Downsizing the Linear PM Generator in Wave Energy Conversion for Improved Economic Feasibility
Abstract
1. Introduction
2. Review of the Application of Linear Generator in Wave Energy Conversion
- Hydraulic PTO: In hydraulic PTO, the motion of a buoy drives the hydraulic piston to increase the pressure of the working medium. Then, the pressure of the medium is raised sufficiently high in an accumulator to rotate the hydraulic motor. The hydraulic PTO is robust and able to provide large forces at low frequencies, which highly matches the dynamic characteristics of WECs. Hydraulic PTO systems were widely used in WECs, such as Pelamis and Edinburgh Duck [15,16,17]. However, hydraulic PTO systems contain plenty of moving parts, which results in their complex structure. So, regular system maintenance and inspection are normally required, which is time-consuming and costly [2]. In addition, the conversion efficiencies of hydraulic PTO systems are relatively low [18].
- Hydro PTO: The hydro PTO mainly refers to the hydro turbine. Hydro turbines transfer the fluid flow to electricity. This type of PTO systems is commonly employed in overtopping devices, such as WaveDragon [19].
- Pneumatic PTO: The pneumatic turbine generally refers to the air turbine, which is driven by the oscillating air pressure. This technology is usually utilized in oscillating water column converters [20].
- Mechanical PTO: In the mechanical PTO system, a gearbox is used to convert the linear movement of the buoy of WECs to rotary motion for fitting conventional rotary generators. The oscillation of the buoy of WECs is of low speed due to the characteristics of ocean waves. For improving efficiency, another important function of the gearbox is to increase the speed of motion. In [21], a point absorber equipped with a bidirectional gearbox and rotary generator was introduced. More recently, WECs with mechanical PTO mechanism have been further investigated by numerical modeling [22] and small-scale testing [23].
- Direct-drive linear generator: The linear generator could be used as the direct-drive PTO system in the oscillating body WECs, and they are usually used in point absorber wave energy converters, such as AWS [24]. In direct-drive linear generators, intermediate transmission interfaces, such as gearbox and hydraulic motors, are not necessary. Instead, the oscillating buoy is directly coupled with the translator of the linear generator. The linear generators are commonly associated with higher efficiencies compared with other PTO systems. This is because there are less transmission losses resulting from a reduced number of energy conversion steps [2,24]. In addition, the reduced number of components in the PTO system increases the reliability of the whole WEC system [25].
3. Description of WEC Concept
4. Methodology
4.1. Hydrodynamic Modeling
4.2. Generator Modeling
4.3. Generator Sizing
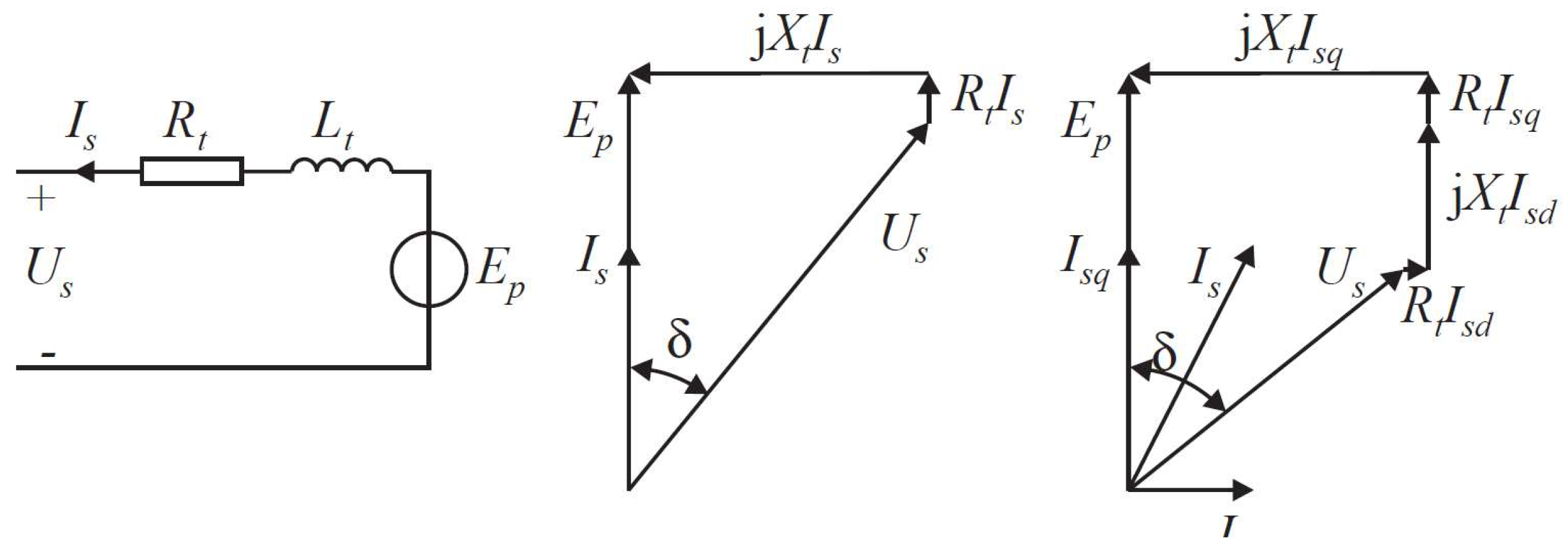
- Method 1: Scaling lawThe scaling principle of electrical generators is based on the fact that the force density per unit surface area of the machine remains rather constant when its dimension changes [40]. The force density is mainly related to two factors. The first one is the magnetic flux density in the air gap, and it is limited by the effect of magnetic saturation. The second one is the linear current density of the machine, and it is limited by the maximum allowed heat dissipation. These two factors could hardly be changed with the dimension if the topology design of the machine does not vary. In this paper, the machine is resized to suit various maximum forces. The force density of resized machines remains identical to the reference machine.For convenience, a scale factor is introduced here as,where and embody the geometrical lengths of the original and the scaled generator. In this method, stator, translator and stack length are sized based on an identical scale factor. However, in principle, they can be sized independently as implemented in method 2 introduced in the following text. Besides, only the stator, translator and stack lengths are considered in scaling, and other geometrical parameters of the machine are kept identical. For a fair comparison of differently sized generators, the stroke and speed limits are maintained to be the same. Then, the other parameters are scaled as follows:where subscripts “s” and “o” indicate the scaled machine and original machine.The rating of the converter is accordingly scaled for each machine. The rated apparent power, current and terminal voltage should be selected during the rating. As the linear current density is assumed to remain identical for differently sized machines, the maximum phase current of the scaled converter is selected to be unchanged, namely of 400 A. At the rated operating condition, the velocity of the buoy is of 1.25 m/s, and then the resulting no-load voltage can be obtained by (13). Additionally, the no-load voltage at the rated point is assumed to be in phase with the current. As a consequence, the rated terminal voltage of the scaled converter, , and the phase angle between the current and terminal voltage, namely , can be calculated according to the first phasor diagram in Figure 3. Therefore, the rated apparent power of the scaled converter is obtained as
- Method 2: Scaling with optimizationIn this method, the main parameters of the machine, including the translator length, stator length and stack length are optimized during sizing for the lowest LCOE. The optimization for each designed maximum generator force is expressed aswhere is the force density of the reference machine, and is the designed maximum generator force. In (26), constraint 1 is associated with the force density. The force density adopted here is considered as 46 , which is calculated based on the performance identification of the AWS generator in [27]. A factor of 2 is included on the left side of the constraint 1 because the machine is double-sided. Constraint 2 indicates that the translator length is required to be larger than 1.2 times the stator length, which is used to mitigate the effect of partial overlap between stator and translator. The maximum phase current, voltage and the rated apparent power of the scaled converter are calculated based on the same way as introduced in Method 1. As the objective function is computationally expensive in this case, the surrogate algorithm is adopted. In the algorithm, the objective function is approximated by a surrogate function, and therefore the optimization speed can be significantly improved [45]. The optimization is implemented in the Matlab environment (version 2020). The tolerance of the function and the maximum iteration steps are set to and 3000, respectively, and the iteration process is terminated when any of the criteria is crossed.
- Method 3: Scaling with assuming a constant generator efficiencyFor simplification, in studies discussing the effects of the sizing of WECs, the sizing of WECs was commonly implemented in the absence of the consideration of the variation of generator efficiencies. Instead, a constant energy conversion efficiency from the absorption stage to the grid was assumed. In this method, the generator size acts simply as a PTO force constraint in the hydrodynamic modeling. This method is discussed in this paper for a comparison with the other two above methods to demonstrate the effects of this simplification on the generator size determination and the LCOE estimation. In this paper, this constant efficiency is considered to be 70%, as usually used in literature [9,46]. Moreover, as the design of the generator is not taken into account in this method, the cost could not be derived explicitly. To evaluate the techno-economic performance of WECs, the PTO related cost in this method is assumed to be the same as that estimated in method 2 for each designed maximum generator force limit.
4.4. Economic Modeling
5. Results and Discussion
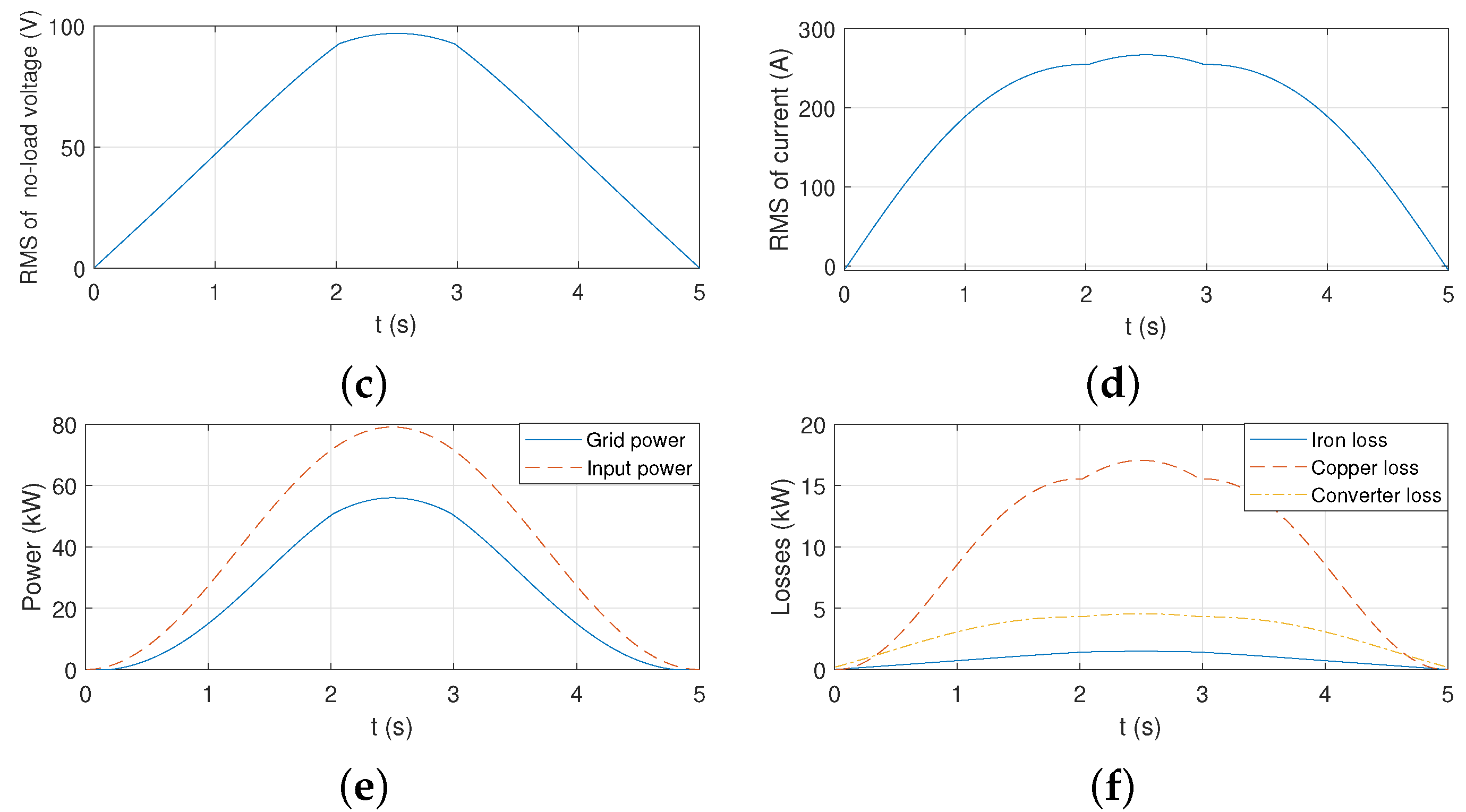
5.1. Generator Performance
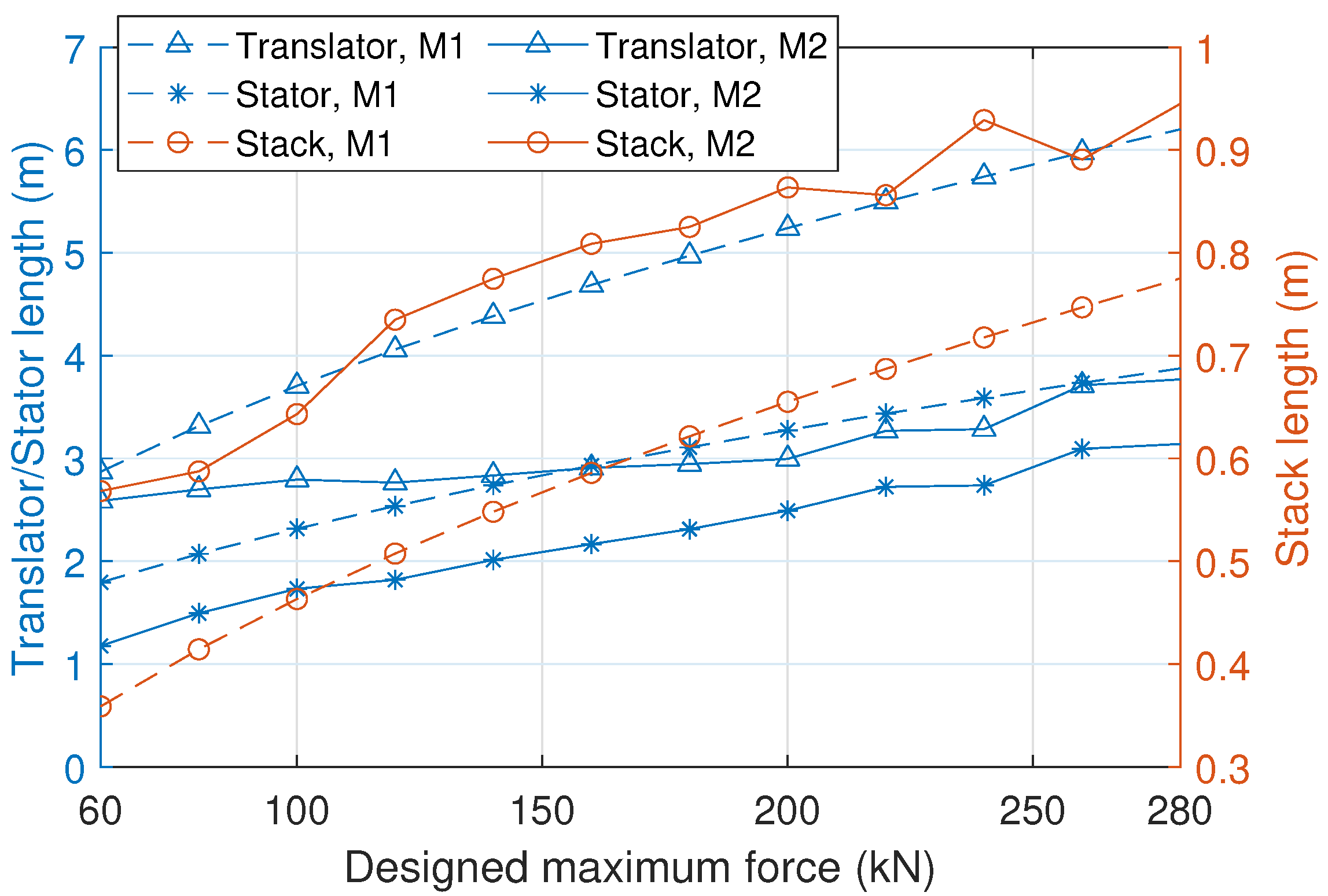
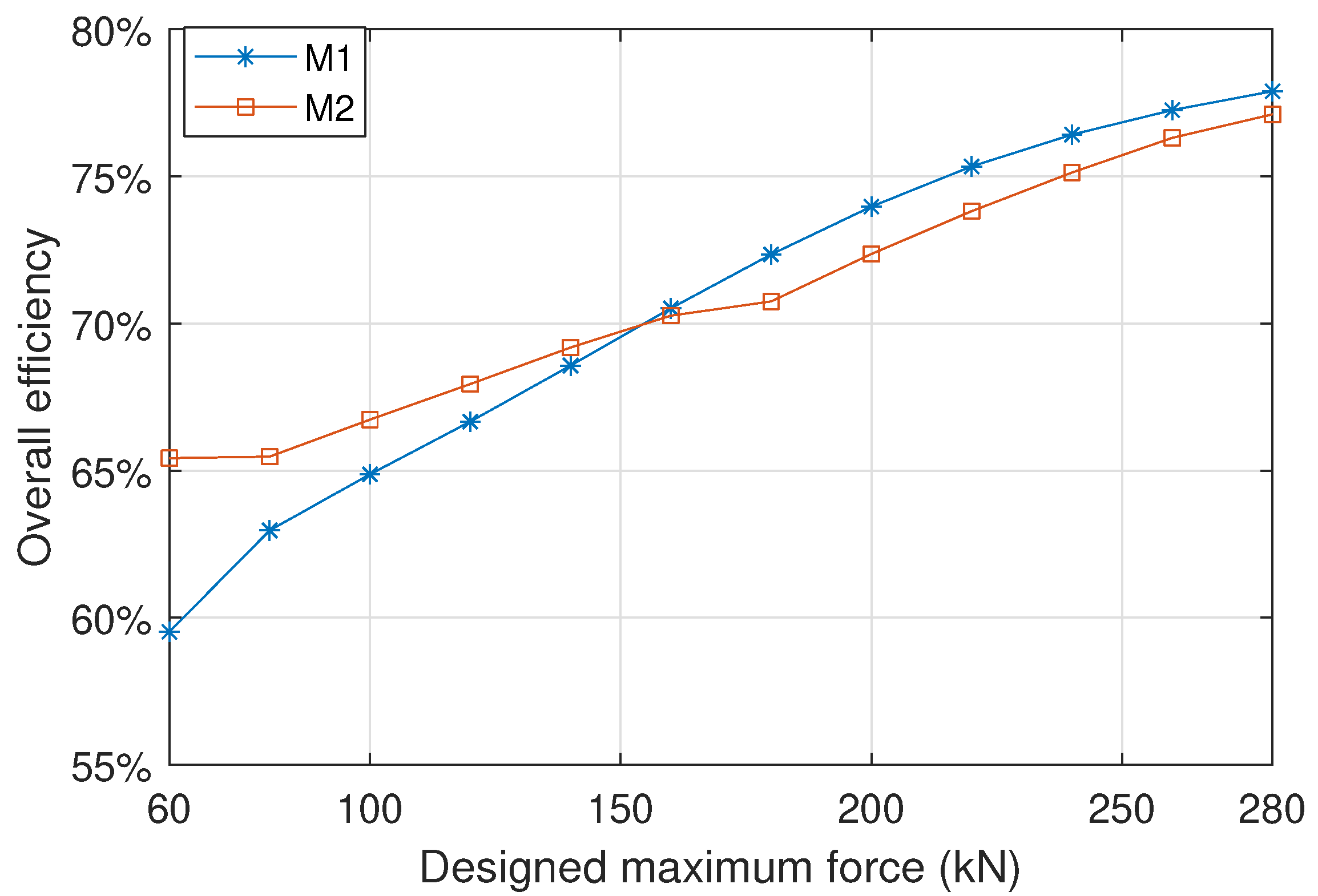
5.2. Comparison of Sizing Methods
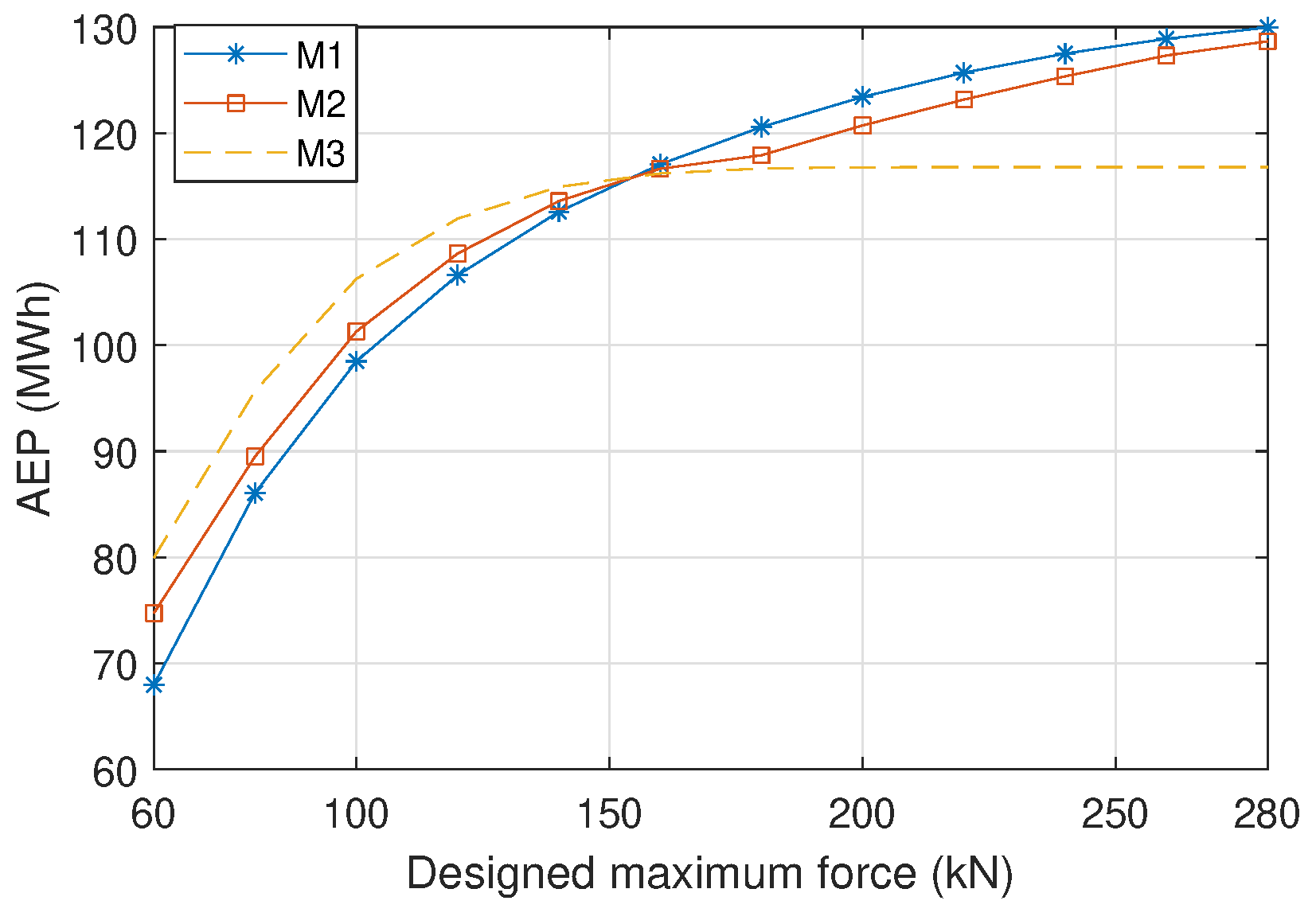
5.2.1. On the Generator Performance
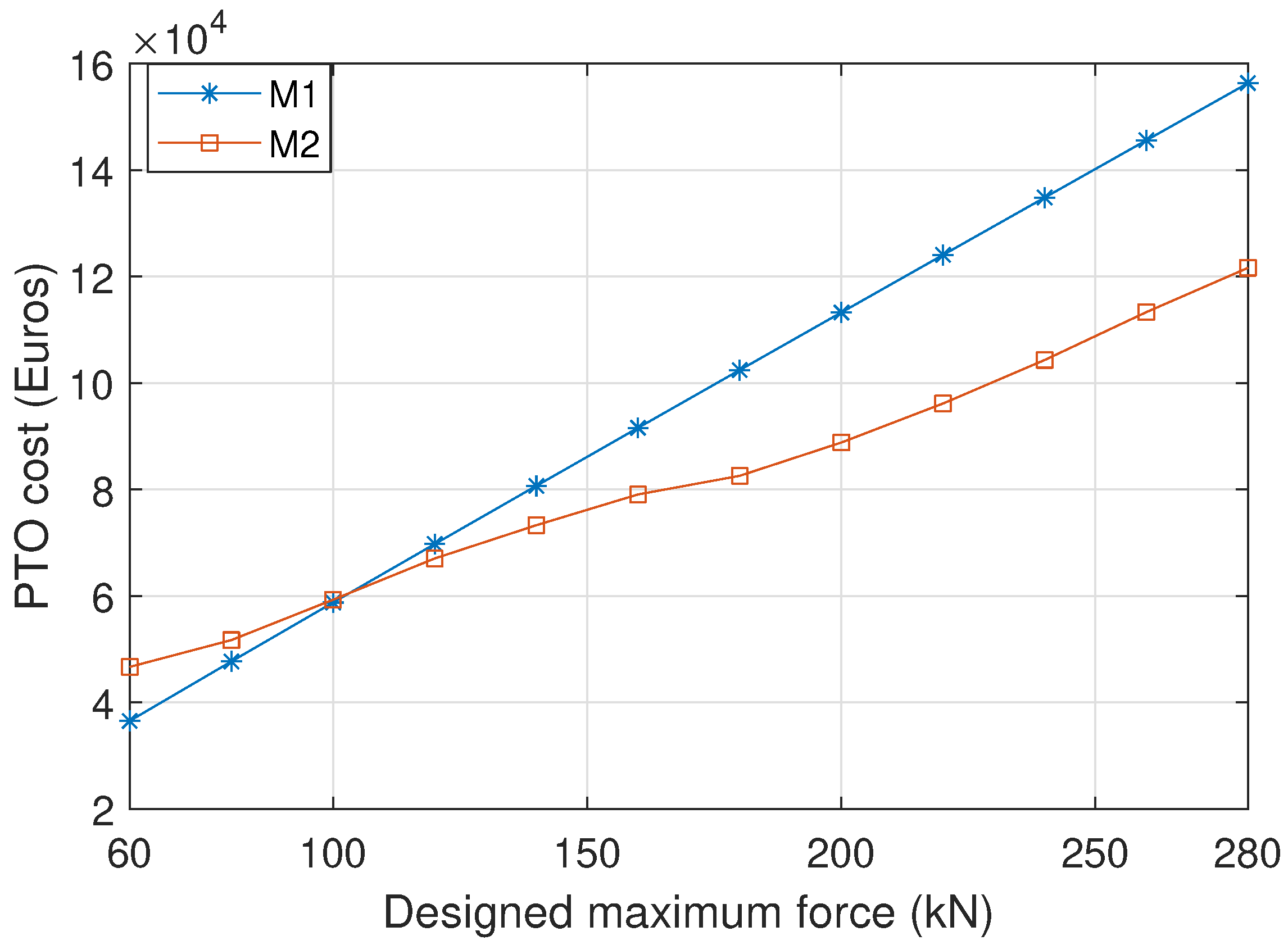
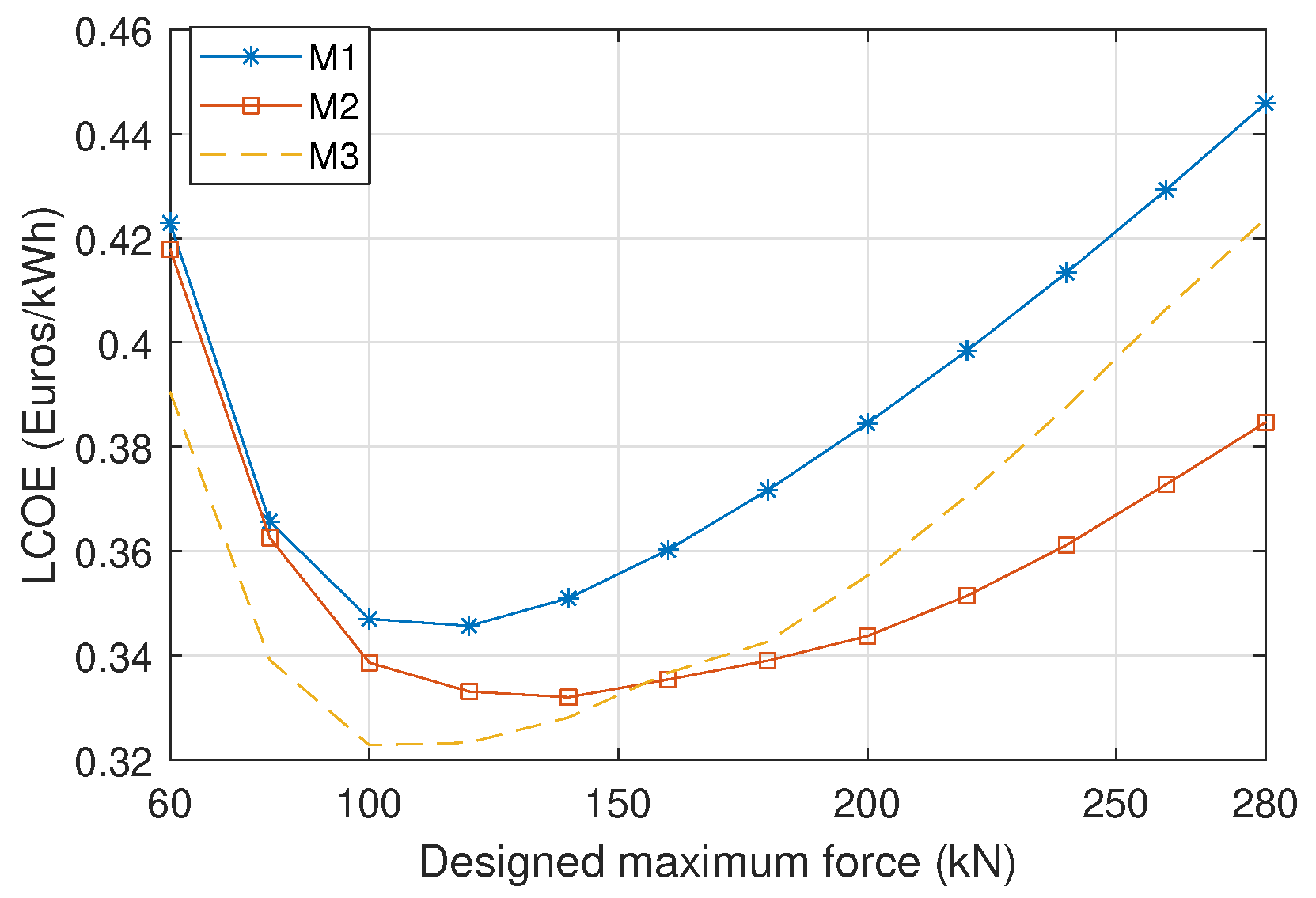
5.2.2. On the Techno-Economics and the PTO Size Determination
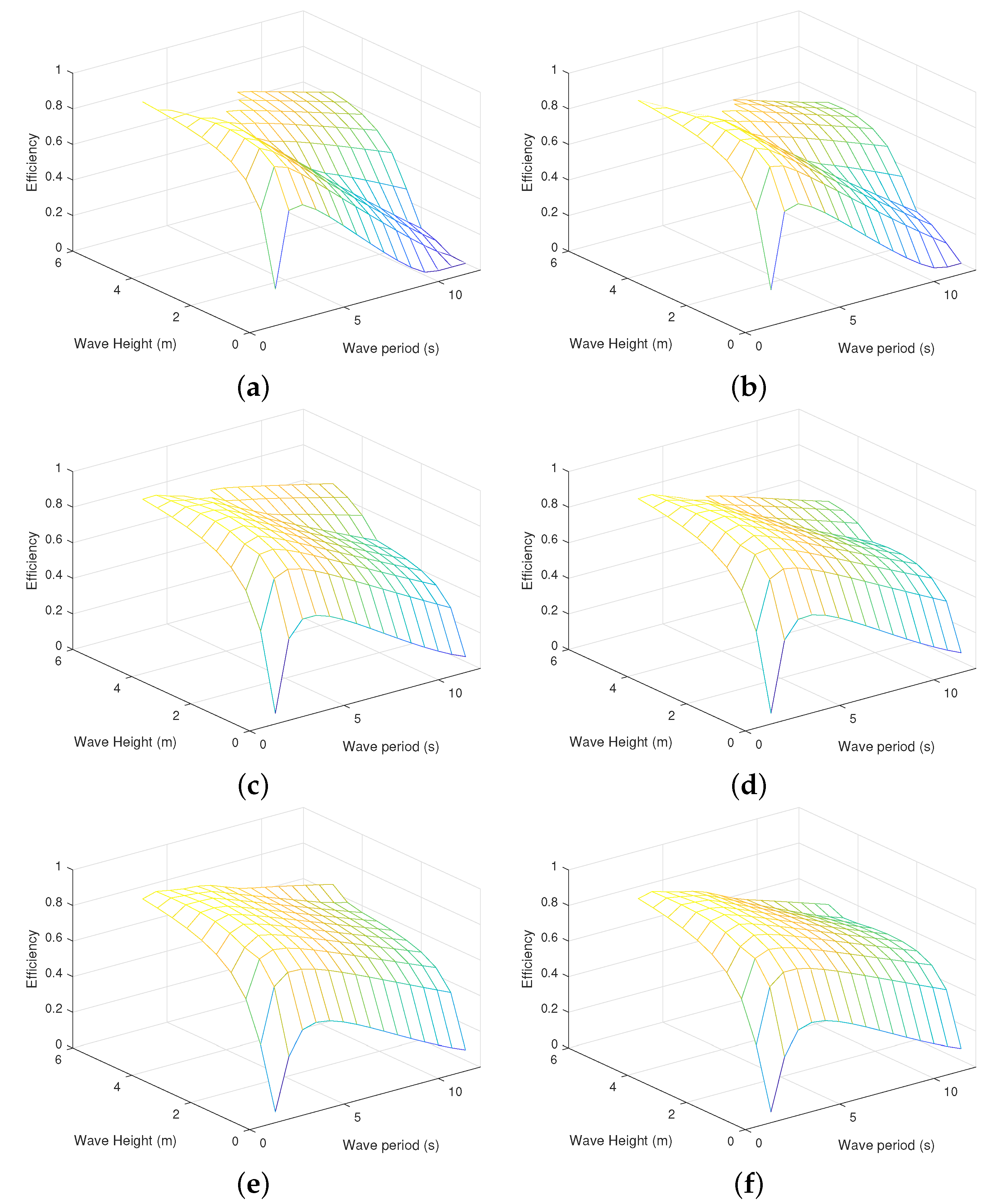
5.3. Dependence of the Generator Sizing on Wave Resources
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

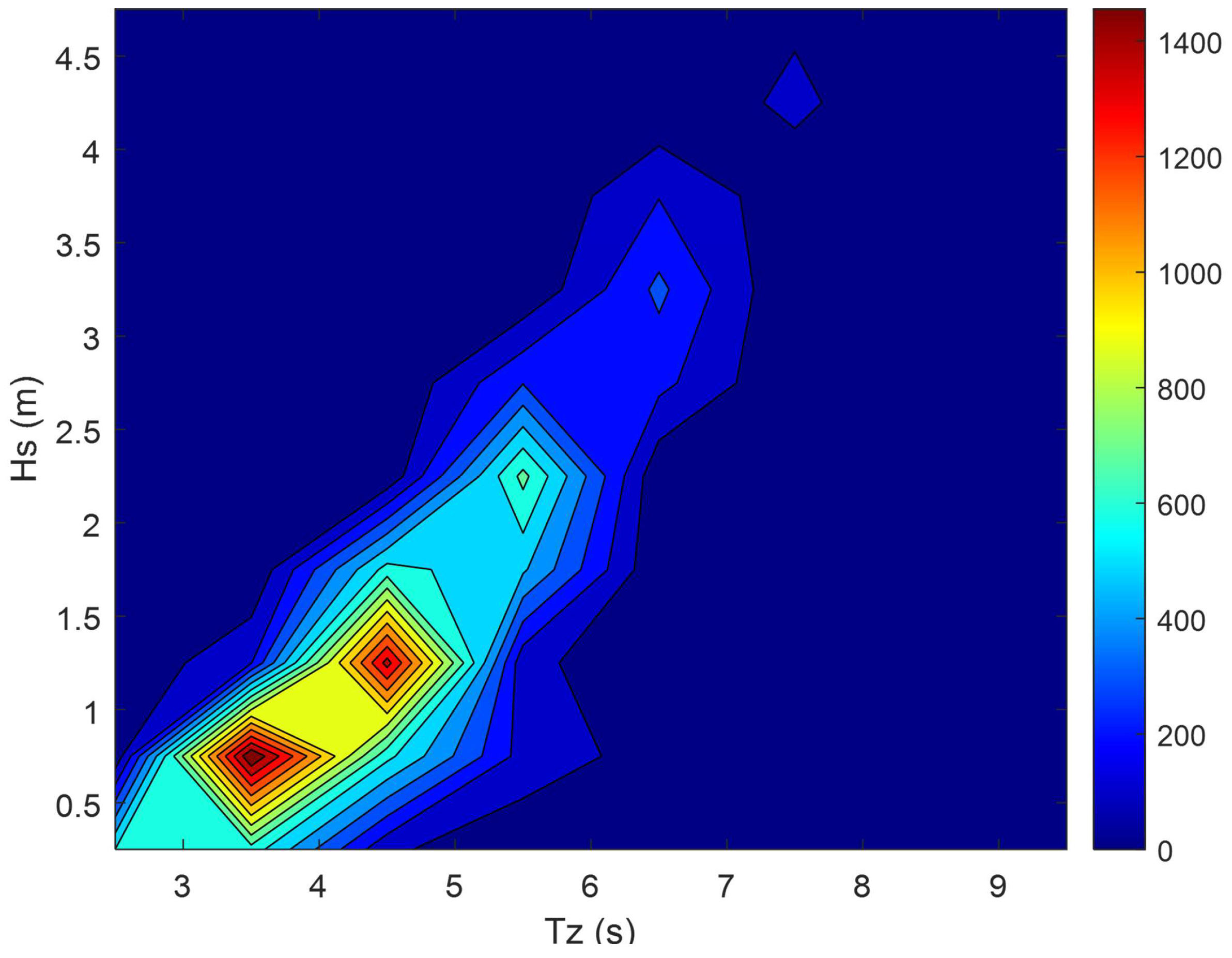
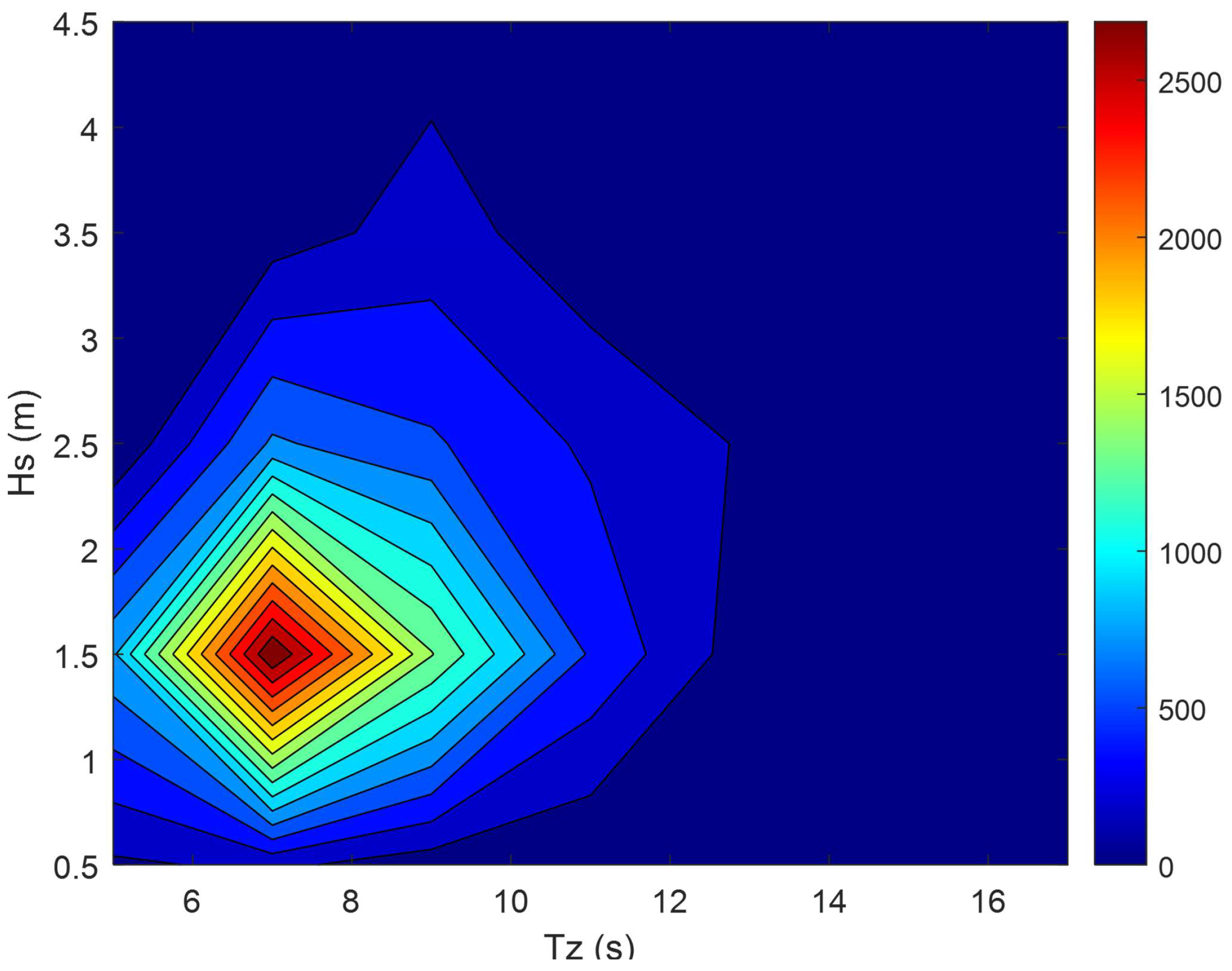
References
- Tan, J.; Wang, X.; Jarquin Laguna, A.; Polinder, H.; Miedema, S. The Influence of Linear Permanent Magnet Generator Sizing on the Techno-Economic Performance of a Wave Energy Converter. In Proceedings of the 2021 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 1 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Ahamed, R.; McKee, K.; Howard, I. Advancements of wave energy converters based on power take off (PTO) systems: A review. Ocean. Eng. 2020, 204, 107248. [Google Scholar] [CrossRef]
- Aderinto, T.; Li, H. Ocean Wave energy converters: Status and challenges. Energies 2018, 11, 1250. [Google Scholar] [CrossRef]
- Shen, W.; Chen, X.; Qiu, J.; Hayward, J.A.; Sayeef, S.; Osman, P.; Meng, K.; Dong, Z.Y. A comprehensive review of variable renewable energy levelized cost of electricity. Renew. Sustain. Energy Rev. 2020, 133, 110301. [Google Scholar] [CrossRef]
- Lavidas, G.; Blok, K. Shifting wave energy perceptions: The case for wave energy converter (WEC) feasibility at milder resources. Renew. Energy 2021, 170, 1143–1155. [Google Scholar] [CrossRef]
- Iglesias, G.; Astariz, S.; Vazquez, A. The economics of wave and tidal energy. Wave Tidal Energy 2018, 513–532. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, T.; Lin, M.; Li, H. Towards realistic power performance and techno-economic performance of wave power farms: The impact of control strategies and wave climates. Ocean Eng. 2022, 248, 110754. [Google Scholar] [CrossRef]
- Pecher, A. Handbook of Ocean Wave Energy; Springer: Berlin/Heidelberg, Germany, 2017; Volume 7. [Google Scholar] [CrossRef]
- Tan, J.; Polinder, H.; Laguna, A.J.; Wellens, P.; Miedema, S. The Influence of Sizing of Wave Energy Converters on the Techno-Economic Performance. J. Mar. Sci. Eng. 2021, 9, 52. [Google Scholar] [CrossRef]
- Tan, J.; Polinder, H.; Wellens, P.; Miedema, S. A feasibility study on downsizing of power take off system of wave energy converters. Dev. Renew. Energies Offshore 2020, 140–148. [Google Scholar] [CrossRef]
- Tan, J.; Polinder, H.; Miedema, S. The Fair Evaluation of Wave Energy Converters. In Proceedings of the 39th International Conference on Ocean, Offshore and Arctic Engineering, Online, 3–7 August 2020; Volume 84416, p. V009T09A016. [Google Scholar] [CrossRef]
- Tokat, P. Performance Evaluation and Life Cycle Cost Analysis of the Electrical Generation Unit of a Wave Energy Converter; Chalmers Tekniska Hogskola: Göteborg, Sweden, 2018. [Google Scholar]
- Cappelli, L.; Marignetti, F.; Mattiazzo, G.; Giorcelli, E.; Bracco, G.; Carbone, S.; Attaianese, C. Linear tubular permanent-magnet generators for the inertial sea wave energy converter. IEEE Trans. Ind. Appl. 2014, 50, 1817–1828. [Google Scholar] [CrossRef]
- de Andres, A.; Maillet, J.; Todalshaug, J.H.; Möller, P.; Bould, D.; Jeffrey, H. Techno-economic related metrics for a wave energy converters feasibility assessment. Sustainability 2016, 8, 1109. [Google Scholar] [CrossRef]
- Henderson, R. Design, simulation, and testing of a novel hydraulic power take-off system for the Pelamis wave energy converter. Renew. Energy 2006, 31, 271–283. [Google Scholar] [CrossRef]
- Wang, L.; Isberg, J.; Tedeschi, E. Review of control strategies for wave energy conversion systems and their validation: The wave-to-wire approach. Renew. Sustain. Energy Rev. 2018, 81, 366–379. [Google Scholar] [CrossRef]
- He, X.; Xiao, G.; Hu, B.; Tan, L.; Tang, H.; He, S.; He, Z. The applications of energy regeneration and conversion technologies based on hydraulic transmission systems: A review. Energy Convers. Manag. 2020, 205, 112413. [Google Scholar] [CrossRef]
- Golbaz, D.; Asadi, R.; Amini, E.; Mehdipour, H.; Nasiri, M.; Nezhad, M.M.; Naeeni, S.T.O.; Neshat, M. Ocean Wave Energy Converters Optimization: A Comprehensive Review on Research Directions. arXiv 2021, arXiv:2105.07180. [Google Scholar]
- Kofoed, J.P.; Frigaard, P.; Friis-Madsen, E.; Sørensen, H.C. Prototype testing of the wave energy converter wave dragon. Renew. Energy 2006, 31, 181–189. [Google Scholar] [CrossRef]
- Heath, T.V. A review of oscillating water columns. Philos. Trans. R. Soc. A 2012, 370, 235–245. [Google Scholar] [CrossRef]
- Binh, P.C.; Tri, N.M.; Dung, D.T.; Ahn, K.K.; Kim, S.J.; Koo, W. Analysis, design and experiment investigation of a novel wave energy converter. IET Gener. Transm. Distrib. 2016, 10, 460–469. [Google Scholar] [CrossRef]
- Wu, J.; Qin, L.; Chen, N.; Qian, C.; Zheng, S. Investigation on a spring-integrated mechanical power take-off system for wave energy conversion purpose. Energy 2022, 245, 123318. [Google Scholar] [CrossRef]
- Stansby, P.; Moreno, E.C.; Draycott, S.; Stallard, T. Total wave power absorption by a multi-float wave energy converter and a semi-submersible wind platform with a fast far field model for arrays. J. Ocean. Eng. Mar. Energy 2022, 8, 43–63. [Google Scholar] [CrossRef]
- Falcão, A.F.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Prado, M.; Polinder, H. Direct Drive Wave Energy Conversion Systems: An Introduction; Woodhead Publishing Limited: Oxford, UK, 2013; pp. 175–194. [Google Scholar] [CrossRef]
- Eriksson, M. Modelling and Experimental Verification of Direct Drive Wave Energy Conversion; Chalmers Tekniska Hogskola: Göteborg, Sweden, 2007. [Google Scholar]
- Polinder, H.; Damen, M.E.C.; Gardner, F. Linear PM generator system for wave energy conversion in the AWS. IEEE Trans. Energy Convers. 2004, 19, 583–589. [Google Scholar] [CrossRef]
- Hong, Y.; Temiz, I.; Pan, J.; Eriksson, M.; Boström, C. Damping Studies on PMLG-Based Wave Energy Converter under Oceanic Wave Climates. Energies 2021, 14, 920. [Google Scholar] [CrossRef]
- Elwood, D.; Yim, S.C.; Prudell, J.; Stillinger, C.; von Jouanne, A.; Brekken, T.; Brown, A.; Paasch, R. Design, construction, and ocean testing of a taut-moored dual-body wave energy converter with a linear generator power take-off. Renew. Energy 2010, 35, 348–354. [Google Scholar] [CrossRef]
- Faiz, J.; Nematsaberi, A. Linear permanent magnet generator concepts for direct-drive wave energy converters: A comprehensive review. In Proceedings of the 2017 12th IEEE Conference on Industrial Electronics and Applications, Siem Reap, Cambodia, 18–20 June 2017; pp. 618–623. [Google Scholar] [CrossRef]
- Shuheng, Q.; Haifeng, W. Simulation of Tubular Transverse Flux Permanent Magnet Linear Generator. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Korea, 7–10 October 2018; pp. 1766–1770. [Google Scholar] [CrossRef]
- Chen, M.; Huang, L.; Hu, M.; Hu, B.; Ahmad, G. A Spiral Translator Permanent Magnet Transverse Flux Linear Generator Used in Direct Drive Wave Energy Converter. IEEE Trans. Magn. 2021, 57, 1–5. [Google Scholar] [CrossRef]
- Chen, M.; Huang, L.; Li, Y.; Tan, P.; Ahmad, G.; Liu, Y.; Hu, M. Analysis of Magnetic Gearing Effect in Field-modulated Transverse Flux Linear Generator for Direct Drive Wave Energy Conversion. IEEE Trans. Magn. 2021, 58, 1–5. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.; Al Shami, E.; Baker, N.J.; Ji, X. A study of a speed amplified linear generator for low-frequency wave energy conversion. Mech. Syst. Signal Process. 2021, 149, 107226. [Google Scholar] [CrossRef]
- Jing, H.; Maki, N.; Ida, T.; Izumi, M. Electromechanical design of an MW class wave energy converter with an HTS tubular linear generator. IEEE Trans. Appl. Supercond. 2018, 28, 1–4. [Google Scholar] [CrossRef]
- Keysan, O.; Mueller, M.A. A linear superconducting generator for wave energy converters. In Proceedings of the 6th IET International Conference on Power Electronics, Machines and Drives (PEMD 2012), Bristol, UK, 27–29 March 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Jing, H.; Maki, N.; Ida, T.; Izumi, M. Design study of large-scale HTS linear generators for wave energy conversion. IEEE Trans. Appl. Supercond. 2017, 27, 1–5. [Google Scholar] [CrossRef]
- Polinder, H.; Damen, M.E.; Gardner, F. Design, modelling and test results of the AWS PM linear generator. Eur. Trans. Electr. Power 2005, 15, 245–256. [Google Scholar] [CrossRef]
- Prado, M.; Polinder, H. Case Study of the Archimedes Wave Swing (AWS) Direct Drive Wave Energy Pilot Plant; Woodhead Publishing Limited: Oxford, MI, USA, 2013; pp. 195–218. [Google Scholar] [CrossRef]
- Polinder, H. Principles of Electrical Design of Permanent Magnet Generators for Direct Drive Renewable Energy Systems; Woodhead Publishing Limited: Oxford, MI, USA, 2013; pp. 30–50. [Google Scholar] [CrossRef]
- Falnes, J.; Kurniawan, A. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar] [CrossRef]
- Penalba, M.; Kelly, T.; Ringwood, J.V. Using NEMOH for Modelling Wave Energy Converters: A Comparative Study with WAMIT. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017; p. 10. [Google Scholar]
- Shek, J.K.; Macpherson, D.E.; Mueller, M.A. Experimental verification of linear generator control for direct drive wave energy conversion. IET Renew. Power Gener. 2010, 4, 395–403. [Google Scholar] [CrossRef]
- Polinder, H.; Van Der Pijl, F.F.; De Vilder, G.J.; Tavner, P.J. Comparison of direct-drive and geared generator concepts for wind turbines. IEEE Trans. Energy Convers. 2006, 21, 725–733. [Google Scholar] [CrossRef]
- Queipo, N.V.; Haftka, R.T.; Shyy, W.; Goel, T.; Vaidyanathan, R.; Tucker, P.K. Surrogate-based analysis and optimization. Prog. Aerosp. Sci. 2005, 41, 1–28. [Google Scholar] [CrossRef]
- De Andres, A.; Medina-Lopez, E.; Crooks, D.; Roberts, O.; Jeffrey, H. On the reversed LCOE calculation: Design constraints for wave energy commercialization. Int. J. Mar. Energy 2017, 18, 88–108. [Google Scholar] [CrossRef]
- Kramer, M.M.; Marquis, L.; Frigaard, P. Performance Evaluation of the Wavestar Prototype. In Proceedings of the 9th European Wave and Tidal Conference, Southampton, UK, 5–9 September 2011; pp. 5–9. [Google Scholar]
- Tokat, P.; Thiringer, T. Sizing of IPM Generator for a Single Point Absorber Type Wave Energy Converter. IEEE Trans. Energy Convers. 2018, 33, 10–19. [Google Scholar] [CrossRef]
- Tan, J.; Polinder, H.; Laguna, A.J.; Miedema, S. The application of the spectral domain modeling to the power take-off sizing of heaving wave energy converters. Appl. Ocean Res. 2022, 122, 103110. [Google Scholar] [CrossRef]
- Rinaldi, G.; Portillo, J.; Khalid, F.; Henriques, J.; Thies, P.; Gato, L.; Johanning, L. Multivariate analysis of the reliability, availability, and maintainability characterizations of a Spar–Buoy wave energy converter farm. J. Ocean Eng. Mar. Energy 2018, 4, 199–215. [Google Scholar] [CrossRef]
- López-Ruiz, A.; Bergillos, R.J.; Lira-Loarca, A.; Ortega-Sánchez, M. A methodology for the long-term simulation and uncertainty analysis of the operational lifetime performance of wave energy converter arrays. Energy 2018, 153, 126–135. [Google Scholar] [CrossRef]
- Majidi, A.G.; Bingölbali, B.; Akpınar, A.; Iglesias, G.; Jafali, H. Downscaling wave energy converters for optimum performance in low-energy seas. Renew. Energy 2021, 168, 705–722. [Google Scholar] [CrossRef]
- Babarit, A. A database of capture width ratio of wave energy converters. Renew. Energy 2015, 80, 610–628. [Google Scholar] [CrossRef]
- Babarit, A.; Hals, J.; Muliawan, M.J.; Kurniawan, A.; Moan, T.; Krokstad, J. Numerical benchmarking study of a selection of wave energy converters. Renew. Energy 2012, 41, 44–63. [Google Scholar] [CrossRef]


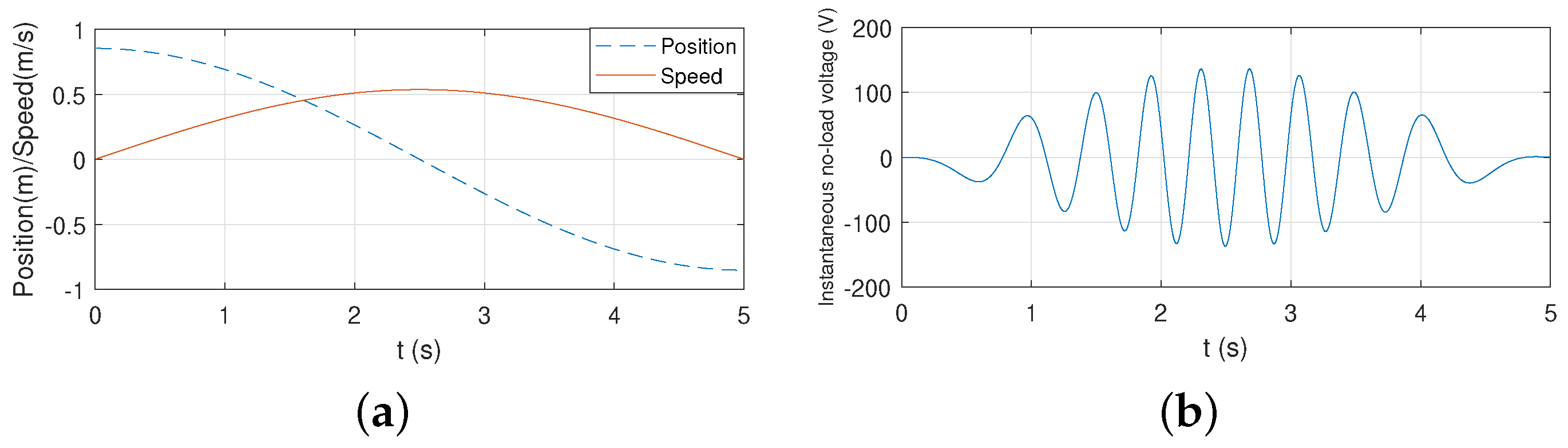

| Parameters | AWS | Uppsala Concept | SeaBeavI |
|---|---|---|---|
| Rated power | 2 MW | 10 kW | 10 kW |
| WEC type | Submerged point absorber | Floating point absorber | Floating point absorber |
| Generator structure | Bottom founded | Bottom founded | Floating |
| Generator topology | Flat and double sided | Flat and four sided | Tubular |
| First tested time | 2004 | 2006 | 2007 |
| Testing site | Portugal | Sweden | USA |
| Parameters | Symbol | Value |
|---|---|---|
| Maximum average power | 1 MW | |
| Maximum force | 933 kN | |
| Maximum velocity | 2.2 m/s | |
| Stroke | S | 7 m |
| Translator length | 8 m | |
| Stator length | 5 m | |
| Air gap length | g | 5 mm |
| Slot width | 15 m | |
| Stack length | 1 m | |
| Magnet pole width | 79 mm | |
| Tooth width | 19 mm | |
| Magnet thickness | 15 mm | |
| Number of conductors per slot | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, J.; Wang, X.; Polinder, H.; Laguna, A.J.; Miedema, S.A. Downsizing the Linear PM Generator in Wave Energy Conversion for Improved Economic Feasibility. J. Mar. Sci. Eng. 2022, 10, 1316. https://doi.org/10.3390/jmse10091316
Tan J, Wang X, Polinder H, Laguna AJ, Miedema SA. Downsizing the Linear PM Generator in Wave Energy Conversion for Improved Economic Feasibility. Journal of Marine Science and Engineering. 2022; 10(9):1316. https://doi.org/10.3390/jmse10091316
Chicago/Turabian StyleTan, Jian, Xuezhou Wang, Henk Polinder, Antonio Jarquin Laguna, and Sape A. Miedema. 2022. "Downsizing the Linear PM Generator in Wave Energy Conversion for Improved Economic Feasibility" Journal of Marine Science and Engineering 10, no. 9: 1316. https://doi.org/10.3390/jmse10091316
APA StyleTan, J., Wang, X., Polinder, H., Laguna, A. J., & Miedema, S. A. (2022). Downsizing the Linear PM Generator in Wave Energy Conversion for Improved Economic Feasibility. Journal of Marine Science and Engineering, 10(9), 1316. https://doi.org/10.3390/jmse10091316








