Construction and Application of Soil–Water Characteristic Curve Model Considering Water Mineralization Degree

Abstract

This study investigated the effects of irrigation water salinity on the soil–water characteristic curve (SWCC) using soil samples collected from a typical irrigated area in Yingjisha County, southern Xinjiang. The SWCC was determined experimentally via centrifugation. The correlation degree among influencing factors was evaluated, and a goodness-of-fit assessment of mainstream traditional SWCC models was conducted using MATLAB 2021a. A modified Van Genuchten (VG) model incorporating the influence of irrigation water salinity was developed. The accuracy and reliability of the proposed model were validated through soil column infiltration experiments and numerical simulations. The results demonstrated that the original VG model provided the best fit for loam soils in southern Xinjiang, albeit with non-negligible deviations, indicating the need for further refinement. Significant correlations were identified between soil characteristic indices and model parameters, ranked in descending order of influence as follows: soil dry bulk density > clay content > inorganic salt content > silt content. Soils with higher clay and silt contents, along with greater bulk density, exhibited enhanced water retention capacity, resulting in a flatter SWCC. Although increased irrigation water salinity initially improved the soil’s water absorption capacity, the rate of enhancement gradually diminished with further increases in salinity, ultimately leading to a reduction in overall water retention performance. This study provides a theoretical foundation for the prevention and amelioration of saline soils and also supports the efficient utilization of water resources.

1. Introduction

The soil–water characteristic curve (SWCC), a fundamental constitutive relationship in unsaturated soil mechanics, determined by applying controlled suction to a soil sample and measuring the corresponding water content. The SWCC serves as a fundamental tool for understanding water retention behavior and pore structure interaction, with broad applications in agricultural irrigation management [1], soil moisture dynamics prediction [2], environmental protection [3], and related disciplines [4,5].

Water scarcity has increasingly become a critical constraint to the synergistic development of industry and agriculture in China. In response to global freshwater shortages, numerous countries are actively advancing the exploitation and utilization of non-conventional water resources. Notably, nations including Israel, the United States, and Canada have conducted extensive research in this domain, yielding substantial outcomes [6,7,8]. In certain regions of Xinjiang, characterized by distinctive geological and climatic conditions, irrigation districts in the southern part are primarily composed of sandy and loamy soils [9]. These areas also exhibit considerable reserves of brackish groundwater, with salinity levels significantly higher than those observed in other regions. Under conditions of severe water scarcity, brackish-saline water—owing to its widespread availability and considerable abundance—has emerged as a potential groundwater resource suitable for utilization [10]. Consequently, investigating the utilization of subsurface brackish-saline water resources and elucidating the transport and transformation mechanisms of such water in sandy soils are of paramount importance. Such research is essential for enabling precise regulation of water and salt dynamics, thereby promoting the efficient use of water resources, particularly brackish-saline water.

The simulation of soil water transport processes fundamentally relies on classical SWCC models—including those developed by Van Genuchten (VG) [11], Brooks-Corey (BC) [12], Gardner (GW) [13], and Fredlund-Xing (FX) [14]—to establish a robust parameterization framework. In a comparative study utilizing one-dimensional horizontal infiltration experiments, Hu et al. [15] confirmed the reliability of Gardner model parameters, demonstrating that the computed unsaturated permeability coefficients were closely aligned with those generated by the VG model. Further supporting the importance of model selection, Tao et al. [16] reported that the FX model exhibited superior fitting performance compared to both the VG and Gardner models. When predicting SWCC across the entire suction range with limited datasets, the FX model yielded predictions that most closely matched experimental measurements, underscoring its robustness under data-constrained conditions. In another investigation focusing on red clay-bentonite mixtures, Amadi and Isah [17] compared the parameter estimation capabilities of the Brooks–Corey (BC) and van Genuchten (VG) models. While both models achieved satisfactory accuracy in describing the SWCC, the VG model demonstrated marginally better overall goodness-of-fit metrics. Complementing these findings, Zhao et al. [18] conducted SWCC analyses on gravel-sand mulched fields with varying cultivation histories. Their results showed that the VG model significantly outperformed the Brooks-Corey model in fitting precision, particularly within both high and low suction regimes. This consistent superiority across different soil types confirms the enhanced reliability and broader applicability of the VG model for characterizing soil moisture characteristics in heterogeneous field conditions. However, the transport mechanisms of brackish and saline water in soils are highly complex, yet current SWCC models often inadequately represent the critical influence of salinity on soil hydraulic properties. This limitation introduces significant uncertainties in managing salinized soils and designing irrigation systems. Therefore, developing high-precision models that explicitly incorporate the effects of saline water irrigation is essential.

The majority of currently employed SWCC models are empirically based. While these models demonstrate robust performance under specific conditions, they are generally constrained by a trade-off among accuracy, universality, and conciseness. To address this limitation, researchers have pursued systematic optimization and innovation of conventional modeling frameworks through diverse methodologies. For example, Shu [19], Li [20] and He [21] utilized fundamental soil properties—including bulk density, specific surface area, and clay content—as inputs to predict the parameters α and n of the VG model via nonlinear regression, back propagation neural networks (BPNN), and support vector machines. Their results indicated that the BPNN provided the most accurate representation of the SWCC. Norouzi et al. [22] introduced a physics-informed neural network (PINN) that significantly outperformed conventional neural networks in predicting the dry-end segment of the curve under data-scarce conditions, achieving a normalized root mean square error (RMSE) of only 0.172. Additionally, the PINN-derived SWCC was differentiable with respect to matric potential, enhancing its integration into numerical simulators. Based on the classical Gardner model, Wang et al. [23] formulated a modified SWCC model that explicitly accounts for soluble salt content, with specific application to high-salinity loess from the Ili region. Through parameter estimation procedures, the proposed model demonstrated enhanced accuracy in characterizing the water retention behavior of saline loess, achieving a coefficient of determination (R²) exceeding 0.995. In a separate methodological contribution, Zhao and Yang [24] established a data-driven optimization framework designed for the precise and efficient calibration of empirical SWCC models under conditions of limited laboratory data availability. Addressing inherent uncertainties in SWCC parameterization, Qian and Rahardjo [25] introduced a systematic mathematical framework for quantifying parameter uncertainty during model calibration. Their analysis further indicated that refinements in experimental design—such as increasing data point density or extending the range of suction measurements—can effectively constrain the posterior distribution of parameters, thereby reducing overall model uncertainty. In summary, while methods for enhancing SWCC models have diversified and shown some success, their subsequent application is under-explored. Thus, building and validating models that consider brackish water influences is an urgent priority for further research.

This study investigates loam soil from a typical irrigation district in Yingjisha County, located in southern Xinjiang. Employing an integrated approach that combines field sampling, laboratory experiments, and numerical simulation, SWCCs were determined for the region’s loam soil. A novel model is proposed that explicitly incorporates solution mineralization level as a key parameter, advancing beyond previous improvements focused primarily on adsorption or thin-film flow mechanisms. The model provides accurate input parameters for simulating brackish water effects, offering a theoretical basis for understanding soil water dynamics under brackish water irrigation in southern Xinjiang. These findings contribute to strategies for protecting agricultural ecosystems and improving groundwater use efficiency across Central Asia.

2. Materials and Methods

2.1. Basic Properties of Test Samples

2.1.1. Tested Soil

The experimental soil was classified as saline-alkali soil. Following the technical guidelines for saline-alkali land improvement in ecological greening engineering (Standard No. DB65/T 4192-2019) [26], three sampling sites were selected within Yingjisha County, representing areas with moderate, severe, and very severe soil salinization, respectively. Soil samples were collected from three designated sites (M1, M2, and M3) in Yingjisha. To maintain consistent sampling depth and ensure the comparability of soil physicochemical properties, the five-point sampling method was employed to obtain surface sandy soil from the 0–20 cm layer. Subsequently, the quartering method was applied to prepare mixed samples, thereby enhancing the representativeness and uniformity of the collected soil. The soil samples utilized in this experiment consisted exclusively of undisturbed soils, which were extracted in situ via the ring knife method. A cylindrical centrifuge test specimen with a base area of 50 cm² and a height of 2 cm was employed during the experimental procedures. To ensure sample representativeness, standard reference samples were prepared for each category of samples under investigation. This study made use of standard stainless steel ring knives with a specified volume of 100 cm³. Following a stratified random sampling strategy, three representative undisturbed soil column samples were collected. Upon collection, all soil samples were immediately sealed in airtight containers and transported to the laboratory for analysis.

The soil textures at the selectively sampled sites were silt loam, silt, and sandy loam, as determined by the United States Department of Agriculture (USDA) soil texture triangle [27]. In addition, samples from the upper soil layer were collected and allocated into aluminum boxes, 30 cm³ ring knives (Hebei Shengxing Instrument Equipment Co., Ltd., Hengshui, China), and sealed bags for further analysis of physico-chemical properties, including soil moisture content, particle size distribution, and soluble salts, thereby facilitating the acquisition of comprehensive soil characteristic datasets. Detailed characteristics of these sites are summarized in

Table 1. Soil Textural Fractions.

Soil Code	Grain Size Composition			Soil Texture
	0.05~2 mm	0.002~0.05 mm	<0.002 mm
M1	43.29	50.53	6.18	Silty Soil
M2	28.86	59.28	11.86	Silt
M3	41.40	51.01	7.58	Sandy Loam

and

Table 2. Ionic Composition of the Soil Samples.

Soil Code	Anion (mg kg−1)				Cation (mg kg−1)			Total (mg kg−1)
	Cl−	HCO3−	CO32−	SO42−	Ca2+	Mg2+	K+ + Na+
M1	3550	256	0	5040	800	146	4053	13,845
M2	3350	305	0	2650	336	139	412	10,279
M3	412	293	0	2136	350	195	679	4065

.

2.1.2. Test Solution

The experiment employed a gradient mineralization approach. Saturated solutions were prepared using analytical-grade NaCl (Tianjin Xiangruixin Chemical Technology Co., Ltd., Tianjin, China) and distilled water. According to the Standard for Classification of Groundwater Chemical Types (DZ/T 0290-2015) [28], the mineralization gradients of the saturated solutions were categorized as brackish water, saline water, and brine. All experimental procedures were carried out in a constant-temperature environment maintained at 25.0 ± 0.5 °C [29]. A series of test solutions with graded mineralization levels were formulated by setting total dissolved solid (TDS) concentration gradients at 1, 3, 5, 7, and 9 g L⁻¹. These concentrations cover the typical thresholds for brackish water (1–3 g L⁻¹), saline water (3–5 g L⁻¹), and brine (>5 g L⁻¹). Ultrapure water (TDS < 0.01 g L⁻¹) served as the standard reference. Detailed parameters are summarized in

Table 3. Test Material.

Number	Mineralization (g L−1)	Soil Salt Content (%)	Saline Soil Types
M1-1	0	1.39	Extremely Severe Saline Soil
M1-2	1	1.39	Extremely Severe Saline Soil
M1-3	3	1.39	Extremely Severe Saline Soil
M1-4	5	1.39	Extremely Severe Saline Soil
M1-5	7	1.39	Extremely Severe Saline Soil
M1-6	9	1.39	Extremely Severe Saline Soil
M2-1	0	1.03	Strongly Saline Soil
M2-2	1	1.03	Strongly Saline Soil
M2-3	3	1.03	Strongly Saline Soil
M2-4	5	1.03	Strongly Saline Soil
M2-5	7	1.03	Strongly Saline Soil
M2-6	9	1.03	Strongly Saline Soil
M3-1	0	0.41	Moderately Saline Soil
M3-2	1	0.41	Moderately Saline Soil
M3-3	3	0.41	Moderately Saline Soil
M3-4	5	0.41	Moderately Saline Soil
M3-5	7	0.41	Moderately Saline Soil
M3-6	9	0.41	Moderately Saline Soil

.

2.2. Experimental and Simulation Methods

In this study, undisturbed soil samples were used to identify influencing factors and perform correlation analysis of the SWCC, in order to accurately represent the in situ soil structure and water retention characteristics under natural bulk density conditions. By contrast, processed disturbed soil was employed in subsequent experiments investigating the effects of irrigation water with different salinity levels on the SWCC, as well as in one-dimensional constant-head soil column infiltration tests. The disturbed soil was prepared by air-drying, crushing, sieving, and recompacting to a predetermined bulk density. This approach allows precise control of key parameters including soil bulk density and initial water content, minimizes interference from the inherent spatial variability associated with undisturbed soils, and helps isolate the influence of irrigation water salinity on soil water movement.

2.2.1. Determination of the Soil Water Characteristic Curve

The centrifuge method (Figure 1) was adopted as the primary technique for determining the SWCC in this study, considering the large sample size and stringent demands for fitting accuracy, stability, curve integrity, and consistency with experimental observations. Measurements were performed using a CR22N high-speed refrigerated centrifuge (EPPENDORF, Hamburg, Germany) to systematically quantify the relationship between soil matric potential and volumetric water content. Each treatment was replicated three times to ensure reliability. The soil sample was initially immersed in water just deep enough to moisten it. Subsequently, additional water was added until the water level was even at the top of the cutting ring. The sample was then soaked until the soil reached a water-saturated state [30]. The centrifuge chamber was maintained at a constant temperature of 4 °C throughout the experiments. A discrete centrifugal force gradient was established by applying stepwise rotational speeds of 980, 1386, 1961, 2405, 2774, 3101, 4385, 6202, 7596, 8771, and 9806 r min⁻¹. This approach enabled continuous loading of matric potential within the unsaturated soil zone. Each speed was maintained for 1 h. The correspondence between centrifugal speed and matric potential is provided in Equation (1).

$$\mathrm{h}=1.118\times {10}^{-3}\times {\mathrm{R}}_0\times {\left(\mathrm{r}\mathrm{p}\mathrm{m}\right)}^2$$

(1)

where R₀ is the radial distance to the midpoint of the soil sample (m).

2.2.2. One-Dimensional Constant-Head Soil Column Infiltration Test

• Tested soil samples:

Due to the presence of uneven soil particle sizes and impurities—such as plastic film, tree roots, and stones—which could adversely affect the simulation outcomes of the indoor soil column experiment, the following pretreatment procedures were conducted to better approximate real-world infiltration dynamics. First, the samples were air-dried to eliminate excess moisture and prevent microbial alteration of soil properties. The dried soil was then ground and sieved through a 2 mm mesh to remove large impurities, thereby ensuring homogeneity and consistency. Laboratory analyses included determinations of particle size distribution, inorganic salt content, and bulk density. After pretreatment, these parameters were measured in the sieved soil samples; corresponding results are summarized in

Table 4. Related Parameters of the Test Material.

Number	Soil Texture	Bulk Density (g cm−3)	Inorganic Salt Content (%)
M1	Silty Soil	1.54	0.41
M2	Silt	1.62	1.03
M3	Sandy Loam	1.32	1.39

. The obtained data provide essential baseline information for subsequent indoor soil column experiments, ensuring that the experimental setup accurately reflects the in situ characteristics of the target soil.

2.

Experimental methods and observation indicators:

As shown in Figure 2, the experimental environment was maintained at a constant temperature of 20 °C. The soil column was packed in 5 cm increments to a total depth of 0.6 m, maintaining the bulk density measured from undisturbed soil samples. After each layer was placed, the surface was scarified and compacted with a soil hammer to enhance interlayer contact. A constant pressure head of 5 cm was maintained using a Mariotte bottle to simulate one-dimensional constant-head infiltration. The top of the column was sealed with plastic wrap to minimize evaporative losses. Soil moisture sensors (TDR-6) were installed at depths of 0.15, 0.30, and 0.45 m to monitor the infiltration rate, cumulative infiltration, and wetting front progression. Each treatment was replicated three times to ensure reliability, and the analysis was based on the mean values. Following infiltration, water supply was ceased, and soil water content dynamics were recorded using the pre-embedded TDR-6 sensors.

Wetting front depth measurement: After the experiment commenced, the wetting front progression was recorded at fixed 1 cm intervals. The time required for the front to advance each centimeter was systematically documented.

Monitoring time: Prior to the commencement of the test, all sensors were assigned identification numbers, with specific calibration performed on the moisture sensors. Upon completion of sensor installation, the units were interconnected with a data logger. A systematic verification procedure was conducted to confirm the proper functionality of every sensor. Following the stabilization of readings, the data acquisition interval was configured to 5 min, aligning with the sampling interval employed in the subsequent infiltration test.

Termination condition: The test was terminated upon the arrival of the wetting front at the base of the soil column.

2.2.3. COMSOL Model Construction Methods

1.

Constitutive equations of the model:

Soil media are characterized by significant heterogeneity, and their hydraulic conductivity exhibits highly nonlinear behavior. This complexity poses considerable challenges for accurately describing water movement in soils. The Richards equation [31], formulated using the Van Genuchten parameterization scheme, is widely employed because it effectively captures the nonlinear dynamics of water flow in unsaturated porous media. The equation rigorously describes fluid filling and drainage processes within soil pores, along with associated changes in hydraulic properties. In practical applications, the VG model incorporates specific parameters (

Table 5. Model Parameter Data Settings.

Description	Unit	M1	M2	M3
Density	Kg m−3	1469.6	1391.6	1369.6
Dynamic Viscosity	Pa s	0.001	0.001	0.001
Porosity	%	0.409	0.427	0.412
Permeability	%	0.00002	0.00018	0.000359
Saturation Water Content	%	30.95	32.83	35.38
Residual Water Content	%	6.23	7.27	9.03
Fluid Density	Kg m−3	1002.5	1002.5	1002.5
Gravity	M s−2	9.82	9.82	9.82
Fluid Compressibility	M s2 kg−1	4.6 × 10−10	4.6 × 10−10	4.6 × 10−10

) to represent soil water retention and hydraulic conductivity functions. The nonlinearity inherent in these parameters enables the model to represent hydraulic behaviors across soils with different textures. Although this nonlinearity increases the model’s complexity, it also enhances its ability to simulate soil water dynamics with higher accuracy. This study investigates water flow in a one-dimensional porous medium column with a length of 0.6 m. The fluid phases are assumed to be incompressible, and relative permeability and porosity are treated as invariant with respect to time and space. Water movement is simulated using the Richards equation. Under one-dimensional conditions and with the stated assumptions, the governing equation for soil water infiltration is expressed as follows:

$${\displaystyle \frac{\partial \mathrm{\theta }}{\partial \mathrm{t}}}={\displaystyle \frac{\partial }{\partial \mathrm{z}}}\left[\mathrm{K}\left(\mathrm{h}\right)\left({\displaystyle \frac{\partial \mathrm{h}}{\partial \mathrm{z}}}+1\right)\right]$$

(2)

$$\mathrm{\theta }\left(\mathrm{h}\right)={\mathrm{\theta }}_{\mathrm{r}}+{\displaystyle \frac{\left(\mathrm{p}{\mathrm{k}}^{\mathrm{q}}+\mathrm{r}\right)-{\mathrm{\theta }}_{\mathrm{r}}}{{\left[1+{\left|\left(\mathrm{f}{\mathrm{k}}^2+\mathrm{i}\mathrm{k}+\mathrm{g}\right)\mathrm{h}\right|}^{\left(\mathrm{d}{\mathrm{k}}^{\mathrm{e}}+\mathrm{s}\right)}\right]}^{\left(1-1/\left(\mathrm{d}{\mathrm{k}}^{\mathrm{e}}+\mathrm{s}\right)\right)}}}$$

(3)

$$\begin{gathered} \mathrm{K}={\mathrm{K}}_{\mathrm{s}}{\left({\displaystyle \frac{\mathrm{h}}{\left(\mathrm{f}{\mathrm{k}}^2+\mathrm{i}\mathrm{k}+\mathrm{g}\right)+\mathrm{h}}}\right)}^{\left(\mathrm{d}{\mathrm{k}}^{\mathrm{e}}+\mathrm{s}\right)}\times \\ {\left(1-{\left(1-\left({\displaystyle \frac{\mathrm{h}}{\left(\mathrm{f}{\mathrm{k}}^2+\mathrm{i}\mathrm{k}+\mathrm{g}\right)+\mathrm{h}}}\right)\right)}^{\left(1-1/\left(\mathrm{d}{\mathrm{k}}^{\mathrm{e}}+\mathrm{s}\right)\right)}\right)}^{\left(1-1/\left(\mathrm{d}{\mathrm{k}}^{\mathrm{e}}+\mathrm{s}\right)\right)} \end{gathered}$$

(4)

where θ is the volumetric water content (%). K(θ) is the unsaturated hydraulic conductivity function, (m s⁻¹). h is the matric potential; t is the time; z is the vertical spatial coordinate (positive upward).

θ(h) is the optimized VG model expression that considers the influence of infiltration water with different salinity levels (k) on the parameters, where d, e, f, g, i, p, q, r, s are all fitting parameters. k is the mineralization degree (g L⁻¹). θr represents the residual volumetric water content (%). Ks denotes the saturated hydraulic conductivity (m s⁻¹), which is the water conductivity of the soil when it is completely saturated.

2.

Initial conditions:

The initial moisture content of the model was set based on the measured soil water content from the soil column tests

Initial Moisture Content θ(x, t = 0) = θ₀(x); h(x, t = 0) = h₀(x)

3.

Boundary conditions:

Upper Boundary Condition: $-\mathrm{K}\left(\mathrm{h}\right){\displaystyle \frac{\partial \mathrm{h}}{\partial \mathrm{z}}}={\mathrm{q}}_{\mathrm{t}\mathrm{o}\mathrm{p}}$(t)

Lower Boundary Condition: $-\mathrm{K}\left(\mathrm{h}\right){\displaystyle \frac{\partial \mathrm{h}}{\partial \mathrm{t}}}=0$

4.

Model material parameters:

5.

Grid convergence:

A grid convergence analysis was performed to eliminate the influence of mesh division on the simulation results. Three models with coarse (9 elements), medium (28 elements), and fine (51 elements) mesh densities were constructed. The relative error between the results of the medium and fine meshes was 1.1%, which is below the specified tolerance of 2%. This confirms the mesh adequacy. Therefore, the medium mesh with 28 elements was selected for all subsequent simulations to ensure computational accuracy while conserving resources.

2.3. Traditional Models

This study evaluated the performance of four SWCC models—the Van Genuchten (VG), Brooks–Corey (BC), Gardner (GW), and Fredlund–Xing (FX) models—in fitting experimentally measured data. The most appropriate model for characterizing the soil moisture properties was identified by comparing the accuracy and reliability of the fitting results. The comparative outcomes are detailed in

Table 6. Fitted Parameter Results of the SWCC Model.

Number	Van Genuchten					Gardner		Fredlund–Xing				Brooks–Corey
	θr	θs	α	n	m	a	b	a	b	c	hr	θr	θs	he	λ
M1-1	0.051	0.483	0.015	1.410	0.291	0.005	0.134	338.30	5.813	0.122	0.242	4.43 × 10−14	0.622	0.177	0.134
M1-2	0.037	0.468	0.014	1.320	0.243	0.004	0.123	1.87 × 10−9	0.232	0.260	41.320	4.24 × 10−14	0.615	0.182	0.123
M1-3	0.024	0.462	0.012	1.312	0.238	0.005	0.131	379.67	4.518	0.113	0.281	2.22 × 10−14	0.626	0.180	0.131
M1-4	0.021	0.458	0.012	1.307	0.235	0.007	0.135	341.99	5.581	0.124	0.388	2.22 × 10−14	0.641	0.183	0.135
M1-5	0.020	0.454	0.013	1.301	0.232	0.004	0.125	3.98 × 10−9	0.214	0.284	44.778	2.22 × 10−14	0.621	0.177	0.125
M1-6	0.020	0.454	0.015	1.300	0.231	0.006	0.131	405.53	4.518	0.131	0.440	4.2 × 10−14	0.645	0.173	0.131
M2-1	0.079	0.458	0.034	1.470	0.320	0.004	0.134	203.25	7.016	0.085	0.161	4.06 × 10−14	0.614	0.168	0.134
M2-2	0.087	0.437	0.028	1.394	0.283	0.006	0.137	178.51	25.827	0.057	0.197	2.33 × 10−14	0.626	0.172	0.137
M2-3	0.069	0.431	0.023	1.371	0.271	0.008	0.149	84.39	9.387	0.098	0.200	1.05 × 10−14	0.629	0.173	0.149
M2-4	0.069	0.424	0.022	1.373	0.272	0.004	0.149	102.38	5.131	0.125	0.028	7.48 × 10−14	0.570	0.161	0.149
M2-5	0.072	0.421	0.025	1.380	0.275	0.003	0.133	194.38	113.691	0.037	0.099	4.31 × 10−14	0.594	0.162	0.133
M2-6	0.064	0.425	0.031	1.363	0.266	0.003	0.140	191.30	4.983	0.114	0.041	3.19 × 10−14	0.579	0.159	0.140
M3-1	0.059	0.685	0.011	1.473	0.321	0.004	0.110	3323.12	0.025	2.68 × 10−7	1.010	4.24 × 10−14	0.652	0.174	0.110
M3-2	0.083	0.641	0.008	1.433	0.302	0.006	0.105	3560.77	212.816	0.041	5.540	3.76 × 10−14	0.697	0.185	0.105
M3-3	0.053	0.577	0.006	1.404	0.288	0.005	0.113	1975.92	180.876	0.045	1.880	3.82 × 10−14	0.666	0.184	0.113
M3-4	0.044	0.569	0.006	1.397	0.284	0.005	0.105	3615.17	213.788	0.041	4.927	3.59 × 10−14	0.702	0.157	0.105
M3-5	0.049	0.558	0.007	1.395	0.283	0.007	0.113	1988.01	181.158	0.047	3.234	1.19 × 10−14	0.690	0.189	0.113
M3-6	0.064	0.555	0.010	1.399	0.285	0.004	0.104	9568.52	2.9 × 10−5	1.04 × 10−4	2.891	4.41×10−14	0.710	0.113	0.104

and

Table 7. Analysis of SWCC Model Evaluation Results.

Number	R2				RMSE				SSE
	Van Genuchten	Gard-ner	Fredlund–Xing	Brooks–Corey	Van Genuchtenn	Gard-ner	Fredlund–Xing	Brooks–Corey	Van Genuchten	Gard-ner	Fredlund–Xing	Brooks–Corey
M1-1	0.9963	0.8729	0.9765	0.8729	0.0063	0.0371	0.016	0.0371	0.00052	0.0179	0.0033	0.0179
M1-2	0.9929	0.8529	0.9272	0.8529	0.0087	0.0396	0.0278	0.0396	0.00099	0.0203	0.0101	0.0203
M1-3	0.9912	0.8899	0.9774	0.8899	0.0098	0.0342	0.0155	0.0342	0.00120	0.0152	0.0031	0.0152
M1-4	0.9928	0.8773	0.9780	0.8773	0.0091	0.0377	0.016	0.0377	0.00110	0.0185	0.0033	0.0185
M1-5	0.9922	0.8473	0.9179	0.8473	0.0092	0.0408	0.0299	0.0408	0.00110	0.0216	0.0116	0.0216
M1-6	0.9941	0.8661	0.9743	0.8661	0.0083	0.0395	0.0173	0.0395	0.00090	0.0203	0.0039	0.0203
M2-1	0.9955	0.9260	0.9803	0.9260	0.0065	0.0265	0.0137	0.0265	0.00055	0.0091	0.0024	0.0091
M2-2	0.9988	0.9503	0.9812	0.9503	0.0034	0.0218	0.0134	0.0218	0.00015	0.0062	0.0024	0.0062
M2-3	0.9986	0.9679	0.9832	0.9679	0.0037	0.0176	0.0127	0.0176	0.00018	0.0040	0.0021	0.0040
M2-4	0.9988	0.9554	0.9849	0.9554	0.0031	0.0188	0.0110	0.0188	0.00013	0.0046	0.0016	0.0046
M2-5	0.9963	0.9445	0.9790	0.9445	0.0057	0.0217	0.0133	0.0217	0.00042	0.0061	0.0023	0.0061
M2-6	0.9987	0.9289	0.9843	0.9289	0.0032	0.0245	0.0115	0.0245	0.00013	0.0078	0.0017	0.0078
M3-1	0.9852	0.8250	0.9156	0.8250	0.0138	0.0448	0.0311	0.0448	0.00250	0.0261	0.0126	0.0261
M3-2	0.9861	0.7697	0.9087	0.7697	0.0147	0.0571	0.0360	0.0571	0.00280	0.0424	0.0168	0.0424
M3-3	0.9916	0.7938	0.9359	0.7938	0.0111	0.0519	0.0289	0.0519	0.00160	0.0350	0.0109	0.0350
M3-4	0.9873	0.7636	0.9032	0.7636	0.0134	0.0575	0.0368	0.0575	0.00230	0.0430	0.0176	0.0430
M3-5	0.9887	0.7930	0.9393	0.7930	0.0127	0.0540	0.0293	0.0540	0.00210	0.0380	0.0111	0.0380
M3-6	0.9874	0.7465	0.8651	0.7465	0.0130	0.0589	0.0430	0.0589	0.00220	0.0451	0.0240	0.0451

. The mathematical formulations of these commonly used SWCC models are provided below.

1.

The Van Genuchten model [11]

$$\mathrm{\Theta }={\displaystyle \frac{\mathrm{\theta }-{\mathrm{\theta }}_{\mathrm{r}}}{{\mathrm{\theta }}_{\mathrm{s}}-{\mathrm{\theta }}_{\mathrm{r}}}}={\left[{\displaystyle \frac{1}{1+{\left(\mathrm{\alpha }\mathrm{\phi }\right)}^{\mathrm{n}}}}\right]}^{\mathrm{m}}$$

(5)

where $\mathrm{\Theta }$ is the effective saturation, or relative water content, (%); $\mathrm{\theta }$ is the volumetric water content, (%); ${\mathrm{\theta }}_{\mathrm{r}}$ is the residual volumetric water content, (%); ${\mathrm{\theta }}_{\mathrm{s}}$ is the saturated volumetric water content, (%); $\mathrm{\phi }$ is the suction, which can be expressed in kPa or by the water head h (where 1 cm of water head equals 0.1 kPa of suction); m and n are parameters controlling the rate of change of the SWCC (Pa⁻¹); $\mathrm{\alpha }$ is a Parameter controlling the relative position of the SWCC, related to the air-entry value.

2.

The Brooks–Corey model [12]

$$\mathrm{\Theta }={\displaystyle \frac{\mathrm{\theta }-{\mathrm{\theta }}_{\mathrm{r}}}{{\mathrm{\theta }}_{\mathrm{s}}-{\mathrm{\theta }}_{\mathrm{r}}}}={\left({\displaystyle \frac{{\mathrm{\phi }}_{\mathrm{a}}}{\mathrm{\phi }}}\right)}^{\mathrm{\lambda }}$$

(6)

where $\mathrm{\Theta }$ is the volumetric water content (%). ${\mathrm{\theta }}_{\mathrm{r}}$ is the residual volumetric water content (%). ${\mathrm{\theta }}_{\mathrm{s}}$ is the saturated volumetric water content (%). $\mathrm{\phi }$ is a air-entry value (kPa). ${\mathrm{\phi }}_{\mathrm{a}}$ is a air-entry value (kPa). $\mathrm{\lambda }$ is a pore-size distribution index.

3.

The Gardner model [13]

$$\mathrm{\theta }\left(\mathrm{h}\right)={\mathrm{\theta }}_{\mathrm{s}}{\left(1+\mathrm{\alpha }\mathrm{h}\right)}^{-\mathrm{\beta }}$$

(7)

where $\mathrm{\theta }\left(\mathrm{h}\right)$ represents the relationship between the soil’s volumetric water content (m³ m³) and the water potential h; ${\mathrm{\theta }}_{\mathrm{s}}$ is the saturated volumetric water content, (%); $\mathrm{\alpha }$ and β are empirical constants obtained by fitting experimental data; h is the soil water potential, (cm or m),a negative value indicates soil moisture suction.

4.

The Fredlund–Xing model [14]

$$\mathrm{\Theta }={\displaystyle \frac{\mathrm{\theta }}{{\mathrm{\theta }}_{\mathrm{s}}}}=\mathrm{C}\left(\mathrm{\phi }\right){\left[{\displaystyle \frac{1}{\ln \left[\mathrm{e}\mathrm{x}\mathrm{p}\left(1\right)+{\left(\raisebox{1ex}{$\mathrm{\phi }$}\!\left/ \!\raisebox{-1ex}{$\mathrm{\alpha }$}\right.\right)}^{\mathrm{n}}\right]}}\right]}^{\mathrm{m}}$$

(8)

where $\mathrm{\Theta }$ is the volumetric water content (%). $\mathrm{\theta }$ is the volumetric water content (%). ${\mathrm{\theta }}_{\mathrm{s}}$ is the saturated volumetric water content (%). $\mathrm{C}\left(\mathrm{\phi }\right)$, correction function, is established based on the assumption that ‘when $\mathrm{\phi }$ = 106 kPa, $\mathrm{\theta }$= 0’. $\mathrm{\phi }$ is the soil matric potential. $\mathrm{\alpha }$ is a Parameter related to the air-entry value; n is the shape parameters for the SWCC (Pa⁻¹).

2.4. Relational Degree Analysis Methods

The diversity of association analysis methods is considerable. Basic graphical tools, such as scatter plots and line charts, are commonly used to intuitively reveal relationships between variables or a pair of factors. In addition, model-based association analysis methods, which build computational models from data, are receiving growing emphasis in contemporary research and are being extensively applied within various modeling frameworks. Notably, grey relational analysis has emerged as one of the most frequently adopted techniques due to its recognized accuracy, universality, and reliability.

1.

Determine the reference series and comparison series

Let the reference series be Y_i = [Y_i(1),Y_i(2),…,Y_i(k)], where i = 1, 2,…, m, and the comparison series be X_j = [X_j(1),X_j(2),…,X_j(k)], where j = 1, 2,…, n. Here, k denotes the sequence length (number of sample points), m represents the number of dependent variables, and n signifies the number of independent variables.

2.

Dimensionless processing of data

To eliminate the effects of differences in units/dimensions across different indicators, standardization processing is performed on the reference series and comparison series.

$$y_i\left(k\right)={\displaystyle \frac{y_i\left(k\right)}{\overline{y_i}\left(k\right)}}$$

(9)

$$x_j\left(k\right)={\displaystyle \frac{x_j\left(k\right)}{\overline{x_j}\left(k\right)}}$$

(10)

3.

Calculate the relational coefficient

Calculate the correlation coefficient between the comparison series X_j and the reference series Y_i at each point k.

$${\Delta }_t\left(k\right)=\left|y_i\left(k\right)-x_j\left(k\right)\right|$$

(11)

$$P_t\left(k\right)={\displaystyle \frac{{\Delta }_t\left(k\right)\left(min\right)+\epsilon {\Delta }_t\left(k\right)\left(max\right)}{{\Delta }_t\left(k\right)+\epsilon {\Delta }_t\left(k\right)\left(max\right)}}$$

(12)

where ε is the resolution coefficient, conventionally set to 0.5; Equations (3)–(10) defines the absolute difference at point k; and (min) and (max) represent the two-level minimum and maximum differences, respectively.

4.

Calculate the relational degree

The grey relational degree ${\varphi }_t$ between series X_j and Y_i is calculated as the average of the correlation coefficients across all observation points, providing a comprehensive metric of their overall relationship.

$${\varphi }_t={\displaystyle \frac{1}{n}}\sum _{k=1}^n{P}_t\left(k\right)$$

(13)

A ${\varphi }_t$ value approaching 1 signifies a stronger association between a given factor and the system’s primary behavior.

In this study, the number of dependent variables (m) is 3, corresponding to the model parameters α, n, and θs. The number of independent variables (n) is 4, representing soil bulk density, clay content, silt content, and inorganic salt content. The sample size is 18. These parameter sets form the basis of the subsequent analysis.

3. Results and Discussion

3.1. Influencing Factors and Correlation Analysis of the SWCC

3.1.1. Effects of Soil Texture

Soil texture is a key physical property and a fundamental parameter that defines the basic physical characteristics of soil. It significantly influences the soil’s water retention capacity, air permeability, and nutrient content, and is crucial in shaping the soil moisture characteristic curve [32]. Figure 3 presents the fitting results of the soil moisture characteristic curve under specific combinations of clay and silt content.

Analysis of the data reveals that at equivalent pressure levels, soil samples with a higher proportion of clay and silt particles exhibit significantly greater moisture content. In contrast, samples with lower clay and silt content display a SWCC with a steeper slope. This difference is attributed to the fine particle size of clay and silt (typically <0.005 mm). An increase in clay content leads to the filling of larger pores [33]. Matric potential, which represents the energy state of water retained in soil via capillary forces and surface adsorption, shows a stronger water-holding capacity (indicated by a larger absolute value) in these fine-textured soils [34]. The concomitant reduction in pore size promotes a more compact soil structure, characterized by an increase in small to medium-sized pores and a greater specific surface area. These factors collectively enhance capillary action, thereby strengthening the soil’s capillary suction and overall water retention capacity [35]. These findings underscore a strong correlation between the evolution of the soil water characteristic curve and soil texture.

3.1.2. Effects of Soil Bulk Density

Soil bulk density, also termed dry bulk density, is defined as the mass of oven-dry soil per unit bulk volume, which encompasses both the solid particles and the pore space. This parameter is a critical physical indicator for assessing soil structure at the macroscopic scale, as it is intrinsically linked to the soil’s state of compaction and consolidation [36]. The fitted results of the soil water characteristic curves across a range of predefined bulk density values are presented in Figure 4.

Figure 4 reveals that an increase in soil bulk density results in a marked flattening of the SWCC. Under equivalent pressure conditions, the volumetric water content exhibits a positive correlation with bulk density. Conversely, soils with lower bulk density are characterized by a steeper curve, indicated by a greater slope value. This behavior can be attributed to the more compact soil structure associated with higher bulk density, which substantially reduces the volume of large pores while increasing the proportion of small and medium-sized pores. The concomitant increase in pore surface area enhances the soil’s water adsorption capacity [37]. Moreover, the abundance of fine pores diminishes the overall connectivity between soil pores. This microstructural change impedes water conduction efficiency but strengthens the soil’s capillary water retention capacity [38]. At low suction stages, water within the soil micropores exists predominantly as bound water due to strong adsorption by soil particles, exhibiting highly constrained mobility. Consequently, a higher suction force is required to remove a unit volume of water [35]. Therefore, it is concluded that a lower soil bulk density contributes to a more pronounced slope in the SWCC.

3.1.3. Effects of Soil Salinity

Soil inorganic salt content serves as a key indicator for evaluating soil salinization degree, since its ionic composition and spatial distribution exert direct impacts on soil fertility and crop development [39,40]. Adhering to the principle of controlling single variables, the soil water characteristic curves were initially measured and subsequently fitted to investigate their correlation with the inorganic salt content. A comparative analysis of these curves under varying salt content conditions is presented in Figure 5, Figure 6 and Figure 7 for soil samples collected from three distinct locations (M1, M2, and M3).

As illustrated in Figure 5, Figure 6 and Figure 7, an increase in soil inorganic salt content is positively correlated with a rightward shift of the SWCC, indicating an enhancement of the soil’s water retention capacity under low to moderate salinity levels. Under equivalent matric potential conditions, the volumetric water content increases with rising salt concentration. This phenomenon can be attributed to changes in the electrochemical properties of soil particles. Specifically, an increase in inorganic salt content elevates the surface charge density of soil particles, promoting the adsorption of cations and enhancing the soil-water interaction energy. The increased ion adsorption not only raises the surface energy of soil particles but also strengthens their water-holding capacity through improved osmotic and matric potential effects.

3.1.4. Correlation Analysis of Soil Physicochemical Properties

Soil basic physicochemical properties are critical determinants of both water retention capacity and the shape of the SWCC. To quantitatively analyze the relationships between these properties and the SWCC, this study applied grey correlation analysis [41]. This method enables a systematic assessment and ranking of multiple potential influencing factors, thereby clarifying their relative importance and contribution to the formation of the water characteristic curve.

The quantitative relationships between soil physicochemical properties and the parameters of the VG model for the SWCC were determined through analysis of 18 datasets. The specific results are summarized in

Table 8. Correlation Degree Results.

Correlation Degree of Parameter	Bulk Density	Clay	Silt	Inorganic Salt
	(X01)	(X02)	(X03)	(X04)
α (Y01)	0.821 ± 0.157	0.821 ± 0.157	0.721 ± 0.275	0.773 ± 0.226
n (Y02)	0.975 ± 0.024	0.975 ± 0.024	0.702 ± 0.221	0.838 ± 0.125
θs (Y03)	0.814 ± 0.179	0.801 ± 0.049	0.801 ± 0.049	0.811 ± 0.175
Ranking	1	2	4	3

.

Correlation analysis between fundamental soil physicochemical properties and the parameters (α, n, and θs) of the VG model reveals statistically significant relationships, as summarized in the table. The influence of these factors follows a consistent order: soil dry bulk density > clay content > inorganic salt content > silt content. The correlation coefficient between each factor and the model parameters exceeds 0.6, indicating substantial associations. Existing studies confirm that soil dry bulk density, clay content, inorganic salt concentration, and silt proportion are key determinants of soil physical properties [42]. The magnitude of their effects on the SWCC varies, with inorganic salts exhibiting a particularly notable influence. Inorganic salts modulate the behavior of the SWCC through multiple direct and indirect mechanisms. Consequently, the role of inorganic salts should be rigorously considered in related research. In practices such as soil water management, irrigation planning, and agricultural production, it is essential to account for soil inorganic salt content and its integrated effects on soil water characteristics.

3.2. Optimization and Reconstruction of SWCC Models Considering Water Mineralization

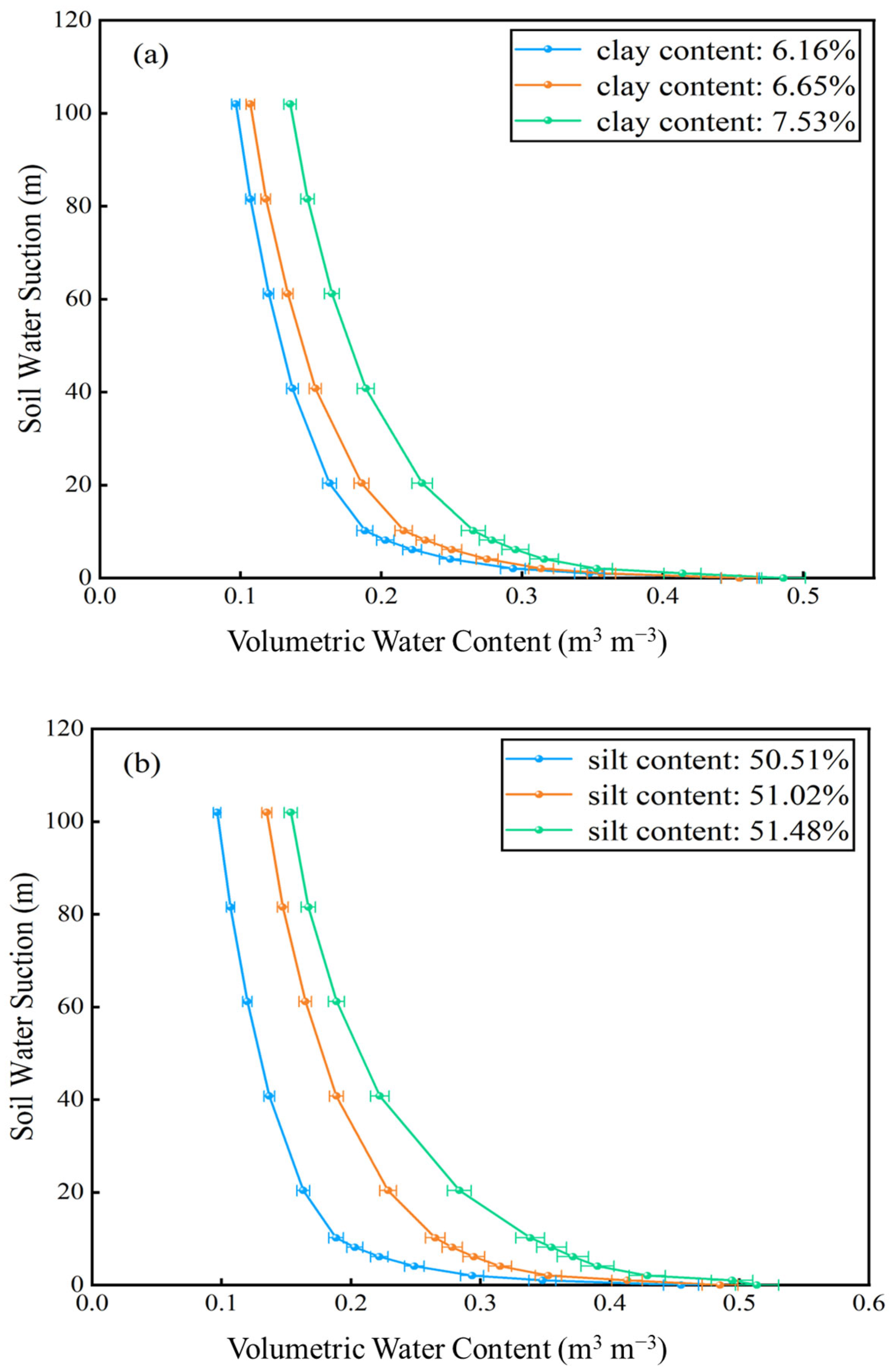
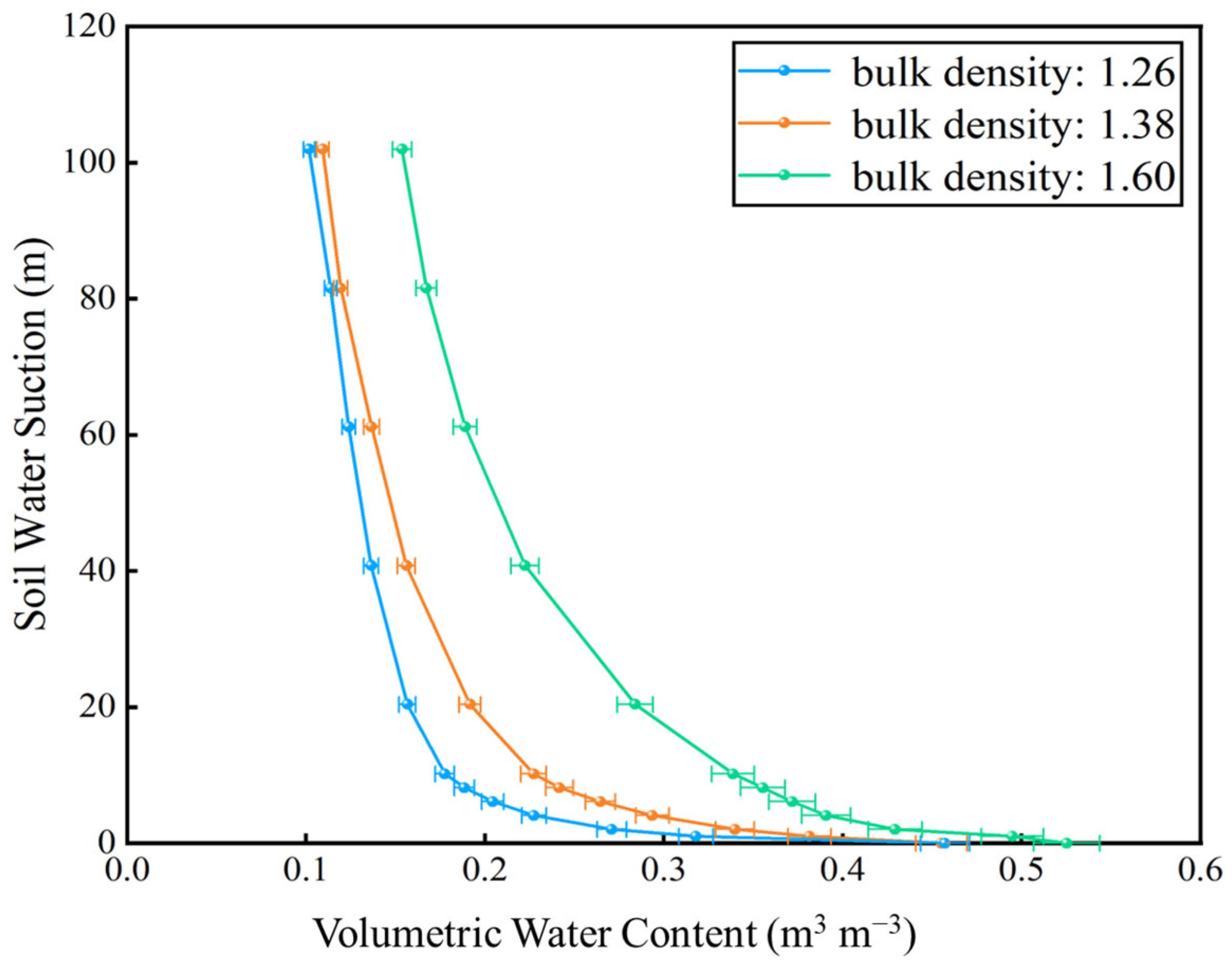
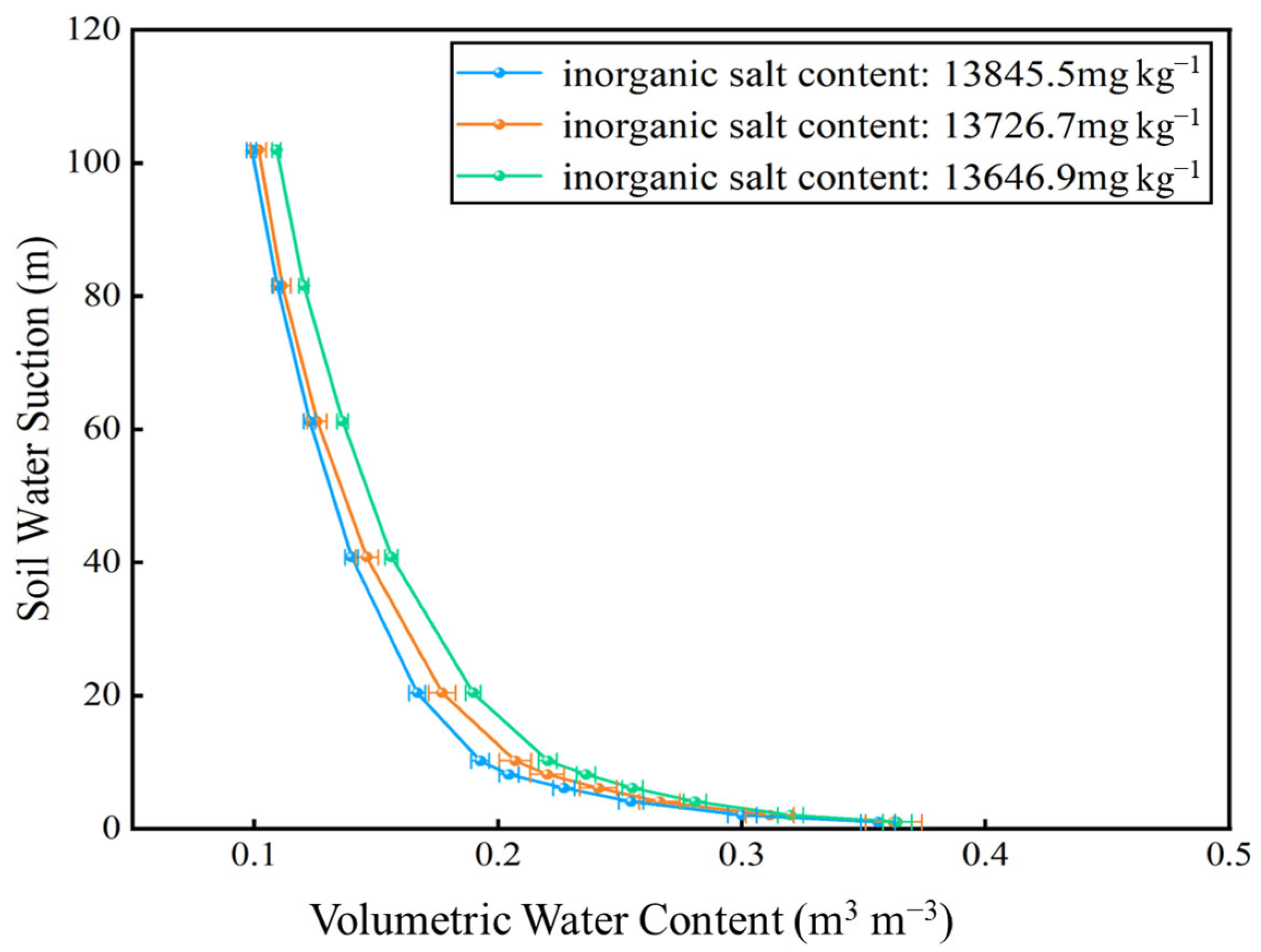
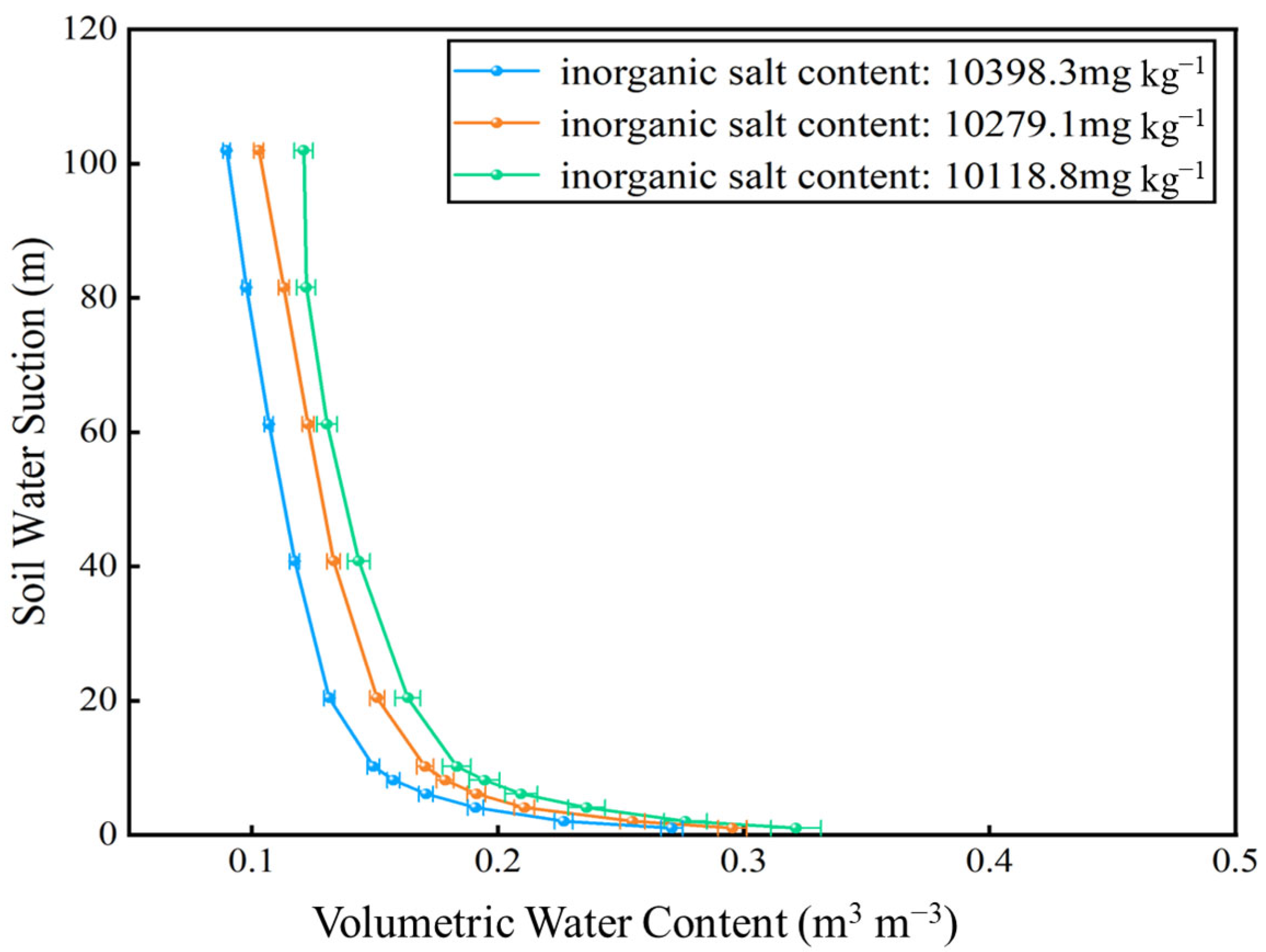
3.2.1. Optimal Model Selection

The applicability of four prediction models was evaluated using 18 soil texture samples collected from the Yingjisha study area. Based on the MATLAB platform, the centrifugation test data were fitted with the four models employing the nonlinear least squares method (via the lsqnonlin function) [43]. The optimal mathematical model, which best matches the three soil textures, was identified by calculating the fitting parameters and the coefficient of determination (R²) for each model. The results are presented in the figure below.

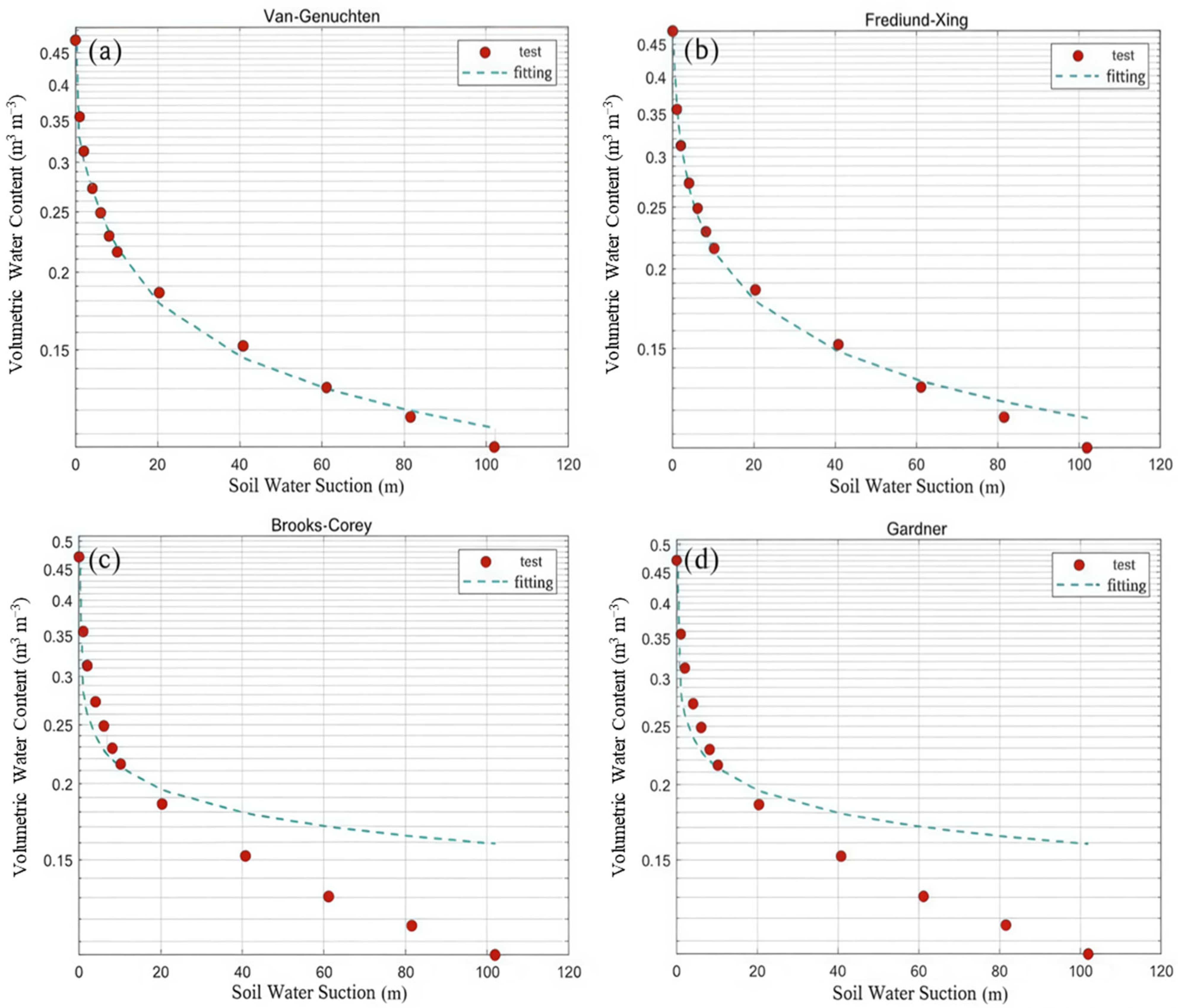
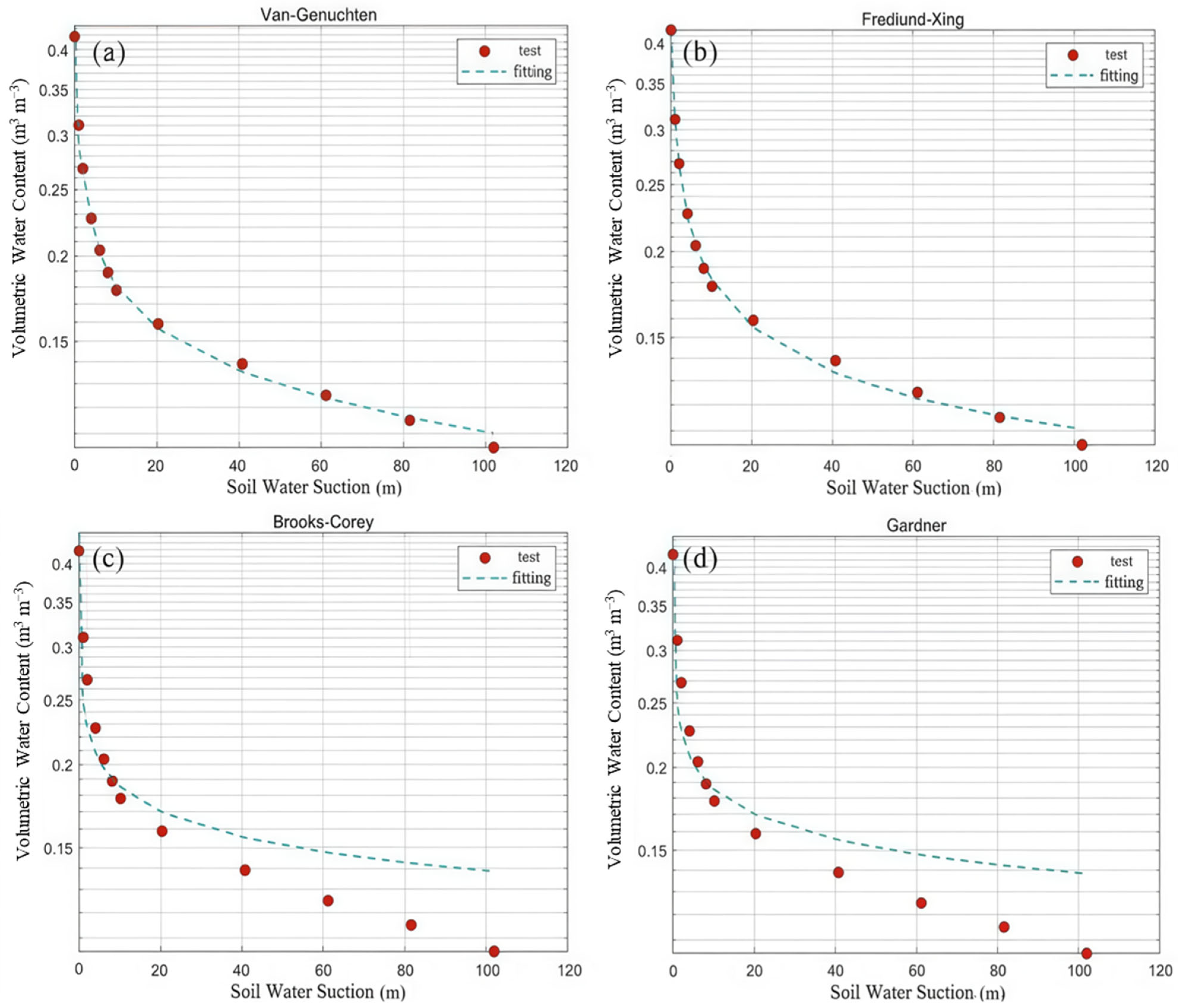
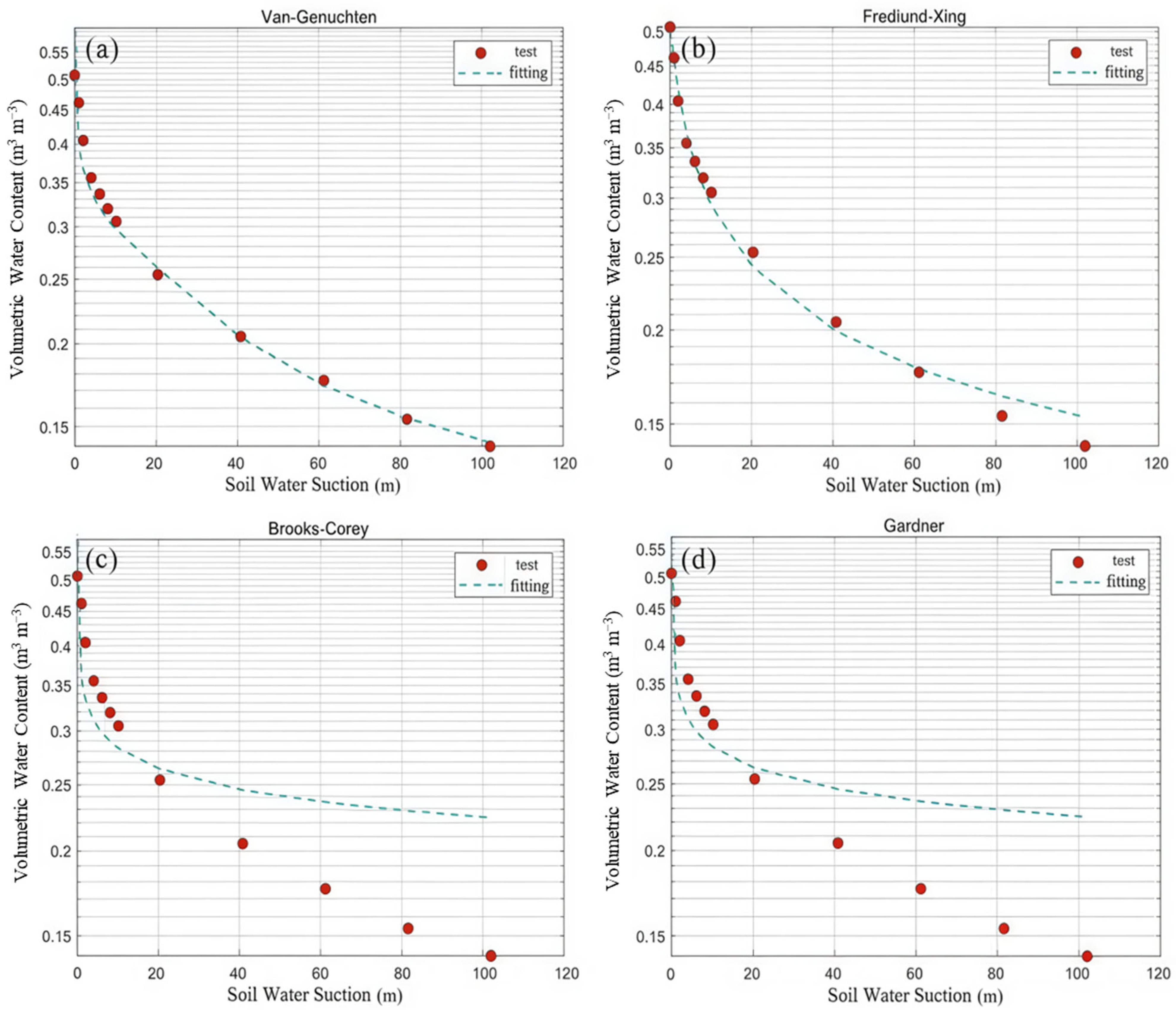
Figure 8, Figure 9 and Figure 10 compare the fitting performance of four SWCC models for soil samples M1, M2, and M3 saturated with water at a salinity level of 5 g L⁻¹. Significant differences in model accuracy are observed. The Brooks-Corey and Gardner models show considerable deviations from the experimentally measured data, indicating suboptimal performance under these conditions. These discrepancies may be attributed to oversimplified theoretical assumptions regarding soil structure and water transport mechanisms in these models, which limit their ability to accurately represent complex soil textures.

In comparison, both the VG and FX models achieved satisfactory fitting performance for the SWCCs. Their high adaptability enabled accurate fitting of SWCC data across three distinct soil textures. The fitted curves exhibited strong agreement with experimental measurements, providing a precise description of soil water adsorption and release dynamics under varying pressure conditions. This outcome underscores the flexibility of the VG and FX models in parameterization and theoretical robustness, allowing them to effectively capture the complexities imposed by soil textural variations. However, while the FX model incorporates particle–particle interactions, thereby offering a more accurate representation of complex soil structures, it entails greater computational complexity. Parameter estimation and numerical implementation are more arduous, limiting its practicality for routine applications but rendering it particularly suitable for specialized soils such as expansive or frozen soils [44].

The fitting accuracy of each model was evaluated based on the parameters derived from the fitting process, which are summarized in Table 7 and Table 8. A comparative analysis of these parameters elucidates the divergence in model performance during the fitting procedure and their respective capacities to characterize the SWCC. This assessment provides critical insights for subsequent model selection.

The fitting performance of the four models was quantitatively assessed by comparing the key evaluation metrics—the coefficient of determination (R²), root mean square error (RMSE), and sum of squared errors (SSE)—derived from the model calibrations. As summarized in Table 8, the VG and FX models, both three-parameter formulations, demonstrated excellent capability in fitting the SWCCs of Yingjisha soil samples under varying salinity conditions. Calibration results indicated that the R² values for both models exceeded 0.85, confirming their ability to accurately capture the variation trends of the SWCCs. Among all models, the VG model yielded the smallest SSE, indicating the smallest discrepancy between the fitted and observed values and thus representing the best overall fit. Furthermore, the VG model achieved the highest fitting accuracy across all three soil samples (M1, M2, M3), whereas the Gardner, FX, and Brooks-Corey models exhibited slightly inferior applicability and stability. In conclusion, the VG model provided the most accurate representation of the soil water characteristics for the investigated samples under different solution mineralization levels, establishing it as the most suitable candidate for subsequent parameter optimization studies. Therefore, the VG model was selected for further optimization work in this research.

A targeted analysis of the fitting evaluation results for the four models presented in Table 8 indicates that all models exhibited superior performance when fitting the M2 (silt soil) samples compared to the M1 (silty sand) and M3 (sandy loam) samples. For the M2 samples, the fitting accuracy, as reflected by the R² values of all four models, was notably high, with each exceeding 0.9. Specifically, samples M2-3 and M2-4 demonstrated the best fit, whereas sample M3-7 showed the poorest performance. This performance discrepancy can be attributed to the finer sand particle size of the M2 soil relative to the M1 and M3 soils, resulting in distinct soil structures and hydrological characteristics. The textural and structural properties of the silt soil promote more regular patterns during water adsorption and release processes. Finer particles generally enhance soil water-holding capacity, and during desorption, capillary suction is more pronounced, leading to a stronger agreement between the fitted SWCC and measured data, thereby facilitating model calibration. In contrast, the M1 and M3 samples contain coarser sand particles. Additionally, the M3 sample exhibits a higher soluble salt content, which can cause soil compaction and alter interparticle pore structure. These changes diminish the effect of capillary suction during desorption, resulting in a less accurate model fit. Furthermore, the overall fitting performance for the M1 samples was generally better than that for the M3 samples, suggesting that the properties of silty sand are more consistent with the assumptions underlying the models, and the variation pattern of the M1 SWCC is more amenable to representation by these models. The complex characteristics of sandy loam soil, however, introduce considerable errors during the fitting process. In summary, the performance of traditional SWCC models is less ideal for sandy loam soils, underscoring the need to optimize existing models or develop alternative approaches tailored to the specific properties of this soil texture.

3.2.2. Development of a SWCC Model Under Various Mineralization Conditions

1.

Effect of different mineralization degrees on the SWCC

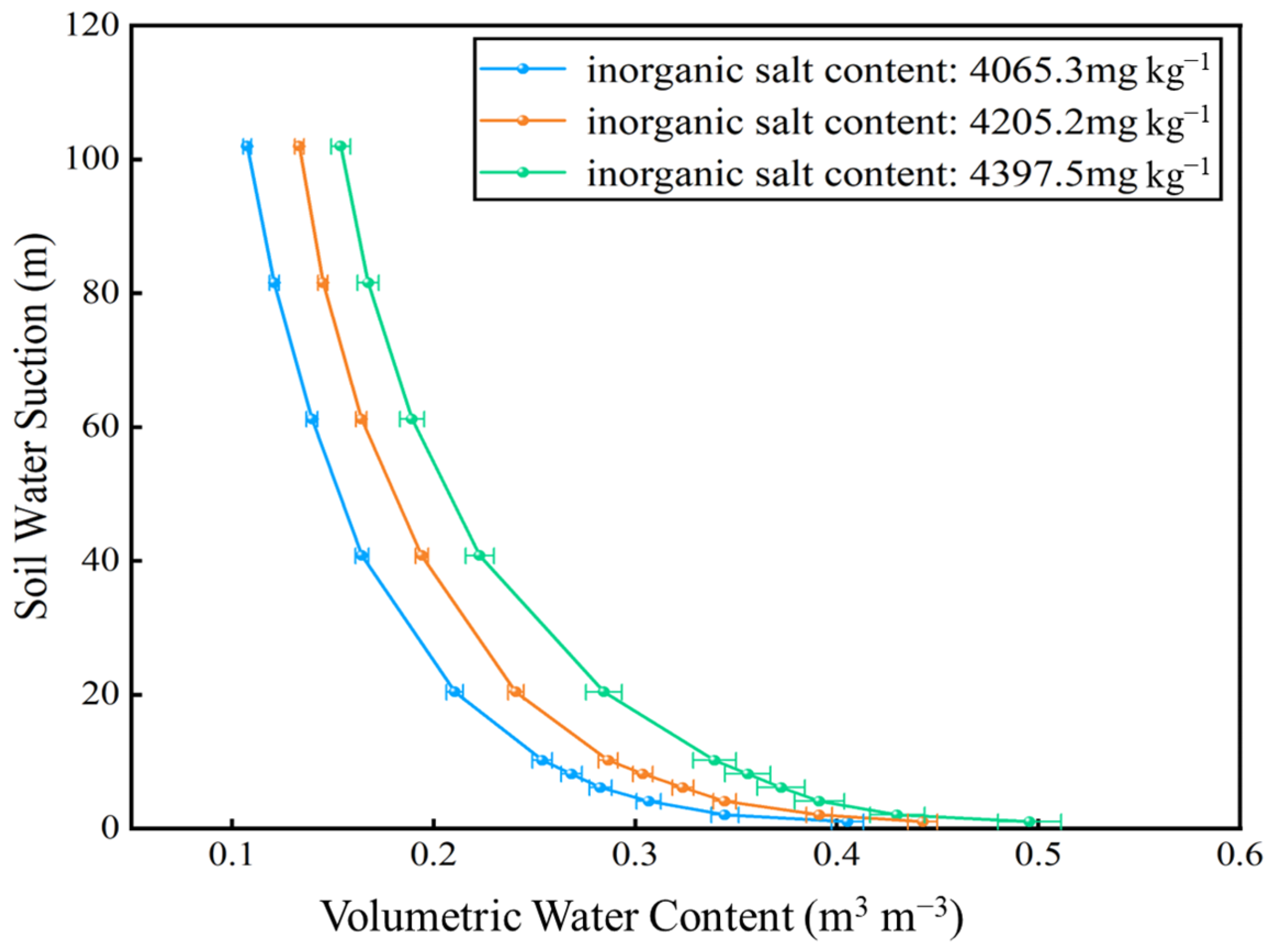
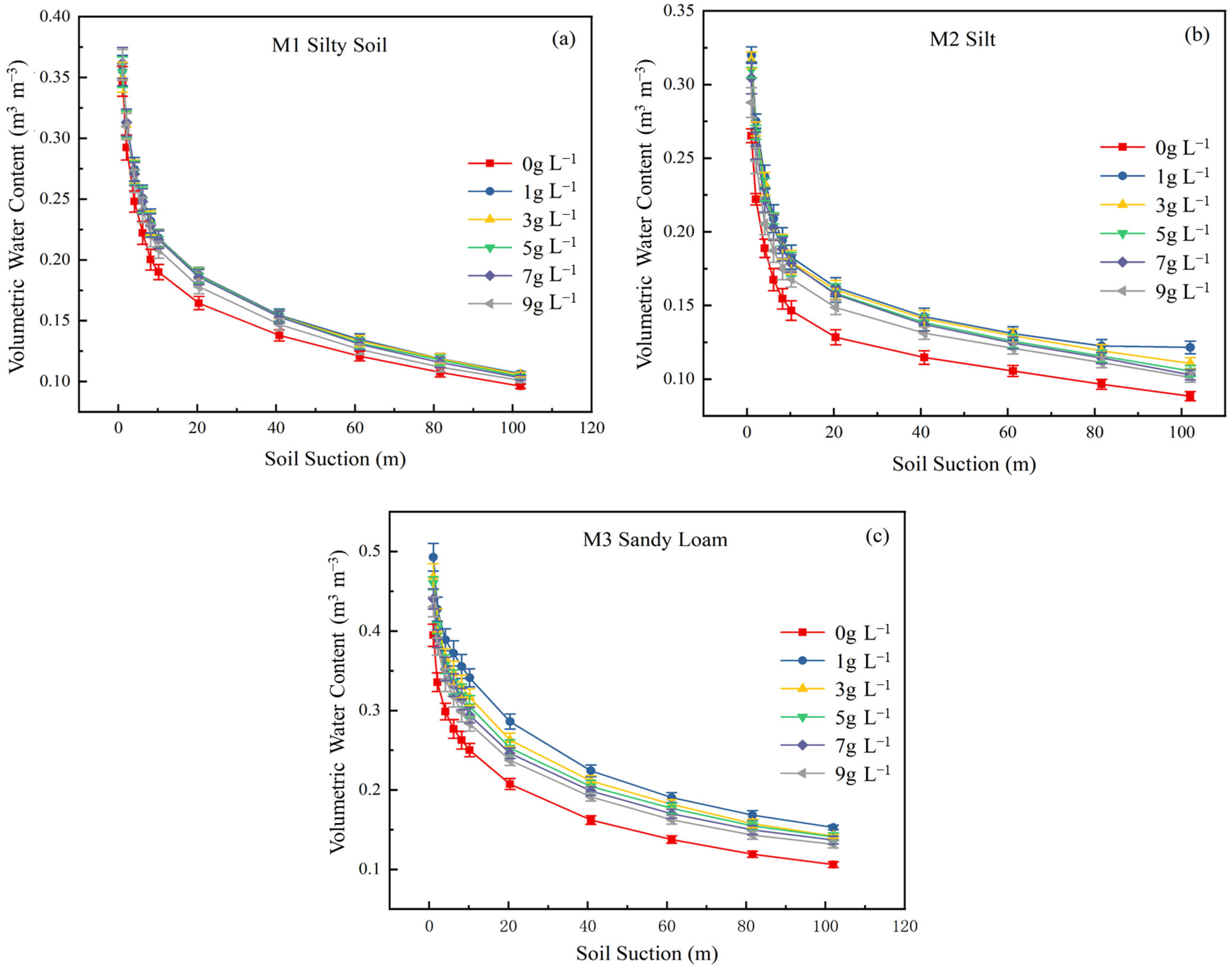
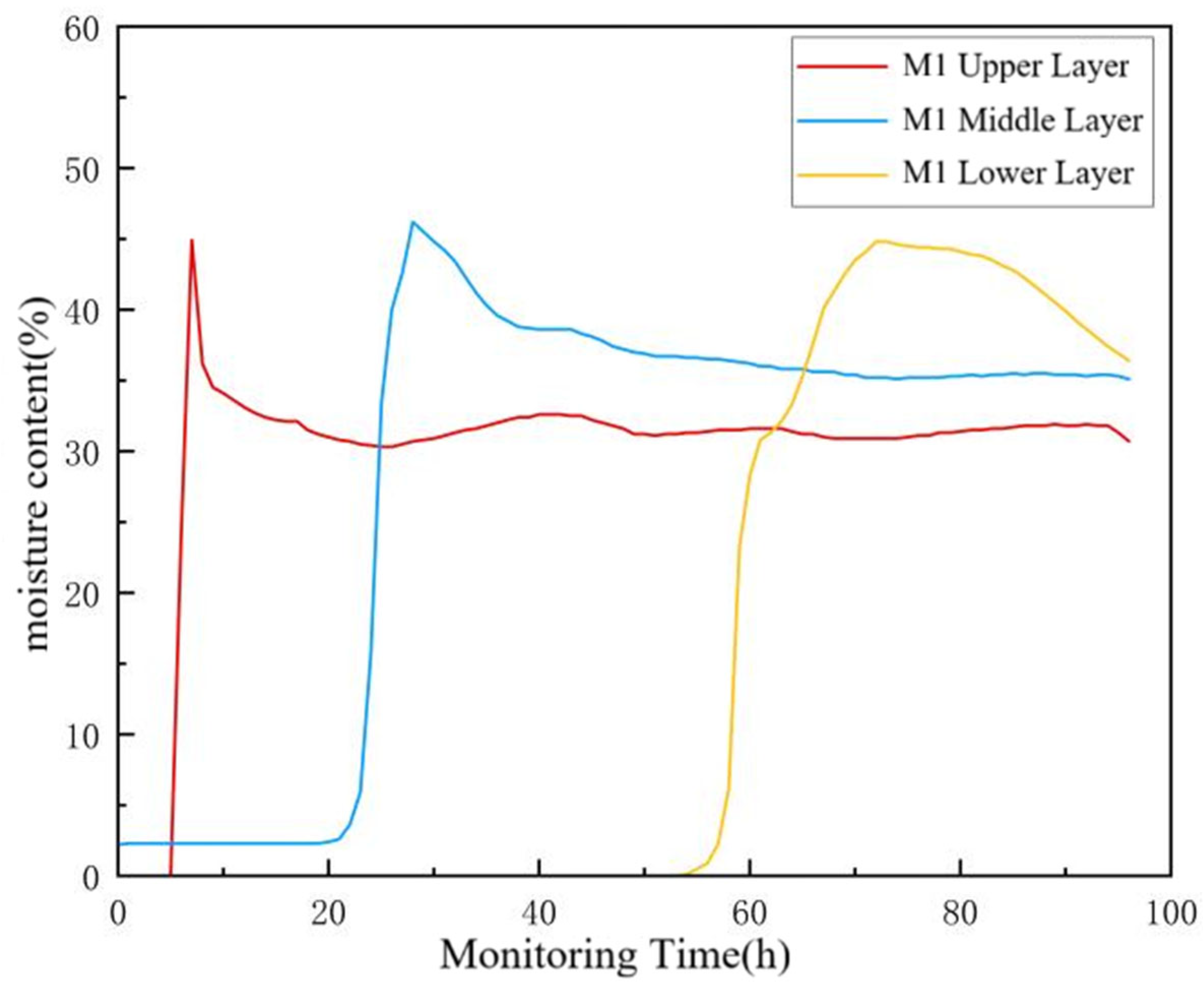
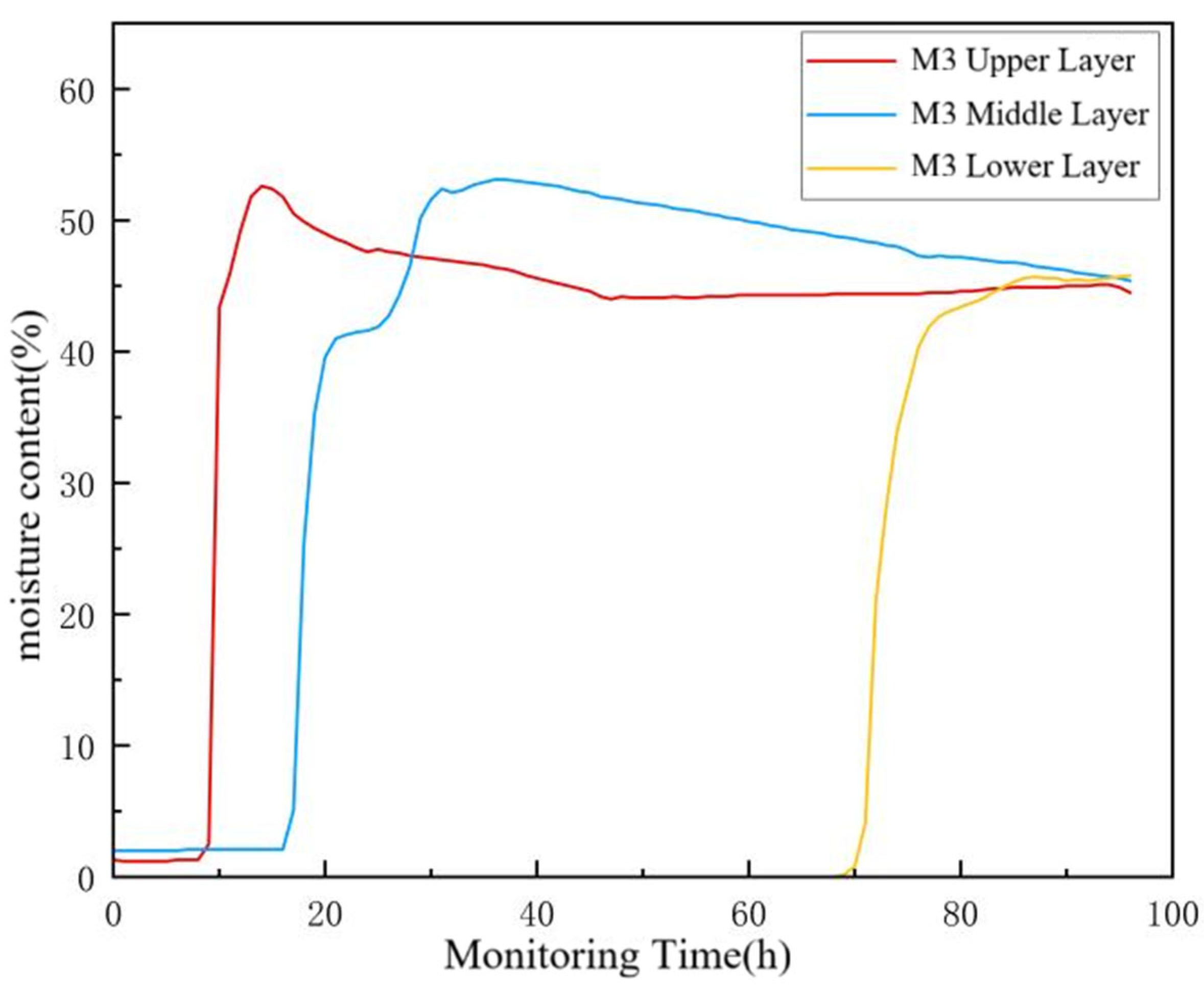
This study employed NaCl solutions with salinity levels of 1, 3, 5, 7, and 9 g L⁻¹ to treat three soil texture samples (M1, M2, M3). The SWCCs for these samples under different salinity conditions are presented in Figure 11. The results indicate that the volumetric water content of all soil samples decreased as soil suction increased. Treatment with saline solutions enhanced the soil water retention capacity to some extent during specific stages. However, the water retention capacity did not increase monotonically with rising salinity levels; instead, it initially increased and then decreased, a trend particularly pronounced under high suction conditions. This phenomenon can be attributed to the following mechanisms: compared to pure water, low-salinity solutions contain a considerable number of ions. Since soil particle surfaces are charged, they can adsorb a significant amount of ions from the solution—typically up to three layers. This adsorption process increases the specific surface area of the soil particles, thereby facilitating the retention of more water molecules. Furthermore, during the desorption process, a portion of the salts originally dissolved in the soil solution precipitates and forms crystals. This precipitation alters the soil microstructure, increases the proportion of small pores, and consequently enhances the water-holding capacity of the soil [45]. However, an excessive accumulation of salt ions increases soil dispersibility. Excessively high salinity accelerates soil salinization, which disrupts soil structure by promoting the dispersion of soil particles and consequently diminishes the water-holding capacity. This explains the observed decline in water-holding capacity of soil samples treated with solutions having a salinity exceeding 1 g/L [46].

Furthermore, the slope of the soil water characteristic curve decreases with increasing soil suction. This occurs because, as soil suction rises, the drainage process within the soil shifts from being dominated by the emptying of large pores to being controlled by the drainage of small and medium-sized pores [47]. The large pore system significantly regulates water movement in the low suction range. With increasing suction, water is progressively retained in smaller pores, making the dewatering process more difficult. Treatments involving water of varying mineralization levels further result in only small pores being able to retain some moisture during the low suction stage. This leads to a significant enhancement of the soil’s water retention capacity, causing the water retention curve to exhibit a steeper shape.

The shift magnitude observed in the SWCCs of the three soil samples (M3, M2, M1) diminished progressively with increasing solution salinity. This pattern suggests that the M1 saline soil, having a high inherent background salt content, responded relatively weakly to variations in solution salinity; consequently, the effect of salinity on its SWCC was minimal. In contrast, the M2 soil, with a lower initial salt content, exhibited a more pronounced response, wherein changes in solution salinity markedly influenced its water characteristic curve. Research indicates that the water-holding capacity of saline soil initially increases with salt content but declines as salinization intensifies beyond a certain threshold. Variations in solution salinity significantly altered the SWCCs of the samples, an effect strongly correlated with their initial salinization degree. Across the examined matrix suction gradients, the SWCCs for different treatments demonstrated notably parallel characteristics. This parallelism implies a consistent influence of matrix potential on the trend of water content change across treatments, whereas localized slope differences are mainly attributed to the differential impact of the salt concentration gradient on pore structure parameters.

2.

Effect of different mineralization degrees on key model parameters

The parameter α in the VG model governs the soil pore-size distribution, primarily influencing the horizontal position of the SWCC. The parameter n characterizes the pore-size distribution uniformity, which dictates the steepness of the curve’s inflection point. The saturated water content [48,49], θs defines the upper limit of the model’s predictive range by representing the maximum volumetric water content under saturated conditions.

Using MATLAB, we simulated and quantitatively analyzed the response of the VG model parameters (α, n, θs) to varying solution mineralization levels (k) for three soil samples. The analysis established explicit functional relationships between the model parameters and k, thereby quantifying the influence of salinity on the soil hydraulic properties. As shown in Figure 12, Figure 13 and Figure 14.

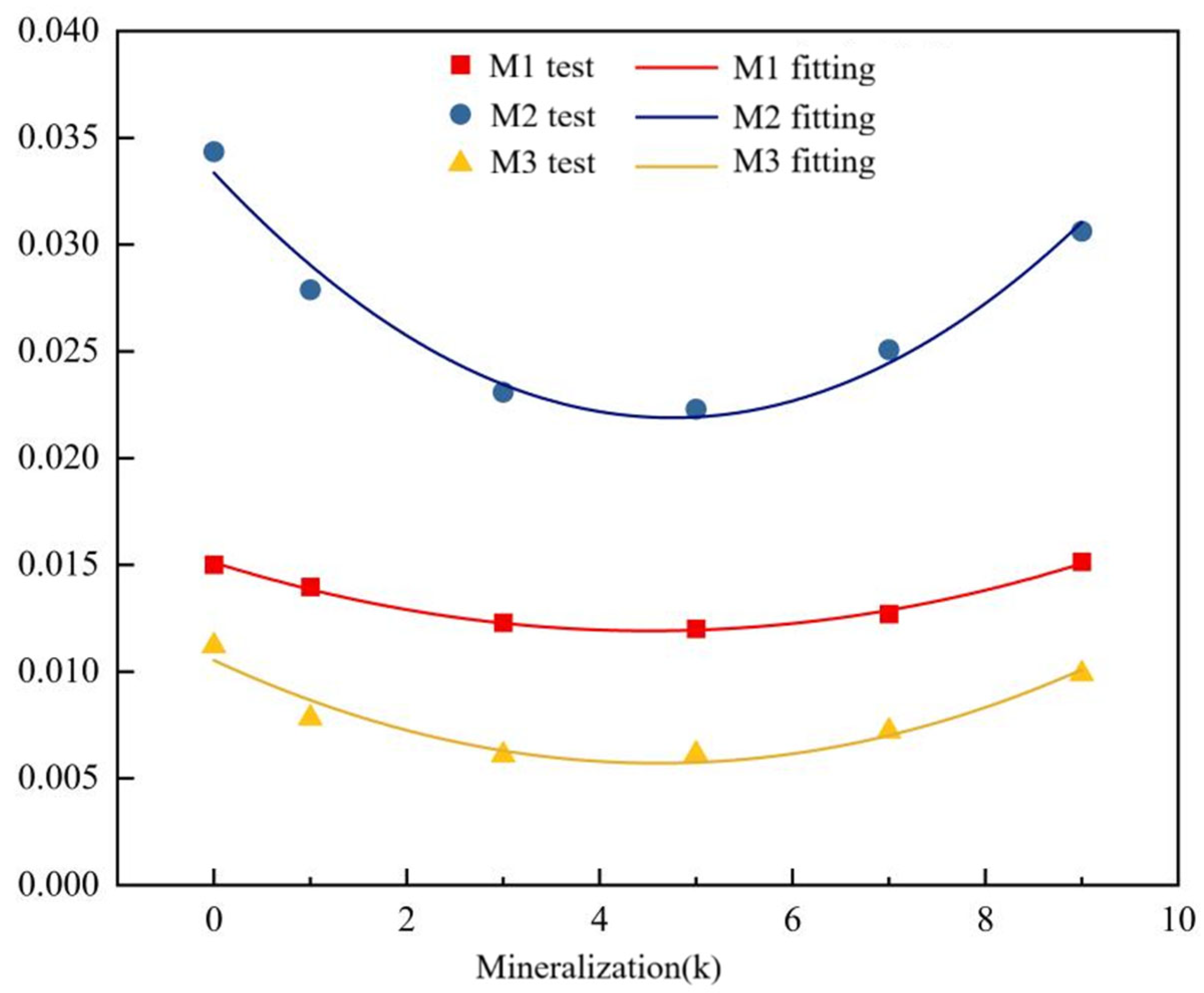
As illustrated in Figure 12, the VG model parameter α for the three soil samples varies non-monotonically with increasing solution mineralization, following a quadratic polynomial trend [50]. Specifically, α initially decreases as mineralization rises, then increases after reaching a minimum, with the symmetry axis of all curves located near approximately 4.3 g/L. The slope change of the curve for sample M3 is markedly steeper than those for M1 and M2, indicating a greater sensitivity of M3 to variations in mineralization. Since α is defined as the reciprocal of the air-entry pressure, it reflects the soil’s hydraulic behavior during initial drying; a higher α value corresponds to more efficient drainage performance.

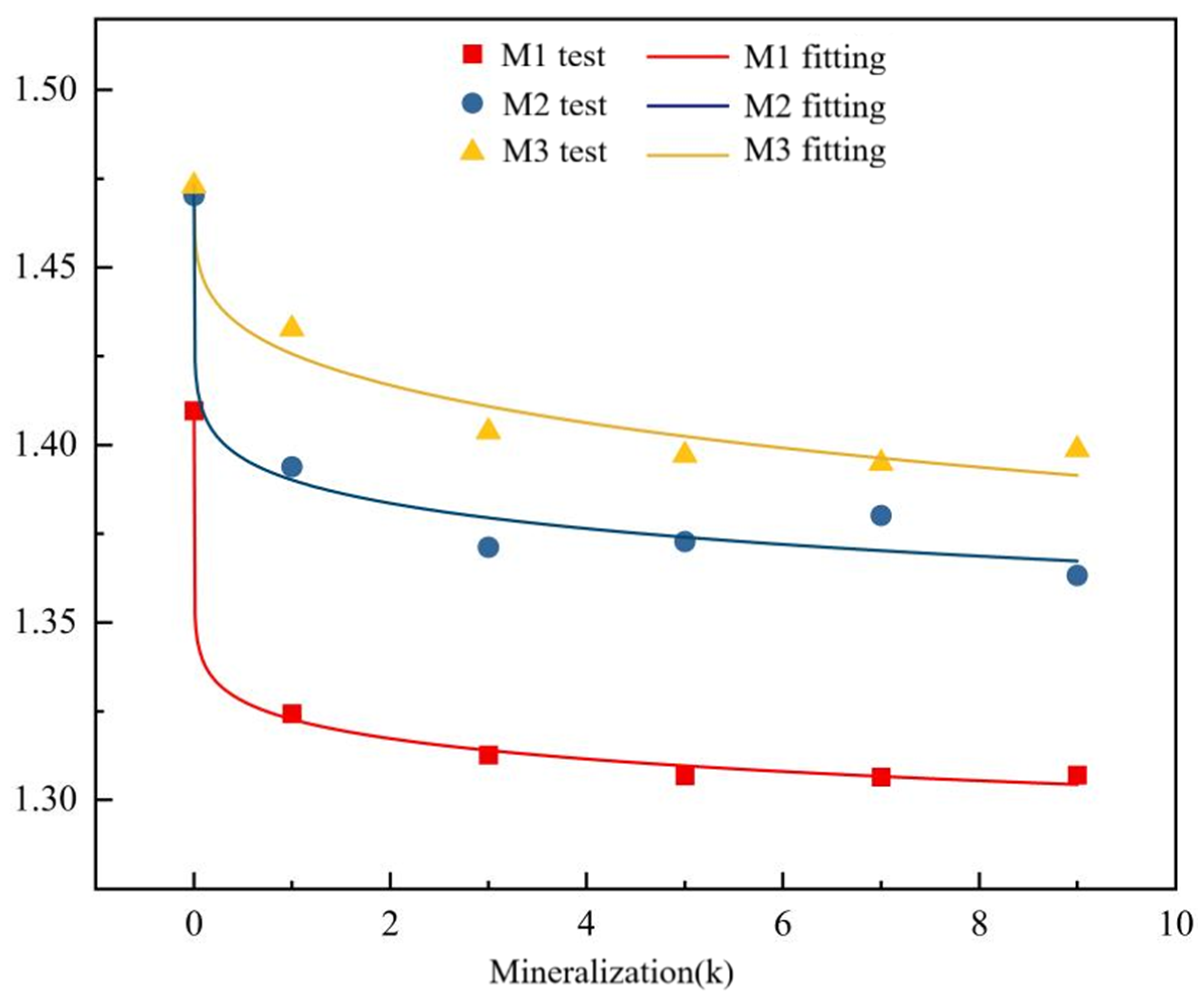
Figure 13 reveals a gradual decline in the parameter n with increasing mineralization, a trend well captured by a power function [50]. The parameter n characterizes the nonlinearity of the soil water retention curve, and its value is indicative of the soil’s water-holding capacity. The slopes of the relationship between n and mineralization decrease consistently across the three soil samples. The inflection point follows the order M3 > M2 > M1. This progression is attributed to increased mineralization promoting soil particle flocculation and altering pore geometry, which in turn influences the shape parameter n of the retention curve.

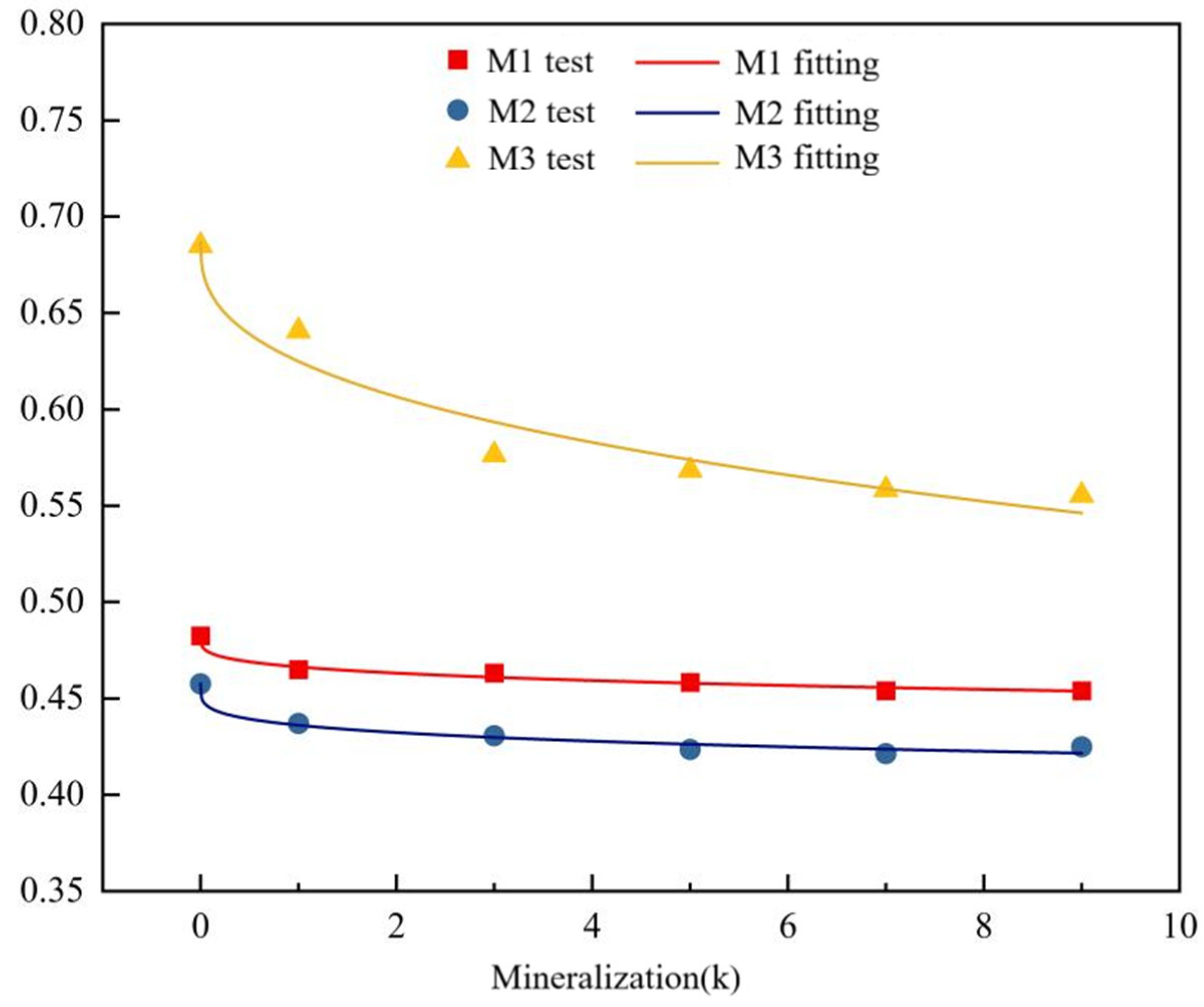
As shown in Figure 14, the saturated water content θs decreases progressively with rising mineralization, demonstrating a reduction in water retention under high salinity conditions. This inverse correlation is effectively modeled by a power function. The slope of the θs-mineralization curve is significantly steeper for M3 than for M1 and M2, and the overall θs values adhere to the ranking M3 > M1 > M2. The more retentive pore structure of M3 allows it to maintain a higher θs even at elevated mineralization levels. The diminishing effect of further increases in mineralization on θs underscores the importance of the soil’s innate salinity level in modulating its response.

3.

Model establishment under different mineralization conditions

For soil samples M1, M2, and M3, the symmetry axes of the fitted function curves were nearly identical, clustering around a mineralization level of approximately 4.3 g L⁻¹. Based on these patterns, the functional relationships for θs(k), n(k), and α(k) were formulated as Equations (14)–(16), respectively. The optimized VG model, incorporating the influence of mineralization level, is presented as Equation (17). This study establishes, for the first time, a quadratic function for α (k) and power functions for n(k) and θs(k), overcoming the limitations of traditional model assumptions and thereby constructing a mineralization-responsive VG model framework. In these equations, (k) represents the solution mineralization level in g/L.

$${\mathrm{\theta }}_{\mathrm{s}}\left(\mathrm{k}\right)=\mathrm{p}{\mathrm{k}}^{\mathrm{q}}+\mathrm{r}$$

(14)

$$\mathrm{n}\left(\mathrm{k}\right)=\mathrm{d}{\mathrm{k}}^{\mathrm{e}}+\mathrm{s}$$

(15)

$$\mathrm{\alpha }\left(\mathrm{k}\right)=\mathrm{f}{\mathrm{k}}^2+\mathrm{i}\mathrm{k}+\mathrm{g}$$

(16)

$$\mathrm{K}={\mathrm{K}}_{\mathrm{s}}{\left({\displaystyle \frac{\mathrm{h}}{\left(\mathrm{f}{\mathrm{k}}^2+\mathrm{i}\mathrm{k}+\mathrm{g}\right)+\mathrm{h}}}\right)}^{\left(\mathrm{d}{\mathrm{k}}^{\mathrm{e}}+\mathrm{s}\right)}\times {\left(1-{\left(1-\left({\displaystyle \frac{\mathrm{h}}{\left(\mathrm{f}{\mathrm{k}}^2+\mathrm{i}\mathrm{k}+\mathrm{g}\right)+\mathrm{h}}}\right)\right)}^{\left(1-1/\left(\mathrm{d}{\mathrm{k}}^{\mathrm{e}}+\mathrm{s}\right)\right)}\right)}^{\left(1-1/\left(\mathrm{d}{\mathrm{k}}^{\mathrm{e}}+\mathrm{s}\right)\right)}$$

(17)

The functional relationships between the key VG model parameters (α, n, θs) and the mineralization level (k), as defined by Equations (14)–(16), were incorporated into the fundamental model equation (Equation (5)). This integration yielded an optimized VG model that explicitly accounts for salinity effects (Equation (17)). The fitting parameters (d, e, f, g, i, p, q, r, s) associated with these functions are provided in

Table 9. Optimized Fitted Values of Model Parameters.

Number	Parameter	Numerical Value	Parameter	Numerical Value	Parameter	Numerical Value
M1	d	−0.08694	e	0.08747	s	1.40972
	f	0.000156941	i	−0.00142	g	0.01511
	p	−0.01603	q	0.26255	r	0.48242
M2	d	−0.08012	e	0.11448	s	1.47034
	f	0.000507893	i	−0.00483	g	0.03337
	p	−0.02157	q	0.23405	r	0.45776
M3	d	−0.04776	e	0.24577	s	1.40972
	f	0.000226969	i	−0.00209	g	0.01053
	p	−0.06172	q	0.3744	r	0.68671

.

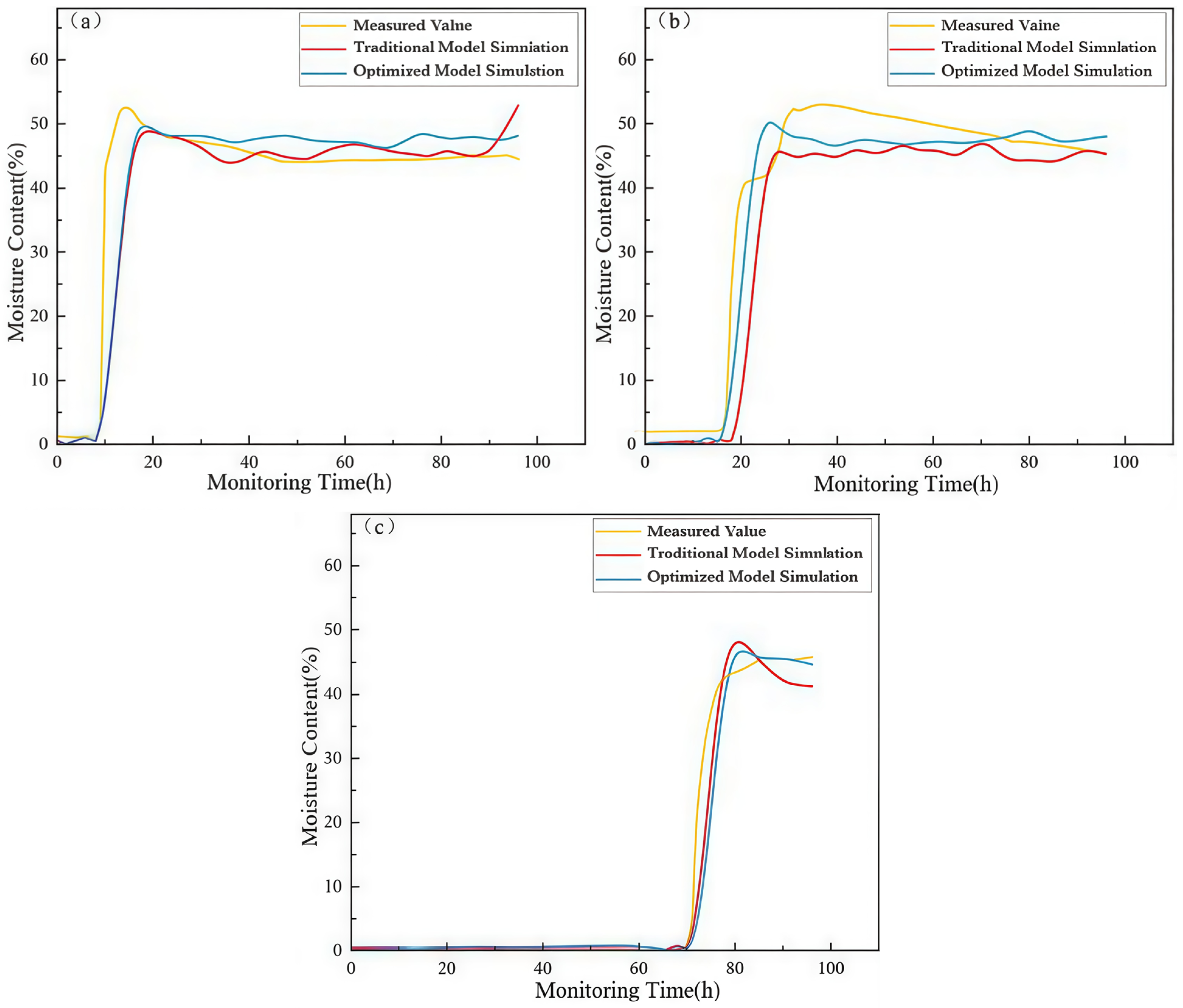
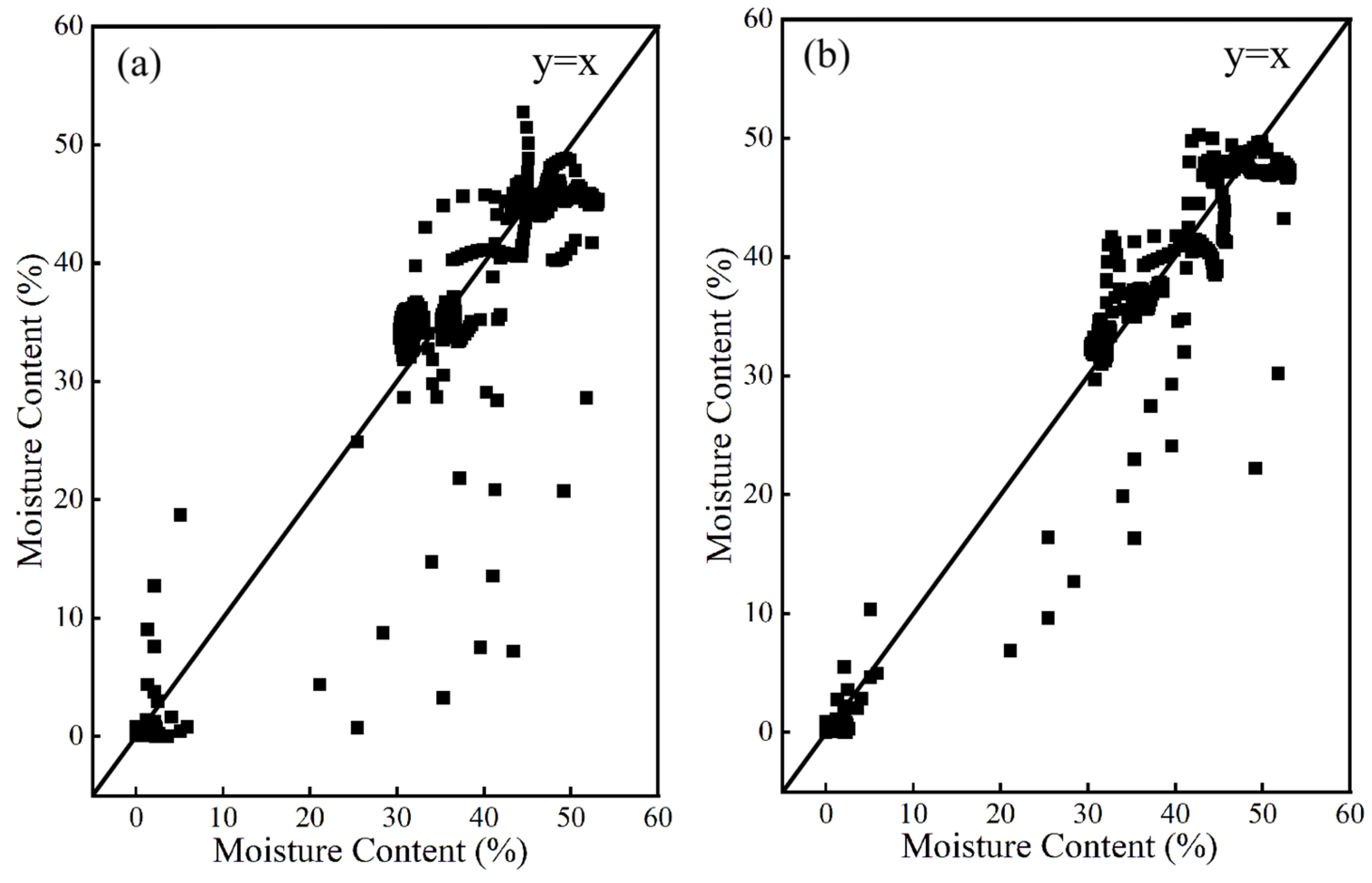
The quadratic/power-law function was selected as an empirical model in this study, guided by the observed patterns in our experimental data. Its validity was confirmed through systematic comparative experiments. Moreover, subsequent results from soil column infiltration tests demonstrate that this model robustly captures the intrinsic relationships between key variables, showing strong explanatory power and reliability.

3.3. Validation of the SWCC Model Incorporating Water Mineralization

3.3.1. Experimental Monitoring Data

The resultant data, depicting the spatial-temporal dynamics of water content for the silty sand (M1), silt soil (M2), and sandy loam (M3) samples, are presented in Figure 15, Figure 16 and Figure 17, respectively, serving as a fundamental dataset for subsequent analytical and model validation purposes.

3.3.2. Numerical Simulation Results

A simulation analysis was conducted on three soil samples with different textures—silty sand (M1), silt soil (M2), and sandy loam (M3). The study employed both the conventional VG model and an optimized version that incorporates the influence of water mineralization. The optimized model featured a customized formula to more accurately represent the effect of salinity on the SWCC. Simulations were performed with a water mineralization level of 4 g/L as an input condition to investigate its impact mechanism on the SWCC.

3.3.3. Evaluation and Analysis

The predictive performance of the optimized VG model was comprehensively evaluated against the traditional model using two standard metrics. A comparative analysis was conducted between the measured data from soil column infiltration experiments and the simulations generated by both models. This comparison allowed for a clear assessment of their respective strengths and weaknesses in capturing soil moisture dynamics. The combined application of these metrics provided a multidimensional evaluation of model performance. The quantitative results of this evaluation are summarized in

Table 10. Evaluation Results of the Two Models.

Number		Upper Layer			Middle Layer			Lower Layer
		RMSE	R2	MAE	RMSE	R2	MAE	RMSE	R2	MAE
M1	Unoptimized	4.81	0.63	3.15	7.16	0.78	3.59	2.63	0.98	1.55
	Optimized	4.16	0.72	2.29	4.04	0.93	2.16	2.53	0.98	1.65
M2	Unoptimized	6.93	0.78	5.16	8.97	0.86	7.41	4.23	0.93	3.17
	Optimized	5.98	0.83	3.08	6.60	0.92	4.68	3.71	0.94	3.11
M3	Unoptimized	6.76	0.76	2.78	7.69	0.83	4.84	3.98	0.95	1.53
	Optimized	6.72	0.76	3.50	4.51	0.94	3.26	3.19	0.97	1.59

. Figure 18, Figure 19 and Figure 20 visually compare the simulated outcomes from the traditional model, the optimized model, and the experimental monitoring data for the three soil types (M1, M2, M3), respectively.

Simulation results demonstrate that the optimized model more accurately captures soil water dynamics under high mineralization conditions. At a mineralization level of 4 g/L, the model exhibits a clear advantage: it precisely tracks the variation in volumetric water content across different soil depths in silty sand (M1), silt soil (M2), and sandy loam (M3), while also delineating the wetting front progression. For instance, in silty sand, the model accurately predicted the wetting front advance velocity, showing high consistency with observed data. In sandy loam, it achieved minimal error in simulating water content. This enhanced accuracy provides robust support for investigating soil water dynamics in saline environments and offers a more reliable basis for practical water management decisions.

A comparative evaluation of the two models across three distinct soil layers (upper, middle, lower) for models M1, M2, and M3 reveals a marked improvement in simulation accuracy offered by the optimized model. The optimized model significantly outperforms the conventional model in the middle and lower layers. Notably, both models exhibited relatively poorer performance in the upper layer compared to the middle and lower layers, likely due to the more porous, heterogeneous structure of the upper soil, which presents greater simulation challenges.

Meanwhile, with reference to Figure 21, the data points from the optimized model simulations and the experimental measurements are distributed closer to the y = x line than those from the traditional model simulations. This indicates that the optimized VG model, which accounts for the influence of salinity, provides more accurate predictions and demonstrates a significant improvement over the traditional approach.

The findings of this study demonstrate that the optimized VG model outperformed the traditional model in simulating the soil water characteristic curves at the Yingjisha County sites (M1, M2, M3). The integration of key influencing factors, particularly water mineralization level, substantially improved the model’s reliability in characterizing soil water infiltration dynamics. This enhancement resulted in greater adaptability across varied soil textures and profile depths, thereby providing valuable insights for future model selection and optimization. The results underscore the necessity of aligning model capabilities with specific dataset characteristics to maximize predictive accuracy.

3.3.4. Research Limitations and Future Prospects

Despite achieving its intended results, this study has several limitations. Nevertheless, these limitations highlight valuable directions for future research improvements and developments.

1.

Limitations in the salinity level validation range

This study is subject to limitations in the coverage of validated salinity levels. Owing to constraints in experimental conditions and duration, the salinity gradient tested may not fully represent the full spectrum of salinity variations found in natural environments—particularly in extreme or complex transitional zones. The research concentrated mainly on the low-to-medium salinity range common in agricultural irrigation contexts, whereas validation under highly saline conditions remains limited. This narrow gradient could compromise the universal applicability and predictive accuracy of the modified VG model when applied to a broader range of salinities. Moreover, the validation was performed primarily under controlled laboratory conditions, with insufficient integration of field observations across varying spatiotemporal scales. The absence of real-world, multi-scenario field data implies that the robustness of the current findings—when exposed to complex environmental factors such as temperature fluctuations, pressure changes, suspended particles, and biological activity—requires further verification. To address these constraints, subsequent research will emphasize validating the method across a wider salinity range. Specifically, we intend to methodically expand the salinity gradient by including extreme salinity conditions in experimental designs. In addition, field-based validation will be enhanced through the establishment of monitoring stations in diverse natural water bodies, enabling the collection of long-term, continuous in situ data. This strategy will allow a thorough assessment and improvement of the method’s accuracy and reliability in practical applications.

2.

Limitations in the theoretical foundation of the model

A limitation of this study concerns the theoretical foundation of the core model employed. As is prevalent in this field, the current work—alongside most existing studies—relies substantially on empirical or semi-empirical formulations, such as the VG model. While these models exhibit satisfactory fitting performance and practical utility under specific conditions, their parameters often lack explicit physical mechanistic interpretations. In essence, they constitute mathematical descriptions of macroscopic phenomena and are thus limited in their ability to uncover the underlying microscopic physical mechanisms and mathematical essence governing processes such as water and salt transport. This reflects a phase-specific constraint in the current state of academic development. Consequently, the depth of mechanistic insight offered in this study remains somewhat limited, and the model’s extrapolation and predictive capability may be compromised when applied to entirely novel scenarios. Nevertheless, acknowledging this limitation does not diminish the value of the present study; rather, it helps to delineate a pathway for further theoretical development. Future work should seek to construct theoretical models with stronger physical foundations, derived from more fundamental microscopic physical processes and mathematical principles. For instance, integrating approaches such as pore-network modeling and molecular dynamics simulations could provide a more fundamental understanding of the migration and transformation mechanisms of salts in complex porous media, thereby facilitating a shift from empirical summarization toward theoretical prediction.

4. Conclusions

Focusing on loam soils from a typical irrigated area in Yingjisha County, southern Xinjiang, this study examined the soil water characteristic curves of three soil textures under different irrigation water mineralization levels through field investigation, sampling, and the centrifuge method. The following conclusions were reached:

1.

Soil physical properties were identified as the dominant factors governing soil water retention capacity. Grey correlation analysis revealed that the influencing factors on the SWCC followed this decreasing order of association: soil dry bulk density > clay content > inorganic salt content > silt content. Soils with higher clay and silt contents, along with greater bulk density, exhibited reduced macropores but enhanced capillary suction, leading to significantly improved water retention capacity and a consequently flattened SWCC.

2.

Irrigation water mineralization demonstrated a non-linear, threshold-dependent influence on water retention. Initially, increasing the total salt content enhanced the soil’s water absorption capacity. However, this relationship was non-monotonic. Beyond a mineralization degree of 1 g L⁻¹, the rate of enhancement in water retention capacity slowed considerably, and the overall water retention performance began to decline.

3.

A comprehensive evaluation of the fitting efficacy and predictive performance of conventional models was performed. Results indicated that the VG model achieved the best fit for loam soils in the characteristic irrigated areas of Southern Xinjiang, although certain deviations persisted, underscoring the necessity for further model refinement.

4.

A modified VG model incorporating irrigation water mineralization as a key parameter was subsequently developed. Validation experiments confirmed that the modified model substantially improved predictive capabilities. In primary application scenarios (middle-layer soil of the M1 and M3), it reduced the RMSE by over 40% and increased the coefficient of determination (R²) by more than 13%, demonstrating a decisive enhancement in fitting accuracy.