Abstract
Environmental air anomaly detection is crucial for ensuring the healthy growth of livestock in smart pig farming systems. This study focuses on four key environmental variables within pig housing: temperature, relative humidity, carbon dioxide concentration, and ammonia concentration. Based on these variables, it proposes a novel encoder–decoder architecture for anomaly detection based on continuous-time models. The proposed framework consists of two embedding layers: an encoder module built around a continuous-time neural network, and a decoder composed of multilayer perceptrons. The model is trained in a self-supervised manner and optimized using a reconstruction-based loss function. Extensive experiments are conducted on a multivariate multi-sequence dataset collected from real-world pig farming environments. Experimental results show that the proposed architecture significantly outperforms existing transformer-based methods, achieving 92.39% accuracy, 92.08% precision, 85.84% recall, and an F1 score of 88.19%. These findings highlight the practical value of accurate anomaly detection in smart farming systems; timely identification of environmental irregularities enables proactive intervention, reduces animal stress, minimizes disease risk, and ultimately improves the sustainability and productivity of livestock operations.
1. Introduction
The rapid growth of the global population and the acceleration of urbanization have elevated the importance of livestock production to unprecedented levels. As a primary source of dietary protein, the livestock industry not only ensures food security but also revitalizes rural economies and contributes significantly to national economic development. However, traditional livestock management practices rely heavily on human experience; as such, they face limitations in simultaneously addressing the complex demands of improving productivity, enhancing animal welfare, and achieving environmental sustainability. In response to these challenges the data-driven management paradigm of precision livestock farming (PLF) has emerged as a critical framework for advancing sustainable livestock production [1,2].
PLF integrates a variety of sensors and IoT-based infrastructure to monitor the physiological status of individual animals and environmental conditions in real time while optimizing management strategies through data analysis. By comprehensively tracking key environmental variables such as temperature (T), relative humidity (RH), ammonia (NH3), and carbon dioxide (CO2) along with physiological indicators such as feed intake [3], activity levels [4], and body temperature [5], PLF aims to enhance both productivity and animal welfare. Notably, the convergence of sensor technologies and machine learning has played a pivotal role in enabling real-time processing of large-scale time series data and the quantitative evaluation of dynamic changes in environmental and physiological conditions [6,7,8,9,10,11,12,13,14].
Although sensor data collected in PLF systems are essential for decision-making, these data often contain anomalies that are not mere errors but rather meaningful signals with the potential to affect animal health and productivity. External factors such as sudden weather changes, equipment degradation, power supply instability, and fluctuations in stocking density can trigger abrupt environmental changes, posing significant threats to animal welfare. For instance, ventilation system failures or sensor malfunctions that cause sudden shifts in temperature or gas concentration may result in respiratory diseases [15] or impaired growth due to reduced feed intake [16]. Thus, anomalies should be considered early warning indicators that demand prompt attention, and their timely detection is essential for ensuring the operational reliability and sustainability of PLF systems.
Early research on anomaly detection was primarily reliant on statistical methods. Techniques such as Z-score analysis [17], interquartile range (IQR) analysis [18], autoregressive integrated moving average (ARIMA) models [19], and linear regression [20] have been used to identify outliers or anomalies based on deviations from normal variable ranges or prediction errors. While these approaches are easy to implement and effective for small-scale datasets, they fall short of capturing the complexity and multivariate dependencies inherent in real-world time series data. In particular, their underlying assumptions such as linearity and stationarity are frequently violated in agricultural datasets, making it difficult to cope with irregular sampling, sensor noise, and long-term dependencies.
To address these limitations, deep learning-based methods for anomaly detection have gained increasing attention. Autoformer [21] introduces a novel transformer-based architecture tailored for long-term time series forecasting, addressing limitations in conventional attention mechanisms. By embedding a progressive series decomposition and replacing standard self-attention with an auto-correlation mechanism, Autoformer effectively models both trend and seasonal components. TimesNet [22] represents a paradigm shift by reinterpreting time series modeling in two dimensions. It converts one-dimensional time series data into two-dimensional tensors in order to decouple intra-period and inter-period variations, allowing for the use of efficient 2D convolutional structures. With its novel TimesBlock architecture, TimesNet achieves state-of-the-art (SOTA) performance in forecasting, classification, anomaly detection, and imputation tasks. Zeng et al. [23] critically examined the rapid adoption of transformer-based models in time series forecasting, arguing that many empirical results are biased due to flawed experimental protocols. Their comprehensive evaluation revealed that transformers do not consistently outperform simpler baselines, underscoring the need to re-examine benchmarking standards and design choices in this domain.
Applying these advanced anomaly detection techniques to PLF, Guo et al. [24] proposed the OTDBO-TCN-GRU model, which integrates the dung beetle optimization algorithm, temporal convolutional networks, and gated recurrent units (GRUs) to predict key environmental parameters in pig houses. This model addresses the low predictive accuracy and limited adaptability of traditional methods, surpassing standard models like Gated Recurrent Units (GRU), Long Short-Term Memory (LSTM), and XGBoost by achieving a mean absolute error of 0.0474, mean squared error of 0.0039, and correlation coefficient of 0.9871. Rong et al. [25] developed an IoT-based environmental monitoring and evaluation system for pig houses. Their approach utilizes median and Kalman filtering for data fusion along with a hybrid weight calculation approach for constructing evaluation indices. This system was shown to significantly improve monitoring accuracy for more precise environmental assessment and control, reducing the temperature error to just 0.12% after Kalman filtering. Park et al. [26] presented a deep learning-based anomaly detection framework for livestock farm equipment that uses optimized recurrent neural networks to monitor and predict equipment malfunctions in real time. Their method detected 93% of artificially induced anomalies, resulting in improved equipment reliability and reduced operational risks. Peng et al. [27] evaluated and compared three traditional machine learning algorithms and three deep learning models for predicting ammonia concentration in pig houses, identifying LSTM and RNN as the most effective after optimization using particle swarm optimization. The PSO-LSTM and PSO-RNN models achieved R2 values of 0.9487 and 0.9458, respectively, demonstrating strong performance in forecasting ammonia levels up to two hours in advance. Jin et al. [28] proposed an improved intelligent control system for regulating temperature and humidity by integrating machine learning with fuzzy control algorithms. Their experimental results showed a 90% reduction in abnormal environmental conditions compared to traditional threshold-based systems. Lastly, Li et al. [29] developed an intelligent control system based on an enhanced three-way K-means clustering algorithm that dynamically allocates control strategies based on real-time environmental data. Compared with natural ventilation and conventional threshold-based methods, their system increased the minimum indoor temperature by 4 °C, decreased the maximum temperature by 8 °C, and reduced the average air humidity from 73.4% to 68.2%, allowing for significantly enhanced environmental stability in pig houses.
Nevertheless, most transformer-based and GRU-based models assume synchronous sampling intervals, which limits their applicability in real-world PLF settings where sensor data are often collected asynchronously and are prone to missing values. Although recent studies have introduced techniques such as time interval embeddings and continuous-time representations, these strategies have yet to fully resolve the challenges posed by temporal irregularities and distortions introduced during preprocessing. Consequently, there is growing interest in modeling paradigms that inherently accommodate the continuous nature of time. In this context, several continuous-time neural network models have recently emerged. The neural ordinary differential equations (Neural ODEs) [30] model hidden state evolution as a continuous-time dynamical system parameterized by neural networks. This allows for flexible representation of complex temporal patterns, particularly in domains with irregular sampling. However, Neural ODEs often suffer from training instability, high computational cost, and sensitivity to numerical solver configurations, limiting their scalability in large-scale or real-time applications. Another related approach involves time-aware recurrent neural networks such as time-aware LSTM (T-LSTM) [31], which incorporate elapsed time intervals into the gating mechanisms of recurrent models. While these models are effective in handling missing values and irregular intervals, they remain fundamentally discrete in nature and may fail to fully capture fine-grained continuous dynamics.
In contrast, newly proposed continuous-time neural architectures such as the liquid time-constant (LTC) model [32] and closed-form continuous-time (CfC) model [33] offer fundamentally different approaches to time series modeling. The CfC model solves ordinary differential equations analytically, enabling exact continuous-time state transitions, while the LTC model dynamically adjusts its neuronal time constants in response to inputs, mimicking the behavior of biological neurons. These formulations provide several advantages over traditional deep RNNs and transformers, including improved parameter efficiency, more stable gradient behavior, and faster convergence. In particular, the closed-form parameterization of CfC offers notable benefits for large-scale and densely-sampled multivariate environmental data such as those found in pig farming thanks to reduced computational overhead and enhanced training robustness. Unlike conventional discrete-time models, these architectures inherently encode elapsed time, allowing them to support more accurate and efficient pattern recognition and anomaly detection in complex agricultural environments.
Based on these insights, in this study we introduce continuous-time neural networks for anomaly detection in pig farm environmental data. Specifically, we propose an encoder–decoder architecture in which the CfC model serves as the core component of the encoder. Environmental data are first processed by an embedding module comprising token and positional embedding layers. The resulting features are then passed through the CfC model to generate continuous-time state updates, which are subsequently projected back to the input space. Given the challenges of obtaining labeled anomalies, the proposed architecture is trained in a self-supervised manner using reconstruction-based loss functions to guide gradient updates. To evaluate the effectiveness of the proposed method, we conduct a comparative study against five SOTA anomaly detection models. Experimental results demonstrate that our approach consistently outperforms these baselines on multi-sequence multivariate time series datasets, achieving superior performance in terms of accuracy, precision, recall, and F1 score. These findings confirm the effectiveness and generalizability of the proposed continuous-time architecture in livestock anomaly detection tasks.
The main contributions of this work are summarized as follows:
- We introduce a novel paradigm of continuous-time neural networks for anomaly detection in pig farming environments. Unlike existing methods, the proposed continuous-time models demonstrate strong ability to capture complex temporal dependencies in multi-sequence multivariate time series data.
- We propose an encoder–decoder architecture based on continuous-time neural networks and adopt an unsupervised learning strategy, enabling end-to-end anomaly detection without the need for labeled data.
- Extensive experiments show that the proposed method consistently outperforms SOTA baseline models in terms of anomaly detection performance, highlighting its robustness and practical applicability in livestock monitoring scenarios.
The remainder of this paper is organized as follows. Section 2 introduces the dataset and preprocessing procedures, followed by a detailed description of the proposed architecture and experimental setup. Section 3 presents the experimental results and comparative analysis with baseline models. Section 4 discusses the limitations of the study and outlines directions for future research. Finally, Section 5 concludes the paper with a summary of the key findings.
2. Materials and Methods
2.1. Dataset
The dataset used in this study was collected from a commercial pig farm located at 121 Dalguji-gil, Jingyo-myeon, Hadong-gun, Gyeongsangnam-do, Korea (35.0671° N, 127.7500° E) as part of the Pork Bioenergy Data project supported by the Industry-Academic Cooperation Group of Jeonbuk National University and available through the Korea AI Hub platform. All monitoring sites were situated within four distinct pig pens on the same farm rather than across geographically separate regions. Each pen housed approximately 50 pigs during the growing-finishing phase, with animal ages ranging from 150 to 180 days. The housing structures were identical across all pens, each measuring 12 m in length, 2.3 m in width, and 2.4 m in height. To ensure a stable internal environment, each pen was equipped with a heating system and ventilation fans, and daily cleaning procedures were performed to maintain sanitation. The roofs were constructed from fiber-reinforced plastic, and all pens shared a north–south orientation. Stocking density and climate control systems were consistent across all pens to standardize environmental conditions.
Environmental data were collected using integrated sensor modules mounted on the wall of each pig pen at a height of 0.5 m above the floor. Each module consisted of an SHT31 or SHT35 (Sensirion, Sensirion AG, Stäfa, Switzerland) sensor for temperature and relative humidity, an MH-Z19C (Winsen, Winsen Electronics Technology Co., Ltd., ZhengZhou, China) sensor for CO2 concentration, and an MICS-6814 sensor for NH3 concentration. One such module was installed in each pig pen, with all environmental parameters measured at the same spatial location. Data were continuously recorded at 5-min intervals from 1 August 2023 to 31 May 2024, yielding 87,840 time series samples per variable. To facilitate the analysis of daily trends, the raw data were averaged over every 288 samples (equivalent to one day), as illustrated in Figure 1. The top row of the figure presents official meteorological data obtained from the Korea Meteorological Administration for the farm’s location. The left panel displays the daily maximum, minimum, and average air temperatures, while the right panel shows the corresponding daily average relative humidity and precipitation levels. These data indicate substantial seasonal variation, with outdoor temperatures ranging from −5 °C to over 35 °C and relative humidity fluctuating between 60% and 90%, often accompanied by episodic rainfall events. In contrast, the middle row of the figure illustrates the measured environmental conditions inside the pig pens. Due to active climate control (heating and ventilation), the daily average indoor temperature remained relatively stable, typically ranging from 25 °C to 27 °C. Similarly, indoor relative humidity was maintained within a narrower and lower range of approximately 25% to 40%, despite the pronounced variability in outdoor conditions. The bottom row of the figure shows the trends in CO2 and NH3 concentrations. Daily mean CO2 levels within the pens generally ranged from 600 to 1000 ppm, while NH3 concentrations were typically maintained between 10 and 12 ppm, with occasional spikes. These values are consistent with expected concentrations in intensively managed livestock housing, and are significantly higher than ambient outdoor levels. Overall, Figure 1 highlights the stark contrast between external climatic variability and the controlled indoor environment maintained for livestock. While outdoor conditions are subject to substantial seasonal and meteorological fluctuations, the indoor microclimate is actively regulated to remain within a stable and optimal range in order to ensure animal health and productivity. This divergence underscores the importance of direct environmental monitoring within livestock facilities to accurately assess animal welfare and the environmental conditions to which animals are exposed.
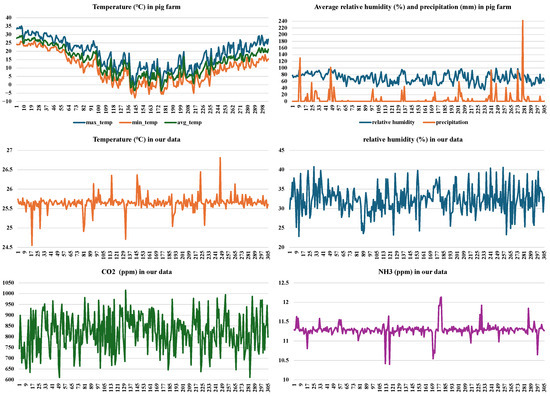
Figure 1.
Visualization of climate information of the pig farm and the dataset. The two graphs in the first row indicate the temperature, relative humidity, and precipitation during data collection, while the other graphs show the daily trends of each environmental variable.
For the purpose of training and evaluating the proposed anomaly detection model, the dataset was partitioned into 52,416 samples for training, 17,280 samples for validation, and 18,144 samples for testing. Descriptive statistics for each environmental variable are presented in Table 1. To structure the input for time series modeling, a sliding window approach was employed to segment the continuous data streams into fixed-length subsequences. For the training set, a window size of 288 and stride of 1 were used, resulting in a large number of overlapping subsequences. This dense segmentation is beneficial in the context of unsupervised learning, where using more data enhances the model’s ability to learn robust feature representations. In contrast, for the validation and test sets, the window size and stride were set to the same value in order to produce non-overlapping subsequences, which ensures that each segment represents a distinct time period and avoids information leakage. Each subsequence is represented as a two-dimensional matrix, with the first dimension corresponding to the sequence length (i.e., number of time steps) and the second encoding the region ID along with the four environmental variables. The training data were used in an entirely unsupervised manner without any labels, while the validation and test sets were annotated with point-level binary anomaly labels to enable performance evaluation. These anomaly annotations were generated through a two-step process. First, a set of classical machine learning-based anomaly detection algorithms (local outlier factor, Z-score analysis, interquartile range (IQR), and one-class support vector machine) was applied to produce candidate anomaly labels. The union of the results from all methods was then taken in order to maximize the coverage of potential anomalous events. Second, manual inspection was conducted to refine the candidate labels by removing unreasonable or inaccurate detections, thereby enhancing the reliability and validity of the final anomaly annotations.

Table 1.
Detailed information of the dataset used in this study. Each sample has four environmental measurements: temperature, relative humidity, carbon dioxide, and ammonia.
2.2. Methods
The overall framework of the proposed method is illustrated in Figure 2. It primarily consists of three modules: data embedding, encoding, and decoding. The data embedding module comprises two components, namely, token embedding and positional embedding. Token embedding projects the raw numerical inputs into a high-dimensional feature space of dimension D, while positional embedding encodes the temporal positions of elements within the input sequence, allowing the model to capture positional dependencies and sequence ordering. The encoder module is constructed using a continuous-time neural model with a residual connection, followed by a layer normalization step. The continuous-time model is capable of learning the intrinsic dynamics of environmental variables and capturing time-dependent abnormal changes, thereby generating informative state feature representations. The decoder module takes these state feature maps as input and projects them back into the original input space. Because the model is trained under an unsupervised learning paradigm, the decoder is optimized to reconstruct the input sequences as accurately as possible. A reconstruction loss function is employed to guide the training process, encouraging the model to learn meaningful representations that effectively capture both normal patterns and potential anomalies.
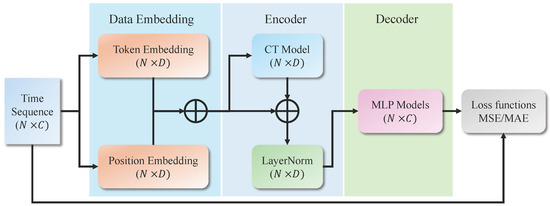
Figure 2.
Overview of the proposed method, which mainly contains three modules: the data embedding module, encoder, and decoder. The data embedding module consists of two parts: token embedding, which maps numerical inputs into the high-dimension feature space, and position embedding, which extracts the positional relationships between input sequences. The encoder module is composed of a continuous-time model, denoted in the figure as CT Model, and a layer normalization step, denoted as LayerNorm. The decoder module is composed of a series of linear layers that reconstruct the hidden states into the input space.
2.2.1. Continuous-Time Model
Modeling temporal dynamics is a fundamental challenge in time series learning. Traditional recurrent neural networks (RNNs), including LSTM and GRU varieties, process sequential data at discrete and fixed time intervals, which limits their ability to model continuous-time dynamics and handle irregularly sampled sequences. In contrast, continuous-time models represent hidden state evolution as a function of time governed by differential equations, offering a more natural and principled framework for capturing real-world temporal processes that unfold continuously and often asynchronously. Compared to traditional RNNs, continuous-time models provide three key advantages: time resolution independence, allowing for flexible handling of variable and irregular time intervals; physically grounded dynamics, making them particularly suitable for domains such as neuroscience or physics-informed modeling; and improved interpretability thanks to their explicit modeling of temporal decay and integration. Two prominent continuous-time neural models have recently been proposed: the liquid time-constant (LTC) network [32], and the closed-form continuous-time (CfC) model [33]. The LTC model simulates neural state evolution using first-order ordinary differential equations (ODEs) approximated via numerical integration. Its formulation is shown in Equation (1):
where is the function of the model, is the input at time step t, and A, , and are learnable parameters. This formulation enables neurons to dynamically adapt their temporal responsiveness, closely mimicking biological time constants. However, LTC is sensitive to numerical instability and incurs increased computational cost, as it requires small integration steps in order to maintain accuracy. To address these limitations, the CfC model introduces a more stable and analytically tractable alternative. It replaces numerical integration with a closed-form solution of the state evolution, assuming piecewise-constant inputs between time points, as shown in Equation (2):
where is a gating factor that is similar to the forgetting mechanism in LSTM model, , , and are learnable parameters, and , , and are three neural network functions. produces gating factors, controlling the the degree of time reliability, while and represent two different ways of updating the state. This elegant formulation provides several significant advantages, including numerical stability by eliminating discretization errors, computational efficiency due to the absence of fine-grained numerical integration, and theoretical clarity through alignment with the analytical behavior of first-order linear systems.
In addition to LTC and CfC, neural ordinary differential equations (neural ODEs) [30] constitute another influential family of continuous-time models. Neural ODEs parameterize the time derivative of the hidden state using a neural network, and estimate the state trajectory by numerically solving the ODE in both the forward and backward passes. While highly flexible and expressive, neural ODEs often suffer from increased computational complexity and training instability due to their reliance on adaptive solvers, which is particularly the case for stiff systems or long prediction horizons. In contrast, the CfC model expresses state transitions via closed-form equations. This offers both theoretical and practical benefits, especially for large-scale long-horizon multivariate time series data such as environmental monitoring data. First, CfC allows for stable and efficient gradient computation through direct backpropagation, eliminating the instability and overhead introduced by adaptive solvers. Second, its constant computational complexity per time step makes it well-suited for real-time and resource-constrained applications, regardless of the underlying system’s stiffness or sampling interval. Third, CfC maintains sufficient expressive power to capture the relatively smooth and continuous dynamics that characterize environmental data while also enhancing model interpretability and robustness. Notably, the closed-form and piecewise-analytical structure of CfC makes each hidden state update transparent and interpretable. The parameters and gating mechanisms directly influence state evolution, facilitating insights into temporal dependencies and system behavior. In contrast, neural ODEs operate as black-box neural networks coupled with numerical solvers. As a result, they offer limited interpretability, particularly in long-term forecasting or safety-critical applications. Furthermore, CfC is inherently suited for irregularly sampled sequences, as it computes state transitions analytically over arbitrary time intervals without requiring resampling or interpolation. While neural ODEs can in principle handle irregular sampling, they rely on adaptive-step solvers, which may be prone to numerical instability and elevated computational cost when processing highly irregular data or stiff systems. By decoupling temporal adaptation from solver dynamics, CfC enables stable, efficient, and interpretable modeling for real-world time series tasks involving asynchronous or sparse observations.
In the context of environmental anomaly detection on pig farms, continuous-time models such as CfC offer substantial advantages over both RNN-based and neural ODE-based approaches. Monitoring environmental variables such as temperature, humidity, , and ammonia concentrations requires models that can efficiently and reliably process large-scale and long-duration time series data. Traditional RNN-based models such as LSTM and GRU are susceptible to vanishing gradients and incur high computational costs on long sequences, limiting both detection performance and deployment scalability. Although offering greater modeling flexibility, neural ODEs often require computationally intensive numerical solvers, resulting in slower training and inference. In contrast, CfC provides closed-form state updates, enabling stable gradient computation, faster convergence, and fixed computational cost per time step. These properties lead to notable improvements in training efficiency, robustness, and deployment feasibility. As a result, CfC is particularly well suited for real-time anomaly detection in livestock farming environments, where accurate, scalable, and resource-efficient processing of environmental time series data is essential.
2.2.2. Unsupervised Anomaly Detection
This study performs anomaly detection on environmental variables in pig farms using an unsupervised learning paradigm. Specifically, the input time sequence is denoted as , where N represents the sliding window size (set to 288) and C denotes the number of channels, which includes four environmental variables (temperature, relative humidity, , and ) along with a region identifier. The input sequence is first processed by a token embedding layer and a position embedding layer, which together map scalar values into a high-dimensional feature space and encode the positional relationships between time steps. This embedding process is defined in Equation (3), where the resulting feature representation is :
The continuous-time model then takes the embedding as input and generates output features along with hidden states. The computation process is similar to that of LSTM, but only the output features are used for residual connections. Taking the CfC model as an example, the output feature (of shape ) is computed as follows:
Finally, the output features are passed through a decoder consisting of three multilayer perceptrons and two activation functions in order to reconstruct the original time sequence . The reconstruction process is formulated as follows:
This self-supervised learning framework enables the model to effectively capture both the local temporal patterns and global trends of the time series without requiring labeled data.
During inference, anomalies are identified by comparing the reconstruction error of each point with a predefined threshold. Through self-supervised training, the model learns to perceive temporal dependencies (i.e., logical continuity in time), short-term regularities (local patterns), and long-term tendencies (global trends). Any point with a reconstruction error exceeding the threshold is classified as an anomalous data point. The deviation of such points from the learned representation indicates that they lie outside the typical distribution of the feature space, meaning that they can be classified as outliers.
2.2.3. Loss Functions
The output of the model consists of reconstructed time sequences, making the task inherently a regression problem. To optimize model training, we employ a combination of the mean squared error (MSE) and mean absolute error (MAE) as the loss function. The MSE is more sensitive to large deviations and penalizes larger errors more heavily, thereby encouraging the model to correct significant anomalies. In contrast, the MAE promotes robustness and leads to more stable reconstructions by treating all errors equally. To leverage the strengths of both metrics, we combine them using a weighting factor , as defined in Equation (6):
3. Experiments
3.1. Experimental Setup
The proposed method was implemented using PyTorch 2.0.0 with Python 3.10. The embedding dimension D for both the token and positional embedding modules was set to 256 and the hidden size of the CfC model was configured to 512. The window size N was fixed at 288, corresponding to a 24-h period, and the stride was set to 1 for the training dataset and 288 for both the validation and test datasets. The choice of a 288-point time window is motivated by the temporal characteristics of the environmental data collected from pig farms. Given that the sensors recorded data every 5 min, a window of 288 data points spans an entire 24-h cycle. This design enables the model to effectively capture daily periodic patterns in environmental variables, which are commonly influenced by farm management routines and external climatic fluctuations. The model was trained with an initial learning rate of 0.0001 and a batch size of 256. The learning rate was scheduled to decay following a cosine annealing policy over 100 epochs. To prevent overfitting, we applied an early stopping mechanism with the patience value set to 10 epochs. Optimization was performed using the Adam optimizer with the default weight decay parameters. All experiments were conducted on a single NVIDIA RTX 4090 GPU running Ubuntu 22.04.
3.2. Evaluation Metrics
In the context of anomaly detection, each prediction may be classified as true positive (TP), true negative (TN), false positive (FP), or false negative (FN). The common classification metrics of accuracy, precision, recall and score were used to evaluate the proposed method, and are defined as shown below.
These metrics capture different aspects of detector performance: accuracy reflects overall success, but can be misleading in highly imbalanced settings (i.e., where anomalies are rare); precision emphasizes the cost of false alarms; recall emphasizes the cost of missed anomalies; finally, the score offers a single scalar that balances these two error types, making it particularly useful when the anomaly and normal classes are of unequal importance.
3.3. Experimental Results
3.3.1. Comparisons with the SOTA Models
Table 2 presents the anomaly detection performance of six representative methods across the four environmental variables. Each method is evaluated using the four metrics of accuracy, precision, recall, and score. In addition, macro-averaged scores across all variables are reported. The proposed method consistently outperforms all baselines across all evaluation metrics. Specifically, it achieves an average accuracy of 92.39%, precision of 92.08%, recall of 85.84%, and score of 88.19%. TimesNet [22] ranks second overall, but lags behind the proposed method by 13.1% in accuracy, 18.5% in precision, 13.4% in recall, and 15.7% in score. Other well-known architectures for time series anomaly detection such as AutoFormer [21], DLinear [23], and the vanilla transformer model [34] perform noticeably worse, with accuracy ranging between 64–79% and precision from 50–73%. These results indicate that simply increasing model depth or expanding receptive fields in the discrete-time domain is insufficient for fine-grained anomaly detection in highly dynamic and complex environments such as livestock housing.

Table 2.
Performance comparisons between the proposed method and other SOTA methods. The four commonly used metrics are listed in the table for all four variables. Average term indicates the mean value of the four variables, while the best performance is indicated in bold typeface.
A direct comparison within the category of continuous-time models further underscores the advantage of the closed-form formulation. While the LTC model [32] already outperforms AutoFormer and DLinear in terms of score, replacing LTC with the CfC model yields an additional gain of 19.4% in accuracy and 26.6% in score. We attribute this improvement to two main factors: first, the analytical solution of CfC enables stable gradient propagation, effectively mitigating issues related to numerical stiffness and allowing precise modeling of subsample temporal dynamics; second, the CfC model employs three distinct neural network functions, which enhances its expressive power and enables more accurate learning of the underlying temporal patterns in environmental time series data.
A variable-wise performance analysis provides further insights. For relative humidity, most models exhibit significant drops in precision, with values ranging from 23.94% to 70.5%, whereas the CfC model maintains a high precision of 91.32%, demonstrating superior robustness to sensor fluctuations. On the variable, our model achieves the highest score of 86.90%, outperforming TimesNet by a margin of 21.2%. Furthermore, the CfC model attains a recall of 96.94% for , highlighting its strong ability to avoid false negatives; this is a particularly critical feature for early warning systems in livestock welfare management. These results provide strong empirical support for the theoretical motivation behind adopting continuous-time modeling for anomaly detection in livestock farm environments. By respecting the differential nature of temporal data streams, the CfC model enhances decision boundaries (as evidenced by its high precision) while simultaneously expanding coverage of abnormal patterns (reflected in high recall), thereby achieving superior performance across all evaluation metrics.
To further illustrate the effectiveness of the proposed method for multivariate time-series anomaly detection across multiple regions, we visualize the scores for each environmental variable in all four regions, as shown in the left subfigure of Figure 3. The radar plot offers a comprehensive comparison of all models across regions and variables, globally emphasizing the superiority of the proposed approach over existing baselines. As depicted in the figure, our method consistently outperforms all competing models for every variable and region. A more fine-grained analysis reveals that most existing models tend to exhibit lower scores on and RH while performing relatively better on T and . Among the baselines, TimesNet shows the least fluctuation in performance across different variables and regions, suggesting a certain degree of robustness; however, its overall performance remains consistently lower than that of the proposed method. Although our model also exhibits slightly lower scores on and RH compared to T and , it significantly narrows the performance gap compared to other methods. This demonstrates that our approach is more balanced and adaptable in addressing variable-specific and region-specific challenges, validating its effectiveness for the complex task of multivariate anomaly detection in pig farm environments.
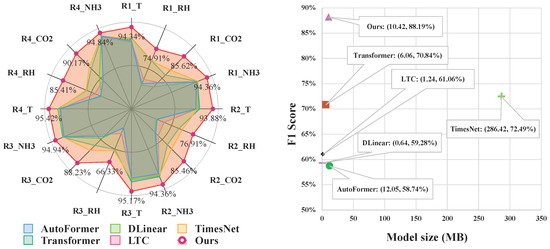
Figure 3.
The left subfigure shows the scores of all models in different regions and variables. Here, R1, R2, R3, and R4 indicate four different regions (pig pens) located in the same pig farm, while T, RH, , and refer to the four environmental variables of temperature, relative humidity, carbon dioxide, and ammonia. AutoFormer, DLinear, TimesNet, and Transformer are four SOTA anomaly detection models, LTC is an anomaly detection method based on a liquid time-constant network, and “Ours” denotes the method proposed in this work. The right subfigure reflects the efficiency of each model, where each bracket contains the score and model size, respectively.
The right subfigure of Figure 3 presents a tradeoff analysis between model size and score across different methods. As shown in the plot, TimesNet has the largest model size at approximately 286 MB. In contrast, all other models maintain a footprint below 12 MB, with DLinear being the most lightweight at only 0.64 MB. Despite being the third-largest model in terms of size, our proposed method achieves the highest score among all competitors. Specifically, our model reduces the parameter size by 276 MB compared to TimesNet while improving the score by 15.7%. When compared to the LTC model, our proposed approach increases model size by only 9.18 MB while yielding a substantial 27.13% improvement in score. These findings indicate that our model achieves an effective balance between model complexity and detection performance. By maintaining a compact architecture without compromising accuracy, the proposed method is particularly well suited for deployment on edge devices in smart farming environments, where computational and memory resources are often constrained.
3.3.2. Performance Analysis by Region
To further assess the effectiveness of the proposed method in multivariate anomaly detection for multi-sequence time series data, Figure 4 visualizes the performance of six representative models across four environmental variables (T, RH, , and ) in each of the four regions. This figure provides a more detailed breakdown of anomaly detection performance, highlighting the multi-sequence and multi-region capability of the proposed method. The visualization allows for a granular evaluation of model robustness and consistency under varying environmental conditions. As illustrated in the figure, our method consistently achieves the highest score for all four variables across every region, significantly outperforming the five baseline models. Although the performance of all six models appears relatively comparable for certain variables across regions, notable disparities emerge for RH and , where several baseline models exhibit substantial drops in detection accuracy. Overall, these results suggest that while all of the evaluated models possess a certain degree of competence in multi-sequence time series anomaly detection, the proposed method demonstrates consistently superior detection performance. Its robustness and strong generalization ability across both spatial dimensions (regions) and feature dimensions (variables) underscore its effectiveness in handling complex and heterogeneous environmental data in real-world livestock farming scenarios.
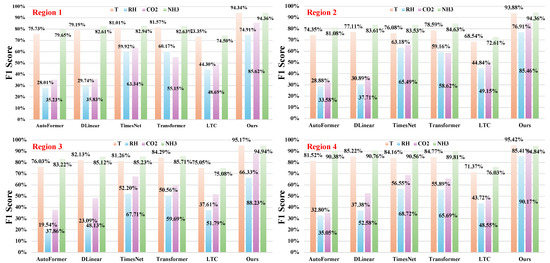
Figure 4.
Comparison of the scores in each region for the four variables. Here, T, RH, , and respectively refer to the four environmental variables of temperature, relative humidity, carbon dioxide, and ammonia; AutoFormer, DLinear, TimesNet, and Transformer are the four SOTA anomaly detection models; LTC is an anomaly detection method based on a liquid time-constant network; and “Ours” denotes the method proposed in this work.
3.3.3. Performance Analysis by Variable
Figure 5 presents a detailed visualization of the scores achieved by the six representative models across the four environmental variables of T, RH, , and in four distinct regions. Overall, the models tend to perform better on T and , while their performance on RH and is relatively lower. This disparity can largely be attributed to the intrinsic characteristics of each environmental variable. Specifically, T and in pig houses typically exhibit clear daily periodic patterns and are more likely to experience abrupt mutation-type anomalies (e.g., due to ventilation failures, heating system malfunctions, or waste accumulation). These pronounced and temporally distinct deviations are easier for data-driven models to detect, resulting in higher scores. In contrast, RH and are influenced by a broader range of interacting and overlapping factors, including animal respiration, ventilation settings, management schedules, and waste removal practices. These influences often vary slightly between pens due to operational differences, leading to smoother fluctuations and gradual drift-type anomalies. The natural variability in these signals tends to blur the distinction between normal and anomalous patterns, increasing both the difficulty of accurate labeling and the complexity of detection.
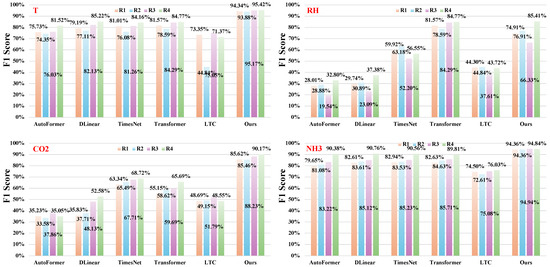
Figure 5.
Comparison of the scores in each regions for the four variables. Here, R1, R2, R3, and R4 indicate four different regions (pig pens) located in the same pig farm; T, RH, , and refer to the four environmental variables of temperature, relative humidity, carbon dioxide, and ammonia; AutoFormer, DLinear, TimesNet, and Transformer are the four SOTA anomaly detection models; LTC is an anomaly detection method based on a liquid time-constant network; and “Ours” denotes the method proposed in this work.
Among the evaluated models, Transformer achieves the highest score on RH, indicating its relatively strong ability to capture dynamic humidity variations. However, the proposed method exhibits only a marginal performance decrease on this variable, while outperforming Transformer on the remaining three environmental variables. Notably, models such as AutoFormer, DLinear, and LTC consistently show inferior performance, particularly on RH and , where scores frequently fall below 50% across all regions. This highlights their limited capacity to capture complex temporal dependencies in multivariate and variable-specific contexts. Overall, the proposed method achieves the highest scores on three out of four environmental variables, reinforcing its effectiveness for multivariate anomaly detection. These results underscore the proposed model’s superior generalization capability across both spatial regions and variable types, establishing it as a promising candidate for real-world deployment in complex environmental monitoring applications.
3.4. Ablation Studies
3.4.1. Selection of Loss Functions
In this subsection, we investigate the impact of different values of the weighting parameter in the loss function on the overall performance of the proposed method. The experimental results are visualized in Figure 6. Recall that in Equation (6), setting corresponds to using the pure mean squared error, while results in the pure mean absolute error. As illustrated in the figure, both of these extreme cases yield suboptimal performance, with scores falling below 80%. As increases from 0, the model’s score gradually improves, reaching a peak at , where the model achieves its best performance with an score of 88.19%. Further increases in lead to a gradual decline in performance beyond this point. These findings indicate that a balanced combination of MSE and MAE yields the most effective loss formulation for this reconstruction-based anomaly detection task. Their combination leverages the sensitivity of MSE to large deviations along with the robustness of MAE to outliers, providing a more comprehensive learning signal. Therefore, in all subsequent experiments we set the loss weight parameter to to achieve optimal accuracy and generalization capability.
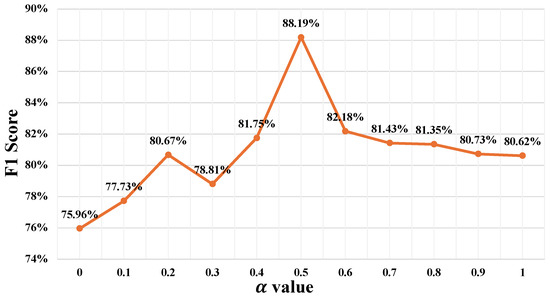
Figure 6.
scores of the proposed method with different weight values.
3.4.2. Threshold Selection
In this study, anomaly points are identified based on reconstruction errors; any data point with a reconstruction loss that exceeds a predefined threshold is classified as being anomalous. Consequently, the selection of an appropriate threshold is critical to the overall effectiveness of the anomaly detection system. For multivariate time series data, two commonly adopted thresholding strategies are considered: (1) a separate-threshold strategy that assigns an individual threshold to each variable; and (2) a unified-threshold strategy that applies a single global threshold across all variables. In the separate-threshold strategy, each variable is assigned its own threshold value, which is automatically determined based on the estimated anomaly ratio for that variable. Specifically, the threshold is calculated as twice the estimated anomaly ratio, following an empirical rule widely used in the prior time series anomaly detection literature. This approach aims to ensure adequate sensitivity to true anomalies while minimizing false positives. Because it is data-driven, this threshold more accurately reflects the variable-specific distribution of reconstruction errors and anomaly characteristics. The final set of threshold values used in this study is reported in Table 3, representing the direct output of this automatic calculation procedure. No additional manual tuning was applied, as these values are inherently adapted to the statistical properties of each variable. In contrast, the unified-threshold strategy applies a single threshold uniformly across all variables. To evaluate this approach, multiple candidate threshold values were systematically tested to examine the model’s sensitivity to different global settings. As shown in Table 3, the separate-threshold strategy achieves the highest score of 88.19%, significantly outperforming the unified strategy, which yields consistently lower results across all tested values. These findings underscore the importance of adopting variable-specific thresholding in multivariate anomaly detection tasks. By tailoring the decision boundary to the unique error distributions and anomaly dynamics of each environmental variable, the separate-threshold strategy enables more accurate and robust anomaly identification in complex monitoring scenarios.

Table 3.
scores of the proposed method with different threshold values.
4. Limitations and Future Work
4.1. Limitations
While the experimental results validate the effectiveness of the proposed method, several limitations should be acknowledged to guide future research and practical deployment. First, the model exhibits relatively lower anomaly detection performance for relative humidity and carbon dioxide compared to temperature and ammonia. This discrepancy may be attributed to the lower signal-to-noise ratio and greater inherent variability in RH and time series, which can obscure clear distinctions between normal and anomalous patterns. In the current study, a unified modeling framework was applied uniformly to all variables without accounting for their distinct statistical characteristics. To address this limitation, future work could explore adaptive strategies such as variable-aware architectures or hybrid models that combine data-driven learning with physics-informed constraints. Such enhancements could further improve detection robustness, particularly for complex and highly dynamic variables such as RH and .
Second, while this study focused on accurate anomaly detection, the post-detection response mechanism remains an open challenge. In practical settings, one promising approach is to implement an early warning accumulation system whereby repeated or consecutive anomalies within a defined time window (e.g., five occurrences) trigger alerts for manual inspection of the affected pig pen. This strategy balances sensitivity and specificity by minimizing false alarms caused by transient fluctuations while also ensuring that persistent or critical anomalies are promptly addressed. Although the current model does not explicitly classify the type or cause of each anomaly, the different environmental variables involved can offer valuable diagnostic insights. For instance, anomalies in temperature and humidity may indicate malfunctions in heating, ventilation, or air conditioning (HVAC) systems; elevated concentrations may suggest issues with waste management or inadequate ventilation; and anomalies may point to insufficient airflow or space congestion problems. In cases where multiple variables simultaneously exhibit anomalies, a comprehensive inspection of environmental control systems may be necessary in order to identify and mitigate underlying systemic failures.
4.2. Future Work
While the present study demonstrates the effectiveness of the proposed approach in a real-world pig farming environment, several directions remain open for future research to enhance the model’s generalizability and practical applicability. First, the current experiments were conducted using data from a single farm in one geographic region. To evaluate the broader applicability of the proposed method, future work should examine its transferability across farms with diverse environmental conditions, management practices, and operational procedures. The model’s design, including closed-form continuous-time networks, multivariate feature learning, and self-supervised training, provides inherent generalization capacity by minimizing reliance on farm-specific data patterns or expert-defined rules; nonetheless, real-world deployment may still face distributional shifts arising from local microclimates or heterogeneous farming practices. To address these challenges, future research will explore domain adaptation techniques, meta-learning frameworks, and multi-site joint training strategies to further improve the proposed model’s robustness and adaptability across diverse farming contexts.
Second, practical deployment in livestock farming often necessitates resource-efficient operation on edge devices with limited computational capacity. The proposed model features a compact architecture of approximately 10 MB and a continuous-time formulation, making it well-suited for execution on embedded controllers and industrial gateways. This enables real-time and low-latency anomaly detection without requiring high-end hardware infrastructure. Moreover, the model’s ability to operate across variable sampling intervals ensures resilience to differences in sensor frequency and data acquisition strategies. Future work will focus on further evaluating and optimizing the model’s computational efficiency, scalability, and fault tolerance to ensure reliable performance in resource-constrained real-world livestock monitoring systems.
5. Conclusions
This study proposes a novel encoder–decoder architecture for unsupervised anomaly detection in pig farm environmental data by leveraging the strengths of continuous-time neural networks, specifically the closed-form continuous-time model. Unlike traditional discrete-time models that rely on synchronous sampling, the proposed method inherently supports irregularly sampled and asynchronous multivariate time series data without the need for resampling or interpolation. Extensive experiments conducted on a real-world dataset comprising four key environmental variables (temperature, relative humidity, carbon dioxide, and ammonia) collected from multiple regions within a commercial pig farm demonstrate that our model consistently outperforms several state-of-the-art baselines. Specifically, the proposed model achieves 92.39% accuracy, 92.08% precision, 85.84% recall, and an score of 88.19%. Ablation studies further validate the effectiveness of the loss function design and threshold selection strategy, showing that a balanced reconstruction loss and variable-specific thresholds significantly enhance detection performance. Overall, these findings highlight the practical value of accurate and efficient anomaly detection in smart livestock systems. As precision livestock farming continues to advance, the approach proposed in this paper offers a robust, generalizable, and lightweight solution for real-time environmental monitoring that can support intelligent decision-making and sustainable management in modern pig production.
Author Contributions
H.Z.: conceptualization, methodology, experiments, writing—original draft; S.C.: data curation, methodology, writing—original draft; M.M.W.: data processing, data labeling; M.I.Z.U.A.: data labeling; A.A.: data labeling; M.A.I.: data labeling; H.K.: supervision; S.K.: funding acquisition, project administration, supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education (RS-2019-NR040079) and the Korea Institute of Planning and Evaluation for Technology in Food, Agriculture and Forestry (IPET) through the Agri-Bioindustry Technology Development Program funded by the Ministry of Agriculture, Food and Rural Affairs (MAFRA) (RS-2025-02307882).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The dataset used in this study is from AI Hub in Korea and is not open-source for others.
Acknowledgments
Heng Zhou is a recipient of the China Scholarship Council (CSC) scholarship (CSC number: 202208260011) and expresses the greatest appreciation for support.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PLF | Precision Livestock Farming |
| SOTA | State-Of-The-Art |
| T | Temperature |
| RH | Relative Humidity |
| Carbon Dioxide | |
| Ammonia | |
| LSTM | Long Short-Term Memory |
| GRU | Gated Recurrent Units |
| RNN | Recurrent Neural Network |
| TP | True Positive |
| TN | True Negative |
| FP | False Positive |
| RN | False Negative |
References
- Kleen, J.L.; Guatteo, R. Precision Livestock Farming: What Does It Contain and What Are the Perspectives? Animals 2023, 13, 779. [Google Scholar] [CrossRef] [PubMed]
- Tullo, E.; Finzi, A.; Guarino, M. Review: Environmental impact of livestock farming and Precision Livestock Farming as a mitigation strategy. Sci. Total Environ. 2019, 650, 2751–2760. [Google Scholar] [CrossRef] [PubMed]
- Williams, L.R.; Moore, S.T.; Bishop-Hurley, G.J.; Swain, D.L. A sensor-based solution to monitor grazing cattle drinking behaviour and water intake. Comput. Electron. Agric. 2020, 168, 105141. [Google Scholar] [CrossRef]
- Biszkup, M.; Vásárhelyi, G.; Setiawan, N.N.; Márton, A.; Szentes, S.; Balogh, P.; Babay-Török, B.; Pajor, G.; Drexler, D. Detectability of multi-dimensional movement and behaviour in cattle using sensor data and machine learning algorithms: Study on a Charolais bull. Artif. Intell. Agric. 2024, 14, 86–98. [Google Scholar] [CrossRef]
- Ma, S.; Yao, Q.; Masuda, T.; Higaki, S.; Yoshioka, K.; Arai, S.; Takamatsu, S.; Itoh, T. Development of Noncontact Body Temperature Monitoring and Prediction System for Livestock Cattle. IEEE Sens. J. 2021, 21, 9367–9376. [Google Scholar] [CrossRef]
- Rebez, E.B.; Sejian, V.; Silpa, M.V.; Kalaignazhal, G.; Thirunavukkarasu, D.; Devaraj, C.; Nikhil, K.T.; Ninan, J.; Sahoo, A.; Lacetera, N.; et al. Applications of Artificial Intelligence for Heat Stress Management in Ruminant Livestock. Sensors 2024, 24, 5890. [Google Scholar] [CrossRef]
- Provolo, G.; Brandolese, C.; Grotto, M.; Marinucci, A.; Fossati, N.; Ferrari, O.; Beretta, E.; Riva, E. An Internet of Things Framework for Monitoring Environmental Conditions in Livestock Housing to Improve Animal Welfare and Assess Environmental Impact. Animals 2025, 15, 644. [Google Scholar] [CrossRef]
- Džermeikaitė, K.; Bačėninaitė, D.; Antanaitis, R. Innovations in Cattle Farming: Application of Innovative Technologies and Sensors in the Diagnosis of Diseases. Animals 2023, 13, 780. [Google Scholar] [CrossRef]
- Han, C.S.; Kaur, U.; Bai, H.; Roqueto dos Reis, B.; White, R.; Nawrocki, R.A.; Voyles, R.M.; Kang, M.G.; Priya, S. Invited review: Sensor technologies for real-time monitoring of the rumen environment. J. Dairy Sci. 2022, 105, 6379–6404. [Google Scholar] [CrossRef]
- Post, C.; Rietz, C.; Büscher, W.; Müller, U. The Importance of Low Daily Risk for the Prediction of Treatment Events of Individual Dairy Cows with Sensor Systems. Sensors 2021, 21, 1389. [Google Scholar] [CrossRef]
- Benjamin, M.; Yik, S. Precision Livestock Farming in Swine Welfare: A Review for Swine Practitioners. Animals 2019, 9, 133. [Google Scholar] [CrossRef] [PubMed]
- Neethirajan, S. Artificial Intelligence and Sensor Innovations: Enhancing Livestock Welfare with a Human-Centric Approach. Hum. Centric Intell. Syst. 2024, 4, 77–92. [Google Scholar] [CrossRef]
- Zhou, H.; Chung, S.; Kakar, J.K.; Kim, S.C.; Kim, H. Pig movement estimation by integrating optical flow with a multi-object tracking model. Sensors 2023, 23, 9499. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Dong, J.; Han, S.; Chung, S.; Ali, H.; Kim, S. Weakly supervised learning through box annotations for pig instance segmentation. Sci. Rep. 2025, 15, 19706. [Google Scholar] [CrossRef]
- Louie, A.; Rowe, J.; Love, W.; Lehenbauer, T.; Aly, S. Effect of the environment on the risk of respiratory disease in preweaning dairy calves during summer months. J. Dairy Sci. 2018, 101, 10230–10247. [Google Scholar] [CrossRef]
- Koknaroglu, H.; Otles, Z.; Mader, T.; Hoffman, M.P. Environmental factors affecting feed intake of steers in different housing systems in the summer. Int. J. Biometeorol. 2008, 52, 419–429. [Google Scholar] [CrossRef]
- Pompeo, J.; Yu, Z.; Zhang, C.; Wu, S.; Zhang, Y.; Gomez, C.; Correll, M. Assessing the stability of indoor farming systems using data outlier detection. Front. Plant Sci. 2025, 15, 1270544. [Google Scholar] [CrossRef]
- Jung, J.M.; Kim, D.H.; Cho, H.; Lee, M.; Jeong, J.; Lee, D.H.; Seo, S.; Lee, W.H. Multi-algorithmic approach for detecting outliers in cattle intake data. J. Agric. Food Res. 2024, 15, 101021. [Google Scholar] [CrossRef]
- Suryavansh, S.; Benna, A.; Guest, C.; Chaterji, S. A data-driven approach to increasing the lifetime of IoT sensor nodes. Sci. Rep. 2021, 11, 22459. [Google Scholar] [CrossRef]
- Ou, C.H.; Chen, Y.A.; Huang, T.W.; Huang, N.F. Design and Implementation of Anomaly Condition Detection in Agricultural IoT Platform System. In Proceedings of the 2020 International Conference on Information Networking (ICOIN), Barcelona, Spain, 7–10 January 2020; pp. 184–189. [Google Scholar] [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. Adv. Neural Inf. Process. Syst. 2021, 34, 22419–22430. [Google Scholar]
- Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; Long, M. TimesNet: Temporal 2D-Variation Modeling for General Time Series Analysis. In Proceedings of the International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are transformers effective for time series forecasting? Proc. AAAI Conf. Artif. Intell. 2023, 37, 11121–11128. [Google Scholar] [CrossRef]
- Guo, Z.; Yin, Z.; Lyu, Y.; Wang, Y.; Chen, S.; Li, Y.; Zhang, W.; Gao, P. Research on indoor environment prediction of pig house based on OTDBO–TCN–GRU algorithm. Animals 2024, 14, 863. [Google Scholar] [CrossRef] [PubMed]
- Rong, L.; Fan, J.; Guo, X.; Tong, Z.; Xu, W.; Pan, Y.; Li, S.; Zhang, W.; Sun, F. Reserach on environmental monitoring and comprehensive evaluation system of pig house based on internet of things technology. INMATEH Agric. Eng. 2025, 75, 501. [Google Scholar] [CrossRef]
- Park, H.; Park, D.; Kim, S. Anomaly detection of operating equipment in livestock farms using deep learning techniques. Electronics 2021, 10, 1958. [Google Scholar] [CrossRef]
- Peng, S.; Zhu, J.; Liu, Z.; Hu, B.; Wang, M.; Pu, S. Prediction of ammonia concentration in a pig house based on machine learning models and environmental parameters. Animals 2022, 13, 165. [Google Scholar] [CrossRef]
- Jin, H.; Meng, G.; Pan, Y.; Zhang, X.; Wang, C. An improved intelligent control system for temperature and humidity in a pig house. Agriculture 2022, 12, 1987. [Google Scholar] [CrossRef]
- Li, H.; Li, H.; Li, B.; Shao, J.; Song, Y.; Liu, Z. Smart temperature and humidity control in pig house by improved three-way K-means. Agriculture 2023, 13, 2020. [Google Scholar] [CrossRef]
- Chen, R.T.Q.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D.K. Neural Ordinary Differential Equations. In Advances in Neural Information Processing Systems; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Baytas, I.M.; Xiao, C.; Zhang, X.; Wang, F.; Jain, A.K.; Zhou, J. Patient subtyping via time-aware LSTM networks. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Montréal, QC, Canada, 2–8 December 2018; pp. 65–74. [Google Scholar]
- Hasani, R.; Lechner, M.; Amini, A.; Rus, D.; Grosu, R. Liquid time-constant networks. Proc. AAAI Conf. Artif. Intell. 2021, 35, 7657–7666. [Google Scholar] [CrossRef]
- Hasani, R.; Lechner, M.; Amini, A.; Liebenwein, L.; Ray, A.; Tschaikowski, M.; Teschl, G.; Rus, D. Closed-form continuous-time neural networks. Nat. Mach. Intell. 2022, 4, 992–1003. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).