3.1. Kinematic Model of the Tracked Vehicle
By analyzing the locomotion mechanism of a single-track vehicle, it is observed that during steering, the track on the braked side remains stationary, while the track on the unbraked side drives the vehicle to rotate. The turning center is located at the contact point of the braked track. This motion behavior can be simplified as a classical differential-drive system.
To facilitate kinematic modeling, the following assumptions are made in this study:
The vehicle moves on a planar (two-dimensional) surface, with the vertical displacement neglected.
The contact between the tracks and the ground is uniform, and no slippage occurs.
The center of mass coincides with the geometric center of the vehicle.
Based on these assumptions, a kinematic model of the tracked vehicle is established in the navigation coordinate frame
XOY, as illustrated in
Figure 3.
To enhance clarity, the definitions of the key symbols used in this model are summarized in
Table 2 below.
According to the kinematic equations of the tracked vehicle, the following can be derived:
The forward velocity
VC of the vehicle, defined as the linear velocity of the vehicle’s center of mass in the forward direction, is given as the average velocity of the two tracks:
When the vehicle turns by braking one track, the angular velocity
ω and turning radius
R are determined by the track width
B and the velocity difference between the two tracks. The turning center is located at the midpoint of the braked track:
When the vehicle turns left, the left track is braked, i.e.,
VL = 0, then:
When the vehicle turns right, the right track is braked, i.e.,
VR = 0, then:
3.2. Segmented Preview Tracking Model
This study adopts a segmented preview tracking model, which divides the path tracking process into two stages: “steering adjustment” and “straight-line motion” (as shown in
Figure 4), in order to accommodate the structural characteristic of fixed turning radius in single-track vehicles. The vehicle first utilizes its single-side braking steering mechanism to adjust its heading by calculating the heading deviation and determining the required turning angle, thereby aligning the vehicle toward the preview point. Subsequently, the vehicle moves along a straight path toward the preview point. Upon reaching it, the next preview point is computed and selected, and the process is repeated until the entire path is successfully tracked.
To realize path tracking control, it is necessary to perform real-time computation and updating of key parameters throughout the tracking process. The lateral deviation
ed represents the perpendicular distance between the vehicle’s current position and the target path, indicating the extent of lateral offset. To ensure computational accuracy, the lateral deviation is calculated based on the local direction of the path. By identifying the nearest index point (
Xn,
Yn), the corresponding path segment (e.g., from (
Xn−1,
Yn−1) to (
Xn+1,
Yn+1)) is obtained, and the tangent direction of the path is calculated accordingly:
where
θp denotes the local heading angle of the path.
Subsequently, the vehicle position vector
is projected onto the direction perpendicular to the path, and the lateral error of the vehicle is calculated as follows:
Note: the sign of ed indicates the vehicle’s relative position with respect to the path; ed > 0 means that the vehicle is on the left side of the path, while ed < 0 means that it is on the right side.
The current preview point of the vehicle is determined based on the preview distance by calculating the Euclidean distance between the vehicle’s current position and the path points and searching for the point whose distance equals or is closest to the preview distance. However, the vehicle may sometimes select a point located behind its current position as the preview point (e.g., selecting point
T0 in
Figure 4), which can lead to path tracking failure. Therefore, a forward-looking constraint must be introduced to ensure that the vehicle progresses along the forward direction of the path. Assuming the path consists of discrete points {(
Xi,
Yi)} for
i = 0, 1, 2, ⋯,
N, a forward constraint is first imposed as follows:
- 2.
Identify the point corresponding to the minimum di as the nearest index point (Xn, Yn), with the index value n (i.e., dn = min(di)).
- 3.
Select the path point that satisfies the preview distance constraint while ensuring that its index satisfies I > n, thereby guaranteeing that the preview point is located ahead of the vehicle. The resulting point is defined as the current preview point.
Meanwhile, to ensure complete path tracking and avoid failures in the final segment caused by the inability to locate a preview point (i.e., (di < Ld2)), it is necessary to assign the endpoint of the planned path as the preview point when it falls within the current preview distance. In such cases, the endpoint Tp is taken as the vehicle’s preview tracking point, thereby ensuring complete path coverage.
After determining the preview point, the current heading deviation
eθ of the vehicle is calculated to guide the steering adjustment. The target heading angle
θ is computed based on the vehicle’s current position (
X,
Y) and the coordinates of the preview point (
XT,
YT) as follows:
The heading deviation
eθ is defined as the difference between the target heading angle
θ and the current heading angle
ψ:
To avoid angular discontinuity,
eθ should be normalized to the interval [−
π,
π].
Note: eθ > 0 indicates that the vehicle needs to turn left, while eθ < 0 indicates a right turn.
To provide a quantitative measure of the dynamic characteristics of the path, the average curvature of the forward path (within the preview range) is calculated. The path curvature
k represents the degree of bending of the path and is mathematically defined as the rate of change of the tangent angle with respect to arc length at a given point on the curve. For circular arcs, where the curvature is constant, the curvature
k is given by the following:
Here, δ represents the central angle corresponding to the arc, and s is the arc length of the arc.
From the nearest point (
Xn,
Yn) of the vehicle, a set of points within the preview distance
Ld is selected along the direction of the path, denoted as (
Xn+1,
Yn+1), …, (
Xn+m,
Yn+m), where
m is determined by the preview distance
Ld. The curvature at each point on the path is estimated using the three-point method. As shown in
Figure 5, three consecutive points (
Xi−1,
Yi−1), (
Xi,
Yi), and (
Xi+1,
Yi+1) are selected. The central angle Δ
δi is approximated by the included angle between the two line segments:
where
,
The arc length Δ
si is approximated based on the three-point arc assumption by taking the average of the lengths of the two segments:
This approximation originates from a geometric simplification in curvature calculations. For a circular arc formed by three points, the true arc length is Δsi = R·|Δδi|, where R is the arc radius. However, calculating R is computationally complex and difficult to obtain in real time. Therefore, the average of the two segment lengths, l1 and l2, is used to approximate the arc length. The resulting error is negligible for small angles, ensuring a balance between real-time performance and accuracy.
The curvature at a single point is given by the following:
The average curvature is calculated over the
m points ahead as follows:
To facilitate the interpretation of
Figure 4, a summary of the associated variables and their definitions is provided in
Table 3.
3.3. Dynamic Adjustment Strategy for Preview Distance
In the preview tracking algorithm for tracked vehicles, the preview distance Ld is a key parameter that determines path tracking performance and turning behavior. However, a fixed preview distance often results in frequent turning or excessive tracking deviation under specific conditions, thereby affecting the smoothness of navigation and operational efficiency.
As shown in
Figure 6, using a large preview distance may cause the vehicle to skip certain path segments, leading to path tracking failure. Conversely, a small preview distance can cause the vehicle to oscillate back and forth near the reference path. Therefore, to enhance the effectiveness of the preview tracking algorithm, it is essential to dynamically select an appropriate preview distance based on road information and vehicle state.
To ensure stable path tracking, the selection of the preview distance must also guarantee the stability of the tracking system [
21]. When the reference path is fully followed, the system must remain in a stable state. The local stability of the nonlinear system under equilibrium conditions can be analyzed by linearizing the system around the equilibrium point.
Based on the geometric preview control model for tracked vehicles, the evolution of lateral error and heading error over time can be described by the following kinematic relationships:
where
ed is the lateral deviation,
eθ is the heading deviation,
v is the vehicle speed,
T is the time constant, and
γ is the vehicle rotation angle.
To ensure closed-loop stability, the controller applies a dynamic regulation rate to adjust
γ based on the observed tracking errors. The adopted regulation law is given as follows:
where
Φeθ,
Φed, and
Φγ are the linearization coefficients of the path tracking system.
Combining the above expressions, the closed-loop state-space system can be written as follows:
The characteristic polynomial of the system is calculated as follows:
Based on the Routh–Hurwitz stability criterion, the stability conditions of the system can be obtained as follows:
If the above conditions are satisfied, the system is locally stable at the equilibrium point. Based on the stability conditions, the following expression is derived:
where
Ld is the preview distance,
T is the system response time, and
v is the vehicle speed.
Through experimental analysis, the system response time of the vehicle was determined to be 0.6 s, and the vehicle speed was set to 2 m/s. As a result, the minimum preview distance was calculated to be 1.2 m, indicating that the system can remain stable when the preview distance satisfies Ld > 1.2 m.
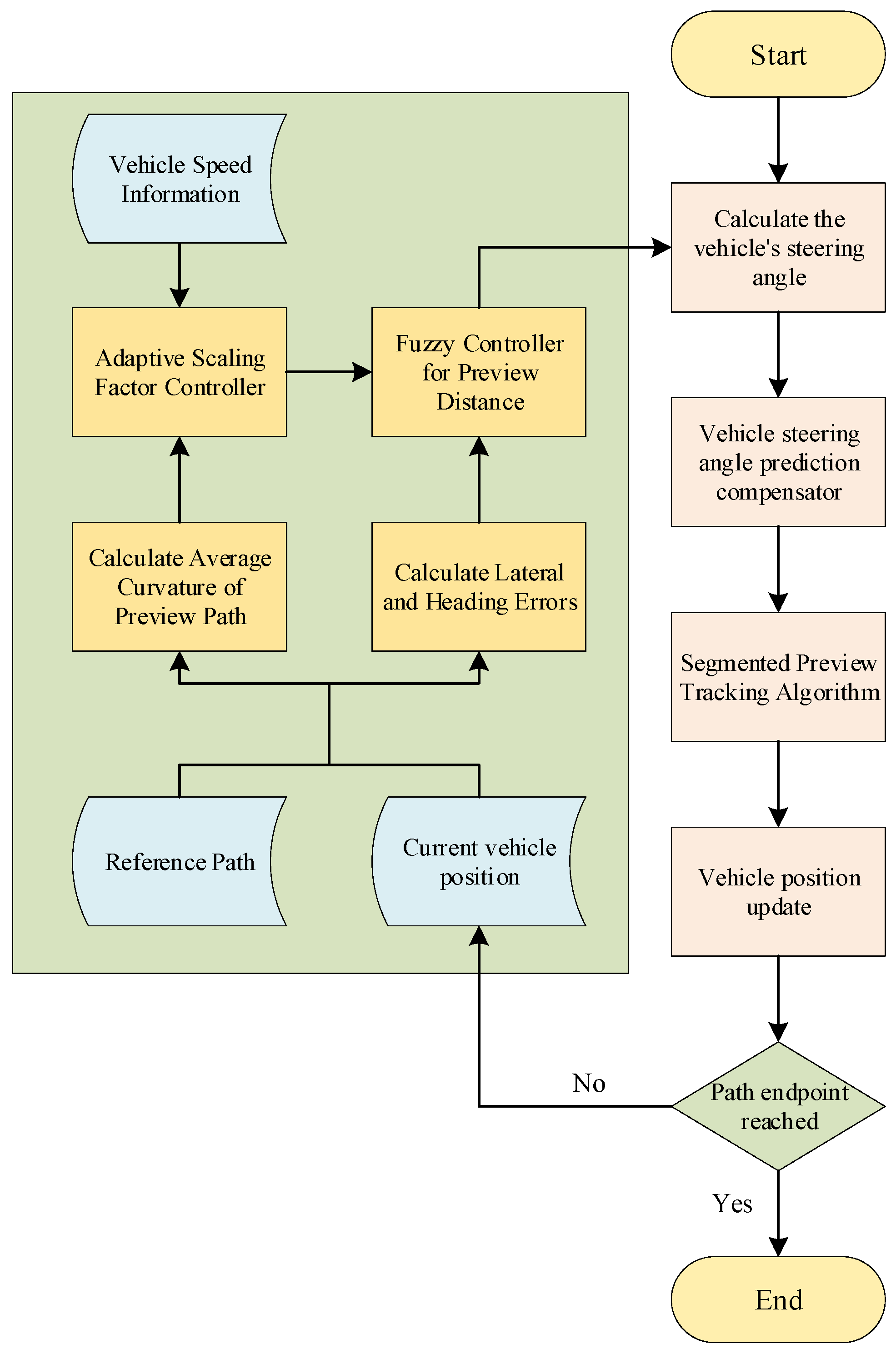
Secondly, this study designs a preview distance adjustment controller based on variable universe fuzzy control. The controller takes the average curvature k of the forward path and the vehicle speed v at a given moment as inputs to an adaptive scaling factor module, which calculates and outputs a universe scaling factor α. Subsequently, the variable universe fuzzy control module adjusts the input universe based on α and performs inference using the current lateral deviation and heading deviation to obtain the optimal preview distance at that moment. Finally, the calculated preview distance is passed into the segmented preview tracking module, which, together with the vehicle’s steering angle prediction compensator, achieves path tracking control.
The algorithm implementation flowchart is shown in
Figure 7. The functions and roles of the key modules involved in the control algorithm, as shown in
Figure 7, are summarized in
Table 4.
3.3.1. Design of the Variable Universe Fuzzy Controller
The essence of the variable universe fuzzy control lies in a dynamically pointwise-converging interpolation method. While keeping the original fuzzy rules of the controller unchanged, it adjusts the scaling factors online, thereby enabling the dynamic modification of the fuzzy universe [
21].
For a dual-input single-output fuzzy preview tracking system, let the fuzzy universe of the input variables be defined as follows:
and the fuzzy universe of the output variable as follows:
The adjusted fuzzy universes after applying the scaling factors are given by the following:
where
α is the universe scaling factor.
The ranges of the input and output fuzzy universes dynamically contract or expand according to the system’s real-time state, such as the average curvature
k of the forward path and the vehicle speed
v. Although the total number of fuzzy rules remains unchanged, when the universe contracts, the fuzzy partitions become finer, thereby increasing the number of effective rules and improving the control accuracy. Conversely, when the universe expands, the fuzzy partitions become coarser, reducing the number of effective rules while accommodating other control requirements. This mechanism enables the controller to apply more appropriate fuzzy rules during different control phases, thereby enhancing the system’s adaptability [
22,
23].
In this study, a dual-input single-output (DISO) fuzzy controller is designed with the objective of enabling the vehicle to follow a predefined trajectory. The initial parameters of the fuzzy controller, including the membership function ranges and rule base, were set based on control experience and standard fuzzy control principles. These parameters were subsequently fine-tuned through offline simulation experiments to enhance the tracking responsiveness and stability of the algorithm under various deviation conditions.
The input variables are the current lateral deviation ed and the heading deviation eθ, while the output variable is the preview distance Ld. Since the segmented preview tracking model divides the vehicle tracking into turning and execution phases, and the turning direction can be determined by the sign of the heading deviation, the design of the preview distance focuses more on the magnitude rather than the direction of the input errors. Therefore, the absolute values of the input parameters are used as inputs to the controller.
The basic universe of discourse for the input and output variables is defined as follows:
ed ∈ [0, 50] cm,
eθ ∈ [0, 90]°, and
Ld ∈ [1, 5] m. The initial value of the scaling factor is set to 1, with its specific value to be determined through system tuning during operation. The input variables are described using three levels of fuzzy linguistic terms: small (
S), medium (
M), and large (
L); the output variable is defined using four levels: very small (
VS), small (
S), medium (
M), and large (
L). To ensure smoothness in the algorithm’s output, all membership functions are modeled using Gaussian membership functions. The membership functions of each variable are shown in
Figure 8.
The mathematical expression is given by the following:
where
μi is the membership degree, and
αi is the center value of the fuzzy set.
Reasonable fuzzy rules are established as follows: when both
ed and
eθ are large, the preview distance
Ld should be reduced to quickly correct the error and improve the tracking accuracy. When
ed and
eθ are small,
Ld should be increased to extend the straight-line distance and reduce unnecessary turning. The fuzzy control rules are listed in
Table 5.
3.3.2. Design of the Adaptive Scaling Factor
Based on the concept of a variable universe, it is necessary to design a reasonable and effective scaling factor. Existing studies commonly adopt mathematical functions to compute the scaling factor, where its magnitude directly depends on the input variables. These function-based approaches have explicit mathematical models, allowing for fast computation and implementation within control systems. However, such methods often rely on empirically defined parameters [
24], which are difficult to tune. Moreover, fixed mathematical formulations cannot fully capture the nonlinear and variable characteristics of complex systems, thereby affecting control accuracy. As a result, they may perform poorly under the diverse operating conditions of agricultural machinery. To enhance the adaptability of the system, this study adopts a fuzzy control approach for scaling factor adjustment. By applying fuzzy inference, the scaling factor is dynamically adjusted in real time based on the average curvature of the path ahead and the vehicle speed. This allows the fuzzy universe to contract more quickly when errors are large—thereby improving the system’s responsiveness—and to expand when errors are small, reducing unnecessary turns and improving the system’s stability.
The adaptive scaling factor controller is designed as a dual-input single-output fuzzy controller. The input variables are the average curvature k of the forward path and the vehicle speed v, while the output variable is the scaling factor α. The adaptive scaling factor controller consists of the following three main steps:
(1) Fuzzification. The fuzzy universe of input variable
k is set to [0, 0.5] m
−1, and the fuzzy range of vehicle speed
v is defined as [2, 12] km/h. Both input variables adopt three levels of fuzzy linguistic terms: small (
S), medium (
M), and large (
L). The fuzzy universe of the output variable
α is set to [0.1, 1.3], with four fuzzy linguistic terms: very small (
VS), small (
S), medium (
M), and large (
L). The membership functions of both input and output variables use triangular functions, which are computationally simple and suitable for real-time control. The general form is as follows: (
μ(
x) =
max(0, 1 − |
x −
c|/
b)), where
c is the center, and
b is the width. The membership functions are illustrated in
Figure 9.
(2) Establishment of the fuzzy rule base. The design principle of the fuzzy rules for the adaptive scaling factor is as follows: When both
k and
v are large, a smaller scaling factor is applied to compress the universe, increase sensitivity to errors, and enhance the path tracking capability. When both
k and
v are small, a larger scaling factor (close to or slightly greater than 1) is used to appropriately expand the universe, reducing excessive adjustments and improving smoothness. When
k is large but
v is small, a moderately small scaling factor is used to improve the tracking accuracy while avoiding unnecessary sharp corrections. When
k is small but
v is large, a moderately large scaling factor is adopted to enhance the vehicle stability while maintaining the required tracking precision. The designed fuzzy rule base is shown in
Table 6.
(3) Defuzzification and fuzzy inference. Fuzzy inference is performed using the Mamdani method. Based on the membership degrees of inputs k and v, the fuzzy rule base is used to compute the fuzzy output of α. The fuzzy output is then defuzzified using the centroid method to obtain a crisp value, calculated as follows: , where μi is the membership degree, and αi is the center value of the fuzzy set. Finally, the computed scaling factor is fed into the variable universe fuzzy controller and applied in the calculation of the vehicle’s preview distance.
3.4. Vehicle Steering Angle Prediction and Compensation Based on SVR and PSO
Heading deviation refers to the difference between the current heading of the vehicle and the desired heading, which determines the vehicle’s turning direction and turning angle. In practical applications, however, due to factors such as muddy terrain and track slippage, the actual angular velocity during single-track steering tends to be discrete or exhibit nonlinear jumps. As a result, the control process shows discontinuous steering behavior, making it difficult to achieve precise control. This often leads to steady-state errors and an inability to maintain low lateral deviation [
25]. Therefore, it is necessary to predict the vehicle’s heading deviation and compensate for the steering angle accordingly so that the vehicle can advance or delay steering actions as needed. Given the highly nonlinear disturbances present in complex farmland environments, it is challenging to develop an accurate model to estimate the actual heading deviation error. In this context, machine learning offers a feasible solution.
Support Vector Regression (SVR), as a nonlinear regression model based on the principle of structural risk minimization, demonstrates strong fitting capabilities for small-sample and high-dimensional data [
26]. It can analyze and learn from actual observational data to infer and predict the vehicle’s state at the next moment. Based on the prediction results, compensation can be applied to certain parameter values to achieve more accurate tracking. Therefore, this study adopts the SVR algorithm to predict the vehicle’s heading at the next time step in real time based on the current heading deviation.
During navigation, due to muddy and uneven terrain, the vehicle’s navigation data
D (including current GPS coordinates, heading angle, and track speed) exhibit continuous fluctuations, containing both sudden changes and noise. To mitigate the impact of noise and abrupt variations, this study employs the exponential moving average (EMA) method:
where
β is the weighting coefficient, which is set to 0.6 in order to enhance the stability of the algorithm and better handle sudden changes.
Di denotes the exponential moving average of the
i-th sample, and
θi represents the original value of the
i-th sample. Each round of exponential smoothing is performed using 300 consecutive sampling points.
Considering that the exponential moving average may misestimate the true value due to insufficient initial data, resulting in a systematic bias, a bias correction formula is introduced for compensation:
SVR can be used to construct a nonlinear mapping relationship between input and output variables. Unlike traditional regression methods, SVR maps input samples into a high-dimensional space using a kernel function and determines the regression hyperplane based on the support vectors [
27]. Its mathematical expression is given as follows:
where
is the kernel function.
During navigation, the 300 most recent navigation data points are processed using exponential moving averaging. The first 70% of the smoothed results are used as the training set, and the remaining 30% as the test set. The input features include vehicle position information, heading deviation, lateral deviation, and vehicle speed. The target output is the predicted heading deviation, which is used to guide steering control. To avoid falling into local optima and to improve the performance of the SVR model, this study introduces the Particle Swarm Optimization (PSO) algorithm to automatically optimize the key SVR parameters, including the penalty coefficient C and the kernel parameter g. In the PSO algorithm, each particle represents a candidate parameter pair (C, g), where C ∈ [0.1, 100] and g ∈ [0.1, 100]. The mean squared error (MSE) of the SVR is adopted as the fitness function in PSO, and the fitness of each particle is evaluated through cross-validation errors.
PSO dynamically updates each particle’s velocity and position by referring to its own historical best position and the current global best position of the entire swarm [
28,
29]. Through multiple iterations, the algorithm converges to an optimal set of parameters that minimizes the prediction error of the SVR model, thereby improving its prediction accuracy and generalization capability. In this study, the PSO hyperparameters—including population size, inertia weight, and learning factors—are empirically set to achieve a good balance between convergence speed and prediction performance.
The equations for updating the particle velocity and position are as follows:
Note: i is the index of the particle; t is the current iteration number; d is the dimension index of the search space (i.e., the d-th parameter); vi,d(t) is the velocity of particle i in dimension d at iteration t; xi,d(t) is the position (i.e., parameter value) of particle i in dimension d at iteration t; Pi,d is the historical best position of particle i in dimension d; Pg,d is the global best position found so far in dimension d; ω is the inertia weight, set to 1; c1 and c2 are learning factors, set to 1.5 and 1.7, respectively; and r1 and r2 are random numbers uniformly distributed in the interval [0, 1].
After training is completed, new navigation data are input into the trained SVR model, which uses the learned weights and bias to compute the predicted heading deviation of the vehicle. For clarity of representation, the heading deviation is denoted as φ.
To improve the prediction accuracy, this study employs the Mean Bias Error (MBE) to correct the prediction results. MBE measures the average deviation between the predicted heading deviation and the actual heading deviation. The calculation formula is as follows:
The predicted heading deviation after
MBE correction is denoted as
, and its calculation formula is as follows:
To further compensate for the heading deviation, a deviation compensation coefficient
μci is defined, and its expression is given as follows:
where
φe is the expected heading deviation, and
is the MBE-corrected predicted heading deviation.
The prediction error is defined as follows:
The corresponding compensation amount is calculated as follows:
The final actual output heading deviation is as follows:
By introducing the heading deviation compensation term to adjust the output of the controller, the heading deviation becomes more consistent with the actual steering behavior of the vehicle, thereby improving the path tracking accuracy of autonomous navigation. The flow of this feedback control algorithm is illustrated in
Figure 10.