Optimization Method for Forecasting Confirmed Cases of COVID-19 in China
Abstract
1. Introduction
- We propose an efficient forecasting model to forecast the confirmed cases of the COVID-19 in China for the upcoming ten days based on previously confirmed cases.
- An improved ANFIS model is proposed using a modified FPA algorithm, using SSA.
- We compare the proposed model with the original ANFIS and existing modified ANFIS models, such as PSO, GA, ABC, and FPA.
2. Material and Methods
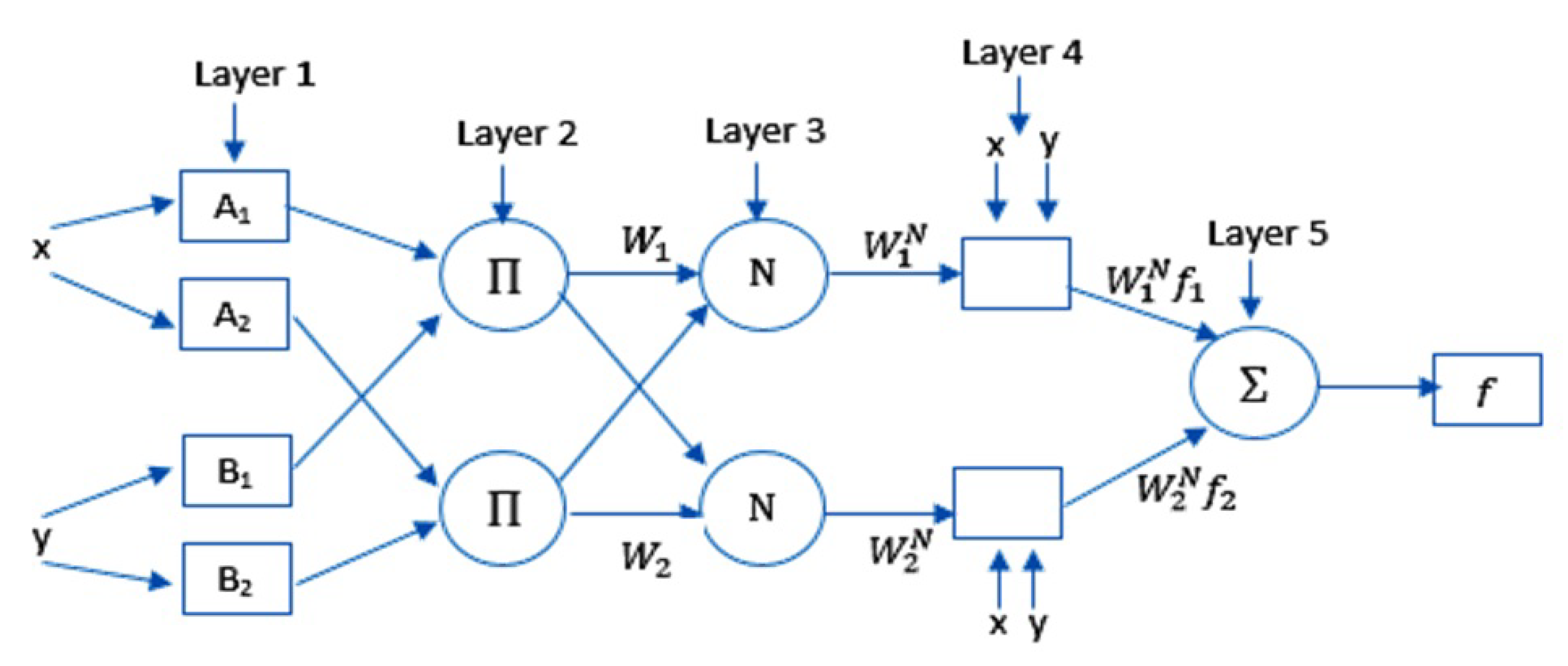
2.1. Adaptive Neuro-Fuzzy Inference System (ANFIS)
2.2. Flower Pollination Algorithm (FPA)
2.3. Salp Swarm Algorithm (SSA)
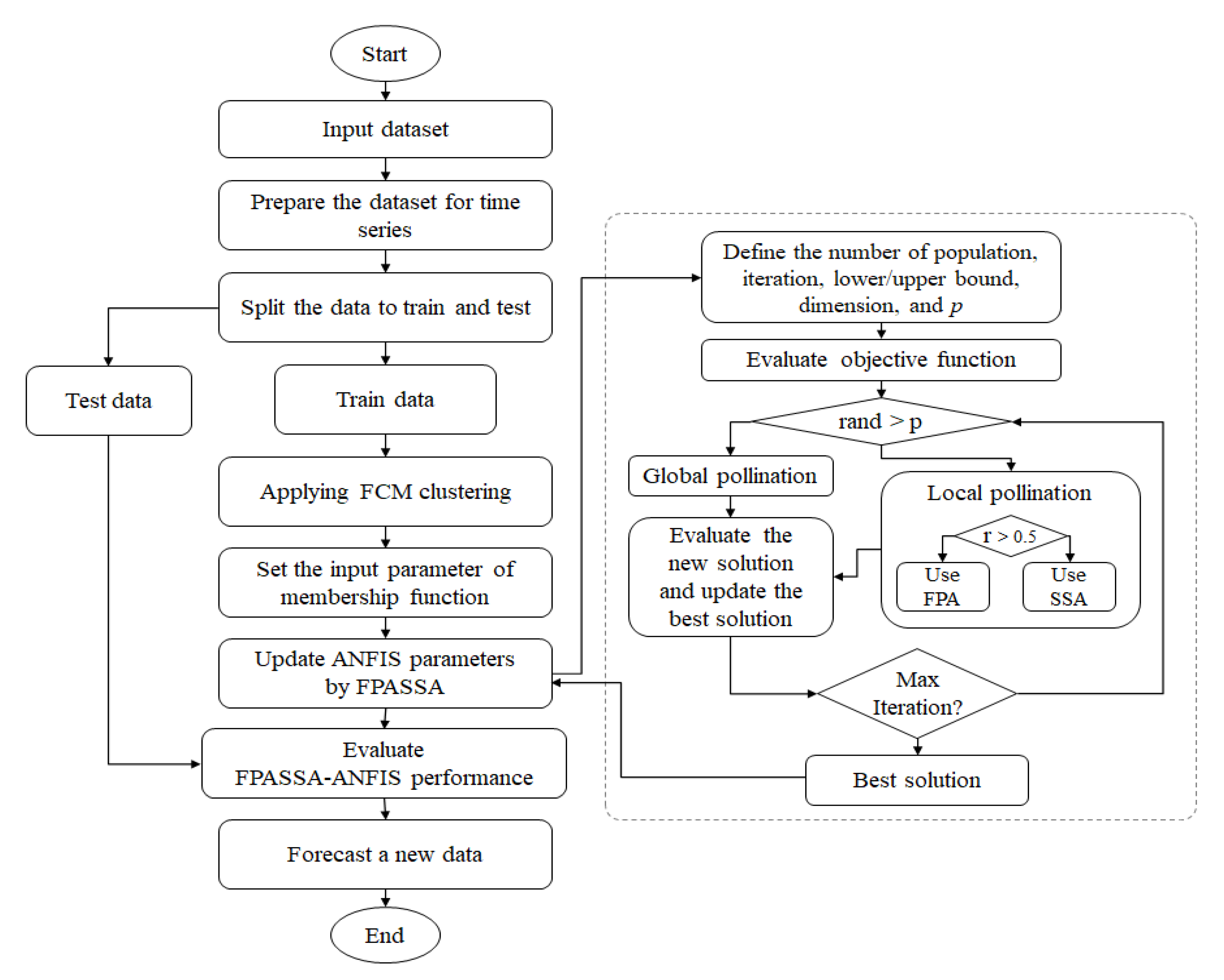
3. The Proposed Method
| Algorithm 1 Proposed FPASSA algorithm |
| Input: Historical COVID-19 dataset, size of population N, total number of iterations . Divide the data into training and testing sets. Using Fuzzy c-mean method to determine the number of membership functions. Constructing the ANFIS network. Set the initial value for N solutions (X). Set . while do Calculate the objective value for each . if then Apply the Global operators of FPA. else if then Using the operators of FPA to update . else Using the operators of SSA. end if end if end while Return the best solution that represents the best configuration for ANFIS. Apply the testing set to the best ANFIS model. Forecasting the COVID-19 for the next ten days. |
4. Experiment
4.1. Datasets Description
4.2. Performance Measures
- Root Mean Square Error (RMSE):where and Y are the predicted and original values, respectively.
- Mean Absolute Error (MAE):
- Mean Absolute Percentage Error (MAPE):
- Root Mean Squared Relative Error (RMSRE):represents the sample size of the data.
- Coefficient of Determination ():where represents the average of Y.
4.3. Parameter Settings
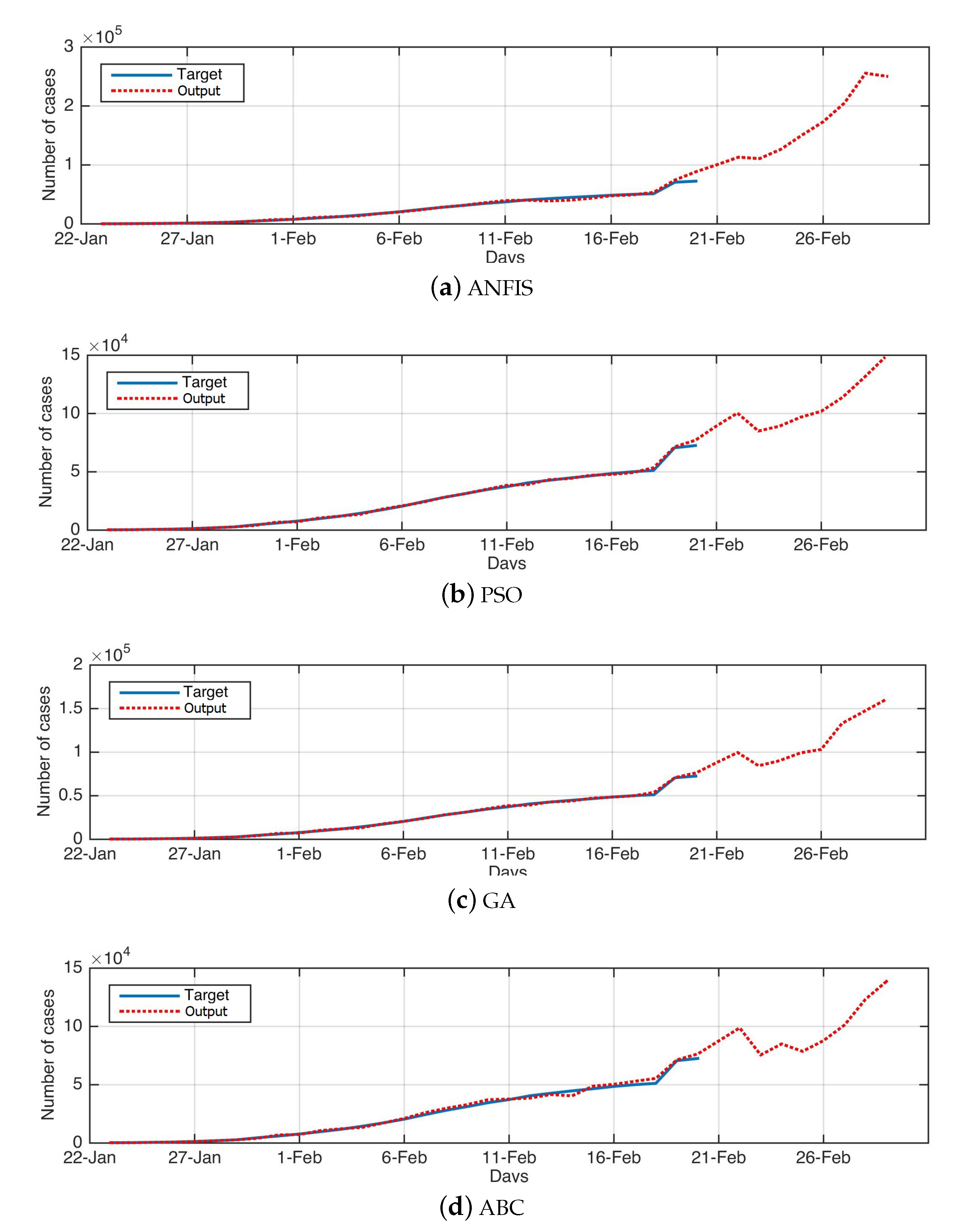
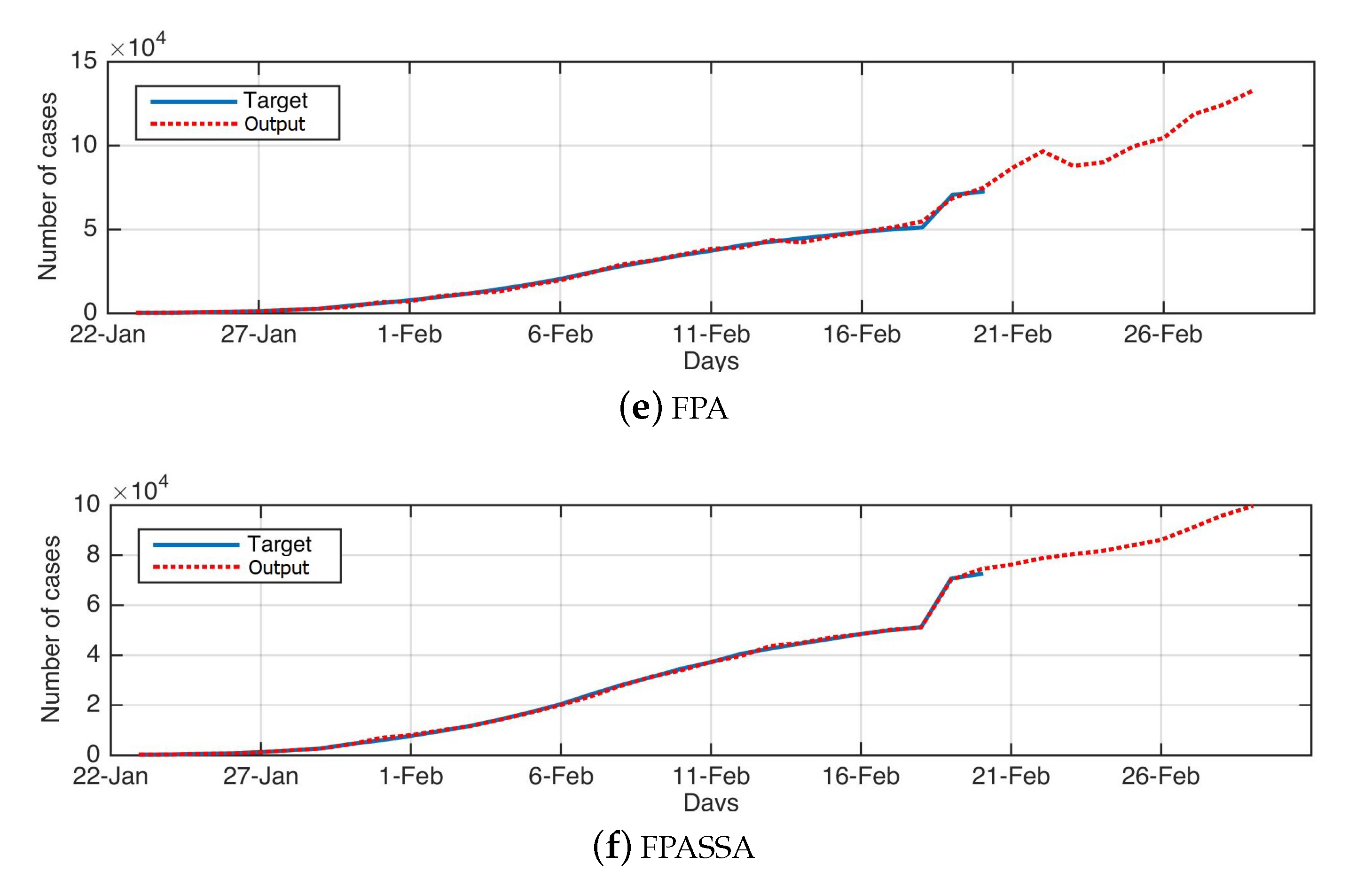
4.4. Performance of FPASSA to Forecast DS1 and DS2
4.5. Influence of FPASSA to Forecast COVID-19
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, Y.; Liu, Q.; Guo, D. Emerging coronaviruses: Genome structure, replication, and pathogenesis. J. Med. Virol. 2020. [Google Scholar] [CrossRef]
- Ge, X.Y.; Li, J.L.; Yang, X.L.; Chmura, A.A.; Zhu, G.; Epstein, J.H.; Mazet, J.K.; Hu, B.; Zhang, W.; Peng, C.; et al. Isolation and characterization of a bat SARS-like coronavirus that uses the ACE2 receptor. Nature 2013, 503, 535–538. [Google Scholar] [CrossRef]
- Wang, L.F.; Shi, Z.; Zhang, S.; Field, H.; Daszak, P.; Eaton, B.T. Review of bats and SARS. Emerg. Infect. Dis. 2006, 12, 1834. [Google Scholar] [CrossRef]
- Cauchemez, S.; Van Kerkhove, M.; Riley, S.; Donnelly, C.; Fraser, C.; Ferguson, N. Transmission scenarios for Middle East Respiratory Syndrome Coronavirus (MERS-CoV) and how to tell them apart. Euro Surveill. Bull. Eur. Sur Les Mal. Transm. Eur. Commun. Dis. Bull. 2013, 18, 20503. [Google Scholar]
- WHO Organization. Novel Coronavirus (2019-nCoV) 2020. Available online: https://www.who.int/ (accessed on 27 January 2020).
- Lu, R.; Zhao, X.; Li, J.; Niu, P.; Yang, B.; Wu, H.; Wang, W.; Song, H.; Huang, B.; Zhu, N.; et al. Genomic characterisation and epidemiology of 2019 novel coronavirus: Implications for virus origins and receptor binding. Lancet 2020, 395, 565–574. [Google Scholar] [CrossRef]
- Cheng, Z.J.; Shan, J. 2019 Novel Coronavirus: Where We are and What We Know. Infection 2020. [Google Scholar] [CrossRef] [PubMed]
- Guan, W.J.; Ni, Z.Y.; Hu, Y.; Liang, W.H.; Ou, C.Q.; He, J.X.; Liu, L.; Shan, H.; Lei, C.L.; Hui, D.S.; et al. Clinical characteristics of 2019 novel coronavirus infection in China. medRxiv 2020. Available online: https://www.medrxiv.org/content/early/2020/02/09/2020.02.06.20020974.full.pdf (accessed on 9 February 2020). [CrossRef]
- Zhao, S.; Musa, S.S.; Lin, Q.; Ran, J.; Yang, G.; Wang, W.; Lou, Y.; Yang, L.; Gao, D.; He, D.; et al. Estimating the Unreported Number of Novel Coronavirus (2019-nCoV) Cases in China in the First Half of January 2020: A Data-Driven Modelling Analysis of the Early Outbreak. J. Clin. Med. 2020, 9, 388. [Google Scholar] [CrossRef]
- Nishiura, H.; Kobayashi, T.; Yang, Y.; Hayashi, K.; Miyama, T.; Kinoshita, R.; Linton, N.M.; Jung, S.m.; Yuan, B.; Suzuki, A.; et al. The Rate of Underascertainment of Novel Coronavirus (2019-nCoV) Infection: Estimation Using Japanese Passengers Data on Evacuation Flights. J. Clin. Med. 2020, 9, 419. [Google Scholar] [CrossRef]
- Tang, B.; Wang, X.; Li, Q.; Bragazzi, N.L.; Tang, S.; Xiao, Y.; Wu, J. Estimation of the Transmission Risk of the 2019-nCoV and Its Implication for Public Health Interventions. J. Clin. Med. 2020, 9, 462. [Google Scholar] [CrossRef]
- Thompson, R.N. Novel Coronavirus Outbreak in Wuhan, China, 2020: Intense Surveillance Is Vital for Preventing Sustained Transmission in New Locations. J. Clin. Med. 2020, 9, 498. [Google Scholar] [CrossRef] [PubMed]
- Jung, S.M.; Akhmetzhanov, A.R.; Hayashi, K.; Linton, N.M.; Yang, Y.; Yuan, B.; Kobayashi, T.; Kinoshita, R.; Nishiura, H. Real time estimation of the risk of death from novel coronavirus (2019-nCoV) infection: Inference using exported cases. J. Clin. Med. 2020, 9, 523. [Google Scholar] [CrossRef] [PubMed]
- DeFelice, N.B.; Little, E.; Campbell, S.R.; Shaman, J. Ensemble forecast of human West Nile virus cases and mosquito infection rates. Nat. Commun. 2017, 8, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Ture, M.; Kurt, I. Comparison of four different time series methods to forecast hepatitis A virus infection. Expert Syst. Appl. 2006, 31, 41–46. [Google Scholar] [CrossRef]
- Shaman, J.; Karspeck, A. Forecasting seasonal outbreaks of influenza. Proc. Natl. Acad. Sci. USA 2012, 109, 20425–20430. [Google Scholar] [CrossRef]
- Shaman, J.; Karspeck, A.; Yang, W.; Tamerius, J.; Lipsitch, M. Real-time influenza forecasts during the 2012–2013 season. Nat. Commun. 2013, 4, 1–10. [Google Scholar] [CrossRef]
- Shaman, J.; Yang, W.; Kandula, S. Inference and forecast of the current West African Ebola outbreak in Guinea, Sierra Leone and Liberia. PLoS Curr. 2014, 6. [Google Scholar] [CrossRef] [PubMed]
- Massad, E.; Burattini, M.N.; Lopez, L.F.; Coutinho, F.A. Forecasting versus projection models in epidemiology: The case of the SARS epidemics. Med. Hypotheses 2005, 65, 17–22. [Google Scholar] [CrossRef]
- Ong, J.B.S.; Mark, I.; Chen, C.; Cook, A.R.; Lee, H.C.; Lee, V.J.; Lin, R.T.P.; Tambyah, P.A.; Goh, L.G. Real-time epidemic monitoring and forecasting of H1N1-2009 using influenza-like illness from general practice and family doctor clinics in Singapore. PLoS ONE 2010, 5. [Google Scholar] [CrossRef]
- Nah, K.; Otsuki, S.; Chowell, G.; Nishiura, H. Predicting the international spread of Middle East respiratory syndrome (MERS). BMC Infect. Dis. 2016, 16, 356. [Google Scholar] [CrossRef]
- Jang, J.S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Wei, L.Y. A hybrid ANFIS model based on empirical mode decomposition for stock time series forecasting. Appl. Soft Comput. 2016, 42, 368–376. [Google Scholar] [CrossRef]
- Cheng, C.H.; Wei, L.Y.; Liu, J.W.; Chen, T.L. OWA-based ANFIS model for TAIEX forecasting. Econ. Model. 2013, 30, 442–448. [Google Scholar] [CrossRef]
- Pousinho, H.M.I.; Mendes, V.; Catalão, J.P.d.S. Short-term electricity prices forecasting in a competitive market by a hybrid PSO–ANFIS approach. Int. J. Electr. Power Energy Syst. 2012, 39, 29–35. [Google Scholar] [CrossRef]
- Svalina, I.; Galzina, V.; Lujić, R.; ŠImunović, G. An adaptive network-based fuzzy inference system (ANFIS) for the forecasting: The case of close price indices. Expert Syst. Appl. 2013, 40, 6055–6063. [Google Scholar] [CrossRef]
- Ekici, B.B.; Aksoy, U.T. Prediction of building energy needs in early stage of design by using ANFIS. Expert Syst. Appl. 2011, 38, 5352–5358. [Google Scholar] [CrossRef]
- Cheng, C.H.; Wei, L.Y. One step-ahead ANFIS time series model for forecasting electricity loads. Optim. Eng. 2010, 11, 303–317. [Google Scholar] [CrossRef]
- Kumar, D.T.; Soleimani, H.; Kannan, G. Forecasting return products in an integrated forward/reverse supply chain utilizing an ANFIS. Int. J. Appl. Math. Comput. Sci. 2014, 24, 669–682. [Google Scholar] [CrossRef]
- Ho, Y.C.; Tsai, C.T. Comparing ANFIS and SEM in linear and nonlinear forecasting of new product development performance. Expert Syst. Appl. 2011, 38, 6498–6507. [Google Scholar] [CrossRef]
- Catalão, J.P.d.S.; Pousinho, H.M.I.; Mendes, V.M.F. Hybrid wavelet-PSO-ANFIS approach for short-term electricity prices forecasting. IEEE Trans. Power Syst. 2010, 26, 137–144. [Google Scholar] [CrossRef]
- Bagheri, A.; Peyhani, H.M.; Akbari, M. Financial forecasting using ANFIS networks with quantum-behaved particle swarm optimization. Expert Syst. Appl. 2014, 41, 6235–6250. [Google Scholar] [CrossRef]
- Ewees, A.A.; El Aziz, M.A.; Elhoseny, M. Social-spider optimization algorithm for improving ANFIS to predict biochar yield. In Proceedings of the 2017 8th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Delhi, India, 3–5 July 2017; pp. 1–6. [Google Scholar]
- Al-Qaness, M.A.; Elaziz, M.A.; Ewees, A.A. Oil consumption forecasting using optimized adaptive neuro-fuzzy inference system based on sine cosine algorithm. IEEE Access 2018, 6, 68394–68402. [Google Scholar] [CrossRef]
- Al-Qaness, M.A.; Abd Elaziz, M.; Ewees, A.A.; Cui, X. A Modified Adaptive Neuro-Fuzzy Inference System Using Multi-Verse Optimizer Algorithm for Oil Consumption Forecasting. Electronics 2019, 8, 1071. [Google Scholar] [CrossRef]
- El Aziz, M.A.; Hemdan, A.M.; Ewees, A.A.; Elhoseny, M.; Shehab, A.; Hassanien, A.E.; Xiong, S. Prediction of biochar yield using adaptive neuro-fuzzy inference system with particle swarm optimization. In Proceedings of the 2017 IEEE PES PowerAfrica, Accra, Ghana, 27–30 June 2017; pp. 115–120. [Google Scholar]
- Elaziz, M.A.; Ewees, A.A.; Alameer, Z. Improving adaptive neuro-fuzzy inference system based on a modified salp swarm algorithm using genetic algorithm to forecast crude oil price. Nat. Resour. Res. 2019, 1–16. [Google Scholar] [CrossRef]
- Yang, X.S. Flower pollination algorithm for global optimization. In International Conference on Unconventional Computing and Natural Computation; Springer: Berlin, Germany, 2012; pp. 240–249. [Google Scholar]
- Alam, D.; Yousri, D.; Eteiba, M. Flower pollination algorithm based solar PV parameter estimation. Energy Convers. Manag. 2015, 101, 410–422. [Google Scholar] [CrossRef]
- Ram, J.P.; Babu, T.S.; Dragicevic, T.; Rajasekar, N. A new hybrid bee pollinator flower pollination algorithm for solar PV parameter estimation. Energy Convers. Manag. 2017, 135, 463–476. [Google Scholar] [CrossRef]
- Abdel-Raouf, O.; El-Henawy, I.; Abdel-Baset, M. A novel hybrid flower pollination algorithm with chaotic harmony search for solving sudoku puzzles. Int. J. Mod. Educ. Comput. Sci. 2014, 6, 38. [Google Scholar] [CrossRef]
- Rodrigues, D.; Yang, X.S.; De Souza, A.N.; Papa, J.P. Binary flower pollination algorithm and its application to feature selection. In Recent Advances in Swarm Intelligence and Evolutionary Computation; Springer: Berlin, Germany, 2015; pp. 85–100. [Google Scholar]
- Salgotra, R.; Singh, U.; Saha, S.; Nagar, A.K. Improved Flower Pollination Algorithm for Linear Antenna Design Problems. In Soft Computing for Problem Solving; Springer: Berlin, Germany, 2020; pp. 79–89. [Google Scholar]
- Priya, K.; Rajasekar, N. Application of flower pollination algorithm for enhanced proton exchange membrane fuel cell modelling. Int. J. Hydrog. Energy 2019, 44, 18438–18449. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Pan, J.S.; Dao, T.K. An improved flower pollination algorithm for optimizing layouts of nodes in wireless sensor network. IEEE Access 2019, 7, 75985–75998. [Google Scholar] [CrossRef]
- Ahmed, K.; Ewees, A.A.; Hassanien, A.E. Prediction and management system for forest fires based on hybrid flower pollination optimization algorithm and adaptive neuro-fuzzy inference system. In Proceedings of the 2017 Eighth International Conference on Intelligent Computing and Information Systems (ICICIS), Cairo, Egypt, 5–7 December 2017; pp. 299–304. [Google Scholar]
- Al-Betar, M.A.; Awadallah, M.A.; Doush, I.A.; Hammouri, A.I.; Mafarja, M.; Alyasseri, Z.A.A. Island flower pollination algorithm for global optimization. J. Supercomput. 2019, 75, 5280–5323. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Tubishat, M.; Idris, N.; Shuib, L.; Abushariah, M.A.; Mirjalili, S. Improved Salp Swarm Algorithm based on opposition based learning and novel local search algorithm for feature selection. Expert Syst. Appl. 2020, 145, 113122. [Google Scholar] [CrossRef]
- Neggaz, N.; Ewees, A.A.; Elaziz, M.A.; Mafarja, M. Boosting salp swarm algorithm by sine cosine algorithm and disrupt operator for feature selection. Expert Syst. Appl. 2020, 145, 113103. [Google Scholar] [CrossRef]
- Panda, N.; Majhi, S.K. How effective is the salp swarm algorithm in data classification. In Computational Intelligence in Pattern Recognition; Springer: Berlin, Germany, 2020; pp. 579–588. [Google Scholar]
- Alwerfali, H.S.N.; Elaziz, M.A.; Al-Qaness, M.A.; Abbasi, A.A.; Lu, S.; Liu, F.; Li, L. A Multilevel Image Thresholding Based on Hybrid Salp Swarm Algorithm and Fuzzy Entropy. IEEE Access 2019, 7, 181405–181422. [Google Scholar] [CrossRef]
- Alresheedi, S.S.; Lu, S.; Elaziz, M.A.; Ewees, A.A. Improved multiobjective salp swarm optimization for virtual machine placement in cloud computing. Hum.-Centric Comput. Inf. Sci. 2019, 9, 15. [Google Scholar] [CrossRef]
- Abualigah, L.; Shehab, M.; Alshinwan, M.; Alabool, H. Salp swarm algorithm: A comprehensive survey. Neural Comput. Appl. 2019. [Google Scholar] [CrossRef]
- Ahmed, K.; Ewees, A.A.; El Aziz, M.A.; Hassanien, A.E.; Gaber, T.; Tsai, P.W.; Pan, J.S. A hybrid krill-ANFIS model for wind speed forecasting. In International Conference on Advanced Intelligent Systems and Informatics; Springer: Berlin, Germany, 2016; pp. 365–372. [Google Scholar]
- Alameer, Z.; Elaziz, M.A.; Ewees, A.A.; Ye, H.; Jianhua, Z. Forecasting copper prices using hybrid adaptive neuro-fuzzy inference system and genetic algorithms. Nat. Resour. Res. 2019, 28, 1385–1401. [Google Scholar] [CrossRef]
| Date (D/M/Y) | Confirmed | Date (D/M/Y) | Confirmed | Date (D/M/Y) | Confirmed |
|---|---|---|---|---|---|
| 21/1/2020 | 278 | 31/1/2020 | 9720 | 10/2/2020 | 40,554 |
| 22/1/2020 | 309 | 1/2/2020 | 11,821 | 11/2/2020 | 42,708 |
| 23/1/2020 | 571 | 2/2/2020 | 14,411 | 12/2/2020 | 44,730 |
| 24/1/2020 | 830 | 3/2/2020 | 17,283 | 13/2/2020 | 46,550 |
| 25/1/2020 | 1297 | 4/2/2020 | 20,471 | 14/2/2020 | 48,548 |
| 26/1/2020 | 1985 | 5/2/2020 | 24,363 | 15/2/2020 | 50,054 |
| 27/1/2020 | 2741 | 6/2/2020 | 28,060 | 16/2/2020 | 51,174 |
| 28/1/2020 | 4537 | 7/2/2020 | 31,211 | 17/2/2020 | 70,635 |
| 29/1/2020 | 5997 | 8/2/2020 | 34,598 | 18/2/2020 | 72,528 |
| 30/1/2020 | 7736 | 9/2/2020 | 37,251 |
| Algorithm | Parameters Setting |
|---|---|
| ANFIS | |
| GA-ANFIS | |
| PSO-ANFIS | |
| ABC-ANFIS | |
| FPA-ANFIS | |
| FPASSA-ANFIS | ∈ [0, 1], ∈ [0, 1] |
| Dataset | Method | RMSE | MAE | MAPE | RMSRE | R2 | Time |
|---|---|---|---|---|---|---|---|
| DS1 | ANFIS | 952 | 570 | 37.61 | 0.551 | 0.969 | - |
| PSO | 798 | 494 | 34.13 | 0.510 | 0.978 | 25.43 | |
| GA | 766 | 480 | 35.44 | 0.530 | 0.98 | 28.70 | |
| ABC | 878 | 564 | 39.79 | 0.593 | 0.972 | 49.27 | |
| FPA | 618 | 411 | 37.69 | 0.570 | 0.979 | 24.58 | |
| FPASSA | 609 | 391 | 32.58 | 0.497 | 0.986 | 24.55 | |
| DS2 | ANFIS | 718 | 405 | 64.20 | 1.198 | 0.858 | - |
| PSO | 620 | 353 | 52.07 | 0.870 | 0.892 | 31.64 | |
| GA | 622 | 362 | 87.91 | 3.216 | 0.902 | 34.83 | |
| ABC | 696 | 433 | 53.30 | 1.101 | 0.887 | 60.87 | |
| FPA | 622 | 371 | 80.55 | 3.152 | 0.898 | 30.42 | |
| FPASSA | 619 | 367 | 45.02 | 0.887 | 0.909 | 30.39 |
| Method | RMSE | MAE | MAPE | RMSRE | R2 | Time |
|---|---|---|---|---|---|---|
| ANN | 8750 | 5413 | 13.09 | 0.204 | 0.8991 | - |
| KNN | 12,100 | 7671 | 8.32 | 0.130 | 0.7710 | - |
| SVR | 7822 | 5354 | 8.40 | 0.080 | 0.8910 | - |
| ANFIS | 7375 | 5523 | 5.32 | 0.09 | 0.9032 | - |
| PSO | 6842 | 4559 | 5.12 | 0.08 | 0.9492 | 24.18 |
| GA | 7194 | 4963 | 5.26 | 0.08 | 0.9575 | 27.02 |
| ABC | 8327 | 6066 | 6.86 | 0.10 | 0.7906 | 46.80 |
| FPA | 6059 | 4379 | 5.04 | 0.07 | 0.9439 | 23.41 |
| FPASSA | 5779 | 4271 | 4.79 | 0.07 | 0.9645 | 23.30 |
| Data | Confirmed Cases (Expected) |
|---|---|
| 19/2/2020 | 74,406 |
| 20/2/2020 | 76,215 |
| 21/2/2020 | 78,728 |
| 22/2/2020 | 80,332 |
| 23/2/2020 | 81,617 |
| 24/2/2020 | 83,858 |
| 25/2/2020 | 86,115 |
| 26/2/2020 | 90,794 |
| 27/2/2020 | 95,695 |
| 28/2/2020 | 99,453 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-qaness, M.A.A.; Ewees, A.A.; Fan, H.; Abd El Aziz, M. Optimization Method for Forecasting Confirmed Cases of COVID-19 in China. J. Clin. Med. 2020, 9, 674. https://doi.org/10.3390/jcm9030674
Al-qaness MAA, Ewees AA, Fan H, Abd El Aziz M. Optimization Method for Forecasting Confirmed Cases of COVID-19 in China. Journal of Clinical Medicine. 2020; 9(3):674. https://doi.org/10.3390/jcm9030674
Chicago/Turabian StyleAl-qaness, Mohammed A. A., Ahmed A. Ewees, Hong Fan, and Mohamed Abd El Aziz. 2020. "Optimization Method for Forecasting Confirmed Cases of COVID-19 in China" Journal of Clinical Medicine 9, no. 3: 674. https://doi.org/10.3390/jcm9030674
APA StyleAl-qaness, M. A. A., Ewees, A. A., Fan, H., & Abd El Aziz, M. (2020). Optimization Method for Forecasting Confirmed Cases of COVID-19 in China. Journal of Clinical Medicine, 9(3), 674. https://doi.org/10.3390/jcm9030674







