Models for Facilitated Transport Membranes: A Review
Abstract
:1. Introduction
Mathematical Background
- C = concentration
- J = flux
- r = dissipative term
- r’ = generative term
- v = velocity
- x, y, z = cartesian directions
- t = time
2. Mobile Carrier Systems
2.1. Models for Mobile Carrier Facilitated Transport Membranes
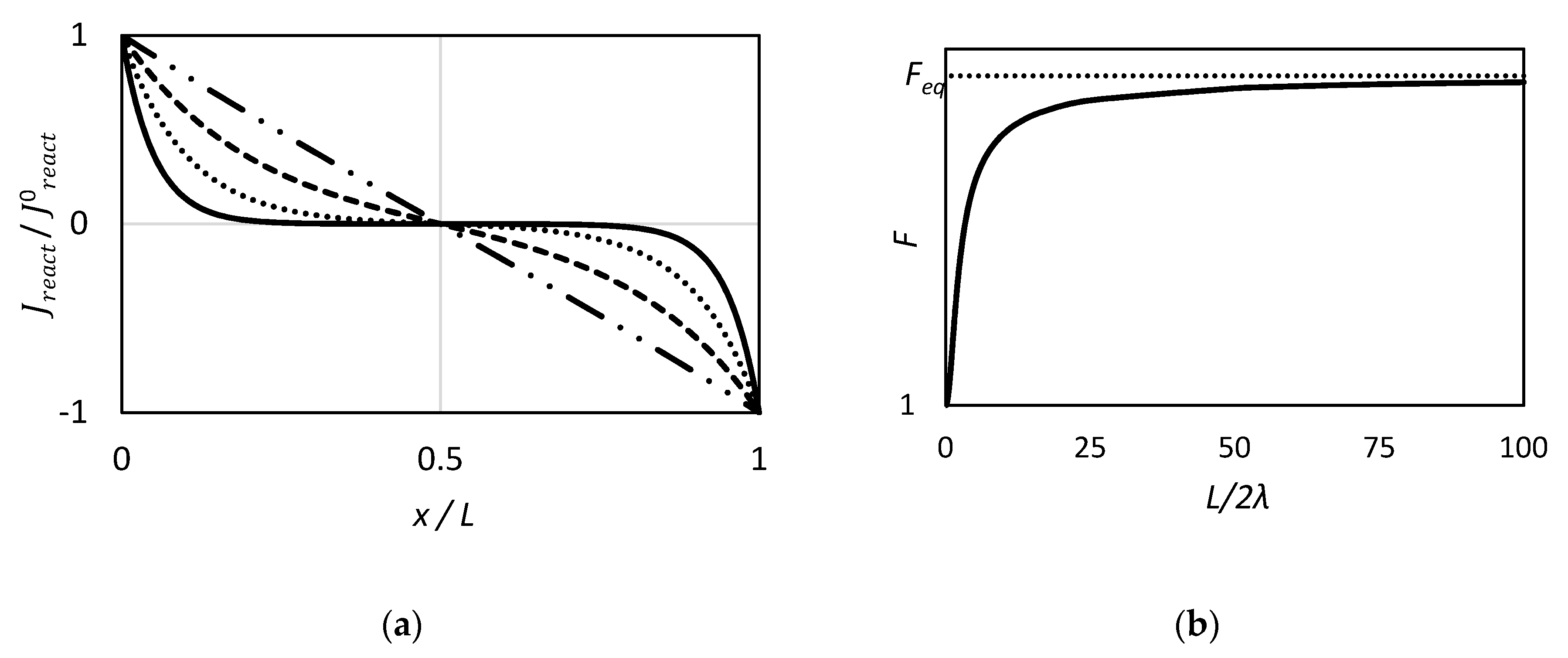
2.1.1. Friedlander and Keller, 1965. Mass Transfer in Reacting System Near Equilibrium: Use of the Affinity Function
2.1.2. Blumenthal and Katchalsky, 1969. The Effect of Carrier Association–Dissociation Rate on Membrane Permeation
2.1.3. Goddard et al., 1969. On Membrane Diffusion with Near Chemical Equilibrium Reaction
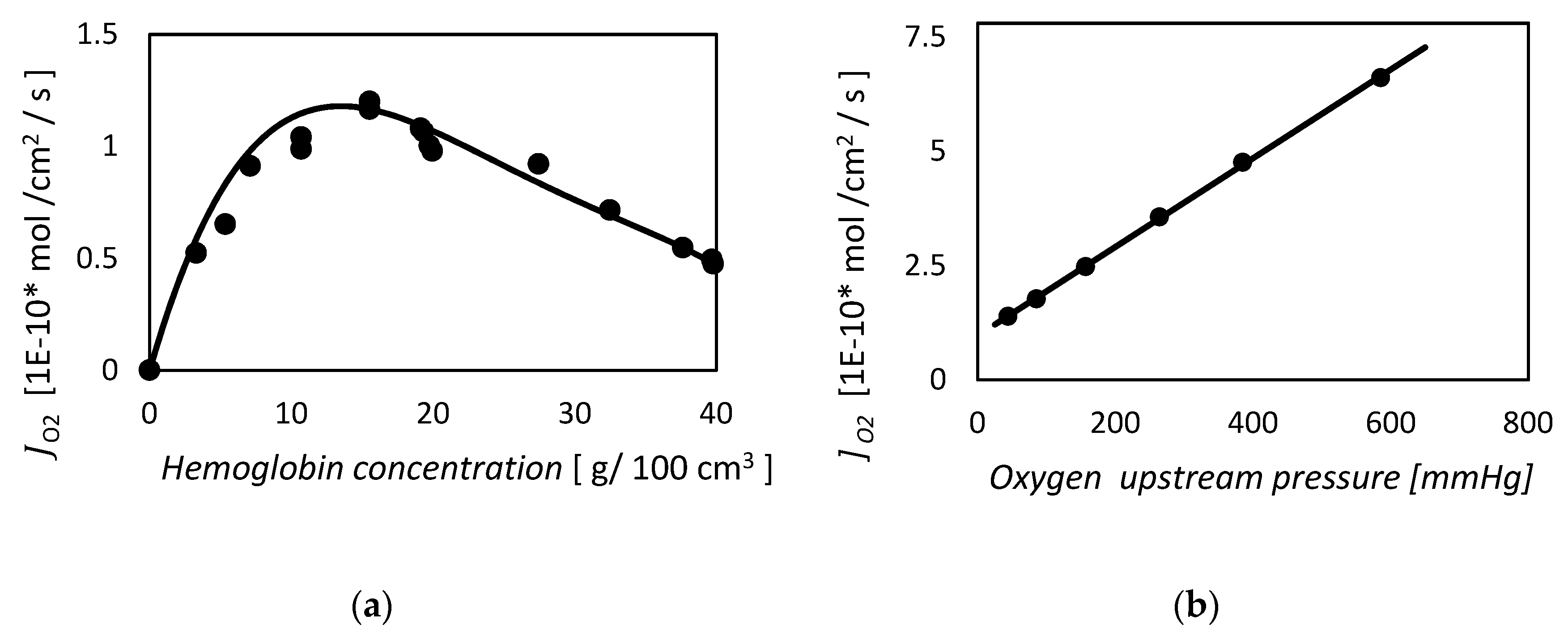
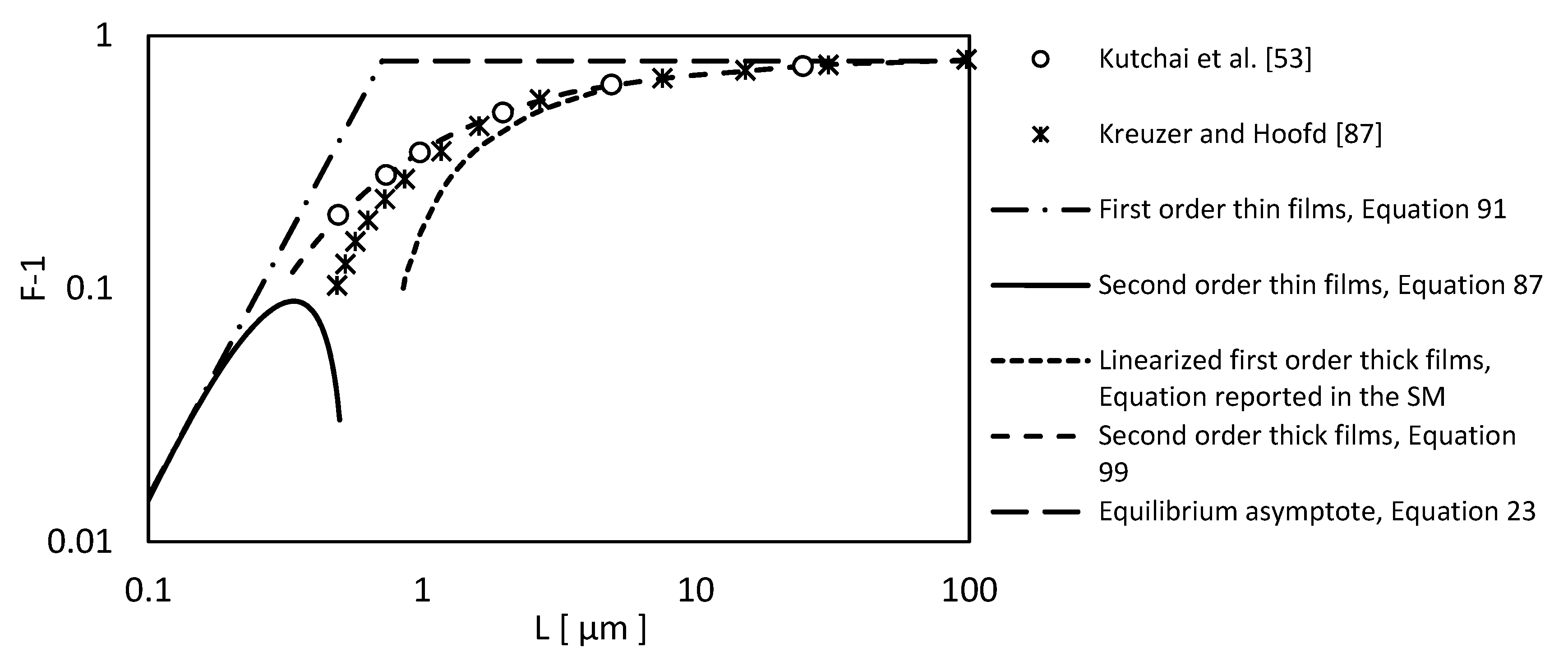
2.1.4. Kreuzer and Hoofd, 1970. Facilitated Diffusion of Oxygen in the Presence of Hemoglobin
2.1.5. Kreuzer and Hoofd, 1972, Factors Influencing Facilitated Diffusion of Oxygen in the Presence of Hemoglobin and Myoglobin
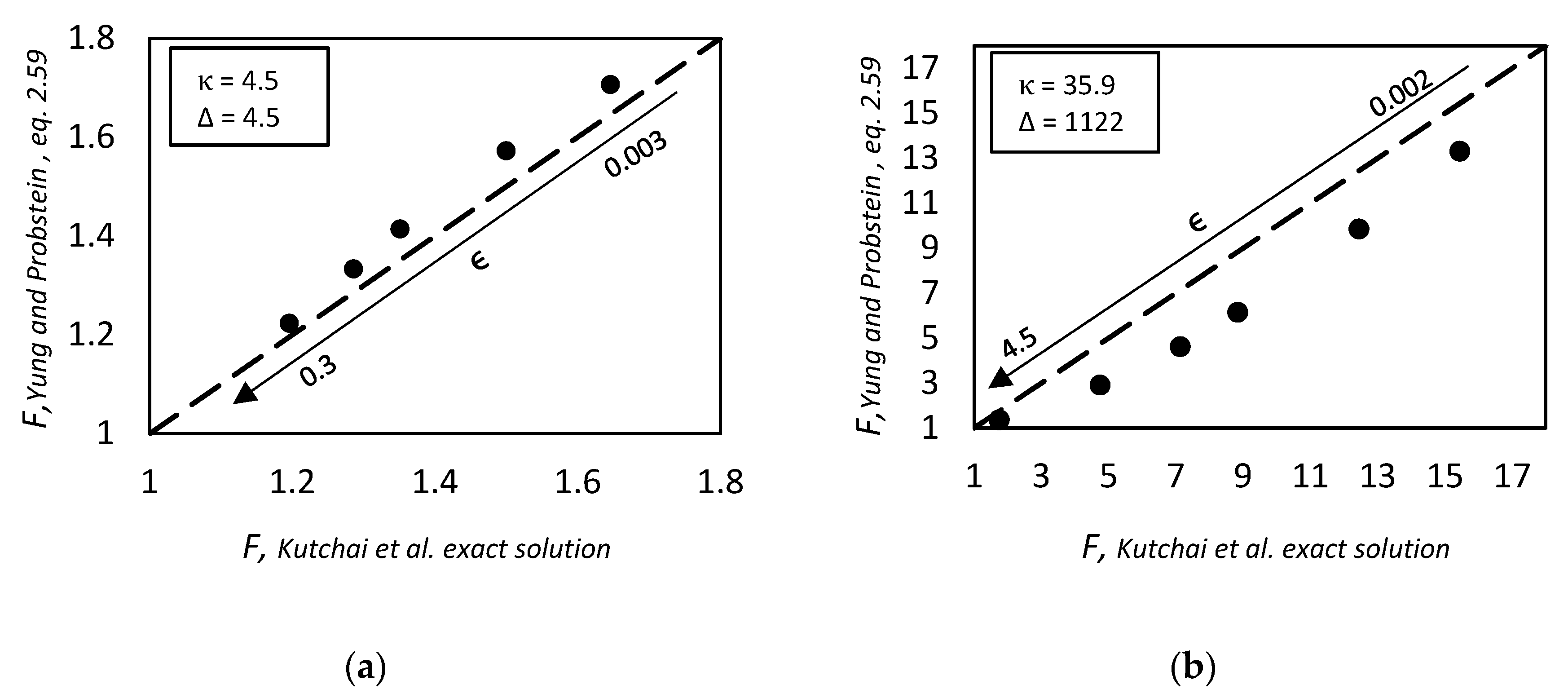
2.1.6. Yung and Probstein, 1973. Similarity Considerations in Facilitated Transport
2.1.7. Smith et al., 1973. An Analysis of Carrier Facilitated Transport
2.1.8. Smith, Quinn, 1979. The Prediction of Facilitation Factors for Reaction-Augmented Membrane Transport
2.1.9. Noble et al., 1986. Effect of Mass Transfer Resistance on Facilitated Transport
2.1.10. Basaran et al., 1989. Facilitated Transport with Unequal Carrier and Complex Diffusivities
2.1.11. Jemaa and Noble, 1992. Improved Analytical Prediction of Facilitation Factors in Facilitated Transport
2.1.12. Teramoto, 1994. Approximate Solution of Facilitation Factor in Facilitated Transport
2.1.13. Morales-Cabrera et al., 2002. Approximate Method for the Solution of Facilitated Transport Problems in Liquid Membranes
3. Fixed Carrier Systems
3.1. Models for Fixed Sites Facilitated Transport Membranes
3.1.1. Dual Mode Theory
- = solute concentration in polymer phase
- = solute concentration trapped in ‘holes’
- = solute concentration dissolved
- = solute partial pressure
- = Henry’s constant
- = holes saturation level concentration
- = affinity constant
3.1.2. Cussler et al., 1989. On the Limits of Facilitated Diffusion
3.1.3. Noble, 1990. Analysis of Facilitated Transport with Fixed Site Carrier Membranes
- -
- the mathematical derivation of the mass balance analog of the mobile carrier case, which allows to use, in analytical approximation methods already known, Equation (2.89) while an excess of carrier is considered.
- -
- the functional dependence of the actual complex diffusivity in such systems on morphological and chemical parameters, Equation (182).
3.1.4. Noble, 1991, Facilitated Transport Mechanism in Fixed Site Carrier Membranes
3.1.5. Noble, 1992, Generalized Microscopic Mechanism of Facilitated Transport in Fixed Site Carrier Membranes
3.1.6. Kang et al., 1995. Analysis of Facilitated Transport in Solid Membranes with Fixed Site Carriers
3.1.7. Zarca et al., 2017. A Practical Approach to Fixed-Site Carrier Facilitated Transport Modeling for the Separation of Propylene/Propane Mixtures Through Silver-Containing Polymeric Membranes
3.1.8. Zarca et al., 2017. Generalized Predictive Modeling for Facilitated Transport Membranes Accounting For Fixed and Mobile Carriers
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Schultz, J.S.; Goddard, J.D.; Suchdeo, S.R. Facilitated transport via carrier-mediated diffusion in membranes: Part I. Mechanistic aspects, experimental systems and characteristic regimes. AIChE J. 1974, 20, 417–445. [Google Scholar] [CrossRef]
- Goddard, J.D.; Schultz, J.S.; Suchdeo, S.R. Facilitated transport via carrier—mediated diffusion in membranes: Part II. Mathematical aspects and analyses. AIChE J. 1974, 20, 625–645. [Google Scholar] [CrossRef]
- Osterhout, W.J.V. Some models of protoplasmic surfaces. Cold Spring Harb. Symp. Quant. Biol. 1940, 8, 51–62. [Google Scholar] [CrossRef]
- Scholander, P.F. Oxygen Transport through Hemoglobin Solutions. Science 1960, 131, 585–590. [Google Scholar] [CrossRef] [PubMed]
- Wittemberg, J.B. The Molecular Mechanism of Hemoglobin-Facilitated Oxygen Diffusion. J. Biol. Chem. 1966, 241, 104–114. [Google Scholar]
- Noble, D.R.; Koval, A.C.; Pellegrino, J. Facilitated Transport Membrane Systems. Chem. Eng. Prog. 1989, 85, 58–70. [Google Scholar]
- Kemena, L.L.; Noble, R.D.; Kemp, N.J. Optimal regimes of facilitated transport. J. Memb. Sci. 1983, 15, 259–274. [Google Scholar] [CrossRef]
- Basaran, O.A.; Burban, P.M.; Auvil, S.R. Facilitated transport with unequal carrier and complex diffusivities. Ind. Eng. Chem. Res. 1989, 28, 108–119. [Google Scholar] [CrossRef]
- Way, J.D.; Noble, R.D.; Flynn, T.M.; Sloan, E.D. Liquid membrane transport: A survey. J. Memb. Sci. 1982, 12, 239–259. [Google Scholar] [CrossRef]
- Basu, A.; Akhtar, J.; Rahman, M.H.; Islam, M.R. A Review of Separation of Gases Using Membrane Systems. Pet. Sci. Technol. 2004, 22, 1343–1368. [Google Scholar] [CrossRef]
- Sholl, D.S.; Lively, R.P. Seven chemical separations to change the world. Nature 2016, 532, 435–437. [Google Scholar] [CrossRef] [PubMed]
- Strathmann, H. Membrane separation processes: Current relevance and future opportunities. AIChE J. 2001, 47, 1077–1087. [Google Scholar] [CrossRef]
- Teramoto, M.; Matsuyama, H.; Yamashiro, T.; Katayama, Y. Separation of ethylene from ethane by supported liquid membranes containing silver nitrate as a carrier. J. Chem. Eng. Jpn. 1986, 19, 419–424. [Google Scholar] [CrossRef]
- Ho, W.S.; Dalrymple, D.C. Facilitated transport of olefins in Ag+-containing polymer membranes. J. Memb. Sci. 1994, 91, 13–25. [Google Scholar] [CrossRef]
- Funke, H.H.; Noble, R.D.; Koval, C.A. Separation of gaseous olefin isomers using facilitated transport membranes. J. Memb. Sci. 1993, 82, 229–236. [Google Scholar] [CrossRef]
- Faiz, R.; Li, K. Olefin/paraffin separation using membrane based facilitated transport/chemical absorption techniques. Chem. Eng. Sci. 2012, 73, 261–284. [Google Scholar] [CrossRef]
- Azizi, S.; Kaghazchi, T.; Kargari, A. Propylene/propane separation using N-methyl pyrrolidone/AgNO3 supported liquid membrane. J. Taiwan Inst. Chem. Eng. 2015, 57, 1–8. [Google Scholar] [CrossRef]
- Zarca, R.; Ortiz, A.; Gorri, D.; Ortiz, I. Generalized predictive modeling for facilitated transport membranes accounting for fixed and mobile carriers. J. Memb. Sci. 2017, 542, 168–176. [Google Scholar] [CrossRef]
- Jung, J.P.; Park, C.H.; Lee, J.H.; Park, J.T.; Kim, J.-H.; Kim, J.H. Facilitated olefin transport through membranes consisting of partially polarized silver nanoparticles and PEMA-g-PPG graft copolymer. J. Memb. Sci. 2018, 548, 149–156. [Google Scholar] [CrossRef]
- Weston, M.H.; Colón, Y.J.; Bae, Y.-S.; Garibay, S.J.; Snurr, R.Q.; Farha, O.K.; Hupp, J.T.; Nguyen, S.T. High propylene/propane adsorption selectivity in a copper(catecholate)-decorated porous organic polymer. J. Mater. Chem. A 2014, 2, 299–302. [Google Scholar] [CrossRef]
- Choi, H.; Lee, J.H.; Kim, Y.R.; Song, D.; Kang, S.W.; Lee, S.S.; Kang, Y.S. Tetrathiafulvalene as an electron acceptor for positive charge induction on the surface of silver nanoparticles for facilitated olefin transport. Chem. Commun. 2014, 50, 3194. [Google Scholar] [CrossRef] [PubMed]
- Chae, I.S.; Kang, S.W.; Park, J.Y.; Lee, Y.-G.; Lee, J.H.; Won, J.; Kang, Y.S. Surface Energy-Level Tuning of Silver Nanoparticles for Facilitated Olefin Transport. Angew. Chem. Int. Ed. 2011, 50, 2982–2985. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.S.; Kang, S.W.; Kim, H.; Kim, J.H.; Won, J.; Kim, C.K.; Char, K. Interaction with Olefins of the Partially Polarized Surface of Silver Nanoparticles Activated byp-Benzoquinone and Its Implications for Facilitated Olefin Transport. Adv. Mater. 2007, 19, 475–479. [Google Scholar] [CrossRef]
- Okahata, Y.; Noguchi, H.; Seki, T. Highly selective transport of molecular oxygen in a polymer containing a cobalt porphyrin complex as a fixed carrier. Macromolecules 1986, 19, 494–496. [Google Scholar] [CrossRef]
- Nishide, H.; Ohyanagi, M.; Okada, O.; Tsuchida, E. Dual-mode transport of molecular oxygen in a membrane containing a cobalt porphyrin complex as a fixed carrier. Macromolecules 1987, 20, 417–422. [Google Scholar] [CrossRef]
- Ohyanagi, M.; Nishide, H.; Suenaga, K.; Tsuchida, E. Effect of Polymer Matrix and Metal Species on Facilitated Oxygen Transport in Metalloporphyrin (Oxygen Carrier) Fixed Membranes. Macromolecules 1988, 21, 1590–1594. [Google Scholar] [CrossRef]
- Chen, S.H.; Lai, J.Y. Polycarbonate/(N,N′-dialicylidene ethylene diamine) cobalt(II) complex membrane for gas separation. J. Appl. Polym. Sci. 1996, 59, 1129–1135. [Google Scholar] [CrossRef]
- Shentu, B.; Nishide, H. Facilitated Oxygen Transport Membranes of Picket-fence Cobaltporphyrin Complexed with Various Polymer Matrixes. Ind. Eng. Chem. Res. 2003, 42. [Google Scholar] [CrossRef]
- Preethi, N.; Shinohara, H.; Nishide, H. Reversible oxygen-binding and facilitated oxygen transport in membranes of polyvinylimidazole complexed with cobalt-phthalocyanine. React. Funct. Polym. 2006, 66, 851–855. [Google Scholar] [CrossRef]
- Li, H.; Choi, W.; Ingole, P.G.; Lee, H.K.; Baek, I.H. Oxygen separation membrane based on facilitated transport using cobalt tetraphenylporphyrin-coated hollow fiber composites. Fuel 2016, 185, 133–141. [Google Scholar] [CrossRef]
- Powell, C.E.; Qiao, G.G. Polymeric CO2/N2 gas separation membranes for the capture of carbon dioxide from power plant flue gases. J. Memb. Sci. 2006, 279, 1–49. [Google Scholar] [CrossRef]
- Adewole, J.K.; Ahmad, A.L.; Ismail, S.; Leo, C.P. Current challenges in membrane separation of CO2 from natural gas: A review. Int. J. Greenh. Gas Control 2013, 17, 46–65. [Google Scholar] [CrossRef]
- Norahim, N.; Yaisanga, P.; Faungnawakij, K.; Charinpanitkul, T.; Klaysom, C. Recent Membrane Developments for CO2 Separation and Capture. Chem. Eng. Technol. 2018, 41, 211–223. [Google Scholar] [CrossRef]
- Summary for Policymakers of IPCC Special Report on Global Warming of 1.5 °C Approved by Governments; IPCC: Geneva, Switzerland, 2018.
- Guha, A.K.; Majumdar, S.; Sirkar, K.K. Facilitated Transport of CO2 through an Immobilized Liquid Membrane of Aqueous Diethanolamine. Ind. Eng. Chem. Res. 1990, 29, 2093–2100. [Google Scholar] [CrossRef]
- Davis, R.A.; Sandall, O.C. CO2/CH4 separation by facilitated transport in amine-polyethylene glycol mixtures. AIChE J. 1993, 39, 1135–1145. [Google Scholar] [CrossRef]
- Teramoto, M.; Nakai, K.; Huang, Q.; Watari, T.; Matsuyama, H. Facilitated Transport of Carbon Dioxide through Supported Liquid Membranes of Aqueous Amine Solutions. Ind. Eng. Chem. Res. 1996, 35, 538–545. [Google Scholar] [CrossRef]
- Matsuyama, H.; Terada, A.; Nakagawara, T.; Kitamura, Y.; Teramoto, M. Facilitated transport of CO2 through polyethylenimine/poly(vinyl alcohol) blend membrane. J. Memb. Sci. 1999, 163, 221–227. [Google Scholar] [CrossRef]
- Huang, J.; Zou, J.; Ho, W.S.W. Carbon Dioxide Capture Using a CO2-Selective Facilitated Transport Membrane. Ind. Eng. Chem. Res. 2008, 47, 1261–1267. [Google Scholar] [CrossRef]
- Zou, J.; Ho, W.S.W. CO2-selective polymeric membranes containing amines in crosslinked poly(vinyl alcohol). J. Memb. Sci. 2006, 286, 310–321. [Google Scholar] [CrossRef]
- Deng, L.; Kim, T.-J.; Hägg, M.-B. Facilitated transport of CO2 in novel PVAm/PVA blend membrane. J. Memb. Sci. 2009, 340, 154–163. [Google Scholar] [CrossRef]
- Sandru, M.; Kim, T.-J.; Capala, W.; Huijbers, M.; Hägg, M.-B. Pilot scale testing of polymeric membranes for CO2 capture from coal fired power plants Selection and/or peer-review under responsibility of GHGT. Energy Procedia 2013, 37, 6473–6480. [Google Scholar] [CrossRef]
- He, X.; Lindbråthen, A.; Kim, T.-J.; Hägg, M.-B. Pilot testing on fixed-site-carrier membranes for CO2 capture from flue gas. Int. J. Greenh. Gas Control 2017, 64, 323–332. [Google Scholar] [CrossRef]
- Ansaloni, L.; Salas-Gay, J.; Ligi, S.; Baschetti, M.G. Nanocellulose-based membranes for CO2 capture. J. Memb. Sci. 2017, 522, 216–225. [Google Scholar] [CrossRef]
- Ansaloni, L.; Zhao, Y.; Jung, B.T.; Ramasubramanian, K.; Baschetti, M.G.; Ho, W.S.W. Facilitated transport membranes containing amino-functionalized multi-walled carbon nanotubes for high-pressure CO2 separations. J. Memb. Sci. 2015, 490, 18–28. [Google Scholar] [CrossRef]
- Fernández-Barquín, A.; Rea, R.; Venturi, D.; Giacinti-Baschetti, M.; De Angelis, M.G.; Casado-Coterillo, C.; Irabien, Á. Effect of relative humidity on the gas transport properties of zeolite A/PTMSP mixed matrix membranes. RSC Adv. 2018, 8, 3536–3546. [Google Scholar] [CrossRef]
- Otvagina, K.V.; Mochalova, A.E.; Sazanova, T.S.; Petukhov, A.N.; Moskvichev, A.A.; Vorotyntsev, A.V.; Afonso, C.A.M.; Vorotyntsev, I.V. Preparation and Characterization of Facilitated Transport Membranes Composed of Chitosan-Styrene and Chitosan-Acrylonitrile Copolymers Modified by Methylimidazolium Based Ionic Liquids for CO2 Separation from CH4 and N2. Membranes 2016, 6, 31. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Kim, T.-J.; Hägg, M.-B. Hybrid fixed-site-carrier membranes for CO2 removal from high pressure natural gas: Membrane optimization and process condition investigation. J. Memb. Sci. 2014, 470, 266–274. [Google Scholar] [CrossRef]
- Hanioka, S.; Maruyama, T.; Sotani, T.; Teramoto, M.; Matsuyama, H.; Nakashima, K.; Hanaki, M.; Kubota, F.; Goto, M. CO2 separation facilitated by task-specific ionic liquids using a supported liquid membrane. J. Memb. Sci. 2008, 314, 1–4. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, C.; Li, L.; Qin, W.; Xu, A. CO2 separation by supported ionic liquid membranes and prediction of separation performance. Int. J. Greenh. Gas Control 2016, 53, 79–84. [Google Scholar] [CrossRef]
- Shin, J.Y.; Yamada, S.A.; Fayer, M.D. Carbon Dioxide in a Supported Ionic Liquid Membrane: Structural and Rotational Dynamics Measured with 2D IR and Pump–Probe Experiments. J. Am. Chem. Soc. 2017, 139, 11222–11232. [Google Scholar] [CrossRef]
- Olivieri, L.; Aboukeila, H.; Giacinti Baschetti, M.; Pizzi, D.; Merlo, L.; Sarti, G.C. Humid permeation of CO2 and hydrocarbons in Aquivion® perfluorosulfonic acid ionomer membranes, experimental and modeling. J. Memb. Sci. 2017, 542, 367–377. [Google Scholar] [CrossRef]
- Kutchai, H.; Jacquez, J.A.; Mather, F.J. Nonequilibrium-Facilitated Oxygen Transport in Hemoglobin Solution. Biophys. J. 1970, 10, 38–54. [Google Scholar] [CrossRef]
- Ward, W.J. Analytical and experimental studies of facilitated transport. AIChE J. 1970, 16, 405–410. [Google Scholar] [CrossRef]
- Collatz, L. The Numerical Treatment of Differential Equations; Springer: Berlin, Germany, 1960; ISBN 3642884342. [Google Scholar]
- Kirkköprü-Dindi, A.; Noble, R.D. Optimal regimes of facilitated transport for multiple site carriers. J. Memb. Sci. 1989, 42, 13–25. [Google Scholar] [CrossRef]
- Carey, G.F.; Finlayson, B.A. Orthogonal collocation on finite elements. Chem. Eng. Sci. 1975, 30, 587–596. [Google Scholar] [CrossRef]
- Jain, R.; Schultz, J. A Numerical technique for solving carrier-mediated transport problems. J. Memb. Sci. 1982, 11, 79–106. [Google Scholar] [CrossRef]
- Barbero, A.J.; Manzanares, J.A.; Mafé, S. A Computational Study of Facilitated Diffusion Using The Boundary Element Method. J. Non-Equilib. Thermodyn. 1995, 20, 332–341. [Google Scholar] [CrossRef]
- Ramachandran, P.A. Application of the boundary element method to non-linear diffusion with reaction problems. Int. J. Numer. Methods Eng. 1990, 29, 1021–1031. [Google Scholar] [CrossRef]
- Ebadi Amooghin, A.; Moftakhari Sharifzadeh, M.M.; Zamani Pedram, M. Rigorous modeling of gas permeation behavior in facilitated transport membranes (FTMs); evaluation of carrier saturation effects and double-reaction mechanism. Greenh. Gases Sci. Technol. 2017, 8, 429–443. [Google Scholar] [CrossRef]
- Graaf, J.M.D. A system of reaction-diffusion equations: Convergence towards the stationary solution. Nonlinear Anal. Theory Methods Appl. 1990, 15, 253–267. [Google Scholar] [CrossRef]
- Feng, W. Coupled system of reaction-diffusion equations and applications in carrier facilitated diffusion. Nonlinear Anal. Theory Methods Appl. 1991, 17, 285–311. [Google Scholar] [CrossRef]
- Desvillettes, L.; Fellner, K.; Pierre, M.; Vovelle, J.; Desvillettes, L.; Fellner, K.; Pierre, M.; Vovelle, J. Global Existence for Quadratic Systems of Reaction-Diffusion. Adv. Nonlinear Stud. 2007, 7, 491–511. [Google Scholar] [CrossRef]
- Britton, N.F. Reaction-Diffusion Equations and Their Application to Biology; Academic Press: London, UK; Orlando, FL, USA, 1986. [Google Scholar]
- Caputo, M.C.; Vasseur, A. Global Regularity of Solutions to Systems of Reaction–Diffusion with Sub-Quadratic Growth in Any Dimension. Commun. Partial Differ. Equ. 2009, 34, 1228–1250. [Google Scholar] [CrossRef]
- Lo, W.-C.; Chen, L.; Wang, M.; Nie, Q. A Robust and Efficient Method for Steady State Patterns in Reaction-Diffusion Systems. J. Comput. Phys. 2012, 231, 5062–5077. [Google Scholar] [CrossRef]
- Friedlander, S.K.; Keller, K.H. Mass transfer in reacting systems near equilibrium. Chem. Eng. Sci. 1965, 20, 121–129. [Google Scholar] [CrossRef]
- Keller, K.H.; Friedlander, S.K. The Steady-State Transport of Oxygen through Hemoglobin Solutions. J. Gen. Physiol. 1966, 49, 663–679. [Google Scholar] [CrossRef]
- Wyman, J. Facilitated Diffusion and the Possible Role of Myoglobin as a Transport Mechanism. J. Biol. Chem. 1966, 241, 115–121. [Google Scholar]
- La Force, R.C.; Fatt, I. Steady-state diffusion of oxygen through whole blood. Trans. Faraday Soc. 1962, 58, 1451. [Google Scholar] [CrossRef]
- Noble, R.D.; Way, J.D.; Powers, L.A. Effect of external mass-transfer resistance on facilitated transport. Ind. Eng. Chem. Fundam. 1986, 25, 450–452. [Google Scholar] [CrossRef]
- Olander, D.R. Simultaneous mass transfer and equilibrium chemical reaction. AIChE J. 1960, 6, 233–239. [Google Scholar] [CrossRef]
- Teramoto, M. Approximate Solution of Facilitation Factors in Facilitated Transport. Ind. Eng. Chem. Res. 1994, 33, 2161–2167. [Google Scholar] [CrossRef]
- Fatt, I.; La Force, R.C. Theory of Oxygen Transport through Hemoglobin Solutions. Science 1961, 133, 1919–1921. [Google Scholar] [CrossRef]
- Zhao, Y.; Ho, W.S.W. CO2 -Selective Membranes Containing Sterically Hindered Amines for CO2 /H2 Separation. Ind. Eng. Chem. Res. 2013, 52, 8774–8782. [Google Scholar] [CrossRef]
- Tong, Z.; Ho, W.S.W. Facilitated transport membranes for CO2 separation and capture. Sep. Sci. Technol. 2017, 52, 156–167. [Google Scholar] [CrossRef]
- Tee, Y.-H.; Zou, J.; Ho, W.S.W. CO2-Selective Membranes Containing Dimethylglycine Mobile Carriers and Polyethylenimine Fixed Carrier. J. Chin. Inst. Chem. Eng. 2006, 37, 37–47. [Google Scholar] [CrossRef]
- Liao, J.; Wang, Z.; Gao, C.; Li, S.; Qiao, Z.; Wang, M.; Zhao, S.; Xie, X.; Wang, J.; Wang, S. Fabrication of high-performance facilitated transport membranes for CO2 separation. Chem. Sci. 2014, 5, 2843–2849. [Google Scholar] [CrossRef]
- Grünauer, J.; Shishatskiy, S.; Abetz, C.; Abetz, V.; Filiz, V. Ionic liquids supported by isoporous membranes for CO2/N2 gas separation applications. J. Memb. Sci. 2015, 494, 224–233. [Google Scholar] [CrossRef]
- Halder, K.; Khan, M.M.; Grünauer, J.; Shishatskiy, S.; Abetz, C.; Filiz, V.; Abetz, V. Blend membranes of ionic liquid and polymers of intrinsic microporosity with improved gas separation characteristics. J. Memb. Sci. 2017, 539, 368–382. [Google Scholar] [CrossRef]
- Zhao, Y.; Winston Ho, W.S. Steric hindrance effect on amine demonstrated in solid polymer membranes for CO2 transport. J. Memb. Sci. 2012, 415–416, 132–138. [Google Scholar] [CrossRef]
- Blumenthal, R.; Katchalsky, A. The effect of the carrier association-dissociation rate on membrane permeation. Biochim. Biophys. Acta 1969, 173, 357–369. [Google Scholar] [CrossRef]
- Goddard, J.D.; Schultz, J.S.; Bassett, R.J. On membrane diffusion with near-equilibrium reaction. Chem. Eng. Sci. 1970, 25, 665–683. [Google Scholar] [CrossRef]
- Van Dyke, M. Perturbation Methods in Fluid Mechanics; Academic Press: New York, NY, USA, 1964; ISBN 10: 0127130500. [Google Scholar]
- Kreuzer, F.; Hoofd, L.J.C. Facilitated diffusion of oxygen in the presence of hemoglobin. Respir. Physiol. 1970, 8, 280–302. [Google Scholar] [CrossRef]
- Kreuzer, F.; Hoofd, L.J.C. Factors influencing facilitated diffusion of oxygen in the presence of hemoglobin and myoglobin. Respir. Physiol. 1972, 15, 104–124. [Google Scholar] [CrossRef]
- Smith, K.A.; Meldon, J.H.; Colton, C.K. An analysis of carrier-facilitated transport. AIChE J. 1973, 19, 102–111. [Google Scholar] [CrossRef]
- Hoofd, L.; Kreuzer, F. A new mathematical approach for solving carrier-facilitated steady-state diffusion problems. J. Math. Biol. 1979, 8, 1–13. [Google Scholar] [CrossRef]
- Yung, D.; Probstein, R.F. Similarity considerations in facilitated transport. J. Phys. Chem. 1973, 77, 2201–2205. [Google Scholar] [CrossRef]
- Airy, G.B. ON the Intensity of Light in the neighbourhood of a Caustic. Trans. Camb. Philos. Soc. 1838, 6, 379–402. [Google Scholar]
- Bdzil, J.; Carlier, C.C.; Frisch, H.L.; Ward, W.J.; Breiter, M.W. Analysis of potential difference in electrically induced carrier transport systems. J. Phys. Chem. 1973, 77, 846–850. [Google Scholar] [CrossRef]
- Smith, D.R.; Quinn, J.A. The prediction of facilitation factors for reaction augmented membrane transport. AIChE J. 1979, 25, 197–200. [Google Scholar] [CrossRef]
- Donaldson, T.L.; Quinn, J.A. Carbon dioxide transport through enzymatically active synthetic membranes. Chem. Eng. Sci. 1975, 30, 103–115. [Google Scholar] [CrossRef]
- Folkner, C.A.; Noble, R.D. Transient response of facilitated transport membranes. J. Memb. Sci. 1983, 12, 289–301. [Google Scholar] [CrossRef]
- Jemaa, N.; Noble, R.D. Improved analytical prediction of facilitation factors in facilitated transport. J. Memb. Sci. 1992, 70, 289–293. [Google Scholar] [CrossRef]
- Van Krevelen, D.W.; Hoftijzer, P.J. Kinetics of gas-liquid reactions part I. General theory. Recl. Trav. Chim. Pays-Bas 2010, 67, 563–586. [Google Scholar] [CrossRef]
- Morales-Cabrera, M.A.; Pérez-Cisneros, E.S.; Ochoa-Tapia, J.A. Approximate Method for the Solution of Facilitated Transport Problems in Liquid Membranes. Ind. Eng. Chem. Res. 2002, 41, 4626–4631. [Google Scholar] [CrossRef]
- Morales-Cabrera, M.A. Factores de mejora en membranas liquidas. Master’s Thesis, Universidad Autonoma Metropolitana, Mexico City, México, 2000. [Google Scholar]
- Cussler, E.L.; Aris, R.; Bhown, A. On the limits of facilitated diffusion. J. Memb. Sci. 1989, 43, 149–164. [Google Scholar] [CrossRef]
- Venturi, D.; Grupkovic, D.; Sisti, L.; Baschetti, M.G. Effect of humidity and nanocellulose content on Polyvinylamine-nanocellulose hybrid membranes for CO2 capture. J. Memb. Sci. 2018, 548, 263–274. [Google Scholar] [CrossRef]
- Rafiq, S.; Deng, L.; Hägg, M.-B. Role of Facilitated Transport Membranes and Composite Membranes for Efficient CO2 Capture—A Review. ChemBioEng Rev. 2016, 3, 68–85. [Google Scholar] [CrossRef]
- Langmuir, I. The Adsorption of Gases on Plane Surfaces of Glass, Mica and Platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Masel, R.I. Principles of Adsorption and Reaction on Solid Surfaces; Wiley: Hoboken, NJ, USA, 1996; ISBN 0471303925. [Google Scholar]
- Nishide, H.; Kawakami, H.; Suzuki, T.; Azechi, Y.; Soejima, Y.; Tsuchida, E. Effect of polymer matrix on the oxygen diffusion via a cobalt porphyrin fixed in a membrane. Macromolecules 1991, 24, 6306–6309. [Google Scholar] [CrossRef]
- Yoshikawa, M.; Ezaki, T.; Sanui, K.; Ogata, N. Selective permeation of carbon dioxide through synthetic polymer membranes having pyridine moiety as a fixed carrier. J. Appl. Polym. Sci. 1988, 35, 145–154. [Google Scholar] [CrossRef]
- Yoshikawa, M.; Fujimoto, K.; Kinugawa, H.; Kitao, T.; Kamiya, Y.; Ogata, N. Specialty polymeric membranes. V. Selective permeation of carbon dioxide through synthetic polymeric membranes having 2-(N,N-dimethyl)aminoethoxycarbonyl moiety. J. Appl. Polym. Sci. 1995, 58, 1771–1778. [Google Scholar] [CrossRef]
- Barrer, R.M. Diffusivities in Glassy Polymers for the Dual Mode Sorption Model. J. Memb. Sci. 1984, 18, 25–35. [Google Scholar] [CrossRef]
- Noble, R.D. Analysis of facilitated transport with fixed site carrier membranes. J. Memb. Sci. 1990, 50, 207–214. [Google Scholar] [CrossRef]
- Noble, R.D. Facilitated transport mechanism in fixed site carrier membranes. J. Memb. Sci. 1991, 60, 297–306. [Google Scholar] [CrossRef]
- Noble, R.D. Generalized microscopic mechanism of facilitated transport in fixed site carrier membranes. J. Memb. Sci. 1992, 75, 121–129. [Google Scholar] [CrossRef]
- Kang, Y.S.; Hong, J.-M.; Jang, J.; Kim, U.Y. Analysis of facilitated transport in solid membranes with fixed site carriers 1. Single RC circuit model. J. Memb. Sci. 1996, 109, 149–157. [Google Scholar] [CrossRef]
- Hong, J.-M.; Kang, Y.S.; Jang, J.; Kim, U.Y. Analysis of facilitated transport in polymeric membrane with fixed site carrier 2. Series RC circuit model. J. Memb. Sci. 1996, 109, 159–163. [Google Scholar] [CrossRef]
- Zarca, R.; Ortiz, A.; Gorri, D.; Ortiz, I. A practical approach to fixed-site-carrier facilitated transport modeling for the separation of propylene/propane mixtures through silver-containing polymeric membranes. Sep. Purif. Technol. 2017, 180, 82–89. [Google Scholar] [CrossRef]
- Henry, W. Experiments on the Quantity of Gases Absorbed by Water, at Different Temperatures, and under Different Pressures. Philos. Trans. R. Soc. Lond. 1803, 93, 29–274. [Google Scholar] [CrossRef]
- Meares, P. The Diffusion of Gases Through Polyvinyl Acetate. J. Am. Chem. Soc. 1954, 76, 3415–3422. [Google Scholar] [CrossRef]
- Barrer, R.M.; Barrie, J.A.; Slater, J. Sorption and diffusion in ethyl cellulose. Part III. Comparison between ethyl cellulose and rubber. J. Polym. Sci. 1958, 27, 177–197. [Google Scholar] [CrossRef]
- Petropoulos, J.H. Quantitative analysis of gaseous diffusion in glassy polymers. J. Polym. Sci. Part A 1970, 8, 1797–1801. [Google Scholar] [CrossRef]
- Michaels, A.S.; Vieth, W.R.; Barrie, J.A. Diffusion of Gases in Polyethylene Terephthalate. J. Appl. Phys. 1963, 34, 13–20. [Google Scholar] [CrossRef]
- Paul, D.R.; Koros, W.J. Effect of partially immobilizing sorption on permeability and the diffusion time lag. J. Polym. Sci. Polym. Phys. Ed. 1976, 14, 675–685. [Google Scholar] [CrossRef]
- Koros, W.J.; Paul, D.R.; Rocha, A.A. Carbon dioxide sorption and transport in polycarbonate. J. Polym. Sci. Polym. Phys. Ed. 1976, 14, 687–702. [Google Scholar] [CrossRef]
- Fredrickson, G.H.; Helfand, E. Dual-mode transport of penetrants in glassy polymers. Macromolecules 1985, 18, 2201–2207. [Google Scholar] [CrossRef]
- Ogata, N.; Sanui, K.; Fujimura, H. Active transport membrane for chlorine ion. J. Appl. Polym. Sci. 1980, 25, 1419–1425. [Google Scholar] [CrossRef]
- Przewoźna, M.; Gajewski, P.; Michalak, N.; Bogacki, M.B.; Skrzypczak, A. Determination of the Percolation Threshold for the Oxalic, Tartaric, and Lactic Acids Transport through Polymer Inclusion Membranes with 1-Alkylimidazoles as a Carrier. Sep. Sci. Technol. 2014, 49, 1745–1755. [Google Scholar] [CrossRef]
- Riggs, J.A.; Smith, B.D. Facilitated Transport of Small Carbohydrates through Plasticized Cellulose Triacetate Membranes. Evidence for Fixed-Site Jumping Transport Mechanism. J. Am. Chem. Soc. 1997, 119, 2765–2766. [Google Scholar] [CrossRef]
- Smith, B.D.; Gardiner, S.J.; Munro, T.A.; Paugam, M.-F.; Riggs, J.A. Facilitated Transport of Carbohydrates, Catecholamines, and Amino Acids Through Liquid and Plasticized Organic Membranes. J. Incl. Phenom. Mol. Recognit. Chem. 1998, 32, 121–131. [Google Scholar] [CrossRef]
- Tsuchida, E.; Nishide, H.; Ohyanagi, M.; Kawakami, H. Facilitated transport of molecular oxygen in the membranes of polymer-coordinated cobalt Schiff base complexes. Macromolecules 1987, 20, 1907–1912. [Google Scholar] [CrossRef]
- Yoshikawa, M.; Shudo, S.; Sanui, K.; Ogata, N. Active transport of organic acids through poly(4-vinylpyridine-co-acrylonitrile) membranes. J. Memb. Sci. 1986, 26, 51–61. [Google Scholar] [CrossRef]
- Noble, R.D. Relationship of system properties to performance in facilitated transport systems. Gas Sep. Purif. 1988, 2, 16–19. [Google Scholar] [CrossRef]
- Way, J.D.; Noble, R.D. Hydrogen sulfide facilitated transport in perfluorosulfonic acid membranes. In Liquid Membranes; American Chemical Society: Washington, DC, USA, 1987; Chapter 9; pp. 123–137. [Google Scholar]
- Way, J.D.; Noble, R.D.; Reed, D.L.; Ginley, G.M.; Jarr, L.A. Facilitated transport of CO2 in ion exchange membranes. AIChE J. 1987, 33, 480–487. [Google Scholar] [CrossRef]
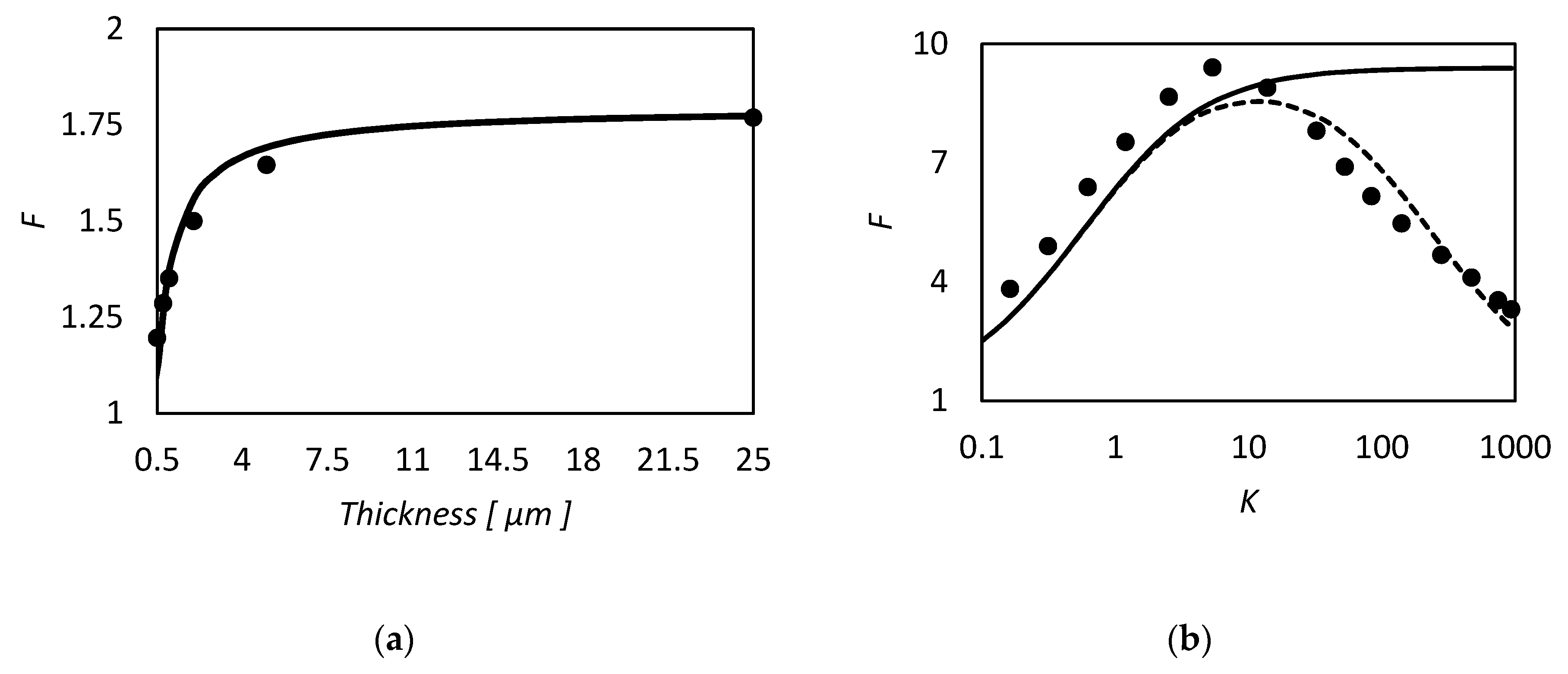
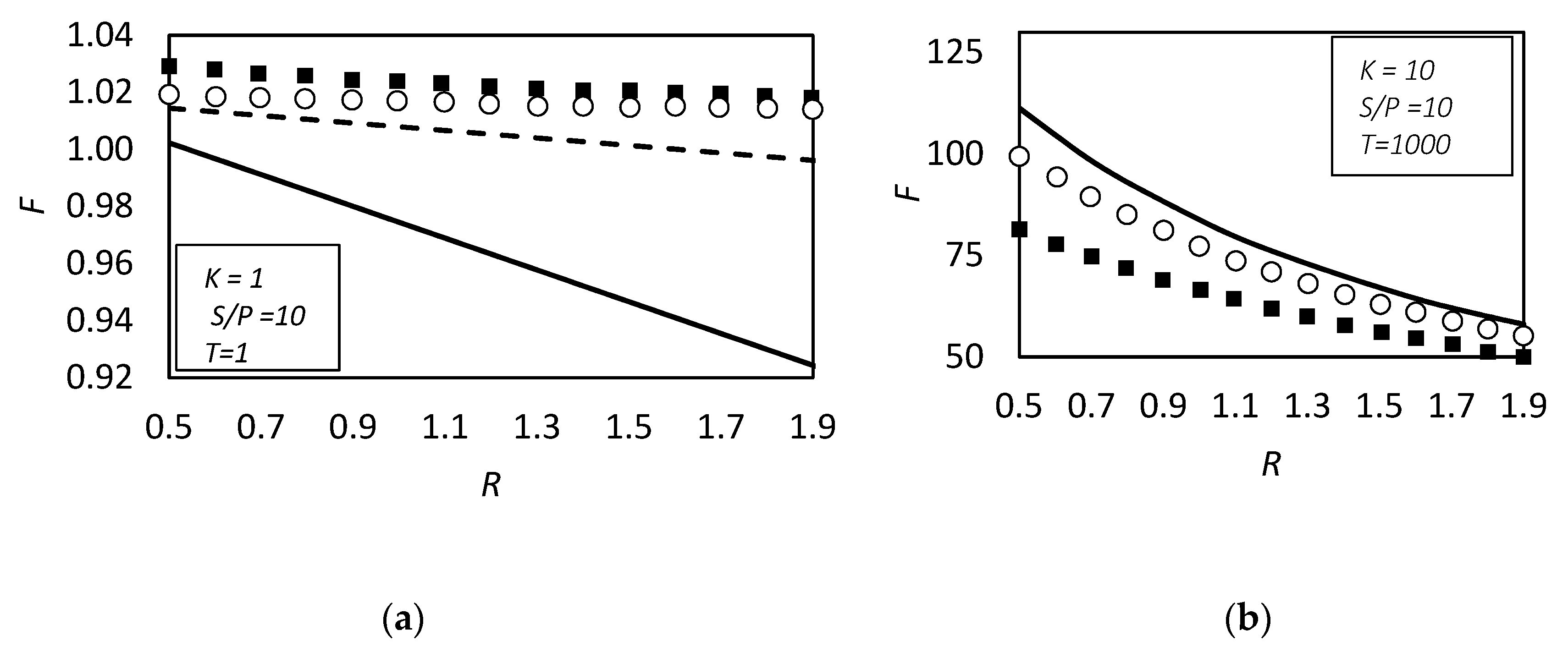
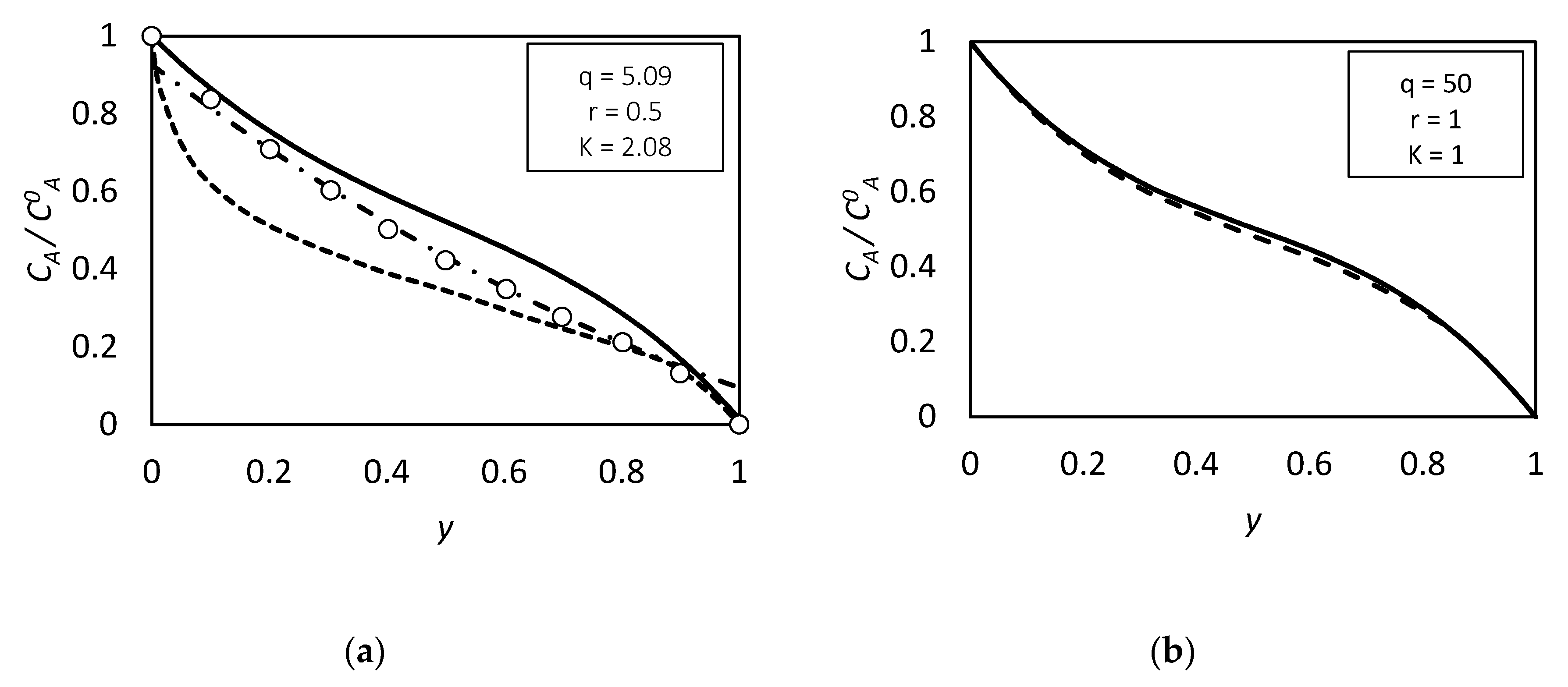
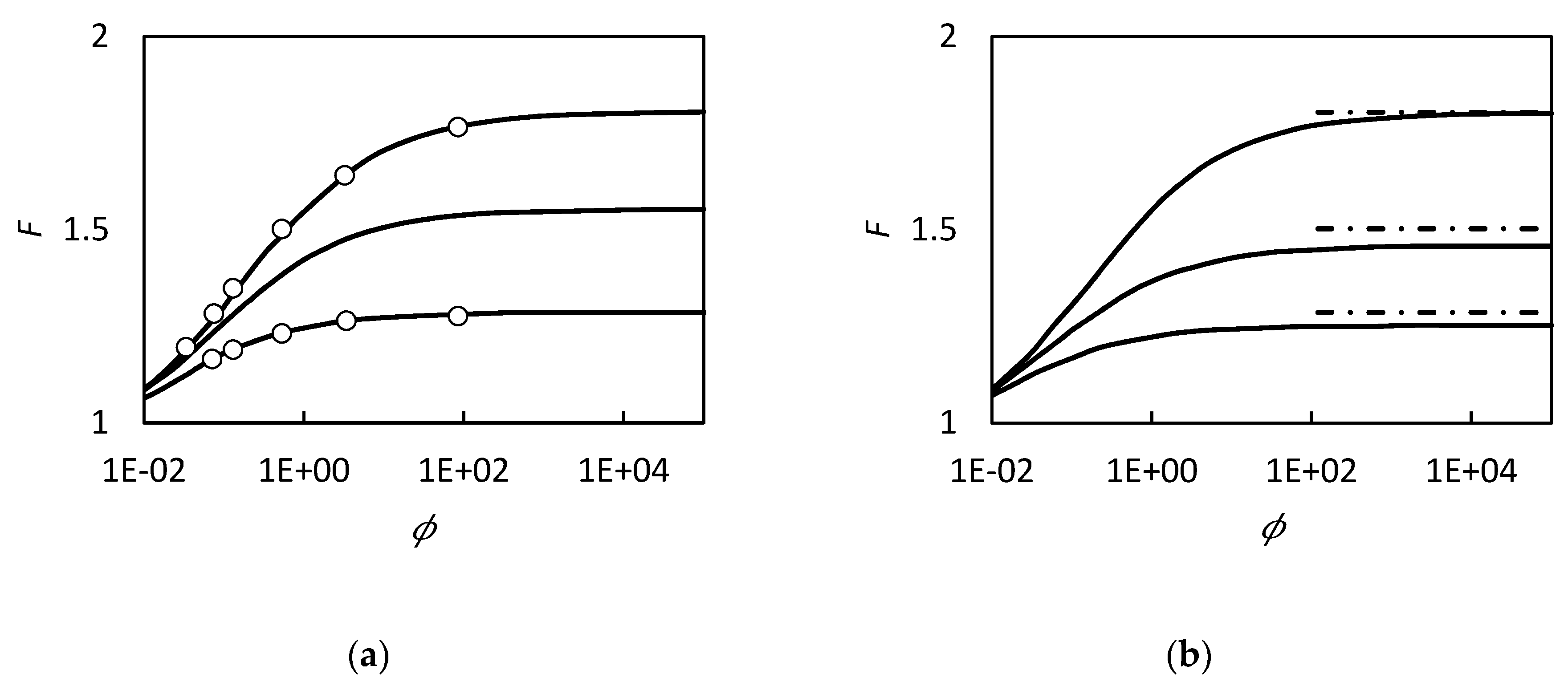
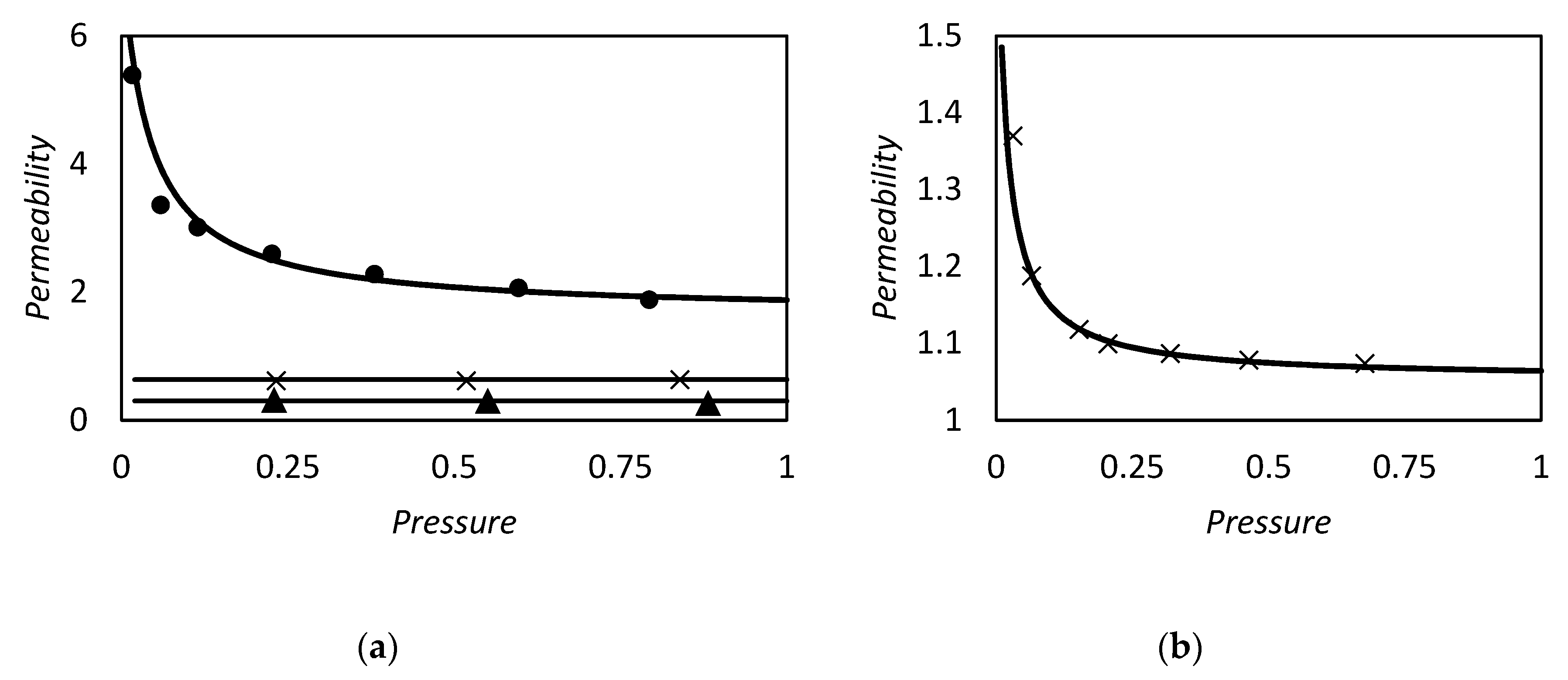
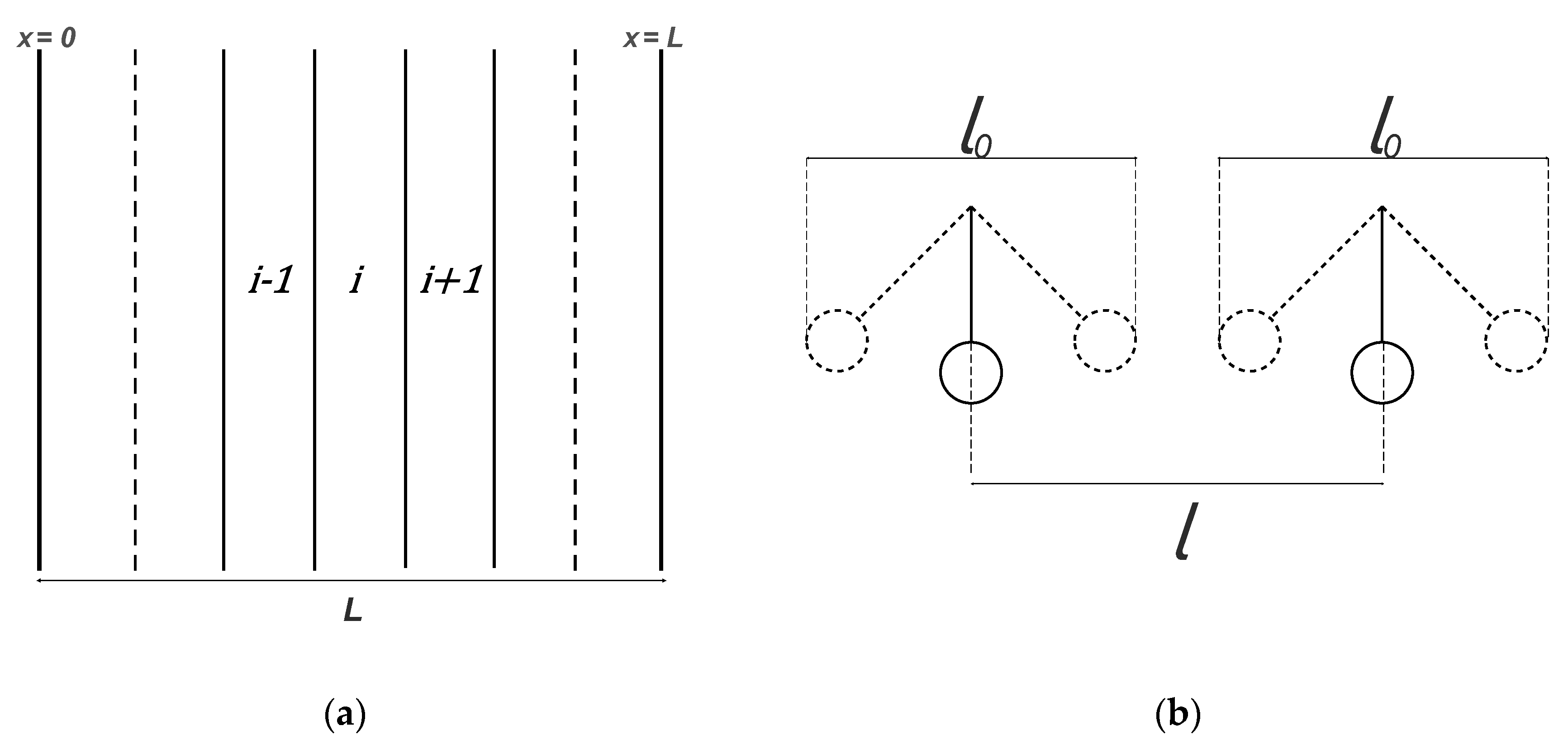
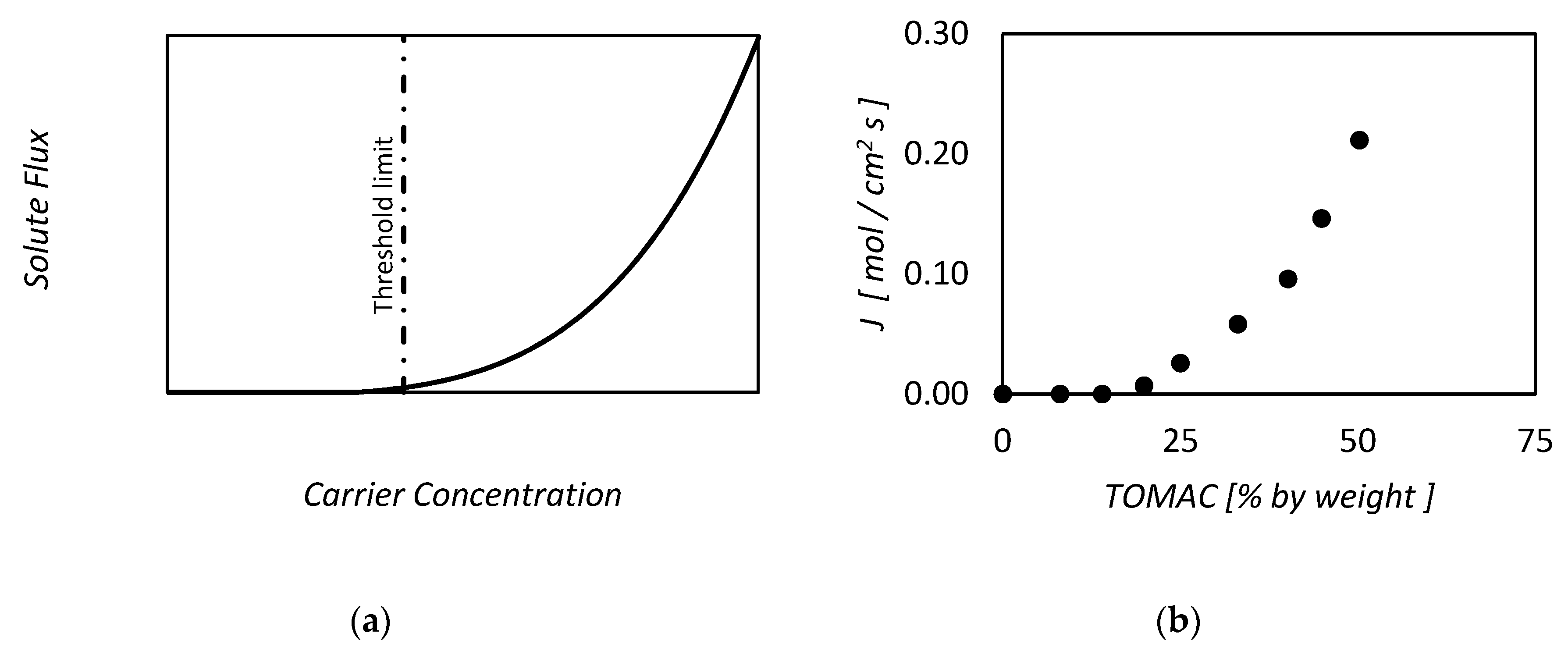
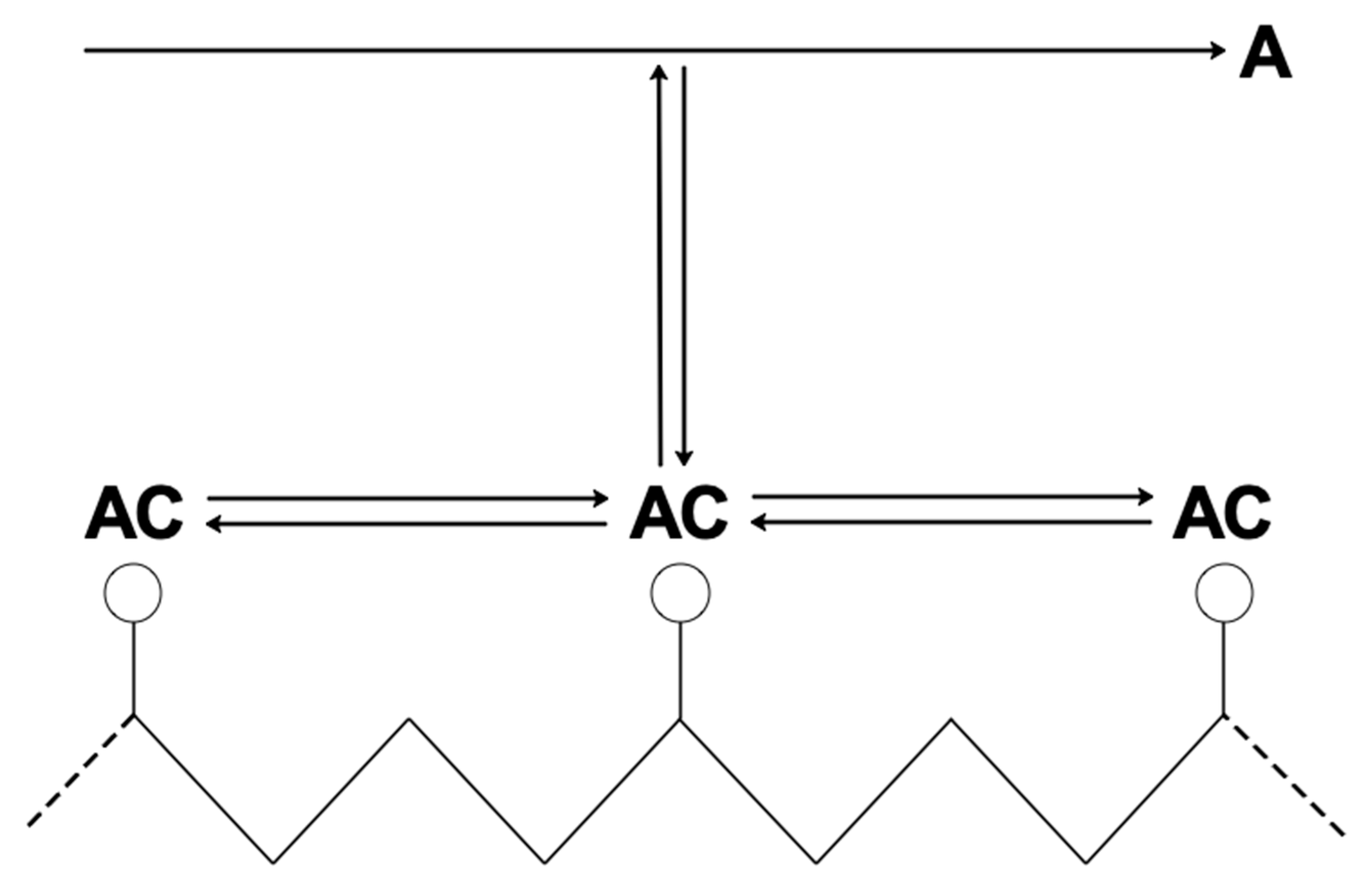
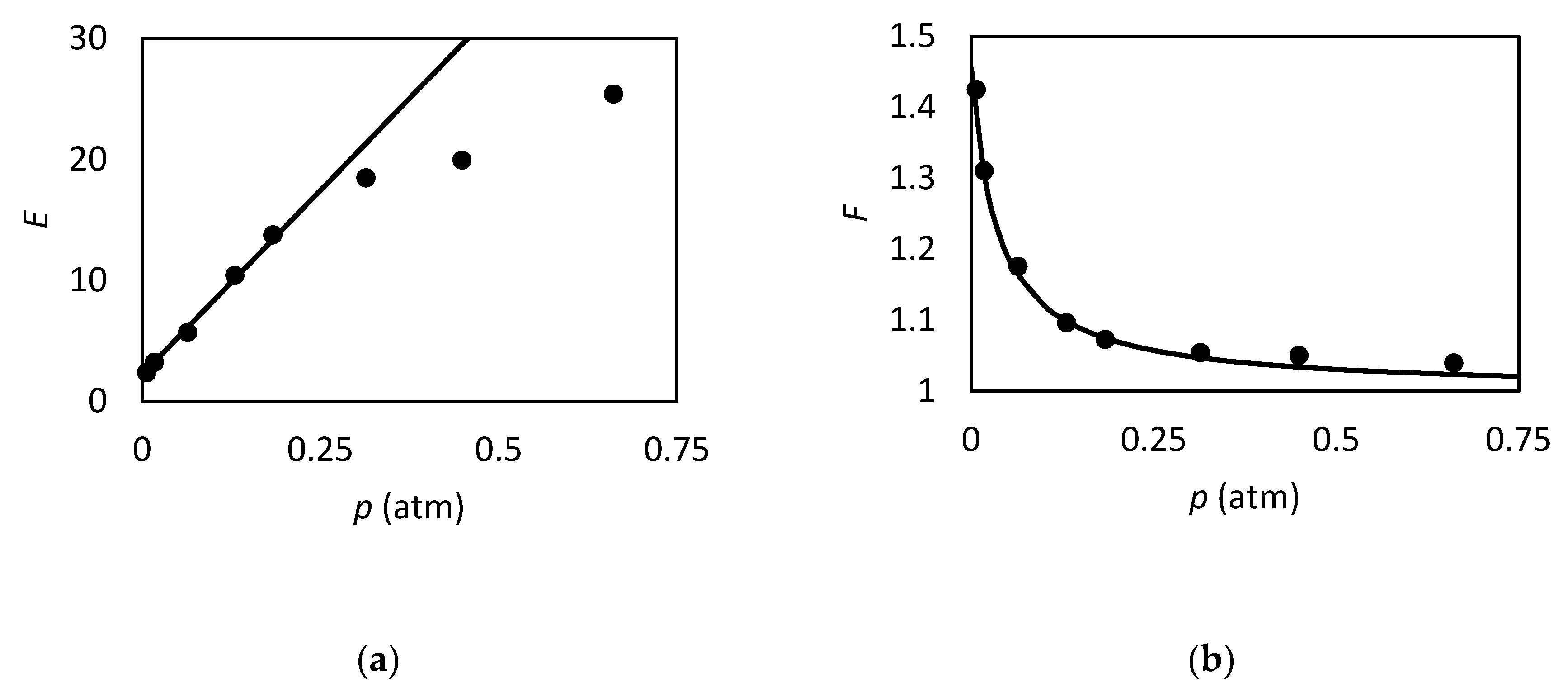
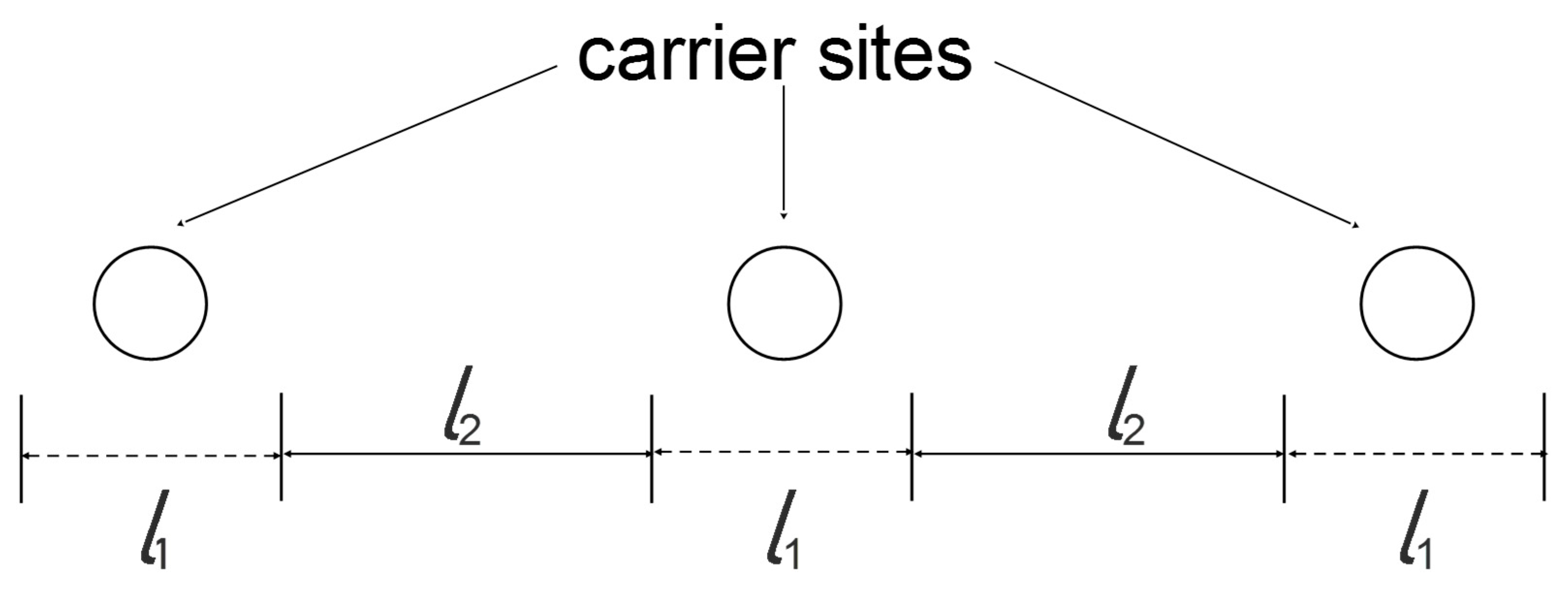
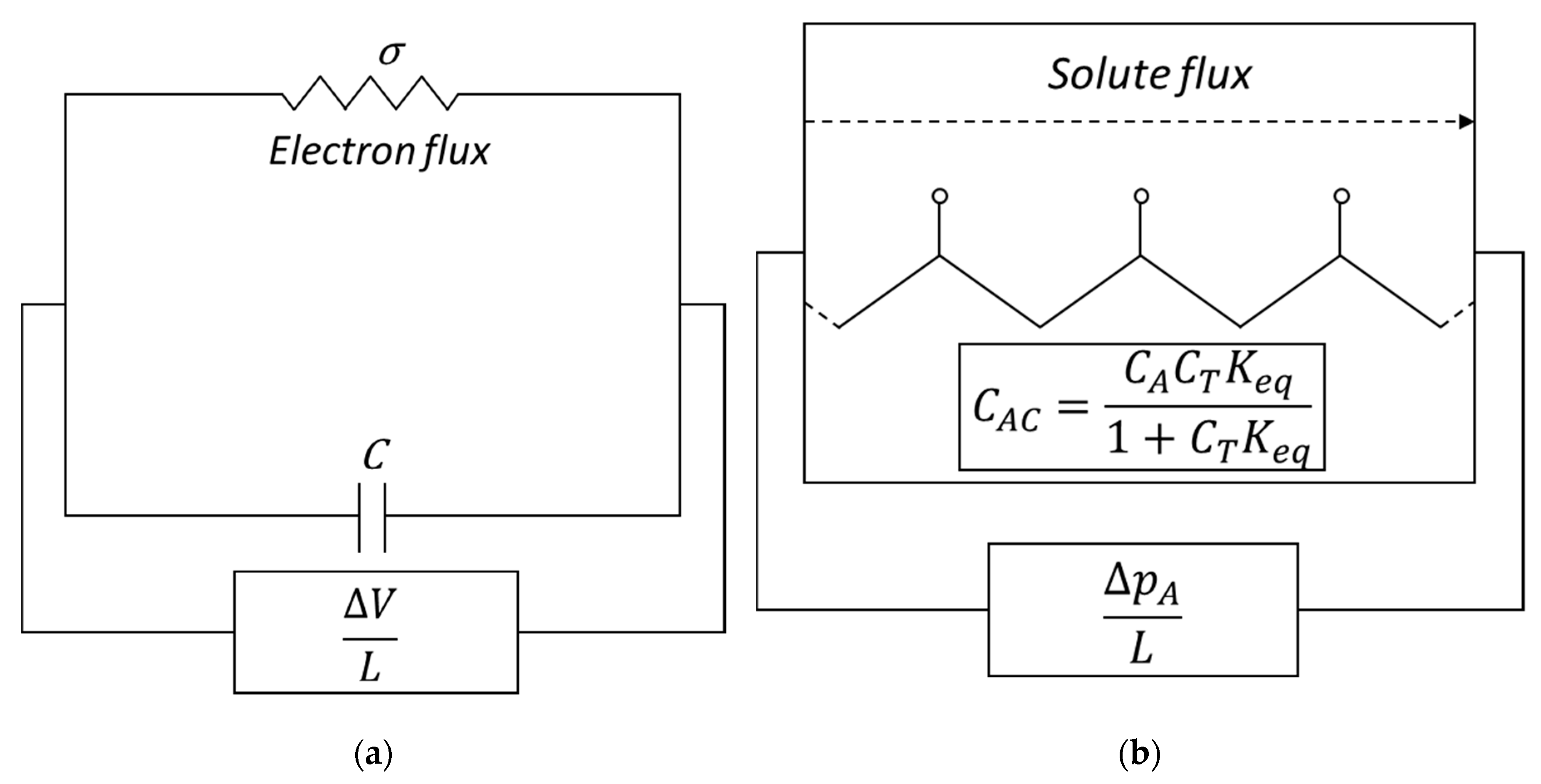
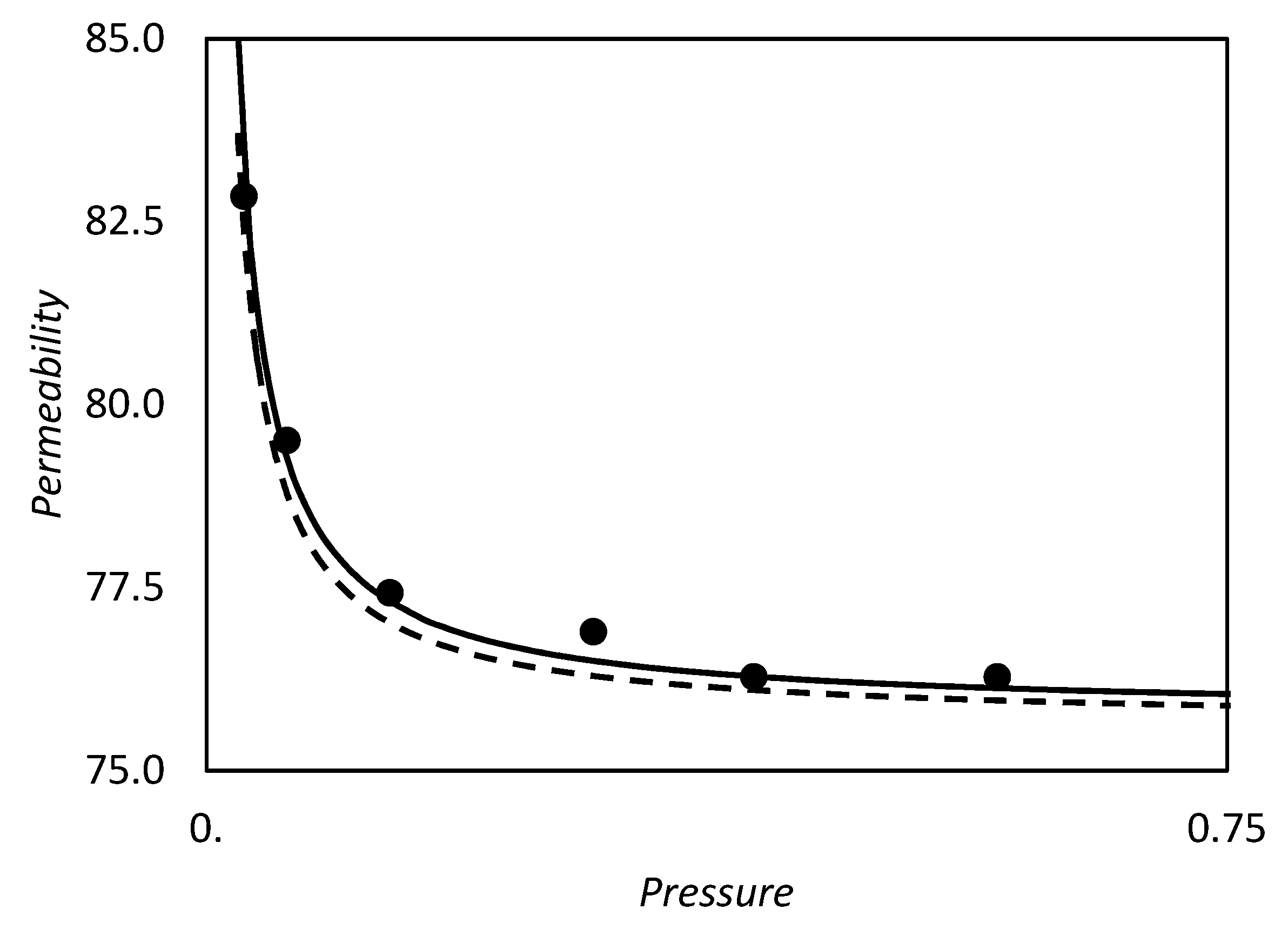
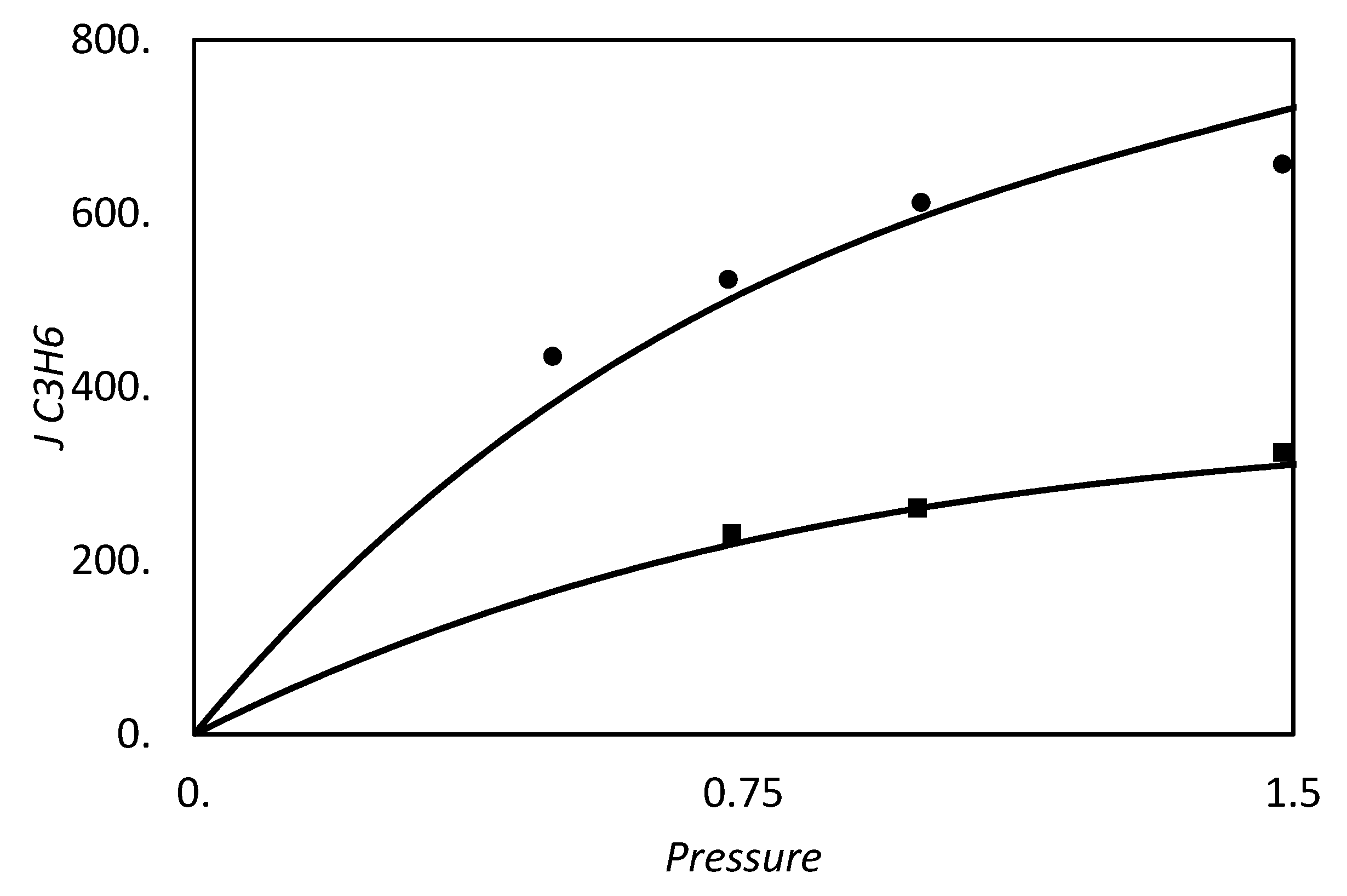
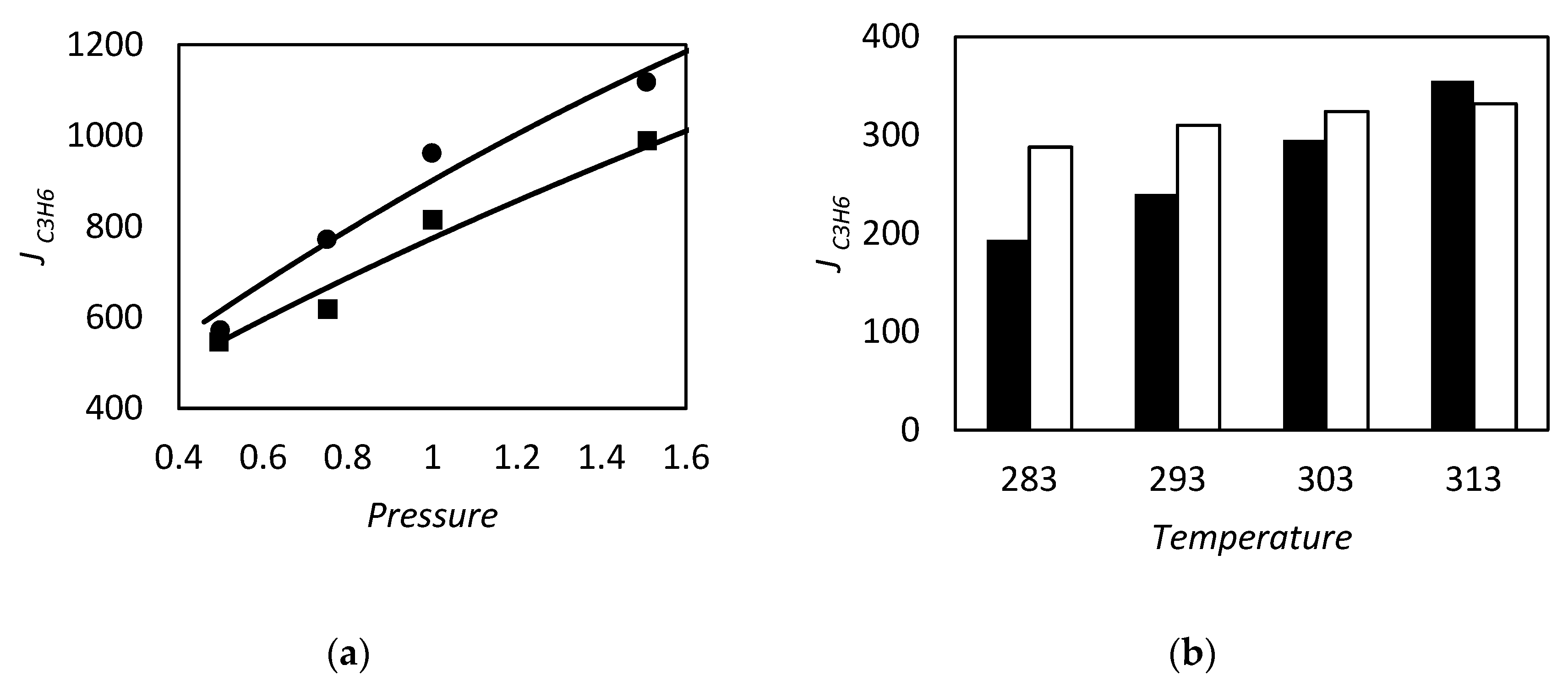
| RC circuit | Facilitated Systems | |
|---|---|---|
| Flux | ||
| Driving Force | ||
| Proportionality | ||
| Capacitor Effect |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rea, R.; De Angelis, M.G.; Baschetti, M.G. Models for Facilitated Transport Membranes: A Review. Membranes 2019, 9, 26. https://doi.org/10.3390/membranes9020026
Rea R, De Angelis MG, Baschetti MG. Models for Facilitated Transport Membranes: A Review. Membranes. 2019; 9(2):26. https://doi.org/10.3390/membranes9020026
Chicago/Turabian StyleRea, Riccardo, Maria Grazia De Angelis, and Marco Giacinti Baschetti. 2019. "Models for Facilitated Transport Membranes: A Review" Membranes 9, no. 2: 26. https://doi.org/10.3390/membranes9020026
APA StyleRea, R., De Angelis, M. G., & Baschetti, M. G. (2019). Models for Facilitated Transport Membranes: A Review. Membranes, 9(2), 26. https://doi.org/10.3390/membranes9020026







