Molecular Modeling Investigations of Sorption and Diffusion of Small Molecules in Glassy Polymers
Abstract
1. Introduction
2. Background and Methodology
2.1. Molecular Dynamics
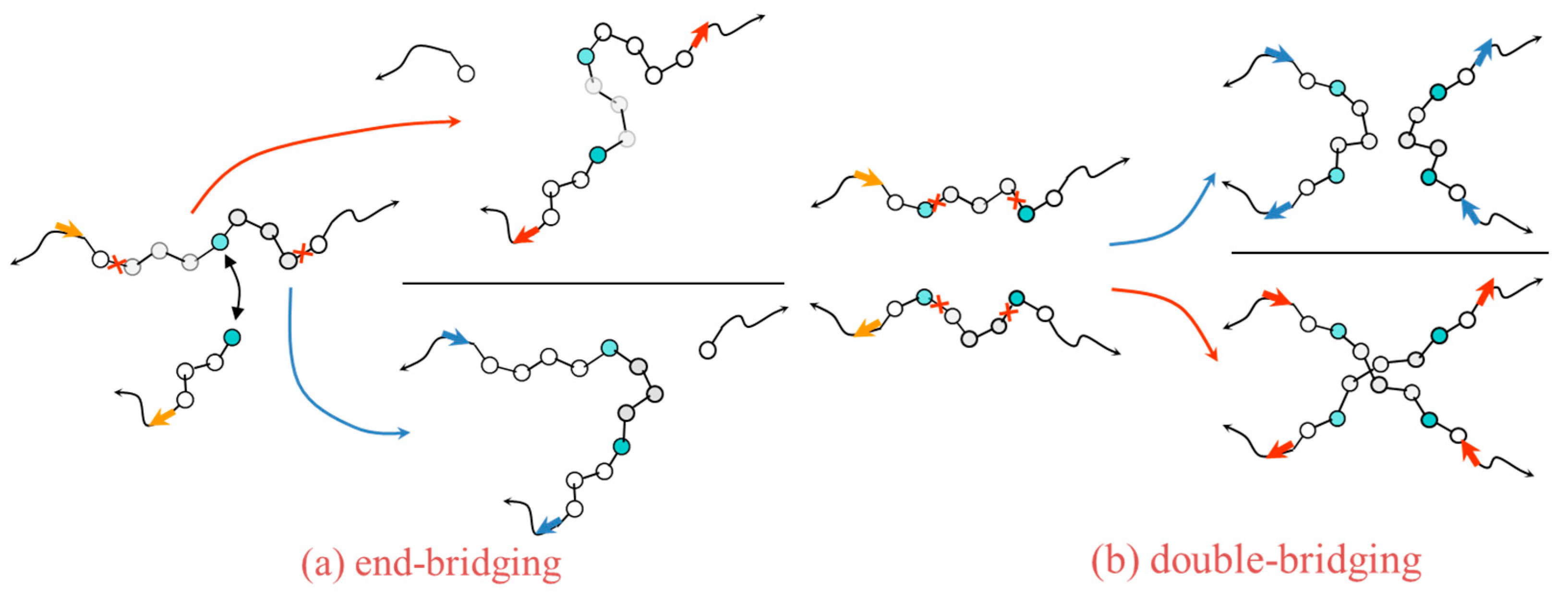
2.2. Monte Carlo
2.3. Methods for the Molecular Simulation of Penetrant Sorption
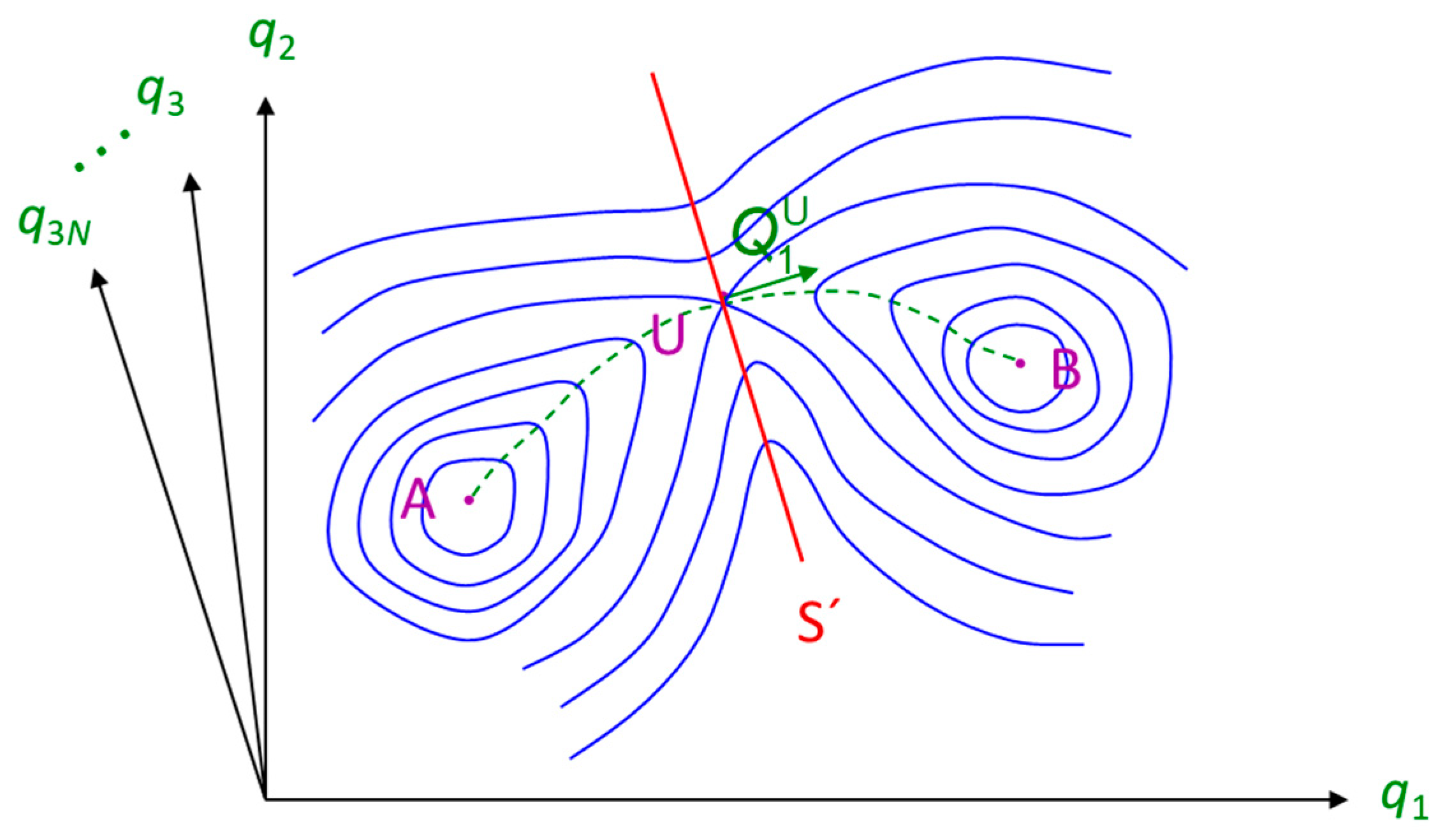
2.4. Molecular Simulation Methods for the Study of Infrequent Events
2.5. Interactions and Generation of Realistic Structures
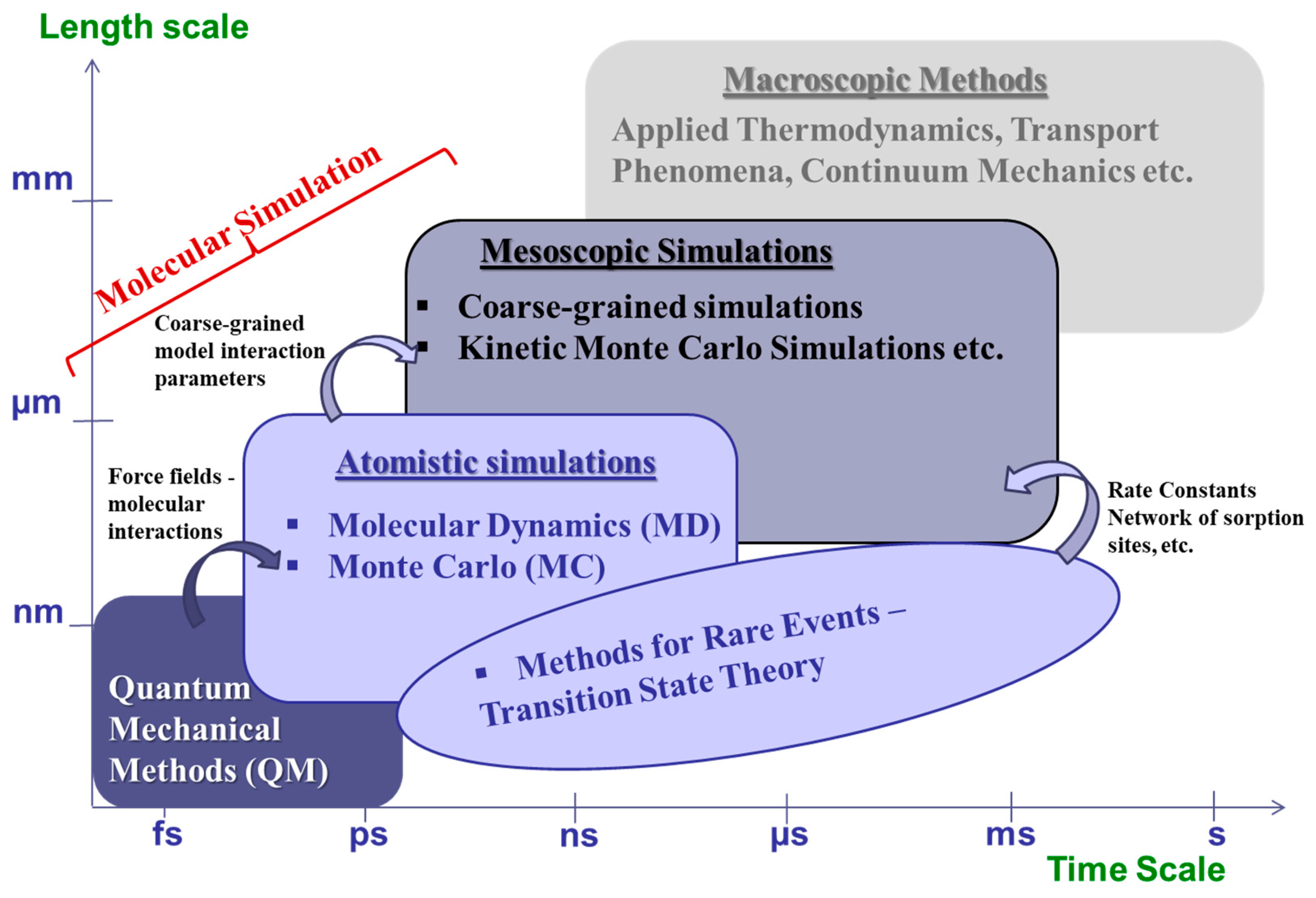
3. Coarse-Graining and Multiscale Approaches in Sorption and Diffusivity Prediction
4. Mechanistic Aspects of Sorption and Transport
4.1. Sorption
4.2. Diffusion
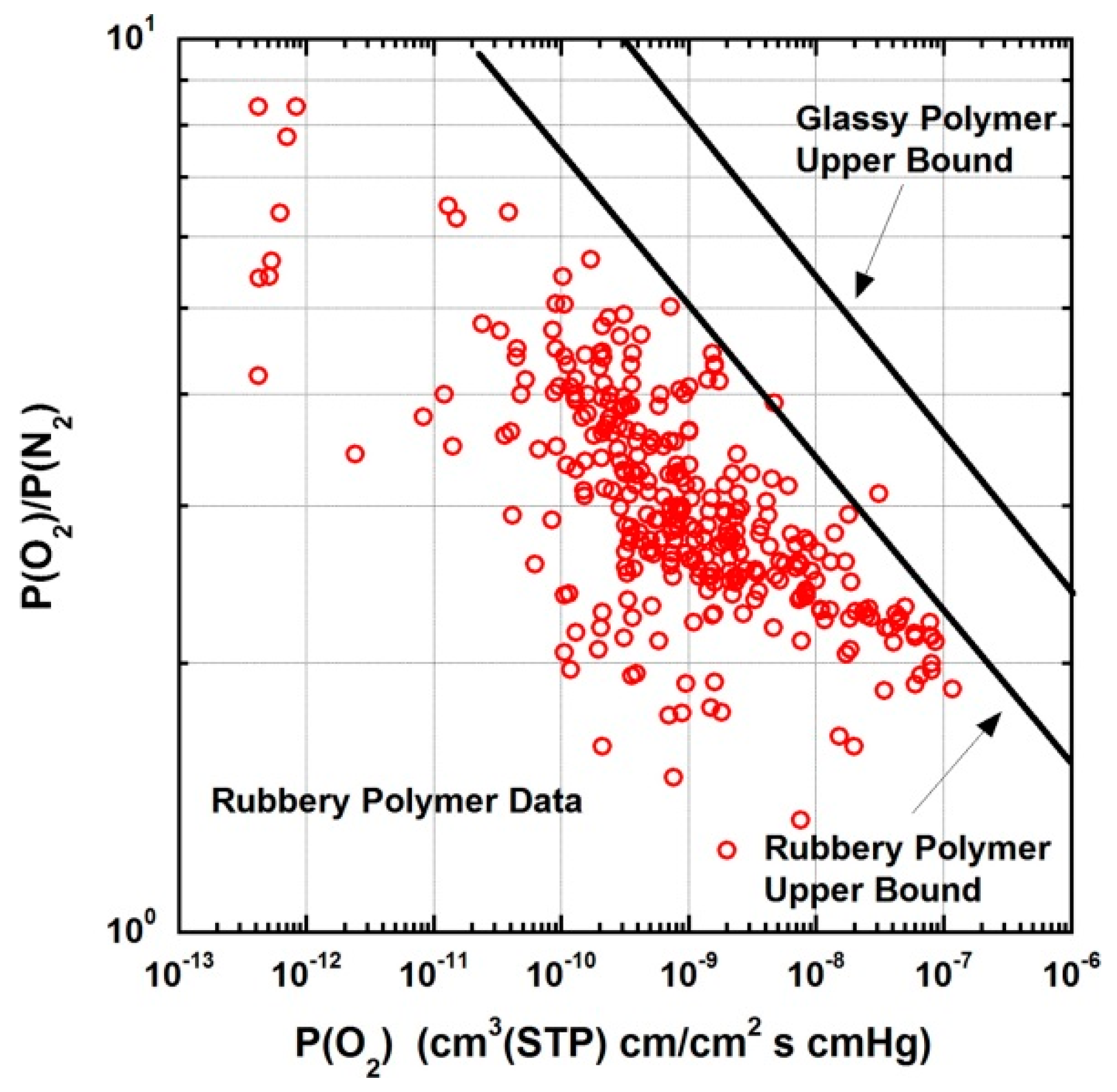
5. New Materials, Challenges and Future Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Maginn, E.J. From discovery to data: What must happen for molecular simulation to become a mainstream chemical engineering tool. AIChE J. 2009, 55, 1304–1310. [Google Scholar] [CrossRef]
- Weiß, H.; Deglmann, P.; in ‘t Veld, P.J.; Cetinkaya, M.; Schreiner, E. Multiscale Materials Modeling in an Industrial Environment. Annu. Rev. Chem. Biomol. Eng. 2016, 7, 65–86. [Google Scholar] [CrossRef] [PubMed]
- Goldbeck, G. The Economic Impact of Molecular Modelling of Chemicals and Materials. Goldbeck Consulting: 2012. Available online: https://gerhardgoldbeck.files.wordpress.com/2014/01/the-economic-impact-of-modelling.pdf (accessed on 15 April 2019).
- Materials Genome Initiative USA. Available online: https://www.mgi.gov (accessed on 15 April 2019).
- OCTA Project Japan. Available online: http://octa.jp/about-octa/project (accessed on 15 April 2019).
- European Materials Modelling Council European Union. Available online: https://emmc.info (accessed on 15 April 2019).
- Gusev, A.A.; Müller-Plathe, F.; van Gunsteren, W.F.; Suter, U.W. Dynamics of small molecules in bulk polymers. In Atomistic Modeling of Physical Properties; Monnerie, L., Suter, U.W., Eds.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 207–247. [Google Scholar] [CrossRef]
- Theodorou, D.N. Molecular Simulations of Sorption and Diffusion in Amorphous Polymers. In Diffusion in Polymers; Neogi, P., Ed.; Marcel Dekker Inc.: New York, NY, USA, 1996; p. 67. [Google Scholar]
- Theodorou, D.N. Principles of Molecular Simulation of Gas Transport in Polymers. In Materials Science of Membranes for Gas and Vapor Separation; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006; pp. 49–94. [Google Scholar]
- Colón, Y.J.; Fairen-Jimenez, D.; Wilmer, C.E.; Snurr, R.Q. High-Throughput Screening of Porous Crystalline Materials for Hydrogen Storage Capacity near Room Temperature. J. Phys. Chem. C 2014, 118, 5383–5389. [Google Scholar] [CrossRef]
- Crank, J.; Park, G.S. Diffusion in Polymers; Academic Press: New York, NY, USA, 1968. [Google Scholar]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Robeson, L.M. The upper bound revisited. J. Membr. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
- Robeson, L.M. Correlation of separation factor versus permeability for polymeric membranes. J. Membr. Sci. 1991, 62, 165–185. [Google Scholar] [CrossRef]
- Robeson, L.M.; Liu, Q.; Freeman, B.D.; Paul, D.R. Comparison of transport properties of rubbery and glassy polymers and the relevance to the upper bound relationship. J. Membr. Sci. 2015, 476, 421–431. [Google Scholar] [CrossRef]
- Robeson, L.M.; Smith, Z.P.; Freeman, B.D.; Paul, D.R. Contributions of diffusion and solubility selectivity to the upper bound analysis for glassy gas separation membranes. J. Membr. Sci. 2014, 453, 71–83. [Google Scholar] [CrossRef]
- Haile, J.M. Molecular Dynamics Simulation: Elementary Methods; John Wiley & Sons, Inc.: New York, NY, USA, 1992; p. 489. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation; Cambridge University Press: New York, NY, USA, 2002. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: New York, NY, USA, 1987. [Google Scholar]
- Pant, P.V.K.; Theodorou, D.N. Variable Connectivity Method for the Atomistic Monte Carlo Simulation of Polydisperse Polymer Melts. Macromolecules 1995, 28, 7224–7234. [Google Scholar] [CrossRef]
- Mavrantzas, V.G.; Boone, T.D.; Zervopoulou, E.; Theodorou, D.N. End-Bridging Monte Carlo: A Fast Algorithm for Atomistic Simulation of Condensed Phases of Long Polymer Chains. Macromolecules 1999, 32, 5072–5096. [Google Scholar] [CrossRef]
- Uhlherr, A.; Mavrantzas, V.G.; Doxastakis, M.; Theodorou, D.N. Directed Bridging Methods for Fast Atomistic Monte Carlo Simulations of Bulk Polymers. Macromolecules 2001, 34, 8554–8568. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Mavrantzas, V.G.; Theodorou, D.N. A novel monte carlo scheme for the rapid equilibration of atomistic model polymer systems of precisely defined molecular architecture. Phys. Rev. Lett. 2002, 88, 105503. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.C.; Giannousaki, A.E.; Mavrantzas, V.G.; Theodorou, D.N. Atomistic Monte Carlo simulation of strictly monodisperse long polyethylene melts through a generalized chain bridging algorithm. J. Chem. Phys. 2002, 117, 5465–5479. [Google Scholar] [CrossRef]
- Peristeras, L.D.; Economou, I.G.; Theodorou, D.N. Structure and Volumetric Properties of Linear and Triarm Star Polyethylenes from Atomistic Monte Carlo Simulation Using New Internal Rearrangement Moves. Macromolecules 2005, 38, 386–397. [Google Scholar] [CrossRef]
- Ramos, F.J.; Peristeras, L.; Theodorou, D.N. Monte Carlo Simulation of Short Chain Branched Polyolefins in the Molten State. Macromolecules 2007, 40, 9640–9650. [Google Scholar] [CrossRef]
- Gusev, A.A.; Suter, U.W. Dynamics of Small Molecules in Dense Polymers Subject to Thermal Motion. J. Chem. Phys. 1993, 99, 2228–2234. [Google Scholar] [CrossRef]
- Gusev, A.A.; Arizzi, S.; Suter, U.W.; Moll, D.J. Dynamics of light gases in rigid matrices of dense polymers. J. Chem. Phys. 1993, 99, 2221–2227. [Google Scholar] [CrossRef]
- Greenfield, M.L.; Theodorou, D.N. Coupling of Penetrant and Polymer Motions during Small-Molecule Diffusion in a Glassy Polymer. Mol. Simul. 1997, 19, 329–361. [Google Scholar] [CrossRef]
- Greenfield, M.L.; Theodorou, D.N. Molecular modeling of methane diffusion in glassy atactic polypropylene via multidimensional transition state theory. Macromolecules 1998, 31, 7068–7090. [Google Scholar] [CrossRef]
- Vergadou, N. Prediction of Gas Permeability of Inflexible Amorphous Polymers via Molecular Simulation. Ph.D. Thesis, University of Athens, Athens, Greece, 2006. [Google Scholar]
- Theodorou, D.N. Hierarchical modelling of polymeric materials. Chem. Eng. Sci. 2007, 62, 5697–5714. [Google Scholar] [CrossRef]
- Xi, L.; Shah, M.; Trout, B.L. Hopping of Water in a Glassy Polymer Studied via Transition Path Sampling and Likelihood Maximization. J. Phys. Chem. B 2013, 117, 3634–3647. [Google Scholar] [CrossRef] [PubMed]
- Greenfield, M.L.; Theodorou, D.N. Coarse-Grained Molecular Simulation of Penetrant Diffusion in a Glassy Polymer Using Reverse and Kinetic Monte Carlo. Macromolecules 2001, 34, 8541–8553. [Google Scholar] [CrossRef]
- Neyertz, S.; Brown, D. A Trajectory-Extending Kinetic Monte Carlo (TEKMC) Method for Estimating Penetrant Diffusion Coefficients in Molecular Dynamics Simulations of Glassy Polymers. Macromolecules 2010, 43, 9210–9214. [Google Scholar] [CrossRef]
- Neyertz, S.; Brown, D.; Pandiyan, S.; van der Vegt, N.F. Carbon dioxide diffusion and plasticization in fluorinated polyimides. Macromolecules 2010, 43, 7813–7827. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Adhikari, N.P.; van der Vegt, N.F.A.; Kremer, K.; Mann, B.A.; Voelkel, R.; Weiss, H.; Liew, C. Ethylbenzene Diffusion in Polystyrene: United Atom Atomistic/Coarse Grained Simulations and Experiments. Macromolecules 2007, 40, 7026–7035. [Google Scholar] [CrossRef]
- Fritz, D.; Herbers, C.R.; Kremer, K.; van der Vegt, N.F.A. Hierarchical Modeling of Polymer Permeation. Soft Matter 2009, 5, 4556–4563. [Google Scholar] [CrossRef]
- Lin, E.; You, X.; Kriegel, R.M.; Moffitt, R.D.; Batra, R.C. Atomistic to coarse grained simulations of diffusion of small molecules into polymeric matrix. Comput. Mater. Sci. 2017, 138, 448–461. [Google Scholar] [CrossRef]
- Zhang, K.; Meng, D.; Müller-Plathe, F.; Kumar, S.K. Coarse-grained molecular dynamics simulation of activated penetrant transport in glassy polymers. Soft Matter 2018, 14, 440–447. [Google Scholar] [CrossRef]
- Müller-Plathe, F.; Rogers, S.C.; van Gunsteren, W.F. Computational Evidence for Anomalous Diffusion of Small Molecules in Amorphous Polymers. Chem. Phys. Lett. 1992, 199, 237–243. [Google Scholar] [CrossRef]
- Raptis, V.E.; Economou, I.G.; Theodorou, D.N.; Petrou, J.; Petropoulos, J.H. Molecular dynamics simulation of structure and thermodynamic properties of poly(dimethylsilamethylene) and hydrocarbon solubility therein: Toward the development of novel membrane materials for hydrocarbon separation. Macromolecules 2004, 37, 1102–1112. [Google Scholar] [CrossRef]
- Yang, Q.; Whiting, W.I. Molecular-level insight of the differences in the diffusion and solubility of penetrants in polypropylene, poly(propylmethylsiloxane) and poly(4-methyl-2-pentyne). J. Membr. Sci. 2018, 549, 173–183. [Google Scholar] [CrossRef]
- Van der Vegt, N.F.A.; Briels, W.J.; Wessling, M.; Strathmann, H. The sorption induced glass transition in amorphous glassy polymers. J. Chem. Phys. 1999, 110, 11061–11069. [Google Scholar] [CrossRef]
- Spyriouni, T.; Boulougouris, G.C.; Theodorou, D.N. Prediction of Sorption of CO2 in Glassy Atactic Polystyrene at Elevated Pressures Through a New Computational Scheme. Macromolecules 2009, 42, 1759–1769. [Google Scholar] [CrossRef]
- Knopp, B.; Suter, U.W. Atomistically Modeling the Chemical Potential of Small Molecules in Dense Polymer Microstructures. 2. Water Sorption by Polyamides. Macromolecules 1997, 30, 6114–6119. [Google Scholar] [CrossRef]
- Knopp, B.; Suter, U.W.; Gusev, A.A. Atomistically Modeling the Chemical Potential of Small Molecules in Dense Polymer Microstructures. 1. Method. Macromolecules 1997, 30, 6107–6113. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tuckerman, M.E.; Tobias, D.J.; Klein, M.L. Explicit reversible integrators for extended systems dynamics. Mol. Phys. 1996, 87, 1117–1157. [Google Scholar] [CrossRef]
- Tuckerman, M.; Berne, B.J.; Martyna, G.J. Reversible multiple time scale molecular dynamics. J. Chem. Phys. 1992, 97, 1990–2001. [Google Scholar] [CrossRef]
- McQuarrie, D.A. Statistical Mechanics; Harper & Row: New York, NY, USA, 1975. [Google Scholar]
- Hansen, J.-P.; McDonald, I.R. Theory of Simple Liquids, 3rd ed.; Academic Press: London, UK, 2006. [Google Scholar]
- Müller-Plathe, F.; Rogers, S.C.; van Gunsteren, W.F. Gas sorption and transport in polyisobutylene: Equilibrium and nonequilibrium molecular dynamics simulations. J. Chem. Phys. 1993, 98, 9895–9904. [Google Scholar] [CrossRef]
- Van der Vegt, N.F.A.; Briels, W.J.; Wessling, M.; Strathmann, H. A Nonequilibrium Simulation Method for Calculating Tracer Diffusion Coefficients of Small Solutes in N-Alkane Liquids and Polymers. J. Chem. Phys. 1998, 108, 9558–9565. [Google Scholar] [CrossRef]
- Frentrup, H.; Hart, E.K.; Colina, M.C.; Müller, A.E. In Silico Determination of Gas Permeabilities by Non-Equilibrium Molecular Dynamics: CO2 and He through PIM-1. Membranes 2015, 5, 99–119. [Google Scholar] [CrossRef]
- Anderson, L.R.; Yang, Q.; Ediger, A.M. Comparing gas transport in three polymers via molecular dynamics simulation. Phys. Chem. Chem. Phys. 2018, 20, 22123–22133. [Google Scholar] [CrossRef] [PubMed]
- Theodorou, D.N. Variable-Connectivity Monte Carlo Algorithms for the Atomistic Simulation of Long-Chain Polymer Systems. In Bridging Time Scales: Molecular Simulations for the Next Decade; Nielaba, P., Mareschal, M., Ciccotti, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 67–127. [Google Scholar]
- Rosenbluth, M.N.; Rosenbluth, A.W. Monte Carlo Calculation of the Average Extension of Molecular Chains. J. Chem. Phys. 1955, 23, 356–359. [Google Scholar] [CrossRef]
- Siepmann, J.I.; Frenkel, D. Configurational bias Monte Carlo: A new sampling scheme for flexible chains. Mol. Phys. 1992, 75, 59–70. [Google Scholar] [CrossRef]
- De Pablo, J.J.; Laso, M.; Suter, U.W. Estimation of the chemical potential of chain molecules by simulation. J. Chem. Phys. 1992, 96, 6157–6162. [Google Scholar] [CrossRef]
- Dodd, L.R.; Boone, T.D.; Theodorou, D.N. A concerted rotation algorithm for atomistic Monte Carlo simulation of polymer melts and glasses. Mol. Phys. 1993, 78, 961–996. [Google Scholar] [CrossRef]
- Panagiotopoulos, A.Z. Direct determination of phase coexistence properties of fluids by Monte Carlo simulation in a new ensemble. Mol. Phys. 1987, 61, 813–826. [Google Scholar] [CrossRef]
- Briano, J.G.; Glandt, E.D. Statistical thermodynamics of polydisperse fluids. J. Chem. Phys. 1984, 80, 3336–3343. [Google Scholar] [CrossRef]
- Kofke, D.A.; Glandt, E.D. Monte carlo simulation of multicomponent equilibria in a semigrand canonical ensemble. Mol. Phys. 1988, 64, 1105–1131. [Google Scholar] [CrossRef]
- Widom, B. Some Topics in the Theory of Fluids. J. Chem. Phys. 1963, 39, 2808–2812. [Google Scholar] [CrossRef]
- Zervopoulou, E.; Mavrantzas, V.G.; Theodorou, D.N. A new Monte Carlo simulation approach for the prediction of sorption equilibria of oligomers in polymer melts: Solubility of long alkanes in linear polyethylene. J. Chem. Phys. 2001, 115, 2860–2875. [Google Scholar] [CrossRef]
- Lyubartsev, A.P.; Martsinovski, A.A.; Shevkunov, S.V.; Vorontsov-Velyaminov, P.N. New approach to Monte Carlo calculation of the free energy: Method of expanded ensembles. J. Chem. Phys. 1992, 96, 1776–1783. [Google Scholar] [CrossRef]
- De Pablo, J.J.; Yan, Q.; Escobedo, F.A. Simulation of Phase Transitions in Fluids. Annu. Rev. Phys. Chem. 1999, 50, 377–411. [Google Scholar] [CrossRef] [PubMed]
- Cuthbert, T.R.; Wagner, N.J.; Paulaitis, M.E. Molecular Simulation of Glassy Polystyrene: Size Effects on Gas Solubilities. Macromolecules 1997, 30, 3058–3065. [Google Scholar] [CrossRef]
- Deitrick, G.L.; Scriven, L.E.; Davis, H.T. Efficient molecular simulation of chemical potentials. J. Chem. Phys. 1989, 90, 2370–2385. [Google Scholar] [CrossRef]
- Tamai, Y.; Tanaka, H.; Nakanishi, K. Molecular Simulation of Permeation of Small Penetrants through Membranes. 2. Solubilities. Macromolecules 1995, 28, 2544–2554. [Google Scholar] [CrossRef]
- Fukuda, M. Solubilities of small molecules in polyethylene evaluated by a test-particle-insertion method. J. Chem. Phys. 1999, 112, 478–486. [Google Scholar] [CrossRef]
- Dömötör, G.; Hentschke, R. Atomistically Modeling the Chemical Potential of Small Molecules in Dense Systems. J. Phys. Chem. B 2004, 108, 2413–2417. [Google Scholar] [CrossRef]
- Dömötör, G.; Hentschke, R. Equilibrium Swelling of an Epoxy-Resin in Contact with Water—A Molecular Dynamics Simulation Study. Macromol. Theory Simul. 2004, 13, 506–511. [Google Scholar] [CrossRef]
- Boulougouris, G.C.; Economou, I.G.; Theodorou, D.N. On the calculation of the chemical potential using the particle deletion scheme. Mol. Phys. 1999, 96, 905–913. [Google Scholar] [CrossRef]
- Boulougouris, G.C.; Economou, I.G.; Theodorou, D.N. Calculation of the chemical potential of chain molecules using the staged particle deletion scheme. J. Chem. Phys. 2001, 115, 8231–8237. [Google Scholar] [CrossRef]
- Van der Vegt, N.F.A.; Briels, W.J. Efficient sampling of solvent free energies in polymers. J. Chem. Phys. 1998, 109, 7578–7582. [Google Scholar] [CrossRef]
- Vrabec, J.; Hasse, H. Grand Equilibrium: Vapour-liquid equilibria by a new molecular simulation method. Mol. Phys. 2002, 100, 3375–3383. [Google Scholar] [CrossRef]
- Hess, B.; Peter, C.; Ozal, T.; van der Vegt, N.F.A. Fast-Growth Thermodynamic Integration: Calculating Excess Chemical Potentials of Additive Molecules in Polymer Microstructures. Macromolecules 2008, 41, 2283–2289. [Google Scholar] [CrossRef]
- Glasstone, S.; Laidler, K.J.; Eyring, H. The Theory of Rate Processes: The Kinetics of Chemical Reactions, Viscosity, Diffusion and Electrochemical Phenomena; McGraw-Hill: New York, NY, USA, 1941. [Google Scholar]
- Voter, A.F.; Doll, J.D. Dynamical Corrections to Transition-State Theory for Multistate Systems—Surface Self-Diffusion in the Rare-Event Regime. J. Chem. Phys. 1985, 82, 80–92. [Google Scholar] [CrossRef]
- Eyring, H. The Activated Complex in Chemical Reactions. J. Chem. Phys. 1935, 3, 107–115. [Google Scholar] [CrossRef]
- van Kampen, N.G. Stochastic Processes in Physics and Chemistry, 3rd ed.; North Holland Publishing Company: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Fukui, K. The Path of Chemical Reactions—The IRC Approach. Acc. Chem. Res. 1981, 14, 363–368. [Google Scholar] [CrossRef]
- Kotelyanskii, M.; Theodorou, D.N. Simulation Methods for Polymers; Marcel Dekker Inc: New York, NY, USA, 2004. [Google Scholar]
- Chandler, D. Statistical mechanics of isomerization dynamics in liquids and the transition state approximation. J. Chem. Phys. 1978, 68, 2959–2970. [Google Scholar] [CrossRef]
- Hofmann, D.; Fritz, L.; Ulbrich, J.; Paul, D. Molecular simulation of small molecule diffusion and solution in dense amorphous polysiloxanes and polyimides. Comp. Theor. Polymer Sci. 2000, 10, 419–436. [Google Scholar] [CrossRef]
- Hofmann, D.; Fritz, L.; Ulbrich, J.; Schepers, C.; Bohning, M. Detailed-Atomistic Molecular Modeling of Small Molecule Diffusion and Solution Processes in Polymeric Membrane Materials. Macromol. Theory Simul. 2000, 9, 293–327. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Mavrantzas, V.G.; Theodorou, D.N. Detailed Atomistic Simulation of the Segmental Dynamics and Barrier Properties of Amorphous Poly(ethylene Terephthalate) and Poly(ethylene Isophthalate). Macromolecules 2004, 37, 2978–2995. [Google Scholar] [CrossRef]
- Greenfield, M.L.; Theodorou, D.N. Geometric analysis of diffusion pathways in glassy and melt atactic polypropylene. Macromolecules 1993, 26, 5461–5472. [Google Scholar] [CrossRef]
- Vergadou, N.; Theodorou, D.N. Molecular simulation of CO2 Diffusion in Glassy Polymers using Multidimensional Transition State Theory. 2019. In preparation. [Google Scholar]
- Bolhuis, P.G. Transition path sampling on diffusive barriers. J. Phys. Condens. Matter 2002, 15, S113–S120. [Google Scholar] [CrossRef]
- Bolhuis, P.G.; Dellago, C.; Chandler, D. Sampling Ensembles of Deterministic Transition Pathways. Faraday Discuss. 1998, 110, 421–436. [Google Scholar] [CrossRef]
- Peters, B.; Trout, B.L. Obtaining Reaction Coordinates by Likelihood Maximization. J. Chem. Phys. 2006, 125, 054108. [Google Scholar] [CrossRef] [PubMed]
- Peters, B.; Beckham, G.T.; Trout, B.L. Extensions to the Likelihood Maximization Approach for Finding Reaction Coordinates. J. Chem. Phys. 2007, 127, 034109. [Google Scholar] [CrossRef] [PubMed]
- Grünwald, M.; Dellago, C.; Geissler, P.L. Precision shooting: Sampling long transition pathways. J. Chem. Phys. 2008, 129, 194101. [Google Scholar] [CrossRef] [PubMed]
- Mullen, R.G.; Shea, J.-E.; Peters, B. Easy Transition Path Sampling Methods: Flexible-Length Aimless Shooting and Permutation Shooting. J. Chem. Theory Comput. 2015, 11, 2421–2428. [Google Scholar] [CrossRef]
- Pan, A.C.; Chandler, D. Dynamics of nucleation in the ising model. J. Phys. Chem. B 2004, 108, 19681. [Google Scholar] [CrossRef]
- Moroni, D.; Ten Wolde, P.R.; Bolhuis, P.G. Interplay between structure and size in a critical crystal nucleus. Phys. Rev. Lett. 2005, 94, 235703. [Google Scholar] [CrossRef]
- Lechner, W.; Dellago, C.; Bolhuis, P.G. Role of the Prestructured Surface Cloud in Crystal Nucleation. Phys. Rev. Lett. 2011, 106, 085701. [Google Scholar] [CrossRef] [PubMed]
- Beckham, G.T.; Peters, B.J. Optimizing Nucleus Size Metrics for Liquid-Solid Nucleation from Transition Paths of Near-Nanosecond Duration. Phys. Chem. Lett. 2011, 2, 1133–1138. [Google Scholar] [CrossRef] [PubMed]
- Chong, L.T.; Saglam, A.S.; Zuckerman, D.M. Path-sampling strategies for simulating rare events in biomolecular systems. Curr. Opin. Struct. Biol. 2017, 43, 88–94. [Google Scholar] [CrossRef] [PubMed]
- Juraszek, J.; Bolhuis, P.G. Rate Constant and Reaction Coordinate of Trp-Cage Folding in Explicit Water. Biophys. J. 2008, 95, 4246–4257. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.W.; Jasnow, D.; Zuckerman, D.M. Efficient and verified simulation of a path ensemble for conformational change in a united-residue model of calmodulin. Proc. Natl. Acad. Sci. USA 2007, 104, 18043. [Google Scholar] [CrossRef]
- Roy, A.; Taraphder, S. Transition Path Sampling Study of the Conformational Fluctuation of His-64 in Human Carbonic Anhydrase II. J. Phys. Chem. B 2009, 113, 12555–12564. [Google Scholar] [CrossRef]
- Keys, A.S.; Hedges, L.O.; Garrahan, J.P.; Glotzer, S.C.; Chandler, D. Excitations Are Localized and Relaxation Is Hierarchical in Glass-Forming Liquids. Phys. Rev. X 2011, 1, 021013. [Google Scholar]
- Pan, B.; Ricci, M.S.; Trout, B.L. A molecular mechanism of hydrolysis of peptide bonds at neutral pH using a model compound. J. Phys. Chem. B 2011, 115, 5958–5970. [Google Scholar] [CrossRef]
- Quaytman, S.L.; Schwartz, S.D. Reaction coordinate of an enzymatic reaction revealed by transition path sampling. Proc. Natl. Acad. Sci. USA 2007, 104, 12253–12258. [Google Scholar] [CrossRef]
- Basner, J.E.; Schwartz, S.D. How Enzyme Dynamics Helps Catalyze a Reaction in Atomic Detail: A Transition Path Sampling Study. J. Am. Chem. Soc. 2005, 127, 13822–13831. [Google Scholar] [CrossRef]
- Vlugt, T.J.H.; Dellago, C.; Smit, B. Diffusion of Isobutane in Silicalite Studied by Transition Path Sampling. J. Chem. Phys. 2000, 113, 8791–8799. [Google Scholar] [CrossRef]
- Peters, B.; Zimmermann, N.E.R.; Beckham, G.T.; Tester, J.W.; Trout, B.L. Path Sampling Calculation of Methane Diffusivity in Natural Gas Hydrates from a Water-Vacancy Assisted Mechanism. J. Am. Chem. Soc. 2008, 130, 17342–17350. [Google Scholar] [CrossRef] [PubMed]
- Boulfelfel, S.E.; Ravikovitch, P.I.; Sholl, D.S. Modeling Diffusion of Linear Hydrocarbons in Silica Zeolite LTA Using Transition Path Sampling. J. Phys. Chem. C 2015, 119, 15643–15653. [Google Scholar] [CrossRef]
- Auhl, R.; Everaers, R.; Grest, G.S.; Kremer, K.; Plimpton, S.J. Equilibration of long chain polymer melts in computer simulations. J. Chem. Phys. 2003, 119, 12718–12728. [Google Scholar] [CrossRef]
- Theodorou, D.N. Equilibration and Coarse-Graining Methods for Polymers. In Computer Simulations in Condensed Matter Systems: From Materials to Chemical Biology Volume 2; Ferrario, M., Ciccotti, G., Binder, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 419–448. [Google Scholar]
- Brown, D.; Clarke, J.H.R.; Okuda, M.; Yamazaki, T. The preparation of polymer melt samples for computer simulation studies. J. Chem. Phys. 1994, 100, 6011–6018. [Google Scholar] [CrossRef]
- Gao, J. An efficient method of generating dense polymer model melts by computer simulation. J. Chem. Phys. 1995, 102, 1074–1077. [Google Scholar] [CrossRef]
- Mondello, M.; Grest, G.S.; Webb, E.B.; Peczak, P. Dynamics of n-alkanes: Comparison to Rouse model. J. Chem. Phys. 1998, 109, 798–805. [Google Scholar] [CrossRef]
- Kröger, M. Efficient hybrid algorithm for the dynamic creation of wormlike chains in solutions, brushes, melts and glasses. Comput. Phys. Commun. 1999, 118, 278–298. [Google Scholar] [CrossRef]
- Sliozberg, Y.R.; Kröger, M.; Chantawansri, T.L. Fast equilibration protocol for million atom systems of highly entangled linear polyethylene chains. J. Chem. Phys. 2016, 144, 154901. [Google Scholar] [CrossRef]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Flory, P. Statistical Mechanics of Chain Molecules; Interscience Publishers: New York, NY, USA, 1969. [Google Scholar]
- Theodorou, D.N.; Suter, U.W. Detailed Molecular-Structure of a Vinyl Polymer Glass. Macromolecules 1985, 18, 1467–1478. [Google Scholar] [CrossRef]
- Rigby, D.; Roe, R.J. Molecular dynamics simulation of polymer liquid and glass. I. Glass transition. J. Chem. Phys. 1987, 87, 7285–7292. [Google Scholar] [CrossRef]
- Gooneie, A.; Schuschnigg, S.; Holzer, C. A Review of Multiscale Computational Methods in Polymeric Materials. Polymers 2017, 9, 16. [Google Scholar] [CrossRef] [PubMed]
- Müller-Plathe, F. Coarse-Graining in Polymer Simulation: From the Atomistic to the Mesoscopic Scale and Back. ChemPhysChem 2002, 3, 754–769. [Google Scholar] [CrossRef]
- Tschöp, W.; Kremer, K.; Batoulis, J.; Bürger, T.; Hahn, O. Simulation of polymer melts. I. Coarse-graining procedure for polycarbonates. Acta Polym. 1998, 49, 61–74. [Google Scholar] [CrossRef]
- Karimi-Varzaneh, H.A.; van der Vegt, N.F.A.; Müller-Plathe, F.; Carbone, P. How Good Are Coarse-Grained Polymer Models? A Comparison for Atactic Polystyrene. ChemPhysChem 2012, 13, 3428–3439. [Google Scholar] [CrossRef]
- Zacharopoulos, N.; Vergadou, N.; Theodorou, D.N. Coarse graining using pretabulated potentials: Liquid benzene. J. Chem. Phys. 2005, 122, 244111. [Google Scholar] [CrossRef]
- Deichmann, G.; Dallavalle, M.; Rosenberger, D.; van der Vegt, N.F.A. Phase Equilibria Modeling with Systematically Coarse-Grained Models—A Comparative Study on State Point Transferability. J. Phys. Chem. B 2019, 123, 504–515. [Google Scholar] [CrossRef]
- Sun, Q.; Faller, R. Systematic Coarse-Graining of a Polymer Blend: Polyisoprene and Polystyrene. J. Chem. Theory Comput. 2006, 2, 607–615. [Google Scholar] [CrossRef]
- Mognetti, B.M.; Virnau, P.; Yelash, L.; Paul, W.; Binder, K.; Müller, M.; MacDowell, L.G. Coarse-grained models for fluids and their mixtures: Comparison of Monte Carlo studies of their phase behavior with perturbation theory and experiment. J. Chem. Phys. 2009, 130, 044101. [Google Scholar] [CrossRef]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; de Vries, A.H. The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef] [PubMed]
- Maerzke, K.A.; Siepmann, J.I. Transferable Potentials for Phase Equilibria−Coarse-Grain Description for Linear Alkanes. J. Phys. Chem. B 2011, 115, 3452–3465. [Google Scholar] [CrossRef] [PubMed]
- Allison, J.R.; Riniker, S.; van Gunsteren, W.F. Coarse-grained models for the solvents dimethyl sulfoxide, chloroform, and methanol. J. Chem. Phys. 2012, 136, 054505. [Google Scholar] [CrossRef] [PubMed]
- Brini, E.; Algaer, E.A.; Ganguly, P.; Li, C.; Rodríguez-Ropero, F.; van der Vegt, N.F.A. Systematic coarse-graining methods for soft matter simulations—A review. Soft Matter 2013, 9, 2108–2119. [Google Scholar] [CrossRef]
- Huang, H.; Wu, L.; Xiong, H.; Sun, H. A Transferrable Coarse-Grained Force Field for Simulations of Polyethers and Polyether Blends. Macromolecules 2019, 52, 249–261. [Google Scholar] [CrossRef]
- Kuo, A.-T.; Okazaki, S.; Shinoda, W. Transferable coarse-grained model for perfluorosulfonic acid polymer membranes. J. Chem. Phys. 2017, 147, 094904. [Google Scholar] [CrossRef] [PubMed]
- Reith, D.; Pütz, M.; Müller-Plathe, F. Deriving effective mesoscale potentials from atomistic simulations. J. Comput. Chem. 2003, 24, 1624–1636. [Google Scholar] [CrossRef]
- Ercolessi, F.; Adams, J.B. Interatomic Potentials from First-Principles Calculations: The Force-Matching Method. Europhys. Lett. (EPL) 1994, 26, 583–588. [Google Scholar] [CrossRef]
- Izvekov, S.; Voth, G.A. Modeling real dynamics in the coarse-grained representation of condensed phase systems. J. Chem. Phys. 2006, 125, 151101. [Google Scholar] [CrossRef]
- Lyubartsev, A.P.; Laaksonen, A. Calculation of effective interaction potentials from radial distribution functions: A reverse Monte Carlo approach. Phys. Rev. E 1995, 52, 3730–3737. [Google Scholar] [CrossRef]
- Chaimovich, A.; Shell, M.S. Coarse-graining errors and numerical optimization using a relative entropy framework. J. Chem. Phys. 2011, 134, 094112. [Google Scholar] [CrossRef] [PubMed]
- Shell, M.S. The relative entropy is fundamental to multiscale and inverse thermodynamic problems. J. Chem. Phys. 2008, 129, 144108. [Google Scholar] [CrossRef] [PubMed]
- Villa, A.; Peter, C.; van der Vegt, N.F.A. Self-assembling dipeptides: Conformational sampling in solvent-free coarse-grained simulation. Phys. Chem. Chem. Phys. 2009, 11, 2077–2086. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Shen, J.; Peter, C.; van der Vegt, N.F.A. A Chemically Accurate Implicit-Solvent Coarse-Grained Model for Polystyrenesulfonate Solutions. Macromolecules 2012, 45, 2551–2561. [Google Scholar] [CrossRef]
- De Nicola, A.; Kawakatsu, T.; Milano, G. Generation of Well-Relaxed All-Atom Models of Large Molecular Weight Polymer Melts: A Hybrid Particle-Continuum Approach Based on Particle-Field Molecular Dynamics Simulations. J. Chem. Theory Comput. 2014, 10, 5651–5667. [Google Scholar] [CrossRef] [PubMed]
- Rosenberger, D.; van der Vegt, N.F.A. Addressing the temperature transferability of structure based coarse graining models. Phys. Chem. Chem. Phys. 2018, 20, 6617–6628. [Google Scholar] [CrossRef] [PubMed]
- Potter, T.D.; Tasche, J.; Wilson, M.R. Assessing the transferability of common top-down and bottom-up coarse-grained molecular models for molecular mixtures. Phys. Chem. Chem. Phys. 2019, 21, 1912–1927. [Google Scholar] [CrossRef] [PubMed]
- Dunn, N.J.H.; Foley, T.T.; Noid, W.G. Van der Waals Perspective on Coarse-Graining: Progress toward Solving Representability and Transferability Problems. Acc. Chem. Res. 2016, 49, 2832–2840. [Google Scholar] [CrossRef]
- Guenza, M.G.; Dinpajooh, M.; McCarty, J.; Lyubimov, I.Y. Accuracy, Transferability, and Efficiency of Coarse-Grained Models of Molecular Liquids. J. Phys. Chem. B 2018, 122, 10257–10278. [Google Scholar] [CrossRef]
- Tschöp, W.; Kremer, K.; Hahn, O.; Batoulis, J.; Bürger, T. Simulation of polymer melts. II. From coarse-grained models back to atomistic description. Acta Polym. 1998, 49, 75–79. [Google Scholar] [CrossRef]
- Hess, B.; León, S.; van der Vegt, N.; Kremer, K. Long time atomistic polymer trajectories from coarse grained simulations: Bisphenol-A polycarbonate. Soft Matter 2006, 2, 409–414. [Google Scholar] [CrossRef]
- Wu, C. Multiscale simulations of the structure and dynamics of stereoregular poly(methyl methacrylate)s. J. Mol. Modeling 2014, 20. [Google Scholar] [CrossRef] [PubMed]
- Ghanbari, A.; Böhm, M.C.; Müller-Plathe, F. A Simple Reverse Mapping Procedure for Coarse-Grained Polymer Models with Rigid Side Groups. Macromolecules 2011, 44, 5520–5526. [Google Scholar] [CrossRef]
- Krajniak, J.; Pandiyan, S.; Nies, E.; Samaey, G. Generic Adaptive Resolution Method for Reverse Mapping of Polymers from Coarse-Grained to Atomistic Descriptions. J. Chem. Theory Comput. 2016, 12, 5549–5562. [Google Scholar] [CrossRef] [PubMed]
- Krajniak, J.; Zhang, Z.; Pandiyan, S.; Nies, E.; Samaey, G. Reverse mapping method for complex polymer systems. J. Comput. Chem. 2018, 39, 648–664. [Google Scholar] [CrossRef]
- Rzepiela, A.J.; Schäfer, L.V.; Goga, N.; Risselada, H.J.; De Vries, A.H.; Marrink, S.J. Reconstruction of atomistic details from coarse-grained structures. J. Comput. Chem. 2010, 31, 1333–1343. [Google Scholar] [CrossRef]
- Wassenaar, T.A.; Pluhackova, K.; Böckmann, R.A.; Marrink, S.J.; Tieleman, D.P. Going Backward: A Flexible Geometric Approach to Reverse Transformation from Coarse Grained to Atomistic Models. J. Chem. Theory Comput. 2014, 10, 676–690. [Google Scholar] [CrossRef]
- Ohkuma, T.; Kremer, K.; Daoulas, K. Equilibrating high-molecular-weight symmetric and miscible polymer blends with hierarchical back-mapping. J. Phys. Condens. Matter 2018, 30, 174001. [Google Scholar] [CrossRef]
- Zhang, G.; Chazirakis, A.; Harmandaris, V.A.; Stuehn, T.; Daoulas, K.C.; Kremer, K. Hierarchical modelling of polystyrene melts: From soft blobs to atomistic resolution. Soft Matter 2019, 15, 289–302. [Google Scholar] [CrossRef]
- Santangelo, G.; Di Matteo, A.; Müller-Plathe, F.; Milano, G. From Mesoscale Back to Atomistic Models: A Fast Reverse-Mapping Procedure for Vinyl Polymer Chains. J. Phys. Chem. B 2007, 111, 2765–2773. [Google Scholar] [CrossRef]
- Bortz, A.; Kalos, M.; Lebowitz, J. A new algorithm for Monte Carlo simulation of Ising spin systems. J. Comput. Phys. 1975, 17, 10–18. [Google Scholar] [CrossRef]
- Young, W.M.; Elcock, E.W. Monte Carlo studies of vacancy migration in binary ordered alloys: I. Proc. Phys. Soc. Lond. 1966, 89, 735. [Google Scholar] [CrossRef]
- Fichthorn, K.A.; Weinberg, W.H. Theoretical foundations of dynamical Monte Carlo simulations. J. Chem. Phys. 1991, 95, 1090–1096. [Google Scholar] [CrossRef]
- Kolokathis, P.D.; Theodorou, D.N. On solving the master equation in spatially periodic systems. J. Chem. Phys. 2012, 137, 034112. [Google Scholar] [CrossRef] [PubMed]
- Tien, W.-J.; Chiu, C.-C. Generic parameters of trajectory-extending kinetic Monte Carlo for calculating diffusion coefficients. AIP Adv. 2018, 8, 065311. [Google Scholar] [CrossRef]
- Hanson, B.; Pryamitsyn, V.; Ganesan, V. Computer Simulations of Gas Diffusion in Polystyrene–C60 Fullerene Nanocomposites Using Trajectory Extending Kinetic Monte Carlo Method. J. Phys. Chem. B 2012, 116, 95–103. [Google Scholar] [CrossRef] [PubMed]
- Mogurampelly, S.; Borodin, O.; Ganesan, V. Computer Simulations of Ion Transport in Polymer Electrolyte Membranes. Annu. Rev. Chem. Biomol. Eng. 2016, 7, 349–371. [Google Scholar] [CrossRef] [PubMed]
- Hanson, B.; Pryamitsyn, V.; Ganesan, V. Mechanisms Underlying Ionic Mobilities in Nanocomposite Polymer Electrolytes. ACS Macro Lett. 2013, 2, 1001–1005. [Google Scholar] [CrossRef]
- Mogurampelly, S.; Ganesan, V. Effect of Nanoparticles on Ion Transport in Polymer Electrolytes. Macromolecules 2015, 48, 2773–2786. [Google Scholar] [CrossRef]
- Mogurampelly, S.; Ganesan, V. Structure and mechanisms underlying ion transport in ternary polymer electrolytes containing ionic liquids. J. Chem. Phys. 2017, 146, 074902. [Google Scholar] [CrossRef]
- Marrink, S.J.; de Vries, A.H.; Mark, A.E. Coarse Grained Model for Semiquantitative Lipid Simulations. J. Phys. Chem. B 2004, 108, 750–760. [Google Scholar] [CrossRef]
- Lee, H.; de Vries, A.H.; Marrink, S.-J.; Pastor, R.W. A Coarse-Grained Model for Polyethylene Oxide and Polyethylene Glycol: Conformation and Hydrodynamics. J. Phys. Chem. B 2009, 113, 13186–13194. [Google Scholar] [CrossRef] [PubMed]
- Bos, A.; Pünt, I.G.M.; Wessling, M.; Strathmann, H. CO2-induced plasticization phenomena in glassy polymers. J. Membr. Sci. 1999, 155, 67–78. [Google Scholar] [CrossRef]
- Wessling, M.; Huisman, I.; Boomgaard, T.v.d.; Smolders, C.A. Dilation kinetics of glassy, aromatic polyimides induced by carbon dioxide sorption. J. Polym. Sci. Part B: Polym. Phys. 1995, 33, 1371–1384. [Google Scholar] [CrossRef]
- Coleman, M.R.; Koros, W.J. Conditioning of Fluorine Containing Polyimides. 1. Effect of Exposure to High Pressure Carbon Dioxide on Permeability. Macromolecules 1997, 30, 6899–6905. [Google Scholar] [CrossRef]
- Coleman, M.R.; Koros, W.J. Conditioning of Fluorine-Containing Polyimides. 2. Effect of Conditioning Protocol at 8 Volume Dilation on Gas-Transport Properties. Macromolecules 1999, 32, 3106–3113. [Google Scholar] [CrossRef]
- Ismail, A.F.; Lorna, W. Penetrant-induced plasticization phenomenon in glassy polymers for gas separation membrane. Sep. Purif. Technol. 2002, 27, 173–194. [Google Scholar] [CrossRef]
- Visser, T.; Wessling, M. When Do Sorption-Induced Relaxations in Glassy Polymers Set In? Macromolecules 2007, 40, 4992–5000. [Google Scholar] [CrossRef]
- Reijerkerk, S.R.; Nijmeijer, K.; Ribeiro, C.P.; Freeman, B.D.; Wessling, M. On the effects of plasticization in CO2/light gas separation using polymeric solubility selective membranes. J. Membr. Sci. 2011, 367, 33–44. [Google Scholar] [CrossRef]
- Duthie, X.; Kentish, S.; Powell, C.; Nagai, K.; Qiao, G.; Stevens, G. Operating temperature effects on the plasticization of polyimide gas separation membranes. J. Membr. Sci. 2007, 294, 40–49. [Google Scholar] [CrossRef]
- Zhang, L.; Xiao, Y.; Chung, T.S.; Jiang, J. Mechanistic understanding of CO2-induced plasticization of a polyimide membrane: A combination of experiment and simulation study. Polymer 2010, 51, 4439–4447. [Google Scholar] [CrossRef]
- Hölck, O.; Böhning, M.; Heuchel, M.; Siegert, M.R.; Hofmann, D. Gas sorption isotherms in swelling glassy polymers—Detailed atomistic simulations. J. Membr. Sci. 2013, 428, 523–532. [Google Scholar] [CrossRef]
- Heuchel, M.; Boehning, M.; Hoelck, O.; Siegert, M.R.; Hofmann, D. Atomistic Packing Models for Experimentally Investigated Swelling States Induced by CO2 in Glassy Polysulfone and Poly(ether sulfone). J. Polym. Sci. Part B: Polym. Phys. 2006, 44, 1874–1897. [Google Scholar] [CrossRef]
- Van der Vegt, N.F.A. Molecular dynamics simulations of sorption and diffusion in rubbery and glassy polymers. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 1998. [Google Scholar]
- Lock, S.S.M.; Lau, K.K.; Shariff, A.M.; Yeong, Y.F.; Bustam, M.A.; Jusoh, N.; Ahmad, F. An atomistic simulation towards elucidation of operating temperature effect in CO2 swelling of polysulfone polymeric membranes. J. Nat. Gas Sci. Eng. 2018, 57, 135–154. [Google Scholar] [CrossRef]
- Balçık, M.; Ahunbay, M.G. Prediction of CO2-induced plasticization pressure in polyimides via atomistic simulations. J. Membr. Sci. 2018, 547, 146–155. [Google Scholar] [CrossRef]
- Kupgan, G.; Demidov, A.G.; Colina, C.M. Plasticization behavior in polymers of intrinsic microporosity (PIM-1): A simulation study from combined Monte Carlo and molecular dynamics. J. Membr. Sci. 2018, 565, 95–103. [Google Scholar] [CrossRef]
- Pandiyan, S.; Brown, D.; Neyertz, S.; van der Vegt, N.F.A. Carbon Dioxide Solubility in Three Fluorinated Polyimides Studied by Molecular Dynamics Simulations. Macromolecules 2010, 43, 2605–2621. [Google Scholar] [CrossRef]
- Spyriouni, T.; Tzoumanekas, C.; Theodorou, D.; Müller-Plathe, F.; Milano, G. Coarse-Grained and Reverse-Mapped United-Atom Simulations of Long-Chain Atactic Polystyrene Melts: Structure, Thermodynamic Properties, Chain Conformation, and Entanglements. Macromolecules 2007, 40, 3876–3885. [Google Scholar] [CrossRef]
- Velioğlu, S.; Ahunbay, M.G.; Tantekin-Ersolmaz, S.B. Investigation of CO2-induced plasticization in fluorinated polyimide membranes via molecular simulation. J. Membr. Sci. 2012, 417-418, 217–227. [Google Scholar] [CrossRef]
- Velioğlu, S.; Ahunbay, M.G.; Tantekin-Ersolmaz, S.B. Propylene/propane plasticization in polyimide membranes. J. Membr. Sci. 2016, 501, 179–190. [Google Scholar] [CrossRef]
- Tullos, G.; Mathias, L. Unexpected thermal conversion of hydroxy-containing polyimides to polybenzoxazoles. Polymer 1999, 40, 3463–3468. [Google Scholar] [CrossRef]
- Liu, Q.; Borjigin, H.; Paul, D.R.; Riffle, J.S.; McGrath, J.E.; Freeman, B.D. Gas permeation properties of thermally rearranged (TR) isomers and their aromatic polyimide precursors. J. Membr. Sci. 2016, 518, 88–99. [Google Scholar] [CrossRef]
- Park, H.B.; Jung, C.H.; Lee, Y.M.; Hill, A.J.; Pas, S.J.; Mudie, S.T.; Van Wagner, E.; Freeman, B.D.; Cookson, D.J. Polymers with Cavities Tuned for Fast Selective Transport of Small Molecules and Ions. Science 2007, 318, 254–258. [Google Scholar] [CrossRef] [PubMed]
- Sanders, D.F.; Smith, Z.P.; Ribeiro, C.P.; Guo, R.; McGrath, J.E.; Paul, D.R.; Freeman, B.D. Gas permeability, diffusivity, and free volume of thermally rearranged polymers based on 3,3′-dihydroxy-4,4′-diamino-biphenyl (HAB) and 2,2′-bis-(3,4-dicarboxyphenyl) hexafluoropropane dianhydride (6FDA). J. Membr. Sci. 2012, 409–410, 232–241. [Google Scholar] [CrossRef]
- Scholes, C.A.; Freeman, B.D. Thermal rearranged poly(imide-co-ethylene glycol) membranes for gas separation. J. Membr. Sci. 2018, 563, 676–683. [Google Scholar] [CrossRef]
- Scholes, C.A.; Freeman, B.D.; Kentish, S.E. Water vapor permeability and competitive sorption in thermally rearranged (TR) membranes. J. Membr. Sci. 2014, 470, 132–137. [Google Scholar] [CrossRef]
- Smith, Z.P.; Hernández, G.; Gleason, K.L.; Anand, A.; Doherty, C.M.; Konstas, K.; Alvarez, C.; Hill, A.J.; Lozano, A.E.; Paul, D.R.; et al. Effect of polymer structure on gas transport properties of selected aromatic polyimides, polyamides and TR polymers. J. Membr. Sci. 2015, 493, 766–781. [Google Scholar] [CrossRef]
- Stevens, K.A.; Smith, Z.P.; Gleason, K.L.; Galizia, M.; Paul, D.R.; Freeman, B.D. Influence of temperature on gas solubility in thermally rearranged (TR) polymers. J. Membr. Sci. 2017, 533, 75–83. [Google Scholar] [CrossRef]
- Calle, M.; Doherty, C.M.; Hill, A.J.; Lee, Y.M. Cross-Linked Thermally Rearranged Poly(benzoxazole-co-imide) Membranes for Gas Separation. Macromolecules 2013, 46, 8179–8189. [Google Scholar] [CrossRef]
- Park, H.B.; Han, S.H.; Jung, C.H.; Lee, Y.M.; Hill, A.J. Thermally rearranged (TR) polymer membranes for CO2 separation. J. Membr. Sci. 2010, 359, 11–24. [Google Scholar] [CrossRef]
- Kim, S.; Jo, H.J.; Lee, Y.M. Sorption and transport of small gas molecules in thermally rearranged (TR) polybenzoxazole membranes based on 2,2-bis(3-amino-4-hydroxyphenyl)-hexafluoropropane (bisAPAF) and 4,4′-hexafluoroisopropylidene diphthalic anhydride (6FDA). J. Membr. Sci. 2013, 441, 1–8. [Google Scholar] [CrossRef]
- Jiang, Y.; Willmore, F.T.; Sanders, D.; Smith, Z.P.; Ribeiro, C.P.; Doherty, C.M.; Thornton, A.; Hill, A.J.; Freeman, B.D.; Sanchez, I.C. Cavity size, sorption and transport characteristics of thermally rearranged (TR) polymers. Polymer 2011, 52, 2244–2254. [Google Scholar] [CrossRef]
- Park, C.H.; Tocci, E.; Lee, Y.M.; Drioli, E. Thermal Treatment Effect on the Structure and Property Change between Hydroxy-Containing Polyimides (HPIs) and Thermally Rearranged Polybenzoxazole (TR-PBO). J. Phys. Chem. B 2012, 116, 12864–12877. [Google Scholar] [CrossRef] [PubMed]
- Chang, K.-S.; Wu, Z.-C.; Kim, S.; Tung, K.-L.; Lee, Y.M.; Lin, Y.-F.; Lai, J.-Y. Molecular modeling of poly(benzoxazole-co-imide) membranes: A structure characterization and performance investigation. J. Membr. Sci. 2014, 454, 1–11. [Google Scholar] [CrossRef]
- Park, C.H.; Tocci, E.; Kim, S.; Kumar, A.; Lee, Y.M.; Drioli, E. A Simulation Study on OH-Containing Polyimide (HPI) and Thermally Rearranged Polybenzoxazoles (TR-PBO): Relationship between Gas Transport Properties and Free Volume Morphology. J. Phys. Chem. B 2014, 118, 2746–2757. [Google Scholar] [CrossRef] [PubMed]
- Rizzuto, C.; Caravella, A.; Brunetti, A.; Park, C.H.; Lee, Y.M.; Drioli, E.; Barbieri, G.; Tocci, E. Sorption and Diffusion of CO2/N2 in gas mixture in thermally-rearranged polymeric membranes: A molecular investigation. J. Membr. Sci. 2017, 528, 135–146. [Google Scholar] [CrossRef]
- Velioğlu, S.; Ahunbay, M.G.; Tantekin-Ersolmaz, S.B. An atomistic insight on CO2 plasticization resistance of thermally rearranged 6FDA-bisAPAF. J. Membr. Sci. 2018, 556, 23–33. [Google Scholar] [CrossRef]
- Brunetti, A.; Tocci, E.; Cersosimo, M.; Kim, J.S.; Lee, W.H.; Seong, J.G.; Lee, Y.M.; Drioli, E.; Barbieri, G. Mutual influence of mixed-gas permeation in thermally rearranged poly(benzoxazole-co-imide) polymer membranes. J. Membr. Sci. 2019, 580, 202–213. [Google Scholar] [CrossRef]
- Hart, K.E.; Colina, C.M. Estimating gas permeability and permselectivity of microporous polymers. J. Membr. Sci. 2014, 468, 259–268. [Google Scholar] [CrossRef]
- Hart, K.E.; Springmeier, J.M.; McKeown, N.B.; Colina, C.M. Simulated swelling during low-temperature N2 adsorption in polymers of intrinsic microporosity. Phys. Chem. Chem. Phys. 2013, 15, 20161–20169. [Google Scholar] [CrossRef]
- Merkel, T.C.; Bondar, V.I.; Nagai, K.; Freeman, B.D.; Pinnau, I. Gas sorption, diffusion, and permeation in poly(dimethylsiloxane). J. Polym. Sci. Part B: Polym. Phys. 2000, 38, 415–434. [Google Scholar] [CrossRef]
- Zhou, C.; Chung, T.-S.; Wang, R.; Liu, Y.; Goh, S.H. The accelerated CO2 plasticization of ultra-thin polyimide films and the effect of surface chemical cross-linking on plasticization and physical aging. J. Membr. Sci. 2003, 225, 125–134. [Google Scholar] [CrossRef]
- Horn, N.R.; Paul, D.R. Carbon dioxide plasticization and conditioning effects in thick vs. thin glassy polymer films. Polymer 2011, 52, 1619–1627. [Google Scholar] [CrossRef]
- Rowe, B.W.; Pas, S.J.; Hill, A.J.; Suzuki, R.; Freeman, B.D.; Paul, D.R. A variable energy positron annihilation lifetime spectroscopy study of physical aging in thin glassy polymer films. Polymer 2009, 50, 6149–6156. [Google Scholar] [CrossRef]
- Kim, J.H.; Koros, W.J.; Paul, D.R. Physical aging of thin 6FDA-based polyimide membranes containing carboxyl acid groups. Part I. Transport properties. Polymer 2006, 47, 3094–3103. [Google Scholar] [CrossRef]
- Kim, J.H.; Koros, W.J.; Paul, D.R. Physical aging of thin 6FDA-based polyimide membranes containing carboxyl acid groups. Part II. Optical properties. Polymer 2006, 47, 3104–3111. [Google Scholar] [CrossRef]
- Kim, J.H.; Koros, W.J.; Paul, D.R. Effects of CO2 exposure and physical aging on the gas permeability of thin 6FDA-based polyimide membranes: Part 1. Without crosslinking. J. Membr. Sci. 2006, 282, 21–31. [Google Scholar] [CrossRef]
- Rowe, B.W.; Freeman, B.D.; Paul, D.R. Physical aging of ultrathin glassy polymer films tracked by gas permeability. Polymer 2009, 50, 5565–5575. [Google Scholar] [CrossRef]
- Murphy, T.M.; Freeman, B.D.; Paul, D.R. Physical aging of polystyrene films tracked by gas permeability. Polymer 2013, 54, 873–880. [Google Scholar] [CrossRef]
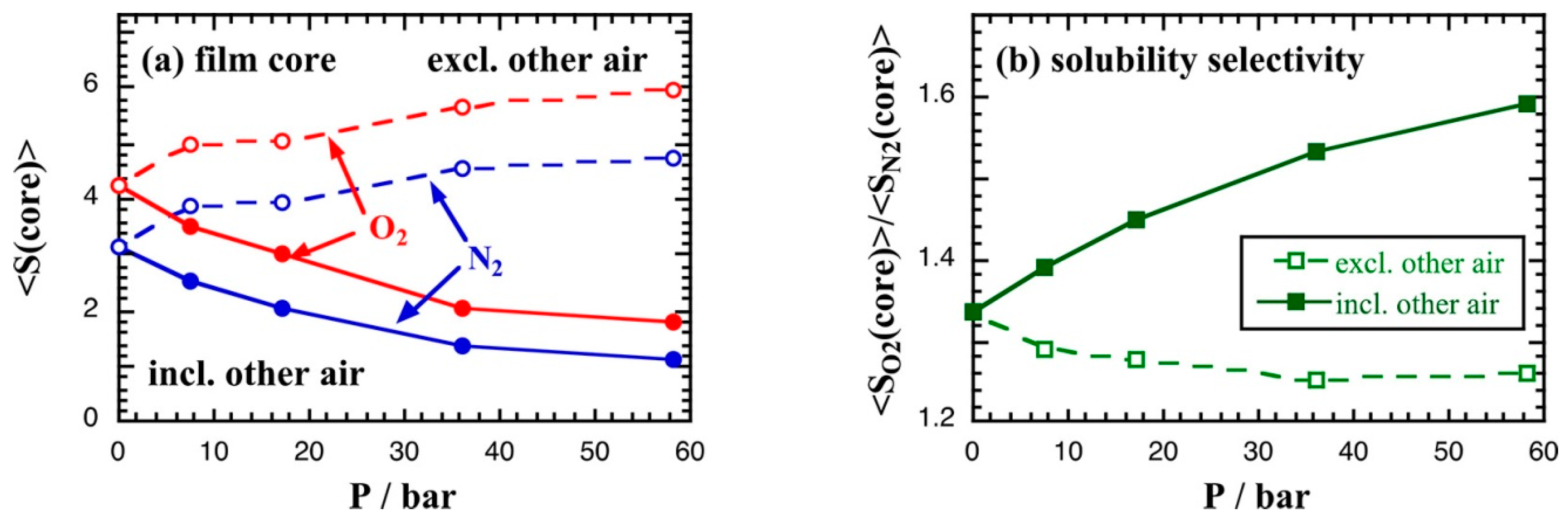
- Neyertz, S.; Brown, D. Air Sorption and Separation by Polymer Films at the Molecular Level. Macromolecules 2018, 51, 7077–7092. [Google Scholar] [CrossRef]
- Lock, S.S.M.; Lau, K.K.; Shariff, A.M.; Yeong, Y.F.; Bustam, M.A. Thickness dependent penetrant gas transport properties and separation performance within ultrathin polysulfone membrane: Insights from atomistic molecular simulation. J. Polym. Sci. Part B Polym. Phys. 2018, 56, 131–158. [Google Scholar] [CrossRef]
- Neyertz, S.; Douanne, A.; Brown, D. Effect of Interfacial Structure on Permeation Properties of Glassy Polymers. Macromolecules 2005, 38, 10286–10298. [Google Scholar] [CrossRef]
- Neyertz, S.; Douanne, A.; Brown, D. A molecular dynamics simulation study of surface effects on gas permeation in free-standing polyimide membranes. J. Membr. Sci. 2006, 280, 517–529. [Google Scholar] [CrossRef]
- Neyertz, S.; Brown, D. Molecular Dynamics Simulations of Oxygen Transport through a Fully Atomistic Polyimide Membrane. Macromolecules 2008, 41, 2711–2721. [Google Scholar] [CrossRef]
- Neyertz, S.; Brown, D. The effect of structural isomerism on carbon dioxide sorption and plasticization at the interface of a glassy polymer membrane. J. Membr. Sci. 2014, 460, 213–228. [Google Scholar] [CrossRef]
- Neyertz, S.; Brown, D. Nanosecond-time-scale reversibility of dilation induced by carbon dioxide sorption in glassy polymer membranes. J. Membr. Sci. 2016, 520, 385–399. [Google Scholar] [CrossRef]
- Gopalan, P.; Brachet, P.; Kristiansen, A.; Männle, F.; Brown, D. Oxygen Transport in Amino-Functionalized Polyhedral Oligomeric Silsesquioxanes (POSS) AU—Neyertz, S. Soft Mater. 2014, 12, 113–123. [Google Scholar] [CrossRef]
- Neyertz, S.; Brown, D. Molecular Dynamics Study of Carbon Dioxide Sorption and Plasticization at the Interface of a Glassy Polymer Membrane. Macromolecules 2013, 46, 2433–2449. [Google Scholar] [CrossRef]
- Yampol’skii, Y.P.; Pinnau, I.; Freeman, B.D. Materials Science of Membranes for Gas and Vapor Separation; John Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Xia, J.; Chung, T.-S.; Paul, D.R. Physical aging and carbon dioxide plasticization of thin polyimide films in mixed gas permeation. J. Membr. Sci. 2014, 450, 457–468. [Google Scholar] [CrossRef]
- O’Brien, K.C.; Koros, W.J.; Barbari, T.A.; Sanders, E.S. A new technique for the measurement of multicomponent gas transport through polymeric films. J. Membr. Sci. 1986, 29, 229–238. [Google Scholar] [CrossRef]
- Genduso, G.; Litwiller, E.; Ma, X.; Zampini, S.; Pinnau, I. Mixed-gas sorption in polymers via a new barometric test system: Sorption and diffusion of CO2-CH4 mixtures in polydimethylsiloxane (PDMS). J. Membr. Sci. 2019, 577, 195–204. [Google Scholar] [CrossRef]
- Fraga, S.C.; Monteleone, M.; Lanč, M.; Esposito, E.; Fuoco, A.; Giorno, L.; Pilnáček, K.; Friess, K.; Carta, M.; McKeown, N.B.; et al. A novel time lag method for the analysis of mixed gas diffusion in polymeric membranes by on-line mass spectrometry: Method development and validation. J. Membr. Sci. 2018, 561, 39–58. [Google Scholar] [CrossRef]
- Tanis, I.; Brown, D.; Neyertz, S.; Heck, R.; Mercier, R.; Vaidya, M.; Ballaguet, J.-P. A comparison of pure and mixed-gas permeation of nitrogen and methane in 6FDA-based polyimides as studied by molecular dynamics simulations. Comput. Mater. Sci. 2018, 141, 243–253. [Google Scholar] [CrossRef]
- Coleman, M.R.; Koros, W.J. Isomeric polyimides based on fluorinated dianhydrides and diamines for gas separation applications. J. Membr. Sci. 1990, 50, 285–297. [Google Scholar] [CrossRef]
- Tanaka, K.; Kita, H.; Okano, M.; Okamoto, K.-I. Permeability and permselectivity of gases in fluorinated and non-fluorinated polyimides. Polymer 1992, 33, 585–592. [Google Scholar] [CrossRef]
- Coleman, M.R.; Koros, W.J. The transport properties of polyimide isomers containing hexafluoroisopropylidene in the diamine residue. J. Polym. Sci. Part B: Polym. Phys. 1994, 32, 1915–1926. [Google Scholar] [CrossRef]
- Cornelius, C.J.; Marand, E. Hybrid silica-polyimide composite membranes: Gas transport properties. J. Membr. Sci. 2002, 202, 97–118. [Google Scholar] [CrossRef]
- Takeuchi, H. A jump motion of small molecules in glassy polymers: A molecular dynamics simulation. J. Chem. Phys. 1990, 93, 2062–2067. [Google Scholar] [CrossRef]
- Müller-Plathe, F.; Laaksonen, L.; van Gunsteren, W.F. Cooperative Effects in the Transport of Small Molecules Through an Amorphous Polymer Matrix. J. Mol. Graph. 1993, 11, 118. [Google Scholar] [CrossRef]
- Haus, J.W.; Kehr, K.W. Diffusion in regular and disordered lattices. Phys. Rep. 1987, 150, 263–406. [Google Scholar] [CrossRef]
- Havlin, S.; Ben-Avraham, D. Diffusion in disordered media. Adv. Phys. 1987, 36, 695–798. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; Taylor & Francis: London, UK, 1992. [Google Scholar]
- Rallabandi, P.S.; Thompson, A.P.; Ford, D.M. A Molecular Modeling Study of Entropic and Energetic Selectivities in Air Separation with Glassy Polymers. Macromolecules 2000, 33, 3142–3152. [Google Scholar] [CrossRef]
- Wind, J.D.; Sirard, S.M.; Paul, D.R.; Green, P.F.; Johnston, K.P.; Koros, W.J. Carbon Dioxide-Induced Plasticization of Polyimide Membranes: Pseudo-Equilibrium Relationships of Diffusion, Sorption, and Swelling. Macromolecules 2003, 36, 6433–6441. [Google Scholar] [CrossRef]
- Pinnau, I.; Toy, L.G. Transport of organic vapors through poly(1-trimethylsilyl-1-propyne). J. Membr. Sci. 1996, 116, 199–209. [Google Scholar] [CrossRef]
- Koros, W.J.; Chern, R.T.; Stannett, V.; Hopfenberg, H.B. A model for permeation of mixed gases and vapors in glassy polymers. J. Polym. Sci. Polym. Phys. Ed. 1981, 19, 1513–1530. [Google Scholar] [CrossRef]
- Park, H.B.; Kamcev, J.; Robeson, L.M.; Elimelech, M.; Freeman, B.D. Maximizing the right stuff: The trade-off between membrane permeability and selectivity. Science 2017, 356, eaab0530. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.-C.; Huang, L.-J.; Wang, Y.-X.; Yang, K.; Tang, J.-G.; Wang, Y.; Cheng, M.-M.; Zhang, Y.; Kipper, M.J.; Belfiore, L.A.; et al. Recent developments in graphene-based polymer composite membranes: Preparation, mass transfer mechanism, and applications. J. Appl. Polym. Sci. 2019, 136, 47761. [Google Scholar] [CrossRef]
- Deng, L.; Hägg, M.-B. Carbon nanotube reinforced PVAm/PVA blend FSC nanocomposite membrane for CO2/CH4 separation. Int. J. Greenh. Gas Control 2014, 26, 127–134. [Google Scholar] [CrossRef]
- Ihsanullah. Carbon nanotube membranes for water purification: Developments, challenges, and prospects for the future. Sep. Purif. Technol. 2019, 209, 307–337. [Google Scholar] [CrossRef]
- Qu, X.; Alvarez, P.J.J.; Li, Q. Applications of nanotechnology in water and wastewater treatment. Water Res. 2013, 47, 3931–3946. [Google Scholar] [CrossRef]
- Celik, E.; Park, H.; Choi, H.; Choi, H. Carbon nanotube blended polyethersulfone membranes for fouling control in water treatment. Water Res. 2011, 45, 274–282. [Google Scholar] [CrossRef] [PubMed]
- Gong, H.; Chuah, C.Y.; Yang, Y.; Bae, T.-H. High performance composite membranes comprising Zn(pyrz)2(SiF6) nanocrystals for CO2/CH4 separation. J. Ind. Eng. Chem. 2018, 60, 279–285. [Google Scholar] [CrossRef]
- Dettori, R.; Yang, Q.; Whiting, W.I. Exploration of anion transport in a composite membrane via experimental and theoretical methods. J. Membr. Sci. 2018, 563, 270–276. [Google Scholar] [CrossRef]
- Vinoba, M.; Bhagiyalakshmi, M.; Alqaheem, Y.; Alomair, A.A.; Pérez, A.; Rana, M.S. Recent progress of fillers in mixed matrix membranes for CO2 separation: A review. Sep. Purif. Technol. 2017, 188, 431–450. [Google Scholar] [CrossRef]
- Favvas, E.P.; Katsaros, F.K.; Papageorgiou, S.K.; Sapalidis, A.A.; Mitropoulos, A.C. A review of the latest development of polyimide based membranes for CO2 separations. React. Funct. Polym. 2017, 120, 104–130. [Google Scholar] [CrossRef]
- Etxeberria-Benavides, M.; David, O.; Johnson, T.; Łozińska, M.M.; Orsi, A.; Wright, P.A.; Mastel, S.; Hillenbrand, R.; Kapteijn, F.; Gascon, J. High performance mixed matrix membranes (MMMs) composed of ZIF-94 filler and 6FDA-DAM polymer. J. Membr. Sci. 2018, 550, 198–207. [Google Scholar] [CrossRef]
- Li, W.; Samarasinghe, S.A.S.C.; Bae, T.-H. Enhancing CO2/CH4 separation performance and mechanical strength of mixed-matrix membrane via combined use of graphene oxide and ZIF-8. J. Ind. Eng. Chem. 2018, 67, 156–163. [Google Scholar] [CrossRef]
- Barooah, M.; Mandal, B. Synthesis, characterization and CO2 separation performance of novel PVA/PG/ZIF-8 mixed matrix membrane. J. Membr. Sci. 2019, 572, 198–209. [Google Scholar] [CrossRef]
- Li, H.; Han, L.; Hou, J.; Liu, J.; Zhang, Y. Oriented Zeolitic imidazolate framework membranes within polymeric matrices for effective N2/CO2 separation. J. Membr. Sci. 2019, 572, 82–91. [Google Scholar] [CrossRef]
- Ding, X.; Tan, F.; Zhao, H.; Hua, M.; Wang, M.; Xin, Q.; Zhang, Y. Enhancing gas permeation and separation performance of polymeric membrane by incorporating hollow polyamide nanoparticles with dense shell. J. Membr. Sci. 2019, 570–571, 53–60. [Google Scholar] [CrossRef]
- Xie, K.; Fu, Q.; Qiao, G.G.; Webley, P.A. Recent progress on fabrication methods of polymeric thin film gas separation membranes for CO2 capture. J. Membr. Sci. 2019, 572, 38–60. [Google Scholar] [CrossRef]
- Akther, N.; Phuntsho, S.; Chen, Y.; Ghaffour, N.; Shon, H.K. Recent advances in nanomaterial-modified polyamide thin-film composite membranes for forward osmosis processes. J. Membr. Sci. 2019, 584, 20–45. [Google Scholar] [CrossRef]
- Liu, G.; Labreche, Y.; Chernikova, V.; Shekhah, O.; Zhang, C.; Belmabkhout, Y.; Eddaoudi, M.; Koros, W.J. Zeolite-like MOF nanocrystals incorporated 6FDA-polyimide mixed-matrix membranes for CO2/CH4 separation. J. Membr. Sci. 2018, 565, 186–193. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, G.; Zhang, C.; Qiu, W.; Yi, S.; Chernikova, V.; Chen, Z.; Belmabkhout, Y.; Shekhah, O.; Eddaoudi, M.; et al. Enhanced CO2/CH4 Separation Performance of a Mixed Matrix Membrane Based on Tailored MOF-Polymer Formulations. Adv. Sci. 2018, 5, 1800982. [Google Scholar] [CrossRef] [PubMed]
- Teodoro, R.M.; Tomé, L.C.; Mantione, D.; Mecerreyes, D.; Marrucho, I.M. Mixing poly(ionic liquid)s and ionic liquids with different cyano anions: Membrane forming ability and CO2/N2 separation properties. J. Membr. Sci. 2018, 552, 341–348. [Google Scholar] [CrossRef]
- Kanehashi, S.; Kishida, M.; Kidesaki, T.; Shindo, R.; Sato, S.; Miyakoshi, T.; Nagai, K. CO2 separation properties of a glassy aromatic polyimide composite membranes containing high-content 1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ionic liquid. J. Membr. Sci. 2013, 430, 211–222. [Google Scholar] [CrossRef]
- Li, J.; Liu, B.; Zhang, X.; Cao, D.; Chen, G. Hydrogen Bond Networks of Glycol Molecules on ZIF-8 Surfaces as Semipermeable Films for Efficient Carbon Capture. J. Phys. Chem. C 2017, 121, 25347–25352. [Google Scholar] [CrossRef]
- Gonciaruk, A.; Althumayri, K.; Harrison, W.J.; Budd, P.M.; Siperstein, F.R. PIM-1/graphene composite: A combined experimental and molecular simulation study. Microporous Mesoporous Mater. 2015, 209, 126–134. [Google Scholar] [CrossRef]
- Kupgan, G.; Abbott, L.J.; Hart, K.E.; Colina, C.M. Modeling Amorphous Microporous Polymers for CO2 Capture and Separations. Chem. Rev. 2018, 118, 5488–5538. [Google Scholar] [CrossRef]
- Vogiatzis, G.G.; Theodorou, D.N. Multiscale Molecular Simulations of Polymer-Matrix Nanocomposites. Arch. Comput. Methods Eng. 2018, 25, 591–645. [Google Scholar] [CrossRef]
- Abedini, A.; Crabtree, E.; Bara, J.E.; Turner, C.H. Molecular Simulation of Ionic Polyimides and Composites with Ionic Liquids as Gas-Separation Membranes. Langmuir 2017, 33, 11377–11389. [Google Scholar] [CrossRef] [PubMed]
- Abedini, A.; Crabtree, E.; Bara, J.E.; Turner, C.H. Molecular analysis of selective gas adsorption within composites of ionic polyimides and ionic liquids as gas separation membranes. Chem. Phys. 2019, 516, 71–83. [Google Scholar] [CrossRef]
- Aryal, D.; Ganesan, V. Reversal of Salt Concentration Dependencies of Salt and Water Diffusivities in Polymer Electrolyte Membranes. ACS Macro Lett. 2018, 7, 739–744. [Google Scholar] [CrossRef]
- Mogurampelly, S.; Sethuraman, V.; Pryamitsyn, V.; Ganesan, V. Influence of nanoparticle-ion and nanoparticle-polymer interactions on ion transport and viscoelastic properties of polymer electrolytes. J. Chem. Phys. 2016, 144, 154905. [Google Scholar] [CrossRef] [PubMed]
- Mogurampelly, S.; Ganesan, V. Influence of nanoparticle surface chemistry on ion transport in polymer nanocomposite electrolytes. Solid State Ion. 2016, 286, 57. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, Z.; Jiang, J. Metal–Organic Framework/Polymer Mixed-Matrix Membranes for H2/CO2 Separation: A Fully Atomistic Simulation Study. J. Phys. Chem. C 2012, 116, 19268–19277. [Google Scholar] [CrossRef]
- Azar, A.N.V.; Velioglu, S.; Keskin, S. Large-Scale Computational Screening of Metal Organic Framework (MOF) Membranes and MOF-Based Polymer Membranes for H2/N2 Separations. ACS Sustain. Chem. Eng. 2019, 7, 9525–9536. [Google Scholar] [CrossRef]
- Yilmaz, G.; Keskin, S. Predicting the Performance of Zeolite Imidazolate Framework/Polymer Mixed Matrix Membranes for CO2, CH4, and H2 Separations Using Molecular Simulations. Ind. Eng. Chem. Res. 2012, 51, 14218–14228. [Google Scholar] [CrossRef]
- Dutta, R.C.; Bhatia, S.K. Structure and Gas Transport at the Polymer–Zeolite Interface: Insights from Molecular Dynamics Simulations. ACS Appl. Mater. Interfaces 2018, 10, 5992–6005. [Google Scholar] [CrossRef]
- Zhang, Q.G.; Liu, Q.L.; Wu, J.Y.; Chen, Y.; Zhu, A.M. Structure-related diffusion in poly(methyl methacrylate)/polyhedral oligomeric silsesquioxanes composites: A molecular dynamics simulation study. J. Membr. Sci. 2009, 342, 105–112. [Google Scholar] [CrossRef]
- Wang, C.; Jagirdar, P.; Naserifar, S.; Sahimi, M. Molecular Simulation Study of Gas Solubility and Diffusion in a Polymer-Boron Nitride Nanotube Composite. J. Phys. Chem. B 2016, 120, 1273–1284. [Google Scholar] [CrossRef]
- Bonakala, S.; Lalitha, A.; Shin, J.E.; Moghadam, F.; Semino, R.; Park, H.B.; Maurin, G. Understanding of the Graphene Oxide/Metal-Organic Framework Interface at the Atomistic Scale. ACS Appl. Mater. Interfaces 2018, 10, 33619–33629. [Google Scholar] [CrossRef] [PubMed]
- Hwang, S.; Semino, R.; Seoane, B.; Zahan, M.; Chmelik, C.; Valiullin, R.; Bertmer, M.; Haase, J.; Kapteijn, F.; Gascon, J.; et al. Revealing the Transient Concentration of CO2 in a Mixed-Matrix Membrane by IR Microimaging and Molecular Modeling. Angew. Chem. Int. Ed. 2018, 57, 5156–5160. [Google Scholar] [CrossRef]
- Semino, R.; Dürholt, J.P.; Schmid, R.; Maurin, G. Multiscale Modeling of the HKUST-1/Poly(vinyl alcohol) Interface: From an Atomistic to a Coarse Graining Approach. J. Phys. Chem. C 2017, 121, 21491–21496. [Google Scholar] [CrossRef]
- Lin, R.; Villacorta Hernandez, B.; Ge, L.; Zhu, Z. Metal organic framework based mixed matrix membranes: An overview on filler/polymer interfaces. J. Mater. Chem. A 2018, 6, 293–312. [Google Scholar] [CrossRef]
- Zhao, J.; He, G.; Liu, G.; Pan, F.; Wu, H.; Jin, W.; Jiang, Z. Manipulation of interactions at membrane interfaces for energy and environmental applications. Prog. Polym. Sci. 2018, 80, 125–152. [Google Scholar] [CrossRef]
- Zavadlav, J.; Bevc, S.; Praprotnik, M. Adaptive resolution simulations of biomolecular systems. Eur. Biophys. J. 2017, 46, 821–835. [Google Scholar] [CrossRef] [PubMed]
- Kreis, K.; Tuckerman, M.E.; Donadio, D.; Kremer, K.; Potestio, R. From Classical to Quantum and Back: A Hamiltonian Scheme for Adaptive Multiresolution Classical/Path-Integral Simulations. J. Chem. Theory Comput. 2016, 12, 3030–3039. [Google Scholar] [CrossRef]
- Kreis, K.; Potestio, R.; Kremer, K.; Fogarty, A.C. Adaptive Resolution Simulations with Self-Adjusting High-Resolution Regions. J. Chem. Theory Comput. 2016, 12, 4067–4081. [Google Scholar] [CrossRef] [PubMed]
- Kreis, K.; Kremer, K.; Potestio, R.; Tuckerman, M.E. From classical to quantum and back: Hamiltonian adaptive resolution path integral, ring polymer, and centroid molecular dynamics. J. Chem. Phys. 2017, 147, 244104. [Google Scholar] [CrossRef]
- Praprotnik, M.; Delle Site, L.; Kremer, K. Adaptive resolution molecular-dynamics simulation: Changing the degrees of freedom on the fly. J. Chem. Phys. 2005, 123, 224106. [Google Scholar] [CrossRef] [PubMed]
- Delle Site, L.; Abrams, C.F.; Alavi, A.; Kremer, K. Polymers near Metal Surfaces: Selective Adsorption and Global Conformations. Phys. Rev. Lett. 2002, 89, 156103. [Google Scholar] [CrossRef] [PubMed]
- Dong, D.; Zhang, W.; Barnett, A.; Lu, J.; Van Duin, C.A.; Molinero, V.; Bedrov, D. Multiscale Modeling of Structure, Transport and Reactivity in Alkaline Fuel Cell Membranes: Combined Coarse-Grained, Atomistic and Reactive Molecular Dynamics Simulations. Polymers 2018, 10, 1289. [Google Scholar] [CrossRef] [PubMed]
- Maghami, S.; Mehrabani-Zeinabad, A.; Sadeghi, M.; Sánchez-Laínez, J.; Zornoza, B.; Téllez, C.; Coronas, J. Mathematical modeling of temperature and pressure effects on permeability, diffusivity and solubility in polymeric and mixed matrix membranes. Chem. Eng. Sci. 2019, 205, 58–73. [Google Scholar] [CrossRef]
- Castro-Muñoz, R.; Iglesia, Ó.d.; Fíla, V.; Téllez, C.; Coronas, J. Pervaporation-Assisted Esterification Reactions by Means of Mixed Matrix Membranes. Ind. Eng. Chem. Res. 2018, 57, 15998–16011. [Google Scholar] [CrossRef]
- Ursino, C.; Castro-Muñoz, R.; Drioli, E.; Gzara, L.; Albeirutty, H.M.; Figoli, A. Progress of Nanocomposite Membranes for Water Treatment. Membranes 2018, 8, 18. [Google Scholar] [CrossRef] [PubMed]
- Sarango, L.; Paseta, L.; Navarro, M.; Zornoza, B.; Coronas, J. Controlled deposition of MOFs by dip-coating in thin film nanocomposite membranes for organic solvent nanofiltration. J. Ind. Eng. Chem. 2018, 59, 8–16. [Google Scholar] [CrossRef]
- Navarro, M.; Benito, J.; Paseta, L.; Gascón, I.; Coronas, J.; Téllez, C. Thin-Film Nanocomposite Membrane with the Minimum Amount of MOF by the Langmuir–Schaefer Technique for Nanofiltration. ACS Appl. Mater. Interfaces 2018, 10, 1278–1287. [Google Scholar] [CrossRef] [PubMed]
- Echaide-Górriz, C.; Navarro, M.; Téllez, C.; Coronas, J. Simultaneous use of MOFs MIL-101(Cr) and ZIF-11 in thin film nanocomposite membranes for organic solvent nanofiltration. Dalton Trans. 2017, 46, 6244–6252. [Google Scholar] [CrossRef]
- Sánchez-Laínez, J.; Zornoza, B.; Orsi, A.F.; Łozińska, M.M.; Dawson, D.M.; Ashbrook, S.E.; Francis, S.M.; Wright, P.A.; Benoit, V.; Llewellyn, P.L.; et al. Synthesis of ZIF-93/11 Hybrid Nanoparticles via Post-Synthetic Modification of ZIF-93 and Their Use for H2/CO2 Separation. Chem. A Eur. J. 2018, 24, 11211–11219. [Google Scholar] [CrossRef]
- Castro-Muñoz, R.; Martin-Gil, V.; Ahmad, M.Z.; Fíla, V. Matrimid® 5218 in preparation of membranes for gas separation: Current state-of-the-art. Chem. Eng. Commun. 2018, 205, 161–196. [Google Scholar] [CrossRef]
- Castro-Muñoz, R.; Fíla, V.; Ahmad, M.Z. Enhancing the CO2 Separation Performance of Matrimid 5218 Membranes for CO2/CH4 Binary Mixtures. Chem. Eng. Technol. 2019, 42, 645–654. [Google Scholar] [CrossRef]
- Castro-Muñoz, R.; Fíla, V.; Martin-Gil, V.; Muller, C. Enhanced CO2 permeability in Matrimid® 5218 mixed matrix membranes for separating binary CO2/CH4 mixtures. Sep. Purif. Technol. 2019, 210, 553–562. [Google Scholar] [CrossRef]
- Mathioudakis, I.G.; Vogiatzis, G.G.; Tzoumanekas, C.; Theodorou, D.N. Molecular modeling and simulation of polymer nanocomposites at multiple length scales. IEEE Trans. Nanotechnol. 2016, 15, 416–422. [Google Scholar] [CrossRef]
- Li, C.; Strachan, A. Molecular simulations of crosslinking process of thermosetting polymers. Polymer 2010, 51, 6058–6070. [Google Scholar] [CrossRef]
- Chmiela, S.; Sauceda, H.E.; Poltavsky, I.; Müller, K.-R.; Tkatchenko, A. sGDML: Constructing accurate and data efficient molecular force fields using machine learning. Comput. Phys. Commun. 2019. [Google Scholar] [CrossRef]
- Bejagam, K.K.; Singh, S.; An, Y.; Deshmukh, S.A. Machine-Learned Coarse-Grained Models. J. Phys. Chem. Lett. 2018, 9, 4667–4672. [Google Scholar] [CrossRef]
- Chan, H.; Narayanan, B.; Cherukara, M.J.; Sen, F.G.; Sasikumar, K.; Gray, S.K.; Chan, M.K.Y.; Sankaranarayanan, S.K.R.S. Machine Learning Classical Interatomic Potentials for Molecular Dynamics from First-Principles Training Data. J. Phys. Chem. C 2019, 123, 6941–6957. [Google Scholar] [CrossRef]
- Wang, J.; Olsson, S.; Wehmeyer, C.; Pérez, A.; Charron, N.E.; de Fabritiis, G.; Noé, F.; Clementi, C. Machine Learning of Coarse-Grained Molecular Dynamics Force Fields. ACS Cent. Sci. 2019, 5, 755–767. [Google Scholar] [CrossRef]
- Zhang, L.; Han, J.; Wang, H.; Car, R.; Weinan, E. Deep Potential Molecular Dynamics: A Scalable Model with the Accuracy of Quantum Mechanics. Phys. Rev. Lett. 2018, 120, 143001. [Google Scholar] [CrossRef]
- Zhang, L.; Han, J.; Wang, H.; Car, R.; Weinan, E. DeePCG: Constructing coarse-grained models via deep neural networks. J. Chem. Phys. 2018, 149, 034101. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhang, L.; Han, J.; Weinan, E. DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics. Comput. Phys. Commun. 2018, 228, 178–184. [Google Scholar] [CrossRef]
- Castro-Muñoz, R.; Galiano, F.; de la Iglesia, Ó.; Fíla, V.; Téllez, C.; Coronas, J.; Figoli, A. Graphene oxide—Filled polyimide membranes in pervaporative separation of azeotropic methanol–MTBE mixtures. Sep. Purif. Technol. 2019, 224, 265–272. [Google Scholar] [CrossRef]
- Baker, R.W.; Wijmans, J.G.; Huang, Y. Permeability, permeance and selectivity: A preferred way of reporting pervaporation performance data. J. Membr. Sci. 2010, 348, 346–352. [Google Scholar] [CrossRef]
- Castro-Muñoz, R.; Buera-González, J.; de la Iglesia, Ó.; Galiano, F.; Fíla, V.; Malankowska, M.; Rubio, C.; Figoli, A.; Téllez, C.; Coronas, J. Towards the dehydration of ethanol using pervaporation cross-linked poly(vinyl alcohol)/graphene oxide membranes. J. Membr. Sci. 2019, 582, 423–434. [Google Scholar] [CrossRef]
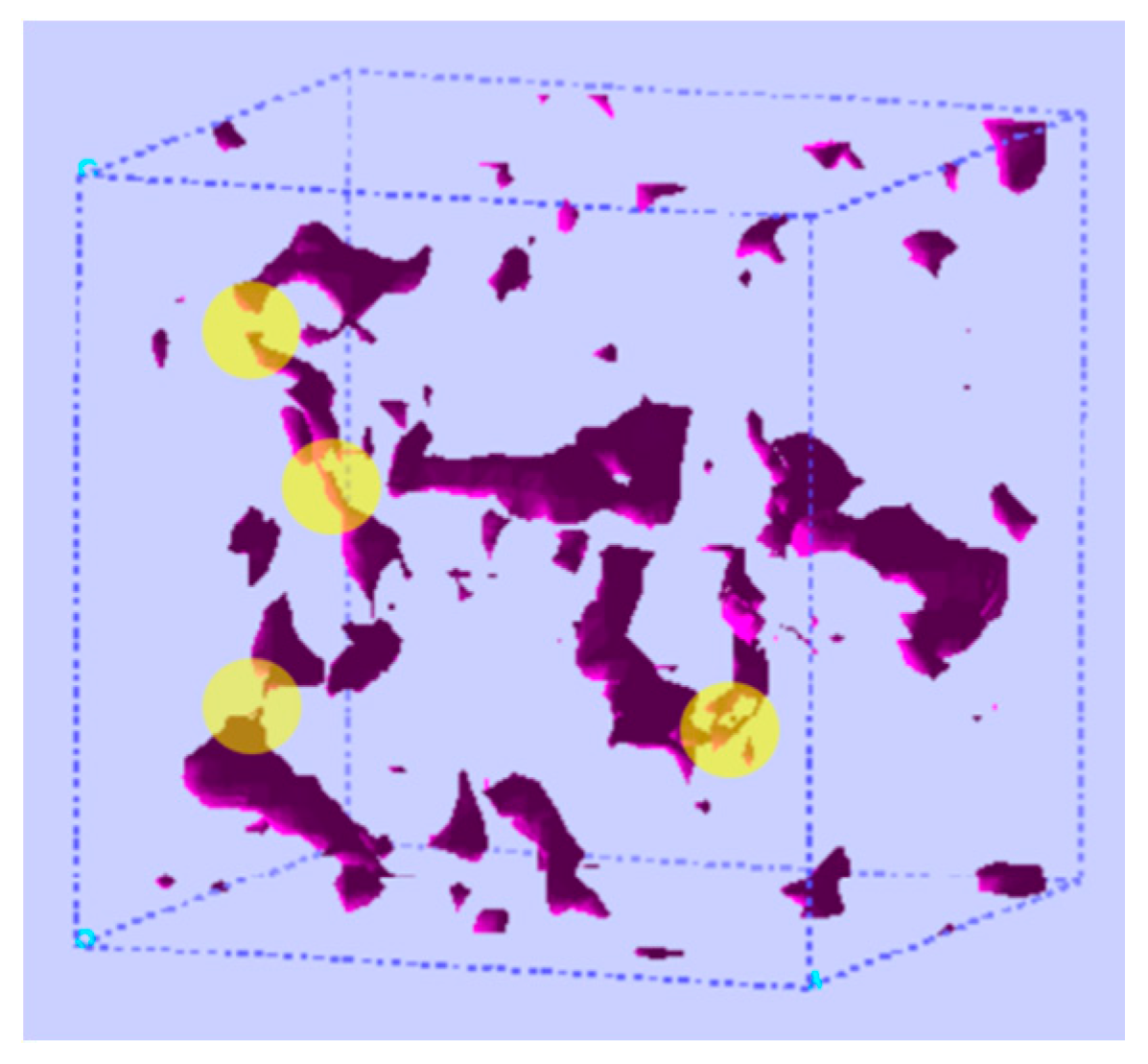
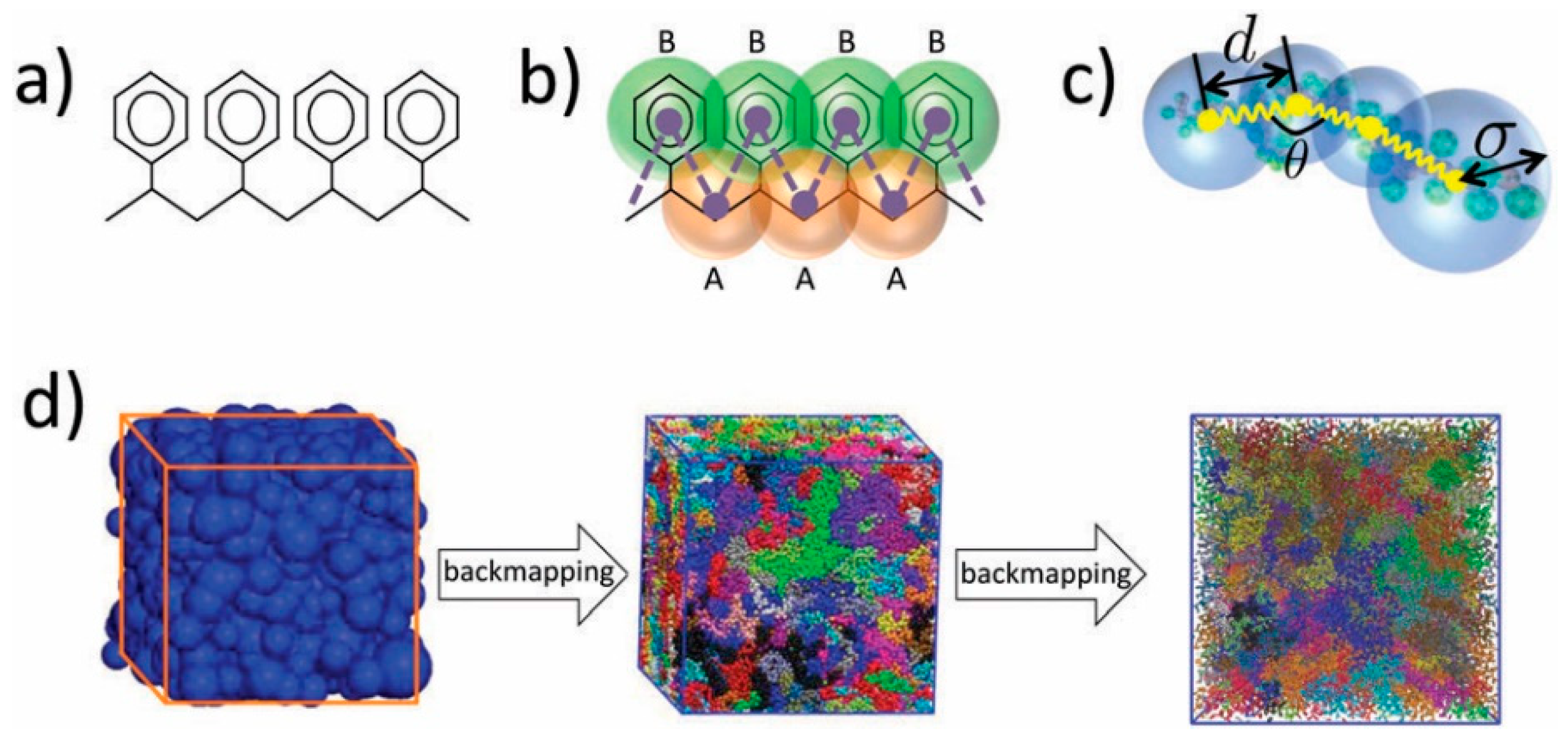
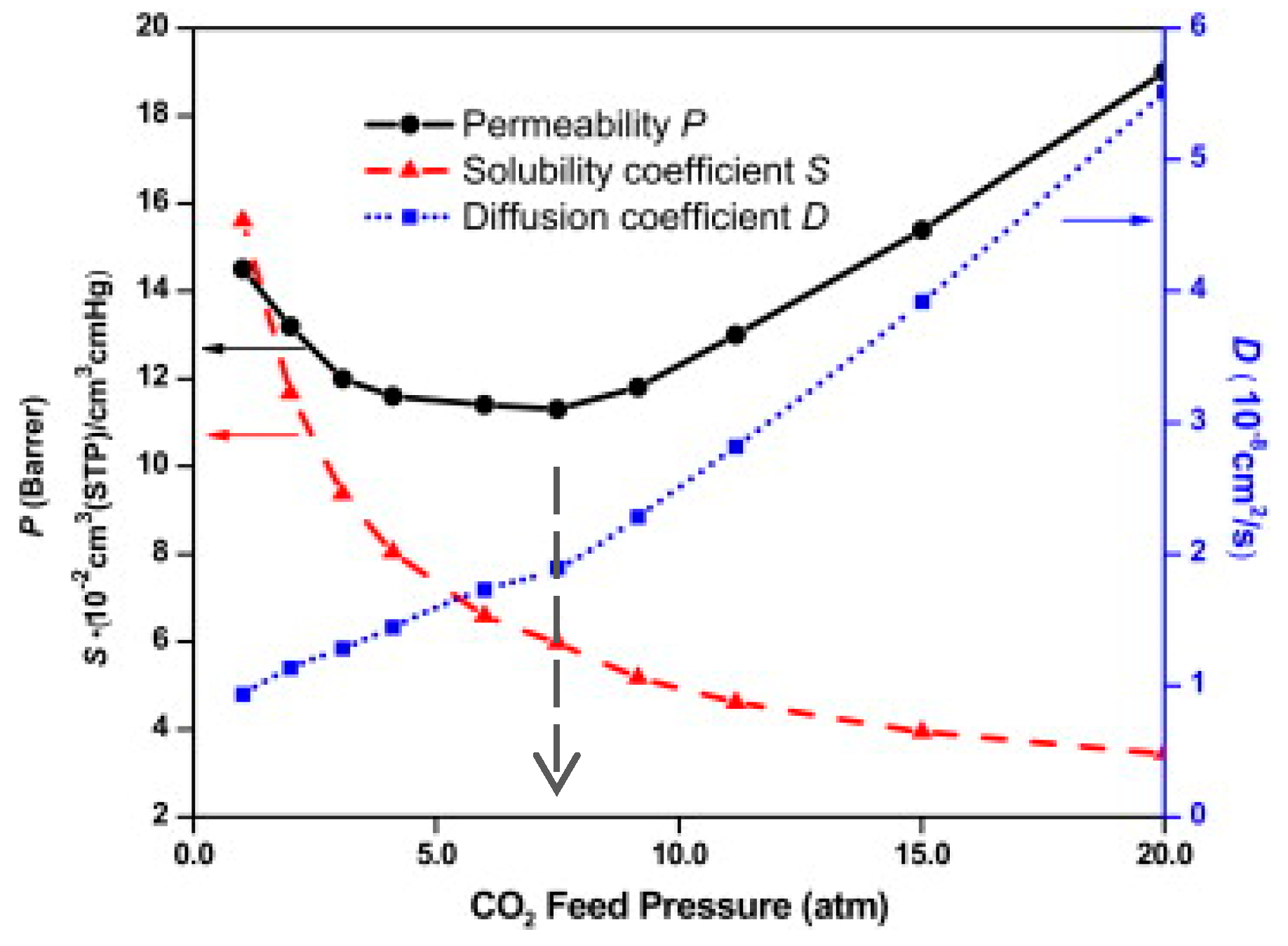
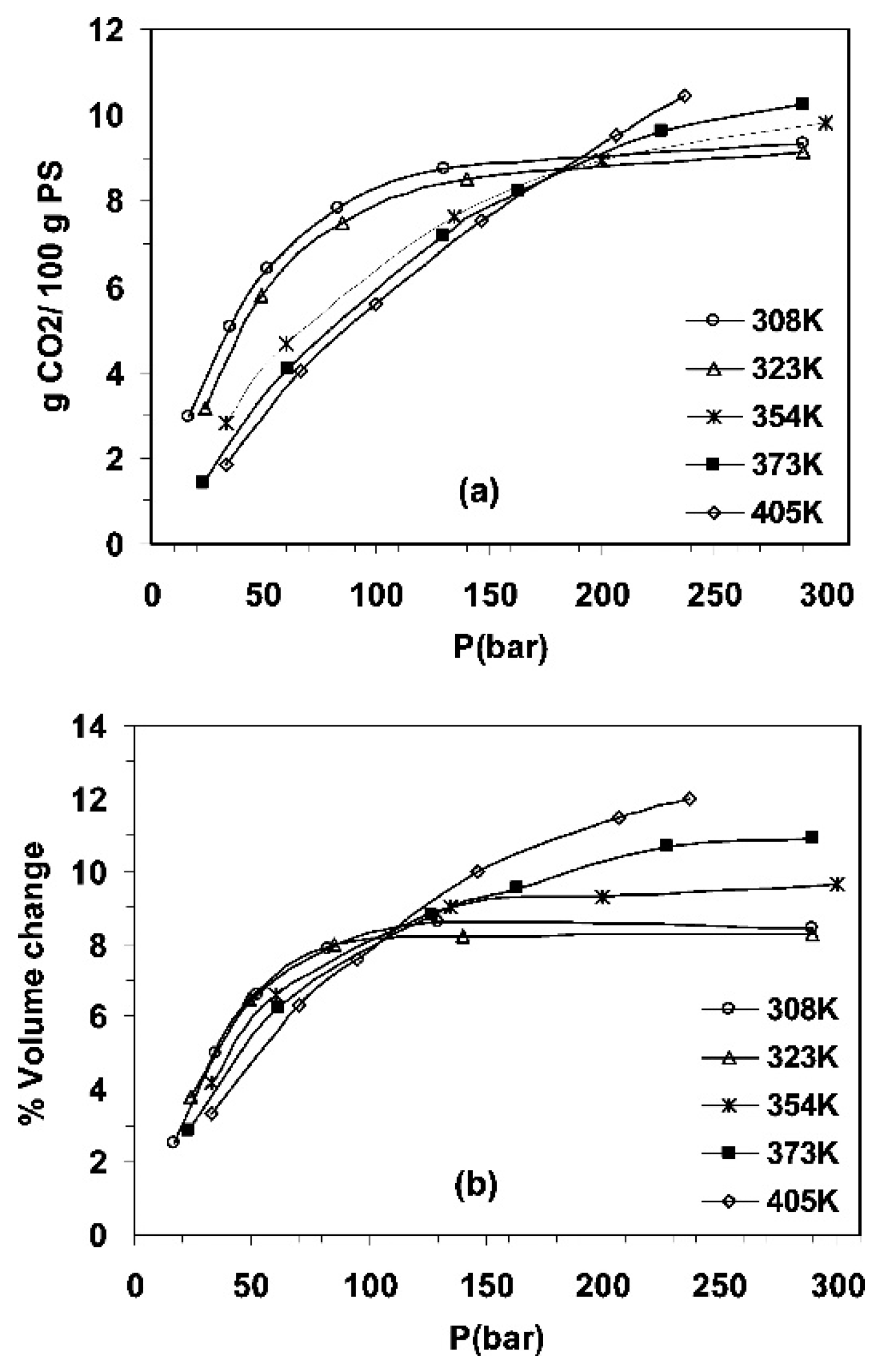
| Method | Application | Advantages | Disadvantages | Refs. |
|---|---|---|---|---|
| Molecular Dynamics | Numerical integration the system’s classical equations of motion | Calculation of thermodynamic, dynamic and transport properties | Not able to correctly sample the dynamics of systems that are characterized by a broad range of time scales or rare events | [17,18,19] |
| Monte Carlo | Stochastic method—generation of a Markov chain sequence of configurations | Efficient in sampling long-chain macromolecular systems when coupled with appropriately designed moves ‡ | Does not account for the system’s time evolution—cannot be used to study the system’s dynamics | [18,20,21] ‡[22,23,24,25,26,27,28] |
| Transition State Theory | Infrequent events | Determination of rate constants and penetrant jump pathways | Multidimensional TST that accounts for polymer cooperative motion is computationally intensive | [8,9,29,30,31,32,33,34] |
| Transition Path Sampling | Infrequent events | Determination of realistic pathways at finite temperatures | Dependence on the limited initial transition pathways extracted by MD simulations | [35] |
| Kinetic Monte Carlo | Mesoscopic simulation of a Poisson process | Calculation of penetrant diffusivity by solving numerically the master equations | Requires information on sorption sites network, rate constants and sorption probabilities determined from the atomistic scale | [8,33,34,36,37,38] |
| Coarse-grained MD | Simulation of dynamics at a mesoscopic scale | Simulation of longer time- and length- scales |
| [39,40,41,42] |
| Widom Test Particle Insertion Method | Sorption | Low concentration sorption of small molecules | Inefficient for dense systems/large solutes | [7,43,44,45] |
| Iterative Widom Schemes | Sorption | Determination of sorption isotherms | Inefficient for dense systems/large solutes | [46,47] |
| Thermodynamic Integration | Sorption | Enhanced efficiency for dense systems | Requires conduction of a series of simulations | [48,49] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vergadou, N.; Theodorou, D.N. Molecular Modeling Investigations of Sorption and Diffusion of Small Molecules in Glassy Polymers. Membranes 2019, 9, 98. https://doi.org/10.3390/membranes9080098
Vergadou N, Theodorou DN. Molecular Modeling Investigations of Sorption and Diffusion of Small Molecules in Glassy Polymers. Membranes. 2019; 9(8):98. https://doi.org/10.3390/membranes9080098
Chicago/Turabian StyleVergadou, Niki, and Doros N. Theodorou. 2019. "Molecular Modeling Investigations of Sorption and Diffusion of Small Molecules in Glassy Polymers" Membranes 9, no. 8: 98. https://doi.org/10.3390/membranes9080098
APA StyleVergadou, N., & Theodorou, D. N. (2019). Molecular Modeling Investigations of Sorption and Diffusion of Small Molecules in Glassy Polymers. Membranes, 9(8), 98. https://doi.org/10.3390/membranes9080098






