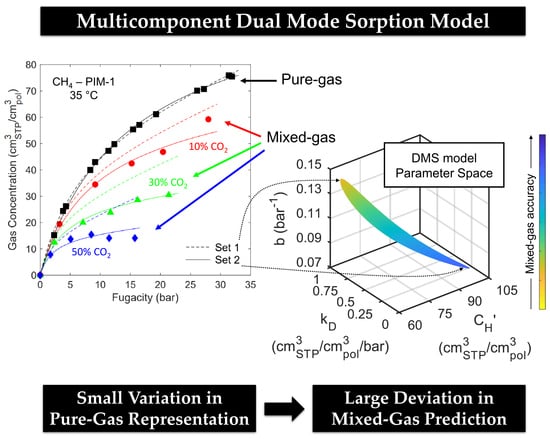
Modelling Mixed-Gas Sorption in Glassy Polymers for CO2 Removal: A Sensitivity Analysis of the Dual Mode Sorption Model
Abstract
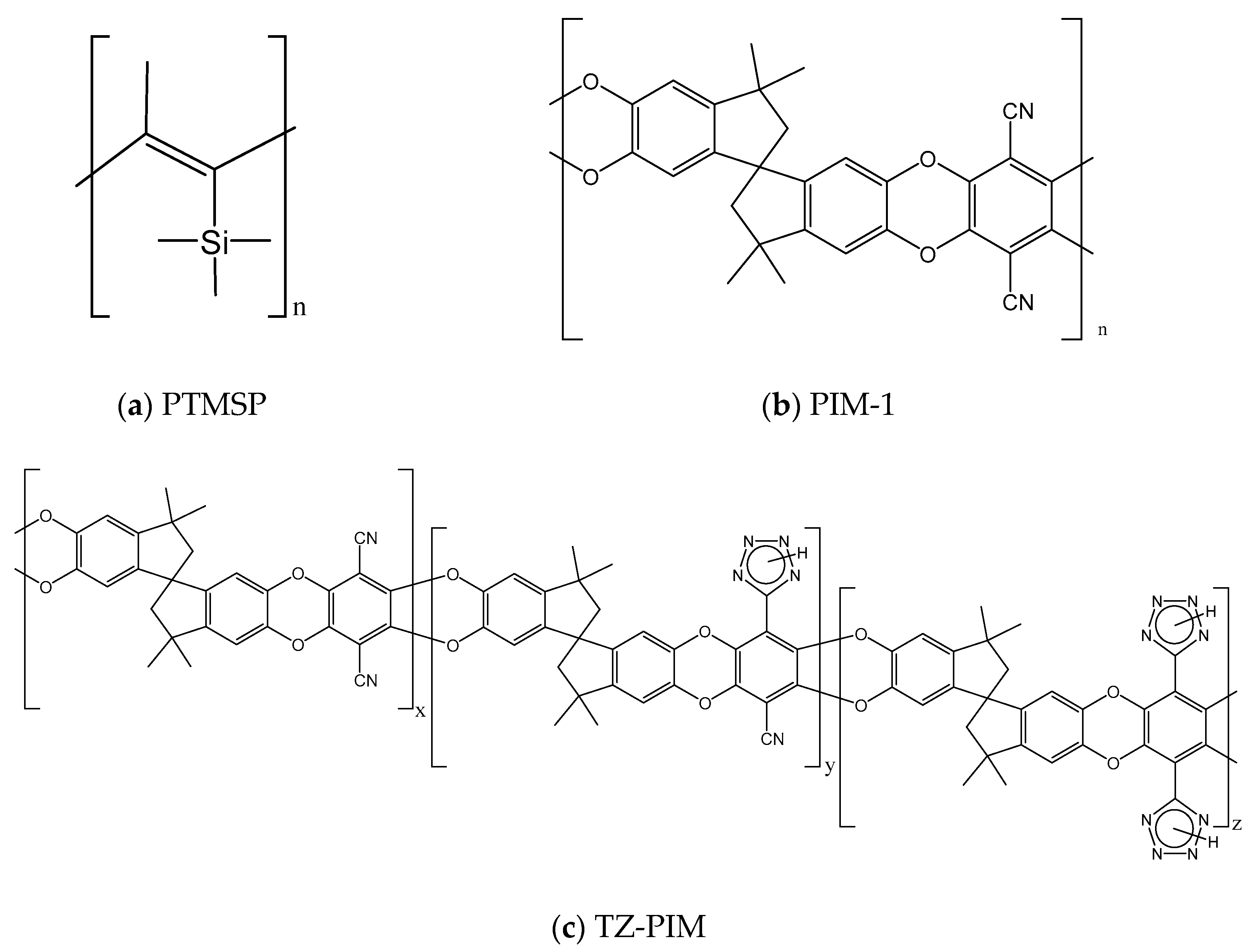
1. Introduction
2. Dual Mode Sorption Model
3. Results
3.1. Pure-Gas Sorption Analysis
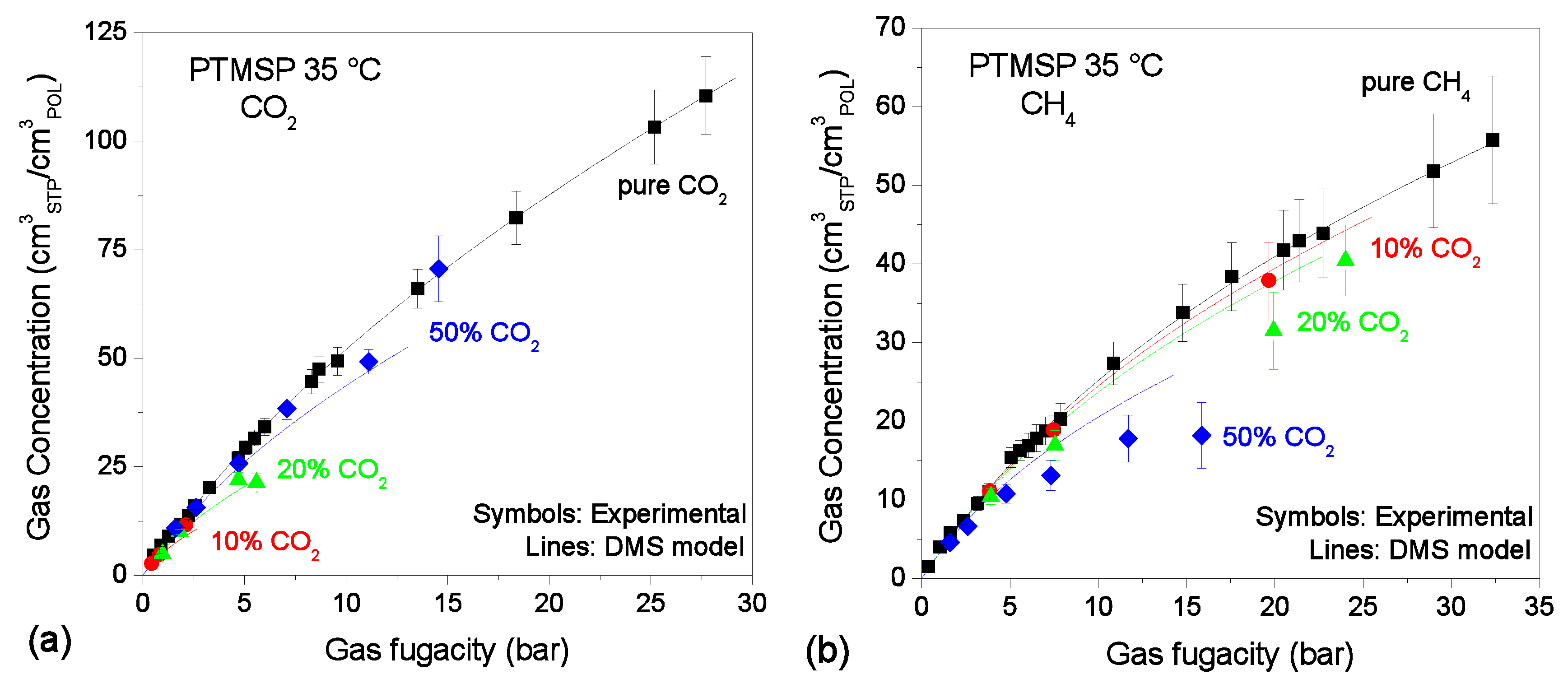
3.2. Mixed-Gas Sorption: PTMSP
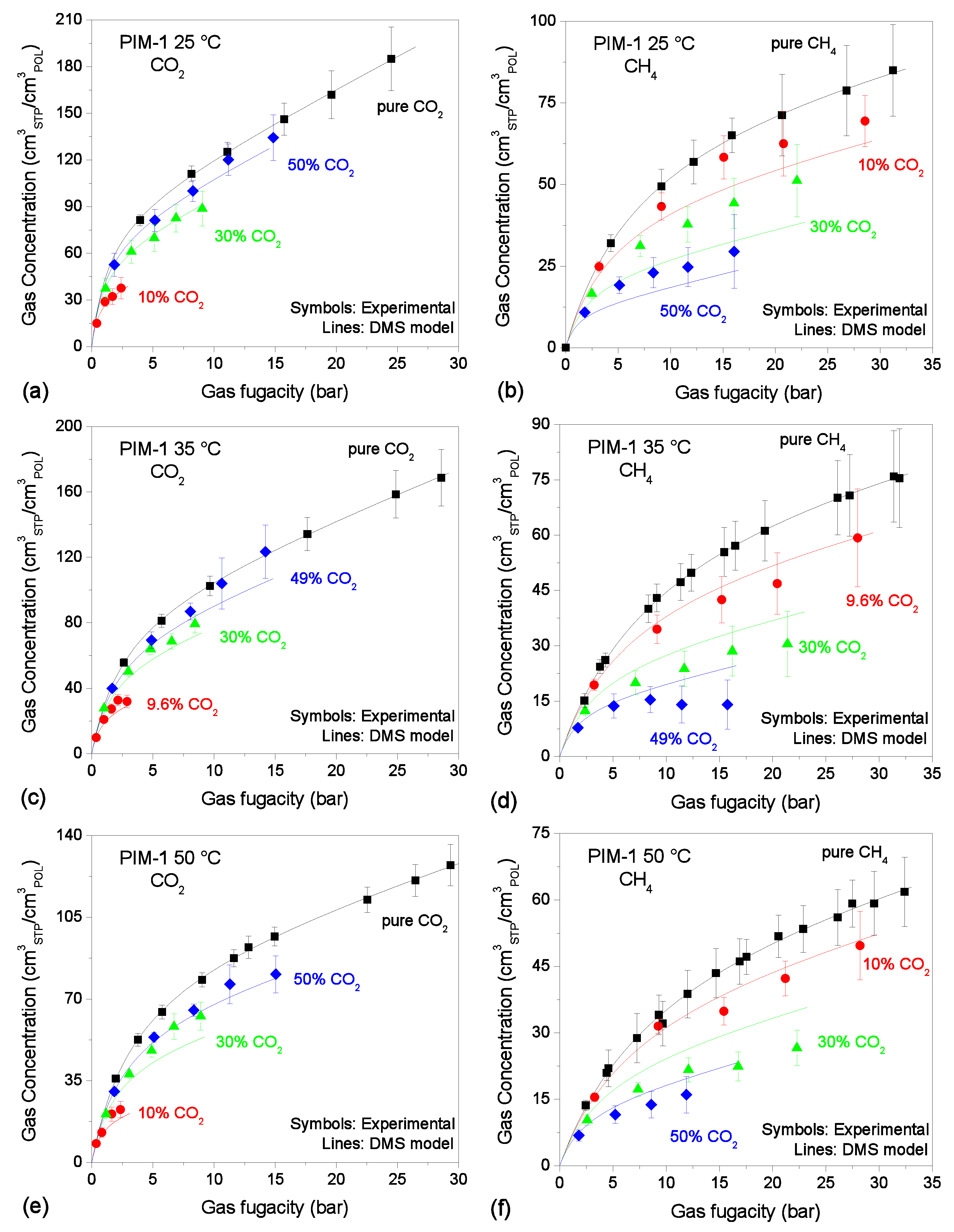
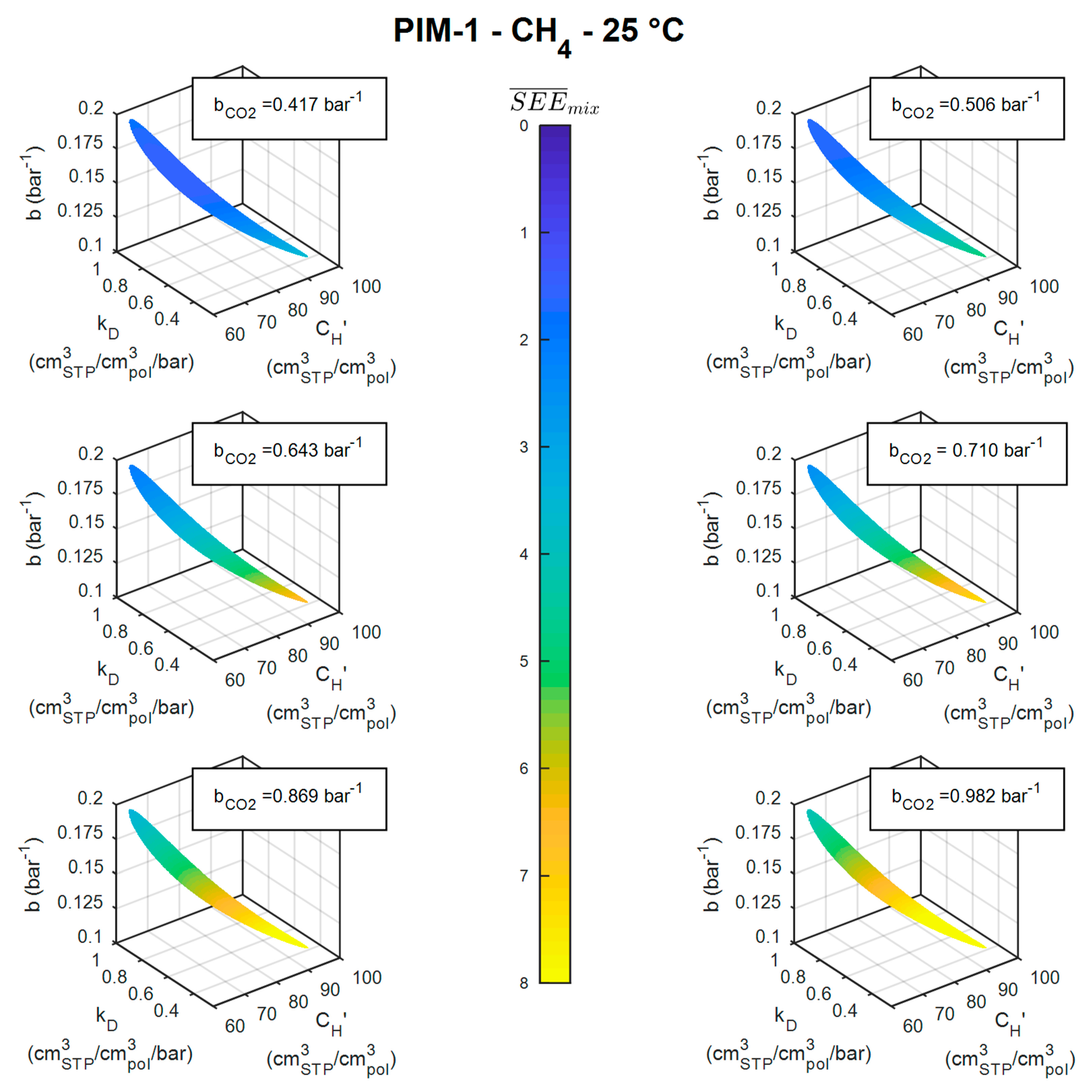
3.3. Mixed-Gas Sorption: PIM-1
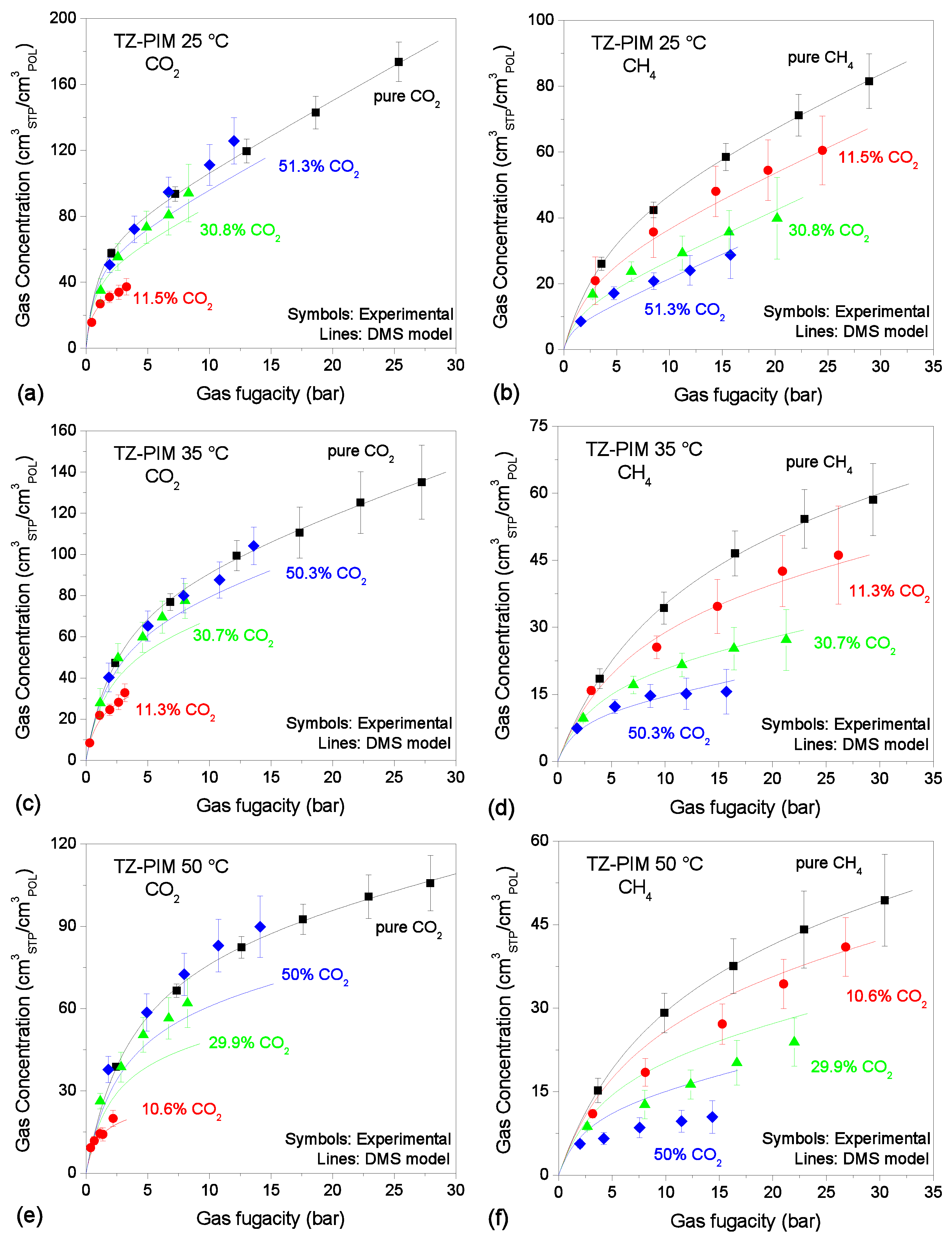
3.4. Mixed-Gas Sorption: TZ-PIM
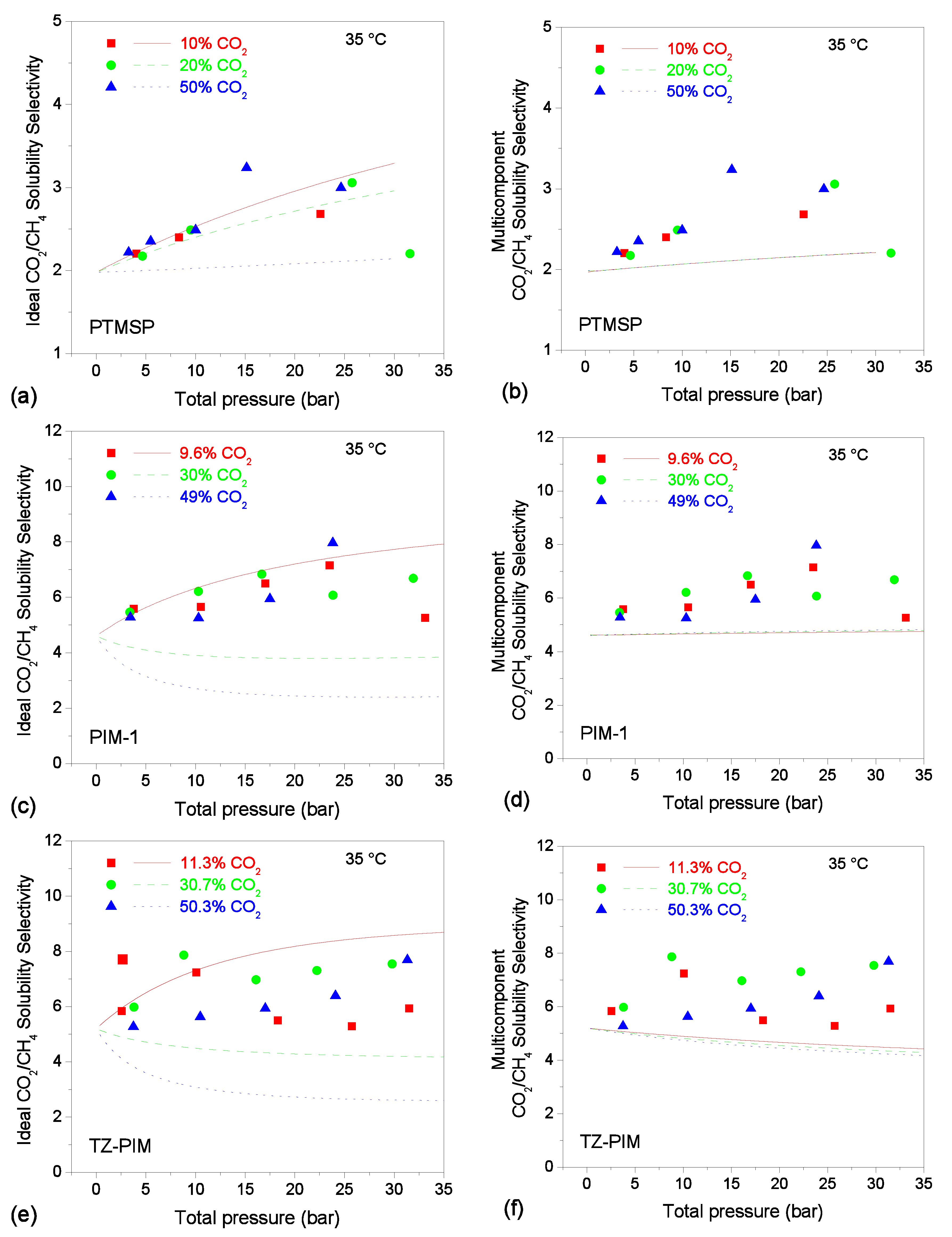
3.5. Solubility-selectivity
4. Sensitivity Analysis
4.1. Pure-Gas Sorption Isotherms Fitting Method
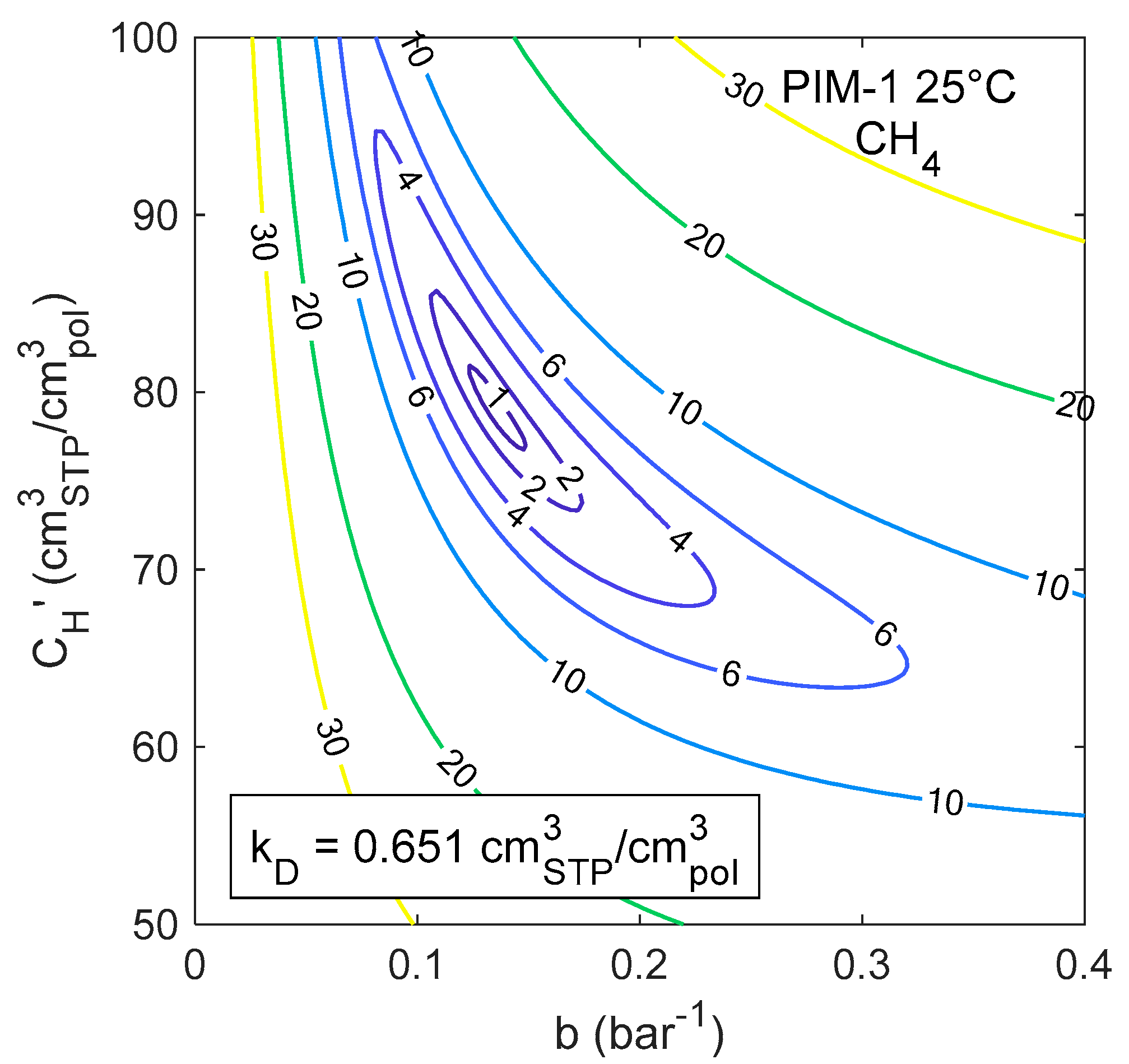
4.2. Confidence Intervals of the DMS Model Parameters
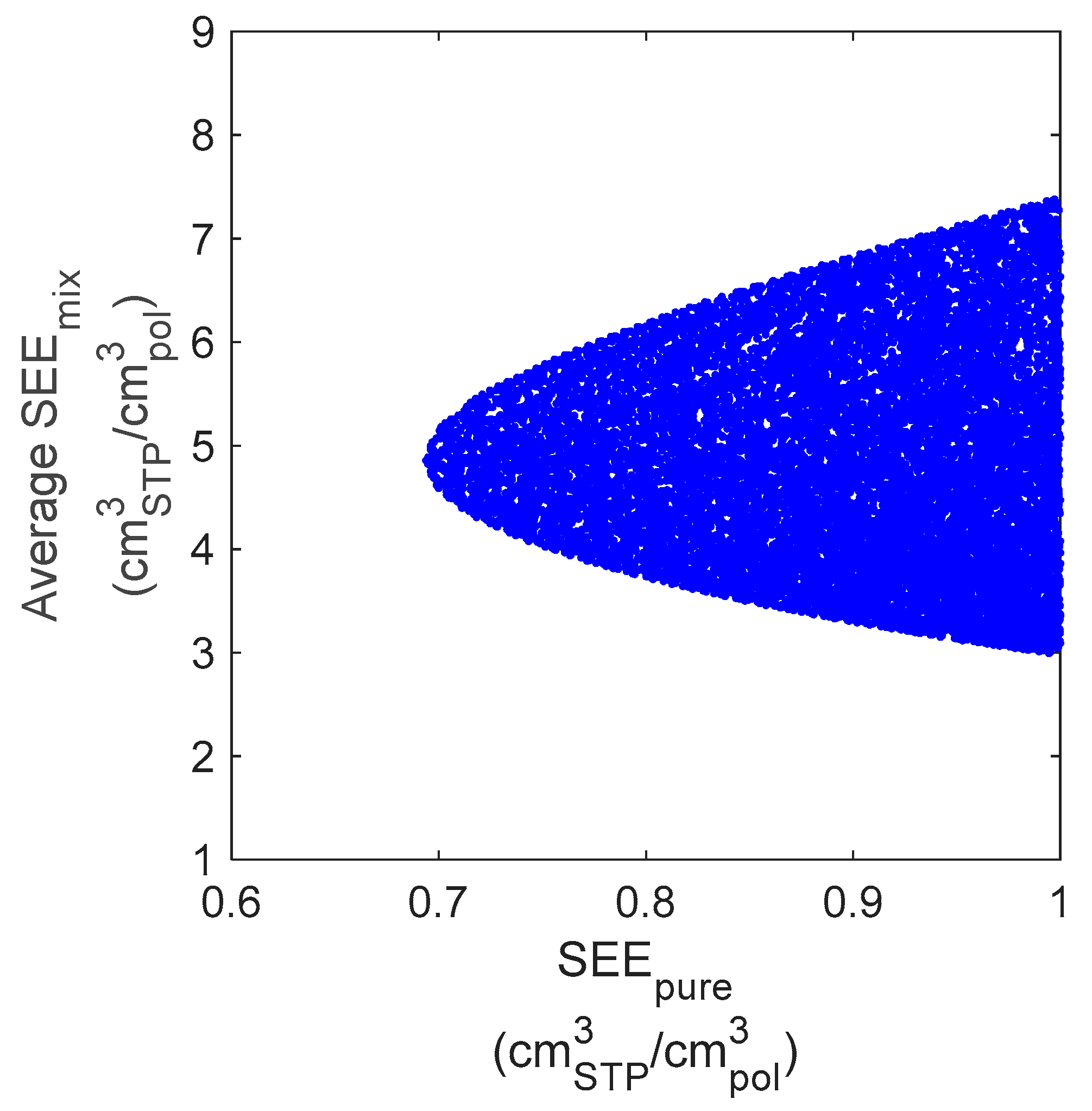
4.3. Evaluation of Mixed-Gas Sorption
4.4. Effect of
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Galizia, M.; Chi, W.S.; Smith, Z.P.; Merkel, T.C.; Baker, R.W.; Freeman, B.D. 50th Anniversary Perspective: Polymers and Mixed Matrix Membranes for Gas and Vapor Separation: A Review and Prospective Opportunities. Macromolecules 2017, 50, 7809–7843. [Google Scholar] [CrossRef]
- Baker, R.W.; Lokhandwala, K. Natural gas processing with membranes: An overview. Ind. Eng. Chem. Res. 2008, 47, 2109–2121. [Google Scholar] [CrossRef]
- Baker, R.W.; Low, B.T. Gas Separation Membrane Materials: A Perspective. Macomolecules 2014, 47, 6999–7013. [Google Scholar] [CrossRef]
- Li, C.; Meckler, S.M.; Smith, Z.P.; Bachman, J.E.; Maserati, L.; Long, J.R.; Helms, B.A. Engineered Transport in Microporous Materials and Membranes for Clean Energy Technologies. Adv. Mater. 2018, 30, 1704953. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.; Zhang, Q.; Zhu, L.; Lin, H.; Kazanowska, B.A.; Doherty, C.M.; Hill, A.J.; Gao, P.; Guo, R. Highly Selective and Permeable Microporous Polymer Membranes for Hydrogen Purification and CO2 Removal from Natural Gas. Chem. Mater. 2018, 30, 5322–5332. [Google Scholar] [CrossRef]
- Low, B.T.; Wang, Y.; Chung, T. Polymeric Membranes for Energy Applications. Encycl. Polym. Sci. Technol. 2013, 1–37. [Google Scholar] [CrossRef]
- Kim, S.; Lee, Y.M. Rigid and microporous polymers for gas separation membranes. Prog. Polym. Sci. 2015, 43, 1–32. [Google Scholar] [CrossRef]
- Kim, W.; Nair, S. Membranes from nanoporous 1D and 2D materials: A review of opportunities, developments, and challenges. Chem. Eng. Sci. 2013, 104, 908–924. [Google Scholar] [CrossRef]
- Zhang, C.; Cao, B.; Li, P. Thermal oxidative crosslinking of phenolphthalein-based cardo polyimides with enhanced gas permeability and selectivity. J. Membr. Sci. 2018, 546, 90–99. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, L.; Tian, Z.; Cao, B.; Li, P. Post-crosslinking of triptycene-based Tröger’s base polymers with enhanced natural gas separation performance. J. Membr. Sci. 2018, 556, 277–284. [Google Scholar] [CrossRef]
- Robeson, L.M. Correlation of separation factor versus permeability for polymeric membranes. J. Membr. Sci. 1991, 62, 165–185. [Google Scholar] [CrossRef]
- Robeson, L.M. The upper bound revisited. J. Membr. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
- Park, H.B.; Kamcev, J.; Robeson, L.M.; Elimelech, M.; Freeman, B.D. Maximizing the right stuff: The trade-off between membrane permeability and selectivity. Science 2017, 365, 1138–1148. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Freeman, B.D. Materials selection guidelines for membranes that remove CO2 from gas mixtures. J. Mol. Struct. 2005, 739, 57–74. [Google Scholar] [CrossRef]
- Budd, P.M.; Ghanem, B.S.; Makhseed, S.; McKeown, N.B.; Msayib, K.J.; Tattershall, C.E. Polymers of intrinsic microporosity (PIMs): Robust, solution-processable, organic nanoporous materials. Chem. Commun. 2004, 230. [Google Scholar] [CrossRef] [PubMed]
- Budd, P.M.; Msayib, K.J.; Tattershall, C.E.; Ghanem, B.S.; Reynolds, K.J.; McKeown, N.B.; Fritsch, D. Gas separation membranes from polymers of intrinsic microporosity. J. Membr. Sci. 2005, 251, 263–269. [Google Scholar] [CrossRef]
- McKeown, N.B.; Budd, P.M. Exploitation of intrinsic microporosity in polymer-based materials. Macromolecules 2010, 43, 5163–5176. [Google Scholar] [CrossRef]
- Swaidan, R.; Ghanem, B.S.; Litwiller, E.; Pinnau, I. Pure- and mixed-gas CO2/CH4 separation properties of PIM-1 and an amidoxime-functionalized PIM-1. J. Membr. Sci. 2014, 457, 95–102. [Google Scholar] [CrossRef]
- Park, H.B.; Jung, C.H.; Lee, Y.M.; Hill, A.J.; Pas, S.J. Polymers with Cavities Tuned for Fast Selective Transport of Small Molecules and Ions. Science 2007, 318, 254–258. [Google Scholar] [CrossRef]
- Park, H.B.; Han, S.H.; Jung, C.H.; Lee, Y.M.; Hill, A.J. Thermally rearranged (TR) polymer membranes for CO2 separation. J. Membr. Sci. 2010, 359, 11–24. [Google Scholar] [CrossRef]
- Gleason, K.L.; Smith, Z.P.; Liu, Q.; Paul, D.R.; Freeman, B.D. Pure- and mixed-gas permeation of CO2 and CH4 in thermally rearranged polymers based on 3,3′-dihydroxy-4,4′-diamino-biphenyl (HAB) and 2,2′-bis-(3,4-dicarboxyphenyl) hexafluoropropane dianhydride (6FDA). J. Membr. Sci. 2015, 475, 204–214. [Google Scholar] [CrossRef]
- Smith, Z.P.; Sanders, D.F.; Ribeiro, C.P.; Guo, R.; Freeman, B.D.; Paul, D.R.; McGrath, J.E.; Swinnea, S. Gas sorption and characterization of thermally rearranged polyimides based on 3,3′-dihydroxy-4,4′-diamino-biphenyl (HAB) and 2,2′-bis-(3,4-dicarboxyphenyl) hexafluoropropane dianhydride (6FDA). J. Membr. Sci. 2012, 415–416, 558–567. [Google Scholar] [CrossRef]
- Sanders, D.F.; Smith, Z.P.; Ribeiro, C.P.; Guo, R.; McGrath, J.E.; Paul, D.R.; Freeman, B.D. Gas permeability, diffusivity, and free volume of thermally rearranged polymers based on 3,3′-dihydroxy-4,4′-diamino-biphenyl (HAB) and 2,2′-bis-(3,4-dicarboxyphenyl) hexafluoropropane dianhydride (6FDA). J. Membr. Sci. 2012, 409, 232–241. [Google Scholar] [CrossRef]
- Vopička, O.; De Angelis, M.G.; Sarti, G.C. Mixed gas sorption in glassy polymeric membranes: I. CO2/CH4 and n-C4/CH4 mixtures sorption in poly(1-trimethylsilyl-1-propyne) (PTMSP). J. Membr. Sci. 2013, 449, 97–108. [Google Scholar] [CrossRef]
- Vopička, O.; De Angelis, M.G.; Du, N.; Li, N.; Guiver, M.D.; Sarti, G.C. Mixed gas sorption in glassy polymeric membranes: II. CO2/CH4 mixtures in a polymer of intrinsic microporosity (PIM-1). J. Membr. Sci. 2014, 459, 264–276. [Google Scholar] [CrossRef]
- Gemeda, A.E.; De Angelis, M.G.; Du, N.; Li, N.; Guiver, M.D.; Sarti, G.C. Mixed gas sorption in glassy polymeric membranes. III. CO2/CH4 mixtures in a polymer of intrinsic microporosity (PIM-1): Effect of temperature. J. Membr. Sci. 2017, 524, 746–757. [Google Scholar] [CrossRef]
- Wijmans, J.G.; Baker, R.W. The solution-diffusion model: A review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Minelli, M.; Friess, K.; Vopička, O.; De Angelis, M.G. Modeling gas and vapor sorption in a polymer of intrinsic microporosity (PIM-1). Fluid Phase Equilib. 2013, 347, 35–44. [Google Scholar] [CrossRef]
- Vieth, W.R.; Tam, P.M.; Michaels, A.S. Dual sorption mechanisms in glassy polystyrene. J. Colloid Interface Sci. 1966, 22, 360–370. [Google Scholar] [CrossRef]
- Koros, W.J.; Paul, D.R. Design considerations for measurement of gas sorption in polymers by pressure decay. J. Polym. Sci. Polym. Phys. Ed. 1976, 14, 1903–1907. [Google Scholar] [CrossRef]
- Michaels, A.S.; Vieth, W.R.; Barrie, J.A. Diffusion of gases in polyethylene terephthalate. J. Appl. Phys. 1963, 34, 13–20. [Google Scholar] [CrossRef]
- Koros, W.J.; Paul, D.R. Carbon dioxide sorption and transport in polycarbonate. J. Polym. Sci. Polym. Phys. 1976, 14, 687–702. [Google Scholar] [CrossRef]
- Paul, D.R.; Koros, W.J. Effect of partially immobilizing sorption on permeability and the diffusion time lag. J. Polym. Sci. Polym. Phys. Ed. 1976, 14, 675–685. [Google Scholar] [CrossRef]
- Fredrickson, G.H.; Helfand, E. Dual-Mode Transport of Penetrants in Glassy Polymers. Macromolecules 1985, 18, 2201–2207. [Google Scholar] [CrossRef]
- Meares, P. The Diffusion of Gases Through Polyvinyl Acetate. J. Am. Chem. Soc. 1954, 76, 3416–3422. [Google Scholar] [CrossRef]
- Meares, P. The solubilities of gases in polyvinyl acetate. Trans. Faraday Soc. 1957, 54, 40–46. [Google Scholar] [CrossRef]
- Barrer, R.M.; Barrie, J.A.; Slater, J. Sorption and Diffusion in Ethyl Cellulose. Part III. Comparison between Ethyl Cellulose and Rubber. J. Polym. Sci. 1958, 27, 177–197. [Google Scholar] [CrossRef]
- Vieth, W.R.; Howell, J.M.; Hsieh, J.H. Dual sorption theory. J. Membr. Sci. 1976, 1, 177–220. [Google Scholar] [CrossRef]
- Vieth, W.R.; Alcalay, H.H.; Frabetti, A.J. Solution of Gases in Oriented Poly(ethylene Terephthalate). J. Appl. Polym. Sci. 1964, 8, 2125–2138. [Google Scholar] [CrossRef]
- Feng, H. Modeling of vapor sorption in glassy polymers using a new dual mode sorption model based on multilayer sorption theory. Polymer 2007, 48, 2988–3002. [Google Scholar] [CrossRef]
- Bondar, V.I.; Kamiya, Y.; Yampol’skii, Y.P. On pressure dependence of the parameters of the dual-mode sorption model. J. Polym. Sci. Part B Polym. Phys. 1996, 34, 369–378. [Google Scholar] [CrossRef]
- Lacombe, R.H.; Sanchez, I.C. Statistical Thermodynamics of Fluid Mixtures. J. Phys. Chem. 1976, 80, 2568–2580. [Google Scholar] [CrossRef]
- Chapman, W.G.; Gubbins, K.E.; Jackson, G.; Razosz, M. SAFT: Equation-of-state solution model for associating fluids. Fluid Phase Equilib. 1989, 52, 31–38. [Google Scholar] [CrossRef]
- Doghieri, F.; Sarti, G.C. Nonequilibrium Lattice Fluids: A Predictive Model for the Solubility in Glassy Polymers. Macromolecules 1996, 29, 7885–7896. [Google Scholar] [CrossRef]
- Minelli, M.; Doghieri, F. Predictive model for gas and vapor solubility and swelling in glassy polymers I: Application to different polymer/penetrant systems. Fluid Phase Equilib. 2014, 381, 1–11. [Google Scholar] [CrossRef]
- Doghieri, F.; Quinzi, M.; Rethwisch, D.G.; Sarti, G.C. Predicting Gas Solubility in Glassy Polymers through Nonequilibrium EOS. In Advanced Materials for Membrane Separations; American Chemical Society: Washington, DC, USA, 2004; pp. 74–90. [Google Scholar]
- Minelli, M.; Campagnoli, S.; De Angelis, M.G.; Doghieri, F.; Sarti, G.C. Predictive model for the solubility of fluid mixtures in glassy polymers. Macromolecules 2011, 44, 4852–4862. [Google Scholar] [CrossRef]
- Ricci, E.; Gemeda, A.E.; Du, N.; Li, N.; De Angelis, M.G.; Guiver, M.D.; Sarti, G.C. Sorption of the CO2/CH4 mixture in TZ-PIM, PIM-1 and PTMSP: Experimental data and NELF-model based analysis of competitive sorption and its impact on the selectivity. J. Membr. Sci. 2018. submitted for publication. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: Wotton-under-Edge, UK, 1989; ISBN 9780198556459. [Google Scholar]
- Widom, B. Some Topics in the Theory of Fluids. J. Chem. Phys. 1963, 39, 2808. [Google Scholar] [CrossRef]
- Ramdin, M.; Balaji, S.P.; Vicent-Luna, J.M.; Gutiérrez-Sevillano, J.J.; Calero, S.; De Loos, T.W.; Vlugt, T.J.H. Solubility of the precombustion gases CO2, CH4, CO, H2, N2, and H2S in the ionic liquid [bmim][Tf2N] from Monte Carlo simulations. J. Phys. Chem. C 2014, 118, 23599–23604. [Google Scholar] [CrossRef]
- Boulougouris, G.C.; Economou, I.G.; Theodorou, D.N. On the calculation of the chemical potential using the particle deletion scheme. Mol. Phys. 1999, 96, 905–913. [Google Scholar] [CrossRef]
- Siegert, M.R.; Heuchel, M.; Hofmann, D. A generalized direct-particle-deletion scheme for the calculation of chemical potential and solubilities of small- and medium-sized molecules in amorphous polymers. J. Comput. Chem. 2007, 28, 877–889. [Google Scholar] [CrossRef] [PubMed]
- Kupgan, G.; Abbott, L.J.; Hart, K.E.; Colina, C.M. Modeling Amorphous Microporous Polymers for CO2 Capture and Separations. Chem. Rev. 2018, 118, 5488–5538. [Google Scholar] [CrossRef] [PubMed]
- Tocci, E.; De Lorenzo, L.; Bernardo, P.; Clarizia, G.; Bazzarelli, F.; McKeown, N.B.; Carta, M.; Malpass-Evans, R.; Friess, K.; Pilnáček, K.; et al. Molecular modeling and gas permeation properties of a polymer of intrinsic microporosity composed of ethanoanthracene and Tröger’s base units. Macromolecules 2014, 47, 7900–7916. [Google Scholar] [CrossRef]
- Hart, K.E.; Colina, C.M. Estimating gas permeability and permselectivity of microporous polymers. J. Membr. Sci. 2014, 468, 259–268. [Google Scholar] [CrossRef]
- Hart, K.E.; Abbott, L.J.; McKeown, N.B.; Colina, C.M. Toward effective CO2/CH4 separations by sulfur-containing PIMs via predictive molecular simulations. Macromolecules 2013, 46, 5371–5380. [Google Scholar] [CrossRef]
- Rose, I.; Bezzu, C.G.; Carta, M.; Comesaña-Gándara, B.; Lasseuguette, E.; Ferrari, M.C.; Bernardo, P.; Clarizia, G.; Fuoco, A.; Jansen, J.C.; et al. Polymer ultrapermeability from the inefficient packing of 2D chains. Nat. Mater. 2017, 1–39. [Google Scholar] [CrossRef]
- Heuchel, M.; Fritsch, D.; Budd, P.M.; McKeown, N.B.; Hofmann, D. Atomistic packing model and free volume distribution of a polymer with intrinsic microporosity (PIM-1). J. Membr. Sci. 2008, 318, 84–99. [Google Scholar] [CrossRef]
- Gusev, A.A.; Arizzi, S.; Suter, U.W.; Moll, D.J. Dynamics of light gases in rigid matrices of dense polymers. J. Chem. Phys. 1993, 99, 2221–2227. [Google Scholar] [CrossRef]
- Gusev, A.A.; Suter, U.W. Dynamics of small molecules in dense polymers subject to thermal motion. J. Chem. Phys. 1993, 99, 2228. [Google Scholar] [CrossRef]
- Fang, W.; Zhang, L.; Jiang, J. Polymers of intrinsic microporosity for gas permeation: A molecular simulation study. Mol. Simul. 2010, 36, 992–1003. [Google Scholar] [CrossRef]
- Fang, W.; Zhang, L.; Jiang, J. Gas Permeation and Separation in Functionalized Polymers of Intrinsic Microporosity: A Combination of Molecular Simulations and Ab Initio Calculations. J. Phys. Chem. C 2011, 115, 14123–14130. [Google Scholar] [CrossRef]
- Kupgan, G.; Demidov, A.G.; Colina, C.M. Plasticization behavior in polymers of intrinsic microporosity (PIM-1): A simulation study from combined Monte Carlo and molecular dynamics. J. Membr. Sci. 2018, 565, 95–103. [Google Scholar] [CrossRef]
- Hölck, O.; Böhning, M.; Heuchel, M.; Siegert, M.R.; Hofmann, D. Gas sorption isotherms in swelling glassy polymers—Detailed atomistic simulations. J. Membr. Sci. 2013, 428, 523–532. [Google Scholar] [CrossRef]
- Frentrup, H.; Hart, K.E.; Colina, C.M.; Müller, E.A. In silico determination of gas permeabilities by non-equilibrium molecular dynamics: CO2 and He through PIM-1. Membranes 2015, 5, 99–119. [Google Scholar] [CrossRef]
- Rizzuto, C.; Caravella, A.; Brunetti, A.; Park, C.H.; Lee, Y.M.; Drioli, E.; Barbieri, G.; Tocci, E. Sorption and Diffusion of CO2/N2 in gas mixture in thermally-rearranged polymeric membranes: A molecular investigation. J. Membr. Sci. 2017, 528, 135–146. [Google Scholar] [CrossRef]
- Myers, A.L.; Prausnitz, J.M. Thermodynamics of mixed-gas adsorption. AIChE J. 1965, 11, 121–127. [Google Scholar] [CrossRef]
- Neyertz, S.; Brown, D. Air Sorption and Separation by Polymer Films at the Molecular Level. Macromolecules 2018, 51, 7077–7092. [Google Scholar] [CrossRef]
- Theodorou, D.N. Principles of Molecular Simulation of Gas Transport in Polymers. In Materials Science of Membranes for Gas and Vapor Separation; John Wiley & Sons: Hoboken, NJ, USA, 2006; ISBN 047085345X. [Google Scholar]
- Larsen, G.S.; Hart, K.E.; Colina, C.M. Predictive simulations of the structural and adsorptive properties for PIM-1 variations. Mol. Simul. 2014, 40, 599–609. [Google Scholar] [CrossRef]
- Spyriouni, T.; Boulougouris, G.C.; Theodorou, D.N. Prediction of sorption of CO2 in glassy atactic polystyrene at elevated pressures through a new computational scheme. Macromolecules 2009, 42, 1759–1769. [Google Scholar] [CrossRef]
- Vogiatzis, G.G.; Theodorou, D.N. Multiscale Molecular Simulations of Polymer-Matrix Nanocomposites. Arch. Comput. Methods Eng. 2017. [Google Scholar] [CrossRef]
- Mathioudakis, I.; Vogiatzis, G.G.; Tzoumanekas, C.; Theodorou, D.N. Molecular modeling and simulation of atactic polystyrene/amorphous silica nanocomposites. J. Phys. Conf. Ser. 2016, 738, 012021. [Google Scholar] [CrossRef]
- Mathioudakis, I.G.; Vogiatzis, G.G.; Tzoumanekas, C.; Theodorou, D.N. Multiscale simulations of PS–SiO2 nanocomposites: From melt to glassy state. Soft Matter 2016, 12, 7585–7605. [Google Scholar] [CrossRef]
- Koros, W.J. Model for sorption of mixed gases in glassy polymers. J. Polym. Sci. Polym. Phys. Ed. 1980, 18, 981–992. [Google Scholar] [CrossRef]
- George, G.; Bhoria, N.; Alhallaq, S.; Abdala, A.; Mittal, V. Polymer membranes for acid gas removal from natural gas. Sep. Purif. Technol. 2016, 158, 333–356. [Google Scholar] [CrossRef]
- Du, N.; Park, H.B.; Robertson, G.P.; Dal-Cin, M.M.; Visser, T.; Scoles, L.; Guiver, M.D. Polymer nanosieve membranes for CO2-capture applications. Nat. Mater. 2011, 10, 372–375. [Google Scholar] [CrossRef] [PubMed]
- Satilmis, B.; Lan, M.; Fuoco, A.; Rizzuto, C.; Tocci, E.; Bernardo, P.; Clarizia, G.; Esposito, E.; Monteleone, M.; Dendisová, M.; et al. Temperature and pressure dependence of gas permeation in amine-modified PIM-1. J. Membr. Sci. 2018, 555, 483–496. [Google Scholar] [CrossRef]
- Lanč, M.; Pilnáček, K.; Mason, C.R.; Budd, P.M.; Rogan, Y.; Malpass-Evans, R.; Carta, M.; Gándara, B.C.; McKeown, N.B.; Jansen, J.C.; et al. Gas sorption in polymers of intrinsic microporosity: The difference between solubility coefficients determined via time-lag and direct sorption experiments. J. Membr. Sci. 2018, 570–571, 522–536. [Google Scholar] [CrossRef]
- Pilnáček, K.; Vopička, O.; Lanč, M.; Dendisová, M.; Zgažar, M.; Budd, P.M.; Carta, M.; Malpass-Evans, R.; McKeown, N.B.; Friess, K. Aging of polymers of intrinsic microporosity tracked by methanol vapour permeation. J. Membr. Sci. 2016, 520, 895–906. [Google Scholar] [CrossRef]
- Ricci, E.; Minelli, M.; De Angelis, M.G. A multiscale approach to predict the mixed gas separation performance of glassy polymeric membranes for CO2 capture: The case of CO2/CH4 mixture in Matrimid®. J. Membr. Sci. 2017, 539. [Google Scholar] [CrossRef]
- Chan, A.H.; Koros, W.J.; Paul, D.R. Analysis of hydrocarbon gas sorption and transport in ethyl cellulose using the dual sorption/partial immobilization models. J. Membr. Sci. 1978, 3, 117–130. [Google Scholar] [CrossRef]
- Kanehashi, S.; Nagai, K. Analysis of dual-mode model parameters for gas sorption in glassy polymers. J. Membr. Sci. 2005, 253, 117–138. [Google Scholar] [CrossRef]
- Koros, W.J.; Paul, D.R. CO2 sorption in poly(ethylene terephthalate) above and below the glass transition. J. Polym. Sci. Part B Polym. Phys. 1978, 16, 1947–1963. [Google Scholar] [CrossRef]
- Koros, W.J.; Sanders, E.S. Multicomponent gas sorption in glassy polymers. J. Polym. Sci. Polym. Symp. 1985, 141–149. [Google Scholar] [CrossRef]
- Sanders, E.S.; Koros, W.J. Sorption of CO2, C2H4, N2O and their Binary Mixtures in Poly(methyl methacrylate). J. Polym. Sci. B 1986, 188, 175–188. [Google Scholar] [CrossRef]
- Sanders, E.S.; Koros, W.J.; Hopfenberg, H.B.; Stannett, V.T. Mixed gas sorption in glassy polymers: Equipment design considerations and preliminary results. J. Membr. Sci. 1983, 13, 161–174. [Google Scholar] [CrossRef]
- Story, B.J.; Koros, W.J. Sorption of CO2/CH4 mixtures in poly(phenylene oxide) and a carboxylated derivative. J. Appl. Polym. Sci. 1991, 42, 2613–2626. [Google Scholar] [CrossRef]
- Peng, D.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Sandler, S.I. Chemical, Biochemical, and Engineering Thermodynamics, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Abadie, J.; Carpentier, J. Generalization of the Wolfe reduced gradient method to the case of nonlinear constraints. In Optimization; Fletcher, R., Ed.; Academic Press: London, UK, 1969; pp. 37–49. [Google Scholar]
- Yamane, T. Statistics: An Introductory Analysis; Harper & Row, John Weatherhill: New York, NY, USA; Evanston, IL, USA; London, UK; Tokyo, Japan, 1973; ISBN 0060473134. [Google Scholar]
- Bevington, P.R.; Robinson, D.K. Data Reduction and Error Analysis for the Physical Sciences, 3rd ed.; McGraw-Hill: Boston, MA, USA, 2003. [Google Scholar]
- Myers, R.H. Classical and Modern Regression with Applications; Duxbury Press: Belmont, CA, USA, 1990. [Google Scholar]
- Koros, W.J.; Paul, R.; Huvard, G.S. Energetics of gas sorption in glassy polymers. Polymer 1979, 20, 956–960. [Google Scholar] [CrossRef]
- Raharjo, R.D.; Freeman, B.D.; Sanders, E.S. Pure and mixed gas CH4 and n-C4H10 sorption and dilation in poly(1-trimethylsilyl-1-propyne). Polymer 2007, 48, 6097–6114. [Google Scholar] [CrossRef]
- Stevens, K.A.; Smith, Z.P.; Gleason, K.L.; Galizia, M.; Paul, D.R.; Freeman, B.D. Influence of temperature on gas solubility in thermally rearranged (TR) polymers. J. Membr. Sci. 2017, 533, 75–83. [Google Scholar] [CrossRef]
- Kamiya, Y.; Hirose, T.; Mizoguchi, K.; Naito, Y. Gravimetric study of high-pressure sorption of gases in polymers. J. Polym. Sci. Part B Polym. Phys. 1986, 24, 1525–1539. [Google Scholar] [CrossRef]
- Chiou, J.S.; Maeda, Y.; Paul, D.R. Gas and vapor sorption in polymers just below Tg. J. Appl. Polym. Sci. 1985, 30, 4019–4029. [Google Scholar] [CrossRef]
- Wang, J.S.; Kamiya, Y. A method of validation and parameter evaluation for dual-mode sorption model. J. Membr. Sci. 1999, 154, 25–32. [Google Scholar] [CrossRef]


| CO2 | ||||||
| T | SEE | mix | ||||
| (°C) | ( | |||||
| PTMSP | 35 | 1.973 | 95.06 | 0.051 | 0.67 | 0.94 |
| PIM-1 | 25 | 4.046 | 90.04 | 0.710 | 1.38 | 2.06 |
| 35 | 2.890 | 94.83 | 0.388 | 0.92 | 3.90 | |
| 50 | 1.596 | 89.30 | 0.290 | 0.80 | 2.08 | |
| TZ-PIM | 25 | 4.127 | 70.58 | 1.127 | 1.28 | 9.77 |
| 35 | 1.982 | 89.53 | 0.378 | 1.57 | 6.66 | |
| 50 | 0.903 | 92.42 | 0.263 | 1.02 | 11.00 | |
| CH4 | ||||||
| T | SEE | mix | ||||
| (°C) | ( | |||||
| PTMSP | 35 | 0.616 | 57.77 | 0.049 | 0.50 | 1.78 |
| PIM-1 | 25 | 0.651 | 78.83 | 0.136 | 0.70 | 4.89 |
| 35 | 0.541 | 75.87 | 0.106 | 0.51 | 2.69 | |
| 50 | 0.543 | 57.90 | 0.105 | 0.89 | 1.70 | |
| TZ-PIM | 25 | 1.400 | 48.09 | 0.214 | 0.55 | 2.54 |
| 35 | 0.378 | 67.12 | 0.087 | 0.97 | 1.40 | |
| 50 | 0.350 | 51.41 | 0.101 | 0.20 | 4.73 | |
| CO2 | ||||||
| T | SEE | mix | ||||
| (°C) | ( | |||||
| PTMSP | 35 | 2.373 | 69.26 | 0.067 | 0.73 | 0.97 |
| PIM-1 | 25 | 3.664 | 100.25 | 0.506 | 1.60 | 3.72 |
| 35 | 3.039 | 90.42 | 0.428 | 1.17 | 3.43 | |
| 50 | 1.666 | 86.84 | 0.306 | 0.84 | 2.57 | |
| TZ-PIM | 25 | 4.023 | 72.88 | 1.019 | 1.44 | 11.21 |
| 35 | 2.168 | 84.61 | 0.420 | 1.82 | 6.16 | |
| 50 | 1.150 | 84.84 | 0.303 | 1.46 | 10.11 | |
| CH4 | ||||||
| T | SEE | mix | ||||
| (°C) | ( | |||||
| PTMSP | 35 | 0.611 | 58.75 | 0.048 | 0.52 | 0.92 |
| PIM-1 | 25 | 0.672 | 78.56 | 0.137 | 0.72 | 3.00 |
| 35 | 0.401 | 82.72 | 0.097 | 0.60 | 1.68 | |
| 50 | 0.684 | 50.99 | 0.124 | 0.94 | 2.08 | |
| TZ-PIM | 25 | 1.526 | 43.65 | 0.250 | 0.76 | 2.97 |
| 35 | 0.282 | 73.42 | 0.079 | 0.98 | 1.61 | |
| 50 | 0.364 | 50.63 | 0.103 | 0.20 | 4.18 | |
| CO2 | ||||||
| T | SEE | mix | ||||
| (°C) | ( | |||||
| PIM-1 | 25 | 4.150 | 90.56 | 0.638 | 2.43 | 1.86 |
| 35 | 2.883 | 89.02 | 0.470 | 4.30 | 3.73 | |
| 50 | 1.742 | 85.63 | 0.308 | 1.11 | 1.44 | |
| TZ-PIM | 25 | 3.625 | 82.25 | 0.676 | 3.54 | 13.43 |
| 35 | 2.473 | 77.23 | 0.511 | 3.13 | 10.04 | |
| 50 | 1.457 | 76.94 | 0.347 | 2.92 | 11.31 | |
| CH4 | ||||||
| T | SEE | mix | ||||
| (°C) | ( | |||||
| PIM-1 | 25 | 0.759 | 78.51 | 0.130 | 1.80 | 3.74 |
| 35 | 0.561 | 72.98 | 0.113 | 0.73 | 2.02 | |
| 50 | 0.369 | 66.17 | 0.093 | 1.00 | 1.12 | |
| TZ-PIM | 25 | 1.275 | 49.29 | 0.206 | 2.73 | 2.41 |
| 35 | 0.865 | 42.49 | 0.171 | 1.99 | 3.87 | |
| 50 | 0.506 | 41.58 | 0.133 | 1.23 | 4.46 | |
| T | |||
|---|---|---|---|
| (°C) | ( | ||
| 25 | |||
| 35 | |||
| 50 |
| T | SEEpure | mix | ||||
|---|---|---|---|---|---|---|
| (°C) | ||||||
| Set 1 | 25 | 0.945 | 65.08 | 0.186 | 0.999 | 3.98 |
| 35 | 0.119 | 101.81 | 0.074 | 0.891 | 1.15 | |
| 50 | 0.125 | 82.00 | 0.070 | 0.797 | 1.35 | |
| Set 2 | 25 | 0.316 | 96.99 | 0.102 | 0.996 | 11.16 |
| 35 | 0.869 | 59.26 | 0.152 | 0.899 | 4.95 | |
| 50 | 0.767 | 45.62 | 0.155 | 0.792 | 3.67 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ricci, E.; De Angelis, M.G. Modelling Mixed-Gas Sorption in Glassy Polymers for CO2 Removal: A Sensitivity Analysis of the Dual Mode Sorption Model. Membranes 2019, 9, 8. https://doi.org/10.3390/membranes9010008
Ricci E, De Angelis MG. Modelling Mixed-Gas Sorption in Glassy Polymers for CO2 Removal: A Sensitivity Analysis of the Dual Mode Sorption Model. Membranes. 2019; 9(1):8. https://doi.org/10.3390/membranes9010008
Chicago/Turabian StyleRicci, Eleonora, and Maria Grazia De Angelis. 2019. "Modelling Mixed-Gas Sorption in Glassy Polymers for CO2 Removal: A Sensitivity Analysis of the Dual Mode Sorption Model" Membranes 9, no. 1: 8. https://doi.org/10.3390/membranes9010008
APA StyleRicci, E., & De Angelis, M. G. (2019). Modelling Mixed-Gas Sorption in Glassy Polymers for CO2 Removal: A Sensitivity Analysis of the Dual Mode Sorption Model. Membranes, 9(1), 8. https://doi.org/10.3390/membranes9010008