Large-Scale Molecular Dynamics of Anion-Exchange Membranes: Molecular Structure of QPAF-4 and Water Transport
Abstract
1. Introduction
2. Model and Methods
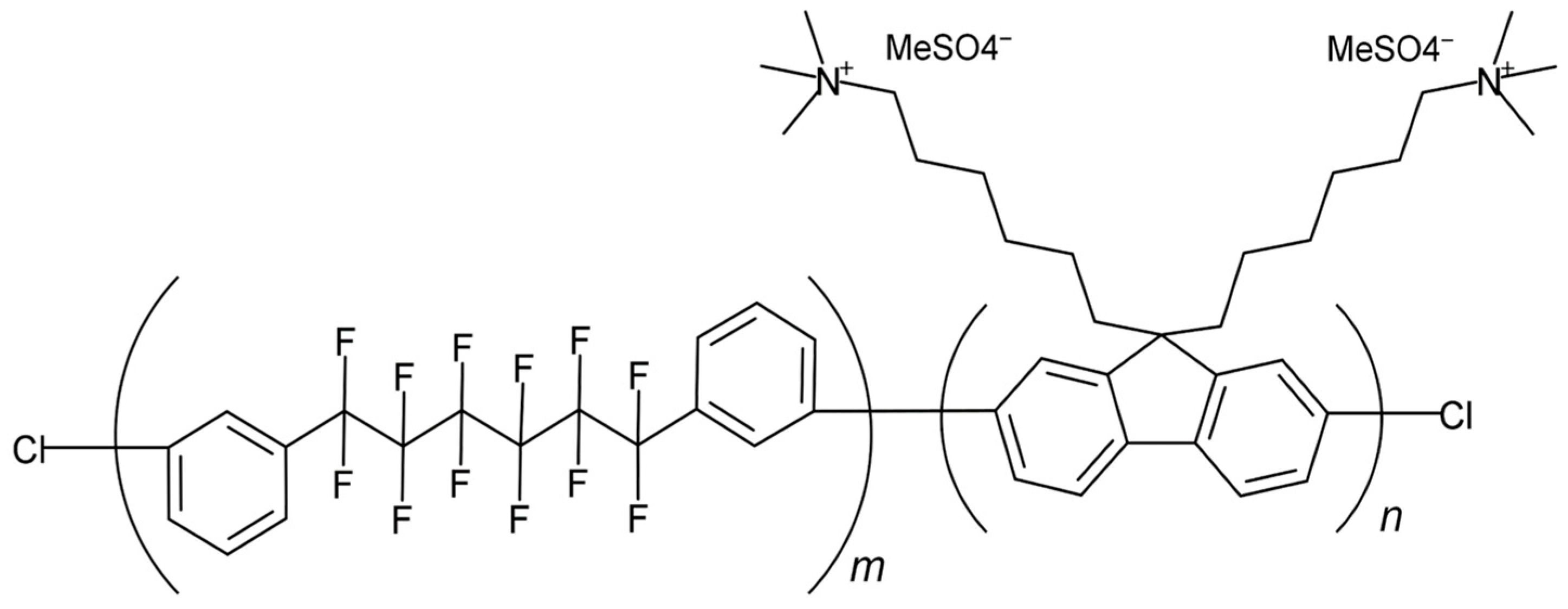
2.1. Outline of Models
2.2. Molecular Dynamics Simulation Details
2.3. X-Ray Scattering Analysis
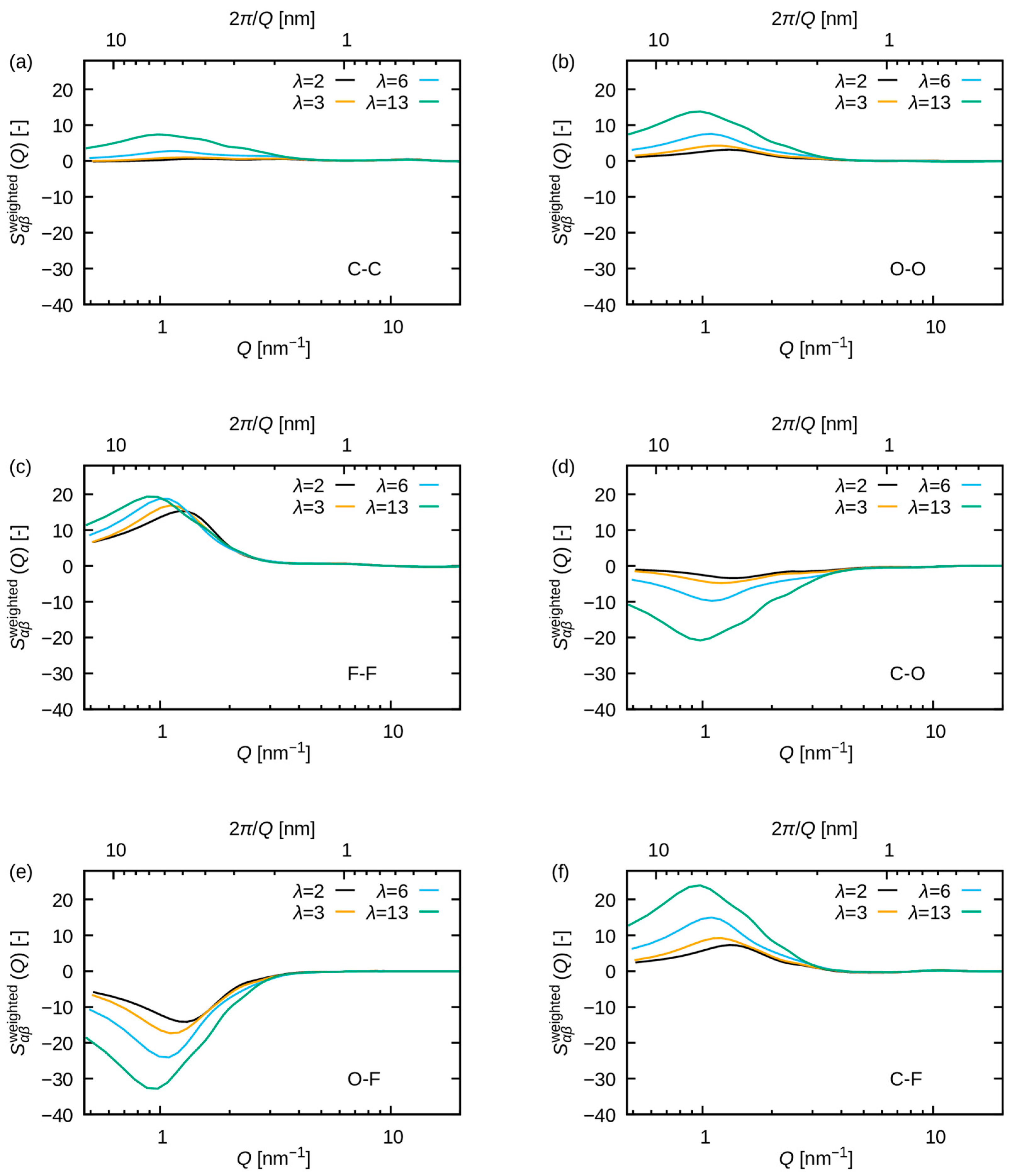
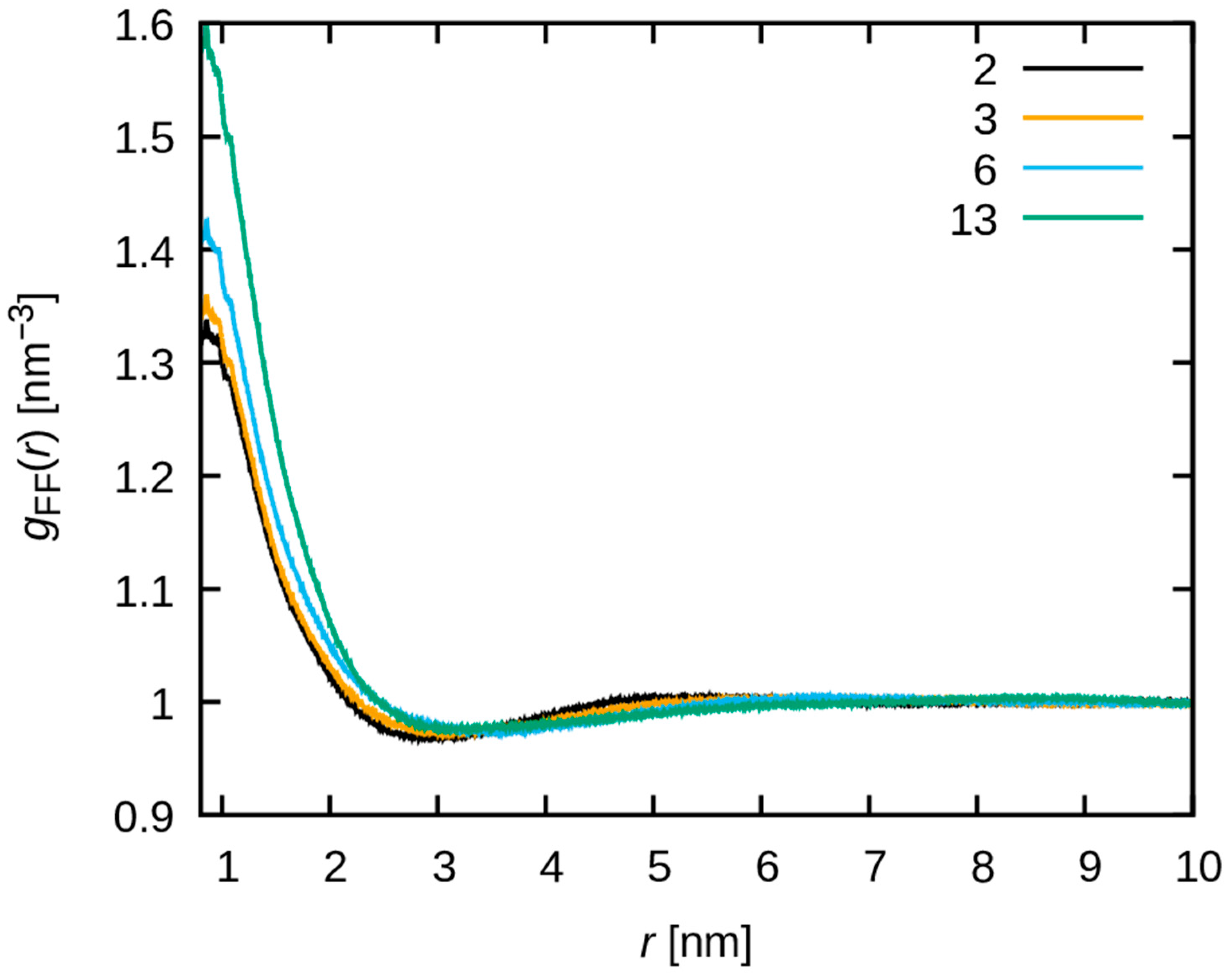
2.4. Analysis of Pair Distribution Function
3. Results and Discussion
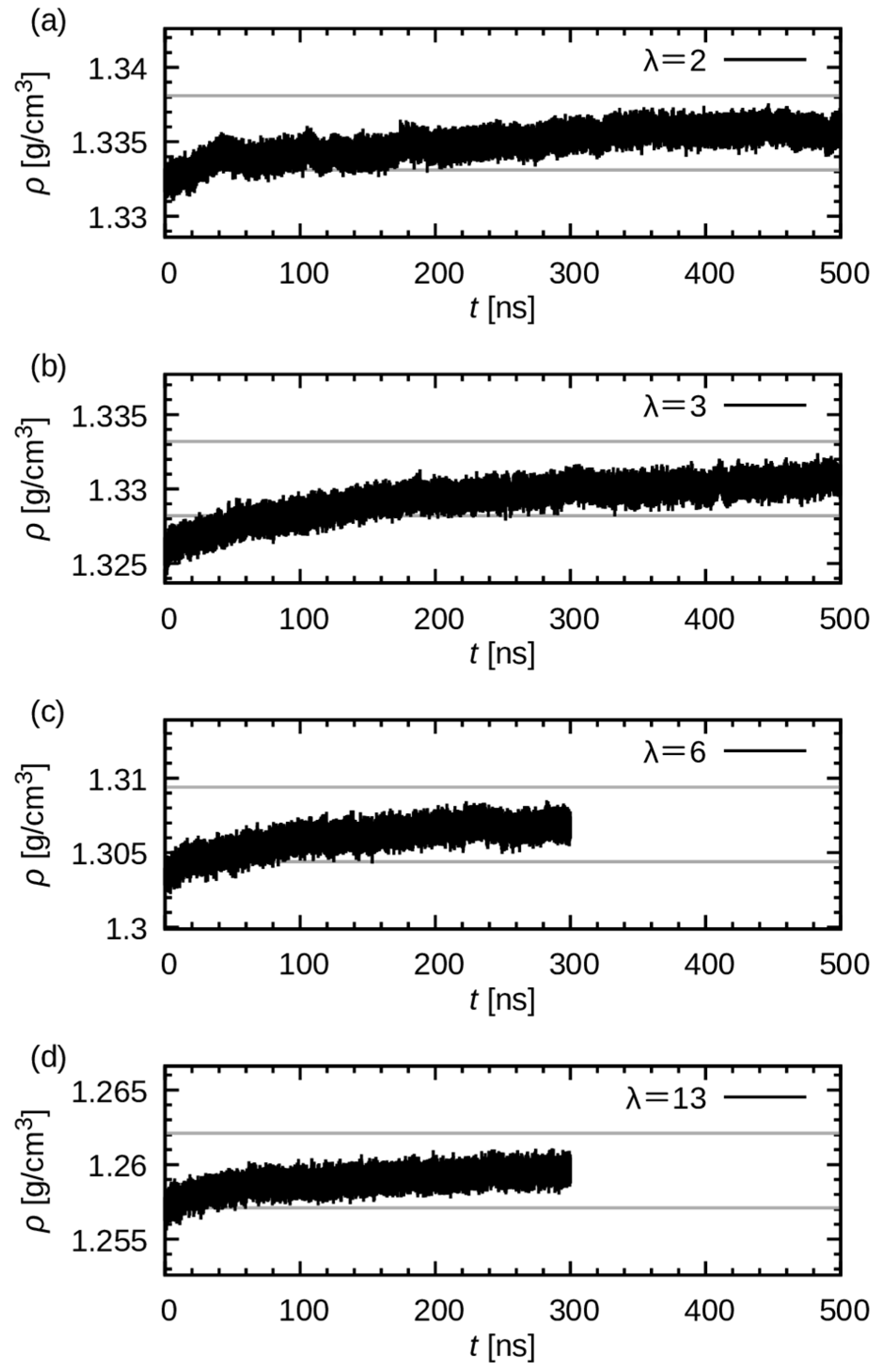
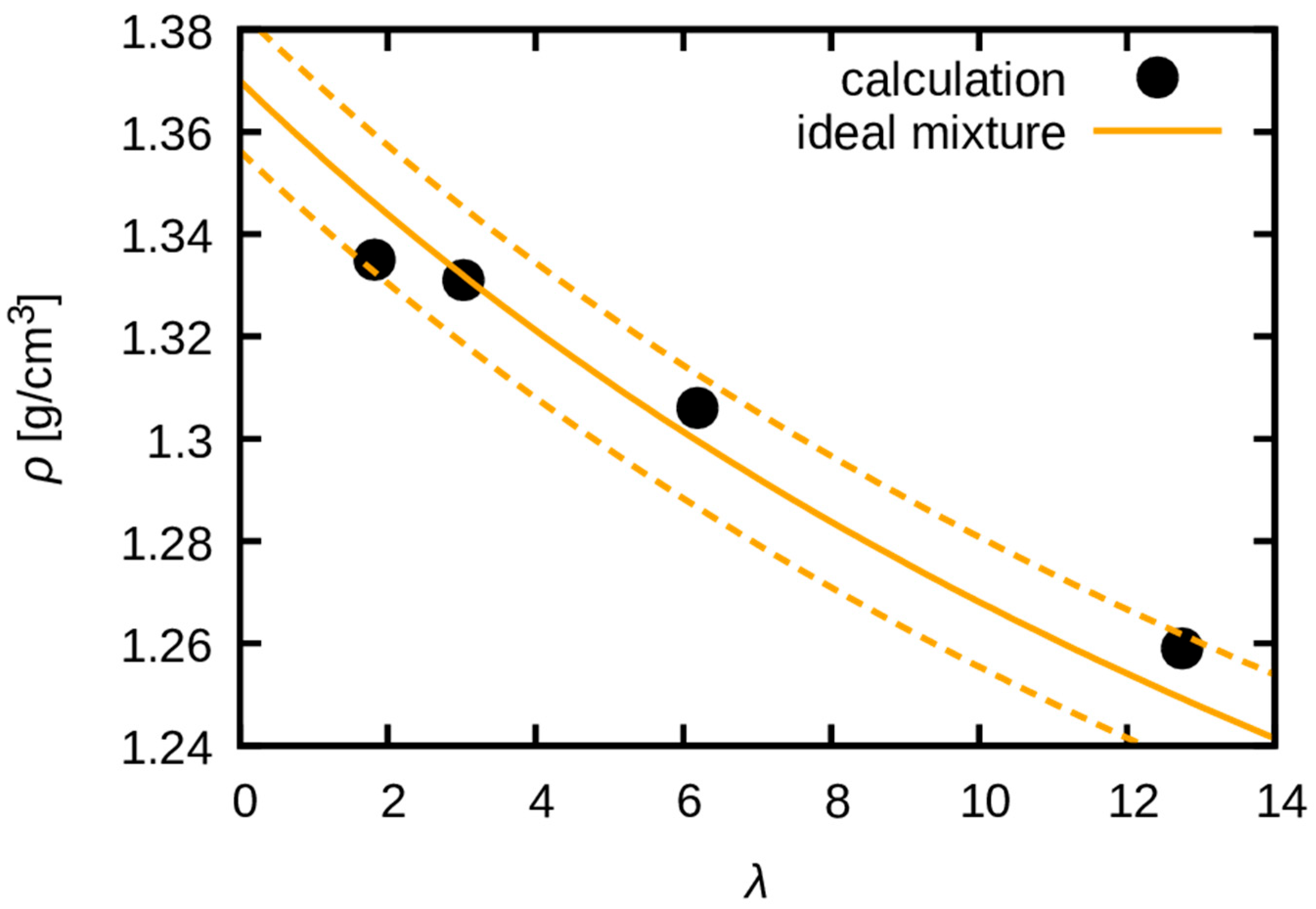
3.1. Equilibration and Mass Density
3.2. Structures and Their Comparison with X-Ray Experiments
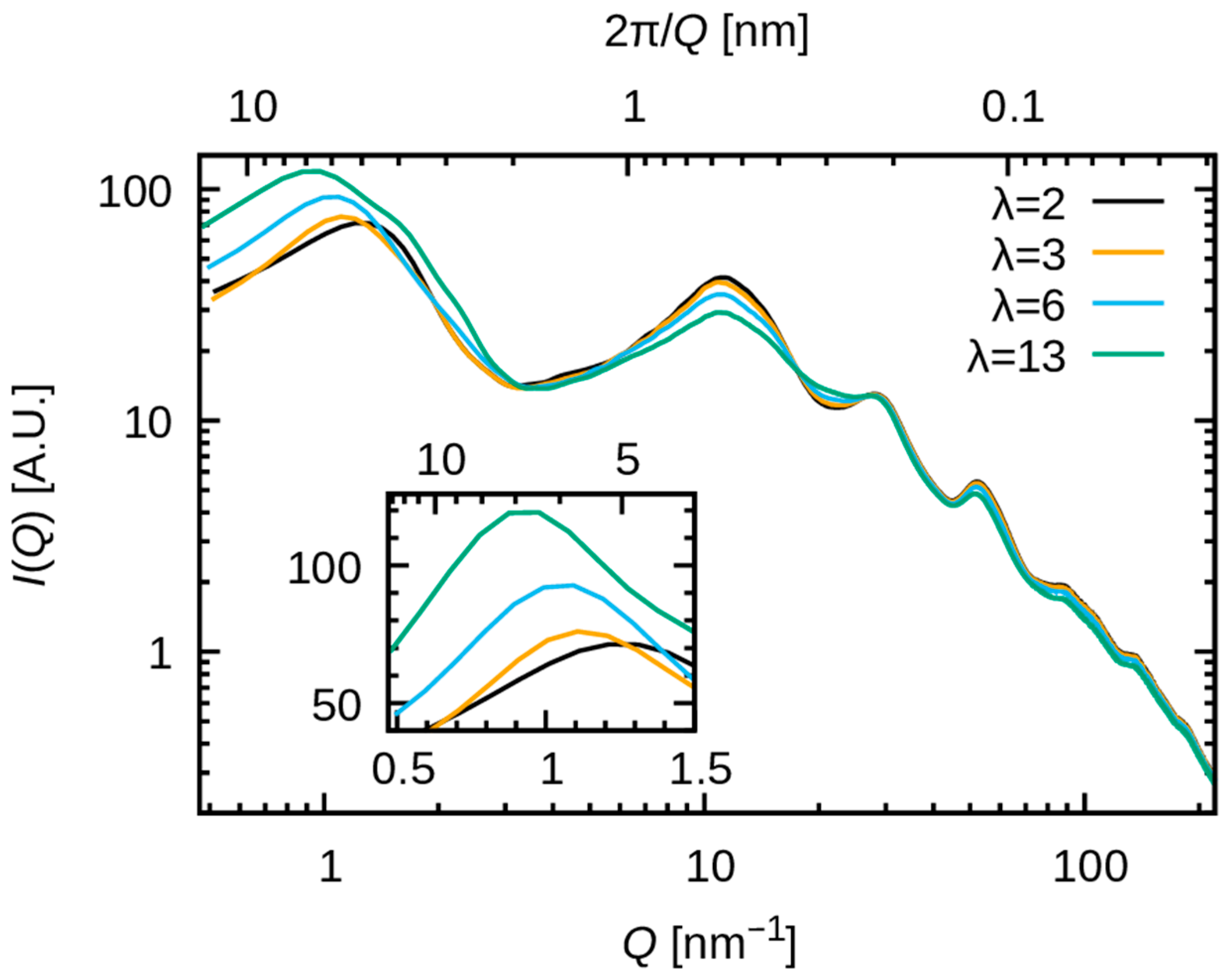
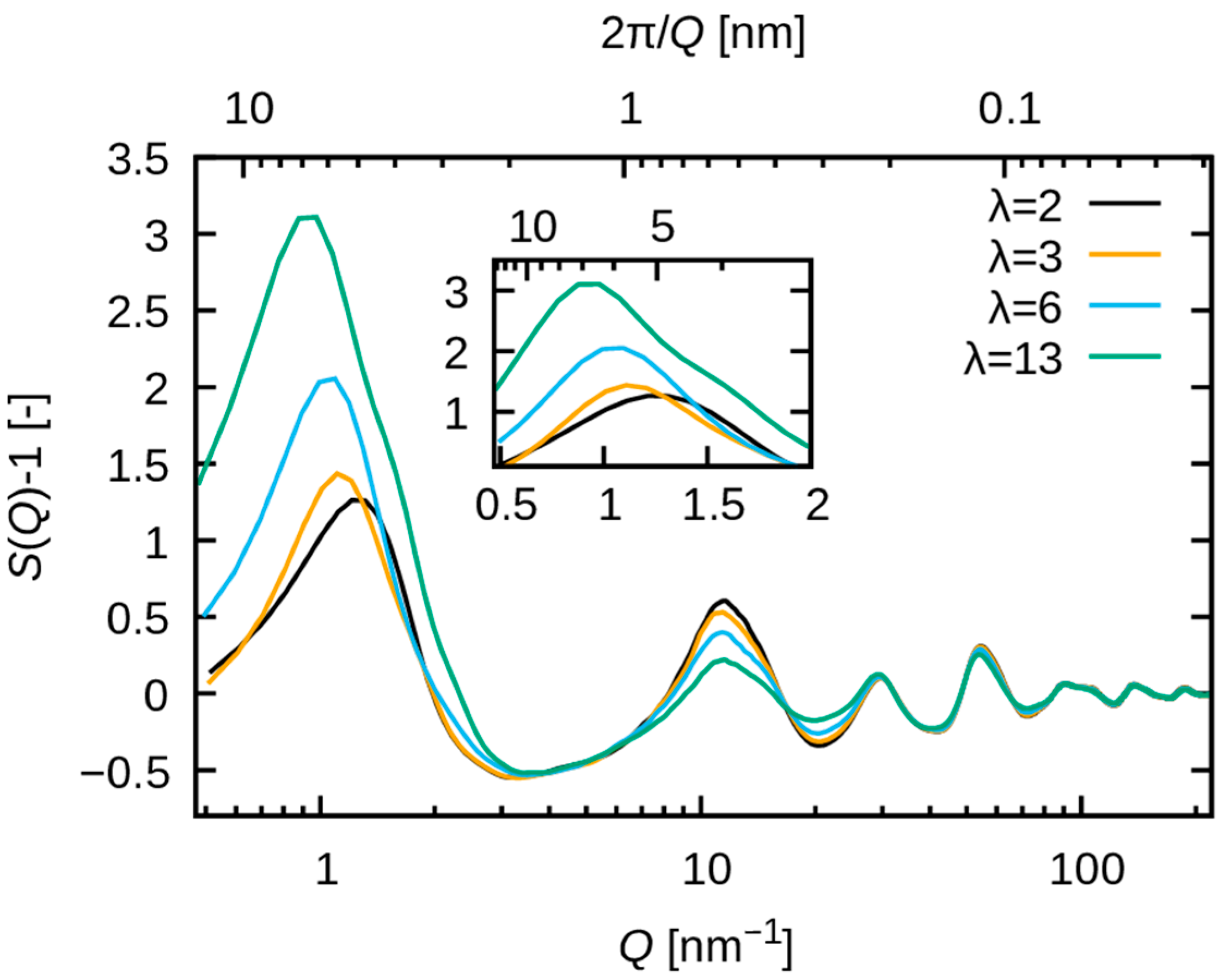
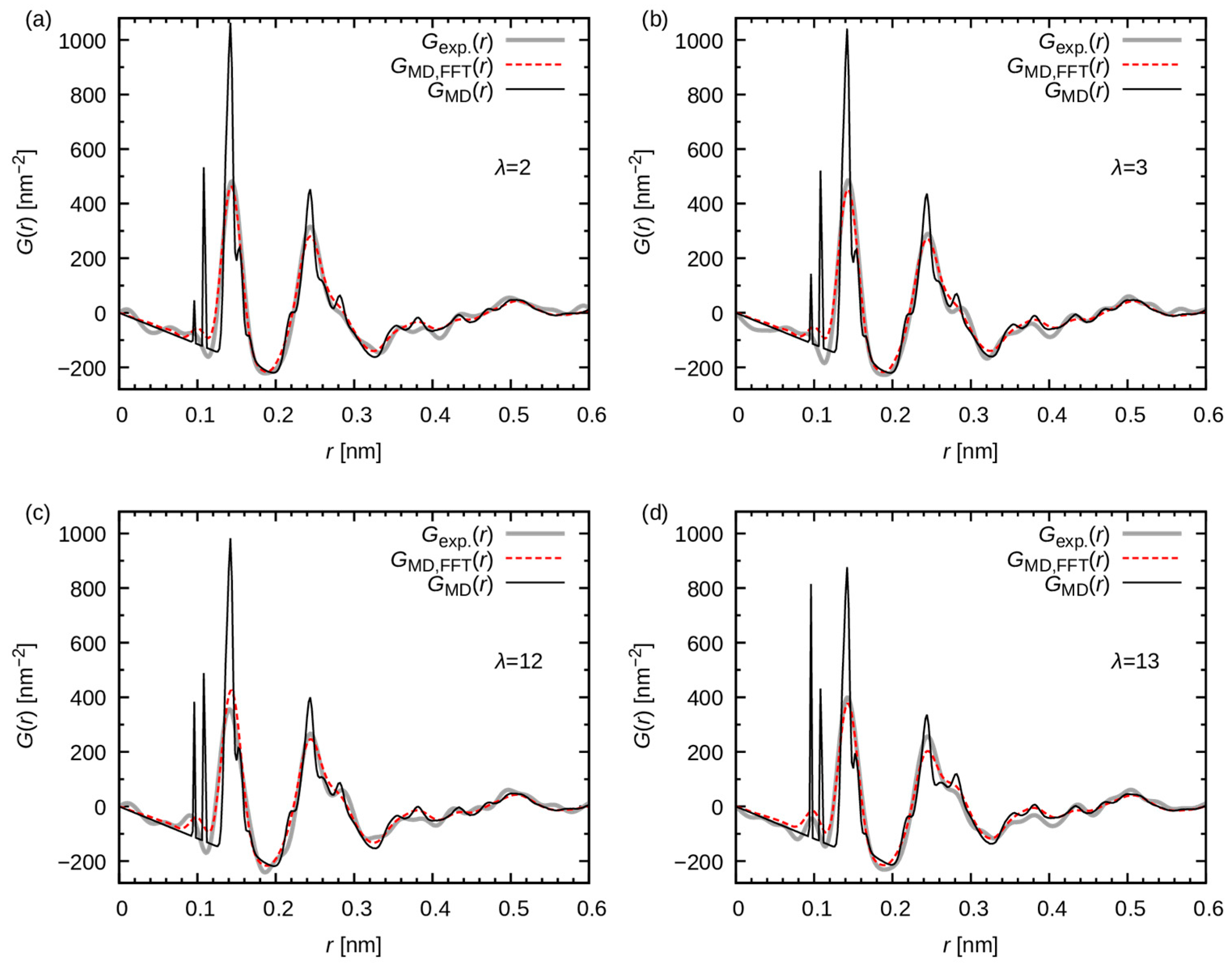
3.2.1. Comparison with SAXS
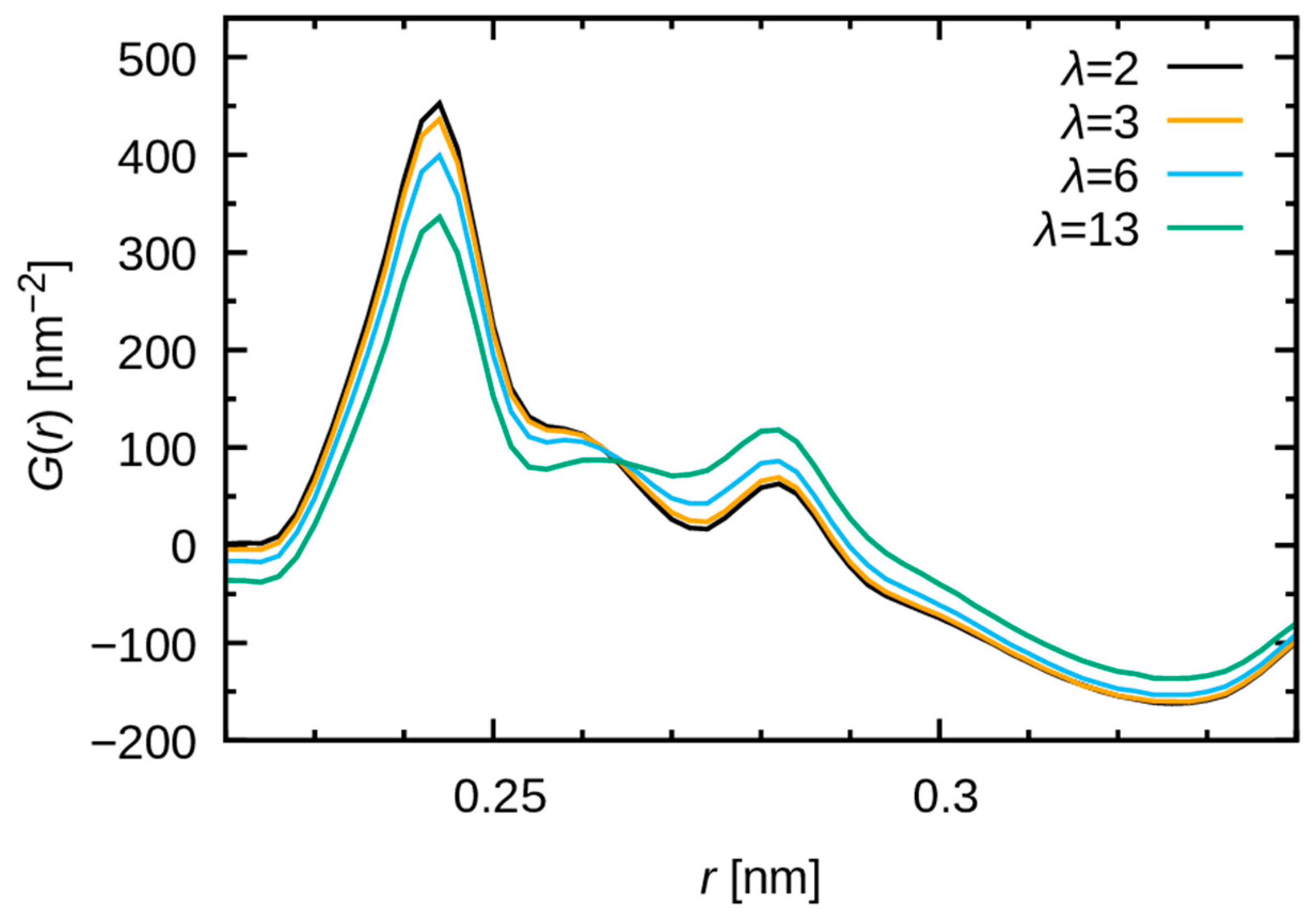
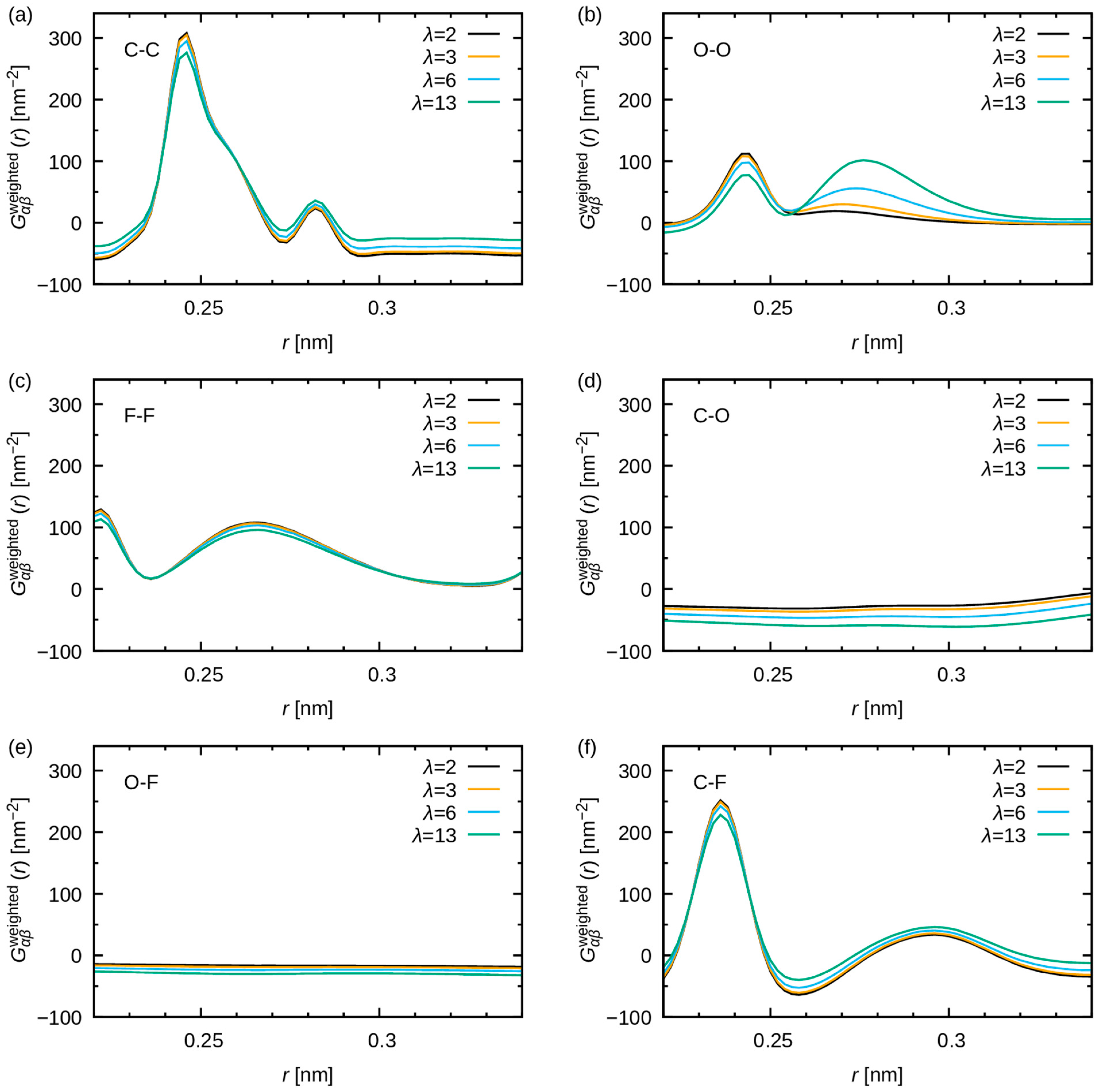
3.2.2. Comparison with WAXS
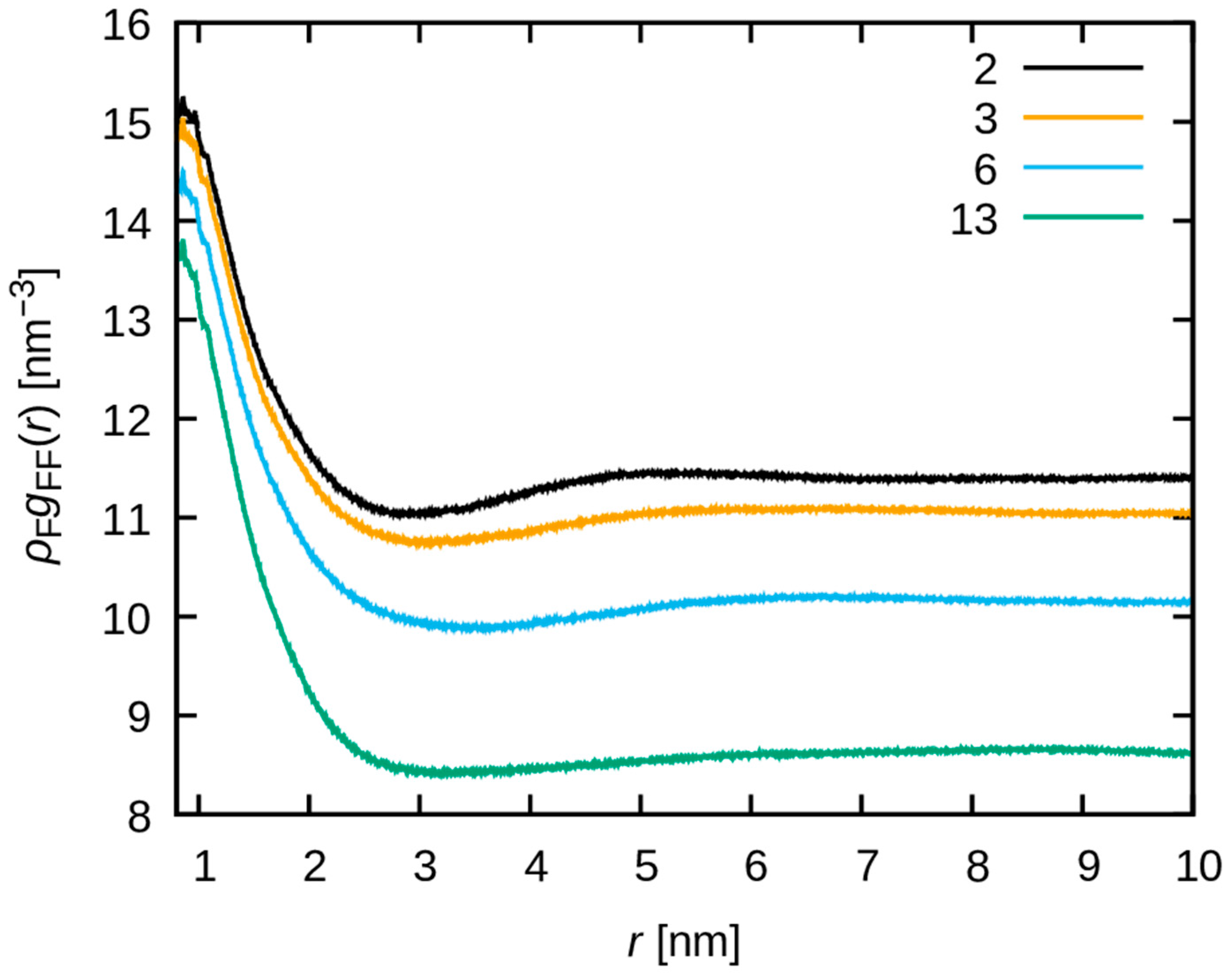
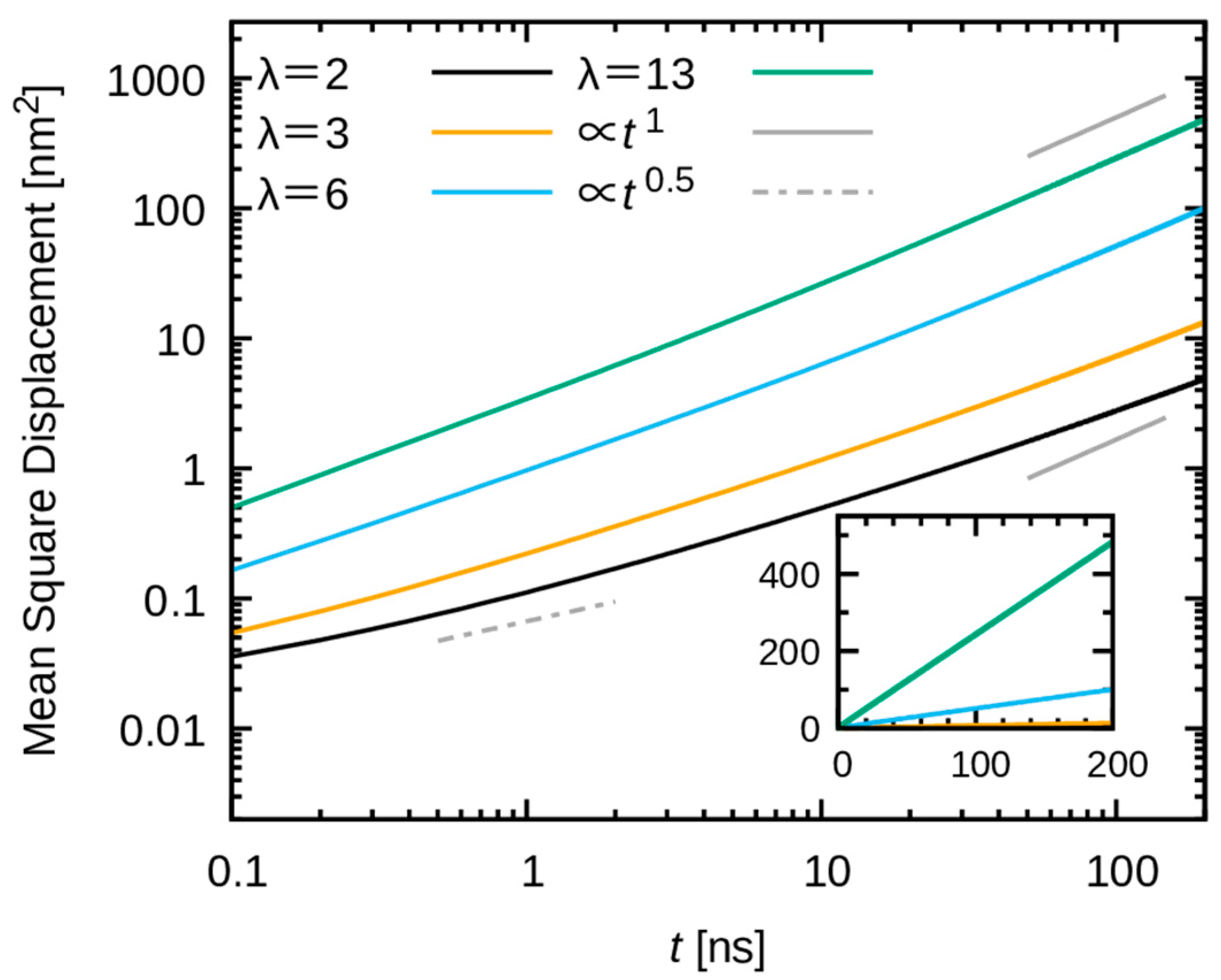
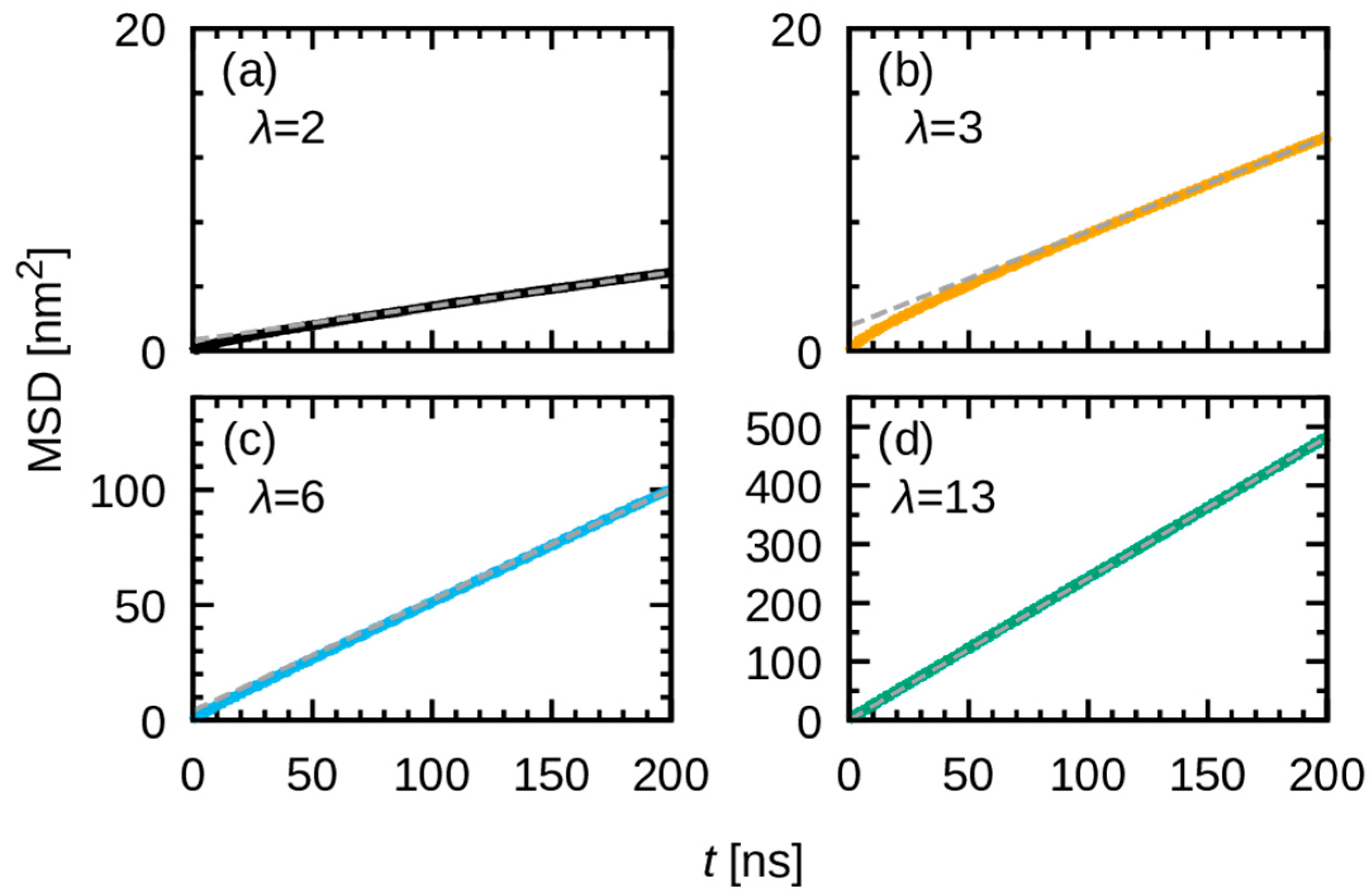
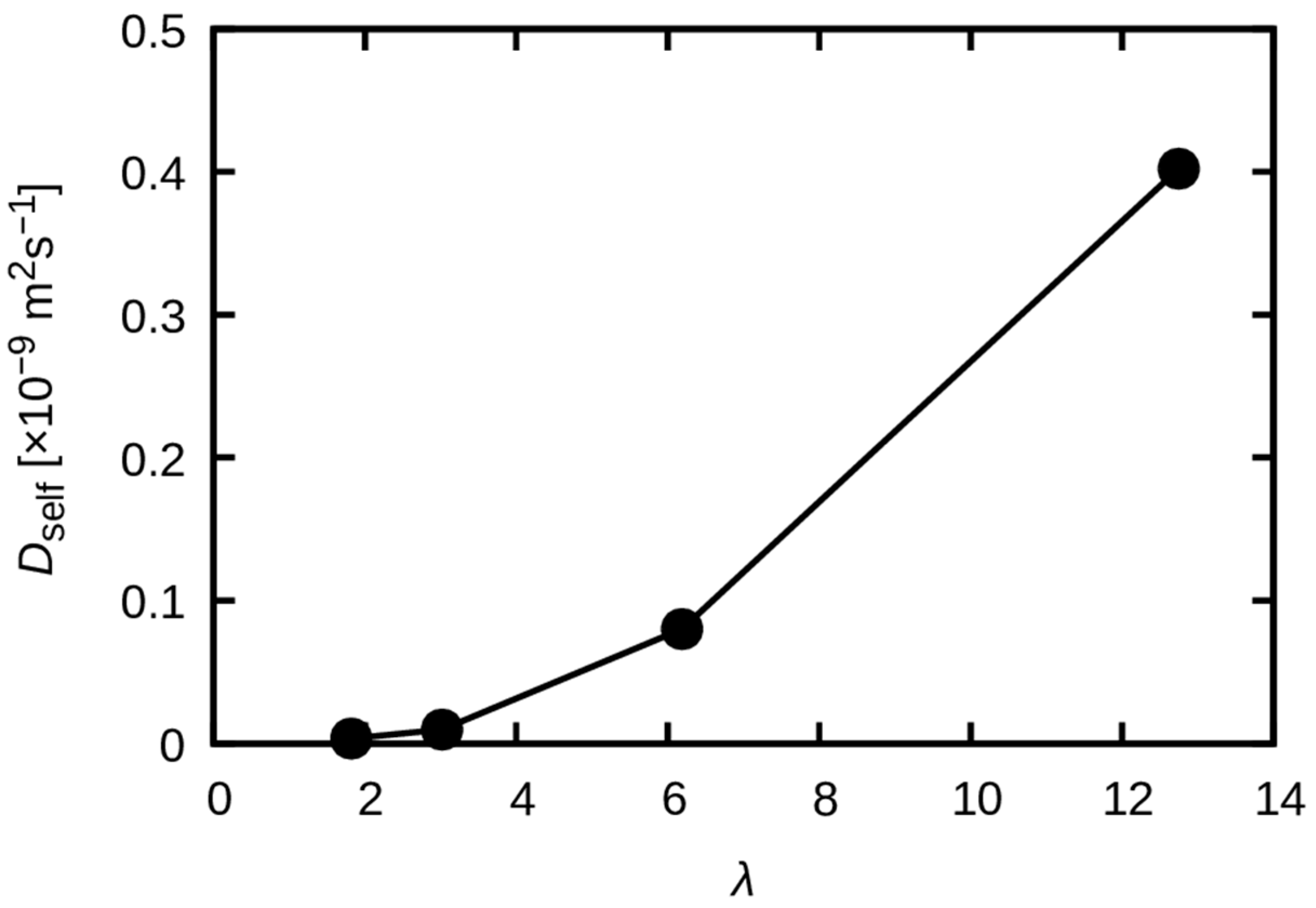
3.3. Dynamics of Water Molecules
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carrette, L.; Friedrich, K.A.; Stimming, U. Fuel Cells—Fundamentals and Applications. Fuel Cells 2001, 1, 5–39. [Google Scholar] [CrossRef]
- Cullen, D.A.; Neyerlin, K.C.; Ahluwalia, R.K.; Mukundan, R.; More, K.L.; Borup, R.L.; Weber, A.Z.; Myers, D.J.; Kusoglu, A. New roads and challenges for fuel cells in heavy-duty transportation. Nat. Energy 2021, 6, 462–474. [Google Scholar] [CrossRef]
- Merle, G.; Wessling, M.; Nijmeijer, K. Anion exchange membranes for alkaline fuel cells: A review. J. Membr. Sci. 2011, 377, 1–35. [Google Scholar] [CrossRef]
- Couture, G.; Alaaeddine, A.; Boschet, F.; Ameduri, B. Polymeric materials as anion-exchange membranes for alkaline fuel cells. Prog. Polym. Sci. 2011, 36, 1521–1557. [Google Scholar] [CrossRef]
- Park, E.J.; Kim, Y.S. Quaternized aryl ether-free polyaromatics for alkaline membrane fuel cells: Synthesis, properties, and performance—A topical review. J. Mater. Chem. A 2018, 6, 15456–15477. [Google Scholar] [CrossRef]
- Gottesfeld, S.; Dekel, D.R.; Page, M.; Bae, C.; Yan, Y.; Zelenay, P.; Kim, Y.S. Anion exchange membrane fuel cells: Current status and remaining challenges. J. Power Sources 2018, 375, 170–184. [Google Scholar] [CrossRef]
- Hickner, M.A.; Herring, A.M.; Coughlin, E.B. Anion exchange membranes: Current status and moving forward. J. Polym. Sci. Part B Polym. Phys. 2013, 51, 1727–1735. [Google Scholar] [CrossRef]
- Varcoe, J.R.; Atanassov, P.; Dekel, D.R.; Herring, A.M.; Hickner, M.A.; Kohl, P.A.; Kucernak, A.R.; Mustain, W.E.; Nijmeijer, K.; Scott, K.; et al. Anion-exchange membranes in electrochemical energy systems. Energy Environ. Sci. 2014, 7, 3135–3191. [Google Scholar] [CrossRef]
- Otsuji, K.; Yokota, N.; Tryk, D.A.; Kakinuma, K.; Miyatake, K.; Uchida, M. Performance hysteresis phenomena of anion exchange membrane fuel cells using an Fe–N–C cathode catalyst and an in-house-developed polymer electrolyte. J. Power Sources 2021, 487, 229407. [Google Scholar] [CrossRef]
- Otsuji, K.; Shirase, Y.; Asakawa, T.; Yokota, N.; Nagase, K.; Xu, W.; Song, P.; Wang, S.; Tryk, D.A.; Kakinuma, K.; et al. Effect of water management in membrane and cathode catalyst layers on suppressing the performance hysteresis phenomenon in anion-exchange membrane fuel cells. J. Power Sources 2022, 522, 230997. [Google Scholar] [CrossRef]
- Ono, H.; Miyake, J.; Shimada, S.; Uchida, M.; Miyatake, K. Anion exchange membranes composed of perfluoroalkylene chains and ammonium-functionalized oligophenylenes. J. Mater. Chem. A 2015, 3, 21779–21788. [Google Scholar] [CrossRef]
- Ozawa, M.; Kimura, T.; Akiyama, R.; Miyake, J.; Inukai, J.; Miyatake, K. Copolymers Composed of Perfluoroalkyl and Ammonium-Functionalized Fluorenyl Groups as Chemically Stable Anion Exchange Membranes. Bull. Chem. Soc. Jpn. 2017, 90, 1088–1094. [Google Scholar] [CrossRef]
- Ozawa, M.; Kimura, T.; Otsuji, K.; Akiyama, R.; Miyake, J.; Uchida, M.; Inukai, J.; Miyatake, K. Structurally Well-Defined Anion-Exchange Membranes Containing Perfluoroalkyl and Ammonium-Functionalized Fluorenyl Groups. ACS Omega 2018, 3, 16143–16149. [Google Scholar] [CrossRef]
- Ono, H.; Miyake, J.; Miyatake, K. Partially fluorinated and ammonium-functionalized terpolymers: Effect of aliphatic groups on the properties of anion conductive membranes. J. Polym. Sci. Part A Polym. Chem. 2017, 55, 1442–1450. [Google Scholar] [CrossRef]
- Mahmoud, A.M.A.; Elsaghier, A.M.M.; Otsuji, K.; Miyatake, K. High Hydroxide Ion Conductivity with Enhanced Alkaline Stability of Partially Fluorinated and Quaternized Aromatic Copolymers as Anion Exchange Membranes. Macromolecules 2017, 50, 4256–4266. [Google Scholar] [CrossRef]
- Ahmed Mahmoud, A.M.; Miyatake, K. Optimization of the pendant chain length in partially fluorinated aromatic anion exchange membranes for alkaline fuel cells. J. Mater. Chem. A 2018, 6, 14400–14409. [Google Scholar] [CrossRef]
- Miyake, J.; Miyatake, K. Quaternized poly(arylene perfluoroalkylene)s (QPAFs) for alkaline fuel cells—A perspective. Sustain. Energy Fuels 2019, 3, 1916–1928. [Google Scholar] [CrossRef]
- Ono, H.; Kimura, T.; Takano, A.; Asazawa, K.; Miyake, J.; Inukai, J.; Miyatake, K. Robust anion conductive polymers containing perfluoroalkylene and pendant ammonium groups for high performance fuel cells. J. Mater. Chem. A 2017, 5, 24804–24812. [Google Scholar] [CrossRef]
- Koronka, D.; Matsumoto, A.; Otsuji, K.; Miyatake, K. Partially fluorinated copolymers containing pendant piperidinium head groups as anion exchange membranes for alkaline fuel cells. RSC Adv. 2019, 9, 37391–37402. [Google Scholar] [CrossRef]
- Yoshida, K.; Nagai, T.; Ohara, K.; Shirase, Y.; Miyatake, K.; Inukai, J. In-situ observation of an anion exchange membrane at various humidity by X-ray scattering. J. Mol. Liq. 2023, 391, 123197. [Google Scholar] [CrossRef]
- Ono, R.; Suzuki, H.; Miyatake, K.; Tokumasu, T. Transport Mechanism of Hydroxide Ions Focused on the Vehicle Mechanism Near the Cation Sites in Anion Exchange Membranes. ECS Trans. 2024, 114, 133–140. [Google Scholar] [CrossRef]
- Shirase, Y.; Matsumoto, A.; Lim, K.L.; Tryk, D.A.; Miyatake, K.; Inukai, J. Properties and Morphologies of Anion-Exchange Membranes with Different Lengths of Fluorinated Hydrophobic Chains. ACS Omega 2022, 7, 13577–13587. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Tirado-Rives, J. Potential energy functions for atomic-level simulations of water and organic and biomolecular systems. Proc. Natl. Acad. Sci. USA 2005, 102, 6665–6670. [Google Scholar] [CrossRef]
- Dodda, L.S.; Cabeza de Vaca, I.; Tirado-Rives, J.; Jorgensen, W.L. LigParGen web server: An automatic OPLS-AA parameter generator for organic ligands. Nucleic Acids Res. 2017, 45, W331–W336. [Google Scholar] [CrossRef]
- Fujimoto, K.; Tang, Z.; Shinoda, W.; Okazaki, S. All-atom molecular dynamics study of impact fracture of glassy polymers. I: Molecular mechanism of brittleness of PMMA and ductility of PC. Polymer 2019, 178, 121570. [Google Scholar] [CrossRef]
- Tang, Z. (Institute for Molecular Science, Okazaki, Aichi, Japan). Personal communication, 2022.
- Fang, C.E.; Tsai, Y.C.; Scheurer, C.; Chiu, C.C. Revised Atomic Charges for OPLS Force Field Model of Poly(Ethylene Oxide): Benchmarks and Applications in Polymer Electrolyte. Polymers 2021, 13, 1131. [Google Scholar] [CrossRef]
- Dodda, L.S.; Vilseck, J.Z.; Tirado-Rives, J.; Jorgensen, W.L. 1.14*CM1A-LBCC: Localized Bond-Charge Corrected CM1A Charges for Condensed-Phase Simulations. J. Phys. Chem. B 2017, 121, 3864–3870. [Google Scholar] [CrossRef]
- Abascal, J.L.; Vega, C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. [Google Scholar] [CrossRef]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Mabuchi, T.; Tokumasu, T. Effect of bound state of water on hydronium ion mobility in hydrated Nafion using molecular dynamics simulations. J. Chem. Phys. 2014, 141, 104904. [Google Scholar] [CrossRef] [PubMed]
- Kuo, A.T.; Shinoda, W.; Okazaki, S. Molecular dynamics study of the morphology of hydrated perfluorosulfonic acid polymer membranes. J. Phys. Chem. C 2016, 120, 25832–25842. [Google Scholar] [CrossRef]
- Nagai, T.; Fujimoto, K.; Okazaki, S. Three-dimensional free-energy landscape of hydrogen and oxygen molecules in polymer electrolyte membranes: Insight into diffusion paths. J. Chem. Phys. 2022, 156, 044507. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páall, S.; Smith, J.C.; Hess, B.; Lindah, E. Gromacs: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [PubMed]
- Bernetti, M.; Bussi, G. Pressure control using stochastic cell rescaling. J. Chem. Phys. 2020, 153, 114107. [Google Scholar] [CrossRef] [PubMed]
- Sivia, D.S. Elementary Scattering Theory: For X-Ray and Neutron Users; Oxford University Press: Oxford, UK, 2011. [Google Scholar] [CrossRef]
- Brown, P.J.; Fox, A.G.; Maslen, E.N.; O’Keefe, M.A.; Willis, B.T.M. Intensity of diffracted intensities. In International Tables for Crystallography Volume C: Mathematical, Physical and Chemical Tables; Springer: Dordrecht, The Netherlands, 2006; pp. 554–595. [Google Scholar] [CrossRef]
- Empirical Potential Structure Refinement. Available online: https://www.isis.stfc.ac.uk/pages/empirical-potential-structure-refinement.aspx (accessed on 12 July 2025).
- Morgado, P.; Gaspar, J.; Filipe, E.J.M. Liquid–liquid interfaces: Water–perfluoroalkanes and water–perfluoroalkylalkanes, experimental interfacial tensions and molecular simulation. J. Mol. Liq. 2020, 312, 113385. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagai, T.; Kawaida, T.; Yoshida, K. Large-Scale Molecular Dynamics of Anion-Exchange Membranes: Molecular Structure of QPAF-4 and Water Transport. Membranes 2025, 15, 266. https://doi.org/10.3390/membranes15090266
Nagai T, Kawaida T, Yoshida K. Large-Scale Molecular Dynamics of Anion-Exchange Membranes: Molecular Structure of QPAF-4 and Water Transport. Membranes. 2025; 15(9):266. https://doi.org/10.3390/membranes15090266
Chicago/Turabian StyleNagai, Tetsuro, Takumi Kawaida, and Koji Yoshida. 2025. "Large-Scale Molecular Dynamics of Anion-Exchange Membranes: Molecular Structure of QPAF-4 and Water Transport" Membranes 15, no. 9: 266. https://doi.org/10.3390/membranes15090266
APA StyleNagai, T., Kawaida, T., & Yoshida, K. (2025). Large-Scale Molecular Dynamics of Anion-Exchange Membranes: Molecular Structure of QPAF-4 and Water Transport. Membranes, 15(9), 266. https://doi.org/10.3390/membranes15090266







