Application of the Transition State Theory in the Study of the Osmotic Permeabilities of AQP7, AQP10 and GlpF
Abstract
1. Introduction
2. Methods
2.1. Model System Setup and Simulation Parameters
2.2. Transition State Theory for Calculation of Water Permeability
3. Results and Discussion
3.1. Single-Channel Osmotic Permeability, pf, of AQP7, GlpF and AQP10
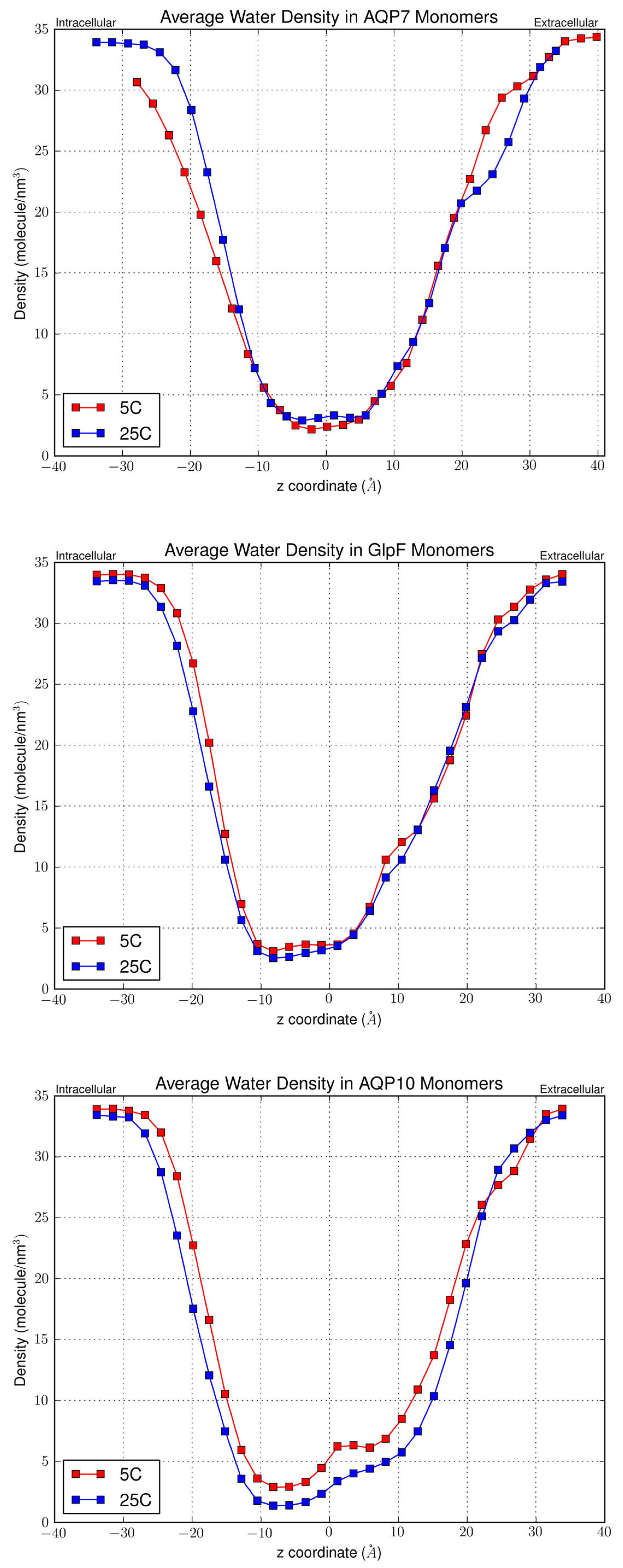
3.2. Effect of Temperature on Osmotic Permeability
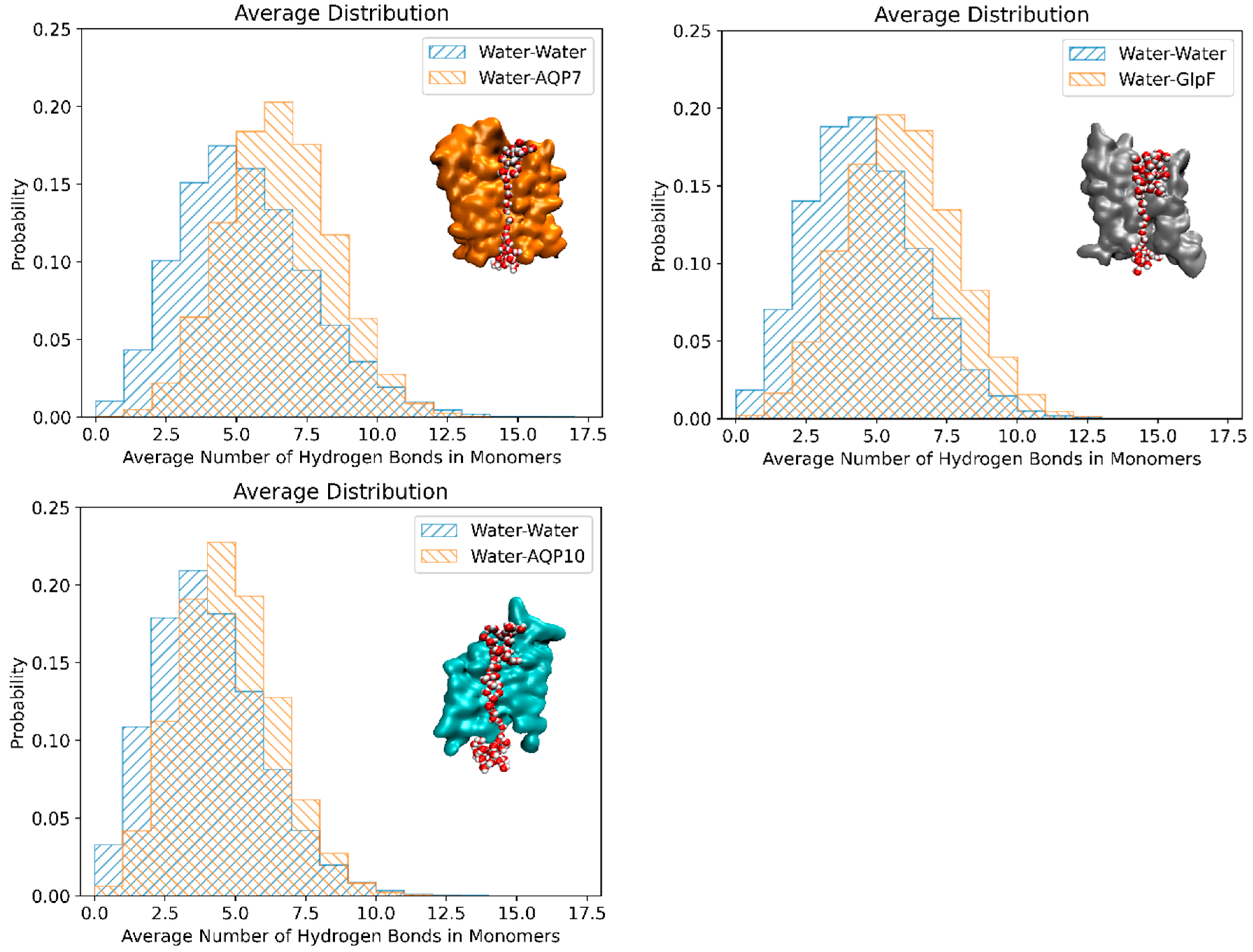
3.3. Correlation Between Osmotic Permeability and Water–Protein Hydrogen Bonds
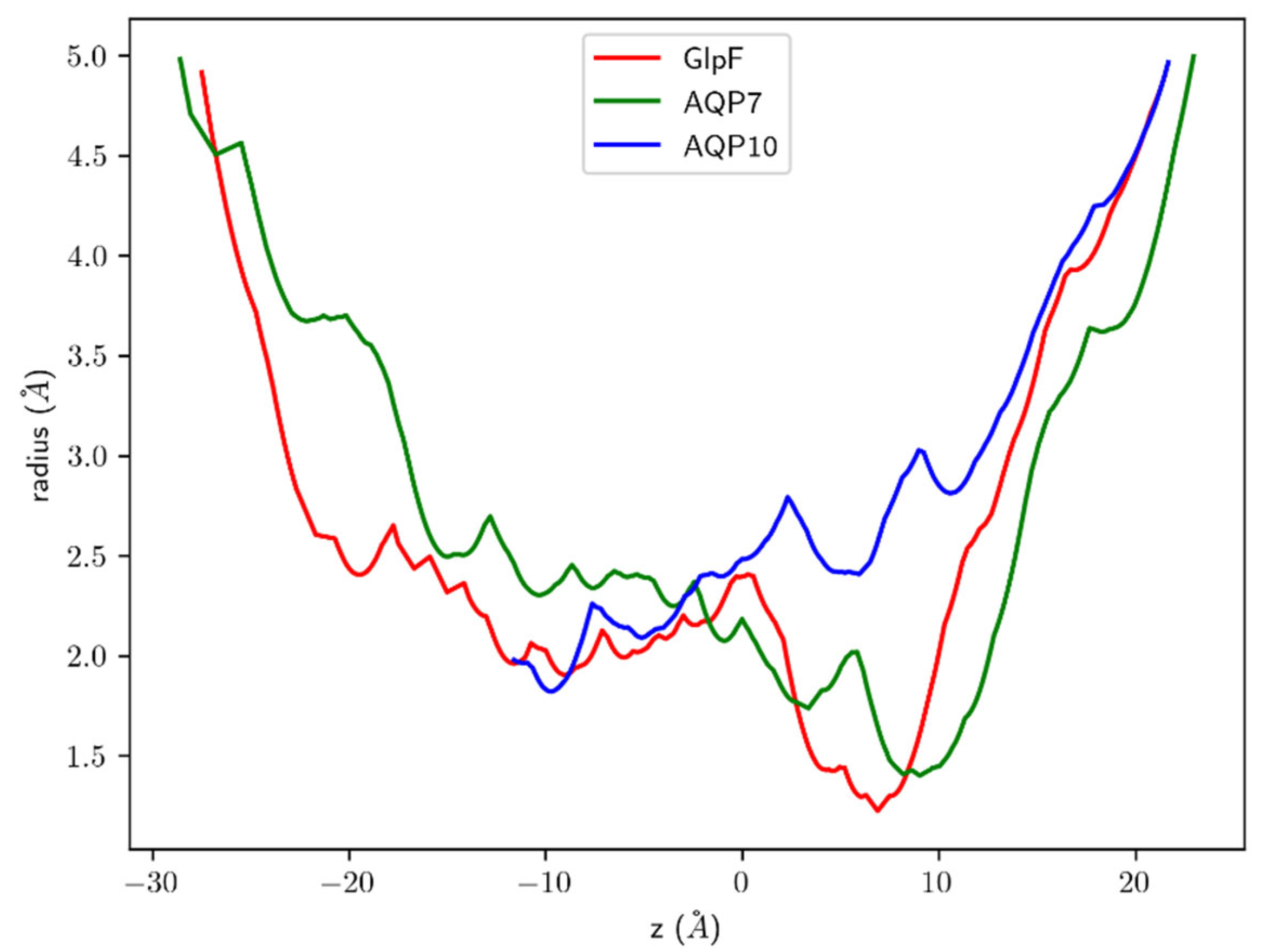
3.4. Effect of Channel Structure on Osmotic Permeability
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fu, D.; Libson, A.; Miercke, L.J.; Weitzman, C.; Nollert, P.; Krucinski, J.; Stroud, R.M. Structure of a glycerol-conducting channel and the basis for its selectivity. Science 2000, 290, 481–486. [Google Scholar] [CrossRef]
- de Groot, B.L.; Grubmüller, H. Water Permeation Across Biological Membranes: Mechanism and Dynamics of Aquaporin-1 and GlpF. Science 2001, 294, 2353–2357. [Google Scholar] [CrossRef]
- Wambo, T.O.; Rodriguez, R.A.; Chen, L.Y. Computing osmotic permeabilities of aquaporins AQP4, AQP5, and GlpF from near-equilibrium simulations. Biochim. Biophys. Acta Biomembr. 2017, 1859, 1310–1316. [Google Scholar] [CrossRef]
- Horner, A.; Zocher, F.; Preiner, J.; Ollinger, N.; Siligan, C.; Akimov, S.A.; Pohl, P. The mobility of single-file water molecules is governed by the number of H-bonds they may form with channel-lining residues. Sci. Adv. 2015, 1, e1400083. [Google Scholar] [CrossRef]
- Chen, L.Y. Glycerol modulates water permeation through Escherichia coli aquaglyceroporin GlpF. Biochim. Biophys. Acta 2013, 1828, 1786–1793. [Google Scholar] [CrossRef]
- Aponte-Santamaria, C.; Hub, J.S.; de Groot, B.L. Dynamics and energetics of solute permeation through the Plasmodium falciparum aquaglyceroporin. Phys. Chem. Chem. Phys. 2010, 12, 10246–10254. [Google Scholar] [CrossRef]
- Jensen, M.; Mouritsen, O.G. Single-channel water permeabilities of Escherichia coli aquaporins AqpZ and GlpF. Biophys. J. 2006, 90, 2270–2284. [Google Scholar] [CrossRef]
- Lee, J.K.; Khademi, S.; Harries, W.; Savage, D.; Miercke, L.; Stroud, R.M. Water and glycerol permeation through the glycerol channel GlpF and the aquaporin family. J. Synchrotron Radiat. 2004, 11, 86–88. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.; Grayson, P.; Schulten, K. Glycerol conductance and physical asymmetry of the Escherichia coli glycerol facilitator GlpF. Biophys. J. 2003, 85, 2977–2987. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Tajkhorshid, E.; Nollert, P.; Jensen, M.Ø.; Miercke, L.J.W.; O’Connell, J.; Stroud, R.M.; Schulten, K. Control of the Selectivity of the Aquaporin Water Channel Family by Global Orientational Tuning. Science 2002, 296, 525–530. [Google Scholar] [CrossRef] [PubMed]
- Jensen, M.; Park, S.; Tajkhorshid, E.; Schulten, K. Energetics of glycerol conduction through aquaglyceroporin GlpF. Proc. Natl. Acad. Sci. USA 2002, 99, 6731–6736. [Google Scholar] [CrossRef]
- Borgnia, M.J.; Agre, P. Reconstitution and functional comparison of purified GlpF and AqpZ, the glycerol and water channels from Escherichia coli. Proc. Natl. Acad. Sci. USA 2001, 98, 2888–2893. [Google Scholar] [CrossRef]
- Maurel, C.; Reizer, J.; Schroeder, J.I.; Chrispeels, M.J.; Saier, M.H., Jr. Functional characterization of the Escherichia coli glycerol facilitator, GlpF, in Xenopus oocytes. J. Biol. Chem. 1994, 269, 11869–11872. [Google Scholar] [CrossRef]
- Heller, K.B.; Lin, E.C.; Wilson, T.H. Substrate specificity and transport properties of the glycerol facilitator of Escherichia coli. J. Bacteriol. 1980, 144, 274–278. [Google Scholar] [CrossRef]
- Hashido, M.; Ikeguchi, M.; Kidera, A. Comparative simulations of aquaporin family: AQP1, AQPZ, AQP0 and GlpF. FEBS Lett. 2005, 579, 5549–5552. [Google Scholar] [CrossRef] [PubMed]
- Jensen, M.Ø.; Tajkhorshid, E.; Schulten, K. Electrostatic tuning of permeation and selectivity in aquaporin water channels. Biophys. J. 2003, 85, 2884–2899. [Google Scholar] [CrossRef] [PubMed]
- Gotfryd, K.; Mósca, A.F.; Missel, J.W.; Truelsen, S.F.; Wang, K.; Spulber, M.; Krabbe, S.; Hélix-Nielsen, C.; Laforenza, U.; Soveral, G.; et al. Human adipose glycerol flux is regulated by a pH gate in AQP10. Nat. Commun. 2018, 9, 4749. [Google Scholar] [CrossRef] [PubMed]
- de Maré, S.W.; Venskutonytė, R.; Eltschkner, S.; de Groot, B.L.; Lindkvist-Petersson, K. Structural Basis for Glycerol Efflux and Selectivity of Human Aquaporin 7. Structure 2020, 28, 215–222.e213. [Google Scholar] [CrossRef]
- Moss, F.J.; Mahinthichaichan, P.; Lodowski, D.T.; Kowatz, T.; Tajkhorshid, E.; Engel, A.; Boron, W.F.; Vahedi-Faridi, A. Aquaporin-7: A Dynamic Aquaglyceroporin With Greater Water and Glycerol Permeability Than Its Bacterial Homolog GlpF. Front. Physiol. 2020, 11, 728. [Google Scholar] [CrossRef]
- Schmidt, J.D.R.; Walloch, P.; Höger, B.; Beitz, E. Aquaporins with lactate/lactic acid permeability at physiological pH conditions. Biochimie 2021, 188, 7–11. [Google Scholar] [CrossRef]
- Madeira, A.; Camps, M.; Zorzano, A.; Moura, T.F.; Soveral, G. Biophysical Assessment of Human Aquaporin-7 as a Water and Glycerol Channel in 3T3-L1 Adipocytes. PLoS ONE 2013, 8, e83442. [Google Scholar] [CrossRef] [PubMed]
- Ishibashi, K.; Kuwahara, M.; Gu, Y.; Kageyama, Y.; Tohsaka, A.; Suzuki, F.; Marumo, F.; Sasaki, S. Cloning and functional expression of a new water channel abundantly expressed in the testis permeable to water, glycerol, and urea. J. Biol. Chem. 1997, 272, 20782–20786. [Google Scholar] [CrossRef]
- Katano, T.; Ito, Y.; Ohta, K.; Yasujima, T.; Inoue, K.; Yuasa, H. Functional Characteristics of Aquaporin 7 as a Facilitative Glycerol Carrier. Drug Metab. Pharmacokinet. 2014, 29, 244–248. [Google Scholar] [CrossRef]
- Hara-Chikuma, M.; Sohara, E.; Rai, T.; Ikawa, M.; Okabe, M.; Sasaki, S.; Uchida, S.; Verkman, A.S. Progressive adipocyte hypertrophy in aquaporin-7-deficient mice: Adipocyte glycerol permeability as a novel regulator of fat accumulation. J. Biol. Chem. 2005, 280, 15493–15496. [Google Scholar] [CrossRef]
- Hibuse, T.; Maeda, N.; Nakatsuji, H.; Tochino, Y.; Fujita, K.; Kihara, S.; Funahashi, T.; Shimomura, I. The heart requires glycerol as an energy substrate through aquaporin 7, a glycerol facilitator. Cardiovasc. Res. 2009, 83, 34–41. [Google Scholar] [CrossRef]
- Mósca, A.F.; de Almeida, A.; Wragg, D.; Martins, A.P.; Sabir, F.; Leoni, S.; Moura, T.F.; Prista, C.; Casini, A.; Soveral, G. Molecular Basis of Aquaporin-7 Permeability Regulation by pH. Cells 2018, 7, 207. [Google Scholar] [CrossRef] [PubMed]
- Ishibashi, K.; Morinaga, T.; Kuwahara, M.; Sasaki, S.; Imai, M. Cloning and identification of a new member of water channel (AQP10) as an aquaglyceroporin. Biochim. Biophys. Acta (BBA)—Gene Struct. Expr. 2002, 1576, 335–340. [Google Scholar] [CrossRef]
- Hatakeyama, S.; Yoshida, Y.; Tani, T.; Koyama, Y.; Nihei, K.; Ohshiro, K.; Kamiie, J.-I.; Yaoita, E.; Suda, T.; Hatakeyama, K.; et al. Cloning of a New Aquaporin (AQP10) Abundantly Expressed in Duodenum and Jejunum. Biochem. Biophys. Res. Commun. 2001, 287, 814–819. [Google Scholar] [CrossRef]
- Ishii, M.; Ohta, K.; Katano, T.; Urano, K.; Watanabe, J.; Miyamoto, A.; Inoue, K.; Yuasa, H. Dual Functional Characteristic of Human Aquaporin 10 for Solute Transport. Cell. Physiol. Biochem. 2011, 27, 749–756. [Google Scholar] [CrossRef] [PubMed]
- Zhu, F.; Tajkhorshid, E.; Schulten, K. Pressure-Induced Water Transport in Membrane Channels Studied by Molecular Dynamics. Biophys. J. 2002, 83, 154–160. [Google Scholar] [CrossRef]
- Zhu, F.; Tajkhorshid, E.; Schulten, K. Collective Diffusion Model for Water Permeation through Microscopic Channels. Phys. Rev. Lett. 2004, 93, 224501. [Google Scholar] [CrossRef]
- Chan, R.; Falato, M.; Liang, H.; Chen, L.Y. In silico simulations of erythrocyte aquaporins with quantitative in vitro validation. RSC Adv. 2020, 10, 21283–21291. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, R.A.; Liang, H.; Chen, L.Y.; Plascencia-Villa, G.; Perry, G. Single-channel permeability and glycerol affinity of human aquaglyceroporin AQP3. Biochim. Biophys. Acta Biomembr. 2019, 1861, 768–775. [Google Scholar] [CrossRef]
- Rodriguez, R.A.; Chan, R.; Liang, H.; Chen, L.Y. Quantitative study of unsaturated transport of glycerol through aquaglyceroporin that has high affinity for glycerol. RSC Adv. 2020, 10, 34203–34214. [Google Scholar] [CrossRef]
- Chen, L.Y. Free-energy landscape of glycerol permeation through aquaglyceroporin GlpF determined from steered molecular dynamics simulations. Biophys. Chem. 2010, 151, 178–180. [Google Scholar] [CrossRef][Green Version]
- Chen, L.Y. Glycerol inhibits water permeation through Plasmodium falciparum aquaglyceroporin. J. Struct. Biol. 2013, 181, 71–76. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kalé, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.; Mittal, J.; Feig, M.; Mackerell, A.D., Jr. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ1 and χ2 dihedral angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef]
- Klauda, J.B.; Venable, R.M.; Freites, J.A.; O’Connor, J.W.; Tobias, D.J.; Mondragon-Ramirez, C.; Vorobyov, I.; MacKerell, A.D., Jr.; Pastor, R.W. Update of the CHARMM all-atom additive force field for lipids: Validation on six lipid types. J. Phys. Chem. B 2010, 114, 7830–7843. [Google Scholar] [CrossRef]
- Wang, Y.; Kiziltas, A.; Blanchard, P.; Walsh, T.R. Calculation of 1D and 2D densities in VMD: A flexible and easy-to-use code. Comput. Phys. Commun. 2021, 266, 108032. [Google Scholar] [CrossRef]
- Verkman, A.S.; Hoek, A.N.v.; Ma, T.; Frigeri, A.; Skach, W.R.; Mitra, A.; Tamarappoo, B.K.; Farinas, J. Water transport across mammalian cell membranes. Am. J. Physiol.-Cell Physiol. 1996, 270, C12–C30. [Google Scholar] [CrossRef] [PubMed]
- Hardiagon, A.; Murail, S.; Huang, L.-B.; Lee, A.v.d.; Sterpone, F.; Barboiu, M.; Baaden, M. Molecular dynamics simulations reveal statistics and microscopic mechanisms of water permeation in membrane-embedded artificial water channel nanoconstructs. J. Chem. Phys. 2021, 154, 184102. [Google Scholar] [CrossRef] [PubMed]
- Wragg, D.; de Almeida, A.; Casini, A.; Leoni, S. Unveiling the Mechanisms of Aquaglyceroporin-3 Water and Glycerol Permeation by Metadynamics. Chem. Eur. J. 2019, 25, 8713–8718. [Google Scholar] [CrossRef] [PubMed]
- Horner, A.; Pohl, P. Single-file transport of water through membrane channels. Faraday Discuss. 2018, 209, 9–33. [Google Scholar] [CrossRef]
- Smart, O.S.; Neduvelil, J.G.; Wang, X.; Wallace, B.A.; Sansom, M.S.P. HOLE: A program for the analysis of the pore dimensions of ion channel structural models. J. Mol. Graph. 1996, 14, 354–360. [Google Scholar] [CrossRef]






| AQP | pf at 5 °C | pf at 25 °C | Ea |
|---|---|---|---|
| AQP7 | 4.664 ± 0.019 | 6.839 ± 0.047 | 3.154 (2.1 [22]) |
| GlpF | 9.657 ± 0.033 (11.7 [4]) | 15.304 ± 0.098 (19.0 [4]) | 3.794 (4.0 [4]) |
| AQP10 | 11.395 ± 0.028 | 17.929 ± 0.028 | 3.734 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chan, R.; Chen, L.Y. Application of the Transition State Theory in the Study of the Osmotic Permeabilities of AQP7, AQP10 and GlpF. Membranes 2025, 15, 265. https://doi.org/10.3390/membranes15090265
Chan R, Chen LY. Application of the Transition State Theory in the Study of the Osmotic Permeabilities of AQP7, AQP10 and GlpF. Membranes. 2025; 15(9):265. https://doi.org/10.3390/membranes15090265
Chicago/Turabian StyleChan, Ruth, and Liao Y. Chen. 2025. "Application of the Transition State Theory in the Study of the Osmotic Permeabilities of AQP7, AQP10 and GlpF" Membranes 15, no. 9: 265. https://doi.org/10.3390/membranes15090265
APA StyleChan, R., & Chen, L. Y. (2025). Application of the Transition State Theory in the Study of the Osmotic Permeabilities of AQP7, AQP10 and GlpF. Membranes, 15(9), 265. https://doi.org/10.3390/membranes15090265






