For understanding the influence of the species present in solution on the properties of the membranes, a speciation diagram for the initial composition of the working solution was constructed with the aid of the Hydra-Medusa software [
40] (
Figure 4). Then, the concentrations of the main ionic species in the initial solution (under pH 12.25) were determined, and the results are presented in
Table 2. As observed, the species present in the highest concentration is the cation Na
+, which is the only species in solution that theoretically crosses the cation-exchange membrane. Regarding the anionic species, those present in the highest concentrations in the solution are OH
−, SO
42−, Zn(EDTA)
2− and Zn(EDTA)OH
3−. The presence of two insoluble species can also be observed: CuO and ZnO, which influenced the results for percent extraction and percent concentration.
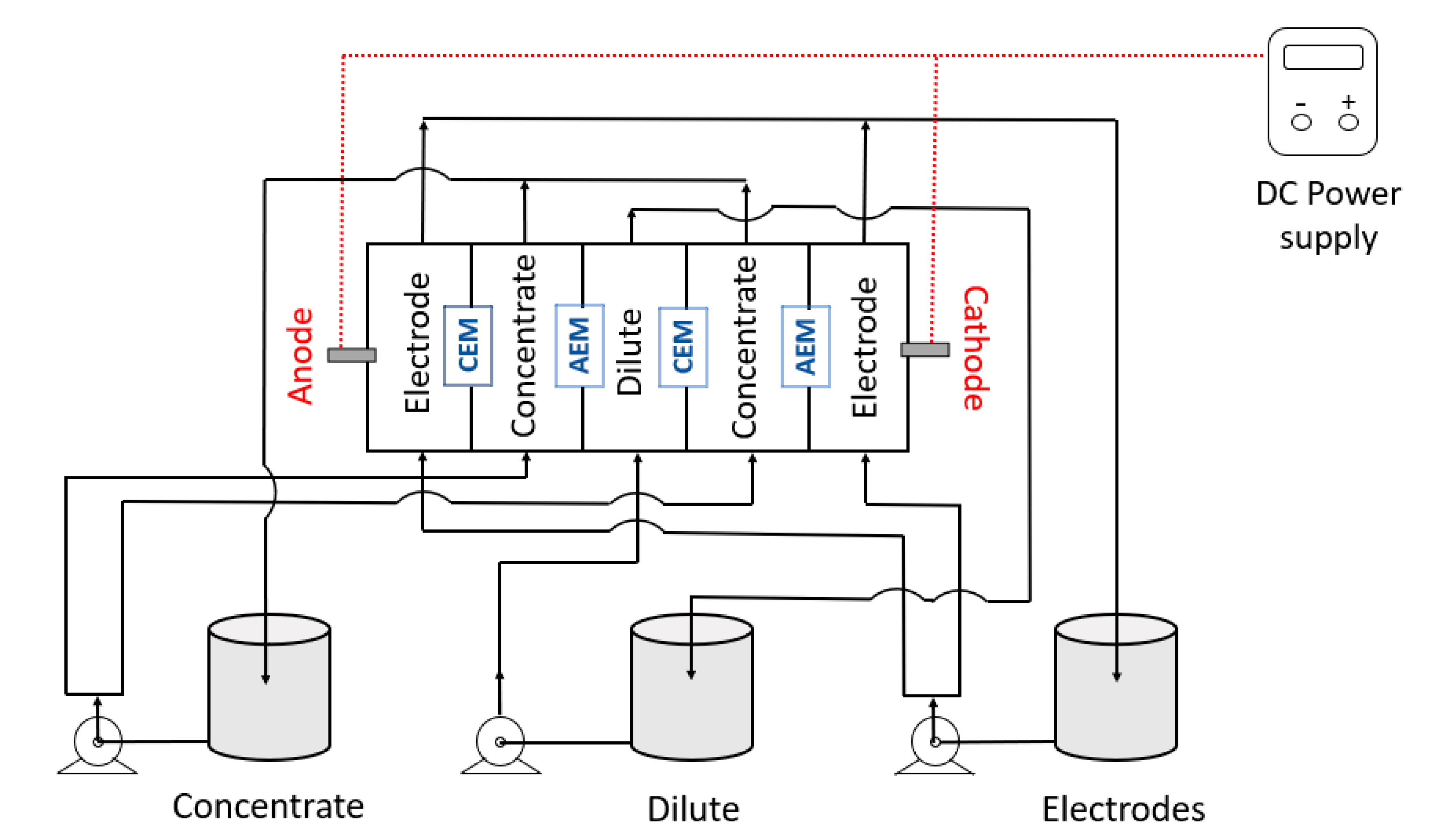
3.1. Obtaining the Current–Voltage Curves in the Stack of Electrodialysis
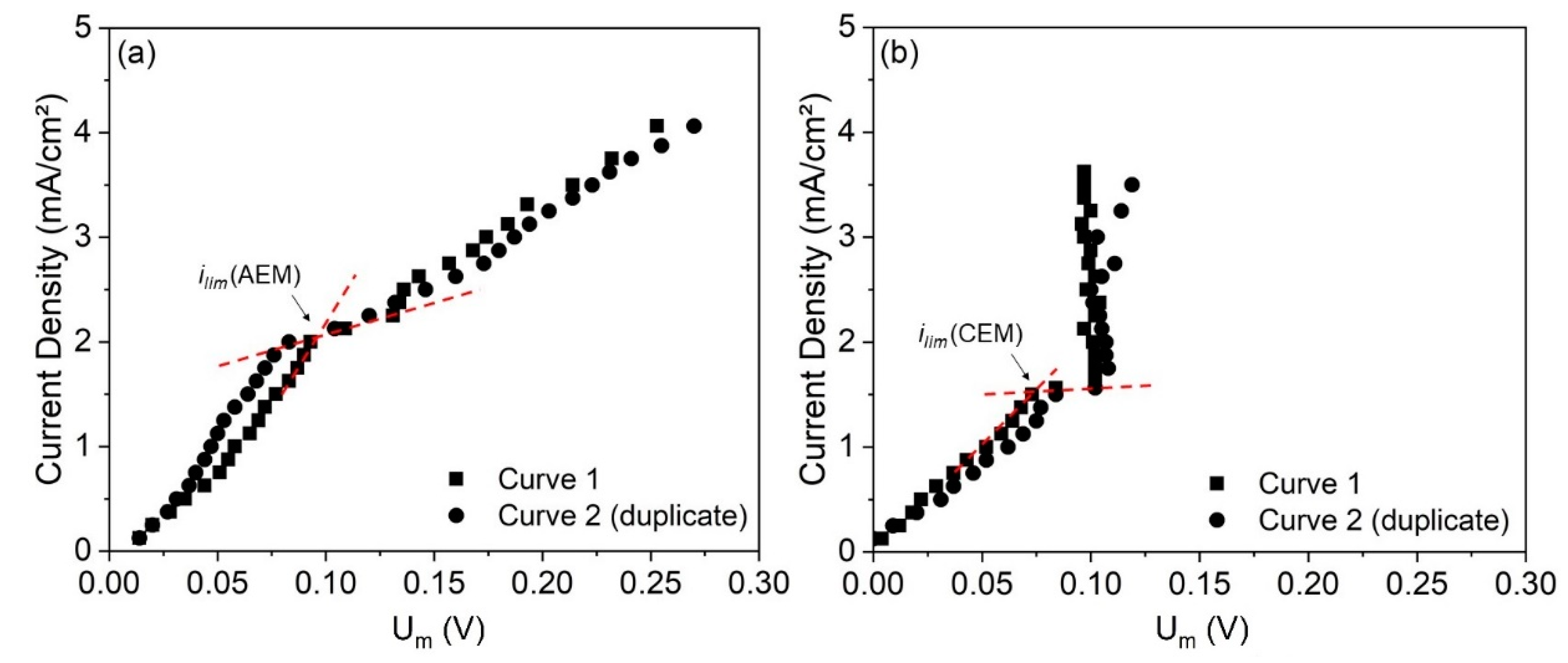
The CVCs of the anion- and cation-exchange membranes were constructed in the electrodialysis stack for determining their limiting current density. The curves obtained are depicted in
Figure 5 and the error in the
ilim determination between the duplicate curves was 3.5% and 0.7% for the AEM and CEM, respectively.
As observed, the AEM curve (
Figure 5a) presented two limiting current densities: one at 0.5 mA/cm
2 and the other at 2.0 mA/cm
2. This behavior was already seen for ampholyte-containing solutions due to the different forms of species depending on the local pH [
41] and for other systems where the prevailing species that passes through the membranes changes as the current density is increased [
42,
43]. The species that passes at each current density depends on its size, molar concentration and mobility/diffusion coefficient. Here, the first limiting current density for the AEM (
ilim1,AEM = 0.5 mA/cm
2) must be related to the depletion of OH
− ions, due to the greater concentration and mobility of these ions (
Table 2), whereas the second one (
ilim2,AEM = 2.0 mA/cm
2) must be related to the depletion of anionic species present in lower concentrations, such as SO
42− and complexes with EDTA. Then, a plateau was reached, and the third region showed the usual linear behavior. For defining the current applied to the electrodialysis test in the overlimiting condition, we considered the
ilim of the AEM as 2.0 mA/cm
2, since only at current densities above this can we see the third region of the current–voltage curve, where overlimiting phenomena occur.
For the cation-exchange membrane (
Figure 5b), the curve showed a linear relationship in the first region, but in the third one, the potential drop remained practically constant with the increase in current density. This occurred due to the very fast and intense ionic transport through the CEM under overlimiting conditions, as will be discussed. Despite the absence of the linear behavior in the third region, it was possible to determine the limiting current density for the CEM (i
lim,CEM = 1.5 mA/cm
2), since the change in the slope after the first region was evident.
Finally, the higher value of limiting current density for the AEM was due to the greater concentration of the anionic species than of the cationic species in the solution (
Table 2), besides the high mobility of OH
−.
3.2. Electrodialysis
Two electrodialysis experiments were performed.
Table 3 presents the current density applied to each test performed, with the relationships between these current densities and the limiting current densities of both membranes.
As observed, in the underlimiting experiment, the applied current density was lower than the ilim of both membranes (80% and 60% of the ilim of the CEM and AEM, respectively). In the overlimiting experiment, both membranes were in overlimiting conditions, since the i applied was 60% and 20% above the ilim of the CEM and AEM, respectively. The limiting current densities were determined with the working solution in its initial state. As the concentration of the dilute compartment decreased throughout the tests, the limiting current density also decreased. Hence, in the underlimiting test, the system may have operated in the overlimiting condition when the applied current density surpassed the limiting current density of the membranes/electrolyte system.
Figure 6 presents the visual aspects of the four solutions involved in the overlimiting test: the original bath solution before its dilution, the synthetic rinsing water (or working solution), the diluted (treated) and concentrated solutions obtained after the fourth cycle.
3.2.1. Evaluation of the Conductivity
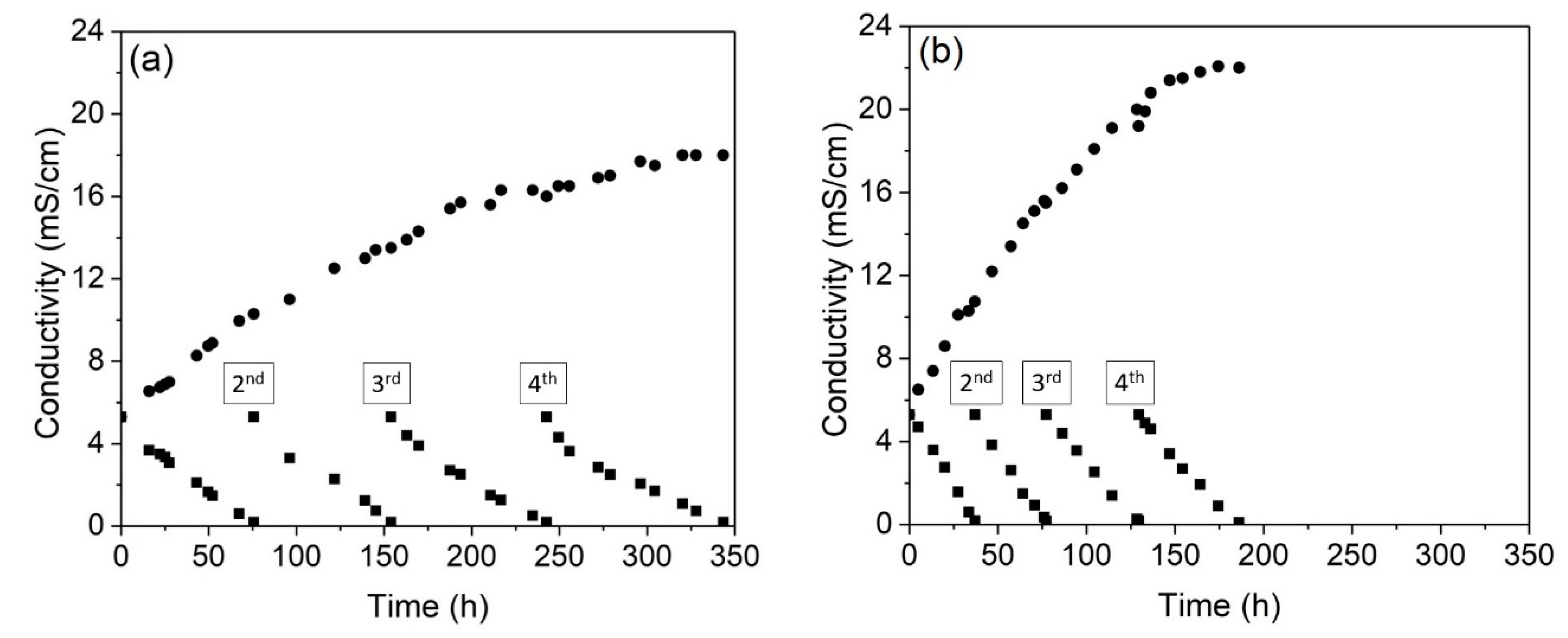
Figure 7 presents the conductivity of the concentrate and dilute compartments throughout the four cycles performed in the ED tests. As expected, the increase in the current density strongly decreased the operation time, from 344 h to 186 h. In relation to the conductivity of the concentrate compartment after each cycle,
Figure 7 shows that the overlimiting test accounted for the highest conductivity achieved in all cycles. As the conductivity of the dilute compartment was the same after all the cycles in the experiments (~0.2 mS/cm), the difference in the conductivity of the concentrated solutions suggests that the increase in the current density caused a change in the type of species that preferentially passed through the membranes. This is also going to be shown in the chemical analyses. The final pH values of the diluted and concentrated solutions after each cycle of the electrodialysis tests are presented in
Table 4.
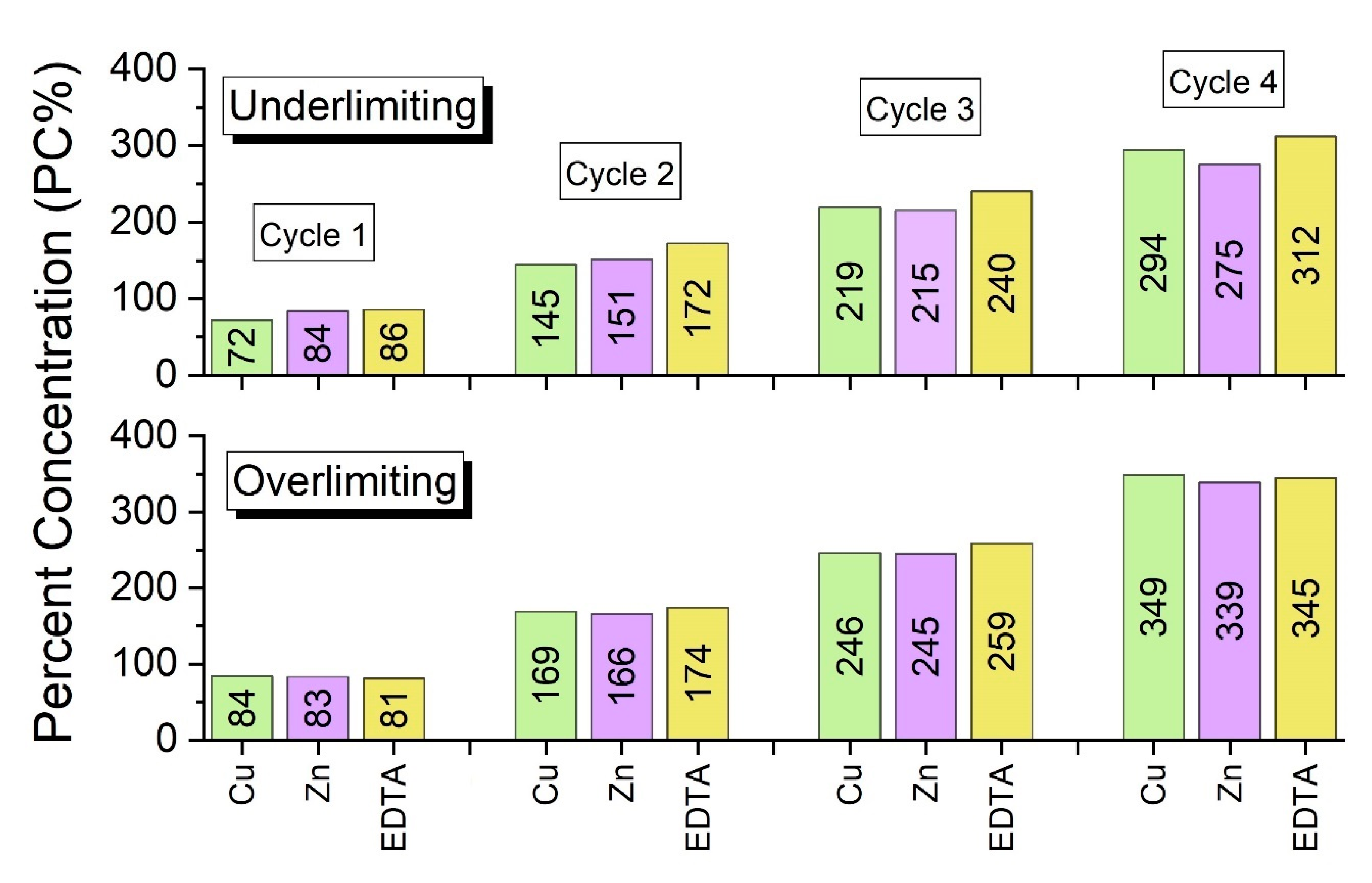
3.2.2. Percent Concentration and Percent Extraction
Table 5 presents the concentration, in ppm, of the species copper, zinc, EDTA, sodium and sulfate in the concentrate and dilute compartments. Here, the concentration of sodium present in EDTA was discounted. Although the initial solution of the synthetic rinsing water was prepared with 0.0014 mol/L of Zn
2+ (
Table 1), or ~90 ppm of Zn
2+,
Table 5 shows that its initial concentration in the experiments, as determined by analytical method, was about 60 ppm. This difference occurred due to the formation of a precipitate with zinc, which was visually observed before the ED tests. The precipitate formation was expected, as shown in the speciation diagram in
Figure 4.
The results of the desalination of the feed solution in each of the four cycles were expected to be similar in the experiments, since the system was carried out in quasi steady-state conditions. The differences shown in
Table 5, for both ED tests, are explained by the formation of insoluble species and by their reactions with protons during overlimiting phenomena, as will be discussed. With the data from
Table 5, the percent concentrations of Cu, Zn and EDTA were calculated, and this is shown in
Figure 8.
According to
Figure 8, the species that preferentially crossed the membranes and their concentrations depended on the applied current density, as suggested by
Figure 7, regarding the values of the final conductivities of the concentrate compartment. It should be noted that, in general, the highest percent concentrations of copper and zinc were those obtained in the overlimiting test. For EDTA, the percent concentration remained practically constant in the first two cycles, whereas it increased in the third and fourth cycles, in the overlimiting test.
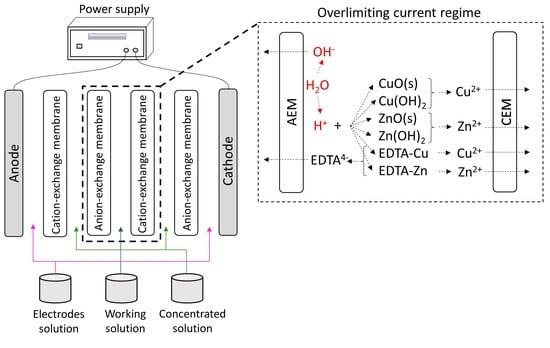
The highest percent concentrations of copper, zinc and EDTA in the overlimiting test can be explained by the occurrence of water dissociation. Zabolotsky et al. [
44] studied this phenomenon using different configurations of electrodialysis and observed that in overlimiting conditions, some of the H
+ ions at the CEM may have migrated from the AEM as a result of water dissociation at this membrane. Hence, the results presented in
Figure 8, and those that will be shown, suggest that intense water dissociation occurred on the surface of the AEM in the overlimiting condition. It is well-known that water dissociation occurs mainly at anion-exchange membranes, due to their higher catalytic activity with respect to this phenomenon [
45,
46]. During the intense migration of hydroxyl ions through the anion-exchange membrane, protons may have accumulated on its cathodic side, leading to a pH decrease. This would have caused the reaction of insoluble species, such as CuO and ZnO, with protons, which would have led to the formation of Cu
2+ and Zn
2+ (Equations (3) and (4)). As shown in
Figure 4, at a pH lower than approximately 8.3 and 7, there is no ZnO and CuO, respectively, in the working solution. Considering the very dynamic behavior of electrodialysis in relation to the concentration and pH of the diluted solution, especially on the membrane surface, the reactions present in Equations (5) to (8) may also have taken place, which also form Cu
2+ and Zn
2+ ions. The values of the equilibrium constant at 25 °C for the equations are from references [
47,
48], except for Equation (5) and Equation (7). For Equation (5),
log K was calculated by combining the values from Equation (6) and Equation (9), whereas for Equation (7),
log K was calculated by combining Equation (8) and Equation (10). The reactions of the hydroxides of copper and zinc with protons are also shown in Equation (11) and Equation (12) [
48]. Similar results regarding the decrease in the occurrence of fouling on the AEM-diluate side due to water dissociation were obtained by Cifuentes-Araya et al. [
49].
The free metals Cu
2+ and Zn
2+ may then have migrated from the AEM to the CEM as a result of the intense electric field and electroconvection, which would have allowed their transport to the concentrate compartment through the cation-exchange membrane. As presented in
Table 3, the
i applied to the overlimiting test was 160% of the
ilim of the CEM, which means that the attraction of cations towards this membrane was very intense. This also explains the current–voltage curve presented in
Figure 5 for the CEM, since the resistance of its third region was very low due to the intense transport of cations. The reaction of the complexes of Cu-EDTA and Zn-EDTA with protons also occurred during water dissociation, which led to an increase of EDTA transfer through the anion-exchange membrane, mainly during the third and fourth cycles (
Figure 8).
| | (3) |
| | (4) |
| | (5) |
| | (6) |
| | (7) |
| | (8) |
| | (9) |
| | (10) |
| | (11) |
| | (12) |
Finally, it is known that in the case of CEMs, water dissociation is enhanced due to the protonation-deprotonation reactions of metallic precipitates, such as copper and zinc hydroxides and oxides. The general water dissociation reaction involving metal ions was formulated by Ganych et al. [
50], and it can be seen in Equations (13) and (14). For AEM, the formation of metal complexes can also catalyze the water dissociation, since they participate as active sites in the protonation-deprotonation reactions [
51]. Hence, the presence of insoluble species and metal complexes may also have favored water dissociation at both membranes facing the diluted solution.
The suggestion of the occurrence of intense water dissociation is also in agreement with the recent work carried out by Barros et al. [
23]; in our previous work, we verified, by chronopotentiometry, that an insoluble species was formed at the AEM surface. Oscillations typical of fouling/scaling by insoluble species were observed in the chronopotentiograms, besides the absence of the third region in the current–voltage curve for the solution with the same composition evaluated herein, but with pH = 10.
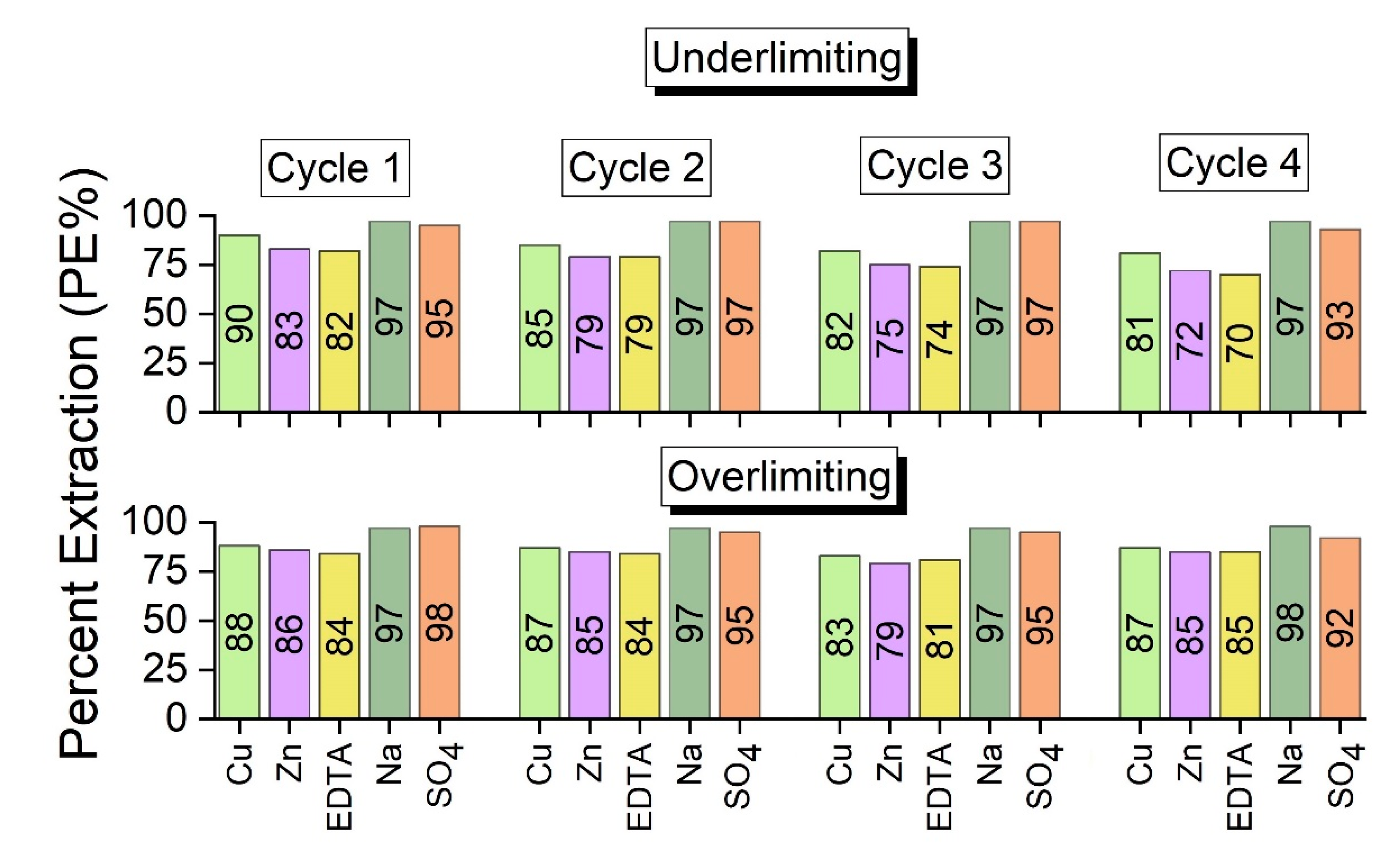
With the data from the diluted solutions from
Table 5, the percent extractions (PE%) of copper, zinc, EDTA, sodium and sulfate were calculated. As verified in
Figure 9, in general, the values of percent extraction of the species are relatively close in both experiments, except for Zn in cycle 2; EDTA in cycle 3; and Cu, Zn and EDTA in cycle 4.
The percent extraction was calculated as a function of the concentration of the species in the dilute compartment after each cycle in relation to its initial concentration. Therefore, similar PE% values for Cu and Zn were obtained in both experiments because in the underlimiting test, some species were present in the solid state and were not quantified in the chemical analyses, whereas in the overlimiting experiment, these species were transported to the concentrate compartment due to water dissociation. For EDTA, the complex dissociation occurred more intensively during the third and fourth cycles, which explains the highest values of PE%. These results are in accordance with the results for percent concentration already shown and will be confirmed by a mass balance. For Na
+ and SO
42− species, differences in the PE% were not verified by the experiments, since they were already present in the free form (
Table 2). Hence, they were not strongly influenced by the water dissociation phenomenon.
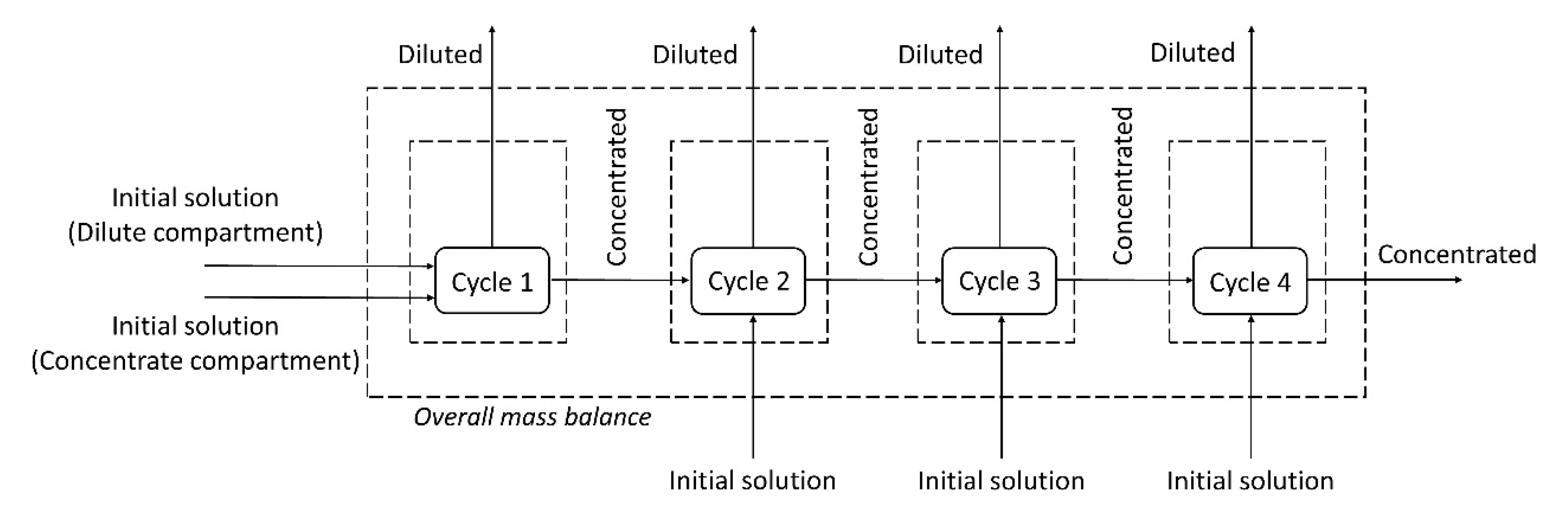
3.2.3. Mass Balance
A mass balance of each species (copper, zinc and EDTA) was performed using the molar flow rates of the species in each cycle. The mass balance for the system was also performed considering all inputs and outputs of the four cycles (overall mass balance), as shown in
Figure 10.
The results of the mass balance are presented in
Table 6, which shows the percentage of the species leaving each control volume (diluted and concentrated solutions) in relation to the species entering it. The values slightly above 100% in the mass balance of some species (~3%) are due to the deviations in the chemical analysis. Note that in the underlimiting test, only 91% and 93% of the Cu and Zn, respectively, of the initial solution were present in the final solutions (dilute and concentrate compartments). In turn, the overall mass balance of metals in the overlimiting test was 100%.
As in the underlimiting experiment, water dissociation (and the reaction of protons with insoluble species) did not occur; part of the metals remained in the solid state and were not quantified in the chemical analysis, which explains why their values were below 100%. These results support our suggestion that the overlimiting experiment led to the reaction of protons with insoluble species of copper and zinc present in the working solution, which allowed the metals passage to the concentrate compartment.
3.3. Chronopotentiometric Measurements after the ED Tests
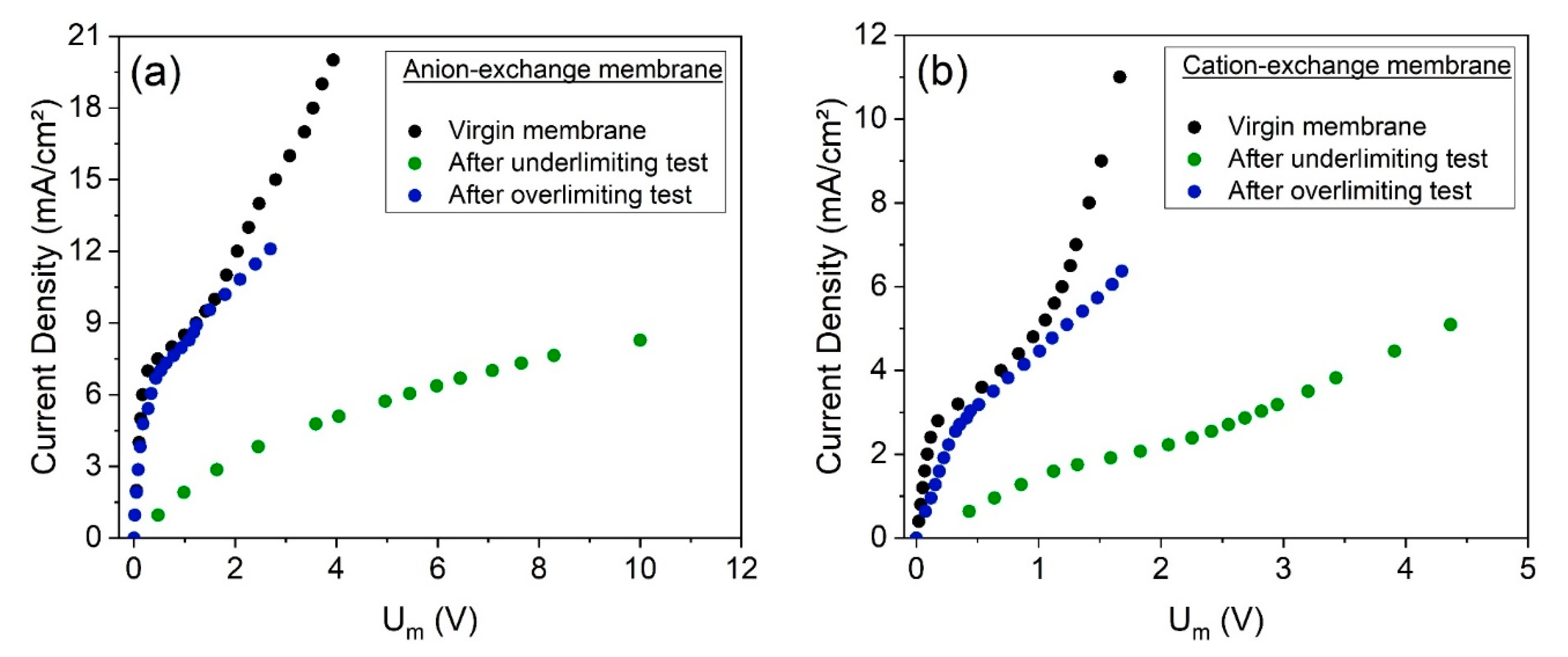
The cation- and anion-exchange membranes were forwarded for chronopotentiometric measurements after both electrodialysis tests, for evaluating their transport properties, such as their limiting current density and ohmic resistance. The virgin membranes, not exposed to electrodialysis, were also evaluated.
Figure 11 presents the current–voltage curves obtained for the AEMs (
Figure 11a) and CEMs (
Figure 11b) by chronopotentiometry, whereas
Table 7 presents the obtained values of limiting current density and ohmic resistance. The errors between the results from the duplicate curves, which are lower than 4%, are also presented in
Table 7.
As observed, the behaviors of the CVCs and the properties obtained for the membranes from the underlimiting test are very distant from those for the virgin membranes. On the other hand, the CVCs of the membranes used in the overlimiting test are very close to those of the virgin membranes. Hence, the overlimiting operation did not cause remarkable modifications in the limiting current density or in the ohmic resistance.
The CVCs of the membranes used in the overlimiting test suggest the lower tendency of fouling to occur when operating in this condition, which may be explained by the intense electroconvective vortices. Bukhovets et al. [
52] proposed the “washing out” effect of electroconvection on organic fouling. According to the authors, the water dissociation phenomenon at the AEM enhances the flux of hydroxyl ions and, together with electroosmotic convection and the effect of current exaltation, contributes to the “washing out” the species fouled. Hence, considering the differences of the current–voltage curves of the CEMs and AEMs after each electrodialysis (
Figure 11) and the intense occurrence of water dissociation in the overlimiting test, it may be suggested that in this experiment, fouling/scaling occurrence was not verified in either membrane. Finally, although the “washing out” phenomenon is valid only for anion-exchange membranes, the results here show that the overlimiting operation also helps to mitigate scaling in cation-exchange membranes, as suggested by Mikhaylin et al. [
53], but with a lower intensity than for AEMs.
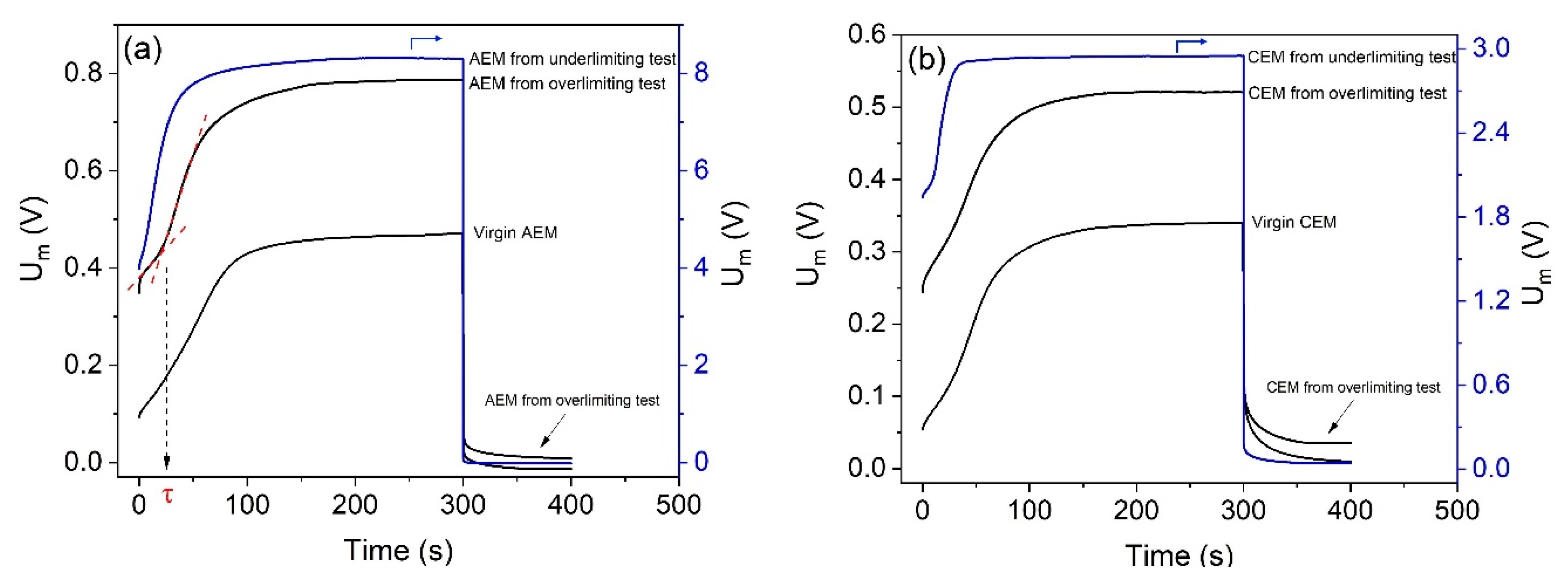
Figure 12 shows the chronopotentiograms constructed for the anion- (
Figure 12a) and cation-exchange membranes (
Figure 12b), both after electrodialysis in the overlimiting and underlimiting tests, and virgin. In
Figure 12, the current density applied to the AEMs was 7.6 mA/cm
2, whereas for the CEMs, it was 3.2 mA/cm
2. The potential drop presented is the total one (measured), in order to show the additional influence of electrodialysis on the ohmic resistance, although in some comparisons of different membranes, some authors represent the “reduced potential drop” by excluding the ohmic potential drop [
54]. All curves obtained were typical of monopolar membranes, without the formation of additional inflexion points during the concentration polarization or the relaxation of the system.
For the anion-exchange membranes (
Figure 12a), the initial potential drop of the virgin one was close to 0.1V, whereas for the membranes used in electrodialysis, higher potential drop values were obtained, especially for the AEM from the underlimiting test. This occurred mainly due to the higher ohmic resistance after the electrodialysis [
55]. The final values of the potential drop in the steady-state condition also showed very different values after each electrodialysis current mode. Note that for the anion-exchange membrane used in the overlimiting test, the final potential drop is closer to that for the virgin membrane if compared to the AEM from the underlimiting test. This occurred due to the greater membrane resistance after the underlimiting test. For the cation-exchange membranes (
Figure 12b), similar behaviors of the AEMs were obtained: for the virgin CEM, the initial potential drop was close to 0.05V, whereas for the membranes used in electrodialysis, higher potential drop values were obtained.
Differences between transition times (τ) were also verified, which correspond to the moment when the concentration of electrolyte at the membrane surface is practically zero and the potential drop tends to infinity. This can be experimentally determined by the intersection of the tangential lines of the first and second stages of the chronopotentiograms [
35], as represented in
Figure 12a. For
i = 7.6 mA/cm
2, the transition time obtained for the virgin AEM was approximately 28 s, whereas for the membranes used in the overlimiting and underlimiting tests, it was 24 s and 6 s, respectively. Hence, the time required for the depletion of counterions in the diffusion boundary layer in the underlimiting test is considerably lower, which means the concentration polarization occurs earlier. This may be explained by the fouling occurrence and the reduction of the fraction of conductive area in the underlimiting test, as verified in the CVC evaluation. For the cation-exchange membranes, transition times also showed remarkable differences between the experiments. For
i = 3.2 mA/cm
2, the transition time obtained for the virgin CEM was 29 s, whereas for the membrane after the overlimiting and underlimiting tests, it was 27 s and 11 s, respectively. As verified for the anion-exchange membrane, lower τ values for the CEM after the underlimiting test are due to the occurrence of fouling/scaling. In
Figure 12, the potential drop values during the relaxation of the system, i.e., when the current was switched off, showed the following order: membranes from the underlimiting test > membranes from the overlimiting test > virgin membranes. The highest potential drop values for the membranes from the underlimiting test are also due to the presence of fouled species.
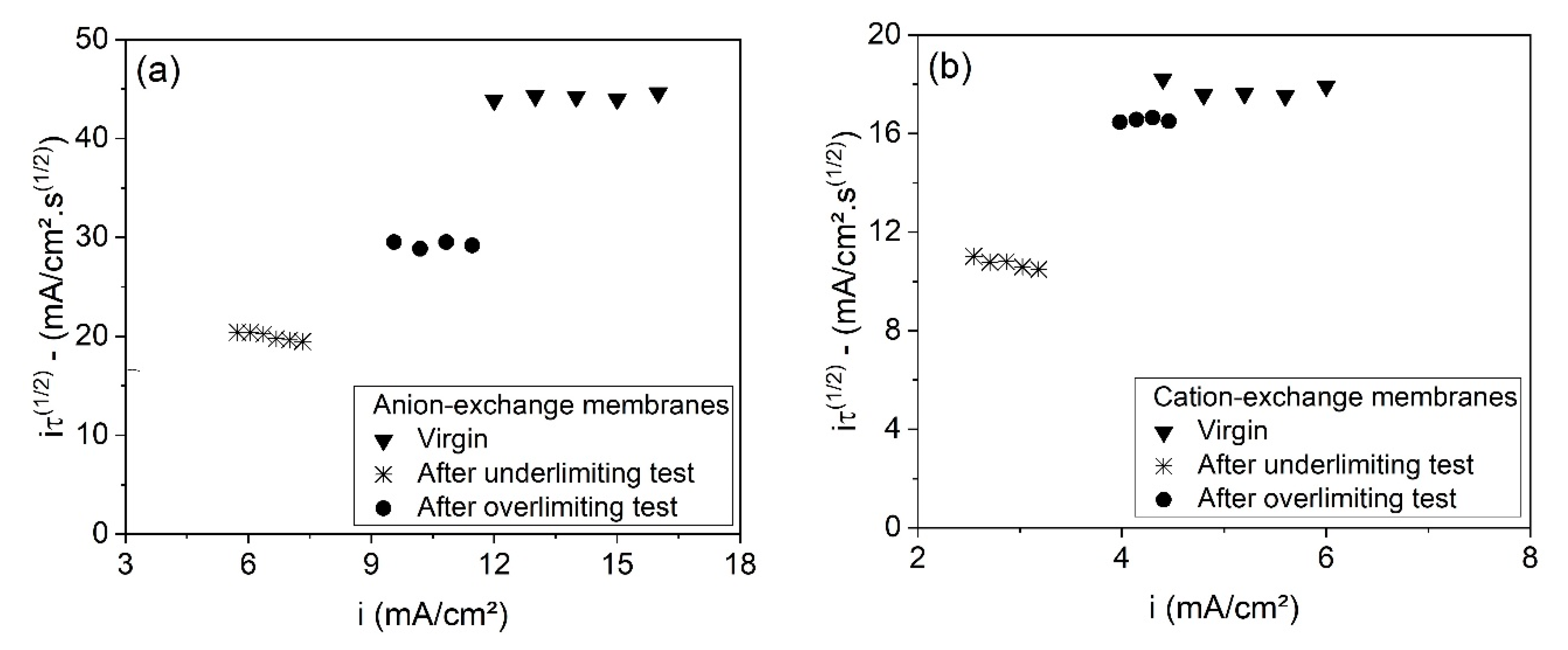
The relationship between transition time (τ) and fouling/scaling may also be evaluated by using the modified Sand’s equation [
56] (Equation (15)), where ε is the fraction of conductive area,
D is the electrolyte diffusion coefficient,
C0 is the electrolyte concentration at
t = 0 s,
z is the counterion charge,
F is the Faraday constant,
i is the applied current density, and
and
are the counterion transport numbers in the membrane and in the solution, respectively. This equation shows that the
values are constant, independent of current density, at a given concentration of electrolytes, and it allows the determination of the fraction of conductive area.
Figure 13 shows the dependence of transition time on current density, represented in Sand’s coordinates for each membrane used in the electrodialysis tests, as well as for the virgin membranes. Here, the plotted transition times were those associated to current densities at least 1.5 times higher than the limiting current density of the membrane/electrolyte systems, as suggested by Mareev et al. [
57]. As can be seen, the
values of the anion- (
Figure 13a) and cation-exchange membranes (
Figure 13b) were fairly constant, independent of the current density, and showed the following order: virgin membranes > membranes from the overlimiting test > membranes from the underlimiting test. This supports the previous discussion about the fraction of conductive area; membranes from the underlimiting test present the lowest ε values due to the occurrence of fouling/scaling. These results confirm the lower tendency of fouling to occur at both membranes when operating in the overlimiting condition. Finally, the greater heterogeneity (lower ε) of the membrane after the underlimiting test may also have favored the “funnel effect” [
58], which occurs due to the accumulation of current lines within the well conducting areas of the membrane surface. This also leads to the reduction of transition time, since the potential drop increases more rapidly [
59].