Particle Track and Trace during Membrane Filtration by Direct Observation with a High Speed Camera
Abstract
:1. Introduction
- FG is the gravitational force of particles transported towards the membrane by permeation,
- FD, a drag force of particles being dragged across the membrane by the crossflow,
- FF, a frictional force of particles moving along the membrane acting against the crossflow, hence slowing down the particles as the move across the membrane, and
- FL, lifting force, acting opposite to the permeate flow as pressure increase when the water velocity decrease near the surface.
2. Materials and Methods
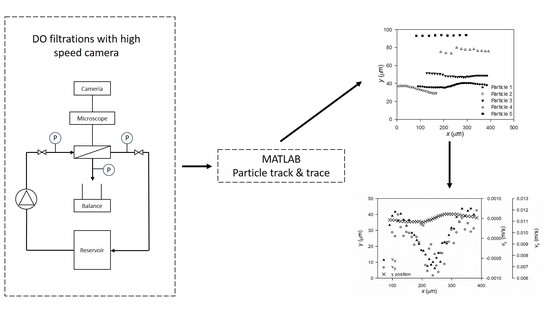
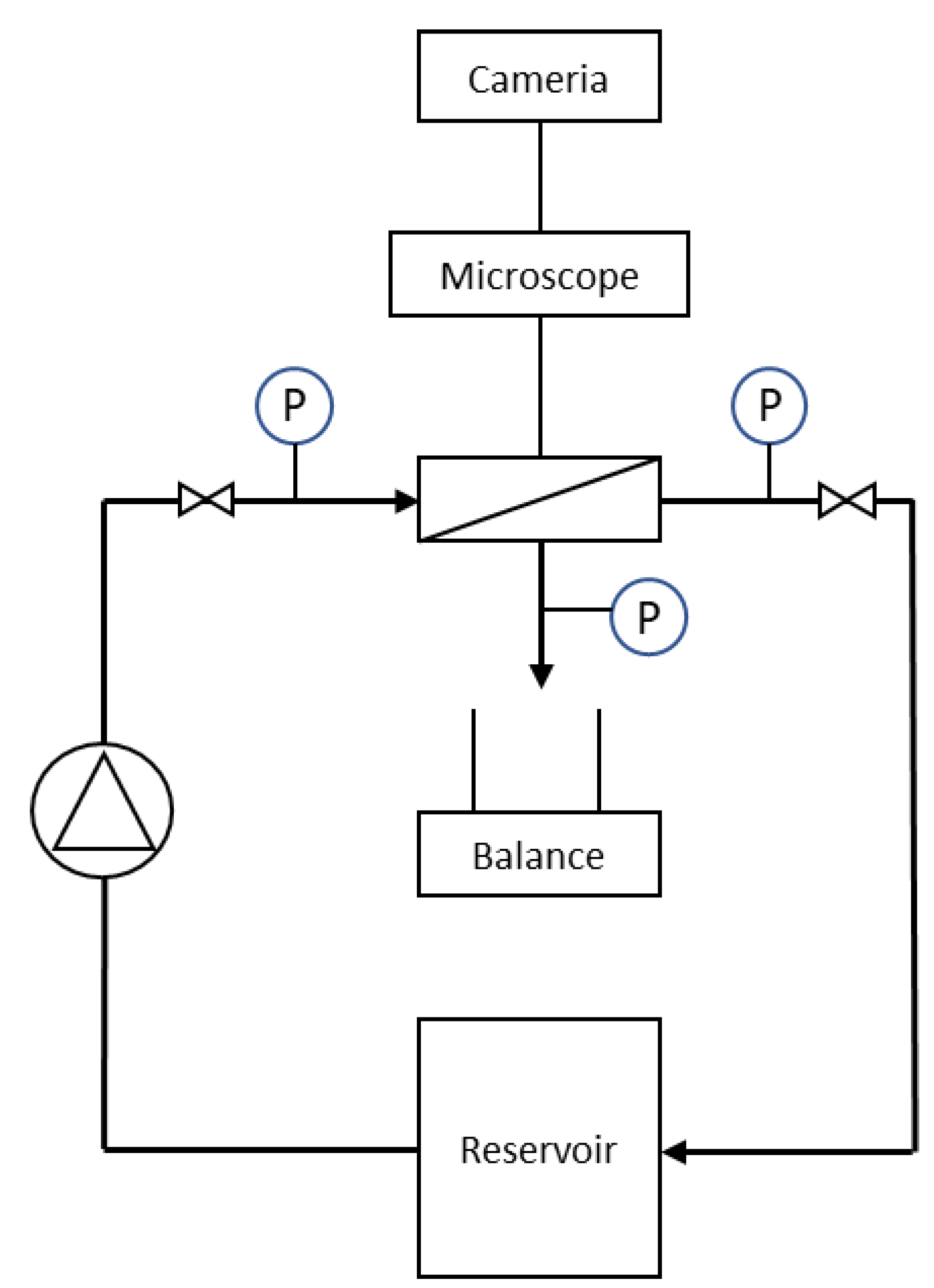
2.1. Direct Observation Setup
2.2. Filtrations
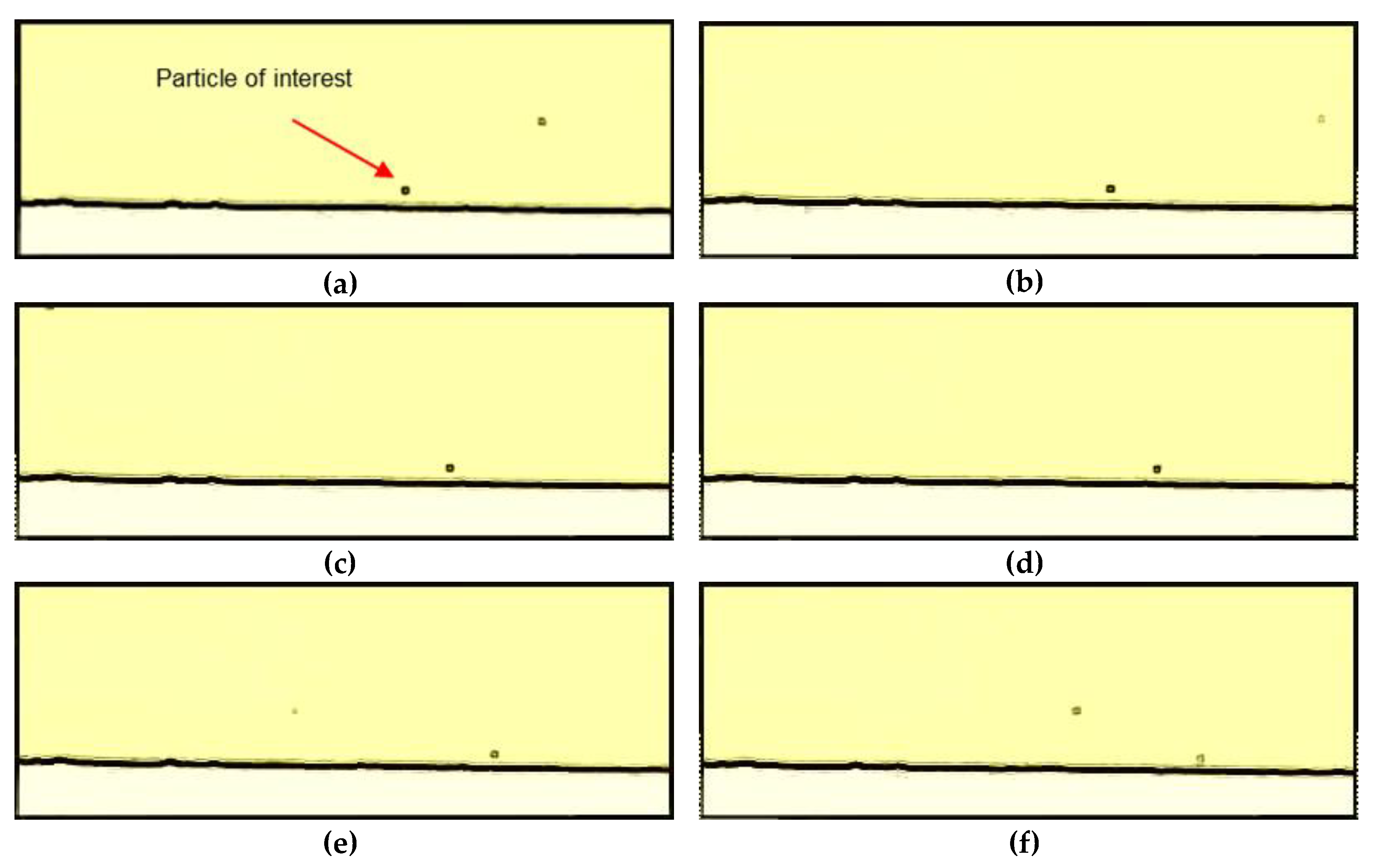
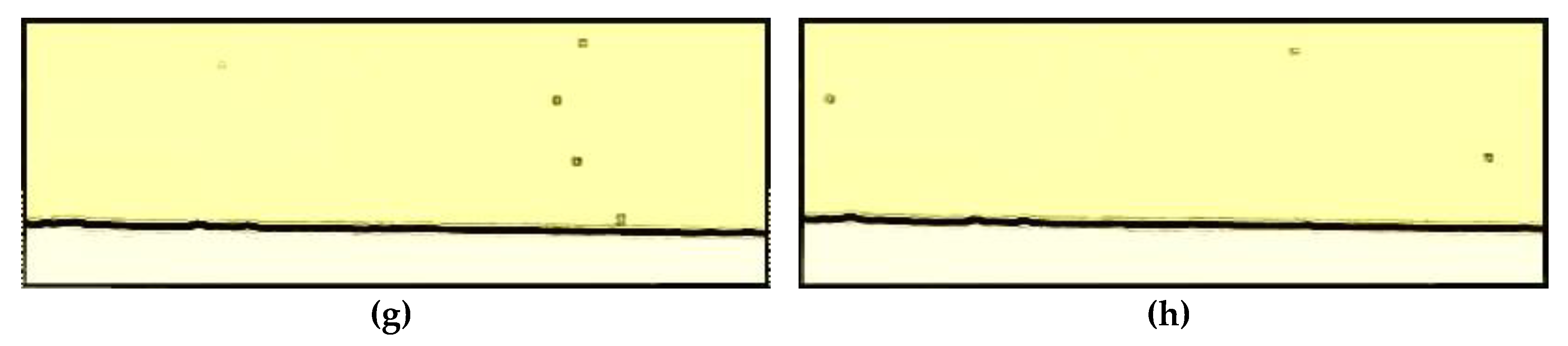
2.3. Microscopy and Video Analysis
2.4. Computational Fluid Dynamics Simulation
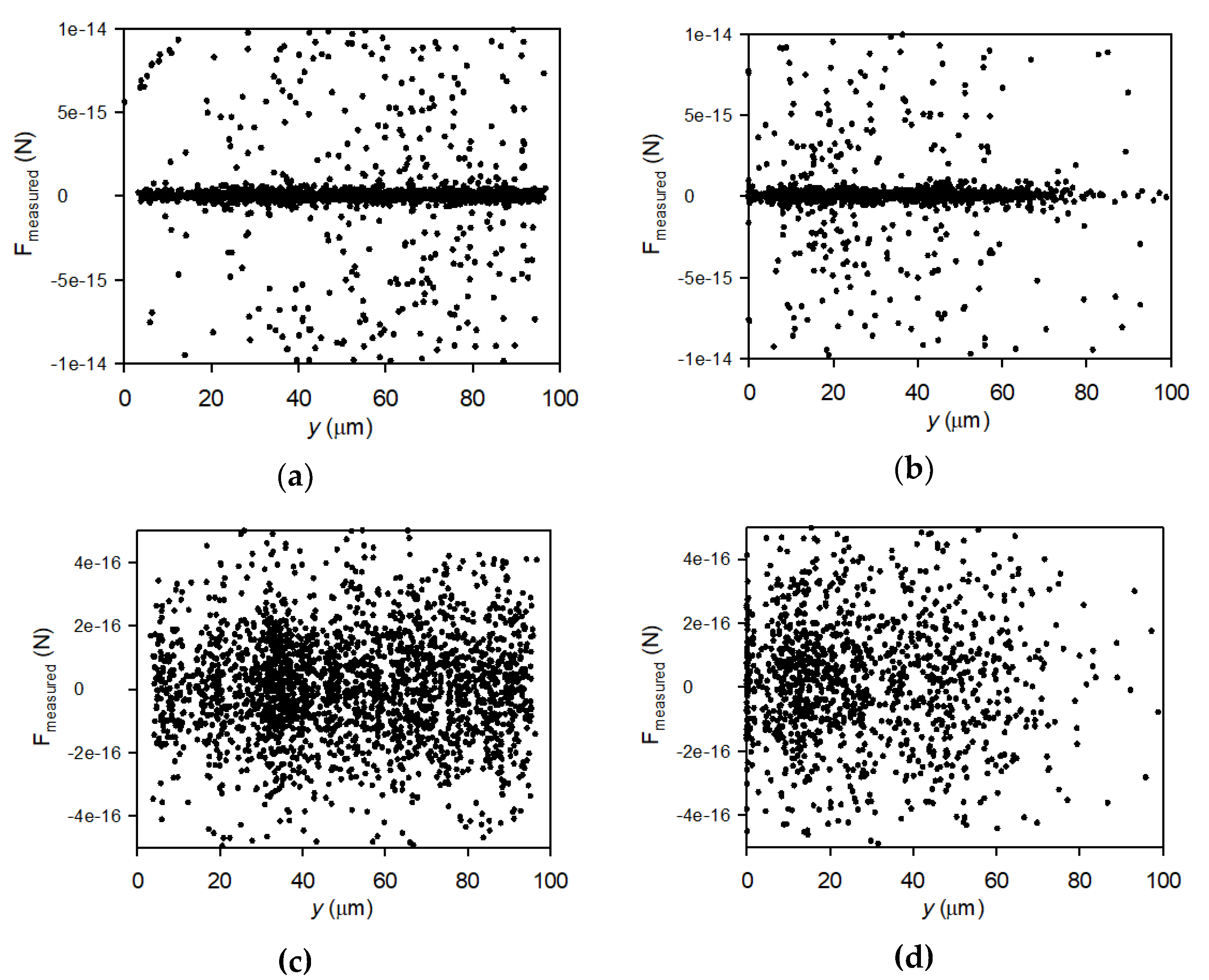
3. Results
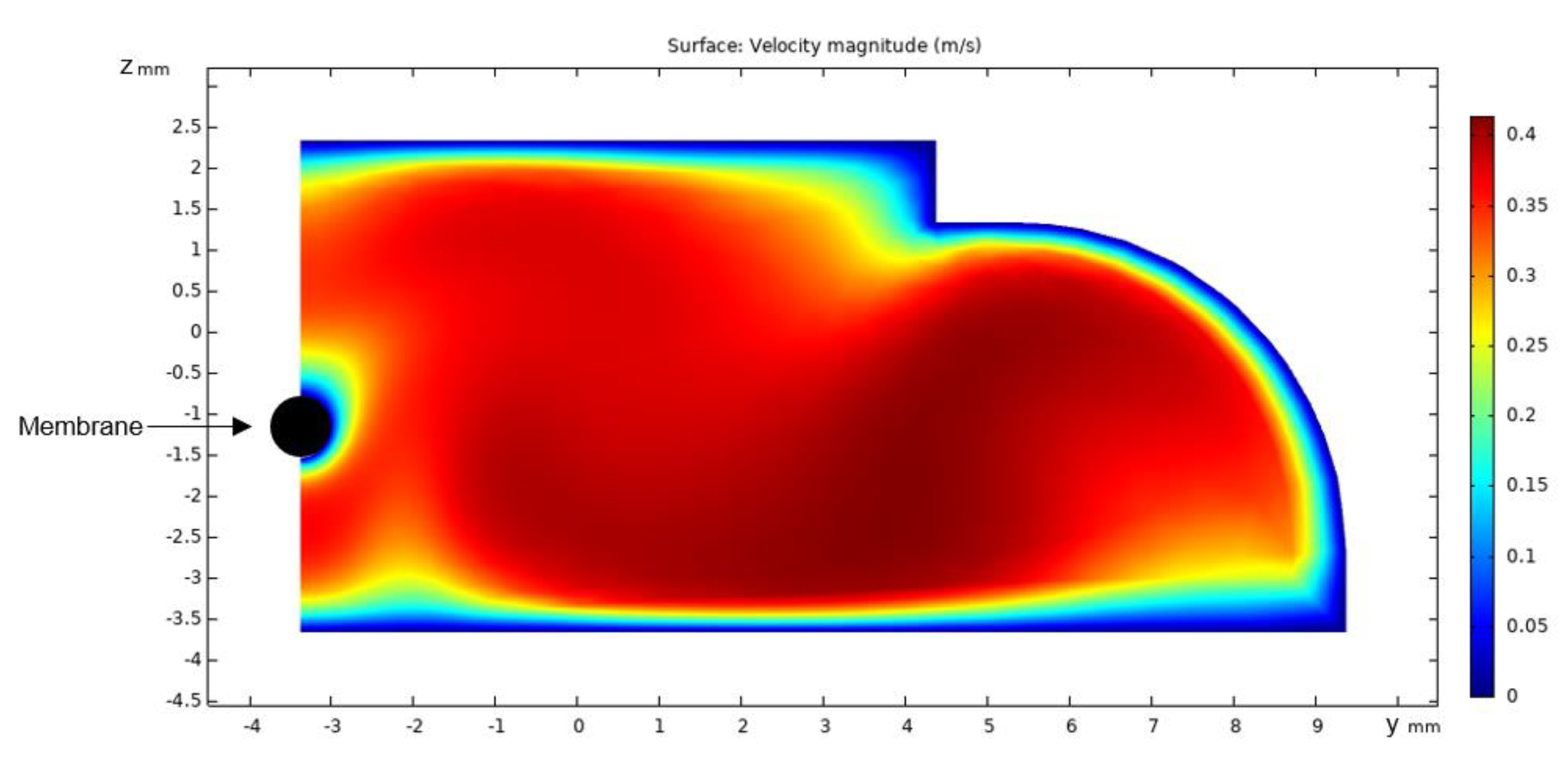
3.1. Flow Simulations
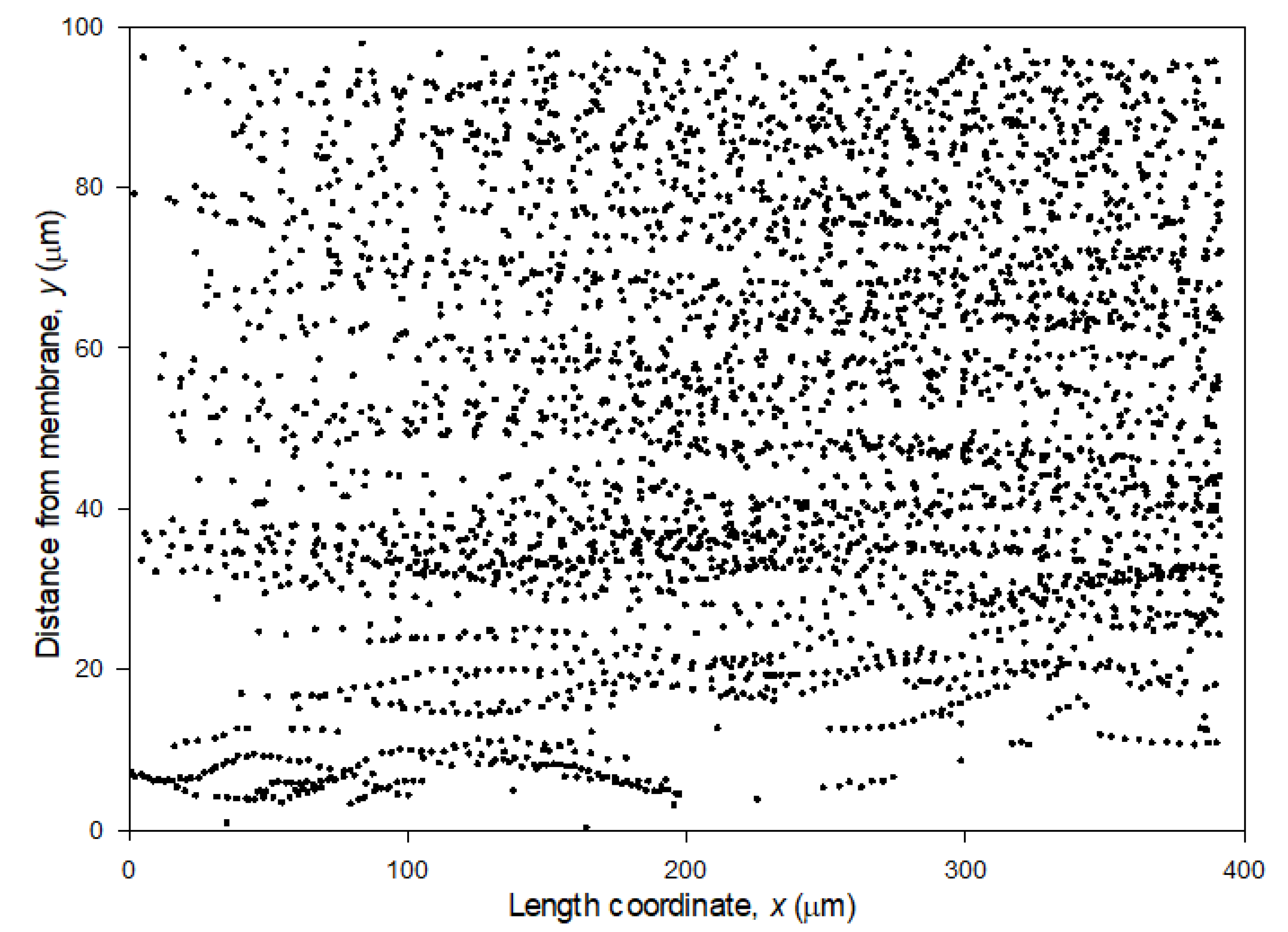
3.2. Particle Track and Trace
3.3. Longitudinal Velocity Profiles
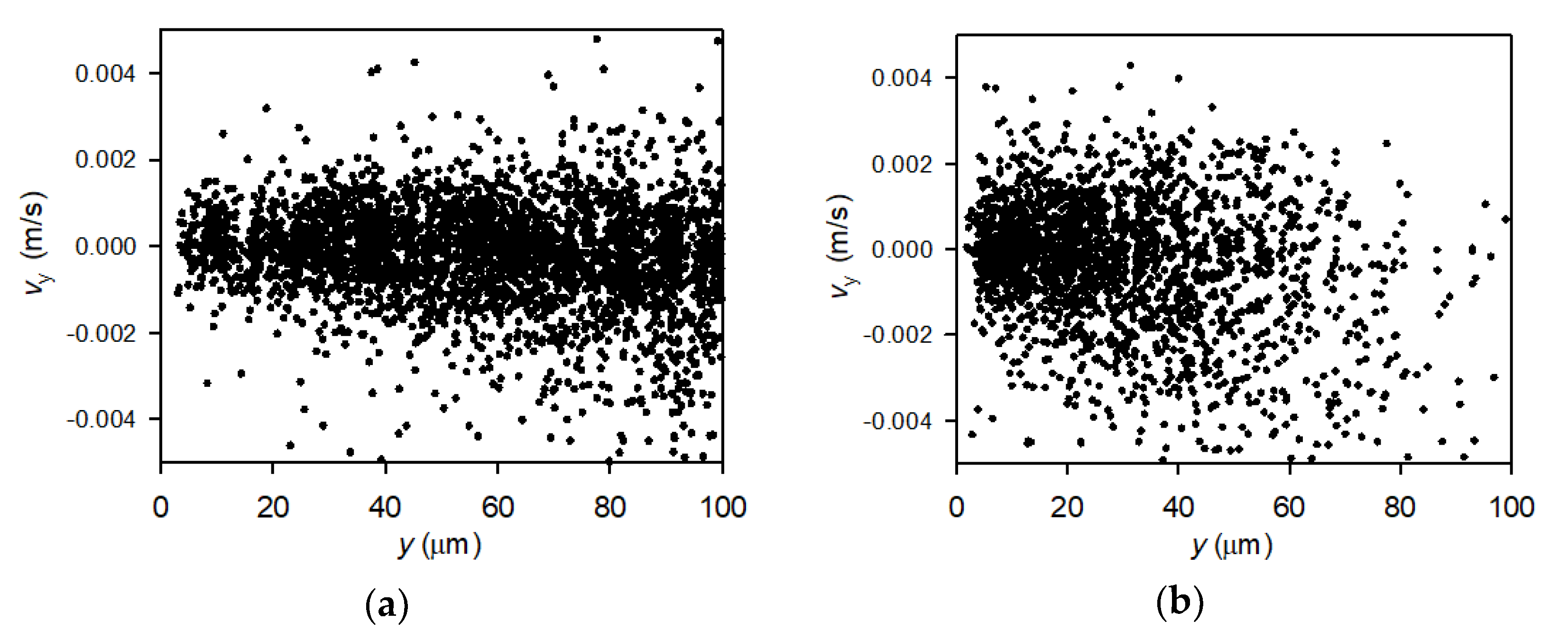
3.4. Perpendicular Velocity Profiles
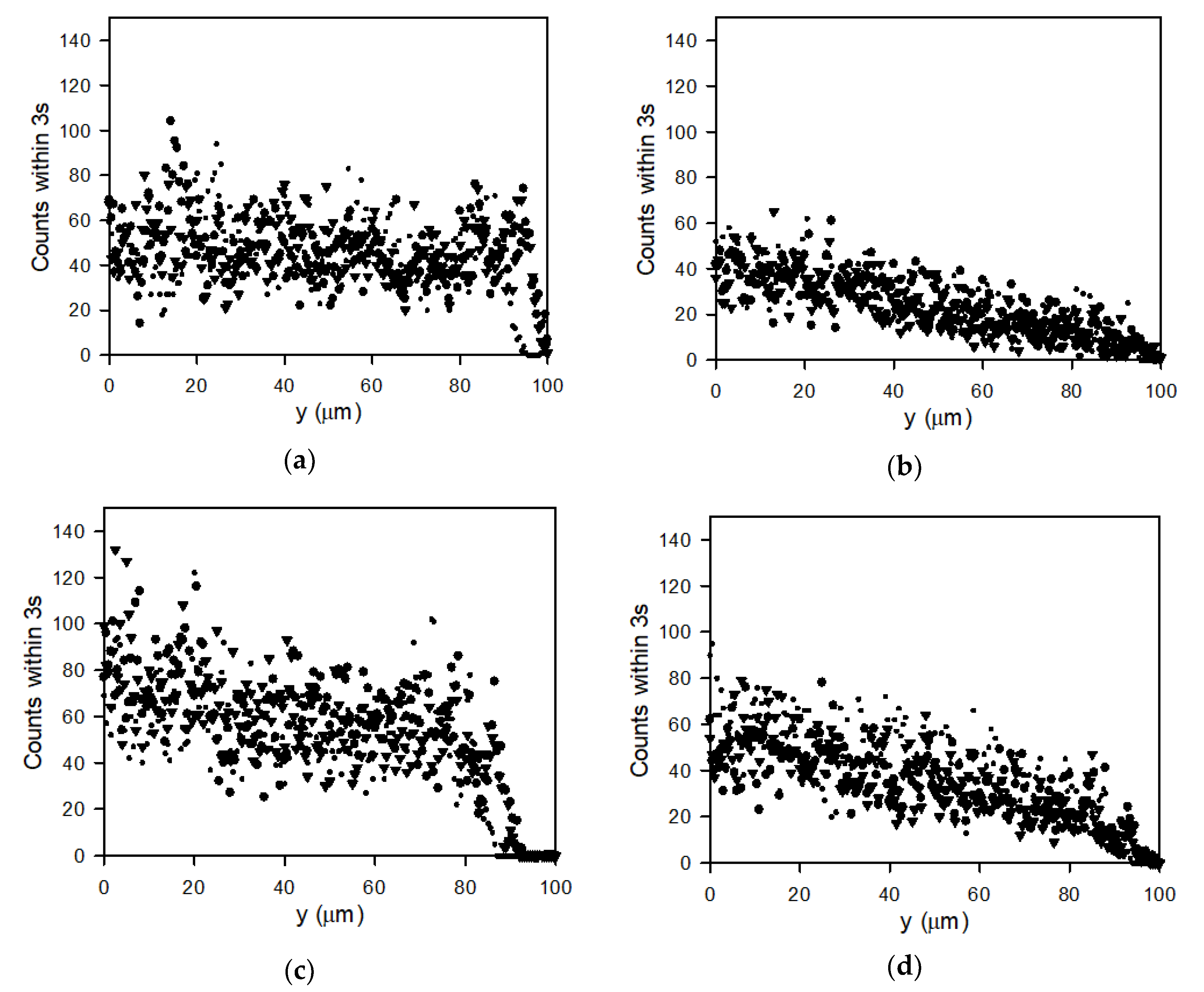
3.5. Particle Count Profiles
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
MATLAB Particle Tracking
- img = img(:, :, 3);
- img = ~imbinarize(img, ‘adaptive’,’Sensitivity’,0.7);
- img = imdilate(img, strel(‘disk’, 1));
- img = imopen(img, strel(‘disk’, 1));
- p = regionprops(img, {‘Centroid’, ‘Area’});
- ind = [p.Area] > minsize;
- cent = reshape([p.Centroid], 2, length(ind));
- cent = cent(:, ind);
MATLAB Particle Tracing
- L = linspace(0,2*pi,6); –sets up graph space
- xv = ParPos(frame).xy(1,particlenumber) – 30 + cos(L)*50’; -x part of polar function
- yv = ParPos(frame).xy(2,particlenumber) + 2 + sin(L)*5’; -y part of polar function
- Xq = ParPos(frame+1).xy(1,:); –x position for all particles in the next frame
- yq = ParPos(frame+1).xy(2,:); –y position for all particles in the next frame
- [in] = inpolygon(xq,yq,xv,yv); –Here the particles are tested if they are inside the polygon
- for lengthin=1:length(in) –Makes a loop that goes through the length of “in”
- lengthins=lengthin;
- if in(lengthin)==true –Goes through the “in vector and checks for points in the polygon
- if ismember(ParPos(frame).xy(1,particlenumber),tracer(:,:))==true -Tests if original particle has been seen before
- [row,col]=find(tracer==ParPos(frame).xy(1,particlenumber));
- kolonne=col;
- tracer(row(end),col(end)+1)=ParPos(frame+1).xy(1,lengthins);
- tracer(row(end)+1,col(end)+1)=ParPos(frame+1).xy(2,lengthins);
- else -If they haven’t been found before both particles are saved here
- tracer(tracenumber*2-1,1)=ParPos(frame).xy(1,particlenumber);
- tracer(tracenumber*2,1)=ParPos(frame).xy(2,particlenumber);
- tracer(tracenumber*2-1,2)=ParPos(frame+1).xy(1,lengthins);
- tracer(tracenumber*2,2)=ParPos(frame+1).xy(2,lengthins);
- tracenumber=tracenumber+1;
- end
- end
- end
MATLAB Scripts and Their Functions
- videotracking.m: Tracks particles in converted videos. Input: Filtered video file directory. Output: Particle positions “ParPos”.
- tracing.m: Traces particle positions. Input: particle positions “ParPos” from videotracking.m. Output: Traced particle data “tracer”.
- Filterfunction: Filters tracked particles. Input: “tracer”. Output: “tracer”.
- Velocities.m: Calculates velocities along and towards the membrane. Input: “tracer”. Output: “Velocities”.
- PlotParticles.m: Plots traced particles and saves their position in Excel file.. Input: “tracer”. Output: “ALLPAR”, Excel file and Plot of particle positions.
- Plots.m: Generates plots of particle velocities and saves velocity data. Input: “tracer”. Output: Plots and Excel file.
Appendix B
References
- Guo, W.; Ngo, H.H.; Li, J. A mini-review on membrane fouling. Bioresour. Technol. 2012, 122, 27–34. [Google Scholar] [CrossRef] [PubMed]
- Hoek, E.M.V.; Agarwal, G.K. Extended DLVO interactions between spherical particles and rough surfaces. J. Colloid Interface Sci. 2006, 298, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Tiller, F.M.; Kwon, J.H. Role of porosity in filtration: XIII. Behavior of highly compactible cakes. AIChE J. 1998, 44, 2159–2167. [Google Scholar] [CrossRef]
- Altmann, J.; Ripperger, S. Particle deposition and layer formation at the crossflow microfiltration. J. Memb. Sci. 1997, 124, 119–128. [Google Scholar] [CrossRef]
- Li, J.; Sanderson, R.D.; Jacobs, E.P. Non-invasive visualization of the fouling of microfiltration membranes by ultrasonic time-domain reflectometry. J. Memb. Sci. 2002, 201, 17–29. [Google Scholar] [CrossRef]
- Hwang, B.K.; Lee, C.H.; Chang, I.S.; Drews, A.; Field, R. Membrane bioreactor: TMP rise and characterization of bio-cake structure using CLSM-image analysis. J. Memb. Sci. 2012, 419–420, 33–41. [Google Scholar] [CrossRef]
- Rudolph, G.; Virtanen, T.; Güell, C.; Lipnizki, F.; Kallioinen, M. A review of in situ real-time monitoring techniques for membrane fouling in the biotechnology, biorefinery and food sectors. J. Memb. Sci. 2019, 588, 117221. [Google Scholar] [CrossRef]
- Kujundzic, E.; Greenberg, A.R.; Fong, R.; Moore, B.; Kujundzic, D.; Hernandez, M. Biofouling potential of industrial fermentation broth components during microfiltration. J. Memb. Sci. 2010, 349, 44–55. [Google Scholar] [CrossRef]
- Jørgensen, M.K.; Kujundzic, E.; Greenberg, A.R. Effect of pressure on fouling of microfiltration membranes by activated sludge. Desalin. Water Treat. 2016, 57, 6159–6171. [Google Scholar] [CrossRef]
- Loulergue, P.; André, C.; Laux, D.; Ferrandis, J.-Y.; Guigui, C.; Cabassud, C. In-situ characterization of fouling layers: Which tool for which measurement? Desalin. Water Treat. 2011, 34, 156–162. [Google Scholar] [CrossRef]
- Lewis, W.J.T.; Agg, A.; Clarke, A.; Mattsson, T.; Chew, Y.M.J.; Bird, M.R. Development of an automated, advanced fluid dynamic gauge for cake fouling studies in cross-flow filtrations. Sensors Actuators A. Phys. 2016, 238, 282–296. [Google Scholar] [CrossRef]
- Zhou, M.; Mattsson, T. Effect of crossflow regime on the deposit and cohesive strength of membrane surface fouling. Food Bioprod. Process. 2019, 115, 185–193. [Google Scholar] [CrossRef]
- Ye, Y.; Chen, V.; Le-Clech, P. Evolution of fouling deposition and removal on hollow fibre membrane during filtration with periodical backwash. Desalination 2011, 283, 198–205. [Google Scholar] [CrossRef]
- Marselina, Y.; Lifia Le-Clech, P.; Stuetz, R.M.; Chen, V. Characterisation of membrane fouling deposition and removal by direct observation technique. J. Memb. Sci. 2009, 341, 163–171. [Google Scholar] [CrossRef]
- Li, H.; Fane, A.G.; Coster, H.G.L.; Vigneswaran, S. An assessment of depolarisation models of crossflow microfiltration by direct observation through the membrane. J. Memb. Sci. 2000, 172, 135–147. [Google Scholar] [CrossRef]
- Li, H.; Fane, A.G.; Coster, H.G.L.; Vigneswaran, S. Direct observation of particle deposition on the membrane surface during crossflow microfiltration. J. Memb. Sci. 1998, 149, 83–97. [Google Scholar] [CrossRef]
- Lorenzen, S.; Ye, Y.; Chen, V.; Christensen, M.L. Direct observation of fouling phenomena during cross-flow filtration: Influence of particle surface charge. J. Memb. Sci. 2016, 510, 546–558. [Google Scholar] [CrossRef]
- Christensen, M.L.; Niessen, W.; Sørensen, N.B.; Hansen, S.H.; Jørgensen, M.K.; Nielsen, P.H. Sludge fractionation as a method to study and predict fouling in MBR systems. Sep. Purif. Technol. 2018, 194, 329–337. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jørgensen, M.K.; Eriksen, K.B.; Christensen, M.L. Particle Track and Trace during Membrane Filtration by Direct Observation with a High Speed Camera. Membranes 2020, 10, 68. https://doi.org/10.3390/membranes10040068
Jørgensen MK, Eriksen KB, Christensen ML. Particle Track and Trace during Membrane Filtration by Direct Observation with a High Speed Camera. Membranes. 2020; 10(4):68. https://doi.org/10.3390/membranes10040068
Chicago/Turabian StyleJørgensen, Mads Koustrup, Kristian Boe Eriksen, and Morten Lykkegaard Christensen. 2020. "Particle Track and Trace during Membrane Filtration by Direct Observation with a High Speed Camera" Membranes 10, no. 4: 68. https://doi.org/10.3390/membranes10040068
APA StyleJørgensen, M. K., Eriksen, K. B., & Christensen, M. L. (2020). Particle Track and Trace during Membrane Filtration by Direct Observation with a High Speed Camera. Membranes, 10(4), 68. https://doi.org/10.3390/membranes10040068