Deep Cerebellar Transcranial Direct Current Stimulation of the Dentate Nucleus to Facilitate Standing Balance in Chronic Stroke Survivors—A Pilot Study
Abstract
1. Introduction
2. Materials and Methods
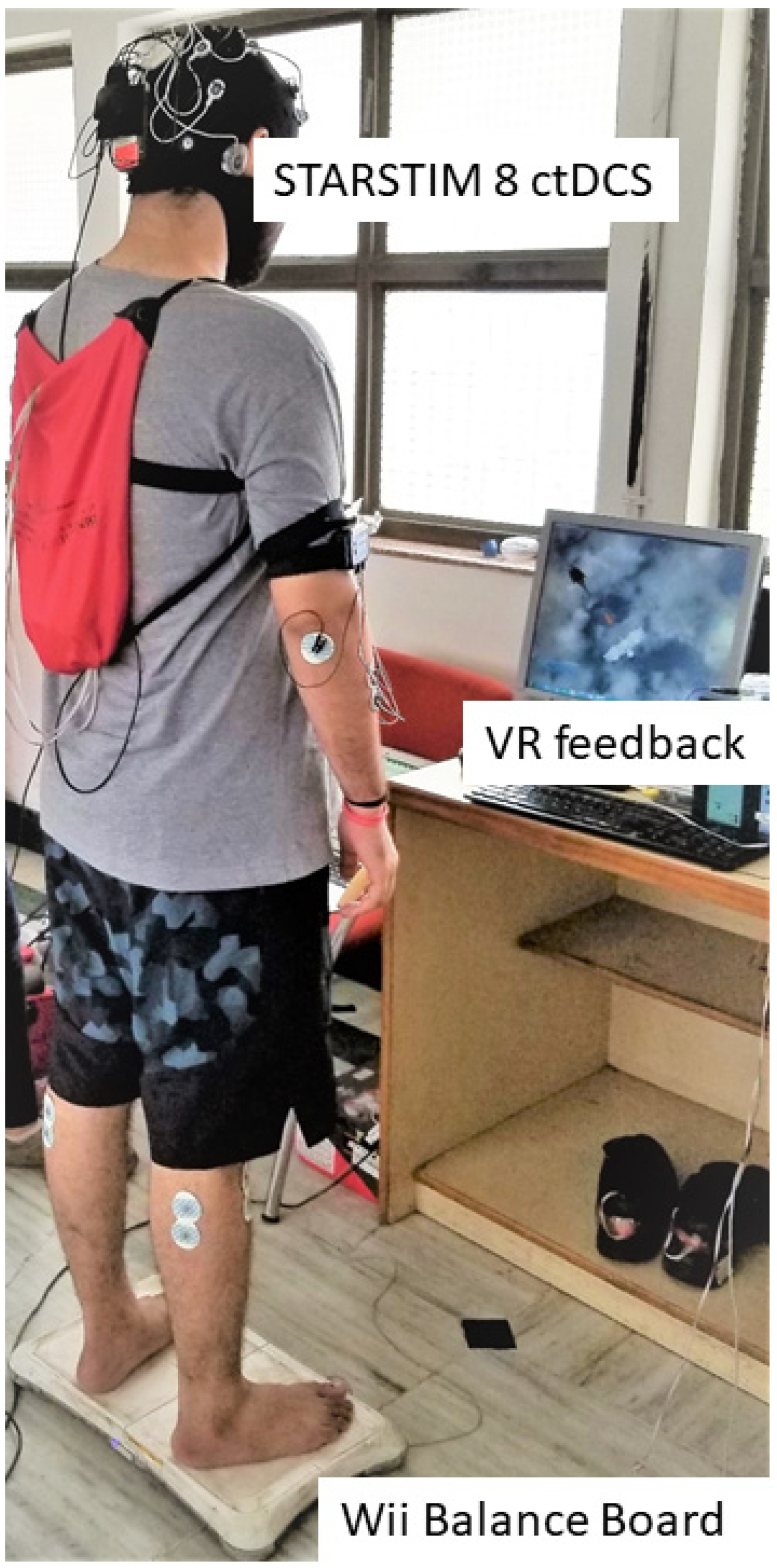
2.1. Experimental Setup and Study Design
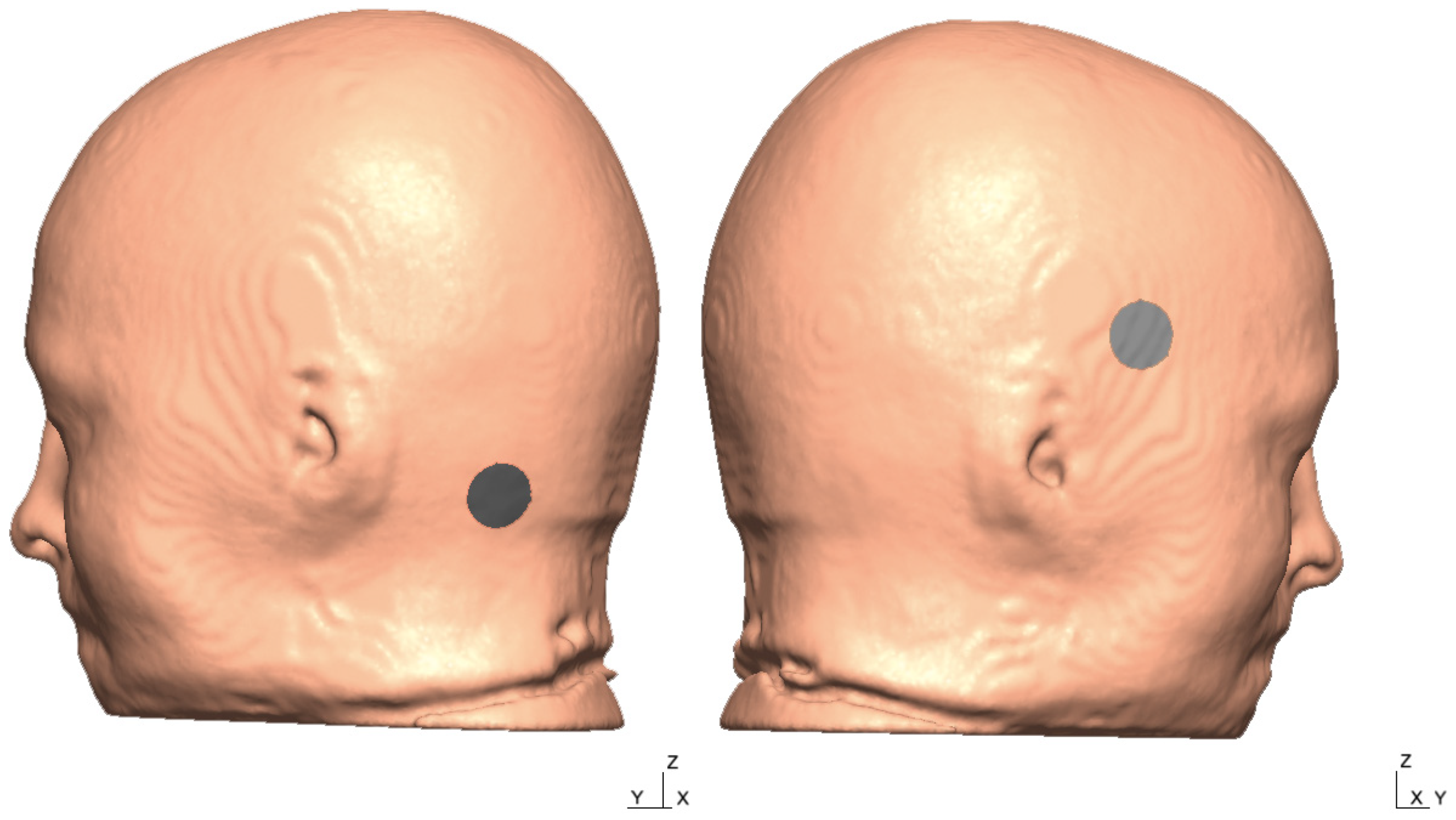
2.2. Data Acquisition and Head Modeling
2.3. Finite Element Analysis (FEA) for ctDCS Optimization Based on the MRI Template of 55 to 59 Years Old
2.3.1. Computational Modeling and Optimization Based on MRI Template of 55 to 59 Years Age-Group
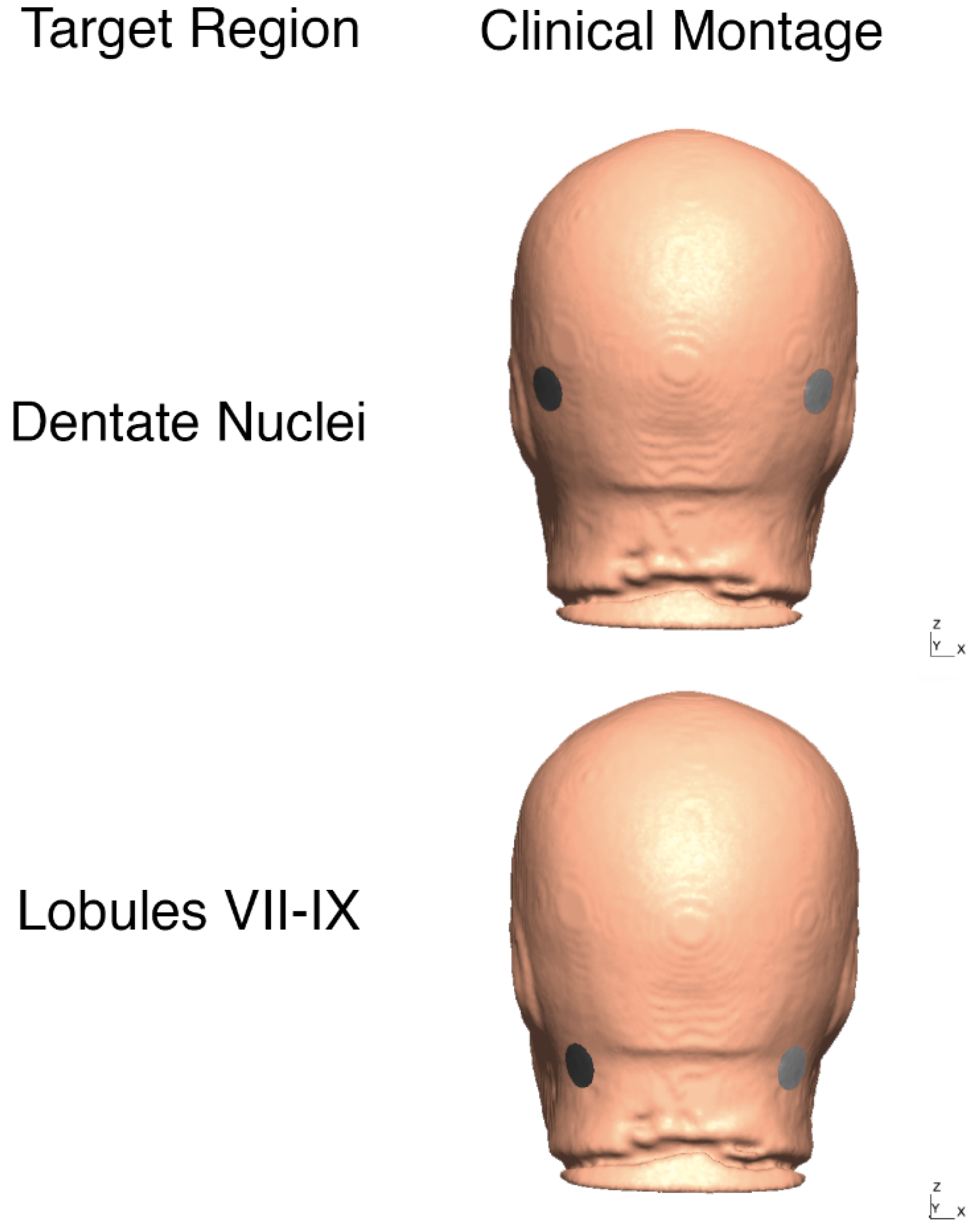
2.3.2. Cerebellar tDCS Optimization Using the Head Model for the Age Group of 55–59 Years
2.3.3. Computational Modeling for the Post-Stroke Subjects
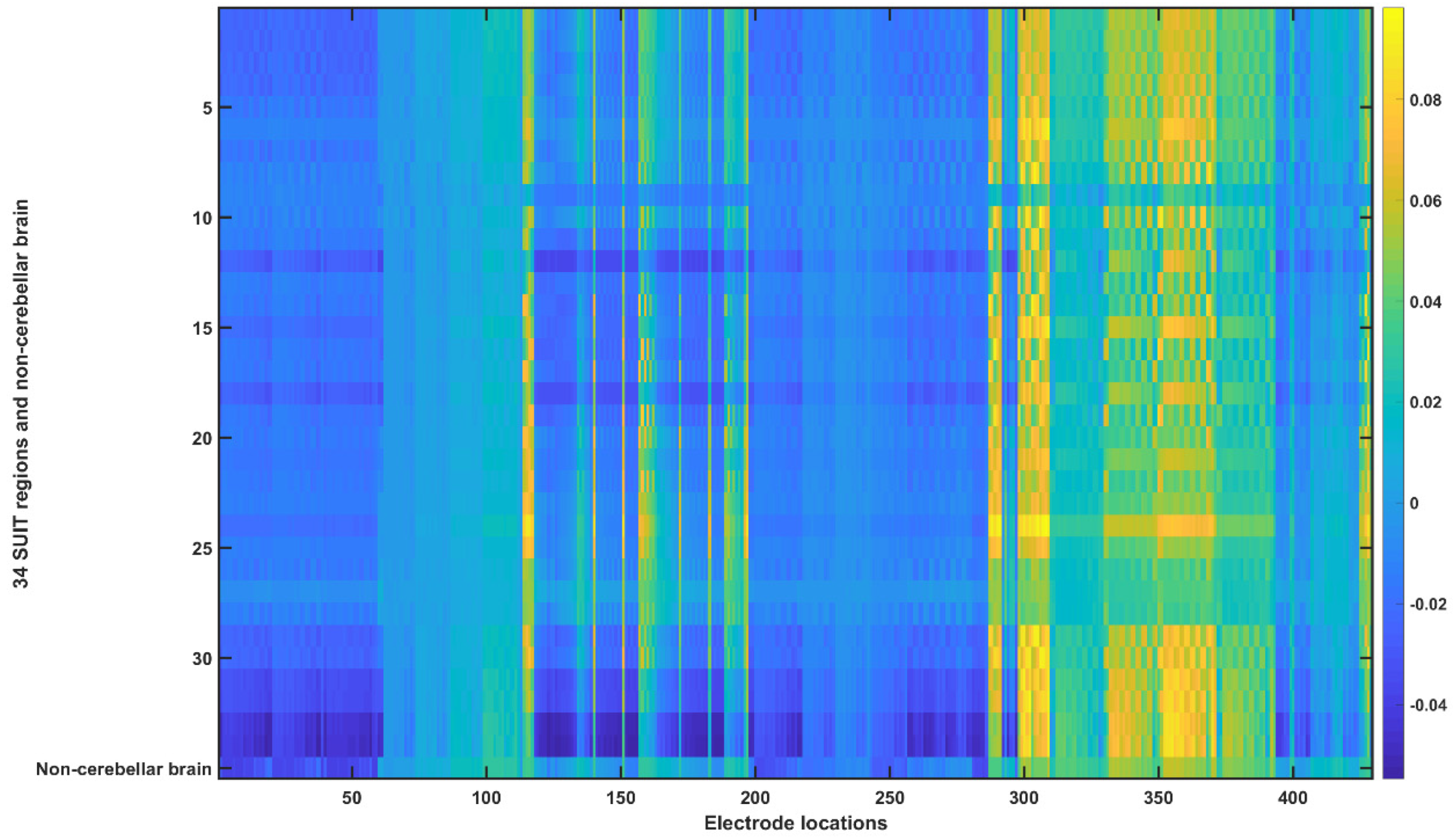
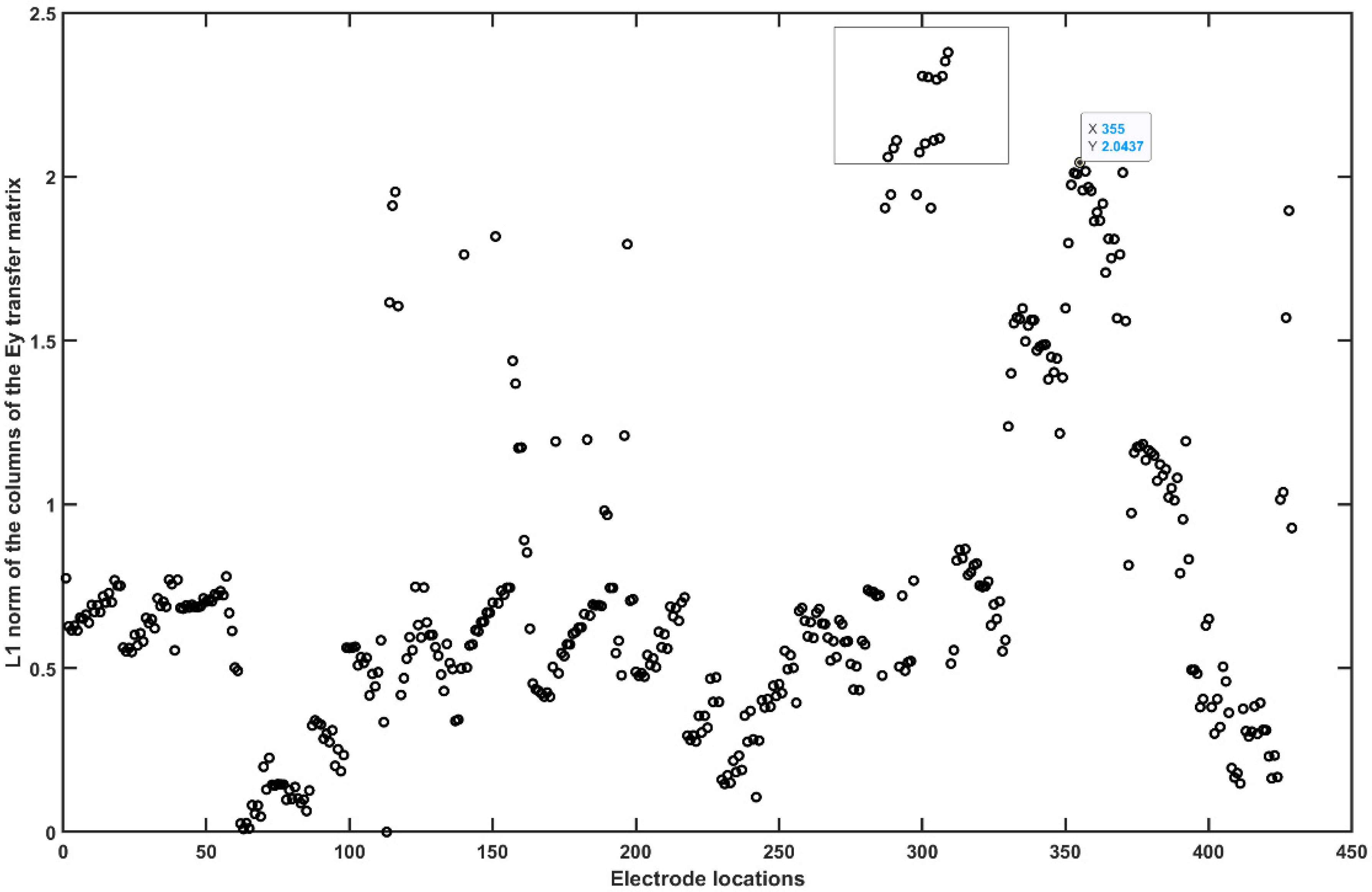
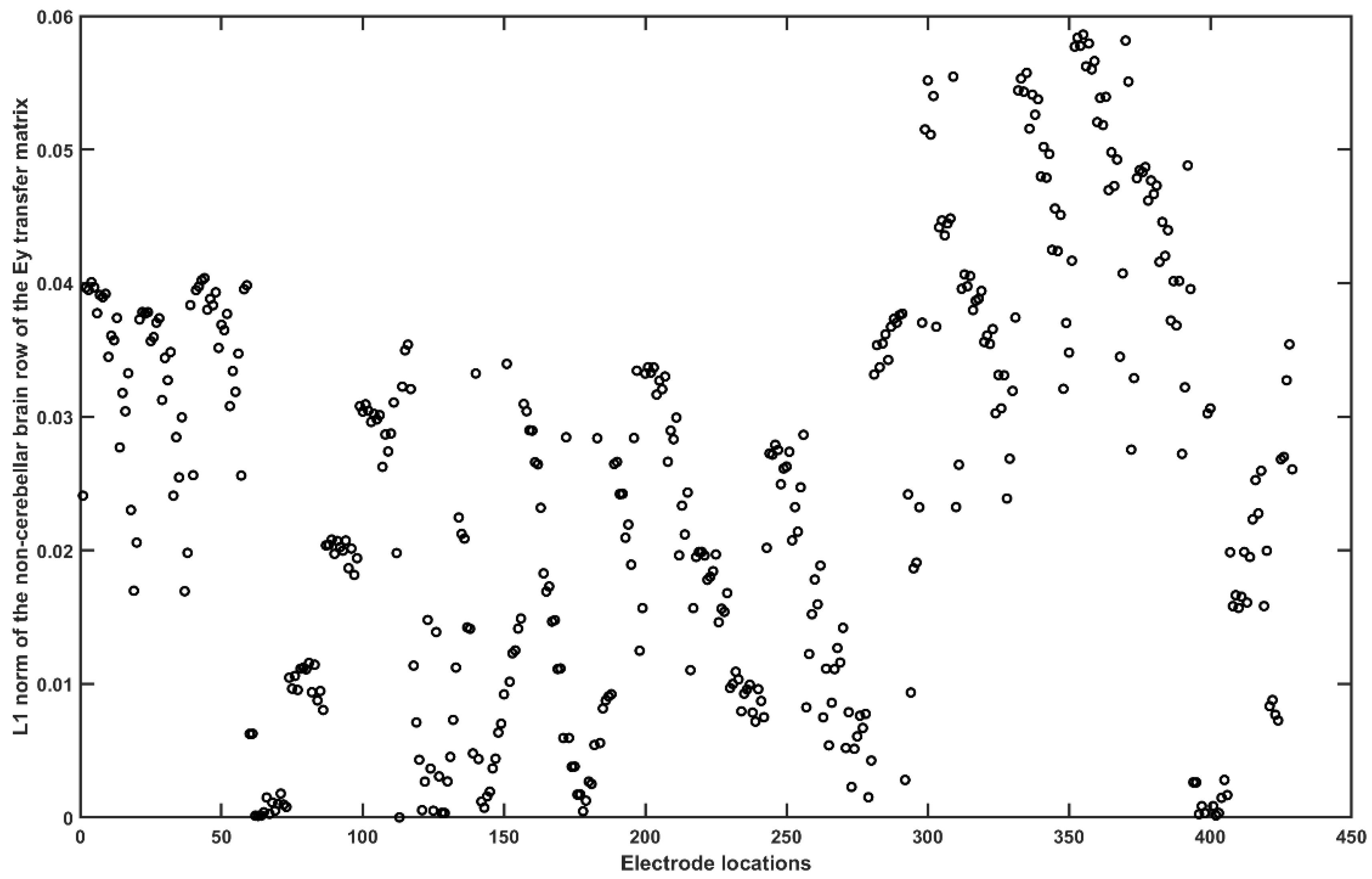
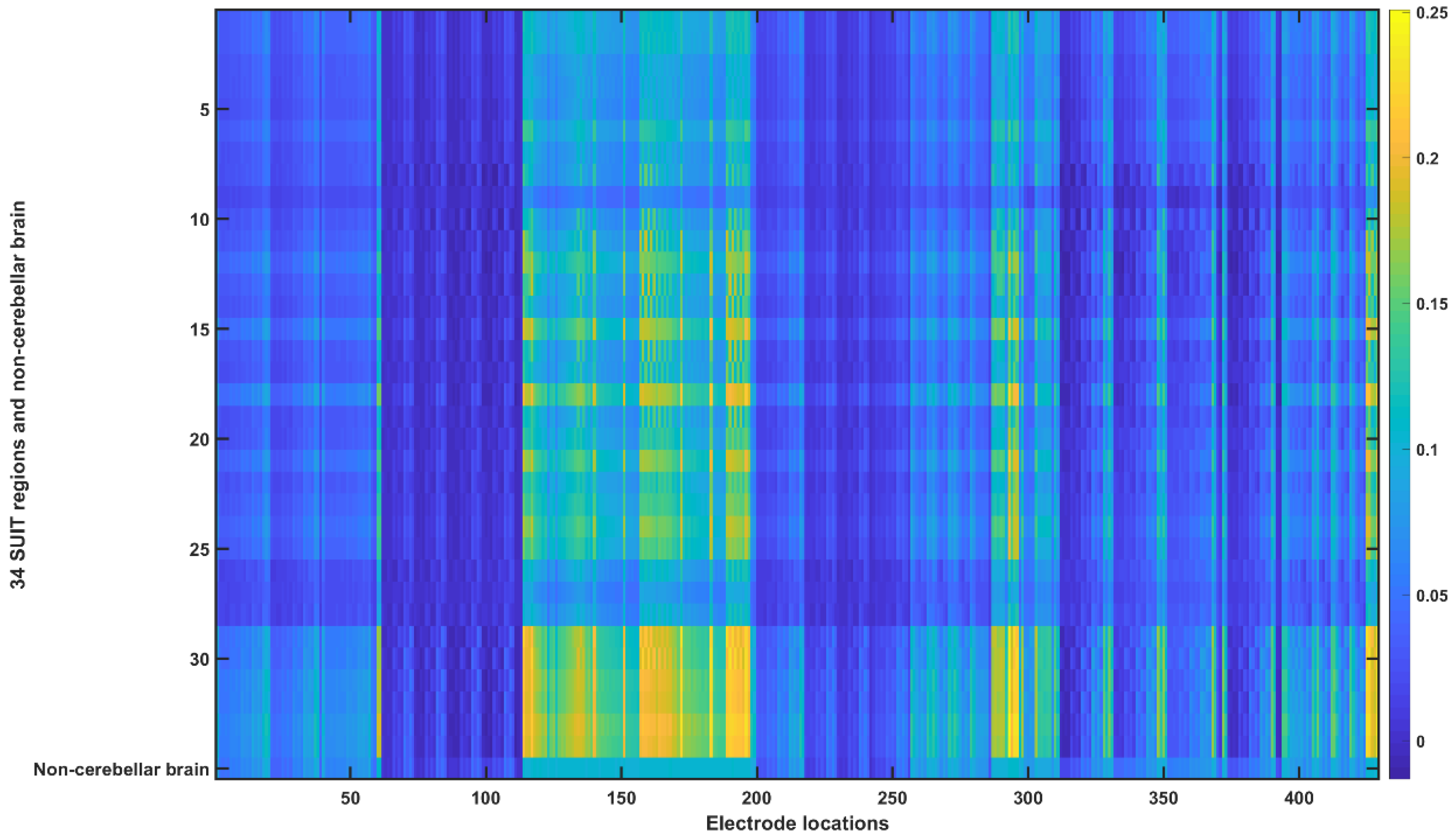
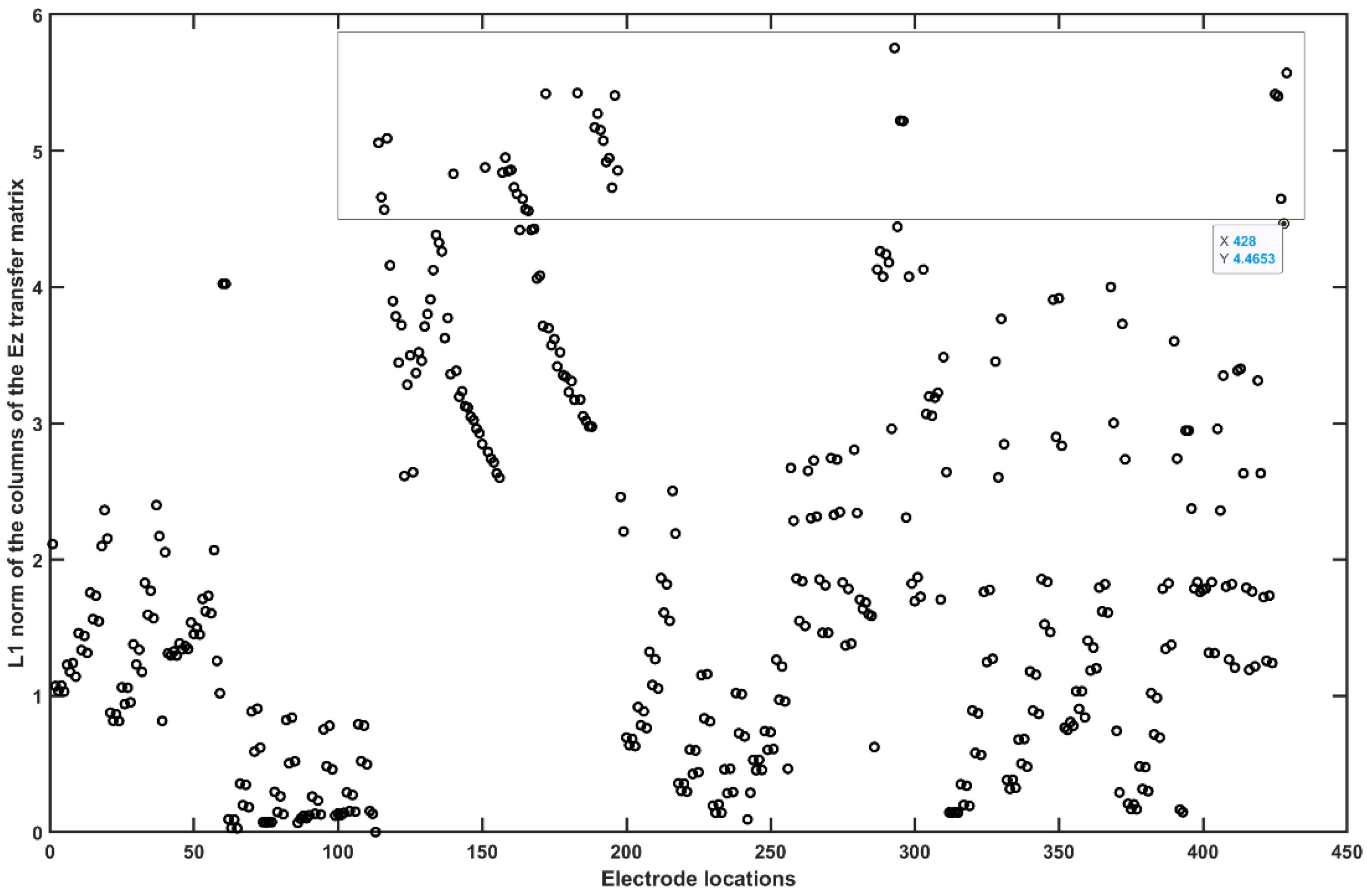
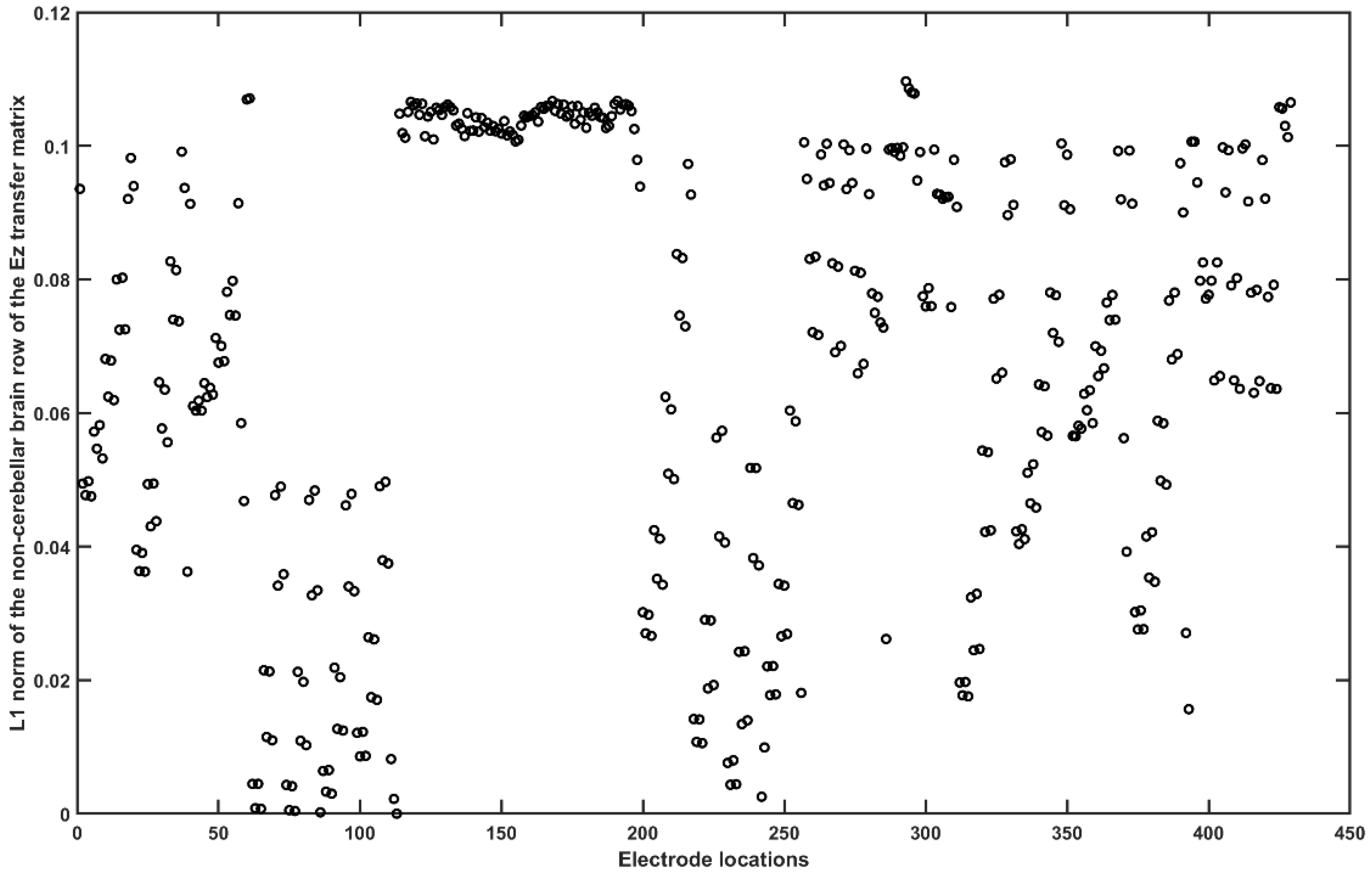
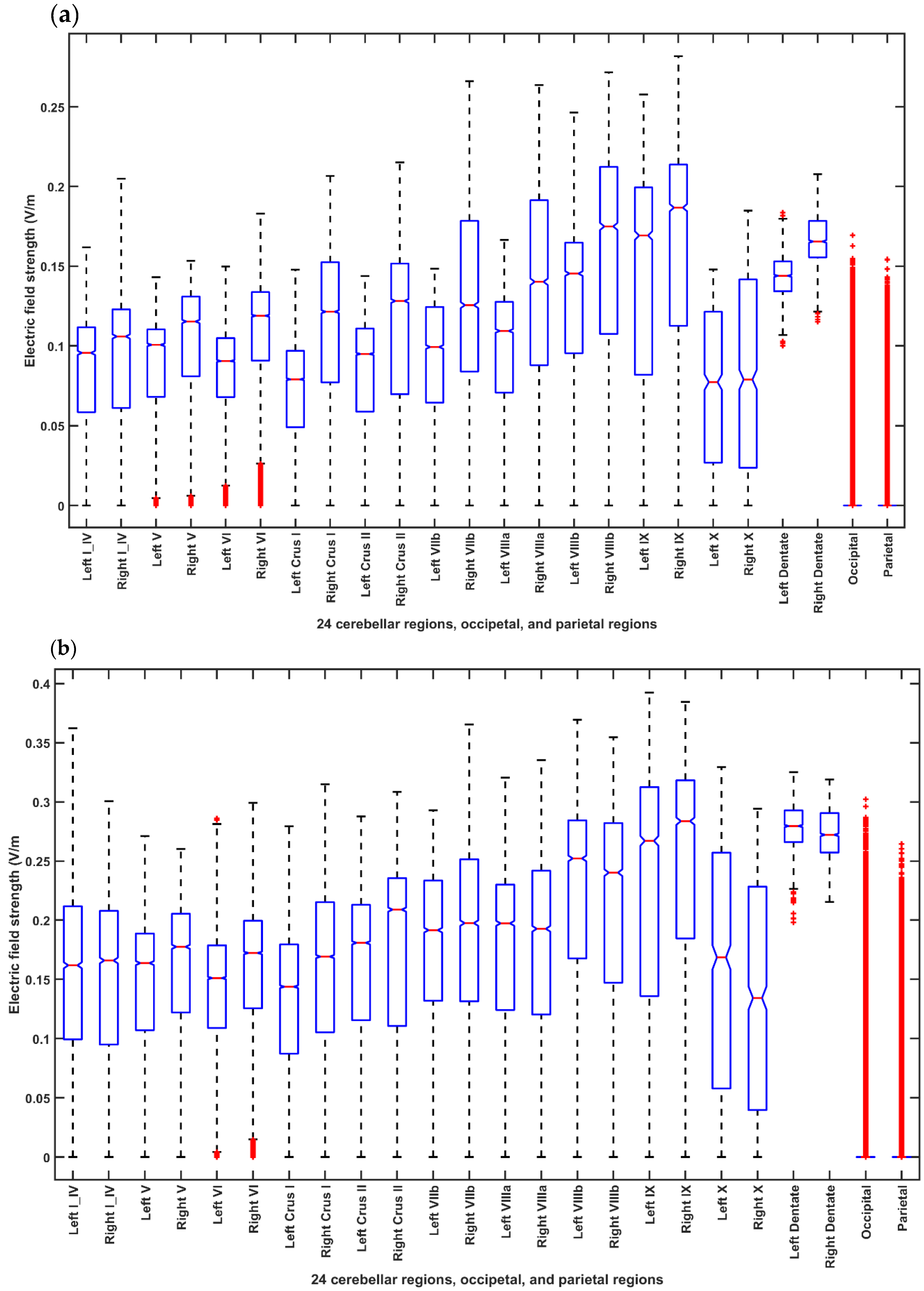
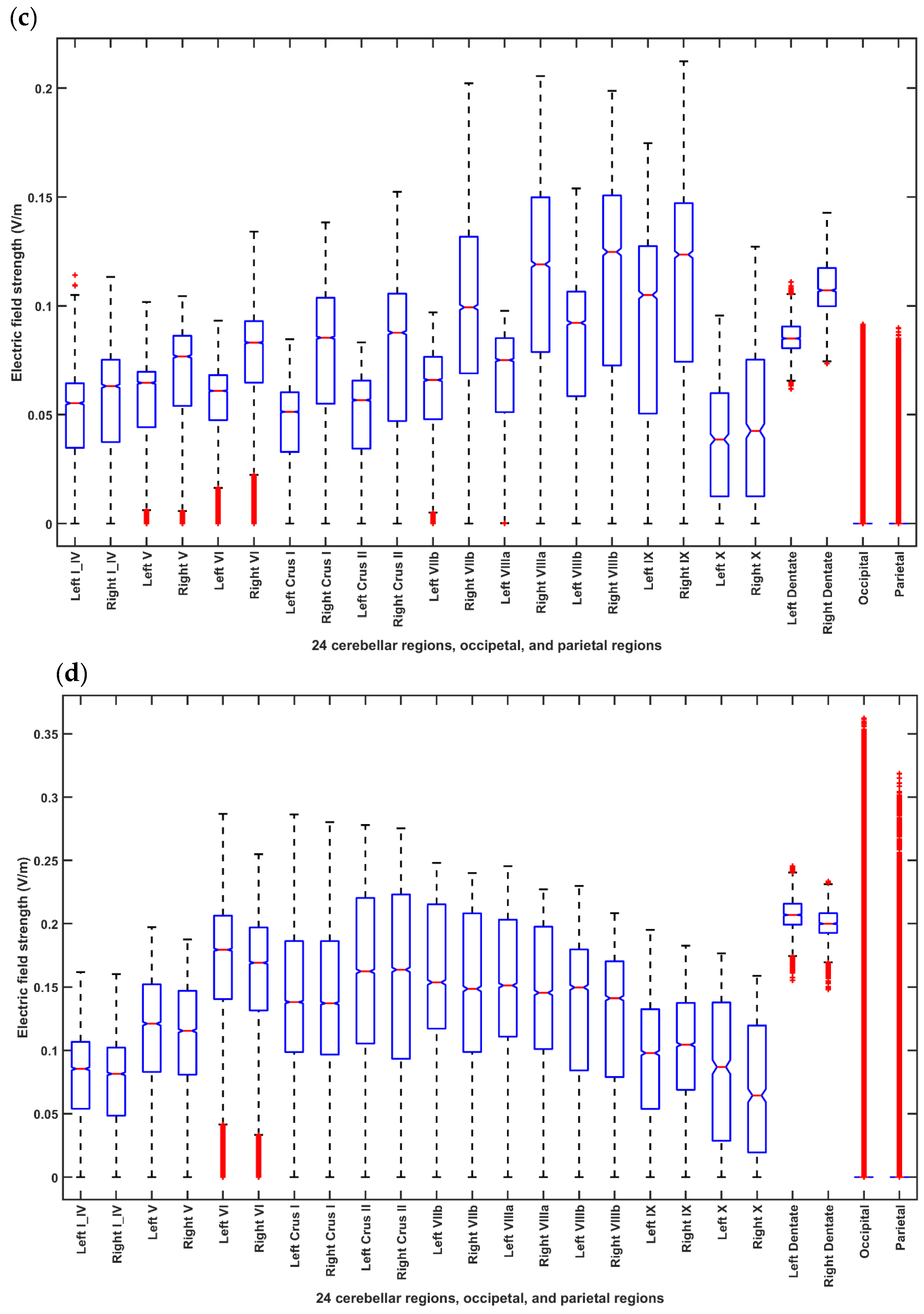
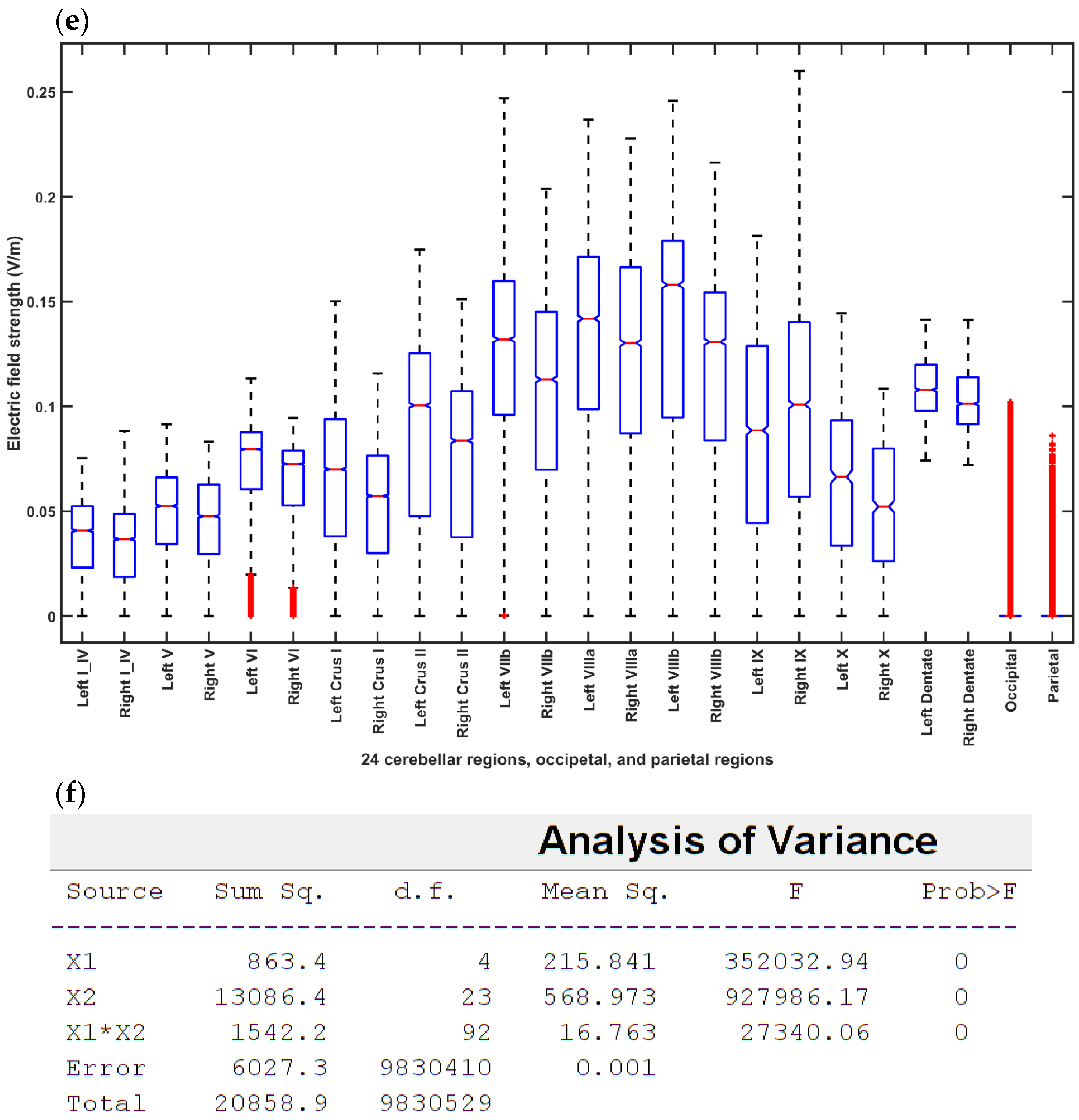
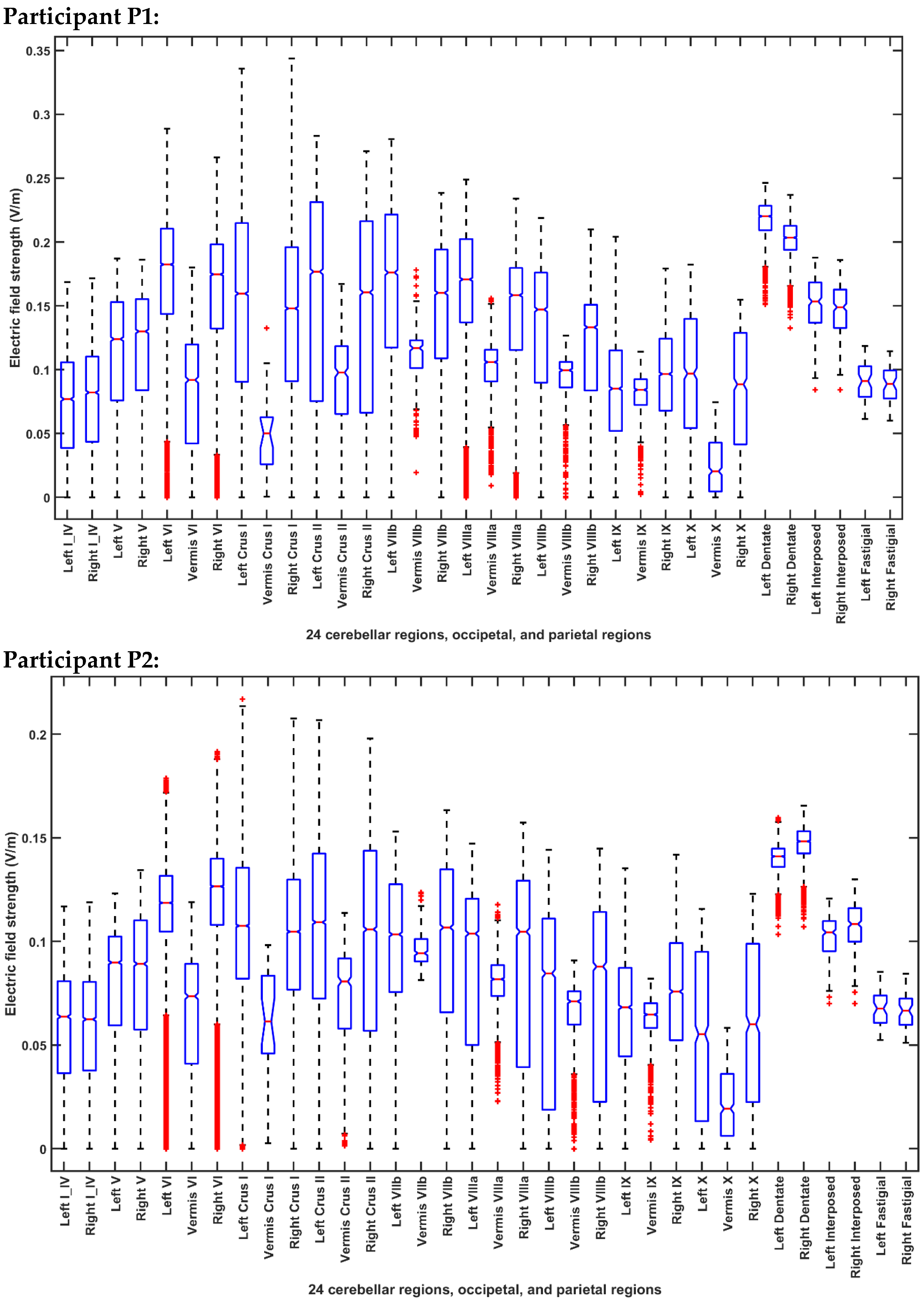
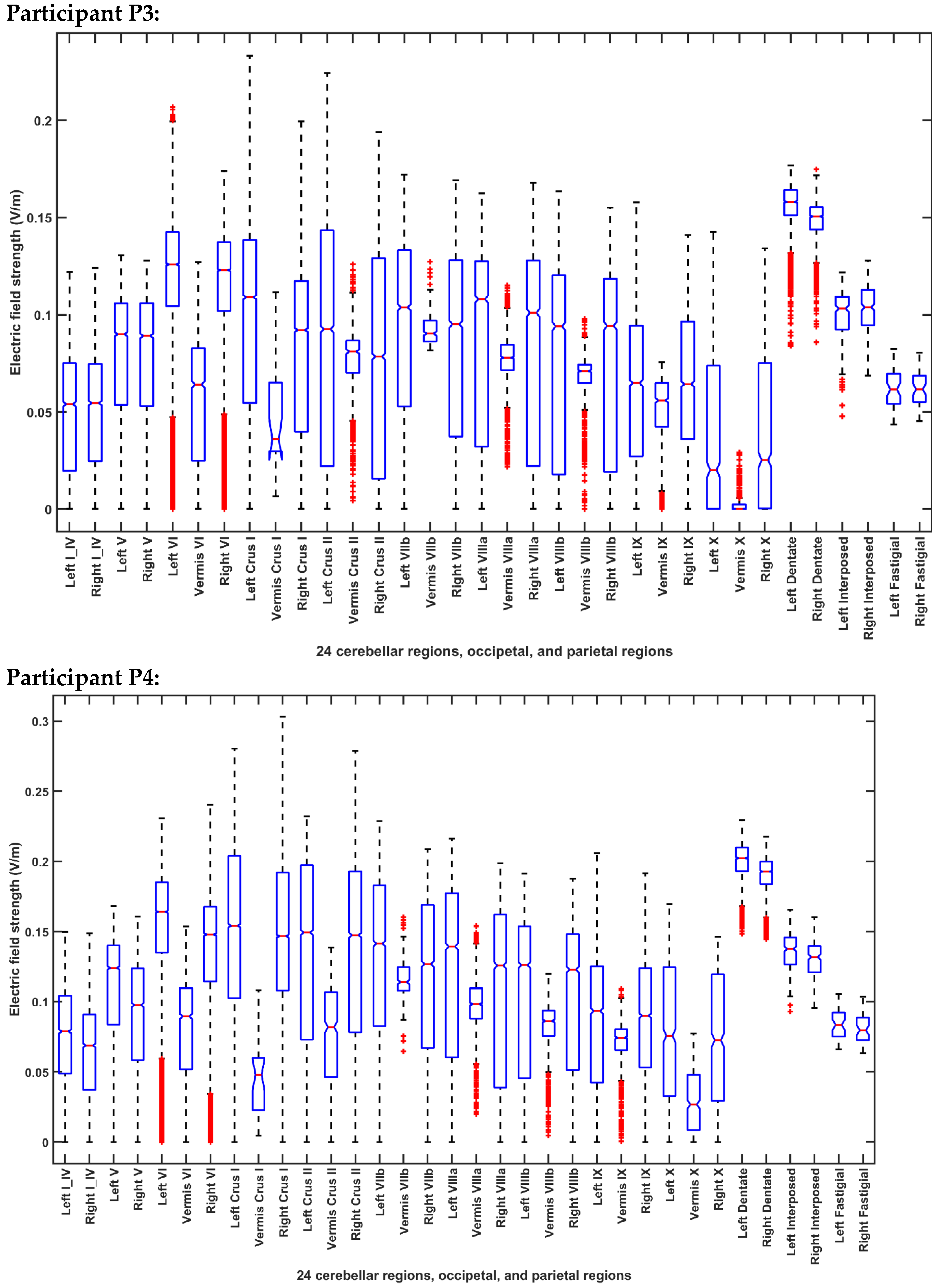
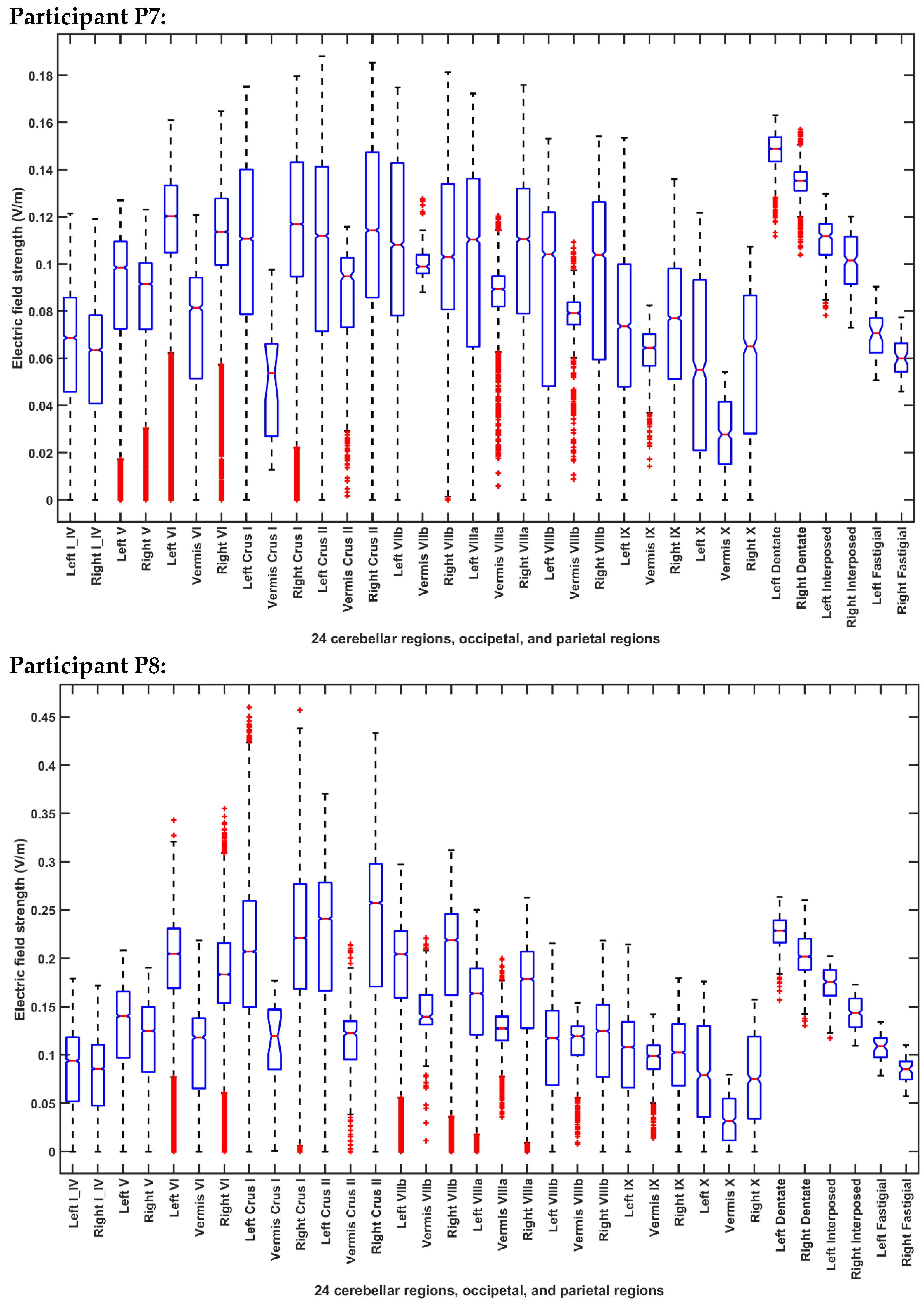
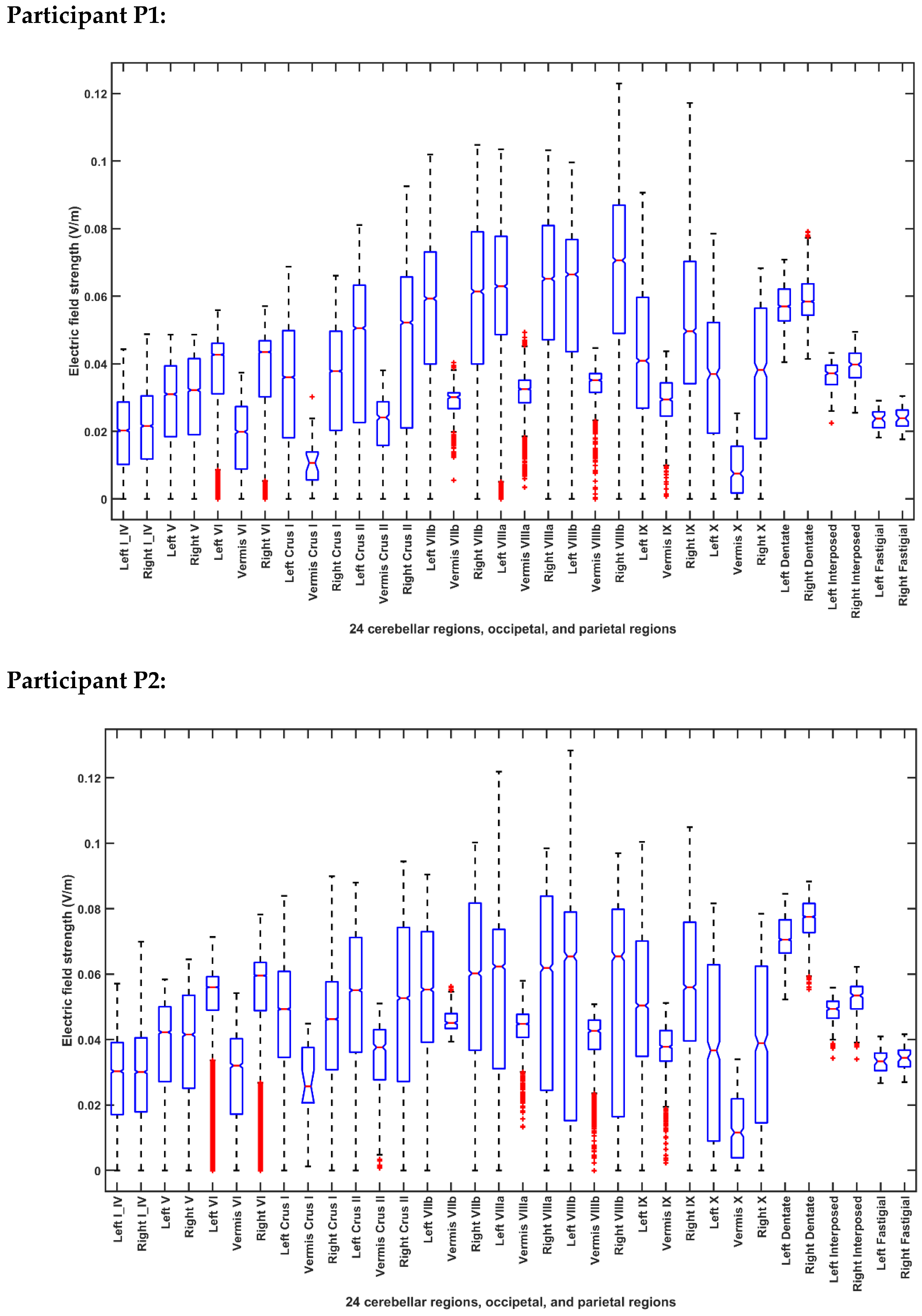
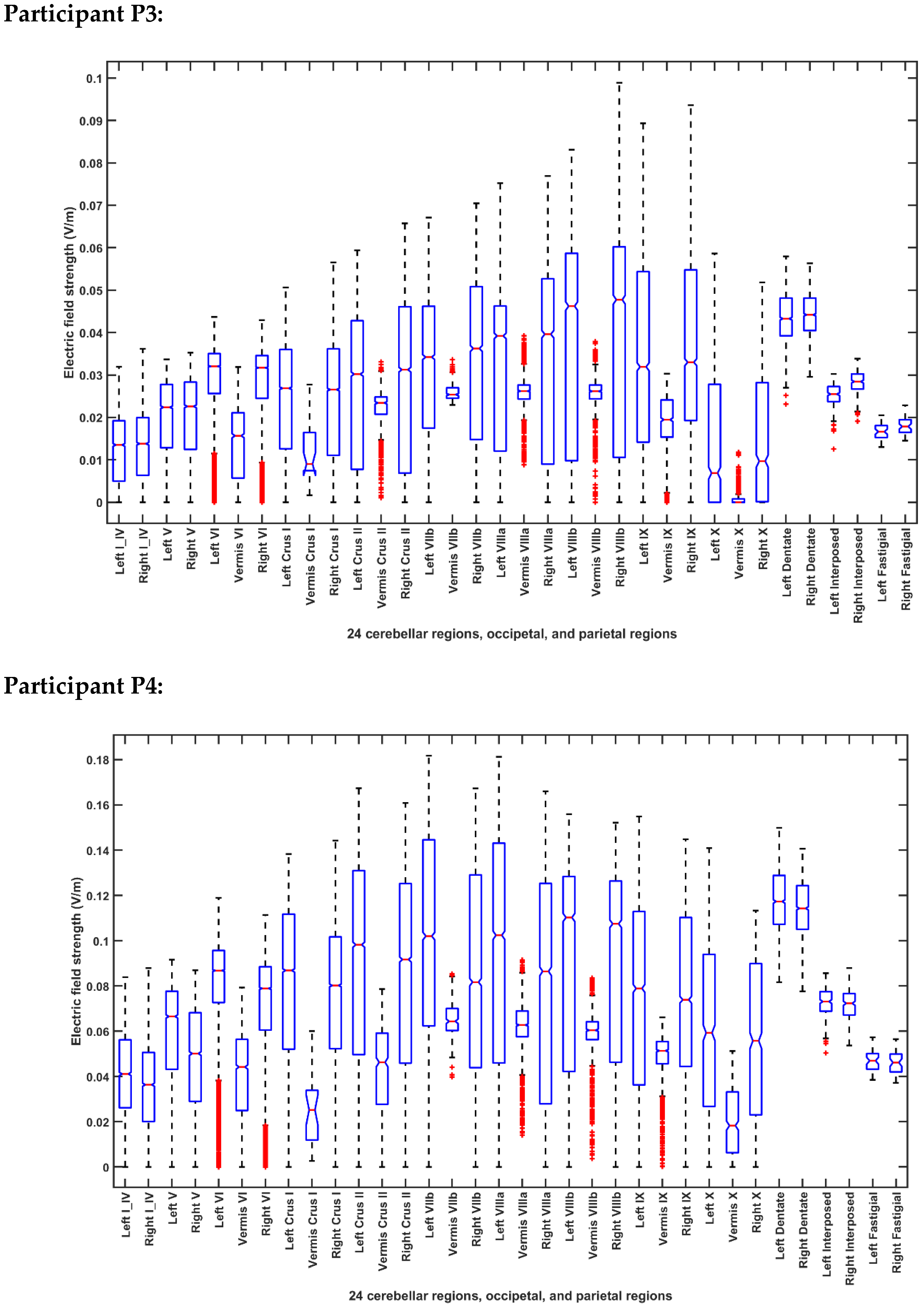
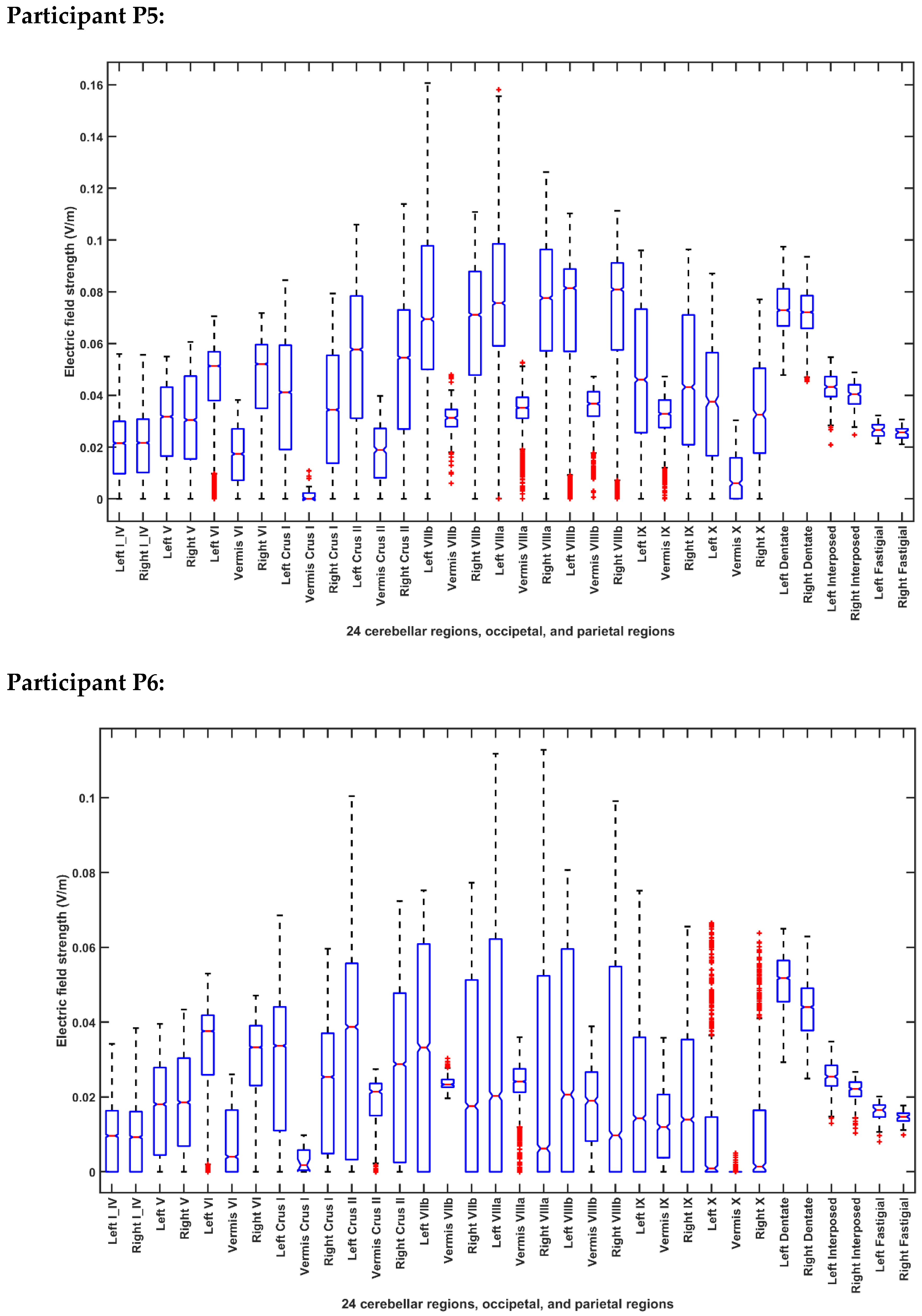
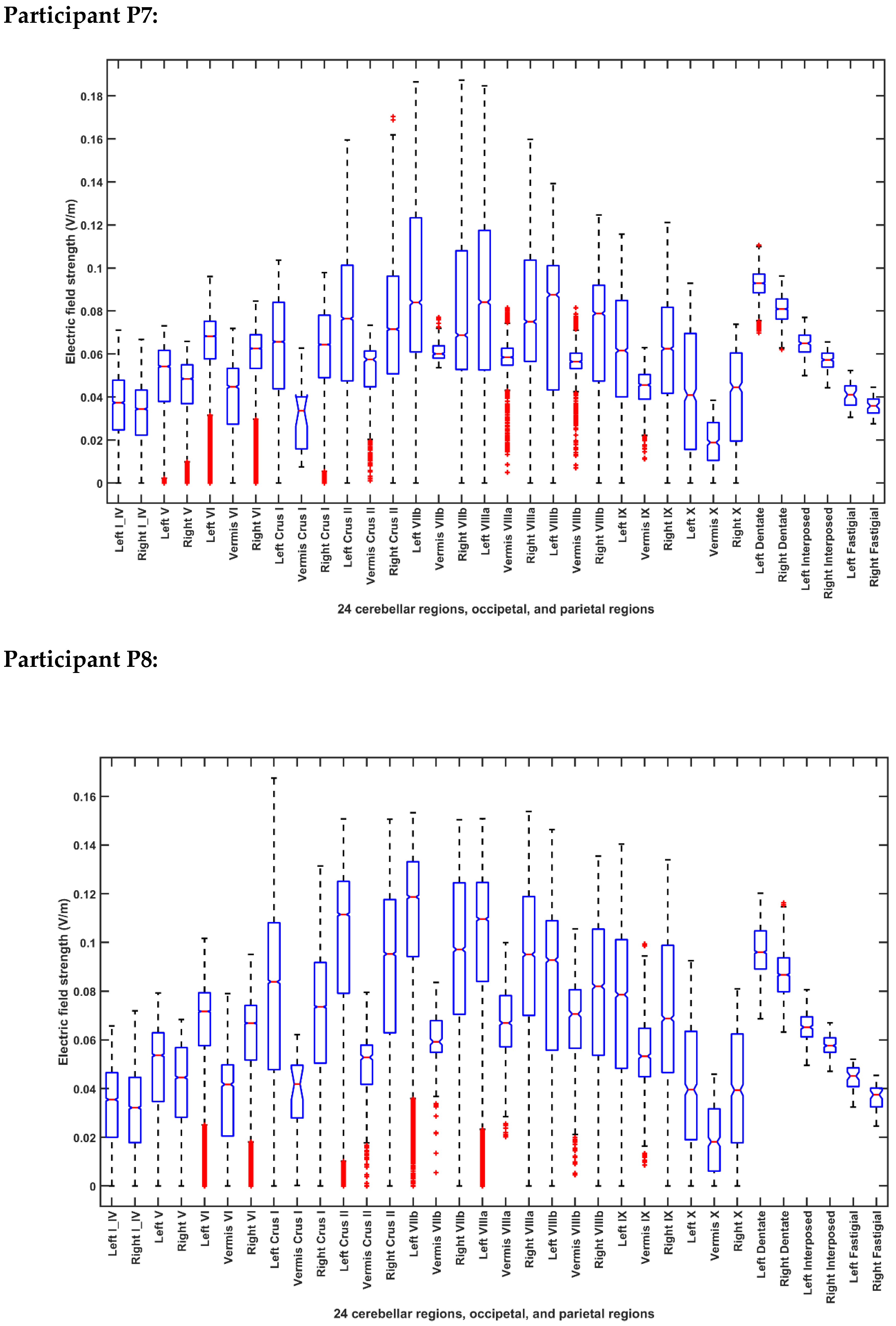
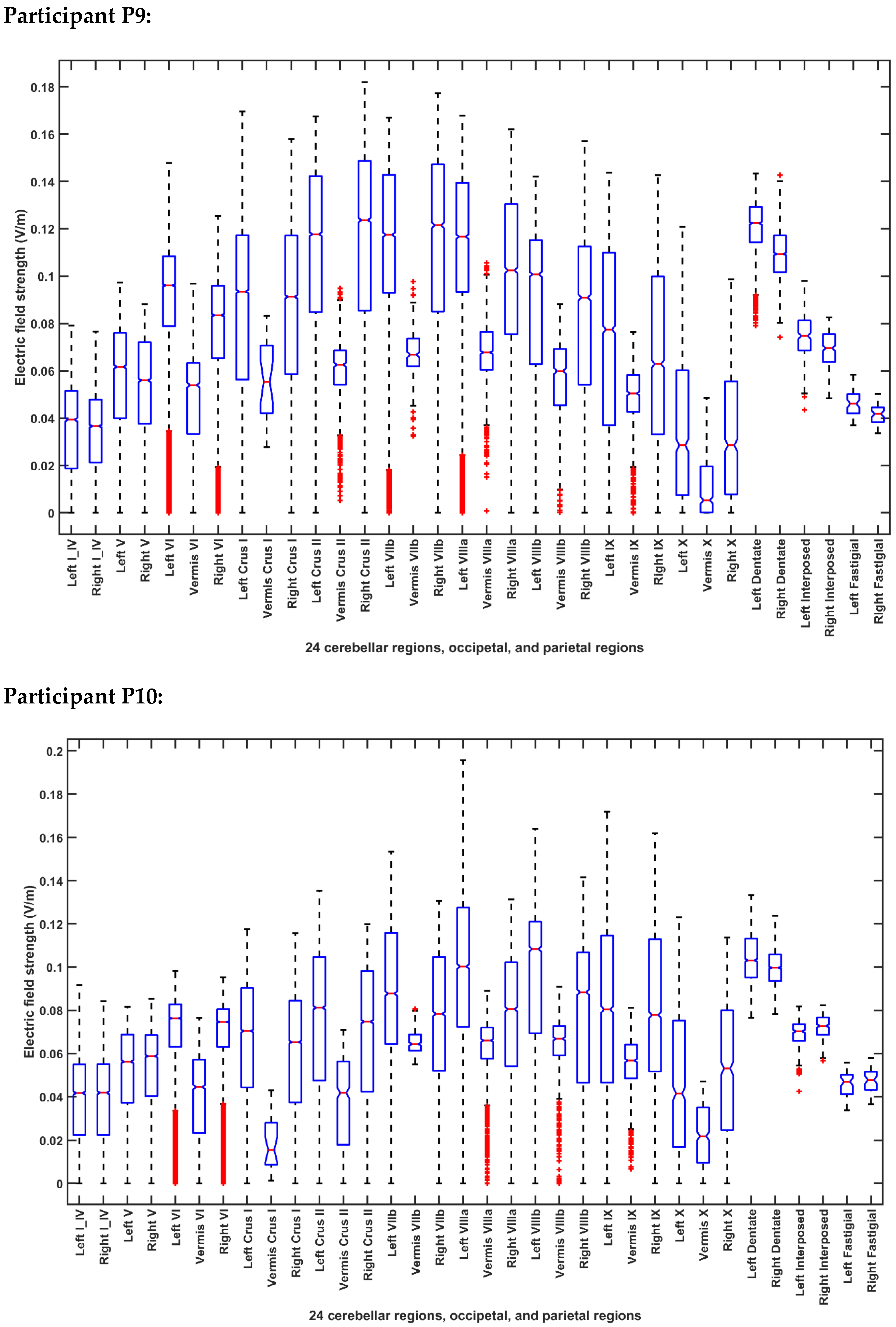
2.3.4. Assessing the Electric Field Distribution in the Cerebellar Lobules
2.3.5. Assessing the Electric Field Distribution in the Occipital and Parietal Lobes
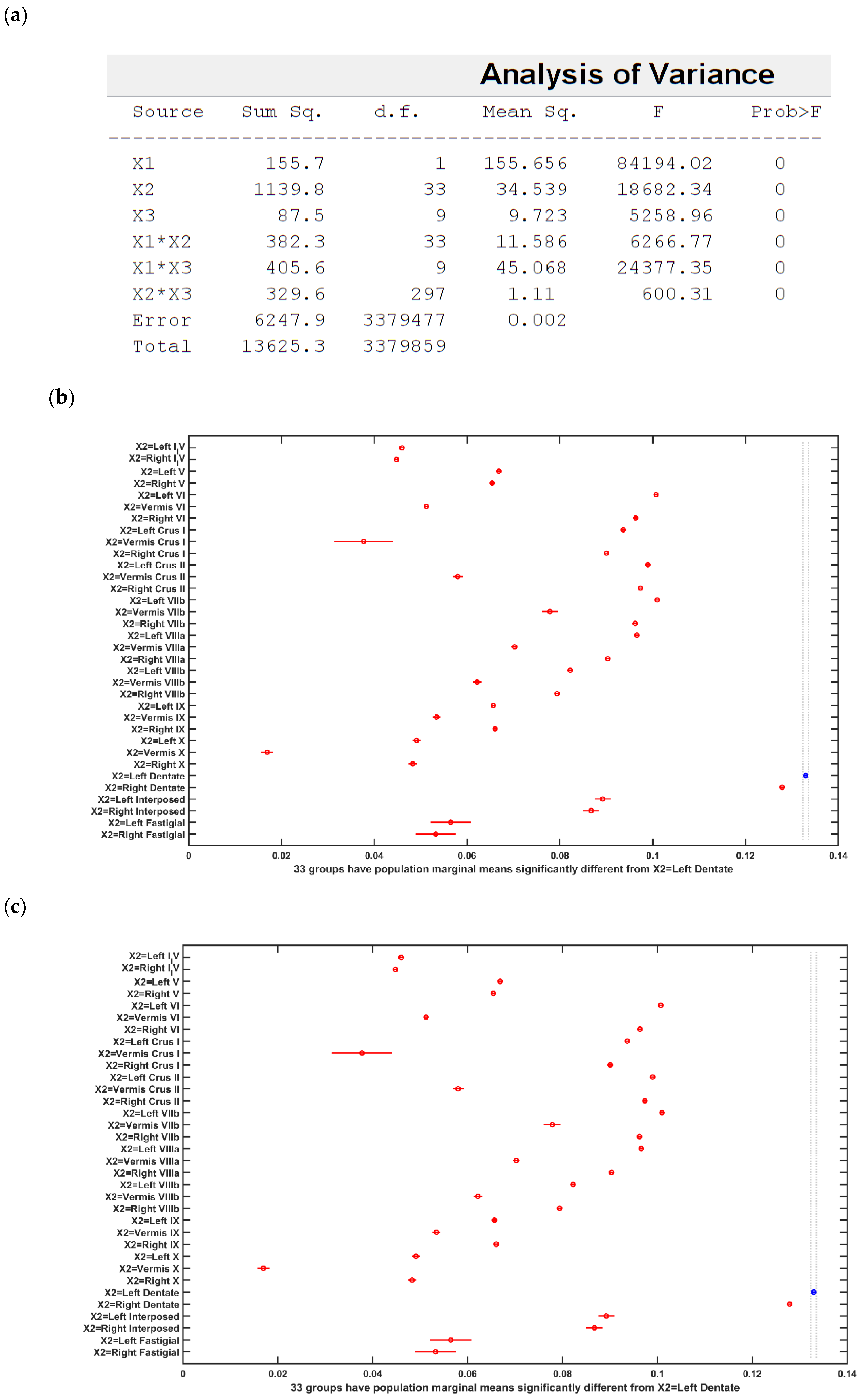
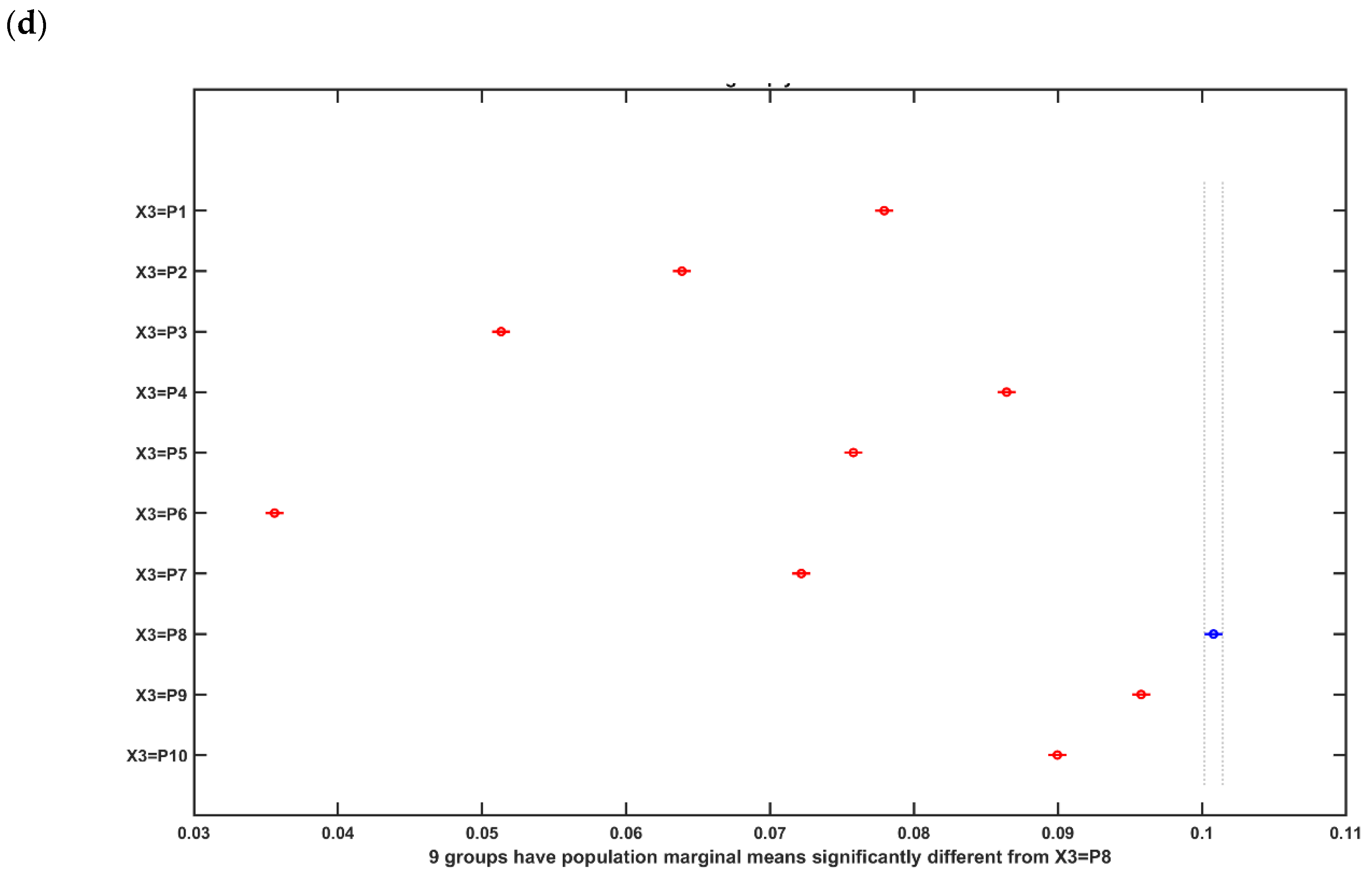
2.4. Statistical Analysis of the Electric Field Distribution in the Head Model of the 55 to 59 Years Old
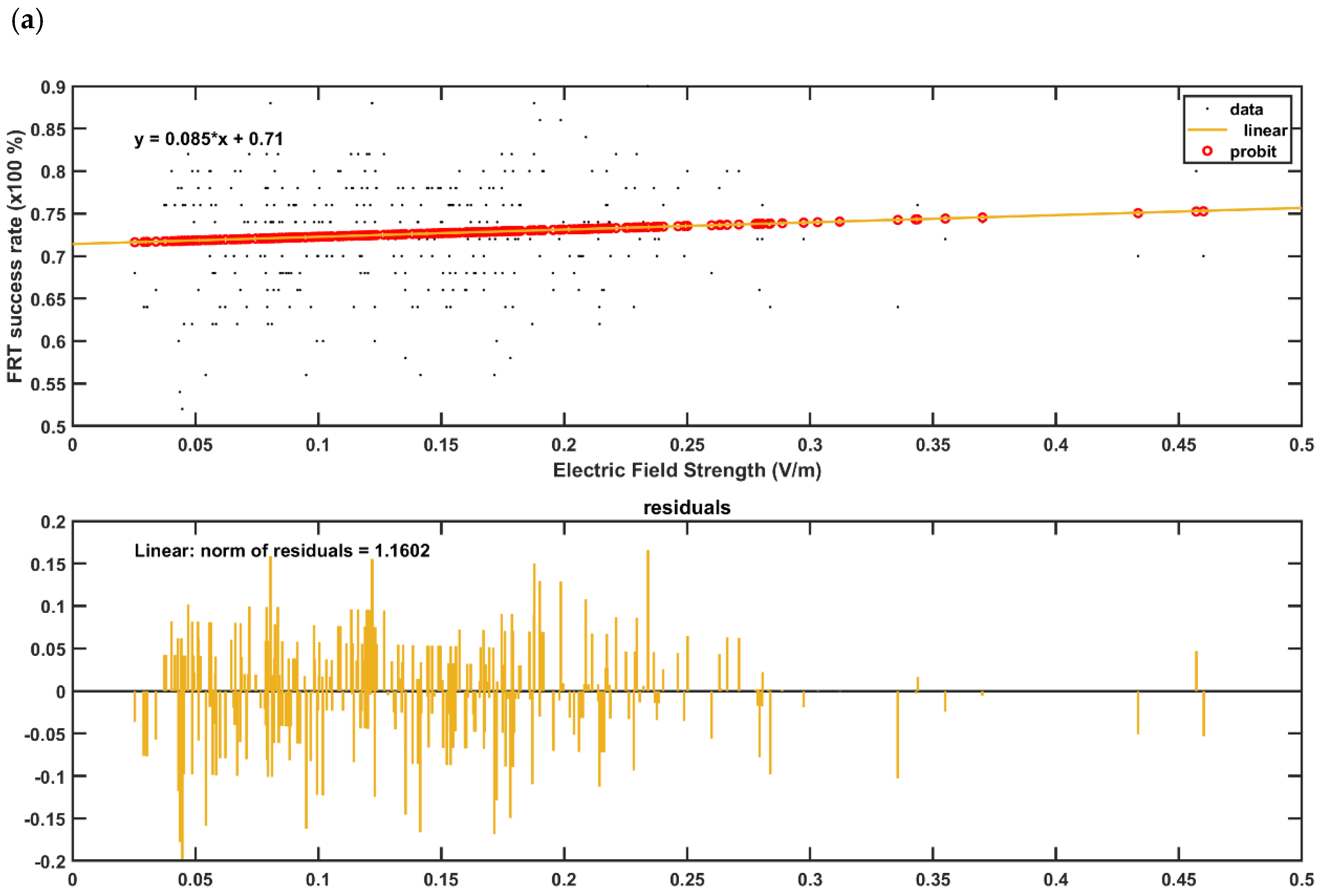
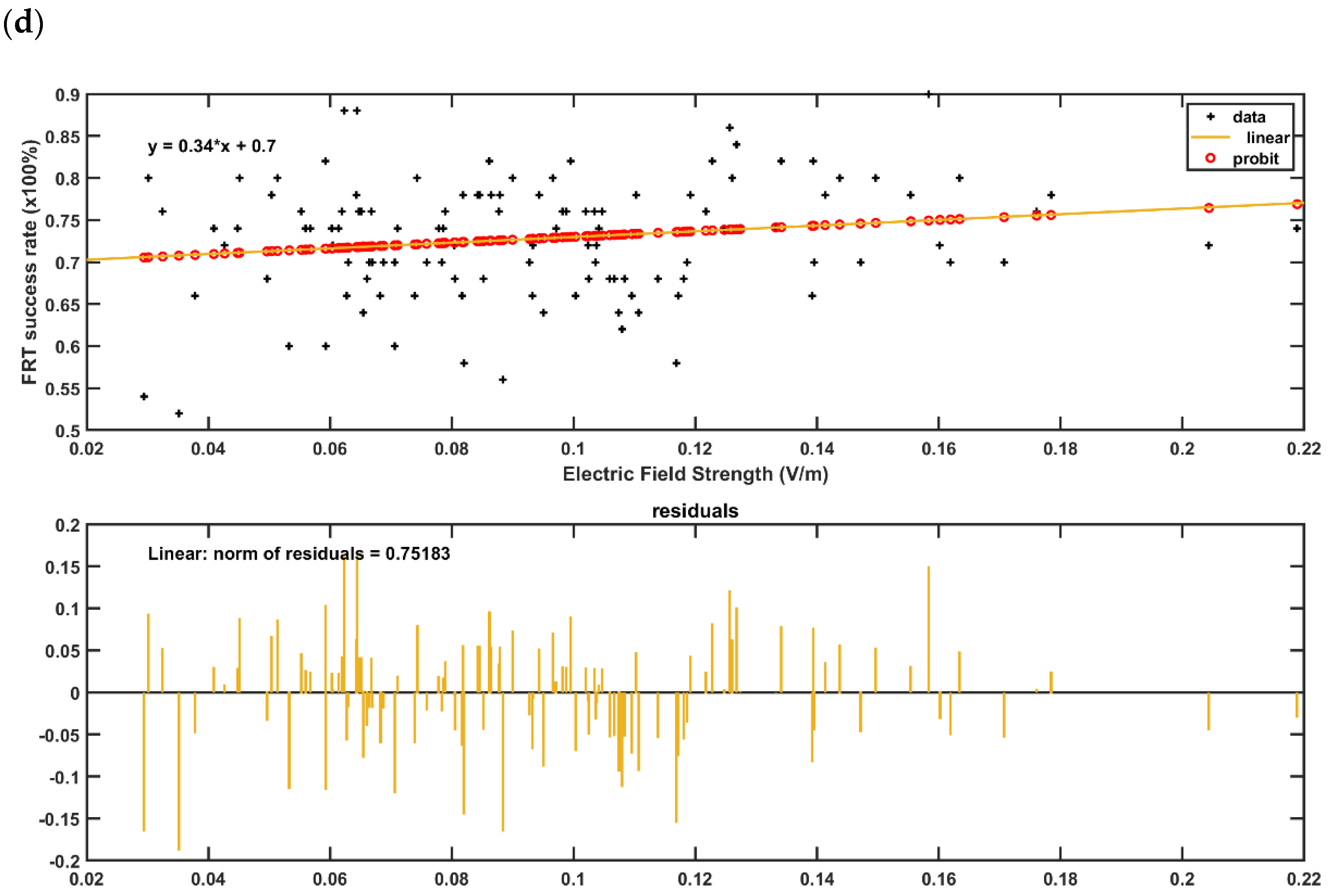
2.5. Regression Analysis of the Electric Field Distribution with the Behavioral Outcome in the Post-Stroke Subjects
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| 1 | Left I_IV | 10 | Right Crus I | 19 | Right VIIIa | 28 | Right X |
| 2 | Right I_IV | 11 | Left Crus II | 20 | Left VIIIb | 29 | Left Dentate |
| 3 | Left V | 12 | Vermis Crus II | 21 | Vermis VIIIb | 30 | Right Dentate |
| 4 | Right V | 13 | Right Crus II | 22 | Right VIIIb | 31 | Left Interposed |
| 5 | Left VI | 14 | Left VIIb | 23 | Left IX | 32 | Right Interposed |
| 6 | Vermis VI | 15 | Vermis VIIb | 24 | Vermis IX | 33 | Left Fastigial |
| 7 | Right VI | 16 | Right VIIb | 25 | Right IX | 34 | Right Fastigial |
| 8 | Left Crus I | 17 | Left VIIIa | 26 | Left X | ||
| 9 | Vermis Crus I | 18 | Vermis VIIIa | 27 | Vermis X |
Appendix B
| No. | Location | x | y | z | No. | Location | x | y | z |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Fp1 | −22.5592 | 82.90488 | 13.87207 | 216 | P5h | −62.6435 | −55.417 | 48.50705 |
| 2 | Fpz | 3.842296 | 87.03616 | 17.49313 | 217 | P3h | −44.5991 | −62.2382 | 71.54874 |
| 3 | Fp2 | 28.52678 | 83.55578 | 13.67529 | 218 | P1h | −15.6894 | −68.0947 | 83.5882 |
| 4 | AF7 | −41.9976 | 71.24048 | 12.12234 | 219 | P2h | 19.79522 | −68.738 | 83.61536 |
| 5 | AF5 | −34.6647 | 75.10938 | 25.48365 | 220 | P4h | 49.80881 | −62.9955 | 71.23532 |
| 6 | AF3 | -25.3904 | 78.60305 | 35.73096 | 221 | P6h | 67.89475 | -54.8502 | 47.65088 |
| 7 | AF1 | -11.941 | 79.80824 | 43.49709 | 222 | P8h | 73.34005 | −48.4089 | 22.94698 |
| 8 | AFz | 2.700881 | 80.83209 | 45.4243 | 223 | P10h | 74.35319 | −44.3501 | −5.70373 |
| 9 | AF2 | 18.38834 | 80.3016 | 43.27522 | 224 | PO9h | −55.5975 | −70.1245 | −6.82361 |
| 10 | AF4 | 32.66851 | 78.83771 | 35.49923 | 225 | PO7h | −54.5191 | −76.0335 | 19.40764 |
| 11 | AF6 | 41.63063 | 75.41405 | 25.66882 | 226 | PO5h | −45.1531 | −82.1967 | 35.4382 |
| 12 | AF8 | 47.49697 | 72.00578 | 13.61991 | 227 | PO3h | −29.3346 | −88.0844 | 47.25826 |
| 13 | F9 | −55.94 | 50.26538 | −18.4116 | 228 | PO1h | −8.08273 | −90.9205 | 53.45393 |
| 14 | F7 | −56.1724 | 53.03701 | 11.21066 | 229 | PO2h | 13.28204 | −91.068 | 52.90984 |
| 15 | F5 | −50.8744 | 56.21025 | 31.86567 | 230 | PO4h | 32.52896 | −88.4084 | 47.14226 |
| 16 | F3 | −39.0952 | 59.77218 | 50.02259 | 231 | PO6h | 50.25244 | −81.431 | 35.07223 |
| 17 | F1 | −20.1033 | 63.803 | 63.89388 | 232 | PO8h | 59.58925 | −74.9128 | 19.71736 |
| 18 | Fz | 2.99712 | 65.08257 | 69.42619 | 233 | PO10h | 61.64832 | −69.6594 | −5.77207 |
| 19 | F2 | 27.36842 | 63.47771 | 64.33418 | 234 | O1h | −16.0684 | −100.448 | 16.96381 |
| 20 | F4 | 45.65995 | 60.44671 | 50.90544 | 235 | O2h | 20.76301 | −100.285 | 15.9655 |
| 21 | F6 | 57.03421 | 57.12775 | 33.22234 | 236 | I1h | −11.759 | −96.2474 | −22.6608 |
| 22 | F8 | 62.18449 | 53.92647 | 12.13087 | 237 | I2h | 16.51372 | −96.2668 | −21.869 |
| 23 | F10 | 61.52017 | 51.90641 | −17.3684 | 238 | AFp7 | −32.0664 | 78.3587 | 13.15924 |
| 24 | FT9 | −66.2371 | 32.61463 | −20.9561 | 239 | AFp5 | −25.9275 | 80.75012 | 21.30455 |
| 25 | FT7 | −65.3194 | 31.50805 | 11.14653 | 240 | AFp3 | −19.2884 | 82.73908 | 28.30598 |
| 26 | FC5 | −62.0899 | 32.15929 | 37.65389 | 241 | AFp1 | −8.28792 | 84.68655 | 31.39793 |
| 27 | FC3 | −49.3727 | 33.4715 | 61.182 | 242 | AFpz | 3.526845 | 85.00818 | 32.90711 |
| 28 | FC1 | −26.791 | 37.68753 | 80.24023 | 243 | AFp2 | 14.7652 | 84.92751 | 31.13003 |
| 29 | FCz | 4.253833 | 38.91969 | 87.41366 | 244 | AFp4 | 24.73355 | 83.55391 | 28.15581 |
| 30 | FC2 | 33.31507 | 37.83103 | 80.37218 | 245 | AFp6 | 33.52511 | 80.75925 | 22.74153 |
| 31 | FC4 | 56.8832 | 33.78278 | 61.13577 | 246 | AFp8 | 37.81402 | 79.40772 | 12.13282 |
| 32 | FC6 | 69.41998 | 31.88483 | 37.35075 | 247 | AFF9 | −48.1636 | 62.60542 | −15.9273 |
| 33 | FT8 | 72.12511 | 31.09664 | 11.29649 | 248 | AFF7 | −49.5452 | 63.06089 | 11.20612 |
| 34 | FT10 | 72.28736 | 31.96451 | −21.5403 | 249 | AFF5 | −43.4247 | 66.72266 | 28.63601 |
| 35 | T9 | −68.4998 | 8.249681 | −22.4725 | 250 | AFF3 | −32.7211 | 69.92124 | 43.53524 |
| 36 | T7 | −71.3853 | 5.05698 | 11.08433 | 251 | AFF1 | −16.6866 | 72.82261 | 53.58292 |
| 37 | C5 | −69.229 | 3.884095 | 42.42783 | 252 | AFFz | 4.288832 | 74.71173 | 57.53587 |
| 38 | C3 | −57.747 | 3.717831 | 67.76955 | 253 | AFF2 | 22.84423 | 73.16779 | 54.42189 |
| 39 | C1 | −31.5817 | 4.967477 | 89.48766 | 254 | AFF4 | 38.48791 | 71.41055 | 43.94503 |
| 40 | Cz | 3.456495 | 5.329642 | 99.52775 | 255 | AFF6 | 50.03043 | 67.02973 | 29.6401 |
| 41 | C2 | 38.09238 | 5.82291 | 88.99616 | 256 | AFF8 | 55.65077 | 63.6887 | 11.91936 |
| 42 | C4 | 64.26701 | 4.369621 | 67.62971 | 257 | AFF10 | 54.26406 | 62.65546 | −16.8431 |
| 43 | C6 | 75.43402 | 6.505909 | 42.33944 | 258 | FFT9 | −62.323 | 41.66684 | −20.9349 |
| 44 | T8 | 77.38602 | 6.530228 | 9.717833 | 259 | FFT7 | −61.3234 | 42.58761 | 10.88625 |
| 45 | T10 | 74.50288 | 7.909821 | −22.3627 | 260 | FFC5 | −57.0247 | 44.441 | 34.49869 |
| 46 | TP7 | −73.5016 | −21.5145 | 10.67297 | 261 | FFC3 | −44.6976 | 46.61251 | 56.76297 |
| 47 | CP5 | −71.524 | −24.3614 | 42.38637 | 262 | FFC1 | −24.2908 | 51.55225 | 72.34157 |
| 48 | CP3 | −61.6892 | −27.3726 | 69.56094 | 263 | FFCz | 3.465133 | 54.22735 | 79.14475 |
| 49 | CP1 | −33.5793 | −28.5314 | 92.61813 | 264 | FFC2 | 31.00001 | 51.91758 | 72.89468 |
| 50 | CPz | 3.611006 | −29.6046 | 102.548 | 265 | FFC4 | 51.2962 | 48.01261 | 57.39484 |
| 51 | CP2 | 40.46755 | −28.5723 | 92.68565 | 266 | FFC6 | 64.18185 | 44.11128 | 35.40215 |
| 52 | CP4 | 67.15958 | −26.2549 | 70.12574 | 267 | FFT8 | 68.26 | 42.44242 | 10.99613 |
| 53 | CP6 | 77.5511 | −23.1143 | 40.75406 | 268 | FFT10 | 67.77986 | 42.6417 | −21.5682 |
| 54 | TP8 | 79.52268 | −20.9995 | 9.849888 | 269 | FTT9 | −68.2673 | 19.54876 | −20.5511 |
| 55 | P9 | −67.2474 | −45.3603 | −21.1713 | 270 | FTT7 | −68.4895 | 19.30654 | 10.96369 |
| 56 | P7 | −68.778 | −46.0653 | 11.4691 | 271 | FCC5 | −66.1508 | 19.10656 | 40.53259 |
| 57 | P5 | −66.2887 | −52.513 | 36.08666 | 272 | FCC3 | −54.2756 | 17.88662 | 64.73584 |
| 58 | P3 | −54.9608 | −59.6442 | 60.7231 | 273 | FCC1 | −29.3821 | 20.95851 | 86.31815 |
| 59 | P1 | −29.4783 | −66.3772 | 79.33228 | 274 | FCCz | 3.958818 | 22.00332 | 94.121 |
| 60 | Pz | 1.16076 | −67.0461 | 86.85532 | 275 | FCC2 | 35.52612 | 22.59816 | 85.42201 |
| 61 | P2 | 35.68975 | −66.3795 | 79.29573 | 276 | FCC4 | 60.75797 | 19.88735 | 64.52368 |
| 62 | P4 | 60.31538 | −59.8885 | 59.73956 | 277 | FCC6 | 72.32896 | 21.06874 | 40.94543 |
| 63 | P6 | 71.43842 | −51.4954 | 35.46394 | 278 | FTT8 | 75.15998 | 19.07234 | 11.70313 |
| 64 | P8 | 74.42983 | −46.1598 | 10.89193 | 279 | FTT10 | 74.18301 | 19.9038 | −19.5862 |
| 65 | P10 | 73.05866 | −44.5554 | −22.0247 | 280 | TTP7 | −73.2764 | −8.59877 | 11.85397 |
| 66 | PO9 | −55.4014 | −66.2734 | −22.0704 | 281 | CCP5 | −71.2532 | −9.33826 | 42.32324 |
| 67 | PO7 | −57.4879 | −72.0804 | 11.77603 | 282 | CCP3 | −61.0012 | −11.1267 | 68.91452 |
| 68 | PO5 | −50.2619 | −79.2832 | 27.65109 | 283 | CCP1 | −33.6162 | −11.7103 | 91.75061 |
| 69 | PO3 | −38.3293 | −85.4101 | 41.33633 | 284 | CCPz | 3.522455 | −12.3699 | 102.5344 |
| 70 | PO1 | −18.2358 | −90.253 | 50.93382 | 285 | CCP2 | 40.14838 | −11.1746 | 92.32234 |
| 71 | POz | 3.252028 | −91.057 | 54.66248 | 286 | CCP4 | 66.77457 | −10.8469 | 70.0064 |
| 72 | PO2 | 24.01926 | −90.0057 | 50.48114 | 287 | CCP6 | 77.44537 | −8.49465 | 41.47523 |
| 73 | PO4 | 42.66196 | −85.4391 | 40.63985 | 288 | TTP8 | 79.36731 | −7.57537 | 11.90171 |
| 74 | PO6 | 55.28989 | −78.3901 | 27.5132 | 289 | TPP9 | −69.0679 | −26.4722 | −22.8065 |
| 75 | PO8 | 62.37442 | −71.6847 | 11.74387 | 290 | TPP7 | −72.1635 | −32.9648 | 10.49897 |
| 76 | PO10 | 60.72315 | −67.1283 | −20.8686 | 291 | CPP5 | −70.2081 | −37.2139 | 39.19454 |
| 77 | O1 | −32.7194 | −94.0121 | 14.27106 | 292 | CPP3 | −60.0331 | −43.4354 | 65.72448 |
| 78 | Oz | 3.040962 | −102.261 | 17.13088 | 293 | CPP1 | −33.7106 | −48.8915 | 88.78305 |
| 79 | O2 | 38.5953 | −93.1054 | 13.28896 | 294 | CPPz | 3.471033 | −50.1578 | 96.55543 |
| 80 | O9 | −31.4911 | −90.3528 | −22.2667 | 295 | CPP2 | 41.27761 | −47.5401 | 88.19879 |
| 81 | O10 | 35.9837 | −91.066 | −21.1492 | 296 | CPP4 | 65.71957 | −43.0657 | 65.24334 |
| 82 | I1 | −31.4911 | −90.3528 | −22.2667 | 297 | CPP6 | 75.38837 | −37.5137 | 39.31531 |
| 83 | I2 | 35.9837 | −91.066 | −21.1492 | 298 | TPP8 | 78.0984 | −32.6421 | 11.23656 |
| 84 | AFp9h | −33.4931 | 79.64136 | −1.93019 | 299 | TPP10 | 77.33778 | −26.388 | −23.5285 |
| 85 | AFp7h | −29.075 | 79.48131 | 17.76607 | 300 | PPO9 | −62.4592 | −53.9455 | −21.5535 |
| 86 | AFp5h | −22.3499 | 82.01069 | 25.16756 | 301 | PPO7 | −64.3126 | −60.0043 | 11.86185 |
| 87 | AFp3h | −14.4406 | 83.74335 | 30.16004 | 302 | PPO5 | −60.4425 | −66.1359 | 31.64876 |
| 88 | AFp1h | −2.90148 | 85.04022 | 31.85801 | 303 | PPO3 | −47.0598 | −74.4885 | 51.85476 |
| 89 | AFp2h | 9.675535 | 85.09084 | 32.41395 | 304 | PPO1 | −25.6341 | −79.8341 | 65.64269 |
| 90 | AFp4h | 19.4288 | 84.61374 | 29.56817 | 305 | PPOz | 2.544747 | −82.1084 | 69.75008 |
| 91 | AFp6h | 28.54921 | 82.69922 | 24.88188 | 306 | PPO2 | 30.92945 | −80.0041 | 65.53837 |
| 92 | AFp8h | 34.67982 | 80.53532 | 17.90698 | 307 | PPO4 | 52.82137 | −73.5944 | 51.12067 |
| 93 | AFp10h | 39.61572 | 79.72829 | −3.10175 | 308 | PPO6 | 65.23055 | −65.1262 | 31.95901 |
| 94 | AFF9h | −50.3731 | 65.10702 | −5.09855 | 309 | PPO8 | 69.65572 | −58.325 | 10.88854 |
| 95 | AFF7h | −47.2197 | 64.64239 | 21.10871 | 310 | PPO10 | 67.54266 | −54.4292 | −22.6903 |
| 96 | AFF5h | −38.0659 | 69.20643 | 35.60582 | 311 | POO9 | −46.5394 | −78.0818 | −22.3323 |
| 97 | AFF3h | −25.6713 | 71.1931 | 49.07541 | 312 | POO7 | −47.1039 | −83.4091 | 13.77876 |
| 98 | AFF1h | −6.32591 | 73.72855 | 57.30378 | 313 | POO5 | −38.0156 | −90.045 | 22.25939 |
| 99 | AFF2h | 13.28156 | 74.02155 | 57.3758 | 314 | POO3 | −26.5354 | −95.0087 | 30.24876 |
| 100 | AFF4h | 32.14301 | 72.00444 | 49.46066 | 315 | POO1 | −11.3729 | −97.5071 | 35.97657 |
| 101 | AFF6h | 45.62772 | 68.72171 | 37.0618 | 316 | POOz | 1.421684 | −98.1703 | 36.50932 |
| 102 | AFF8h | 52.96668 | 66.07579 | 20.63462 | 317 | POO2 | 18.62236 | −97.2628 | 34.81373 |
| 103 | AFF10h | 56.20926 | 65.41907 | −5.3522 | 318 | POO4 | 33.08083 | −93.8825 | 29.92061 |
| 104 | FFT9h | −62.2082 | 42.18876 | −7.02438 | 319 | POO6 | 43.59314 | −89.0643 | 22.69428 |
| 105 | FFT7h | −60.208 | 43.71072 | 22.80203 | 320 | POO8 | 52.61583 | −82.9258 | 13.22738 |
| 106 | FFC5h | −52.1008 | 45.21527 | 46.08334 | 321 | POO10 | 52.20508 | −78.4769 | −21.0116 |
| 107 | FFC3h | −35.2463 | 49.01726 | 65.63649 | 322 | OI1 | −33.6804 | −92.1769 | −4.83753 |
| 108 | FFC1h | −10.0519 | 51.67205 | 78.71602 | 323 | OIz | 2.777775 | −101.21 | −5.77148 |
| 109 | FFC2h | 16.63637 | 52.14783 | 78.93129 | 324 | OI2 | 38.28328 | −92.2741 | −4.78841 |
| 110 | FFC4h | 41.65304 | 50.35553 | 66.03575 | 325 | T3 | −71.3853 | 5.05698 | 11.08433 |
| 111 | FFC6h | 58.85195 | 46.52834 | 46.21732 | 326 | T5 | −68.778 | −46.0653 | 11.4691 |
| 112 | FFT8h | 67.11803 | 42.89774 | 24.38205 | 327 | T4 | 77.38602 | 6.530228 | 9.717833 |
| 113 | FFT10h | 68.23584 | 42.95902 | −6.70591 | 328 | T6 | 74.42983 | −46.1598 | 10.89193 |
| 114 | FTT9h | −68.3143 | 20.6105 | −6.39526 | 329 | Exz | 3.413347 | −94.1549 | −34.1897 |
| 115 | FTT7h | −68.134 | 19.9404 | 27.09219 | 330 | Ex1 | −8.96197 | −94.2189 | −34.75 |
| 116 | FCC5h | −62.2303 | 17.18796 | 52.15804 | 331 | Ex2 | 13.74652 | −94.1877 | −33.868 |
| 117 | FCC3h | −42.1513 | 19.75226 | 77.24973 | 332 | Ex3 | −36.2817 | −82.5359 | −38.5457 |
| 118 | FCC1h | −12.9036 | 22.0511 | 91.96693 | 333 | Ex4 | 43.2247 | −80.4344 | −40.514 |
| 119 | FCC2h | 19.41887 | 22.7243 | 91.5395 | 334 | Ex5 | −45.9755 | −71.6576 | −39.8934 |
| 120 | FCC4h | 49.69143 | 20.55158 | 76.14634 | 335 | Ex6 | 51.25343 | −72.2088 | −40.2305 |
| 121 | FCC6h | 68.2901 | 18.7172 | 53.31686 | 336 | Ex7 | −53.701 | −60.5663 | −40.0393 |
| 122 | FTT8h | 75.10453 | 19.11036 | 25.89622 | 337 | Ex8 | 60.58237 | −59.2705 | −39.1244 |
| 123 | FTT10h | 74.3296 | 21.48304 | −7.01454 | 338 | Ex9 | −59.7161 | −48.2031 | −38.4779 |
| 124 | TTP7h | −73.2487 | −9.19111 | 26.35322 | 339 | Ex10 | 65.82136 | −47.2179 | −39.1501 |
| 125 | CCP5h | −68.0965 | −11.9187 | 56.38265 | 340 | Ex11 | −61.9403 | −42.6414 | −39.7219 |
| 126 | CCP3h | −49.0741 | −11.6074 | 82.11982 | 341 | Ex12 | 68.00566 | −42.5266 | −39.2374 |
| 127 | CCP1h | −15.7263 | −11.6781 | 99.48219 | 342 | Ex13 | −65.1545 | −22.0944 | −31.4051 |
| 128 | CCP2h | 21.99551 | −11.2966 | 99.28143 | 343 | Ex14 | 69.53552 | −21.2467 | −32.9172 |
| 129 | CCP4h | 55.17046 | −11.6881 | 82.76363 | 344 | Ex19 | −67.1288 | 8.122559 | −35.3273 |
| 130 | CCP6h | 74.18729 | −8.89512 | 55.26226 | 345 | Ex20 | 72.7148 | 8.95946 | −35.0052 |
| 131 | TTP8h | 79.55205 | −7.03237 | 25.88526 | 346 | Ex21 | −65.7359 | 19.52943 | −34.2457 |
| 132 | TPP9h | −73.1609 | −31.863 | −6.42023 | 347 | Ex22 | 71.67707 | 20.64119 | −34.9331 |
| 133 | TPP7h | −71.2541 | −35.6643 | 25.71736 | 348 | Ex23 | −64.4187 | 30.91435 | −34.9063 |
| 134 | CPP5h | −66.9441 | −40.7847 | 52.23498 | 349 | Ex24 | 70.69261 | 30.84808 | −34.6901 |
| 135 | CPP3h | −48.5238 | −46.0193 | 78.62906 | 350 | Ex25 | −61.0794 | 41.18943 | −35.0183 |
| 136 | CPP1h | −16.212 | −48.3473 | 95.56354 | 351 | Ex26 | 66.73764 | 41.93864 | −34.4454 |
| 137 | CPP2h | 22.19478 | −48.9157 | 95.74229 | 352 | Ex27 | −54.5623 | 51.50744 | −34.1932 |
| 138 | CPP4h | 54.62639 | −44.8678 | 78.57848 | 353 | Ex28 | 60.44307 | 51.08272 | −33.6067 |
| 139 | CPP6h | 72.4343 | −40.4486 | 51.81738 | 354 | Ex29 | −46.6597 | 58.25651 | −33.7596 |
| 140 | TPP8h | 77.38898 | −35.5248 | 24.96803 | 355 | Ex30 | 52.00837 | 59.01769 | −33.3612 |
| 141 | TPP10h | 78.72811 | −31.5109 | −7.08444 | 356 | Ex31 | −37.3566 | 64.40849 | −32.5878 |
| 142 | PPO9h | −63.5017 | −57.5402 | −6.52086 | 357 | Ex32 | 42.79809 | 64.87608 | −33.3054 |
| 143 | PPO7h | −63.334 | −62.1435 | 22.93271 | 358 | Ex33 | −27.8098 | 69.11741 | −31.0611 |
| 144 | PPO5h | −54.6809 | −70.9147 | 42.44857 | 359 | Ex34 | 34.60232 | 69.6494 | −30.5847 |
| 145 | PPO3h | −37.0488 | −78.1767 | 59.33378 | 360 | Exxz | 2.600347 | −88.223 | −53.4067 |
| 146 | PPO1h | −11.9075 | −81.2245 | 69.38043 | 361 | Exx1 | −14.7184 | −87.6082 | −53.7016 |
| 147 | PPO2h | 17.13343 | −81.2939 | 69.21624 | 362 | Exx2 | 12.11622 | −88.1398 | −53.8715 |
| 148 | PPO4h | 43.56473 | −76.6983 | 59.87423 | 363 | Exx3 | −39.6464 | −73.0199 | −51.5006 |
| 149 | PPO6h | 60.5297 | −69.1201 | 42.01922 | 364 | Exx4 | 44.51721 | −73.1659 | −52.6129 |
| 150 | PPO8h | 67.73132 | −61.8571 | 21.41818 | 365 | Exx5 | −49.3719 | −59.3122 | −53.2278 |
| 151 | PPO10h | 69.40595 | −56.9527 | −5.5405 | 366 | Exx6 | 54.64212 | −60.8592 | −52.4478 |
| 152 | POO9h | −46.5702 | −81.4362 | −6.27118 | 367 | Exx7 | −54.6454 | −44.98 | −54.0367 |
| 153 | POO7h | −42.5362 | −87.1419 | 17.76792 | 368 | Exx8 | 59.84738 | −49.264 | −52.8618 |
| 154 | POO5h | −32.906 | −92.4566 | 26.75433 | 369 | Exx9 | −56.4254 | −37.1207 | −53.3956 |
| 155 | POO3h | −18.1407 | −97.0718 | 32.9983 | 370 | Exx10 | 63.56102 | −35.4075 | −53.3598 |
| 156 | POO1h | −4.35032 | −98.1974 | 36.47809 | 371 | Exx11 | −57.4456 | −29.9627 | −53.944 |
| 157 | POO2h | 10.44098 | −98.1735 | 35.64018 | 372 | Exx12 | 64.68636 | −31.6225 | −53.0232 |
| 158 | POO4h | 24.9554 | −96.0371 | 33.98659 | 373 | Exx13 | −59.97 | −21.5577 | −55.1901 |
| 159 | POO6h | 39.33543 | −91.2763 | 26.13067 | 374 | Exx14 | 66.54841 | −22.0255 | −55.3961 |
| 160 | POO8h | 48.66409 | −85.8521 | 17.3463 | 375 | Exx15 | −62.8827 | −8.8041 | −51.3662 |
| 161 | POO10h | 51.90488 | −81.7238 | −3.61663 | 376 | Exx16 | 69.73143 | −8.80946 | −51.6004 |
| 162 | OI1h | −16.2967 | −99.2963 | −5.70751 | 377 | Exx19 | −62.6843 | 10.32494 | −49.7987 |
| 163 | OI2h | 19.77029 | −99.3035 | −5.48463 | 378 | Exx20 | 68.79898 | 10.01529 | −50.2973 |
| 164 | Fp1h | −11.069 | 85.78906 | 16.19175 | 379 | Exx21 | −62.7266 | 18.11554 | −47.6526 |
| 165 | Fp2h | 17.40425 | 86.00068 | 16.62331 | 380 | Exx22 | 68.68758 | 18.27113 | −48.8729 |
| 166 | AF9h | −43.1299 | 73.41663 | −3.09828 | 381 | Exx23 | −62.6512 | 26.49811 | −46.3039 |
| 167 | AF7h | −38.0283 | 73.39389 | 20.26724 | 382 | Exx24 | 68.65659 | 28.04243 | −48.9772 |
| 168 | AF5h | −31.289 | 76.66604 | 30.64554 | 383 | Exx25 | −60.7794 | 38.99 | −46.6925 |
| 169 | AF3h | −19.7298 | 79.67746 | 38.74554 | 384 | Exx26 | 65.71754 | 41.25271 | −46.1681 |
| 170 | AF1h | −5.34166 | 80.65797 | 44.42367 | 385 | Exx27 | −54.8926 | 50.79774 | −45.9224 |
| 171 | AF2h | 11.62486 | 80.66363 | 44.63826 | 386 | Exx28 | 61.09327 | 49.51846 | −47.248 |
| 172 | AF4h | 25.92847 | 79.96298 | 39.45565 | 387 | Exx29 | −46.6684 | 60.09819 | −43.8871 |
| 173 | AF6h | 37.10209 | 77.53429 | 31.11362 | 388 | Exx30 | 53.15618 | 59.38957 | −44.2863 |
| 174 | AF8h | 44.79905 | 73.63746 | 20.56396 | 389 | Exx31 | −34.8663 | 66.18984 | −42.5205 |
| 175 | AF10h | 48.30704 | 74.28571 | −3.70438 | 390 | Exx32 | 39.06328 | 67.17146 | −42.6776 |
| 176 | F9h | −56.2794 | 53.9874 | −4.8204 | 391 | Exx33 | −25.3427 | 69.17799 | −42.3267 |
| 177 | F7h | −54.1276 | 54.83297 | 21.29189 | 392 | Exx34 | 32.09887 | 69.18816 | −42.7444 |
| 178 | F5h | −46.1711 | 57.41139 | 41.39215 | 393 | Nz | 3.045649 | 85.78599 | −13.0592 |
| 179 | F3h | −30.6328 | 61.49756 | 57.99867 | 394 | Iz | 2.468983 | −97.0978 | −20.8705 |
| 180 | F1h | −8.29532 | 64.8715 | 67.98486 | 395 | LPA | −68.4998 | 8.249681 | −22.4725 |
| 181 | F2h | 15.81096 | 64.36282 | 68.75623 | 396 | RPA | 74.50288 | 7.909821 | −22.3627 |
| 182 | F4h | 36.61898 | 62.49406 | 58.716 | 397 | E91 | −61.6492 | −8.67609 | −54.4837 |
| 183 | F6h | 53.18107 | 57.77425 | 42.0475 | 398 | E145 | −17.7096 | −92.294 | −40.2247 |
| 184 | F8h | 60.83748 | 54.7282 | 22.34931 | 399 | E146 | −6.71912 | −95.1286 | −29.8033 |
| 185 | F10h | 63.2029 | 52.89882 | −6.03739 | 400 | E156 | 12.13489 | −95.1305 | −28.0012 |
| 186 | FT9h | −66.2717 | 31.36578 | −6.40502 | 401 | E165 | 22.84798 | −92.1301 | −40.7906 |
| 187 | FT7h | −65.0153 | 31.08678 | 25.53057 | 402 | E216 | 68.56397 | −9.00269 | −54.6747 |
| 188 | FC5h | −57.3659 | 31.34863 | 50.01614 | 403 | E229 | 66.97836 | 8.062315 | −56.7868 |
| 189 | FC3h | −39.1293 | 34.07175 | 72.53582 | 404 | E233 | 67.45635 | 24.21528 | −61.932 |
| 190 | FC1h | −11.5736 | 38.04508 | 86.22924 | 405 | E236 | 60.26823 | 48.67714 | −55.5136 |
| 191 | FC2h | 19.26051 | 37.39407 | 86.27477 | 406 | E237 | 63.47423 | 39.36662 | −66.5048 |
| 192 | FC4h | 45.08233 | 36.48935 | 72.40091 | 407 | E238 | 37.47127 | 68.77808 | −30.4581 |
| 193 | FC6h | 64.20741 | 32.13495 | 50.49309 | 408 | E239 | 51.7936 | 60.47199 | −51.2174 |
| 194 | FT8h | 71.35658 | 32.40674 | 25.6693 | 409 | E240 | 54.81123 | 54.56659 | −60.9892 |
| 195 | FT10h | 72.24158 | 31.60956 | −6.88527 | 410 | E241 | −32.4799 | 67.65216 | −30.8595 |
| 196 | T9h | −70.0675 | 5.813199 | −4.69129 | 411 | E242 | −45.6637 | 60.77062 | −52.4213 |
| 197 | T7h | −71.3325 | 5.365419 | 26.65917 | 412 | E243 | −49.1741 | 55.07184 | −61.148 |
| 198 | C5h | −65.0858 | 3.171895 | 55.58735 | 413 | E246 | −55.5859 | 48.38052 | −54.9718 |
| 199 | C3h | −46.1586 | 5.295424 | 79.522 | 414 | E247 | −58.3659 | 39.83813 | −66.754 |
| 200 | C1h | −15.5144 | 5.296714 | 96.40534 | 415 | E251 | −60.6583 | 23.2251 | −61.7857 |
| 201 | C2h | 21.45332 | 6.008428 | 96.20527 | 416 | E256 | −60.8025 | 7.515017 | −56.689 |
| 202 | C4h | 52.60489 | 5.316879 | 79.24145 | 417 | Z1 (CUSTOM1) | −23.8825 | −83.2177 | −58.0362 |
| 203 | C6h | 72.16673 | 4.238553 | 53.78267 | 418 | Z2 (CUSTOM2) | 28.18846 | −84.073 | −57.3271 |
| 204 | T8h | 77.50304 | 7.381789 | 26.59993 | 419 | NkB | 0.964145 | −87.1275 | −81.3772 |
| 205 | T10h | 75.50536 | 8.118926 | −5.99068 | 420 | NkF | 4.987046 | 34.93547 | −110.5 |
| 206 | TP7h | −73.3161 | −21.7404 | 24.86315 | 421 | NkL | −53.381 | −43.9806 | −86.5306 |
| 207 | CP5h | −68.7413 | −26.2843 | 55.30541 | 422 | NkR | 57.15611 | −46.0686 | −81.5096 |
| 208 | CP3h | −50.1834 | −27.5033 | 82.00723 | 423 | Z7 (CUSTOM7) | −38.1961 | −83.0703 | −32.9412 |
| 209 | CP1h | −16.7946 | −29.913 | 99.5545 | 424 | Z8 (CUSTOM8) | 29.06139 | −92.9926 | −27.3526 |
| 210 | CP2h | 22.80005 | −28.7106 | 99.65032 | 425 | Z9 (CUSTOM9) | 1.175956 | −87.1841 | −64.4326 |
| 211 | CP4h | 56.18856 | −27.8068 | 81.92991 | 426 | BuccR | 64.76903 | 22.15443 | −76.1383 |
| 212 | CP6h | 74.4538 | −24.369 | 55.76225 | 427 | BuccL | −59.1864 | 22.08333 | −76.1964 |
| 213 | TP8h | 79.55327 | −21.2631 | 25.87299 | 428 | TP9 | −72.7334 | −34.6841 | −21.3735 |
| 214 | P9h | −68.3091 | −45.6398 | −5.21867 | 429 | TP10 | 78.42117 | −34.7148 | −20.7991 |
| 215 | P7h | −68.2502 | −48.8372 | 24.32609 |
Appendix C
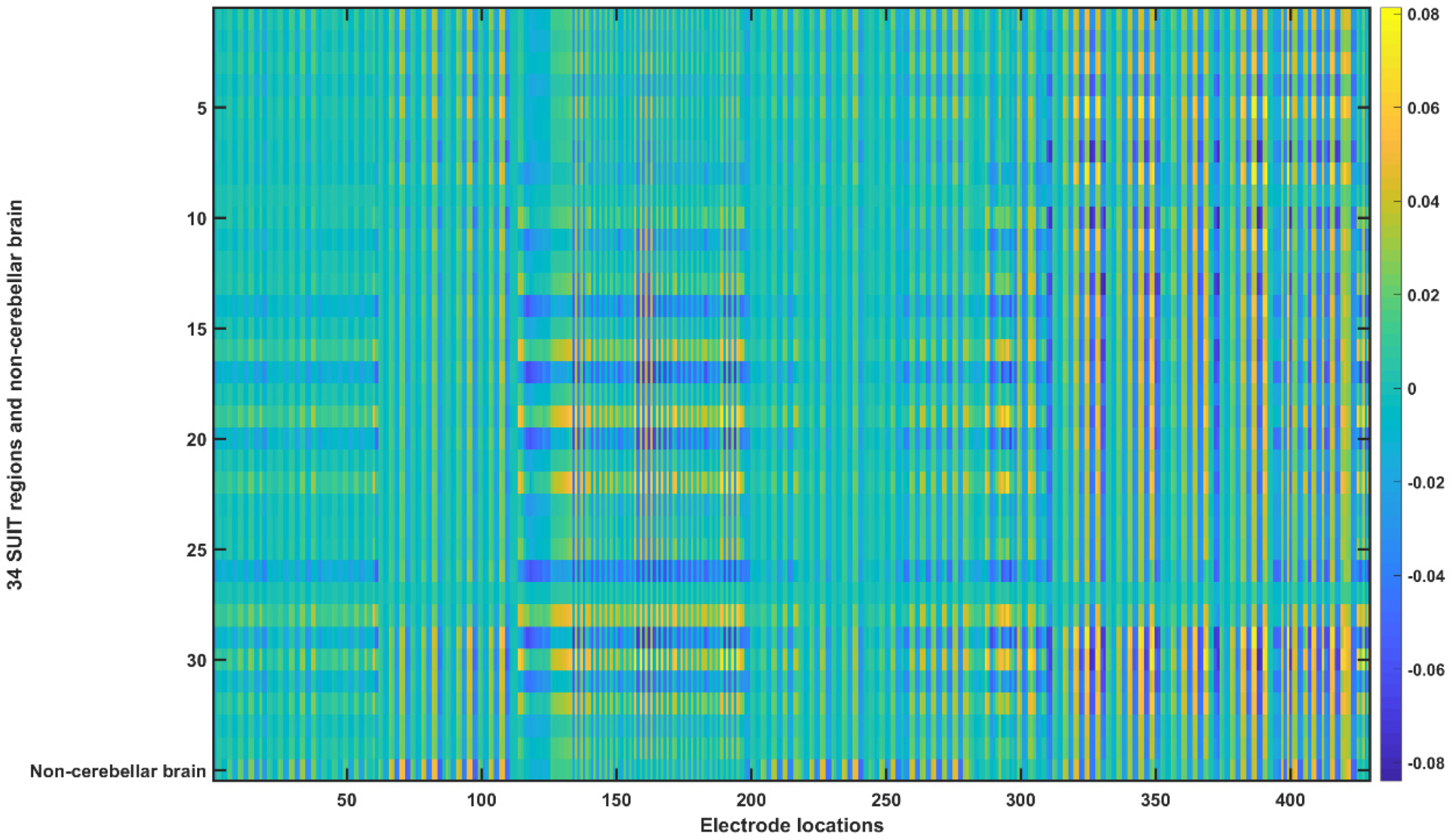
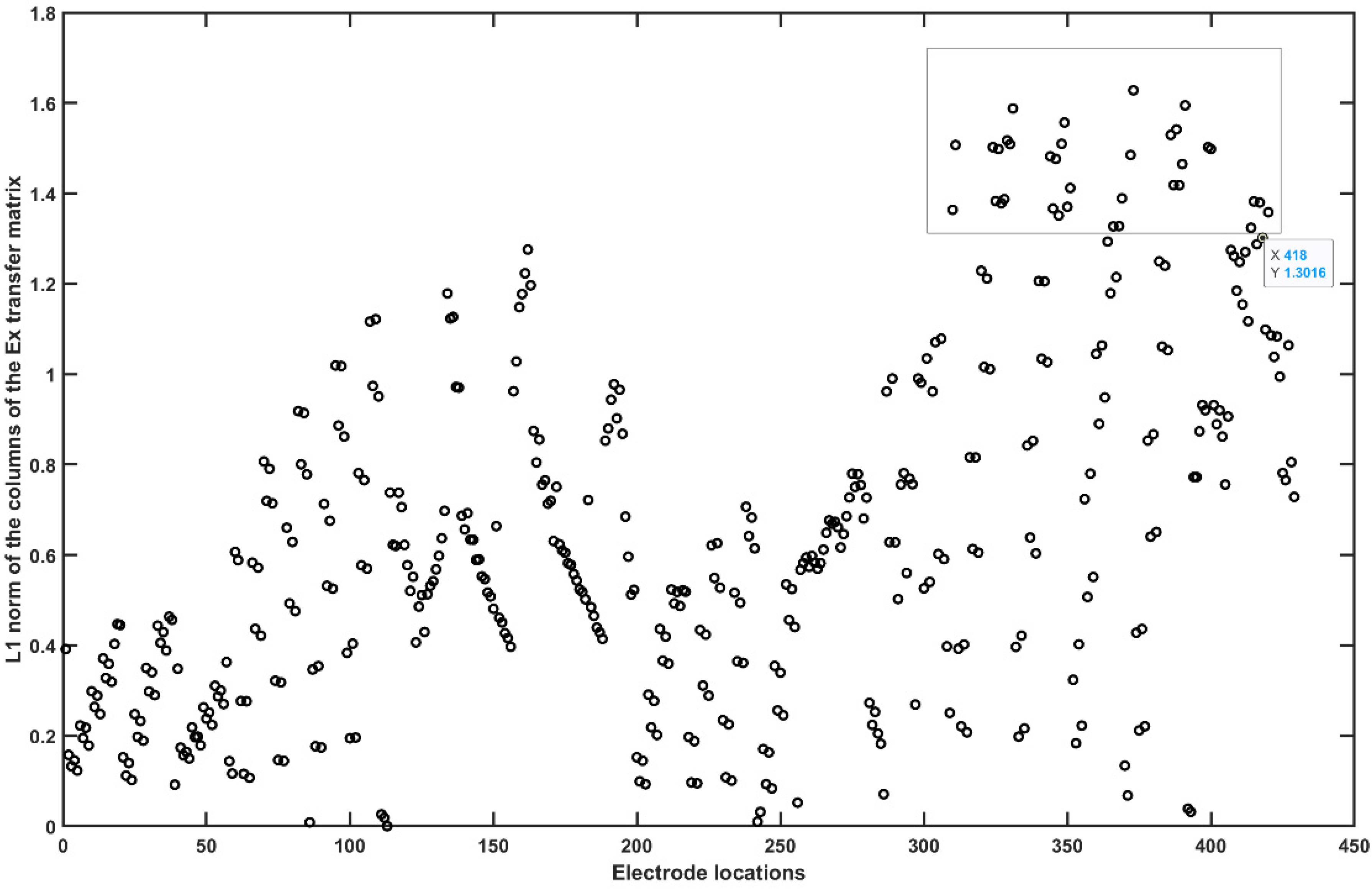
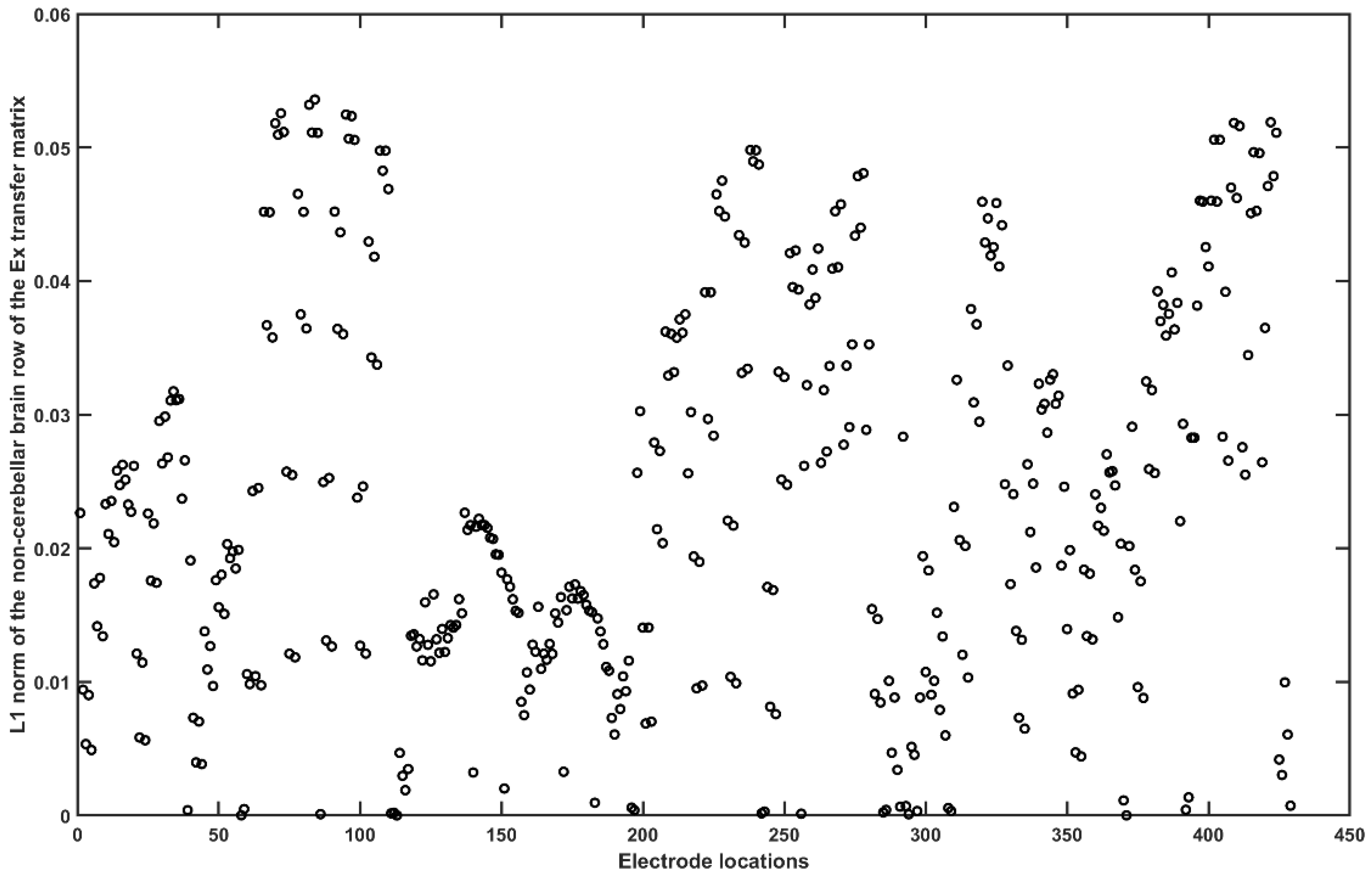
| 1 | “P10” | 10 | “PO10h” | 19 | “POO8” | 28 | “PPO9” |
| 2 | “P10h” | 11 | “PO7” | 20 | “POO9” | 29 | “PPO9h” |
| 3 | “P7” | 12 | “PO7h” | 21 | “POO9h” | 30 | “T5” |
| 4 | “P7h” | 13 | “PO8” | 22 | “PPO10” | 31 | “T6” |
| 5 | “P8” | 14 | “PO8h” | 23 | “PPO10h” | 32 | “TPP10h” |
| 6 | “P8h” | 15 | “PO9” | 24 | “PPO7” | 33 | “TPP7” |
| 7 | “P9” | 16 | “PO9h” | 25 | “PPO7h” | 34 | “TPP8” |
| 8 | “P9h” | 17 | “POO10” | 26 | “PPO8” | 35 | “TPP8h” |
| 9 | “PO10” | 18 | “POO10h” | 27 | “PPO8h” | 36 | “TPP9h” |
| 1 | “I1h” | 10 | “OI2” |
| 2 | “I2h” | 11 | “OI2h” |
| 3 | “Iz” | 12 | “OIz” |
| 4 | “O1” | 13 | “Oz” |
| 5 | “O1h” | 14 | “POO1h” |
| 6 | “O2” | 15 | “POO2” |
| 7 | “O2h” | 16 | “POO2h” |
| 8 | “OI1” | 17 | “POO3h” |
| 9 | “OI1h” | 18 | “POOz” |
| 1 | “E145” | 10 | “Ex6” | 19 | “Exx4” | 28 | “NkL” |
| 2 | “E146” | 11 | “Ex7” | 20 | “Exx5” | 29 | “NkR” |
| 3 | “E156” | 12 | “Ex8” | 21 | “Exx6” | 30 | “CUSTOM1” |
| 4 | “E165” | 13 | “Exx10” | 22 | “Exx7” | 31 | “CUSTOM2” |
| 5 | “Ex1” | 14 | “Exx11” | 23 | “Exx8” | 32 | “CUSTOM7” |
| 6 | “Ex2” | 15 | “Exx12” | 24 | “Exx9” | 33 | “CUSTOM9” |
| 7 | “Ex3” | 16 | “Exx1” | 25 | “Exxz” | ||
| 8 | “Ex4” | 17 | “Exx2” | 26 | “Exz” | ||
| 9 | “Ex5” | 18 | “Exx3” | 27 | “NkB” |
Appendix D

References
- Feigin, V.L.; Forouzanfar, M.H.; Krishnamurthi, R.; Mensah, G.A.; Connor, M.; Bennett, D.A.; Moran, A.E.; Sacco, R.L.; Anderson, L.; Truelsen, T.; et al. Global and regional burden of stroke during 1990–2010: Findings from the global burden of disease study 2010. Lancet 2014, 383, 245–255. [Google Scholar] [CrossRef]
- Pandian, J.D.; Sudhan, P. Stroke epidemiology and stroke care services in India. J. Stroke 2013, 15, 128–134. [Google Scholar] [CrossRef]
- Kamalakannan, S.; Gudlavalleti, A.S.V.; Gudlavalleti, V.S.M.; Goenka, S.; Kuper, H. Incidence and prevalence of stroke in India: A systematic review. Indian J. Med. Res. 2017, 146, 175–185. [Google Scholar] [CrossRef]
- Das, A.; Botticello, A.L.; Wylie, G.R.; Radhakrishnan, K. Neurologic disability: A hidden epidemic for India. Neurology 2012, 79, 2146–2147. [Google Scholar] [CrossRef]
- Wathen, C.A.; Frizon, L.A.; Maiti, T.K.; Baker, K.B.; Machado, A.G. Deep brain stimulation of the cerebellum for poststroke motor rehabilitation: From laboratory to clinical trial. Neurosurg. Focus 2018, 45, E13. [Google Scholar] [CrossRef]
- Bond, K.M.; Brinjikji, W.; Eckel, L.J.; Kallmes, D.F.; McDonald, R.J.; Carr, C.M. Dentate update: Imaging features of entities that affect the dentate nucleus. Am. J. Neuroradiol. 2017, 38, 1467–1474. [Google Scholar] [CrossRef] [PubMed]
- Rezaee, Z.; Dutta, A. Cerebellar lobules optimal stimulation (CLOS): A computational pipeline to optimize cerebellar lobule-specific electric field distribution. Front. Neurosci. 2019, 13, 266. [Google Scholar] [CrossRef] [PubMed]
- Grimaldi, G.; Argyropoulos, G.P.; Bastian, A.; Cortes, M.; Davis, N.J.; Edwards, D.J.; Ferrucci, R.; Fregni, F.; Galea, J.M.; Hamada, M.; et al. Cerebellar transcranial direct current stimulation (ctDCS). Neuroscientist 2016, 22, 83–97. [Google Scholar] [CrossRef] [PubMed]
- Van Dun, K.; Bodranghien, F.C.A.A.; Mariën, P.; Manto, M.U. tDCS of the cerebellum: Where do we stand in 2016? Technical issues and critical review of the literature. Front. Hum. Neurosci. 2016, 10, 199. [Google Scholar] [CrossRef] [PubMed]
- Jayaram, G.; Tang, B.; Pallegadda, R.; Vasudevan, E.V.L.; Celnik, P.; Bastian, A. Modulating locomotor adaptation with cerebellar stimulation. J. Neurophysiol. 2012, 107, 2950–2957. [Google Scholar] [CrossRef]
- Poortvliet, P.; Hsieh, B.; Cresswell, A.; Au, J.; Meinzer, M. Cerebellar transcranial direct current stimulation improves adaptive postural control. Clin. Neurophysiol. Off. J. Int. Fed. Clin. Neurophysiol. 2018, 129, 33–41. [Google Scholar] [CrossRef]
- Ferrucci, R.; Bocci, T.; Cortese, F.; Ruggiero, F.; Priori, A. Cerebellar transcranial direct current stimulation in neurological disease. Cerebellum Ataxias 2016, 3, 16. [Google Scholar] [CrossRef] [PubMed]
- Galea, J.M.; Jayaram, G.; Ajagbe, L.; Celnik, P. Modulation of cerebellar excitability by polarity-specific noninvasive direct current stimulation. J. Neurosci. Off. J. Soc. Neurosci. 2009, 29, 9115–9122. [Google Scholar] [CrossRef] [PubMed]
- Timmann, D.; Drepper, J.; Frings, M.; Maschke, M.; Richter, S.; Gerwig, M.; Kolb, F.P. The human cerebellum contributes to motor, emotional and cognitive associative learning. A review. Cortex J. Devoted Study Nerv. Syst. Behav. 2010, 46, 845–857. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, T.; Tomatsu, S.; Tsunoda, Y.; Lee, J.; Hoffman, D.S.; Kakei, S. Releasing dentate nucleus cells from Purkinje cell inhibition generates output from the cerebrocerebellum. PLoS ONE 2014, 9, e108774. [Google Scholar] [CrossRef] [PubMed]
- Kumar, D.; Das, A.; Lahiri, U.; Dutta, A. A Human-machine-interface integrating low-cost sensors with a neuromuscular electrical stimulation system for post-stroke balance rehabilitation. JoVE 2016, e52394. [Google Scholar] [CrossRef] [PubMed]
- Jalali, R.; Miall, R.C.; Galea, J.M. No consistent effect of cerebellar transcranial direct current stimulation on visuomotor adaptation. J. Neurophysiol. 2017, 118, 655–665. [Google Scholar] [CrossRef]
- Jalali, R.; Chowdhury, A.; Wilson, M.; Miall, R.C.; Galea, J.M. Neural changes associated with cerebellar tDCS studied using MR spectroscopy. Exp. Brain Res. 2018, 236, 997–1006. [Google Scholar] [CrossRef]
- Zandvliet, S.B.; Meskers, C.G.M.; Kwakkel, G.; van Wegen, E.E.H. Short-term effects of cerebellar tDCS on standing balance performance in patients with chronic stroke and healthy age-matched elderly. Cerebellum Lond. Engl. 2018, 17, 575–589. [Google Scholar] [CrossRef]
- Yosephi, M.H.; Ehsani, F.; Zoghi, M.; Jaberzadeh, S. Multi-session anodal tDCS enhances the effects of postural training on balance and postural stability in older adults with high fall risk: Primary motor cortex versus cerebellar stimulation. Brain Stimulat. 2018, 11, 1239–1250. [Google Scholar] [CrossRef]
- Batsikadze, G.; Rezaee, Z.; Chang, D.-I.; Gerwig, M.; Herlitze, S.; Dutta, A.; Nitsche, M.A.; Timmann, D. Effects of cerebellar transcranial direct current stimulation on cerebellar-brain inhibition in humans: A systematic evaluation. Brain Stimul. 2019, 12, 1177–1186. [Google Scholar] [CrossRef] [PubMed]
- Van de Winckel, A.; Carey, J.R.; Bisson, T.A.; Hauschildt, E.C.; Streib, C.D.; Durfee, W.K. Home-based transcranial direct current stimulation plus tracking training therapy in people with stroke: An open-label feasibility study. J. NeuroEngineering Rehabil. 2018, 15, 83. [Google Scholar] [CrossRef] [PubMed]
- Verma, S.; Kumar, D.; Kumawat, A.; Dutta, A.; Lahiri, U. A low-cost adaptive balance training platform for stroke patients: A usability study. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 935–944. [Google Scholar] [CrossRef] [PubMed]
- Dutta, A.; Lahiri, U.; Das, A.; Nitsche, M.A.; Guiraud, D. Post-stroke balance rehabilitation under multi-level electrotherapy: A conceptual review. Front. Neurosci. 2014, 8, 403. [Google Scholar] [CrossRef]
- Dutta, A.; Banerjee, A.; Dutta, A. Low-cost visual postural feedback with Wii balance board and Microsoft Kinect—A feasibility study. In Proceedings of the 2013 IEEE Point-of-Care Healthcare Technologies (PHT), Bangalore, India, 16–18 January 2013; pp. 291–294. [Google Scholar]
- Dutta, A.; Chugh, S.; Banerjee, A.; Dutta, A. Point-of-care-testing of standing posture with Wii balance board and Microsoft Kinect during transcranial direct current stimulation: A feasibility study. NeuroRehabilitation 2014, 34, 789–798. [Google Scholar] [CrossRef]
- Huang, Y.; Datta, A.; Bikson, M.; Parra, L.C. ROAST: An open-source, fully-automated, realistic volumetric-approach-based simulator for TES. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018. [Google Scholar]
- Jurcak, V.; Tsuzuki, D.; Dan, I. 10/20, 10/10, and 10/5 systems revisited: Their validity as relative head-surface-based positioning systems. NeuroImage 2007, 34, 1600–1611. [Google Scholar] [CrossRef]
- Thielscher, A.; Opitz, A.; Windhoff, M. Impact of the gyral geometry on the electric field induced by transcranial magnetic stimulation. NeuroImage 2011, 54, 234–243. [Google Scholar] [CrossRef]
- Windhoff, M.; Opitz, A.; Thielscher, A. Electric field calculations in brain stimulation based on finite elements: An optimized processing pipeline for the generation and usage of accurate individual head models. Hum. Brain Mapp. 2013, 34, 923–935. [Google Scholar] [CrossRef]
- Fillmore, P.T.; Phillips-Meek, M.C.; Richards, J.E. Age-specific MRI brain and head templates for healthy adults from 20 through 89 years of age. Front. Aging Neurosci. 2015, 7, 44. [Google Scholar] [CrossRef]
- Avants, B.B.; Epstein, C.L.; Grossman, M.; Gee, J.C. Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Med. Image Anal. 2008, 12, 26–41. [Google Scholar] [CrossRef]
- Escalona, P.R.; Early, B.; McDonald, W.M.; Doraiswamy, P.M.; Shah, S.A.; Husain, M.M.; Boyko, O.B.; Figiel, G.S.; Ellinwood, E.H.; Nemeroff, C.B.; et al. Reduction of cerebellar volume in major depression: A controlled MRI study. Depression 1993, 1, 156–158. [Google Scholar] [CrossRef]
- Richards, J.E.; Xie, W. Brains for all the ages: Structural neurodevelopment in infants and children from a life-span perspective. In Advances in Child Development and Behavior; Benson, J.B., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 48, pp. 1–52. ISBN 0065-2407. [Google Scholar]
- Richards, J.E.; Sanchez, C.; Phillips-Meek, M.; Xie, W. A database of age-appropriate average MRI templates. Shar. Wealth Brain Imaging Repos. 2015 2016, 124, 1254–1259. [Google Scholar] [CrossRef]
- Sanchez, C.E.; Richards, J.E.; Almli, C.R. Age-specific MRI templates for pediatric neuroimaging. Dev. Neuropsychol. 2012, 37, 379–399. [Google Scholar] [CrossRef]
- Penny, W.D.; Friston, K.J.; Ashburner, J.T.; Kiebel, S.J.; Nichols, T.E. Statistical Parametric Mapping: The Analysis of Functional Brain Images; Elsevier: Amsterdam, The Netherlands, 2011; ISBN 978-0-08-046650-7. [Google Scholar]
- Fang, Q.; Boas, D.A. Tetrahedral mesh generation from volumetric binary and grayscale images. In Proceedings of the 2009 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Boston, MA, USA, 28 June–1 July 2009; pp. 1142–1145. [Google Scholar]
- Dular, P.; Geuzaine, C.; Henrotte, F.; Legros, W. A general environment for the treatment of discrete problems and its application to the finite element method. IEEE Trans. Magn. 1998, 34, 3395–3398. [Google Scholar] [CrossRef]
- SPM. Statistical Parametric Mapping. Available online: http://www.fil.ion.ucl.ac.uk/spm/ (accessed on 16 June 2018).
- Datta, A.; Bansal, V.; Diaz, J.; Patel, J.; Reato, D.; Bikson, M. Gyri-precise head model of transcranial direct current stimulation: Improved spatial focality using a ring electrode versus conventional rectangular pad. Brain Stimulat. 2009, 2, 201–207.e1. [Google Scholar] [CrossRef]
- Foerster, Á.S.; Rezaee, Z.; Paulus, W.; Nitsche, M.A.; Dutta, A. Effects of cathode location and the size of anode on anodal transcranial direct current stimulation over the leg motor area in healthy humans. Front. Neurosci. 2018, 12, 443. [Google Scholar] [CrossRef]
- Oostenveld, R.; Praamstra, P. The five percent electrode system for high-resolution EEG and ERP measurements. Clin. Neurophysiol. 2001, 112, 713–719. [Google Scholar] [CrossRef]
- Otal, B.; Dutta, A.; Foerster, Á.; Ripolles, O.; Kuceyeski, A.; Miranda, P.C.; Edwards, D.J.; Ilić, T.V.; Nitsche, M.A.; Ruffini, G. Opportunities for guided multichannel non-invasive transcranial current stimulation in poststroke rehabilitation. Front. Neurol. 2016, 7, 21. [Google Scholar] [CrossRef]
- Grimaldi, G.; Manto, M. Anodal transcranial direct current stimulation (tDCS) decreases the amplitudes of long-latency stretch reflexes in cerebellar ataxia. Ann. Biomed. Eng. 2013, 41, 2437–2447. [Google Scholar] [CrossRef]
- Dmochowski, J.P.; Datta, A.; Bikson, M.; Su, Y.; Parra, L.C. Optimized multi-electrode stimulation increases focality and intensity at target. J. Neural Eng. 2011, 8, 046011. [Google Scholar] [CrossRef]
- Lee, C.; Kim, E.; Im, C.-H. Techniques for efficient computation of electric fields generated by transcranial direct-current stimulation. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Neumaier, A. Solving ill-conditioned and singular linear systems: A tutorial on regularization. SIAM Rev. 1998, 40, 636–666. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Saturnino, G.B.; Siebner, H.R.; Thielscher, A.; Madsen, K.H. Accessibility of cortical regions to focal TES: Dependence on spatial position, safety, and practical constraints. NeuroImage 2019, 203, 116183. [Google Scholar] [CrossRef] [PubMed]
- Buckner, R.L.; Krienen, F.M.; Castellanos, A.; Diaz, J.C.; Yeo, B.T.T. The organization of the human cerebellum estimated by intrinsic functional connectivity. J. Neurophysiol. 2011, 106, 2322–2345. [Google Scholar] [CrossRef]
- Diedrichsen, J. A spatially unbiased atlas template of the human cerebellum. NeuroImage 2006, 33, 127–138. [Google Scholar] [CrossRef]
- Diedrichsen, J.; Balsters, J.H.; Flavell, J.; Cussans, E.; Ramnani, N. A probabilistic MR atlas of the human cerebellum. NeuroImage 2009, 46, 39–46. [Google Scholar] [CrossRef]
- Giacometti, P.; Perdue, K.L.; Diamond, S.G. Algorithm to find high density EEG scalp coordinates and analysis of their correspondence to structural and functional regions of the brain. J. Neurosci. Methods 2014, 229, 84–96. [Google Scholar] [CrossRef]
- FSL. FslWiki. Available online: https://fsl.fmrib.ox.ac.uk/fsl/fslwiki (accessed on 17 February 2018).
- Diedrichsen, J.; Kriegeskorte, N. Representational models: A common framework for understanding encoding, pattern-component, and representational-similarity analysis. PLoS Comput. Biol. 2017, 13, e1005508. [Google Scholar] [CrossRef]
- King, M.; Hernandez-Castillo, C.R.; Poldrack, R.A.; Ivry, R.B.; Diedrichsen, J. Functional boundaries in the human cerebellum revealed by a multi-domain task battery. Nat. Neurosci. 2019, 22, 1371–1378. [Google Scholar] [CrossRef]
- Diedrichsen, J.; King, M.; Hernandez-Castillo, C.; Sereno, M.; Ivry, R.B. Universal transform or multiple functionality? Understanding the contribution of the human cerebellum across task domains. Neuron 2019, 102, 918–928. [Google Scholar] [CrossRef]
- Mariën, P.; van Dun, K.; Verhoeven, J. Cerebellum and apraxia. Cerebellum Lond. Engl. 2015, 14, 39–42. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Guell, X.; D’Mello, A.M.; Hubbard, N.A.; Romeo, R.R.; Gabrieli, J.D.; Whitfield-Gabrieli, S.; Schmahmann, J.D.; Anteraper, S.A. Functional territories of human dentate nucleus. bioRxiv 2019, 608620. [Google Scholar] [CrossRef] [PubMed]
- Guell, X.; Schmahmann, J.D.; Gabrieli, J.D.; Ghosh, S.S. Functional gradients of the cerebellum. eLife 2018, 7, e36652. [Google Scholar] [CrossRef] [PubMed]
- Stoodley, C.J.; Schmahmann, J.D. Evidence for topographic organization in the cerebellum of motor control versus cognitive and affective processing. Cortex J. Devoted Study Nerv. Syst. Behav. 2010, 46, 831–844. [Google Scholar] [CrossRef] [PubMed]
- Dutta, A.; Kumar, R.; Malhotra, S.; Chugh, S.; Banerjee, A.; Dutta, A. A low-cost point-of-care testing system for psychomotor symptoms of depression affecting standing balance: A preliminary study in India. Depress. Res. Treat. 2013, 2013, 640861. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kumar, D.; González, A.; Das, A.; Dutta, A.; Fraisse, P.; Hayashibe, M.; Lahiri, U. Virtual reality-based center of mass-assisted personalized balance training system. Front. Bioeng. Biotechnol. 2018, 5, 85. [Google Scholar] [CrossRef]
- Clark, R.A.; Pua, Y.-H.; Bryant, A.L.; Hunt, M.A. Validity of the Microsoft Kinect for providing lateral trunk lean feedback during gait retraining. Gait Posture 2013, 38, 1064–1066. [Google Scholar] [CrossRef]
- Clark, R.A.; Bryant, A.L.; Pua, Y.; McCrory, P.; Bennell, K.; Hunt, M. Validity and reliability of the Nintendo Wii balance board for assessment of standing balance. Gait Posture 2010, 31, 307–310. [Google Scholar] [CrossRef]
- Kumar, D.; Sinha, N.; Dutta, A.; Lahiri, U. Virtual reality-based balance training system augmented with operant conditioning paradigm. Biomed. Eng. OnLine 2019, 18, 90. [Google Scholar] [CrossRef]
- Dutta, A.; Kumar, D.; Lahiri, U.; Das, A.; Padma, M.V. Post-stroke engagement-sensitive balance rehabilitation under an adaptive multi-level electrotherapy: Clinical hypothesis and computational framework. Neurosci. Biomed. Eng. 2014, 2, 66–80. [Google Scholar] [CrossRef]
- Ebner, T.J. Cerebellum and internal models. In Handbook of the Cerebellum and Cerebellar Disorders; Springer: Dordrecht, The Netherlands, 2013; pp. 1279–1295. ISBN 978-94-007-1332-1. [Google Scholar]
- Van Duijnhoven, H.J.R.; Heeren, A.; Peters, M.A.M.; Veerbeek, J.M.; Kwakkel, G.; Geurts, A.C.H.; Weerdesteyn, V. Effects of exercise therapy on balance capacity in chronic stroke: Systematic review and meta-analysis. Stroke 2016, 47, 2603–2610. [Google Scholar] [CrossRef] [PubMed]
- De Rooij, I.J.M.; van de Port, I.G.L.; Meijer, J.-W.G. Effect of virtual reality training on balance and gait ability in patients with stroke: Systematic review and meta-analysis. Phys. Ther. 2016, 96, 1905–1918. [Google Scholar] [CrossRef] [PubMed]
- Schröder, J.; van Criekinge, T.; Embrechts, E.; Celis, X.; Van Schuppen, J.; Truijen, S.; Saeys, W. Combining the benefits of tele-rehabilitation and virtual reality-based balance training: A systematic review on feasibility and effectiveness. Disabil. Rehabil. Assist. Technol. 2019, 14, 2–11. [Google Scholar] [CrossRef] [PubMed]
- Denissen, S.; Staring, W.; Kunkel, D.; Pickering, R.M.; Lennon, S.; Geurts, A.C.; Weerdesteyn, V.; Verheyden, G.S. Interventions for preventing falls in people after stroke. Cochrane Database Syst. Rev. 2019, 10, CD008728. [Google Scholar] [CrossRef]
- Zadikoff, C.; Lang, A.E. Apraxia in movement disorders. Brain J. Neurol. 2005, 128, 1480–1497. [Google Scholar] [CrossRef]
- Ambrosoni, E.; Sala, S.D.; Motto, C.; Oddo, S.; Spinnler, H. Gesture imitation with lower limbs following left hemisphere stroke. Arch. Clin. Neuropsychol. 2006, 21, 349–358. [Google Scholar] [CrossRef]
- Buchmann, I.; Randerath, J. Selection and application of familiar and novel tools in patients with left and right hemispheric stroke: Psychometrics and normative data. Cortex 2017, 94, 49–62. [Google Scholar] [CrossRef]
- Dobigny-Roman, N.; Dieudonne-moinet, B.; Tortrat, D.; Verny, M.; Forotte, B. Ideomotor apraxia test: A new test of imitation of gestures for elderly people. Eur. J. Neurol. 1998, 5, 571–578. [Google Scholar] [CrossRef]
- Rezaee, Z.; Dutta, A. Lobule-Specific Dosage Considerations for Cerebellar Transcranial Direct Current Stimulation During Healthy Aging: A Computational Modeling Study Using Age-Specific Magnetic Resonance Imaging Templates. Neuromodulation Technol. Neural Interface 2020. [Google Scholar] [CrossRef]
- Mutha, P.K.; Stapp, L.H.; Sainburg, R.L.; Haaland, K.Y. Motor adaptation deficits in ideomotor apraxia. J. Int. Neuropsychol. Soc. JINS 2017, 23, 139–149. [Google Scholar] [CrossRef]
- Teasell, R.; McRae, M.; Foley, N.; Bhardwaj, A. The incidence and consequences of falls in stroke patients during inpatient rehabilitation: Factors associated with high risk. Arch. Phys. Med. Rehabil. 2002, 83, 329–333. [Google Scholar] [CrossRef] [PubMed]
- Laakso, I.; Mikkonen, M.; Koyama, S.; Hirata, A.; Tanaka, S. Can electric fields explain inter-individual variability in transcranial direct current stimulation of the motor cortex? Sci. Rep. 2019, 9, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Khattar, B.; Banerjee, A.; Reddi, R.; Dutta, A. Feasibility of functional electrical stimulation-assisted neurorehabilitation following stroke in India: A case series. Case Rep. Neurol. Med. 2012, 2012, 830873. [Google Scholar] [CrossRef]
- Lindley, R.I.; Anderson, C.S.; Billot, L.; Forster, A.; Hackett, M.L.; Harvey, L.A.; Jan, S.; Li, Q.; Liu, H.; Langhorne, P.; et al. Family-led rehabilitation after stroke in India (ATTEND): A randomised controlled trial. Lancet 2017, 390, 588–599. [Google Scholar] [CrossRef]
- Sharma, S.; Padma, M.V.; Bhardwaj, A.; Sharma, A.; Sawal, N.; Thakur, S. Telestroke in resource-poor developing country model. Neurol. India 2016, 64, 934. [Google Scholar] [CrossRef] [PubMed]
- Khanna, M.; Gowda, G.S.; Bagevadi, V.I.; Gupta, A.; Kulkarni, K.; S Shyam, R.P.; Basavaraju, V.; Ramesh, M.B.; Sashidhara, H.N.; Manjunatha, N.; et al. Feasibility and utility of tele-neurorehabilitation service in India: Experience from a quaternary center. J. Neurosci. Rural Pract. 2018, 9, 541–544. [Google Scholar]
- Kamalakannan, S.; Gudlavalleti Venkata, M.; Prost, A.; Natarajan, S.; Pant, H.; Chitalurri, N.; Goenka, S.; Kuper, H. Rehabilitation needs of stroke survivors after discharge from hospital in India. Arch. Phys. Med. Rehabil. 2016, 97, 1526–1532.e9. [Google Scholar] [CrossRef]
- Banerjee, A.; Kumar, R.; Khattar, B.; Reddi, R.; Dutta, A. Customizing functional electrical therapy using a ’rehabilitation problem-solving form’—A preliminary study. In Converging Clinical and Engineering Research on Neurorehabilitation; Pons, J.L., Torricelli, D., Pajaro, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 183–188. [Google Scholar]
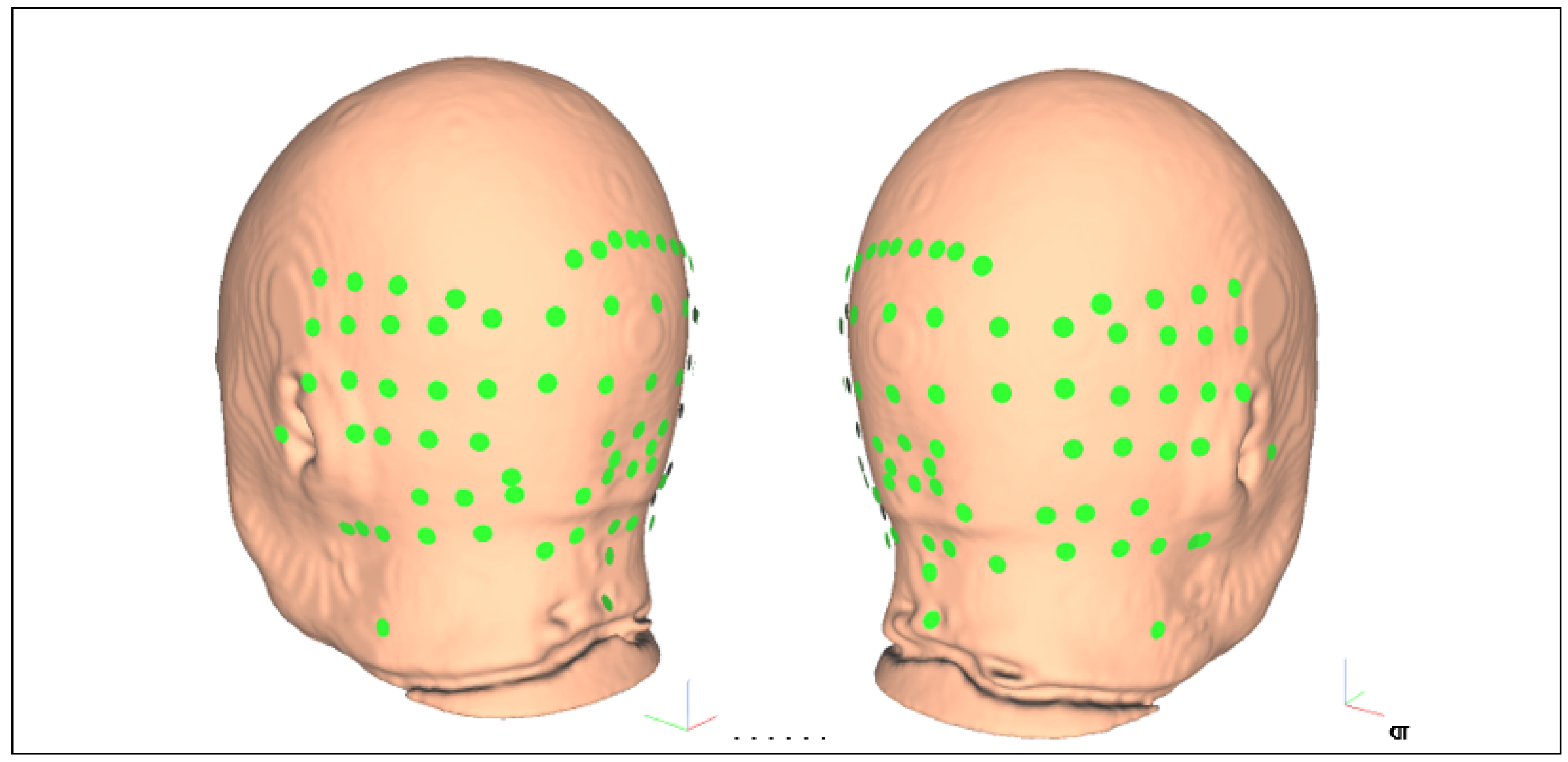



| Participant ID | Age | Gender | Hemiplegic Side |
|---|---|---|---|
| P1 * | 48 years | Male | LEFT |
| P2 * | 38 years | Male | RIGHT |
| P3 | 35 years | Male | LEFT |
| P4 * | 44 years | Male | RIGHT |
| P5 | 56 years | Male | RIGHT |
| P6 | 59 years | Male | RIGHT |
| P7 | 28 years | Male | LEFT |
| P8 * | 50 years | Male | LEFT |
| P9 | 50 years | Male | LEFT |
| P10 * | 32 years | Male | RIGHT |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezaee, Z.; Kaura, S.; Solanki, D.; Dash, A.; Srivastava, M.V.P.; Lahiri, U.; Dutta, A. Deep Cerebellar Transcranial Direct Current Stimulation of the Dentate Nucleus to Facilitate Standing Balance in Chronic Stroke Survivors—A Pilot Study. Brain Sci. 2020, 10, 94. https://doi.org/10.3390/brainsci10020094
Rezaee Z, Kaura S, Solanki D, Dash A, Srivastava MVP, Lahiri U, Dutta A. Deep Cerebellar Transcranial Direct Current Stimulation of the Dentate Nucleus to Facilitate Standing Balance in Chronic Stroke Survivors—A Pilot Study. Brain Sciences. 2020; 10(2):94. https://doi.org/10.3390/brainsci10020094
Chicago/Turabian StyleRezaee, Zeynab, Surbhi Kaura, Dhaval Solanki, Adyasha Dash, M V Padma Srivastava, Uttama Lahiri, and Anirban Dutta. 2020. "Deep Cerebellar Transcranial Direct Current Stimulation of the Dentate Nucleus to Facilitate Standing Balance in Chronic Stroke Survivors—A Pilot Study" Brain Sciences 10, no. 2: 94. https://doi.org/10.3390/brainsci10020094
APA StyleRezaee, Z., Kaura, S., Solanki, D., Dash, A., Srivastava, M. V. P., Lahiri, U., & Dutta, A. (2020). Deep Cerebellar Transcranial Direct Current Stimulation of the Dentate Nucleus to Facilitate Standing Balance in Chronic Stroke Survivors—A Pilot Study. Brain Sciences, 10(2), 94. https://doi.org/10.3390/brainsci10020094






