Modified Multi-Support Response Spectrum Analysis of Structures with Multiple Supports under Incoherent Ground Excitation
Abstract
:1. Introduction
2. The Response Spectrum Method under Coherent Ground Excitations
3. The MSRS Method under Incoherent Ground Excitations
3.1. The Equation of Motion
3.2. Solution of Equation (10)
4. The Modified MSRS Method
4.1. Problems in the MSRS Method
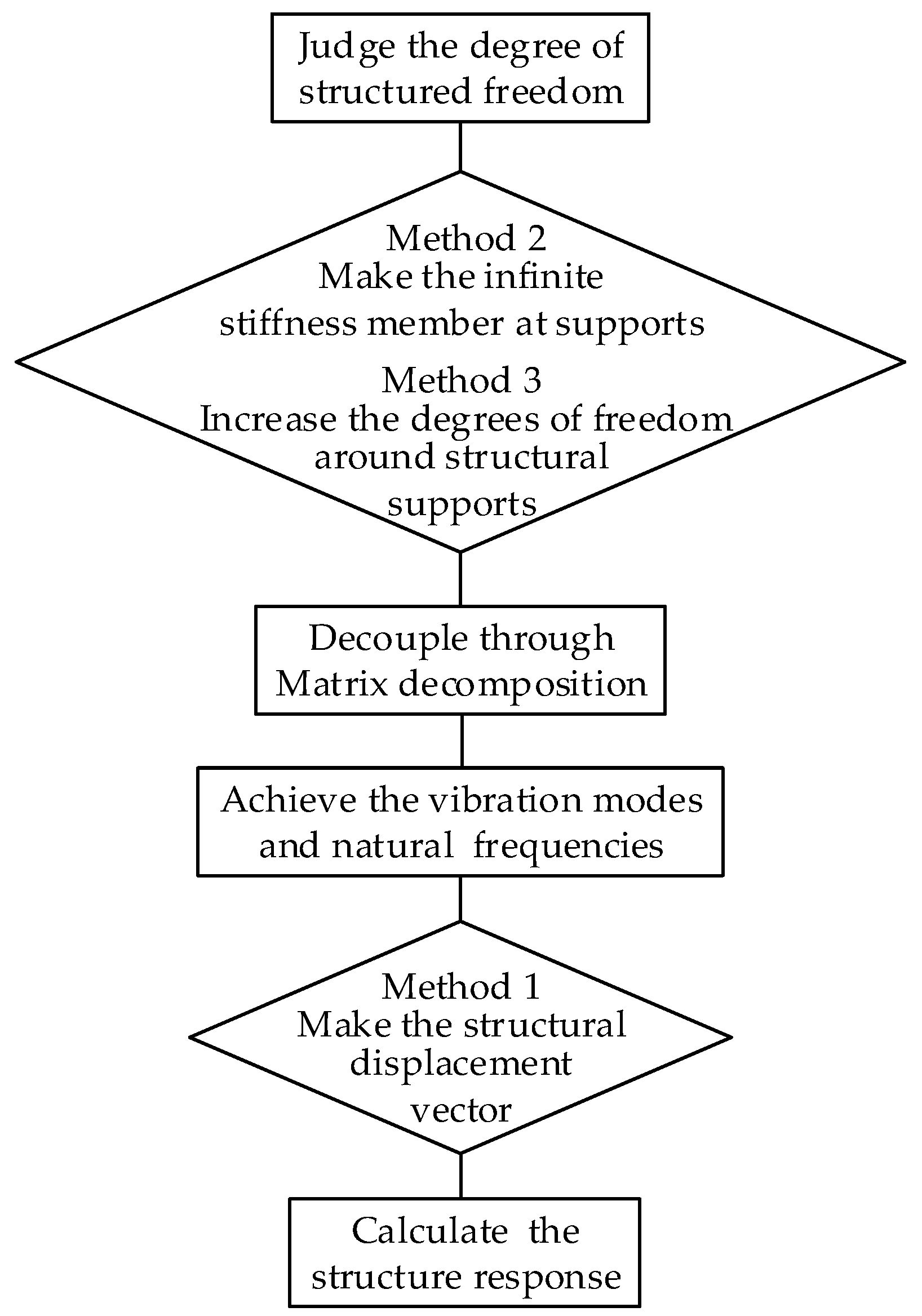
4.2. Method 1: Making the Structural Displacement Vector
4.3. Method 2: Making the Infinite Stiffness Member at Supports
4.4. Method 3: Increasing the Degrees of Freedom around Structural Supports
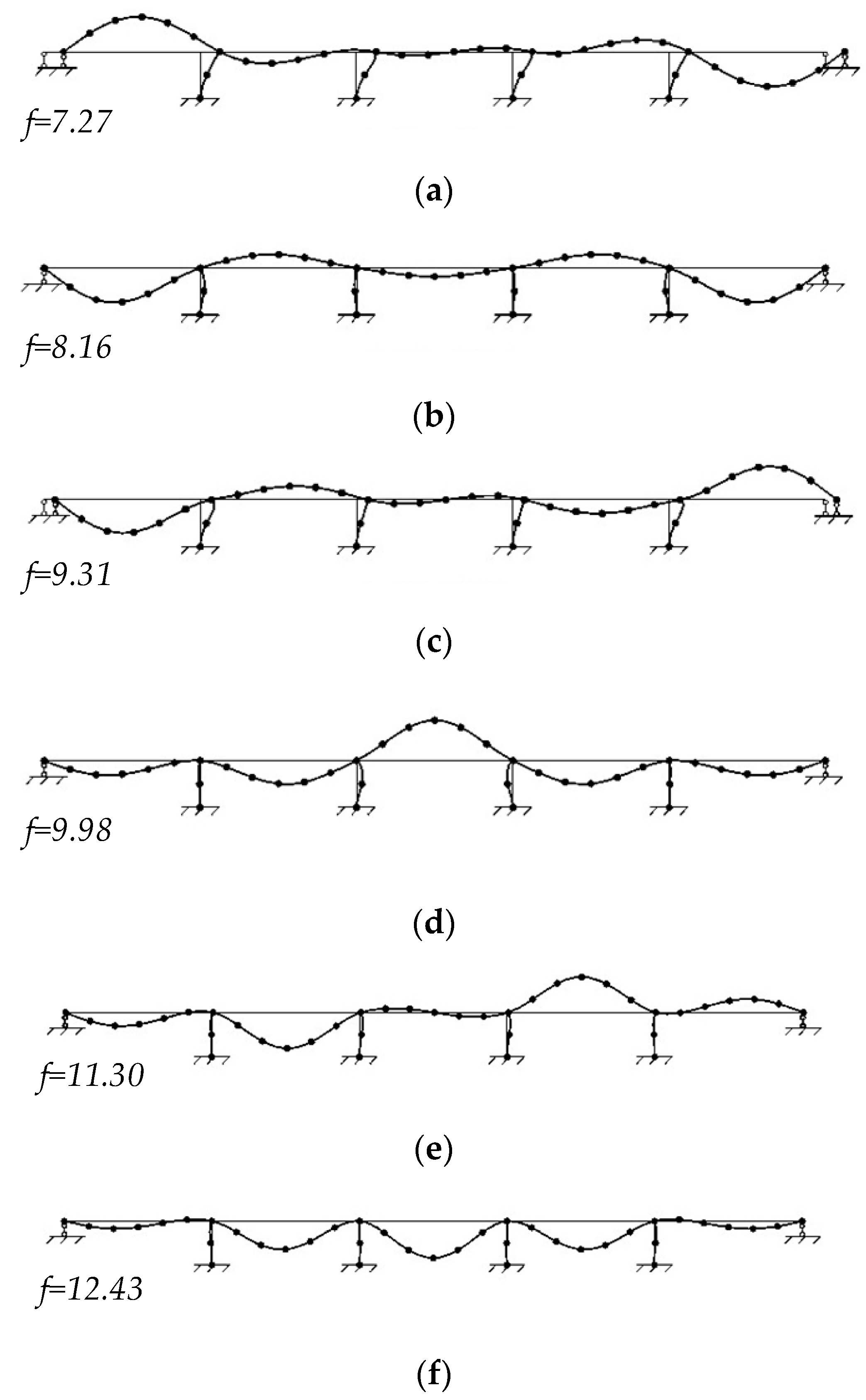
5. The Verification of the Modified MSRS Method
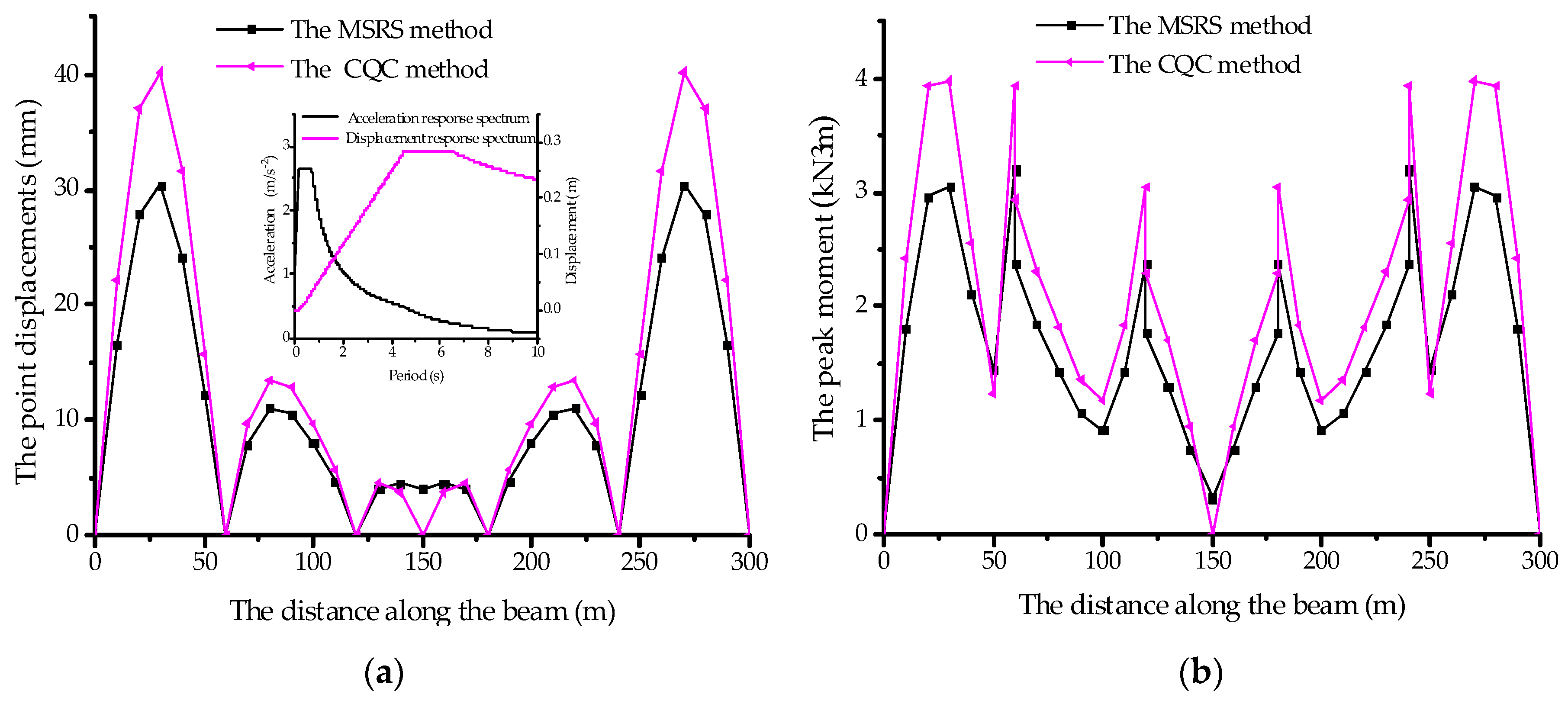
5.1. Comparison of the MSRS Method with the CQC Method
5.2. Comparison of the Modified MSRS Method with the MSRS Method
- The bending moment values and the peak bending moment at the girder points calculated by the two methods are almost the same;
- The bending moments at the points far from supports calculated by the two methods are close to each other;
- The bending moments at the points of the piers close to the supports calculated by the existing MSRS method are much different from those calculated by the modified MSRS method, with even the biggest deviation is up to several tens of times different. Clearly, the MSRS method is inaccurate in calculating the responses near the supports when compared with the modified MSRS method. Therefore, the comparison based on Table 1 validates the modified MSRS method.
6. The Spectrum Methods for Incoherent Ground Displacement Excitations
6.1. The Differential Equation of Motion for Incoherent Ground Displacement Excitations
6.2. The Power Spectrum Method (Solution)
6.3. The Response Spectrum Method for Incoherent Ground Displacement Excitations
6.4. The Simplified Power Spectrum Method
- and in Equations (62) and (63) simplify the peak response factors, and , in Equations (48) and (49). and can calculate the peak response and the variance of the peak response in the structural linear-elastic stage under incoherent ground motion.
- and have three merits when compared with the peak response factors, and : less computation, less process extent in simplifying and approximating, and without involving in the response spectrum.
- When compared with the existing power spectrum method introduced above, the collective response spectrum method reduces the computational effort by about 50%.
6.5. The Validity of the Power Spectrum/Collective Response Spectrum Methods
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Andersen, M.S.; Brandt, A. Aerodynamic Instability Investigations of a Novel, Flexible and Lightweight Triple-Box Girder Design for Long-Span Bridges. J. Bridge Eng. 2018, 23. [Google Scholar] [CrossRef]
- Kamada, T.; Fujita, T. State of the Art of Development and Application of Antiseismic Systems in Japan. In Proceedings of the 2008 Seismic Engineering Conference: Commemorating the 1908 Messina and Reggio Calabria Earthquake, Reggio Calabria, Italy, 8–11 July 2008; American Institute of Physics: New York, NY, USA; Volume 1020, pp. 1255–1271. [Google Scholar]
- Ashraf, A. Seismic analysis of wood building structures. Eng. Struct. 2006, 29, 213–223. [Google Scholar] [CrossRef]
- Seo, J.; Rogers, L.P. Comparison of curved prestressed concrete bridge population response between area and spine modeling approaches toward efficient seismic vulnerability analysis. Eng. Struct. 2017, 150, 176–189. [Google Scholar] [CrossRef]
- Ghadban, A.A.; Wehbe, N.I.; Pauly, T. Seismic performance of self-consolidating concrete bridge columns. Eng. Struct. 2018, 160, 461–472. [Google Scholar] [CrossRef]
- Elmy, M.H.; Nakamura, S. Static and seismic behaviours of innovative hybrid steel reinforced concrete bridge. J. Constr. Steel. Res. 2017, 138, 701–713. [Google Scholar] [CrossRef]
- Soleimani, F.; Vidakovic, B.; Desroches, R.; Padgett, J.E. Identification of the significant uncertain parameters in the seismic response of irregular bridges. Eng. Struct. 2017, 141, 356–372. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, H. Experimental study on a new type of earthquake resilient shear wall. Earthq. Eng. Struct. Dyn. 2017, 46, 2479–2497. [Google Scholar] [CrossRef]
- Dario, D.D.; Giuseppe, R. Earthquake-resilient design of base isolated buildings with TMD at basement: Application to a case study. Soil Dyn. Earthq. Eng. 2018, 113, 503–521. [Google Scholar] [CrossRef]
- Le, H.T.N.; Poh, L.H.; Wang, S.; Zhang, M.H. Critical parameters for the compressive strength of high-strength concrete. Cem. Concr. Compos. 2017, 82, 202–216. [Google Scholar] [CrossRef]
- D’Ambrisi, A.; Focacci, F.; Luciano, R.; Alecci, V.; Stefano de, M. Carbon-FRCM materials for structural upgrade of masonry arch road bridges. Compos. Pt. B-Eng. 2015, 75, 355–366. [Google Scholar] [CrossRef]
- Hollaway, L.C. Advanced Fibre-Reinforced Polymer (FRP) Composite Materials in Bridge Engineering; Woodhead Publishing: Sawston, Cambridge, UK, 2013; pp. 582–630. ISBN 978-0-85709-418-6. [Google Scholar]
- Zhang, A.L.; Li, S.H.; Jiang, Z.Q.; Fang, H.; Dou, C. Design theory of earthquake-resilient prefabricated sinusoidal corrugated web beam-column joint. Eng. Struct. 2017, 150, 665–673. [Google Scholar] [CrossRef]
- Zhang, A.L.; Li, R.; Jiang, Z.Q.; Zhang, Z.Y. Experimental study of earthquake-resilient PBCSC with double flange cover plates. J. Constr. Steel. Res. 2018, 143, 343–356. [Google Scholar] [CrossRef]
- Deng, K.; Wang, T.; Kurata, M.; Zhao, C.H.; Wang, K.K. Numerical study on a fully-prefabricated damage- tolerant beam to column connection for an earthquake-resilient frame. Eng. Struct. 2018, 159, 320–331. [Google Scholar] [CrossRef]
- Gou, H.Y.; Wen, Z.; Yi, B.; Li, X.B.; Pu, Q.H. Experimental Study on Dynamic Effects of a Long-span Railway Continuous Beam Bridge. Appl. Sci. 2018, 8, 669. [Google Scholar] [CrossRef]
- Zong, Z.H.; Xia, Z.H.; Liu, H.H.; Li, Y.L. Collapse Failure of Prestressed Concrete Continuous Rigid-Frame Bridge under Strong Earthquake Excitation: Testing and Simulation. J. Bridge Eng. 2016. [Google Scholar] [CrossRef]
- Kiureghian, A.D.; Neuenhofer, A. Response spectrum method for multi-support seismic excitations. Earthq. Eng. Struct. Dyn. 1992, 21, 713–740. [Google Scholar] [CrossRef]
- Allam, S.M.; Datta, T.K. Response Spectrum Analysis of Suspension Bridges for Random Ground Motion. J. Bridge Eng. 2002, 7, 325–337. [Google Scholar] [CrossRef]
- Cowan, D.R.; Consolazio, G.R.; Davidson, M.T. Response-Spectrum Analysis for Barge Impacts on Bridge Structures. J. Bridge Eng. 2015. [Google Scholar] [CrossRef]
- Wang, Q.X.; Wu, G.Z. Response of frame under multi-support excitations or disturbing forces. Earthq. Eng. Eng. Vib. 1983, 2, 3–17. (In Chinese) [Google Scholar] [CrossRef]
- Shi, Z.L.; Li, Z.X. Methods of seismic response analysis for long-span bridges under multi-support excitations of random earthquake ground motion. Earthq. Eng. Eng. Vib. 2003, 23, 124–130. (In Chinese) [Google Scholar] [CrossRef]
- Bai, F.L.; Li, H.N. Seismic response analysis of long-span spatial truss structure under multi-support excitations. Eng. Mech. 2010, 27, 67–73. (In Chinese) [Google Scholar]
- Ding, Y.; Lin, W.; Li, Z.X. Non-Stationary random seismic response analysis of long-span structures under multi-support and multi-dimensional earthquake excitation. Eng. Mech. 2007, 24, 97–103. (In Chinese) [Google Scholar] [CrossRef]
- Berrah, M.; Kausel, E. Response Spectrum Analysis of Structures Subjected to Spatially Varying Motions. Earthq. Eng. Struct. Dyn. 1992, 21, 461–470. [Google Scholar] [CrossRef]
- Berrah, M.; Kausel, E. A Modal Combination Rule for Spatially Varying Seismic Motions. Earthq. Eng. Struct. Dyn. 1993, 22, 791–800. [Google Scholar] [CrossRef]
- Clough, R.W.; Penzien, J. Dynamics of Structures; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar] [CrossRef]
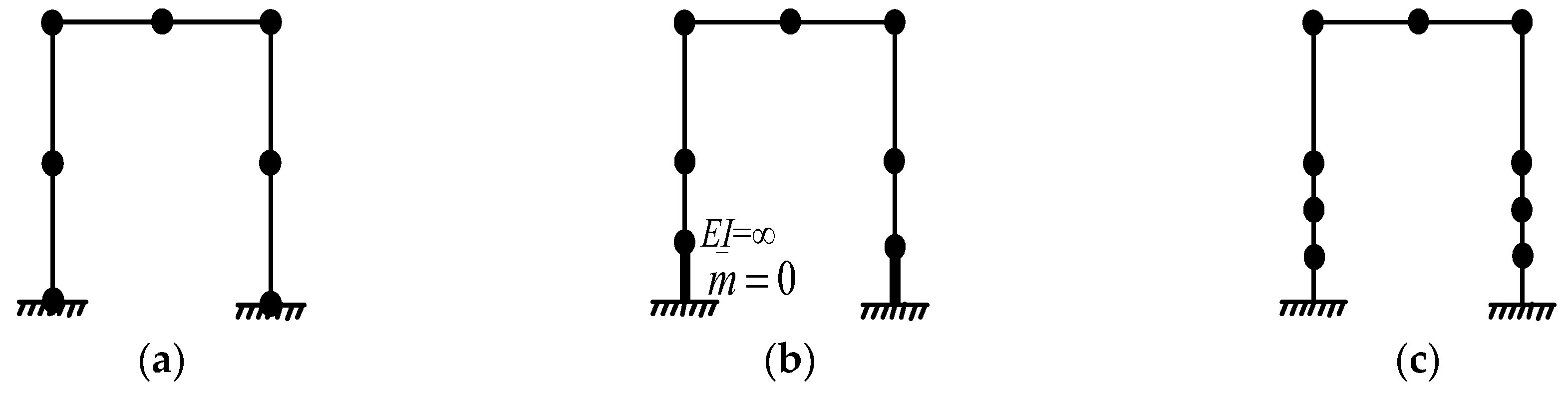


| Position | Bending Moment M (×103 kN∙m) | ||
|---|---|---|---|
| Method | The MSRS Method | The Modified MSRS Method 1 1 | The Modified MSRS Method 2 1 |
| Girder point 4 | 2.99 | 3.06 | 3.06 |
| Girder point 10 | 1.06 | 1.06 | 1.06 |
| Girder point 16 | 0.30 | 0.30 | 0.32 |
| Pier point 7 | 14.30 | 39.50 | 39.50 |
| Pier point 13 | 14.20 | 37.50 | 37.50 |
| Pier point 32 | 35.40 | 1.36 | 1.36 |
| Pier point 33 | 35.30 | 0.79 | 0.79 |
| Position | Peak Factor | Position | Peak Factor | ||
|---|---|---|---|---|---|
| VD 1 at Point 2 | 2.79 | 0.50 | BBM at the left of Point 13 | 2.72 | 0.52 |
| VD at Point 3 | 2.78 | 0.50 | BBM at the right of Point 13 | 2.72 | 0.52 |
| VD at Point 4 | 2.78 | 0.50 | BBM at Point 14 | 2.72 | 0.52 |
| VD at Point 5 | 2.77 | 0.50 | BBM at Point 15 | 2.73 | 0.51 |
| VD at Point 6 | 2.76 | 0.51 | BBM at Point 16 | 2.80 | 0.50 |
| VD at point 8 | 2.75 | 0.51 | PBM 2 at Point 7 | 2.76 | 0.51 |
| VD at Point 9 | 2.78 | 0.50 | PBM at Point 13 | 2.70 | 0.52 |
| VD at Point 10 | 2.81 | 0.49 | PBM at Point 32 | 2.73 | 0.51 |
| VD at Point 11 | 2.82 | 0.49 | PBM at Point 33 | 2.72 | 0.52 |
| VD at Point 12 | 2.78 | 0.50 | SBM 2 at Point 36 | 2.71 | 0.52 |
| VD at Point 14 | 2.72 | 0.51 | SBM at Point 37 | 2.70 | 0.52 |
| VD at Point 15 | 2.73 | 0.51 | SF 3 in Beam 1–2 | 2.80 | 0.50 |
| VD at Point 16 | 2.79 | 0.50 | SF in Beam 2–3 | 2.79 | 0.50 |
| HD 1 at bridge deck | 2.70 | 0.52 | SF in Beam 3–4 | 2.69 | 0.52 |
| HD at Point 32 | 2.70 | 0.52 | SF in Beam 4–5 | 2.80 | 0.50 |
| HD at Point 33 | 2.69 | 0.52 | SF in Beam 5–6 | 2.80 | 0.50 |
| HD at Point 36 | 2.73 | 0.51 | SF in Beam 6–7 | 2.80 | 0.50 |
| HD at Point 37 | 2.69 | 0.52 | SF in beam 7–8 | 2.82 | 0.49 |
| BBM 2 at Point 2 | 2.79 | 0.50 | SF in Beam 8–9 | 2.79 | 0.50 |
| BBM at Point 3 | 2.79 | 0.50 | SF in beam 9–10 | 2.72 | 0.51 |
| BBM at Point 4 | 2.79 | 0.50 | SF in Beam 10–11 | 2.72 | 0.52 |
| BBM at Point 5 | 2.77 | 0.50 | SF in beam 11–12 | 2.75 | 0.51 |
| BBM at Point 6 | 2.71 | 0.52 | SF in Beam 12–13 | 2.78 | 0.50 |
| BBM at the left of Point 7 | 2.79 | 0.50 | SF in Beam 13–14 | 2.73 | 0.51 |
| BBM at the right of Point 7 | 2.73 | 0.51 | SF in Beam 14–15 | 2.72 | 0.51 |
| BBM at Point 8 | 2.71 | 0.52 | SF in Beam 15–16 | 2.72 | 0.51 |
| BBM at Point 9 | 2.75 | 0.51 | SF in Pier 7–32 | 2.73 | 0.51 |
| BBM at Point 10 | 2.82 | 0.49 | SF in Beam 13–33 | 2.70 | 0.52 |
| BBM at Point 11 | 2.78 | 0.50 | SF in Beam 32–36 | 2.73 | 0.51 |
| BBM at Point 12 | 2.70 | 0.52 | SF in Beam 33–37 | 2.70 | 0.52 |
| 0.05 | 2.72 | 0.51 |
| 0.05 | 2.72 | 0.52 |
| 0.04 | 2.73 | 0.51 |
| 0.04 | 2.73 | 0.51 |
| 0.03 | 2.74 | 0.51 |
| 0.03 | 2.74 | 0.51 |
| 0.02 | 2.75 | 0.51 |
| 0.01 | 2.76 | 0.51 |
| ω1 = 4.81 | 2.71 | 0.51 | ω6 = 8.97 | 2.81 | 0.49 |
| ω2 = 5.61 | 2.75 | 0.50 | ω7 = 18.71 | 2.65 | 0.53 |
| ω3 = 6.11 | 2.77 | 0.50 | ω8 = 18.88 | 2.65 | 0.53 |
| ω4 = 6.92 | 2.79 | 0.49 | ω9 = 20.93 | 2.62 | 0.53 |
| ω5 = 7.98 | 2.81 | 0.49 | ω10 = 23.03 | 2.60 | 0.54 |
| Structural Response | The MSRS Method | The Power Spectrum Method | The Simplified Power Spectrum Method | The Collective Response Spectrum Method | ||
|---|---|---|---|---|---|---|
| BBM 1 at Point 02 | 0.61 | 1.81 | 0.62 | 1.54 | 1.71 | 1.76 |
| BBM at Point 03 | 1.00 | 2.97 | 1.01 | 2.51 | 2.78 | 2.91 |
| BBM at Point 04 | 1.02 | 3.06 | 1.03 | 2.54 | 2.82 | 3.02 |
| BBM at Point 05 | 0.67 | 2.12 | 0.67 | 1.66 | 1.85 | 2.10 |
| BBM at Point 06 | 0.31 | 1.45 | 0.43 | 1.04 | 1.19 | 1.14 |
| BBM at the left of Point 07 | 0.97 | 3.20 | 1.10 | 2.72 | 3.01 | 2.72 |
| BBM at the right of Point 07 | 0.76 | 2.37 | 0.88 | 2.14 | 2.42 | 2.76 |
| BBM at Point 08 | 0.61 | 1.84 | 0.69 | 1.66 | 1.90 | 2.21 |
| BBM at Point 09 | 0.47 | 1.43 | 0.51 | 1.24 | 1.40 | 1.58 |
| BBM at Point 10 | 0.34 | 1.06 | 0.34 | 0.86 | 0.94 | 0.90 |
| BBM at Point 11 | 0.29 | 0.92 | 0.34 | 0.83 | 0.92 | 0.92 |
| BBM at Point 12 | 0.48 | 1.44 | 0.59 | 1.41 | 1.62 | 1.83 |
| BBM at the left of Point 13 | 0.80 | 2.38 | 0.93 | 2.25 | 2.57 | 2.90 |
| BBM at the right of Point 13 | 0.58 | 1.77 | 0.75 | 1.80 | 2.05 | 2.19 |
| BBM at point 14 | 0.43 | 1.31 | 0.55 | 1.32 | 1.50 | 1.60 |
| BBM at Point 15 | 0.24 | 0.75 | 0.30 | 0.73 | 0.83 | 0.87 |
| BBM at Point 16 | 0.06 | 0.32 | 0.07 | 0.17 | 0.19 | 0.14 |
| PBM at Point 07 | 1.20 | 3.95 | 1.53 | 3.75 | 4.21 | 3.91 |
| PBM at Point 13 | 1.28 | 3.75 | 1.59 | 3.80 | 4.37 | 4.90 |
| PBM at Point 32 | 0.44 | 1.36 | 0.47 | 1.15 | 1.31 | 1.52 |
| PBM at Point 33 | 0.24 | 0.79 | 0.31 | 0.74 | 0.85 | 0.90 |
| PBM at Point 36 | 1.59 | 5.32 | 2.09 | 5.04 | 5.75 | 6.00 |
| PBM at Point 37 | 1.77 | 5.30 | 2.23 | 5.35 | 6.14 | 6.82 |
| Structural Response (mm) | The MSRS Method | The Power Spectrum Method | The Simplified Power Spectrum Method | The Collective Response Spectrum Method | ||
|---|---|---|---|---|---|---|
| VD 1 at Point 2 | 6.46 | 16.66 | 6.46 | 18.02 | 17.76 | 17.93 |
| VD at Point 3 | 10.83 | 27.94 | 10.83 | 30.19 | 29.77 | 30.26 |
| VD at Point 4 | 11.80 | 30.48 | 11.80 | 32.86 | 32.44 | 33.38 |
| VD at Point 5 | 9.33 | 24.15 | 9.35 | 25.98 | 25.71 | 26.95 |
| VD at Point 6 | 4.68 | 12.23 | 4.76 | 13.17 | 13.10 | 14.09 |
| VD at Point 8 | 2.90 | 7.93 | 3.07 | 8.44 | 8.43 | 9.01 |
| VD at Point 9 | 3.96 | 11.00 | 4.05 | 11.27 | 11.14 | 11.33 |
| VD at Point 10 | 3.68 | 10.54 | 3.68 | 10.37 | 10.12 | 9.41 |
| VD at Point 11 | 2.69 | 8.01 | 2.80 | 7.92 | 7.70 | 6.53 |
| VD at Point 12 | 1.57 | 4.72 | 1.86 | 5.18 | 5.13 | 4.63 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, J.; Li, R.; Shi, J.; Zhou, G. Modified Multi-Support Response Spectrum Analysis of Structures with Multiple Supports under Incoherent Ground Excitation. Appl. Sci. 2019, 9, 1744. https://doi.org/10.3390/app9091744
Shen J, Li R, Shi J, Zhou G. Modified Multi-Support Response Spectrum Analysis of Structures with Multiple Supports under Incoherent Ground Excitation. Applied Sciences. 2019; 9(9):1744. https://doi.org/10.3390/app9091744
Chicago/Turabian StyleShen, Jiyang, Rui Li, Jun Shi, and Guangchun Zhou. 2019. "Modified Multi-Support Response Spectrum Analysis of Structures with Multiple Supports under Incoherent Ground Excitation" Applied Sciences 9, no. 9: 1744. https://doi.org/10.3390/app9091744
APA StyleShen, J., Li, R., Shi, J., & Zhou, G. (2019). Modified Multi-Support Response Spectrum Analysis of Structures with Multiple Supports under Incoherent Ground Excitation. Applied Sciences, 9(9), 1744. https://doi.org/10.3390/app9091744




