1. Introduction
The quantum mechanics (QM) and information theory (IT) establish a solid basis for both determining the electronic structure of molecules and understanding, in chemical terms, general trends in their chemical behavior. The energy principle of QM has been recently interpreted [
1,
2,
3] as equivalent variational rule for the overall content of the gradient information in the system electronic wavefunction, proportional to the state average kinetic energy. In the grand-ensemble representation of thermodynamic (mixed) states they both determine the same equilibrium of an externally open molecular system. This equivalence parallels identical predictions resulting from the minimum-energy and maximum-entropy principles in ordinary thermodynamics [
4].
The generalized, Fisher-type gradient information in the specified electronic state is proportional to the system average kinetic energy. This allows one to interpret the variational principle for electronic energy as equivalent information rule. The energy and resultant-information/kinetic-energy rules thus represent equivalent sources of reactivity criteria, the populational derivatives of ensemble-average values of electronic energy or overall information, e.g., the system chemical potential (negative electronegativity) and hardness/softness descriptors. The IT transcription of the variational principle for the minimum of electronic energy allows one to interpret the familiar (energetical) criteria of chemical reactivity, the populational derivatives of electronic energy, in terms of the corresponding derivatives of the state-resultant information content. The latter combines the classical (probability) and nonclassical (current) contributions to the state kinetic energy of electrons, generated by the modulus and phase components of molecular wavefunctions, respectively. This proportionality between the state resultant gradient information and its kinetic energy also allows one to use the molecular virial theorem [
5] in general reactivity considerations [
1,
2,
3].
The resultant measures combining the probability and phase/current contributions allow one to distinguish the information content of states generating the same electron density but differing in their phase/current composition. To paraphrase Prigogine [
6], the electron density alone reflects only the molecular static structure of “being”, missing the dynamic structure of “becoming” contained in the state current distribution. Both these manifestations of electronic “organization” in molecules ultimately contribute to resultant IT descriptors of the structural entropy/information content in generally complex electronic wavefunctions [
7,
8,
9,
10]. In quantum information theory (QIT) [
7], the classical information contribution probes the entropic content of incoherent (disentangled) local “events” while its nonclassical supplement provides the information complement due to their coherence (entanglement).
The classical IT [
11,
12,
13,
14,
15,
16,
17,
18] has been already successfully applied to interpret the molecular probability distributions, e.g., References [
19,
20,
21,
22]. Information principles have been explored [
1,
2,
3,
23,
24,
25,
26,
27,
28] and density pieces attributed to atoms-in-molecules (AIM) have been approached [
22,
26,
27,
28,
29,
30] providing the information basis of the intuitive (stockholder) division of Hirshfeld [
31]. Patterns of chemical bonds have been extracted from electronic communications in molecules [
7,
19,
20,
21,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42] and entropy/information distributions in molecules have been explored [
7,
19,
20,
21,
43,
44]. The nonadditive Fisher information [
7,
19,
20,
21,
45,
46] has been linked to electron localization function (ELF) [
47,
48,
49] of modern density functional theory (DFT) [
50,
51,
52,
53,
54,
55]. This analysis has also formulated the contragradience (CG) probe [
7,
19,
20,
21,
56] for localizaing chemical bonds and the orbital communication theory (OCT) of the chemical bond has identified the bridge bonds originating from the cascade propagations of information between AIM, which involve intermediate orbitals [
7,
21,
57,
58,
59,
60,
61,
62].
In entropic theories of molecular electronic structure, one ultimately requires the quantum (resultant) extensions of the familiar complementary measures of Fisher [
11] and Shannon [
13], of the information and entropy content in probability distributions, which are appropriate for the complex probability amplitudes (wavefunctions) of molecular QM. The wavefunction phase, or its gradient determining the current density and the associated velocity field, gives rise to nonclassical supplements in resultant measures of an overall entropic content of molecular states [
7,
63,
64,
65,
66,
67,
68]. The information distinction between the bonded (entangled) and nonbonded (disentangled) states of subsystems, e.g., molecular substrates of a chemical reaction, also calls for such generalized information descriptors [
69,
70,
71,
72]. The extremum principles for the global and local measures of the resultant entropy have been used to determine the phase-equilibrium states of molecular systems, identified by their optimum (local, probability-dependent) “thermodynamic” phase.
Various DFT-based approaches to classical issues in reactivity theory [
73,
74,
75,
76,
77,
78,
79] use the energy-centered arguments in justifying the observed reaction paths and relative yields of their products. Qualitative considerations on preferences in chemical reactions usually emphasize changes in energies of both reactants and of the whole reactive system, which are induced by displacements (perturbations) in parameters describing the relevant (real or hypothetical) electronic state. In such classical treatments, also covering the linear responses to these primary shifts, one also explores reactivity implications of the electronic equilibrium and stability criteria. For example, in charge sensitivity analysis (CSA) [
73,
74] the “principal” (energy) derivatives with respect to the system external potential (
v), due to the fixed nuclei defining molecular geometry, and its overall number of electrons (
N), as well as the associated charge responses of both the whole reactive system and its constituent subsystems, have been used as reactivity criteria. In R = acid(A)← base(B) ≡ A–B complexes, consisting of the coordinated electron-acceptor and electron-donor reactants, respectively, such responses can be subsequently combined into the corresponding in situ descriptors characterizing the B→A charge transfer (CT).
We begin this overview with a summary of the probability and current distributions, the physical attributes reflecting the modulus and phase components of quantum states, and an introduction to the resultant QIT descriptors. The phase equilibria, representing extrema of the overall entropy measures, will be explored and molecular orbital (MO) contributions to the overall gradient-information measure will be examined. Using the molecular virial theorem, the role of electronic kinetic energy, also reflecting the system resultant information, in shaping the electronic structure of molecules, will be examined. This analysis of the theorem implications will cover the bond-formation process and the qualitative Hammond [
80] postulate of reactivity theory. The hypothetical stages of chemical reactions invoked in reactivity theory will be explored and the in situ populational derivatives will be applied to determine the optimum amount of CT in donor-acceptor coordinations. Populational derivatives of the resultant gradient information will be advocated as alternative indices of chemical reactivity, related to their energetical analogs. They will be shown to be capable of predicting both the direction and magnitude of electron flows in A–B systems. The frontier-electron (FE) [
81,
82,
83] framework for describing molecular interactions will be used to reexamine Pearson’s [
84] hard (soft) acids and bases (HSAB) principle of structural chemistry (see also Reference [
85]) and electron communications between reactants will be commented upon. The ionic and covalent interactions between the “frontier” MO will be invoked to fully explain the HSAB stability predictions, and the “complementary” A–B complex will be compared with its regional-HSAB analog. The complementary preference will be explained by examining physical implications of the polarizational and relaxational flows in these alternative reactive complexes. In appendices, the continuity relations for the probability and phase distributions of molecular electronic states resulting from the Schrödinger equation (SE) of QM will be summarized, the dynamics of resultant gradient information will be addressed, the nonclassical origin of the overall gradient-information production will be demonstrated, and the grand-ensemble representation of open molecular systems will be outlined.
2. Physical Attributes of Quantum States and Generalized Information Descriptors
The electronic wavefunctions of molecules are determined by SE of QM. This fundamental equation also determines the dynamics of the modulus (probability) and phase (current) attributes of such elementary quantum states. In a discussion of “productions” of the resultant entropy/information quantities [
7,
69,
72], it is of interest to examine implications of SE for the dynamics of these fundamental physical distributions of quantum states. For simplicity, let us first consider a single electron at time
t in state |
ψ(
t)〉 ≡ |
ψ(
t)〉 ≡ |
ψ〉, described by the (complex) wavefunction in position representation,
where the real functions
R(
r,
t) ≡
R(
t) and
ϕ(
r,
t) ≡
ϕ(
t) stand for its modulus and phase parts, respectively. It determines the state probability distribution at the specified time
t,
and its current density
The effective velocity field
V(
r,
t) =
j(
t)/
p(
t) ≡
V(
t) of the probability “fluid” measures the local current-per-particle and reflects the state phase gradient:
The wavefunction modulus, the classical amplitude of the particle probability density, and the state phase, or its gradient determining the effective velocity of the probability flux, thus constitute two physical degrees-of-freedom in the full IT treatment of quantum states of a monoelectronic system:
One envisages the electron moving in the external potential
v(
r), due to the “frozen” nuclei of the Born–Oppenheimer (BO) approximation determining the system geometry, described by the electronic Hamiltonian
where
denotes its kinetic part. The quantum dynamics of a general electronic state of Equation (1) is generated by SE
which also determines temporal evolutions of the state physical distributions: The (instantaneous) probability density
p(
t) and (local) phase
ϕ(
t) or its gradient reflecting the velocity field
V(
t), the current-per-particle of the probability “fluid” [
7,
69,
72]. The relevant continuity relations resulting from SE are summarized in
Appendix A.
To simplify the notation for the the specified time
t =
t0, let us suppress this parameter in the list of state arguments, e.g.,
ψ(
r,
t0) ≡
ψ(
r) = 〈
r|
ψ〉, etc. We, again, examine the mono-electron system in (pure) quantum state |
ψ〉. The average Fisher’s measure [
11,
12] of the classical gradient information for locality events, called the intrinsic accuracy, which is contained in the molecular probability density
p(
r) =
R(
r)
2 is reminiscent of von Weizsäcker’s [
86] inhomogeneity correction to the density functional for electronic kinetic energy:
This local measure characterizes an effective “narrowness” of the particle spatial probability distribution, i.e., a degree of the particle position determinicity. It represents the complementary measure to the global entropy of Shannon [
13,
14], the position-uncertainty index,
which reflects the particle position indeterminicity, a “spread” of probability distribution. This classical descriptor also measures the amount of information received when the uncertainty about particle’s location is removed by an appropriate experiment:
IS[
p] ≡
S[
p].
In QM, these classical measures can be supplemented by the associated nonclassical contributions in the corresponding resultant QIT descriptors [
7,
45,
63,
64,
65,
66,
67]. The intrinsic accuracy concept then naturally generalizes into the associated overall descriptor, a functional of the quantum state |
ψ〉 itself. This generalized Fisher-type measure is defined by the expectation value of the Hermitian operator
[
7,
45] of the overall gradient information,
related to kinetic energy operator
of Equation (6). Using integration by parts then gives:
The classical and nonclassical densities-per-electron of this information functional read:
The quantum-information concept
I[
ψ] =
I[
p,
ϕ] =
I[
p,
j] thus combines the classical (probability) contribution
I[
p] of Fisher and the nonclassical (phase/current) supplement
I[
ϕ] =
I[
j]. The positive sign of the latter expresses the fact that a nonvanishing current pattern introduces more structural determinicity (order information) about the system, which also implies less state indeterminicity (disorder information). This dimensionless measure is seen to reflect the average kinetic energy
T[
ψ] = 〈
ψ|
|
ψ〉:
One similarly generalizes the entropy (uncertainty) concept of the disorder information in probability density, e.g., the global quantity of Shannon or the gradient descriptor of Fisher, by supplementing the relevant classical measure of the information contained in probability distribution with the corresponding nonclassical complement due to the state (positive) phase or the associated current pattern [
7,
8,
9,
10]. The resultant Shannon-type global-entropy measure then reads
It includes the (positive) probability information
IS[
p] ≡
S[
p] and (negative) nonclassical supplement
S[
ϕ] reflecting the state average phase. These entropy contributions also reflect the real and imaginary parts of the associated complex-entropy concept [
8], the quantum expectation value of the non-Hermitian entropy operator
S(
r) = − 2ln
ψ(
r),
The resultant gradient entropy similarly combines the (positive) Fisher probability information and (negative) phase contribution due to the current density:
The sign of the latter reflects an extra decrease of the state overall structure indeterminicity due to its nonvanishing current pattern.
The extrema of these resultant entropies identify the same optimum, equilibrium-phase solution
ϕeq. ≥ 0 [
7,
63,
64,
65,
66,
67]:
This local “thermodynamic” phase generates the associated current contribution reflecting the negative probability gradient:
The above one-electron development can be straightforwardly generalized into a general case of
N-electron system in the specified (pure) quantum state |Ψ(
N)〉, exhibiting the electron density
ρ(
r) =
Np(
r), where
p(
r) stands for the density probability (shape) factor. The corresponding
N-electron information operator then combines terms due to each particle,
and determines the state overall gradient information,
proportional to the expectation value
T(
N) of the system kinetic-energy operator
. The relevant separation of the modulus and phase components of such general
N-electron states calls for a wavefunction yielding the specified electron density [
52]. For example, this goal can be accomplished using the Harriman–Zumbach–Maschke (HZM) [
87,
88] construction of DFT. It uses
N (complex) equidensity orbitals, each generating the molecular probability distribution
p(
r) and exhibiting the density-dependent spatial phases,
f(
r) =
f[
ρ;
r], which safeguard the MO orthogonality.
Consider the Slater-determinant describing an electron configuration defined by
N (singly) occupied spin MO,
The kinetic-energy/gradient-information descriptors then combine additive contributions due to each particle:
In the analytical (LCAO MO) representation, with MO expressed as linear combinations of the (orthogonalized) atomic orbitals (AO)
χ= (
χ1,
χ2, …,
χk, …),
the average gradient information in Ψ(
N) for the unit matrix
n = {
ns δs,s′} = {
δs,s′} of MO occupations, then reads
Here, the AO matrix representation of the
gradient-information operator,
and the charge/bond-order (CBO) (density) matrix of LCAO MO theory,
is the associated matrix representation of the projection operator onto the occupied MO-subspace,
proportional to the density operator
of the configuration MO “ensemble”.
This expression for the average overall information in Ψ(
N) thus assumes thermodynamic-like form, as trace of the product of the CBO matrix, the AO representation of the (occupation-weighted) MO projector determining the configuration density operator
, and the corresponding AO matrix of the resultant gradient information related to that of the kinetic energy of electrons. It has been argued elsewhere [
7,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42] that elements of the CBO matrix generate amplitudes of electronic “communications” between AO “events” in the molecule. Therefore, the average gradient information of Equation (24) is seen to represent the communication-weighted (dimentionless) kinetic-energy descriptor.
The SE (7) also determines a temporal evolution of the average resultant descriptor of the gradient-information content in the specified (pure) quantum state (see Equation (11)). The time derivative of this overall information functional
I[
ψ] is addressed in
Appendix B.
3. Probing Formation of the Chemical Bond
The association between the overall gradient information and electronic kinetic energy suggests the use of molecular virial theorem in extracting the physical origins of the chemical bonding [
89,
90,
91,
92] and for understanding general reactivity rules [
1,
2,
3,
5]. The previous analyses [
89,
90,
91] have focused on the interplay between the longitudinal (in the bond direction, along “
z” coordinate) and transverse (perpendicular to the bond axis, due to coordinates “
x” and “
y”) components of electronic kinetic energy. The former appears as the true driving force of the covalent-bond formation and the accompanying electron-delocalization process at an early approach by the two atoms, while the latter reflects an overall transverse contraction of the electron density in the attractive field of both nuclei.
It is of interest to examine the global production (Equation (A20)) of the resultant gradient measure of the electronic information due to the equilibrium current of Equation (18),
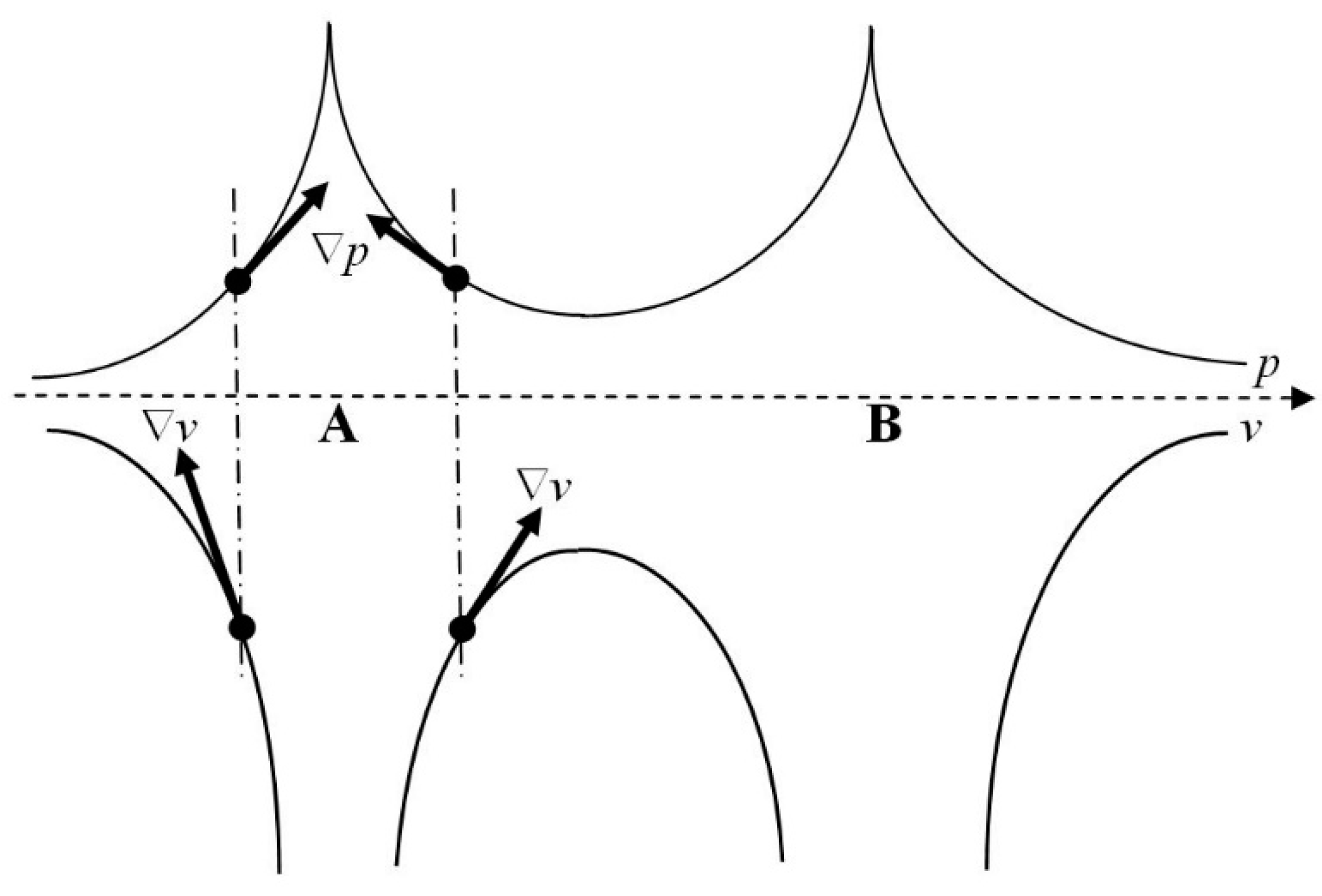
which accompanies a formation of the covalent chemical bond A–B (
Figure 1). Reference to this figure shows that in the axial (bond) section of the molecule ∇
p(
r)⋅∇
v(
r) < 0, thus confirming a derease of the longitudinal contribution to the average structure information, i.e., an increase in the axial component of the overall gradient entropy (Equation (A24)) as a result of the chemical bond formation:
σIeq.(axial) < 0 and
σMeq(axial)
. > 0. This accords with the chemical intuition: electron delocalization in the covalent chemical bond at its equilibrium length
R =
Re should produce a higher indeterminicity (disorder, entropy) measure and a lower level of the determinicity (order, information) descriptor, particularly in the axial bond region between the two nuclei.
Since the gradient measure of the state overall gradient information reflects the system kinetic-energy content, one could indeed relate these conclusions to the known profiles of the longitudinal and transverse components of this energy contribution [
89,
90,
91]. The former contribution effectively lowers the longitudinal inhomogeneity of molecular probability density,
σIeq.(axial) < 0, particularly in the bond region between the two nuclei, while the (dominating) latter component implies an effective transverse contraction of the electron distribution, i.e.,
σIeq.(transverse) > 0. The bonded system thus exhibits a net increase in the probability inhomogeneity, i.e., a higher gradient information compared to the separated-atoms limit (SAL). This is independently confirmed by a lowering of the system overall potential-energy displacement Δ
W(
R) =
W(
R) −
W(SAL) at the equilibrium bond-length
Re,
Here,
combines the (electron-nuclear) attraction (
V) and repulsion (
U =
Ue +
Un) energies between electrons (
Ue) and nuclei (
Un).
It is also of interest to examine variations of the resultant gradient information in specific geometrical displacements Δ
R of this diatomic system. Its proportionality to the system kinetic-energy component again calls for using the molecular virial theorem, which allows one to partition the relative BO potential Δ
E(
R) = Δ
T(
R) + Δ
W(
R) into the SAL-related changes in the electronic kinetic energy [Δ
T(
R)] and its overall potential complement [Δ
W(
R)]. In the BO approximation the virial theorem for diatomics reads:
It implies the following kinetic and potential energy components:
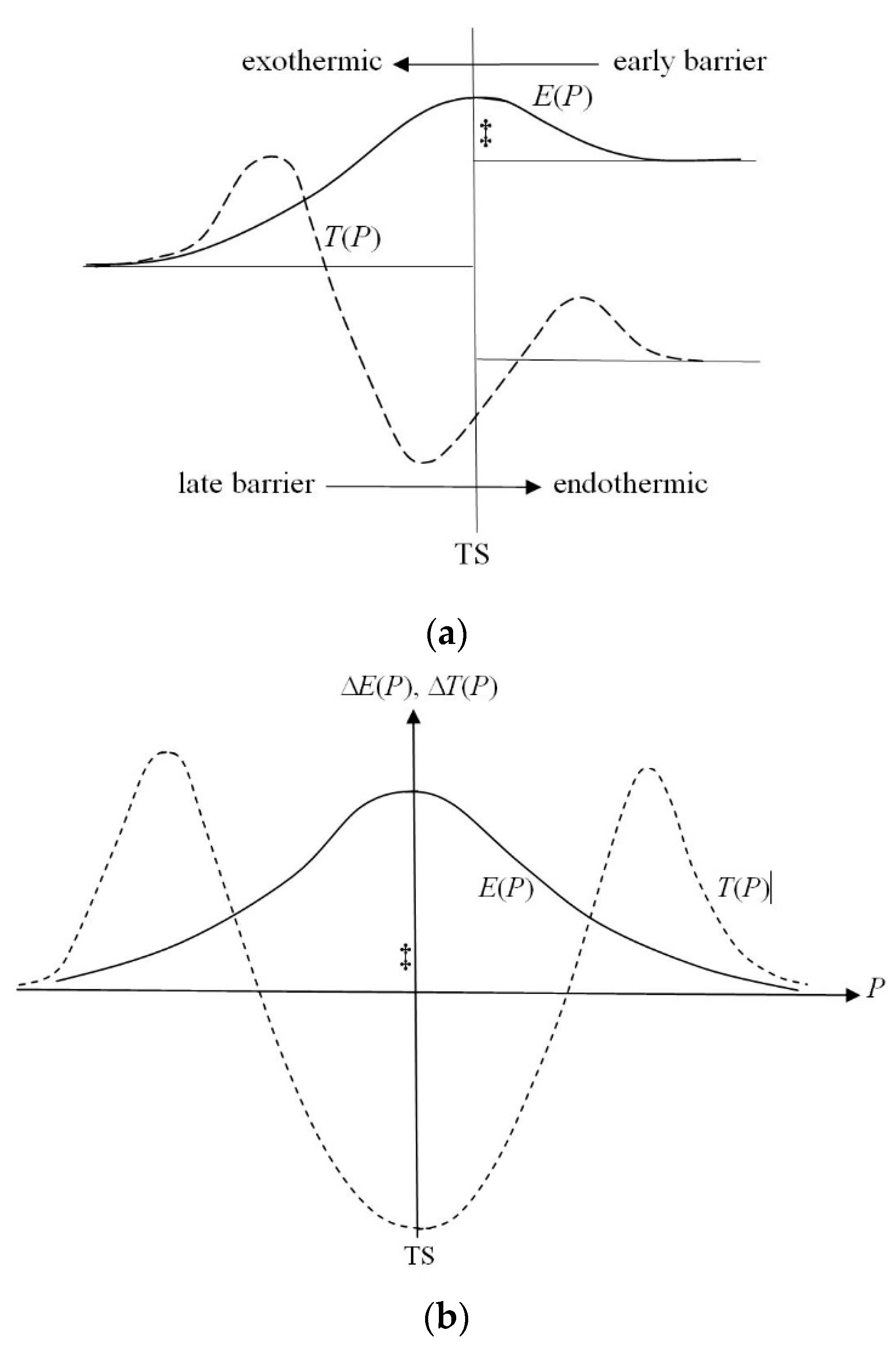
Figure 2 presents qualitative plots of the BO potential Δ
E(
R) and its kinetic-energy contribution Δ
T(
R) in diatomics. The latter also reflects the associated displacement plots for the resultant gradient information Δ
I(
R) =
σ Δ
T(
R). It follows from this qualitative diagram that, during a mutual approach by two constituent atoms, the kinetic-energy/gradient information is first diminished relative to SAL, due to the dominating longitudinal contribution related to Cartesian coordinate “
z” (along the bond axis). However, at the equilibrium distance
Re the resultant information already rises above the SAL value, due to the dominating increase in transverse components of the kinetic-energy/information (corresponding to coordinates “
x” and “
y” perpendicular to the bond axis). Therefore, at the equilibrium separation
Re between atoms the bond-formation results in a net increase of the resultant gradient-information relative to SAL, due to—on average—more compact electron distribution in the field of both nuclei.
Consider next the (intrinsic) reaction coordinate
Rc, or the associated progress variable
P = |
Rc|, of the arc length along this trajectory, for which the virial relations also assume the diatomic-like form. The virial theorem decomposition of the energy profile
E(
P) along
Rc in bimolecular reaction
where the R
‡ denotes the transition-state (TS) complex, then generates the associated profile of its kinetic-energy component
T(
P), which also reflects the associated resultant gradient information
I(
P). Such an application of the molecular virial theorem to endo- and exo-ergic reactions is presented in the upper panel of
Figure 3, while the energy-neutral case of such a chemical process, on a “symmetric” potential energy surface (PES), refers to a lower panel in the figure.
The (qualitative) Hammond postulate [
80] of reactivity theory relates a general resemblance/proximity of the reaction TS complex R
‡ to either its substrates
α ∈ (A, B) or products
β ∈ (C, D) to the reaction energy Δ
Er =
E(
Pprod.) −
E(
Psub.): in
exo-ergic (Δ
Er < 0) processes, R
‡ ≈
α and in endo-ergic (Δ
Er > 0) reactions, R
‡ ≈
β. Accordingly, for the vanishing reaction energy Δ
Er = 0, the position of TS complex is expected to be located symmetrically between the reaction substrates and products. A reference to
Figure 3 indeed shows that the activation barrier appears “early” in exo-ergic reaction, e.g., H
2 + F → H + HF, with the reaction substrates being only slightly modified in TS, R
‡ ≈ [A–B]. Accordingly, in the endo-ergic bond-breaking–bond-forming process, e.g., H + HF → H
2 + F, the barrier is “late” along the reaction coordinate
P and the activated complex resembles more reaction products: R
‡ ≈ [C–D]. This qualitative statement has been subsequently given several more quantitative formulations and theoretical explanations using both the energetic and entropic arguments [
93,
94,
95,
96,
97,
98,
99,
100]
Previous virial-theorem analyses [
1,
2,
3,
5] have shown that this qualitative rule is fully indexed by the sign of the
P-derivative of the average kinetic energy or of the resultant gradient information at TS complex. The energy profile along the reaction “progress” coordinate
P, Δ
E(
P) =
E(
P) −
E(
Psub.) is again directly “translated” by the virial theorem into the associated displacement in its kinetic-energy contribution Δ
T(
P) =
T(
P) −
T(
Psub.), proportional to the corresponding change Δ
I(
P) =
I(
P) −
I(
Psub.) in the system resultant gradient information, Δ
I(
P) =
σ Δ
T(
P),
A reference to qualitative plots in
Figure 3 shows that the related Δ
T(
P) or Δ
I(
P) criteria distinguish these two directions by the sign of their geometrical derivative at TS complex:
This observation demonstrates that the RC derivative of the resultant gradient information at TS complex, proportional to
dT/dP|
‡, can indeed serve as an alternative detector of the reaction energetic character: its positive/negative values respectively identify the endo/exo-ergic processes, exhibiting the late/early activation barriers, respectively, with the neutral case, Δ
Er = 0 or
dT/dP|
‡ = 0, exhibiting an “equidistant” position of TS between the reaction substrates and products on a symmetric PES, e.g., in the hydrogen exchange reaction H + H
2 →H
2 + H.
The reaction energy ΔEr determines the corresponding change in the resultant gradient information, ΔIr = I(Pprod.) − I(Psub.) = σ ΔTr, proportional to ΔTr = T(Pprod.) − T(Psub.) = −ΔEr. The virial theorem thus implies a net decrease of the resultant gradient information in endo-ergic processes, ΔIr(endo) < 0, its increase in exo-ergic reactions, ΔIr(exo) > 0, and a conservation of the resultant gradient information in the energy-neutral chemical processes: ΔIr(neutral) = 0. One also recalls that the classical part of this information displacement probes an average inhomogeneity of electronic density. Therefore, the endo-ergic processes, requiring a net supply of energy to R, give rise to more diffused electron distributions in the reaction products, compared to substrates. Accordingly, the exo-ergic transitions, which release the energy from R, generate a more compact electron distributions in products and no such change is predicted for the energy-neutral case.
4. Reactivity Criteria
The grand-ensemble basis of populational derivatives of the energy or information descritors in the externally open molecular systems [
1,
2,
3,
53,
101,
102] has been briefly summarized in
Appendix C. The equilibrium energy function
is determined by the optimum probabilities {
Pji(
μ,
T;
v)} of the ensemble stationary states {|
ψji〉}, eigenstates of Hamiltonians {
}:
|
ψji〉 =
Eji |
ψji〉. These state probabilities correspond to the grand-potential minimum with respect to the ensemble density operator (see Equations (A29) and (A38)):
Thermodynamic energy of Equation (33) identifies the two Lagrange multipliers involved in this variational rule as corresponding partial derivatives with respect to the constraint values:
The minimum-energy principle of Equation (34) (see also Equation (A38)) can be alternatively interpreted as the associated extremum rule for the overall gradient information [
1,
2,
3,
19,
45],
where the ensemble-average value of the system potential energy again combines the electron-nuclear attraction (
) and the repulsion (
) contributions:
=
+
. This gradient-information/kinetic-energy principle is seen to contain the additional constraint of the fixed overall potential energy, 〈
W〉
ens. =
, multiplied by the Lagrange multiplier
It also includes modified “intensities” associated with the remaining constraints: information potential
information “temperature”
The conjugate thermodynamic principles, for the constrained extrema of the ensemble-average energy,
and thermodynamic gradient information,
have the same state-probability solutions [
1,
2,
3]. This manifests the physical equivalence of the energetic and entropic principles for determining the equilibrium states in thermodynamics [
4].
The equilibrium value of resultant gradient information, given by the weighted expression in terms of the equilibrium probabilities in the grand-canonical mixed state,
is related to the ensemble average kinetic energy
:
In this grand-ensemble approach the system chemical potential appears as the first (partial) populational derivative [
53,
73,
74,
101,
102,
103,
104,
105] of the system average energy. This interpretation also applies to the diagonal and mixed second derivatives of equilibrium electronic energy, which involve differentiation with respect to the electron-population variable
. In this energy representation, the chemical hardness reflects
-derivative of the chemical potential [
53,
73,
74,
106],
while the information hardness measures
-derivative of the information potential:
By the Maxwell cross-differentiation relation, the mixed derivative of the energy,
measuring the global Fukui Function (FF) [
53,
73,
74,
107], can be alternatively interpreted as either the density response per unit populational displacement, or the global chemical-potential response per unit local change in the external potential. The associated mixed derivative of the resultant gradient information then reads:
The positive signs of the diagonal descriptors assure the external stability of a molecule with respect to external flows of electrons, between the molecular system and its electron reservoir. Indeed, they imply an increase (a decrease) of the global energetic and information “intensities” conjugate to
=
N, the chemical (
μ), and information (
ξ) potentials, in response to a perturbation created by an electron inflow (outflow) Δ
N. This is in accordance with the familiar Le Châtelier and Le Châtelier–Braun principles of thermodynamics [
4], that the secondary (spontaneous) responses in system intensities to an initial population displacement diminish effects of this primary perturbation.
Since reactivity phenomena involve electron flows between the mutually open substrates, only in such generalized, grand-ensemble framework can one precisely define the relevant CT criteria, determine the hypothetical “states” of subsystems, and eventually measure the effects of their mutual interaction. The open microscopic systems require the mixed-state description, in terms of the ensemble-average physical quantities, capable of reflecting the externally imposed thermodynamic conditions and defining the infinitesimal populational displacements invoked in reactivity theory. In this ensemble approach, the energetic and information principles are physically equivalent, giving rise to the same equilibrium probabilities. This basic equivalence is consistent with the alternative energetic and entropic principles invoked in equilibrium thermodynamics of macroscopic systems [
4].
5. Donor-Acceptor Systems
In reactivity considerations one conventionally recognizes several hypothetical stages of chemical processes involving either the mutually closed (nonbonded, disentangled) or open (bonded, entangled) reactants
α = {A, B} [
1,
2,
3,
73,
74], e.g., substrates in a typical bimolecular reactive system R = A–B involving the acidic (A, electron acceptor) and basic (B, electron donor) subsystems. The nonbonded status of these fragments, when they conserve their initial (integer) overall numbers of electrons {
Nα =
Nα0} in the isolated (separated) reactants {
α0}, is symbolized by the solid vertical line, e.g., in the intermediate, polarized reactive system R
+ ≡ (A
+|B
+) combining the internally polarized but mutually closed subsystems. It should be emphasized that only due to this mutual closure the substrate identity remains a meaningful concept. Their descriptors in the final, equilibrium-reactive system R
* ≡ (A
*¦B
*) ≡ R, combining the mutually open (bonded) fragments, as symbolized by the vertical broken line separating the two subsystems, can be inferred only indirectly [
1,
2,
3], by externally opening the two mutually closed subsystems of R
+ with respect to their separate (macroscopic) electron reservoirs {
α} in the composite polarized system
The subsystem densities {ρα = Nα pα}, with pα denoting the internal probability distribution in fragment α, are “frozen” in the promolecular reference R0 = (A0|B0) consisting of the isolated-reactant distributions {ρα0 = Nα0 pα0} shifted to their actual positions in the “molecular” system R. The polarized reactive system R+ combines the relaxed subsystem densities, modified in presence of the reaction partner at finite separation between both subsystems: {ρα+ = Nα+pα+, Nα+ = ∫ρα+dr = Nα0}. In the global equilibrium state of R as a whole, these polarized subsystem densities are additionally modified by the effective inter-reactant CT: {ρα* = Nα*pα*, Nα* = ∫ρα*dr ≠ Nα0}.
The overall electron density in the whole R
+ is given by the sum of reactant densities, polarized due to “molecular” external potential
v =
vA +
vB combining contributions due to the fixed nuclei in both substrates at their final mutual separation,
Here, {
pα+ =
ρα+/
Nα+} stand for the internal probability densities in such promoted fragments, and the global probability distribution reflects the “shape” factor of the overall electron density,
where condensed reactant probabilities {
Pα+ =
Nα+/
NR =
Nα0/
NR =
Pα0} denote fragment shares in
NR. At this polarization stage, both fragments exhibit internally equalized chemical potentials {
μα+ =
μ[
Nα0,
v]}, different from the separate-reactant levels {
μα0 =
μ[
Nα0,
vα]}.
The two molecular subsystems lose their identity in the bonded status, as the mutually open parts of the externally closed reactive system R
*, which allows for the inter-fragment (intra-R) flows of electrons. In such a global equilibrium each “part” effectively extends over the whole molecular system since the hypothetical boundary defining the fragment identity does not exists any more. Both subsystems then effectively exhaust the molecular electron distribution, their electron populations are equal to the global number of electrons,
and subsystem chemical potentials in R are equalized at molecular level
μR: {
μα* =
μR}.
One can contemplate, however, the external flows of electrons, between the mutually closed (nonbonded) but externally open reactants and their separate (macroscopic) reservoirs {
α}. The mutual closure then implies the relevancy of subsystem identities established at the polarization stage of R
+, while the external openness in the composite subsystems {
α+ = (
α+¦
α+)} allows one to independently “regulate” the external chemical potentials of both parts, {
μα+ =
μ(
α)}, and hence also their average densities {
ρα+ =
Nα+pα+} and electron populations
Nα+ = ∫
ρα+dr. In particular, the substrate chemical potentials equalized at the molecular level in both subsystems, {
μα+ ≡
μ[
Nα*,
v] =
μR ≡
μ[
NR,
v]}, which then also describes a common molecular reservoir {
α(
μR) =
(
μR)} coupled to both reactants, (
(
μR)¦A
*¦B
*), formally define the global equilibrium state in the molecular part R
* = (A
*¦B
*) of the composite system which (indirectly) represents the global equilibrium in R as a whole:
This reactive system indeed implies an effective mutual openess of both reactants, realized through the direct external openness of both substrates to a common (molecular) reservoir
(
μR). It allows for an effective donor(B)→acceptor(A) flow of electrons, between subsystems of the molecular fragment R
* of
R*, while retaining the reactant identities assured by the direct mutual closeness of the polarized molecular part R
+ in
R+.
The final reactant distributions {
ρα* =
ρα+(
μR)} in R
* and the associated electron populations {
Nα* =
Nα+(
μR)} are then modified by effects of the inter-reactant CT
for the conserved overall (average) number of electrons in the globally isoelectronic processes in the reactive system as a whole:
Density changes due to these equilibrium redistributions of electrons are indexed by the corresponding in situ FF. In CSA [
73,
74], one introduces the reactant-resolved FF matrix of the substrate density responses to displacements in the fragment electron populations, for the fixed (molecular) external potential (geometry),
which generate the FF indices of reactants in the B→A CT:
One recalls, that these relative responses of reactants eventually combine into the corresponding global CT derivative, of the reactive system as a whole,
which represents the populational sensitivity of R
* with respect to the effective internal CT, between the externally open but mutually closed reactants.
To summarize, the fragment identity remains a meaningful concept only for the mutually closed (nonbonded) status of the acidic and basic reactants, e.g., in the polarized reactive system R+ or in the R+ part of R+. The global equilibrium in R as a whole, R = R*, combining the effectively “bonded”, externally open but mutually closed subsystems {α*} in R*, accounts for the extra CT-induced polarization of reactants compared to R+. Descriptors of this state, of the mutually “bonded” reactants, can be inferred only indirectly, by examining the chemical potential equalization in the equilibrium composite system R*. Similar external reservoirs are involved when one examines independent population displacements on reactants, e.g., in defining the fragment chemical potentials and their hardness tensor in the substrate fragment of R+. In this hypothetical chain of reaction “events”, the polarized system R+ thus appears as the launching stage for the subsequent CT and the accompanying induced polarization, after the hypothetical barrier for the flow of electrons between subsystems has been effectively lifted.
Thus, the equilibrium case
R* of
R+ also represents the effectively open reactants in R
*. The equilibrium substrates {
α*} indeed display the final equilibrium densities {
ρα* =
ρα(
μR)} after the B→A CT, giving rise to molecular electron distribution
and the associated populations {∫
ρα+(
μR)
dr =
Nα+(
μR) =
Nα*} corresponding to the chemical potential equalization in R = R
* as a whole:
μA* =
μB* =
μR. One observes that the reactant chemical potentials have not been equalized at the preceding polarization stage in the molecular part R
n+ = (A
+|B
+) of a general composite system
when
μA+[
ρA+] <
μB+[
ρB+].
In the polarized reactive system, the fragment chemical potentials
μR+= {
μα+ =
μα[
Nα0,
v]} and the resulting elements of the hardness matrix
ηR+ = {
ηα,β} represent populational derivatives of the system average electronic energy in reactant resolution,
Ev({
Nβ}). They are properly defined in
R+, calculated for the fixed external potential
v reflecting the “frozen” molecular geometry. These quantities represent the corresponding partials of the system ensemble-average energy with respect to ensemble-average populations {
Nα} on subsystems in the mutually closed (externally open) composite subsystems {
α+ = (
α+¦
α+)} in
R+ = (
A+|
B+):
The global reactivity descriptors, of the R = (A
*¦B
*) ≡ R
* part of
R*, similarly involve differentiations with respect to the average number of electrons of R in the combined system
R* = (R
*¦
*) = (A
*¦B
*¦
*):
The optimum amount of the (fractional) CT is determined by the populational “force”, measuring the difference between chemical potentials of the polarized acidic and basic reactants which defines the effective CT gradient,
and the in situ hardness (
ηCT) or softness (
SCT) for this process,
representing the effective CT Hessian and its inverse, respectively, proportional to the CT information hardness Hessian
ωCT. The optimum amount of the inter-reactant CT,
then generates the associated second-order stabilization energy due to CT,
proportional to the associated change
ICT in the resultant gradient information.
6. HSAB Principle Revisited
The physical equivalence of reactivity concepts formulated in the energy and resultant gradient-information representations has direct implications for OCT, in which one treats a molecule as an information network propagating signals of the AO origins of electrons in the bond system determined by the configuration occupied MO. It has been argued that elements of the CBO matrix
γ = {
γk,l} of Equation (26), weighting factors in Equation (24), determine amplitudes of conditional probabilities defining molecular (direct) communications between AO. Entropic descriptors of such information channel generate the entropic bond orders and measures of their covalent/ionic components, which ultimately facilitate an IT understanding of molecular electronic structure in chemical terms [
7,
19,
20,
21,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42]. The communication “noise” (orbital indeterminicity) in this network, measured by the channel conditional entropy, is due to the electron delocalization in the bond system of a molecule. It represents the system overall bond “covalency”, while the channel information “capacity” (orbital determinicity), reflected by the mutual information of the molecular communication network, measures its resultant bond “iconicity”. The more scattering (indeterminate) is the molecular information system, the higher its covalent character; a more deterministic (less noisy) channel thus represents a more ionic molecular system. These two bond attributes thus compete with one another.
In chemistry, the bond covalency, a common possession of electrons by interacting atoms, is indeed synonymous with an electron delocalization generating a communication noise. A classical example of a purely covalent interaction constitute bonds connecting identical atoms, e.g., hydrogens in H2 or carbons in ethylene, when the interacting AO in the familiar MO diagrams of chemistry exhibit the same AO energies. The bond ionicity accompanies large differences in electronegativities, generating a substantial CT between the interacting atoms. Such bonds correspond to a wide separation of AO energies in MO diagrams. The ionic bond component diminishes noise and introduces more determinicity into AO communications, thus representing the bond mechanism competitive with the bond covalency.
One of the celebrated (qualitative) rules of chemistry deals with stability preferences in molecular coordinations. The HSAB principle [
84,
85,
106] predicts that chemically hard (H) acids prefer to coordinate hard bases in the [HH] complexes A–B, and soft (S) acids prefer to coordinate soft bases in the [SS] complexes, whereas the “mixed” [HS] or [SH] coordinations, of hard acids with soft bases or of soft acids with hard bases, are relatively unstable. Little is known about the communication implications of this principle. In such a communication perspective on reactive systems the H and S reactants correspond to internally ionic (deterministic) and covalent (noisy) substrate channels, respectively. The former involves relatively localized communications between AO, while the latter corresponds to delocalized probability scatterings between the basis states.
In the reactivity context, the following additional questions arise:
What is an overall character of communications responsible for the mutual interaction between reactants?
How does the HSAB rule influence the inter-reactant propagations of information, i.e., how do the [HH] and [SS] preferences shape the inter-reactant communications in these complexes?
Do the S substrates in [SS] complex predominantly interact “covalently”, and H substrates in the [HH] complex “ionically”?
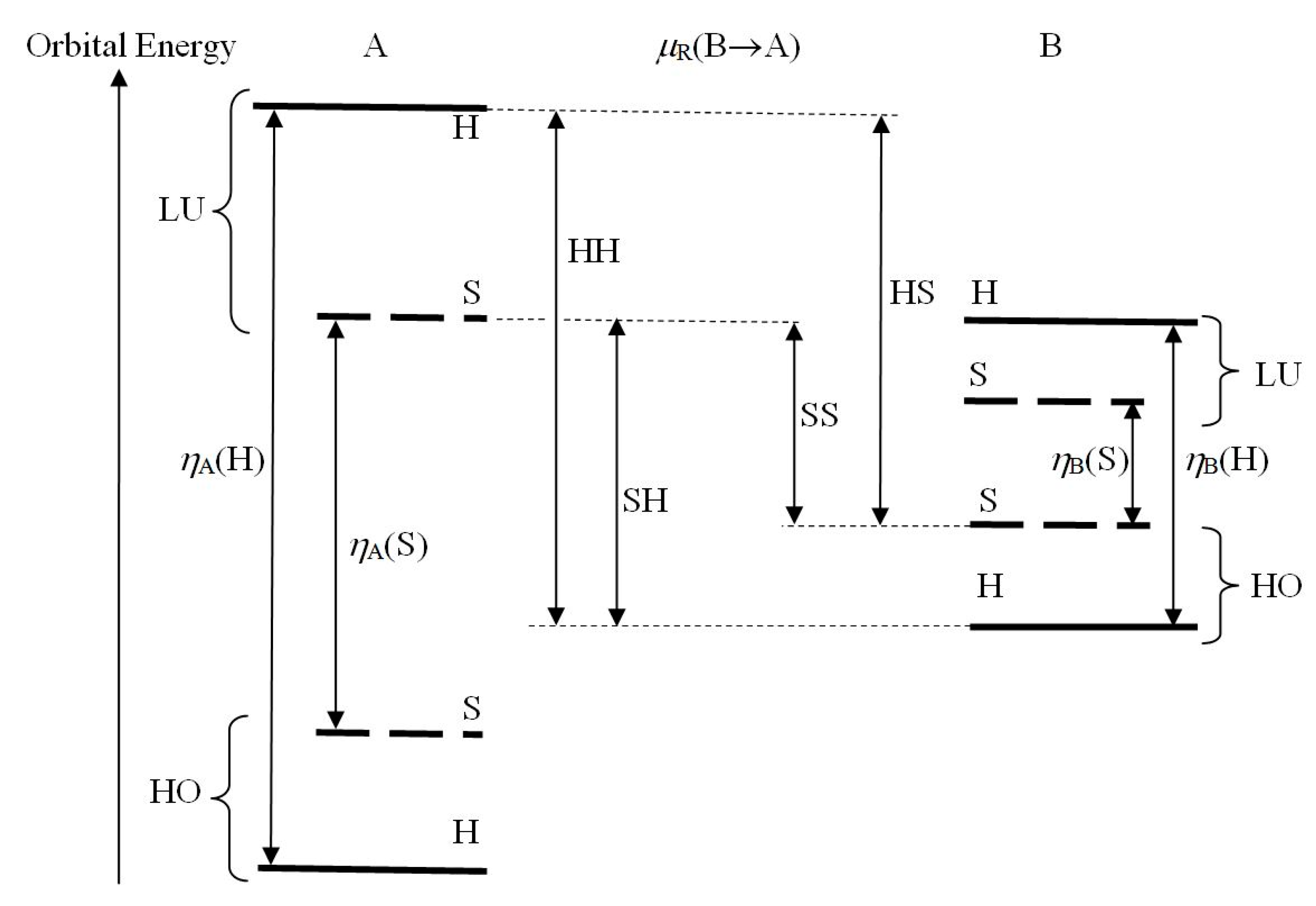
In the frontier electron (FE) [
81,
82,
83] approach to molecular interactions and CT phenomena, the orbital energy of the substrate highest occupied MO (HOMO) determines its donor (basic) level of the chemical potential, while the lowest unoccupied MO (LUMO) energy establishes its acceptor (acidic) capacity (see
Figure 4). The HOMO–LUMO energy gaps in subsystems then reflect the substrate molecular hardnesses. The interaction between the reactant frontier MO of comparable orbital energies is predominantly covalent (chemically “soft”) in character, while that between the subsystem MO of distinctly different energies becomes mostly ionic (chemically “hard”).
Figure 4 summarizes the alternative relative positions of the donor (HOMO) levels of the basic reactant, relative to the acceptor (LUMO) levels of its acidic partner, for all admissible hardness combinations in the reactive system R = A–B. In view of the proportionality relations between the energetic and information reactivity criteria, these relative MO energy levels also reflect the corresponding information potential and hardness descriptors of subsystems, including the in situ derivatives driving the information transfer between reactants.
A magnitude of the ionic, CT-stabilization energy in A–B systems is then determined by the corresponding in situ populational derivatives in R,
where
μCT and
ηCT stand for the effective chemical potential and hardness descriptors of R involving the FE of reactants. Since the donor/acceptor properties of reactants are already implied by their known relative acidic or basic character, one applies the biased estimate of the CT chemical potential. In FE approximation, the chemical potential difference
μCT for the effective internal B→A CT then reads (see
Figure 4):
It determines the associated first-order energy change for the B→A transfer of
NCT electrons:
The CT chemical potential of Equation (66) thus combines the electron-removal potential of the basic reactant, i.e., its negative ionization potential
IB =
E(B
+1) −
E(B
0) > 0,
and the electron-insertion potential of the acidic substrate, i.e., its negative electron affinity
The energy of the CT disproportionation process,
then generates the (unbiased) finite-difference measure of the effective hardness descriptor for this implicit CT:
These in situ derivatives ultimately determine a magnitude of the CT stabilization energy of Equation (65), which reflects the ionic part of the overall interaction energy,
In the FE framework of
Figure 4, the CT-interaction energy is thus proportional to the squared gap between the LUMO orbital energy of the acidic reactant and the HOMO level of the basic substrate. This ionic interaction is thus predicted to be strongest in [HH] pairs of subsystems and weakest in [SS] arrangements, with the mixed [HS] and [SH] combinations representing the intermediate magnitudes of this ionic-stabilization effect.
It should be realized, however, that ionic and covalent energy contributions complement each other in the resultant bond energy [
85]. Therefore, the [SS] complex, for which the energy gap
εA(LUMO)−
εB(HOMO) between the interacting orbitals reaches the minimum value, implies the strongest covalent stabilization in the reactive complex. Indeed, the lowest (bonding) energy level
εb of this FE interaction, corresponding to the bonding combination of the (positively overlapping) frontier MO of subsystems,
then exhibits the maximum bonding energy due to the covalent interaction:
It follows from the familiar secular equations of the Ritz method that this covalent energy can be approximated by the limiting MO expression
where the matrix element of the system electronic Hamiltonian, which couples the two states,
is expected to be proportional to the overlap integral
S between the frontier MO involved. It indeed follows from Equation (75) that the maximum covalent component of the inter-reactant chemical bond is expected in interactions between soft, strongly overlapping reactants, since then the numerator assumes the highest value while the denominator reaches its minimum. For the same reason one predicts the smallest covalent stabilization in interactions between the hard, weakly overlapping substrates, with the mixed hardness combinations giving rise to intermediate bond covalencies.
To summarize, the [HH] complex exhibits the maximum ionic stabilization, the [SS] complex the maximum covalent interaction, while the mixed combinations of reactant hardnesses in [HS] and [SH] coordinations exhibit a mixture of moderate covalent and ionic bond components between the acidic and basic subsystems. Therefore, communications representing the inter-reactant bonds between the chemically soft (covalent) reactants are also expected to be predominantly “soft” (delocalized, indeterministic) in character, while those between the chemically hard (ionic) subsystems are predicted to be dominated by the “hard” (localized, deterministic) propagations in the communication system for R as a whole.
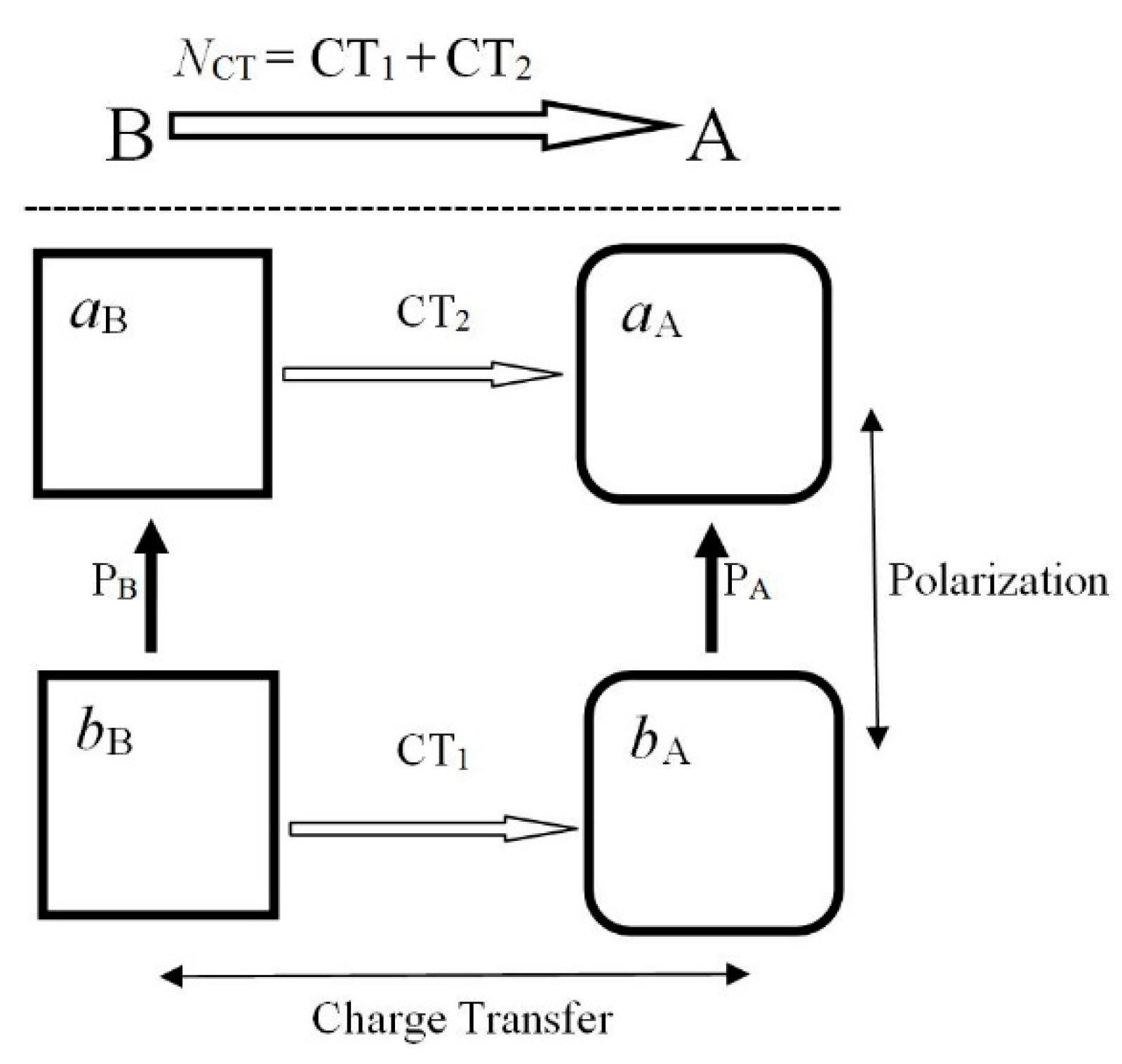
The electron communications between reactants {
α = A, B} in the acceptor-donor reactive system R = A–B are determined by the corresponding matrix of conditional probabilities (or of their amplitudes) in AO resolution, which can be partitioned into diagonal blocks of the intra-reactant (internal) communications within individual substrates and off-diagonal blocks of the inter-reactant (external) communications between different subsystems:
The [SS] complexes combining the “soft” (noisy, delocalized) internal blocks of such probability propagations imply similar covalent character of the external blocks of electron AO communications between reactanta, i.e., strongly indeterministic scatterings between subsystems: {intra-S} ⇒ {inter-S}. The “hard” (ionic) internal channels are similarly associated with the ionic (localized) external communications: {intra-H} ⇒ {inter-H}. This observation adds a new communication angle to the classical HSAB principle of chemistry.
7. Regional HSAB versus Complementary Coordinations
One of the still problematic issues in reactivity theory is the most favorable mutual arrangement of the acidic and basic parts of molecular reactants in donor-acceptor systems. It appears that the global HSAB preference is no longer valid regionally, in interactions between fragments of reactants, where the complementarity principle [
108,
109] establishes the preferred arrangement between the acidic and basic parts of both substrates. These more subtle reactivity preferences result from the induced electron flows in reactive systems, reflecting responses to the primary displacements in molecular complexes. Such flow patterns can be diagnosed, estimated, and compared using either the energetical or information reactivity criteria defined above.
Consider the reactive A–B complex consisting of the basic reactant B = (aB|…|bB) ≡ (aB|bB) and the acidic substrate A = (aA|…|bA) ≡ (aA|bA), where aX and bX denote the acidic and basic parts of X, respectively. The acidic (electron acceptor) part is relatively hard, i.e., less responsive to external perturbations, exhibiting lower values of the fragment FF descriptor, while the basic (electron donor) fragment is relatively soft and more polarizable, as reflected by its higher density or population response descriptors. The acidic part aX exerts an electron-accepting (stabilizing) influence on the neighboring part of another reactant Y, while the basic fragment bX produces an electron-donor (destabilizing) effect on a fragment of Y in its vicinity.
There are two ways in which both reactants can mutually coordinate in the reactive complexes. In the complementary (
c) arrangement of
Figure 5,
the reactants orient themselves in such a way that geometrically accessible
a-fragment of one reactant faces the geometrically accessible
b-fragment of the other substrate. This pattern follows from the maximum complementarity (MC) rule of chemical reactivity [
108,
109], which reflects an electrostatic preference: an electron-rich (repulsive, basic) fragment of one reactant prefers to face an electron-deficient (attractive, acidic) part of the reaction partner. In the alternative regional HSAB-type structure of
Figure 6,
the acidic (basic) fragment of one reactant faces the like-fragment of the other substrate.
The complementary complex, in which the “excessive” electrons of
bX are placed in the attractive field generated by the electron “deficient”
aY, is expected to be favored electrostatically since the other arrangement produces regional repulsions between two acidic and two basic sites of reactants. Additional rationale for this complementary preference over the regional HSAB alignment comes from examining charge flows created by the dominating shifts in the site chemical potential due to the presence of the (“frozen”) coordinated site of the nearby part of the reaction partner. At finite separations between the two subsystems, these displacements trigger the polarizational flows {P
X} shown in
Figure 5 and
Figure 6, which restore the internal equilibria in subsystems, initially displaced by the presence of the other reactant.
In R
c, the harder (acidic) site
aY initially lowers the chemical potential of the softer (basic) site
bX, while
bY rises the chemical potential level of
aX. These shifts trigger the internal polariaztional flows {
aX→
bX} in both reactants, which enhance the acceptor capacity of
aX and donor ability of
bX, thus creating more favourable conditions for the subsequent inter-reactant CT of
Figure 5. A similar analysis of R
HSAB (
Figure 6) predicts the
bX→
aX polarizational flows, which lower the acceptor capacity of
aX and donor ability of
bX, i.e., produce an excess electron accumulation on
aX and stronger electron depletion on
bX, thus creating less favourable conditions for the subsequent inter-reactant CT.
The complementary preference also follows from the electronic stability considerations, in spirit of the familiar Le Châtelier–Braun principle in ordinary thermodynamics [
4]. In
Figure 5 and
Figure 6, the CT responses follow the preceding polarizations of reactants, the equilibrium responses to displacements {Δ
vX} in the external potential on subsystems. In stability considerations one first assumes the primary (inter-reactant) CT displacements {ΔCT
1, ΔCT
2} of
Figure 5 and
Figure 6, in the internally “frozen” but externally open reactants, and then examines the induced secondary (intra-reactant) relaxational responses {I
X} to these populational shifts in the CT-perturbed substrates.
Let us first examine the CT-displaced complementary structure R
c,
It corresponds to the primary CT perturbations of
Figure 5:
In accordance with the Le Châtelier principle, an inflow/outflow of electrons to/from a given site
x increases/decreases the site chemical potential, as indeed reflected by the positive value of the site diagonal hardness descriptor
The initial perturbations of the partial CT flows {ΔCT
k} thus create the following shifts in the site chemical potentials, compared to the initially equalized levels in isolated reactants A
0 = (
aA0¦
bA0) and B
0 = (
aB0¦
bB0),
These CT-induced shifts in the fragment electronegativities thus trigger the following secondary (induced) relaxational flows {I
X} in R
cCT,
which diminish effects of the CT perturbations by reducing the extra charge accumulations/ depletions created by the primary populational displacements.
Consider next the CT-displaced HSAB complex R
HSAB,
The primary CT shifts in the site electron populations,
where inequality reflects expected magnitudes of the associated in situ chemical potentials,
now induce the following internal
relaxations in reactants:
These charge responses further exaggerate charge depletions/accumulations created by the primary CT perturbations, thus giving rise to less stable reactive complex.