Performance Enhancement of Internal Combustion Engines through Vibration Control: State of the Art and Challenges
Abstract
:1. Introduction
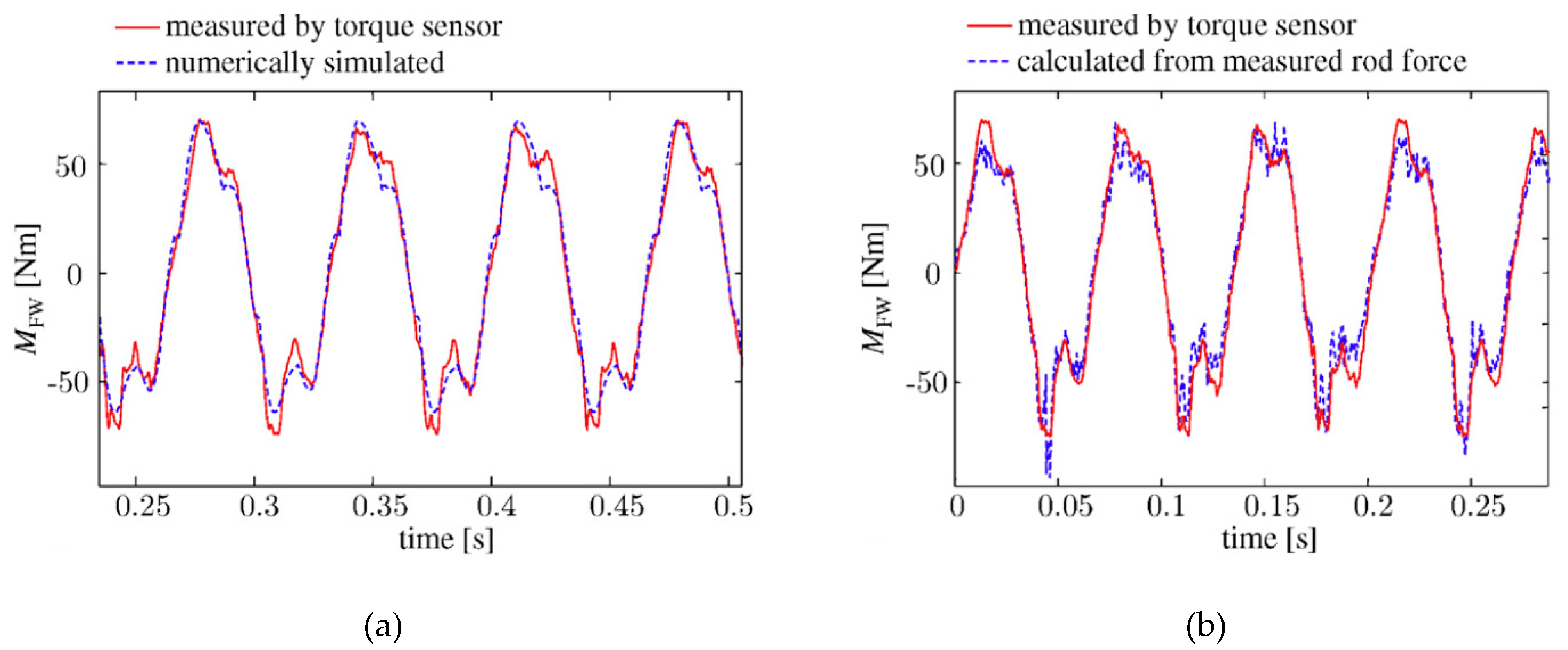
2. Measurement of Torsional Vibrations in ICEs
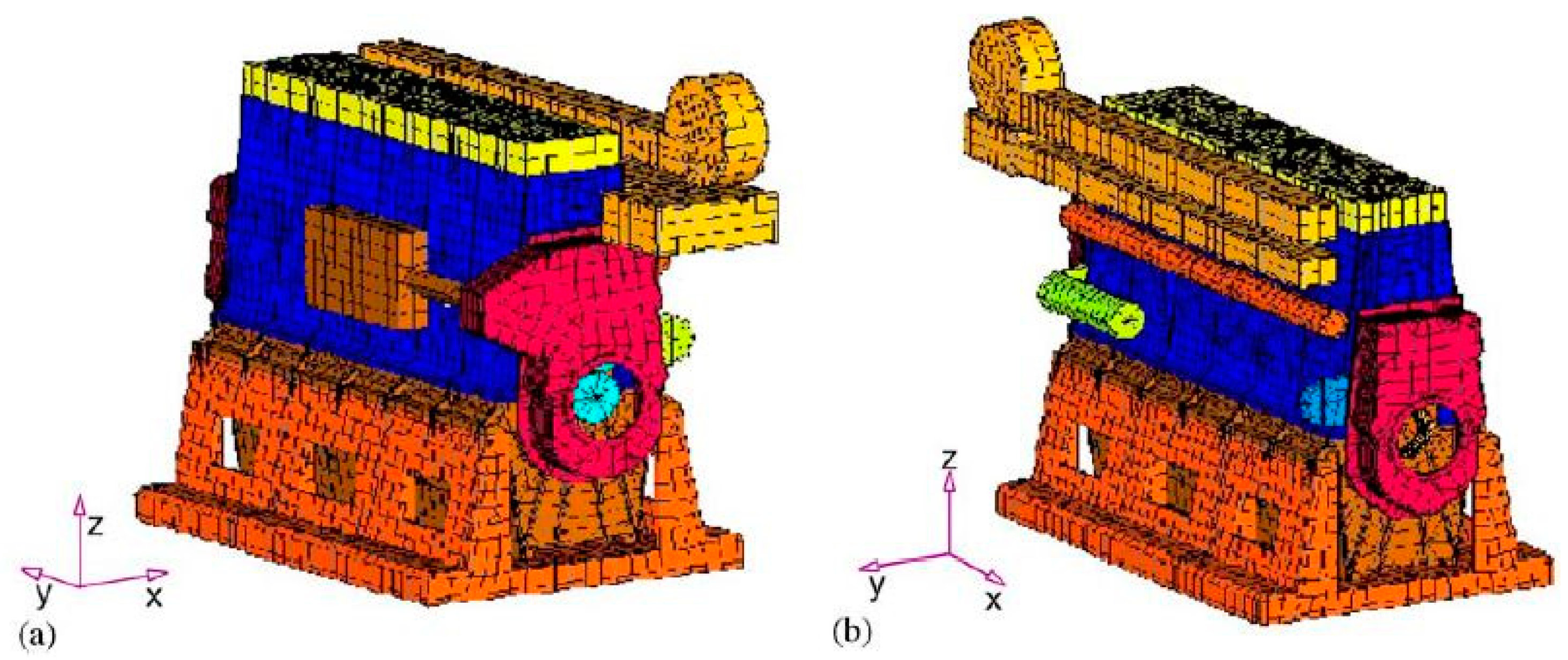
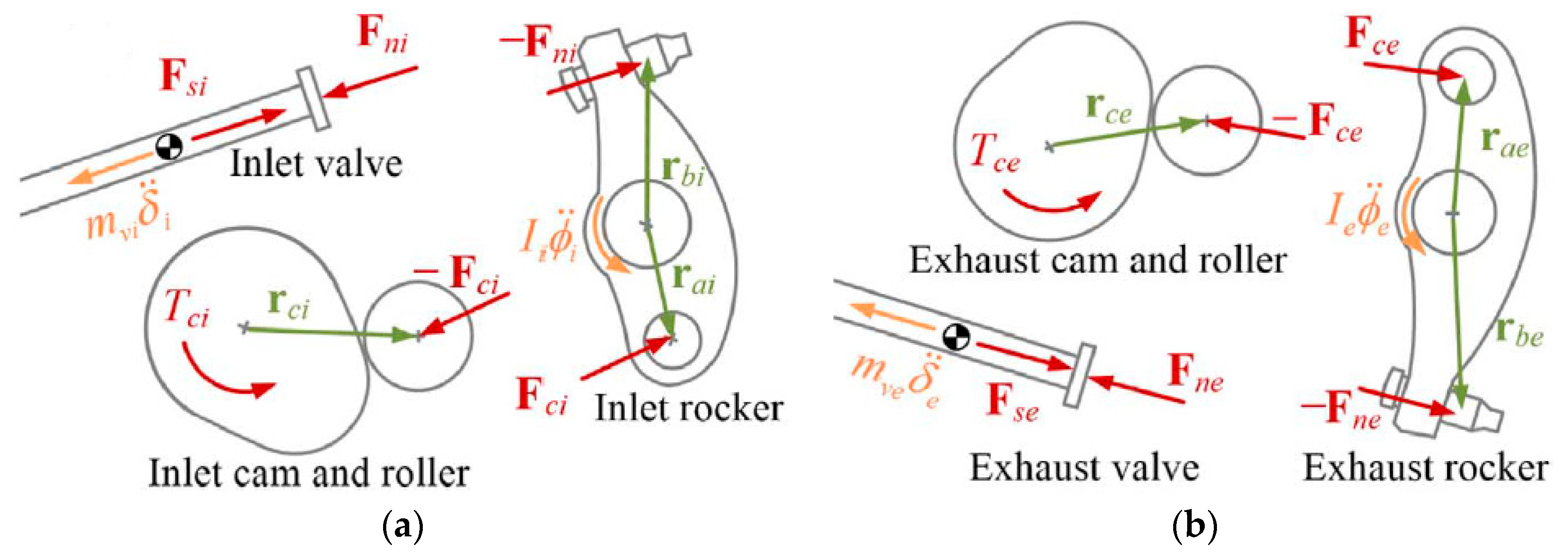
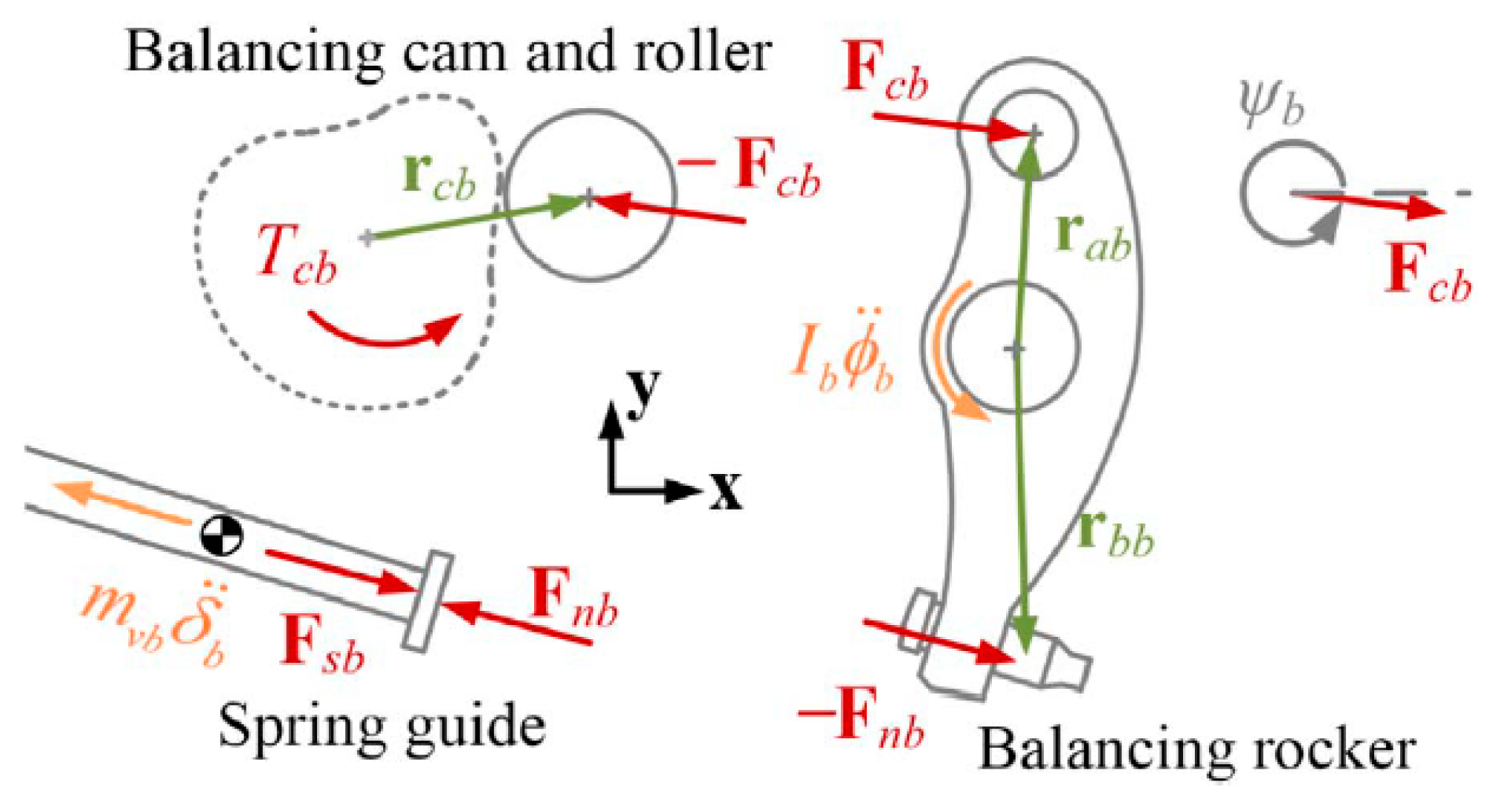
3. Engine Modifications and Mechanism Design
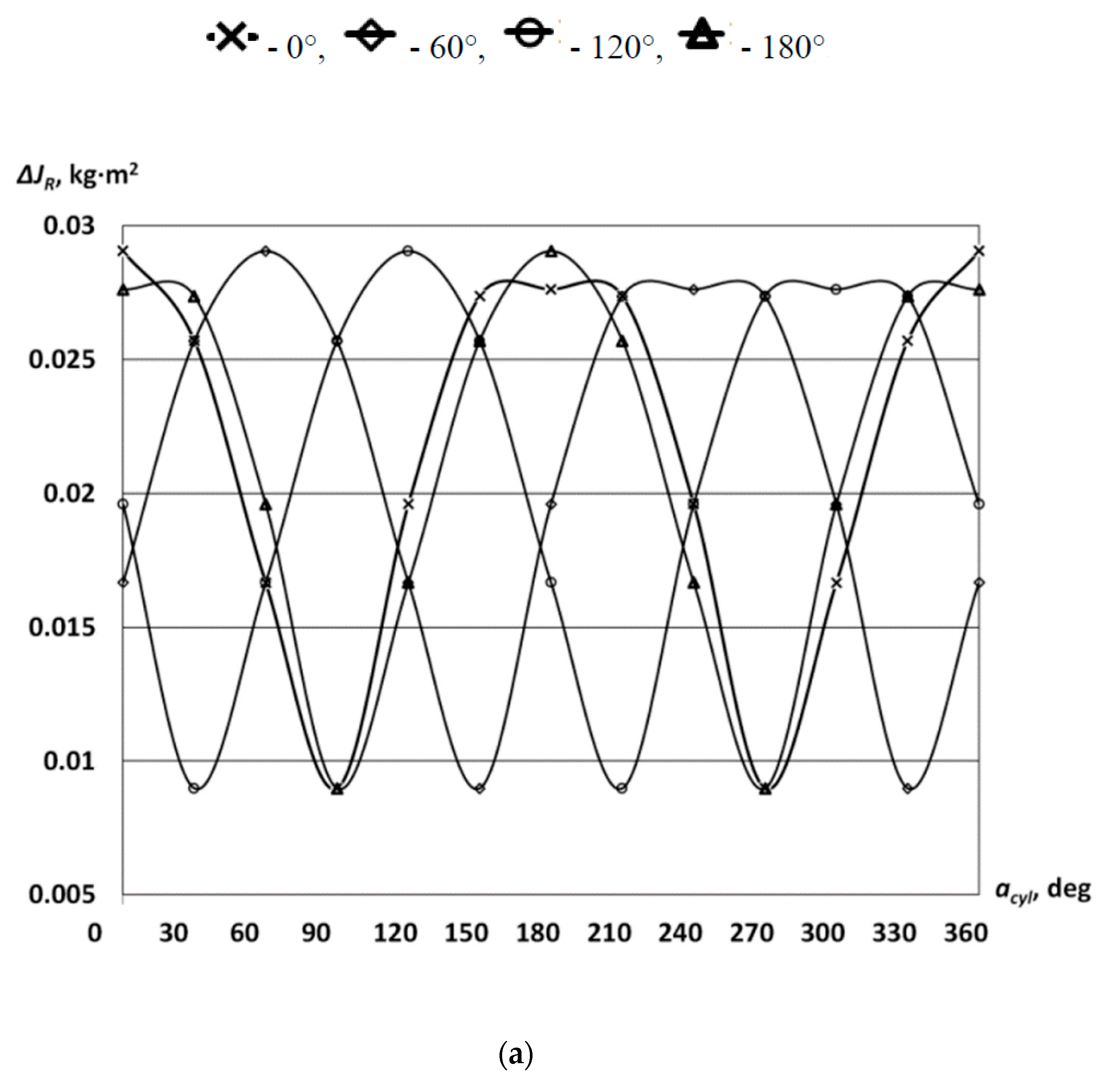
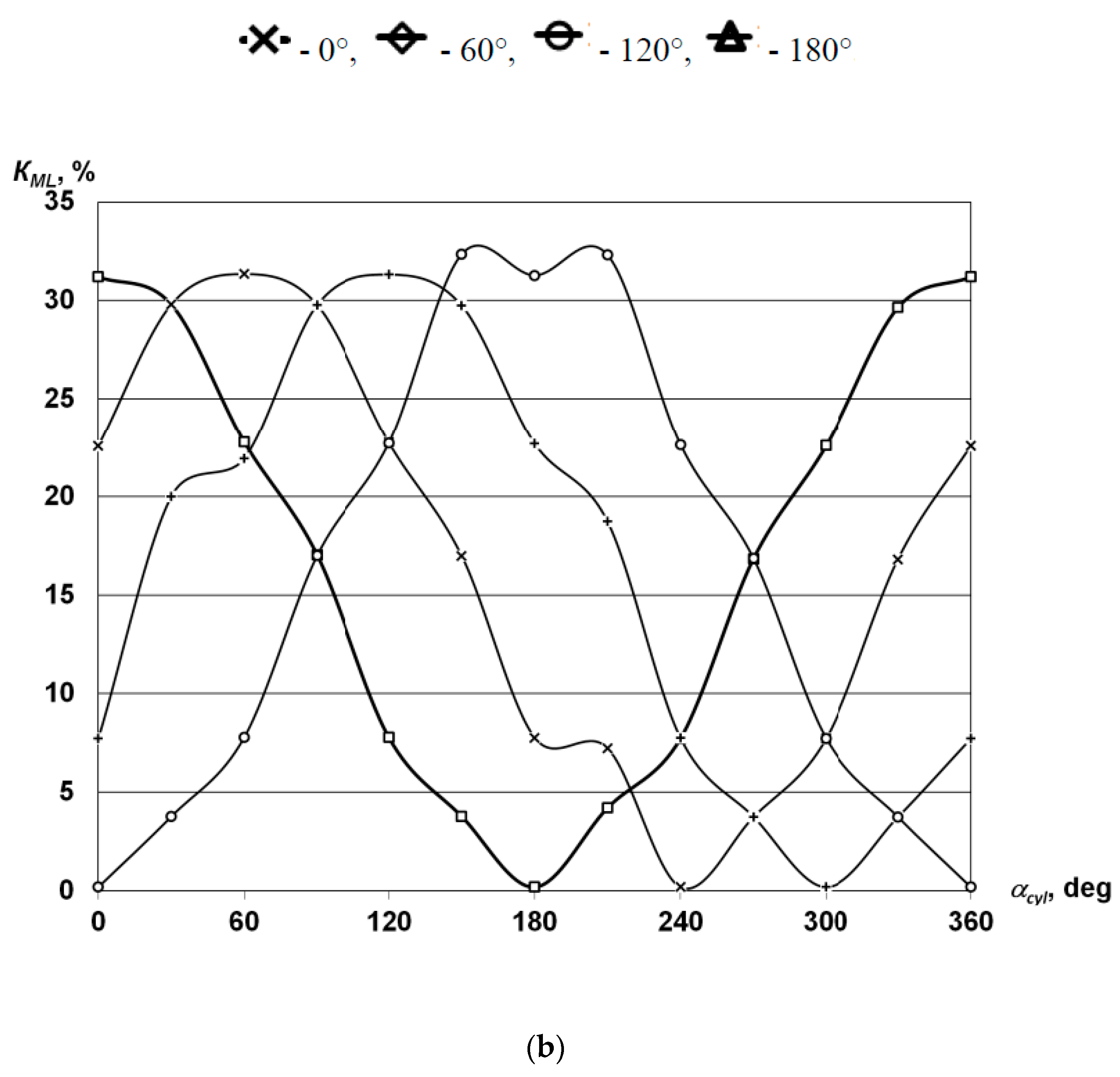
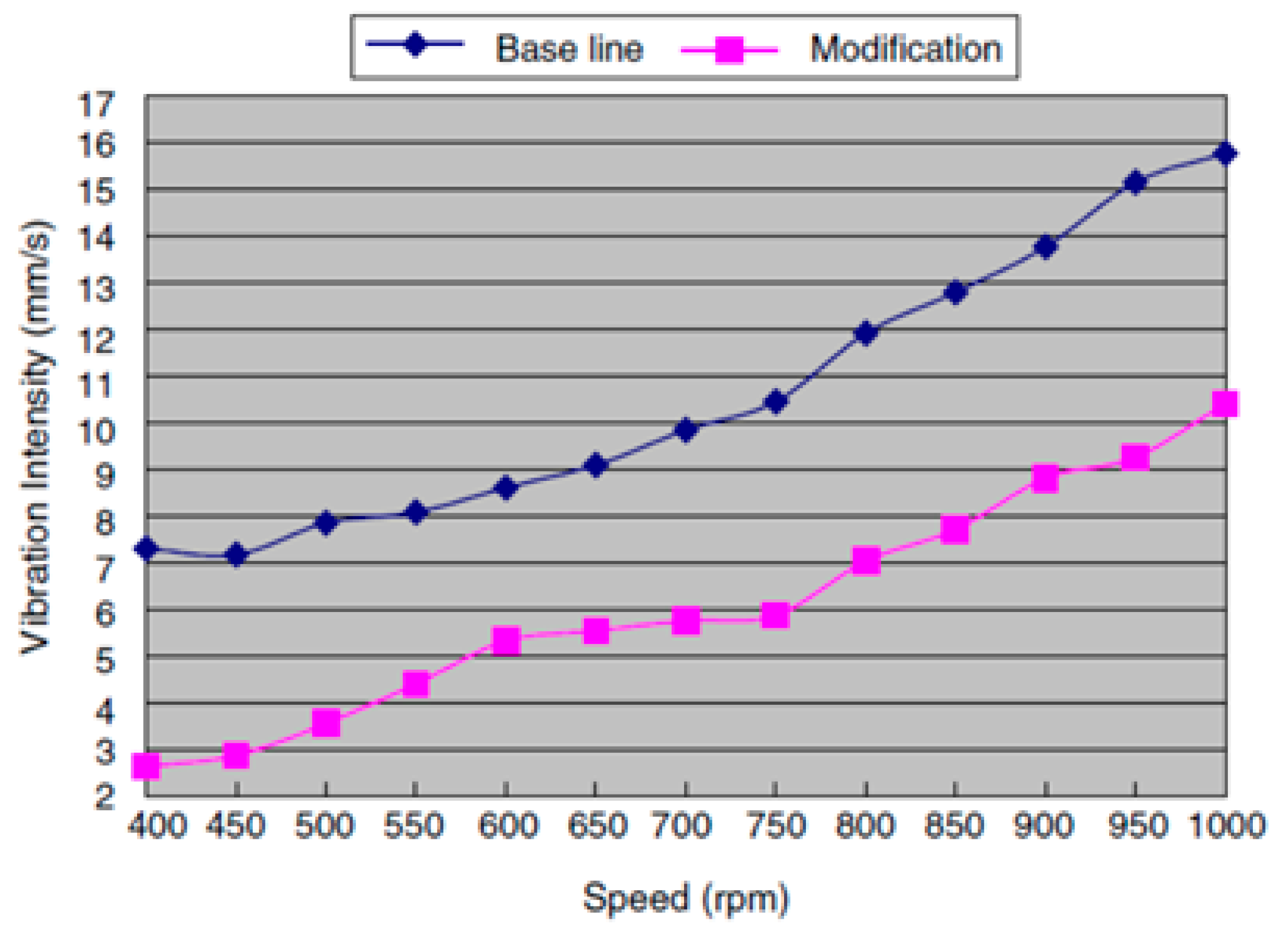
3.1. Engine Modifications
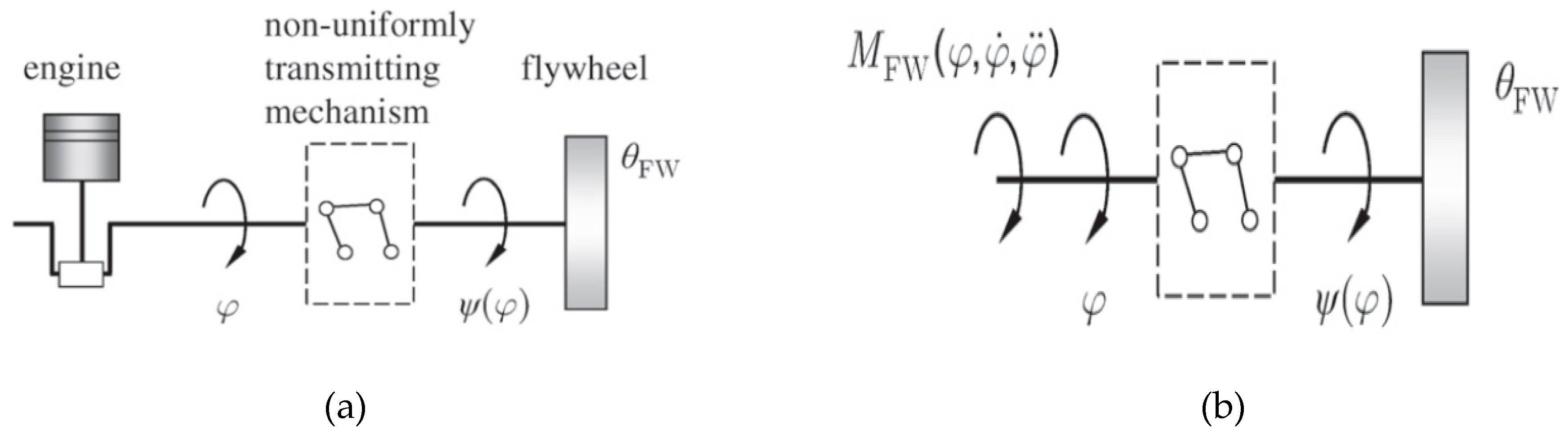
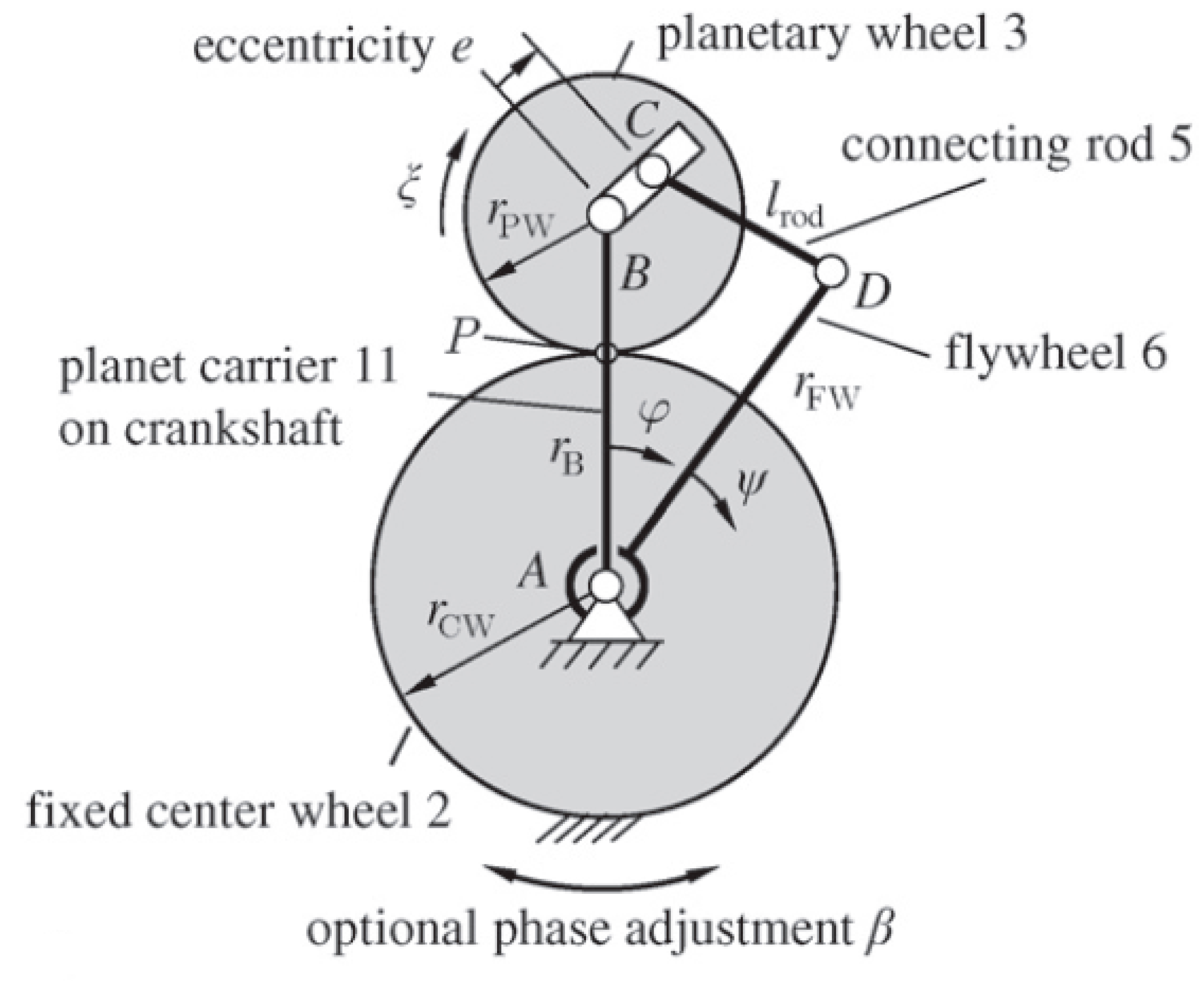
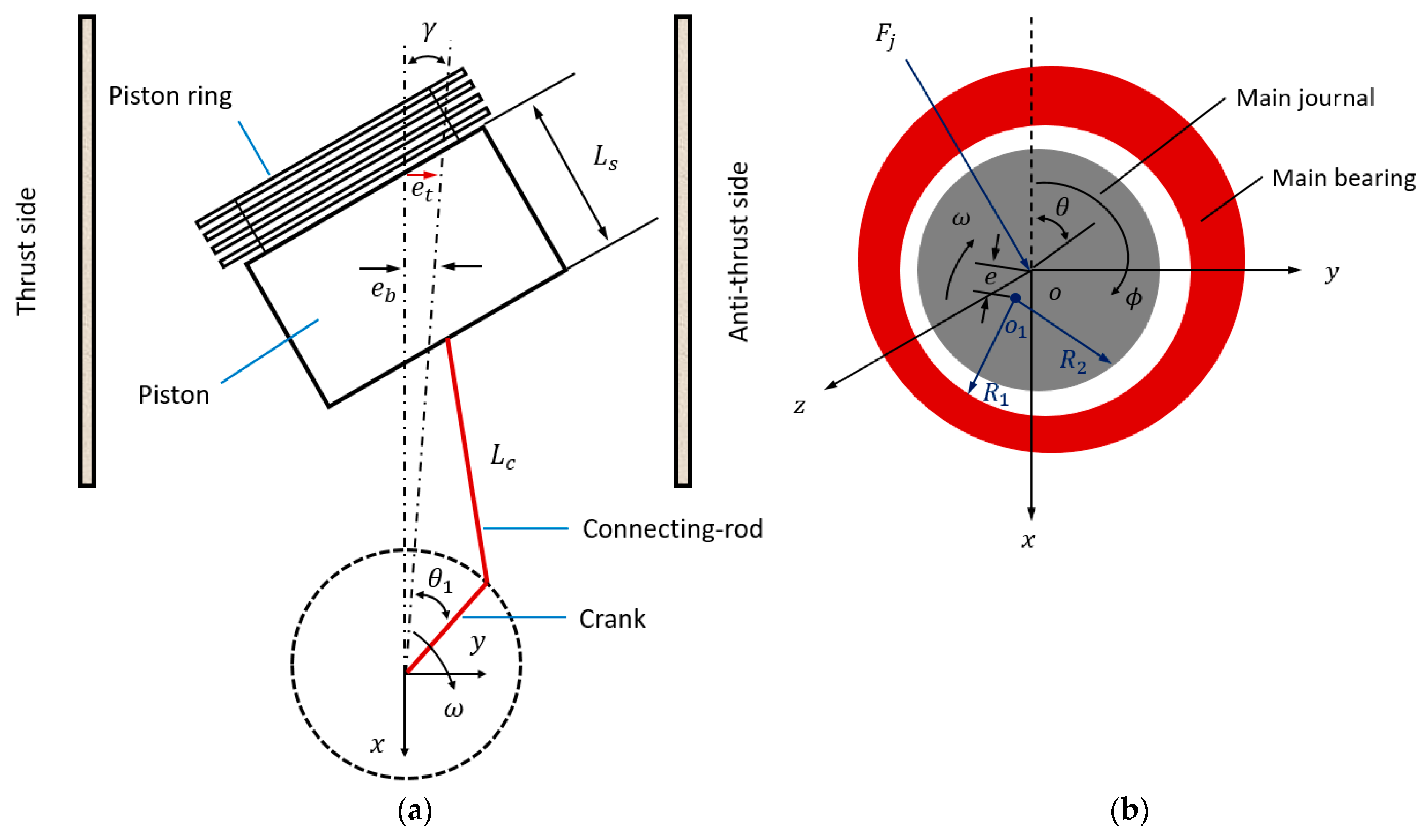
3.2. Mechanism Design
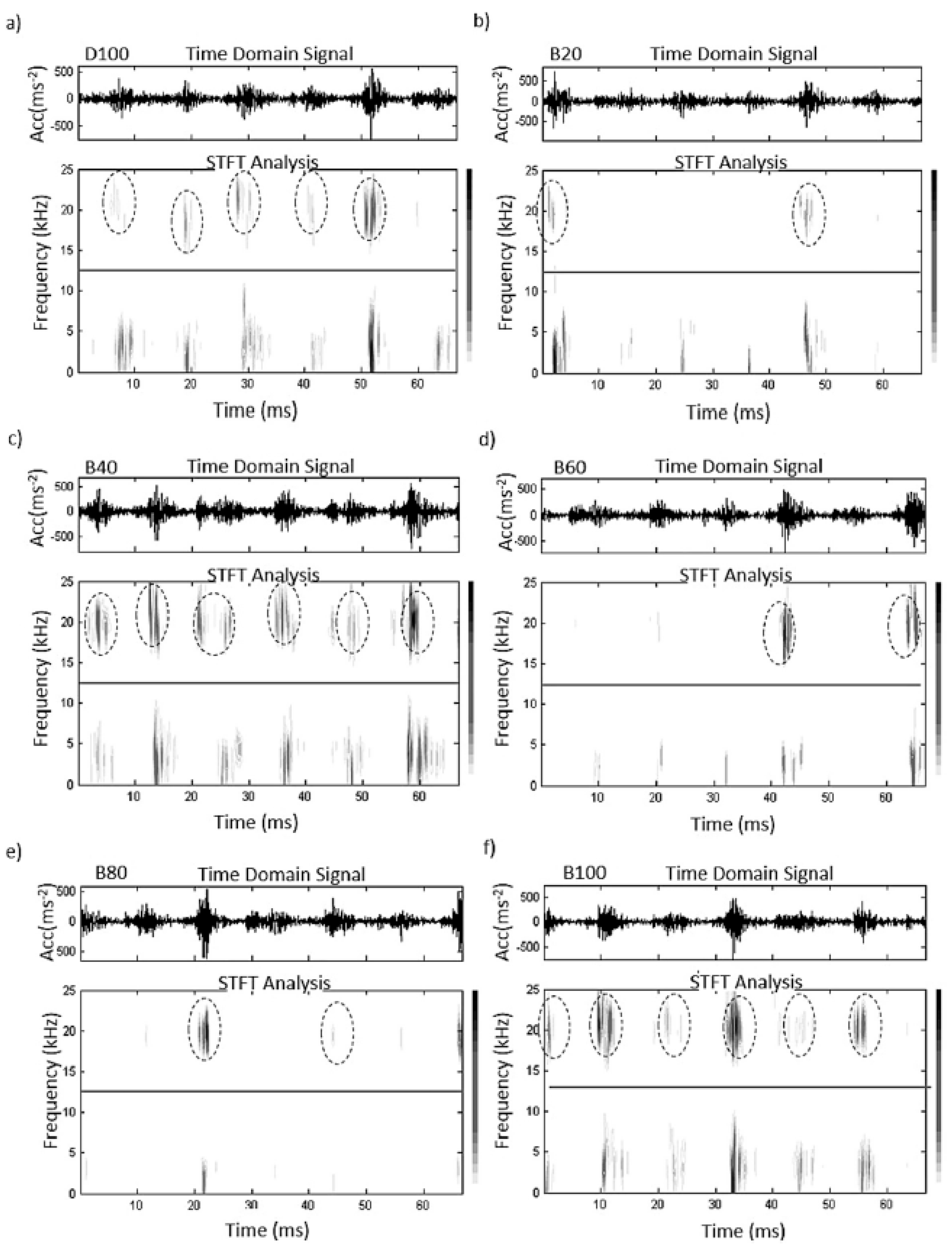
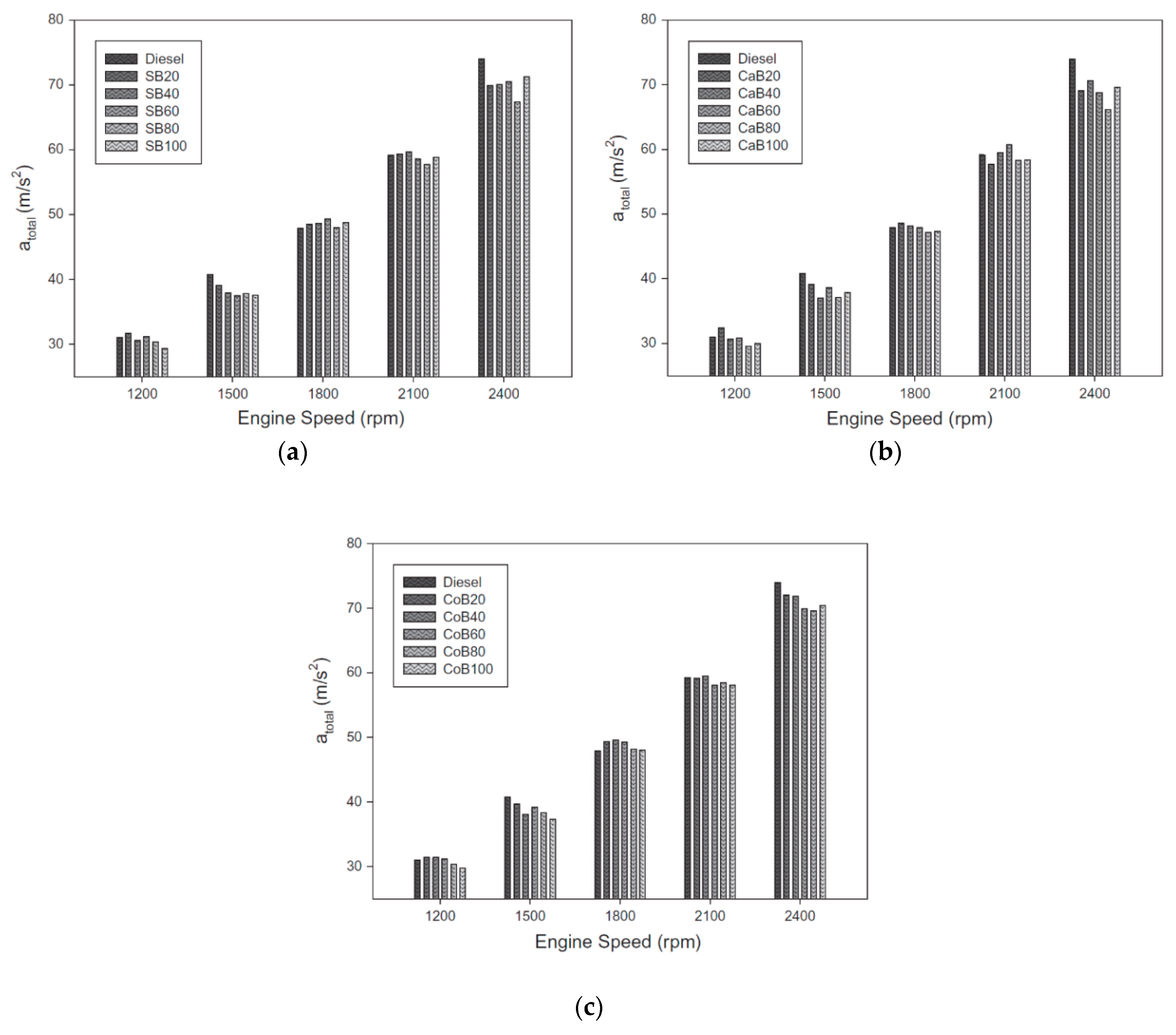
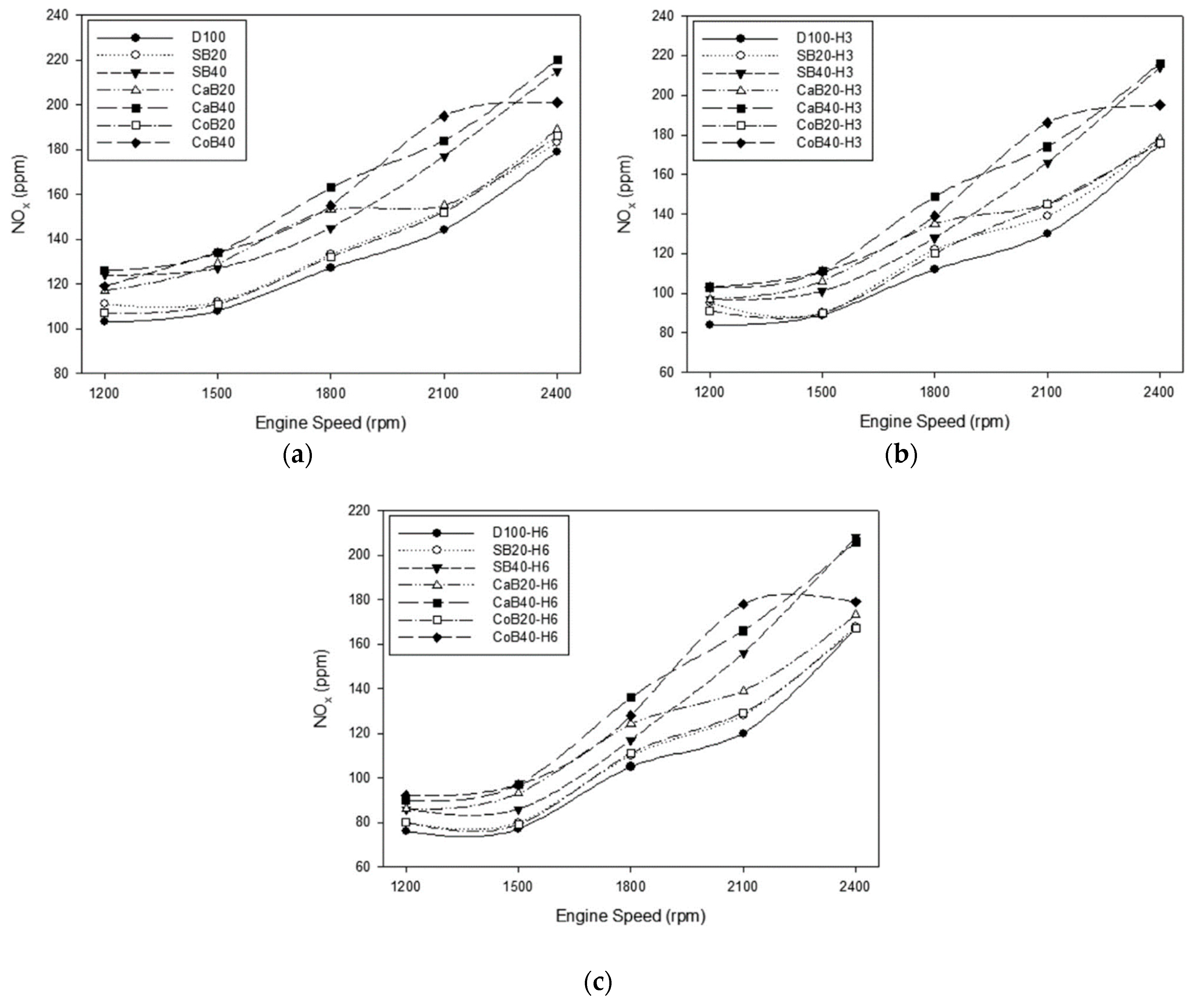
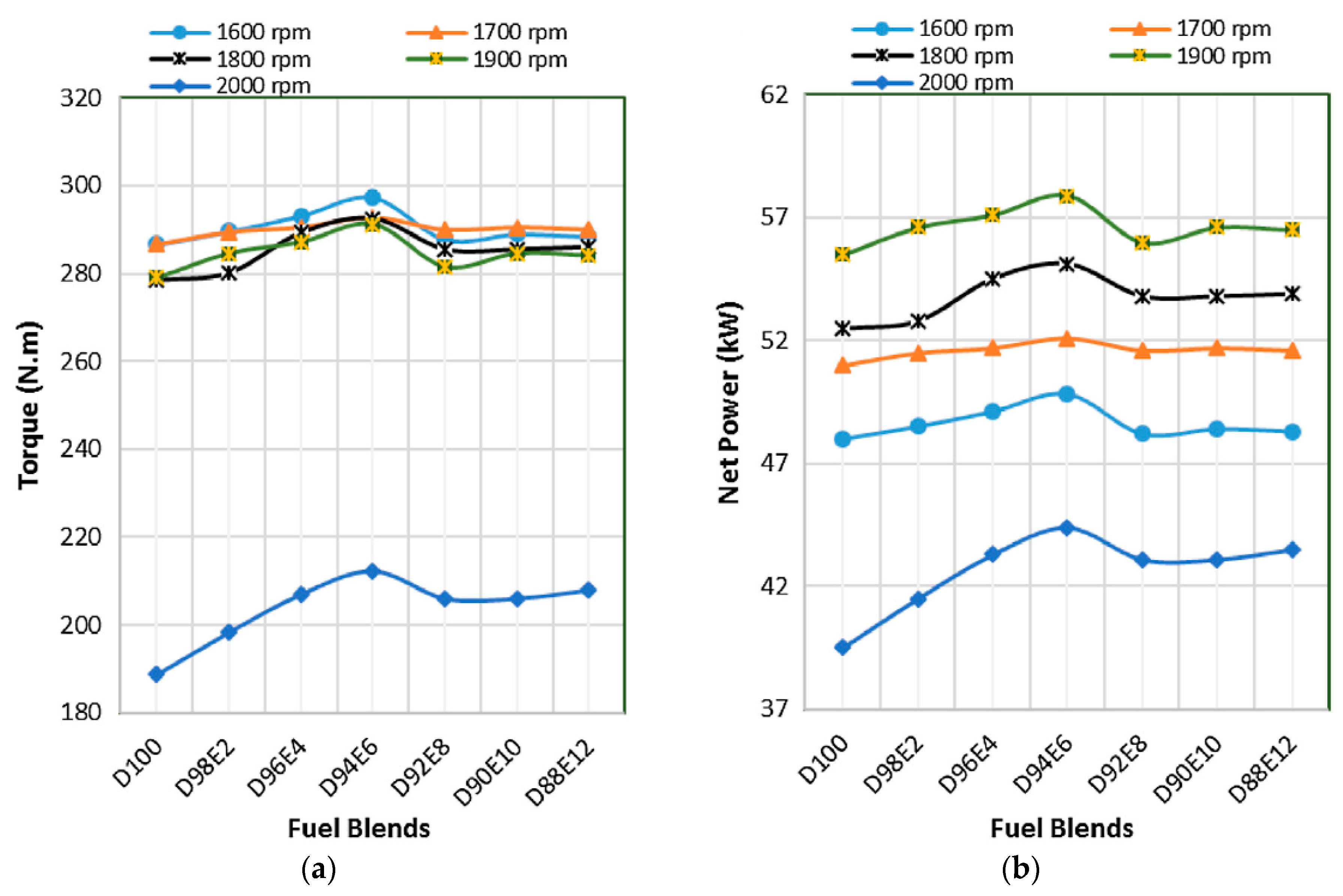
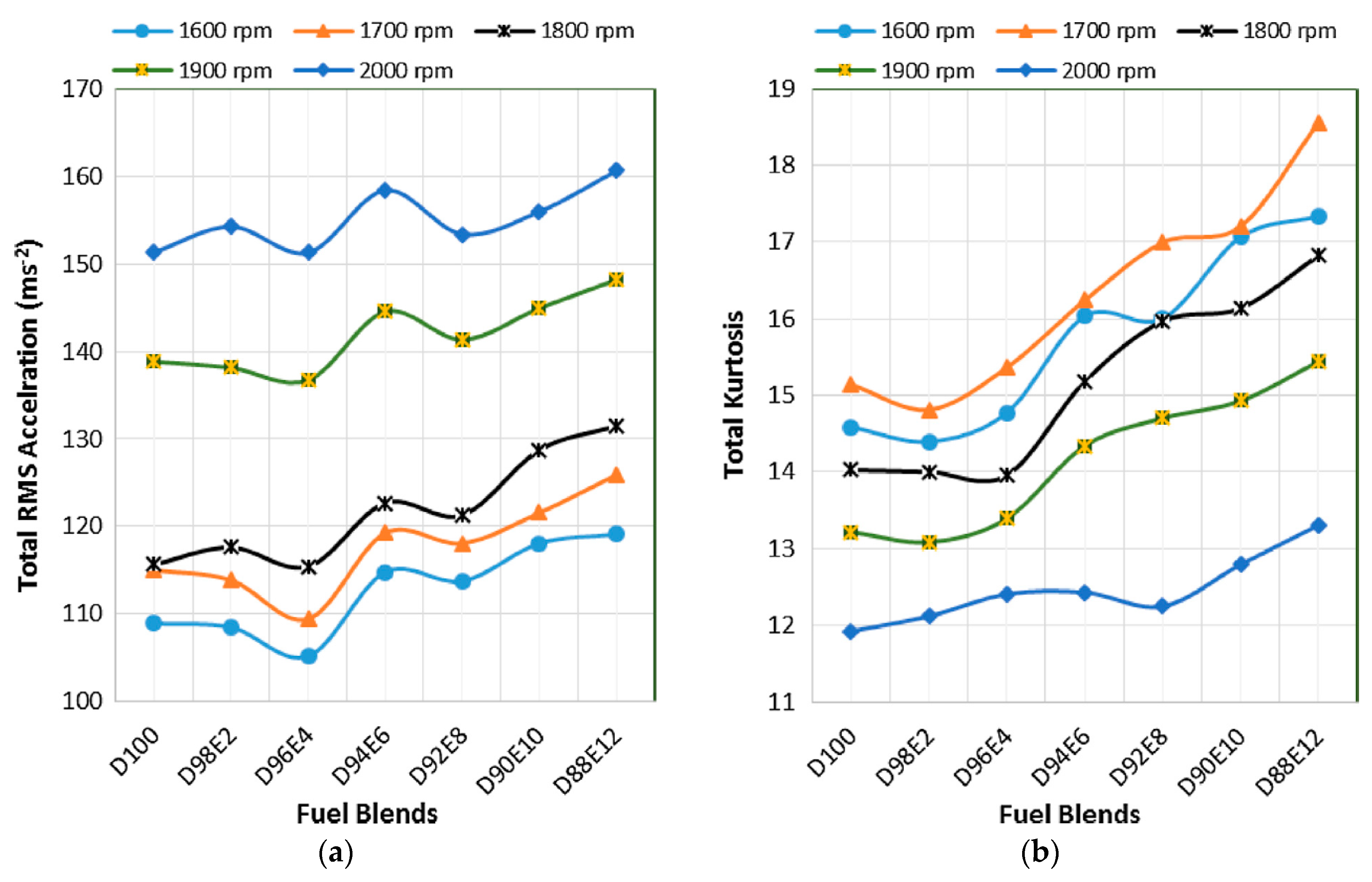
4. Biodiesel Fuels
- the mass flow rate of H2;
- the mass flow rate of fuel blends;
- lower heating value of fuel blends.
5. Conclusions
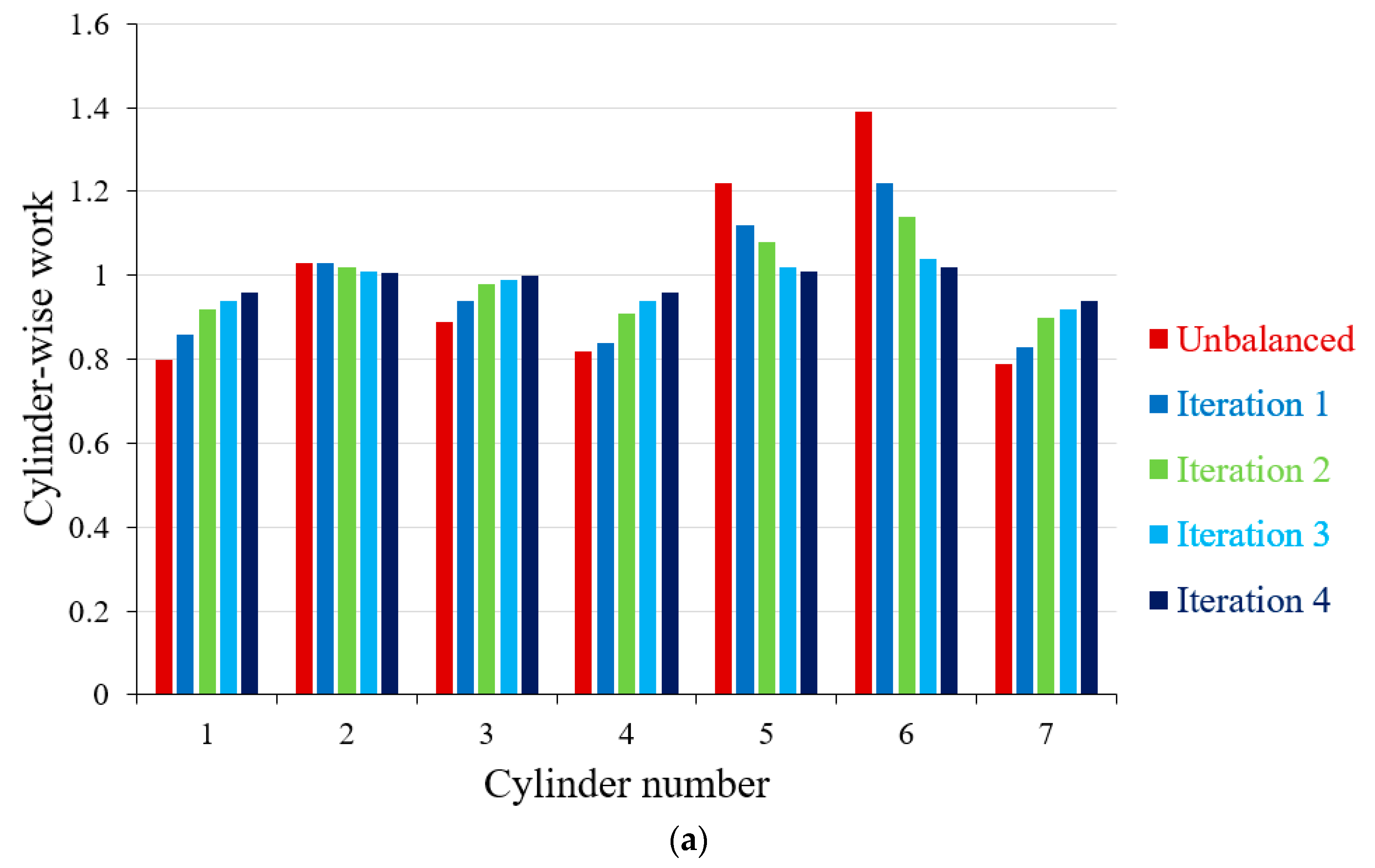
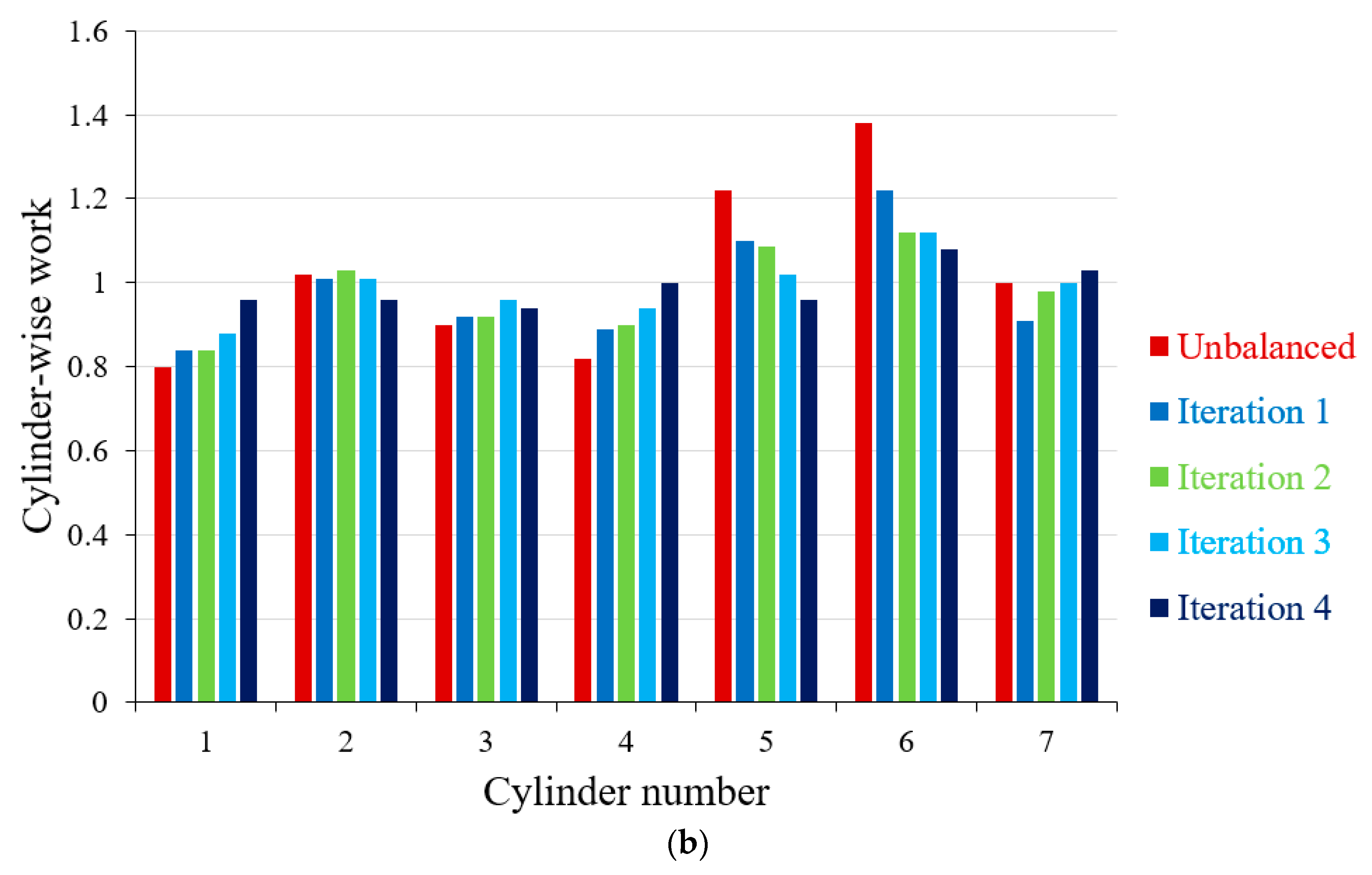
- Introducing new balancing algorithms accompanied by time- and frequency-domain analyses enables reduction of the torsional vibration in rotary components of ICEs operating under high dynamic loading conditions.
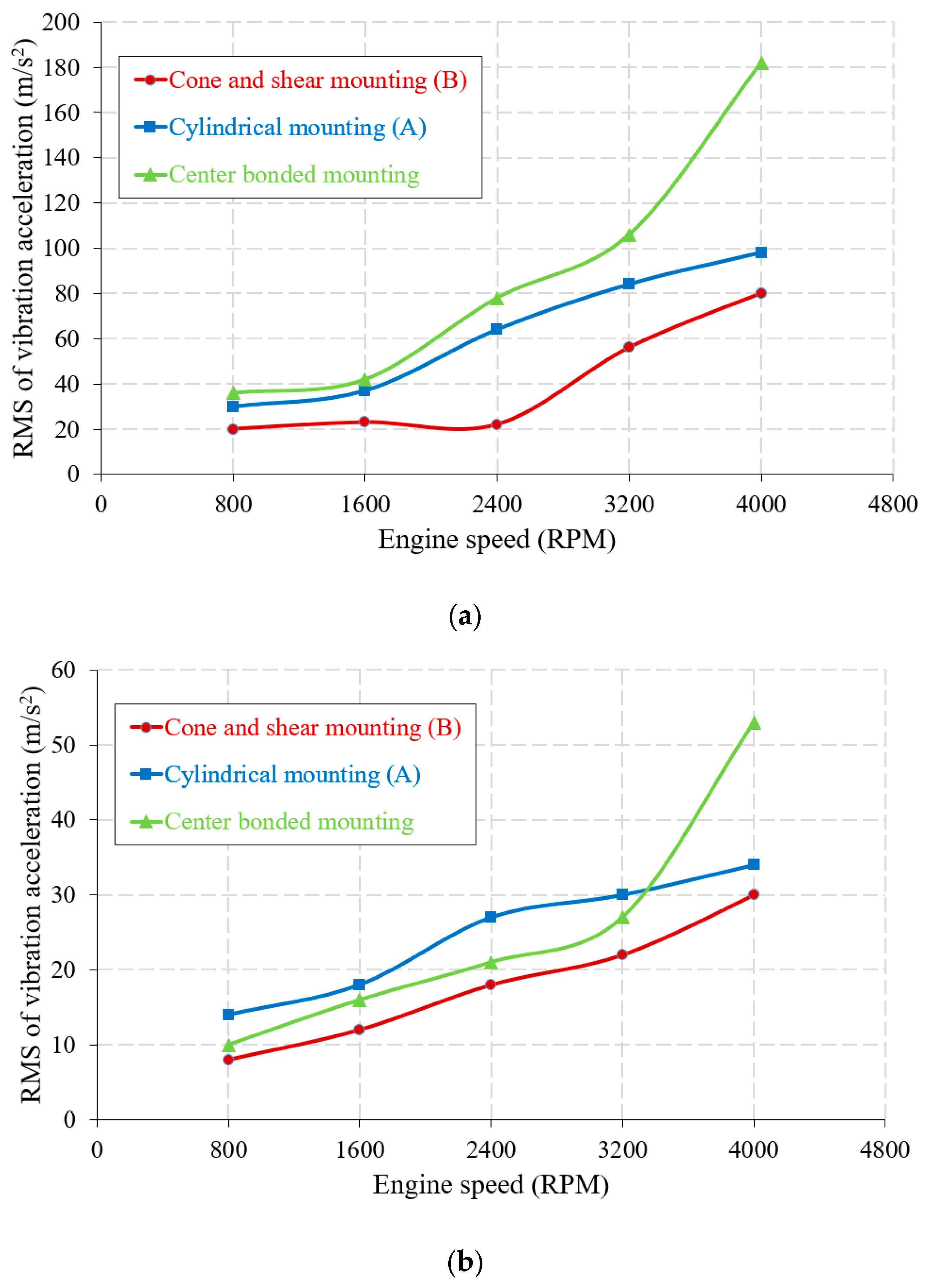
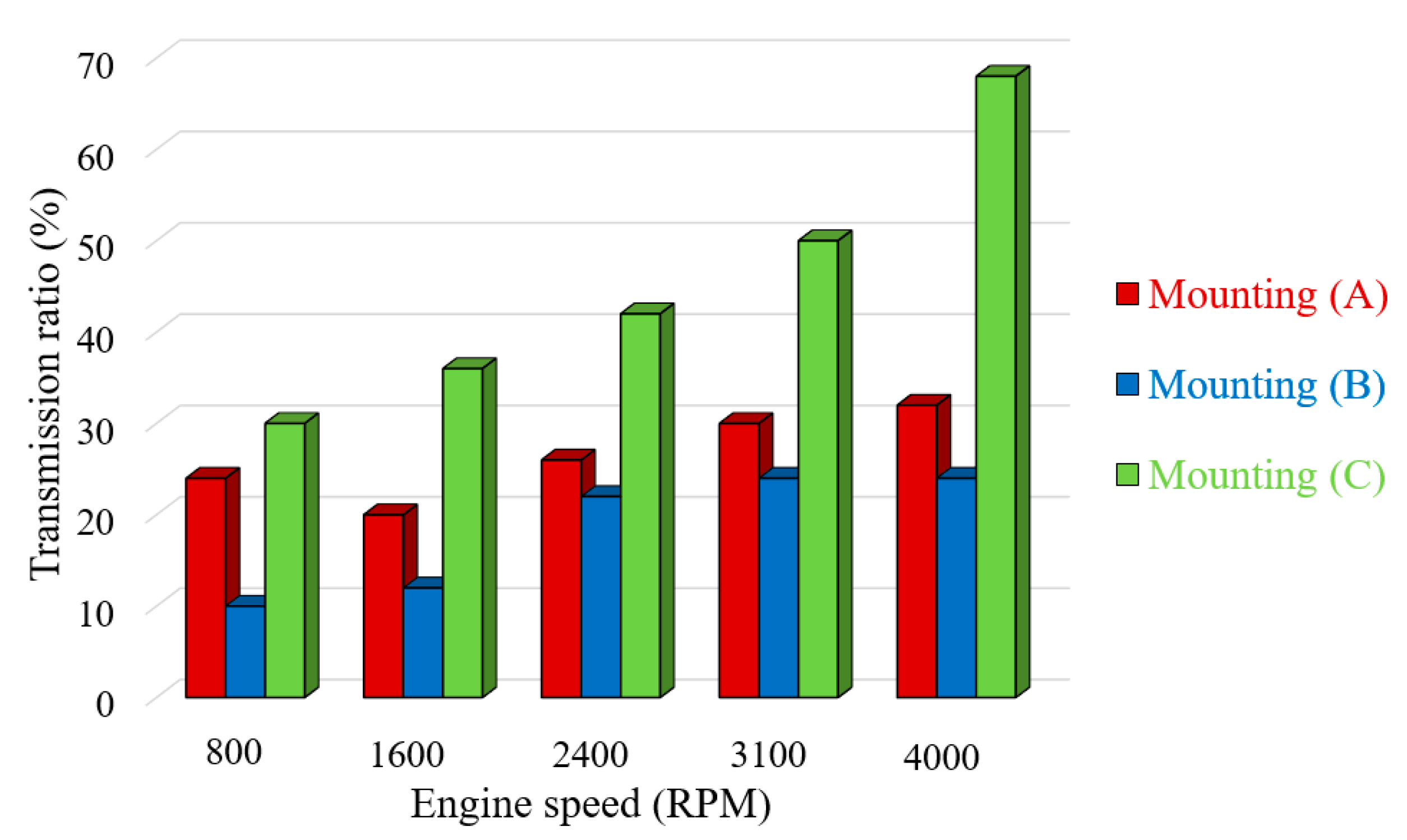
- By proper use of engine mounting system (EMS), when a high transmission ratio is selected, the vibration and noise can be remarkably isolated before they are transferred to chassis and body of a vehicle.
- Accurate prediction of time and frequencies of the piston slap events during the engine cycle can be achieved by taking into account the impact of elastohydrodynamic lubrication (EHL) and piston transient dynamics.
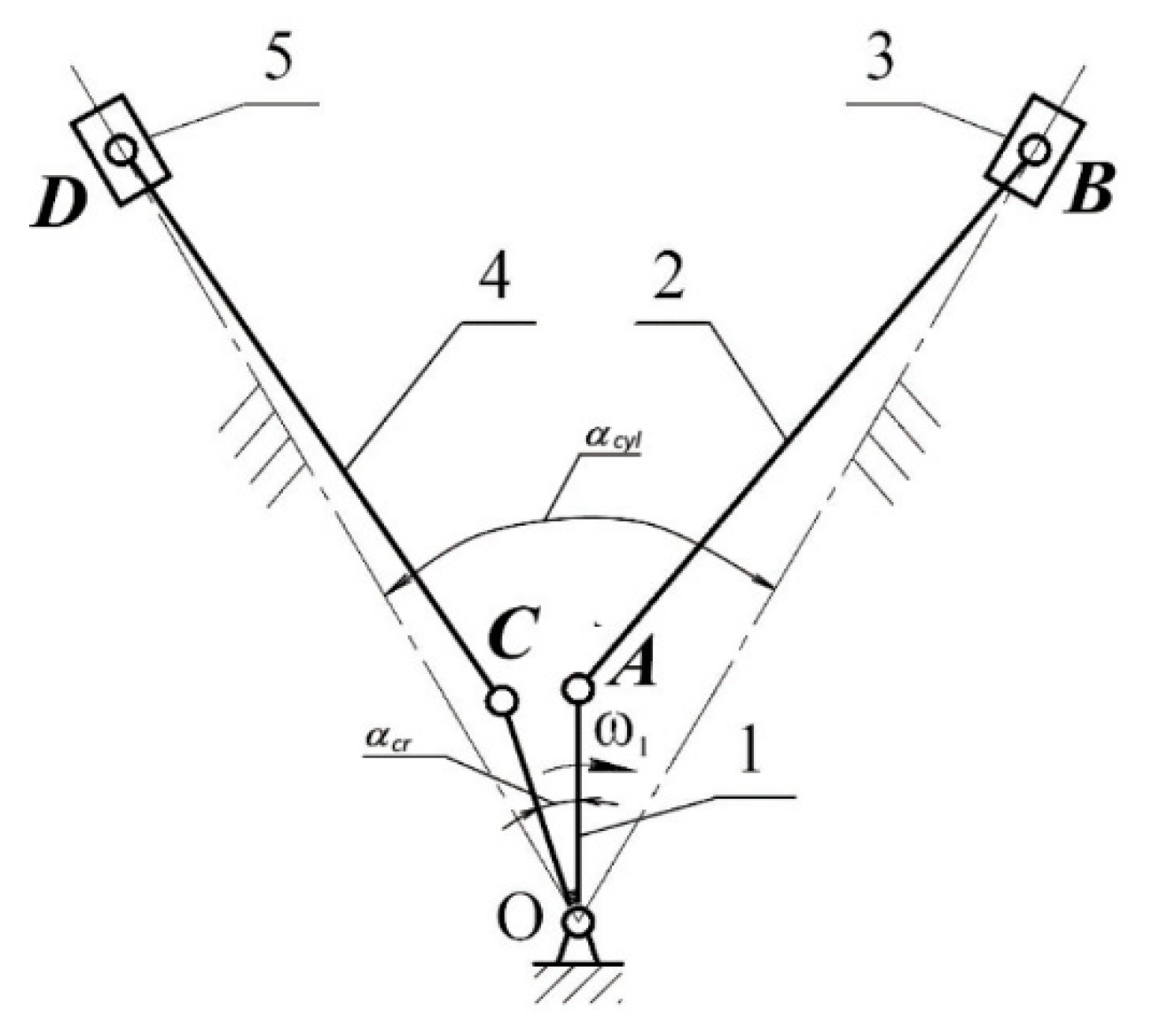
- The torsional vibration of ICEs can be significantly mitigated by optimizing the geometrical parameters of the engine’s crank-slider mechanism and designing a novel kinematically driven flywheel (KDF).
- To minimize the transmitting vibrations, the stiffness of the engine block can be enhanced by applying structural modifications such as thickening the crankcase walls, front gear cover, back flywheel cover, as well as adding ribs to its driveshaft.
- The resistive torque fluctuations of an engine camshaft can be passively compensated by carefully designing a balancing cam mechanism.
- RMS, kurtosis, STFT, FFT, and Morlet wavelet are among the most common statistical tools that are used for vibration and noise analyses in ICEs.
- A biodiesel fuel (or biofuel) offers better physicochemical properties (i.e., density, viscosity, distillation, bulk modulus, surface tension, etc.), to control the injection process.
- Canola and corn vegetable oil fuel additives can avoid an abrupt combustion process due to increasing the oxygen content in the biodiesel fuels.
- When hydrogen gas is added to the fuel blend, it improves the combustion quality, ignition delay, and variation in peak pressure rise rate, resulting in a reduction of the noise and total vibration of the engine.
- The vibration performance of ICEs can be significantly enhanced by adding ZnO nanoparticles to biofuels, as they have a higher heat release rate (HRR), metal vaporization and oxidation, catalytic behavior, and combustion rate.
- Finally, fatty acid methyl ether (FAME) biofuels containing ether group alcohols can reduce the ignition delay time and NOx pollutants, leading to better biodiesel fuel combustion.
Author Contributions
Funding
Conflicts of Interest
References
- Ramachandran, T.; Padmanaban, K.P. Review on internal combustion engine vibrations and mountings. Int. J. Eng. Sci. Emerg. Technol. 2012, 3, 63–73. [Google Scholar]
- Meng, F.; Li, Q. Analysis of main journal vibration of internal combustion engine by systematic method considering oil film forces. Proc. Inst. Mech. Eng. Part J 2014, 228, 756–769. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, S.; Zhang, F.; Zhao, C.; Ling, Q.; Wang, H. Non-linear torsional vibration characteristics of an internal combustion engine crankshaft assembly. Chin. J. Mech. Eng. 2012, 25, 797–808. [Google Scholar] [CrossRef]
- Shim, D.; Park, J.; Khargonekar, P.P.; Ribbns, W. Reducing automotive engine speed fluctuation at idle. IEEE Trans. Control Syst. Technol. 1996, 4, 404–410. [Google Scholar] [CrossRef]
- Li, P.; Shen, T. Overlap model based unknown offset-free MPC scheme for torque balancing control in multi-cylinder SI engines. In Proceedings of the 30th Chinese Control Conference, Yantai, China, 22–24 July 2011; pp. 6239–6244. [Google Scholar]
- Walter, A.; Lingenfelser, C.; Kiencke, U.; Jones, S.; Winkler, T. Cylinder balancing based on reconstructed engine torque for vehicles fitted with a dual mass flywheel (DMF). SAE Int. J. Passenger Cars-Mech. Syst. 2008, 1, 810–819. [Google Scholar] [CrossRef]
- Macian, V.; Lujan, J.M.; Guardiola, C.; Yuste, P. DFT-based controller for fuel injection unevenness correction in turbocharged diesel engines. IEEE Trans. Control Syst. Technol. 2006, 14, 819–827. [Google Scholar] [CrossRef]
- Desbazeille, M.; Randall, R.; Guillet, F.; El Badaoui, M.; Hoisnard, C. Model-based diagnosis of large diesel engines based on angular speed variations of the crankshaft. Mech. Syst. Signal Process. 2010, 24, 1529–1541. [Google Scholar] [CrossRef]
- Saxén, J.-E.; Hyvämäki, T.; Björkqvist, J.; Ostman, F.; Toivonen, H.T. Power Balancing of Internal Combustion Engines–A Time and Frequency Domain Analysis. Int. Fed. Autom. Control 2014, 47, 10802–10807. [Google Scholar] [CrossRef]
- Yu, Y.; Naganathan, N.G.; Dukkipati, R.V. A literature review of automotive vehicle engine mounting systems. Mech. Mach. Theory 2001, 36, 123–142. [Google Scholar] [CrossRef]
- Barton, D.C.; Fieldhouse, J.D. Noise, Vibration and Harshness (NVH). In Automotive Chassis Engineering; Springer: London, UK, 2018; pp. 255–317. [Google Scholar]
- Ghosh, C.; Parmar, A.; Chatterjee, J. Challenges of Hydraulic Engine Mount Development for NVH Refinement; SAE Technical Paper; SAE: Chennai, India, 2018. [Google Scholar]
- Van Keymeulen, J.; Nussmann, C.; Steffens, C.; Eisele, G. NVH Aspects of Powertrain Mounting Systems Layout. ATZ Worldwide 2016, 118, 26–31. [Google Scholar] [CrossRef]
- Mohamed, E.S.; Saad, A.A.; Hassan, S.S. Assessment of vibration and transmissibility behaviour of a rubber engine mount considering vibration tuned modification. Int. J. Veh. Noise Vib. 2016, 12, 24–41. [Google Scholar] [CrossRef]
- Hajikhodaverdikhan, P.; Nazari, M.; Mohsenizadeh, M.; Shamshirband, S.; Chau, K.-W. Earthquake prediction with meteorological data by particle filter-based support vector regression. Eng. Appl. Comput. Fluid Mech. 2018, 12, 679–688. [Google Scholar] [CrossRef]
- Zuo, Q.; Zhu, X.; Liu, Z.; Zhang, J.; Wu, G.; Li, Y. Prediction of the performance and emissions of a spark ignition engine fueled with butanol-gasoline blends based on support vector regression. Environ. Progress Sustain. Energy 2018. [Google Scholar] [CrossRef]
- Kong, D.; Chen, Y.; Li, N.; Tan, S. Tool wear monitoring based on kernel principal component analysis and v-support vector regression. Int. J. Adv. Manuf. Technol. 2017, 89, 175–190. [Google Scholar] [CrossRef]
- Li, N.; Chen, Y.; Kong, D.; Tan, S. Force-based tool condition monitoring for turning process using v-support vector regression. Int. J. Adv. Manuf. Technol. 2017, 91, 351–361. [Google Scholar] [CrossRef]
- Omar, F.K.; Selim, M.Y.; Emam, S.A. Time and frequency analyses of dual-fuel engine block vibration. Fuel 2017, 203, 884–893. [Google Scholar] [CrossRef]
- Çalık, A. Determination of vibration characteristics of a compression ignition engine operated by hydrogen enriched diesel and biodiesel fuels. Fuel 2018, 230, 355–358. [Google Scholar] [CrossRef]
- Uludamar, E.; Tosun, E.; Tüccar, G.; Yıldızhan, Ş.; Çalık, A.; Yıldırım, S.; Serin, H.; Özcanlı, M. Evaluation of vibration characteristics of a hydroxyl (HHO) gas generator installed diesel engine fuelled with different diesel–biodiesel blends. Int. J. Hydrog. Energy 2017, 42, 23352–23360. [Google Scholar] [CrossRef]
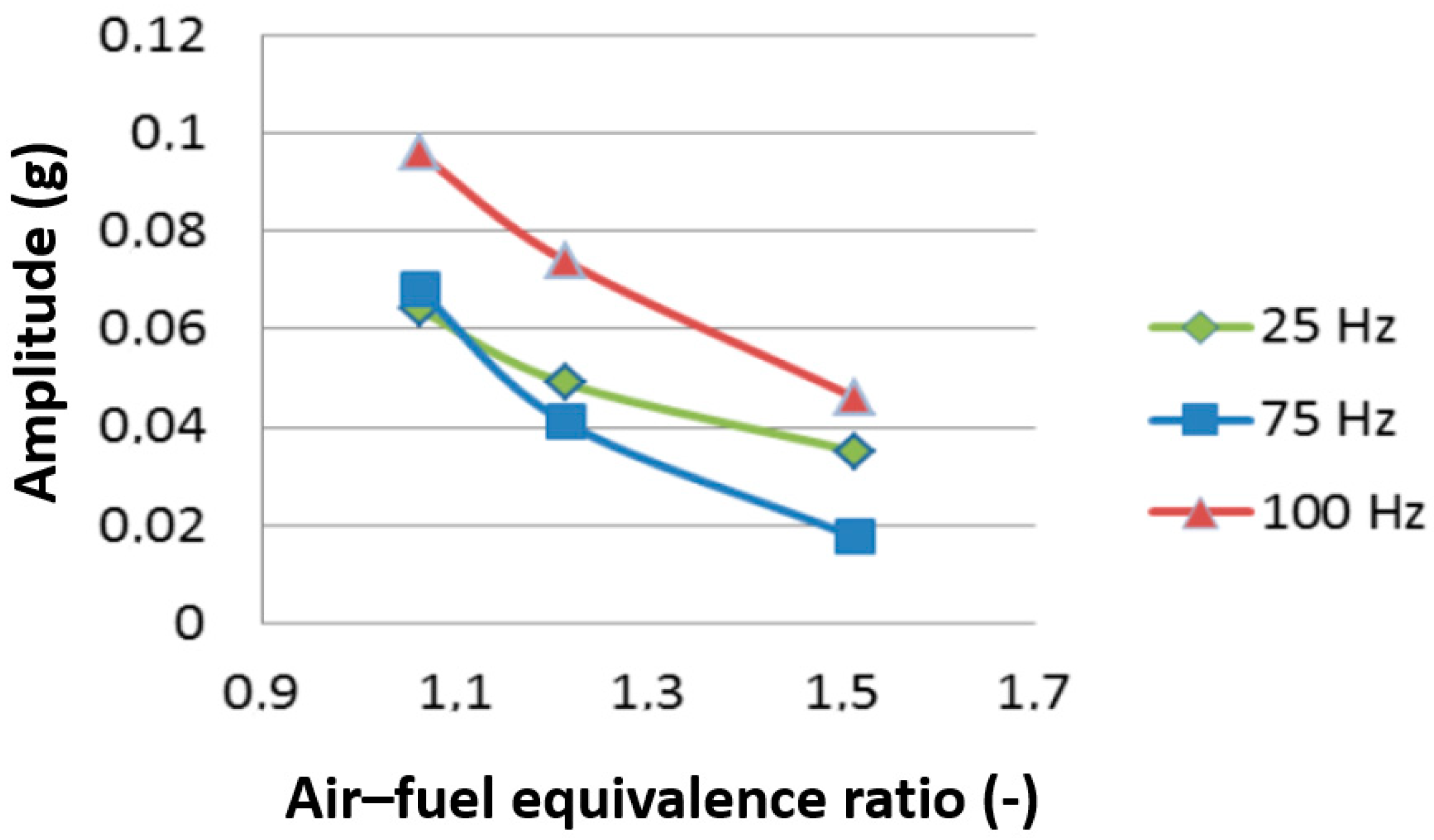
- Manhertz, G.; Antal, A. The effect of air-fuel equivalence ratio change on the vibration components of an internal-combustion engine. Recent Innov. Mech. 2015, 2, 1–6. [Google Scholar] [CrossRef]
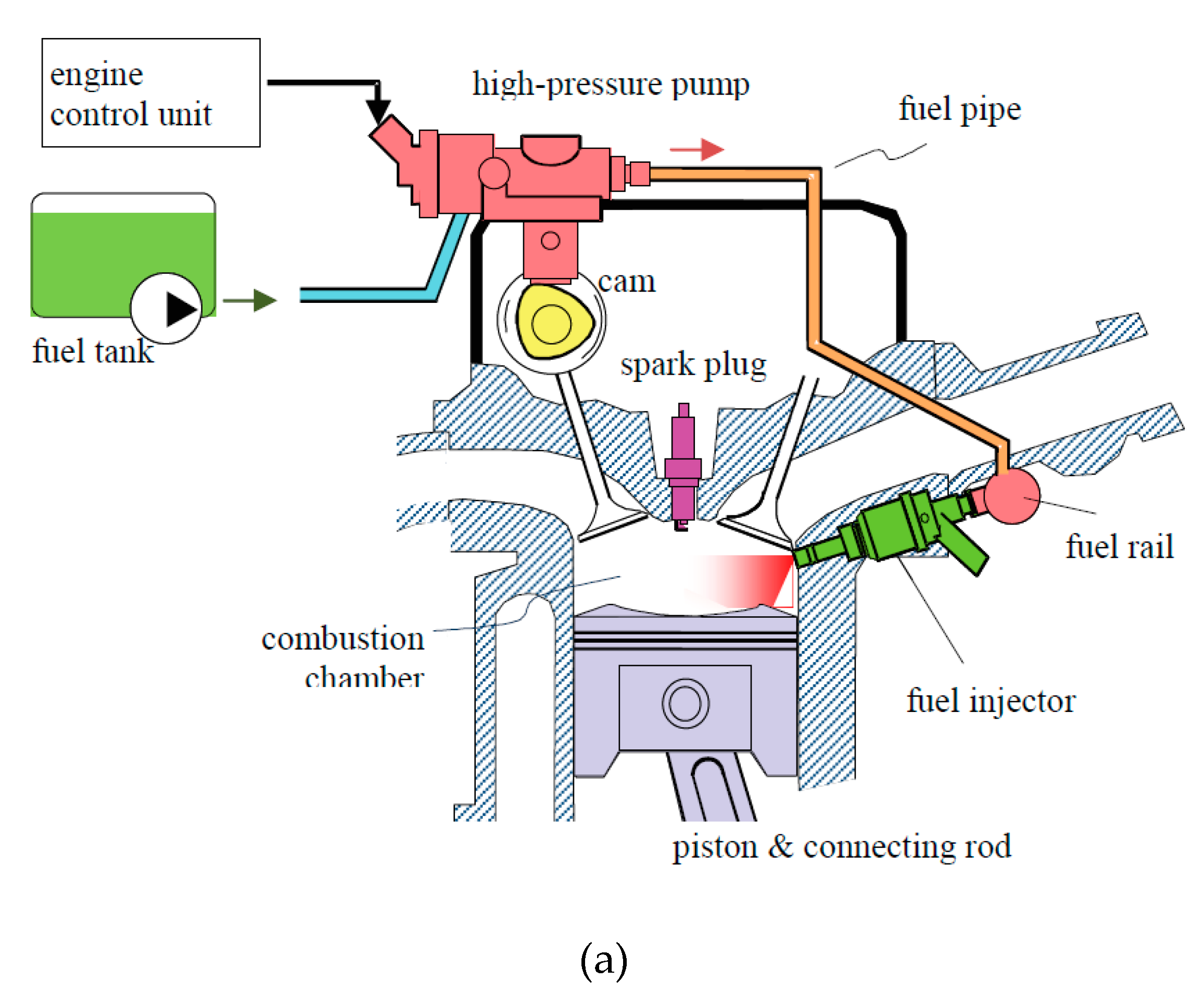
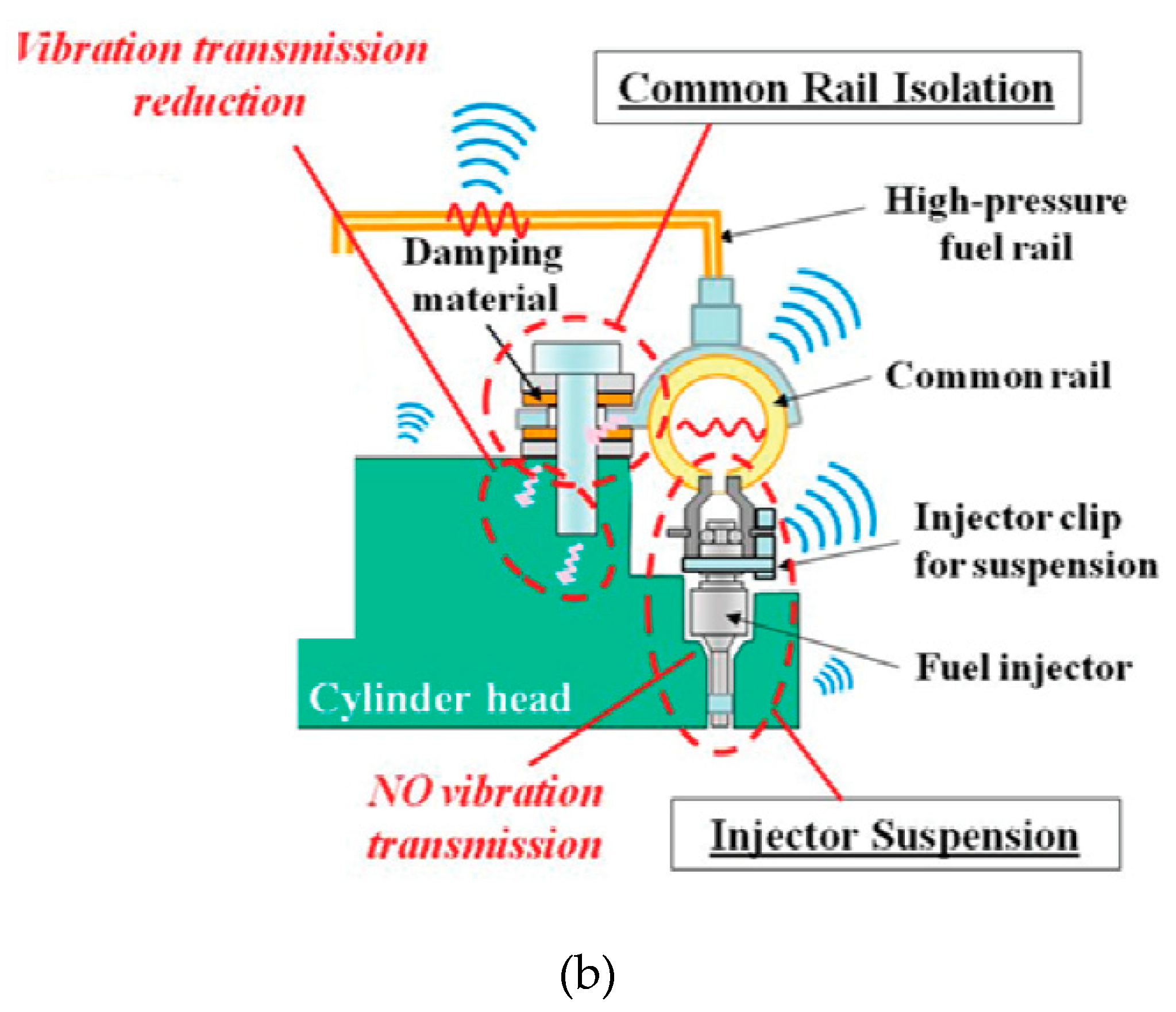
- Borg, J.; Watanabe, A.; Tokuo, K. Mitigation of noise and vibration in the high-pressure fuel system of a gasoline direct injection engine. Procedia-Soc. Behav. Sci. 2012, 48, 3170–3178. [Google Scholar] [CrossRef]
- Zavos, A.; Nikolakopoulos, P.G. Measurement of friction and noise from piston assembly of a single-cylinder motorbike engine at realistic speeds. Proc. Inst. Mech. Eng. Part D 2018, 232, 1715–1735. [Google Scholar] [CrossRef]
- Dolatabadi, N.; Littlefair, B.; De la Cruz, M.; Theodossiades, S.; Rothberg, S.; Rahnejat, H. A transient tribodynamic approach for the calculation of internal combustion engine piston slap noise. J. Sound Vib. 2015, 352, 192–209. [Google Scholar] [CrossRef]
- Kosenok, B.B.; Balyakin, V.B. Study of the Dynamic Characteristics of a Two-Cylinder Internal Combustion Engine Using Vector Models. Procedia Eng. 2015, 106, 183–191. [Google Scholar] [CrossRef]
- Pfabe, M.; Woernle, C. Reducing torsional vibrations by means of a kinematically driven flywheel—Theory and experiment. Mech. Mach. Theory 2016, 102, 217–228. [Google Scholar] [CrossRef]
- Junhong, Z.; Jun, H. CAE process to simulate and optimise engine noise and vibration. Mech. Syst. Signal Process. 2006, 20, 1400–1409. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H. Application of average flow model to lubrication between rough sliding surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Meng, F.; Hu, Y.; Wang, H.; Zhang, Y. Analysis of the dynamic performances of a piston-crankshaft system considering oil-film forces reconstructed by a neural network. Proc. Inst. Mech. Eng. Part D 2007, 221, 171–180. [Google Scholar] [CrossRef]
- Albarbar, A.; Gu, F.; Ball, A.; Starr, A. Internal combustion engine lubricating oil condition monitoring based on vibro-acoustic measurements. Insight-Non-Destr. Test. Cond. Monit. 2007, 49, 715–718. [Google Scholar] [CrossRef]
- Shadloo, M.; Poultangari, R.; Jamalabadi, M.A.; Rashidi, M. A new and efficient mechanism for spark ignition engines. Energy Convers. Manag. 2015, 96, 418–429. [Google Scholar] [CrossRef]
- Lin, D.-Y.; Hou, B.-J.; Lan, C.-C. A balancing cam mechanism for minimizing the torque fluctuation of engine camshafts. Mech. Mach. Theory 2017, 108, 160–175. [Google Scholar] [CrossRef]
- Capuano, D.; Costa, M.; Di Fraia, S.; Massarotti, N.; Vanoli, L. Direct use of waste vegetable oil in internal combustion engines. Renew. Sustain. Energy Rev. 2017, 69, 759–770. [Google Scholar] [CrossRef]
- Yilmaz, N.; Atmanli, A.; Vigil, F.M. Quaternary blends of diesel, biodiesel, higher alcohols and vegetable oil in a compression ignition engine. Fuel 2018, 212, 462–469. [Google Scholar] [CrossRef]
- Shah, P.R.; Gaitonde, U.; Ganesh, A. Influence of soy-lecithin as bio-additive with straight vegetable oil on CI engine characteristics. Renew. Energy 2018, 115, 685–696. [Google Scholar] [CrossRef]
- Can, Ö.; Öztürk, E.; Yücesu, H.S. Combustion and exhaust emissions of canola biodiesel blends in a single cylinder DI diesel engine. Renew. Energy 2017, 109, 73–82. [Google Scholar] [CrossRef]
- Qasim, M.; Ansari, T.M.; Hussain, M. Emissions and performance characteristics of a diesel engine operated with fuel blends obtained from a mixture of pretreated waste engine oil and waste vegetable oil methyl esters. Environ. Prog. Sustain. Energy 2018, 37, 2148–2155. [Google Scholar] [CrossRef]
- Domínguez-Sáez, A.; Rattá, G.A.; Barrios, C.C. Prediction of exhaust emission in transient conditions of a diesel engine fueled with animal fat using Artificial Neural Network and Symbolic Regression. Energy 2018, 149, 675–683. [Google Scholar] [CrossRef]
- Alexandru, C.; Constantin, P.; Niculae, N.; Cristian, N.; Adrian, N. Butanol Effects on the Fuelled Diesel Engine Operation with Preheated Diesel Fuel-Animal Fat Blends. In Proceedings of the 4th International Congress of Automotive and Transport Engineering, Cluj, Romania, 17–19 October 2018; pp. 609–616. [Google Scholar]
- Varuvel, E.G.; Mrad, N.; Tazerout, M.; Aloui, F. Combustion Analysis of Biofuel Derived from Waste Fish Fat. In Exergy for A Better Environment and Improved Sustainability 1; Springer: Berlin, Germany, 2018; pp. 1311–1328. [Google Scholar]
- Wei, L.; Cheung, C.; Ning, Z. Influence of waste cooking oil biodiesel on combustion, unregulated gaseous emissions and particulate emissions of a direct-injection diesel engine. Energy 2017, 127, 175–185. [Google Scholar] [CrossRef]
- Şen, M.; Emiroğlu, A.O.; Keskin, A. Production of Biodiesel from Broiler Chicken Rendering Fat and Investigation of Its Effects on Combustion, Performance, and Emissions of a Diesel Engine. Energy Fuels 2018, 32, 5209–5217. [Google Scholar] [CrossRef]
- Emiroğlu, A.O.; Keskin, A.; Şen, M. Experimental investigation of the effects of turkey rendering fat biodiesel on combustion, performance and exhaust emissions of a diesel engine. Fuel 2018, 216, 266–273. [Google Scholar] [CrossRef]
- Akar, M.A.; Kekilli, E.; Bas, O.; Yildizhan, S.; Serin, H.; Ozcanli, M. Hydrogen enriched waste oil biodiesel usage in compression ignition engine. Int. J. Hydrog. Energy 2018, 43, 18046–18052. [Google Scholar] [CrossRef]
- Kumar, R.; Gakkhar, R. Influence of nozzle opening pressure on combustion, performance and emission analysis of waste cooking oil biodiesel fuelled diesel engine. Int. J. Renew. Energy Technol. 2018, 9, 244–259. [Google Scholar] [CrossRef]
- Geng, P.; Mao, H.; Zhang, Y.; Wei, L.; You, K.; Ju, J.; Chen, T. Combustion characteristics and NOx emissions of a waste cooking oil biodiesel blend in a marine auxiliary diesel engine. Appl. Thermal Eng. 2017, 115, 947–954. [Google Scholar] [CrossRef]
- Geng, L.; Chen, Y.; Chen, X.; Chia-fon, F.L. Study on combustion characteristics and particulate emissions of a common-rail diesel engine fueled with n-butanol and waste cooking oil blends. J. Energy Inst. 2018. [Google Scholar] [CrossRef]
- Ranjan, A.; Dawn, S.; Jayaprabakar, J.; Nirmala, N.; Saikiran, K.; Sriram, S.S. Experimental investigation on effect of MgO nanoparticles on cold flow properties, performance, emission and combustion characteristics of waste cooking oil biodiesel. Fuel 2018, 220, 780–791. [Google Scholar] [CrossRef]
- Jiaqiang, E.; Liu, T.; Yang, W.; Li, J.; Gong, J.; Deng, Y. Effects of fatty acid methyl esters proportion on combustion and emission characteristics of a biodiesel fueled diesel engine. Energy Convers. Manag. 2016, 117, 410–419. [Google Scholar]
- Xue, J.; Grift, T.E.; Hansen, A.C. Effect of biodiesel on engine performances and emissions. Renew. Sustain. Energy Rev. 2011, 15, 1098–1116. [Google Scholar] [CrossRef]
- Sun, J.; Caton, J.A.; Jacobs, T.J. Oxides of nitrogen emissions from biodiesel-fuelled diesel engines. Prog. Energy Combust. Sci. 2010, 36, 677–695. [Google Scholar] [CrossRef]
- Ma, Y.; Huang, R.; Huang, S.; Zhang, Y.; Xu, S.; Wang, Z. Experimental investigation on the effect of n-pentanol blending on spray, ignition and combustion characteristics of waste cooking oil biodiesel. Energy Convers. Manag. 2017, 148, 440–455. [Google Scholar] [CrossRef]
- Fattah, I.R.; Ming, C.; Chan, Q.N.; Wehrfritz, A.; Pham, P.X.; Yang, W.; Kook, S.; Medwell, P.R.; Yeoh, G.-H.; Hawkes, E.R. Spray and Combustion Investigation of Post Injections under Low-Temperature Combustion Conditions with Biodiesel. Energy Fuels 2018, 32, 8727–8742. [Google Scholar] [CrossRef]
- Torres-Jimenez, E.; Dorado, R.; Kegl, B.; Kegl, M. One-dimensional modeling and simulation of injection processes of bioethanol-biodiesel and bioethanol-diesel fuel blends. Fuel 2018, 227, 334–344. [Google Scholar] [CrossRef]
- Taghizadeh-Alisaraei, A.; Ghobadian, B.; Tavakoli-Hashjin, T.; Mohtasebi, S.S. Vibration analysis of a diesel engine using biodiesel and petrodiesel fuel blends. Fuel 2012, 102, 414–422. [Google Scholar] [CrossRef]
- Aydin, H.; Bayindir, H. Performance and emission analysis of cottonseed oil methyl ester in a diesel engine. Renew. Energy 2010, 35, 588–592. [Google Scholar] [CrossRef]
- Buyukkaya, E. Effects of biodiesel on a DI diesel engine performance, emission and combustion characteristics. Fuel 2010, 89, 3099–3105. [Google Scholar] [CrossRef]
- Taghizadeh-Alisaraei, A.; Ghobadian, B.; Tavakoli-Hashjin, T.; Mohtasebi, S.S.; Rezaei-asl, A.; Azadbakht, M. Characterization of engine’s combustion-vibration using diesel and biodiesel fuel blends by time-frequency methods: A case study. Renew. Energy 2016, 95, 422–432. [Google Scholar] [CrossRef]
- Lin, J.; Qu, L. Feature extraction based on Morlet wavelet and its application for mechanical fault diagnosis. J. Sound Vib. 2000, 234, 135–148. [Google Scholar] [CrossRef]
- Wu, J.-D.; Chen, J.-C. Continuous wavelet transform technique for fault signal diagnosis of internal combustion engines. NDT Int. 2006, 39, 304–311. [Google Scholar] [CrossRef]
- Moosavian, A.; Najafi, G.; Ghobadian, B.; Mirsalim, M. The effect of piston scratching fault on the vibration behavior of an IC engine. Appl. Acoust. 2017, 126, 91–100. [Google Scholar] [CrossRef]
- Riaz, S.; Elahi, H.; Javaid, K.; Shahzad, T. Vibration feature extraction and analysis for fault diagnosis of rotating machinery-A literature survey. Asia Pac. J. Multidiscipl. Res. 2017, 5, 103–110. [Google Scholar]
- Taghizadeh-Alisaraei, A.; Mahdavian, A. Fault detection of injectors in diesel engines using vibration time-frequency analysis. Appl. Acoust. 2019, 143, 48–58. [Google Scholar] [CrossRef]
- Ftoutou, E.; Chouchane, M. Injection fault detection of a diesel engine by vibration analysis. In Proceedings of the International Conference Design and Modeling of Mechanical Systems, Hammame, Tunisia, 27–29 March 2017; pp. 11–20. [Google Scholar]
- Hodgins, S. A Wireless Sensor for Fault Detection and Diagnosis of Internal Combustion Engines; McMaster University: Hamilton, ON, Canada, 2017. [Google Scholar]
- Al-Badour, F.; Sunar, M.; Cheded, L. Vibration analysis of rotating machinery using time–frequency analysis and wavelet techniques. Mech. Syst. Signal Process. 2011, 25, 2083–2101. [Google Scholar] [CrossRef]
- Klinchaeam, S.; Nivesrangsan, P.; Lokitsangthong, M. Condition monitoring of a small four-stroke petrol engine using vibration signals. Curr. Appl. Sci. Technol. 2009, 9, 9–17. [Google Scholar]
- Vulli, S.; Dunne, J.; Potenza, R.; Richardson, D.; King, P. Time-frequency analysis of single-point engine-block vibration measurements for multiple excitation-event identification. J. Sound Vib. 2009, 321, 1129–1143. [Google Scholar] [CrossRef]
- Uludamar, E.; Tosun, E.; Aydın, K. Experimental and regression analysis of noise and vibration of a compression ignition engine fuelled with various biodiesels. Fuel 2016, 177, 326–333. [Google Scholar] [CrossRef]
- Uludamar, E.; Yıldızhan, Ş.; Aydın, K.; Özcanlı, M. Vibration, noise and exhaust emissions analyses of an unmodified compression ignition engine fuelled with low sulphur diesel and biodiesel blends with hydrogen addition. Int. J. Hydrog. Energy 2016, 41, 11481–11490. [Google Scholar] [CrossRef]
- Zhou, J.; Cheung, C.; Zhao, W.; Leung, C. Diesel–hydrogen dual-fuel combustion and its impact on unregulated gaseous emissions and particulate emissions under different engine loads and engine speeds. Energy 2016, 94, 110–123. [Google Scholar] [CrossRef]
- Zhou, J.; Cheung, C.; Leung, C. Combustion, performance, regulated and unregulated emissions of a diesel engine with hydrogen addition. Appl. Energy 2014, 126, 1–12. [Google Scholar] [CrossRef]
- Jhang, S.-R.; Chen, K.-S.; Lin, S.-L.; Lin, Y.-C.; Cheng, W.L. Reducing pollutant emissions from a heavy-duty diesel engine by using hydrogen additions. Fuel 2016, 172, 89–95. [Google Scholar] [CrossRef]
- Giakoumis, E.G.; Rakopoulos, D.C.; Rakopoulos, C.D. Combustion noise radiation during dynamic diesel engine operation including effects of various biofuel blends: A review. Renew. Sustain. Energy Rev. 2016, 54, 1099–1113. [Google Scholar] [CrossRef]
- Seifi, M.R.; Hassan-Beygi, S.R.; Ghobadian, B.; Desideri, U.; Antonelli, M. Experimental investigation of a diesel engine power, torque and noise emission using water–diesel emulsions. Fuel 2016, 166, 392–399. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Mikami, M. Effect of hydrogen addition to intake air on combustion noise from a diesel engine. Int. J. Hydrog. Energy 2013, 38, 4153–4162. [Google Scholar] [CrossRef]
- How, H.; Masjuki, H.; Kalam, M.; Teoh, Y. An investigation of the engine performance, emissions and combustion characteristics of coconut biodiesel in a high-pressure common-rail diesel engine. Energy 2014, 69, 749–759. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, X.; Wei, L.; Zhang, J.; Tang, C.; Huang, Z. Experimental and modeling study on auto-ignition characteristics of methane/hydrogen blends under engine relevant pressure. Int. J. Hydrog. Energy 2012, 37, 19168–19176. [Google Scholar] [CrossRef]
- Dimitriou, P.; Kumar, M.; Tsujimura, T.; Suzuki, Y. Combustion and emission characteristics of a hydrogen-diesel dual-fuel engine. Int. J. Hydrog. Energy 2018, 43, 13605–13617. [Google Scholar] [CrossRef]
- Akansu, S.O.; Dulger, Z.; Kahraman, N.; Veziroǧlu, T.N. Internal combustion engines fueled by natural gas—hydrogen mixtures. Int. J. Hydrog. Energy 2004, 29, 1527–1539. [Google Scholar] [CrossRef]
- Velmurugan, K.; Sathiyagnanam, A. Impact of antioxidants on NOx emissions from a mango seed biodiesel powered DI diesel engine. Alexandria Eng. J. 2016, 55, 715–722. [Google Scholar] [CrossRef]
- Rao, K.P.; Rao, B.A.; Babu, V.R. Heat release rate and engine vibration correlation to investigate combustion propensity of an IDI engine run with biodiesel (MME) and methanol additive as an alternative to diesel fuel. Biofuels 2015, 6, 45–54. [Google Scholar] [CrossRef]
- Taghizadeh-Alisaraei, A.; Rezaei-Asl, A. The effect of added ethanol to diesel fuel on performance, vibration, combustion and knocking of a CI engine. Fuel 2016, 185, 718–733. [Google Scholar] [CrossRef]
- Wang, Y.; Xiang, J.; Markert, R.; Liang, M. Spectral kurtosis for fault detection, diagnosis and prognostics of rotating machines: A review with applications. Mech. Syst. Signal Process. 2016, 66, 679–698. [Google Scholar] [CrossRef]
- Chen, J.; Randall, R.B.; Peeters, B. Advanced diagnostic system for piston slap faults in IC engines, based on the non-stationary characteristics of the vibration signals. Mech. Syst. Signal Process. 2016, 75, 434–454. [Google Scholar] [CrossRef]
- Grajales, J.A.; Quintero, H.F.; Romero, C.A.; Henao, E. Engine diagnosis based on vibration analysis using different fuel blends. In Advances in Condition Monitoring of Machinery in Non-Stationary Operations; Springer: Berlin, Germany, 2017; pp. 27–36. [Google Scholar]
- Djaidir, B.; Guemana, M.; Kouzou, A.; Hafaifa, A. Failure monitoring of gas turbine based on vibration analysis and detection. In Proceedings of the 2017 6th International Conference on Systems and Control (ICSC), Batna, Algeria, 7–9 May 2017; pp. 397–402. [Google Scholar]
- Mohamed, E.S. Performance analysis and condition monitoring of ICE piston-ring based on combustion and thermal characteristics. Appl. Therm. Eng. 2018, 132, 824–840. [Google Scholar] [CrossRef]
- Delvecchio, S.; Bonfiglio, P.; Pompoli, F. Vibro-acoustic condition monitoring of internal combustion engines: A critical review of existing techniques. Mech. Syst. Signal Process. 2018, 99, 661–683. [Google Scholar] [CrossRef]
- Ravi, M.; Kumar, K.V.; Murugesan, A. Certain Investigations on the Performance of Emission, Vibration and Noise Characteristics of CI Engine Using Bio Gas and Bio Diesel as Alternate Fuel. Int. J. PharmTech Res. 2015, 8, 11–19. [Google Scholar]
- Javed, S.; Murthy, Y.S.; Baig, R.U.; Rao, T.N. Vibration analysis of a diesel engine using biodiesel fuel blended with nano particles by dual fueling of hydrogen. J. Nat. Gas Sci. Eng. 2016, 33, 217–230. [Google Scholar] [CrossRef]
- Patel, C.; Lee, S.; Tiwari, N.; Agarwal, A.K.; Lee, C.S.; Park, S. Spray characterization, combustion, noise and vibrations investigations of Jatropha biodiesel fuelled genset engine. Fuel 2016, 185, 410–420. [Google Scholar] [CrossRef]
- Patel, C.; Agarwal, A.K.; Tiwari, N.; Lee, S.; Lee, C.S.; Park, S. Combustion, noise, vibrations and spray characterization for Karanja biodiesel fuelled engine. Appl. Therm. Eng. 2016, 106, 506–517. [Google Scholar] [CrossRef]
- Liu, S.; Chen, W.; Zhu, Z.; Jiang, S.; Ren, T.; Guo, H. A Review of the Developed New Model Biodiesels and Their Effects on Engine Combustion and Emissions. Appl. Sci. 2018, 8, 2303. [Google Scholar] [CrossRef]



| λ | O2 (%) | Amax (s) | Amin (s) |
|---|---|---|---|
| 1.06 | 1.3 | 46.57 | −54.65 |
| 1.24 | 3.9 | 36.81 | −38.31 |
| 1.51 | 7.6 | 31.51 | −32.49 |
| ∞ | 0.0 | 29.38 | −28.97 |
| Notation | Description | Notation | Description |
|---|---|---|---|
| Mass of inlet/exhaust valve | Inlet/exhaust spring force | ||
| Force from adjustment screw to inlet/exhaust valve | Force from inlet/exhaust cam to rocker | ||
| Position vector from rocker pivot to roller center | Position vector from rocker pivot to adjustment screw | ||
| Moment of inertia of inlet/exhaust rocker | Position vector from inlet/exhaust cam axis to roller center | ||
| Required inlet/exhaust torque on camshaft to balance with force | Total camshaft torque | ||
| Inlet/exhaust valve linear displacement | Inlet/exhaust rocker angular displacement | ||
| Unit vector along inlet/exhaust valve | Unit vector along rotation vector |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahdisoozani, H.; Mohsenizadeh, M.; Bahiraei, M.; Kasaeian, A.; Daneshvar, A.; Goodarzi, M.; Safaei, M.R. Performance Enhancement of Internal Combustion Engines through Vibration Control: State of the Art and Challenges. Appl. Sci. 2019, 9, 406. https://doi.org/10.3390/app9030406
Mahdisoozani H, Mohsenizadeh M, Bahiraei M, Kasaeian A, Daneshvar A, Goodarzi M, Safaei MR. Performance Enhancement of Internal Combustion Engines through Vibration Control: State of the Art and Challenges. Applied Sciences. 2019; 9(3):406. https://doi.org/10.3390/app9030406
Chicago/Turabian StyleMahdisoozani, Hojat, Mehrdad Mohsenizadeh, Mehdi Bahiraei, Alibakhsh Kasaeian, Armin Daneshvar, Marjan Goodarzi, and Mohammad Reza Safaei. 2019. "Performance Enhancement of Internal Combustion Engines through Vibration Control: State of the Art and Challenges" Applied Sciences 9, no. 3: 406. https://doi.org/10.3390/app9030406
APA StyleMahdisoozani, H., Mohsenizadeh, M., Bahiraei, M., Kasaeian, A., Daneshvar, A., Goodarzi, M., & Safaei, M. R. (2019). Performance Enhancement of Internal Combustion Engines through Vibration Control: State of the Art and Challenges. Applied Sciences, 9(3), 406. https://doi.org/10.3390/app9030406






