Abstract
In this work, we studied the propagation of ultrasonic waves of lysozyme solutions characterized by different degrees of aggregation and networking. The experimental investigation was performed by means of the transient grating (TG) spectroscopy as a function of temperature, which enabled measurement of the ultrasonic acoustic proprieties over a wide time window, ranging from nanoseconds to milliseconds. The fitting of the measured TG signal allowed the extraction of several dynamic properties, here we focused on the speed and the damping rate of sound. The temperature variation induced a series of processes in the lysozyme solutions: Protein folding-unfolding, aggregation and sol–gel transition. Our TG investigation showed how these self-assembling phenomena modulate the sound propagation, affecting both the velocity and the damping rate of the ultrasonic waves. In particular, the damping of ultrasonic acoustic waves proved to be a dynamic property very sensitive to the protein conformational rearrangements and aggregation processes.
1. Introduction
In order to fulfill protein functions, the polypeptide chains must be organized in their native conformation. In fact, after protein biosynthesis the folding process occurs, giving the protein a three-dimensional structure that makes it biologically active. Sometimes, erroneous protein structuring (misfolding) may occur, resulting in the onset of many diseases [1]. In general, the development of protein structural organization is given by the tendency to minimize interactions between the hydrophobic residues and the polar solvent. Depending on solvating conditions, folding or misfolding and aggregation can be favored. It is possible to modulate the protein’s unfolding and aggregation processes by changing the environmental conditions, such as pH, ionic strength, solvent composition and temperature. These self-assembling phenomena are characterized by different steps, in which the protein undergoes conformational rearrangements and intermolecular associations to form stable structures of increasing complexity [2,3], such as amyloid fibrils and hydrogel networks [4,5]. Protein-based hydrogels have recently received great attention since they can be the key to develop novel biomaterials. In fact, hydrogels have the capability to retain inside their matrix a great amount of water (up to 97%) [6], which make these materials similar to biological tissues [7,8]. Protein hydrogels are therefore of great interest in many fields spanning from the medical to the nanotechnological [9,10,11]. Moreover, hydrogels hold the promise to help in the understanding of tissue formation and transformation. For example, the β-sheet intermolecular motifs, that are responsible of several diseases, form hydrogel structures, which self-organize into three-dimensional networks. The hydrogel matrices have been utilized as scaffolds for stem cells [12], highlighting how the mechanical properties of the gel can modulate cellular differentiation processes.
In the class of globular proteins, an excellent study case is hen egg white lysozyme (HEWL). In fact, HEWL is a small globular protein easy to find, that is capable of producing a variety of aggregated structures, including the intermolecular β-sheet. The self-assembly of HEWL—and more in general of globular proteins—give rise to much interest in biomaterial science since they can originate biocompatible hydrogels whose properties can be modulated by changing the aggregation condition. Lysozyme hydrogels are promising candidates to produce successful cell scaffolds, thanks to their high cytocompatibility [13]. With the aim of studying the protein aggregation processes and following the evolution of the system gelation, we choose to work with an acid (pH = 1.4) and highly concentrated (240 mg/mL) HEWL solution [14]. In particular, the low pH value favors the unfolding process and the high protein concentration facilitates the aggregation/gelation of the system [15].
The investigation of protein solutions and hydrogels by ultrasonic propagation has been performed by a series of research studies [16,17,18,19,20,21]. In fact, the sound speed and the acoustic wave damping can be used to provide information about protein hydration in an aqueous environment and their conformational changes or phase transformations induced by the external stimuli [22]. In particular, C. M. Bryant and D. J. McClements [16] study the behavior of the acoustic wave through a solution of whey proteins, finding that the acoustic attenuation in protein solutions is due both to scattering contributions and protein relaxation phenomena. The latter could be related to hydration, proton transfer [23,24,25] and conformational changes [26,27]. Despite several studies on this argument, one of the major challenges of research in the field of soft matter remains that of relating intra- and intermolecular interactions that govern the structure of individual proteins and their aggregates with the elastic macroscopic characteristics of the whole system. In this respect, we investigated the propagation of ultrasonic acoustic waves in the lysozyme solution and hydrogel, by heterodyne transient grating (HD-TG) spectroscopy [28]. This is a powerful tool that provides valuable information about the elastic properties and their relationship with the relaxation and structural phenomena, both in homogeneous matter [29,30,31,32,33] and in materials characterized by complex structures [34,35,36,37,38,39]. HD-TG experiments can be considered an important advance in the investigation of hydrogels, thanks to their ability to measure collective relaxation times in a wide time/frequency window, hardly accessible by other methods. Moreover, the HD-TG technique is able to measure both acoustic wave damping and sound speed with very high accuracy in a frequency range unexplored by the Brillouin and ultrasonic spectroscopic techniques. HD-TG measurements as a function of the environmental conditions can support a more comprehensive understanding of the relationship between the elastic and structural properties of the self-assembling phenomena taking place in biologic samples.
2. Experimental Methods
2.1. Sample Preparation
The dialyzed and lyophilized powder of HEWL (Sigma Aldrich, 62970, Saint Louis, MO, USA) was dissolved without further purification in deuterium oxide (99.9 atom % D, Sigma Aldrich), to prepare solutions with concentrations of 120 mg/mL and 240 mg/mL. The protein solubilization was increased by leaving the sample at 50 °C for an hour, allowing the exchangeable hydrogens of the proteins to be replaced by deuterium. Deuterium oxide was chosen as a solvent because it will be of interest in the future to compare the TG measurements with those of infrared absorption. After the total dissolution, the pH was adjusted with a 2 M deuterium chloride (DCl) solution, to have a final pH value of 1.4. The solution was filtered with Millex-HV sterilized syringe filter, 0.45 μm pore size, directly into a cuvette. The filtration was mandatory to remove the larger impurities that would disturb the signal acquisition. Regarding the preparation of the gel, we started from the solution with the highest concentration, which was filtered and placed in a cuvette. The solution was left in the thermostat at 55 °C for two hours and then quickly cooled by placing the cuvette in water at room temperature. A very viscous solution was obtained and left at room temperature for about 10 h, to obtain a transparent gel.
2.2. Transient Grating Experiments
The HD-TG experiment is a time-resolved optical technique, based on the third-order non-linear optical response. The experimental details have been described in previous works [28,33,37,40] and here we summarize only the main experimental aspects. Two infrared (1064 nm) laser pulses, with a temporal duration of 20 ps, interfere and produce into the sample temperature and density spatially periodic variation that generates a refractive index grating. The angle between the two pump pulses defines the wave-vector q, which characterizes the spatial modulation of the sample optical properties. Its modulus is where and are the wavelength and the incidence angle of the exciting pulses, respectively. A third continuous-wave laser beam, at 532 nm, is used to probe the modulation of the material optical properties, induced by the pump beams. The time-resolved intensity of the diffracted probe provide information on collective relaxation phenomena in a wide temporal range, from nanoseconds to milliseconds, in a single experiment. To measure the natural damping of the induced acoustic oscillations properly, the pump was focused with a cylindrical shape to have on the sample an excitation grating extended in the q-direction, while the probe beam was focused to a circular spot in order to have a probe area with smaller dimensions in q-direction. The pump beams produced two acoustic pressure waves (i.e., two longitudinal bulk ultrasonic waves), which counter-propagated in the q-direction, their superposition created a stationary wave. The probe beam was scattered by the standing wave, which produced the oscillations in the acoustic signal. The induced standing wave had a lifetime related to the pump spatial extension in the q-direction (geometrical damping time). The natural damping time of the acoustic wave was properly extracted if it was shorter, compared to the geometrical one. Since in our samples the natural damping time was quite long (tens and hundreds of ns), a very precise alignment of the pump and the probe beams was required in order to measure the natural damping. Therefore, the alignment was done through a camera, which permitted micrometer control on the centering and on the spatial superposition of the beams.
2.3. Data Collection
We record the data using a fast time window (0–80 ns range with a 50 ps time step of sampling) and a long one (0–2 μs range with 800 ps time step). The measurements are merged in a single data file. Each data were the average of 1000 records, this procedure produced an excellent signal to noise ratio. The HD-TG signal can be defined according to the following equation [28,37]:
where is the electric field diffracted by the grating, is the local field and is the phase difference between the and . If the local field contribution, , is higher than the diffracted one, , the homodyne contribution becomes negligible and the time variation of the signal is dominated by the heterodyne term, . In addition, the heterodyne detection enables the cancelling of eventual spurious contributions present in the signal. We recorded two HD-TG signals with different phases of the local field, the first signal with and a second one with , we then subtracted from . This procedure extracted the pure HD signal from the not phase sensitive contributions, including the homodyne and local field ones:
We measured the relaxation processes of our samples at in the temperature range 20–80 °C. The samples were kept directly in the cuvette, introduced in a copper cell holder, connected to a thermostat and a thermocouple to feedback the temperature control. During the data collection, the diluted 120 mg/mL HEWL solution remained liquid in all the investigated temperature ranges. Instead, both the 240 mg/mL HEWL solution and the hydrogel at 60 °C became opaque, making it impossible to extend the measurements at temperatures higher than 60 °C.
3. Results and Discussion
In the HD-TG experiments, the pump fields interacted with the material, inducing into the sample a density grating; this is build up by both a weak absorption of the laser pulses and the electrostriction effects. The absorption was due to the presence in the sample of harmonic/combination vibrational bands having frequencies resonant with the laser wavelength, 1064 nm. The electrostriction was due to the migration of the induced dipole in the regions of the maximum of the electric field gradient. These mentioned effects produced two standing acoustic waves characterized by a phase difference of π/2. Both the standing waves decayed in time with the exponential law, . The laser absorption phenomena induced in the sample a third interaction effect, the thermal grating. This is static grating that decays through the heat diffusion processes; represented by the exponential law, . The thermal diffusion time constant, , was typically much longer than the damping time of the acoustic oscillation, .
The can be found using the generalized hydrodynamic equations and can be expressed as follows [28,30,41]:
This expression has been utilized to perform the fitting of the measured HD-TG signals. The fitting parameters are: The acoustic angular frequency, , the acoustic damping rate, , the thermal decay rate, , and the corresponding amplitude constants, A, B and C. In this work, we focused our attention on the speed of sound, , and the acoustic damping rate, . In particular, we focused on the trend of and as a function of temperature. The relative uncertainties associated with these values were those related to the fitting procedure, which were 0.1% and 1%, respectively.
In the HD-TG measures performed in this work, the angle between the pump laser beams was 10.4° and this condition defined a wave vector of , which corresponded to a sound wavelength of 3 μm. Figure 1 shows the linear log plot of the HD-TG signal and the relative fit of the 120 mg/mL lysozyme solution at room temperature.

Figure 1.
Heterodyne transient grating (HD-TG) decay signal (gray dots) and its relative fit (red line) of 120 mg/mL lysozyme aqueous solution at T = 23 °C and wave-vector q = 2.1 μm−1.
Figure 2 shows the linear-log plot of the HD-TG decay signals and their relative fit of both lysozyme solutions and of the gel system, at room temperature and at 60 °C. Figure 2 shows that at room temperature (left panel of Figure 2). The damping rate of the acoustic oscillation was higher in the solution with the highest protein concentration ( = 14.7 MHz), and even higher in the gel system ( = 20.0 MHz). Such behavior was related to the increase of the sample viscosity, going from the diluted solution to the gel matrix, and to the amount of the relaxation channels that an acoustic wave comes across propagating in the sample. Furthermore, scattering processes could start to play a role during the propagation of ultrasonic waves in these complex materials. The increase of damping rates reflected the increase of the system complexity.
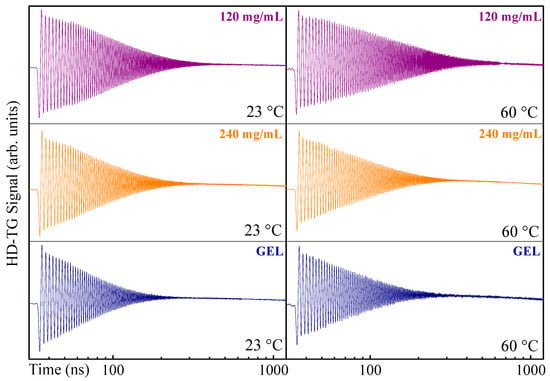
Figure 2.
HD-TG decay signals for the wave vector q = 2.1 μm−1 of: Hen egg white lysozyme (HEWL) 120 mg/mL solution (purple line), 240 mg/mL solution (orange line) and gel (blue line) at 23 °C (left panel) and 60 °C (right panel).
With regard to the 120 mg/mL HEWL solution, the damping rate of the acoustic oscillation at 60 °C (right panel of Figure 2) was lower compared to that at 23 °C (left panel of Figure 2). In fact, at high temperature, a decrease of solution viscosity occurred, due to the increase of the thermal motions of the molecules. Concerning the concentrated solution and the gel matrix at 60 °C, their HD-TG decay signals were comparable. In fact, the parameters that described the propagation of the acoustic wave into the materials were = 13.2 MHz, = 1.52 km/s for the concentrated solution and = 14.3 MHz, = 1.53 km/s for the gel system.
Figure 3 plots the variation of the speed of sound in the studied samples. In all conditions, the speed of sound curves had a similar trend as a function of temperature. This was related to the sound velocity temperature behavior of deuterium oxide (D2O), in fact, the solvent was the most abundant component in the samples. Figure 3a shows the temperature dependence of the speed of sound of the diluted HEWL solution, which was very close to that of the pure solvent. In fact, increased rapidly with temperature, until 50 °C, and less rapidly between 50–75 °C and then decreased after 75 °C, as experimentally observed in D2O [42] and H2O [29]. The data of the concentrated (240 mg/mL) HEWL solution, reported in Figure 3b, showed an overall increase of the velocities with a monotonic temperature dependence similar to the diluted solution dependence up to 55 °C. At this temperature value, there was a small but clear deviation. The gel material also showed the solvent trend, but again a dip in the sound velocity showed up at a lower temperature of about 45 °C.
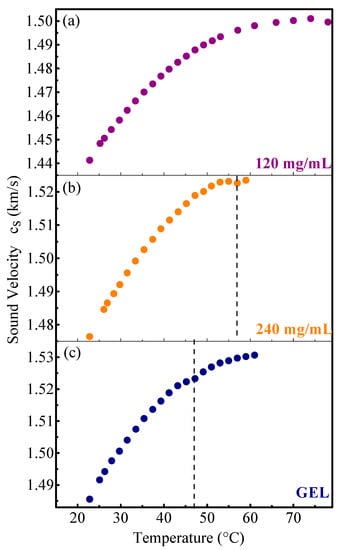
Figure 3.
Temperature dependence of the sound velocity on: (a) The diluted (120 mg/mL) lysozyme solution, (b) the concentrated (240 mg/mL) lysozyme solution and (c) the gel system. The vertical lines point out the temperatures where the speed sound variations take place.
We must remember that the present HD-TG experiment measured the propagation of longitudinal acoustic bulk waves, whereas the gel/aggregation formations were expected to modulate mainly the transverse components of the sound velocities. Nevertheless, the self-assembling phenomena modulated the sound velocities, changing its overall value and producing the observed dips at about 55 °C (Figure 3b), due to the formation of a high content of aggregate species. With regard to the gel matrix, the deviation of the sound velocity data trend occurred at 45 °C due to the transition from gel to liquid state (Figure 3c). This was also in agreement with the damping rate trends that are considered in the following.
Figure 4 shows the temperature dependence of the acoustic damping rate of the studied samples. For the 120 mg/mL HEWL solution (Figure 4a), starting from room temperature to ~45 °C, a decrease from 11.1 MHz to 7.3 MHz of the damping rate occurred, similar to what was observed for a pure liquid [30]. In the range 45–55 °C, the damping rate remained constant, this behavior could be connected to the transition of proteins from a folded to unfolded state. The literature reports a temperature of about 75 °C [4,43] for the folding–unfolding transition of the lysozyme in pure aqueous solution. Nevertheless, in our sample, the acidification of the solution destabilized the protein’s tertiary and secondary structure, so that the unfolding process occurred at lower temperature [44], in agreement with the damping rate observed variation. During the folding-unfolding transition, the damping rate did not change, which could be due to a stabilization of the solution viscosity, induced by the increasing concentration of denatured proteins. After 55 °C, the trend of the damping rate became almost linear with the temperature, recovering the expected behavior of the solvent, D2O. Another slight deviation from the quasi-linear T-dependence occurred around 70 °C. This could again be related to the unfolding of a residual fraction of HEWL proteins less affected b the acid addition [6]. Figure 4b reports the temperature trend of the damping rate for the 240 mg/mL HEWL solution. In this experimental condition, the damping rate behavior was totally different with respect to that of the diluted solution. In particular, in the 23–45 °C temperature range, decreased due to the reduction of solution viscosity. Above 45 °C, the damping of the acoustic wave oscillation increased strongly with temperature, which could be due to the formation of protein aggregates. Indeed, at 45 °C the percentage of proteins in the unfolded state was high enough to promote both the deviation of the acoustic damping rate from the linear T-dependence (visible from Figure 4a) and to promote the aggregation process (visible from Figure 4b). From the literature, it is well known that even a relatively low percentage of unfolded proteins promote aggregation processes [45]. Figure 4c reports the temperature behavior of the gel system. The damping rate showed a linear temperature dependence from 23 °C to 45 °C, and at above 45 °C remained almost constant. We interpreted this trend with the breaking of the gel network, which implied the transition to the liquid state. In other words, according to our results the gel–sol transition takes place at 45 °C.
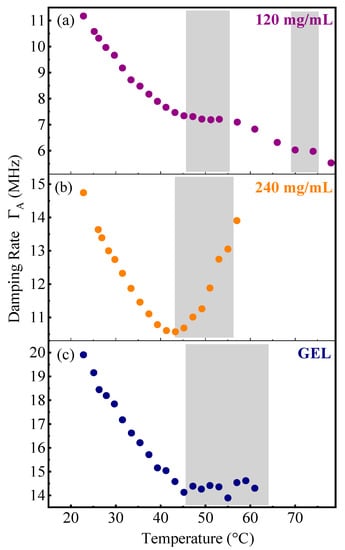
Figure 4.
Temperature dependence of the acoustic damping rate measured on the samples for the 2.1 μm−1 q-vector. (a) The diluted (120 mg/mL) lysozyme solution, (b) the concentrated (240 mg/mL) lysozyme solution, and (c) the gel system. The shaded band underlines the temperature zones characterized by different dynamic regimes.
According to our investigations, the ultrasonic velocities and attenuation processes were both sensitive to the aggregation phenomena. Nevertheless, it seemed that the attenuation processes were more sensitive to the self-assembling even from its earlier stages of the process, in agreement with other investigations [17]. For both the solution samples, the deviation in the damping rates occurred around 45 °C, where the aggregates started to form without necessarily modifying the overall elasticity of the sample. Afterward, the increase of temperature induces the formation of a great amount of lysozyme aggregates [17,46]. For the low concentrated solution, the unfolding of the native lysozyme stabilized the damping rate, whereas, in the highly concentrated solution, the unfolded species promoted aggregate formation, which produced a strong increase of the attenuation phenomena. This could be due to a different level of coordination between the lysozyme aggregated species or to their different structure and/or dimensions. Our outcomes were in agreement with previous studies on other protein solutions [16,27]. The authors found that the protein’s conformational rearrangements and the aggregate’s formation highly affect the attenuation of the acoustic waves.
Instead, the sound speed seemed to be less sensitive to these phenomena, which turn to be important only at 55 °C, where the aggregation extent was high enough to largely affect the sample elasticity.
For the gel system, we must consider a different scenario. In fact, both the ultrasonic parameters, speed and damping, were affected by the gel–solution transition of the system taking place at 45 °C. According to our results, the speed of longitudinal ultrasonic acoustic waves of the gel system was dominated by the solvent proprieties (Figure 3c), whereas the damping rate showed clear differences from solvent features. We must note that the gel–liquid phase did not have the same acoustic proprieties of the highly concentrated solution (Figure 4c,b, respectively), which showed a different structural nature of the lysozyme aggregates and depended only on the thermal treatment.
4. Conclusions
We have studied the acoustic properties of lysozyme aqueous systems at a wave vector of 2.1 μm−1, corresponding to an ultrasonic frequency MHz. Our results showed that both the speed and the attenuation of sound showed articulate temperature dependences, clearly affected by the concentration and phase nature of the system. In this work, we demonstrated that HD-TG provided a versatile approach to study the dynamical behavior of proteins, such as unfolding, aggregation and gelation processes. This technique offered fast data acquisition and the possibility to probe at the same time the viscoelastic properties and its relationship with the self-assembling phenomena. In particular, the acoustic wave damping showed a great sensibility to the aggregate’s formation and phase transitions.
The damping of the HD-TG signal was clearly due to the presence of lysozyme proteins and its temperature dependence was very likely due to the transition from a folded to unfolded state. In fact, the two different protein conformations (folded and unfolded) led to a markedly different environment, due to the exposition of the hydrophobic sites in the unfolded structure, compared to the folded one and the following local arrangement and aggregation phenomena. In particular, in the lysozyme solutions the variation of with temperature occurred for the double effect of viscosity and aggregation processes, whereas in the lysozyme gel the damping regimes reflected the matter phases. Moreover, some scattering processes could have contributed to the damping effects [16] when the aggregate structures reached an adequate stiffness contrast and a dimension comparable to the sound wavelength, μm. The lysozyme solution presented a hydrodynamic behavior that was more complex than a pure viscoelastic liquid, this was related with the continuous protein conformational rearrangements due to the temperature increase. Following the simple viscoelastic model, the maximum damping rate corresponded to the condition, where is the acoustic frequency and is the structural time [41]. In our experiment, this condition would be met when was approximately some hundreds of picoseconds. The unfolding process modified the interactions between the proteins, modulating the structural relaxation channels. It is meaningful to note that the unfolding was supported by the breaking of the protein H-bonds, that took place in hundreds of ps. This could explain the new dynamic regime, which appeared in all the investigated samples around 45 °C, where the unfolding processes began to be active.
Author Contributions
Experimental investigations, S.C., A.T. and P.B.; writing and original draft preparation, S.C. and R.T.; writing, review and editing, all the authors; supervision, P.F. and R.T.
Funding
This research was funded by Ente Cassa di Risparmio Firenze, 2016-0866 and European Community by Laserlab-Europe, H2020 EC-GA-654148.
Acknowledgments
We thank M. Paolantoni, P. Sassi and L. Comez for the idea of studying the thermal behavior of lysozyme in conditions of high concentration and low pH; and B. Rossi for providing the lysozyme sample; the technical staff of LENS for supporting our mechanical and electronic experimental needs; and the student C. Rediti for attending to some experimental investigations.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dobson, C.M. Principles of protein folding, misfolding and aggregation. Semin. Cell Dev. Biol. 2004, 15, 3–16. [Google Scholar] [CrossRef] [PubMed]
- Stradner, A.; Sedgwick, H.; Cardinaux, F.; Poon, W.C.; Egelhaaf, S.U.; Schurtenberger, P. Equilibrium cluster formation in concentrated protein solutions and colloids. Nature 2004, 432, 492–495. [Google Scholar] [CrossRef] [PubMed]
- Porcar, L.; Falus, P.; Chen, W.R.; Faraone, A.; Fratini, E.; Hong, K.L.; Baglioni, P.; Liu, Y. Formation of the Dynamic Clusters in Concentrated Lysozyme Protein Solutions. J. Phys. Chem. Lett. 2010, 1, 126–129. [Google Scholar] [CrossRef]
- Sassi, P.; Onori, G.; Giugliarelli, A.; Paolantoni, M.; Cinelli, S.; Morresi, A. Conformational changes in the unfolding process of lysozyme in water and ethanol/water solutions. J. Mol. Liquids 2011, 159, 112–116. [Google Scholar] [CrossRef]
- Giugliarelli, A.; Tarpani, L.; Latterini, L.; Morresi, A.; Paolantoni, M.; Sassi, P. Spectroscopic and Microscopic Studies of Aggregation and Fibrillation of Lysozyme in Water/Ethanol Solutions. J. Phys. Chem. B 2015, 119, 13009–13017. [Google Scholar] [CrossRef] [PubMed]
- Yan, H.; Frielinghaus, H.; Nykanen, A.; Ruokolainen, J.; Saiani, A.; Miller, A.F. Thermoreversible lysozyme hydrogels: Properties and an insight into the gelation pathway. Soft Matter 2008, 4, 1313–1325. [Google Scholar] [CrossRef]
- Sassi, P.; Giugliarelli, A.; Paolantoni, M.; Morresi, A.; Onori, G. Unfolding and aggregation of lysozyme: A thermodynamic and kinetic study by FTIR spectroscopy. Biophys. Chem. 2011, 158, 46–53. [Google Scholar] [CrossRef]
- Yan, C.; Pochan, D.J. Rheological properties of peptide-based hydrogels for biomedical and other applications. Chem. Soc. Rev. 2010, 39, 3528–3540. [Google Scholar] [CrossRef]
- Jonker, A.M.; Lowik, D.W.P.M.; van Hest, J.C.M. Peptide- and Protein-Based Hydrogels. Chem. Mater. 2012, 24, 759–773. [Google Scholar] [CrossRef]
- Yan, H.; Saiani, A.; Gough, J.E.; Miller, A.F. Thermoreversible protein hydrogel as cell scaffold. Biomacromolecules 2006, 7, 2776–2782. [Google Scholar] [CrossRef]
- Khoury, L.R.; Nowitzke, J.; Shmilovich, K.; Popa, I. Study of Biomechanical Properties of Protein-Based Hydrogels Using Force-Clamp Rheometry. Macromolecules 2018, 51, 1441–1452. [Google Scholar] [CrossRef]
- Sahoo, S.; Ouyang, H.; Goh, J.C.; Tay, T.E.; Toh, S.L. Characterization of a novel polymeric scaffold for potential application in tendon/ligament tissue engineering. Tissue Eng. 2006, 12, 91–99. [Google Scholar] [CrossRef] [PubMed]
- Yan, H.; Nykanen, A.; Ruokolainen, J.; Farrar, D.; Gough, J.E.; Saiani, A.; Miller, A.F. Thermo-reversible protein fibrillar hydrogels as cell scaffolds. Faraday Discuss. 2008, 139, 71–84. [Google Scholar] [CrossRef] [PubMed]
- Catalini, S. Studio Spettroscopico dei Processi di Aggregazione e Gelificazione del Lisozima in Soluzione Acida. Master Thesis, Dip. di Chimica, Biologia e Biotecnologie, Università di Perugia, Perugia, Italy, 2016. [Google Scholar]
- Raccosta, S.; Manno, M.; Bulone, D.; Giacomazza, D.; Militello, V.; Martorana, V.; San Biagio, P.L. Irreversible gelation of thermally unfolded proteins: Structural and mechanical properties of lysozyme aggregates. Eur. Biophys. J. 2010, 39, 1007. [Google Scholar] [CrossRef] [PubMed]
- Bryant, C.M.; McClements, D.J. Ultrasonic spectroscopy study of relaxation and scattering in whey protein solutions. J. Sci. Food Agric. 1999, 79, 1754–1760. [Google Scholar] [CrossRef]
- Corredig, M.; Alexander, M.; Dalgleish, D.G. The application of ultrasonic spectroscopy to the study of the gelation of milk components. Food Res. Int. 2004, 37, 557–565. [Google Scholar] [CrossRef]
- Parker, N.G.; Povey, M.J.W. Ultrasonic study of the gelation of gelatin: Phase diagram, hysteresis and kinetics. Food Hydrocoll. 2012, 26, 99–107. [Google Scholar] [CrossRef]
- Lamanna, L.; Rizzi, F.; Demitri, C.; Pisanello, M.; Scarpa, E.; Qualtieri, A.; Sannino, A.; De Vittorio, M. Determination of absorption and structural properties of cellulose-based hydrogel via ultrasonic pulse-echo time-of-flight approach. Cellulose 2018, 25, 4331–4343. [Google Scholar] [CrossRef]
- Meng, Z.; Thakur, T.; Chitrakar, C.; Jaiswal, M.K.; Gaharwar, A.K.; Yakovlev, V.V. Assessment of Local Heterogeneity in Mechanical Properties of Nanostructured Hydrogel Networks. ACS Nano 2017, 11, 7690–7696. [Google Scholar] [CrossRef]
- Bottari, C.; Comez, L.; Corezzi, S.; D’Amico, F.; Gessini, A.; Mele, A.; Punta, C.; Melone, L.; Pugliese, A.; Masciovecchio, C.; et al. Correlation between collective and molecular dynamics in pH-responsive cyclodextrin-based hydrogels. Phys. Chem. Chem. Phys. PCCP 2017, 19, 22555–22563. [Google Scholar] [CrossRef]
- Pavlovskaya, G.; Mcclements, D.J.; Povey, M.J.W. Ultrasonic Investigation of Aqueous-Solutions of a Globular Protein. Food Hydrocoll. 1992, 6, 253–262. [Google Scholar] [CrossRef]
- O’Brien, W.D., Jr.; Dunn, F. Ultrasonic absorption mechanisms in aqueous solutions of bovine hemoglobin. J. Phys. Chem. 1972, 76, 528–533. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.C.; Leung, W.P.; Mok, H.Y.; Choy, C.L. Ultrasonic absorption in myoglobin and other globular proteins. Biochim. Biophys. Acta 1985, 830, 36–44. [Google Scholar] [CrossRef]
- Kanda, H.; Ookubo, N.; Nakajima, H.; Suzuki, Y.; Minato, M. Ultrasonic absorption in aqueous solution of lysozyme. Biopolymers 1976, 15, 785–795. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, G. On the Kinetics of the Helix-Coil Transition of Polypeptides in Solution. J. Mol. Biol. 1965, 11, 64–77. [Google Scholar] [CrossRef]
- Kessler, L.W.; Dunn, F. Ultrasonic investigation of the conformal changes of bovine serum albumin in aqueous solution. J. Phys. Chem. 1969, 73, 4256–4263. [Google Scholar] [CrossRef]
- Taschin, A.; Eramo, R.; Bartolini, P.; Torre, R. Transient Grating Experiments in Glass-Former Liquids, A Unique Tool to Investigate Complex Dynamics. In Time-Resolved Spectroscopy in Complex Liquids; Torre, R., Ed.; Springer: Boston, MA, USA, 2008. [Google Scholar] [CrossRef]
- Taschin, A.; Cucini, R.; Bartolini, P.; Torre, R. Does there exist an anomalous sound dispersion in supercooled water? Philos. Mag. 2011, 91, 1796–1800. [Google Scholar] [CrossRef]
- Taschin, A.; Bartolini, P.; Eramo, R.; Torre, R. Supercooled water relaxation dynamics probed with heterodyne transient grating experiments. Phys. Rev. E 2006, 74, 031502. [Google Scholar] [CrossRef]
- Pratesi, G.; Bartolini, P.; Senatra, D.; Ricci, M.; Righini, R.; Barocchi, F.; Torre, R. Experimental studies of the ortho-toluidine glass transition. Phys. Rev. E 2003, 67, 021505. [Google Scholar] [CrossRef]
- Pick, R.M.; Dreyfus, C.; Azzimani, a.; Gupta, R.; Torre, R.; Taschin, a.; Franosch, T. Heterodyne detected transient gratings in supercooled molecular liquids. Eur. Phys. J. B 2004, 39, 169–197. [Google Scholar] [CrossRef]
- Amirkhani, M.; Taschin, A.; Cucini, R.; Bartolini, P.; Leporini, D.; Torre, R. Polymer thermal and acoustic properties using heterodyne detected transient grating technique. J. Polym. Sci. Part B Polym. Phys. 2011, 49, 685–690. [Google Scholar] [CrossRef]
- Malfanti, I.; Taschin, a.; Bartolini, P.; Bonello, B.; Torre, R. Propagation of acoustic surface waves on a phononic surface investigated by transient reflecting grating spectroscopy. J. Mech. Phys. Solids 2011, 59, 2370–2381. [Google Scholar] [CrossRef]
- Taschin, A.; Cucini, R.; Bartolini, P.; Torre, R. Temperature of maximum density of water in hydrophilic confinement measured by transient grating spectroscopy. EPL (Europhys. Lett.) 2010, 92, 26005. [Google Scholar] [CrossRef]
- Plazanet, M.; Bartolini, P.; Torre, R.; Petrillo, C.; Sacchetti, F. Structure and acoustic properties of hydrated nafion membranes. J. Phys. Chem. B 2009, 113, 10121–10127. [Google Scholar] [CrossRef] [PubMed]
- Cucini, R.; Taschin, a.; Bartolini, P.; Torre, R. Acoustic, thermal and flow processes in a water filled nanoporous glass by time-resolved optical spectroscopy. J. Mech. Phys. Solids 2010, 58, 1302–1317. [Google Scholar] [CrossRef]
- Taschin, A.; Cucini, R.; Bartolini, P.; Torre, R. Acoustic phenomena in porous media studied by transient grating spectroscopy: A critical test of the Biot theory. EPL (Europhys. Lett.) 2008, 81, 58003. [Google Scholar] [CrossRef]
- Taschin, A.; Bartolini, P.; Sánchez-Ferrer, A.; Mezzenga, R.; Mrzel, A.; Torre, R. Investigation of Relaxation Processes in Nanocomposites by Transient Grating Experiments. Mater. Sci. Forum 2012, 714, 79–83. [Google Scholar] [CrossRef]
- Cucini, R.; Taschin, a.; Bartolini, P.; Torre, R. Acoustic phenomena and hydrodynamic flow in a water filled nano-porous glass studied by transient grating spectroscopy. J. Phys. Conf. Ser. 2010, 214, 012032. [Google Scholar] [CrossRef]
- Azzimani, A.; Dreyfus, C.; Pick, R.; Bartolini, P.; Taschin, a.; Torre, R. Analysis of a heterodyne-detected transient-grating experiment on a molecular supercooled liquid. I. Basic formulation of the problem. Phys. Rev. E 2007, 76, 011509. [Google Scholar] [CrossRef] [PubMed]
- Wegge, R.; Richter, M.; Span, R. Speed of sound measurements in deuterium oxide (D2O) over the temperature range from (278.2 to 353.2) K at pressures up to 20 MPa. Fluid Phase Equilibria 2016, 418, 175–180. [Google Scholar] [CrossRef]
- Matheus, S.; Friess, W.; Mahler, H.C. FTIR and nDSC as analytical tools for high-concentration protein formulations. Pharm Res 2006, 23, 1350–1363. [Google Scholar] [CrossRef] [PubMed]
- Zou, Y.; Li, Y.; Hao, W.; Hu, X.; Ma, G. Parallel beta-sheet fibril and antiparallel beta-sheet oligomer: New insights into amyloid formation of hen egg white lysozyme under heat and acidic condition from FTIR spectroscopy. J. Phys. Chem. B 2013, 117, 4003–4013. [Google Scholar] [CrossRef]
- Giugliarelli, A.; Paolantoni, M.; Morresi, A.; Sassi, P. Denaturation and preservation of globular proteins: The role of DMSO. J. Phys. Chem. B 2012, 116, 13361–13367. [Google Scholar] [CrossRef] [PubMed]
- Corredig, M.; Dalgleish, D.G. Effect of temperature and pH on the interactions of whey proteins with casein micelles in skim milk. Food Res. Int. 1996, 29, 49–55. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).