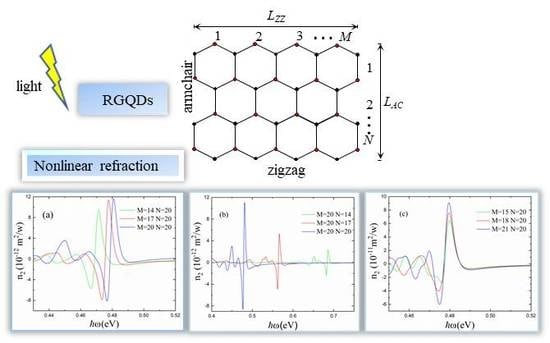
Nonlinear Refractive Index in Rectangular Graphene Quantum Dots
Abstract
:1. Introduction
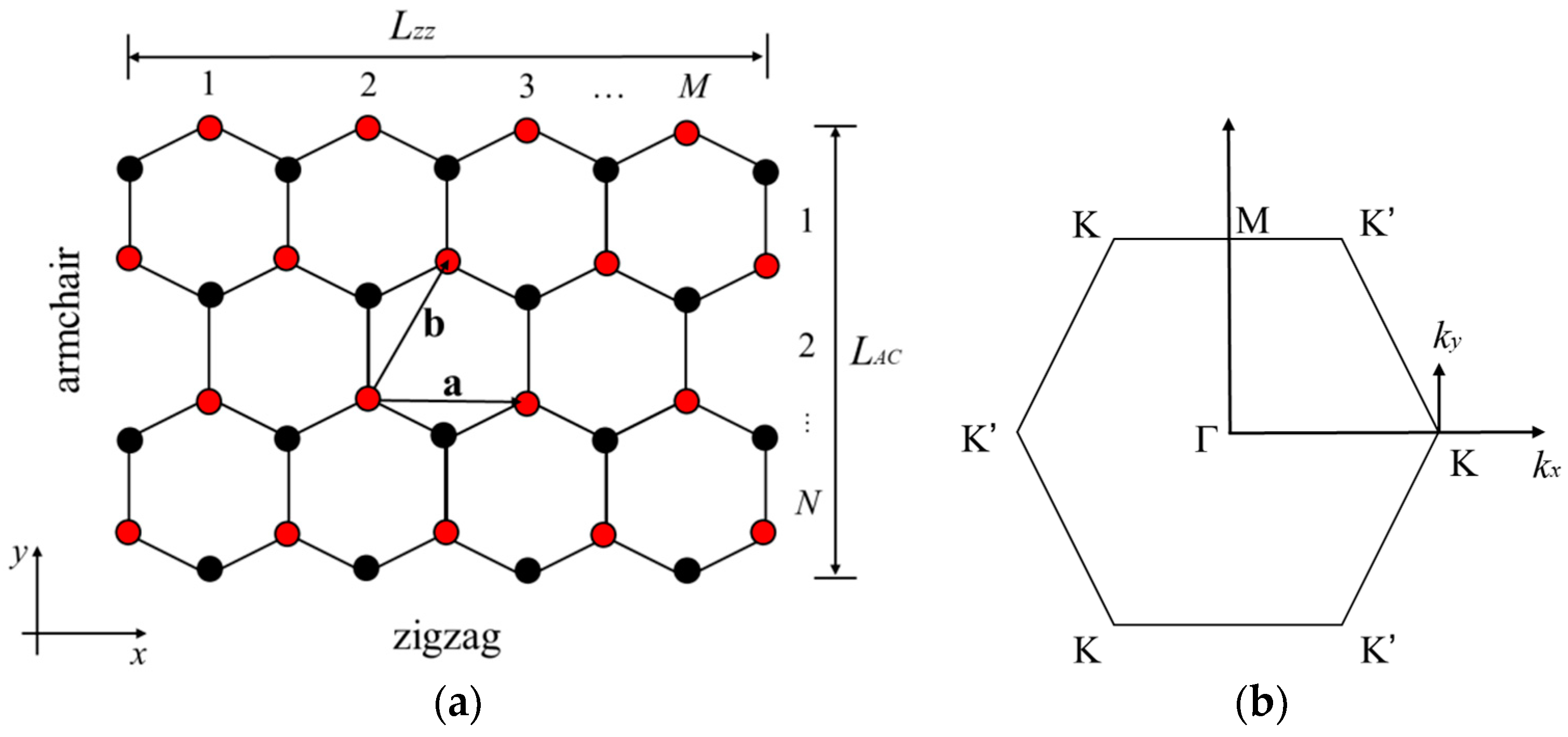
2. Theory and Calculation
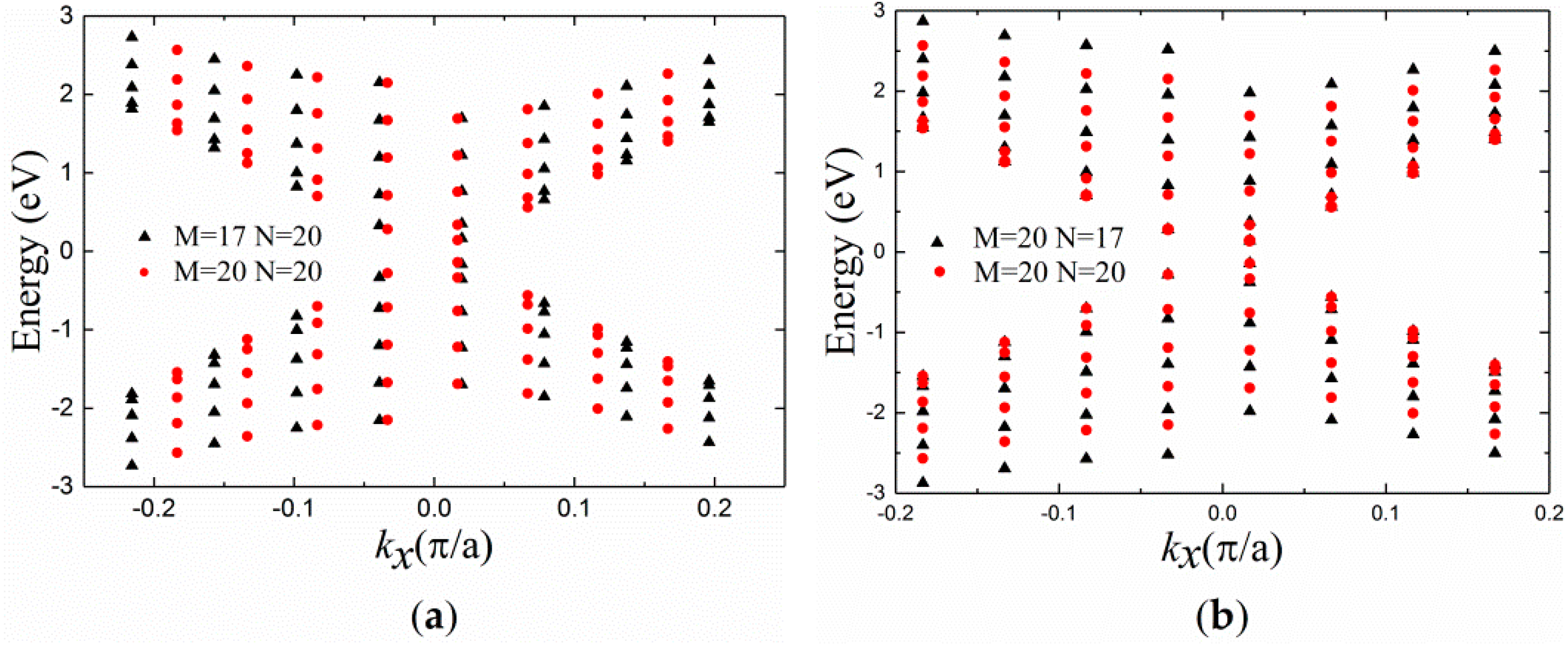
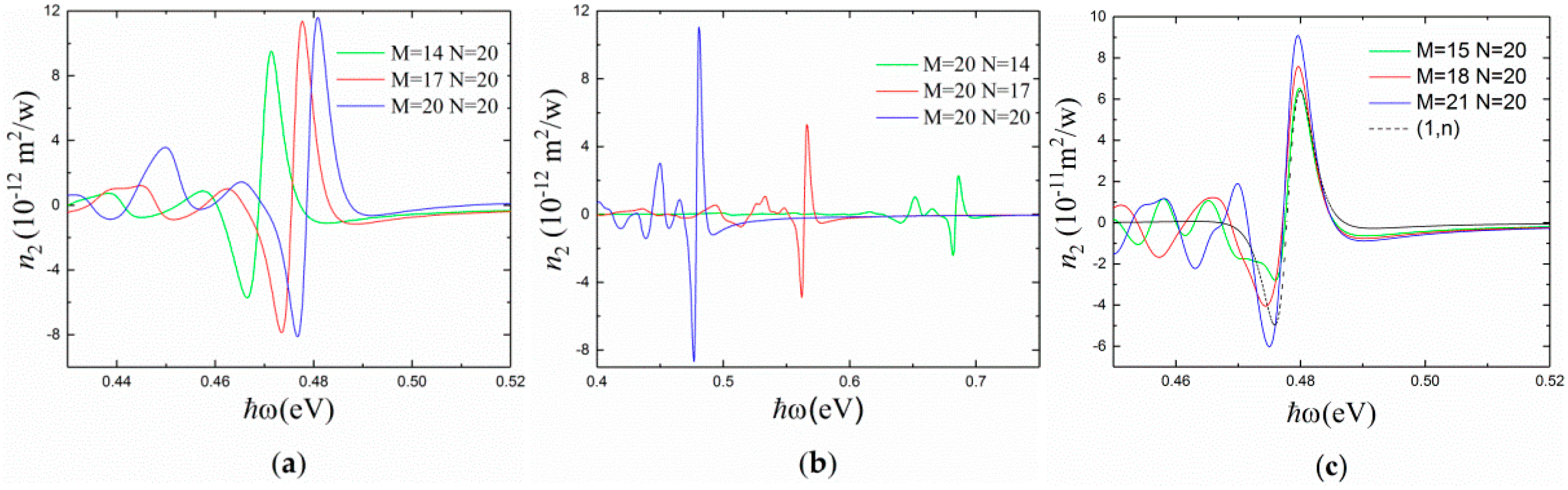
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhu, Y.; Murali, S.; Cai, W.; Li, X.; Suk, J.W.; Potts, J.R.; Ruoff, R.S. Graphene and graphene oxide: Synthesis, properties, and applications. Adv. Mater. 2010, 22, 3906–3924. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K. Graphene: Status and prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Gunlycke, D.; Lawler, H.M.; White, C.T. Room-temperature ballistic transport in narrow graphene strips. Phys. Rev. B 2007, 75, 085418-1–085418-5. [Google Scholar] [CrossRef]
- Güttinger, J.; Stampfer, C.; Hellmüller, S.; Molitor, F.; Ihn, T.; Ensslin, K. Charge detection in graphene quantum dots. Appl. Phys. Lett. 2008, 93, 212102-1–212102-3. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hiura, H. Tailoring graphite layers by scanning tunneling microscopy. Appl. Surf. Sci. 2004, 222, 374–381. [Google Scholar] [CrossRef]
- Zheng, X.T.; Ananthanarayanan, A.; Luo, K.Q.; Chen, P. Glowing graphene quantum dots and carbon dots: Properties, syntheses, and biological applications. Small 2015, 11, 1620–1636. [Google Scholar] [CrossRef] [PubMed]
- Tang, L.; Ji, R.; Cao, X.; Lin, J.; Jiang, H.; Li, X.; Teng, K.S.; Luk, C.M.; Zeng, S.; Hao, J.; et al. Deep ultraviolet photoluminescence of water-soluble self-passivated graphene quantum dots. ACS Nano 2012, 6, 5102–5110. [Google Scholar] [CrossRef]
- Sun, H.; Li, W.; Wei, W.; Qu, X. Recent advances in graphene quantum dots for sensing. Mater. Today 2013, 16, 433–442. [Google Scholar] [CrossRef]
- Thakur, S.; Semnani, B.; Majedi, A.H. Spectrally-dependent Z-scan measurement of the nonlinear refractive index of graphene. In Proceedings of the 2017 Photonics North, Ottawa, ON, Canada, 6–8 June 2017. [Google Scholar] [CrossRef]
- Zhang, H.; Virally, S.; Bao, Q.; Ping, L.K.; Massar, S.; Godbout, N.; Kochaert, P. Z-scan measurement of the nonlinear refractive index of graphene. Opt. Lett. 2012, 37, 1856–1858. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Zhang, S.; Umran, F.A.; Cheng, X.; Dong, N.; Coghlan, D.; Cheng, Y.; Zhang, L.; Blau, W.J.; Wang, J. Tunable effective nonlinear refractive index of graphene dispersions during the distortion of spatial self-phase modulation. Appl. Phys. Lett. 2014, 104, 141909-1–141909-5. [Google Scholar] [CrossRef]
- Dremetsika, E.; Dlubak, B.; Gorza, S.P.; Ciret, C.; Martin, M.B.; Hofmann, S.; Seneor, P.; Dolfi, D.; Massar, S.; Emplit, P.; et al. Measuring the nonlinear refractive index of graphene using the optical Kerr effect method. Opt. Lett. 2016, 41, 3281–3284. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Qin, Y.; Liu, Y. Size and edge dependence of two-photon absorption in rectangular graphene quantum dots. Opt. Express 2018, 26, 7132–7139. [Google Scholar] [CrossRef] [PubMed]
- Coso, R.; Solis, J. Relation between nonlinear refractive index and third-order susceptibility in absorbing media. J. Opt. Soc. Am. B 2004, 21, 640–644. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Li, J.; Xiong, G. Studies of the third-order nonlinear optical susceptibility for InxGa1−xN/GaN cylinder quantum dots. Physica E 2005, 25, 466–471. [Google Scholar] [CrossRef]
- Shen, Y.R. The Principles of Nonlinear Optics; John Wiley & Sons: New York, NY, USA, 1984; pp. 13–41. ISBN 978-0-471-43080-3. [Google Scholar]
- Ando, T.; Nakanishi, T. Impurity Scattering in Carbon Nanotubes Absence of Back Scattering. J. Phys. Soc. Jpn. 1998, 67, 1704–1713. [Google Scholar] [CrossRef]
- Tang, C.; Yan, W.; Zheng, Y.; Li, G.; Li, L. Dirac equation description on the electronic states and magnetic properties of a square graphene quantum dots. Nanotechnology 2008, 19, 435401-1–435401-10. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef] [Green Version]
- Suzuura, H.; Ando, T. Phonons and electron-phonon scattering in carbon nanotubes. Phys. Rev. B 2002, 65, 205412-1–205412-15. [Google Scholar] [CrossRef]
- Qian, J.; Dutta, M.; Stroscio, M.A. Phonon bottleneck effects in rectangular graphene quantum dots. J. Comput. Electron. 2012, 11, 293–301. [Google Scholar] [CrossRef]
- Fang, T.; Konar, A.; Xing, H.; Jena, D. Mobility in semiconducting graphene nanoribbons: Phonon, impurity, and edge roughness scattering. Phys. Rev. B 2008, 78, 205403-1–205403-8. [Google Scholar] [CrossRef]
- Gong, H.M.; Wang, X.H.; Du, Y.M.; Wang, Q.Q. Optical nonlinear absorption and refraction of CdS and CdS-Ag core-shell quantum dots. J. Chem. Phys. 2006, 125, 024707-1–024707-4. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.L.; Zhu, C.S.; Gan, F.X. Nonlinear optical absorption and refraction by CdTe microcrystals doped in glass. J. Appl. Phys. 2000, 87, 1759–1761. [Google Scholar] [CrossRef]
- Wang, K.P.; Feng, Y.Y.; Chang, C.X.; Zhan, J.X.; Wang, C.W.; Zhao, Q.Z.; Coleman, J.N.; Zhang, L.; Blau, W.J.; Wang, J. Broadband ultrafast nonlinear absorption and nonlinear refraction of layered molybdenum dichalcogenide semiconductors. Nanoscale 2014, 6, 10530–10535. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Zhang, Y.W.; Chen, R.Z.; Cheng, X.A.; Xu, Z.J.; Jiang, T. Z-scan measurement of the nonlinear refractive index of monolayer WS2. Opt. Express 2015, 23, 15616–15623. [Google Scholar] [CrossRef] [PubMed]
- Dong, N.N.; Li, Y.X.; Zhang, S.F.; Mcevoy, N.; Zhang, X.Y.; Cui, Y.; Zhang, L.; Duesberg, G.S.; Wang, J. Dispersion of nonlinear refractive index in layered WS2 and WSe2 semiconductor films induced by two-photon absorption. Opt. Lett. 2016, 41, 3936–3969. [Google Scholar] [CrossRef]

| Materials | Size | Wavelength | n2 (×10−12 m2/W) | |
|---|---|---|---|---|
| (nm) | Experiment | Theory | ||
| CdS QDs | 6.4 nm | 790 | 10−7 [25] | |
| CdS-Ag QDs | 10.1 nm | 790 | −2.3 × 10−5 [25] | |
| CdTe QDs | 20 nm | 1060 | −6 × 10−5 [26] | |
| Graphene | 1–6 layers | 1550 | 10 [12] | |
| monolayer | 1600 | −1.1 × 10−1 [14] | ||
| 1050 | 1.7 [11] | |||
| 1064 | −13.7 [27] | |||
| 532 | −2.34 [27] | |||
| MoS2 | 1064 | −(0.207 ± 0.021) [27] | ||
| 532 | −(2.5 ± 1.2) [27] | |||
| WS2 | monolayer | 800 | 0.8 [28] | |
| 0.75 nm thick | 1040 | (1.28 ± 0.03) × 10−2 [29] | ||
| 18.8 nm thick | 1040 | (−8.55 ± 0.63) × 10−4 [29] | ||
| RGQDs | 6.4 nm × 6.4 nm | 790 | −2.13 × 10−2 | |
| 5.2 nm × 4.3 nm | 699 | −1.75 × 10−2 | ||
| 5.2 nm × 4.3 nm | 1064 | −6.33 × 10−2 | ||
| 3.4 nm × 4.3 nm | 2638 | 9.5 | ||
| 4.2 nm × 4.3 nm | 2594 | 11.4 | ||
| 4.9 nm × 4.3 nm | 2583 | 11.6 | ||
| 4.9 nm × 3.7 nm | 2175 | 5.24 | ||
| 3.7 nm × 4.3 nm | 2583 | 65.2 | ||
| 4.4 nm × 4.3 nm | 2583 | 75.9 | ||
| 5.2 nm × 4.3 nm | 2583 | 90.8 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Y.; Feng, X.; Liu, Y. Nonlinear Refractive Index in Rectangular Graphene Quantum Dots. Appl. Sci. 2019, 9, 325. https://doi.org/10.3390/app9020325
Qin Y, Feng X, Liu Y. Nonlinear Refractive Index in Rectangular Graphene Quantum Dots. Applied Sciences. 2019; 9(2):325. https://doi.org/10.3390/app9020325
Chicago/Turabian StyleQin, Yonggang, Xiaobo Feng, and Yu Liu. 2019. "Nonlinear Refractive Index in Rectangular Graphene Quantum Dots" Applied Sciences 9, no. 2: 325. https://doi.org/10.3390/app9020325
APA StyleQin, Y., Feng, X., & Liu, Y. (2019). Nonlinear Refractive Index in Rectangular Graphene Quantum Dots. Applied Sciences, 9(2), 325. https://doi.org/10.3390/app9020325