Resonance Instability of Photovoltaic E-Bike Charging Stations: Control Parameters Analysis, Modeling and Experiment
Abstract
1. Introduction
2. Experimental Study
2.1. Experimental Set-Up
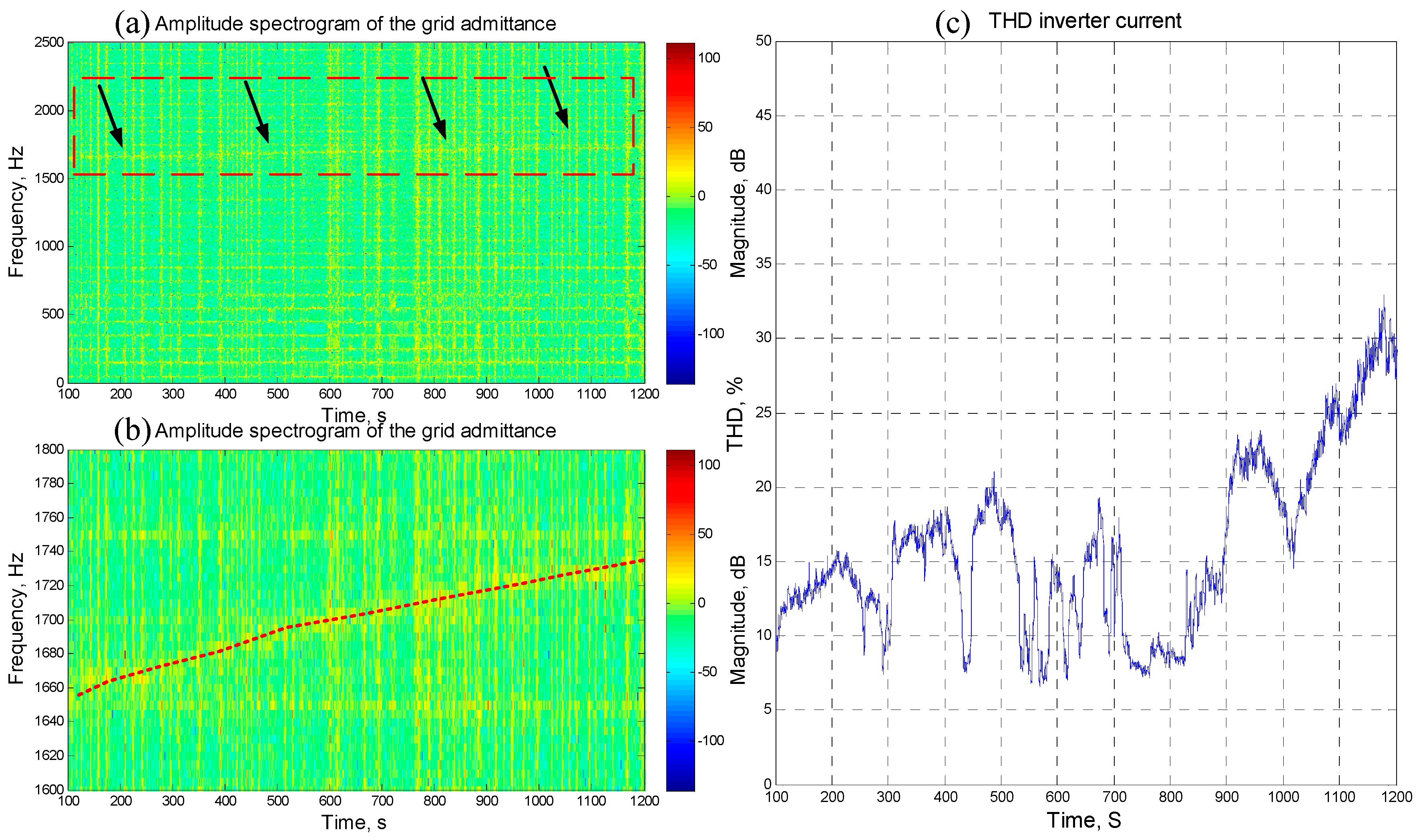
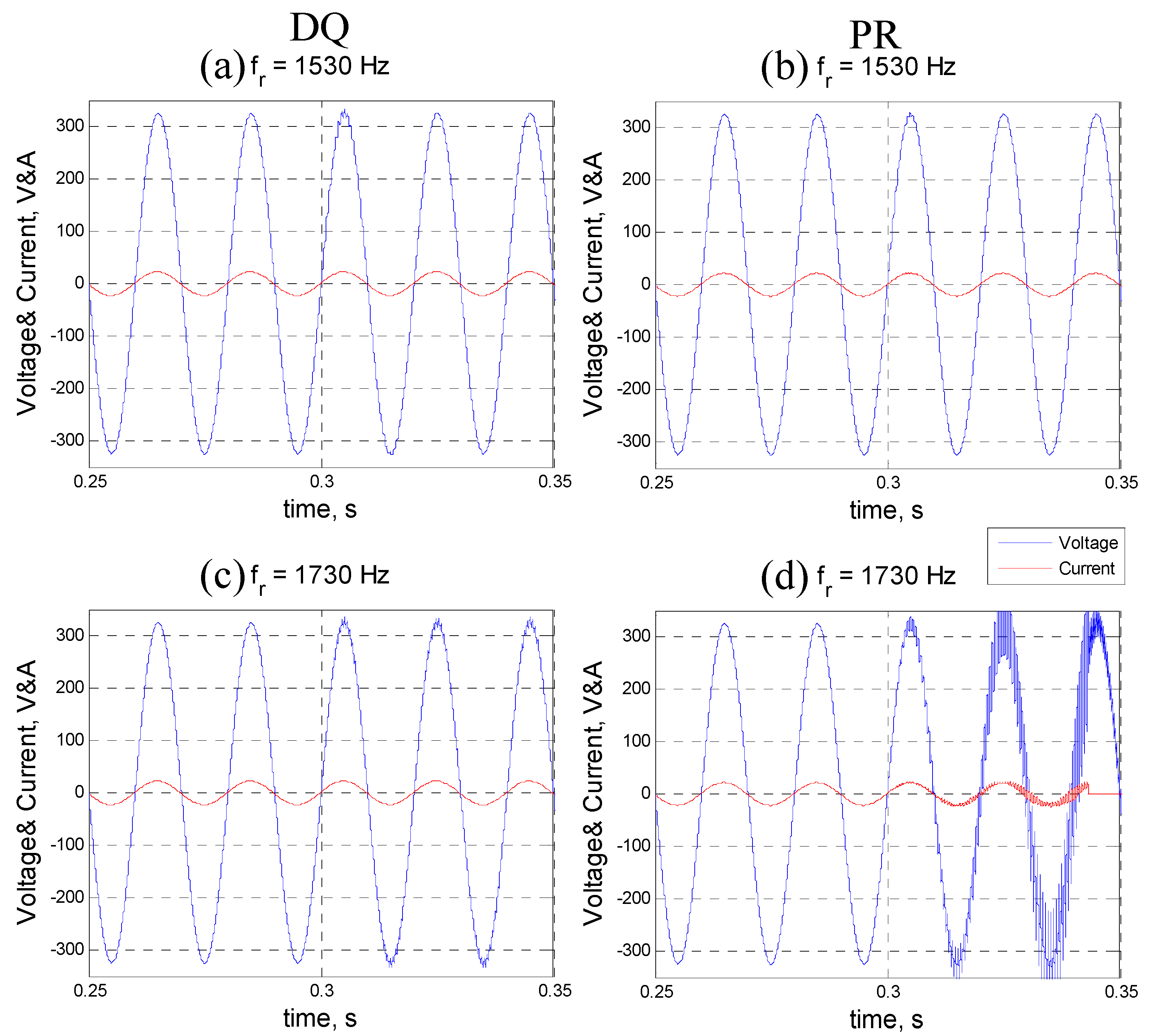
2.2. Experimental Results
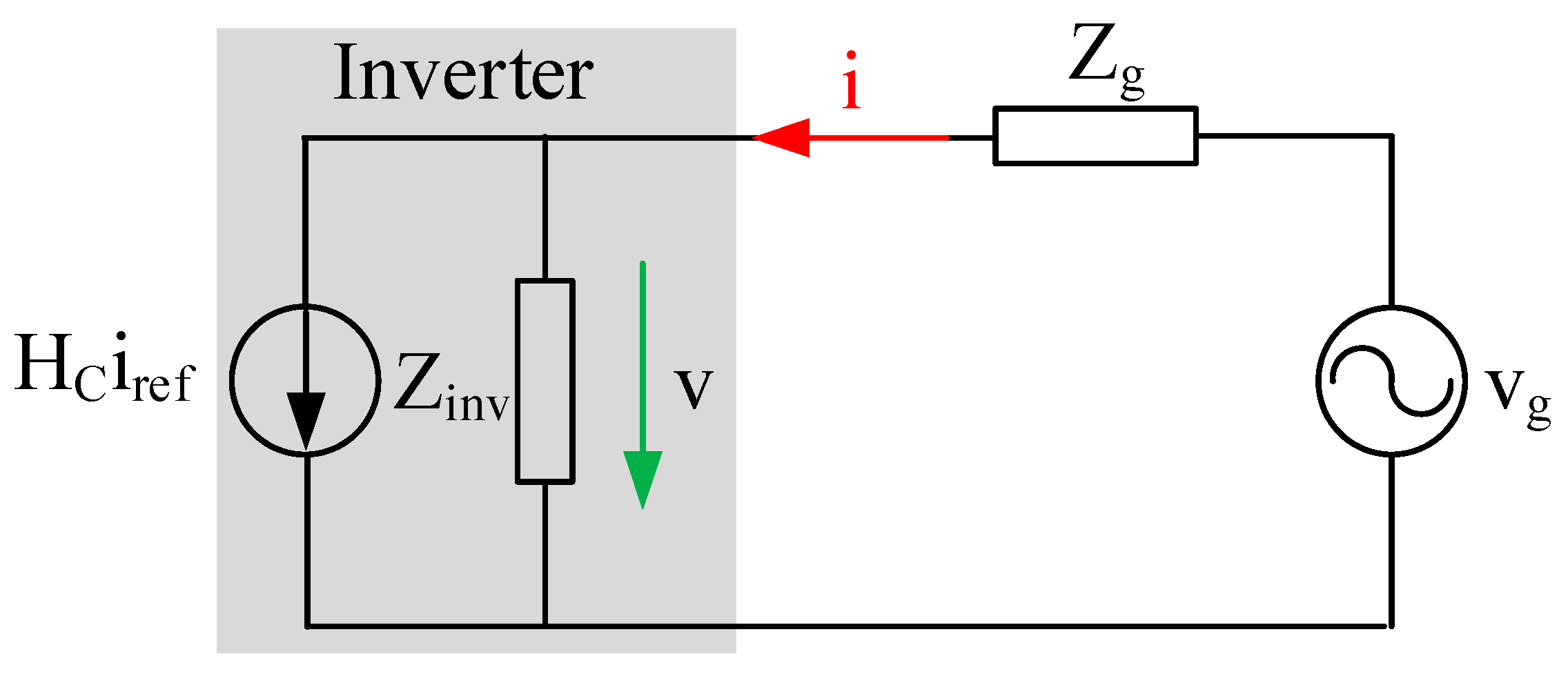
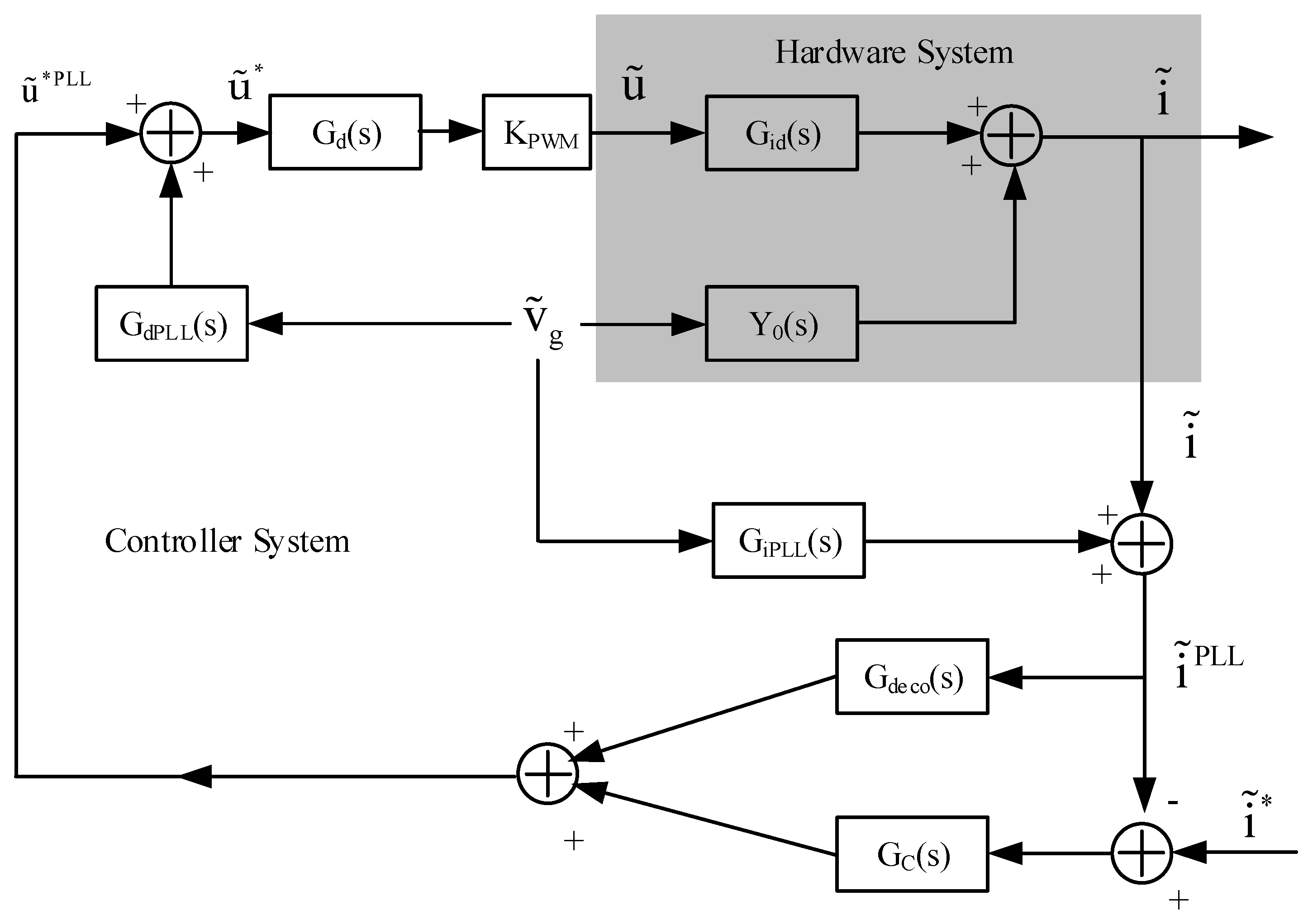
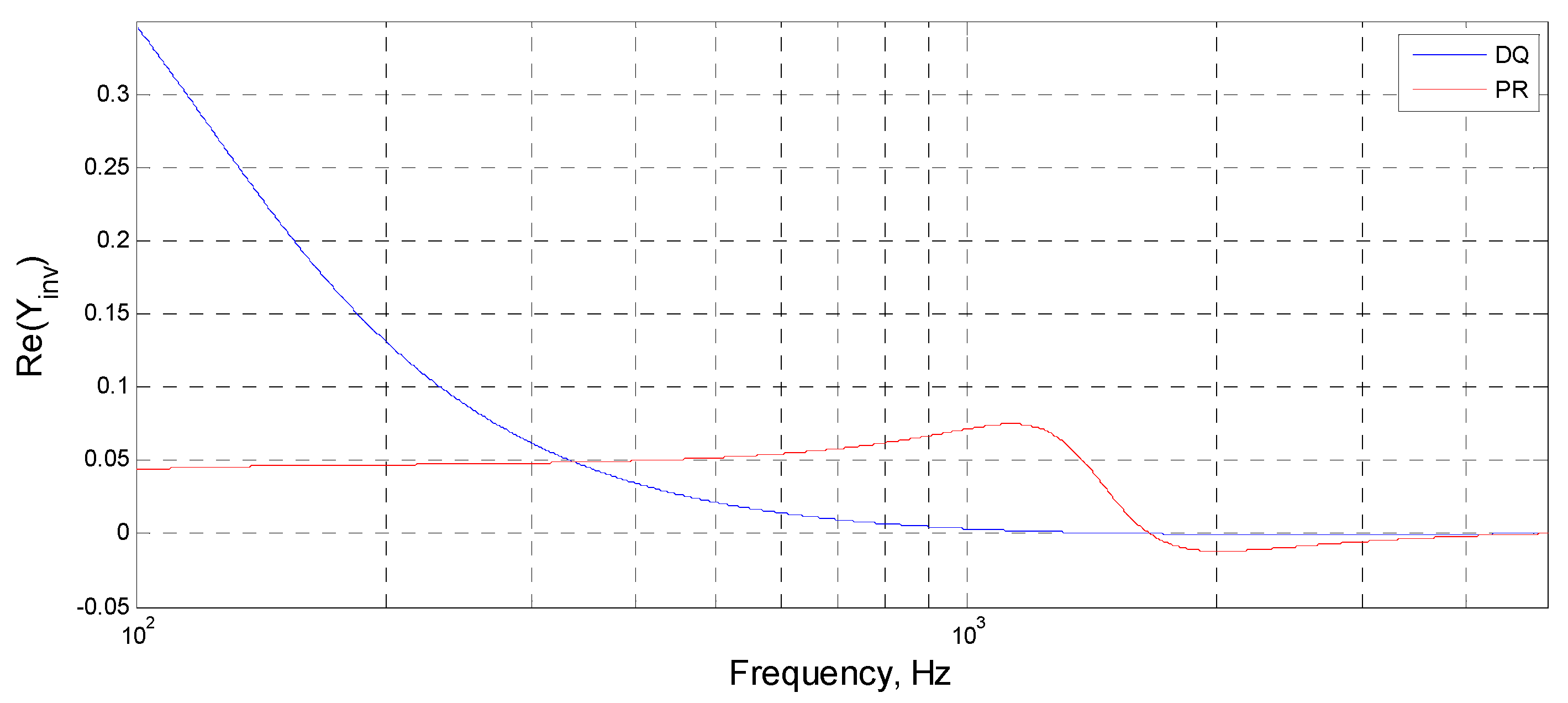
2.3. Passivity Impedance-Based Stability Criterion
- Y(s) is stable and;
- −π ≤ arg[Y(jω)] ≤ π and can also be expressed equivalently as;
- Re{Y(jω)} ≥ 0, ∀ω ∈ (0,fL].which means that the transfer function is passive in the interval (0,fL].
3. Modeling the Inverter in the Frequency-Domain
- proportional resonance (PR) based current control
- synchronous rotating frame (dq-transformation) based current control
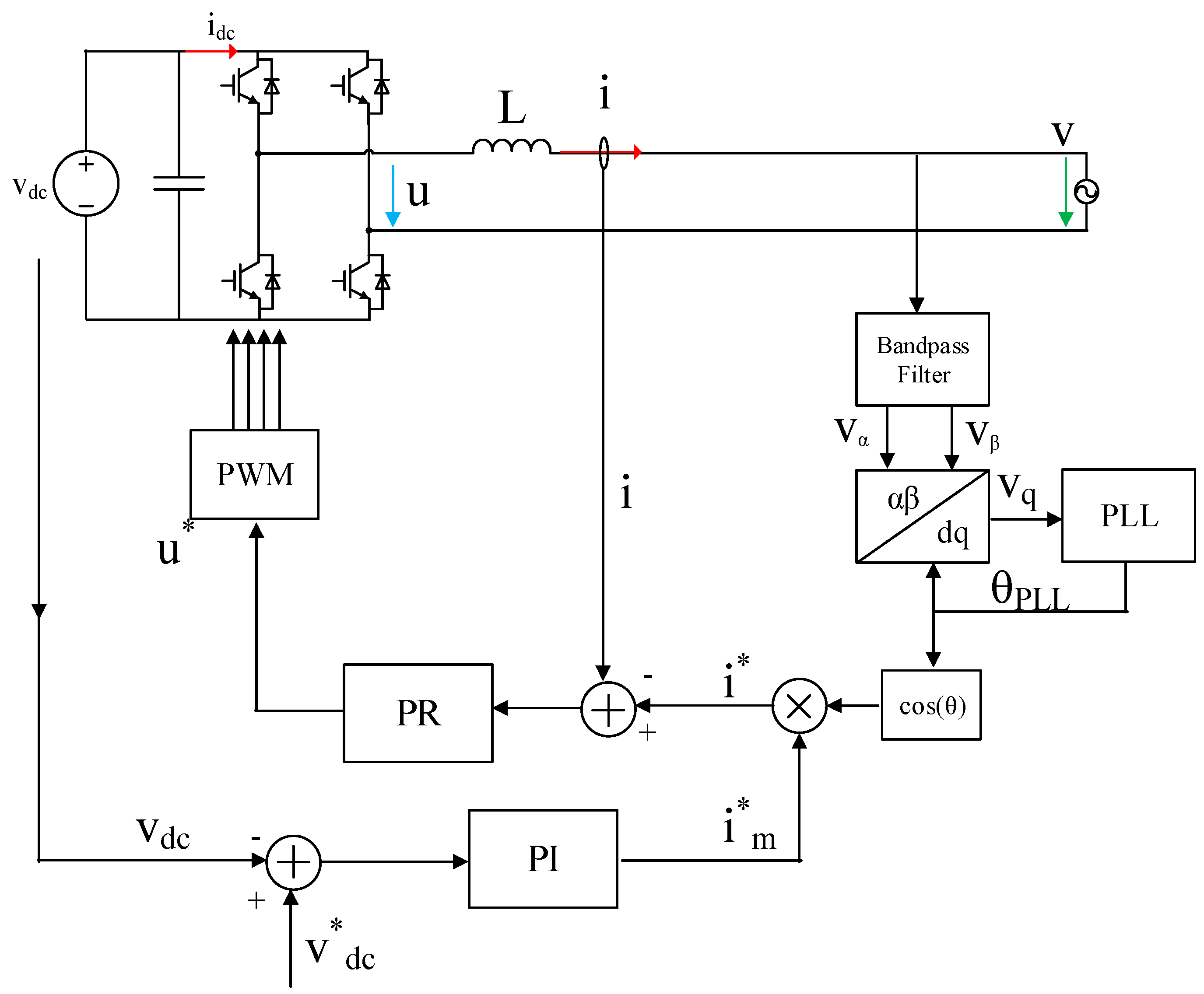
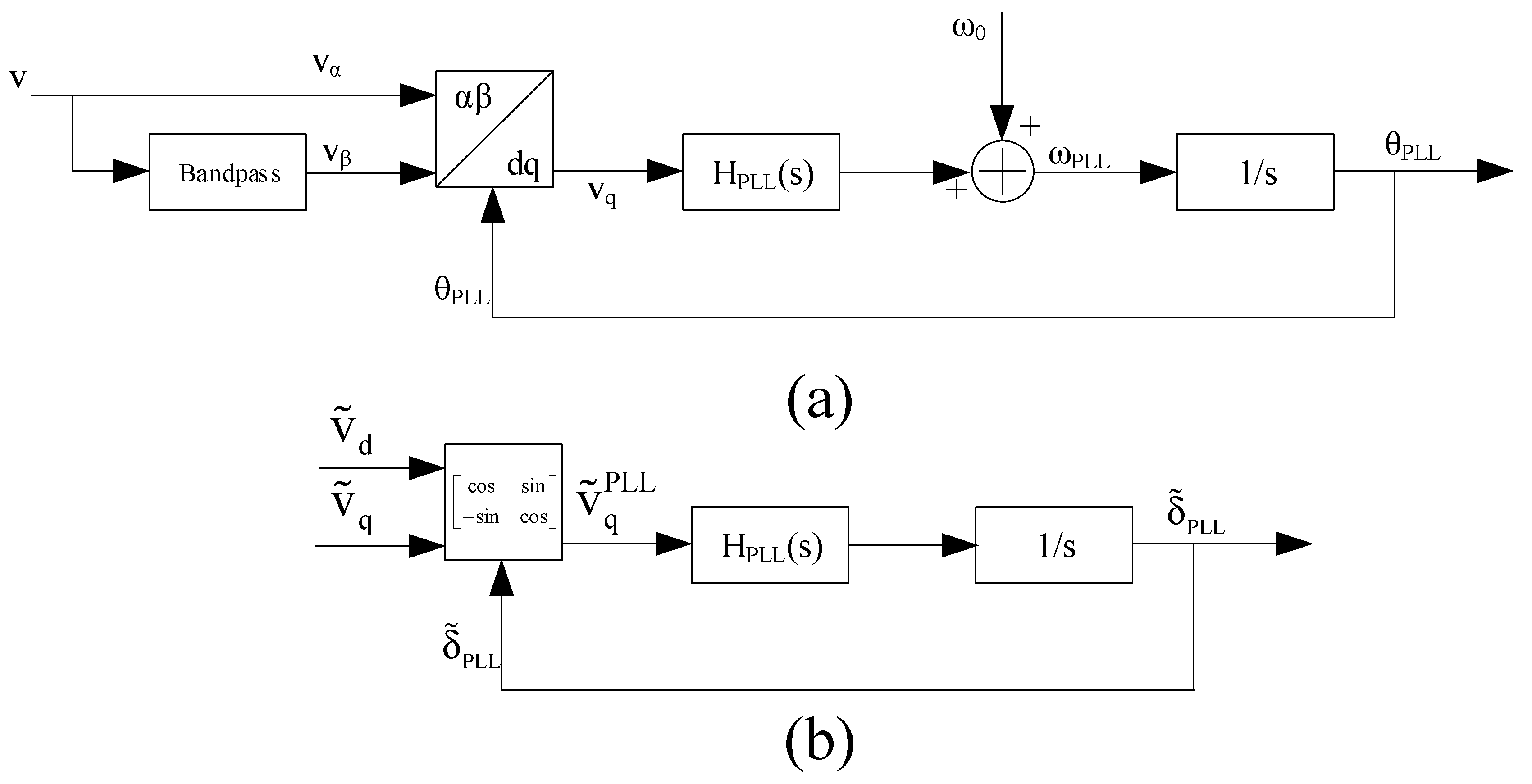
3.1. PR-Based Current Control Method
3.2. Synchronous Rotating Frame Based Current Control Method
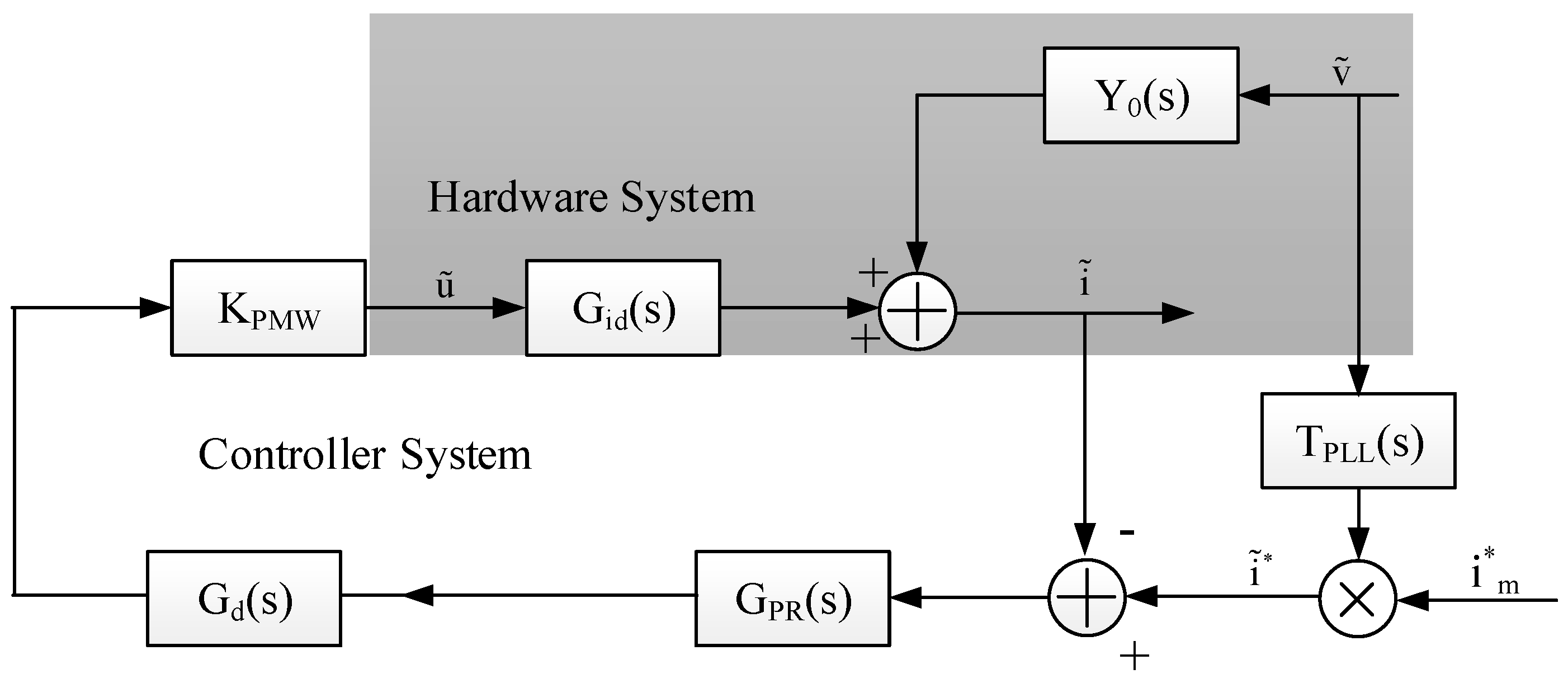
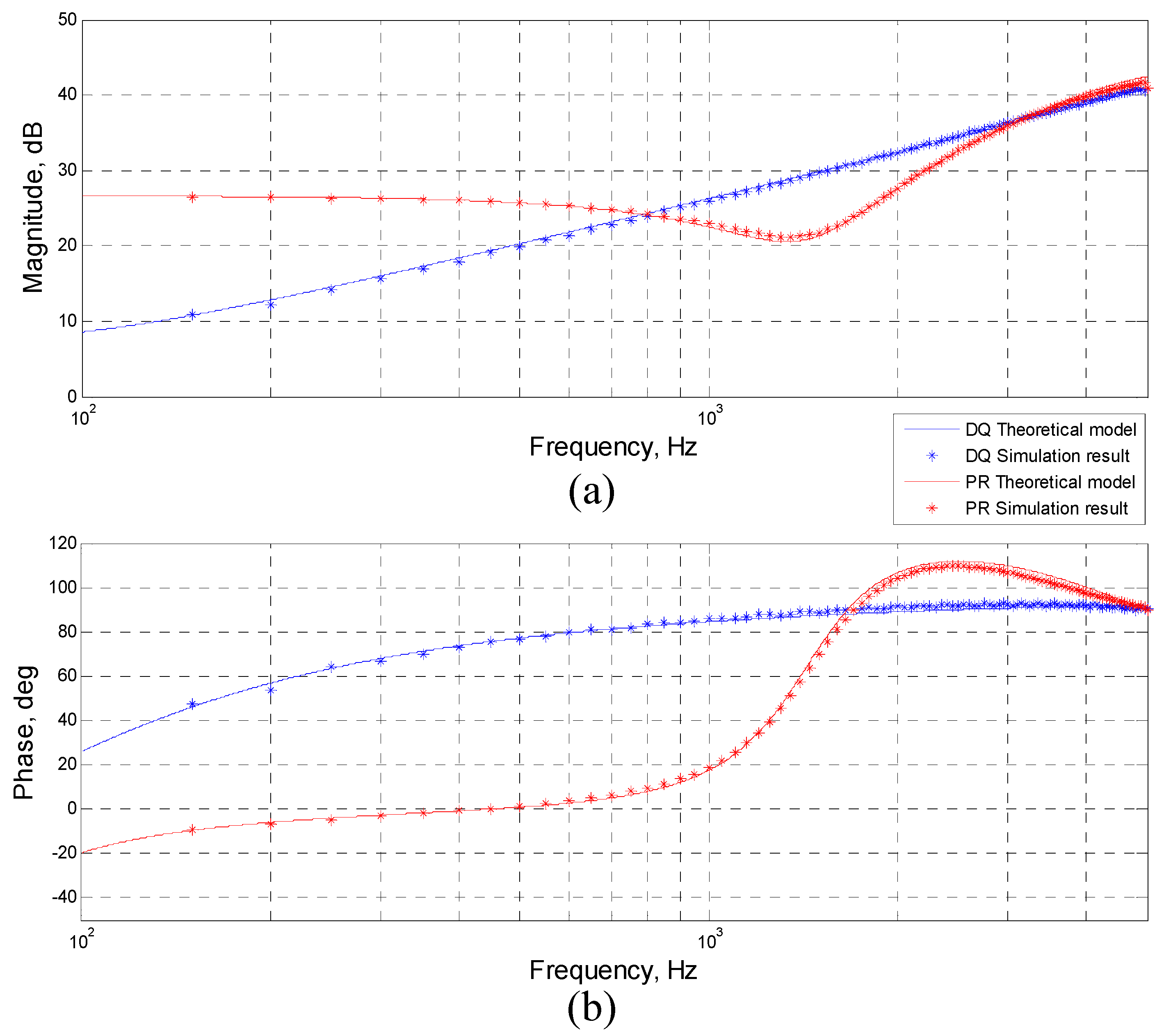
4. Simulation Verification
Verification
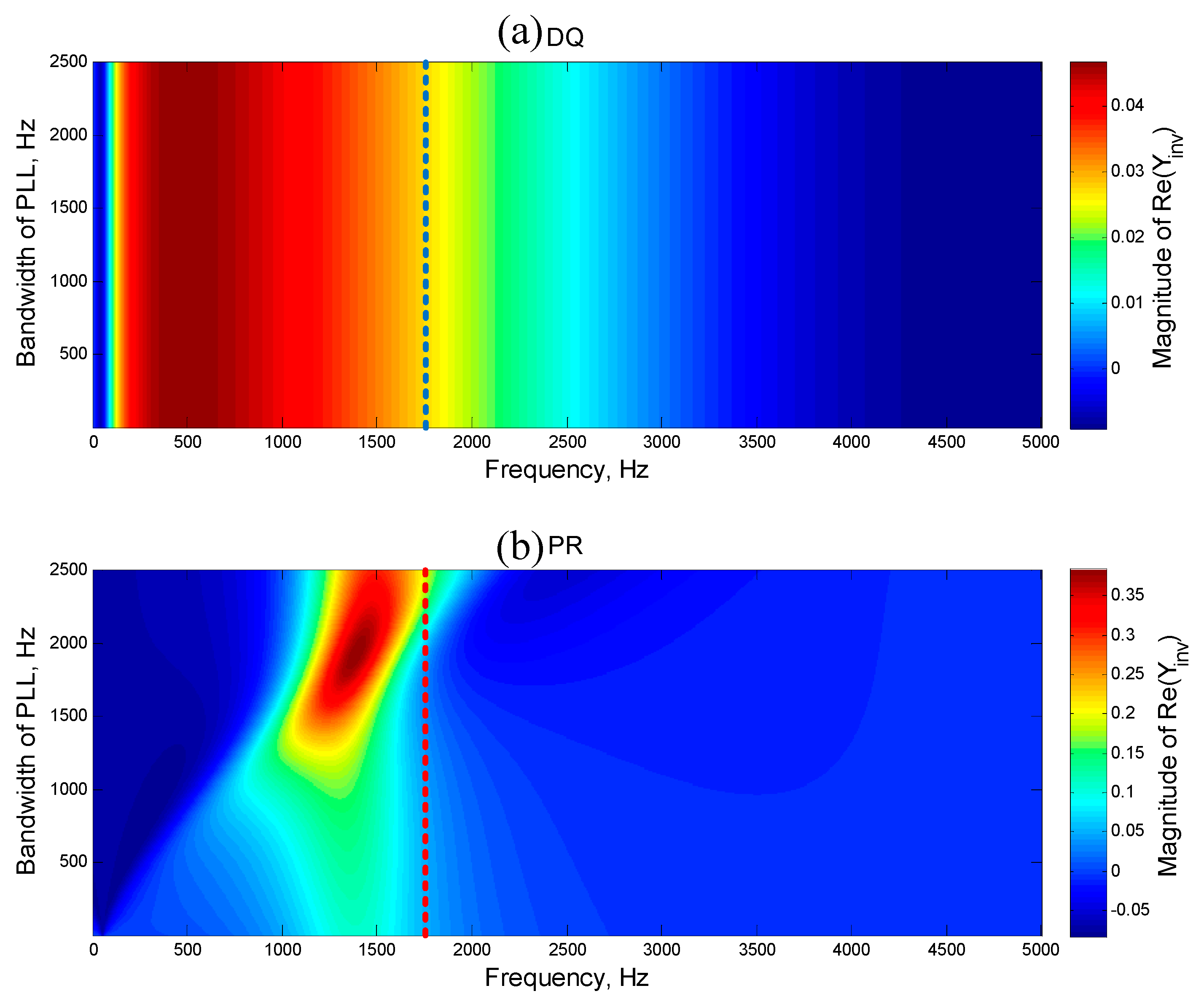
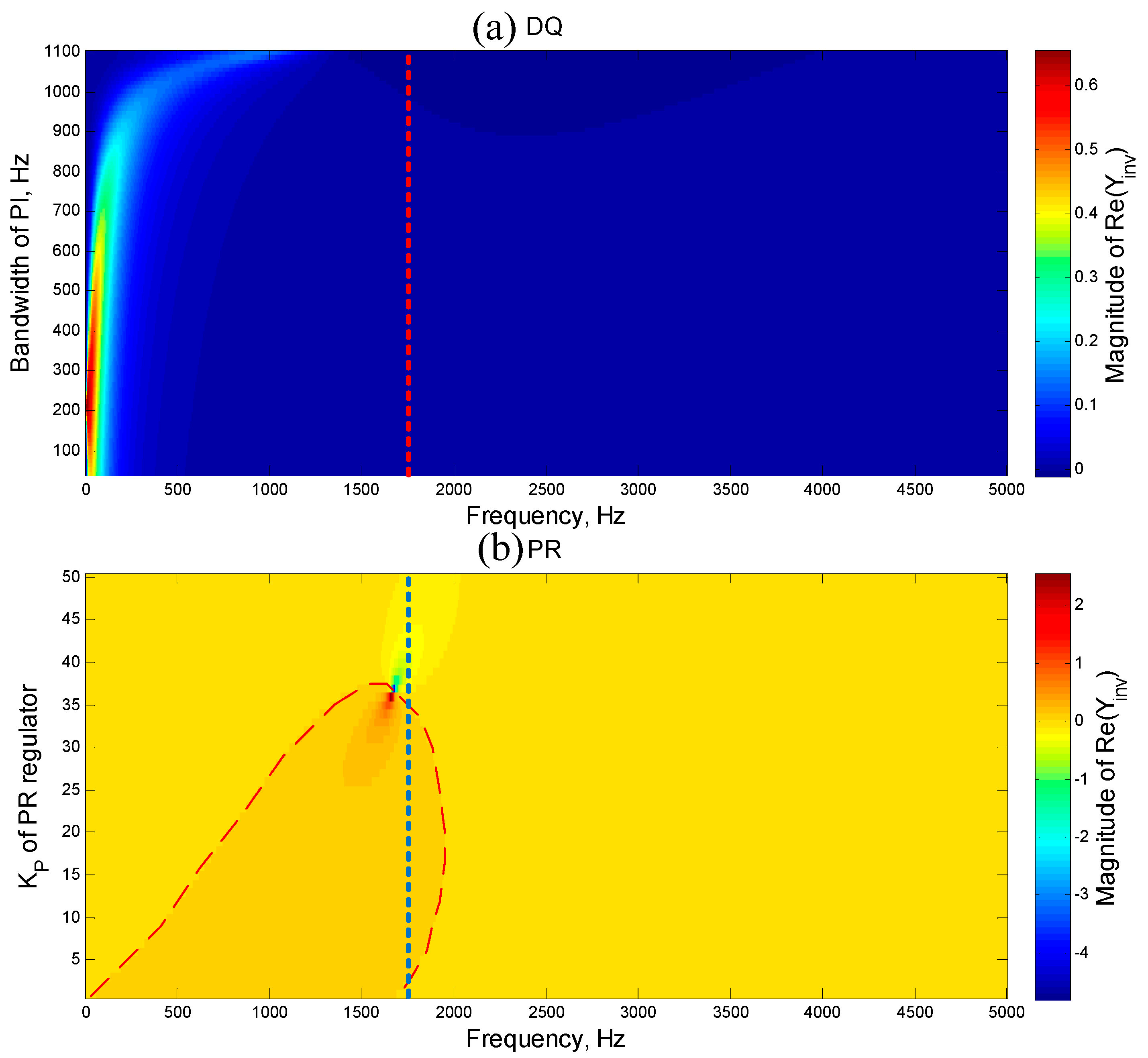
5. Analysis of the Influence of the Control Parameter and Improvement Methods
5.1. Analysis of the Influence of the Control Parameter
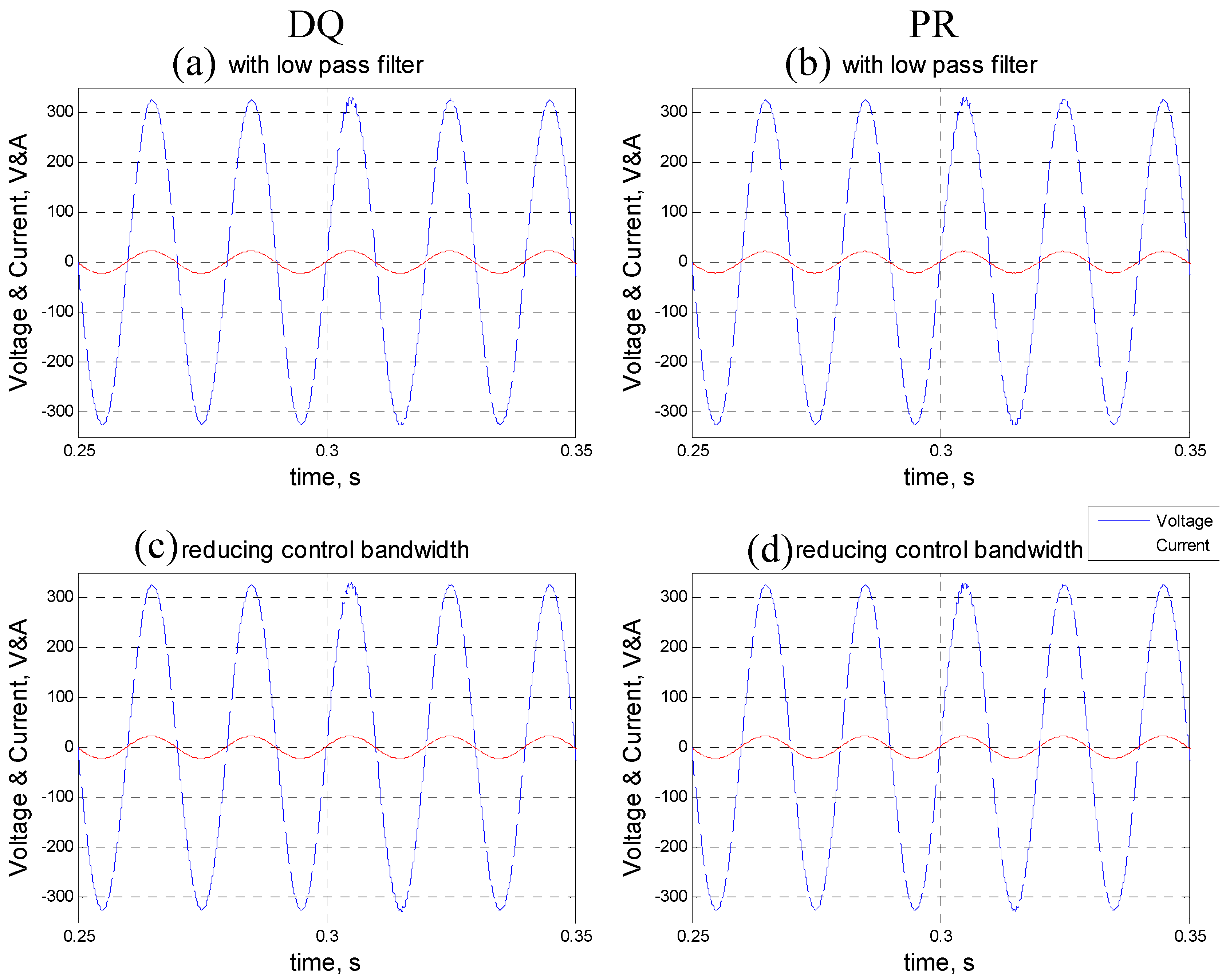
5.2. Improvement Methods
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Disclaimer
References
- Biresselioglu, M.E.; Demirbag Kaplan, M.; Yilmaz, B.K. Electric mobility in Europe: A comprehensive review of motivators and barriers in decision making processes. Transp. Res. Part A Policy Pract. 2018, 109, 1–13. [Google Scholar] [CrossRef]
- Fathabadi, H. Novel grid-connected solar/wind powered electric vehicle charging station with vehicle-to-grid technology. Energy 2017, 132, 1–11. [Google Scholar] [CrossRef]
- Nunes, P.; Figueiredo, R.; Brito, M.C. The use of parking lots to solar-charge electric vehicles. Renew. Sustain. Energy Rev. 2016, 66, 679–693. [Google Scholar] [CrossRef]
- Redpath, D.A.G.; McIlveen-Wright, D.; Kattakayam, T.; Hewitt, N.J.; Karlowski, J.; Bardi, U. Battery powered electric vehicles charged via solar photovoltaic arrays developed for light agricultural duties in remote hilly areas in the Southern Mediterranean region. J. Clean. Prod. 2011, 19, 2034–2048. [Google Scholar] [CrossRef]
- Ji, S.; Cherry, C.R.; Han, L.D.; Jordan, D.A. Electric bike sharing: Simulation of user demand and system availability. J. Clean. Prod. 2014, 85, 250–257. [Google Scholar] [CrossRef]
- Apostolou, G.; Reinders, A.; Geurs, K. An Overview of Existing Experiences with Solar-Powered E-Bikes. Energies 2018, 11, 2129. [Google Scholar] [CrossRef]
- Apostolou, G.; Guers, K.; Reinders, A. Technical performance and user aspects of solar powered e-bikes—Results of a field study in The Netherlands. Presented at the DIT–ESEIA Conference on Smart Energy Systems in Cities and Regions, Dublin, Ireland, 10–12 April 2018. [Google Scholar]
- Zhao, M.; Yuan, X.; Hu, J.; Yan, Y. Voltage Dynamics of Current Control Time-Scale in a VSC-Connected Weak Grid. IEEE Trans. Power Syst. 2016, 31, 2925–2937. [Google Scholar] [CrossRef]
- Krein, P.T.; Bentsman, J.; Bass, R.M.; Lesieutre, B.L. On the use of averaging for the analysis of power electronic systems. IEEE Trans. Power Electron. 1990, 5, 182–190. [Google Scholar] [CrossRef]
- Sun, J. AC power electronic systems: Stability and power quality. In Proceedings of the 2008 11th Workshop on Control and Modeling for Power Electronics, Zurich, Switzerland, 17–20 August 2008; pp. 1–10. [Google Scholar]
- Kroutikova, N.; Hernandez-Aramburo, C.A.; Green, T.C. State-space model of grid-connected inverters under current control mode. IET Electr. Power Appl. 2007, 1, 329. [Google Scholar] [CrossRef]
- Bengtsson, T.; Bickel, P.; Li, B. Curse-of-dimensionality revisited: Collapse of the particle filter in very large scale systems. In Institute of Mathematical Statistics Collections; Institute of Mathematical Statistics: Beachwood, OH, USA, 2008; pp. 316–334. ISBN 978-0-940600-74-4. [Google Scholar]
- Sun, J. Impedance-Based Stability Criterion for Grid-Connected Inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Willems, J.C. Dissipative Dynamical Systems. Eur. J. Control 2007, 13, 134–151. [Google Scholar] [CrossRef]
- Hu, H.; Tao, H.; Blaabjerg, F.; Wang, X.; He, Z.; Gao, S. Train–Network Interactions and Stability Evaluation in High-Speed Railways–Part I: Phenomena and Modeling. IEEE Trans. Power Electron. 2018, 33, 4627–4642. [Google Scholar] [CrossRef]
- Pan, P.; Hu, H.; Yang, X.; Blaabjerg, F.; Wang, X.; He, Z. Impedance Measurement of Traction Network and Electric Train for Stability Analysis in High-Speed Railways. IEEE Trans. Power Electron. 2018, 33, 10086–10100. [Google Scholar] [CrossRef]
- Reinders, A.; de Respinis, M.; van Loon, J.; Stekelenburg, A.; Bliek, F.; Schram, W.; van Sark, W.; Esteri, T.; Uebermasser, S.; Lehfuss, F.; et al. Co-evolution of smart energy products and services: A novel approach towards smart grids. In Proceedings of the 2016 Asian Conference on Energy, Power and Transportation Electrification, Singapore, 25–27 October 2016; pp. 1–6. [Google Scholar]
- Canadian Solar. All-Black CS6K-270-275-280 M. Available online: https://www.canadiansolar.com/downloads/datasheets/v5.531/canadian_solar-datasheet-allblack-CS6K-M-v5.531en.pdf (accessed on 30 November 2018).
- olax Power. X1 Series User Manual. Available online: https://www.solaxpower.com/wp-content/uploads/2017/01/X1-Mini-Install-Manual.pdf (accessed on 30 November 2018).
- Ciobotaru, M.; Agelidis, V.; Teodorescu, R. Line impedance estimation using model based identification technique. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011; pp. 1–9. [Google Scholar]
- Guo, X.; Wu, W.; Chen, Z. Multiple-Complex Coefficient-Filter-Based Phase-Locked Loop and Synchronization Technique for Three-Phase Grid-Interfaced Converters in Distributed Utility Networks. IEEE Trans. Ind. Electron. 2011, 58, 1194–1204. [Google Scholar] [CrossRef]
- Pendharkar, I. A generalized Input Admittance Criterion for resonance stability in electrical railway networks. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 690–695. [Google Scholar]
- Ban, M.; Shen, K.; Wang, J.; Ji, Y. A novel circulating current suppressor for modular multilevel converters based on quasi-proportional-resonant control. China Acad. J. Electron. Publ. House 2014, 85–89. [Google Scholar] [CrossRef]
- Lu, M.; Wang, X.; Loh, P.C.; Blaabjerg, F.; Dragicevic, T. Graphical Evaluation of Time-Delay Compensation Techniques for Digitally Controlled Converters. IEEE Trans. Power Electron. 2018, 33, 2601–2614. [Google Scholar] [CrossRef]
- Mattavelli, P.; Polo, F.; Dal Lago, F.; Saggini, S. Analysis of Control-Delay Reduction for the Improvement of UPS Voltage-Loop Bandwidth. IEEE Trans. Ind. Electron. 2008, 55, 2903–2911. [Google Scholar] [CrossRef]
- Wu, H.; Ruan, X.; Yang, D. Research on the stability caused by phase-locked loop for LCL-type grid-connected inverter in weak grid condition. Zhongguo Dianji Gongcheng Xuebao/Proc. Chin. Soc. Electr. Eng. 2014, 34. [Google Scholar] [CrossRef]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Analysis of D-Q Small-Signal Impedance of Grid-Tied Inverters. IEEE Trans. Power Electron. 2016, 31, 675–687. [Google Scholar] [CrossRef]



| Parameter | DQ | PR |
|---|---|---|
| Rated power | 3.3 kW | |
| Rated voltage | 230 V | |
| Filter inductor | 3.5 mH | |
| PLL bandwidth | 25 Hz | |
| Sampling frequency | 10 kHz | |
| KP-C | 2.46 | / |
| KI-C | 548.81 | / |
| KP-PR | / | 34.99 |
| KR-PR | / | 400 |
| ωc | / | π |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Gercek, C.; Renner, H.; Reinders, A.; Fickert, L. Resonance Instability of Photovoltaic E-Bike Charging Stations: Control Parameters Analysis, Modeling and Experiment. Appl. Sci. 2019, 9, 252. https://doi.org/10.3390/app9020252
Zhang Z, Gercek C, Renner H, Reinders A, Fickert L. Resonance Instability of Photovoltaic E-Bike Charging Stations: Control Parameters Analysis, Modeling and Experiment. Applied Sciences. 2019; 9(2):252. https://doi.org/10.3390/app9020252
Chicago/Turabian StyleZhang, Ziqian, Cihan Gercek, Herwig Renner, Angèle Reinders, and Lothar Fickert. 2019. "Resonance Instability of Photovoltaic E-Bike Charging Stations: Control Parameters Analysis, Modeling and Experiment" Applied Sciences 9, no. 2: 252. https://doi.org/10.3390/app9020252
APA StyleZhang, Z., Gercek, C., Renner, H., Reinders, A., & Fickert, L. (2019). Resonance Instability of Photovoltaic E-Bike Charging Stations: Control Parameters Analysis, Modeling and Experiment. Applied Sciences, 9(2), 252. https://doi.org/10.3390/app9020252





