EUV-Induced Plasma: A Peculiar Phenomenon of a Modern Lithographic Technology
Abstract
Featured Application
Abstract
1. Introduction
EUV-Induced Plasma and Its Relation to Photolithography
2. EUV-Induced Plasma
2.1. Observation of a Peculiar Phenomenon: EUV-Induced Plasma
2.2. Key Parameters of EUV-Induced Plasma
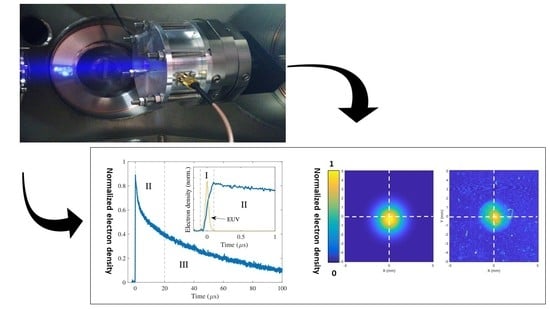
2.2.1. Electron Density
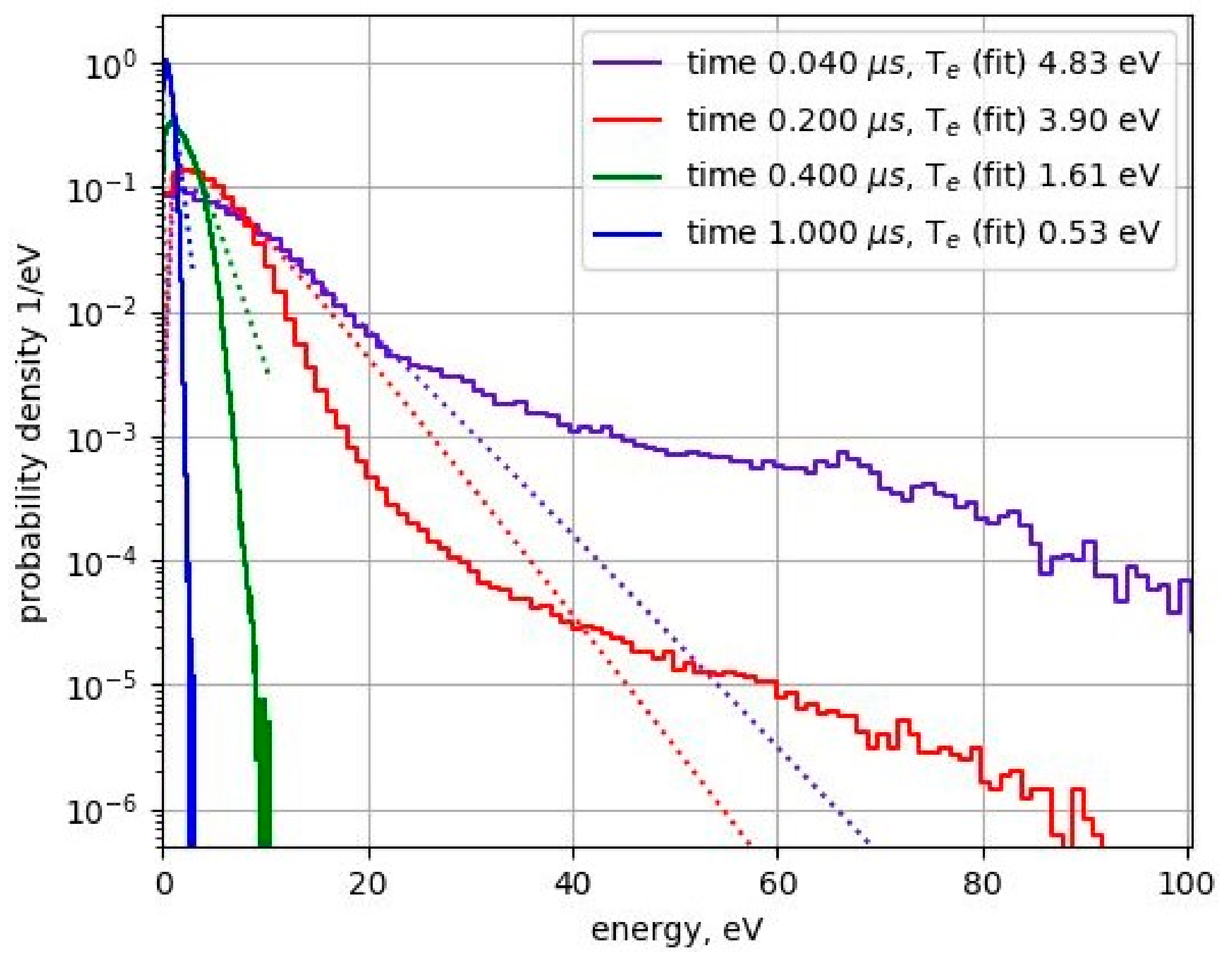
2.2.2. Electron Temperature
2.3. Recent Numerical Work on EUV-Induced Bulk Plasmas
2.4. Recent Experimental Work on EUV-Induced Bulk Plasmas
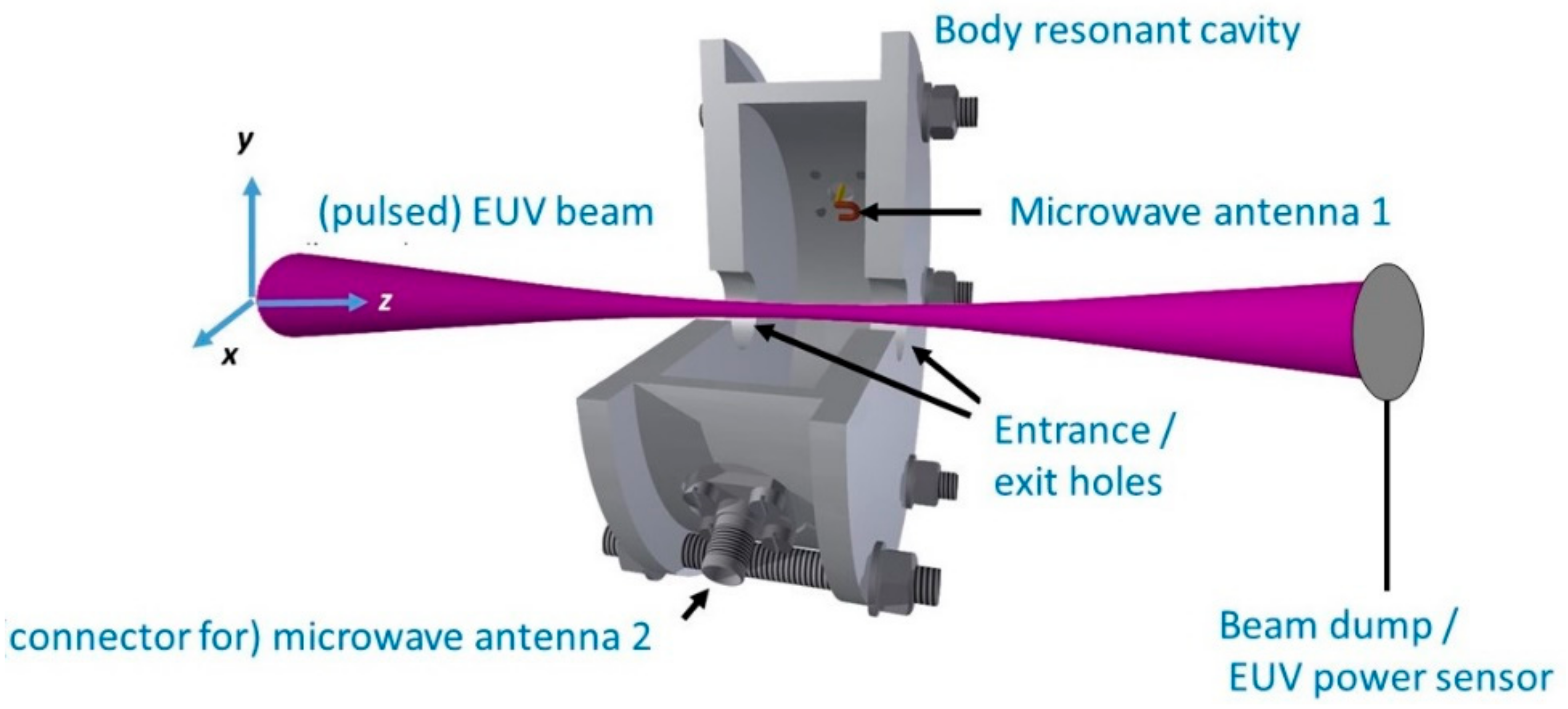
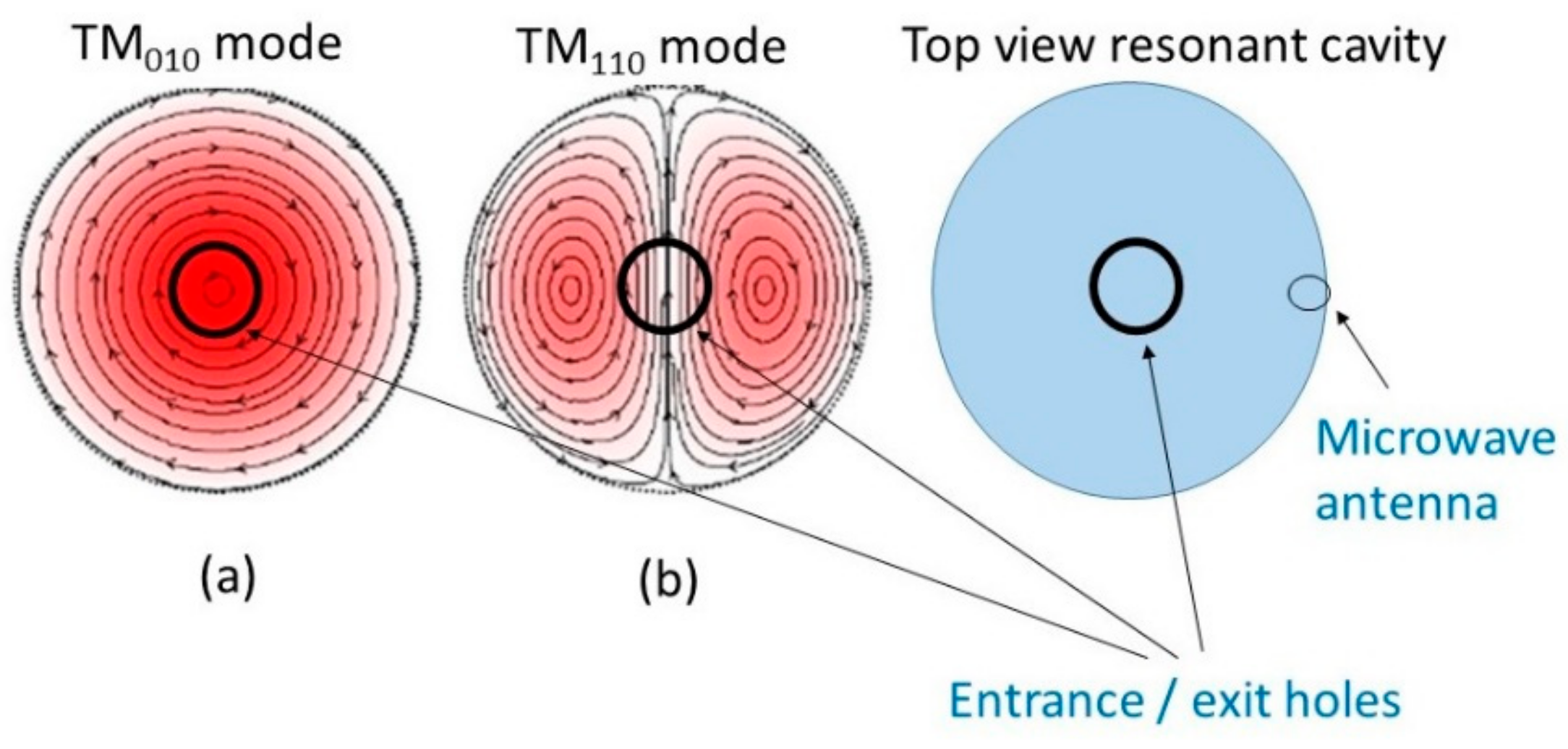
Microwave Cavity Resonance Spectroscopy (MCRS)
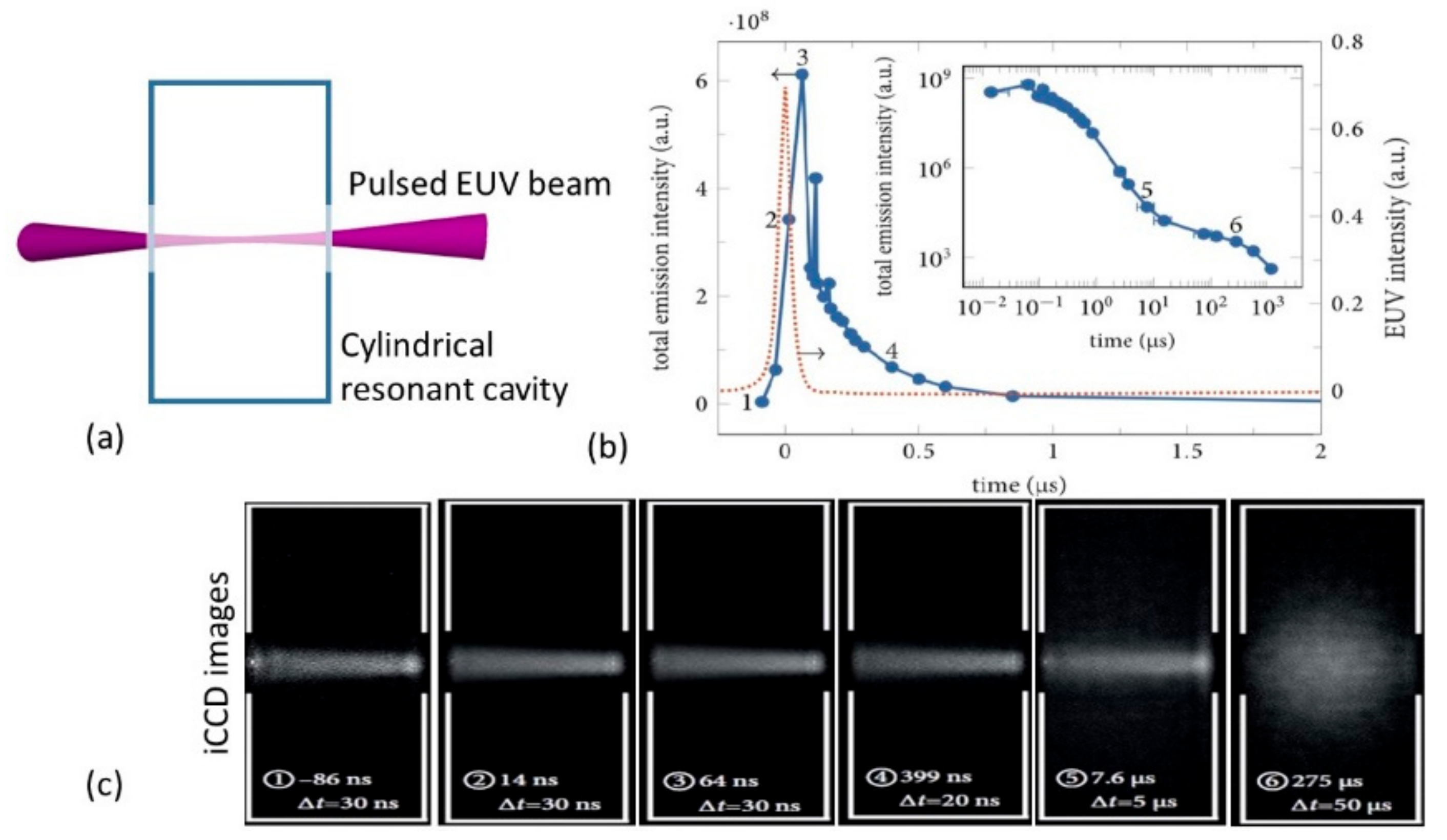
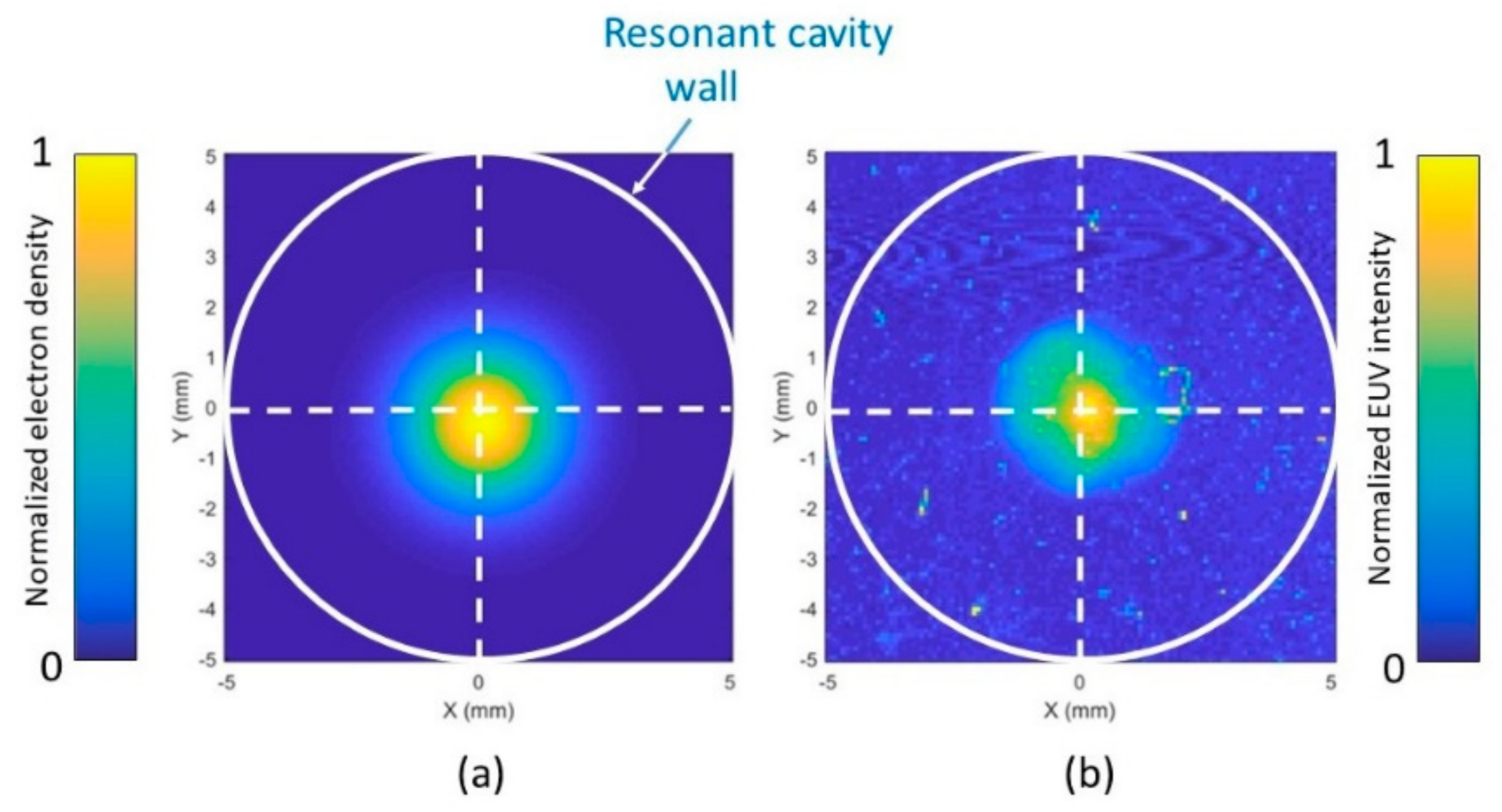
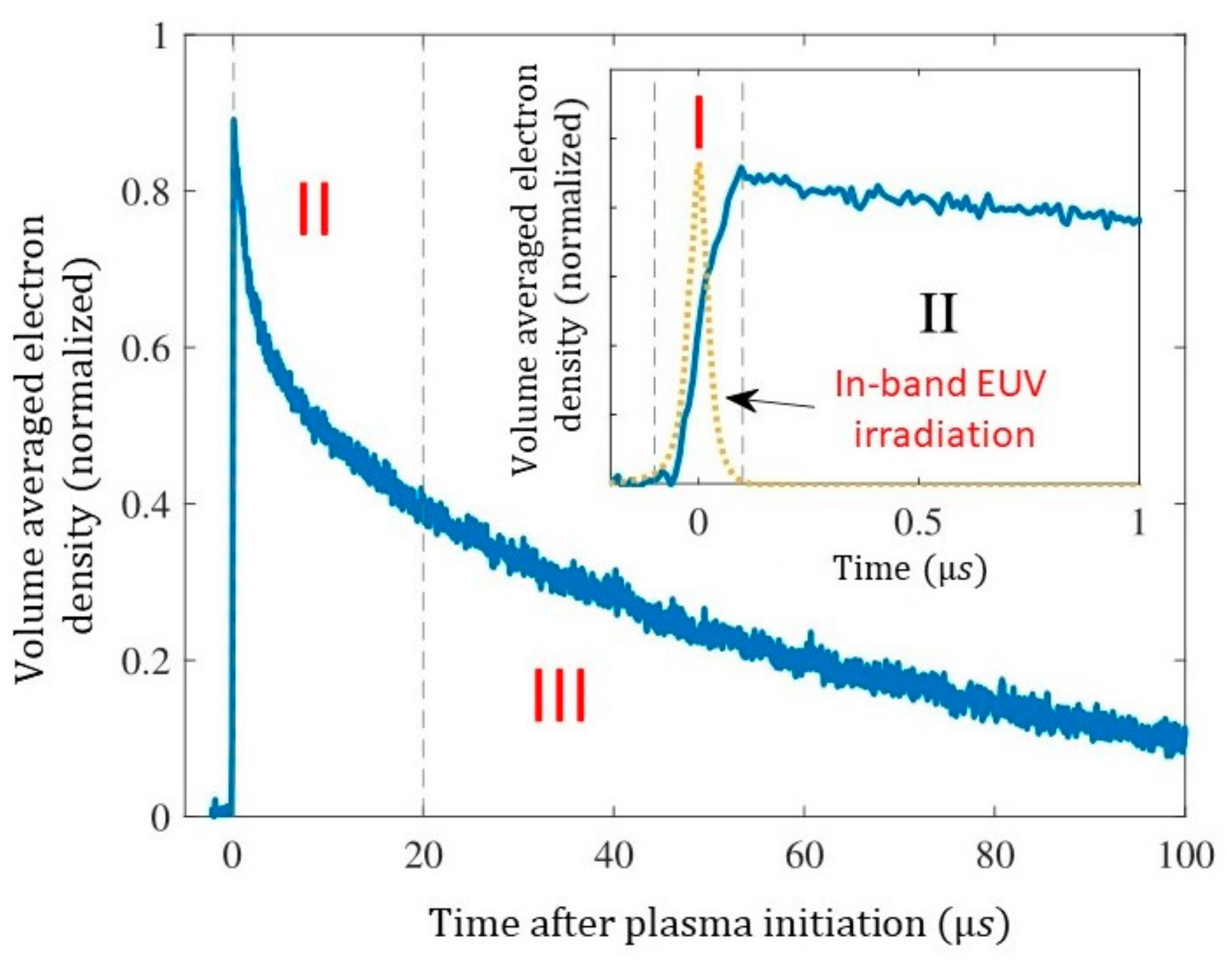
2.5. Dynamics of EUV-Induced Plasmas
2.5.1. Phase I: Plasma Creation by Photoionization and Electron Impact Ionization
Photoionization
Electron Impact Ionization
2.5.2. Phase II: Strong Decrease of
2.5.3. Phase III: Exponential Decay of ne
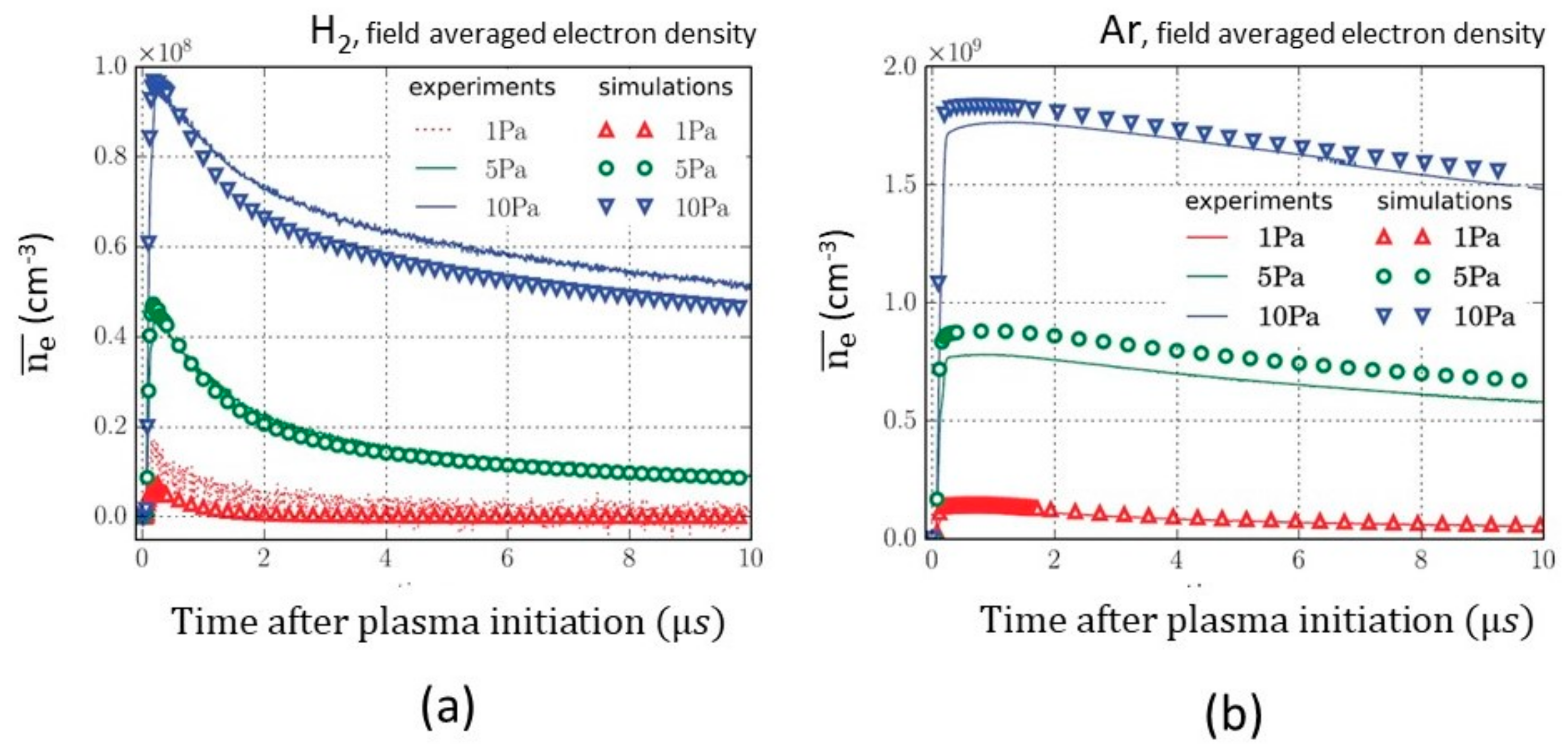
2.6. Scaling Laws
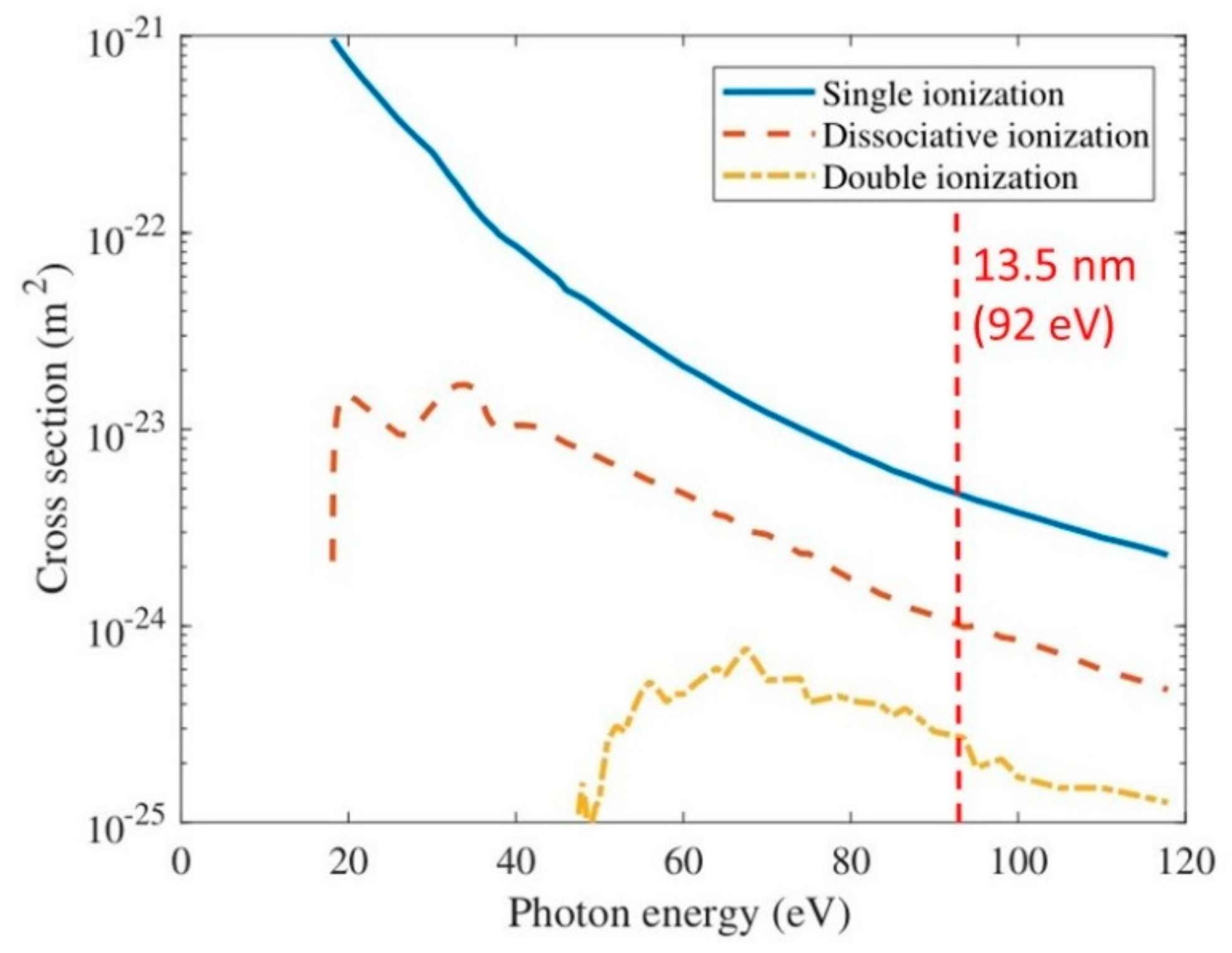
- Influence of EUV spectrum
- Gas pressure scaling
- Pulse energy scaling
- Source repetition rate scaling
- Different gases
3. Bulk Materials Facing EUV Photon Induced Plasma
3.1. Observation of Cleaning and Degradation of Exposed Surfaces
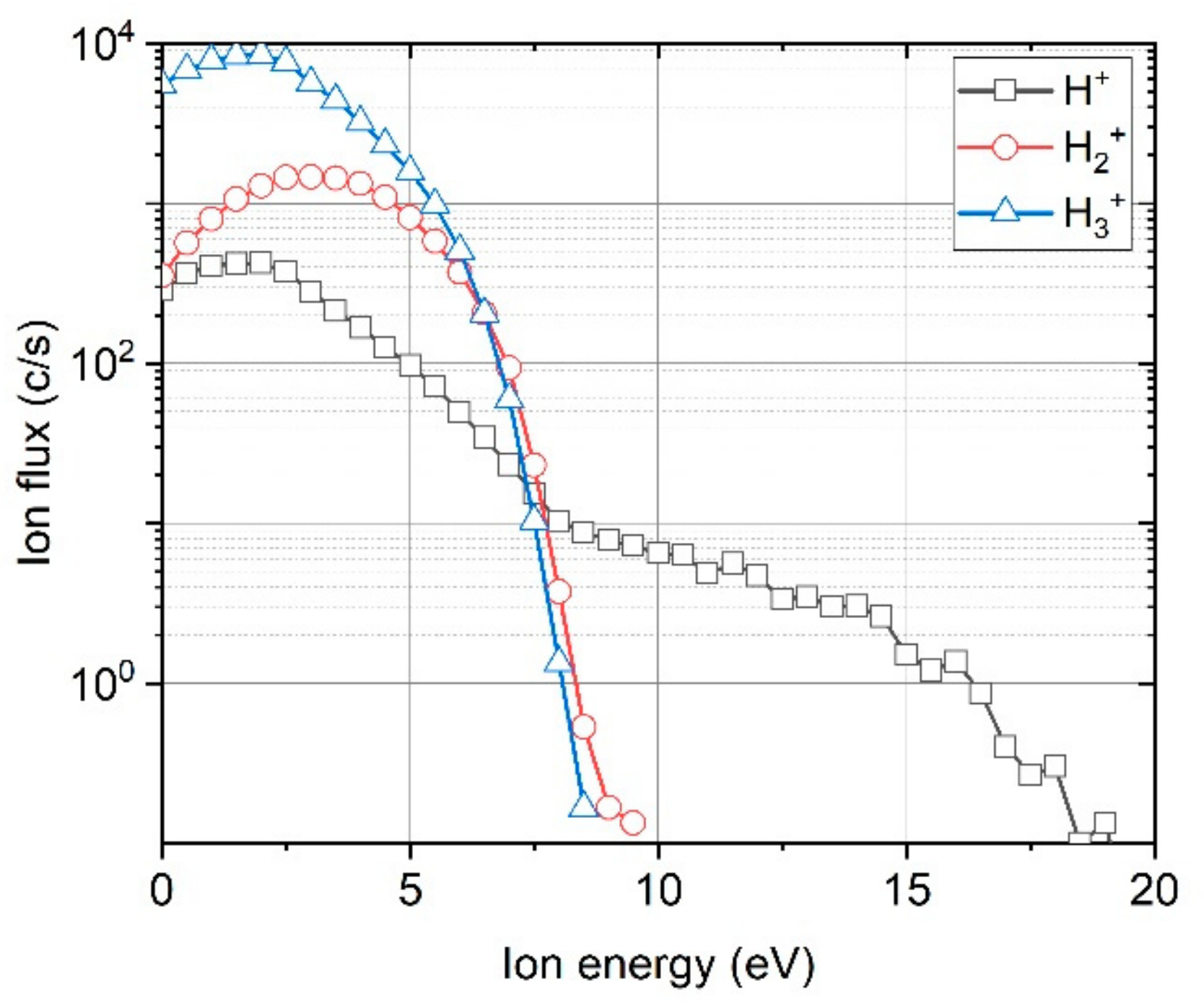
3.2. Ionic Particle Fluxes
3.3. Identification of Reaction Mechanisms
3.3.1. Carbon Removal
3.3.2. Multilayer Delamination
4. Discussion, Conclusions, and Outlook
- Radical production
- Gas admixtures (e.g., N2)
- Interaction with nano- to micrometer sized particles
Funding
Conflicts of Interest
References
- Born, M.; Wolf, E. Principles of Optics; Pegamon Press: Oxford, UK, 1980. [Google Scholar]
- Lin, B.J. The future of subhalf-micrometer optical lithography. Microelectron. Eng. 1987, 6, 31–51. [Google Scholar] [CrossRef]
- EUV Lithography, 2nd ed.; Bakshi, V., Ed.; SPIE Press: Bellingham, WA, USA, 2018. [Google Scholar]
- Benschop, J.; Banine, V.; Lok, S.; Loopstra, E. Extreme ultraviolet lithography: Status and prospects. J. Vac. Sci. Technol. B 2008, 26, 2204–2207. [Google Scholar] [CrossRef]
- Bergmann, K.; Schriever, G.; Rosier, O.; Müller, M.; Neff, W.; Lebert, R. Highly repetitive, extreme-ultraviolet radiation source based on a gas-discharge plasma. Appl. Opt. 1999, 38, 5413–5417. [Google Scholar] [CrossRef] [PubMed]
- Fomenkov, I.V.; Brandt, D.C.; Farrar, N.R.; La Fontaine, B.; Böwering, N.R.; Brown, D.J.; Ershov, A.I.; Myers, D.W. Laser Produced Plasma EUV Light Source for EUVL Patterning at 20nm Node and Beyond. Extreme Ultrav. (EUV) Lithogr. IV 2013, 8679, 86792I. [Google Scholar]
- Brandt, D.C.; Fomenkov, I.V.; Farrar, N.R.; La Fontaine, B.; Myers, D.W.; Brown, D.J.; Ershov, A.I.; Böwering, N.R.; Riggs, D.J.; Rafac, R.J.; et al. LPP EUV source readiness for NXE 3300B. Extreme Ultrav. (EUV) Lithogr. V 2014, 9048, 90480C. [Google Scholar]
- Ueno, Y.; Hori, T.; Kawasuji, Y.; Shiraishi, Y.; Yanagida, T.; Miyao, K.; Hayashi, H.; Ishii, T.; Watanabe, Y.; Okamoto, T.; et al. Key Components Development Progress Updates of the 250W High Power LPP-EUV Light Source. Extreme Ultrav. (EUV) Lithogr. IX 2018, 10583, 1058328. [Google Scholar]
- Teramoto, Y.; Santos, B.; Mertens, G.; Kops, R.; Kops, M.; von Wezyk, A.; Bergmann, K.; Yabuta, H.; Nagano, A.; Ashizawa, N.; et al. High-radiance LDP source for mask inspection and beam line applications (Conference Presentation). Extreme Ultrav. (EUV) Lithogr. VIII 2017, 10143, 101431L. [Google Scholar]
- Van der Velden, M.H.L.; Brok, W.J.M.; Van der Mullen, J.J.A.M.; Banine, V. Kinetic simulation of an extreme ultraviolet radiation driven plasma near a multilayer mirror. J. Appl. Phys. 2006, 100, 73303. [Google Scholar] [CrossRef]
- Van Der Horst, R.M.; Beckers, J.; Osorio, E.A.; Banine, V.Y. Exploring the electron density in plasmas induced by extreme ultraviolet radiation in argon. J. Phys. D Appl. Phys. 2015, 48, 285203. [Google Scholar] [CrossRef][Green Version]
- Astakhov, D. Numerical Study of Extreme-Ultra-Violet Generated Plasmas in Hydrogen; Universiteit Twente: Enschede, The Netherlands, 2016. [Google Scholar]
- Yoon, J.S.; Song, M.Y.; Han, J.M.; Hwang, S.H.; Chang, W.S.; Lee, B.; Itikawa, Y. Cross Sections for Electron Collisions with Hydrogen Molecules. J. Phys. Chem. Ref. Data 2008, 37, 913–931. [Google Scholar] [CrossRef]
- Ehrhardt, H.; Langhans, L.; Linder, F.; Taylor, H.S. Resonance scattering of slow electrons from H 2 and CO angular distributions. Phys. Rev. 1968, 173, 222–230. [Google Scholar] [CrossRef]
- Bakshi, V. EUV Sources for Lithography; Bakshi, V., Ed.; Spie Press: Bellingham, WA, USA, 2006. [Google Scholar]
- Van der Horst, R.M. Electron Dynamics in EUV-Induced Plasmas; Eindhoven University of Technology: Eindhoven, The Netherlands, 2015. [Google Scholar]
- Van Der Horst, R.M.; Beckers, J.; Osorio, E.A.; Astakhov, D.I.; Goedheer, W.J.; Lee, C.J.; Ivanov, V.V.; Krivtsum, V.M.; Koshelev, K.N.; Lopaev, D.V.; et al. Exploring the electron density in plasma induced by EUV radiation: I. Experimental study in hydrogen. J. Phys. D Appl. Phys. 2016, 19, 145203. [Google Scholar] [CrossRef]
- Beckers, J.; van Der Horst, R.M.; Osorio, E.A.; Kroesen, G.M.W.; Banine, V.Y. Thermalization of electrons in decaying extreme ultraviolet photons induced low pressure argon plasma. Plasma Source Sci. Technol. 2016, 15, 35010. [Google Scholar] [CrossRef]
- Birdsall, A.; Langdon, C. Plasma Physics via Computer Simulation; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
- Wieggers, R.C.; Goedheer, W.J.; Louis, E.; Bijkerk, F. Plasma-induced damage of multilayer coatings in EUVL. Proc. SPIE 6586 Damage VUV EUV X-ray Opt. 2007, 6586, 65860L. [Google Scholar]
- Astakhov, D.I.; Goedheer, W.J.; Lee, C.J.; Ivanov, V.V.; Krivtsun, V.M.; Koshelev, K.N.; Lopaev, D.V.; Van Der Horst, R.M.; Beckers, J.; Osorio, E.A.; et al. Exploring the electron density in plasma induced by EUV radiation: II. Numerical studies in argon and hydrogen. J. Phys. D Appl. Phys. 2016, 49, 295204. [Google Scholar] [CrossRef]
- Astakhov, D.I.; Goedheer, W.J.; Lee, C.J.; Ivanov, V.V.; Krivtsun, V.M.; Zotovich, A.I.; Zyryanov, S.M.; Lopaev, D.V.; Bijkerk, F. Plasma probe characteristics in low density hydrogen pulsed plasmas. Plasma Source Sci. Technol. 2015, 24, 55018. [Google Scholar] [CrossRef]
- Mokrov, M.S.; Raizer, Y.P. Monte Carlo method for finding the ionization and secondary emission coefficients and I–V characteristic of a Townsend discharge in hydrogen. Tech. Phys. 2008, 53, 436–444. [Google Scholar] [CrossRef]
- Van de Ven, T.H.M. Ion Fluxes Towards Surfaces Exposed to EUV-Induced Plasmas; Eindhoven University of Technology: Eindhoven, The Netherlands, 2018. [Google Scholar]
- Hobbs, G.D.; Wesson, J.A. Heat flow through a Langmuir sheath in the presence of electron emission. Plasma Phys. 1967, 9, 85. [Google Scholar] [CrossRef]
- Van der Horst, R.M.; Beckers, J.; Osorio, E.A.; van de Ven, T.H.M.; Banine, V.Y. Radiating plasma species density distribution in EUV-induced plasma in argon: A spatiotemporal experimental study. Plasma Source Sci. Technol. 2015, 24, 065016. [Google Scholar] [CrossRef]
- Bartnik, A.; Skrzeczanowski, W.; Wachulak, P.; Saber, I.; Fiedorowicz, H.; Fok, T. Low-temperature photoionized plasmas induced in Xe gas using an EUV source driven by nanosecond laser pulses. Laser Part. Beams 2017, 35, 42–47. [Google Scholar] [CrossRef]
- Bartnik, A.; Fiedorowicz, H.; Wachulak, P.; Fok, T. Time-resolved measurements of extreme ultraviolet (EUV) emission, from EUV-induced He, Ne, and Ar plasmas. Laser Part. Beams 2019, 37, 49–54. [Google Scholar] [CrossRef]
- Bartnik, A.; Wachulak, P.; Fiedorowicz, H.; Fok, T.; Jarocki, R.; Szczurek, M. Extreme ultraviolet-induced photoionized plasmas. Phys. Scr. 2014, T161, 14061. [Google Scholar] [CrossRef]
- Bartnik, A.; Wachulak, P.; Fok, T.; Fiedorowicz, H.; Skrzeczanowski, W.; Pisarczyk, T.; Chodukowski, T.; Kalinowska, Z.; Dudzak, R.; Dostal, J.; et al. Photoionized argon plasmas induced with intense soft x-ray and extreme ultraviolet pulses. Plasma Phys. Control. Fusion 2015, 58, 14009. [Google Scholar] [CrossRef]
- Saber, I.; Bartnik, A.; Wachulak, P.; Skrzeczanowski, W.; Jarocki, R.; Fiedorowicz, H. Temporal variations of electron density and temperature in Kr/Ne/H2 photoionized plasma induced by nanosecond pulses from extreme ultraviolet source. Phys. Plasmas 2017, 24, 063501. [Google Scholar] [CrossRef]
- Carbone, E.; Nijdam, S. Thomson scattering on non-equilibrium low density plasmas: Principles, practice and challenges. Plasma Phys. Control. Fusion 2015, 57, 014026. [Google Scholar] [CrossRef]
- Van der Velden, M. Radiation Generated Plasmas: A Challenge in Modern Lithography; University of Technology Eindhoven: Eindhoven, The Netherlands, 2008. [Google Scholar]
- Van der Horst, R.M.; Beckers, J.; Nijdam, S.; Kroesen, G.M.W. Exploring the temporally resolved electron density evolution in extreme ultra-violet induced plasmas. J. Phys. D Appl. Phys. 2014, 47, 302001. [Google Scholar] [CrossRef][Green Version]
- Van der Horst, R.M.; Osorio, E.A.; Banine, V.Y.; Beckers, J. The influence of the EUV spectrum on plasma induced by EUV radiation in argon and hydrogen gas. Plasma Source Sci. Technol. 2016, 25, 015012. [Google Scholar] [CrossRef]
- De Wetering, F. Dust Particle Formation in Silane Plasmas. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2005. [Google Scholar]
- Brown, S.C.; Rose, D.J. Methods of measuring the properties of ionized gases at high frequencies. I. Measurements of Q. J. Appl. Phys. 1952, 23, 711–718. [Google Scholar] [CrossRef]
- Rose, D.J.; Brown, S.C. Methods of measuring the properties of ionized gases at high frequencies. II. Measurement of electric field. J. Appl. Phys. 1952, 23, 719–722. [Google Scholar] [CrossRef]
- Rose, D.J.; Brown, S.C. Methods of measuring the properties of ionized gases at high frequencies. III. Measurement of discharge admittance and electron density. J. Appl. Phys. 1952, 23, 1028–1032. [Google Scholar] [CrossRef]
- Haverlag, M.; Kroesen, G.M.W.; Bisschops, T.H.J.; DeHoog, F.J. Measurement of electron-densities by a microwave cavity method 13.56-MHz RF plasmas of AR, CF4, C2F6, and CHF3. Plasma Chem. Plasma Process. 1991, 11, 357–370. [Google Scholar] [CrossRef]
- Stoffels, E.; Stoffels, W.W.; Vender, D.; Kando, M.; Kroesen, G.M.W.; DeHoog, F.J. Negative ions in a radiofrequency oxygen plasmas. Phys. Rev. E 1995, 51, 2425–2435. [Google Scholar] [CrossRef]
- Stoffels, E.; Stoffels, W.W. Electrons, Ions and Dust in a Radio-Frequency Discharge. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 1994. [Google Scholar]
- Vender, D.; Stoffels, W.W.; Stoffels, E.; Kroesen, G.M.W.; DeHoog, F.J. Charged-species profiles in electronegative radiofrequency plasmas. Phys. Rev. E 1995, 51, 2436–2444. [Google Scholar] [CrossRef]
- Stoffels, W.W.; Sorokin, M.; Remy, J. Charge and charging of nanoparticles in a SiH4 rf-plasma. Faraday Discuss. 2008, 137, 115–126. [Google Scholar] [CrossRef] [PubMed]
- Van de Wetering, F.M.J.H.; Beckers, J.; Kroesen, G.M.W. Anion dynamics in the first 10 milliseconds of an argon-acetylene radio-frequency plasma. J. Phys. D Appl. Phys. 2012, 45, 485205. [Google Scholar] [CrossRef]
- Van de Wetering, F.M.J.H.; Brooimans, R.J.C.; Nijdam, S.; Beckers, J.; Kroesen, G.M.W. Fast and interrupted expansion in cyclic void growth in dusty plasma. J. Phys. D Appl. Phys. 2015, 48, 035204. [Google Scholar] [CrossRef][Green Version]
- Beckers, J.; Stoffels, W.W.; Kroesen, G.M.W. Temperature dependence of nucleation and growth of nanoparticles in low pressure Ar/CH4 RF discharges. J. Phys. D Appl. Phys. 2009, 42, 155206. [Google Scholar] [CrossRef]
- Beckers, J. Dust Particle(s) (as) Diagnostics in Plasmas. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2011. [Google Scholar]
- Van der Schans, M.; Platier, B.; Koelman, P.; van de Wetering, F.; van Dijk, J.; Beckers, J.; Nijdam, S.; IJzerman, W. Decay of the electron density and the electron collision frequency between successive discharges of a pulsed plasma jet in N2. Plasma Source Sci. Technol. 2019, 28, 35020. [Google Scholar] [CrossRef]
- Van der Horst, R.M.; Beckers, J.; Osorio, E.A.; Banine, V.Y. Dynamics of the spatial electron density distribution of EUV-induced plasmas. J. Phys. D Appl. Phys. 2015, 48, 432001. [Google Scholar] [CrossRef]
- Beckers, J.; Van De Wetering, F.M.J.H.; Platier, B.; Van Ninhuijs, M.A.W.; Brussaard, G.J.H.; Banine, V.Y.; Luiten, O.J. Mapping electron dynamics in highly transient {EUV} photon-induced plasmas: A novel diagnostic approach using multi-mode microwave cavity resonance spectroscopy. J. Phys. D Appl. Phys. 2018, 52, 34004. [Google Scholar] [CrossRef]
- Banine, V.Y. Radiation sensor apparatus. US-20180058928-A1 1 March 2018. [Google Scholar]
- Chung, Y.M.; Lee, E.M.; Masuoka, T.; Samson, J.A.R. Dissociative Photoionization Of H2 From 18 To 124-Ev. J. Chem. Phys. 1993, 99, 885–889. [Google Scholar] [CrossRef]
- Kossmann, H.; Schwarzkopf, O.; Kammerling, B.; Braun, W.; Schmidt, V. Photoionisation cross-section of h-2. J. Phys. B Atomic Mol. Opt. Phys. 1989, 22, L411–L414. [Google Scholar] [CrossRef]
- Dujardin, G.; Besnard, M.J.; Hellner, L.; Malinovitch, Y. Double photoionization of H2: An experimental test of electronic-correlation models in molecules. Phys. Rev. A 1987, 35, 5012–5019. [Google Scholar] [CrossRef]
- Berkowiz, J. Atomic and Molecular Photoabsorption: Absolute Partial Cross Sections. Elsevier Science Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- McCulloh, K.E.; Rosenstock, H.M. Experimental Test of the Franck—Condon Principle: Double Ionization of Molecular Hydrogen. J. Chem. Phys. 1968, 48, 2084–2089. [Google Scholar] [CrossRef]
- Tabata, T.; Shirai, T. Analytic Cross Sections For Collisions Of H+, H2+, H3+, H, H2, And H− With Hydrogen Molecules. At. Data Nucl. Data Tables 2000, 76, 1–25. [Google Scholar] [CrossRef]
- Van De Ven, T.H.M.; Reefman, P.; De Meijere, C.A.; Van Der Horst, R.M.; Van Kampen, M.; Banine, V.Y.; Beckers, J. Ion energy distributions in highly transient EUV induced plasma in hydrogen. J. Appl. Phys. 2018, 123, 063301. [Google Scholar] [CrossRef]
- Lieberman, M.A.; Lichtenberg, A.J. Principles of Plasma Discharges and Materials Processing, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Van der Velden, M.; Brok, W.; van der Mullen, J.; Goedheer, W.; Banine, V. Particle-in-cell Monte Carlo simulations of an extreme ultraviolet radiation driven plasma. Phys. Rev. E 2006, 73, 36406. [Google Scholar] [CrossRef]
- Samson, J.A.; Masuoka, T.; Pareek, P.N.; Angel, G.C. Total and dissociative photoionization cross sections of N2 from threshold to 107 eV. J. Chem. Phys. 1987, 86, 6128. [Google Scholar] [CrossRef]
- Beckers, J.; de Ven, T.H.M.; de Meijere, C.A.; der Horst, R.M.; van Kampen, M.; Banine, V.Y. Energy distribution functions for ions from pulsed EUV-induced plasmas in low pressure N2-diluted H2 gas. Appl. Phys. Lett. 2019, 114, 133502. [Google Scholar] [CrossRef]
- Dolgov, A.; Lopaev, D.; Rachimova, T.; Kovalev, A.; Vasil’Eva, A.; Lee, C.J.; Krivtsun, V.M.; Yakushev, O.; Bijkerk, F. Comparison of H2 and He carbon cleaning mechanisms in extreme ultraviolet induced and surface wave discharge plasmas. J. Phys. D Appl. Phys. 2014, 47, 65205. [Google Scholar] [CrossRef]
- Dolgov, A.; Lopaev, D.; Lee, C.J.; Zoethout, E.; Medvedev, V.; Yakushev, O.; Bijkerk, F. Characterization of carbon contamination under ion and hot atom bombardment in a tin-plasma extreme ultraviolet light source. Appl. Surf. Sci. 2015, 353, 708–713. [Google Scholar] [CrossRef]
- Boller, K.; Haelbich, R.P.; Hogrefe, H.; Jark, W.; Kunz, C. Investigation of carbon contamination of mirror surfaces exposed to synchrotron radiation. Nucl. Instrum. Methods Phys. Res. 1983, 208, 273–279. [Google Scholar] [CrossRef]
- Koster, N.; Mertens, B.; Jansen, R.; Van De Runstraat, A.; Stietz, F.; Wedowski, M.; Meiling, H.; Klein, R.; Gottwald, A.; Scholze, F.; et al. Molecular contamination mitigation in EUVL by environmental control. Microelectron. Eng. 2002, 61, 65–76. [Google Scholar] [CrossRef]
- Malinowski, M.E.; Steinhaus, C.; Clift, W.M.; Klebanoff, L.E.; Mrowka, S. Controlling contamination in Mo/Si multilayer mirrors by Si surface capping modifications. Proc. SPIE 2002, 4688, 442–453. [Google Scholar]
- Meiling, H.; Meijer, H.; Banine, V.; Moors, R.; Groeneveld, R.; Voorma, H.J.; Mickan, U.; Wolschrijn, B.; Mertens, B.; van Baars, G.; et al. First performance results of the ASML alpha demo tool. Proc. SPIE 2006, 6151, 615108. [Google Scholar]
- Matsunari, S.; Aoki, T.; Murakami, K.; Gomei, Y.; Terashima, S.; Takase, H.; Tanabe, M.; Watanabe, Y.; Kakutani, Y.; Niibe, M.; et al. Carbon deposition on multi-layer mirrors by extreme ultra violet ray irradiation. Proc. SPIE Int. Soc. Opt. Eng. 2007, 6517, 65172X. [Google Scholar]
- Hollenshead, J.; Klebanoff, L. Modeling radiation-induced carbon contamination of extreme ultraviolet optics. J. Vac. Sci. Technol. B Microelectron. Nanom. Struct. 2006, 24, 64. [Google Scholar] [CrossRef]
- Koster, N.B.; van der Donck, J.C.J.; Stortelder, J.K.; de Jong, A.J.; Molkenboer, F.T. A multistep approach for reticle cleaning. Proc. SPIE 2012, 8322, 83220R. [Google Scholar]
- Chen, J.; Louis, E.; Harmsen, R.; Tsarfati, T.; Wormeester, H.; van Kampen, M.; van Schaik, W.; van de Kruijs, R.; Bijkerk, F. In situ ellipsometry study of atomic hydrogen etching of extreme ultraviolet induced carbon layers. Appl. Surf. Sci. 2011, 258, 7–12. [Google Scholar] [CrossRef]
- Bajt, S.; Alameda, J.B.; Clift, W.M.; Folta, J.A.; Kaufmann, B.; Spiller, E.A. Improved reflectance and stability of Mo-Si multilayers. Opt. Eng. 2002, 41, 1797. [Google Scholar] [CrossRef]
- Yakshinskiy, B.V.; Bartynski, R.A. Carbon film growth on model MLM cap layer: Interaction of selected hydrocarbon vapor with Ru(10(1)over-bar0) surface. Extreme Ultrav. (Euv) Lithogr. 2010, 7636, 76360F. [Google Scholar]
- Oizumi, H.; Izumi, A.; Motai, K.; Nishiyama, I.; Namiki, A. Atomic hydrogen cleaning of surface Ru oxide formed by extreme ultraviolet irradiation of Ru-capped multilayer mirrors in H2O ambience. Jpn. J. Appl. Phys. 2007, 46, L633. [Google Scholar] [CrossRef]
- Bondareva, A.L.; Zmievskaya, G.I. Computer simulation of blistering in multilayer mirrors for EUV lithography. J. Surf. Investig. X-ray, Synchrotron Neutron Tech. 2010, 4, 480–487. [Google Scholar] [CrossRef]
- Enhanced multilayer mirror stability through heterogeneous materials. Available online: https://www.rvo.nl/subsidies-regelingen/projecten/enhanced-multilayer-mirror-stability-through-heterogeneous-materials (accessed on 13 July 2019).
- Wieggers, R.C.; Goedheer, W.J.; Akdim, M.R.; Bijkerk, F.; Zegeling, P.A. A particle-in-cell plus Monte Carlo study of plasma-induced damage of normal incidence collector optics used in extreme ultraviolet lithography. J. Appl. Phys. 2008, 3, 013308. [Google Scholar] [CrossRef]
- Henke, B.L.; Gullikson, E.M.; Davis, J.C. X-Ray Interactions: Photoabsorption, Scattering, Transmission, and Reflection at E = 50-30,000 eV, Z = 1-92. At. Data Nucl. Data Tables 1993, 54, 181–342. [Google Scholar] [CrossRef]
- Abrikosov, A.; Reshetnyak, V.; Astakhov, D.; Dolgov, A.; Yakushev, O.; Lopaev, D.; Krivtsun, V. Numerical simulations based on probe measurements in EUV-induced hydrogen plasma. Plasma Source Sci. Technol. 2017, 26, 45011. [Google Scholar] [CrossRef]
- Abrikosov, A.A.; Yakushev, O.F.; Lopaev, D.V.; Krivtsun, V.M. Dynamics of the ion energy spectrum in EUV-induced hydrogen plasma. Plasma Phys. Rep. 2017, 43, 614–620. [Google Scholar] [CrossRef]
- Jariwala, B.N.; Ciobanu, C.V.; Agarwal, S. Atomic hydrogen interactions with amorphous carbon thin films. J. Appl. Phys. 2009, 106, 073305. [Google Scholar] [CrossRef]
- Hopf, C.; von Keudell, A.; Jacob, W. Chemical sputtering of hydrocarbon films. J. Appl. Phys. 2003, 94, 2373–2380. [Google Scholar] [CrossRef]
- Schlüter, M.; Hopf, C.; Jacob, W. Chemical sputtering of carbon by combined exposure to nitrogen ions and atomic hydrogen. New J. Phys. 2008, 10, 53037. [Google Scholar] [CrossRef]
- Liu, S.; Sun, J.; Dai, S.; Stirner, T.; Wang, D. A general model for chemical erosion of carbon materials due to low-energy H+ impact. J. Appl. Phys. 2010, 108, 073302. [Google Scholar] [CrossRef]
- Nishiyama, Y.; Anazawa, T.; Oizumi, H.; Nishiyama, I.; Suga, O.; Abe, K.; Kagata, S.; Izumi, A. Carbon contamination of EUV mask: Film characterization, impact on lithographic performance, and cleaning. Emerg. Lithogr. Technol. XII PTS 1 2 2008, 6921, 692116. [Google Scholar]
- Meyer, F.W.; Zhang, H.; Lance, M.J.; Krause, H.F. Chemical sputtering and surface damage of graphite by low-energy atomic and molecular hydrogen and deuterium projectiles. Vacuum 2008, 82, 880–887. [Google Scholar] [CrossRef]
- Elg, D.T.; Panici, G.A.; Srivastava, S.N.; Ruzic, D.N. Collector Optic Cleaning by In-Situ Hydrogen Plasma. Extreme Ultrav. (EUV) Lithogr. VI 2015, 9422, 94222H. [Google Scholar]
- Chen, J.; Louis, E.; Wormeester, H.; Harmsen, R.; van de Kruijs, R.; Lee, C.J.; van Schaik, W.; Bijkerk, F. Carbon-induced extreme ultraviolet reflectance loss characterized using visible-light ellipsometry. Meas. Sci. Technol. 2011, 22, 105705. [Google Scholar] [CrossRef]
- Astakhov, D.I.; Goedheer, W.J.; Lee, C.J.; Ivanov, V.V.; Krivtsun, V.M.; Yakushev, O.; Koshelev, K.N.; Lopaev, D.V.; Bijkerk, F. Numerical and experimental studies of the carbon etching in EUV-induced plasma. arXiv 2016, arXiv:1507.02705. [Google Scholar]
- Biener, J.; Schenk, A.; Winter, B.; Lutterloh, C.; Horn, A.; Kuppers, J. Elementary Steps Of The Interaction Of C-H Film Surfaces With Thermal H/D Atoms. Vacuum 1995, 46, 903–906. [Google Scholar] [CrossRef]
- Meiling, H.; Banine, V.; Kurz, P.; Blum, B.; Heerens, G.J.; Harned, N. The EUV program at ASML: An update. Emerg. Lithogr. Technol. VII Pts 1 2 2003, 5037, 24–35. [Google Scholar]
- Kuznetsov, A.S.; Kruijs, R.W.E.; Gleeson, M.A.; Schmid, K.; Bijkerk, F. Hydrogen interaction with EUVL-relevant optical materials. J. Surf. Investig. X-ray, Synchrotron Neutron Tech. 2010, 4, 563–566. [Google Scholar] [CrossRef]
- Kuznetsov, A.S.; Gleeson, M.A.; Bijkerk, F. Ion effects in hydrogen-induced blistering of Mo/Si multilayers. J. Appl. Phys. 2013, 114, 113507. [Google Scholar] [CrossRef]
- Van den Bos, R.A.J.M.; Lee, C.J.; Benschop, J.P.H.; Bijkerk, F. Blister formation in Mo/Si multilayered structures induced by hydrogen ions. J. Phys. D Appl. Phys. 2017, 50, 265302. [Google Scholar] [CrossRef]
- Van den Bos, R.A.J.M.; Reshetniak, V.; Lee, C.J.; Benschop, J.; Bijkerk, F. A model for pressurized hydrogen induced thin film blisters. J. Appl. Phys. 2016, 120, 235304. [Google Scholar] [CrossRef]
- Pelizzo, M.G.; Corso, A.J.; Zuppella, P.; Windt, D.L.; Mattei, G. Stability of extreme ultraviolet multilayer coatings to low energy proton bombardment. Opt. Express 2011, 19, 14838–14844. [Google Scholar] [CrossRef]
- Kuznetsov, A.S.; Gleeson, M.A.; van de Kruijs, R.W.E.; Bijkerk, F. Blistering behavior in Mo/Si multilayers. Damage VUV, EUV X-ray Optics III 2011, 8077, 807713. [Google Scholar]
- Bouchoule, A. Dusty Plamsas; Physics, Chemistry and Technological Impacts in Plasma Processing; John Wiley And Sons Ltd.: Chichester, UK, 1999. [Google Scholar]
- Beckers, J.; Ockenga, T.; Wolter, M.; Stoffels, W.W.; Van Dijk, J.; Kersten, H.; Kroesen, G.M.W. Microparticles in a collisional rf plasma sheath under hypergravity conditions as probes for the electric field strength and the particle charge. Phys. Rev. Lett. 2011, 106, 115002. [Google Scholar] [CrossRef] [PubMed]
- Beckers, J.; Trienekens, D.J.M.; Kroesen, G.M.W. Absolute measurement of the total ion-drag force on a single plasma-confined microparticle at the void edge under microgravity conditions. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2013, 88, 055101. [Google Scholar] [CrossRef] [PubMed]
- Ivlev, A.V.; Kretschmer, M.; Zuzic, M.; Morfill, G.E.; Rothermel, H.; Thomas, H.M.; Fortov, V.E.; Molotkov, V.I.; Nefedov, A.P.; Lipaev, A.M.; et al. Decharging of complex plasmas: First kinetic observations. Phys. Rev. Lett. 2003, 90, 055003/1–055003/4. [Google Scholar] [CrossRef] [PubMed]
- Van Minderhout, B.; Peijnenburg, T.; Blom, P.; Vogels, J.M.; Kroesen, G.M.; Beckers, J. The charge of micro-particles in a low pressure spatial plasma afterglow. J. Phys. D Appl. Phys. 2019, 52, 32. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beckers, J.; van de Ven, T.; van der Horst, R.; Astakhov, D.; Banine, V. EUV-Induced Plasma: A Peculiar Phenomenon of a Modern Lithographic Technology. Appl. Sci. 2019, 9, 2827. https://doi.org/10.3390/app9142827
Beckers J, van de Ven T, van der Horst R, Astakhov D, Banine V. EUV-Induced Plasma: A Peculiar Phenomenon of a Modern Lithographic Technology. Applied Sciences. 2019; 9(14):2827. https://doi.org/10.3390/app9142827
Chicago/Turabian StyleBeckers, Job, Tijn van de Ven, Ruud van der Horst, Dmitry Astakhov, and Vadim Banine. 2019. "EUV-Induced Plasma: A Peculiar Phenomenon of a Modern Lithographic Technology" Applied Sciences 9, no. 14: 2827. https://doi.org/10.3390/app9142827
APA StyleBeckers, J., van de Ven, T., van der Horst, R., Astakhov, D., & Banine, V. (2019). EUV-Induced Plasma: A Peculiar Phenomenon of a Modern Lithographic Technology. Applied Sciences, 9(14), 2827. https://doi.org/10.3390/app9142827