High-Speed Holographic Shape and Full-Field Displacement Measurements of the Tympanic Membrane in Normal and Experimentally Simulated Pathological Ears
Abstract
1. Introduction
2. Materials and Methods
2.1. Principle of High-Speed Holographic for Shape and Displacement Measurements
2.1.1. Multiple Wavelength Holographic Interferometry (MWHI) Method for Shape Measurement
2.1.2. High-Speed Digital Holographic (HDH) Method for Displacement Measurement
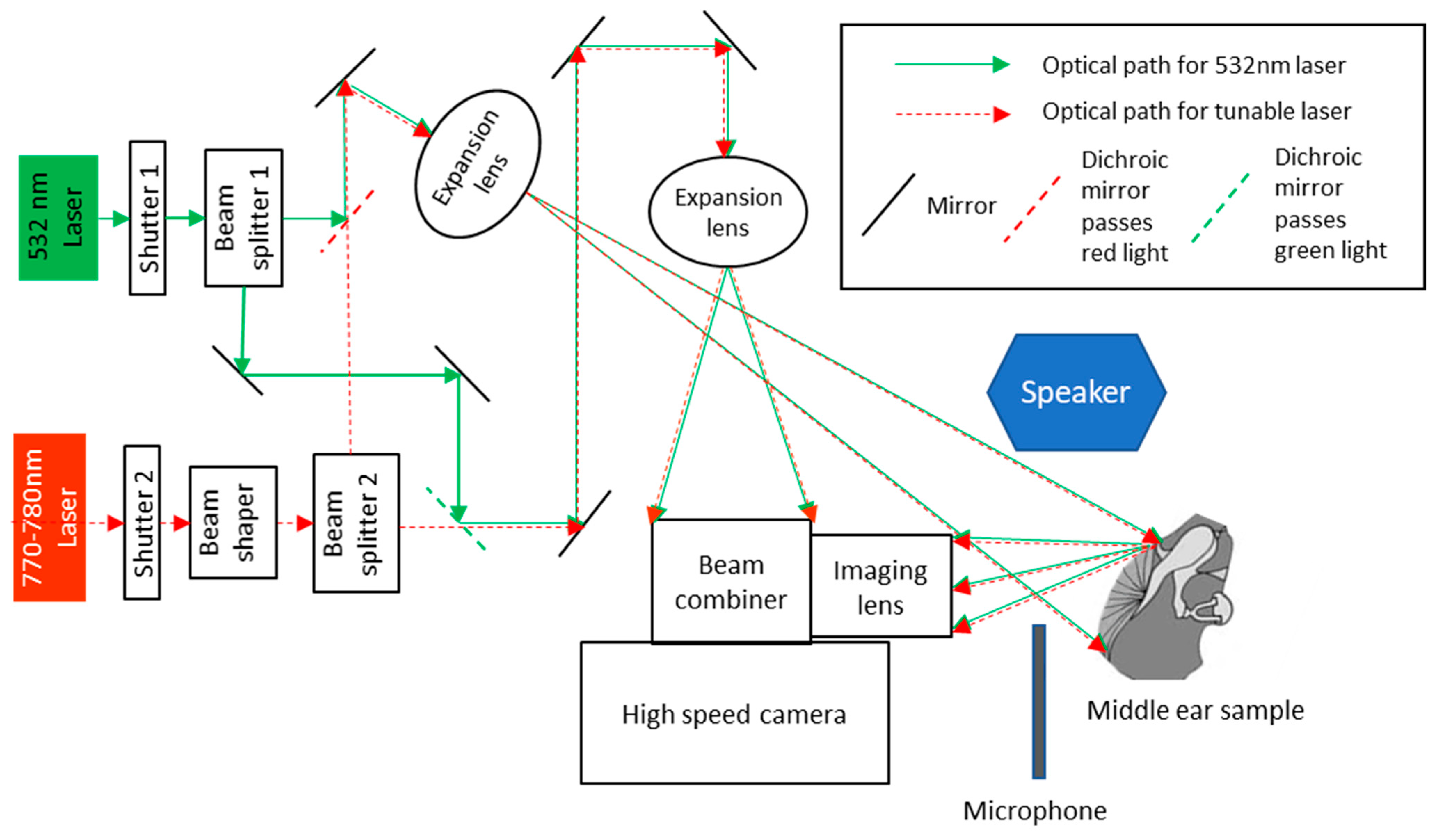
2.2. Experimental Setup and Procedures
2.3. Experimental Modal Analysis
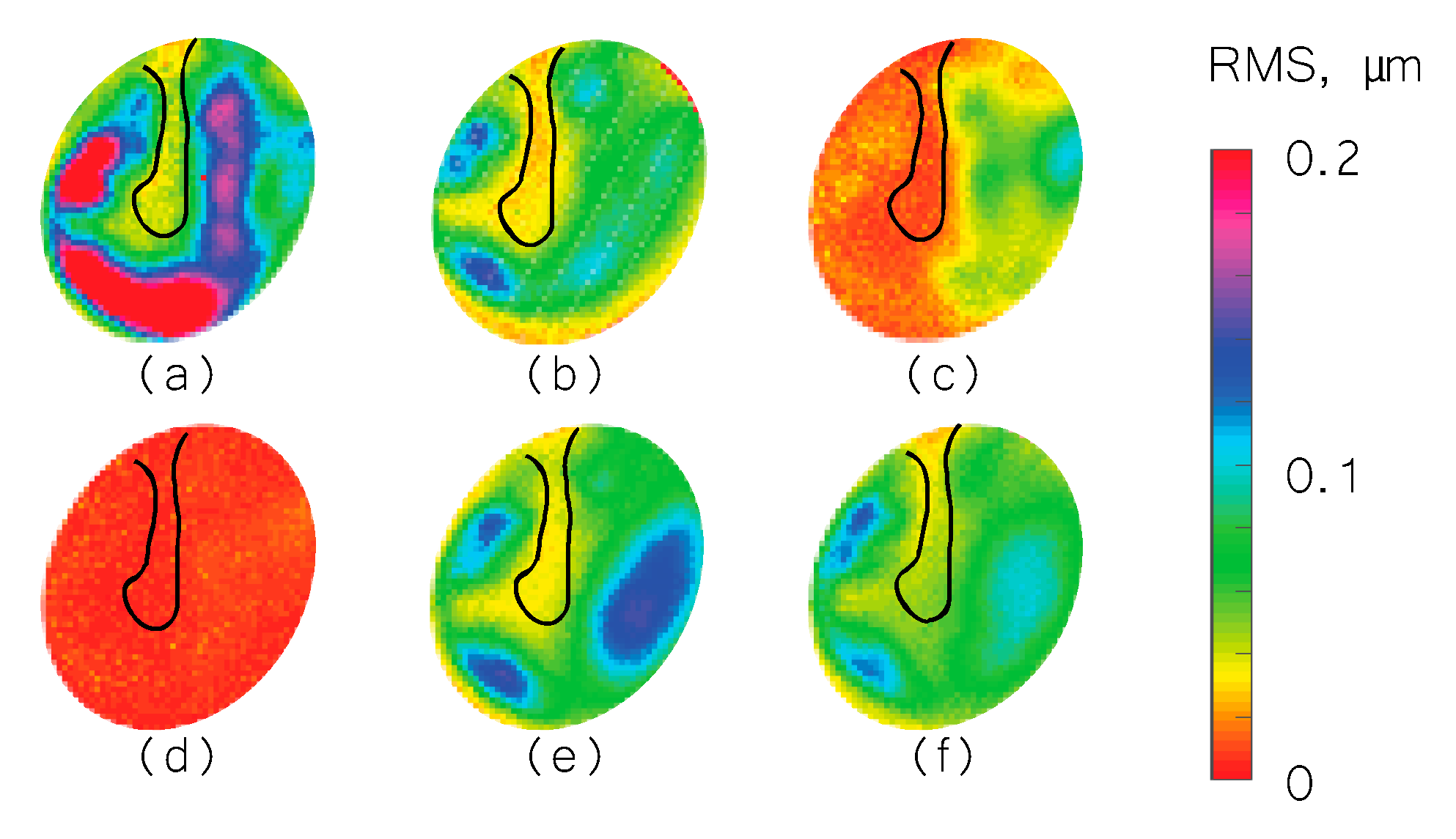
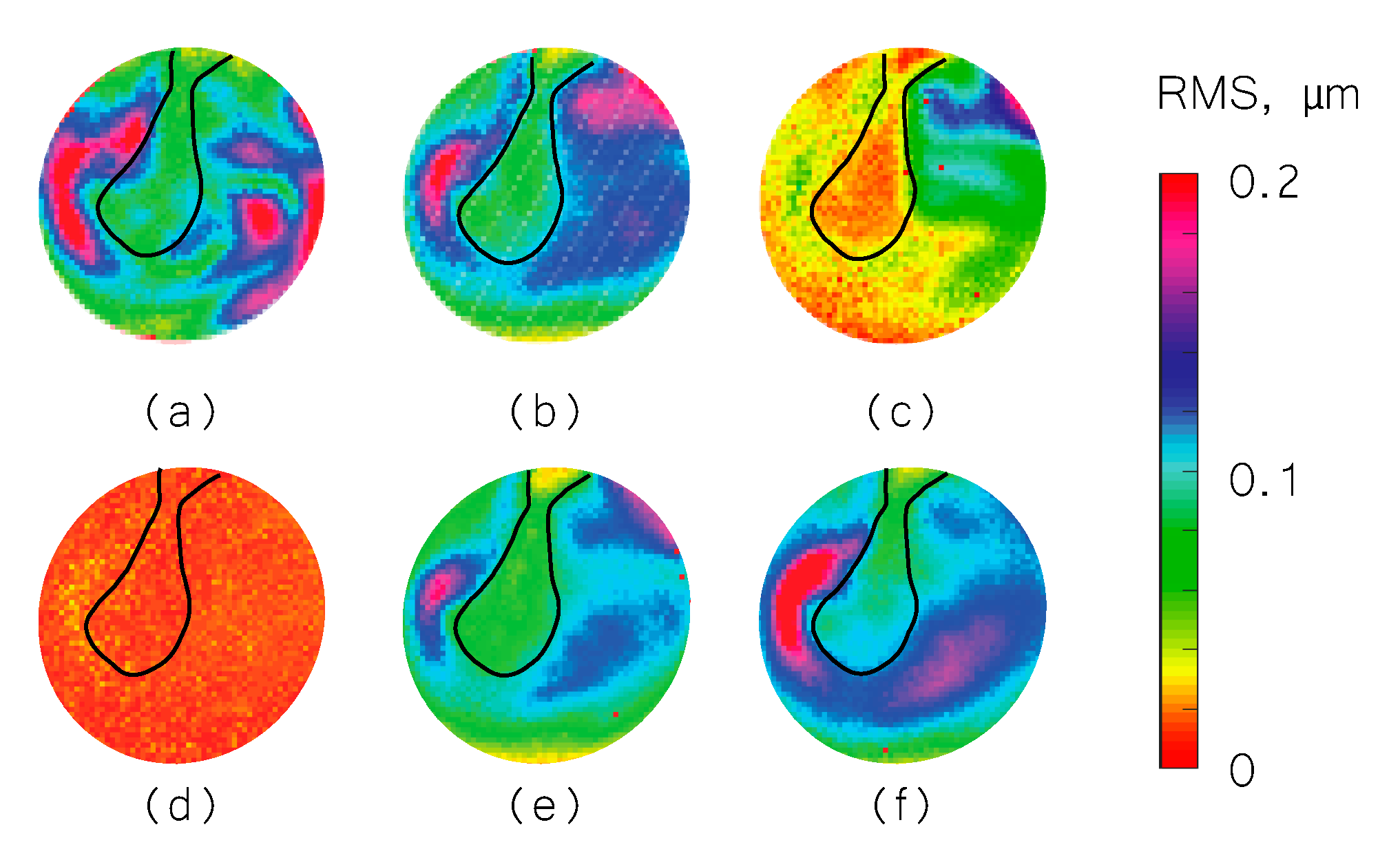
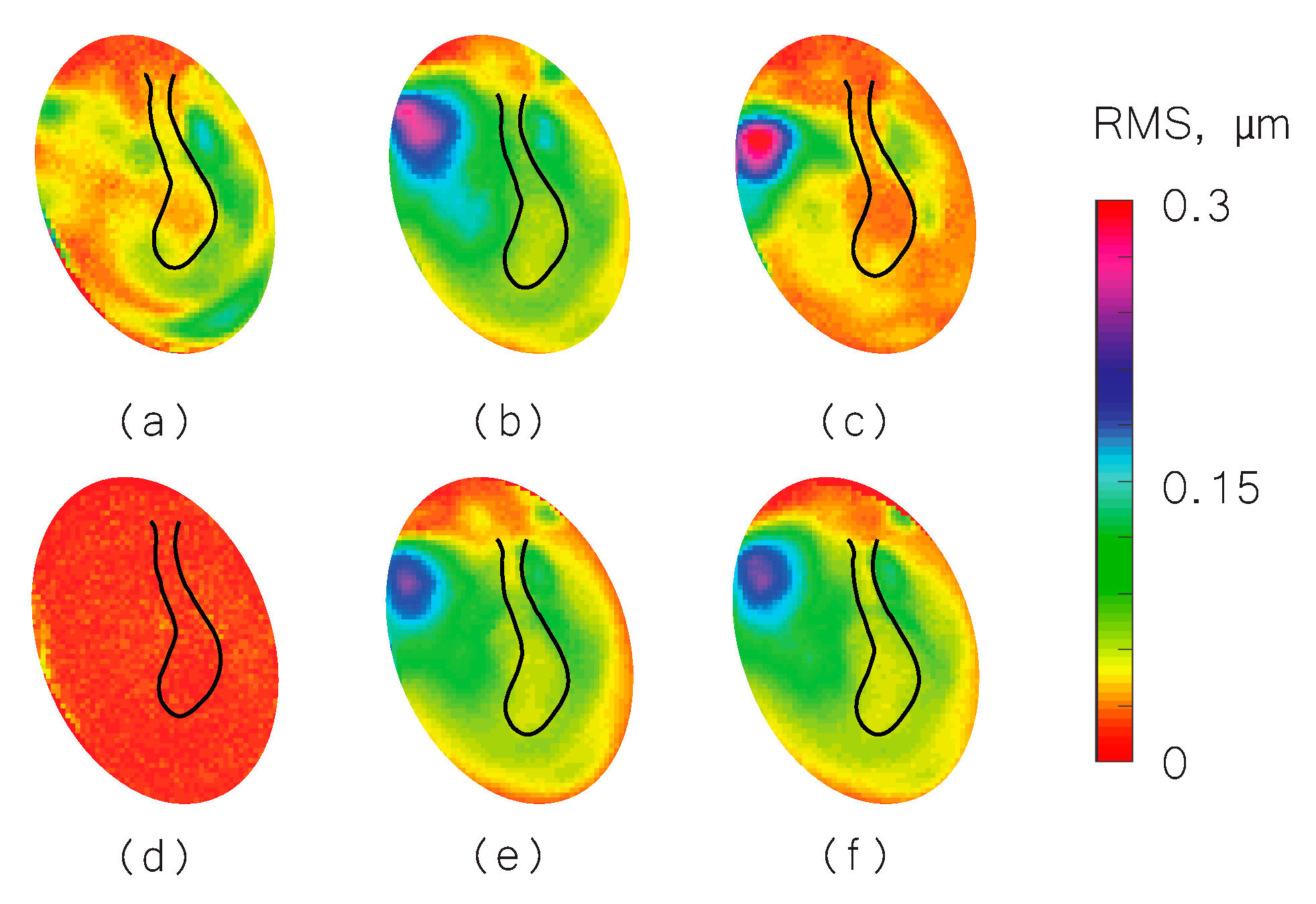
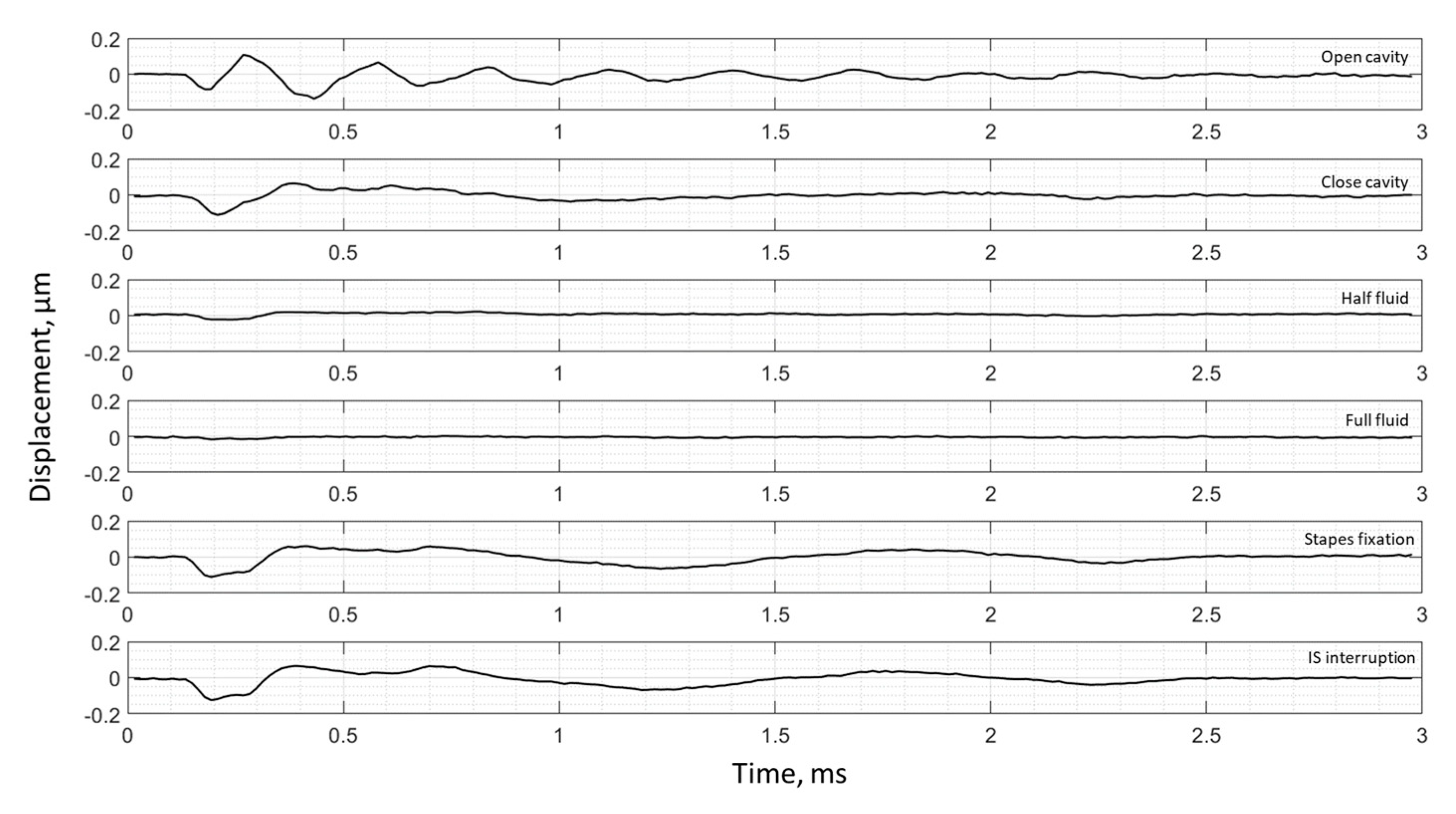
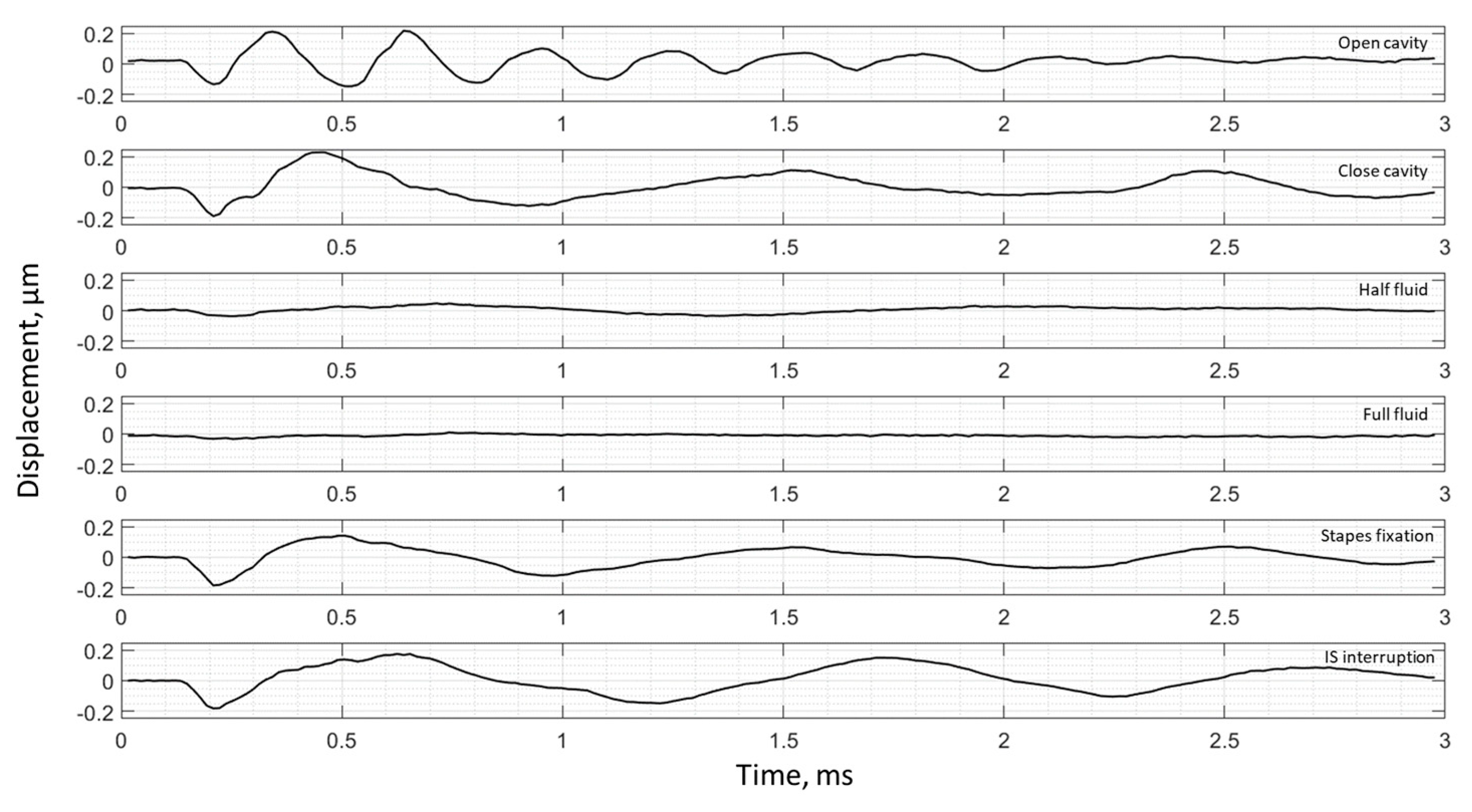
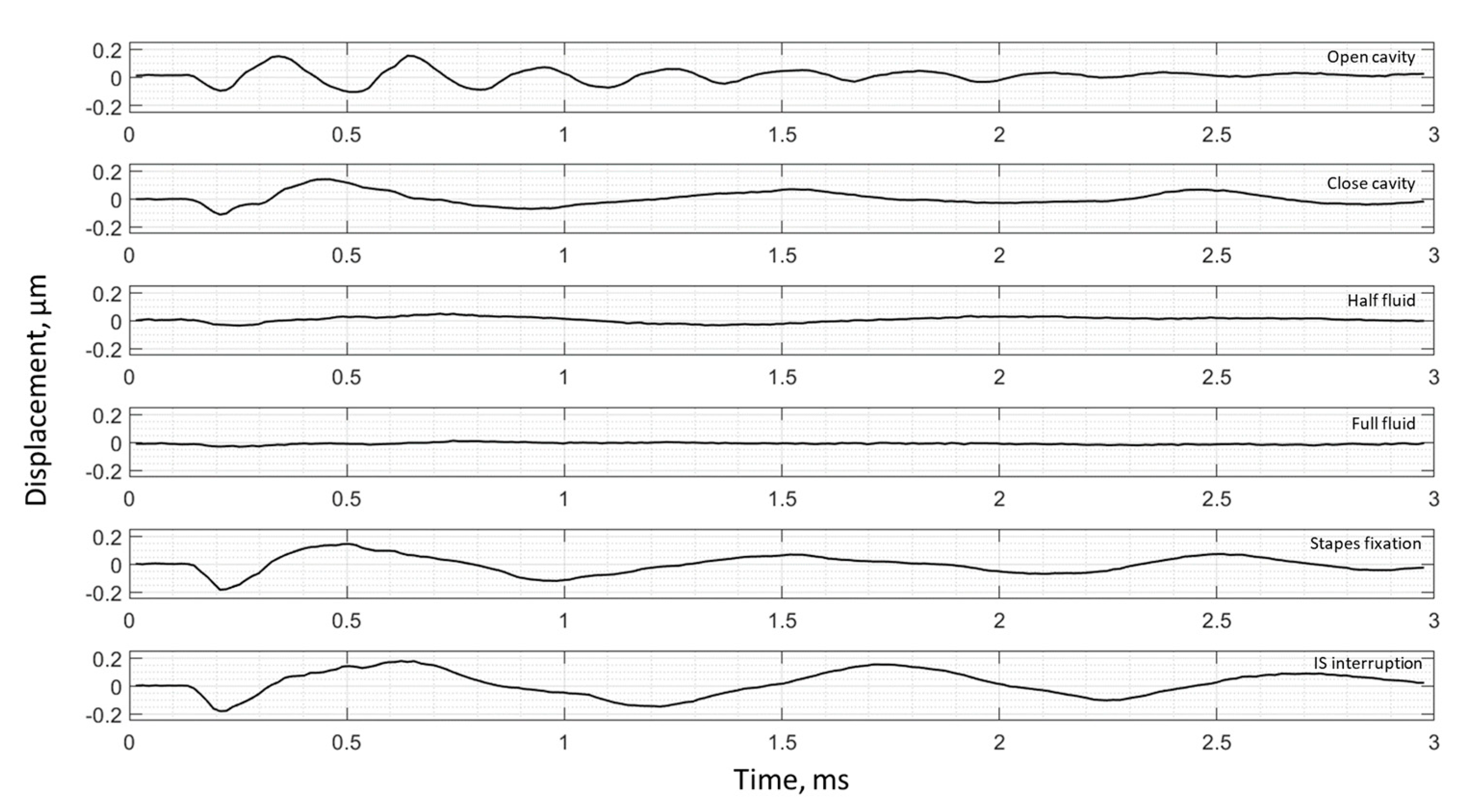
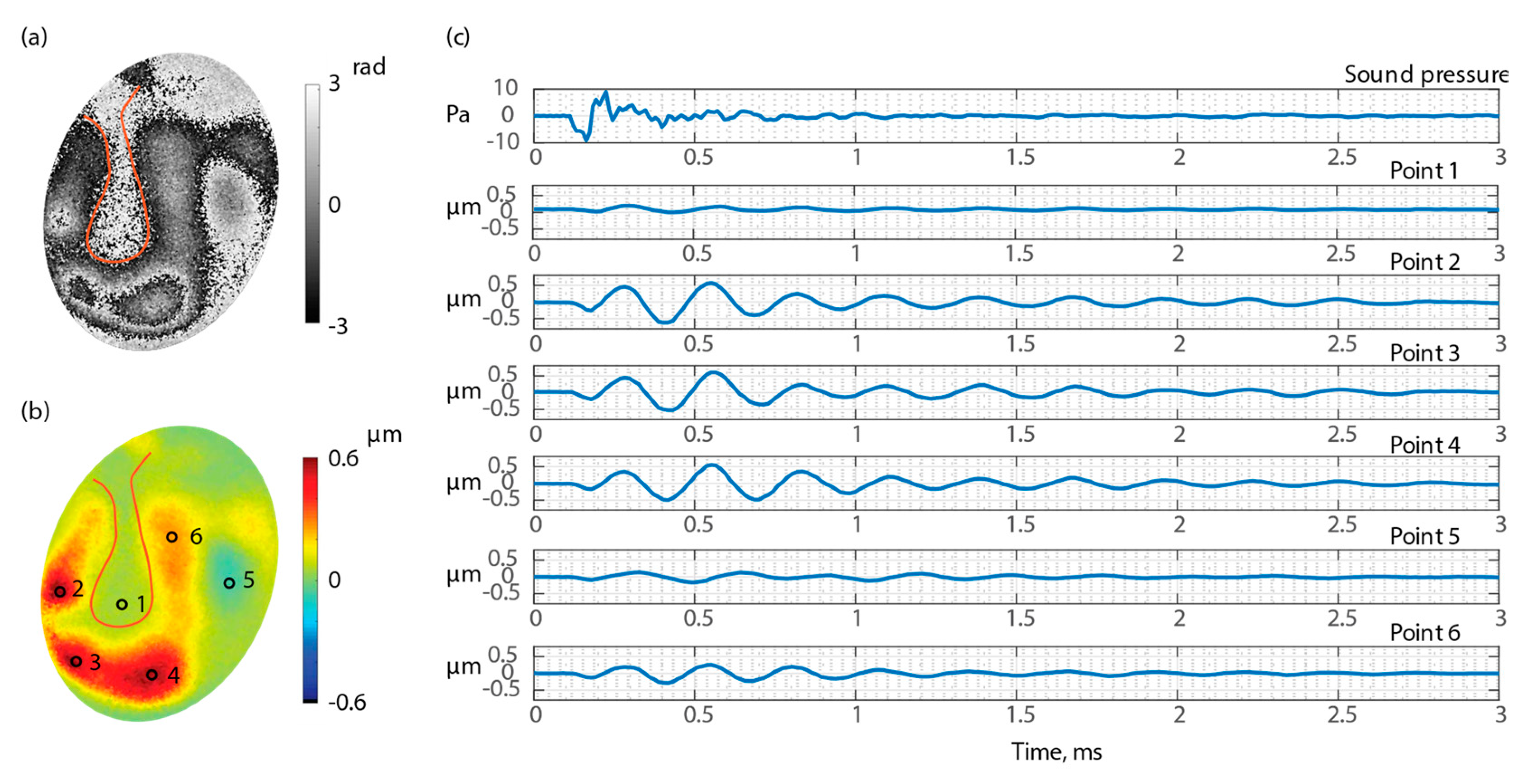
3. Results
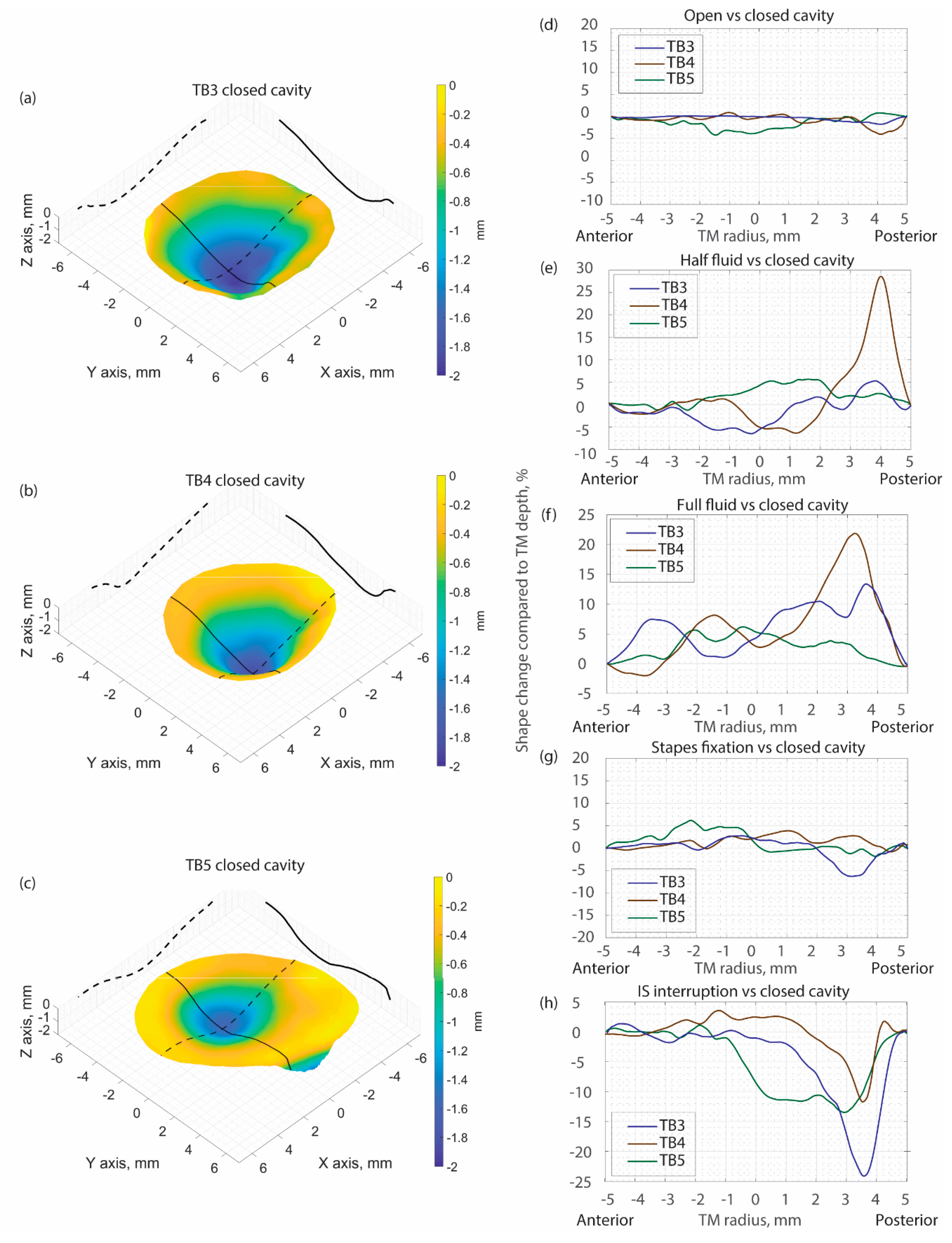
3.1. Representative Shape Measurement Results
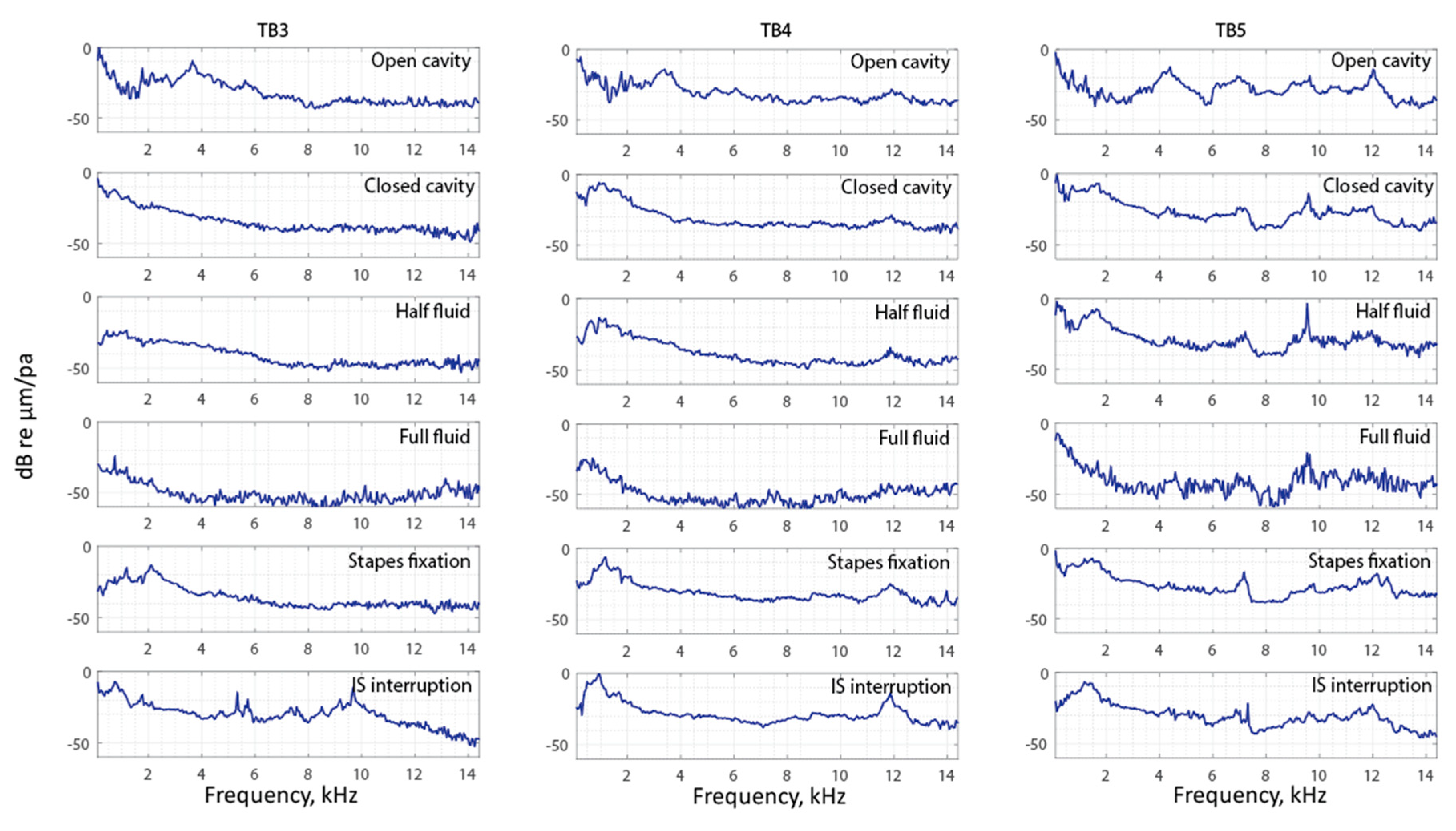
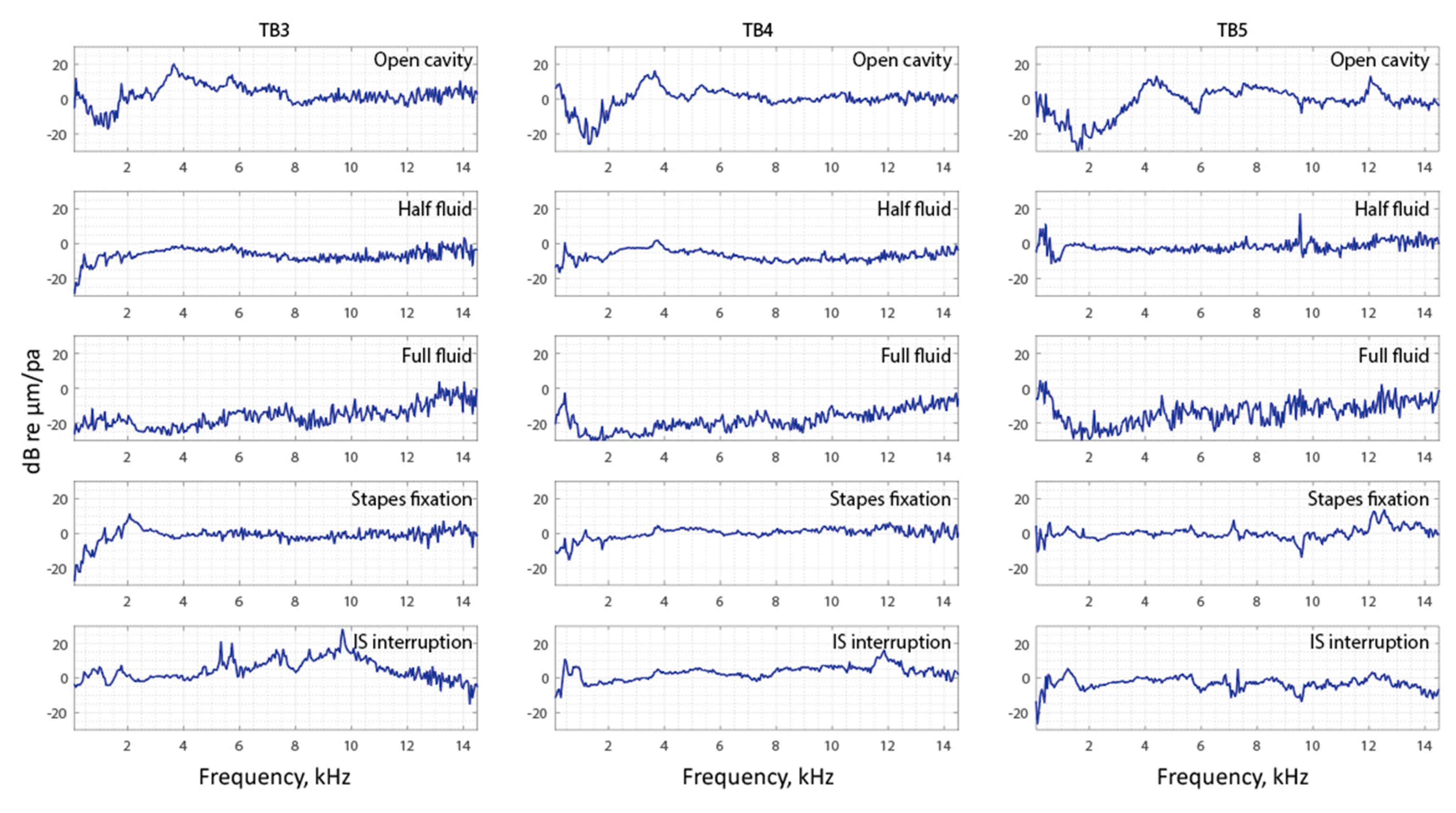
3.2. Frequency Analysis: Complex Mode Indicator Functions
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rosowwski, J.J. Outer and Middle Ears. Comparative Hearing: Mammals; Fay, R.R., Popper, A.N., Eds.; Springer: New York, NY, USA, 1994; pp. 172–247. [Google Scholar]
- Geisler, C.D. From Sound to Synapse: Physiology of the Mammalian Ear; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Wang, X.; Guan, X.; Pineda, M.; Gan, R.Z. Motion of tympanic membrane in guinea pig otitis media model measured by scanning laser Doppler vibrometry. Hear. Res. 2016, 339, 184–194. [Google Scholar] [CrossRef] [PubMed]
- Fay, J.P.; Puria, S.; Steele, C.R. The discordant eardrum. Proc. Natl. Acad. Sci. USA 2006, 103, 19743–19748. [Google Scholar] [CrossRef] [PubMed]
- Volandri, G.; di Puccio, F.; Forte, P.; Carmignani, C. Biomechanics of the tympanic membrane. J. Biomech. 2011, 44, 1219–1236. [Google Scholar] [CrossRef] [PubMed]
- Cheng, T.; Dai, C.; Gan, R.Z. Viscoelastic Properties of Human Tympanic Membrane. Ann. Biomed. Eng. 2007, 35, 305–314. [Google Scholar] [CrossRef] [PubMed]
- Fay, J.; Puria, S.; Decraemer, W.F.; Steele, C. Three approaches for estimating the elastic modulus of the tympanic membrane. J. Biomech. 2005, 38, 1807–1815. [Google Scholar] [CrossRef] [PubMed]
- Greef, D.; Buytaert, J.A.; Aerts, J.R.; Van, L.; Dierick, M.; Dirckx, J. Details of human middle ear morphology based on micro-CT imaging of phosphotungstic acid stained samples. J. Morphol. 2015, 276, 1025–1046. [Google Scholar] [CrossRef]
- Van der Jeught, S.; Dirckx, J.J.J.; Aerts, J.R.M.; Bradu, A.; Podoleanu, A.G.; Buytaert, J.A.N. Full-Field Thickness Distribution of Human Tympanic Membrane Obtained with Optical Coherence Tomography. J. Assoc. Res. Otolaryngol. 2013, 14, 483–494. [Google Scholar] [CrossRef] [PubMed]
- Aernouts, J.; Aerts, J.R.M.; Dirckx, J.J.J. Mechanical properties of human tympanic membrane in the quasi-static regime from in situ point indentation measurements. Hear. Res. 2012, 290, 45–54. [Google Scholar] [CrossRef]
- Rosowski, J.J.; Cheng, J.T.; Ravicz, M.; Hulli, N.; Montes, M.H.; Harrington, E.; Furlong, C. Computer-assisted time-averaged holograms of the motion of the surface of the mammalian tympanic membrane with sound stimuli of 0.4–25 kHz. Hear. Res. 2009, 253, 83–96. [Google Scholar] [CrossRef]
- Rosowski, J.J.; Hawkins, H.L.; McMullen, T.A.; Popper, A.N.; Fay, R.R. Models of External- and Middle-Ear Function. In Auditory Computation; Springer: New York, NY, USA, 1996; pp. 15–61. [Google Scholar]
- Lim, D.J. Human Tympanic Membrane. Acta Oto Laryngol. 1970, 70, 176–186. [Google Scholar] [CrossRef]
- Khaleghi, M. Development of Holographic Interferometric Methodologies for Characterization of Shape and Function of the Human Tympanic Membrane. Ph.D. Thesis, Worcester Polytechnic Institute, Worcester, MA, USA, April 2015. [Google Scholar]
- Milazzo, M.; Fallah, E.; Carapezza, M.; Kumar, N.S.; Lei, J.H.; Olson, E.S. The path of a click stimulus from ear canal to umbo. Hear. Res. 2017, 346, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.T.; Aarnisalo, A.A.; Harrington, E.; Montes, S.H.; Furlong, C.; Merchant, S.N.; Rosowski, J.J. Motion of the surface of the human tympanic membrane measured with stroboscopic holography. Hear. Res. 2010, 263, 66–77. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Montes, S.; Furlong, C.; Rosowski, J.J.; Hulli, N.; Harrington, E.; Cheng, J.T.; Ravicz, M.E.; Santoyo, F.M. Optoelectronic holographic otoscope for measurement of nano-displacements in tympanic membranes. J. Biomed. Opt. 2009, 14, 034021. [Google Scholar]
- Solís, S.M.; Hernández-Montes, M.D.; Santoyo, F.M. Tympanic membrane contour measurement with two source positions in digital holographic interferometry. Biomed. Opt. Express 2012, 3, 3203–3210. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Solís, S.M.; Santoyo, F.M.; Hernández-Montes, M.D. 3D displacement measurements of the tympanic membrane with digital holographic interferometry. Opt. Express 2012, 20, 5613–5621. [Google Scholar] [CrossRef] [PubMed]
- Rosowski, J.J.; Dobrev, I.; Khaleghi, M.; Lu, W.; Cheng, J.T.; Harrington, E.; Furlong, C. Measurements of three-dimensional shape and sound-induced motion of the chinchilla tympanic membrane. Hear. Res. 2013, 301, 44–52. [Google Scholar] [CrossRef] [PubMed]
- Rutledge, C.; Thyden, M.; Furlong, C.; Rosowski, J.J.; Cheng, J.T. Mapping the Histology of the Human Tympanic Membrane by Spatial Domain Optical Coherence Tomography. MEMS Nanotechnol. 2013, 6, 125–129. [Google Scholar]
- Khaleghi, M.; Furlong, C.; Cheng, J.T.; Rosowski, J.J. Characterization of Acoustically-Induced Forces of the Human Eardrum. Mech. Biol. Syst. Mater. 2016, 6, 147–154. [Google Scholar]
- Santiago-Lona, C.V.; Hernández-Montes, M.D.; Mendoza-Santoyo, F.; Esquivel-Tejeda, J. Quantitative comparison of tympanic membrane displacements using two optical methods to recover the optical phase. J. Mod. Opt. 2018, 65, 275–286. [Google Scholar] [CrossRef]
- Dobrev, I.; Furlong, C.; Cheng, J.T.; Rosowski, J.J. Full-field transient vibrometry of the human tympanic membrane by local phase correlation and high-speed holography. J. Biomed. Opt. 2014, 19, 96001. [Google Scholar] [CrossRef]
- De Greef, D.; Aernounts, J.; Aerts, J.; Cheng, J.T.; Horwitz, R.; Rosowski, J.J.; Dirckx, J. Viscoelastic properties of the human tympanic membrane studied with stroboscopic holography and finite element modeling. Hear. Res. 2014, 312, 69–80. [Google Scholar] [CrossRef] [PubMed]
- Khaleghi, M.; Guignard, J.; Furlong, C.; Rosowski, J.J. Simultaneous full-field 3-D vibrometry of the human eardrum using spatial-bandwidth multiplexed holography. J. Biomed. Opt. 2015, 20, 111202. [Google Scholar] [CrossRef] [PubMed]
- Dobrev, I. Full-Field Vibrometry by High-Speed Digital Holography for Middle-ear Mechanics. Ph.D. Thesis, Worcester Polytechnic Institute, Worcester, MA, USA, July 2014. [Google Scholar]
- Razavi, P.; Ravicz, M.E.; Dobrev, I.; Cheng, J.T.; Furlong, C.; Rosowski, J.J. Response of the human tympanic membrane to transient acoustic and mechanical stimuli: Preliminary results. Hear. Res. 2016, 340, 15–24. [Google Scholar] [CrossRef] [PubMed]
- Razavi, P.; Dobrev, I.; Ravicz, M.E.; Cheng, J.T.; Furlong, C.; Rosowski, J.J. Transient Response of the Eardrum Excited by Localized Mechanical Forces. Mech. Biol. Syst. Mater. 2016, 6, 31–37. [Google Scholar]
- Razavi, P.; Cheng, J.T.; Furlong, C.; Rosowski, J.J. High-Speed Holography for In-Vivo Measurement of Acoustically Induced Motions of Mammalian Tympanic Membrane. Mech. Biol. Syst. Mater. 2016, 6, 75–81. [Google Scholar]
- Razavi, P.; Tang, H.; Rosowski, J.J.; Furlong, C.; Cheng, J.T. Combined high-speed holographic shape and full-field displacement measurements of tympanic membrane. J. Biomed. Opt. 2018, 24, 031008. [Google Scholar] [CrossRef] [PubMed]
- Razavi, P. Development of High-Speed Digital Holographic Shape and Displacement Measurement Methods for Middle-Ear Mechanics In-vivo. Ph.D. Thesis, Worcester Polytechnic Institute, Worcester, MA, USA, March 2018. [Google Scholar]
- Yamaguchi, I.; Ida, T.; Yokota, M.; Yamashita, K. Surface shape measurement by phase-shifting digital holography with dual wavelengths. Interferom. Tech. Anal. 2006, 6292, 62920V. [Google Scholar]
- Kuwamura, S.; Yamaguchi, I. Wavelength scanning profilometry for real-time surface shape measurement. Appl. Opt. 1997, 36, 4473–4482. [Google Scholar] [CrossRef]
- Seebacher, S.; Osten, W.; Jueptner, W.P.O. Measuring shape and deformation of small objects using digital holography. Laser Interferom. Appl. 1998, 3479, 104–116. [Google Scholar]
- Furlong, C.; Pryputniewicz, R.J. Absolute shape measurements using high-resolution optoelectronic holography methods. Opt. Eng. 2000, 39, 216–224. [Google Scholar] [CrossRef]
- Osten, W.; Seebacher, S.; Baumbach, T.; Jueptner, W.P.O. Absolute shape control of microcomponents using digital holography and multiwavelength contouring. Metrol. Based Control Micro Manuf. 2001, 4275, 71–85. [Google Scholar]
- Harvey, K.C.; Myatt, C.J. External-cavity diode laser using a grazing-incidence diffraction grating. Opt. Lett. 1991, 16, 910. [Google Scholar] [CrossRef] [PubMed]
- Kreis, T. Handbook of Holographic Interferometry: Optical and Digital Methods; VCH Publishers: New York, NY, USA, 2005; ISBN 978-3-527-60492-0. [Google Scholar]
- Ghiglia, D.C.; Pritt, M.D. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software; Wiley: New York, NY, USA, 1998; Volume 4. [Google Scholar]
- Khaleghi, M.; Cheng, J.T.; Furlong, C.; Rosowski, J.J. In-plane and out-of-plane motions of the human tympanic membrane. J. Acoust. Soc. Am. 2016, 139, 104–117. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, H.; Razavi, P.; Pooladvand, K.; Psota, P.; Maftoon, N.; Rosowski, J.J.; Furlong, C.; Cheng, J.T. High-Speed Holographic Shape and Full-Field Displacement Measurements of the Tympanic Membrane in Normal and Experimentally Simulated Pathological Ears. Appl. Sci. 2019, 9, 2809. https://doi.org/10.3390/app9142809
Tang H, Razavi P, Pooladvand K, Psota P, Maftoon N, Rosowski JJ, Furlong C, Cheng JT. High-Speed Holographic Shape and Full-Field Displacement Measurements of the Tympanic Membrane in Normal and Experimentally Simulated Pathological Ears. Applied Sciences. 2019; 9(14):2809. https://doi.org/10.3390/app9142809
Chicago/Turabian StyleTang, Haimi, Payam Razavi, Koohyar Pooladvand, Pavel Psota, Nima Maftoon, John J. Rosowski, Cosme Furlong, and Jeffrey T. Cheng. 2019. "High-Speed Holographic Shape and Full-Field Displacement Measurements of the Tympanic Membrane in Normal and Experimentally Simulated Pathological Ears" Applied Sciences 9, no. 14: 2809. https://doi.org/10.3390/app9142809
APA StyleTang, H., Razavi, P., Pooladvand, K., Psota, P., Maftoon, N., Rosowski, J. J., Furlong, C., & Cheng, J. T. (2019). High-Speed Holographic Shape and Full-Field Displacement Measurements of the Tympanic Membrane in Normal and Experimentally Simulated Pathological Ears. Applied Sciences, 9(14), 2809. https://doi.org/10.3390/app9142809





