Potential of Liquid-Crystal Materials for Millimeter-Wave Application
Abstract
1. Introduction
2. Measurement of Complex Refractive Indices in Millimeter Wave
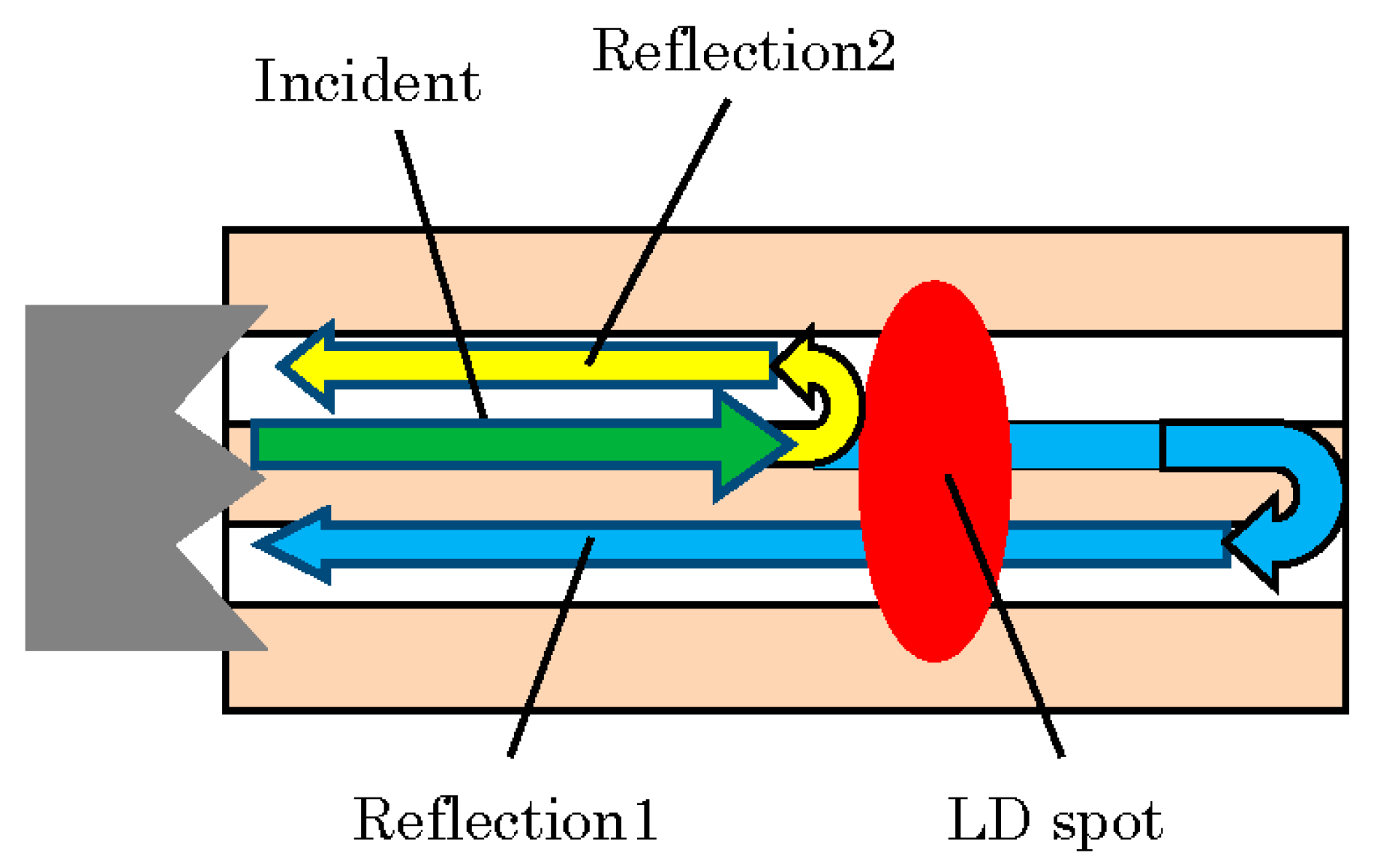
2.1. Principle of Measurement
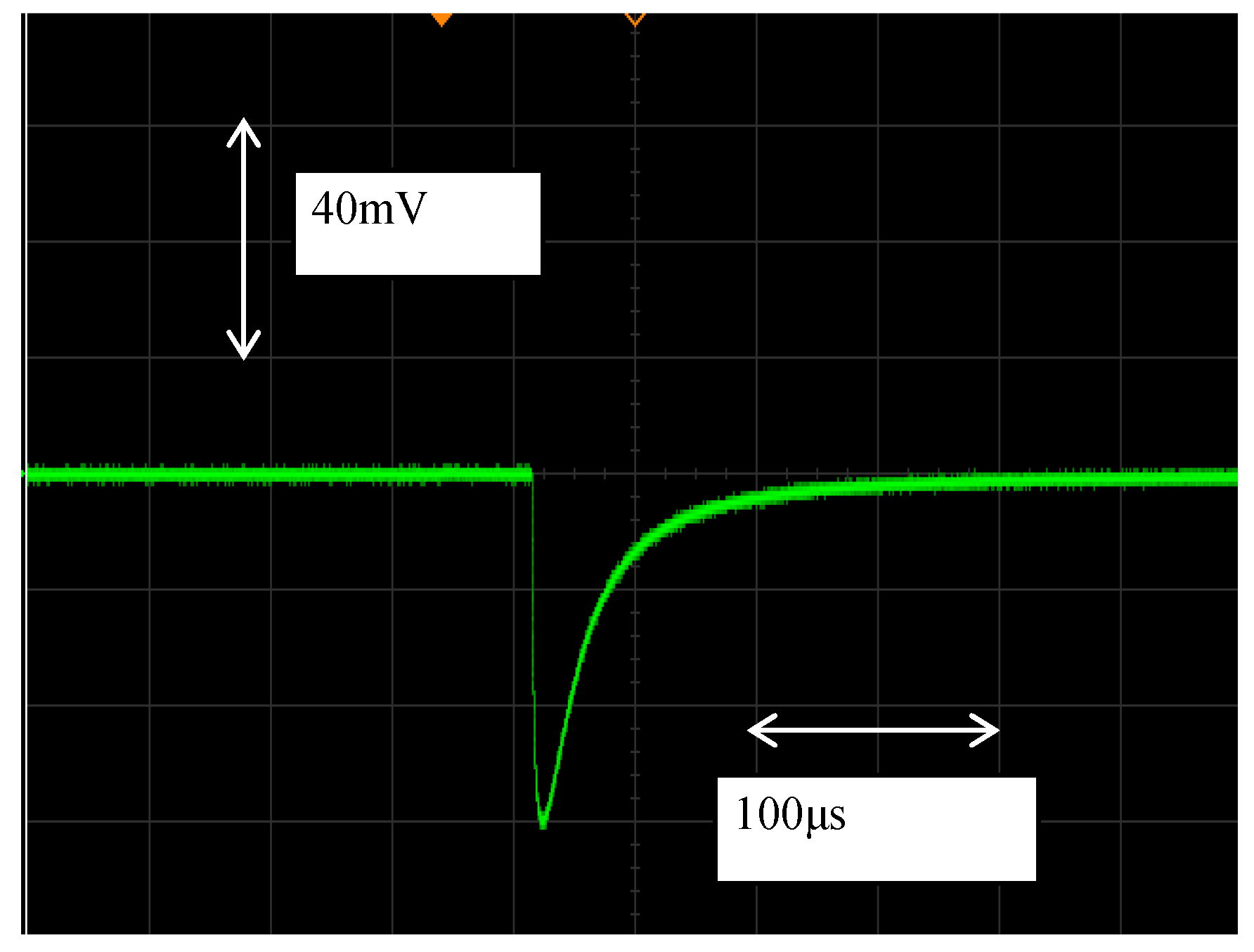
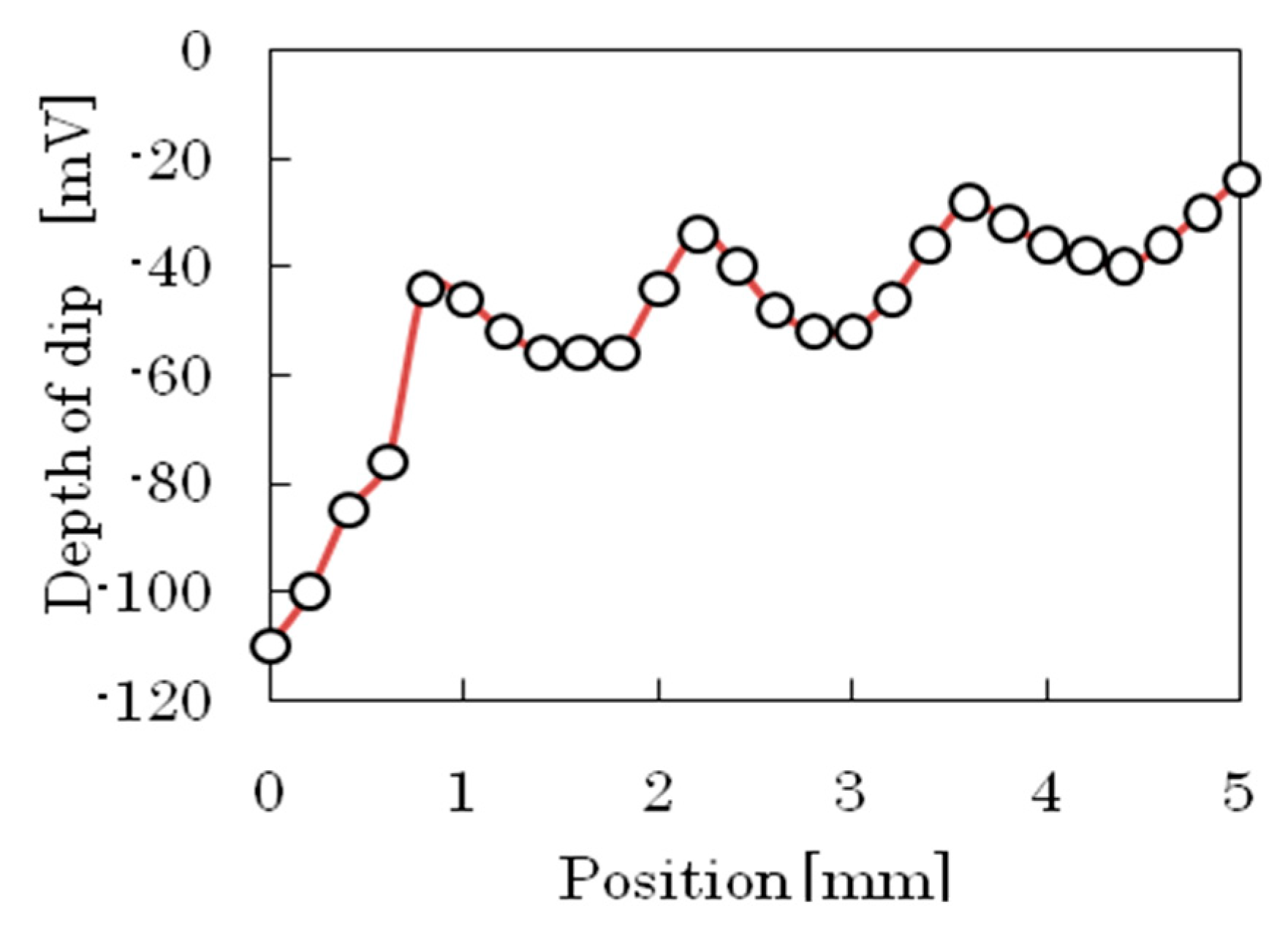
2.2. Evaluation of Refractive Index and Absorption Coefficient
3. Millimeter Wave Fresnel Lens Fabricated Using 3D Printer
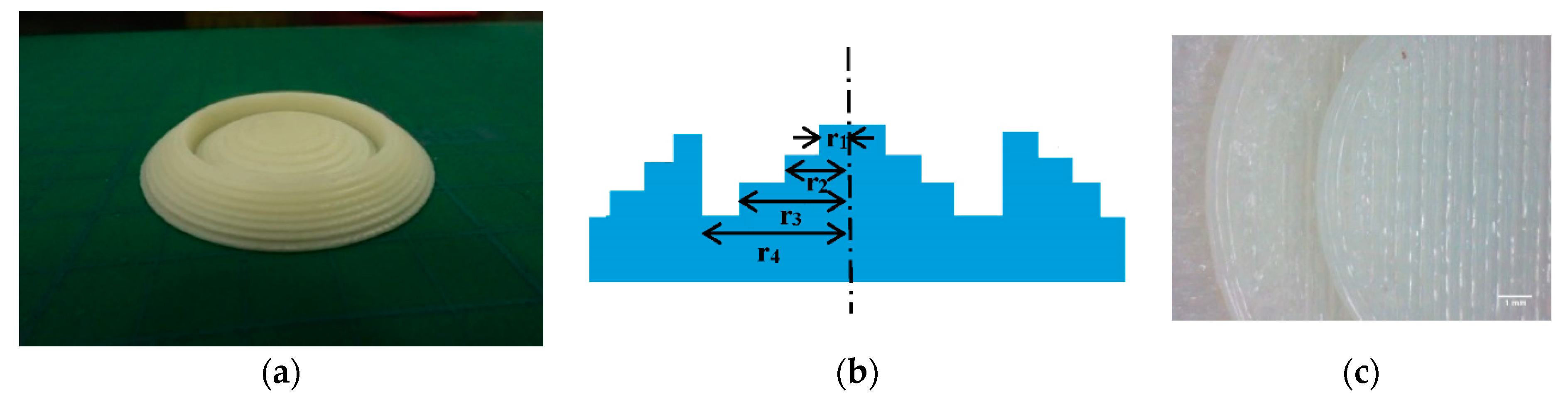
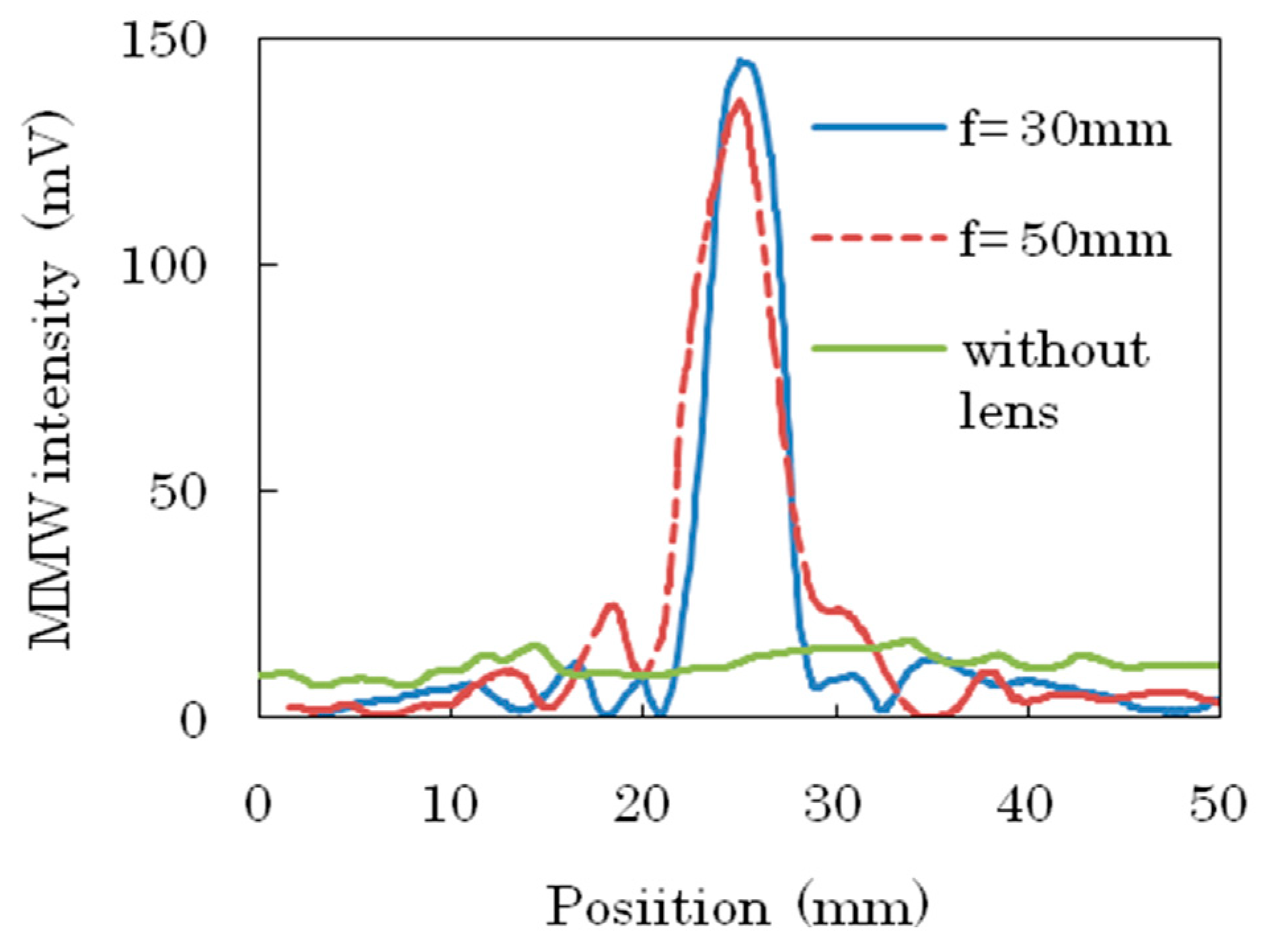
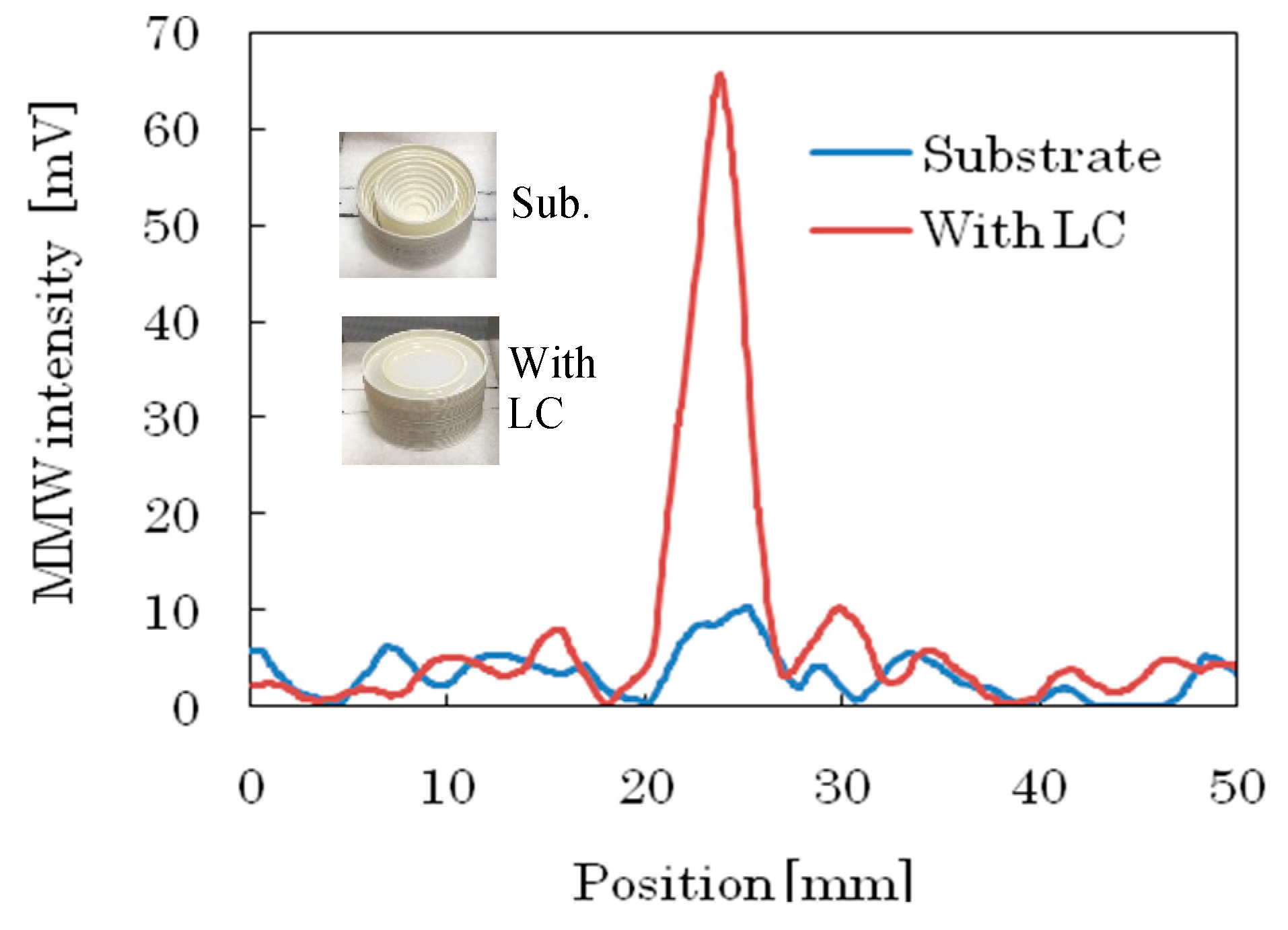
3.1. Design of Fresnel Lens Substrate
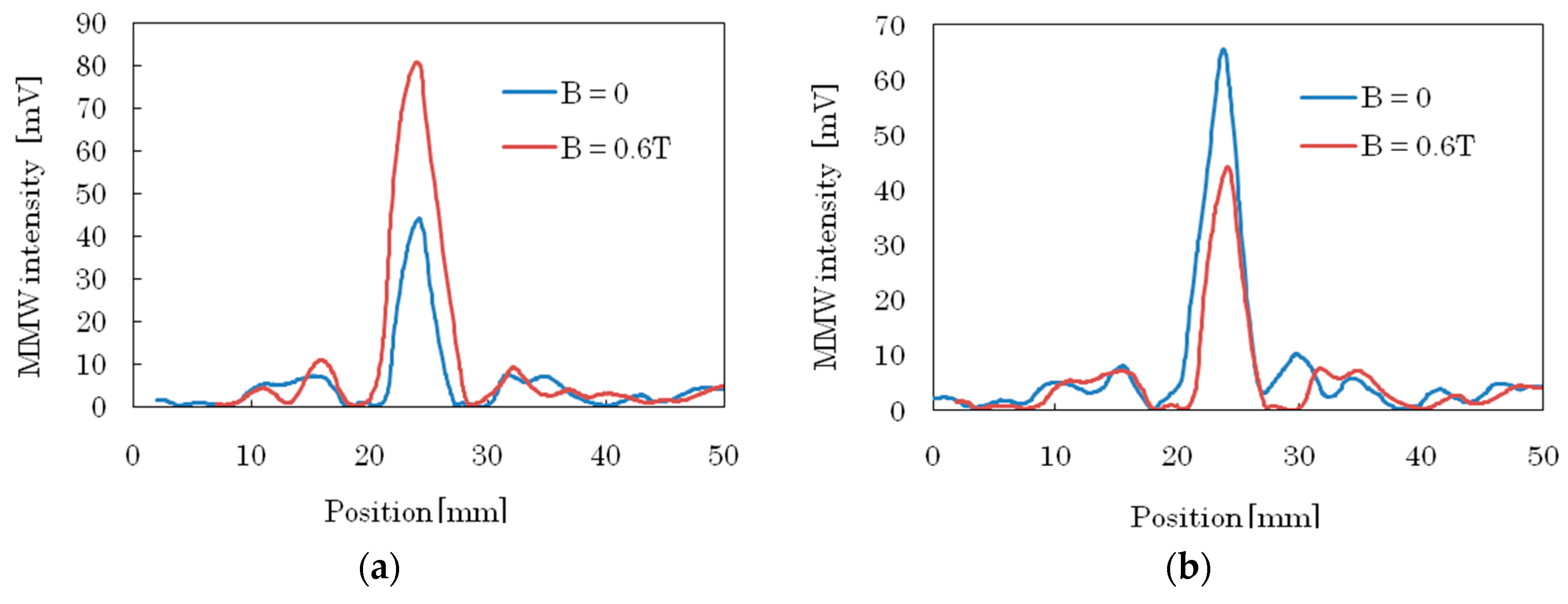
3.2. Magnetic Field Tunable Properties of LC Composite Fresnel Lens
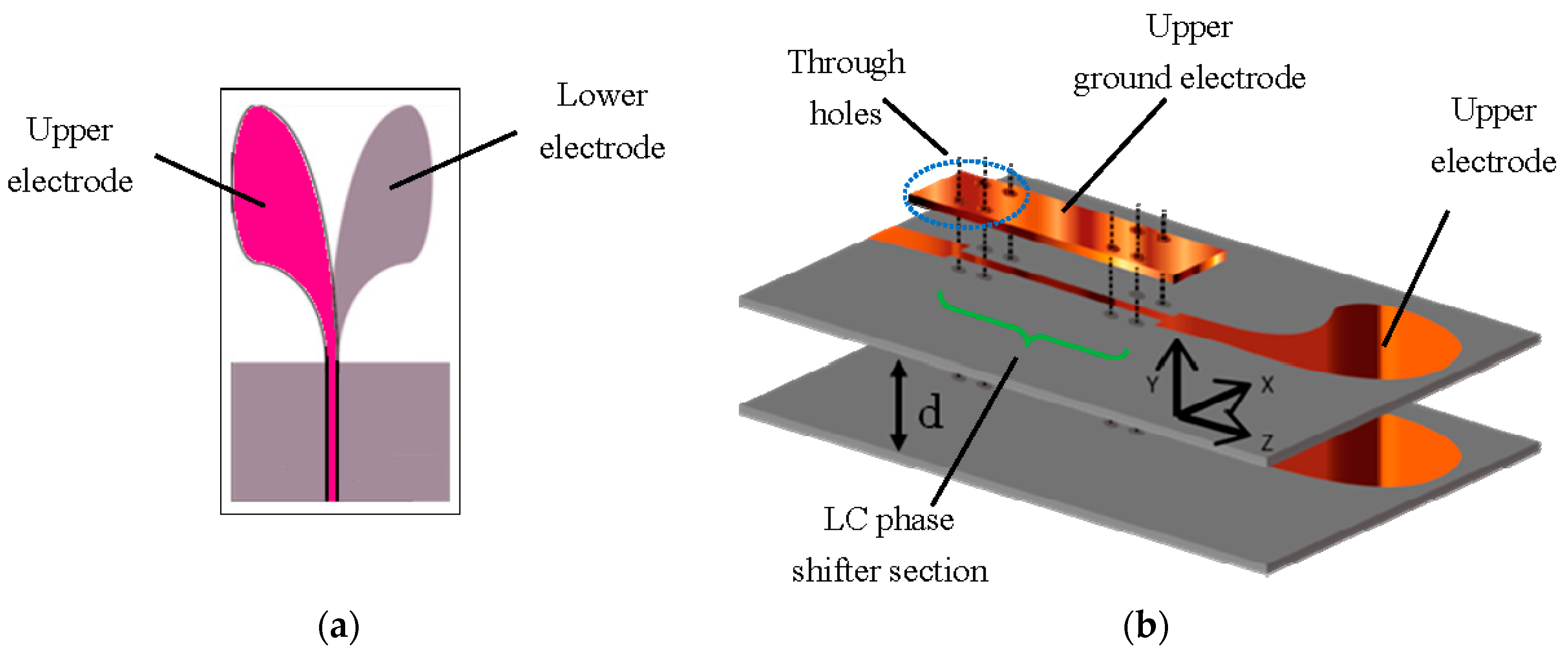
4. Microstrip-Line-Type Liquid Crystal Phase Shifter
Basic Performance of Antenna Array
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Vicari, L. Optical Application of Liquid Crystals, 1st ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Larsen, T.T.; Bjarklev, A.; Hermann, D.S.; Broeng, J. Optical devices based on liquid crystal photonics bandgap filter. Opt. Express 2003, 11, 2589–2596. [Google Scholar] [CrossRef]
- Bitou, Y. Digital phase-shift interferometer with an electrically addressed liquid crystal spatial light modulator. Opt. Lett. 2003, 28, 1576–1578. [Google Scholar] [CrossRef] [PubMed]
- Honma, M.; Horiuchi, T.; Nose, T. Oblique extraction of polarized light from light-emitting liquid crystal cells doped with a fluorescent dye. Jpn. J. Appl. Phys. 2013, 52, 070205. [Google Scholar] [CrossRef]
- Nose, T.; Kamata, K.; Takeuchi, T.; Okano, K.; Fujita, N.; Muraguchi, H.; Ozaki, N.; Honma, M.; Ito, R. Determination of birefringence and slow axis distribution using an interferometric measurement system with liquid crystal phase shifter. Appl. Opt. 2014, 53, 7230–7235. [Google Scholar] [CrossRef]
- Yang, D.K.; Wu, S.T. Fundamentals of Liquid Crystal Devices, 2nd ed.; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Wang, L.; Dong, H.; Li, Y.; Xue, C.; Sun, L.; Yan, C.; Li, Q. Reversible near infrared light directed reflection in a self-organized helical superstructure loaded with upconversion nanoparticles. JACS 2014, 136, 4480–4483. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Dong, H.; Li, Y.; Liu, R.; Wang, Y.; Bisoyi, H.K.; Sun, L.; Yan, C.; Li, Q. Luminescence-driven reversible handedness inversion of self-organized helical superstructures enabled by a novel near infrared light nanotransducer. Adv. Mater. 2015, 27, 2065–2069. [Google Scholar] [CrossRef] [PubMed]
- Buchnev, O.; Podoliak, N.; Kaczmarck, M.; Zheludev, N.I.; Fedotov, V.A. Electrically controlled nanostructured metasurface loaded with liquid crystal: toward multifunctional photonic switch. Adv. Opt. Mater. 2015, 3, 674–679. [Google Scholar] [CrossRef]
- Wang, L.; Li, Q. Stimuli-directing directing self-organized 3D liquid crystalline nanostructures: from material design to photonic applications. Adv. Funct. Mater. 2016, 26, 10–28. [Google Scholar] [CrossRef]
- Wang, L. Self-activating liquid crystal devices for smart laser projection. Liq. Cryst. 2016, 43, 2062–2078. [Google Scholar] [CrossRef]
- Nose, T.; Ishizaka, S.; Okano, K.; Fujita, N.; Murata, J.; Muraguchi, H.; Ozaki, N.; Honma, M.; Ito, R. Differential interference contrast imaging using a pair of twisted nematic cells. Opt. Lett. 2016, 41, 4012–4015. [Google Scholar] [CrossRef]
- Honma, M.; Nose, T. Polarization conversion system with liquid crystal geometric-phase-based cylinder lens. Jpn. J. Appl. Phys. 2016, 55, 012202. [Google Scholar] [CrossRef]
- Honma, M.; Miura, T.; Nose, T. Liquid-crystal-grating-based optical displacement sensors. Appl. Opt. 2016, 55, 10045–10052. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Huang, D.; Lam, L.; Cheng, Z. Bowkics: history, advances and application. Liq. Cryst. Today 2017, 26, 85–111. [Google Scholar] [CrossRef]
- Wang, L.; Bisoni, H.K.; Zheng, Z.; Gutierrez-Cuevas, K.G.; Singh, G.; Kumar, S.; Bunning, T.J.; Li, Q. Stimuli-directed self-organized chiral superstructures for adaptive windows enabled by mesogen-functionalized grapheme. Mater. Today 2017, 20, 230–236. [Google Scholar] [CrossRef]
- Gorkunov, M.V.; Kasyanova, I.V.; Artenov, V.V.; Barnik, M.I.; Geivandov, A.R.; Palto, S.P. Fast surface-plasmon-mediated electro-optics of a liquid rystal on a metal grating. Phys. Rev. Appl. 2017, 8, 054051. [Google Scholar] [CrossRef]
- Komar, A.; P-Dominguez, R.; Miroshnichenko, A.; Yu, Y.F.; Kivshar, Y.S.; Kuznetsov, A.I.; Neshev, D. Dynamic beam switching by liquid crystal tunable dielectric metasurfaces. ACS Photonics 2018, 5, 1742–1748. [Google Scholar] [CrossRef]
- Nose, T.; Mizuno, S.S.K.; Bae, J.; Nozokido, T. Refractive index of nematic liquid crystals in the submillimeter wave region. Appl. Opt. 1997, 36, 6383–6387. [Google Scholar] [CrossRef]
- Lim, K.C.; Margerum, J.D. Liquid-crystal optical propertiesand applications in the millimeter-wave range. Proc. SPIE 1992, 1815, 99–103. [Google Scholar]
- Lackner, A.M.; Lim, K.C.; Margerum, J.D.; Sherman, E. Microtubule particle dispersion in liquid crystal hosts. Liq. Cryst. 1993, 14, 351–359. [Google Scholar] [CrossRef]
- Lim, K.C.; Margerum, J.D.; Lackner, A.M.; Sherman, E.; Ho, M.-S.; Fung, B.M.; Genetti, W.B.; Grady, B.P. Aliquid crystal based polymer for applications in MMW modulationdevices. Mol. Cryst. Liq. Cryst. 1997, 302, 187–197. [Google Scholar] [CrossRef]
- Kamoda, H.; Kuki, T.; Fujikake, H.; Nomoto, T. Measurementof microwave dielectric properties of liquid crystal usingcoaxial line. Trans. IEICE C 2002, J85, 776–777. [Google Scholar]
- Kamei, T.; Utsumi, Y.; Moritake, H.; Toda, K.; Suzuki, H. Dielectric properties measurement of nematic liquid crystalat 10 kHz–40 GHz and its application for variable delay line. Trans. IEICE C 2002, J85, 1149–1158. [Google Scholar]
- Nose, T.; Honma, M.; Nozokido, T.; Mizuno, K. Determinationof the insertion loss and refractive index anisotropy innematic liquid crystal materials using a V-band waveguidetransmission cell. Mol. Cryst. Liq. Cryst. 2004, 409, 199–207. [Google Scholar] [CrossRef]
- Nose, T.; Honma, M.; Nozokido, T.; Mizuno, K. Simple method for the determination of refractive indices and loss parameters for liquid-crystal materials in the millimeter-wave region. Appl. Opt. 2005, 44, 1150–1155. [Google Scholar] [CrossRef] [PubMed]
- Ito, R.; Yanagihara, S.; Ito, K.; Watanabe, T.; Nose, T.; Honma, M. Basic performance of refractive index measurement method for LC materials in super high frequency region by using coplanar wave guide. Mol. Cryst. Liq. Cryst. 2011, 543, 92–100. [Google Scholar] [CrossRef]
- Vogel, T.; Dodel, G.; Holzhauer, E.; Salzmann, H.; Theurer, A. High-speed switching of far-infrared radiation by photoionization in a semiconductor. Appl. Opt. 1992, 31, 329–337. [Google Scholar] [CrossRef] [PubMed]
- Nozokido, T.; Minamide, H.; Mizuno, K. Modulation of submillimeter wave radiation by laser-produced free carriers in semiconductor. IEICE Trans. Electron. C 1997, 6, 259–266. (In Japanese) [Google Scholar] [CrossRef]
- Tanaka, M.; Sato, S. Focusing properties of liquid crystal lens cells with stacked-layered structure in the millimeter-wave region. IEEE Microw. Wirel. Compon. Lett. 2002, 12, 163–165. [Google Scholar] [CrossRef]
- Kamoda, H.; Kuki, T.; Fujikake, H.; Nomoto, T. Millimeter-wave beam former using liquid crystal. In Proceedings of the 34th European Microwave Conference, Amsterdam, The Netherlands, 12–14 October 2004; pp. 1141–1144. [Google Scholar]
- Nozokido, T.; Maeda, S.; Okada, H.; Nose, T.; Murai, T. A millimeter-wave quasi-optical grid phase shifter using liquid crystal. IEICE Electron. Express 2010, 7, 67–72. [Google Scholar] [CrossRef]
- Nose, T.; Ito, T.; Watanabe, T.; Ito, K.; Yanagihara, S.; Ito, R.; Honma, M. Preparation of porous polymer materials for bulky liquid crystal devices. Proc. SPIE 2012, 8279. [Google Scholar] [CrossRef]
- Ohno, S.; Toshima, N.; Honma, R.I.M.; Nose, T. Modified microscopic structure and its LC molecular orientation effects in the stretched porous PMMA films. In Proceedings of the 21st International Display Workshops 2014 (IDW’14), Niigata, Japan, 3–5 December 2014; pp. 129–130, (Nagoya, Japan). [Google Scholar]
- Nose, T.; Ohno, S.; Masaka, M.; Ito, K.; Ito, R.; Honma, M. Basic performance of a liquid crystal millimeter wave Fresnel lens fabricated using machinable porous polymethylmethacrylate materials. Mol. Cryst. Liq. Cryst. 2017, 647, 341–350. [Google Scholar] [CrossRef]
- Lim, K.C.; Margerum, J.D.; Lackner, A.M.; Miller, L.J.; Sherman, E.; Smith, W.H., Jr. Liquid crystal birefringence for millimeter wave radar. Liq. Cryst. 1993, 14, 327–337. [Google Scholar] [CrossRef]
- Lim, K.C.; Margerum, J.D.; Lackner, A.M. Liquid crystal millimeter wave electronic phase shifter. Appl. Phys. Lett. 1993, 62, 1065–1067. [Google Scholar] [CrossRef]
- Strunck, S.; Karabey, O.H.; Gaebler, A.; Jakoby, R. Reconfigurable waveguide polariser based on liquid crystal for continuous tuning of linear polarization. Electron. Lett. 2012, 48, 441–443. [Google Scholar] [CrossRef]
- Dolfi, D.; Labeyrie, M.; Joffre, P.; Huignard, J.P. Liquid crystal microwave phase shifter. Electron. Lett. 1993, 29, 926–927. [Google Scholar] [CrossRef]
- Guerin, F.; Chappe, J.M.; Joffre, P.; Dolfi, D. Modeling, synthesis and characterization of a millimeter-wave multilayer microstrip liquid crystal phase shifter. Jpn. J. Appl. Phys. 1997, 36, 4409–44413. [Google Scholar] [CrossRef]
- Kuki, T.; Fujikake, H.; Nomoto, T.; Utsumi, Y. Design of a microwave variable delay line using liquid crystal, and a study of its insertion loss. IEICE Trans. C 2001, J84, 90–96. (In Japanese) [Google Scholar] [CrossRef]
- Kuki, T.; Fjikake, H.; Kamoda, H.; Nomoto, T. Microwave variable delay line using a membrane impregnated with liquid crystal. In Proceedings of the 2002 IEEE MTT-S International Microwave Symposium Digest, Seattle, WA, USA, 2–7 June 2002; pp. 363–365. [Google Scholar]
- Splingart, B.; Tentillier, N.; Huret, F.; Legrand, C. Liquid crystals application to R. F. and microwave tunable components. Mol. Cryst. Liq. Cryst. 2001, 368, 183–190. [Google Scholar] [CrossRef]
- Weil, C.; Luessem, G.; Jakoby, R. Tunable inverted-microstrip phase shifter device using nematic liquid crystals. In Proceedings of the 2002 IEEE MTT-S International Microwave Symposium Digest, Seattle, WA, USA, 2–7 June 2002; pp. 367–370. [Google Scholar]
- Karabey, O.H.; Bildik, S.; Strunck, S.; Gaebler, A.; Jakoby, R. Continuously polarisation reconfigurable antenna element by using liquid crystal based tunable coupled line. Electron. Lett. 2012, 48, 141–143. [Google Scholar] [CrossRef]
- Garbvskiy, Y.; Zagoridnii, V.; Krivosik, P.; Lovejoy, J.; Camley, R.E.; Celinski, Z.; Glushchenko, A.; Dziaduszek, J.; Dabroeski, R. Liquid crystal phase shifter at millimeter wave frequencies. J. Appl. Phys. 2012, 111, 054504. [Google Scholar] [CrossRef]
- Ito, R.; Kawakami, T.; Ito, Y.; Sasamori, T.; Isota, Y.; Honma, M.; Nose, T. Fundamental properties of novel design microstrip line type of liquid crystal phase shifter in microwave region. Jpn. J. Appl. Phys. 2012, 51, 044104-1–044104-5. [Google Scholar] [CrossRef]
- Nose, T.; Chien, L.; Catanescu, O.; Golvin, A.; Ito, Y.; Sasamori, T.; Isota, Y.; Ito, R.; Honma, M. Improved high-frequency performance of microstrip-line-type liquid crystal phase shifter. Jpn. J. Appl. Phys. 2013, 52, 091701-1–091701-5. [Google Scholar] [CrossRef]
- Nose, T.; Ito, Y.; Iisaka, T.; Chien, L.; Catanescu, O.; Golvin, A.; Isota, Y.; Sasamori, T.; Ito, R.; Honma, M. High-frequency performance extending to millimeter-waves in inverted-microstrip-line-type LC phase shifter. Proc. SPIE 2013, 8642, 864206. [Google Scholar]
- Nose, T.; Komuro, T.; Sasamori, T.; Isota, Y.; Watanabe, T.; Ito, K.; Ito, R.; Honma, M. Fundamental performance of liquid crystal millimeter-wave phase shifter using negative dielectric anisotropic material. In Proceedings of the 2014 39th International Conference on Infrared, Millimeter, and Terahertz waves (IRMMW-THz), Tucson, AZ, USA, 14–19 September 2014. [Google Scholar]
- Nose, T.; Saito, S.; Yanagihara, S.; Honma, M. Molecular orientation effects in the CPW type LC phase shifters for MMW phase shifting. Proc. SPIE 2006, 6135, 6135F. [Google Scholar]
- Nose, T.; Yanagihara, S.; Honma, M. Operational mode of millimeter-wave phase shifter using liquid crystal materials with coplanar waveguide. Jpn. J. Appl. Phys. 2007, 46, 1114–1117. [Google Scholar] [CrossRef]
- Nose, T.; Yanagihara, S.; Sato, Y.; Ito, R.; Honma, M. Improvement of phase-shifting properties in coplanar waveguide-type liquid crystal millimeter-wave phase shifter by introducing a resonant phenomenon. Jpn. J. Appl. Phys. 2008, 47, 8483–8486. [Google Scholar] [CrossRef]
- Wiltse, J.C. Recent developments in Fresnel zone plate antennas at microwave/millimeter wave. Proc. SPIE 1998, 3464, 146–154. [Google Scholar]

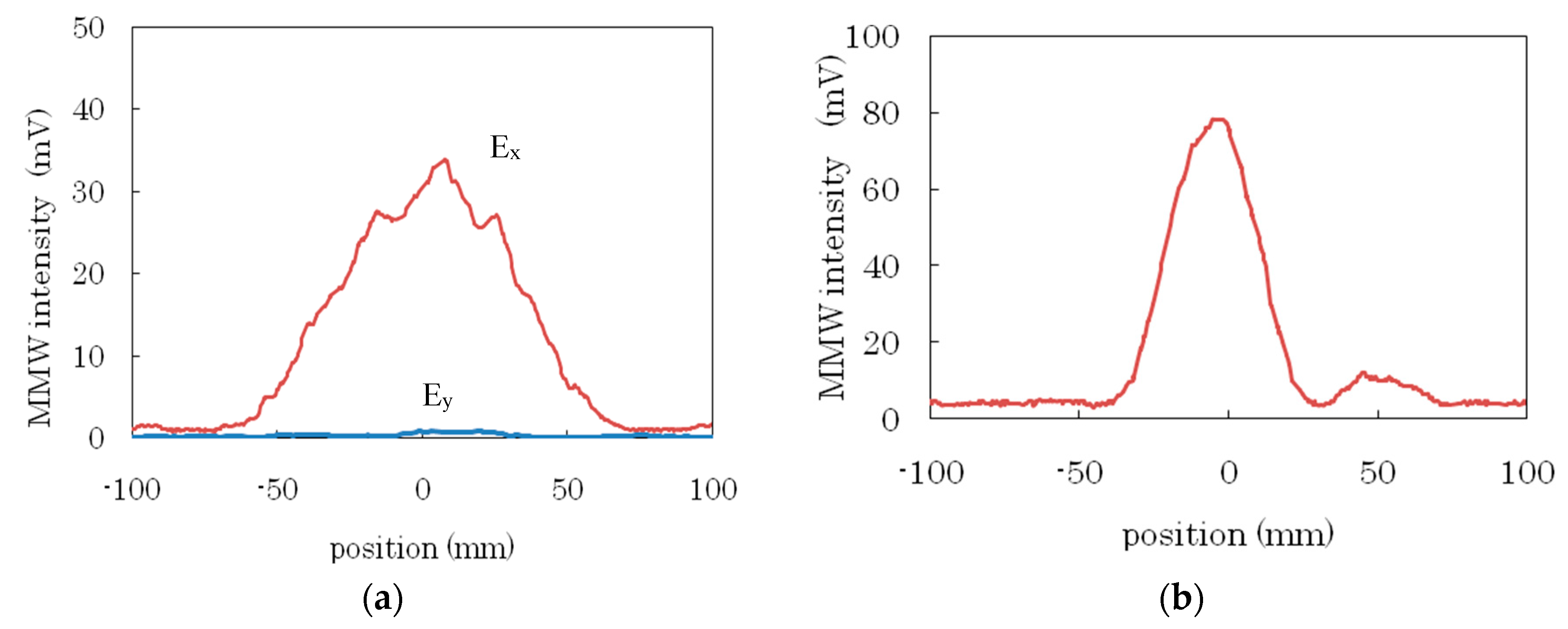
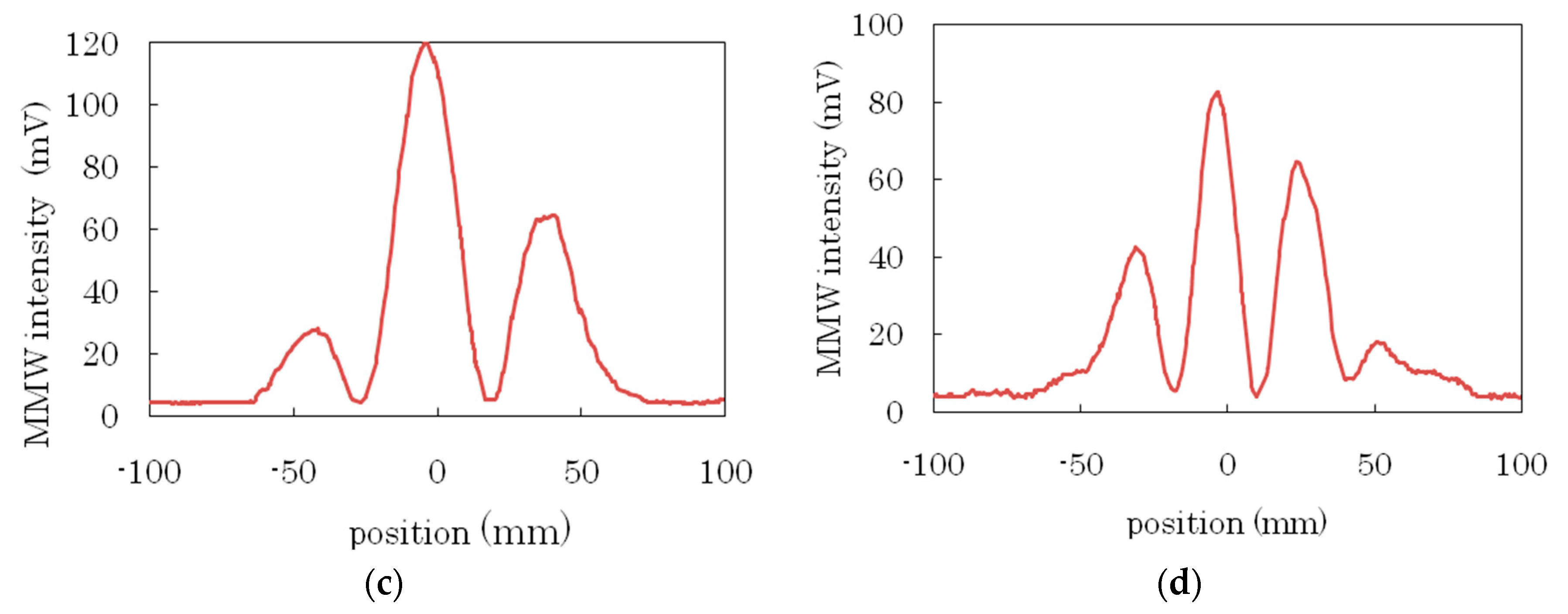
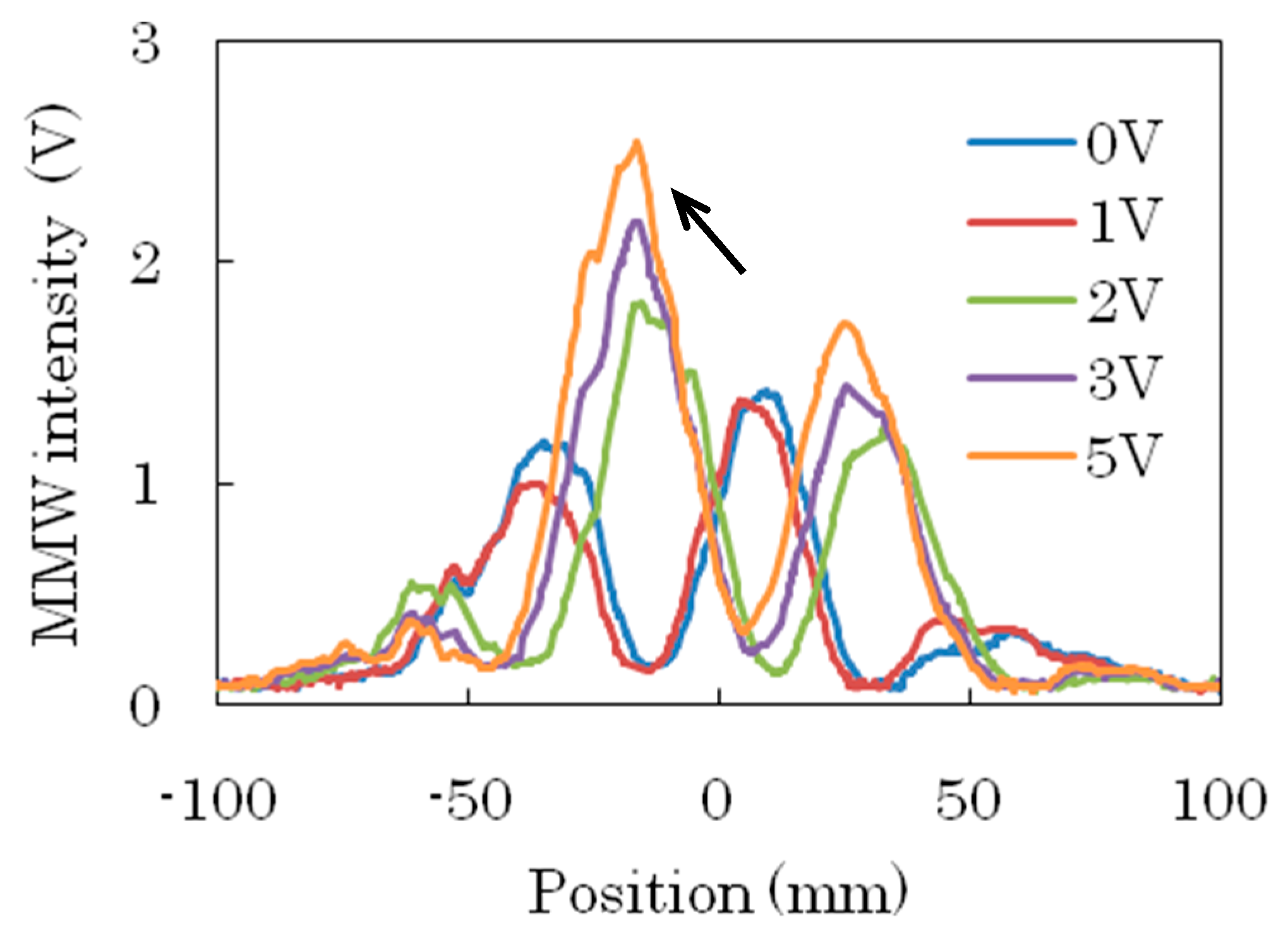
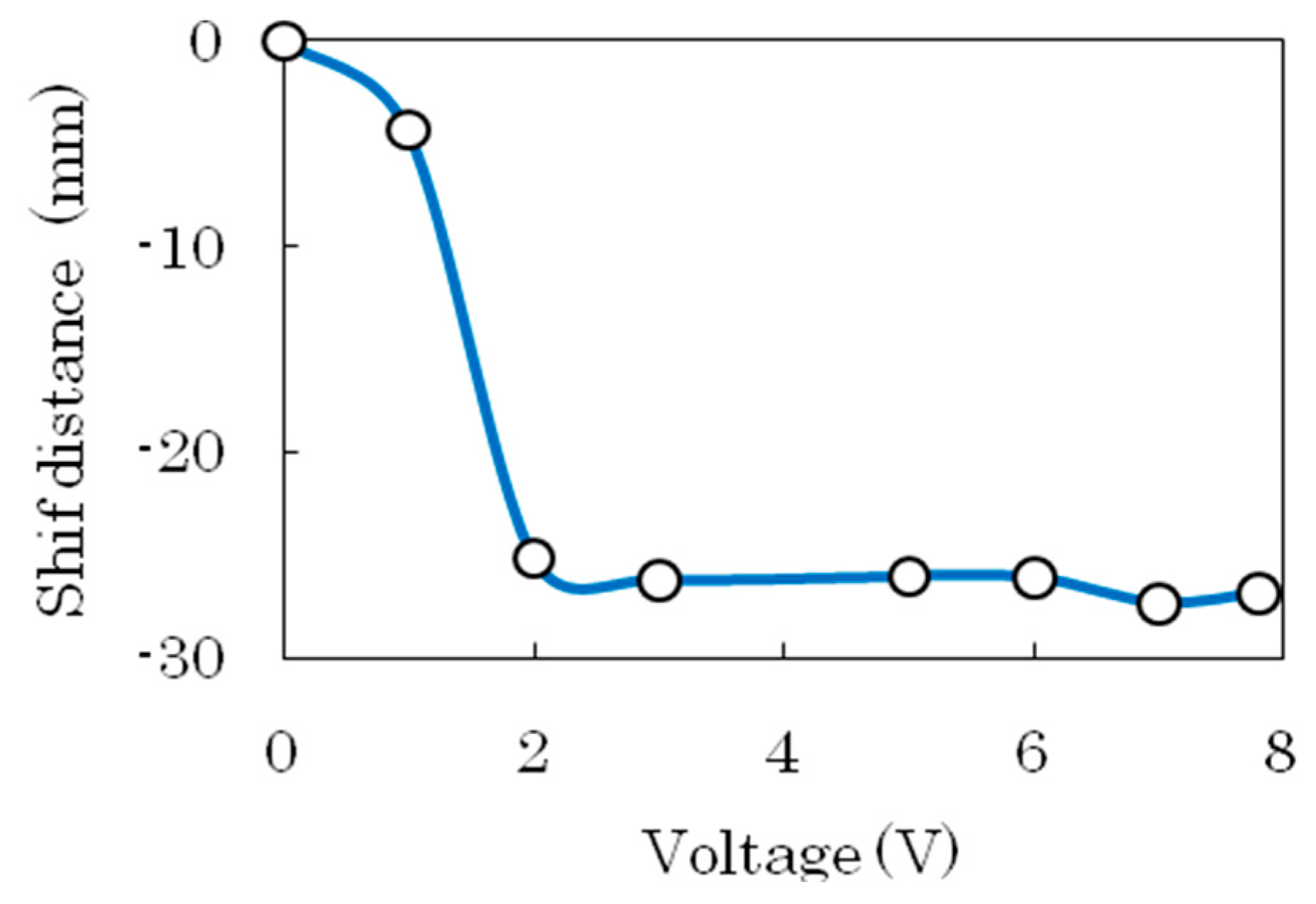
| λg (mm) | n | εr | α (mm−1) | |
|---|---|---|---|---|
| Measurement | 2.77 | 2.71 | 7.34 | 0.079 |
| Reference | - | 3.6 | 13 | 0.011 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nose, T.; Ito, R.; Honma, M. Potential of Liquid-Crystal Materials for Millimeter-Wave Application. Appl. Sci. 2018, 8, 2544. https://doi.org/10.3390/app8122544
Nose T, Ito R, Honma M. Potential of Liquid-Crystal Materials for Millimeter-Wave Application. Applied Sciences. 2018; 8(12):2544. https://doi.org/10.3390/app8122544
Chicago/Turabian StyleNose, Toshiaki, Ryota Ito, and Michinori Honma. 2018. "Potential of Liquid-Crystal Materials for Millimeter-Wave Application" Applied Sciences 8, no. 12: 2544. https://doi.org/10.3390/app8122544
APA StyleNose, T., Ito, R., & Honma, M. (2018). Potential of Liquid-Crystal Materials for Millimeter-Wave Application. Applied Sciences, 8(12), 2544. https://doi.org/10.3390/app8122544




