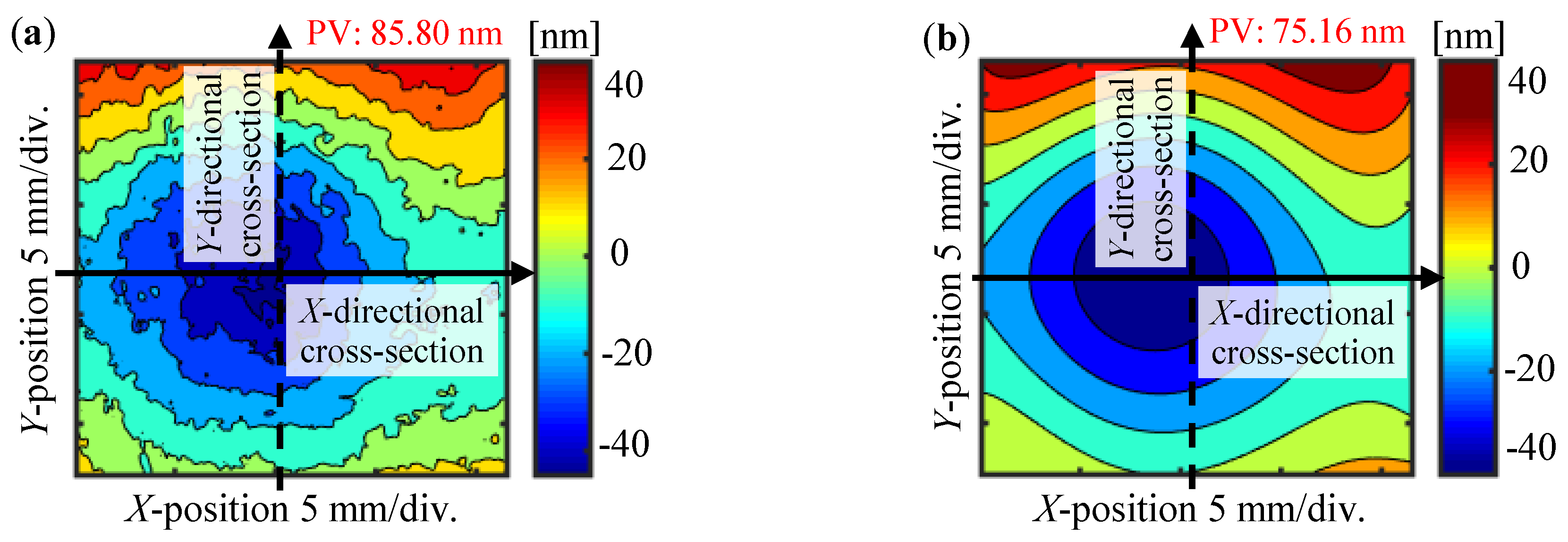
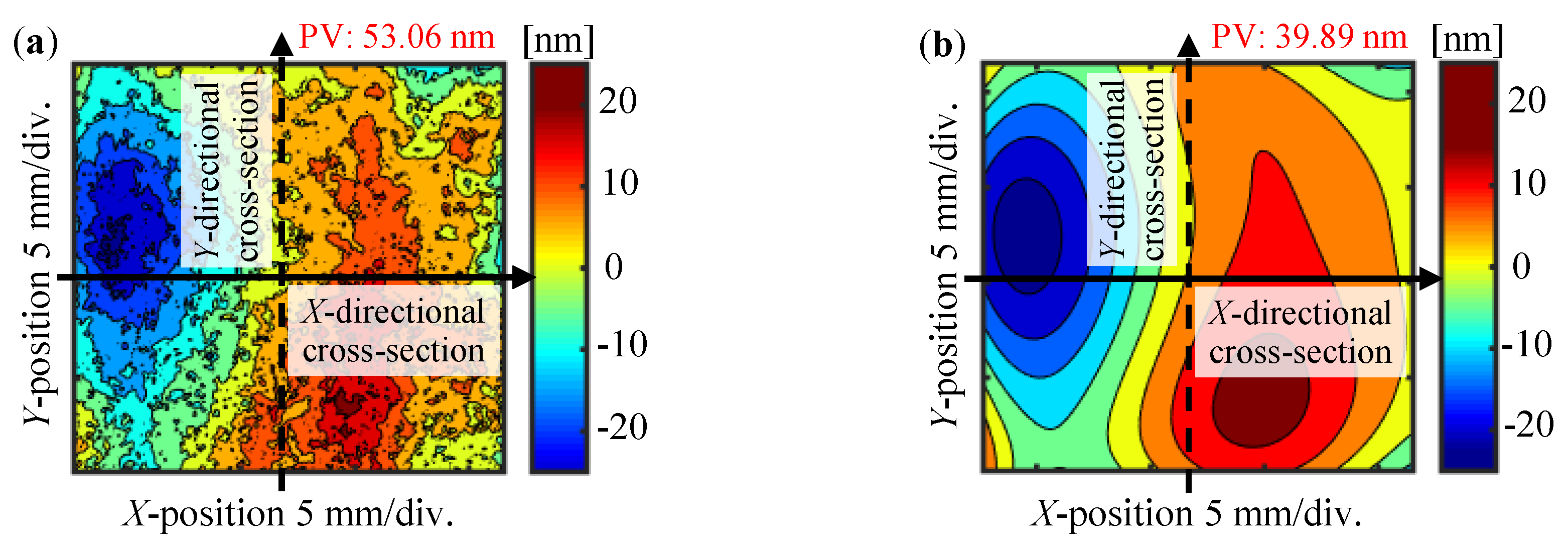
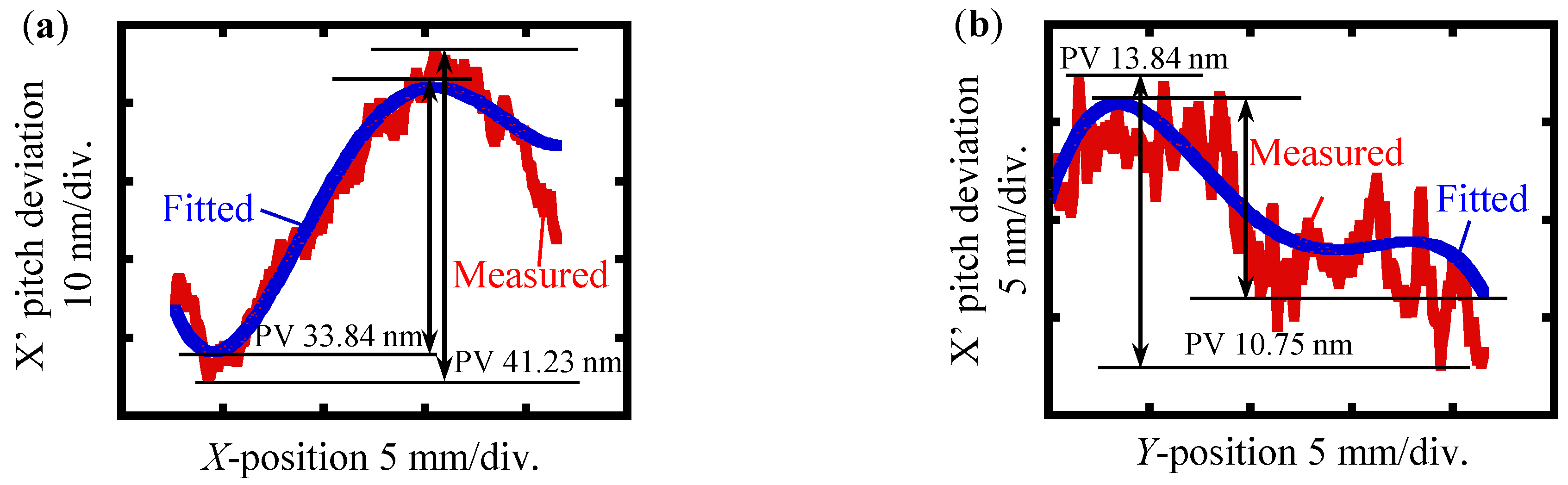
1. Introduction
An optical encoder, which is mainly composed of an optical sensor head and a scale grating, is one of the most commonly used sensors for precision positioning in production engineering [
1], due to the advantages of non-contact measurement, a high resolution, and a wide bandwidth [
2]. In the case of incremental type one-axis encoders, a diffraction grating having periodic line pattern structures is employed as a scale for measurement of relative translational displacement between the scale grating and an optical sensor head [
3]. With the employment of a planar scale grating having two-dimensional grating pattern structures [
4], the dimension of displacement/position measurement can be expanded to two or more [
5,
6]. Among the components in a multi-axis planar encoder system [
5], a planar scale grating having periodical structures along the
X- and
Y-directions is one of the key components that influence the accuracy of measurement, since the period of interference signal in the optical head, which will be interpolated and used to calculate the displacement, is directly influenced by the pitch of the scale grating, in principle [
4]. Moreover, the
Z-directional out-of-flatness of the scale grating could also be a source of measurement uncertainty in the planar encoder system. The
X- and
Y-directional pitch deviations, as well as the out-of-flatness of the scale grating, are thus required to be evaluated and calibrated over the entire surface of a scale grating for high precision measurement applications [
7].
Line scale comparator [
8,
9] and scanning probe microscopes (SPMs) [
10,
11] are available as conventional solutions to evaluate the pitch deviations of a planar scale granting. The line scale comparator has long been used in the enterprises that manufacture linear encoders and national standard institutes for testing one-axis linear scale gratings [
8,
9]. However, it is too expensive to construct a measurement system for two-dimensional scale grating that is based on the line scale comparator. Another drawback of the line scale comparator is that the out-of-flatness of a planar scale grating cannot be measured in principle. Meanwhile, SPMs can measure both the grating pitch deviations and the out-of-flatness of a planar scale grating. However, on the other hand, a limited scanning area and a measurement throughput of SPMs [
11] prevent them being applied for the evaluation of planar scale grating, especially for the condition of laboratory-level, it may take hours and days to conduct the measurement of a large size planar scale grating over its whole area.
In responding to the background described above, the authors’ group has proposed a method to simultaneously evaluate both the
X- and
Y-directional pitch deviations and the
Z-directional out-of-flatness of a planar scale grating by utilizing a Fizeau interferometer in the previous work [
7]. In the propose method, wavefront of the zeroth-order diffracted beam and wavefronts of positive and negative first-order diffracted beams from a scale grating obtained in Littrow configurations were utilized to perform a non-contact evaluation of a planar scale grating over the entire area. The feasibility of proposed method has been verified in experiments [
7]. In addition, the proposed method has been improved so that the self-calibration of the Fizeau interferometer and the planar scale grating can be conducted simultaneously while considering the out-of-flatness of the reference optical flat and the change of the coordinate system in the Littrow configuration [
12]. As the first step of the research, a preliminary verification of the improved method has been performed successfully through the simulation in both the noise-free and noisy cases [
12]. The key advantage of this method is that the measurement using the Fizeau interferometer can be carried out without significant investments in time and/or capital to assess the out-of-flatness and pitch deviations of the planar scale grating accurately compared with other measurement techniques. Nevertheless, further experimental demonstration as well as the uncertainty analysis of the proposed method have not been conducted yet, and they remain to be addressed.
In this paper, as the second step of the research, experimental verification of the feasibility of the improved method [
12] has been conducted as well as the uncertainty analysis when considering the possible error factors influencing the measurement uncertainties, such as the form error of the reference surface in a Fizeau interferometer or the inclination error of a scale grating in measurement. Theoretical equations are derived to evaluate the influence of the error factors on the final uncertainties in the measured
Z-directional out-of-flatness as well as the
X- and
Y-directional pitch deviations of a scale grating. Moreover, when considering the drawbacks of the traditional uncertainty matrix approach [
13], which is intellectually satisfying but difficult to handle or specify the surface form in a straightforward way, a method aiming to evaluate the uncertainty by using one of the simplest but most commonly used peak-to-valley (P-V) deviation of the surface form is proposed. Experiments are also conducted to demonstrate the feasibility of the proposed method.
2. Measurement Principle
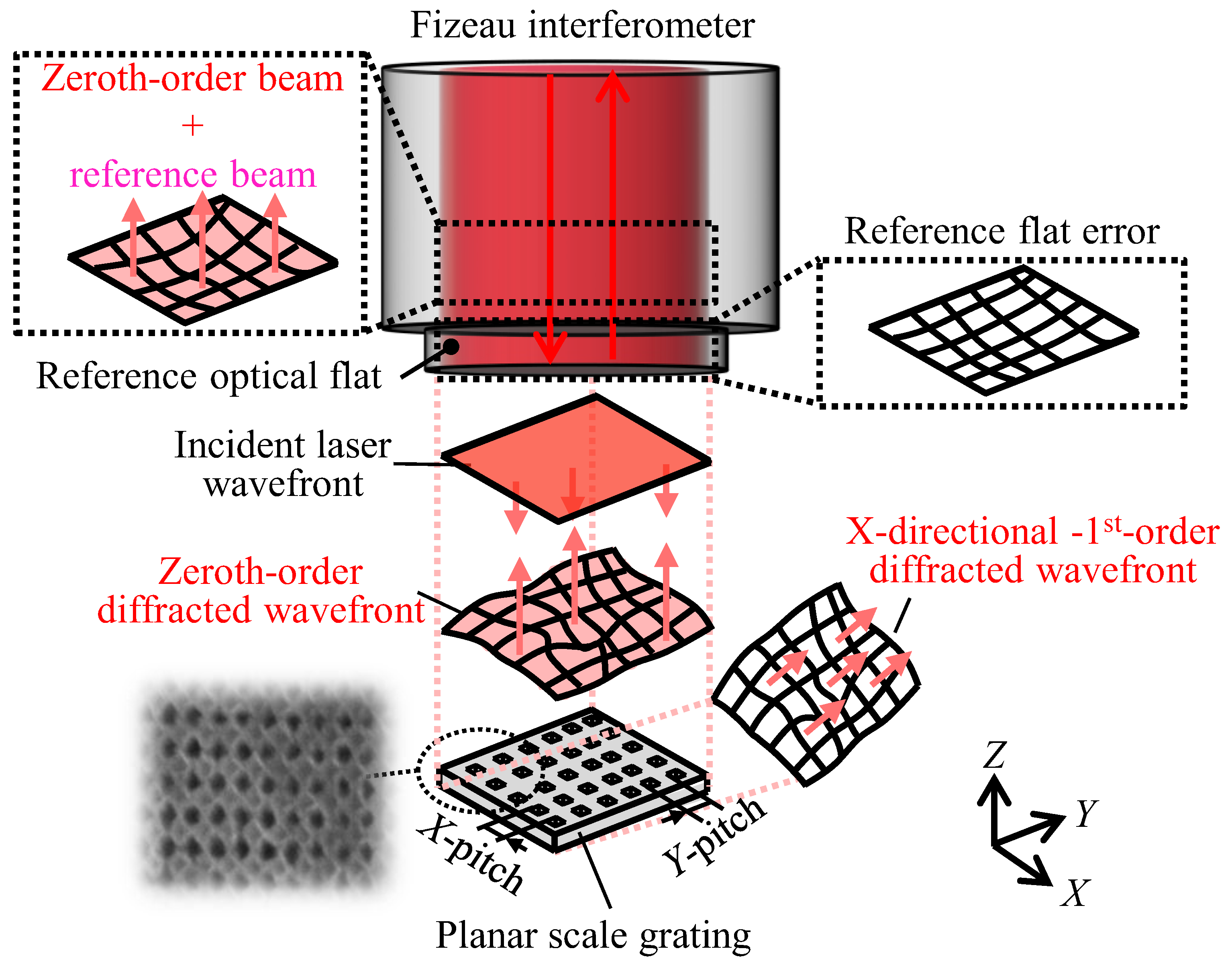
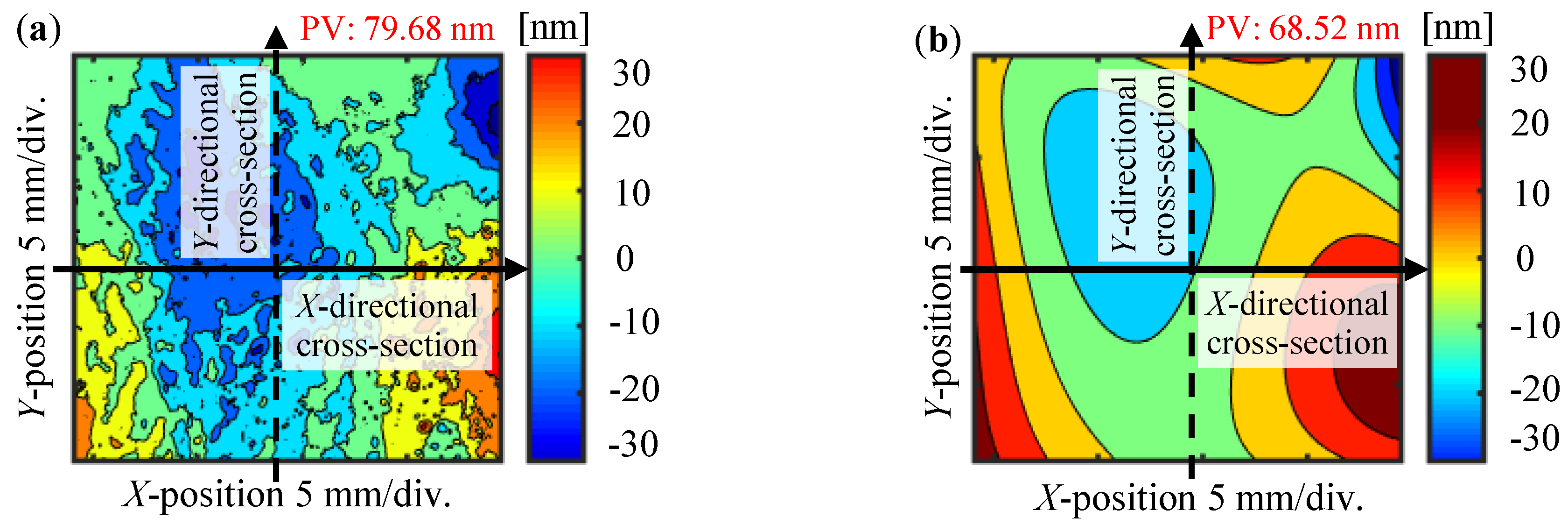
Figure 1 demonstrates the measurement of the
Z-directional out-of-flatness of a planar scale grating
eZ(
x,
y) using the typical function of the Fizeau interferomter. Assume that the field-of-view (FOV) of the Fizeau interferometer is larger than the size of the grating employed for measurement. As can be seen in the figure, the wavefront of the zeroth-order diffracted beam from the grating superimposed on the wavefront of the reflected beam from the reference optical flat. Consequently, the zeroth-order phase output
I0(
x,
y) from the interferometer can be expressed by the following equation [
7]:
where
λ represents the light wavelength of the laser source and
eR(
x,
y) represents the out-of-flatness of the reference optical flat in the Fizeau interferometer. The out-of-flatness of the grating
eZ(
x,
y) can be obtained by the following equation according to Equation (1):
As can be seen in Equation (2), the result of
eZ(
x,
y) contains the out-of-flatness of the reference flat
eR(
x,
y). Since the calibration of the absolute flatness of the reference flat is quite complicated in practice [
14], in this paper, the mean (average or expectation) of
eR(
x,
y) is taken to be zero and its uncertainty being the specified peak-to-valley (PV) value, which is typically less than
λ/20 over the whole field of view (FOV) of a commercial Fizeau interferometer.
For the evaluation of
X-directional pitch deviation
eX(
x,
y) and
Y- directional pitch deviation
eY(
x,
y) of the planar scale grating, measurement of the wavefronts of the
X and
Y-directional positive and negative first-order diffracted beams in Littrow configurations is needed.
Figure 2 shows an example of the Littrow configuration for the measurement of the wavefront of
X-directional positive first-order diffracted beam, where the grating is tilted clockwise, so that the
X-directional positive first-order diffracted beam is back-reflected directly into the direction of the incident laser beam and superimposed with the reference beam in the Fizeau interferometer. Assume that the actual inclination angle in measurement
θ1 can be represented by
θ1 =
θ/2 +
ε1, where
θ = arcsin(
λ/
g) is the first-order diffraction angle,
ε1 is the misalignment of
θ, and
g is the nominal pitch of the grating along the
X-direction. The
X-directional pitch deviation
eX(
x,
y) of the planar scale grating causes a phase shift in the wavefront of the diffracted beam [
7]. As depicted in
Figure 2, the coordinate system has changed after setting the grating in Littrow configuration. Since the measurement results should correspond to the original grating coordinate system, the
X-directional positive first-order phase output
IX+1(
x,
y) that was obtained in the Fizeau measurement can be described, as follows:
where
α1 = cos
θ1. In the same manner, the wavefront of the
X-directional negative first-order diffracted beam can be measured by tilting the scale grating counterclockwise with an opposite inclination angle, the
X-directional negative first-order phase output
IX−1(
x,
y) can be obtained, as follows:
where
α2 = cos
θ2. By using the error
ε2 in the alignment of
θ2 in measurement of the negative first-order diffracted beam,
θ2 can be represented as
θ2 = −
θ/2 +
ε2. According to Equations (3) and (4), the following equation can be obtained:
In the same manner, the
Y-directional pitch deviation
eY(
x,
y) of the planar scale grating can be obtained as follows by measuring the
Y-directional positive and negative first-order phase outputs
IY+1(
x,
y) and
IY−1(
x,
y), respectively:
where
= cos
θ′
1 = cos(
θ/2 +
ε′
1) and
α’
2 = cos
θ’
2 = cos(
θ/2 +
ε′
2).
ε′
1 and
ε′
2 represent the misalignments of
θ in the measurement of the wavefronts of the
Y-directional positive and negative first-order diffracted beams, respectively. Note here that the nominal pitches of the planar scale grating along the
X- and
Y-directions are assumed to be the same for the sake of simplicity. According to Equations (6) and (7), the following equation can be obtained:
In the following section of this paper, how to further obtain the mean values and uncertainties of eZ(x,y), eX(x,y), and eY(x,y) according to Equations (2), (5), and (8) are presented. Since the evaluations of the mean value and uncertainty of eY(x,y) are similar to those of eX(x,y), only the latter is focused in the following for the sake of clarity.
3. Uncertainty Evaluation
Major sources of uncertainty in the evaluation of out-of-flatness
eZ(
x,
y) and pitch deviation
eX(
x,
y) of a planar scale grating by a Fizeau interferometer primarily arise from uncertainties in the measured phase outputs
I0(
x,
y) and
IX±1(
x,
y). In addition, out-of-flatness
eR(
x,
y) of the reference flat in a Fizeau interferometer and uncertainties in the nominal pitch
g of the planar scale grating under test, as well as the inclination angles
θ1 and
θ2, could also be major sources of uncertainty. According to the GUM (guide to the expression of uncertainty in measurement) [
13], the uncertainties in
I0(
x,
y) and
IX±1(
x,
y) attribute to the Type A evaluation, while those in
eR(
x,
y),
g,
θ1 and
θ2 attribute to the Type B evaluation. Through the uncertainty analysis, The
E(·),
σ(·) and
σ2(·) are used to represent the mean, standard deviation, and variance of a random variable, respectively. The expanded uncertainty of a random variable is given by
u(·) =
kσ(·), where
k denotes the coverage factor;
k = 2 produces a confidence interval of approximately 95%; and,
k = 3 produces an interval with a confidence of approximately 99%.
As mentioned in
Section 2, in this paper, the mean and 3
σ uncertainty of
eR(
x,
y) are treated to be zero and the specified PV value, respectively. The uncertainty in the inclination angles
θ1 and
θ2 contains two components; one is the uncertainty induced by the deviation of the nominal grating pitch with respect to its true value, and another is induced by the misalignments in measurement. In the uncertainty analysis, the means of
θ1 and
θ2 are taken to be
θ/2 and −
θ/2, respectively, and the uncertainties that are induced by the misalignments are assumed to be identical; namely,
σ(
ε1) =
σ(
ε2). Due to the independence between
θ and
ε1 (
ε2), the means of
α1 and
α2 will be cos(
θ/2), which is denoted as
α in the following (
α = cos(
θ/2)). By taking the means for both sides of Equations (2) and (5), the following equations can be obtained:
It should be pointed out that here has E[α1eZ(x/α1,y)] = E[α2eZ(x/α2,y)] mathematically. In practical experiments, the second term of the right side of Equation (5) could be minimized by making interference fringes of the Fizeau interferometer minimum though adjusting the tilt stage on which the scale grating is fixed. Although the influence from the out-of-flatness of the substrate surface cannot completely be eliminated by the differential operation, when considering the holographic grating with a good surface quality, the effect on the evaluation of the pitch deviation can be ignored by conducting the operation mentioned above.
A straightforward approach to evaluate the uncertainty in the obtained
eZ(
x,
y) and
eX(
x,
y) is to generate a matrix, called the uncertainty matrix [
15], which has the same size to
eZ(
x,
y) or
eX(
x,
y) and it contains the corresponding uncertainty of
eZ(
x,
y) or
eX(
x,
y) at every pixel position (
xi,
yj) (
I = 1, 2, …,
M;
j = 1, 2, …,
N). Taking the propagation of errors into consideration, the variances
σ2[
eZ(
x,
y)] and
σ2[
eX(
x/
α,
y)] can be represented, as follows:
where the variance
σ2(
α) is evaluated by the following equation:
The first and second terms in curly brackets of the right side of Equation (13) correspond to the uncertainties that are induced by the deviation of the nominal grating pitch to its true value and the misalignment in measurement, respectively. It should be noted from Equations (11) and (12) that, for
eZ(
x,
y), the corresponding uncertainty matrix can be obtained, while for
eX(
x,
y) it cannot, because of the change in the coordinate system after tilting the scale gating. Moreover, as shown in Equation (12), even for
eX(
x/
α,
y), the corresponding uncertainty matrix cannot be obtained either due to the involvement of the evaluation of the unknown
eZ(
x/
α,
y), ∂
eZ(
x/
α,
y)/∂
α, and
σ2[
eZ(
x/
α,
y)]. On the other hand, it should be pointed out that the uncertainty matrix approach has a number of drawbacks in practice. As stated in [
16], the information density that is contained in the uncertainty matrix is too high for users who only want a single number. In addition, the uncertainty matrix cannot easily be used for the decision of either acceptance or rejection. Evaluations of measurement uncertainty should be expressed in a manner that is informative and actionable [
17]. Therefore, in this paper, a PV value is adopted to evaluate the quality of the obtained form errors. Although a PV value also has inadequacies in charactering surfaces, it is still widely recognized that a PV value remains one of the most commonly used specifications of surface form errors [
18]. Next, the details are presented in evaluating a PV value and its uncertainty for the characterization of
eZ(
x,
y) and
eX(
x,
y).
In this paper, the form errors
eZ(
x,
y) and
eX(
x,
y) are assumed can be characterized in terms of polynomials. This assumption is reasonable, since, as stated in [
19], the low-frequency errors can be completely modeled by the set of polynomials and are of the main concern in the application. Moreover, modeling the form errors in terms of polynomials is also favorable to evaluate the associated PV values since the estimated PV values will not be biased by the high-frequency noises contained in the raw data. Without losing generality, the
n-degree bivariate polynomials are used to fit the discrete form errors (
xi,
yj,
E[
eZ(
xi,
yj)]) and (
xi,
yj,
E[
eX(
xi/
α,
yj)]) obtained at each pixel position (
xi,
yj), according to Equations (9) and (10), as follows:
where the matrices
A and
B′ contain the undetermined coefficients of the fitted bivariate polynomials. As noted from Equations (14) and (15), here the set of
n-degree bivariate polynomials are used to fit the form errors of the scale grating. In addition, the highest degree for
x and
y coordinates is not necessary to be identical, but it depends on the actual fitting performance. With Equations (14) and (15), the
eZ(
x/
α,
y) and
eX(
x,
y) can be obtained, as follows:
where
According to Equations (14), (16), and (18), once the matrix A is obtained, the eZ(x/α,y), ∂eZ(x/α,y)/∂α, σ2[eZ(x/α,y)] can also be calculated successively, and finally σ2[eX(x/α,y)] by Equation (12), eZ(x/α,y) by Equation (16), eX(x,y) by Equations (17) and (19), and also σ2[eX(x,y)]. With the obtained eZ(x,y), σ2[eZ(x,y)], eX(x,y), and σ2[eX(x,y)], evaluation of the PV values and the associated uncertainty for both eZ(x,y) and eX(x,y) can also be conducted. Since the procedures for obtaining the matrices A and B′ are similar, only the determination of the matrix A is presented in the following.
Taking the vectorization operator on both sides of Equation (14) leads to
where vec(·) signifies the vectorization operator that converts a matrix into a column vector, and the symbol
represents the Kronecker product. Discarding the zero elements in vec(
A) and denoting the processed vec(
A) as a vector
a = [
a0,
a1,
a2, …,
aK−1]
T (
K = (
n + 1)(
n + 2)/2) and then choosing new basis functions Ξ
k (
k = 0, 1, 2, …,
K−1), where Ξ
k {1,
x,
y,
x2,
xy,
y2, …,
xyn−1,
yn}, the Equation (20) can be rewritten, as follows:
where the variable
ξ represents the value of the terms
x,
y,
x2,
xy,
y2, …,
xyn−1,
yn at any pixel position (
xi,
yj) (
i = 1, 2, …,
M;
j = 1, 2, …,
N), and
η(
ξ) represents the value of vec[
eZ(
x,
y)] at the corresponding pixel position. To determine the elements in vector
a, the general linear least-squares method [
20] is used by defining a merit function, as follows:
where
ηl corresponds to the value
E[
eZ(
xi,
yj)] given in Equation (9) and
σ(
ηl) is corresponding standard deviation
σ[
eZ(
xi,
yj)], as obtained by Equation (11). In addition, an
MN ×
K matrix
D, which is also called the design matrix of the fitting problem, is defined with elements given as follows:
Also, define a vector
b of length
MN with elements, as follows:
The minimum of Equation (22) occurs where the derivative of
χ2 with respect to all
K parameters
ak vanish. This condition yields the following matrix equation:
According to Equation (25), the least-squares estimation of vector a can be obtained, as follows:
where
D+ = (
DTD)
−1DT is the Moore-Penrose pseudo-inverse of
D. Let’s denote the matrix (
DTD)
−1 as
C, namely,
C = (
DTD)
−1, which is also called the covariance matrix and it has a close relation with the uncertainties of the estimated parameters
ak (
k = 0, 1, 2, …,
K − 1) by Equation (26). Specifically, the variance in
ak can be evaluated by
where
Ckk is the
k-th diagonal element of the matrix
C. According to Equations (26) and (27), the least-square estimation
Apq (
p,
q = 0, 1, 2, …,
n) of all elements in matrix
A as well as their uncertainties
u(
Apq) can be finally obtained.
With the estimated elements
Apq and their uncertainties
u(
Apq), the uncertainty of
eZ(
x,
y) at any pixel position (
xi,
yj) can be further evaluated. Specifically, according to Equation (14), there is
eZ(
xi,
yj) =
xiTAyj, which can be regarded as a linear function of the coefficients
Apq. The evaluation of the upper and lower bounds of
eZ(
xi,
yj) can be transformed into a simple linear programming problem [
21], described as follows:
where Equations (28a) and (28b) yield the upper and lower bounds of
eZ(
xi,
yj), respectively. The uncertainty of
eZ(
x,
y) at the pixel position of (
xi,
yj) is then evaluated by
In addition, according to Equation (18), the least-squares estimation
A′
pq of elements in matrix A′ can be calculated, as follows:
It follows that the uncertainty in
A′
pq can be evaluated by the following equation:
With A′pq and u(Apq), the values of eZ(x/α,y) and ∂eZ(x/α,y)/∂α can be obtained at any pixel position of (xi,yj). The uncertainty of eZ(x/α,y) at any pixel position (xi,yj) can be also evaluated in a similar manner to Equation (28). Likewise, the value of eX(x,y) and its uncertainty u[eX(x,y)] at any pixel position (xi,yj) can be calculated as well.
The PV value of
eZ(
x,
y) in the region Ω of interest can be evaluated by
where max(·) and min(·) represent the maximum and minimum of a function. The peak and valley values of
eZ(
x,
y), max[
eZ(
x,
y)], and min[
eZ(
x,
y)] can be readily calculated according to the obtained expression of
eZ(
x,
y). The uncertainty in the calculated PV of
eZ(
x,
y) can then be evaluated, as follows:
where
up[
eZ(
x,
y)] and
uv[
eZ(
x,
y)] represent the uncertainties of
eZ(
x,
y) at the peak and valley positions, respectively, which can be directly obtained by substituting the coordinates of the peak and valley positions into Equation (29).
Other approaches to evaluate the uncertainty in PV could simply double the maximum value of the uncertainty matrix or applying the Monte Carlo (MC) simulation. However, the former method obviously overestimates the uncertainty in the PV, except coincidence. The MC method could estimate the PV uncertainty by collecting the PV value in each trail assuming that all of the significant errors are included and the probability distributions of each error source is known. Nevertheless, it is burdensome to run the simulation when routine experiment is conducted in a similar condition and the noise could exist explicitly in the evaluated results. Therefore, in this paper, the MC method is not employed, but just the part of error form is analyzed directly to evaluate the uncertainty in the peak and valley separately, and then combine them together. Since the PV of each error form is usually larger than the uncertainty in this experiment, this method is thus a reasonable way to obtain the uncertainty in PV.
As can be noted from the above description, the success of the proposed evaluation method lies on the fitting performance of the polynomials fitted to
eZ(
x,
y) and
eX(
x/
α,
y). There are two measures that are commonly used to evaluate the goodness-of-fit in statistics. One is the coefficient of determination
R2, while another is the reduced chi-square
χ2, which for the polynomial fitted to
eZ(
x,
y) are defined, as follows:
where
v =
MN ×
K signifies the degree-of-freedom in the least-square regression. Typically, 0 <
R2 < 1, and the larger the
R2 is, the better the polynomial model fits the data. For the reduced chi-square,
χv2 = 1 indicates that the model properly fits the data, while
> 1 indicates that the fit does not fully capture the data (or that the variance
σ2(
ηl) is underestimated) and
< 1 indicates that the model overly fits the data (either the model improperly fits the noise or the variance
σ2(
ηl) is overestimated). According to the value of
, the variance of
ak that is represented in Equation (27) is usually rescaled as follows in order to pass the
χ2-test:
In addition, as illustrated in Equation (26), the least-squares estimation of vector a can be obtained by calculating the Moore-Penrose pseudo-inverse of the design matrix
D. It should be pointed out that this solving approach is susceptible to round-off error in practice and it will lead to errors in both the solution
a and its uncertainty, especially when the variance
σ2(
ηl) (corresponds to the variance
σ2(
eZ(
xi,
yj))) is not uniform at different pixel positions. To relieve the round-off problem, the solution by use of the singular value decomposition is recommended [
22].