1. Introduction
The energy performance of heat emitters is a key factor in the energy demand of the building sector, which is primarily determined by space heating [
1,
2,
3]. Such devices can be of very different type (panel radiators, convectors, ceiling and underfloor heating …), each determining the energy demand in a specific way [
4,
5,
6,
7,
8]. For these reasons, several studies have investigated the emitters’ performance on both the experimental and theoretical viewpoint [
9,
10,
11], focusing especially on the design, specific type and room placement of panel radiators (e.g., close to a window or slightly detached from a wall) [
4,
12,
13,
14,
15,
16,
17,
18]. For instance, measurements have shown a better performance of low temperature panel radiators [
19], and a sensibly different outcome for serial and parallel connected radiators [
9].
Despite such recent advances, this kind of investigation seems to be very involved, for a variety of reasons. Contrasting results also exist: an experimental investigation of a convector, a radiant and a baseboard heater showed a lower energy consumption by the convector [
7], in contrast with the classic work by Olesen et al. [
4], written in the early 80s. While it was concluded in [
7] that the cause was probably the improved flow outlet design of the newer convector, an older study already considering this improvement [
13] agreed instead with [
4].
Previous research regarding the energy performance of heat emitters has largely dealt with matters of emission efficiency and losses within the system. In such a framework, one typically addresses the emitted power and energy usage by the system under predefined boundary conditions [
20,
21]. So far, this approach has been effective enough for product characterisation. However, the methodology fails to take into account the different levels of thermal comfort provided by the heaters at equal air temperature (which is the target value that is kept constant throughout product comparison). Such a difference in the thermal environment can affect negatively even the perceived productivity in the workplace, with a seizable economical impact [
22,
23]. More importantly, accounting for this phenomenon could allow for some direct energy savings if different set-points within the heating systems could be used.
Thermal comfort within an enclosure can be quantified with the so-called operative temperature (hereinafter op.t. or
), which is finding an increasing use recently [
9,
13,
18,
24]. This is defined as the uniform temperature of an enclosure in which an occupant would exchange the same amount of heat by radiation and convection as in the existing non-uniform environment [
25].
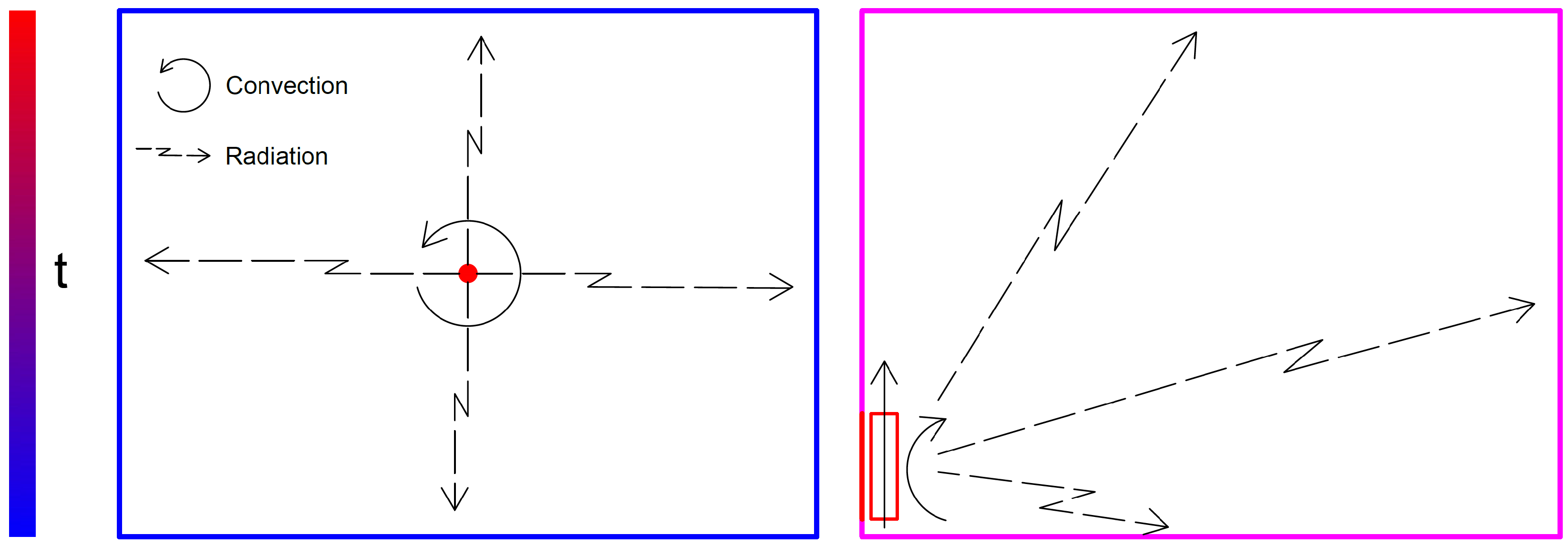
Unfortunately, such a formulation generates a fundamental problem for product comparison, as it does not provide one clear “ideal” emitter to benchmark others against. For ordinary systems where the air temperature is controlled, such an ideal heater is generally described as a dimensionless point (
Figure 1). Heat is transferred by convection to the thermal node of indoor air, and by radiation to the surrounding surfaces. A higher convective transfer fraction induces lower surface temperatures on the surrounding surfaces with minimal heat loss, as in
Figure 1. To reach the desired air temperature set-point
, an emitter with convective fraction of 1 (pure convection) thus requires the lowest possible heat output. In this sense, it represents an “ideal” heater.
By the definition of operative temperature however,
is inversely proportional to the surrounding surfaces’ temperatures. In this respect, the “ideal” device described above should now exhibit a lower performance, as it heats the surrounding surfaces only minimally. As we will illustrate in the following, preliminary simulations with the software IDA ICE [
26] confirm indeed that several real emitter configurations can outperform the point heater (or convector). In other words, defining an ideal benchmark heater for operative temperature control is non-trivial, and needs to be addressed for better comparison between different heat emitter systems.
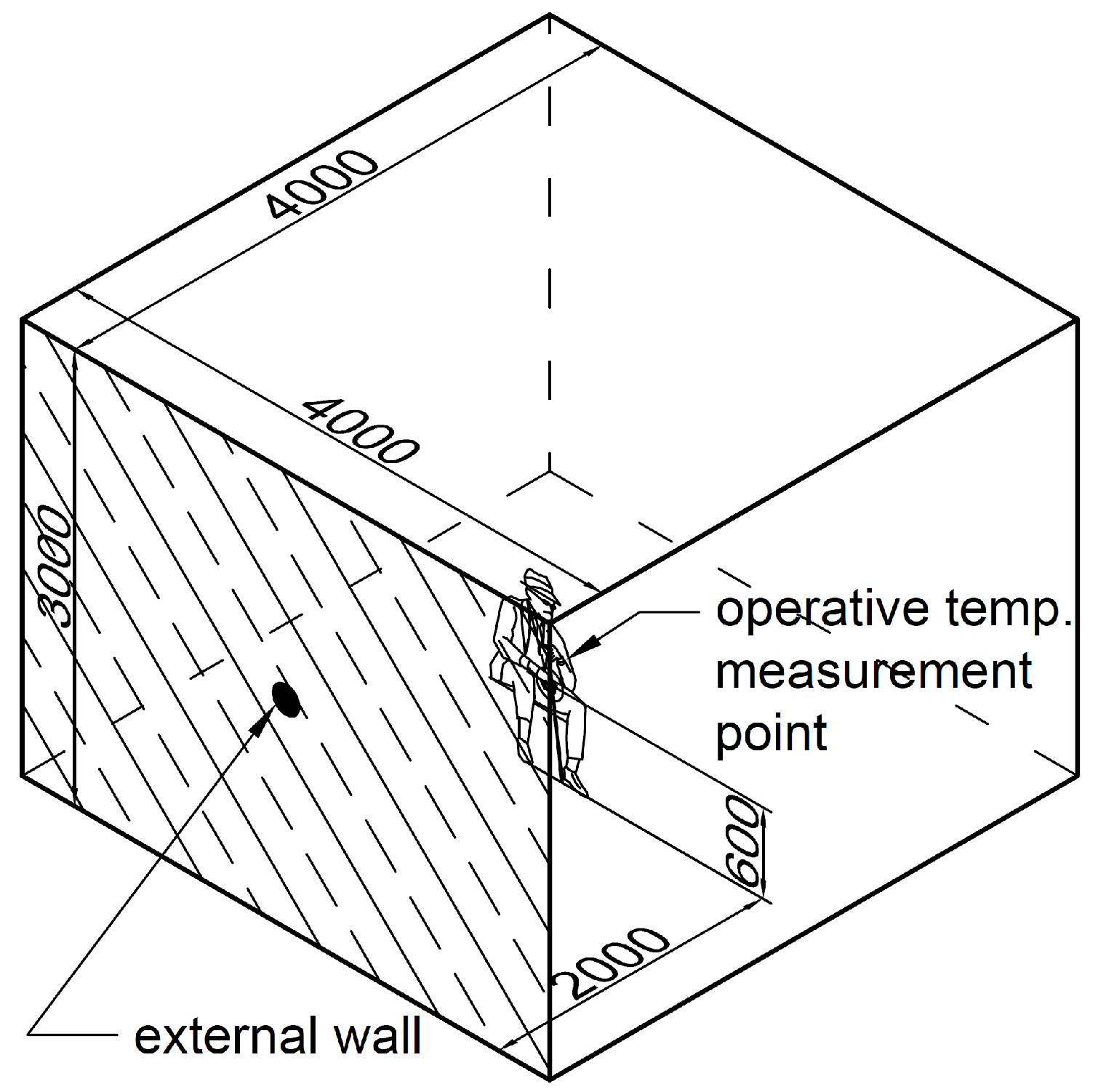
To this aim, in the present paper, we consider an average-sized enclosure provided by the CEN technical committee TC130 working group WG13, with a user sitting in the middle (
Figure 2). We investigate how the operative temperature sensed by this user changes with the typology and size of emitter, and whether there exist optimal configurations corresponding to the highest
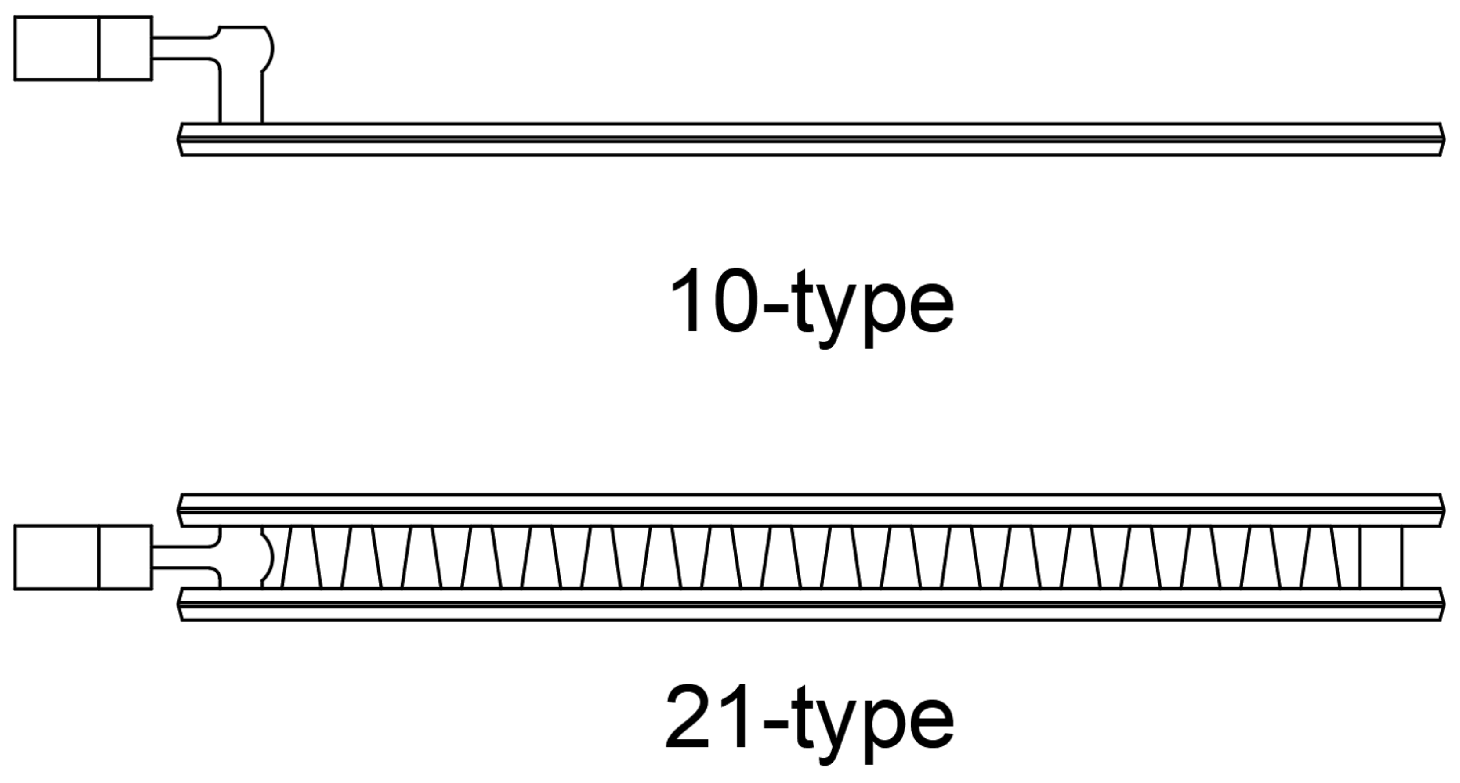
. We address panel radiators (10- and 21-type), underfloor (UFH) square, UFH strip and ceiling heater. A 10-type radiator has only one panel and no convector fins, while the 21-type has two panels with one set of fins in between, bas illustrated in
Figure 3. They are placed on the cold wall, with centrelines aligned, as in
Figure 4.
bWe adopt a combined numerical-analytical model that follows the ISO Standard [
25], coupled with a simple interpolation method which was introduced in [
27] when assessing domestic hot water consumption. We first obtain the surface temperatures of the enclosure numerically, with IDA ICE, for each heat emitter type and for different sizes; these temperatures are then used as boundary conditions for an analytical calculation of the according operative temperature. The resulting
is finally studied as a function of the emitters’ dimensions to identify general trends, comparing the different devices and finding optimal configurations.
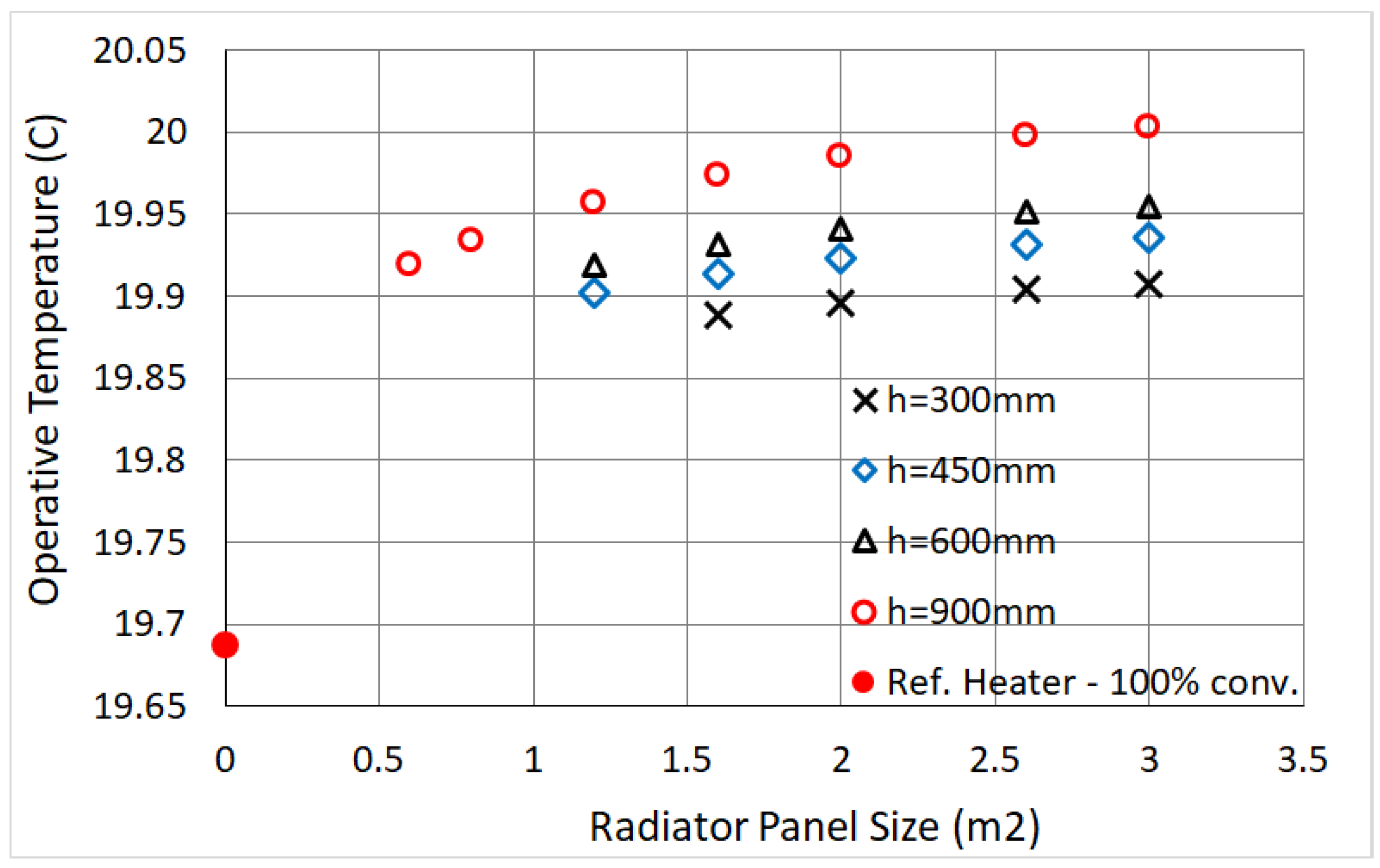
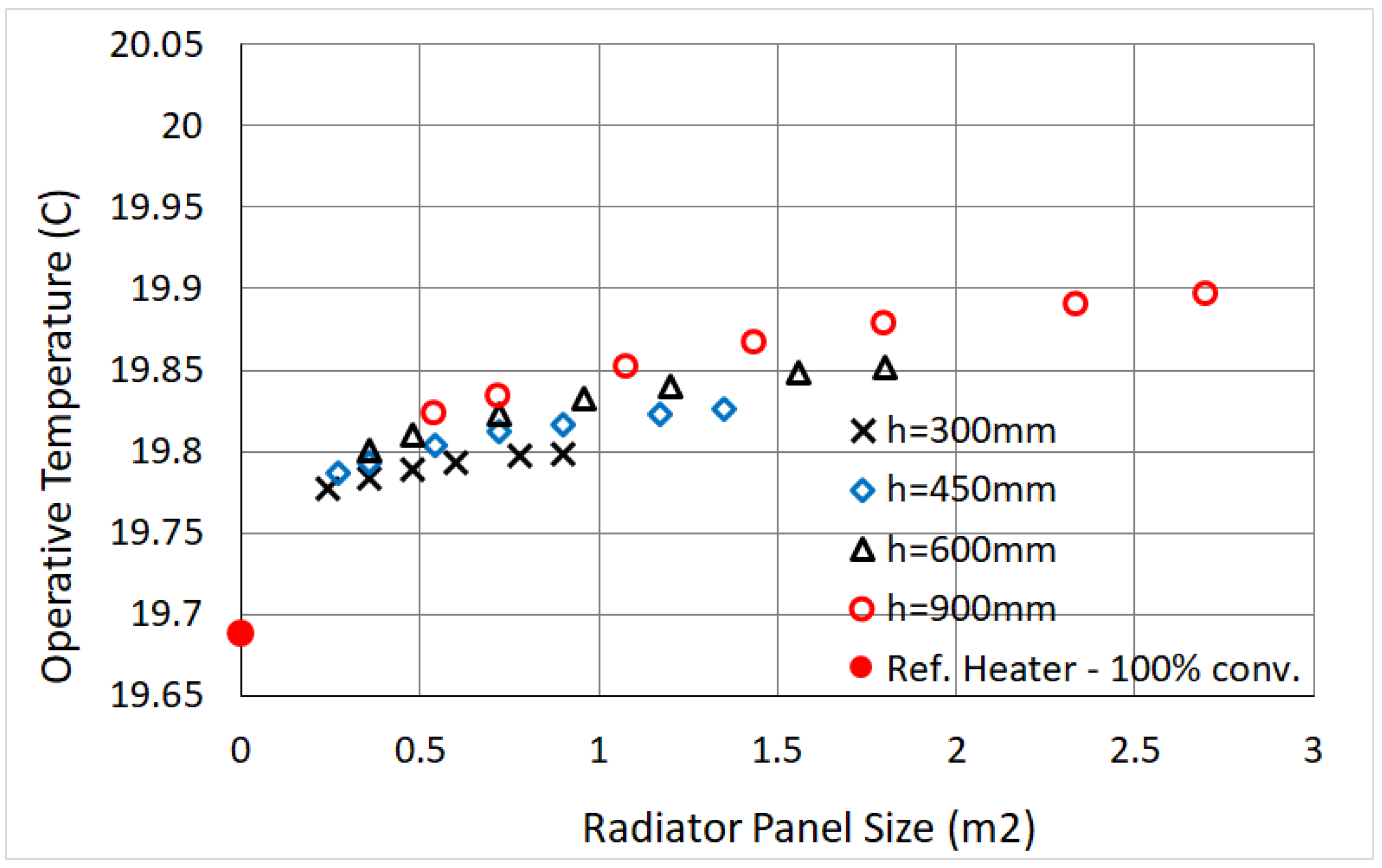
Concerning panel radiators, by keeping the heat output constant we determine analytical curves in function of their panel dimensions, finding an optimal width range of both the 10- and 21-type. We prove that the thermal comfort performance of radiators is more sensitive to the height than to the width, and that the convector and 21-type provide the lowest operative temperatures. On the other hand, the 10-type can provide a as high as the air temperature, and accordingly it can be identified as our “ideal” emitter. For the case at hand, we also list a series of analytical formulas for calculating for radiators of 10- or 21-type, with panel size in the range considered and excluding back wall losses (Adiabatic internal surfaces are used in the model; namely, no additional heat is transferred from the ceiling heater and UFH to the colder rooms above and below. This additional heat loss is also omitted for the radiators, to guarantee an accurate comparison.).
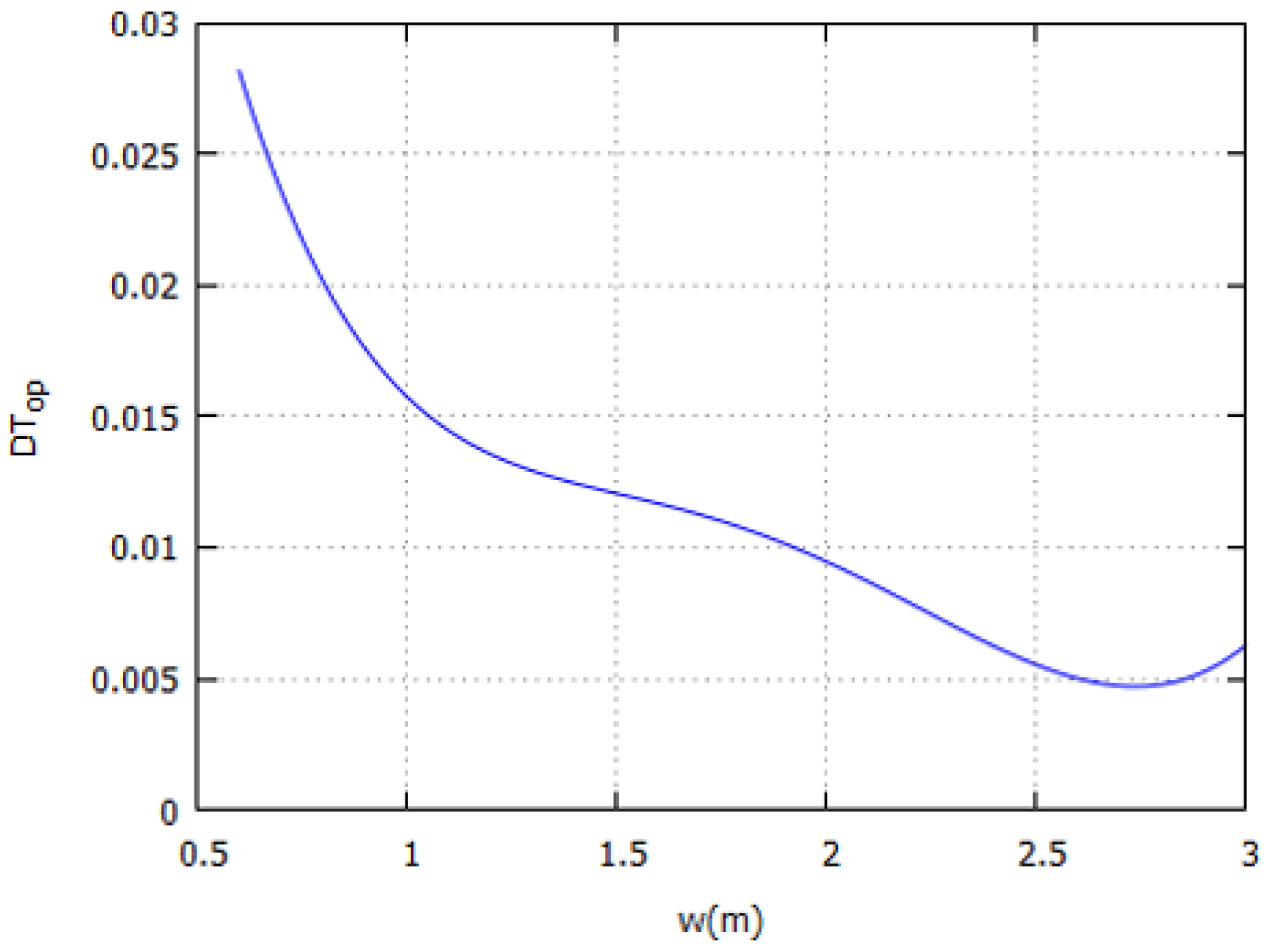
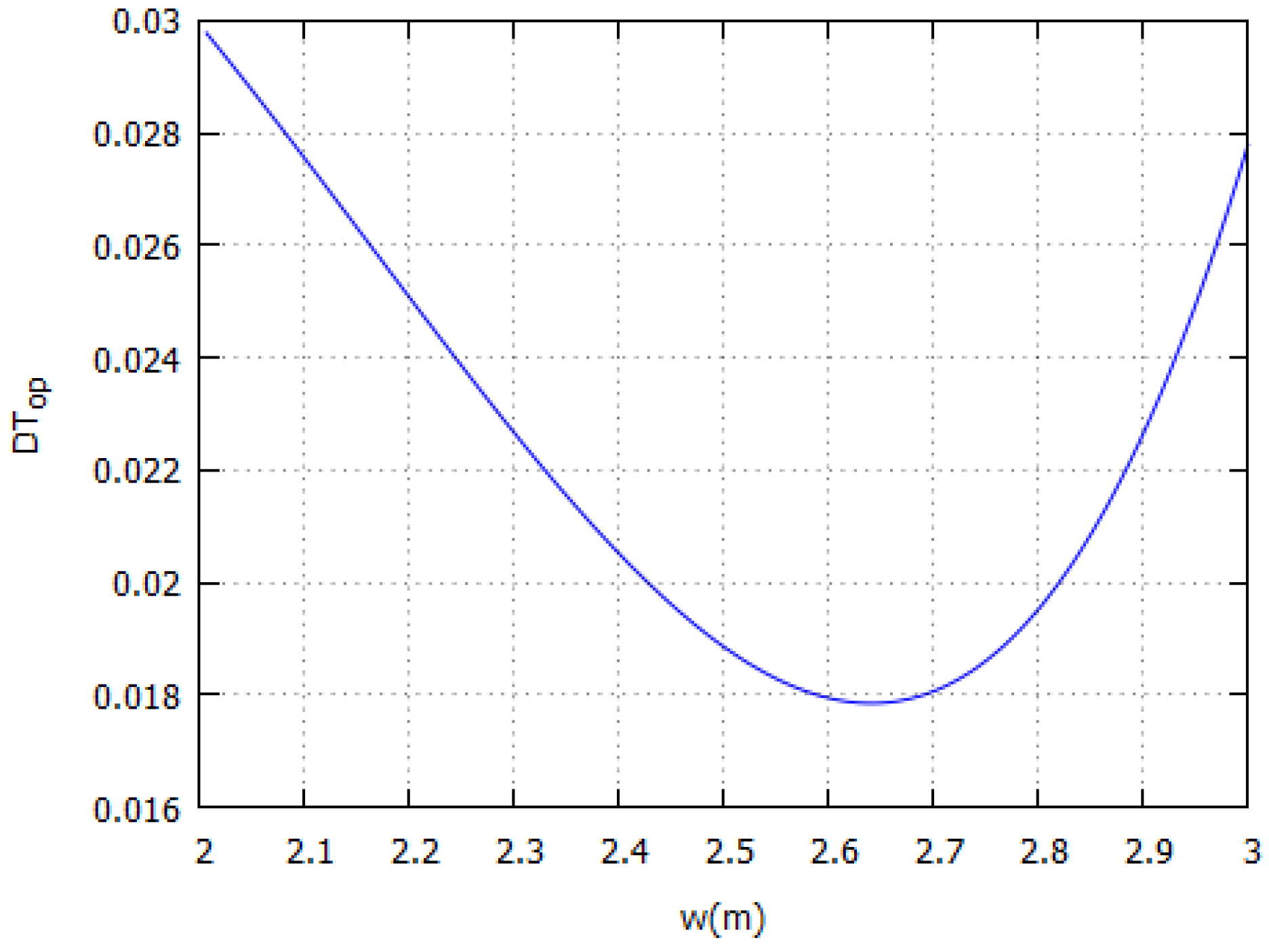
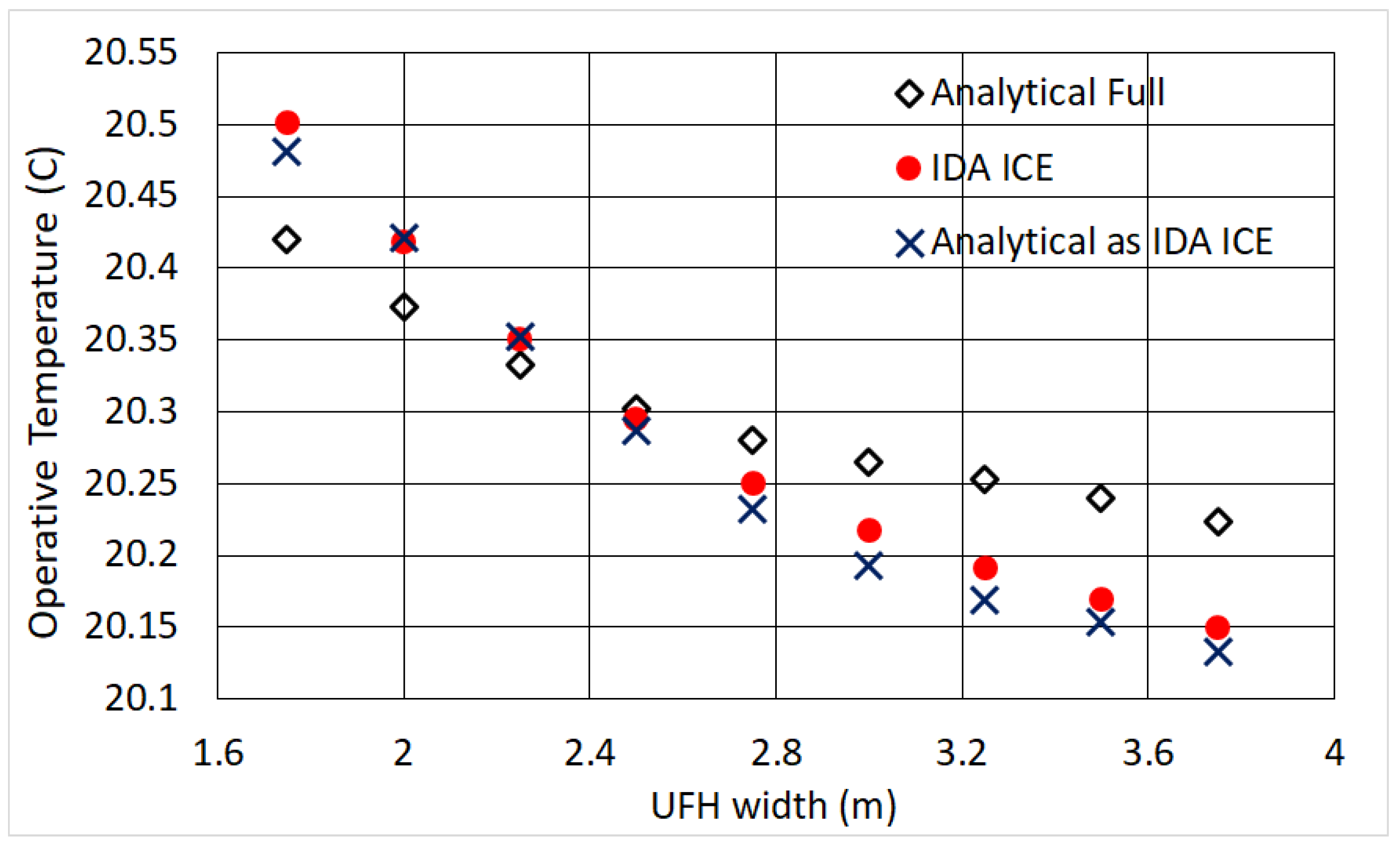
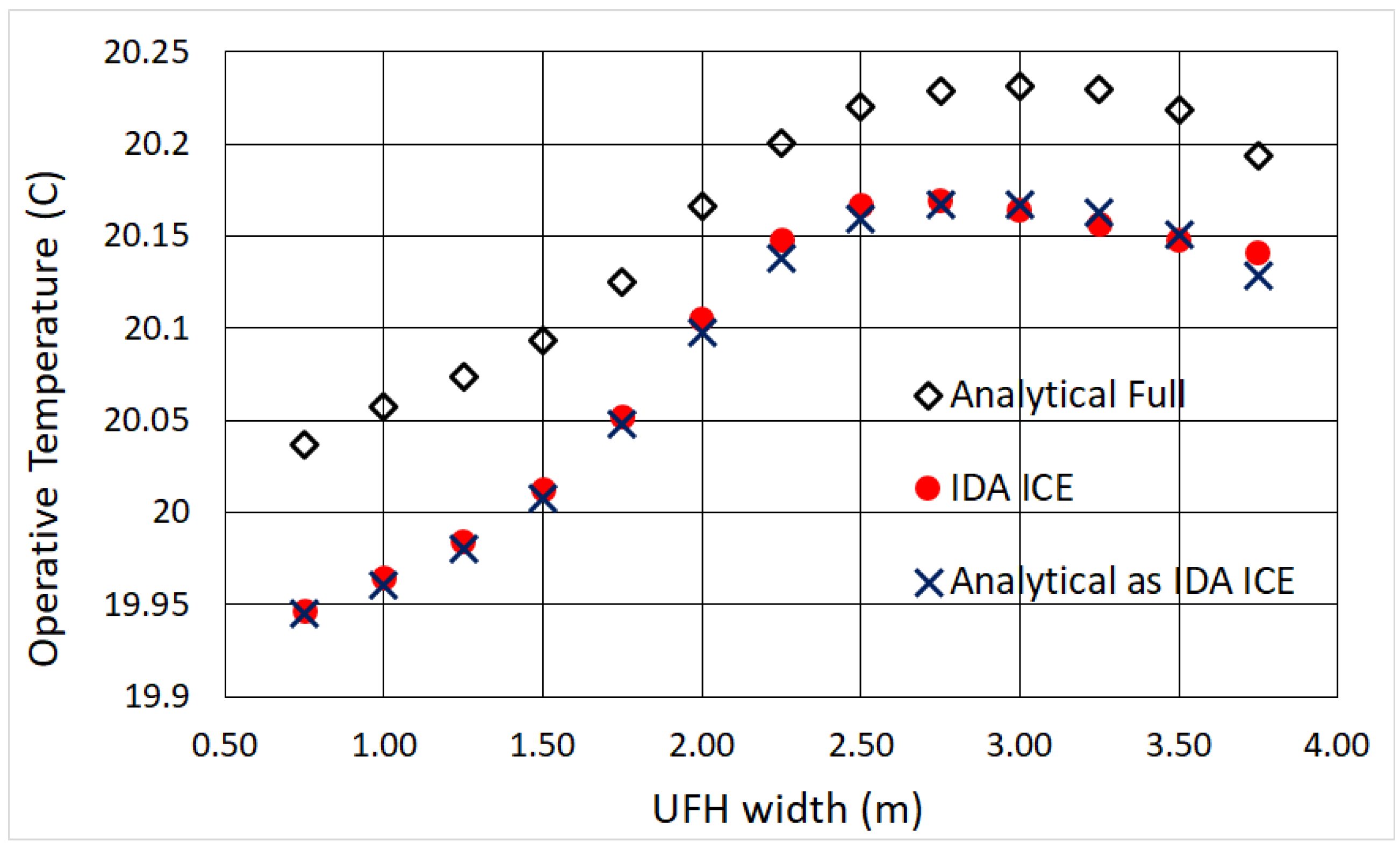
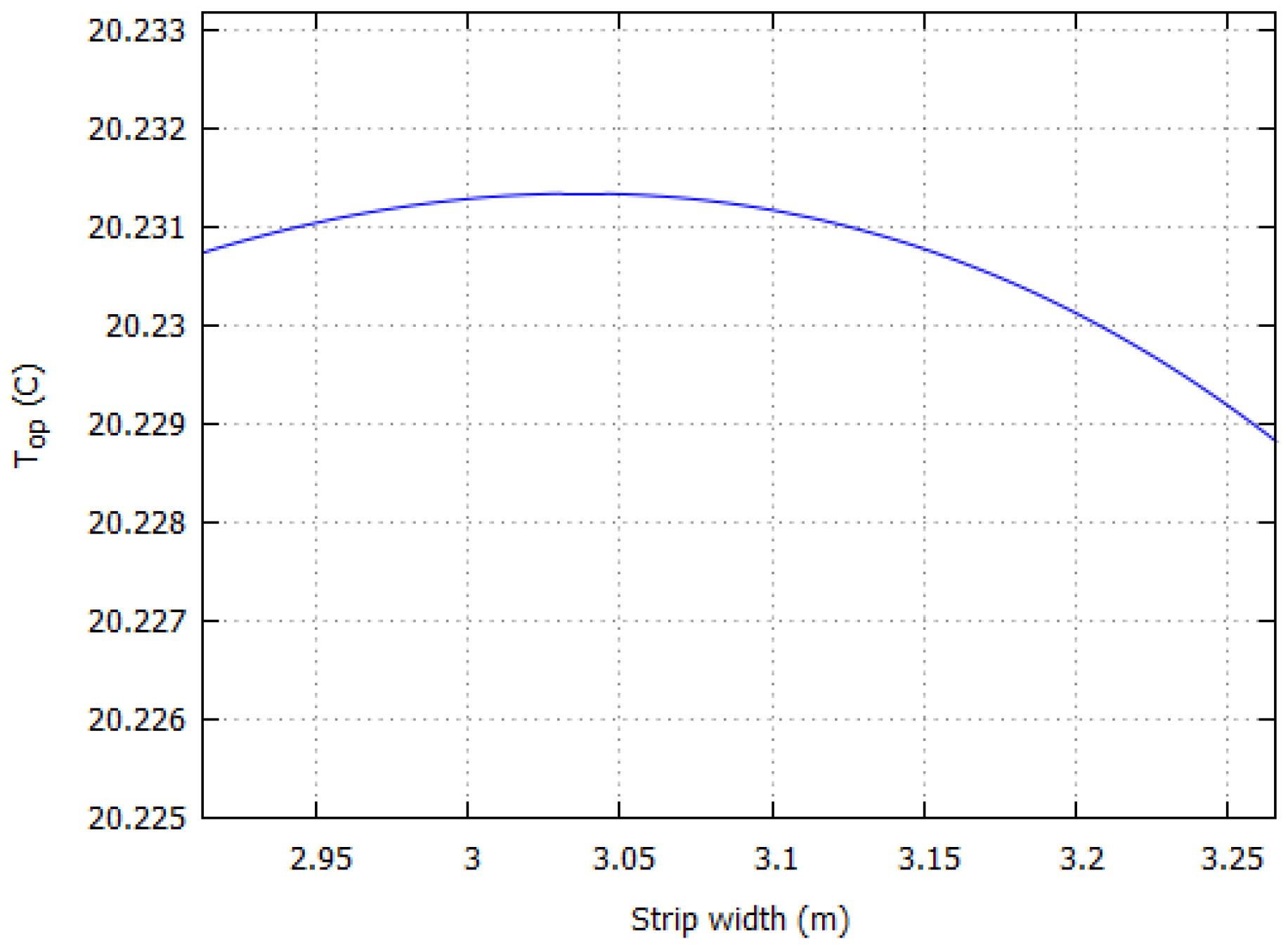
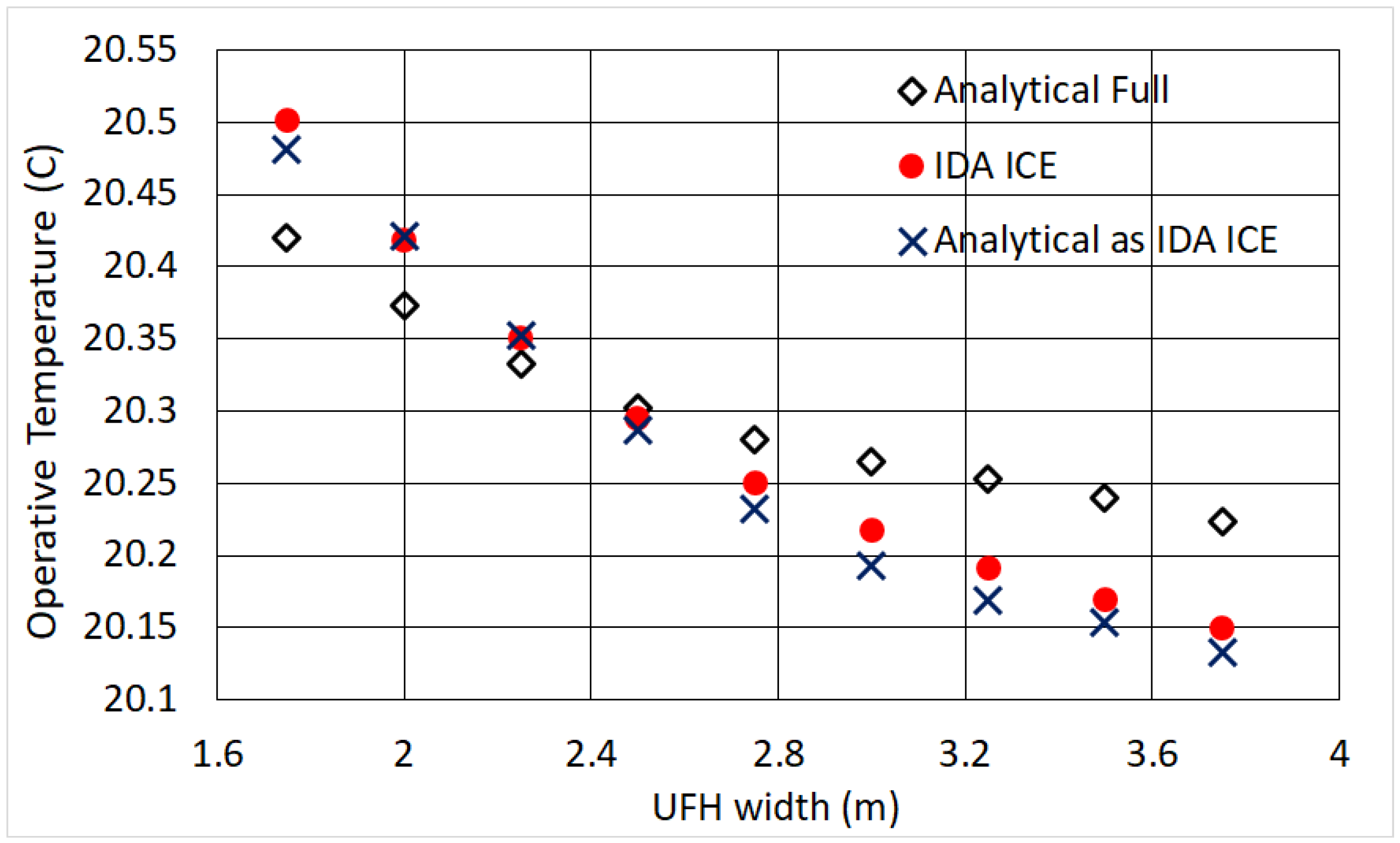
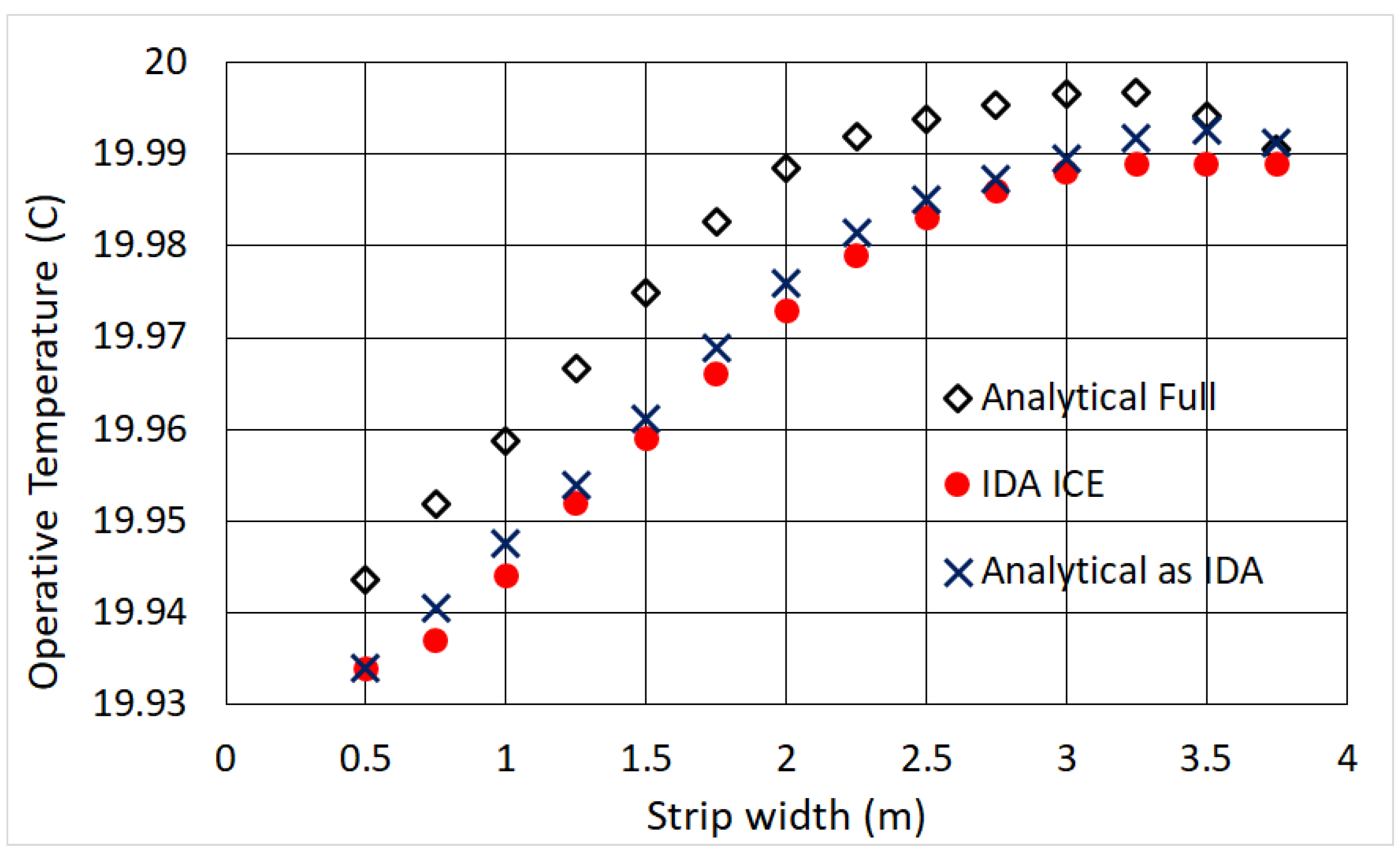
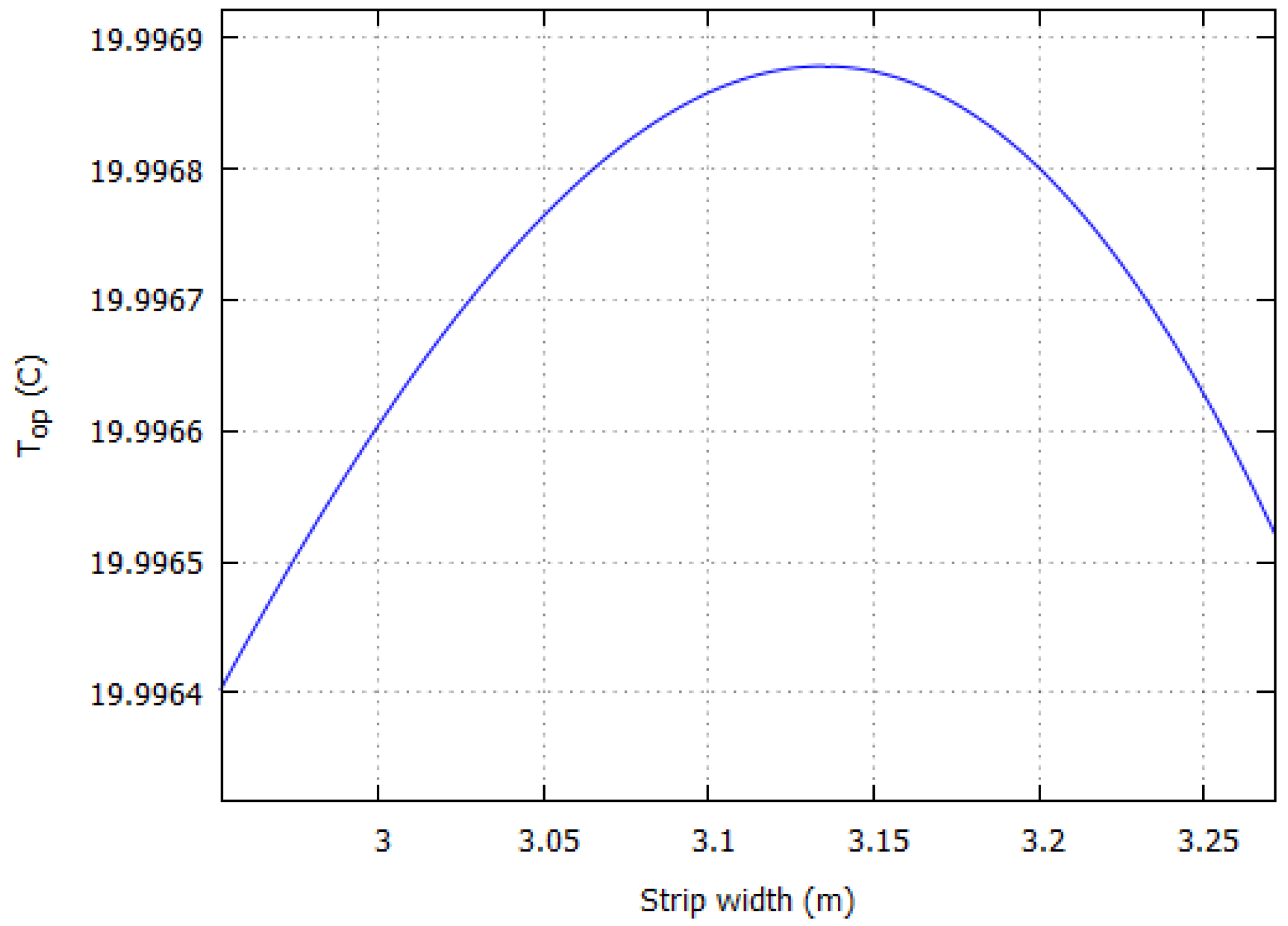
The UFH and ceiling heater provide in general higher operative temperatures, approaching, and often exceeding, the air temperature. We find, both analytically and numerically, a maximum
for sizes smaller than the whole width of the room: the analytical solution allows to locate them precisely, up to three digits. Remarkably, if one considers typical radiator sizes with height 0.6 m, when compared to a 10-type the UFH provides a
that is higher by 0.25 K–0.3 K, and by 0.35 K in the case of a 21-type (In theory one might conclude that the UFH is our ideal heater, but in practical cases the embedded emission losses are relevant [
8].).
The present paper is organized as follows: in
Section 2 we describe the test chamber, the simulation setup and the different methods for computing the operative temperature. In
Section 3 we report our results for each single case, some general discussion then appears in
Section 4 and finally,
Section 5 contains a summary of our findings and concluding remarks. In
Appendix A we include considerations about the view factors, a comparison between our analytical and numerical methods and the analytical formulas to determine the operative temperature for any radiator size discussed in the study.
2. Method
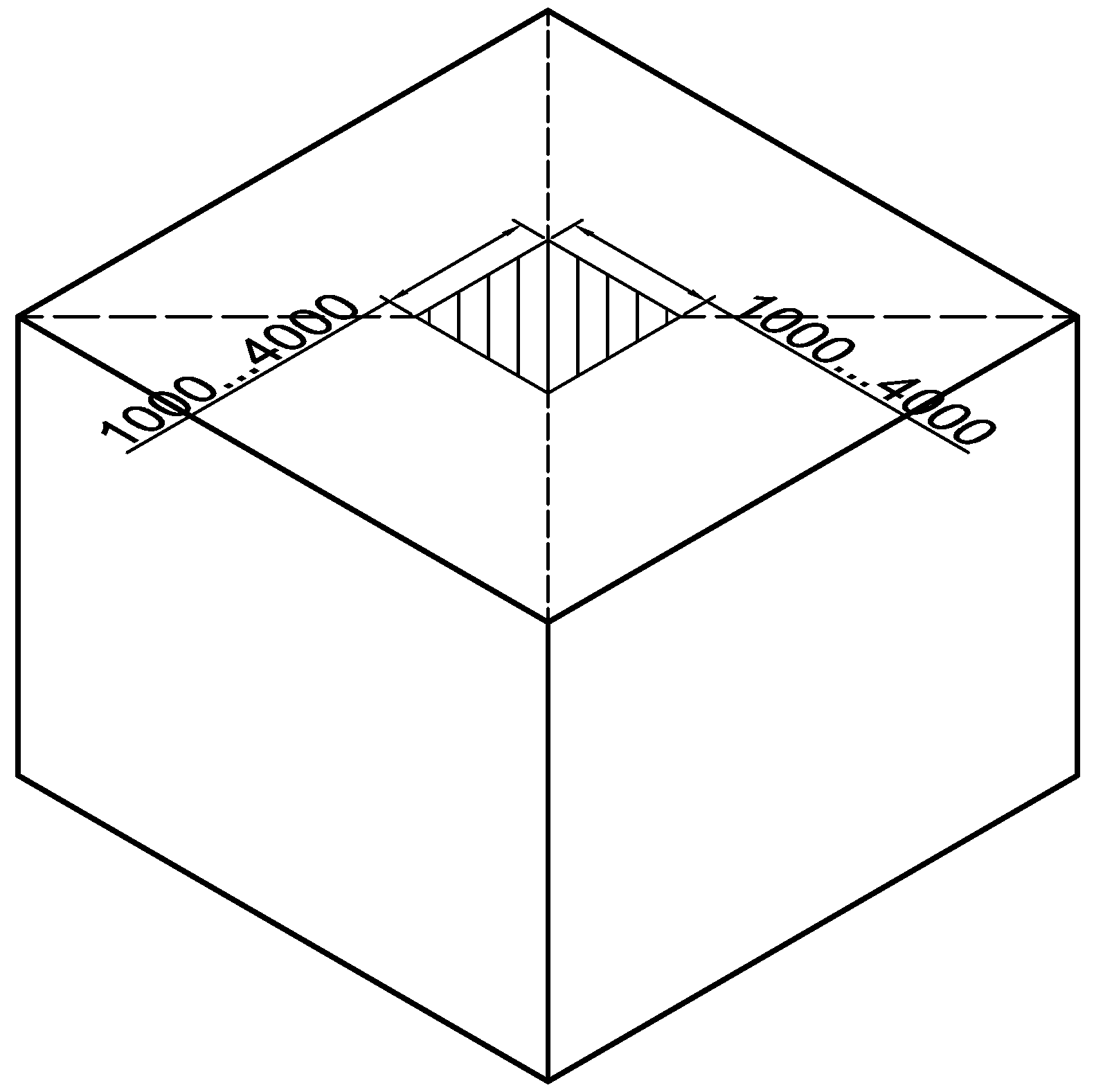
In this study, we consider an enclosure with thermal layer properties and dimensions 4 m × 4 m × 3 m specified by the CEN TC130 European Committee, shown in
Figure 2. The external wall has U-value 0.25 W/m
K, and heat recovery ventilation in the room provided an air change rate of 1 ACH bwith temperature efficiency 0.8.
Vertical temperature gradients are mainly influenced by the amount of air circulation within an enclosure. As it was shown in [
8], gradients measured for radiators and UFH were approximately 0 K/m for ventilated rooms. The ventilation flow rates and room geometry (mainly the height of the room) within the referenced study are similar to the room considered in this paper. We accordingly neglect the possible effects of a vertical temperature gradient, assuming indoor air mixing and lack of stratification to be similar. This approximation is therefore true at least for radiators and UFH, however no information exists for ceiling heater. We do note that including a vertical gradient would yield marginally different surface (and thus operative) temperatures, since the temperature differences for convection calculation purposes would change between the room air and enclosing surfaces only slightly. A more detailed study on this phenomenon would certainly be interesting, however it would require extensive measurements to accurately assess the variation in the gradient values, as the size of the emitters changes within a broad range.
We locate the calculation point, namely the centre of mass of an average sitting user, at 0.6 m above the floor in the room centre (i.e., at 2 m distance from each wall) [
25]. The most performing heater configuration will then be the one providing the highest operative temperature, with the same heater nominal output. The steady-state boundary conditions are the following: Indoor air temperature
= 20
C, external air temperature
= −15
C. Both direct normal and diffuse horizontal irradiance are set to zero. 134 W of power are required to heat up the room under these predefined conditions (the heat outputs throughout the simulations were within ±0.5 W of this value).
IDA ICE calculates the heat emission from any hydronic heating device as follows. The characteristic equation used to determine and model the device’s heat output comes in the form of an empirical power law [
21],
where
k and
n are coefficients determined individually for each emitter type, with
l its length and
the logarithmic mean temperature difference between heating water and indoor air. This governing equation therefore holds true for radiators, ceiling panels and UFH. The detailed version of the model, containing the heat balance equations used in the IDA ICE software for e.g., the calculation of relevant flow and surface temperatures, can be found in [
28].
For underfloor heating, the pipe installation depth and the fluid-to-slab heat transfer coefficient are provided by the user along with the nominal heat output
at a given temperature drop
for the underfloor heating system. The maximal mass flow
through the underfloor piping is then calculated as
where
is the specific heat capacity of water at constant pressure. The exact heat output, return temperature and mass flow depend on the actual amount of heat required within the room.
Heat transfer from the heating water to the surfaces of heating pipe and floor is modelled with an n-layered RC-network, see [
28] for exact model descriptions. The piping layer is basically given by a heat exchanger, with an active plane at constant surface temperature located inside the floor slab. In the resulting floor coil model, the heat transfer between fluid and active plane is computed via their logarithmic temperature difference; the according heat transfer coefficient includes convection between medium and tube wall, heat conduction through the tube walls and “fin efficiency” given by the distance between immersed tubes or actual fins. In steady state, this approach corresponds to the resistance method of the EN 15377-1 standard [
29].
For a selection of IDA ICE model and software validations, see, e.g., [
30,
31,
32,
33,
34].
The operative temperature
is computed analytically, according to the prescriptions of the ISO 7726 standard, as we explain in the following. Considering the contributions of all the six surfaces in the enclosure, we obtain an expression for
that is a function of the radiator height
a and width
b. The eventual global maxima of this function in the
plane would then correspond to the optimal configuration for that specific heater. Such full analytical solution is then numerically validated by the finite difference method software IDA ICE [
26] in the same CEN TC130 test room, in the limit when only the contribution of the surfaces that are parallel to the principal calculation surface is accounted for.
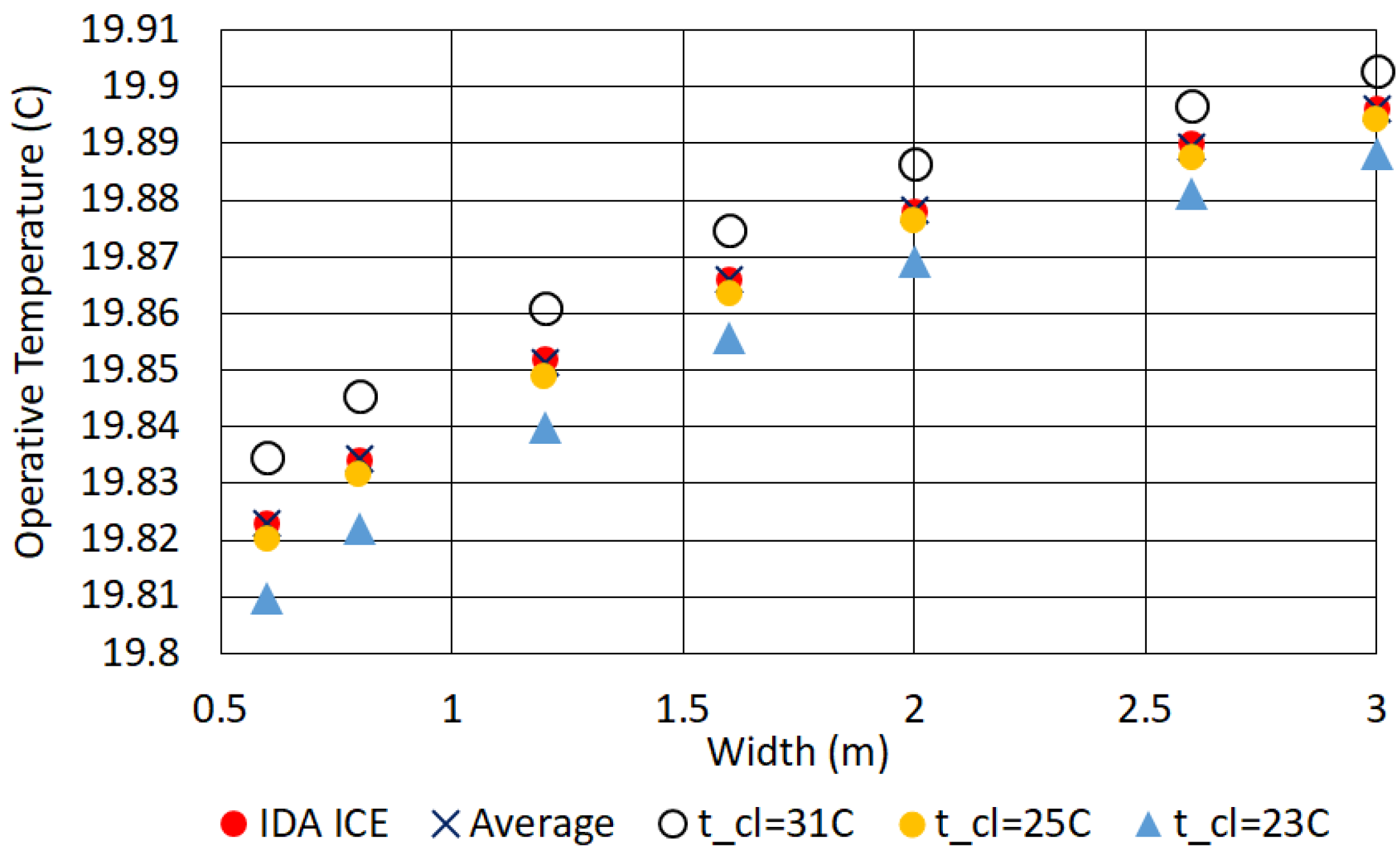
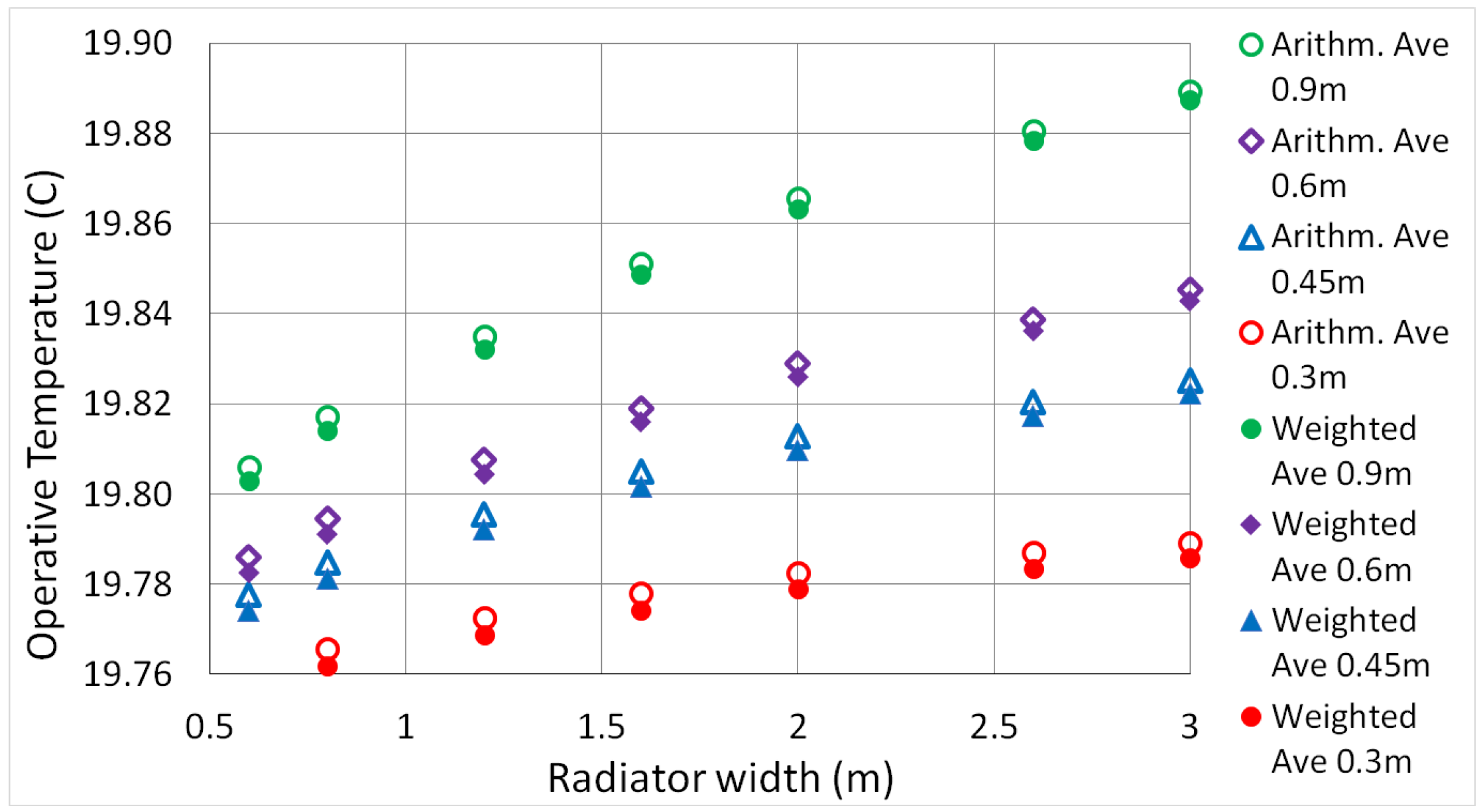
The operative temperature at the above location is not uniquely defined. In IDA ICE this is evaluated as the simple arithmetic average of air temperature
and mean radiant temp.
[
26],
(throughout this paper, [
] = [
C] and [
] = [K]). This differs from the exact definition given in the ISO 7726 [
25],
where the average is weighted by the radiation and convection heat transfer coefficients
and
at the calculation point (As we demonstrate in
Appendix A, in reality the different operative temperature values which are obtained with either method show no sizeable difference). The explicit formula for the coefficient
A, which is itself a function of
and
, is given in
Appendix A; for our setup, it lies within the range
.
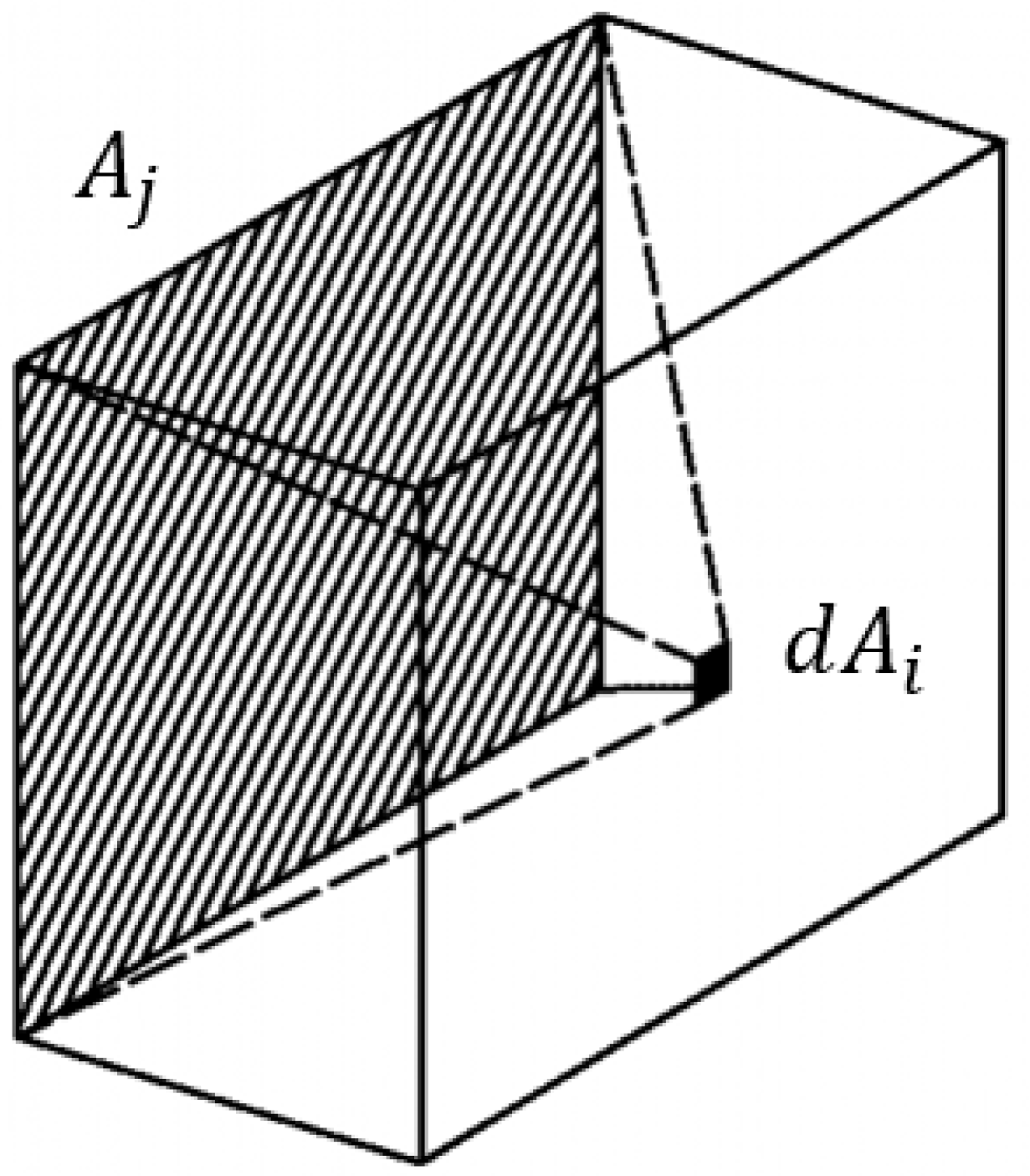
Another difference between the ISO standard and IDA ICE is that the numerical software has a peculiar way of computing the mean radiant temperature
. It considers only the surfaces that are
parallel to the principal calculation surface, therefore the sum of view factors in a principal direction is <1 (
Figure 5). Moreover,
is obtained as the average of mean radiant temperatures from the six principal directions, weighted by the respective view factors,
where the
are computed for a small area (the observer) that is only parallel to the radiating surface.
In contrast, the ISO 7726 prescribes that for each direction one considers both parallel
and perpendicular surfaces (see
Figure 6), obtaining the plane radiant temperature [
14,
25],
with the angle factors
reported in
Appendix A. Now the sum of view factors in each direction is accordingly =1, and the mean radiant temperature is given by [
25],
namely by a weighted average over the projected area factors
of a person, listed in
Table 1.
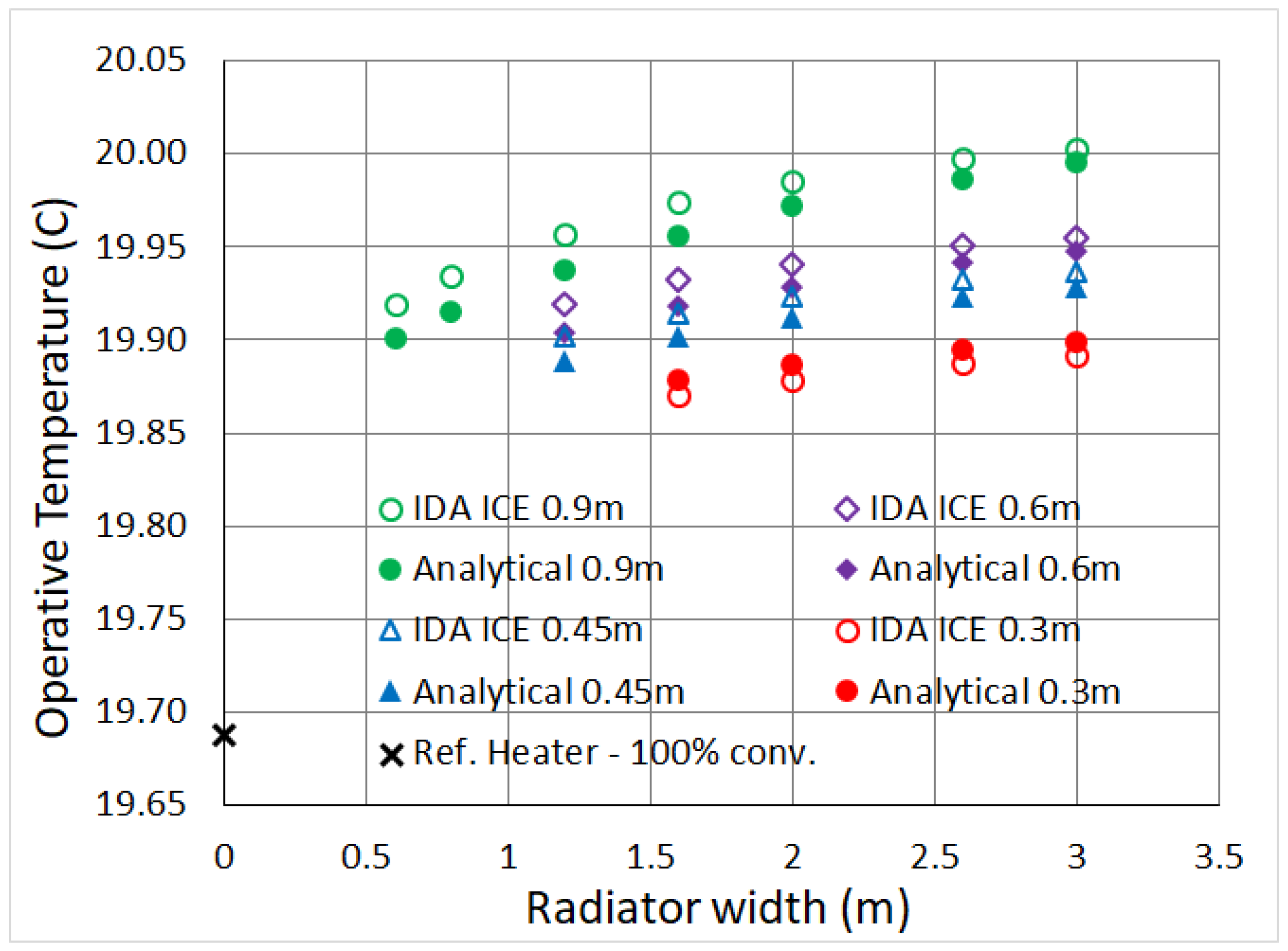
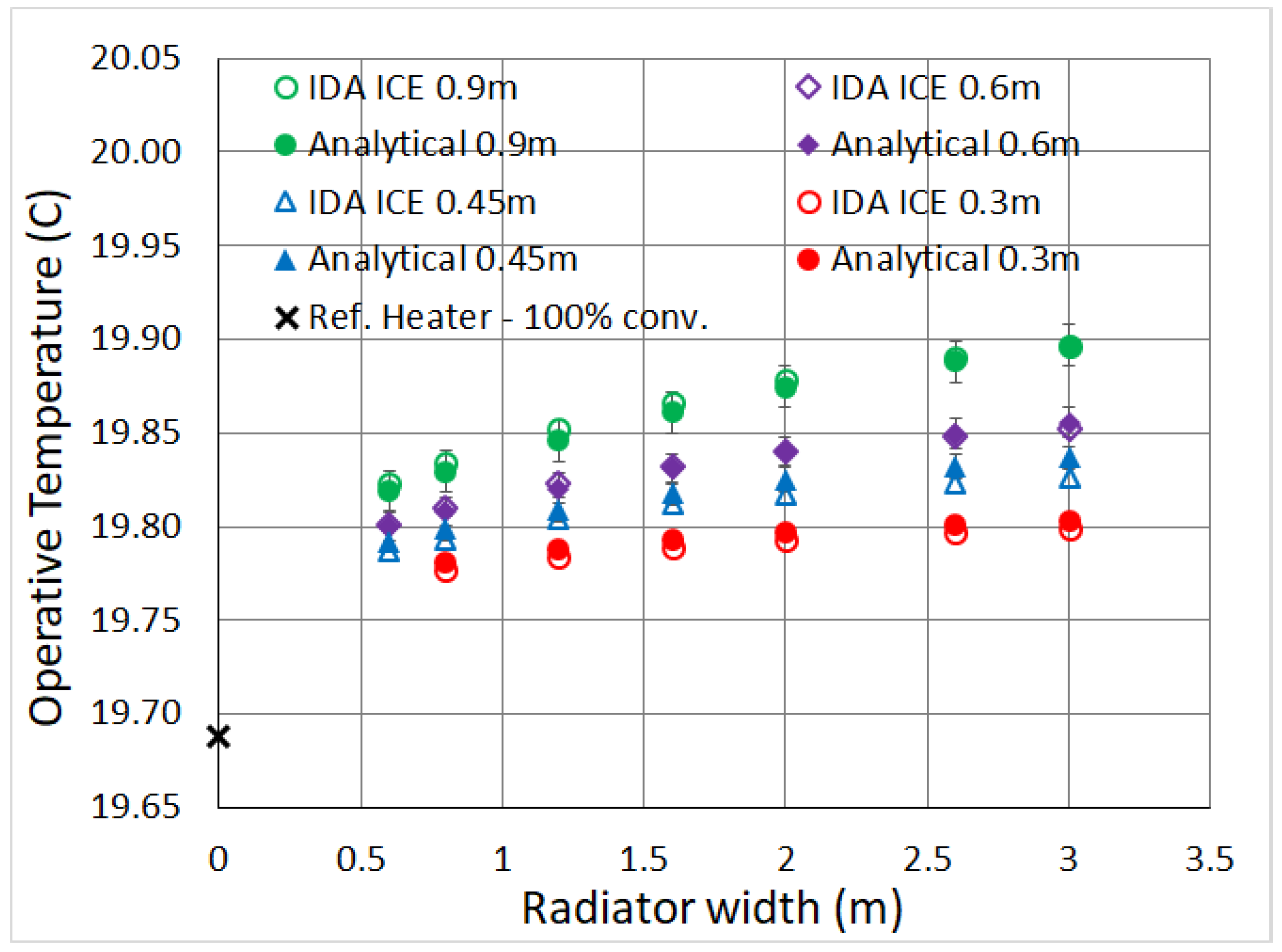
Specifically, in this work all the “Analytical Full”
points in the graphs are calculated with Equations (
4) and (
7), therefore following the ISO standard completely throughout this paper. The only point in common with IDA ICE consists of the surface temperatures
, which are written as polynomial interpolations from the data provided by the software. Since both the definitions of operative and mean radiant
T are different, the analytical
is independent of the numerical
.
On the other hand, for the "Analytical as IDA ICE" points, while still computing analytically, we use Equations (
3) and (
5), consistently with the software. This provides validation of both our view factors and the temperature interpolations
, where
x is a length that is specific to the particular case (either
a or
b). The interpolations are implemented towards a more general form of the operative temperature than by using the raw data for the surface temperatures. This way, instead of calculating
for each point, we can write
and accordingly formulate general considerations and predictions on the operative temperature for
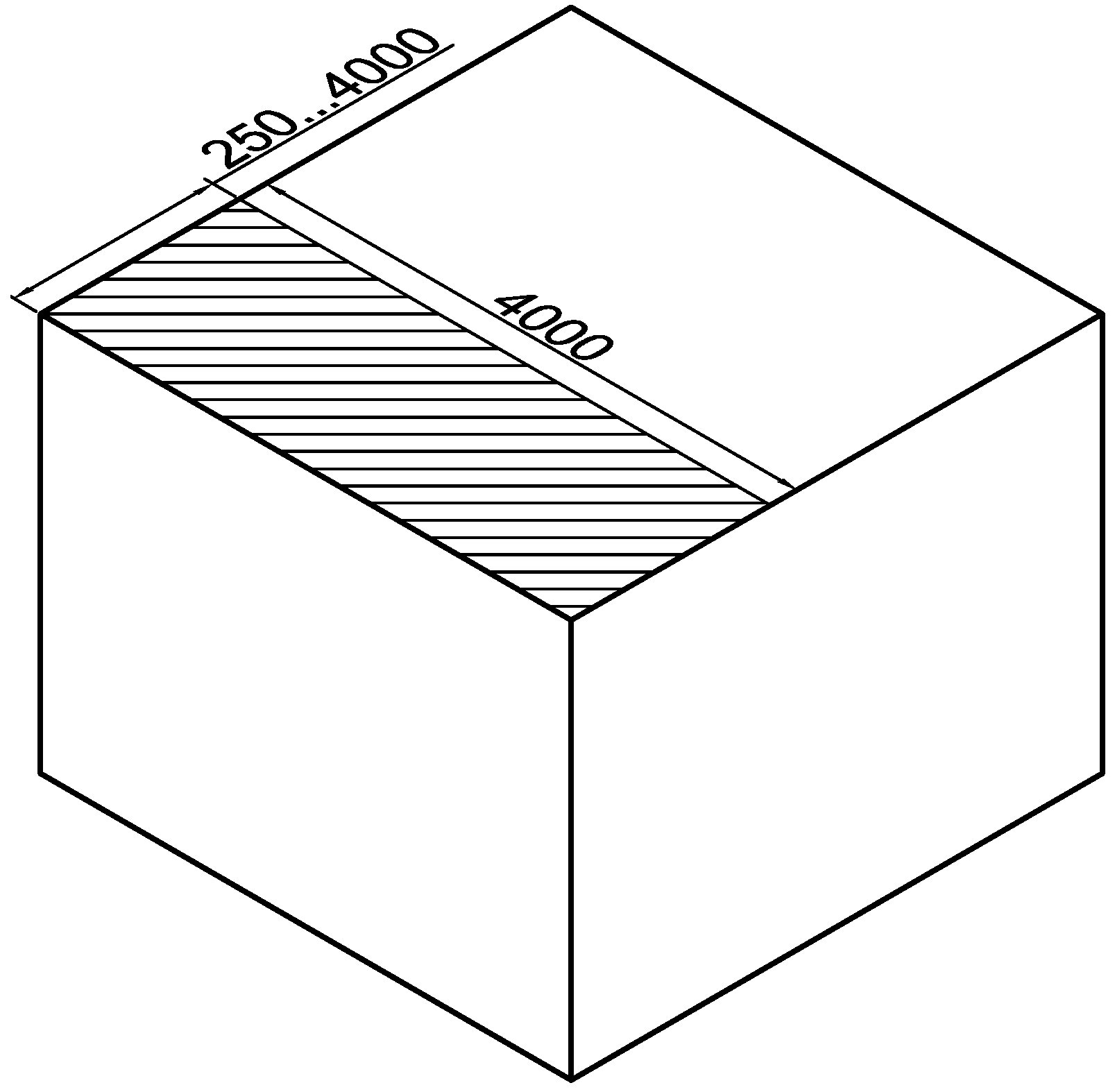
any possible configuration consistent with the test room setup. In the case of UFH and ceiling heater, the "square" configuration consists of a square heater placed under the floor or ceiling surface, centred in the middle of the room, where the user is sitting. The “strip” configuration instead considers a heated strip running from the cold (or external) wall. Further descriptions are given in
Section 3.2 and
Section 3.3.
4. Discussion
Besides several specific results, in this paper we have shown quantitatively two general features: how the radiator performance bfor thermal comfort changes with panel area, and the existence of optimal sizes for the UFH and ceiling heater.
These findings are supported by well-tested approaches such as the view factors (see e.g., the standard [
25]), which constitute the foundation of our analysis. In this respect, the analytical calculation is necessary for two main reasons: first, IDA ICE calculates the operative temperature in a very specific way that is different from the ISO prescription (As we have shown, the
obtained this way is not radically different from the analytical result.). Since we are aiming to contribute to the heat emission code EN 15316-2-1:200, a more standard procedure is preferable.
Secondly, and more importantly, we are able to extrapolate and generalize our results to
any 10- or 21-type emitter with size included in the studied range, by virtue of the simple interpolation method introduced in [
27]. The exact formulas listed in
Table A1,
Table A2,
Table A3 and
Table A4 can be of practical use for qualitative assessments of thermal comfort induced by radiators of 10- or 21-type, with dimensions
and
and assuming no back wall losses.
In our simulation setup, temperature limits for the water supplied to the emitters are imposed on their systems for a variety of reasons. In theory, any size of emitter in any configuration could be used to offset the heat loss through the external wall, with smaller devices needing hotter surfaces (thus requiring a higher supply water temperature). However, practical reasons bound these temperatures greatly. For example, floor surfaces with UFH in living rooms are limited to 27/29
C to avoid thermal discomfort [
35]. Moreover, large surface temperature differences in opposing directions can cause local discomfort via a phenomena called “radiant temperature asymmetry” [
25]. In addition, supply water at low temperature can be generated by ground and air source heat pumps with a higher thermal efficiency. Finally, warmer supply water would also yield higher embedded losses.
It should be also noted that if a UFH heated square could follow and track an occupant location, this solution would represent the best performing heater with the highest operative temperature, a result that may have practical implications for personal thermal comfort solutions (Clearly, though the UFH and ceiling smallest squares provided the highest op.t., such cases are not realistic, because a small square heater cannot track the occupants when they move around the room).
As the differential between outdoor and indoor air temperature decreases, we expect the corresponding
to do the same, since each and every wall surface temperature tends to approach
. The emitters’ surface temperatures will decrease as well, affecting
and therefore
accordingly. In other words, for a more realistic (higher) outdoor temperature we expect
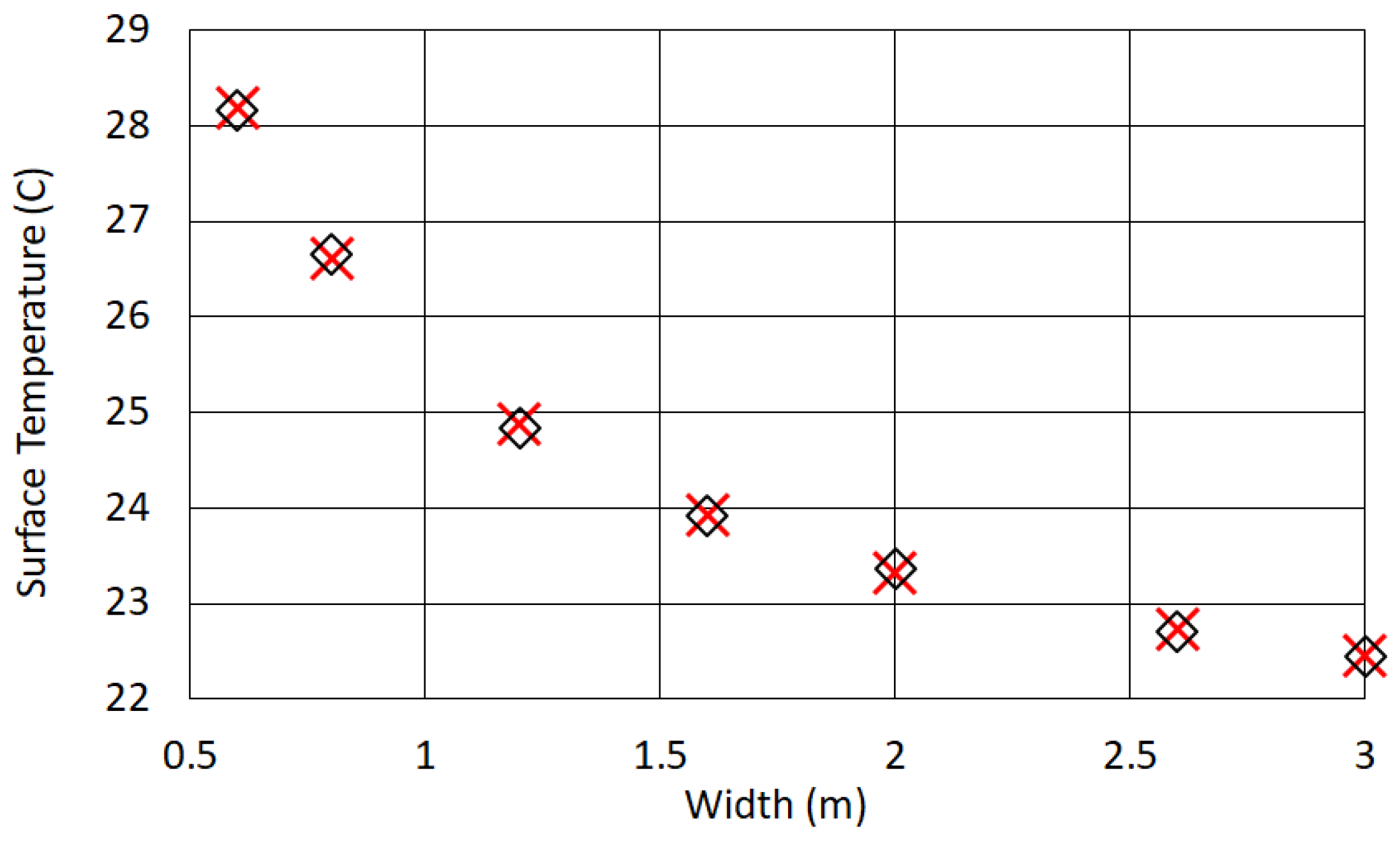
to be generally smaller than what reported in this study. The surface temperatures for our enclosure are listed in
Table 2 for the smallest size of each emitter type addressed in this study.
The occurrence of a maximum
for UFH and ceiling heater strips that do not cover the floor or ceiling entirely implies that the remaining area does not contribute to thermal comfort, which might be interesting for energy saving purposes. More generally, the finding that
approaches in some cases
is very advantageous for energy saving, as it was shown e.g., in [
36] that the energy demand is very sensitive to operative temperature corrections. In particular, a difference of only 0.1
C can increase the annual heating need by 1–2% [
36]: such effect is found for both the convector and the 21-type panel radiator, which are therefore fairly underperforming.
All these results are obtained by a rather general methodology. Our model can easily be extended to any study where it is possible to express the quantity of interest in function of the system variables: in the case of HVAC for instance, one could investigate how the indoor changes according to different inlet velocities and/or temperatures, to the diffusers and windows location and so on.
5. Conclusions
In this paper we have compared quantitatively the operative temperature induced by different types of heat emitters, in the search for the most performing, or "ideal", heater for thermal comfort. We considered several configurations of practical interest, with analytical and numerical calculations of performed in a test room with a standard size defined by updated European Standards.
We first addressed panel radiators of 10- and 21-type installed on the cold wall, for a variety of sizes and surface temperatures. Compared with an ideal convector providing the same output ∼134 W, we found the 10-type to be the most performing radiator, and accordingly the "ideal" radiator for the setup considered in this paper. By means of our analytical calculations, we were able to draw several considerations, proving for instance that the thermal comfort performance of radiators is more sensitive to the height than to the width.
For underfloor UFH and ceiling heater strips, we identified the occurrence of non-trivial global maxima, corresponding to the highest temperature sensed by a person sitting in the middle of the room. Furthermore, compared to typical radiator sizes with height 0.6 m, the UFH provides 0.25 K–0.3 K higher relative to the 10-type and 0.35 K relative to the 21-type. In general, we found the convector and the 21-type panel radiator to be fairly underperforming. Specifically, the former shows the worst performance: the op.temp. is lower by 0.55 K when compared to UFH. Let us remark anyway that the air and operative temperature differences calculated in this study should not be directly applied for energy saving assessment, because they are valid at the outdoor temperature −15C, which is much lower than the average heating season value.
In conclusion, the investigation presented in this paper constitutes a good starting point for several improvements in the search for an ideal heater. Here we have addressed the operative temperature as the sole parameter that is responsible for thermal comfort; we therefore do not claim by any means to have provided an ultimate method for determining an ideal heater. Taken as a whole, the phenomenology of heat transfer and thermal comfort inside an enclosure depends indeed on several factors that are very difficult to track simultaneously.
For these reasons, there definitely exists some ground for future work. As remarked in the Introduction, our method can be easily applied to HVAC as a way to fine-tune the room ventilation. Also, we can investigate how any quantity of interest (such as the op.t.) is affected by e.g., the emitters position, the location and size of the windows, the emissivity of materials and so on. Furthermore, parametric studies on the relationship between view factors, room and geometry of the emitter might show a more general pattern, whose impact on the whole energy demand could be quantified with e.g., annual simulations.