Delamination Buckling and Crack Propagation Simulations in Fiber-Metal Laminates Using xFEM and Cohesive Elements
Abstract
Featured Application
Abstract
1. Introduction
2. Numerical Models
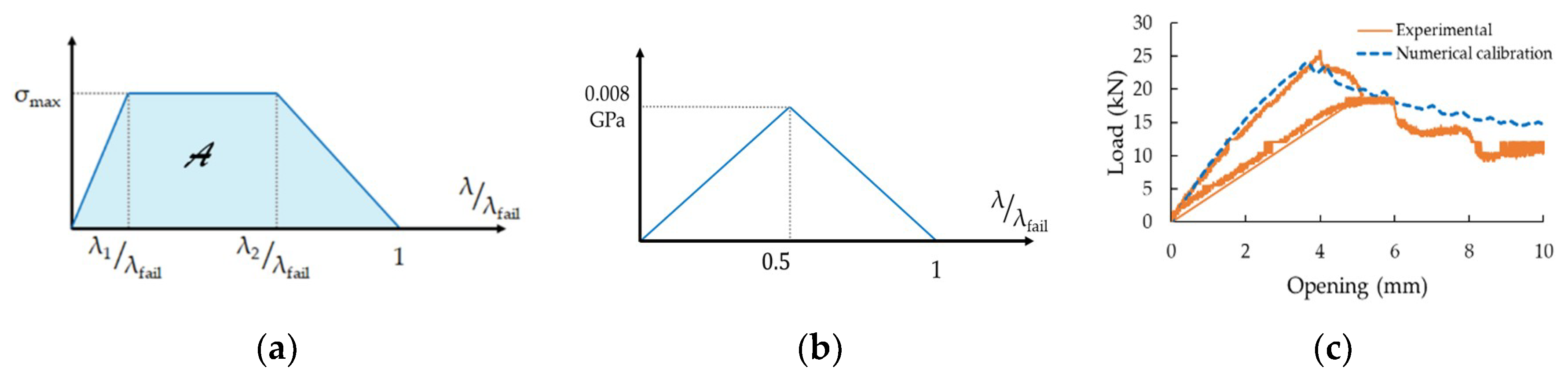
2.1. Material Model for Cohesive and xFEM Elements
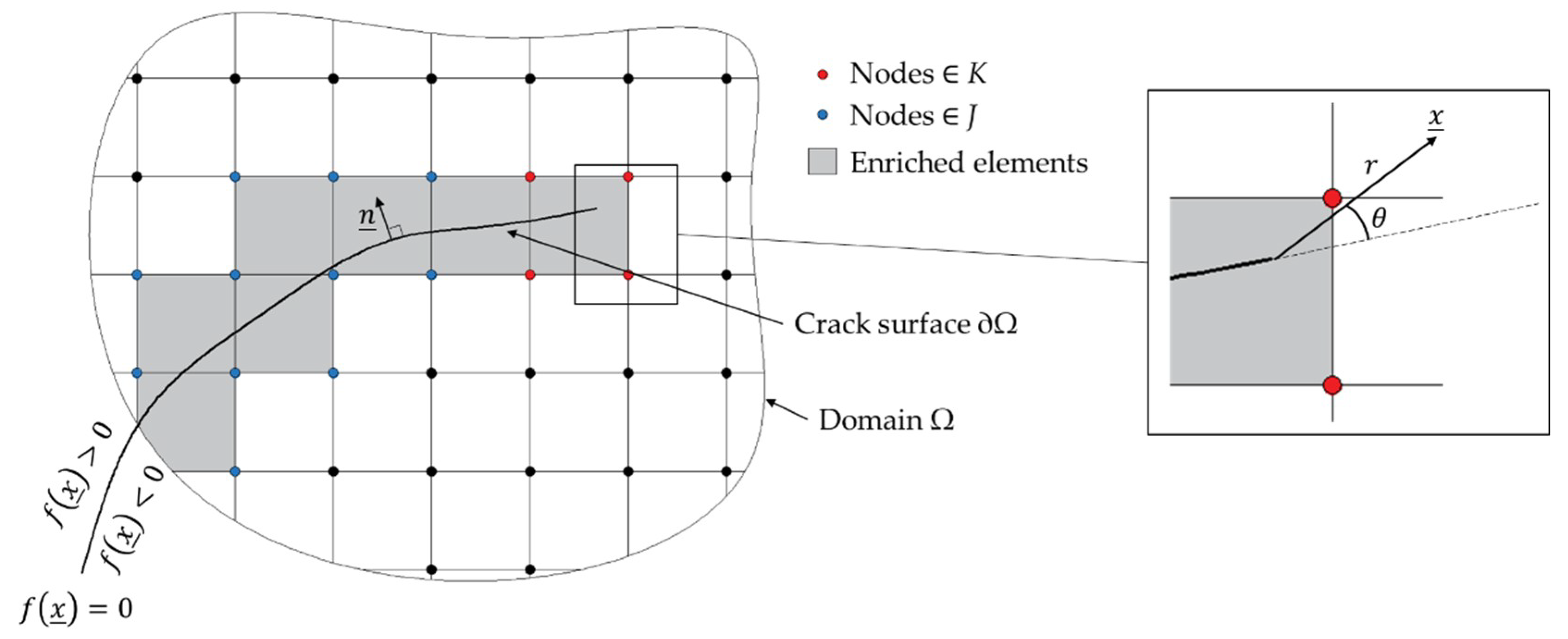
2.2. xFEM’s Formulation
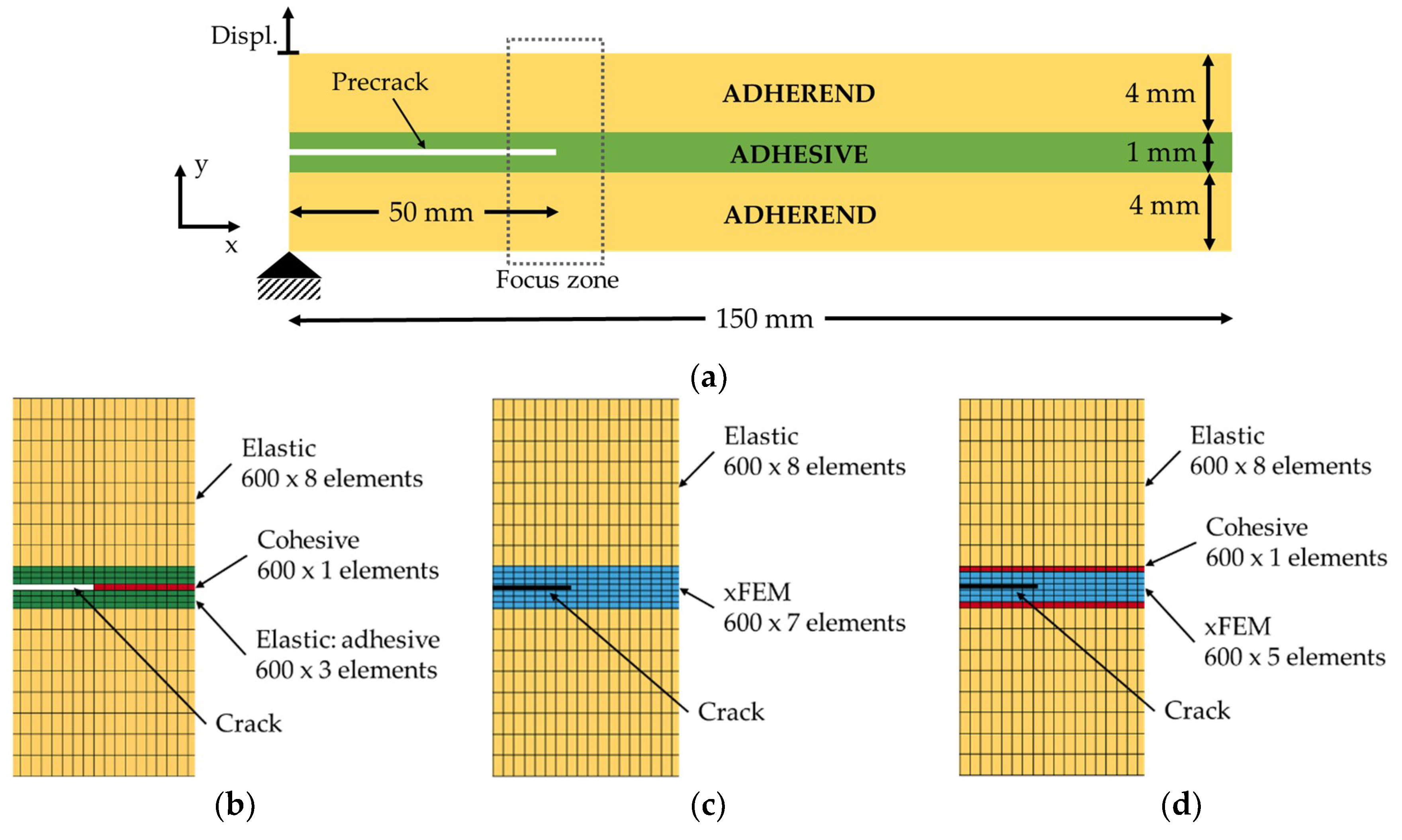
2.3. Double Cantilever Beam Model
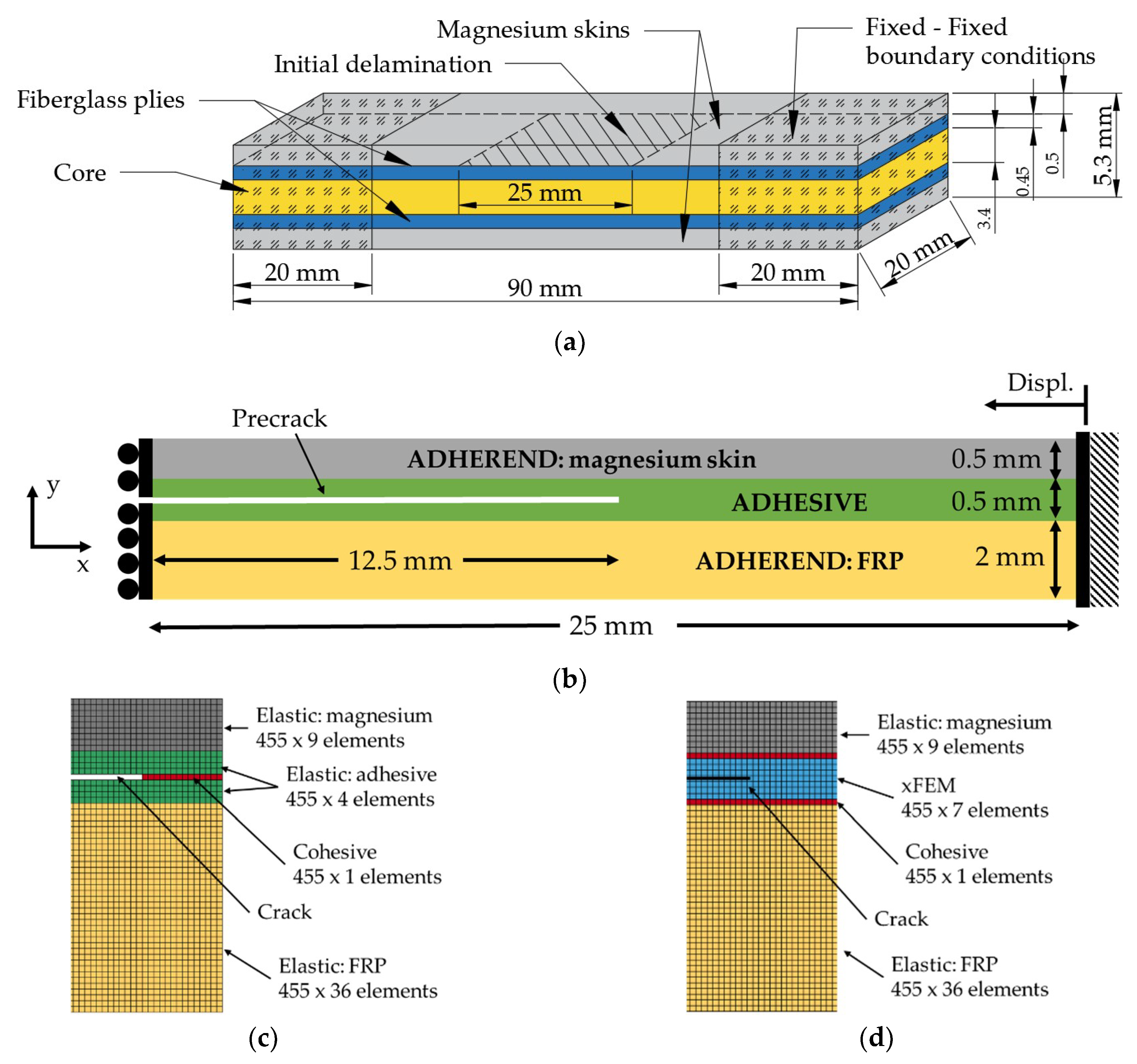
2.4. Delamination-Buckling Analysis
3. Results and Discussion
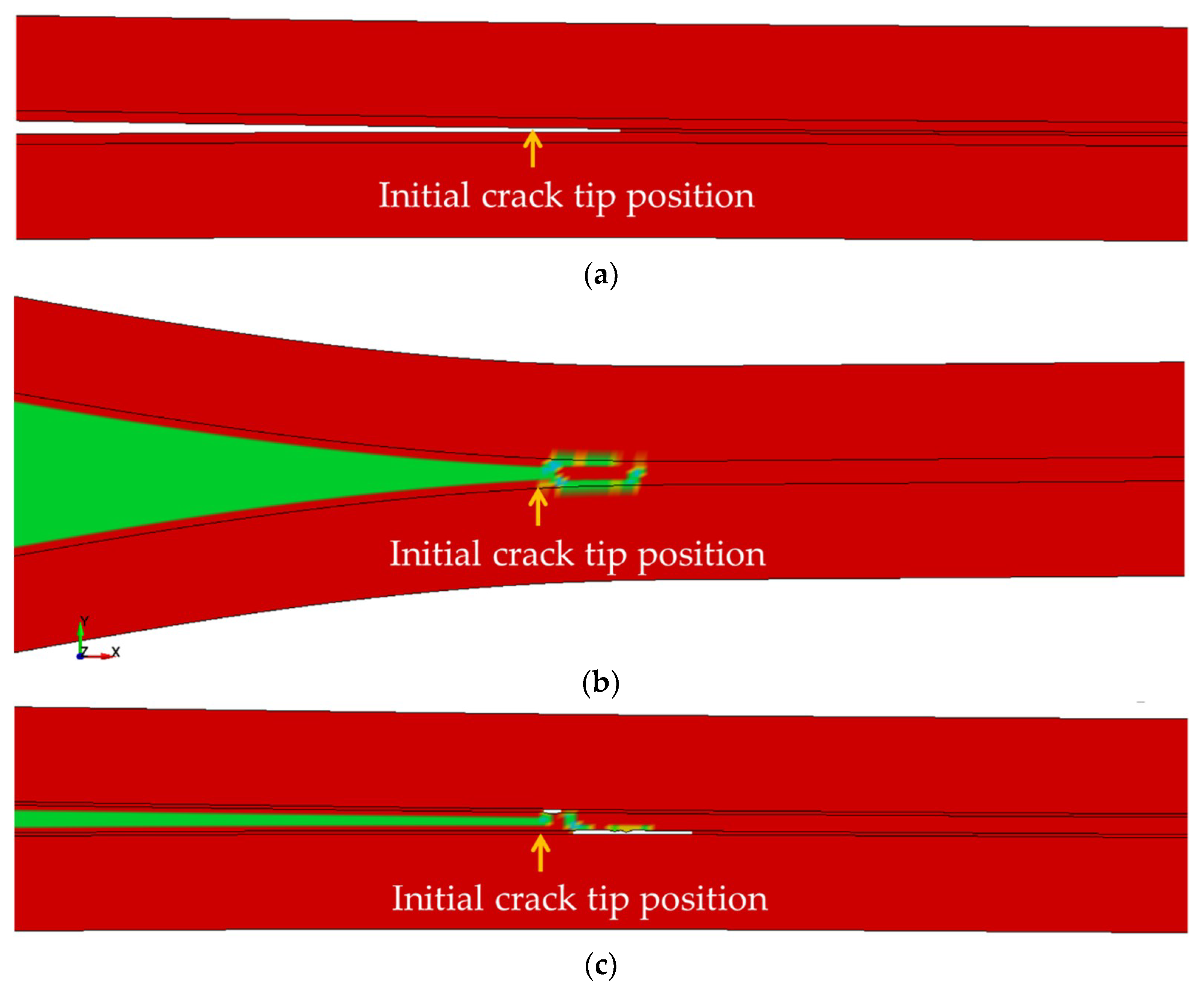
3.1. Double Cantilever Beam Simulation Results
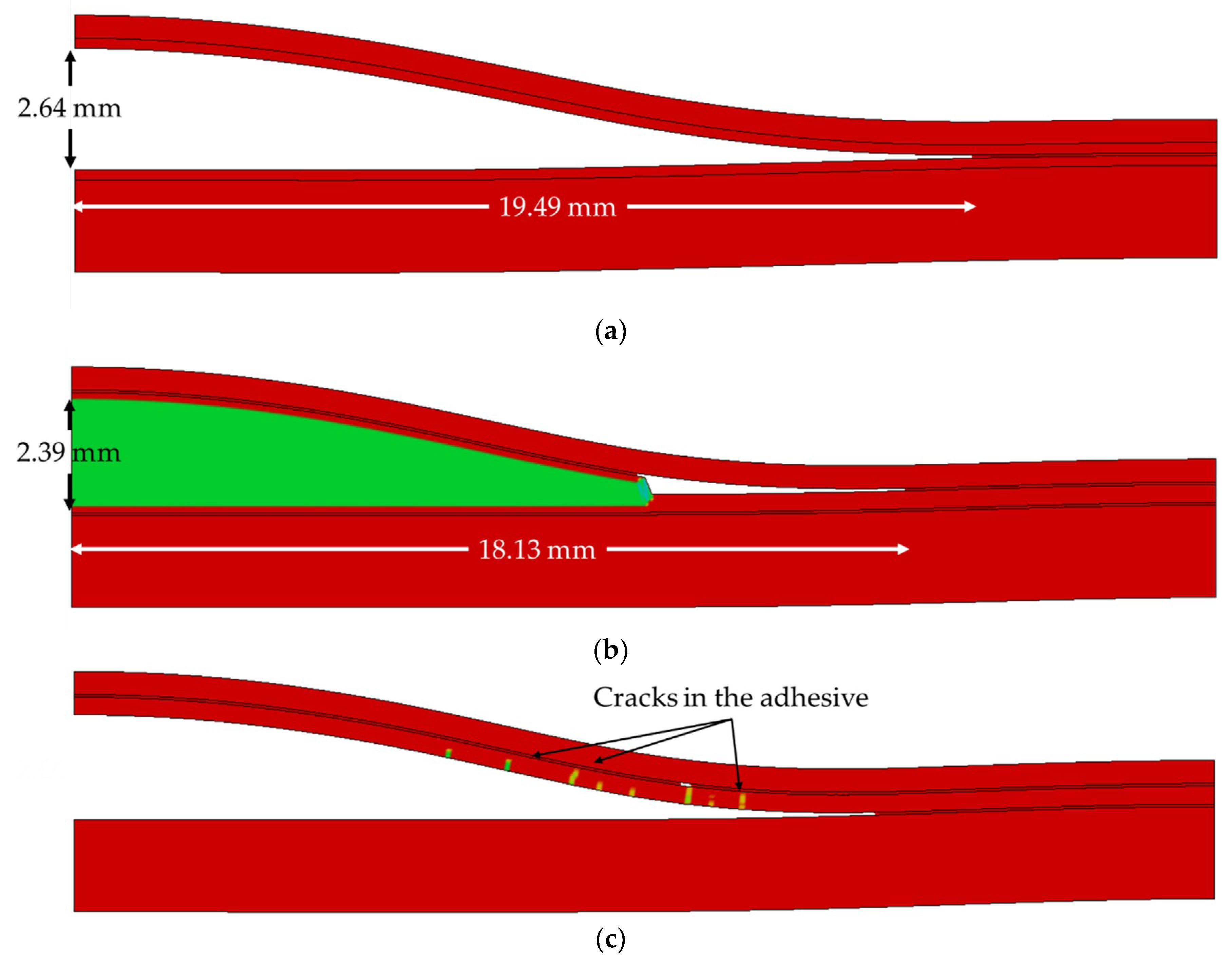
3.2. Delamination-Buckling Simulation Results
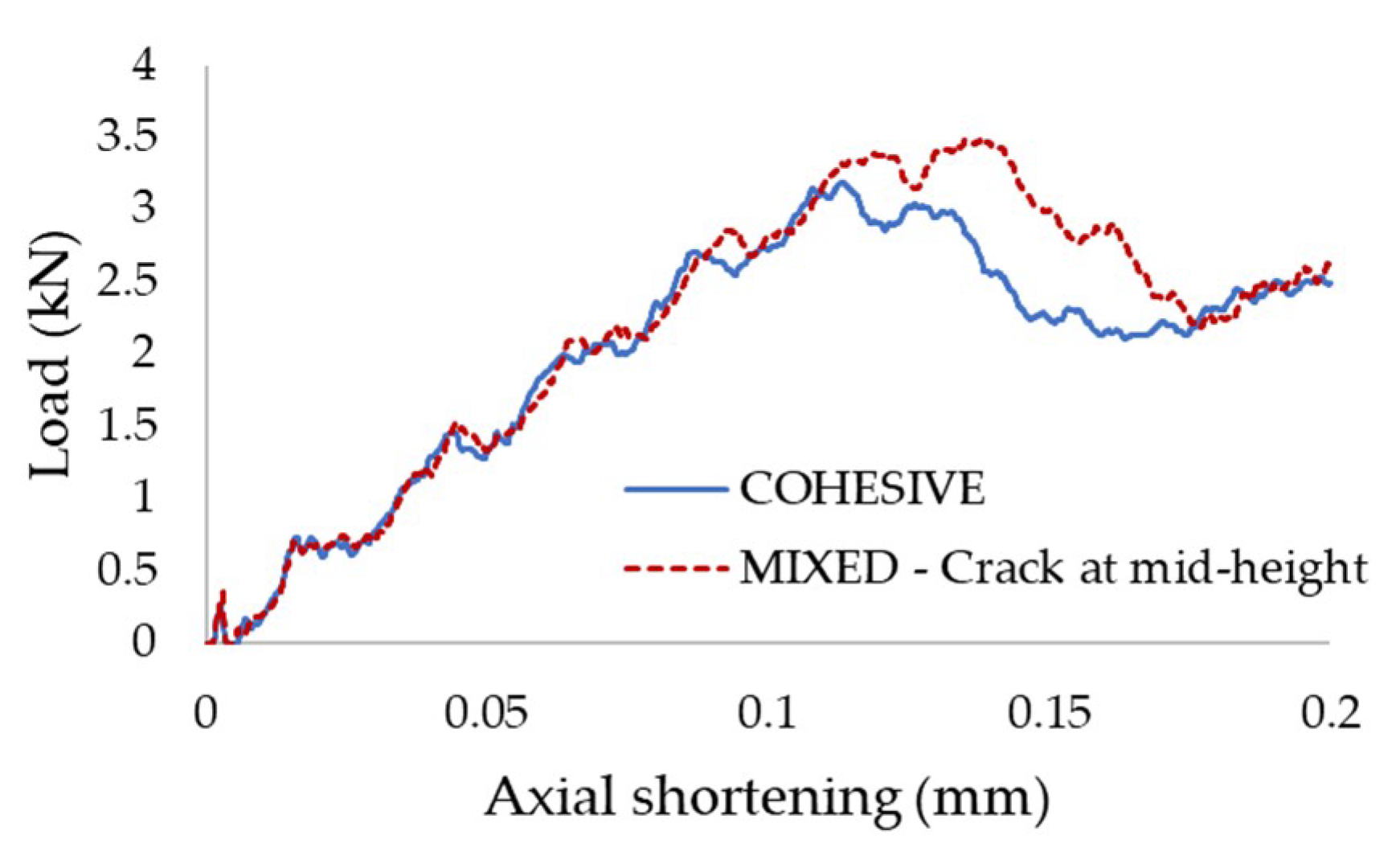
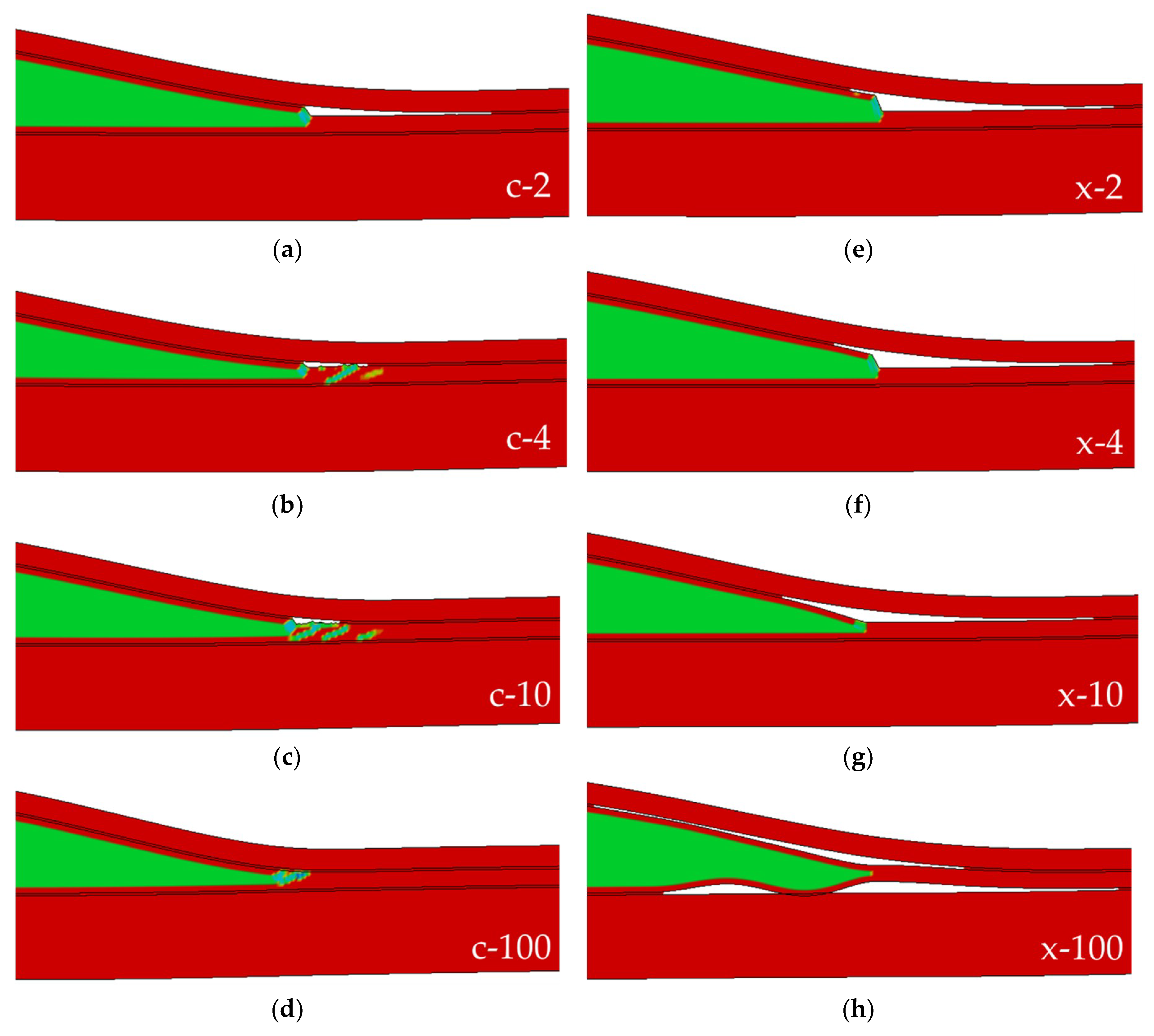
3.2.1. Influence of the Fracture Simulation Algorithms
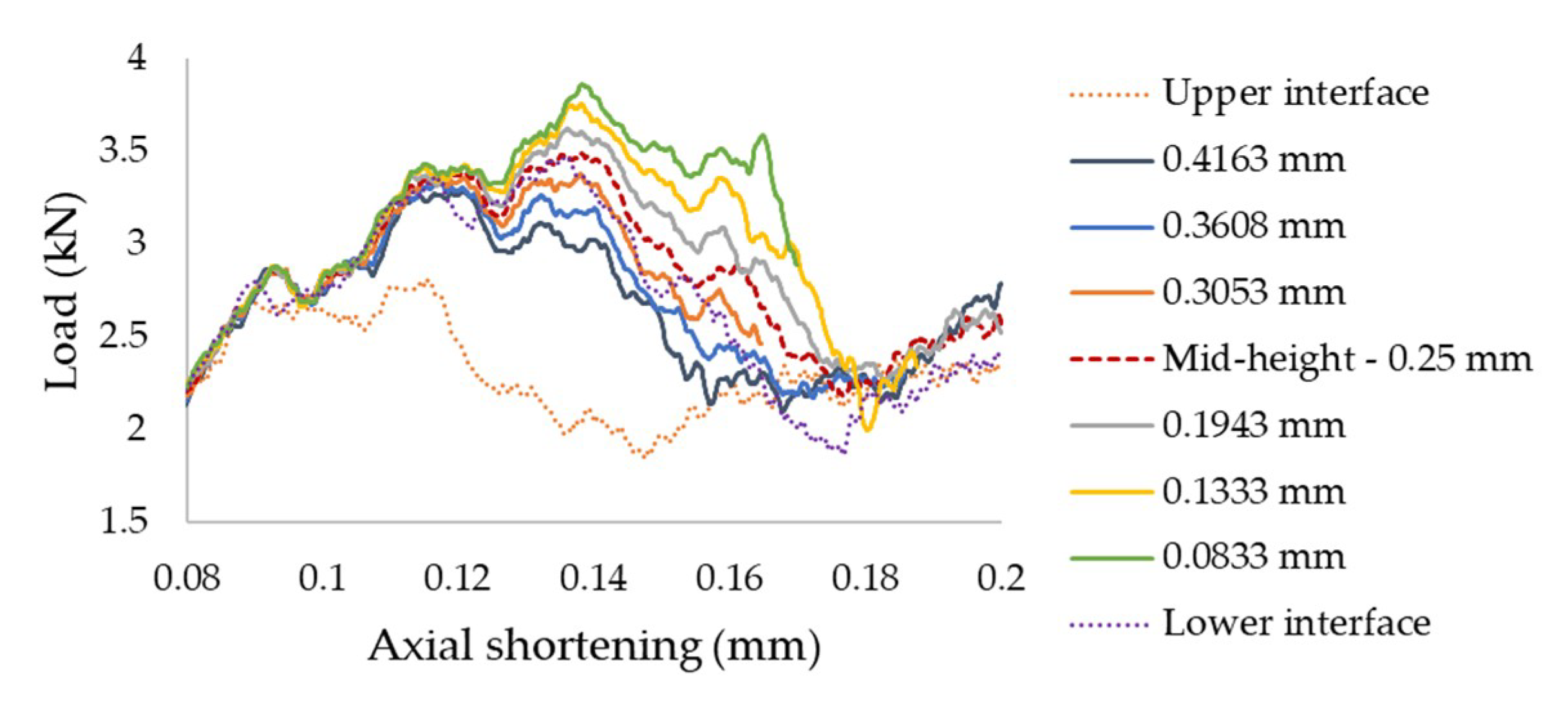
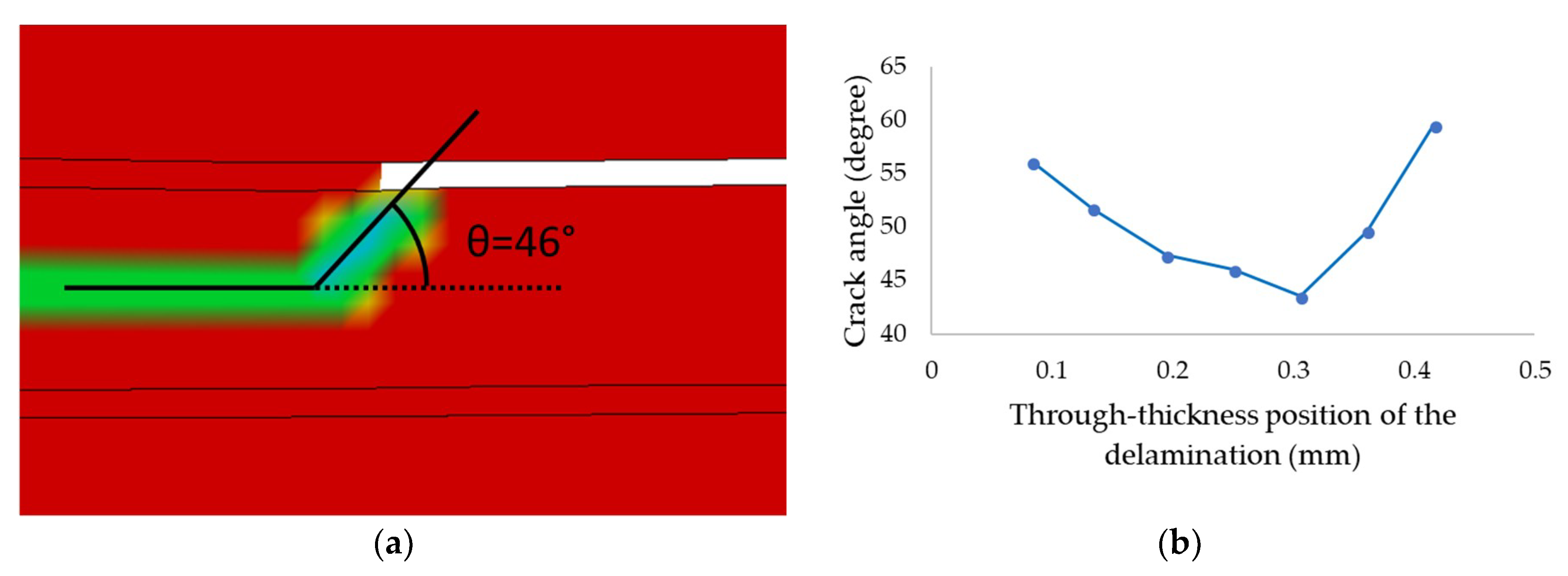
3.2.2. Influence of the Through-Thickness Position of Delamination
3.2.3. Influence of the Strength Ratio and the Reference Strength
3.3. Computation Time
4. Summary and Conclusions
- LS-DYNA’s shell elements could be used to simulate plane strain conditions in circumstances when plane strain elements cannot be used to conduct the analysis.
- The analysis of the DCB specimens using the combined xFEM and cohesive approach proved that the crack kinking that was experimentally observed to occur within the adhesive could be simulated precisely. The model that used only the xFEM elements could not capture the phenomenon.
- The above-mentioned combined approaches could also successfully simulate the delamination buckling response of the FML model with good accuracy. The delamination was demonstrated to change its propagation path that was initially within the adhesive (i.e., through the xFEM elements) towards the adhesive/metal interface, and subsequently propagating along the interface (i.e., through the cohesive elements). The delamination path deviation response highlights the importance of the role of surface preparation (i.e., interfacial integrity) in enhancing the performances of such FMLs under compressive loading states.
- Using the same material model and properties, the model constructed using only xFEM elements appeared to overestimate the energy required for the crack/delamination to propagate in comparison with the model constructed with the cohesive elements.
- The use of xFEM elements resulted in more accurate predictions of crack initiation and propagation. However, from a solution time perspective, especially when large complex geometries are to be modeled, the use of cohesive elements is deemed preferable, so long as the crack or delamination path is known a priori.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| *SECTION_SHELL | ELFORM = 2, NIP = 1 |
| *SECTION_SHELL_XFEM | ELFORM = 54, NIP = 4, CMID = id of the cohesive material, BASELM = 16, DOMINT = 0, FAILCR = 1 |
| *MAT_COHESIVE_TH | INTFALL = 1, STFSF = 100 |
| *DATABASE_EXTENT_BINARY | NEIPS = 1 |
| Elastic (*MAT_ELASTIC) | |||
| FRP | ρ = 1630 kg/m3 | E = 25 GPa | ν = 0.254 |
| Magnesium | ρ = 1740 kg/m3 | E = 36 GPa | ν = 0.35 |
| Adhesive | ρ = 1200 kg/m3 | E = 3 GPa | ν = 0.3 |
| Cohesive (*MAT_COHESIVE_TH) | |||
| ρ = 1200 kg/m3 | σmax = 0.008 GPa ♣ | δnorm = 0.015 mm | δtan = 0.02 mm |
| λ1 = 0.5 | λ2 = 0.5 | λfail = 1 | |
References
- Tsuda, T.; Ohnishi, Y.; Ohtagaki, R.; Cho, K.; Fujimoto, T. Three-Point Bending Crack Propagation Analysis of Beam Subjected to Eccentric Impact Loading by X-FEM. In Proceedings of the 10th European LS-DYNA Conference, Würzburg, Germany, 15–17 June 2015; Livermore Software Technology Corporation: Würwburg, Germany, 2015; p. 10. [Google Scholar]
- Barenblatt, G.I. The mathematical theory of equilibrium cracks in brittle fracture. In Advances in Applied Mechanics; Elsevier: New York, NY, USA, 1962; Volume 7, pp. 55–129. ISBN 0065-2156. [Google Scholar]
- Xu, X.-P.; Needleman, A. Numerical simulations of fast crack growth in brittle solids. J. Mech. Phys. Solids 1994, 42, 1397–1434. [Google Scholar] [CrossRef]
- Wang, Y.; Waisman, H. From diffuse damage to sharp cohesive cracks: A coupled XFEM framework for failure analysis of quasi-brittle materials. Comput. Methods Appl. Mech. Eng. 2016, 299, 57–89. [Google Scholar] [CrossRef]
- Ranatunga, V. Finite Element Modeling of Delamination Crack Propagation in Laminated Composites. In Proceedings of the World Congress on Engineering 2011, London, UK, 6–8 July 2011; Volume III, ISBN 9789881925152. [Google Scholar]
- Yelve, N.P.; Khan, N.N. Analysis of Traction Separation in Double Cantilever Beam Using Cohesive Zone Modeling. In Proceedings of the International Conference on Mechanical and Industrial Engineering (ICMIE), Penang, Malaysia, 28–29 August 2013; pp. 47–50, ISBN 9789382208815. [Google Scholar]
- Alfano, G.; de Barros, S.; Champaney, L.; Valoroso, N. Comparison Between Two Cohesive-Zone Models for the Analysis of Interface Debonding. In Proceedings of the European Congress on Computational Methods in Applied Sciences and Engineering ECCOMAS, Jyväskylä, Finland, 24–28 July 2004; pp. 1–18. [Google Scholar]
- Sapora, A.; Paggi, M. A coupled cohesive zone model for transient analysis of thermoelastic interface debonding. Comput. Mech. 2014, 53, 845–857. [Google Scholar] [CrossRef]
- Sugiman, S.; Crocombe, A.D.; Aschroft, I.A. Experimental and numerical investigation of the static response of environmentally aged adhesively bonded joints. Int. J. Adhes. Adhes. 2013, 40, 224–237. [Google Scholar] [CrossRef]
- Giuliese, G.; Pirondi, A.; Moroni, F. A Cohesive Zone Model for Three-dimensional Fatigue Debonding/Delamination. Procedia Mater. Sci. 2014, 3, 1473–1478. [Google Scholar] [CrossRef]
- Johar, M.; Kosnan, M.S.E.; Tamin, M.N. Cyclic Cohesive Zone Model for Simulation of Fatigue Failure Process in Adhesive Joints. Appl. Mech. Mater. 2014, 606, 217–221. [Google Scholar] [CrossRef]
- Marzi, S.; Ramon-Villalonga, L.; Poklitar, M.; Kleiner, F. Usage of cohesive elements in crash analysis of large, bonded vehicle structures. Experimental tests and simulation. In German LS-Dyna Forum; DYNAmore GmbH: Bamberg, Germany, 2008; pp. 1–20. [Google Scholar]
- Lemmen, P.; Meijer, G.-J.; Rasmussen, E.A. Dynamic behavior of composite ship structures (DYCOSS). Failure prediction tool. In Proceedings of the 70th Shock and Vibration Symposium, Albuquerque, NM, USA, 15–19 November 1999; pp. 15–19. [Google Scholar]
- Dogan, F.; Hadavinia, H.; Donchev, T.; Bhonge, P.S. Delamination of impacted composite structures by cohesive zone interface elements and tiebreak contact. Cent. Eur. J. Eng. 2012, 2, 612–626. [Google Scholar] [CrossRef]
- Moes, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Krueger, R. Virtual crack closure technique: History, approach, and applications. Appl. Mech. Rev. 2004, 57, 109–143. [Google Scholar] [CrossRef]
- Pascoe, J.A.; Alderliesten, R.C.; Benedictus, R. Methods for the prediction of fatigue delamination growth in composites and adhesive bonds—A critical review. Eng. Fract. Mech. 2013, 112–113, 72–96. [Google Scholar] [CrossRef]
- Serna Moreno, M.C.; Curiel-Sosa, J.L.; Navarro-Zafra, J.; Martínez Vicente, J.L.; López Cela, J.J. Crack propagation in a chopped glass-reinforced composite under biaxial testing by means of XFEM. Compos. Struct. 2014, 119, 264–271. [Google Scholar] [CrossRef]
- Wang, Y.; Waisman, H. Progressive delamination analysis of composite materials using XFEM and a discrete damage zone model. Comput. Mech. 2015, 55, 1–26. [Google Scholar] [CrossRef]
- Mollenhauer, D.; Zhou, E.; Hoos, K.; Iarve, E.; Braginsky, M.; Breitzman, T.; Rapking, D. Multi-Scale Simulation of Delamination Migration. In Proceedings of the American Society for Composites: Thirty-First Technical Conference, Williamsburg, VA, USA, 19–22 September 2016; DEStech Publications, Inc.: Williamsburg, VA, USA, 2016; p. 10. [Google Scholar]
- Wang, Y.; Waisman, H. Material-dependent crack-tip enrichment functions in XFEM for modeling interfacial cracks in bimaterials. Int. J. Numer. Methods Eng. 2017, 112, 1495–1518. [Google Scholar] [CrossRef]
- Wang, Y.; Cerigato, C.; Waisman, H.; Benvenuti, E. XFEM with high-order material-dependent enrichment functions for stress intensity factors calculation of interface cracks using Irwin’s crack closure integral. Eng. Fract. Mech. 2017, 178, 148–168. [Google Scholar] [CrossRef]
- Curiel Sosa, J.L.; Karapurath, N. Delamination modelling of GLARE using the extended finite element method. Compos. Sci. Technol. 2012, 72, 788–791. [Google Scholar] [CrossRef]
- Asaee, Z.; Shadlou, S.; Taheri, F. Low-velocity impact response of fiberglass/magnesium FMLs with a new 3D fiberglass fabric. Compos. Struct. 2015, 122, 155–165. [Google Scholar] [CrossRef]
- De Cicco, D.; Taheri, F. Delamination Buckling Response of 3D Fiber-Metal Laminates Subjected to Different Loading Rates. In Proceedings of the American Society for Composites: Thirty-First Technical Conference, Williamsburg, VA, USA, 19–22 September 2016; DEStech Publications, Inc.: Williamsburg, VA, USA, 2016; p. 12. [Google Scholar]
- De Cicco, D.; Taheri, F. Understanding the parameters that influence buckling of 3D fiber-metal laminates. In Proceedings of the 10th Canadian-International Conference on Composites (CANCOM2017), Ottawa, ON, Canada, 17–20 July 2017. [Google Scholar]
- De Cicco, D.; Taheri, F. Robust numerical approaches for simulating the buckling response of 3D fiber-metal laminates under axial impact—Validation with experimental results. J. Sandw. Struct. Mater. 2018, 1–30. [Google Scholar] [CrossRef]
- Tvergaard, V.; Hutchinson, J.W. The relation between crack growth resistance and fracture process parameters in elastic-plastic solids. J. Mech. Phys. Solids 1992, 40, 1377–1397. [Google Scholar] [CrossRef]
- KEYWORD USER’S MANUAL VOLUME II; LS-DYNA R9.0; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2016; Volume II, ISBN 9254492507.
- Sam, C.; Papoulia, K.D.; Vavasis, S.A. Obtaining initially rigid cohesive finite element models that are temporally convergent. Eng. Fract. Mech. 2005, 72, 2247–2267. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, C.T. XFEM and EFG Cohesive Fracture Analysis for Brittle and Semi-Brittle Materials. In Proceedings of the 11th International LS-DYNA Users Conference, Dearborn, MI, USA, 6–8 June 2010; pp. 21–32. [Google Scholar]
- ASTM D5528: Standard Test Method for Mode I Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites. Am. Stand. Test. Methods 2014, 3, 1–12. [CrossRef]
- Tabiei, A.; Zhang, W. Evaluation of Various Numerical Methods in LS-DYNA for 3D Crack Propagation. In Proceedings of the 14th International LS-DYNA Users Conference, Dearborn, MI, USA, 12–14 June 2016; Livermore Software Technology Corporation: Detroit, MI, USA, 2016; pp. 1–19. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Cicco, D.; Taheri, F. Delamination Buckling and Crack Propagation Simulations in Fiber-Metal Laminates Using xFEM and Cohesive Elements. Appl. Sci. 2018, 8, 2440. https://doi.org/10.3390/app8122440
De Cicco D, Taheri F. Delamination Buckling and Crack Propagation Simulations in Fiber-Metal Laminates Using xFEM and Cohesive Elements. Applied Sciences. 2018; 8(12):2440. https://doi.org/10.3390/app8122440
Chicago/Turabian StyleDe Cicco, Davide, and Farid Taheri. 2018. "Delamination Buckling and Crack Propagation Simulations in Fiber-Metal Laminates Using xFEM and Cohesive Elements" Applied Sciences 8, no. 12: 2440. https://doi.org/10.3390/app8122440
APA StyleDe Cicco, D., & Taheri, F. (2018). Delamination Buckling and Crack Propagation Simulations in Fiber-Metal Laminates Using xFEM and Cohesive Elements. Applied Sciences, 8(12), 2440. https://doi.org/10.3390/app8122440





