Featured Application
accurate and reliable modeling of crack path in delamination of composite materials, specifically in fiber-metal laminates.
Abstract
Simulation of fracture in fiber-reinforced plastics (FRP) and hybrid composites is a challenging task. This paper investigates the potential of combining the extended finite element method (xFEM) and cohesive zone method (CZM), available through LS-DYNA commercial finite element software, for effectively modeling delamination buckling and crack propagation in fiber metal laminates (FML). The investigation includes modeling the response of the standard double cantilever beam test specimen, and delamination-buckling of a 3D-FML under axial impact loading. It is shown that the adopted approach could effectively simulate the complex state of crack propagation in such materials, which involves crack propagation within the adhesive layer along the interface, and its diversion from one interface to the other. The corroboration of the numerical predictions and actual experimental observations is also demonstrated. In addition, the limitations of these numerical methodologies are discussed.
1. Introduction
The effective assessment of performances of today’s lightweight hybrid materials and complex structural components made by such materials requires cost-effective numerical methodologies and approaches. The currently available advanced numerical methods and simulation techniques are considered as effective and efficient tools for assessing the response of materials, engineering components and structures, and their certification. Even though remarkable advancements have been made in computational mechanics in the past few decades, the reliable simulation and prediction of fracture and failure of bulk materials and bonded interfaces are still challenging. In finite element modeling, the main techniques used to simulate fracture are the (i) element erosion approach, (ii) cohesive zone modeling (CZM), and (iii) extended finite element method (xFEM). It should be noted that other techniques, like the Virtual Crack Closure Technique (VCCT), may also be coupled with other algorithms to simulate crack propagation in a body; however, only the techniques that could individually simulate crack propagation are briefly discussed.
The element erosion approach entails deleting elements based on an appropriate stress or strain criterion, therefore, leading to the formation of a crack path. It is the simplest of the mentioned methods but is significantly mesh-dependent, thus, often lacking accuracy [1].
CZM is a relatively easy method to implement [2]; however, it requires a priori knowledge of the crack path, unless coupled with an advanced re-meshing technique [3,4]. The technique has been used in a variety of applications [5,6,7], because it is especially suitable for modeling interfaces in hybrid material systems; it also works well under large deformation conditions. Moreover, CZM can also be used to account for thermal [8] and moisture [9] effects, and also fatigue [10,11]. For instance, Marzi et al. [12] used CZM to model the low-velocity impact of a vehicle’s sub-structure constituted of various bonded components. Accurate results were obtained when the mesh discretizing the cohesive zone was significantly fine. Moreover, the suitability of the method for large-scale simulations was also demonstrated. Lemmen et al. [13] showed another application of CZM, when it was used to assess the performance of bonded joints mating composite components in a ship, obtaining close an agreement between the numerical results and experimental data. Dogan et al. [14] used cohesive elements and tiebreak contact in LS-DYNA to simulate delamination between plies of fiber-reinforced polymers (note that tiebreak contact is also based on a cohesive zone algorithm). They obtained excellent results compared to their experimental results. In that study, each composite ply was modeled separately with either thin or thick shell elements, and the elements were then mated using cohesive elements or tiebreak contact.
The xFEM approach involves “enriching” the finite element formulation to account for the presence of a discontinuity, without the need for creating an actual discontinuity between the elements, thus removing the need for remeshing [15,16,17]. A detailed explanation of the method’s implementation in LS-DYNA can be found in [18]. The use of xFEM would be most effective when the crack path is unknown, or in cases where a crack is suspected to kink or bifurcate. This method has been recently utilized by several researchers to simulate crack initiation and propagation in various media. For instance, Serna Moreno et al. [19] analyzed the failure of a biaxially loaded cruciform specimen made of quasi-isotropic chopped strand mat-reinforced composite using xFEM and showed that no prior knowledge of the onset location of the crack was necessary to obtain an accurate prediction of crack initiation and propagation. This is a significant advantage of xFEM compared to CZM. Wang and Waisman [20] used xFEM to model delamination in composites and showed that the interfacial failure of the plies and cracking of the laminate could be simulated with virtually no-mesh dependency. Mollenhauer et al. [21] demonstrated the capability of the tiebreak contact and xFEM for modeling crack propagation in a precracked thick beam, under mode I loading. They showed the deviation of the crack that originally started in 0°/90° ply-interface, propagating into the adjacent 90°/0° interface.
It should be noted that in general, however, the accuracy of the results is highly dependent on the xFEM formulation, which is considerably more complex than the conventional finite element formulations [22,23]. As a result, xFEM is not readily available in all commercial finite element software, and if it is, the formulation is usually limited to a set of element types.
Moreover, it is worth mentioning that there are a few studies that have compared the integrity of the three approaches when used in simulating crack propagation. For instance, Tsuda et al. [1] used the erosion and xFEM elements of LS-DYNA for simulating the crack propagation resulting from the impact of a rectangular cast iron specimen in three-point bending configuration. The xFEM results were found to be in excellent agreement with the experimental results, while the erosion elements could not accurately simulate the experimentally observed response. Curiel Sosa and Karapurath [24] compared capabilities of the xFEM element against both cohesive and erosion elements for simulating the response of a standard double cantilever beam modeled using 3D elements in ABAQUS. They found the xFEM results to be more consistent and closer to the experiment results, and not too sensitive to mesh density. However, they observed xFEM’s tendency to underestimate the fracture energy, while CZM overestimated it.
As stated, all the modeling facilities mentioned above are available in LS-DYNA. In this paper, we will focus on CZM and xFEM and, more precisely, on the possibility of combining them for conducting a more accurate modeling of crack propagation resulting from delamination buckling of a relatively complex 3D hybrid composite material (i.e., a new class of FML). This new material referred to as 3D-FML, takes advantage of the properties of a lightweight magnesium alloy, coupled with a recently developed truly 3D fiberglass fabric and a light-weight foam, thus rendering a cost-effective lightweight material with remarkable stiffness, strength, and resiliency against impact [25]. However, it is well-known that the Achilles’ heel of all laminated composites is their relatively weaker interlaminar strength compared to their bending and axial strengths, and the 3D-FML is no exception. The likelihood of delamination initiation in such materials becomes even greater when they become subjected to a suddenly applied axial compressive loading [26,27,28]. Under such a circumstance, the metallic constituent often debonds from the core section. Therefore, the presence of a delamination, even a small one, would adversely affect the performance of laminated composites and FMLs subjected to compressive loadings. The authors are, therefore, interested in better understanding the response of 3D-FMLs under compressive impact loading, and the ensuing failure mechanism during their delamination buckling in order (i) to accurately predict their behavior through numerical simulation and (ii) to enhance their load-carrying capacity of the 3D-FML by appropriate means.
2. Numerical Models
A systematic numerical investigation was conducted in this study, using a total of three different models in order to establish the integrity of the xFEM and CZM facilities of LS-DYNA. First, a model that was analyzed by another investigator [1] was tried to validate the integrity of our approach. Then, since the configuration of the materials forming our 3D-FML is relatively complex, it was decided to initially simulate the response of the standard double cantilever beam to further hone our skill in using the xFEM and calibrate the properties required for conducing such analysis. Finally, the response of a less-complex equivalent model of our 3D-FML material, subjected to an axial impact, was simulated.
As briefly mentioned, the first trial involved simulation of the response of a simply-supported rectangular cross-section cast iron beam specimen subjected to an impact load at its mid-span using xFEM. The parameters required for xFEM simulation of the specimen were extracted from reference [1]. It should be noted that the efficient approach commonly used in simulating such simple 3D geometries is by modeling them as either 2D plane-stress or plane-strain geometry, depending on the aspect ratios of the specimen. Therefore, an attempt was made to simulate the beam’s response by a plane-strain model. However, a convergent result could not be achieved when the xFEM was used in conjunction with the 2D plane strain element of LS-DYNA (even though LS-DYNA user-manual explicitly states admissibility of that element type in conjunction with xFEM). Consequently, LS-DYNA’s shell elements (type 54 in conjunction with the fully integrated base element 16) were used to continue the modeling effort. It is reckoned that shell elements are not used conventionally to simulate such geometries (i.e., geometries with an appreciable thickness-to-depth ratio); nonetheless, an accurate fracture response could be successfully predicted in comparison to the experimental results reported by Tsuda et al. [1] (who incidentally used the same approach in modeling the specimen’s response). A detailed explanation of the modeling approach, as well as the discussion of the required parameters, are presented in the Appendix A. In addition, the value of the parameters used in our models are given in Table A1.
The simulated results confirmed the integrity of the selected algorithm and element type; thus, they were used in the subsequent phases of the analysis. However, before continuing with the remaining analyses, it warrants to discuss the material model and the required parameters that will be required when conducting xFEM modeling.
2.1. Material Model for Cohesive and xFEM Elements
In LS-DYNA, only one material model is currently available for use in conjunction with the xFEM formulation, which is: *MAT_COHESIVE_TH. This is a cohesive material law proposed by Tvergaard and Hutchinson [29] with tri-linear traction-separation behavior (see Figure 1a), where the maximum traction stress and normal or tangential ultimate displacements are the governing and required parameters [30]. The model accepts only one value of the maximum stress; therefore, it could be either the maximum normal stress or maximum shear stress, accordingly. In this study, because mode I fracture is the dominant failure mode, the maximum tensile stress is chosen as the maximum stress governing the failure of the material. Note that the lack of differentiation between the maximum normal and shear stresses is an important limitation of this model.
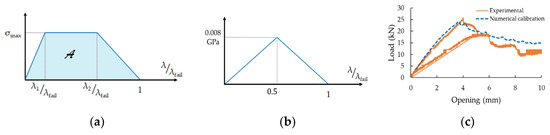
Figure 1.
(a) Representation of the traction-separation law of the *COHESIVE_TH material model, and (b) the bi-linear traction-separation cohesive model used in this investigation. Note that A refers to the total area under the curve. (c) the load-opening curves of the double cantilever beam (DCB) experimental test used for establishing the cohesive zone method (CZM) parameters.
This cohesive model is based on the non-dimensional parameters λ1, λ2, and λfail, defining the traction-separation law behavior, as shown in Figure 1. These parameters correspond to various segments of the traction-separation curve (i.e., the peak traction, the beginning of softening segment, and the final failure, respectively). In other words, these parameters are used to represent a measure of the global dimensionless separation, λ, mathematically represented for the two-dimensional case as follows:
where and are the normal and tangent separation displacements, and are the respective separation values at failure, and the operator ⟨⟩ refers to the Mc-Cauley brackets, used to differentiate the behavior under tension and compression.
The stress state is computed, using the trilinear traction-separation law parameters (see Figure 1), as follows:
where refers to the maximum tensile or shear stress, as mentioned previously.
Using a potential function, φ, defined as:
and the normal surface traction, , and the tangential surface traction, , are expressed by the following derivatives:
Finally, the development of the derivatives leads to the traction vector, expressed as:
This model is totally reversible, in other words, the loading and unloading follow the same path. In addition, the difference in behavior between tension and compression is accounted for, with the following equation describing the behavior for :
where κ is the penetration stiffness multiplier, defined by the user.
As mentioned previously, the tri-linear behavior is controlled by the three non-dimensional parameters, which affect term A in the following equation. These parameters are related to the material’s fracture toughness, GIC or GIIC in the following manner:
where the subscript “i” relates to the normal or tangential directions and A is the area under the normalized traction-separation curve (see Figure 1a,b).
GiC = A δi,
The cohesive parameters used in this investigation, as reported in the Appendix A, were obtained by calibrating the trial values in such a way that the numerical simulation-produced results would closely match the results obtained through the actual testing of the double cantilever beam (DCB) specimen, using the load-opening curve as the criterion, as shown in Figure 1c. It should be noted that the experimental test data of DCB was obtained under a static loading, while the simulation of the 3D-FML specimen of our interest, as will be presented later, was carried out when the specimen was subjected to an impact loading state; therefore, there would be some discrepancies between the evaluated values and those exhibited by the actual specimen dynamically. The establishment of the CZM parameters as explained is based on matching the overall behavior, which would not include while the fluctuations that could potentially develop locally. However, in this paper, the authors’ intent is to demonstrate the feasibility of the described method, not its accuracy. The selected calibration method is meant to simply establish the values of the cohesive zone’s parameters used to facilitate the simulation. Moreover, the xFEM formulation is currently only available under the dynamic, explicit solution scheme of LS-DYNA. Therefore, to ensure a reasonable solution time, all the simulations were run in dynamic mode, with the simulated event being in the order of a millisecond.
It is also worth mentioning that, during the calibration, no significant difference was found when reducing the tri-linear law to a bi-linear one (see Figure 1b), which facilitates a more CPU-efficient numerical solution. Consequently, λ1 and λ2 were both set to 0.5, thereby reducing the tri-linear model to a bi-linear model. Note that some researchers [31,32] have recommended the use of an initially-rigid cohesive law (i.e., λ1 = λ2 ≅ 0) for obtaining a more reliable estimation of the state of stress prior to the onset of a crack. However, numerical instabilities were encountered when the approach was adopted in this study. Moreover, this is not to say that adaptation of the tri-linear law and/or the initially rigid cohesive response would lead to similar issues when simulating other cases. It should be noted that the main objective of the study presented here is to demonstrate the potential of the xFEM method in simulating the response of a complex material system under a relatively complex loading state, as opposed to targeting the degree of accuracy that could be attained when using the technique. Consequently, no further calibration effort was expended towards this issue.
Finally, as mentioned earlier, this cohesive model is the only one available for use within xFEM in LS-DYNA. Therefore, for the sake of consistency, this model was also used with the cohesive elements, even though other cohesive models are available that could potentially produce more accurate predictions in the case of mixed mode fracture.
2.2. xFEM’s Formulation
Here, a brief description of the xFEM formulation is presented. Consider a domain, noted Ω, that includes a crack represented by a surface discontinuity ∂Ω, as shown in Figure 2. In xFEM, the following distance function (i.e., the function mapping the position of the closest points to the discontinuity), is used to represent the crack in Ω:
where is the position vector, is the position of the closest point that is projected onto the discontinuity surface ∂Ω, and is the unity vector normal to ∂Ω. Therefore, the discontinuity is represented by , and the sign of the function refers to each part of the domain, with positivity determined by .
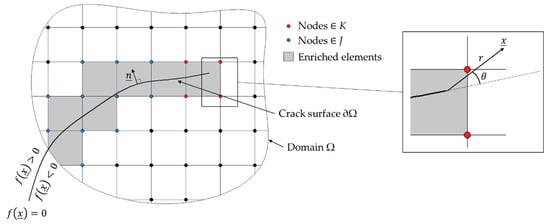
Figure 2.
Illustration of the extended finite element method (xFEM) approach.
In order to account for the presence of the discontinuity, the element formulation is enriched for the elements concerned by the crack. Let I be the set of all the nodes within the domain Ω and J be the set of all the nodes belonging to the enriched elements, excluding the one containing the crack tip, which is assigned to the set K. The nodal variable (e.g., displacement) can, therefore, be represented by [1]:
where , and are the regular and enriched nodal variables and , and are the regular and enriched shape functions. The enriched shape functions are as follow:
and
where H is the Heaviside function and , with r and θ given in Figure 2.
Note that the previously defined cohesive material behavior is used to obtain the crack opening displacement, and either the maximum principal stress or the maximum shear stress can be used as a criterion to establish the onset of crack propagation and its direction (noting that the former criterion is used in our models). When the criterion is reached within the element containing the current crack tip, the element is considered as failed and the crack tip is advanced by one element.
2.3. Double Cantilever Beam Model
The first of the two models, whose results are presented in this study, is the double cantilever beam (DCB), which is commonly used to assess the interlaminar fracture toughness of composite materials [33]. This model, whose geometry and boundary conditions are illustrated in Figure 3a, was used to assess the feasibility of the contemporary use of xFEM and cohesive elements for modeling crack propagation within the adhesive layer bonding the two adherends of DCB. In addition, as briefly explained earlier, the case was used to tune the materials properties that are required as input by both xFEM and cohesive elements.
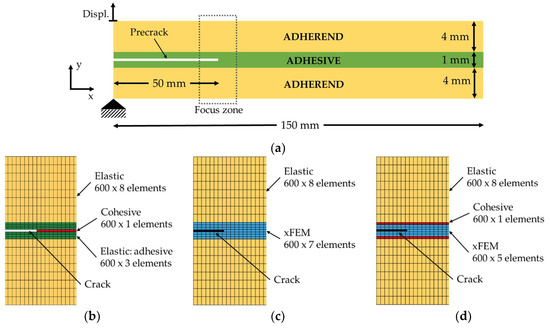
Figure 3.
(a) DCB specimen’s geometry, boundary conditions (not to scale), and zoom-up of the mesh around the crack-tip in the (b) COHESIVE model, (c) XFEM model, and (d) MIXED model.
The overall model’s specimen dimensions are 150 mm × 25 mm × 9 mm, with the initial crack length of 50 mm embedded within the mid-plane of the adhesive, in one end of the specimen, (see Figure 3a). This model is a simplification of the hybrid composite used for the experimental tests, consisting of a hybrid magnesium sheet and FRP forming the upper adherend, and biaxial FRP forming the lower adherend. It should be noted that, to further simplify the analysis (without compromising the overall accuracy), each of the two 4-mm thick adherends was homoginzed into an equivalent elstic material. In this way, the equivalent materials had the same flexural stiffness as the combined hybrid materials, but the analysis would concume significantly less CPU. The adopted scheme also facilitates more effective debugging. The 1-mm thick adhesive layer was modeled in three ways, by using (i) a combination of elastic and cohesive elements, as shown in Figure 3b, (ii) xFEM elements only, as shown in Figure 3c, and (iii) a combination of xFEM and cohesive elements, as shown in Figure 3d. These models are referred to as COHESIVE, XFEM, and MIXED, respectively, hereafter. The same cohesive material model was used in conjunction with both cohesive and xFEM elements; moreover, the xFEM elements were also assigned elastic model properties. In other words, the elements defined as xFEM would initially behave elastically until the stresses reach to a level at which xFEM’s enrichment is activated, thereby using the assigned cohesive properties. It should be noted that one could also assign other material models (e.g., elasto-plastic) to the xFEM elements instead of the elastic model [32].
The generation of the precrack, for the XFEM and MIXED models, was done using the *BOUNDARY_PRECRACK keyword, which enriches the elements to account for the presence of an initial crack. Note that the conventional practice in fracture mechanics, that is, having a series of disconnected adjacent layers of elements to model the crack, cannot be used in conjunction with xFEM elements. This is because xFEM element formulation allows for the crack to propagate only within the element. For the COHESIVE case, however, the crack was generated as done conventionally, that is by simply deleting the appropriate number of elements corresponding to the location of the actual crack/delamination. Therefore, to maintain consistency of the results when comparing the results generated by the three models, only the elements forming a portion of the adhesive that would be cracking (i.e., at the midplane of adhesive) were modeled by the cohesive material model, while the remaining portions were modeled with the elastic model, hereafter referred to as “elastic element”. This approach also saves the CPU time.
Finally, the adhesive layer was discretized with seven layers of elements as shown in Figure 3 and its density was kept constant along the bond length. The mesh density was stablished upon conducting a convergence study by which a reasonable accuracy could be attained by consuming an optimal CPU time.
2.4. Delamination-Buckling Analysis
The delamination-buckling of an initially partially delaminated clamped-clamped fiber-metal laminate subjected to an axial impact was simulated, with the geometry and dimensions of the original sample reported in Figure 4a. An equivalent simplified model, as shown in Figure 4b, consisting of three components was constructed. The model consisted of a 0.5-mm thick magnesium skin, a 0.5-mm thick adhesive layer, and a 2-mm thick fiberglass substrate. The symmetry in geometry and boundary conditions warranted modeling only one-half of the specimen, thus, reducing CPU computation. As shown in Figure 4b, the transverse displacement (uy) of the nodes located at the far-end of the specimen was restrained, and the same nodes were displaced at a rate of 1 m/s in the negative x-direction (-ux), to simulate the applied impact. In addition, the rotation (in xy-plane) of the nodes were also restrained. This combination of restrains mimics the actual clamped boundary condition. As also shown in the figure, the symmetric boundary condition at the left end of the half-symmetry model was ensured by restraining the longitudinal displacement (ux) and rotation about the y-axis at that location, while displacement in the transverse direction was permitted. Lastly, the out-of-plane displacement of all nodes (i.e., (uz)) was restrained to guarantee a purely planar deformation.
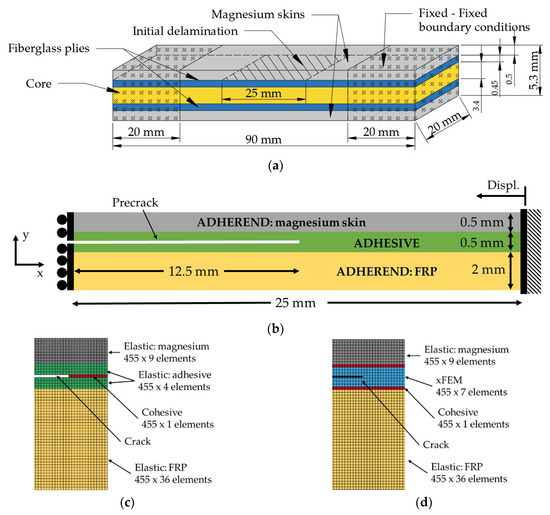
Figure 4.
Geometry and boundary conditions of the partially delaminated fiber metal laminates (FML) specimen (not to scale): (a) Sketch of the actual specimen (not to scale) (b) model used for numerical analysis, and the zoom-up views of the mesh around the delamination-tip in (c) the COHESIVE model and (d) the MIXED model.
Similar to the DCB specimen’s model, the adherends of the FML were modeled using elastic elements, while the adhesive layer was modeled using (i) the cohesive element only and (ii) a combination of both xFEM and cohesive elements. Moreover, similar to the previous case-study, the models will be referred to as COHESIVE and MIXED. The XFEM model was not considered here because of the inconsistent results obtained when the xFEM element was used in modeling the DCB, as will be discussed in Section 3.1. Moreover, the adhesive thickness was assumed to be 0.5 mm, so to facilitate more discrete simulation of the influence of the through-thickness location of a crack within the adhesive layer. Therefore, the mesh, established based on a convergence study, has nine layers of elements through the thickness of the adhesive.
In addition, the upper and lower delaminated portions of the specimen were assumed to have a sinusoidal geometric imperfection with small amplitudes of 0.1 mm and −0.02 mm in the y-direction, respectively, to promote the instability and to ensure that the upper and lower adherends would deflect in two opposite directions.
3. Results and Discussion
3.1. Double Cantilever Beam Simulation Results
The simulations of the DCB were conducted to examine the feasibility and advantage of the proposed combined simulation methods (i.e., combined xFEM and cohesive elements). It is noted that the DCB tests were conducted under static loading scenario, which differs from the loading states our 3D-FML specimens were subjected to. However, as briefly stated earlier, the accuracy of the results is not a focus of this preliminary stage of our research, since the main objective was to examine the capabilities of the various approaches used here to model the crack propagation within a complex hybrid system subjected to a critical loading state (i.e., impact). The predicted crack propagation paths are reported in Figure 5. Note that LS-DYNA’s post-processor exhibits the crack propagation path captured by XFEM models by a change in the elements’ color, while the deleted-element scheme exhibits the path in the case of COHESIVE models. In the COHESIVE model, as expected, the crack propagated in a straight path along the cohesive elements. In the XFEM model, the crack did not propagate when the same magnitude of displacement as applied in the case of the COHESIVE model was used. However, upon the application of a greater magnitude of displacement (i.e., +45% for initiating the crack and +1132% at the end of calculations), the crack started propagating and deviated from its course towards the upper adherend/adhesive interface, traveling along that interface. At that stage, a second crack appeared at the initial kink location, propagating along the direction of the lower interface. It should be noted that the simulated crack propagation is not consistent with the experimental observations. Moreover, the resistance of crack to propagate led to an exaggerated opening of the delaminated portions of DCB when compared to the COHESIVE model.
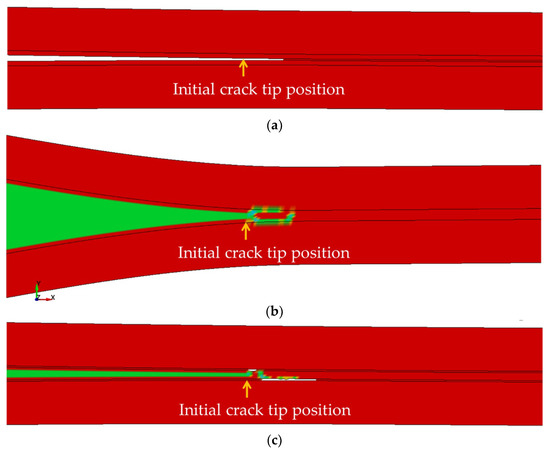
Figure 5.
Qualitative comparison of the crack propagation under the DCB test predicted by the various models (a) COHESIVE, (b) XFEM, and (c) MIXED. For the sake of clarity, only the zone near the crack tip is shown.
It should be noted that, when a combination of the elements was used (i.e., the MIXED model), the resulting crack propagation path was found to be yet different, as shown in Figure 5c. In that case, first the crack propagated through one element, and then it diverted towards the upper interface and propagated along that interface. It subsequently changed its path towards the lower interface and traveled along that interface. The total length of propagation during the described event was limited to 6 mm, after which the simulation was halted due to computational issues caused by the development of a negative volume in one of the elements; nevertheless, the approach illustrates the potential of the method.
The initial stage of crack propagation obtained with the MIXED model is compared to that observed during the static testing of the DCB described in Section 2.2, as illustrated in Figure 6. Note that the tested adhesive layer of 1 mm is greater than the actual thickness of 0.2 mm used in the actual test. The change in the thickness had to be done to resolve the extremely fine mesh that would have been required, had we used the 0.2 mm thickness. In addition, it is necessary to mention that the hybrid DCB specimen was designed so that the difference in flexural stiffness between the two cantilever beam portions of DCB specimen was relatively equal (in fact, they differed by a mere 2%, and the variation of longitudinal strain induced by the applied load was limited to 8%). This unconventional DCB specimen was constructed for the sole purpose of being able to obtain satisfactory experimental data using the available 0.5-mm thin magnesium sheets. Therefore, could appreciate that the qualitative results obtained through the presented model and the experimental results are comparable. The figure shows that the real crack deviated from its initial orientation towards the magnesium/adhesive interface, which is what the simulation captured. This kinking phenomenon can be captured by xFEM elements only, while in the case of the COHESIVE model, the crack had to follow the path occupied by the cohesive elements. The accuracy of the crack kinking captured by xFEM, however, will be discussed further in the following sections.

Figure 6.
Close-up views of the crack propagation in the DCB, in which a magnesium skin is bonded to an epoxy/fiberglass composite, using a 0.2 mm thick layer of epoxy resin. Specimen (a) with the white coating used for monitoring crack propagation and (b) without the coating.
3.2. Delamination-Buckling Simulation Results
As mentioned previously, one of the main objectives of this study was to gain a better appreciation of the predictive capability of the described approaches in simulating a more complicated response. The interest was to determine whether the simulation techniques could capture the response of the 3D magnesium/FRP FML introduced earlier; specifically, when the FML is subjected to an in-plane impact loading, which would potentially cause delamination buckling of its magnesium skins. In this phase of the study, the MIXED model’s response is compared to that of the COHESIVE model, qualitatively (i.e., by comparison of the delamination propagation paths) and quantitatively (by comparison of the resulting axial-load shortening curves). The models consider the presence of a delamination (crack) located at the mid-plane, through-the-thickness of the adhesive. In addition, the effect of two parameters on the delamination behavior is analyzed; the parameters are: (i) the through-thickness position of the delamination, and (ii) the ratio of the cohesive strength of the adhesive to the interfacial strength (i.e., the properties used in the xFEM and cohesive elements’ material models).
3.2.1. Influence of the Fracture Simulation Algorithms
The qualitative results are illustrated in Figure 7. The final delamination length captured by the COHESIVE model is 7.5% longer than that of the MIXED model, and the deflection of the delaminated skin is 10.5% greater, respectively. However, the deformed shapes are quite similar. The comparison of the axial-load shortening curves is presented in Figure 8. As seen, the two models predicted a similar response up to the stage when delamination starts propagating (i.e., when the elements are damaged but not yet failed); this stage corresponds to an axial shortening of approximately 0.12 mm. After that stage, the MIXED model depicted a stiffer response in comparison to the COHESIVE model. The areas under the axial-load shortening curves, evaluated from the stage at which delamination starts propagating, which represent the impact resisting energies, are also compared. The comparison indicates that the specimen analyzed by the MIXED model could sustain 20%more energy than the one modeled by the COHESIVE model. Interestingly, this behavior is opposite to what was reported by Curiel Sosa and Karapurath [24], who showed that CZM has a tendency to overestimate fracture energy. The sustaining energies become closer to one another towards the end of the computation time. This is attributed to the presence of the residual stress captured by the xFEM elements. In other words, after xFEM elements fail, the stress inside the elements does not become null, which is in contrast to the behaviour exhibited by the cohesive elements. However, since the delamination continues propagating through the cohesive elements and the number of failed xFEM elements remains constant, the effect of the residual stress is reduced.
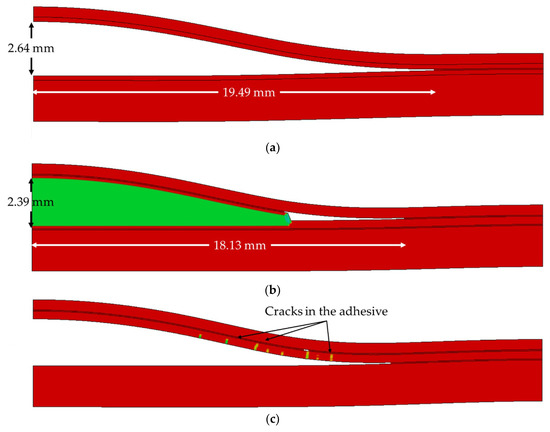
Figure 7.
Delamination propagation and resulting deformed shapes captured by the (a) COHESIVE model, (b) MIXED model with initial delamination at the mid-height, and (c) MIXED model with initial delamination at the lower interface.
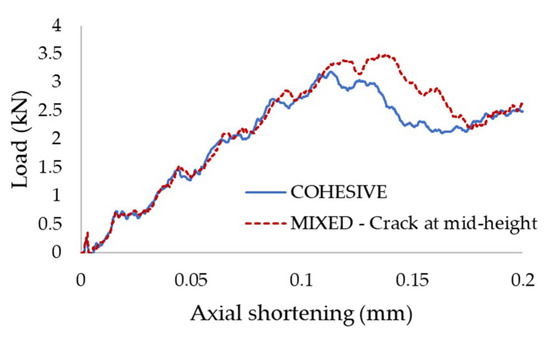
Figure 8.
Axial-load shortening curve produced by COHESIVE and MIXED models.
3.2.2. Influence of the Through-Thickness Position of Delamination
The analysis concerning the through-thickness position of the initial delamination, whose results are reported in Figure 9, indicates that a delamination located closer to the magnesium skin would lead to a lower load sustaining capacity (apart from the cases where the delamination is located at any of the interfaces). This is attributed to a combination of factors. Firstly, the delamination path would become longer when it propagates towards the interface. Secondly, the skin will have higher apparent rigidity, because a thicker layer of resin is bonded to it. Lastly, a greater number of xFEM elements would have to be traversed by the delamination front, which would imply that there would be a higher number of elements with residual stress. The results, however, do not follow the mentioned pattern when the delamination is initiated within the cohesive elements. The lowest load sustaining capacity is observed when the delamination is located at the upper interface; that is because no xFEM element is affected by the delamination. When the delamination is initiated at the lower interface, it does not propagate towards the upper interface, because the stress necessary for the delamination to kink is not attained. However, as can be seen from Figure 7c, several cracks appear in the adhesive layer due to the bending (note that all the cracks are oriented normal to the delaminated surface); notwithstanding, experimental tests would be required to corroborate these findings.
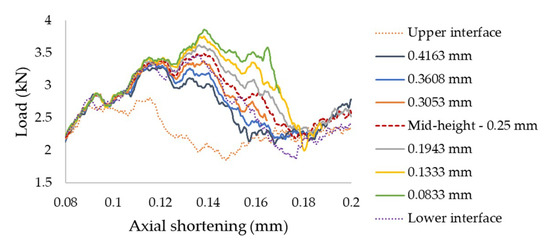
Figure 9.
Axial-load shortening curves produced by the MIXED model for case studies having various through-thickness positions of the initial delamination. Note that the first portion of the graphs has been omitted for clarity, as it is the same for all the cases.
Another important observation exposed by the result is that xFEM elements failed at a higher stress level in comparison to the cohesive elements, despite the fact that both element types were fed the same material properties (note that both cohesive and xFEM elements were described by the same bi-linear traction-separation law, cf. Section 2.1). For practical applications, it is therefore recommended to consider a slightly larger traction when using the cohesive element in comparison to the xFEM element. The exact amount of the traction value would have to be established by tuning the numerical models with experimental data.
Another interesting phenomenon observed during this phase of the study is the change in the ensuing delamination kink angle. This angle is defined as the angle between a hypothetical non-kinked delamination path and the delamination orientation after it kinks, as shown in Figure 10a. Note that for the reasons mentioned earlier, only the variation of the delamination in the xFEM elements could be considered.
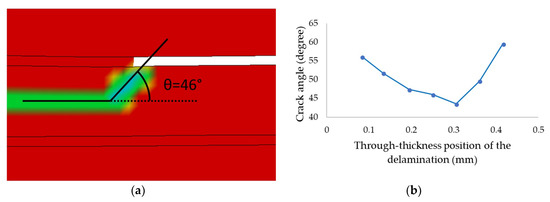
Figure 10.
(a) Kinking of the delaminated front predicted by the MIXED model (initial delamination at the mid-height); (b) delamination kink angles for various through-thickness positions of the delamination, for the specimen under impact.
As seen from Figure 10b, the closer the delamination is to the interfaces, the greater is the delamination kink angle (i.e., ~60°), while the minimum angle of 43° is observed when the delamination is located near the mid-thickness of the adhesive. This would indicate that, as the delamination becomes closer to an interface, its advancement will involve a greater presence of mode I compared to mode II. This is attributed to the stress state and the difference in the deformation responses of the relatively more flexible skins and the more rigid FRP core. Therefore, this could explain why an optimal surface preparation is of paramount importance for obtaining the maximum performance in such 3D-FMLs, in particular when the constituents bonded together have low chemical compatibility ( such as in our case).
It should be noted that in another work that will be soon published, we proposed a new bonding technique for improving the interface adhesion strength between magnesium and fiber-reinforced epoxy composites. In that work, it is experimentally demonstrated that the overall observed improvement in the delamination-buckling response of 3D-FML was, in part, due to the transition of fracture from mode I to mixed mode. The numerical results presented here, therefore, has enabled us to gain a better understanding of the basis that facilitated the improved performances we observed experimentally.
3.2.3. Influence of the Strength Ratio and the Reference Strength
The choice of adhesive type is of primordial importance to guarantee a sound 3D-FML. However, an adhesive with excellent bonding capabilities may not have an adequate strength, and a very strong adhesive may succumb to interfacial failure because of the lack of adhesion compatibility with the mating adherends. Therefore, another aspect that was investigated was the influence of the ratio of the cohesive strength of the adhesive (modeled using xFEM) to the interfacial strength (modeled using CZM). Surprisingly, no significant difference was observed in the resulting axial-load shortening curves among all the considered cases; therefore, these results are not reported.
However, the influence of the reference (or the maximum traction) strength was investigated. For that, values of 0.016, 0.032, 0.08, and 0.8 GPa were considered. The results are illustrated in Figure 11. The following conventions are used to distinguish the models’ results. In the figures, “c” and “x” refer to the results produced by the cohesive and xFEM elements, respectively. The numbers appearing after “c” and “x” signify the value (multiplier) by which the base strength (traction) value reported in Table A2 was increased. For instance, c-100 references to the COHESIVE model with the base strength of 0.8 GPa (i.e., 0.008 GPa × 100).
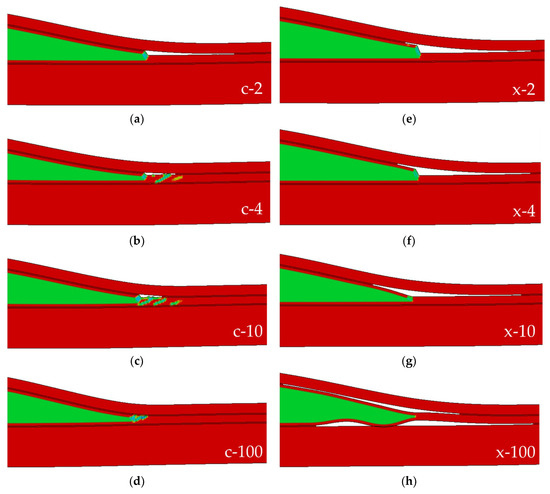
Figure 11.
Influence of the base (traction) strength on delamination propagation captured by the MIXED model when the strength of the cohesive elements is 2-100 times greater than the strength of the xFEM elements (subfigures (a) to (d), respectively) and when the strength of the xFEM elements is 2-100 times greater than the strength of the cohesive elements (subfigures (e) to (h), respectively).
As seen, the higher is the adhesive strength, the more difficult would be for the delamination to propagate along the interface. This results in the evolution of successive cracks, all having the same inclination. However, an apparent limit is reached when the base strength approaches a relatively large value (i.e., c-100), in which case the delamination would no longer propagate longitudinally, leading to extensive local damage at the delamination tip. Note that the delamination initially kinks towards the upper interface but could not propagate within the cohesive elements due to the high traction strength. Moreover, due to the limitation of the xFEM formulation, the delamination was not capable of propagating along the interface of xFEM/cohesive elements either. This resulted in the development of successive delaminations parallel to the initial delamination. Of interest is also the behaviors of models x-2 to x-10. In these models, the delamination propagated towards the interface, and then traveled along that interface in both forward and reverse directions. This response became increasingly noticeable as the base strength was increased, which is facilitated by the comparatively lower interface strength. In the extreme case (x-100), where the interface strength is significantly weaker than the traction strength, the adhesive detaches almost completely from both neighboring materials. Note that the minute interpenetration seen in model x-100 (see Figure 11h) is the result of the failure of the cohesive elements, and the absence of a contact algorithm. It should be noted that incorporation of an appropriate contact algorithm would have increased CPU consumption significantly, resulting in no appreciable benefit in terms of further understanding of the behavior.
3.3. Computation Time
The final aspect of the analyses being investigated is the computation time, which is one of the most important constraints in a numerical analysis, especially in large-scale simulations. For the relatively small and geometrically simple models considered in this study, the COHESIVE model consumed 1445 s solution time on a workstation using eight cores of an E5520 Xeon processor. In contrast, the MIXED model analysis took 2320 s (i.e., 60% more time compared with the COHESIVE model). Therefore, the use of the MIXED approach has its merits for understanding the crack propagation mechanisms but may not be feasible for large-scale simulations. However, its use may be justifiable if the crack path is either not known a priori or has a high influence on the outcome of the simulation. In cases where the crack path is predictable or confined, such as modeling the interfacial delamination in fiber-metal laminates, the use of cohesive elements could be considered as a more suitable choice.
4. Summary and Conclusions
In this study, the integrity and efficiency of the two modelling approaches used for assessing crack and delamination propagations in hybrid composites were examined. The approaches involved the use of cohesive and extended finite element (xFEM) elements available through the commercial finite element software LS-DYNA. More specifically, two separate case-studies were considered. First, crack propagation in a double cantilever beam (DCB) test specimen formed by two dissimilar adherends was considered. Then, delamination buckling response of a 3D fiber-metal laminate, subjected to a compressive impact loading, was simulated. The study also examined the integrity of a mixed approach; that is, the use of xFEM and cohesive elements within a single model. In the latter analysis, the cohesive elements were used to simulate the adhesive/adherend interface, while the xFEM elements were used to simulate the bulk portion of the adhesive. The summary of our findings is as follows:
- LS-DYNA’s shell elements could be used to simulate plane strain conditions in circumstances when plane strain elements cannot be used to conduct the analysis.
- The analysis of the DCB specimens using the combined xFEM and cohesive approach proved that the crack kinking that was experimentally observed to occur within the adhesive could be simulated precisely. The model that used only the xFEM elements could not capture the phenomenon.
- The above-mentioned combined approaches could also successfully simulate the delamination buckling response of the FML model with good accuracy. The delamination was demonstrated to change its propagation path that was initially within the adhesive (i.e., through the xFEM elements) towards the adhesive/metal interface, and subsequently propagating along the interface (i.e., through the cohesive elements). The delamination path deviation response highlights the importance of the role of surface preparation (i.e., interfacial integrity) in enhancing the performances of such FMLs under compressive loading states.
- Using the same material model and properties, the model constructed using only xFEM elements appeared to overestimate the energy required for the crack/delamination to propagate in comparison with the model constructed with the cohesive elements.
- The use of xFEM elements resulted in more accurate predictions of crack initiation and propagation. However, from a solution time perspective, especially when large complex geometries are to be modeled, the use of cohesive elements is deemed preferable, so long as the crack or delamination path is known a priori.
In closing, while the potentials of the different numerical approaches were demonstrated throughout this study, nonetheless, further effort is necessary to establish the accuracy of the solutions that are produced by these approaches. For instance, the future works should consider (i) precise calibration of the cohesive parameters required by the methods by experimental means, including investigation of strain effect on the properties, and (ii) verify the accuracy of the numerical results by comparing them with consistent experimental results. Another aspect that requires further investigation is understanding the origins of the numerical instabilities that at times halt and limit such solution processes. Finally, it would be worth exploring the capabilities of the element-free approaches, such as the element-free Galerkin (EFG) method and the discrete element method (DEM). These approaches have been proven to be efficient in simulating crack propagation [32,34] and are available through LS-DYNA for both 2D and 3D simulations.
Author Contributions
D.D.C. constructed and run the models, analyzed the data and wrote the draft manuscript. F.T. provided the idea, guided the research and edited the manuscript.
Funding
This research was supported by the National Sciences and Engineering Research Council of Canada (NSERC) and the MITACS Globalink fellowship program.
Acknowledgments
The grants received from the above agencies facilitated the study; the authors are grateful to the above agencies. The authors are also indebted to the LSTC support personnel (J. Day and Y. Guo) for their invaluable suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The authors wish to provide further information regarding the models’ implementation in LS-DYNA, to facilitate the use of the presented modeling approaches. The xFEM formulation is assigned to the elements via *SECTION_SHELL_XFEM keyword. For shell elements, the formulation ELFORM = 54 is used, while the parameter would be 52 when using the 2D plane strain element formulation. A base element (BASELM) must be designated as 16 for shell elements and 13 for the plane strain elements. Finally, the cohesive material model (CMID) is assigned. It should be noted that at the time the analyses were conducted, only *MAT_COHESIVE_TH was available for xFEM. The section properties are assigned to the mesh via the *PART keyword, which also requires a material model. As mentioned in Section 2.2, this input material model will govern the behavior until the stress state leads to the activation of the xFEM formulation, thereby switching the material behavior to those assigned through the selected cohesive zone model. In our study, a linear elastic orthotropic material model was used (*MAT_ELASTIC); however, other models, such as a plasticity model, can also be used if large deformations or material non-linearity are to be taken into account. Finally, the crack propagation path was captured by specifying an additional history variable for the output, by using the keyword *DATABASE_EXTENT_BINARY. This would enable the user to visualize the results in LS-DYNA’s post-processor (LS-PrePost).

Table A1.
Supplementary information related to the parameters required for implementation of the models in LS-DYNA.
Table A1.
Supplementary information related to the parameters required for implementation of the models in LS-DYNA.
| *SECTION_SHELL | ELFORM = 2, NIP = 1 |
| *SECTION_SHELL_XFEM | ELFORM = 54, NIP = 4, CMID = id of the cohesive material, BASELM = 16, DOMINT = 0, FAILCR = 1 |
| *MAT_COHESIVE_TH | INTFALL = 1, STFSF = 100 |
| *DATABASE_EXTENT_BINARY | NEIPS = 1 |

Table A2.
Material properties and parameters of the material models.
Table A2.
Material properties and parameters of the material models.
| Elastic (*MAT_ELASTIC) | |||
| FRP | ρ = 1630 kg/m3 | E = 25 GPa | ν = 0.254 |
| Magnesium | ρ = 1740 kg/m3 | E = 36 GPa | ν = 0.35 |
| Adhesive | ρ = 1200 kg/m3 | E = 3 GPa | ν = 0.3 |
| Cohesive (*MAT_COHESIVE_TH) | |||
| ρ = 1200 kg/m3 | σmax = 0.008 GPa ♣ | δnorm = 0.015 mm | δtan = 0.02 mm |
| λ1 = 0.5 | λ2 = 0.5 | λfail = 1 | |
♣ The reference strength value. The values of 0.016, 0.032, 0.08, and 0.8 GPa are used in conducting the influence of material’s strength study, outlined in Section 3.2.
References
- Tsuda, T.; Ohnishi, Y.; Ohtagaki, R.; Cho, K.; Fujimoto, T. Three-Point Bending Crack Propagation Analysis of Beam Subjected to Eccentric Impact Loading by X-FEM. In Proceedings of the 10th European LS-DYNA Conference, Würzburg, Germany, 15–17 June 2015; Livermore Software Technology Corporation: Würwburg, Germany, 2015; p. 10. [Google Scholar]
- Barenblatt, G.I. The mathematical theory of equilibrium cracks in brittle fracture. In Advances in Applied Mechanics; Elsevier: New York, NY, USA, 1962; Volume 7, pp. 55–129. ISBN 0065-2156. [Google Scholar]
- Xu, X.-P.; Needleman, A. Numerical simulations of fast crack growth in brittle solids. J. Mech. Phys. Solids 1994, 42, 1397–1434. [Google Scholar] [CrossRef]
- Wang, Y.; Waisman, H. From diffuse damage to sharp cohesive cracks: A coupled XFEM framework for failure analysis of quasi-brittle materials. Comput. Methods Appl. Mech. Eng. 2016, 299, 57–89. [Google Scholar] [CrossRef]
- Ranatunga, V. Finite Element Modeling of Delamination Crack Propagation in Laminated Composites. In Proceedings of the World Congress on Engineering 2011, London, UK, 6–8 July 2011; Volume III, ISBN 9789881925152. [Google Scholar]
- Yelve, N.P.; Khan, N.N. Analysis of Traction Separation in Double Cantilever Beam Using Cohesive Zone Modeling. In Proceedings of the International Conference on Mechanical and Industrial Engineering (ICMIE), Penang, Malaysia, 28–29 August 2013; pp. 47–50, ISBN 9789382208815. [Google Scholar]
- Alfano, G.; de Barros, S.; Champaney, L.; Valoroso, N. Comparison Between Two Cohesive-Zone Models for the Analysis of Interface Debonding. In Proceedings of the European Congress on Computational Methods in Applied Sciences and Engineering ECCOMAS, Jyväskylä, Finland, 24–28 July 2004; pp. 1–18. [Google Scholar]
- Sapora, A.; Paggi, M. A coupled cohesive zone model for transient analysis of thermoelastic interface debonding. Comput. Mech. 2014, 53, 845–857. [Google Scholar] [CrossRef]
- Sugiman, S.; Crocombe, A.D.; Aschroft, I.A. Experimental and numerical investigation of the static response of environmentally aged adhesively bonded joints. Int. J. Adhes. Adhes. 2013, 40, 224–237. [Google Scholar] [CrossRef]
- Giuliese, G.; Pirondi, A.; Moroni, F. A Cohesive Zone Model for Three-dimensional Fatigue Debonding/Delamination. Procedia Mater. Sci. 2014, 3, 1473–1478. [Google Scholar] [CrossRef]
- Johar, M.; Kosnan, M.S.E.; Tamin, M.N. Cyclic Cohesive Zone Model for Simulation of Fatigue Failure Process in Adhesive Joints. Appl. Mech. Mater. 2014, 606, 217–221. [Google Scholar] [CrossRef]
- Marzi, S.; Ramon-Villalonga, L.; Poklitar, M.; Kleiner, F. Usage of cohesive elements in crash analysis of large, bonded vehicle structures. Experimental tests and simulation. In German LS-Dyna Forum; DYNAmore GmbH: Bamberg, Germany, 2008; pp. 1–20. [Google Scholar]
- Lemmen, P.; Meijer, G.-J.; Rasmussen, E.A. Dynamic behavior of composite ship structures (DYCOSS). Failure prediction tool. In Proceedings of the 70th Shock and Vibration Symposium, Albuquerque, NM, USA, 15–19 November 1999; pp. 15–19. [Google Scholar]
- Dogan, F.; Hadavinia, H.; Donchev, T.; Bhonge, P.S. Delamination of impacted composite structures by cohesive zone interface elements and tiebreak contact. Cent. Eur. J. Eng. 2012, 2, 612–626. [Google Scholar] [CrossRef]
- Moes, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Krueger, R. Virtual crack closure technique: History, approach, and applications. Appl. Mech. Rev. 2004, 57, 109–143. [Google Scholar] [CrossRef]
- Pascoe, J.A.; Alderliesten, R.C.; Benedictus, R. Methods for the prediction of fatigue delamination growth in composites and adhesive bonds—A critical review. Eng. Fract. Mech. 2013, 112–113, 72–96. [Google Scholar] [CrossRef]
- Serna Moreno, M.C.; Curiel-Sosa, J.L.; Navarro-Zafra, J.; Martínez Vicente, J.L.; López Cela, J.J. Crack propagation in a chopped glass-reinforced composite under biaxial testing by means of XFEM. Compos. Struct. 2014, 119, 264–271. [Google Scholar] [CrossRef]
- Wang, Y.; Waisman, H. Progressive delamination analysis of composite materials using XFEM and a discrete damage zone model. Comput. Mech. 2015, 55, 1–26. [Google Scholar] [CrossRef]
- Mollenhauer, D.; Zhou, E.; Hoos, K.; Iarve, E.; Braginsky, M.; Breitzman, T.; Rapking, D. Multi-Scale Simulation of Delamination Migration. In Proceedings of the American Society for Composites: Thirty-First Technical Conference, Williamsburg, VA, USA, 19–22 September 2016; DEStech Publications, Inc.: Williamsburg, VA, USA, 2016; p. 10. [Google Scholar]
- Wang, Y.; Waisman, H. Material-dependent crack-tip enrichment functions in XFEM for modeling interfacial cracks in bimaterials. Int. J. Numer. Methods Eng. 2017, 112, 1495–1518. [Google Scholar] [CrossRef]
- Wang, Y.; Cerigato, C.; Waisman, H.; Benvenuti, E. XFEM with high-order material-dependent enrichment functions for stress intensity factors calculation of interface cracks using Irwin’s crack closure integral. Eng. Fract. Mech. 2017, 178, 148–168. [Google Scholar] [CrossRef]
- Curiel Sosa, J.L.; Karapurath, N. Delamination modelling of GLARE using the extended finite element method. Compos. Sci. Technol. 2012, 72, 788–791. [Google Scholar] [CrossRef]
- Asaee, Z.; Shadlou, S.; Taheri, F. Low-velocity impact response of fiberglass/magnesium FMLs with a new 3D fiberglass fabric. Compos. Struct. 2015, 122, 155–165. [Google Scholar] [CrossRef]
- De Cicco, D.; Taheri, F. Delamination Buckling Response of 3D Fiber-Metal Laminates Subjected to Different Loading Rates. In Proceedings of the American Society for Composites: Thirty-First Technical Conference, Williamsburg, VA, USA, 19–22 September 2016; DEStech Publications, Inc.: Williamsburg, VA, USA, 2016; p. 12. [Google Scholar]
- De Cicco, D.; Taheri, F. Understanding the parameters that influence buckling of 3D fiber-metal laminates. In Proceedings of the 10th Canadian-International Conference on Composites (CANCOM2017), Ottawa, ON, Canada, 17–20 July 2017. [Google Scholar]
- De Cicco, D.; Taheri, F. Robust numerical approaches for simulating the buckling response of 3D fiber-metal laminates under axial impact—Validation with experimental results. J. Sandw. Struct. Mater. 2018, 1–30. [Google Scholar] [CrossRef]
- Tvergaard, V.; Hutchinson, J.W. The relation between crack growth resistance and fracture process parameters in elastic-plastic solids. J. Mech. Phys. Solids 1992, 40, 1377–1397. [Google Scholar] [CrossRef]
- KEYWORD USER’S MANUAL VOLUME II; LS-DYNA R9.0; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2016; Volume II, ISBN 9254492507.
- Sam, C.; Papoulia, K.D.; Vavasis, S.A. Obtaining initially rigid cohesive finite element models that are temporally convergent. Eng. Fract. Mech. 2005, 72, 2247–2267. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, C.T. XFEM and EFG Cohesive Fracture Analysis for Brittle and Semi-Brittle Materials. In Proceedings of the 11th International LS-DYNA Users Conference, Dearborn, MI, USA, 6–8 June 2010; pp. 21–32. [Google Scholar]
- ASTM D5528: Standard Test Method for Mode I Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites. Am. Stand. Test. Methods 2014, 3, 1–12. [CrossRef]
- Tabiei, A.; Zhang, W. Evaluation of Various Numerical Methods in LS-DYNA for 3D Crack Propagation. In Proceedings of the 14th International LS-DYNA Users Conference, Dearborn, MI, USA, 12–14 June 2016; Livermore Software Technology Corporation: Detroit, MI, USA, 2016; pp. 1–19. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).