Mobile Music, Sensors, Physical Modeling, and Digital Fabrication: Articulating the Augmented Mobile Instrument ^†

Abstract

Two concepts are presented, extended, and unified in this paper: mobile device augmentation towards musical instruments design and the concept of hybrid instruments. The first consists of using mobile devices at the heart of novel musical instruments. Smartphones and tablets are augmented with passive and active elements that can take part in the production of sound (e.g., resonators, exciter, etc.), add new affordances to the device, or change its global aesthetics and shape. Hybrid instruments combine physical/acoustical and “physically informed” virtual/digital elements. Recent progress in physical modeling of musical instruments and digital fabrication is exploited to treat instrument parts in a multidimensional way, allowing any physical element to be substituted with a virtual one and vice versa (as long as it is physically possible). A wide range of tools to design mobile hybrid instruments is introduced and evaluated. Aesthetic and design considerations when making such instruments are also presented through a series of examples.

1. Introduction

1.1. Physical Interfaces and Virtual Instruments: Remutualizing the Instrument

The concept of musical controller is not new and was perhaps invented when the first organs were made centuries ago. However, the rise of analog synthesizers in the middle of the twentieth century, followed a few decades later by digital synthesizers almost systematized the dissociation of the control-interface and sound-generation in musical instrument design. This gave birth to a new family of musical instruments known as “Digital Musical Instruments” (DMIs).

Marc Battier defines DMIs from a “human computer interaction (HCI) standpoint” as “instruments that include a separate gestural interface (or gestural controller unit) from a sound generation unit [1].” Thus, this feature that originally resulted from logical engineering decisions encouraged by the use of flexible new technologies, became one of the defining components of DMIs [2,3]. This characteristic has been extensively commented upon and studied in the New Interfaces for Musical Expression (NIME) literature. In particular, Marcello Wanderley highlights the fact that “with the separation of the DMI into two independent units, basic interaction characteristics of existing instruments may be lost and/or difficult to reproduce” [4].

Perry Cook provides an exhaustive overview of the risks associated with “abstracting the controller from the synthesizer,” [5] which might sometimes result in a “loss of intimacy” between performer and instrument. More specifically, he associates the flaws of “demutualized instruments” to the lack of haptic feedback (which has been extensively studied [4,6]), the lack of “fidelity in the connections from the controller to the generator,” and the fact that “no meaningful physics goes on in the controller.”

This paper addresses the first and the third issues pointed out by Cook and builds upon his work by providing a framework to design remutualized instruments reconciling the haptic, the physical, and the virtual.

1.2. Augmented and Acoustically Driven Hybrid Instruments: Thinking DMIs As a Whole

Augmented and acoustically driven hybrid instruments are two special kinds of DMIs combining acoustical and virtual elements to make sound. By doing so, they often blur the interface/synthesizer boundary, making them more mutualized and unified as a whole, partly solving the issue presented in Section 1.1.

Augmented instruments are based on acoustic instruments that are “enhanced” using virtual elements. Digital technologies can be added to the existing tool-set of instrument designers. There exist dozens of examples of such instruments in the computer music literature [7,8,9,10,11,12].

Instead of being based on existing acoustic instruments, acoustically driven hybrid instruments use acoustic elements (e.g., membrane, solid surfaces, strings, etc.) to drive virtual (i.e., electronic, digital, etc.) ones. The electric guitar is a good example of this kind of instrument. Acoustically driven hybrid instruments have been extensively studied and theorized by Roberto Aimi in his PhD thesis [13]. Their goal is to play to the strengths of physical/acoustical elements (e.g., imperfection, tangibility, randomness, etc.) and combine them with the infinite possibilities of digital ones.

A specific kind of acoustically driven hybrid instruments uses digital physical models (see Section 1.5) as the virtual portion of the instrument. The Korg Wavedrum (http://www.korg.com/us/products/drums/wavedrum_global_edition/—All URLs were verified on 1 December 2017.) is probably one of the earliest examples of this type of instrument. It uses the sound excitations created on a physical drum membrane to drive a wide range of physical models. The same technique has been used as the core of a wide range of other musical instruments [13,14,15,16,17].

By using acoustical elements as an interface, instruments presented in this section implement a form of “passive haptic feedback,” (i.e., the performer physically feels these elements while actuating them, even though they are not transmitting information from the virtual simulation via active force feedback). Moreover, they force the instrument maker to “co-design synthesis algorithms and controllers” (see Section 1.1 and [5]) reinforcing “the sense of intimacy, connectedness, and embodiment for the player and audience” [5].

1.3. Mobile Devices as Musical Instruments

Mobile devices (smart-phones, tablets, etc.) have been used as musical instruments for the past ten years both in the industry (e.g., GarageBand (http://www.apple.com/ios/garageband) for iPad, Smule’s apps (https://www.smule.com), moForte’s GeoShred (http://www.moforte.com/geoshredapp), etc.) and in the academic community [18,19,20,21,22]. As stand alone devices they present a promising platform for the creation of versatile instruments for live music performance. Within a single entity, sounds can be generated and controlled, differentiating them from most Digital Musical Instruments (DMIs), and allowing the creation of instruments much closer to “traditional” acoustic instruments in this respect. This resemblance is pushed even further with mobile phone orchestras such as MoPhO (http://mopho.stanford.edu) [23], where each performer uses a mobile phone as a independent musical instrument.

1.4. Augmenting Mobile Devices

Despite all their qualities, mobile devices were never designed to be used as musical instruments and lack some crucial elements to compete with their acoustic counterparts. This problem can be solved by adding prosthetics to the device implementing missing features or enhancing existing ones. Augmentations can be classified in two categories: passive and active.

Passive augmentations leverage built-in elements of the device (e.g., speaker, microphone, motion sensors, touchscreen, etc.) to implement new features or improve existing ones. Thus, the scope of this kind of augmentation is limited to what the host device can offer. There exist many examples of this type of augmentation ranging from passive amplifiers (e.g., Etsy Amplifiers (https://www.etsy.com/market/iphone_amplifier)) to smart-phone-based motion synthesizer controller (e.g., AAUG Motion Synth Controller (http://www.auug.com/)).

Active augmentations rely on electronic elements to add new features to mobile devices. Thus, they must be connected to it using one of its input or output ports (e.g., headphone jack, USB, etc.). Unlike passive augmentations, their scope is more or less infinite. Active augmentations range from external speakers to smart-phone-based musical instruments such as the Artiphon INSTRUMENT 1 (https://artiphon.com/).

1.5. Physical Modeling

Waveguide synthesis has been used since the second half of the 1980’s to model a wide range of musical instruments [24,25,26,27]. The main advantages of this technique are its simplicity and efficiency while still sounding adequately real. It allows for the accurate modeling of a wide range of instruments (string and wind instruments, tonal percussion, etc.) just with a single “filtered delay loop.” This technique was used in many commercial synthesizers in the 1990s such as the Yamaha VL1.

While any instrument part implementing a quasi harmonic series (e.g., a linear string, tube, etc.) can be modeled with a single digital waveguide, other parts must be modeled using other techniques such as modal synthesis.

Modal synthesis [28] consists of implementing each mode of a linear system as an exponentially decaying sine wave. Each mode can then be configured with its frequency, gain, and resonance duration (T60). Since each harmonic is implemented with an independent sine wave generator, this technique is a lot more computationally expensive than waveguide modeling. The parameters of a modal synthesizer (essentially a list of frequencies, gains, and T60s) can be calculated from the impulse response of a physical object [29] or by using the Finite Element Method (FEM) on a volumetric mesh [30]. This technique strengthens the link between physical elements and their virtual counterparts as it allows for the design of an instrument part on a computer using CAD software, and turn it into a physical model that could also be materialized using digital fabrication. This concept is further developed in Section 5.2.

Other methods such as finite-difference schemes [31] can be used to implement physical models of musical instruments and provide more flexibility and accuracy in some cases. However, most of them are computationally more expensive than waveguide models and modal synthesis. An overview of these techniques is provided in [27]. Since this paper is targeting the use of physical models on mobile platforms with a limited computational power, we’re focusing on CPU-efficient techniques.

1.6. 3D Printing, Acoustics, and Musical Instrument Design/Lutherie

3D printing has been used extensively in the past few years to make novel, traditional, acoustic, digital, etc., musical instruments [32]. While high-end 3D printers can be used to make full size traditional acoustic musical instruments, cheaper printers are often utilized to augment or modify existing instruments or to make new ones from random objects. Fast prototyping and iterative design are at the heart of this new approach to lutherie and musical instrument making in general [33].

While string instruments are particularly well represented [34,35,36,37,38], many experiments around wind instruments have been conducted as well [39,40,41].

1.7. Towards the Hybrid Mobile Instrument

In a previous publication [42], we introduced the concept of “augmented mobile-device” and we presented the BladeAxe: an acoustically driven hybrid instrument partly based on acoustic elements used to generate sound excitations and an iPad. The iPad was used both as a controller, and to implement virtual physical-model-based elements of the instrument. The BladeAxe was the last iteration of a series of mobile-device-based instruments that we developed during the past four years.

In this paper, we generalize the various concepts introduced by the BladeAxe and propose a framework centered around the Faust programming language [43] to facilitate the design of “hybrid mobile instruments.” Such instruments combine physical/acoustical elements and physically informed virtual/digital elements (i.e., physical models) (Throughout this paper, “physical elements” designate tangible acoustical musical instrument parts and “virtual elements” designate digital, physically informed (based on a physical model) instrument parts.). Virtual elements are implemented on the mobile device that serves as the “core” of the system. Modern digital fabrication (e.g., 3D printing, etc.) is combined to physical modeling techniques to approach musical instrument design in a multidimensional way. By being standalone, implementing passive haptic feedback, and having a unified design between the interface and the sound generation unit, we believe that hybrid mobile instruments solve some of the flaws of DMIs highlighted by Perry Cook [5].

First, we present faust2smartkeyb, a Faust-based tool facilitating the design of musical apps and focusing on skill transfer. It serves as the “glue” between the different building blocks of mobile-device-based hybrid musical instruments (i.e., physically modeled parts, built-in and external sensors, touchscreen interface, connections to digitally fabricated elements, etc.). Next, we introduce Mobile3D, an OpenScad (http://www.openscad.org) library to help design mobile device passive augmentations using DIY (Do It Yourself) digital fabrication techniques such as 3D printing and laser cutting. We give an exhaustive overview of the taxonomy of the various types of passive augmentations that can be implemented on mobile devices through a series of examples and we demonstrate how they leverage existing components on the device. Next, a framework based on the Teensy board (https://www.pjrc.com/teensy/) and Faust, to design and make active mobile device augmentations is presented and evaluated through the results of a workshop. Finally, the concept of “acoustically driven hybrid mobile instrument” is studied and a framework centered around the Faust Physical Modeling Toolkit to design virtual and physical musical instrument parts is presented.

2. faust2smartkeyb: Facilitating Musical Apps Design and Skill Transfer

Making musical apps for mobile devices involves the use and mastery of various technologies, standards, programming languages, and techniques ranging from low level C++ programming for real-time DSP (Digital Signal Processing) to advanced interface design. This adds up to the variety of the platforms (e.g., iOS, Android, etc.) and of their associated tools (e.g., Xcode, Android Studio, etc.), standards, and languages (e.g., JAVA, C++, Objective-C, etc.).

While there exists a few tools to facilitate the design of musical apps such as libpd, [44] Mobile CSOUND [45], and more recently JUCE (https://www.juce.com) and SuperPowered (http://superpowered.com), none of them provides a comprehensive cross-platform environment for musical touchscreen interface design, high level DSP programming, turnkey instrument physical model prototyping, built-in sensors handling and mapping, MIDI and OSC compatibility, etc.

Earlier works inspired the system presented in this section and served as its basis. faust2ios and faust2android [46] are command line tools to convert Faust codes into fully working Android and iOS applications. The user interface of apps generated using this system corresponds to the standard UI specifications provided in the Faust code and is made out of sliders, buttons, groups, etc. More recently, faust2api, a lower level tool to generate audio engines with Faust featuring polyphony, built-in sensors mapping, MIDI and OSC (Open Sound Control) support, etc., for a wide range of platforms including Android and iOS was introduced [47].

Despite the fact that user interfaces better adapted to musical applications (e.g., piano keyboards, $(x,y)$ controllers, etc.) can replace the standard UI of a Faust object in apps generated by faust2android [48], they are far from providing a generic solution to capture musical gestures on a touchscreen and to allow for musical skill transfer.

In this section, we present faust2smartkeyb (faust2smartkeyb is now part of the Faust distribution.), a tool based on faust2api to facilitate the creation of musical apps for Android and iOS. The use of musical instrument physical models in this context and in that of acoustically driven hybrid instrument design (see Section 5) is emphasized. Similarly, allowing the design of interfaces implementing skill transfer from existing musical instruments is one of our main focus.

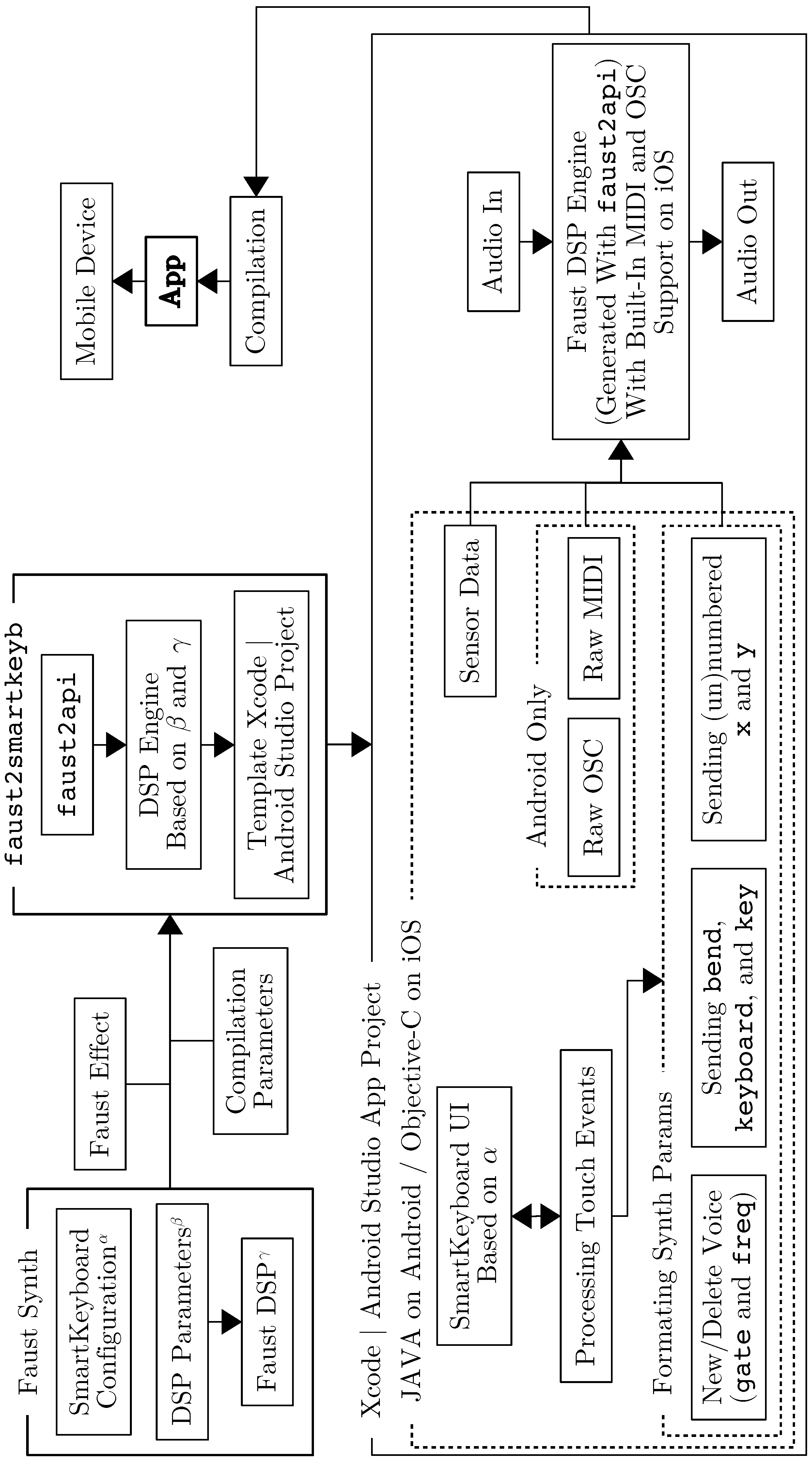
2.1. Apps Generation and General Implementation

faust2smartkeyb works the same way than most Faust targets/“architectures” [49] and can be called using the faust2smartkeyb command-line tool: where faustFile.dsp is a Faust file declaring a SmartKeyboard interface (see Section 2.2) and [options] is a set of options to configure general parameters of the generated app (e.g., Android vs. iOS app, internal number of polyphony voices, etc.). An exhaustive list of these options is available in the faust2smartkeyb documentation [50].

The only required option is the app type (-android or -ios). Unless specified otherwise (e.g., using the -source option), faust2smartkeyb will compile the app directly in the terminal and upload it on any Android device connected to the computer if the -install option is provided. If -source is used, an Xcode (https://developer.apple.com/xcode/) or an Android Studio (https://developer.android.com/studio) project is generated, depending on the selected app type (see Figure 1).

faust2smartkeyb is based on faust2api [47] and takes advantage of most of the features of this system. It provides polyphony, MIDI, and OSC support and allows for SmartKeyboard interfaces to interact with the DSP portion of the app at a very high level (see Figure 1).

faust2smartkeyb inherits some of faust2api’s options. For example, an external audio effect Faust file can be specified using -effect. This is very useful to save computation when implementing a polyphonic synthesizer [47]. Similarly, -nvoices can be used to override the default maximum number of polyphony voices (twelve) of the DSP engine generated by faust2api (see Figure 1).

The DSP engine generated by faust2api is transferred to a template Xcode or Android Studio project (see Figure 1) and contains the SmartKeyboard declaration (see Section 2.2). The interface of the app, which is implemented in JAVA on Android and in Objective-C on iOS, is built from this declaration. While OSC support is built-in in the DSP engine and works both on iOS and Android, MIDI support is only available on iOS thanks to Rt-MIDI [47] (see Figure 1). On Android, raw MIDI messages are retrieved in the JAVA portion of the app and “pushed” to the DSP engine. MIDI is only supported since Android-23 so faust2smartkeyb apps wont have MIDI support on older Android versions.

2.2. Architecture of a Simple faust2smartkeyb Code

The SmartKeyboard interface can be declared anywhere in a Faust file using the SmartKeyboard{} metadata:

It is based on the idea that any touchscreen musical interface can be implemented as a set of keyboards with different key numbers (like a table with columns and cells, essentially). Various interfaces ranging from drum pads, isomorphic keyboards, $(x,y)$ controllers, wind instruments fingerings, etc. can be implemented using this paradigm. The position of fingers in the interface can be continuously tracked and transmitted to the DSP engine both as high level parameters formatted by the system (e.g., frequency, note on/off, gain, etc.) or low level parameters (e.g., $(x,y)$ position, key and keyboard ID, etc.). These parameters are declared in the Faust code using default parameter names (see [50] for an exhaustive list).

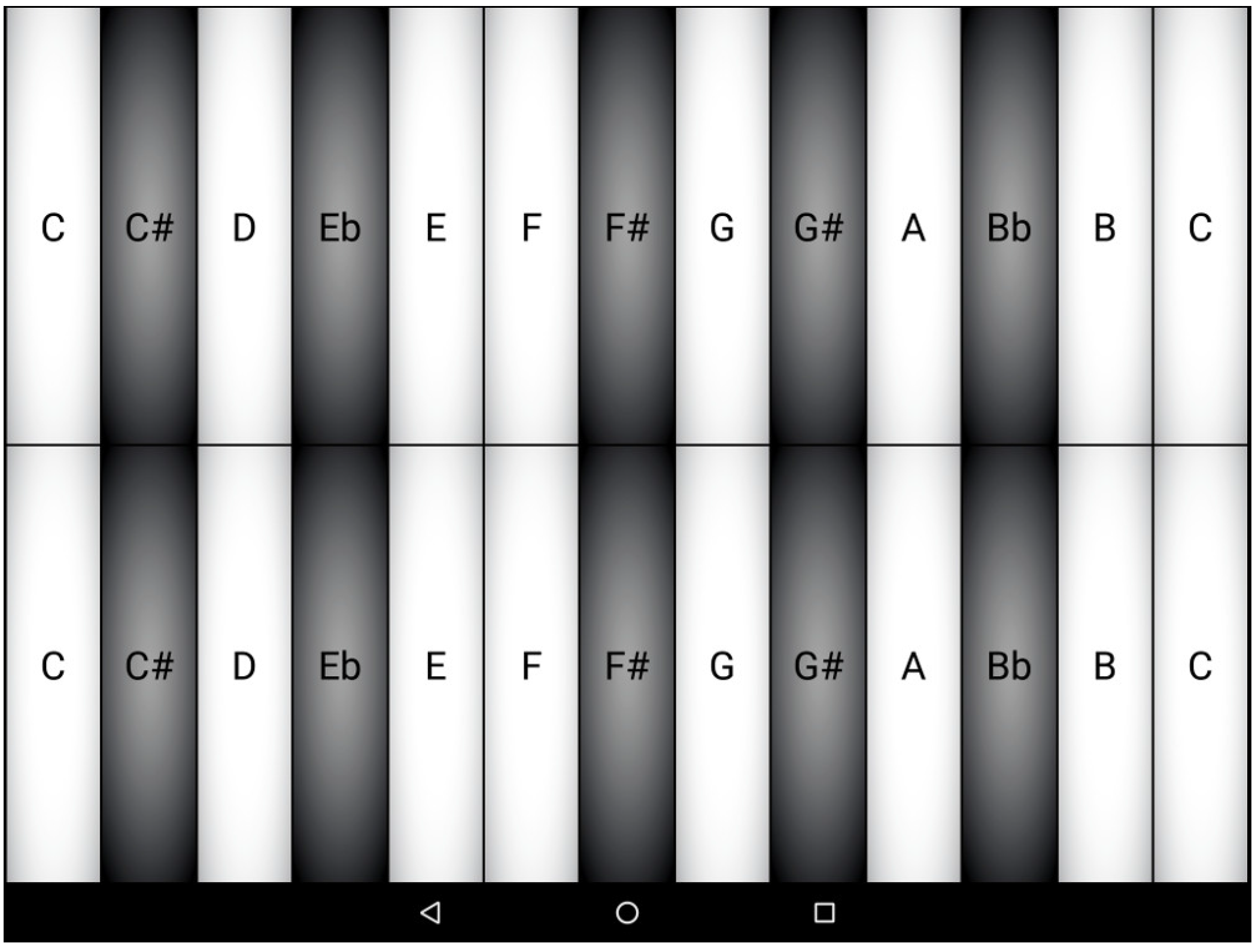
By default, the screen interface is a polyphonic chromatic keyboard with thirteen keys whose lowest key is a C5 (MIDI note number 60). A set of key/value pairs can be used to override the default look and behavior of the interface (see [50] for an exhaustive list). Code Listing 1 presents the Faust code of a simple app where two identical keyboards can be used to control a simple synthesizer based on a band-limited sawtooth wave oscillator and a simple exponential envelope generator. Since MIDI support is enabled by default in apps generated by faust2smartkeyb and that the SmartKeyboard standard parameters are the same as the one used for MIDI in Faust, this app is also controllable by any MIDI keyboard connected to the device running it. A screen-shot of the interface of the app generated from Code Listing 1 can be seen in Figure 2.

2.3. Preparing a Faust Code for Continuous Pitch Control

In faust2smartkeyb programs, pitch is handled using the freq and bend standard parameters [50]. The behavior of the formatting of these parameters can be configured using specific keys.

freq gives the “reference frequency” of a note and is tied to the gate parameter. Every time gate goes from 0 to 1 (which correlates with a new note event), the value of freq is updated. freq always corresponds to an integer MIDI pitch number which implies that its value is always quantized to the nearest semitone.

Pitch can be continuously updated by using the bend standard parameter. bend is a ratio that should be multiplied to freq. E.g.,:The state of polyphonic voices is conserved in memory until the app is ended. Thus, the value of bend might jump from one value to another when a new voice is activated. polySmooth() is used here to smooth the value of bend to prevent clicks, only after the voice started. This suppresses any potential “sweep” that might occur if the value of bend changes abruptly at the beginning of a note.

2.4. Configuring Continuous Pitch Control

The Rounding Mode configuration key has a significant impact on the behavior of freq, bend, and gate. When Rounding Mode = 0, pitch is fully “quantized,” and the value of bend is always 1. Additionally, a new note is triggered every time a finger slides to a new key, impacting the value of freq and gate. When Rounding Mode = 1, continuous pitch control is activated, and the value of bend is constantly updated in function the position of the finger on the screen. New note events updating the value of freq and gate are only triggered when fingers start touching the screen. While this mode might be useful in some cases, it is hard to use when playing tonal music as any new note might be “out of tune.”

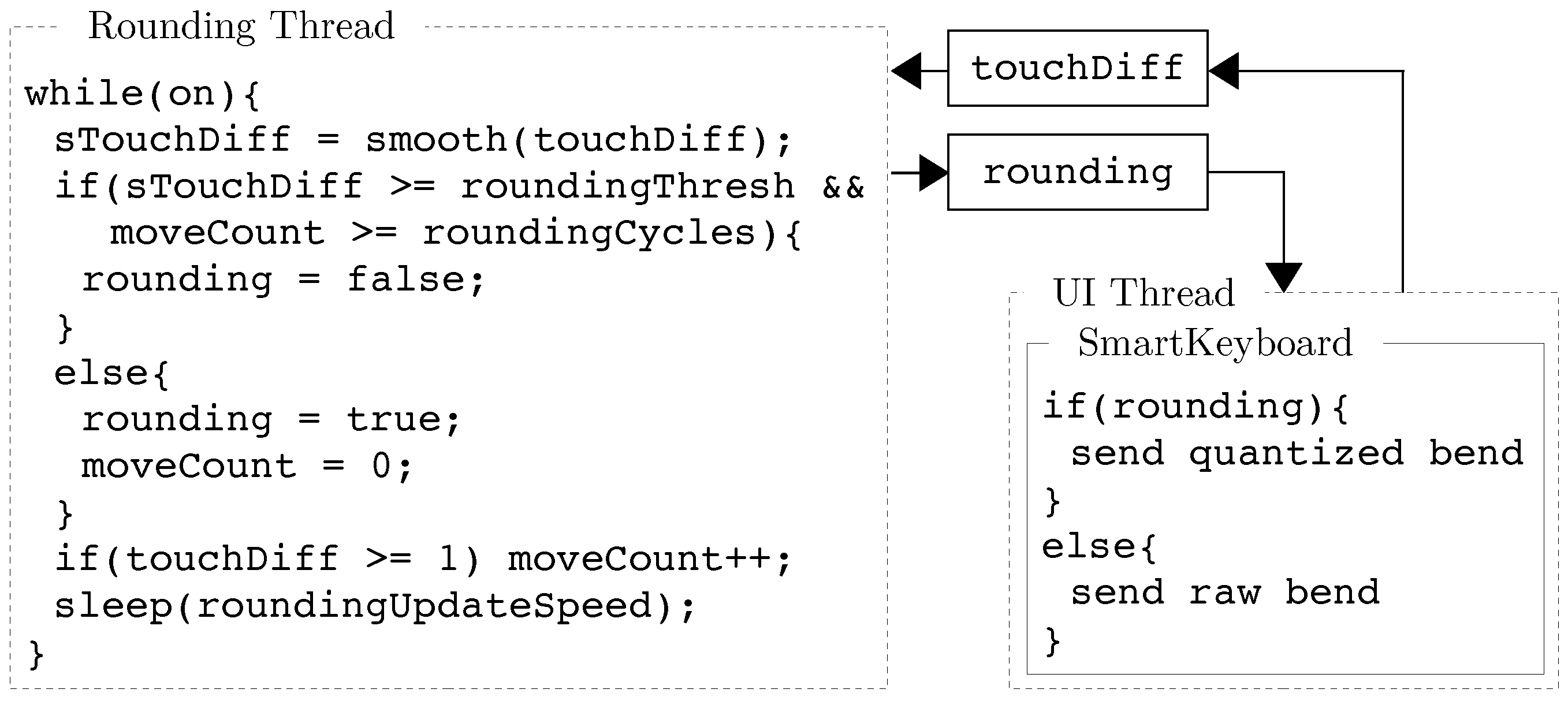
When Rounding Mode = 2, “pitch rounding” is activated and the value of bend is rounded to match the nearest quantized semitone when the finger is not moving on the screen. This allows for generated sounds to be “in tune” without preventing slides, vibratos, etc. While the design of such a system has been previously studied [51], we decided to implement our own algorithm for this (see Figure 3). touchDiff is the distance on the screen between two touch events for a specific finger. This value is smoothed (sTouchDiff) using a unity-dc-gain one pole lowpass filter in a separate thread running at a rate defined by configuration key Rounding Update Speed. Rounding Smooth corresponds to the pole of the lowpass filter used for smoothing (0.9 by default). A separate thread is needed since the callback of touch events is only called when events are received. If sTouchDiff is greater than Rounding Threshold during a certain number of cycles defined by Rounding Cycles, then rounding is deactivated and the value of bend corresponds to the exact position of the finger on the screen. If rounding is activated, the value of bend is rounded to match the nearest pitch of the chromatic scale.

2.5. Using Specific Scales

A wide range of musical scales (see [50] for an exhaustive list), all compatible with the system described in Section 2.4, can be used with the SmartKeyboard interface and configured using the Keyboard N - Scale key. When other scales than the chromatic scale are used, keys on the keyboard all have the same color.

Custom scales and temperaments can be implemented using the Keyboard N - Scale configuration key. It allows us to specify a series of intervals to be repeated along the keyboard (not necessarily at the octave). Intervals are provided as semitones and can have a decimal value. For example, the chromatic scale can be implemented as:Similarly, the standard equal-tempered major scale can be specified as:A 5-limit just intoned major scale (rounded to the nearest 0.01 cents) could be:Equal-tempered Bohlen-Pierce (dividing 3:1 into 13 equal intervals) would be:

Alternatively, custom scales and pitch mappings can be implemented directly from the Faust code using some of the lower level standard parameters returned by the SmartKeyboard interface (e.g., x, y, key, keyboard, etc.).

2.6. Handling Polyphony and Monophony

By default, the DSP engine generated by faust2api has twelve polyphony voices. This parameter can be overridden using the -nvoices option when executing the faust2smartkeyb command. This system works independently from the monophonic/polyphonic configuration of the SmartKeyboard interface. Indeed, even when a keyboard is monophonic, a polyphonic synthesizer might still be needed to leave time for the release of an envelope generator, for example.

The Max Keyboard Polyphony key defines the maximum number of voices of polyphony of a SmartKeyboard interface. Polyphony is tied to fingers present on the screen, in other words, one finger corresponds to one voice. If Max Keyboard Polyphony = 1, then the interface becomes “monophonic.” The monophonic behavior of the system is configured using the Mono Mode key [50].

2.7. Other Modes

In some cases, both the monophonic and the polyphonic paradigms are not adapted. For example, when implementing an instrument based on a physical model, it might be necessary to use a single voice and constantly run it. This might be the case of a virtual wind instrument where notes are “triggered” by some of the continuous parameters of the embouchure and not by discrete events such as the one created by a key. This type of system can be implemented by setting the Max Keyboard Polyphony key to zero. In that case, the first available voice is triggered and ran until the app is killed. Adding new fingers on the screen will have no impact on that and the gate parameter wont be sent to the DSP engine. freq will keep being sent unless the Keyboard N - Send Freq is set to zero. Since this parameter is keyboard specific, some keyboards in the interface might be used for pitch control while others might be used for other types of applications (e.g., X/Y controller, etc.).

It might be useful in some cases to number the standard x and y parameters in function of the fingers present on the screen. This can be easily accomplished by setting the Keyboard N - Count Fingers key to one. In that case, the first finger to touch the screen will send the x0 and y0 standard parameters to the DSP engine, the second finger x1 and y1, and so on.

2.8. Example: Violin App

Implementation strategies greatly varies from one instrument to another, so giving a fully representative example is impossible. Instead, we focus on a specific implementation of a violin here where strings are excited by an interface independent from the keyboards used to control their pitch. This illustrates a “typical” physical model mapping where the MIDI concept of note on/off event is not used. More examples are available on-line (Making Faust-Based Smartphone Musical Instruments On-Line Tutorial: https://ccrma.stanford.edu/~rmichon/faustTutorials/#making-faust-based-smartphone-musical-instruments).

Unlike plucked string instruments, bowed string instruments must be constantly excited to generate sound. Thus, parameters linked to bowing (i.e., bow pressure, bow velocity, etc.) must be continuously controlled. The faust2smartkeyb code presented in Listing 2 is a violin app where each string is represented by one keyboard in the interface. An independent surface can be used to control the bow pressure and velocity. This system is common to all strings that are activated when they are touched on the screen. This virtual touchscreen interface could be easily be substituted by a physical one using the technique presented in Section 4.

The SmartKeyboard configuration declares 5 keyboards (4 strings and one control surface for bowing). “String keyboards” are tuned like on a violin (G, D, A, E) and are configured to be monophonic and implement “pitch stealing” when a higher pitch is selected. Bow velocity is computed by measuring the displacement of the finger touching the 5th keyboard (bowVel). Bow pressure just corresponds to the y position of the finger on this keyboard. Strings are activated when at least one finger is touching the corresponding keyboard (as(i)).

The app doesn’t take advantage of the polyphony support of faust2smartkeyb and a single voice is constantly ran after the app is launched (Max Keyboard Polyphony = 0). Four virtual strings based on a simple violin string model (violinModel()) implemented in the Faust Physical Modeling Library (see Section 5.2) are declared in parallel and activated in function of events happening on the screen.

Alternatively, the bowing interface could be removed and the bow velocity could be calculated based on the displacement on the y axis of a finger on a keyboard, allowing one to excite the string and control its pitch with a single finger. However, concentrating so many parameters on a single gesture tends to limit the affordances of the instrument. The code presented in Listing 2 could be easily modified to implement this behavior.

Mastering a musical instrument, should it be fully acoustic, digital, or hybrid, is a time consuming process. While skill transfer can help reduce its duration, we do not claim that the instruments presented in this paper are faster to learn than any other type of instrument. Virtuosity can be afforded by the instrument, but it still depends on the musicianship of the performer.

This section just gave an overview of some of the features of faust2smartkeyb. More details about this tool can be found in its documentation [50] as well as on the corresponding on-line tutorials.

3. Passively Augmenting Mobile Devices

In this section, we try to generalize the concept of “passively augmented mobile device” briefly introduced in Section 1.4 and we provide a framework to design this kind of instrument. We focus on “passive augmentations” leveraging existing components of hand-held mobile devices in a very lightweight, non-invasive way (as opposed to “active augmentation” presented in Section 4 that require the use of electronic components). We introduce Mobile3D, an OpenScad (http://www.openscad.org) library to help design mobile device augmentations using DIY digital fabrication techniques such as 3D printing and laser cutting. We give an exhaustive overview of the taxonomy of the various types of passive augmentations that can be implemented on mobile devices through a series of examples and we demonstrate how they leverage existing components on the device. Finally, we evaluate our framework and propose future directions for this type of research.

3.1. Mobile 3D

Mobile3D is an OpenScad library facilitating the design of mobile device augmentations. OpenScad is an open-source Computer Assisted Design (CAD) software using a high level functional programming language to specify the shape of any object. It supports fully parametric parts, permitting users to rapidly adapt geometries to the variety of devices available on the market.

Mobile3D is organized in different files that are all based on a single library containing generic standard elements (basics.scad) ranging from simple useful shapes to more advanced augmentations such as the ones presented in the following sections. A series of device-specific files adapt the elements of basics.scad and are also available for the iPhone 5, 6, and 6 Plus and for the iPod Touch. For example, a generic horn usable as a passive amplifier for the built-in speaker of a mobile device can be simply created with the following call in OpenScad: To generate the same object specifically for the iPhone 5, the following code can be written:

Finally, the shape of an object can be easily modified either by providing parameters as arguments to the corresponding function, or by overriding them globally before the function is called. If this approach is chosen, all the parts called in the OpenScad code will be updated, which can be very convenient in some cases. For example, the radius (expressed in millimeters here) of iPhone5_SmallPassiveAmp() can be modified locally by writing:or globally by writing:

Mobile3D is based on two fundamental elements that can be used to quickly attach any prosthetic to the device: the top and bottom holders (see Figure 4). They were designed to be 3D printed using elastomeric material such as NinjaFlex^® (https://ninjatek.com) in order to easily install and remove the device without damaging it. They also help reducing printing duration, which is often a major issue during prototyping. These two holders glued to a laser-cut plastic plate form a sturdy case, whereas completely printing this part would take much more time.

Figure 4 presents an example of an iPhone 5 augmented with a passive amplifier. The bottom holder and the horn were printed separately and glued together, but they could also have been printed as one piece. In this example, the bottom and top holders were printed with PLA (PolyLactic Acid), which is a hard plastic, and they were mounted on the plate using Velcro^®. This is an alternative solution to using NinjaFlex^® that can be useful when augmenting the mobile device with large appendixes requiring a stronger support.

The passive amplifier presented in Figure 4 was made by overriding the default parameters of the iPhone5_SmallPassiveAmp() function:

An exhaustive list of all the elements available in Mobile3D can be found on the project webpage (https://ccrma.stanford.edu/~rmichon/mobile3D).

3.2. Leveraging Built-In Sensors and Elements

Mobile devices host a wide range of built-in sensors and elements that can be used to control sound synthesizers (see Section 2). While the variety of available sensors and elements differs from one device to another, most smart-phones have at least a touch screen, a loudspeaker, a microphone, and some type of motion sensor (accelerometer, gyroscope, etc.). In this section, we’ll focus on these four elements and we’ll demonstrate how they can be “augmented” for specific musical applications.

3.2.1. Microphone

While the built-in microphone of a mobile device can simply serve as a source for any kind of sound process (e.g., audio effect, physical model, etc.), it can also be used as a versatile, high rate sensor [52]. In this section, we demonstrate how it can be augmented for different kinds of uses.

One of the first concrete uses of the built-in microphone of a mobile device to control some sound synthesis process was done with Smule’s Ocarina [22]. There, the microphone serves as a blow sensor by measuring the gain of the signal created when blowing on it to control the gain of an ocarina sound synthesizer.

Mobile3D contains an object that can be used to leverage this principle when placed in front of the microphone (see Figure 5). It essentially allows for the performer to blow into a mouthpiece mounted on the device. The air-flow is directed through a small aperture inside the pipe, creating a sound that can be recorded by the microphone and analyzed in the app using standard amplitude tracking techniques. The air-flow is then sent outside of the pipe, preventing it from ever being in direct contact with the microphone.

The acquired signal is much cleaner than when the performer blows directly onto the mic, allowing us to generate precise control data. Additionally, condensation never accumulates on the mic which can help extend the duration of its life, etc.

The built-in microphone of mobile devices has already been used as a data acquisition system to implement various kinds of sensors using frequency analysis techniques [53]. Mobile3D contains an object using similar principles that can be used to control some of the parameters of a synthesizer running on a mobile device. It is based on a conical tube (see Figure 5) where dozens of small tines of different length and diameter are placed inside it. These tines get thicker towards the end of the tube and their length varies linearly around it. When the performer blows inside the tube, the resulting airflow hits the nails, creating sounds with varying harmonic content. By directing the airflow towards different locations inside the tube, the performer can generate various kind of sounds that can be recognized in the app using frequency analysis techniques. The intensity and the position of the airflow around the tube can be measured by keeping track of the spectral centroid of the generated sound, and used to control synthesis parameters.

The same approach can be used with an infinite number of augmentations with different shapes. While our basic spectral-centroid-based analysis technique only allows us to extract two continuous parameters from the generated signal, it should be possible to get more of them using more advanced techniques.

3.2.2. Speaker

Even though their quality and power has significantly increased during the last decade, mobile device built-in speakers are generally only good for speech, not music. This is mostly due to their small size and the lack of a proper resonance chamber to boost bass, resulting in a very curvy frequency response and a lack of power.

There exists a wide range of passive amplifiers on the market to boost the sound generated by the built-in speakers of mobile devices, also attempting to flatten their frequency response (see Section 1.4). These passive amplifiers can be seen as resonators driven by the speaker. In this section, we present various kinds of resonators that can be connected to the built-in speaker of mobile devices to amplify and/or modify their sound.

Mobile3D contains multiple passive amplifiers of various kinds that can be used to boost the loudness of the built-in speaker of mobile devices (e.g., see Figure 4). Some of them were designed to maximize their effect on the generated sound [54]. Their shape can vary greatly and will usually be determined by the type of the instrument. For example, if the instrument requires the performer to make fast movements, a small passive amplifier will be preferred to a large one, etc. Similarly, the orientation of the output of the amplifier will often be determined by the way the performer holds the instrument, etc. These are design decisions that are left up to the instrument designer.

3D printed musical instrument resonators (e.g., guitar body, etc.) can be seen as a special case of passive amplifiers. Mobile3D contains a few examples of such resonators that can be driven by the device’s built-in speakers. While they don’t offer any significant advantage over “standard” passive amplifiers like the one presented in the previous paragraph, they are aesthetically interesting and perfectly translate the idea of hybrid instrument developed in Section 5.

Another way to use the signal generated by the built-in speakers of mobile devices is to modify it using dynamic resonators. For example, in the instrument presented in Figure 6, the performer’s hand can filter the generated sound to create a wah effect. This can be very expressive, especially if the signal has a dense spectral content. This instrument is featured in the teaser video (https://www.youtube.com/watch?v=dGBDrmvG4Yk) of the workshop presented in Section 3.4.

Similarly, the sound generated by the built-in speaker is sent to the mouth of the performer in the instrument presented in Figure 6. The sound is therefore both modulated acoustically and through the embedded synthesis and touch-screen. The same result can obviously be achieved by directly applying the mouth of the performer to the speaker, but the augmentation presented in Figure 6 increases the effect of the oral cavity on the sound through a passive wave guide.

3.2.3. Motion Sensors

Most mobile devices have at least one kind of built-in motion sensor (e.g., accelerometer, gyroscope, etc.). They are perfect to continuously control the parameters of sound synthesizer and have been used as such since the beginning of mobile music (see Section 1.3).

Augmentations can be made to mobile devices to direct and optimize the use of this type of sensor. This kind of augmentation can be classified in two main categories:

• augmentations to create specific kinds of movements (spin, swing, shake, etc.),
• augmentations related to how the device is held.

Figure 7 presents a “sound toy” where a mobile device can be spun like a top. This creates a slight “Leslie effect”, increased by the passive amplifier. Additionally, the accelerometer and gyroscope data are used to control the synthesizer running on the device. This instrument is featured in the teaser video of the workshop presented in Section 3.4.

Another example of motion-sensor-based augmentation is presented in Figure 8 and described with more details in Section 3.4. It features a smart-phone mounted on a bike wheel where, once again, the gyroscope and accelerometer data are used to control the parameters of a synthesizer running on the device. Similarly, a “rolling smart-phone” is presented in Figure 8 and described in Section 3.4. Mobile3D contains a series of templates and functions to make this kind of augmentation.

Augmentations leveraging built-in sensors related to how the device is held are presented in more detail in Section 3.3.

3.2.4. Other Sensors

Most mobile devices host built-in sensors that exceed the ones presented in the previous sections and are not supported yet in Mobile3D. For example, built-in cameras can be used as very versatile sensors [52], and a wide range of passive augmentations could be applied to them to “customize” their use for musical ends. We plan to support more sensors in Mobile3D in the future.

3.3. Holding Mobile Devices

Mobile devices were designed to be held in a specific way, mostly so that they can be used conveniently both as a phone and to use the touch-screen (see Section 1.3). Passive augmentations can be designed to hold mobile devices in different ways to help carry out specific musical gestures, better leveraging the potential of the touch-screen and of built-in sensors.

More generally, this type of augmentation is targeted towards making mobile-device-based musical instruments more engaging and easier to play.

In this section, we give a brief overview of the different types of augmentations that can be made with Mobile3D to hold mobile devices in different ways.

3.3.1. Wind Instrument Paradigm

One of the first attempts to hold a smart-phone as a wind instrument was Ocarina, where the screen interface was designed to be similar to a traditional ocarina. The idea of holding a smart-phone as such is quite appealing since all fingers (beside the thumbs) of both hands perfectly fit on the screen (thumbs can be placed on the other side of the device to hold it). However, this position is impractical since at least one finger has to be on the screen in order to hold the device securely. The simple augmentation presented in Figure 9 solves this problem by adding “handles” on both sides of the device so that it can be held using the palm of the two hands, leaving all fingers (including the thumbs) free to carry out any action. Several functions and templates are available in Mobile3D to design these types of augmentations.

3.3.2. Holding the Device with One Hand

Mobile3D contains several functions and templates to hold mobile devices with one hand, leaving at least four fingers available to perform on the touch-screen. This way to hold the device opens up a wide range of options to fully take advantage of the built-in motion sensors and easily execute free movements. Additionally, the performer can decide to use two devices in this case (one for each hand).

The instrument presented in Figure 9 uses one of Mobile3D’s ring holders to hold the device with only the thumb.

3.3.3. Other Holding Options

There are obviously many other options to hold mobile-devices to carry out specific musical gestures. For example, one might hold the device in one hand and perform it with the other, etc. In any case, we believe that Mobile3D provides enough options to cover the design needs for most musical instruments.

3.4. More Examples and Evaluation

To evaluate Mobile3D and the framework presented in this paper, we organized a one-week workshop last summer at Stanford’s Center for Computer Research in Music and Acoustics (CCRMA) called The Composed Instrument Workshop: Intersections of 3D Printing and Digital Audio for Mobile Platforms (Workshop Web-Page: https://ccrma.stanford.edu/~rmichon/composedInstrumentWorkshop/). We taught the seven participants how to make basic musical smart-phone apps using faust2smartkeyb (see Section 2) and how to use Mobile3D to design mobile device augmentations. They were free to make any musical instrument or sound toy for their final project. Some examples of these instruments are presented in Figure 4 and Figure 8.

In only one week, participants mastered all these techniques and designed and implemented very original instrument ideas. This helped us debug and improve Mobile3D with new objects and features.

4. Actively Augmenting Mobile Devices

While the non-invasive and lightweight character of passive mobile device augmentations (see Section 3) contributes to the overall physical coherence of hybrid instruments, their simplicity can sometimes be a limitation as they remain tied to what built-in active elements of the device (e.g., touchscreen, microphone, speaker, etc.) can offer. Inversely, active augmentations can take any form and can be used to implement almost anything that mobile devices don’t have. While their level of complexity can be more or less infinite, we praise for an incremental approach where instrument designers should first take advantage of elements already available on mobile devices, and then use active augmentations parsimoniously to implement what they could not have done otherwise.

In this section, we provide a framework/method to make active augmentations for mobile devices, towards mobile hybrid musical instrument design (see Section 5). Unlike passive augmentations, the scope of active augmentations is almost infinite and any musical controller could probably fit in this category. Thus, we will only consider the tools to carry out this task and let design or aesthetic considerations up to the instrument maker.

4.1. Active Augmentation Framework

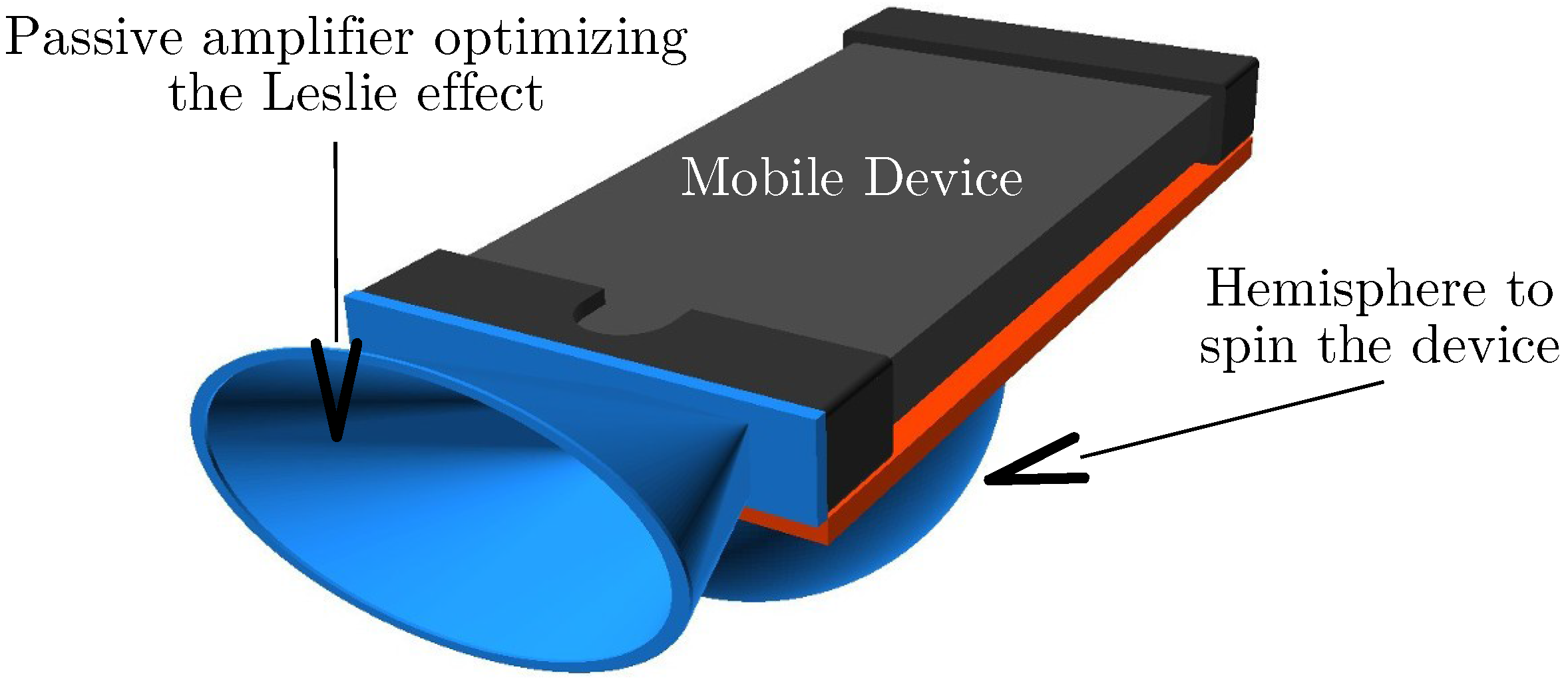
In our view, mobile device augmentations should supplement existing built-in sensors (e.g., touchscreen, motion sensors, etc.) and remain as lightweight and confined as possible. Indeed, there’s often not much to add to a mobile device to turn it into a truly expressive musical instrument. Nuance [55] is a good example of that since it adds a whole new level of expressivity to the touchscreen, simply by using a few sensors. On the other hand, unlike passive augmentations, active augmentations can be used to add an infinite number of features.

In this section, we introduce a framework for designing active mobile device augmentations supplementing sensors already available on the device. This allows us to keep our augmentations lightweight and powered by the device, preserving the standalone aspect and partly the physical coherence of the instrument.

To keep our augmentations simple, we propose to use a wired solution for transmitting sensor data to the mobile device, which also allows us to power the augmentation. Augmentations requiring an external power supply (e.g., battery) are discarded and are not considered in the frame of this work.

MIDI is a standard universal way to transmit real-time musical (and non-musical) control data to mobile devices, so we opted for this solution. Teensys such the Teensy 3.2 (https://www.pjrc.com/store/teensy32.html) are micro-controllers providing built-in USB MIDI support, making them particularly well suited to be used in our framework.

Teensyduino (https://www.pjrc.com/teensy/teensyduino.html) (Teensy’s IDE), comes with a high level library part of Bounce.h for sending MIDI over USB. The code presented in Listing 3 demonstrates how to use this library to send sensor values on a MIDI “Continuous Controller” (CC).

Once uploaded to the microcontroller, the Teensy board can be connected via USB to any MIDI-compatible mobile device (iOS and Android) to control some of the parameters of a faust2smartkeyb app (see Section 2). This will require the use of a USB adapter, depending on the type of USB plug available on the device. MIDI is enabled by default in faust2smartkeyb apps and parameters in the Faust code can be mapped to a specific MIDI CC by using a metadata (see Section 2.2):

Here, the frequency parameter will be controlled by MIDI messages coming from MIDI CC 10 and mapped to the minimum (20 Hz for MIDI CC 10 = 0) and maximum (2000 Hz for MIDI CC 10 = 127) values defined in the nentry declaration. Thus, if this parameter was controlling the frequency of an oscillator and that the Teensy board running the code presented in Listing 3 was connected to the mobile device running the corresponding faust2smartkeyb app, the sensor connected to the A0 pin of the Teensy would be able to control the frequency of the generated sound.

Other types of MIDI messages (e.g., sendNoteOn()) can be sent to a faust2smartkeyb app using the same technique.

Most of the parameters controlled by elements on the touchscreen or by built-in sensors of the app presented in Section 2.8 could be substituted by external sensors or custom interfaces using the technique described above.

4.2. Examples and Evaluation: CCRMA Mobile Synth Summer Workshop

The framework presented in Section 4.1 was evaluated within a two weeks workshop at CCRMA at the end of June 2017 (https://ccrma.stanford.edu/~rmichon/mobileSynth: this webpage contains more details about the different instruments presented in the following subsections.). It was done in continuity with the Faust Workshop taught the previous years (https://ccrma.stanford.edu/~rmichon/faustWorkshops/2016/) and the Composed Instrument Workshop presented in Section 3.4. During the first week (Mobile App Development for Sound Synthesis and Processing in Faust), participants learned how to use Faust through faust2smartkeyb and made a wide range of musical apps. During the second week (3D Printing and Musical Interface Design for Smart-phone Augmentation), they designed various passive (see Section 3) and active augmentations using the framework presented in Section 4.1. They were encouraged to first use elements available on the device (e.g., built-in sensors, touchscreen, etc.) and then think about what was missing to their instrument to make it more expressive and controllable.

This section presents selected works from students of the workshop.

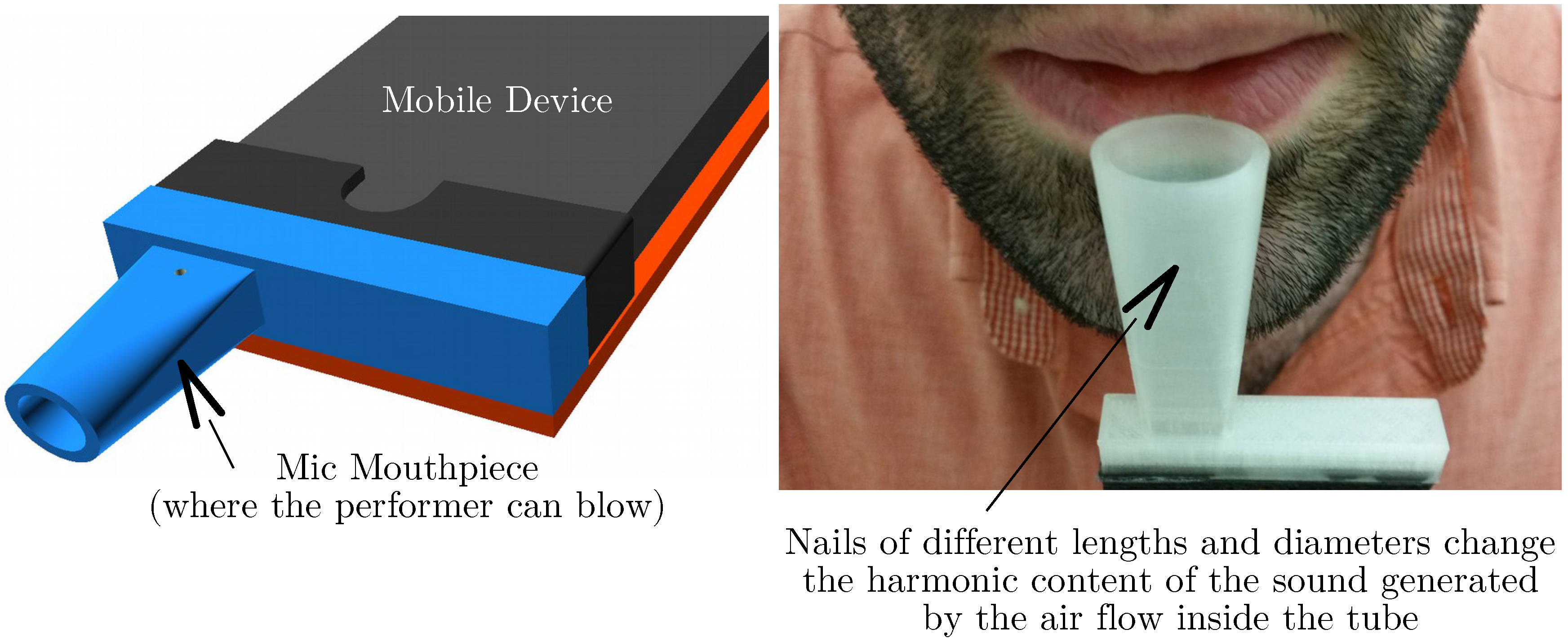
4.2.1. Bouncy-Phone by Casey Kim

Casey Kim designed Bouncy-Phone, an instrument where a 3D printed spring is “sandwiched” between an iPhone and an acrylic plate hosting a set of photo-resistors (see Figure 10). The interface on the touchscreen implements two parallel piano keyboards controlling the pitch of a monophonic synthesizer. The instrument is played by blowing onto the built-in microphone, in a similar way than Ocarina. The x axis of the accelerometer is mapped to the frequency of a lowpass filter applied to the generated sound. The spring is used to better control the position of the device in space in order to finely tune the frequency of the filter. The shades created by the two hands of the performer between the phone and the acrylic plate are used to control the parameters of various audio effects.

4.2.2. Something Else by Edmond Howser

Edmond Howser designed Something Else, an instrument running a set of virtual strings based on physical models from the Faust Physical Modeling Library (see Section 5.2). The touchscreen of an iPhone can be used to trigger sound excitations of different pitches. A set of three photoresistors were placed in 3D printed cavities (see Figure 10) that can be covered by the fingers of the performer to progressively block the light, allowing for a precise control of the parameters associated to them. These sensors were mapped to the parameters of a set of audio effects applied to the sounds generated by the string physical models. The instrument is meant to be held as a trumpet with three fingers on top of it (one per photoresistor) and fingers from the other hand on the side, on the touchscreen.

4.2.3. Mobile Hang by Marit Brademann

Mobile Hang is an instrument based on an iPhone designed by Marit Brademann. A 3D printed prosthetic is mounted on the back of the mobile device (see Figure 10). It hosts a Teensy board as well as a set of force sensitive resistors that can be used to trigger a wide range of percussion sounds based on modal physical models of the Faust Physical Modeling Library (see Section 5.2) with different velocities. A large hole placed in the back of the tapping surface allows for the performer to hold the instrument with the thumb of his right hand. The left hand is then free to interact with the different $(x,y)$ controllers on the touchscreen controlling the parameters of various effects applied to the generated sounds. Mobile Hang also takes advantage of the built-in accelerometer of the device to control additional parameters.

5. Articulating the Hybrid Mobile Instrument

Current technologies allow one to blur the boundary between the physical/acoustical and the virtual/digital world. Transforming a physical object into its virtual approximation can be done easily using various techniques (see Section 1.5). On the other hand, recent progress in digital fabrication, with 3D printing in particular (see Section 1.6), allows us to materialize 3D virtual objects. Even though 3D printed acoustic instruments don’t compete yet with “traditionally made” ones, their quality keeps increasing and they remain perfectly usable.

This section generalizes some of the concepts used by the BladeAxe [42], where sound excitations made by physical objects are used to drive physical-model-based virtual elements. It allows for instrument designers to arbitrarily choose the nature (physical or virtual) of the different parts of their creations.

We introduce a series of tools completing the framework presented in this paper to approach musical instrument design in a multimodal way where physical acoustical parts can be “virtualized” and vice versa. First, we give an overview of our framework to design mobile hybrid instruments. We provide a set of rules to help the instrument designer to make critical decisions about the nature (acoustical or digital) of the different parts of his instrument in the context of mobile devices. Then we introduce the Faust Physical Modeling Library (FPML), “the core” of our framework, that can be used to implement a wide range of physical models of musical instruments to be run on a mobile device (e.g., using faust2smartkeyb). Finally, we demonstrate how custom models can be implemented using mesh2faust [56] and FMPL.

5.1. Framework Overview

5.1.1. From Physical to Virtual

In Section 1.5, we gave an overview of different physical modeling techniques that can be used to make virtual versions of physical objects designed to generate sound (i.e., musical instruments). The framework presented in this section is a bit more limiting and focuses on specific modeling techniques that are flexible and computationally cheap (which is a crucial feature for mobile development).

Various linearizable acoustical physical objects can be easily turned into modal physical models using their impulse response [28]. Pierre-Amaury Grumiaux et al. implemented ir2faust [57], a command-line tool taking an impulse response in audio format and generating the corresponding Faust physical model compatible with the Faust Physical Modeling Library presented in Section 5.2. This technique is commonly used to make signal models of musical instrument parts (e.g., acoustic resonators such as violin and guitar bodies, etc.).

Modal physical models can also be generated by carrying out a finite element analysis (FEM) on a 3D volumetric mesh. Meshes can be made “from scratch” or using a 3D scanner, allowing musical instrument designers to make virtual parts using a CAD model. mesh2faust [56] can be used to carry out this type of task. Modal models generated by this tool are fully compatible with the Faust Physical Modeling Library presented in Section 5.2. While this technique is more flexible and allows us to model elements “from scratch,” generated models are usually not as accurate as the one deduced from the impulse response of a physical object that faithfully reproduce its harmonic content.

Even though it is tempting to model an instrument in its whole using its complete graphical representation, better results are usually obtained using a modular approach where each part of the instrument (e.g., strings, bridge, body, etc.) are modeled as single entities. The Faust Physical Modeling Library introduced in Section 5.2 implements a wide range of ready-to-use musical instrument parts. Missing elements can then be easily created using mesh2faust or ir2faust. Various examples of such models are presented in Section 5.2.2 and Section 5.2.3.

5.1.2. From Virtual to Physical

3D printing can be used to materialize virtual representation of musical instrument parts under certain conditions. Thus, most elements provided to mesh2faust [56] can be printed and turned into physical objects.

5.1.3. Connecting Virtual and Physical Elements

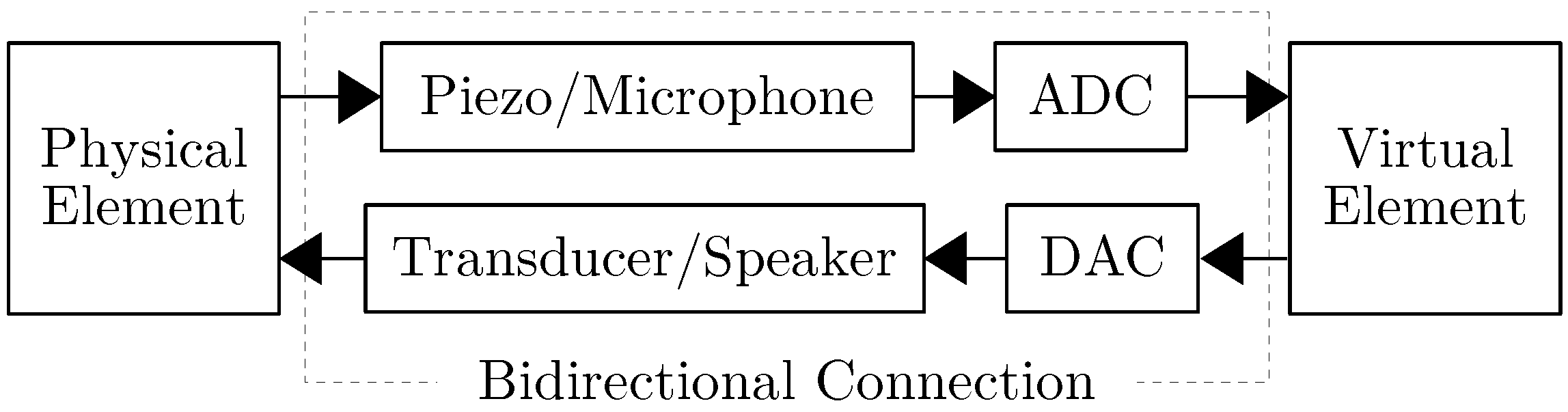
Standard hardware for digitizing mechanical acoustic waves and vice versa can be used to connect the physical and virtual elements of a hybrid instrument (see Figure 11). Piezos (contact microphones) can capture mechanical waves on solid surfaces (e.g., guitar body, string, etc.) and microphones mechanical air waves (e.g., in a tube, etc.). Captured signals can be digitized using an analog to digital converter (ADC). Inversely, digital audio signals can be converted to analog signals using a digital to analog converter (DAC) and then to mechanical waves with a transducer (for solid surfaces) or a speaker (for the air).

In some cases, a unidirectional connection is sufficient as waves travel in only one direction and are not (or almost not) reflected. This is the case of the BladeAxe [42] where sound excitations (i.e., plucks) are picked up using piezos and transmitted to virtual strings. This type of system remains simple and works relatively well as the latency of the DAC or the ADC doesn’t impact the characteristics the generated sound.

On the other hand, a bidirectional connection (see Section 5.2.1) might be necessary in other cases. Indeed, reflection waves play a crucial role in the production of sound in some musical instruments such as woodwinds. For examples, connecting a physical clarinet mouthpiece to a virtual bore will require the use of a bidirectional connection in order for the frequency of vibration of the reed to be coupled to the tube it is connected to. This type of connection extends beyond the instrument to the performer that constantly adjusts its various parameters in function of the generated sound [5]. However, implementing this type of system can be very challenging as the DAC and the ADC will add latency, which in the case of the previous example will artificially increase the length of the virtual bore. Thus, using low latency DACs and ADCs is crucial when implementing this type of systems sometimes involving the use of active control techniques [58,59].

More generally, the use of high-end components with a flat frequency response is very important when implementing any kind of hybrid instruments. Also, hardware can become very invasive in some cases, and it is the musical instrument designer’s responsibility to find the right balance between all these parameters.

5.1.4. Adapting This Framework to Mobile Devices

Beyond this theoretical modularity (keeping in mind that audio latency can be a limiting factor in some cases) where any part of mobile hybrid instruments can either be physical or virtual, some design “templates” are more efficient than others. Here, we give some guidelines/rules to restrain the scope of our framework to optimize its results when making mobile hybrid instruments.

In the context of augmented mobile instruments where standalone aspects and lightness are key factors, the number of physical/acoustical elements of hybrid instruments must be scaled down compared to what is possible with a desktop-based system. Indeed, transducers are large and heavy components requiring the use of an amplifier, which itself needs a large power source other than the mobile device battery, etc. Similarly, multichannel ADCs and DACs can take a fair amount of space and will likely need to be powered with an external battery/power supply.

Even though applications generated with faust2smartkeyb (see Section 2) are fully compatible with external USB ADC/DACs, we believe that restraining hybrid mobile instruments to their built-in ADC/DACs helps preserve their compactness and playability.

Beyond the aesthetic and philosophical implications of hybrid instruments (which are of great interest but are not the object of this paper), their practical goal is to leverage the benefits of physical and virtual elements to combine them. In practice, the digital world is more flexible and allows us to model/approximate many physical elements. However, even with advanced sensor technologies, it often fails to capture the intimacy (see Section 1.1) between a performer and an acoustic instrument allowing us to directly interact with its sound generation unit (e.g., plucked strings, hand drum, etc.) [13].

Thus, a key factor in the success of hybrid mobile instruments lies in the use of a physical/acoustical element as the direct interface for the performer, enabling passive haptic feedback and taking advantage of the randomness and unpredictability of acoustical elements (see Section 1.2). In other words, even though it is possible to combine any acoustical element with any digital one, we encourage instrument designers to use acoustical excitations to drive virtual elements (see Figure 12), implementing the concept of “acoustically driven hybrid instruments” presented in Section 1.2. While the single analog input available on most mobile devices allows for the connection of one acoustical element, having access to more independent analog inputs would significantly expend the scope of the type of instruments implementable with our framework. This remains one of its main limitation.

5.2. Faust Physical Modeling Library

More than just a set of functions, the Faust Physical Modeling Library provides a comprehensive environment to implement physical models of musical instrument parts fully compatible with the hybrid instrument paradigm described in Section 5. This section summarizes its various features.

5.2.1. Bidirectional Block-Diagram Algebra

In the physical world, waves propagate in multiple dimensions and directions across the different parts of musical instruments. Thus, coupling between the constituting elements of an instrument sometimes plays an important role in its general acoustical behavior. In Section 5.1.3, we highlighted the importance of bidirectional connections to implement coupling between the performer, the physical, and the virtual elements of a hybrid instrument. While these types of connections happen naturally between physical elements, it is necessary to implement them when connecting virtual elements together.

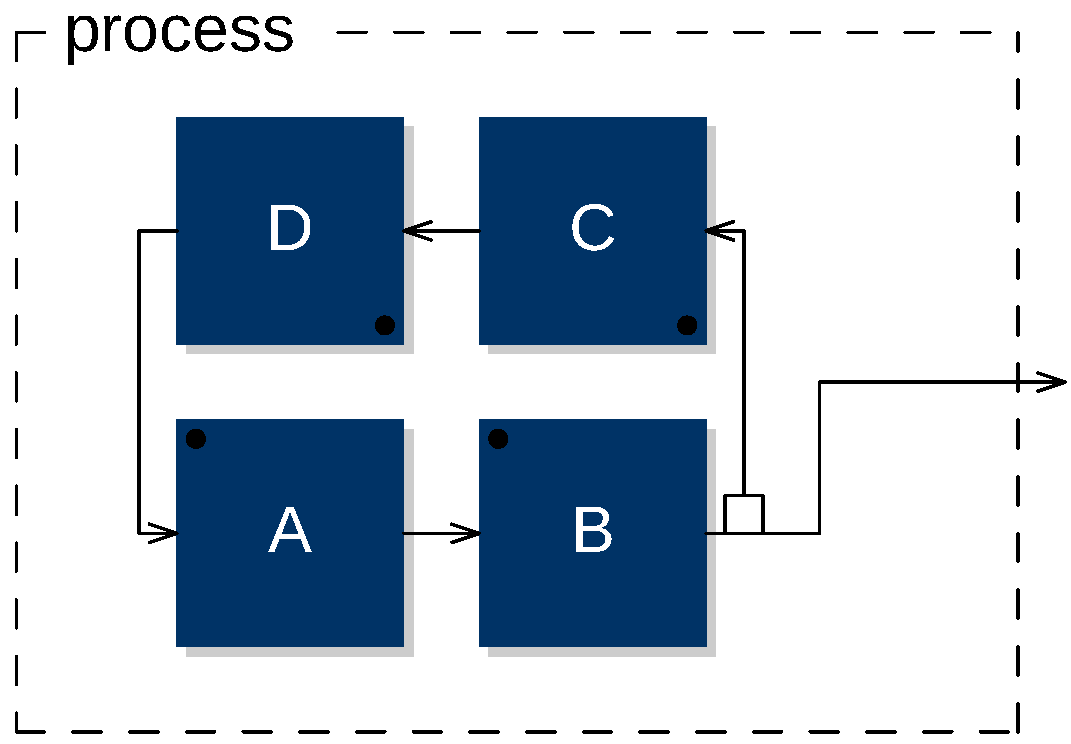
The block-diagram algebra of Faust allows us to connect blocks in a unidirectional way (from left to right) and feedback signals (from right to left) can be implemented using the tilde (~) diagram composition operation: where A, B, C, and D are hypothetical functions with a single argument and a single output. The resulting Faust-generated block diagram can be seen in Figure 13.

In this case, the D/A and the C/B couples can be seen as bidirectional blocks/functions that could implement some musical instrument part. However, the Faust semantics doesn’t allow them to be specified as such from the code, preventing the implementation of “bidirectional functions.” Since this feature is required to create a library of physical modeling elements, we had to implement it.

Bidirectional blocks in the Faust Physical Modeling Library all have three inputs and outputs. Thus, an empty block can be expressed as:

The first input and output correspond to left-going waves (e.g., C and D in Figure 13), the second input and output to right-going waves (e.g., A and B in Figure 13), and the third input and output can be used to carry any signal to the end of the algorithm. As we’ll see in Section 5.2.2, this can be useful when picking up the sound at the middle of a virtual string, for example.

Bidirectional blocks are connected to each other using the chain primitive which is part of physmodels.lib. For example, an open waveguide (no terminations) expressed as: where nMax is the maximum length of the waveguide and n its current length, could be connected to our emptyBlock:Note the use of fdelay4 in waveguide, which is a fourth order fractional delay line [60].

The Faust compiler is not able yet to generate the block diagram corresponding to the previous expression in an organized bidirectional way (see Section 5.3). However, a “hand-made” diagram can be seen in Figure 14.

The placement of elements in a chain matters and corresponds to their order in the physical world. For example, for a set of hypothetical functions implementing the different parts of a violin, we could write:

The main limitation of this system is that it introduces a one sample delay in both directions for each block in the chain due to the internal use of ~ [49]. This has to be taken into account when implementing certain types of elements such as a string or a tube.

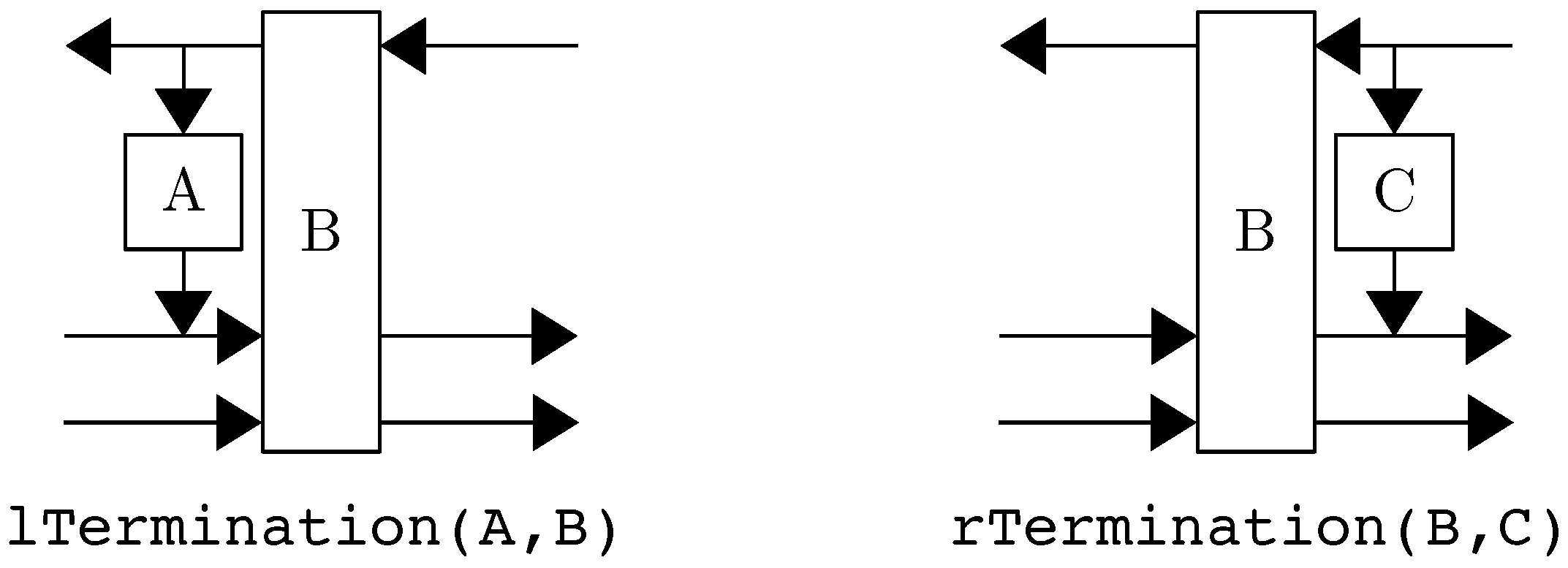
Terminations can be added on both sides of a chain using lTermination(A,B) for a left-side termination and rTerminations(B,C) for a right-side termination where B can be any bidirectional block, including a chain, and A and C are functions that can be put between left and right-going signals (see Figure 15).

A signal x can be fed anywhere in a chain by using the in(x) primitive. Similarly, left and right-going waves can be summed and extracted from a chain using the out primitive (see Code Listing 4).

Finally, a chain of blocks A can be “terminated” using endChain(A) which essentially removes the three inputs and the first two outputs of A.

Assembling a simple waveguide string model with “ideal” rigid terminations is simple using this framework:

In this case, since in and out are placed next to each other in the chain, the position of excitation and the position of the pickup are the same as well.

5.2.2. Assembling High Level Parts: Violin Example

FPML contains a wide range of ready-to-use instrument parts and pre-assembled models. An overview of the content of the library is provided in the Faust libraries documentation [60]. Detailing the implementation of each function of the library would be interesting, however this section focuses on one of its models: violinModel (see Code Listing 5) which implements a simple bowed string connected to a body through a bridge.

violinModel assembles various high-level functions implementing violin parts. violinNuts is a termination applying a light low-pass filter on the reflected signal. violinBowedString is made out of two open string segments allowing us to choose the bowing position. The bow nonlinearity is implemented using a table. violinBridge implements the “right termination” as well as the reflectance and the transmittance filters [27]. Finally, violinBody is a simple violin body modal model.

In addition to its various models and parts, the FPML also implements a series of ready-to-use models hosting their own user interface. The corresponding functions end with the _ui suffix. For example:is a complete Faust program adding a simple user interface to control the violin model presented in Code Listing 5.

While [...]_ui functions associate continuous UI elements (e.g., knobs, sliders, etc.) to the parameters of a model, functions ending with the _ui_midi prefix automatically format the parameters linked the Faust MIDI parameters (i.e., frequency, gain, and note-on/off) using envelope generators. Thus, such functions are ready to be controlled by a MIDI keyboard.

Nonlinear behaviors play an important role in some instruments (e.g., gongs, cymbals, etc.). While waveguide models and modal synthesis are naturally linear, nonlinearities can be introduced using nonlinear allpass ladder filters [61]. allpassNL implements such a filter in the Faust Physical Modeling Library.

Some of the physical models of the Faust-STK [62] were ported to FPML and are available through various functions in the library.

5.2.3. Example: Marimba Physical Model Using FPML and mesh2faust

This section briefly demonstrates how a simple marimba physical model can be made using mesh2faust and FPML (An extended version of this example with more technical details is also available in the corresponding on-line tutorial: https://ccrma.stanford.edu/~rmichon/faustTutorials/#making-custom-elements-using-mesh2faust). The idea is to use a 3D CAD model of a marimba bar, generate the corresponding modal model, and then connect it to a tube model implemented in FPML.

A simple marimba bar 3D model can be made by extruding a marimba bar cross section using the Inkscape to OpenSCAD tool part of mesh2faust [56]. The resulting CAD model is then turned into a volumetric mesh by importing it to MeshLab and by uniformly re-sampling it to have approximately 4500 vertices. The mesh produced during this step (marimbaBar.obj in the following code listing) can then be processed by mesh2faust using the following command (A complete listing of mesh2faust’s options can be found in its on-line documentation: https://github.com/grame-cncm/faust/blob/master-dev/tools/physicalModeling/mesh2faust/README.md.):

The material parameters are those of rosewood which is traditionally used to make marimba bars. The number of modes is limited to 50 and various excitation positions were selected to be uniformly spaced across the horizontal axis of the bar. frequency control mode is activated to be able to transpose the modes of the generated model in function of the fundamental frequency making the model more generic.

A simple marimba resonator was assembled using FPML and is presented in Code Listing 6. It is made out of an open tube where two simple lowpass filters placed at its extremities are used to model the wave reflections. The model is excited on one side of the tube and sound is picked-up on the other side.

Code Listing 7 demonstrates how the marimba bar model generated with mesh2faust (marimbaBarModel) can be simply connected to the marimba resonator. A unidirectional connection can be used in this case since waves are only transmitted from the bar to the resonator.

This model is now part of the Faust Physical Modeling Library. It could be easily used with faust2smartkeyb to implement a marimba app (see Section 2) as well as with any of the Faust targets (e.g., Web App, Plug-In, etc.). More examples of models created using this technique can be found on-line (Faust Physical Modeling Toolkit Webpage: https://ccrma.stanford.edu/~rmichon/pmFaust/).

5.3. Discussion and Future Directions

The framework presented in this section remains limited by several factors. Audio latency induced by ADCs and DACs prevents in some cases the implementation of cohesive bidirectional chains between physical and virtual elements. Audio latency reduction has been an ongoing research topic for many years and more work has to be done in this direction. This problem is exacerbated by the use of mobile devices at the heart of these systems that are far from being specialized for this specific type of application (i.e., operating system optimizations inducing extra latency, number of analog inputs and outputs, etc.). On the other hand, we believe that despite the compromises that they entail, mobile devices remain a versatile, and yet easy to customize platform well suited to implement hybrid instruments (e.g., the BladeAxe [42]).

The Faust Physical Modeling Library is far from being exhaustive and many models and instruments could be added to it. We believe that mesh2faust will help enlarge the set of functions available in this system.

The framework presented in Section 5.2.1 allows us to assemble the different parts of instrument models in a simple way by introducing a bidirectional block diagram algebra to Faust. While it provides a high level approach to physical modeling, Faust is not able to generate the corresponding block diagram in a structured way. This would be a nice feature to add.

Similarly, we would like to extend the idea of being able to make multidimensional block diagrams in Faust by adding new primitives to the language.

More generally, we hope to make more instruments using this framework and use them on stage for live performance.

6. Conclusions

By combining physical and virtual elements, hybrid instruments are “physically coherent” by nature and allow instrument designers to play to the strengths of both acoustical and digital elements. Current technologies and techniques allow us to blur the boundary between the physical and the virtual world enabling musical instrument designers to treat instrument parts in a multidimensional way. The Faust Physical Modeling Toolkit presented in Section 5 facilitates the design of such instruments by providing a way to approach physical modeling of musical instruments at a very high level.

Mobile devices combined with physical passive or active augmentations are well suited to implement hybrid instruments. Their built-in sensors, standalone aspect, and computational capabilities are the core elements required to implement the virtual portion of hybrid instruments. faust2smartkeyb facilitates the design of mobile apps using elements from the Faust Physical Modeling Library, implementing skill transfer, and serving as the glue between the various parts of the instrument. Mobile devices might limit the scope of hybrid instruments by scaling down the number of connections between acoustical and digital elements because of technical limitations. However, we demonstrated that a wide range of instruments can still be implemented using this type of system.

The framework presented in this paper is a toolkit for musical instrument designers. By facilitating skill transfer, it can help accelerate the learning process of instruments made with it. However, musical instruments remain a tool controlled by the performer. Having a well designed instrument leveraging some of the concepts presented here doesn’t mean that it will systematically play beautiful music and generate pleasing sounds: this is mostly up to the performer.

We believe that mobile hybrid instruments presented in this paper help reconcile the haptic, the physical, and the virtual, partially solving some of the flaws of DMIs depicted by Perry Cook [5].

We recently finished releasing the various elements of the framework presented in this paper and we hope to see the development of more mobile-device-based hybrid instruments in the future.