Theoretical Analysis for the Flow Ripple of a Tandem Crescent Pump with Index Angles
Abstract
:Featured Application
Abstract
1. Introduction
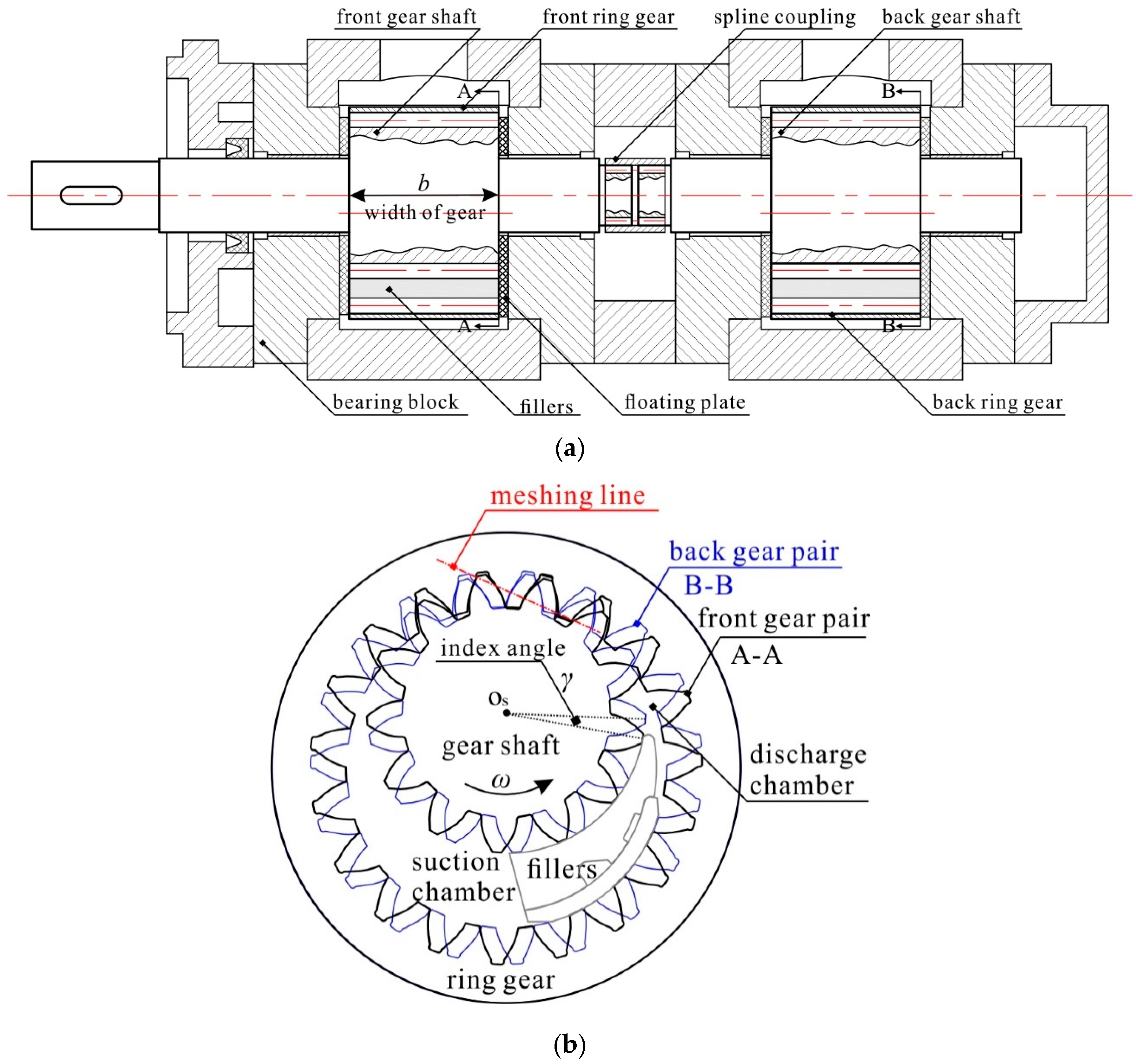
2. Simulation Model
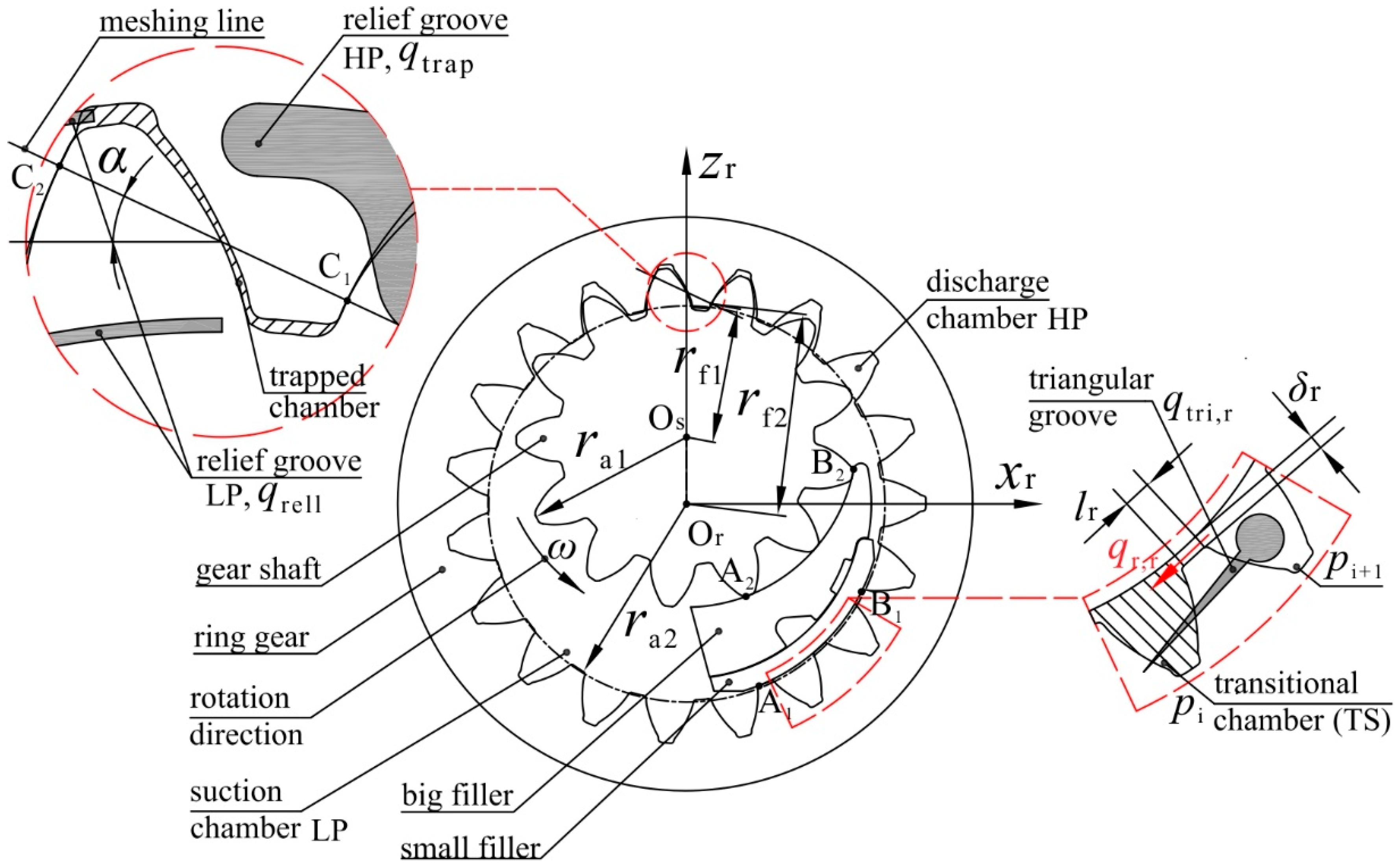
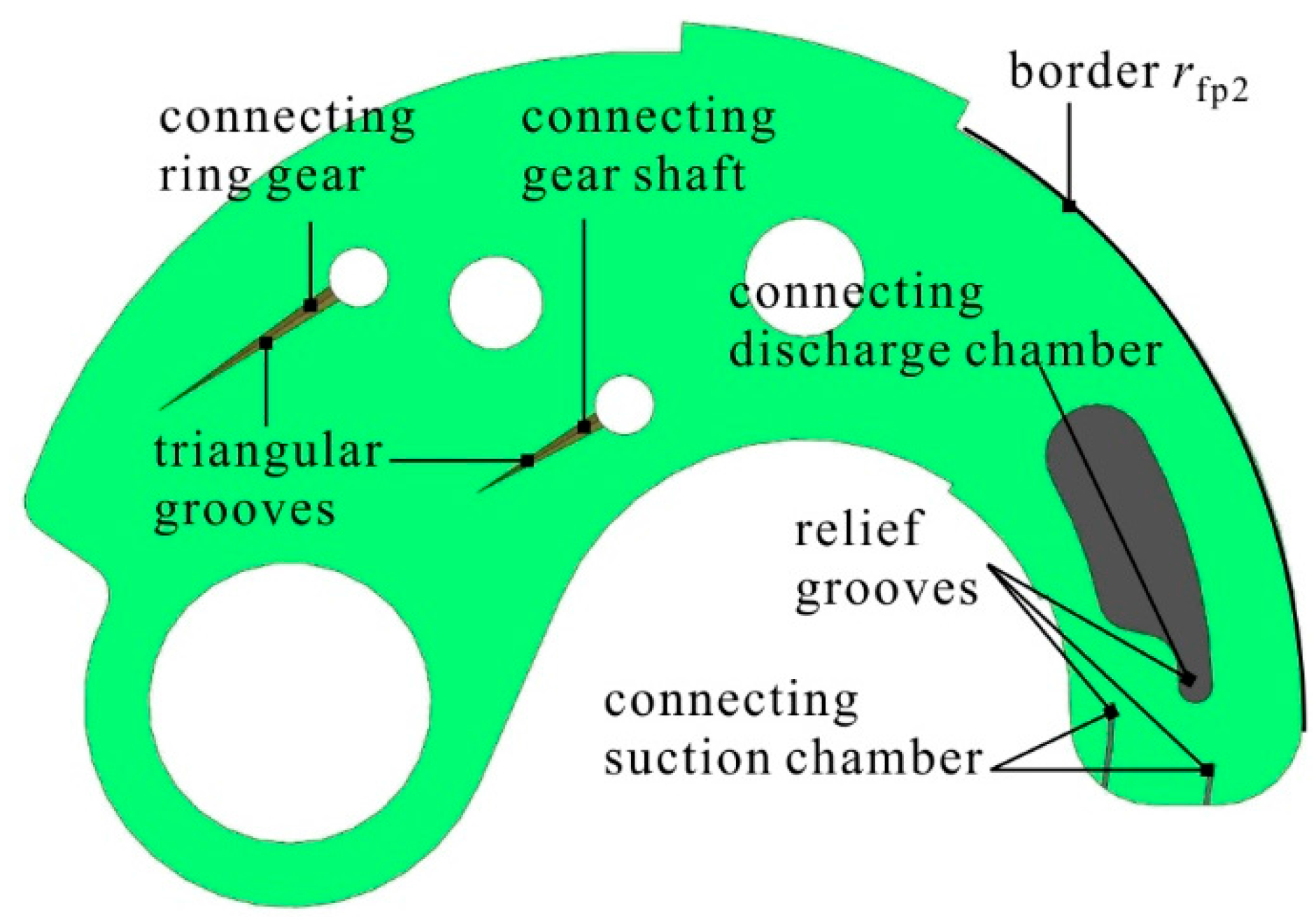
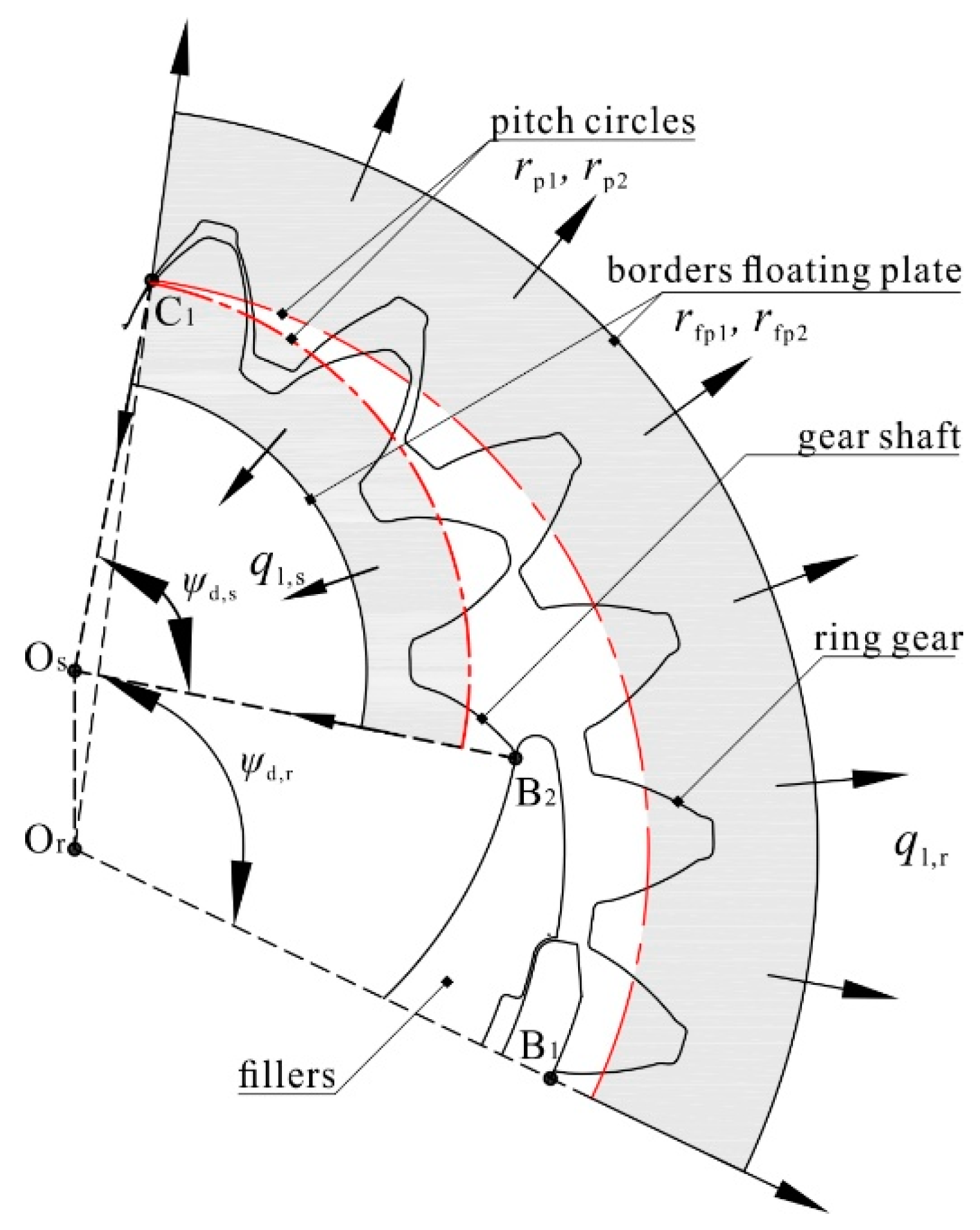
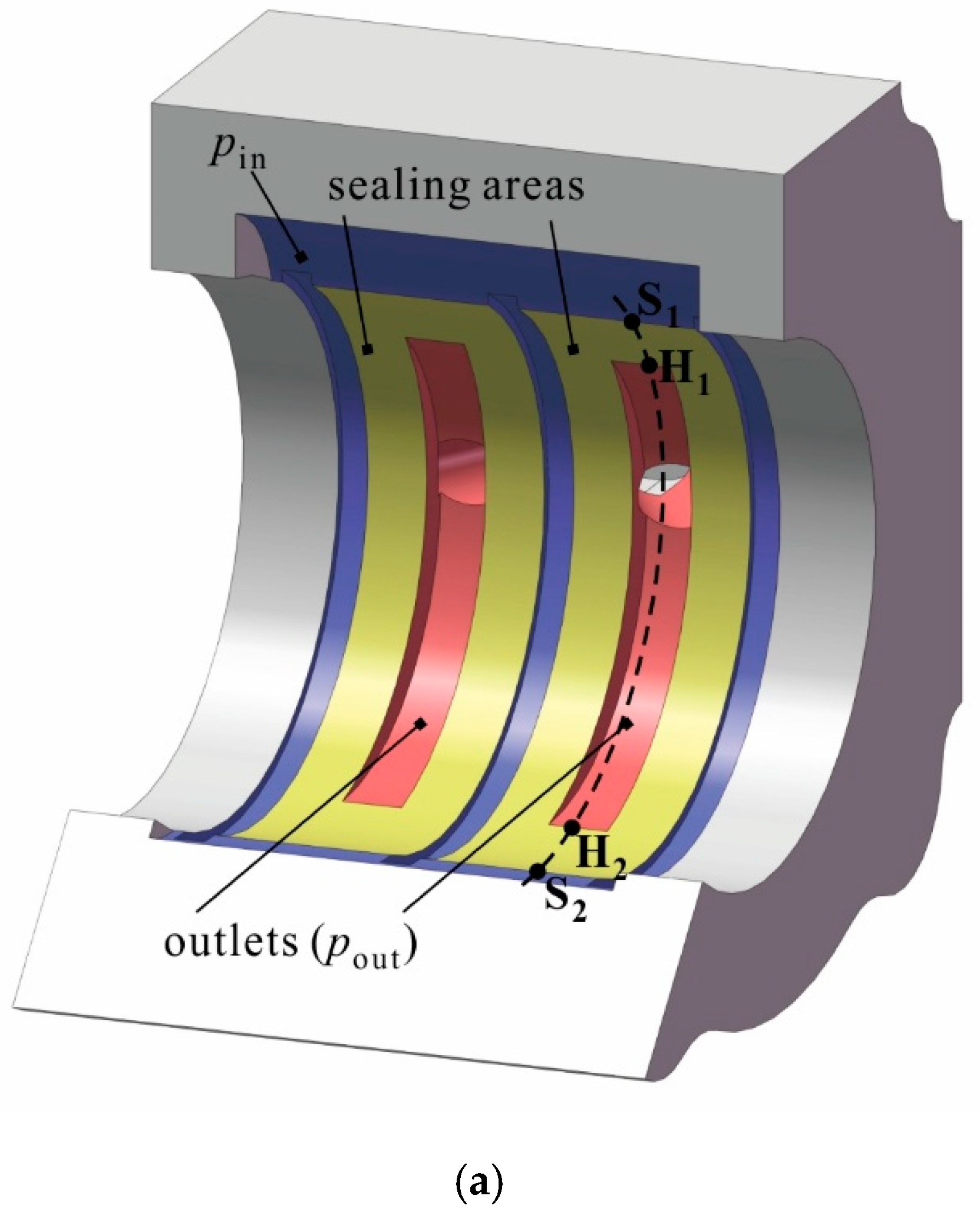
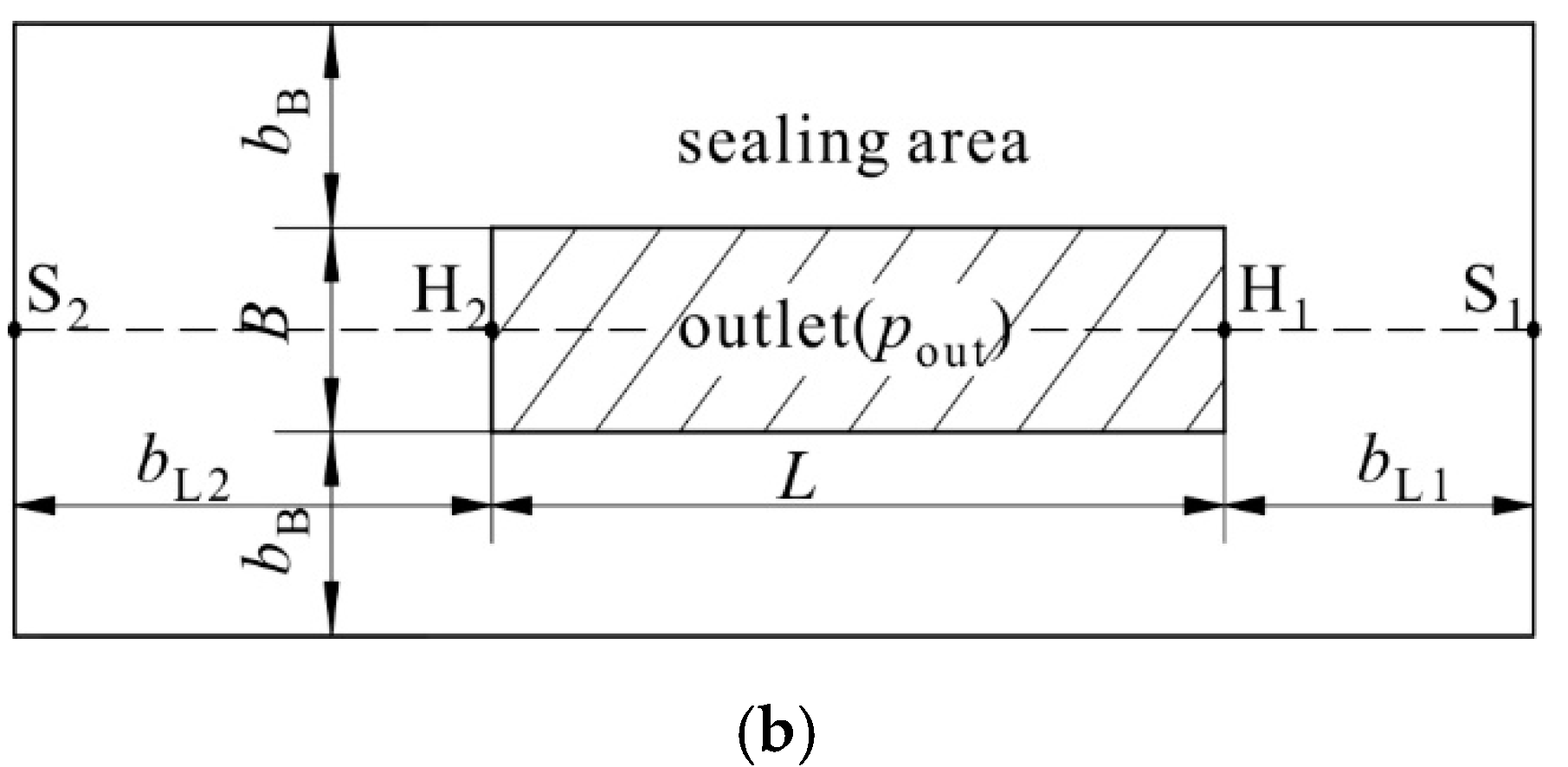
2.1. The Discharge Chamber
2.2. The Trapped Chamber
2.3. The Transitional Chamber
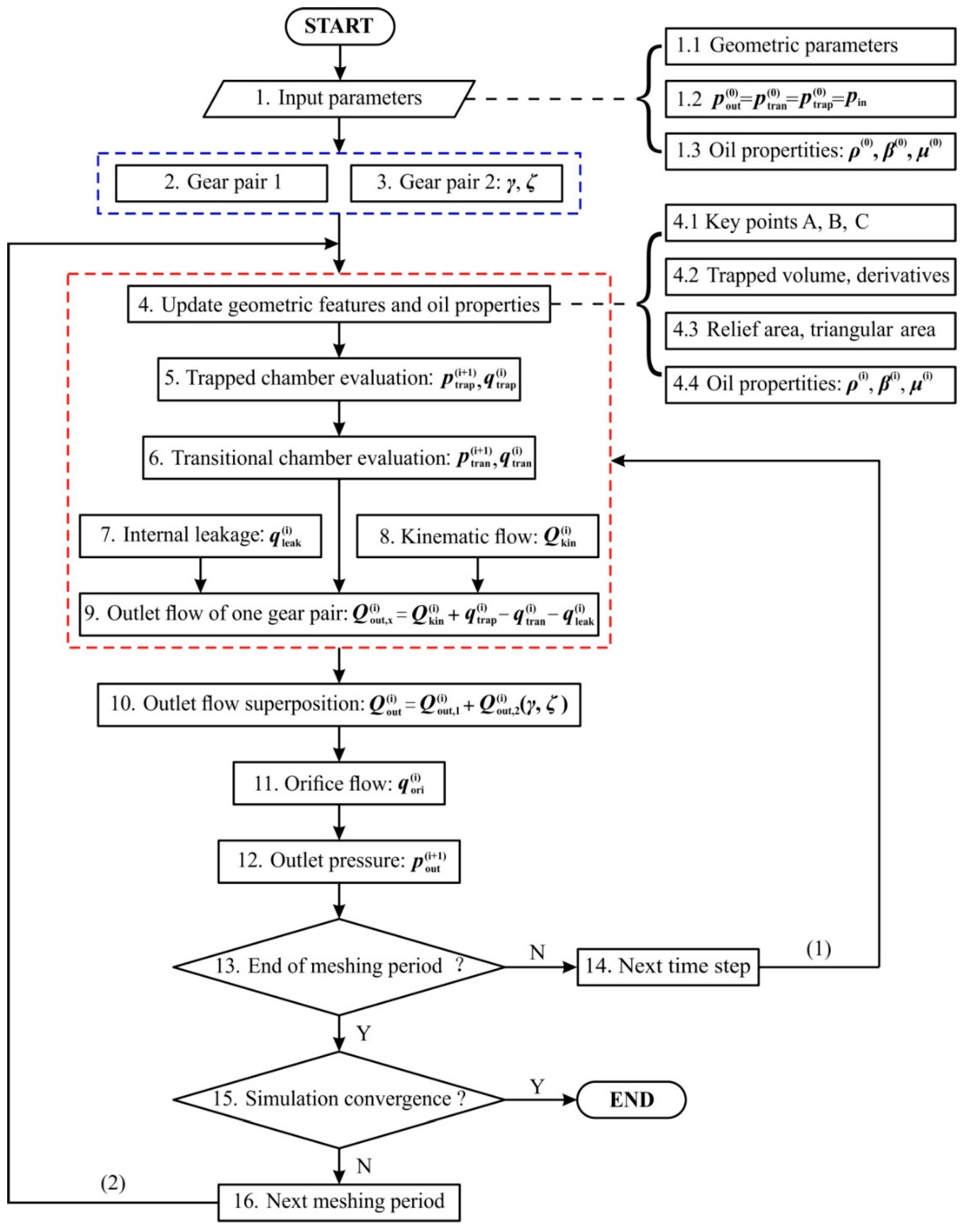
2.4. Simulation Procedure
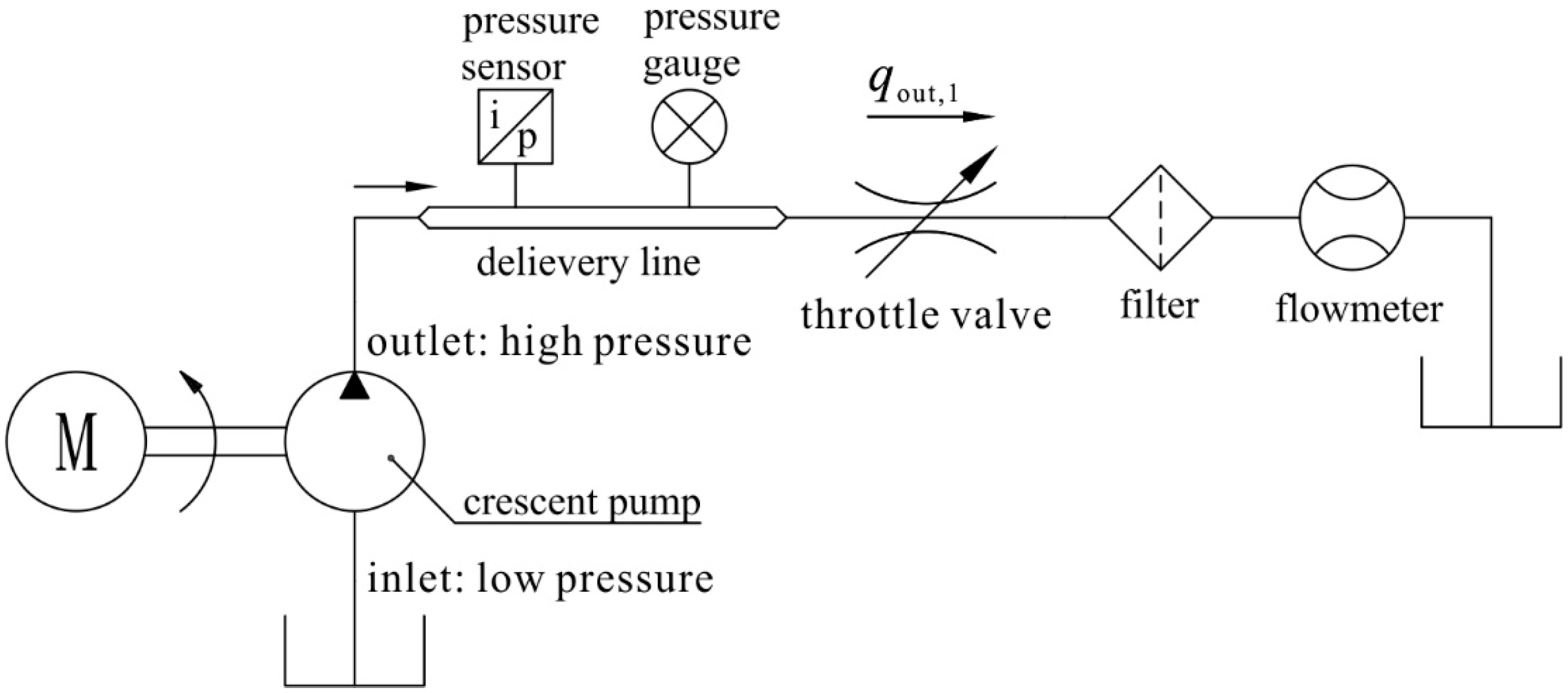
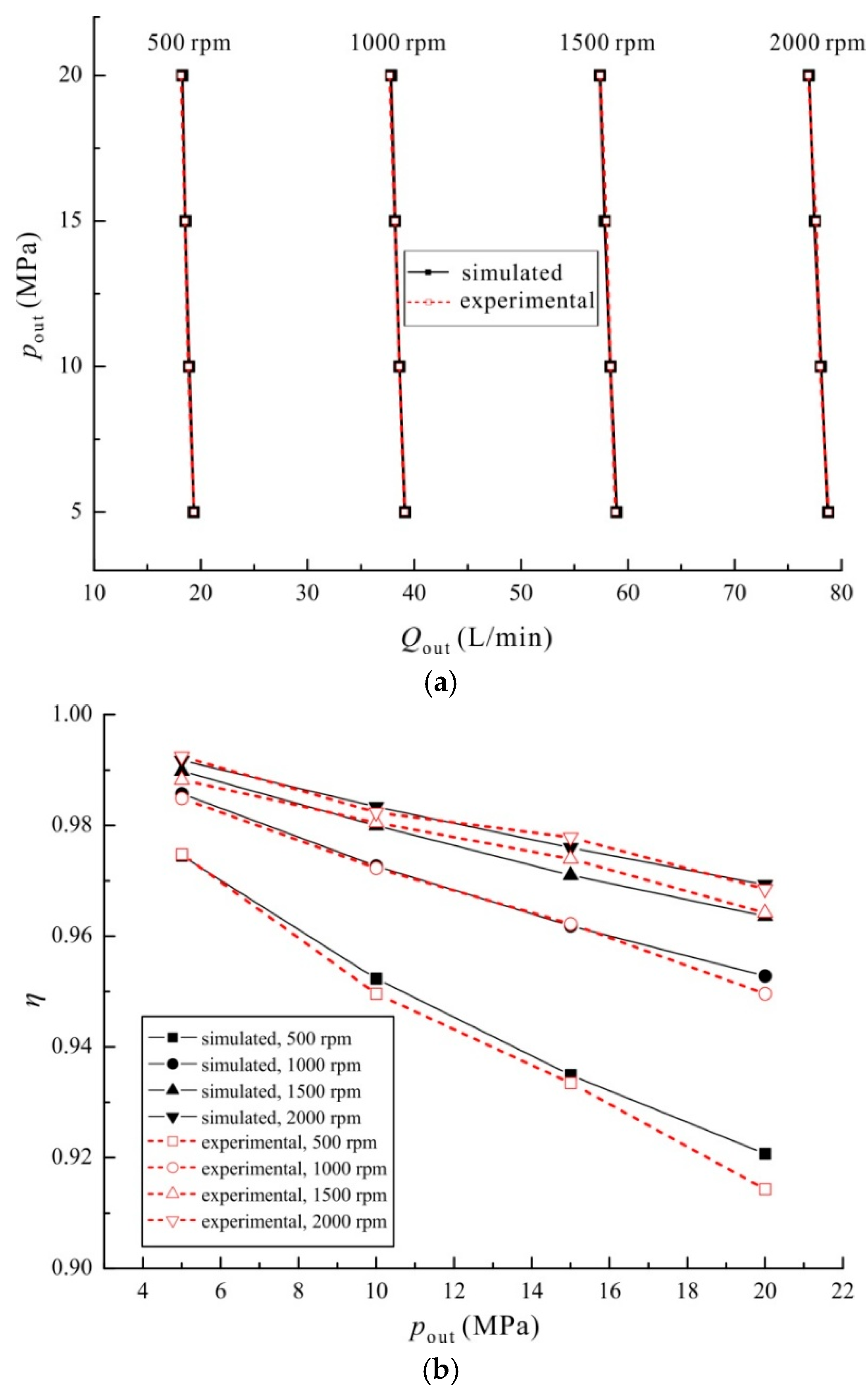
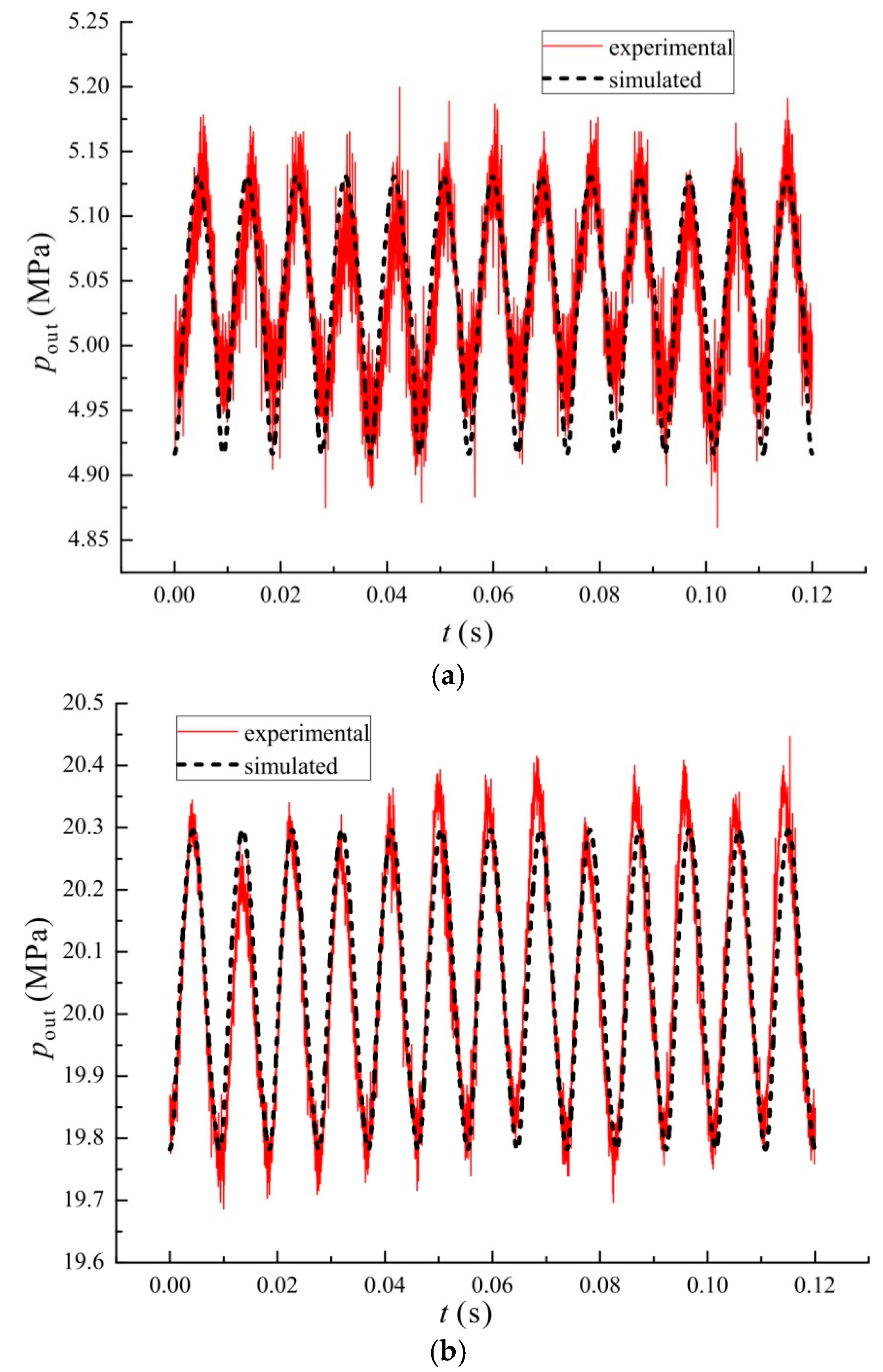
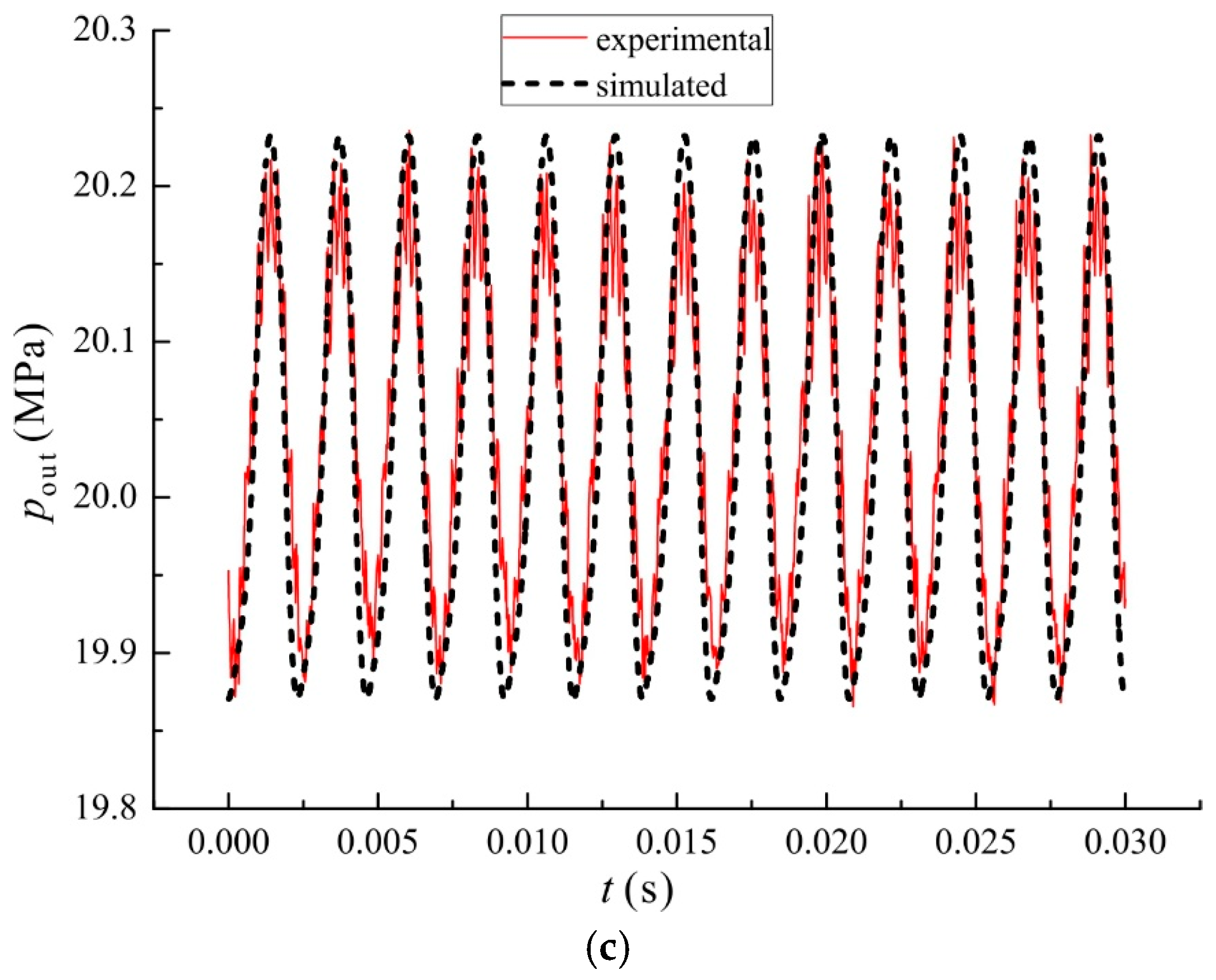
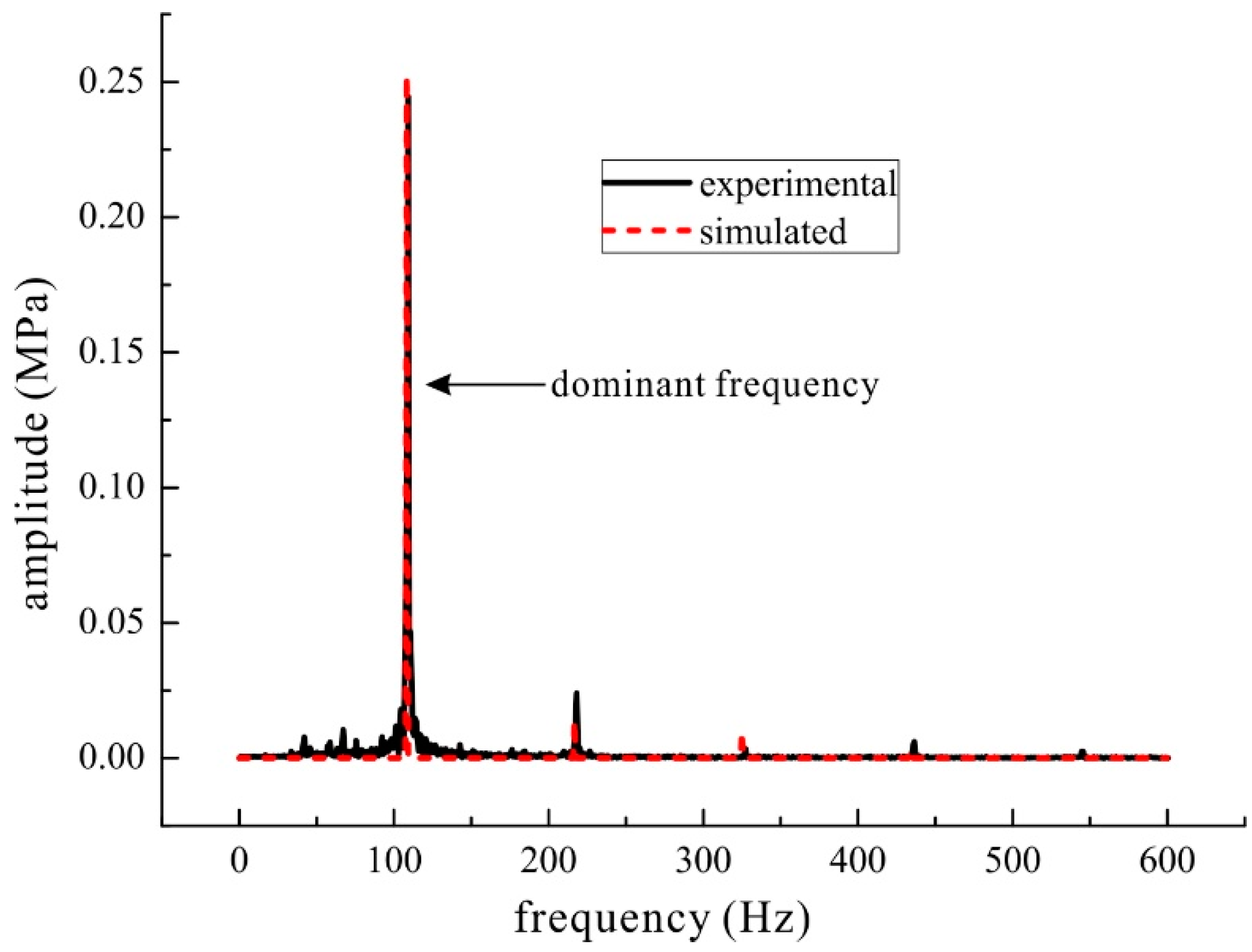
3. Experimental Validation
4. Numerical Results
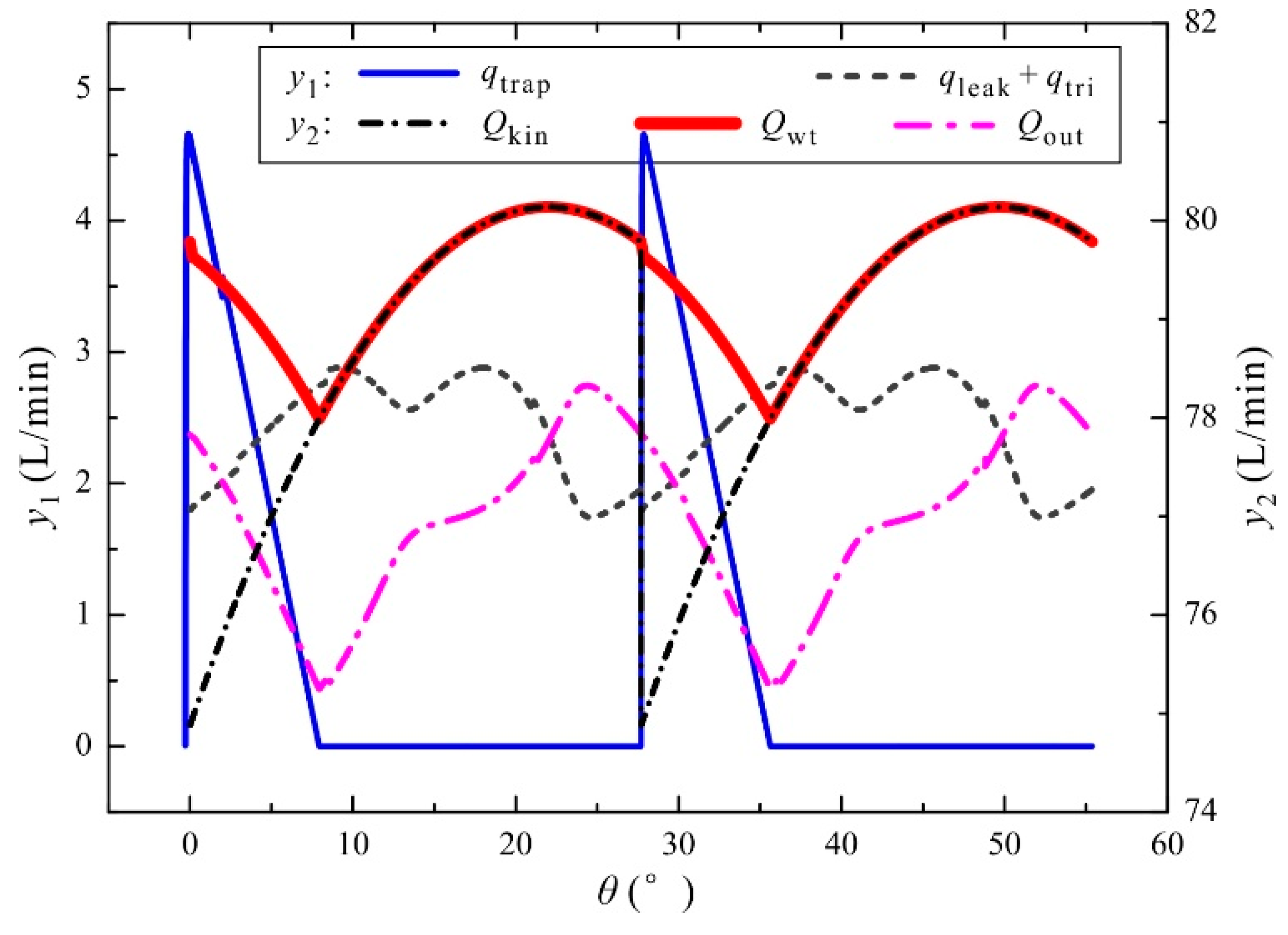
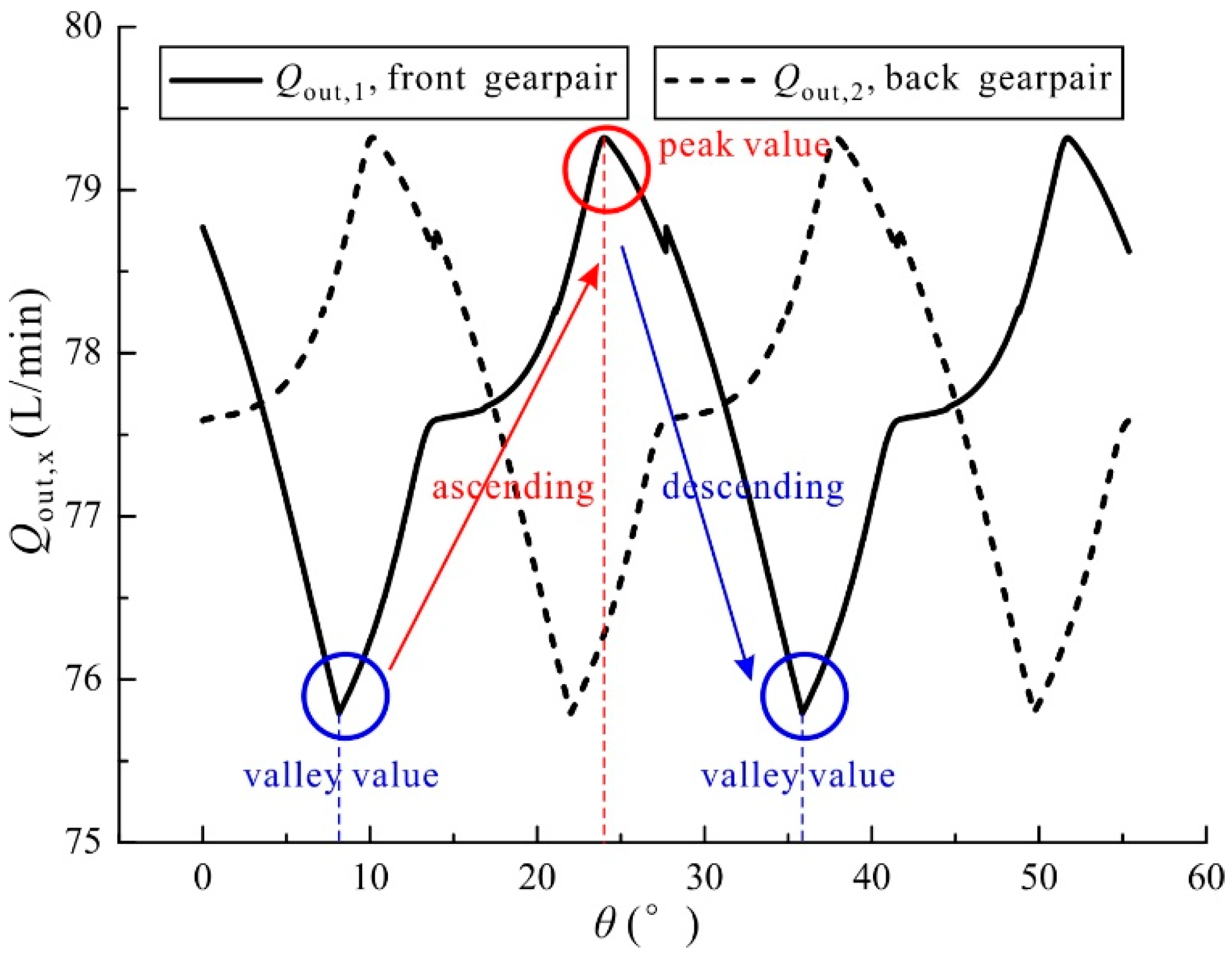
4.1. Outlet Flow of the Crescent Pump
4.2. Flow Ripple under Different Design Parameters
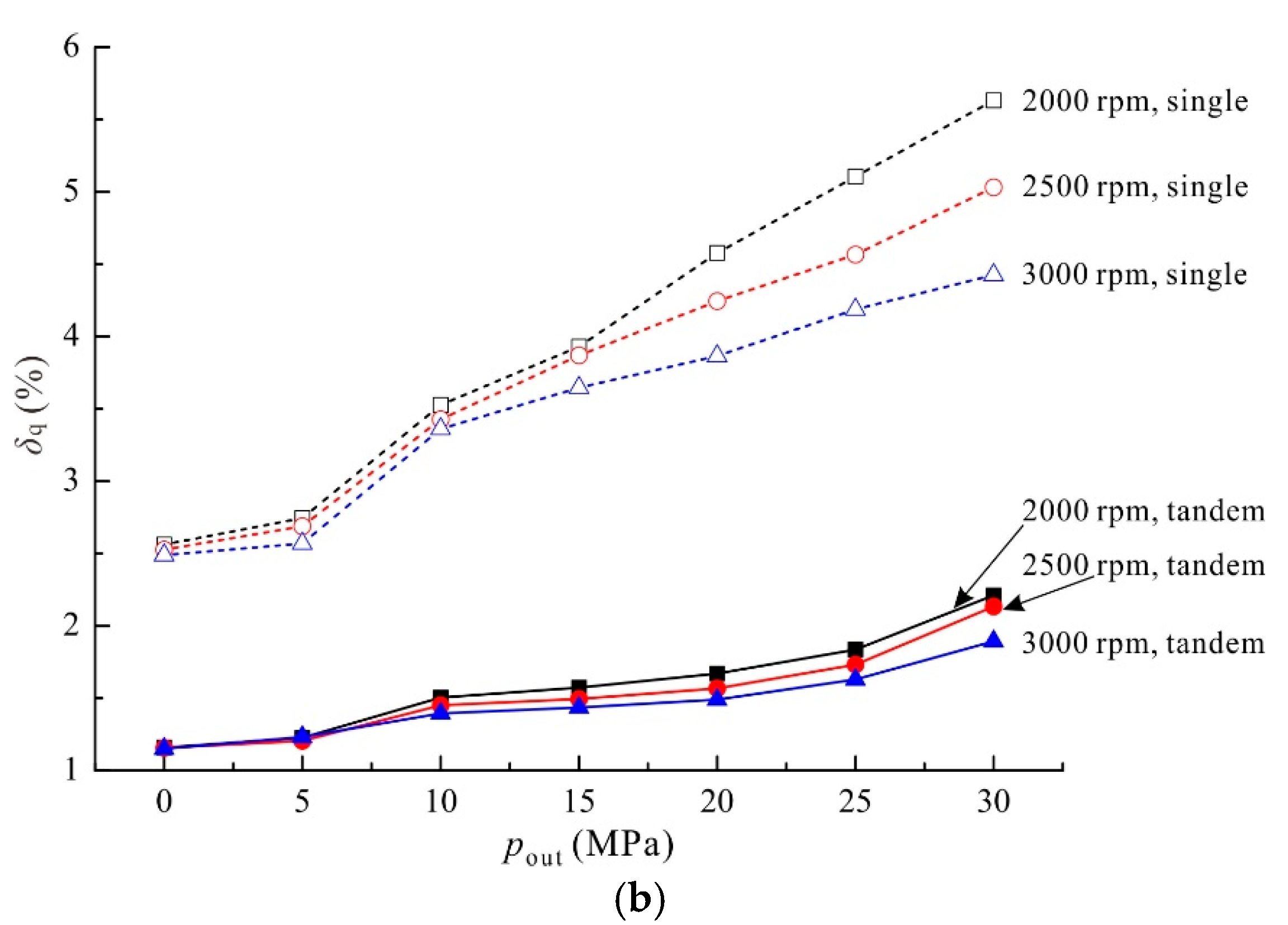
4.3. Flow Ripple under Different Operating Conditions
5. Discussion and Conclusions
5.1. Main Causes of the Flow Ripple
5.2. Influence of Design Parameters
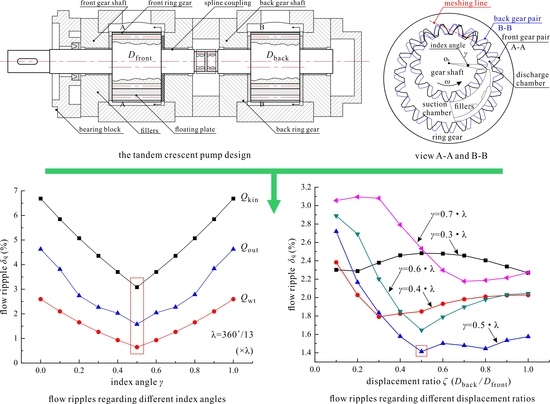
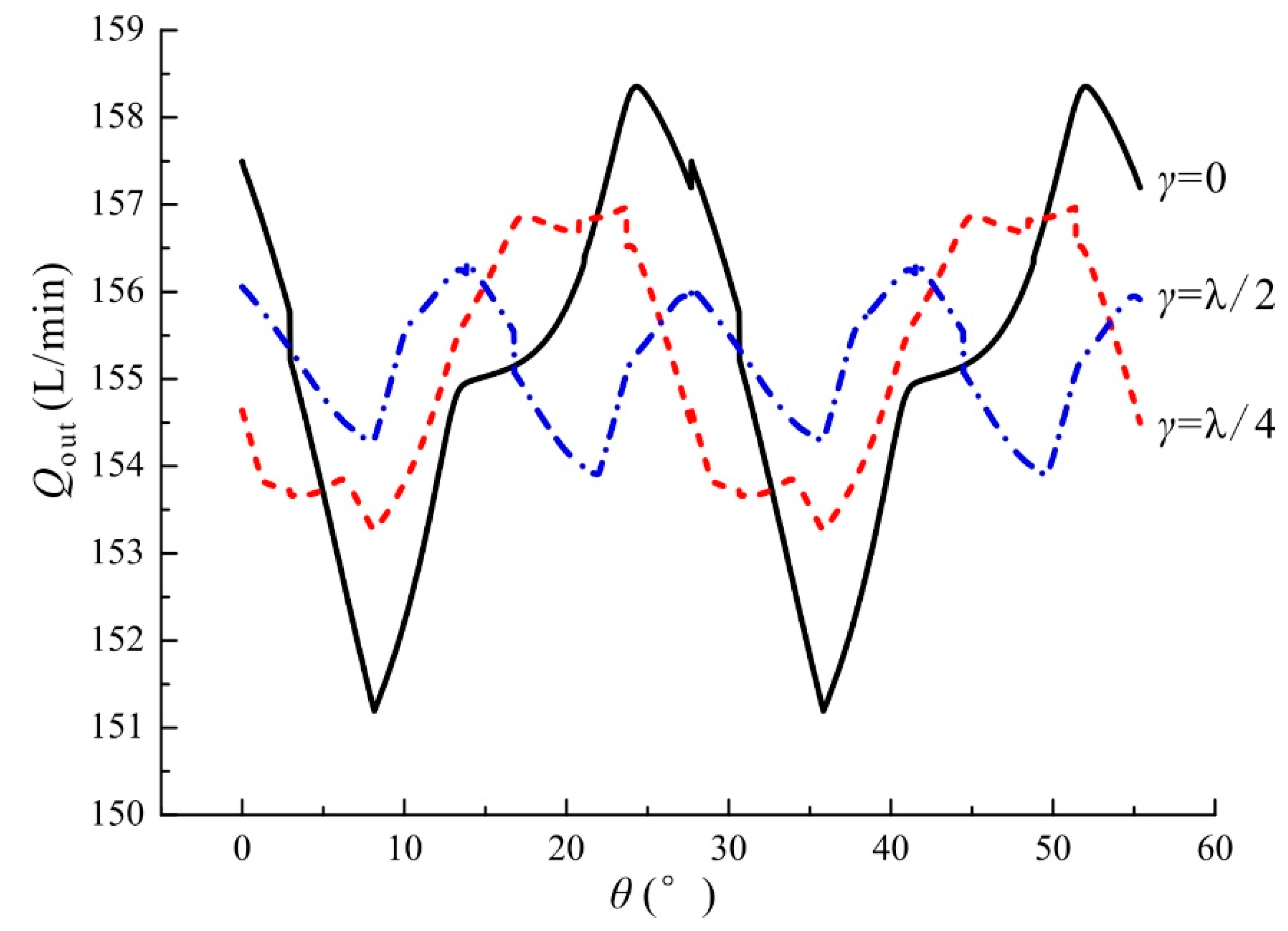
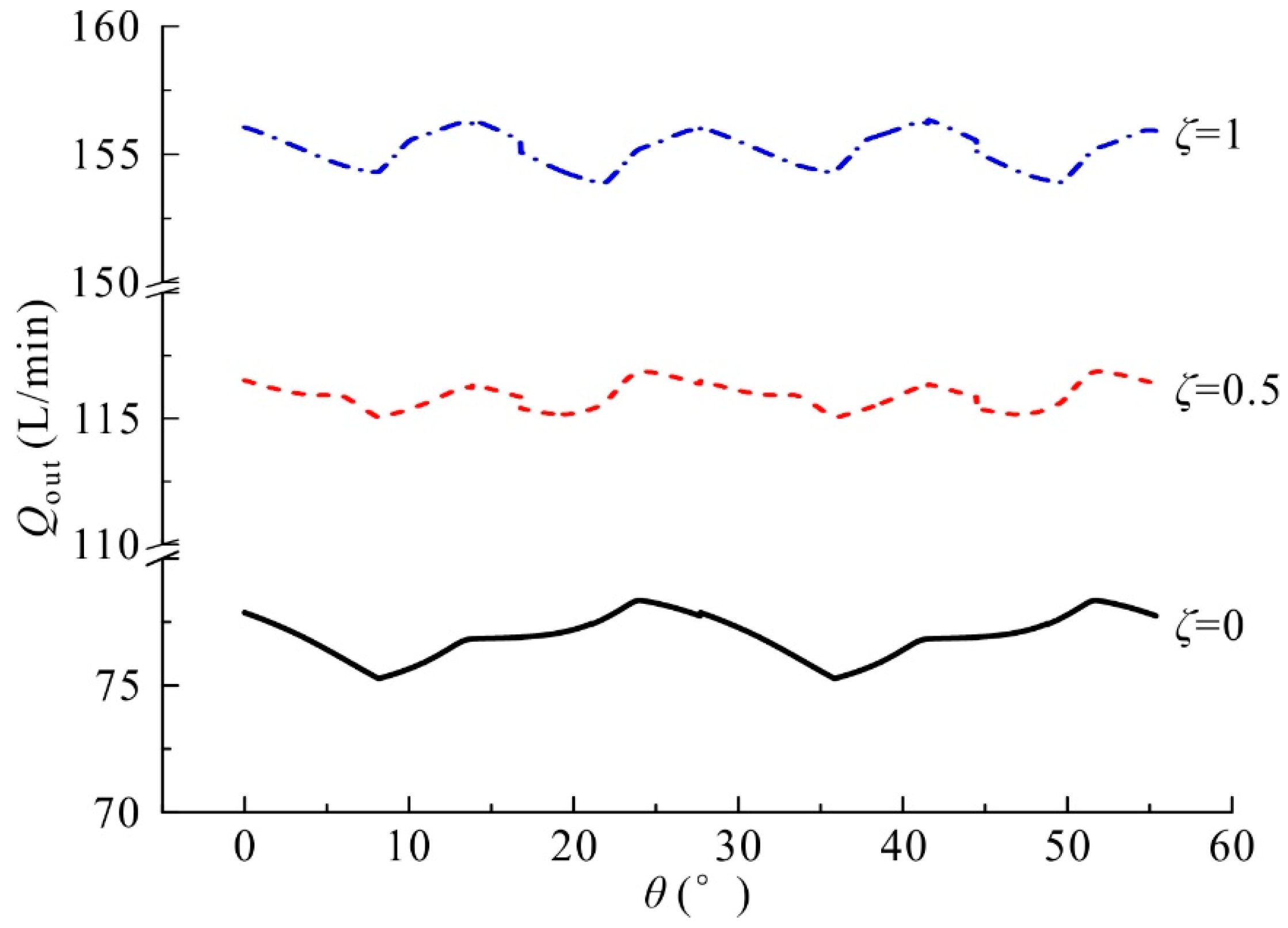
5.2.1. Influence of the Index Angle
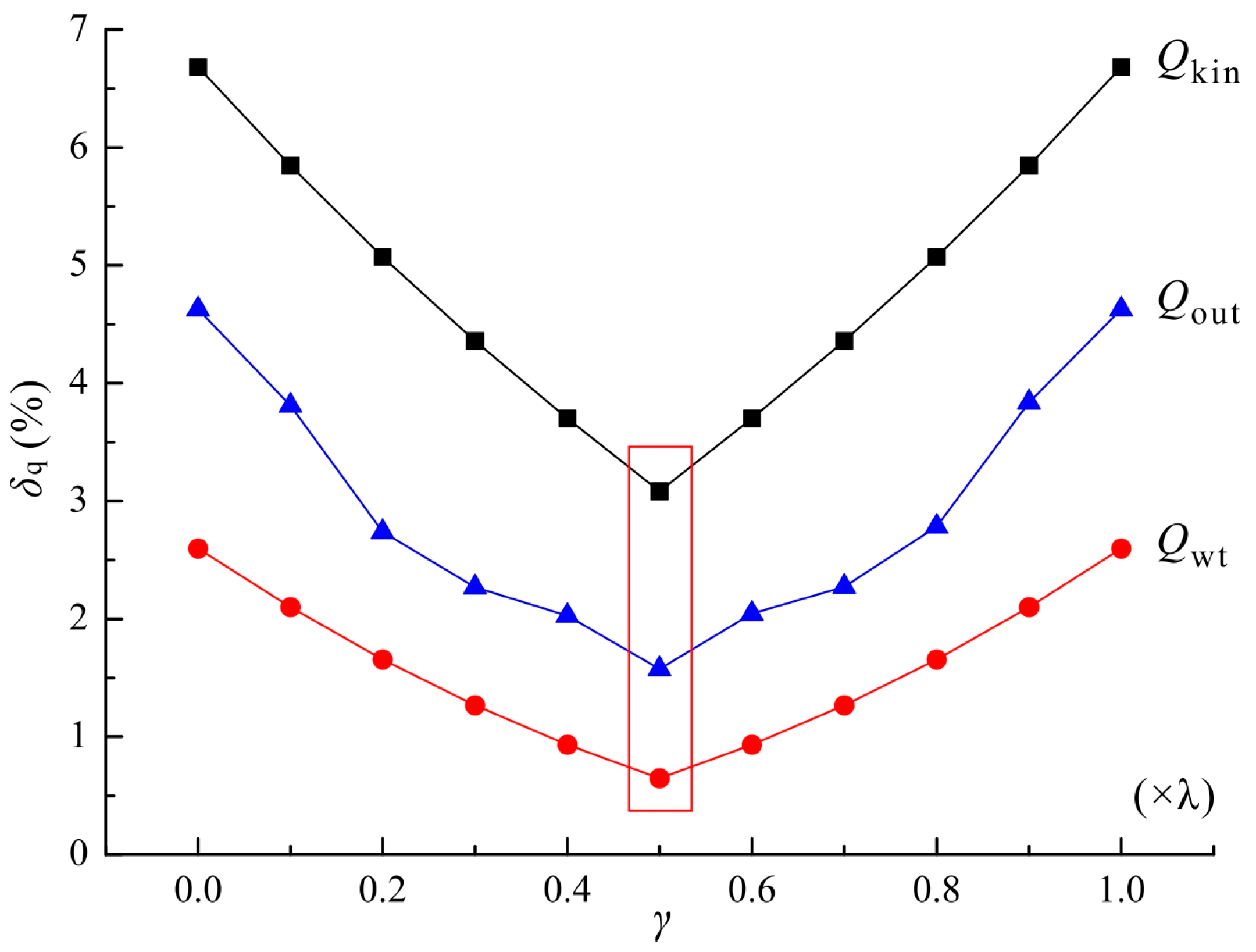
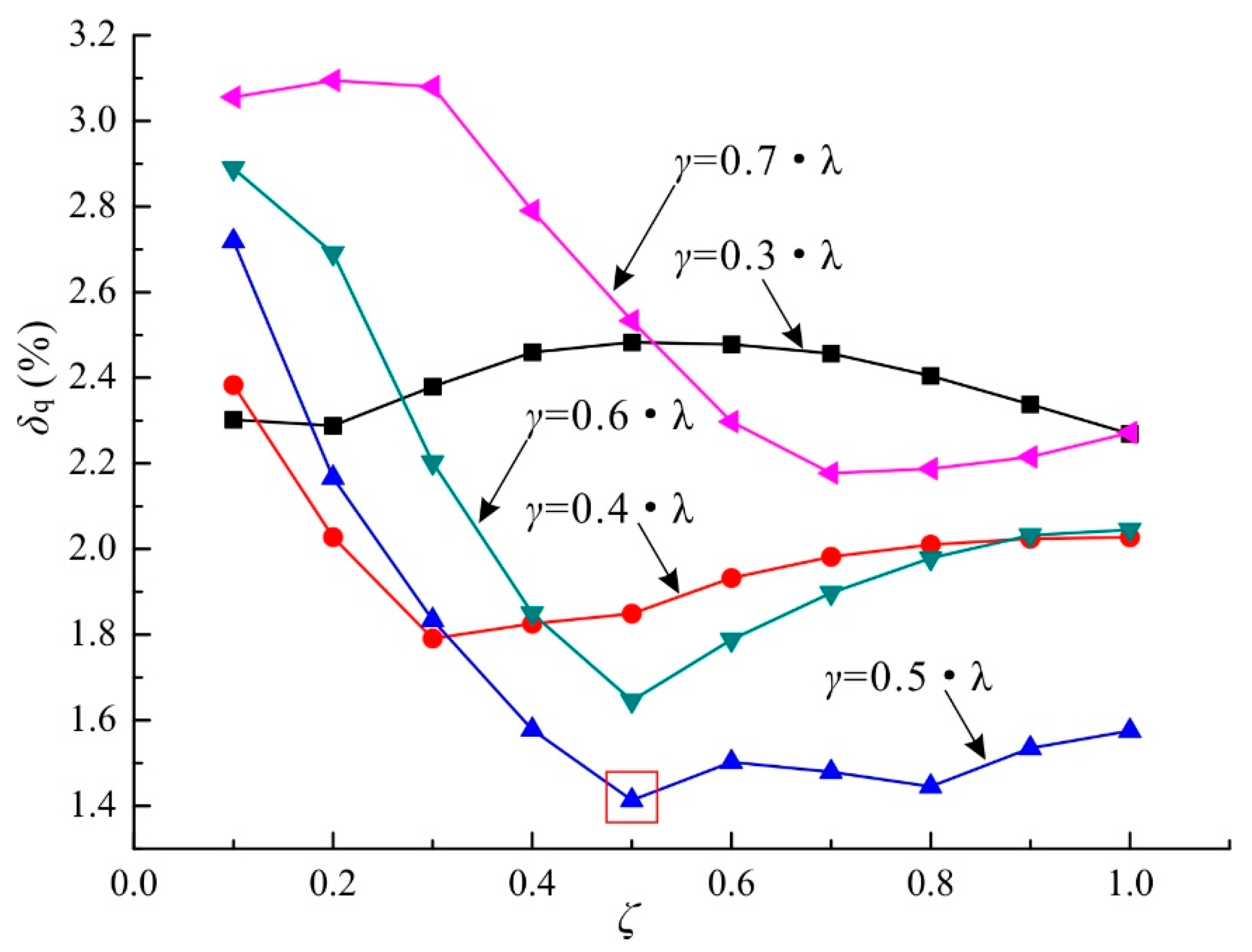
5.2.2. Influence of the Displacement Ratio
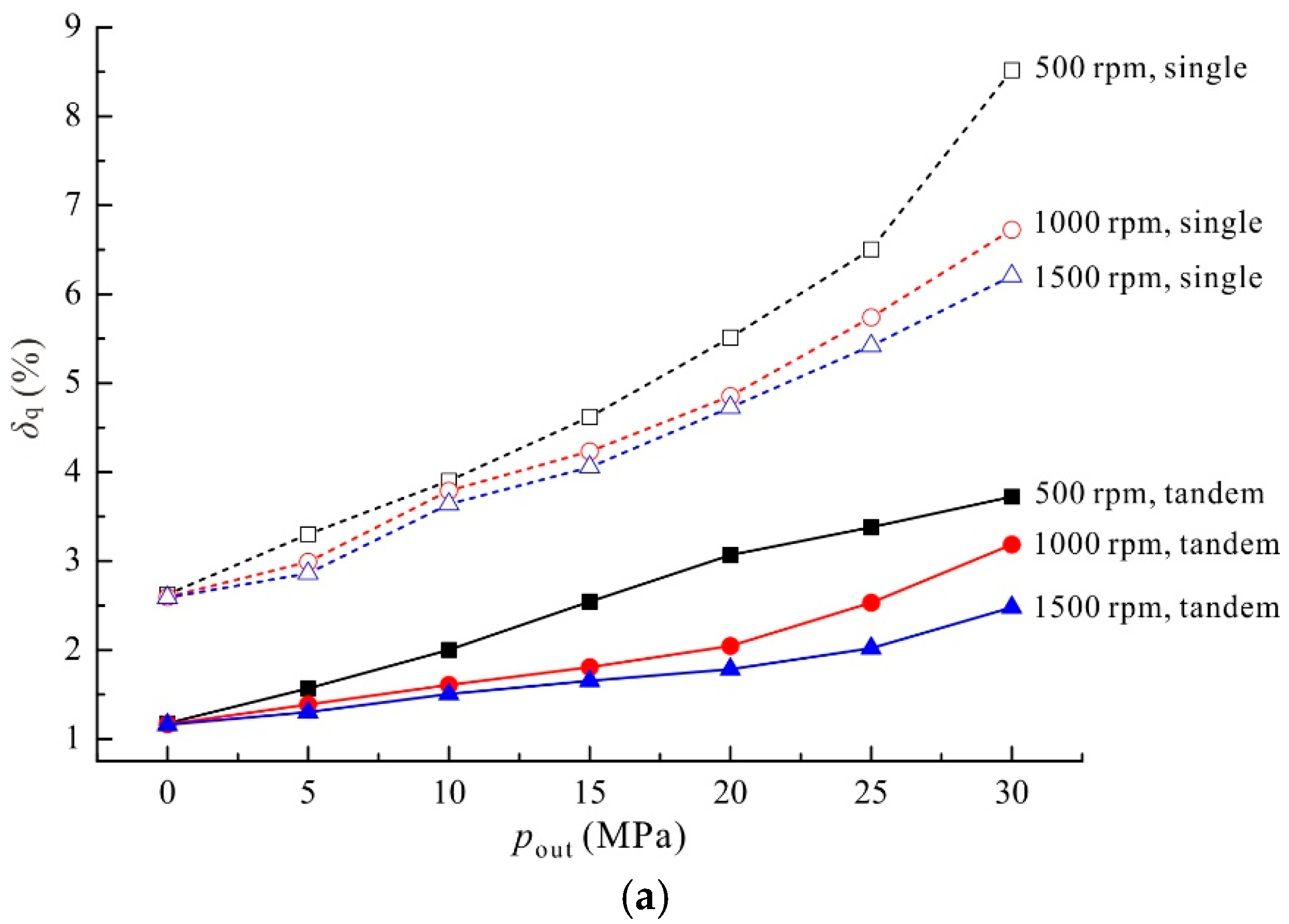
5.3. Influence of Operating Conditions
Acknowledgments
Author Contributions
Conflicts of Interest
Notation
| Aval, rel, tri | flow area of the throttle valve, the relief groove, and the triangular groove (m2) |
| b | width of the gear (m) |
| bB, L1, L2 | parameters of the rectangular sealing area around the outlets (m) |
| Cd | discharge coefficient (-) |
| f | frequency (Hz) |
| l | length of the sealing area in the ring-gear/case interface(m) |
| lr | length of the tooth tip (m) |
| m | module of the gear (m) |
| n | operating speed (rpm) |
| Os,r | centers of the gear shaft and the ring gear (-) |
| p | pressure (Pa) |
| pin, out | inlet or outlet pressure (Pa) |
| ptran | transitional pressure (Pa) |
| ptrap | trapped pressure (Pa) |
| qin, out | flowrate into and out of a chamber (m3/s) |
| ql | lateral leakage of the lateral interface of the gears’ lateral sides and the floating plates (m3/s) |
| qleak | total internal leakage (m3/s) |
| qval, rel, tri | flowrate through the throttle valve, the relief groove and the triangular groove (m3/s) |
| qtri,s; tri,r | triangular flow for the gear shaft and the ring gear (m3/s) |
| qr | radial leakage of the radial interface of the tooth tips and the crescent fillers (m3/s) |
| qrc | leakage of the ring-gear/case interface (m3/s) |
| qtrap | trapped flow, flow out of the trapped chamber through the relief groove (m3/s) |
| Qmax, min | maximum and minimum flowrate (m3/s) |
| Qkin | kinematic outlet flow (m3/s) |
| Qwt | with-trapped flow by adding the kinematic flow and the trapped flow (m3/s) |
| Qout | actual outlet flow by adding the kinematic flow, the trapped flow, the leakage and the triangular flow (m3/s) |
| ra1, a2 | addendum radii of the gear shaft and the ring gear (m) |
| rf1, f2 | distances between the contact point and the centers of the gear shaft and ring gear (m) |
| rfp1, fp2 | radii of the inner and the outer border of the floating plate (m) |
| rp1, p2 | pitch radii of the gear shaft and the ring gear (m) |
| t | time (s) |
| V | volume (m3) |
| Vd | volume of the discharge chamber and the delivery line (m3) |
| Vkin | volume of the discharged fluid when the pump operates for a period of time t from the kinematic aspect (m3) |
| Vtrap | volume of the trapped chamber (m3) |
| VTS | volume of the tooth space (m3) |
| z1, 2 | tooth number of the gear shaft and the ring gear (-) |
| Greek symbols | |
| α0 | pressure angle of the gear (°) |
| α | operating pressure angle of the gear pair (°) |
| β | fluid bulk modulus (Pa) |
| γ | index angle (°) |
| δ | radial clearance between the ring gear and the case (m) |
| δl | lateral clearance between the gears’ lateral sides and the floating plates (m) |
| δq | flow ripple (-) |
| δr | radial clearance between the gears’ tooth tips and the fillers (m) |
| Δt | time interval (s) |
| ζ | displacement ratio (-) |
| η | volumetric efficiency (-) |
| θ | rotation angle of the gear shaft (°) |
| λ | circumferential angle of one tooth in the gear shaft (λ = 360°/z1) |
| μ | fluid viscosity (Pa·s) |
| ρ | fluid density (kg/ m3) |
| φ | angle circumference the sealing area in the ring-gear/case interface (rad) |
| ψ | sector angle of the annular sector for estimation of the lateral leakage (rad) |
| ω, ωr | angular velocity of the gear shaft and the ring gear (rad/s) |
References
- Zhou, H.; Song, W. Optimization of floating plate of water hydraulic internal gear pumps. In Proceedings of the 8th JFPS International Symposium on Fluid Power, Okinawa, Japan, 25–28 October 2011. [Google Scholar]
- Shi, Y.; Wu, T.; Cai, M.; Yixuan, W.; Weiqing, X. Energy conversion characteristics of a hydropneumatic transformer in a sustainable-energy vehicle. Appl. Energy 2016, 171, 77–85. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, Y.; Cai, M.; Zhang, B.; Zhu, J. Study on the aviation oxygen supply system based on a mechanical ventilation model. Chin. J. Aeronaut. 2017. [Google Scholar] [CrossRef]
- Yang, H.; Pan, M. Engineering research in fluid power: A review. J. Zhejiang Univ. Sci. A 2015, 16, 427–442. [Google Scholar] [CrossRef]
- Mimmi, G.; Pennacchi, P. Involute gear pumps versus lobe pumps: A comparison. J. Mech. Des. 1997, 119, 458–465. [Google Scholar] [CrossRef]
- Bonandrini, G.; Mimmi, G.; Rottenbacher, C. Theoretical analysis of internal epitrochoidal and hypotrochoidal machines. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2009, 223, 1469–1480. [Google Scholar] [CrossRef]
- Gamez-Montero, P.J.; Codina, E. Flow characteristics of a trochoidal-gear pump using bond graphs and experimental measurement. Part 1. Proc. Inst. Mech. Eng. I J. Syst. Control Eng. 2007, 221, 331–346. [Google Scholar] [CrossRef]
- Gamez-Montero, P.J.; Codina, E. Flow characteristics of a trochoidal-gear pump using bond graphs and experimental measurement. Part 2. Proc. Inst. Mech. Eng. I J. Syst. Control Eng. 2007, 221, 347–363. [Google Scholar] [CrossRef]
- Gamez-Montero, P.J.; Castilla, R.; del Campo, D.; Ertürk, N.; Raush, G.; Codina, E. Influence of the interteeth clearances on the flow ripple in a gerotor pump for engine lubrication. Proc. Inst. Mech. Eng. D J. Automob. Eng. 2012, 226, 930–942. [Google Scholar] [CrossRef]
- Hsieh, C.-F. Influence of gerotor performance in varied geometrical design parameters. J. Mech. Des. 2009, 131, 121008. [Google Scholar] [CrossRef]
- Hsieh, C.F. Flow characteristics of gerotor pumps with novel variable clearance designs. J. Fluids Eng. 2015, 137, 041107. [Google Scholar] [CrossRef]
- Manco, S.; Nervegna, N.; Rundo, M. A contribution to the design of hydraulic lube pumps. Int. J. Fluid Power 2002, 3, 21–32. [Google Scholar] [CrossRef]
- Schweiger, W.; Schoefmann, W.; Vacca, A. Gerotor pumps for automotive drivetrain applications: A multi domain simulation approach. SAE Int. J. Passeng. Cars-Mech. Syst. 2011, 4, 1358–1376. [Google Scholar] [CrossRef]
- Pellegri, M.; Vacca, A.; Frosina, E.; Buono, D.; Senatore, A. Numerical analysis and experimental validation of gerotor pumps: A comparison between a lumped parameter and a computational fluid dynamics-based approach. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2016. [Google Scholar] [CrossRef]
- Pellegri, M.; Vacca, A. Numerical simulation of gerotor pumps considering rotor micro-motions. Meccanica 2017, 52, 1851–1870. [Google Scholar] [CrossRef]
- Ichikawa, T. Characteristics of internal gear pump. Bull. JSME 1959, 2, 35–39. [Google Scholar] [CrossRef]
- Zhou, H.; Song, W. Theoretical flowrate characteristics of the conjugated involute internal gear pump. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2013, 227, 730–743. [Google Scholar] [CrossRef]
- Song, W.; Chen, Y.; Zhou, H. Investigation of fluid delivery and trapped volume performances of Truninger gear pump by a discretization approach. Adv. Mech. Eng. 2016, 8, 1–15. [Google Scholar] [CrossRef]
- Rundo, M. Theoretical flow rate in crescent pumps. Simul. Model. Pract. Theory 2017, 71, 1–14. [Google Scholar] [CrossRef]
- Rundo, M.; Corvaglia, A. Lumped parameters model of a crescent pump. Energies 2016, 9, 876. [Google Scholar] [CrossRef]
- Manring, N.D.; Mehta, V.S.; Raab, F.J.; Graf, K.J. The shaft torque of a tandem axial-piston pump. J. Dyn. Syst. Meas. Control 2007, 129, 367–371. [Google Scholar] [CrossRef]
- Mehta, V.S. Torque Ripple Attenuation for an Axial Piston Swash Plate Type Hydrostatic Pump: Noise Considerations. Ph.D. Thesis, University of Missouri, Columbia, SC, USA, 2006. [Google Scholar]
- Xu, B.; Ye, S.; Zhang, J. Effects of index angle on flow ripple of a tandem axial piston pump. J. Zhejiang Univ. Sci. A 2015, 16, 404–417. [Google Scholar] [CrossRef]
- Battarra, M.; Mucchi, E.; Dalpiaz, G. A model for the estimation of pressure ripple in tandem gear pumps. In Proceedings of the ASME 2015 International Design Engineering Technical Conference and Computers and Information in Engineering Conference, Boston, MA, USA, 2–5 August 2015. [Google Scholar]
- Xu, B.; Zhang, J.; Yang, H. Simulation research on distribution method of axial piston pump utilizing pressure equalization mechanism. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2013, 227, 459–469. [Google Scholar] [CrossRef]
- Ivantysyn, J.; Ivantysynova, M. Hydrostatic Pumps and Motors, 1st ed.; Academia Books International: New Delhi, India, 2001; ISBN 81-85522-16-2. [Google Scholar]
- Ma, J.; Fang, Y.; Xu, B.; Yang, H. Optimization of cross angle based on the pumping dynamics model. J. Zhejiang Univ. Sci. A 2010, 11, 181–190. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Schmid, S.R.; Jacobson, B.O. Fundamentals of Fluid Film Lubrication, 2nd ed.; Marcel Dekker, Inc.: New York, NY, USA, 2004; ISBN 0-8247-5371-2. [Google Scholar]

| Sensor | Type | Main Feature |
|---|---|---|
| Flowmeter | Kracht®, Germany, VC5F1PV | scale: 1–250 L/min, 0.3% accuracy (from measured value) |
| Pressure sensor | Shuangqiao®, China, CYG1401F | scale: 0–35 MPa, 0.5% FS accuracy, 0.5% nonlinearity, 100 KHz natural frequency |
| Parameter | Notation | Value | Unit |
|---|---|---|---|
| Module of the gear | m | 3 | mm |
| Tooth numbers of the gear shaft and the ring gear | z1, z2 | 13, 19 | -- |
| Pressure angle of the gear | α0 | 22 | ° |
| Operating pressure angle of the gear pair | α | 24.87 | ° |
| Width of the gear | b | 55 | mm |
| Addendum and pitch radii of the gear shaft | ra1, rp1 | 23.43, 19.5 | mm |
| Addendum and pitch radii of the ring gear | ra2, rp2 | 26.95, 28.5 | mm |
| Radii of inner and outer borders of the floating plate | rfp1, rfp2 | 15.5, 38.25 | mm |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Du, R.; Xie, A.; Yang, H. Theoretical Analysis for the Flow Ripple of a Tandem Crescent Pump with Index Angles. Appl. Sci. 2017, 7, 1148. https://doi.org/10.3390/app7111148
Zhou H, Du R, Xie A, Yang H. Theoretical Analysis for the Flow Ripple of a Tandem Crescent Pump with Index Angles. Applied Sciences. 2017; 7(11):1148. https://doi.org/10.3390/app7111148
Chicago/Turabian StyleZhou, Hua, Ruilong Du, Anhuan Xie, and Huayong Yang. 2017. "Theoretical Analysis for the Flow Ripple of a Tandem Crescent Pump with Index Angles" Applied Sciences 7, no. 11: 1148. https://doi.org/10.3390/app7111148
APA StyleZhou, H., Du, R., Xie, A., & Yang, H. (2017). Theoretical Analysis for the Flow Ripple of a Tandem Crescent Pump with Index Angles. Applied Sciences, 7(11), 1148. https://doi.org/10.3390/app7111148