Privacy-Preserving Smart Metering with Authentication in a Smart Grid
Abstract
:1. Introduction
1.1. Related Work
1.2. Contribution
1.3. Organization
2. Smart Grid Architecture
2.1. System Description and Assumptions
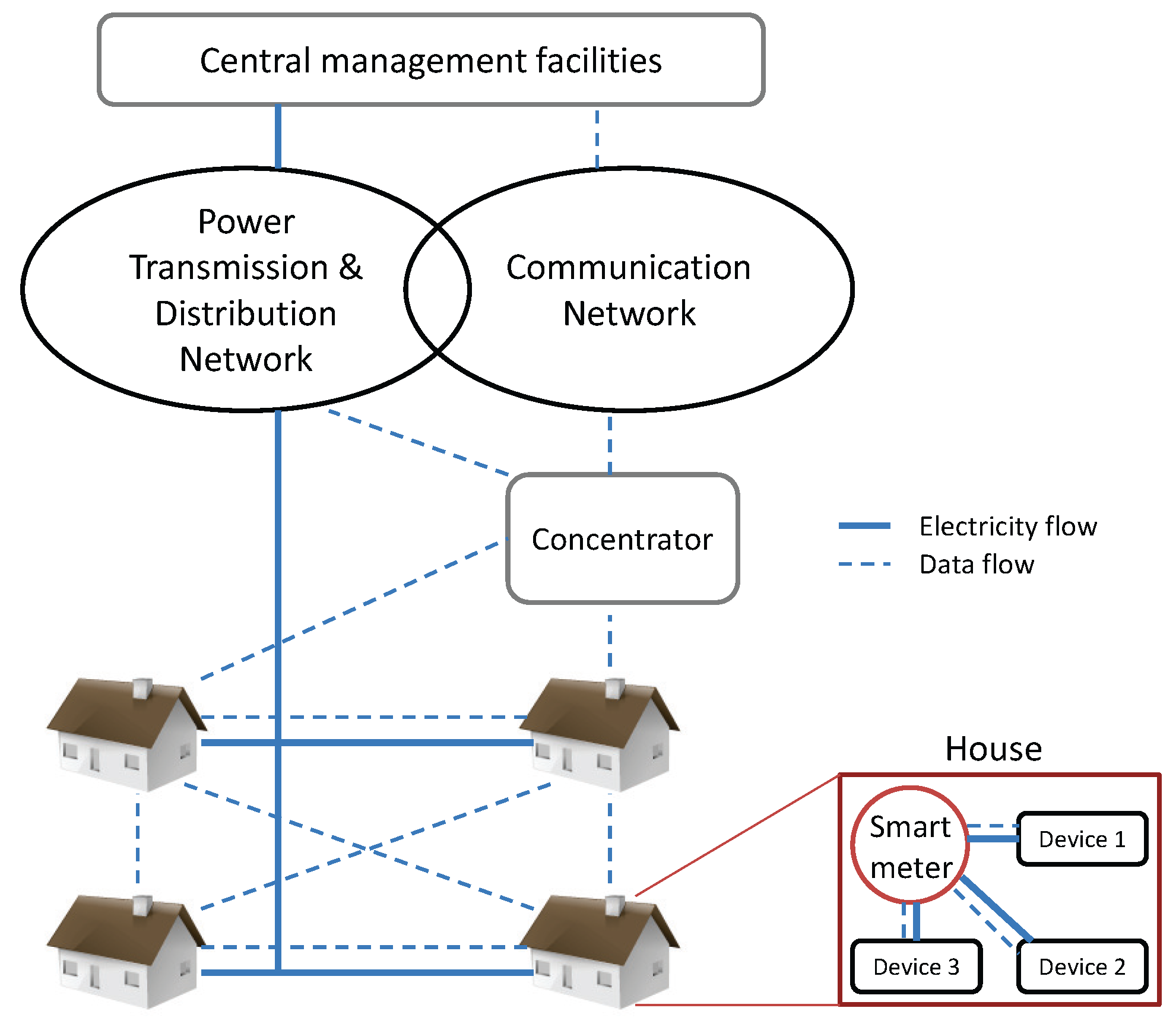

2.2. Threat Model and Security Requirements
- Data confidentiality (user privacy): Individual power usage of a smart meter is considered the private information of the owner. Thus, it should not be revealed to the concentrator or other meters on the routing path during data aggregation and delivery, and passive attacks such as eavesdropping should thus be defended against.
- Data integrity: Dishonest or compromised smart meters in the network could manipulate the intermediate metering data during aggregation, causing inaccurate aggregation results. Thus, manipulation of the aggregate by active inside attack from the compromised meters should be detected by the concentrator.
- Sender authentication: Defending against any active outside attacks, such as false data injection attack by outside adversaries, the concentrator should be able to ensure the authenticity of the smart meters’ identities on the routing path that have contributed to the data aggregation.
3. Preliminaries and Definition
3.1. Cryptographic Background
3.1.1. Notations
3.1.2. Bilinear Pairings
- Bilinearity: For all , , and , .
- Non-degeneracy: .
- Computability: There is an efficient algorithm to compute for any and .
3.1.3. Computational Diffie-Hellman Problem
3.1.4. Identity-based Sequential Aggregate Signature (IBSAS) Problem
3.2. Cryptographic Protocol
3.2.1. Homomorphic Encryption
3.2.2. Aggregate Signatures
4. Privacy-Preserving Smart Metering with Authentication Capability
4.1. Primitive Functions
4.1.1. Symmetric Homomorphic Encryption
- Encryption. Given integer message m and randomly generated key stream k, for where M is a large integer, the algorithm computes (mod M).
- Decryption. Given ciphertext c and key k, the algorithm computes (mod M).
4.1.2. Identity-Based Sequential Aggregate Signature
- Setup. The trusted key generation center (KGC) initially runs the algorithm to generate the master public key and master secret key .
- Key Derivation. The KGC runs the on the input of and user identity , and outputs the private key for the user’s .
- Sign. A signer with runs the algorithm on the input of , message , aggregate-so-far σ, and list of identity-message pairs , and returns new aggregate signature ; or ⊥ if any of the inputs are invalid.
- Verification. The verifier runs the algorithm on the input of , list of identity-message pairs , and aggregate signature σ, and returns 1 or 0.
4.2. Scheme Construction
4.2.1. System Setup
Key Setup
Aggregation Path Setup
4.2.2. Data Encryption
Path Key Establishment
- randomly selects , where M is a large integer. Then, it securely sends to the concentrator via a direct secure connection, and securely sends to the next smart meter .
- For , randomly selects , computes , and forwards it to securely. (For simplicity, we assume that denotes the concentrator.)
- When the concentrator receives from , it computes and stores as a path key for the aggregation path.
Data Encryption
4.2.3. Signing
- ,
- ,
- ,
- .
4.2.4. Verification
4.2.5. Data Decryption
- ,
- .
4.3. Discussion
5. Efficiency
5.1. Security Property
| Scheme | Confidentiality | Data | Sender |
|---|---|---|---|
| (User Privacy) | Integrity | Authentication | |
| GJ [3] | yes | no | no |
| LLL [5,6] | yes | no | no |
| LLYLLS [21] | yes | yes | yes |
| Proposed | yes | yes | yes |
5.2. Theoretical Analysis
| bit size of an element in | |
| bit size of an element in | |
| bit size of an element in (n = p · q where q is a large prime) | |
| bit size of an element in | |
| bit size of an identity string | |
| bit size of a timestamp | |
| bit size of a message (=symmetric key size) | |
| N | the number of smart meters participating in the aggregation |
| System | Communication | Message | Signature | Private Key | Public Key |
|---|---|---|---|---|---|
| GJ [3] | - | ||||
| LLL [5,6] | N | - | - | ||
| LLYLLS [21] | |||||
| Proposed |
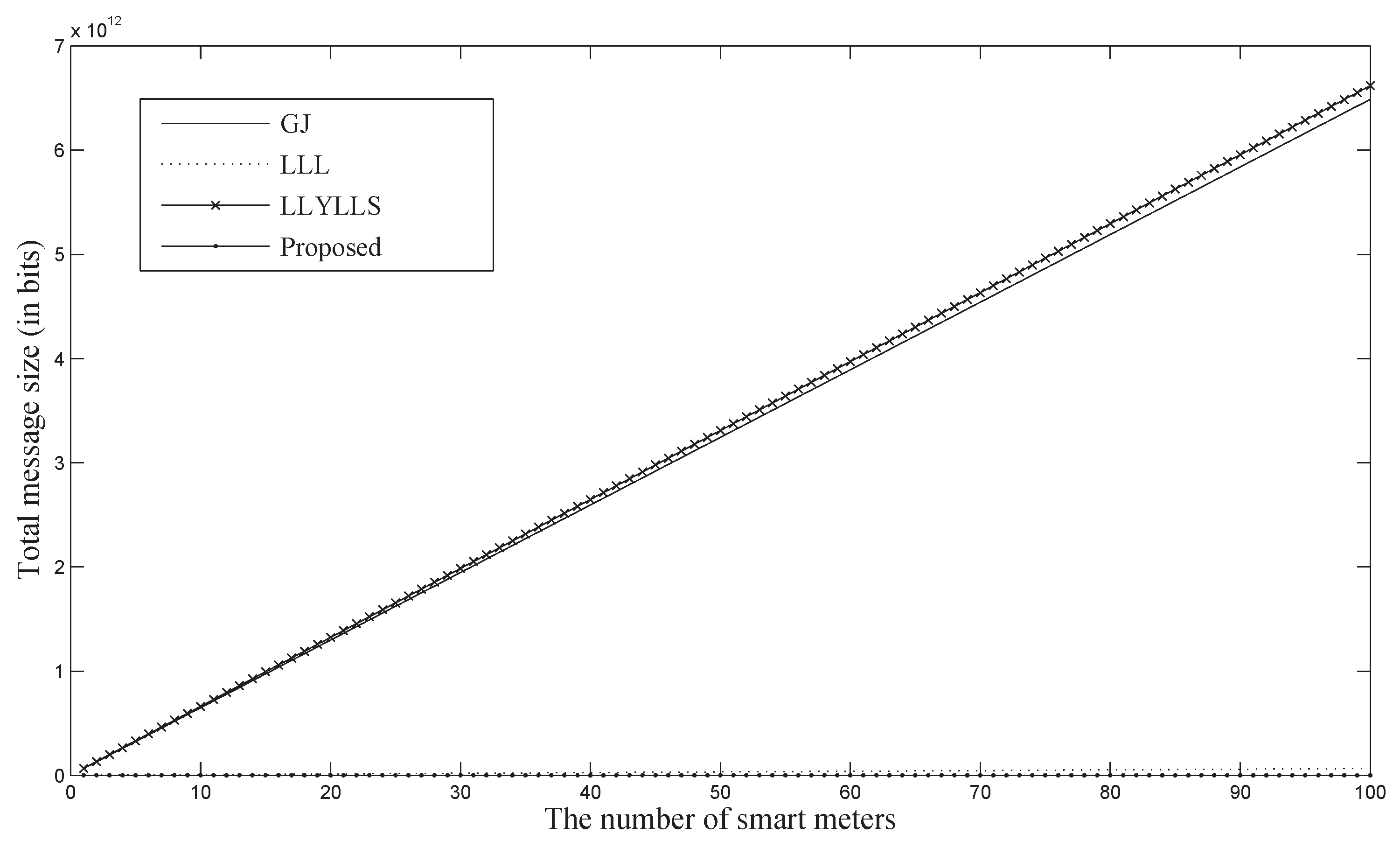
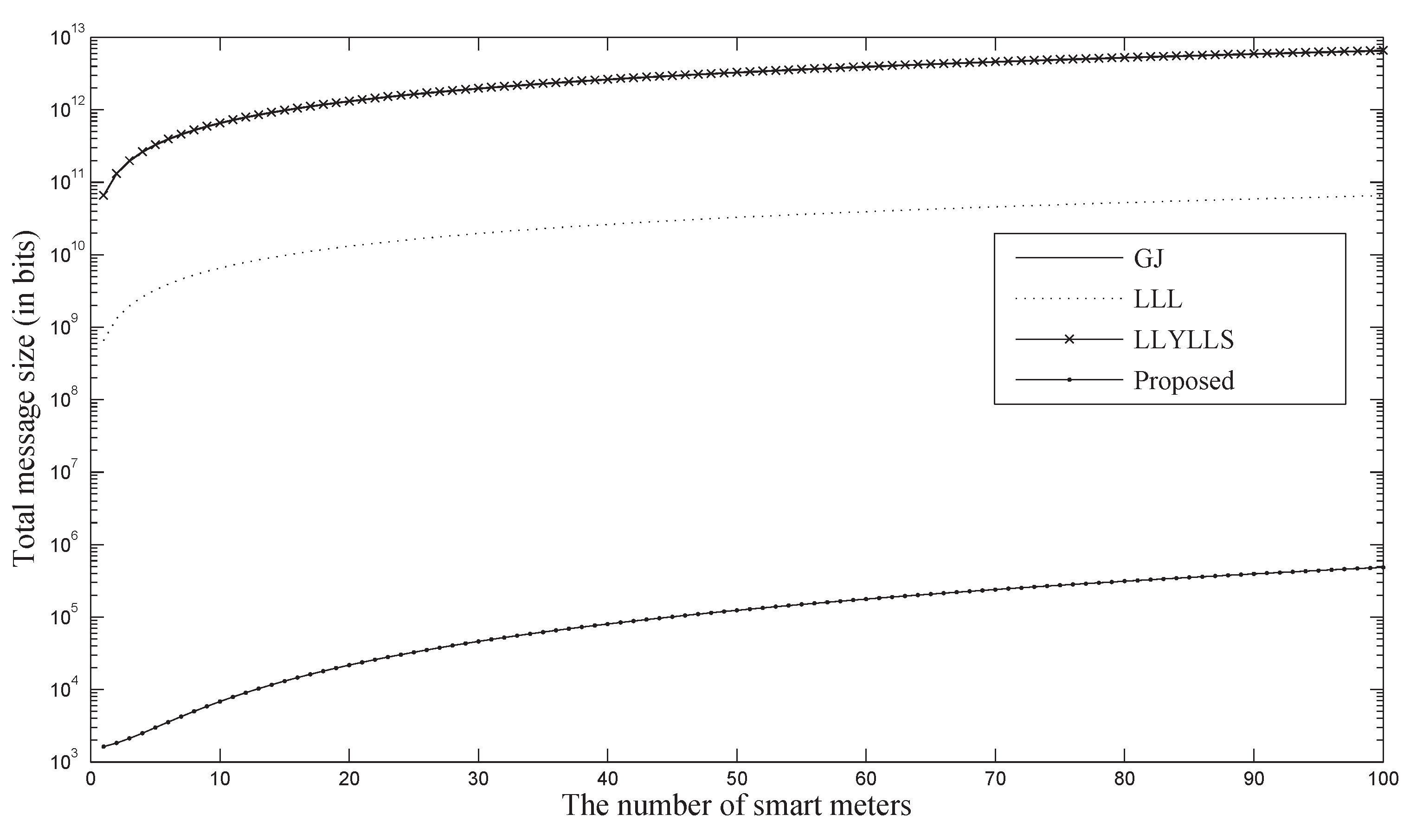
5.3. Implementation
| Operation | Time (ms) | Smart Meter | Concentrator |
|---|---|---|---|
| Pairing | 2.9 | - | 4 |
| Exp. in | 1.0 | 5 | - |
| Exp. in | 0.2 | - | N |
| Computation (ms) | |||
6. Security
6.1. Data Confidentiality (User Privacy)
6.2. Data Integrity and Sender Authentication
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Metke, A.R.; Ekl, R.L. Security Technology for Smart Grid Networks. IEEE Trans. Smart Grid 2010, 1, 99–107. [Google Scholar] [CrossRef]
- Khurana, H.; Hadley, M.; Lu, N.; Frincke, D.A. Smarg-Grid Security Issues. IEEE Secur. Priv. 2010, 8, 81–85. [Google Scholar] [CrossRef]
- Garcia, F.D.; Jacobs, B. Privacy-friendly Energy-Metering via Homomorphic Encryption. In Proceedings of the International Workshop on Security and Trust Management, Athens, Greece, 23–24 September 2010; pp. 226–238.
- Efthymiou, C.; Kalogridis, G. Smart Grid Privacy via Anonymization of Smart Metering Data. In Proceedings of the IEEE International Conference on Smart Grid Communications, Gaithersburg, MD, USA, 4–6 October 2010; pp. 4–6.
- Li, F.; Luo, B.; Liu, P. Secure Information Aggregation for Smart Grids Using Homomorphic Encryption. In Proceedings of the IEEE International Conference on Smart Grid Communications, Gaithersburg, MD, USA, 4–6 October 2010; pp. 327–332.
- Li, F.; Luo, B.; Liu, P. Secure and Privacy-Preserving Information Aggregation for Smart Grids. Int. J. Secur. Netw. 2011, 6, 28–39. [Google Scholar] [CrossRef]
- Rial, A.; Danezis, G. Privacy-Preserving Smart Metering. In Proceedings of the ACM Workshop on Privacy and the Electronic Society, Chicago, IL, USA, 17 October 2011; pp. 49–60.
- Bohli, J.M.; Sorge, C.; Ugus, O. A Privacy Model for Smart Metering. In Proceedings of the IEEE International Conference on Communications Workshops, Capetown, South Africa, 23–27 May 2010; pp. 1–5.
- Paillier, P. Public-Key Cryptosystem Based on Composite Degree Residuosity Classes. In Advances in Cryptology—EUROCRYPT’99; Springer Berlin Heidelberg: Heidelberg, Germany, 1999; Volume 1592, pp. 223–238. [Google Scholar]
- Boneh, D.; Goh, E.; Nissim, K. Evaluating 2-DNF Formulas on Ciphertexts. In Theory of Cryptography; Springer Berlin Heidelberg: Heidelberg, Gemany, 2005; pp. 325–341. [Google Scholar]
- Paillier, P.; Pointcheval, D. Efficient Public-Key Cryptosystems Provably Secure Against Active Adversaries. In Advances in Cryptology-ASIACRYPT’99; Springer Berlin Heidelberg: Heidelberg, Gemany, 1999; pp. 165–179. [Google Scholar]
- McDaniel, P.; McLaughlin, S. Security and Privacy Challenges in the Smart Grid. IEEE Secur. Priv. 2009, 7, 75–77. [Google Scholar] [CrossRef]
- Lee, A.; Brewer, T. The Cyber Security Coordination Task Group, Smart Grid Cyber Security Strategy and Requirements. NIST Tech. Rep. Draft NISTIR 7628. 2009. Available online: http://www.smartgridinformation.info/pdf/1200_doc_1.pdf (accessed on 10 October 2015).
- Seo, D.; Lee, H.; Perrig, A. Secure and Efficient Capability-based Power Management in the Smart Grid. In Proceedings of the IEEE International Symposium on Parallel and Distributed Processing with Applications Workshops, Busan, Korea, 26–28 May 2011; pp. 119–126.
- Garofalakis, M.; Hellerstein, J.M.; Maniatis, P. Proof Sketches: Verifiable In-Network Aggregation. In Proceedings of the International Conference on Data Engineering, Istanbul, Turkey, 15–20 April 2007; pp. 996–1005.
- Castelluccia, C.; Chan, A.C.-F.; Mykletun, E.; Tsudik, G. Efficient and Provably Secure Aggregation of Encrypted Data in Wireless Sensor Networks. ACM Trans. Sens. Netw. 2009, 5, 1–36. [Google Scholar] [CrossRef]
- Boneh, D.; Freeman, D.M. Homomorphic Signatures for Polynomial Functions. In Advances in Cryptology—EUROCRYPT 2011; Springer Berlin Heidelberg: Heidelberg, Gemany, 2011. [Google Scholar]
- Marmol, F.; Sorge, C.; Ugus, O.; Perez, G. Do Not Snoop My Habits: Preserving Privacy in the Smart Grid. IEEE Commun. Mag. 2012, 50, 166–172. [Google Scholar] [CrossRef]
- Cho, S.; Li, H.; Choi, B. PALDA: Efficient Privacy-Preserving Authentication for Lossless Data Aggregation in Smarg Grids. In Proceedings of the IEEE International Conference on Smart Grid Communications, Venice, Italy, 3–6 November 2014; pp. 914–919.
- Alharbi, K.; Lin, X.; Shao, J. A Framework for Privacy-preserving Data Sharing in the Smart Grid. In Proceedings of the IEEE/CIC International Conference on Communications in China, Shanghai, China, 13–15 October 2014; pp. 214–219.
- Li, H.; Lin, X.; Yang, H.; Liang, X.; Lu, R.; Shen, X. EPPDR: An Efficient Privacy-Preserving Demand Response Scheme with Adaptive Key Evolution in Smart Grid. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 2053–2064. [Google Scholar] [CrossRef]
- Borges, F.; Demirel, D.; Bock, L.; Buchmann, J.; Muhlhauser, M. A Privacy-Enhancing Protocol that Provides In-Network Data Aggregation and Verifiable Smart Meter Billing. In Proceedings of the IEEE Symposium on Computers and Communication, Funchal, Portugal, 23–26 June 2014; pp. 1–6.
- Deng, P.; Yang, L. A Secure and Privacy-preserving communication scheme for Advanced Metering Infrastructure. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Washington, DC, USA, 16–20 January 2012; pp. 1–5.
- He, X.; Pun, M.; Kuo, C. Secure and Efficient Cryptosystem for Smart Grid Using Homomorphic Encryption. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, 16–20 January 2012; pp. 1–8.
- Li, F.; Luo, B. Preserving Data Integrity for Smart Grid Data Aggregation. In Proceedings of the IEEE Third International Conference on SmartGridComm, Tainan, Taiwan, 5–8 November 2012; pp. 366–371.
- Rottondi, C.; Savi, M.; Verticale, G.; Kraub, C. Mitigation of Peer-to-Peer Overlay Attacks in the Automatic Metering Infrastructure of Smart Grids. Secur. Commun. Netw. 2015, 8, 343–359. [Google Scholar] [CrossRef]
- Boneh, D.; Franklin, M.K. Identity-Based Encryption from the Weil Pairing. In Advances in Cryptology—CRYPTO 2001; Springer Berlin Heidelberg: Heidelberg, Gemany, 2001; Volume 2139, pp. 213–229. [Google Scholar]
- Galbraith, S.D.; Harrison, K.; Soldera, D. Implementing the Tate Pairing. In Algorithmic Number Theory; Springer Berlin Heidelberg: Heidelberg, Gemany, 2002; Volume 2369, pp. 324–337. [Google Scholar]
- Boldyreva, A.; Gentry, C.; O’Neill, A.; Yum, D. Ordered Multisignatures and Identity-Based Sequential Aggregate Signatures, with Applications to Secure Routing. A Corrected Version of the Paper [35] 2007. Available online: http://www.cc.gatech.edu/~aboldyre/papers/bgoy.pdf (accessed on 11 October 2013).
- Gamal, T.E. A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms. In Advances in Cryptology; Springer Berlin Heidelberg: Heidelberg, Gemany, 1985; pp. 10–18. [Google Scholar]
- Naccache, D.; Stern, J. A New Public Key Cryptosystem Based on Higher Residues. In Proceedings of the ACM Conference on Computer and Communications Security, San Francisco, CA, USA, 2–5 November, 1998; pp. 59–66.
- Boneh, D.; Gentry, C.; Lynn, B.; Shacham, H. Aggregate and Verifiably Encrypted Signatures from Bilinear Maps. In Advances in Cryptology—EUROCRYPT 2003; Springer Berlin Heidelberg: Heidelberg, Gemany, 2003. [Google Scholar]
- Lysyanskaya, A.; Micali, S.; Reyzin, L.; Shacham, H. Sequential Aggregate Signatures from Trapdoor Permutations. In Advances in Cryptology—EUROCRYPT 2004; Springer Berlin Heidelberg: Heidelberg, Gemany, 2004. [Google Scholar]
- Lu, S.; Ostrovsky, R.; Sahai, A.; Shacham, H.; Waters, B. Sequential Aggregate Signatures and Multisignatures without Random Oracles. In Eurocrypt, St. Petersburg, Russia, May 28–June 1, 2006; 2006; pp. 465–485. [Google Scholar]
- Boldyreva, A.; Gentry, C.; O’Neill, A.; Yum, D. Ordered Multisignatures and Identity-Based Sequential Aggregate Signatures, with Applications to Secure Routing. In Proceedings of the ACM Conference on Computer and Communications Security, Alexandria, VA, USA, October 29 – November 2 2007; pp. 276–285.
- Hwang, J.Y.; Lee, D.H.; Yung, M. Universal Forgery of the Identity-Based Sequential Aggregate Signature Scheme. In Proceedings of ACM Symposium on Information, Computer and Communications Security, Sydney, Australia, 10–12 March 2009; pp. 157–160.
- Castelluccia, C.; Mykletun, E.; Tsudik, G. Efficient Aggregation of Encrypted Data in Wireless Sensor Networks. In Proceedings of the The Second Annual International Conference on ACM/IEEE Mobile and Ubiquitous Systems: Networking and Services (Mobiquitous’05), San Diego, CA, USA, 17–21 July 2005; pp. 109–117.
- Fontaine, C.; Galand, F. A Survey of Homomorphic Encryption for Nonspecialists. J. Inf. Secur. 2009, 1, 41–50. [Google Scholar]
- The Pairing-Based Cryptography Library. Available online: http://crypto.stanford.edu/pbc/ (accessed on 23 October 2014).
- Shannon, C. Communication Theory of Secrecy Systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hur, J.B.; Koo, D.Y.; Shin, Y.J. Privacy-Preserving Smart Metering with Authentication in a Smart Grid. Appl. Sci. 2015, 5, 1503-1527. https://doi.org/10.3390/app5041503
Hur JB, Koo DY, Shin YJ. Privacy-Preserving Smart Metering with Authentication in a Smart Grid. Applied Sciences. 2015; 5(4):1503-1527. https://doi.org/10.3390/app5041503
Chicago/Turabian StyleHur, Jun Beom, Dong Young Koo, and Young Joo Shin. 2015. "Privacy-Preserving Smart Metering with Authentication in a Smart Grid" Applied Sciences 5, no. 4: 1503-1527. https://doi.org/10.3390/app5041503
APA StyleHur, J. B., Koo, D. Y., & Shin, Y. J. (2015). Privacy-Preserving Smart Metering with Authentication in a Smart Grid. Applied Sciences, 5(4), 1503-1527. https://doi.org/10.3390/app5041503







