An Efficient Power Scheduling Scheme for Residential Load Management in Smart Homes
Abstract
:1. Introduction
- We build a model by classifying electrical appliances into three groups based on power usage and user comfort requirements. This model incorporates the three proposed classes of appliances based on hourly electricity prices (TOU) during on-peak and off-peak hours in conjunction with user preferences.
- On the proposed model, we devise a binary version of WDO algorithm for minimum electricity cost and maximum user comfort. Moreover, a knapsack-based WDO (K-WDO) algorithm is also designed for maximum electricity cost saving that can be used as a benchmark for the performance evaluation of energy consumption in home area networks. The min-max regret-based knapsack optimization technique is used to minimize the maximum energy consumption.
- The said optimization techniques are mapped for scheduling electrical appliances. Moreover, we incorporate a renewable energy resource during critical hours for grid stability, electricity cost reduction and user comfort (we assume that fixed electric power is stored via a renewable energy resource that can be utilized in peak or crucial hours).
- Finally, we validate our proposed schemes and analytic framework via extensive simulations and comparisons of unscheduled and scheduled cases.
2. Related Work
3. Home Energy Management Architecture
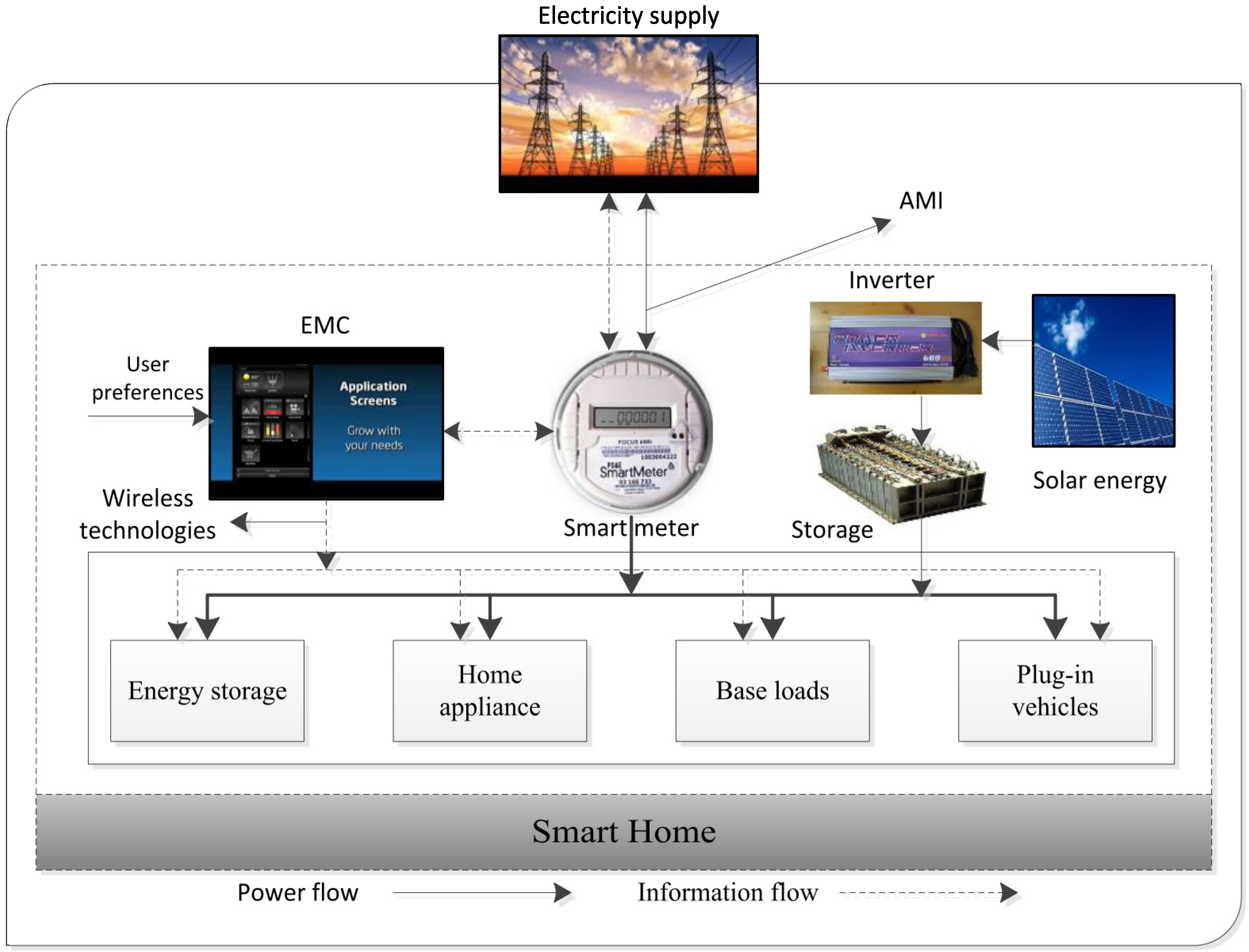
4. Price-Based DR
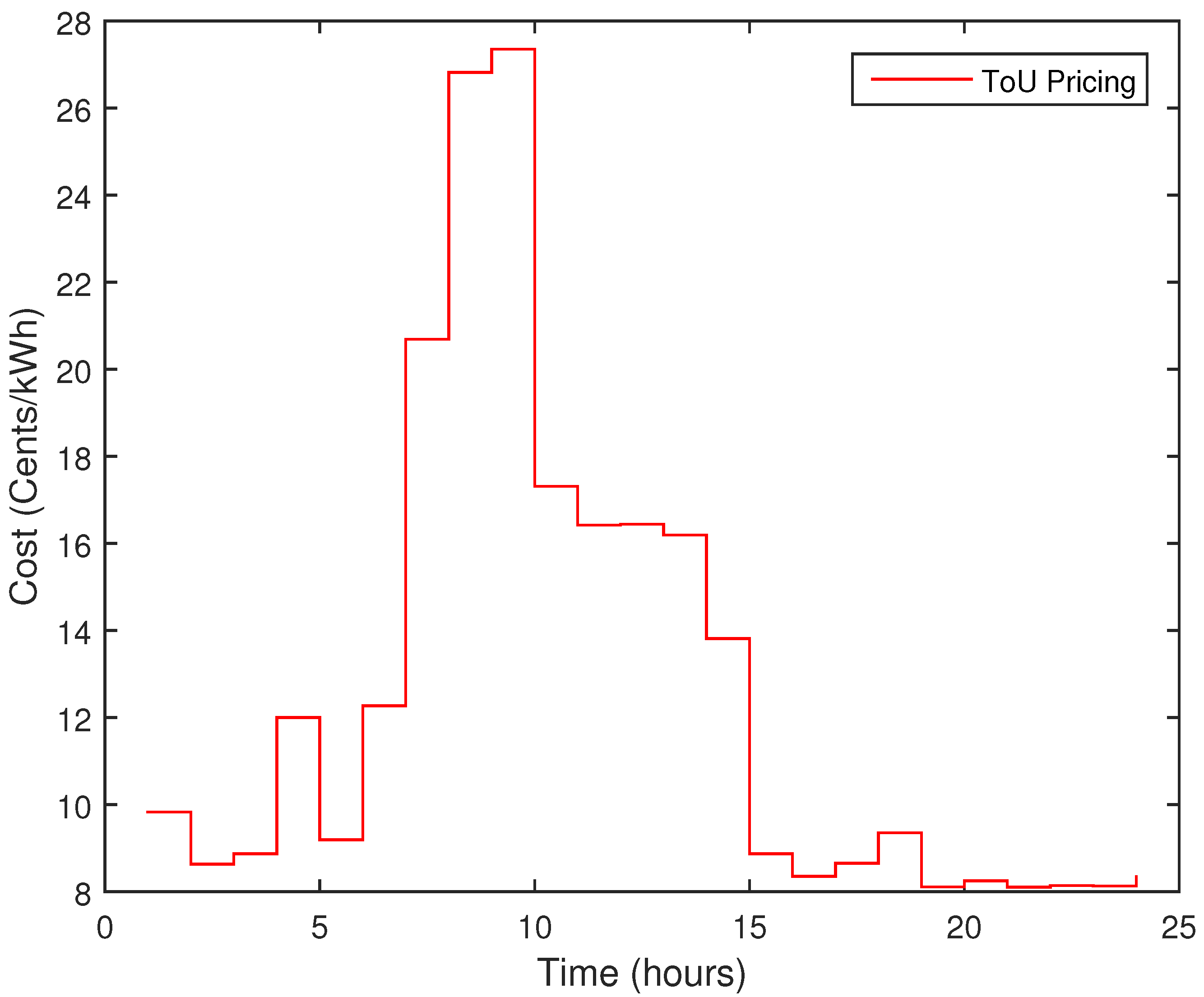
4.1. TOU and DAP
4.2. RTP
4.3. CPP
5. Home Appliance Energy Usage Pattern
5.1. Appliance Waiting Time
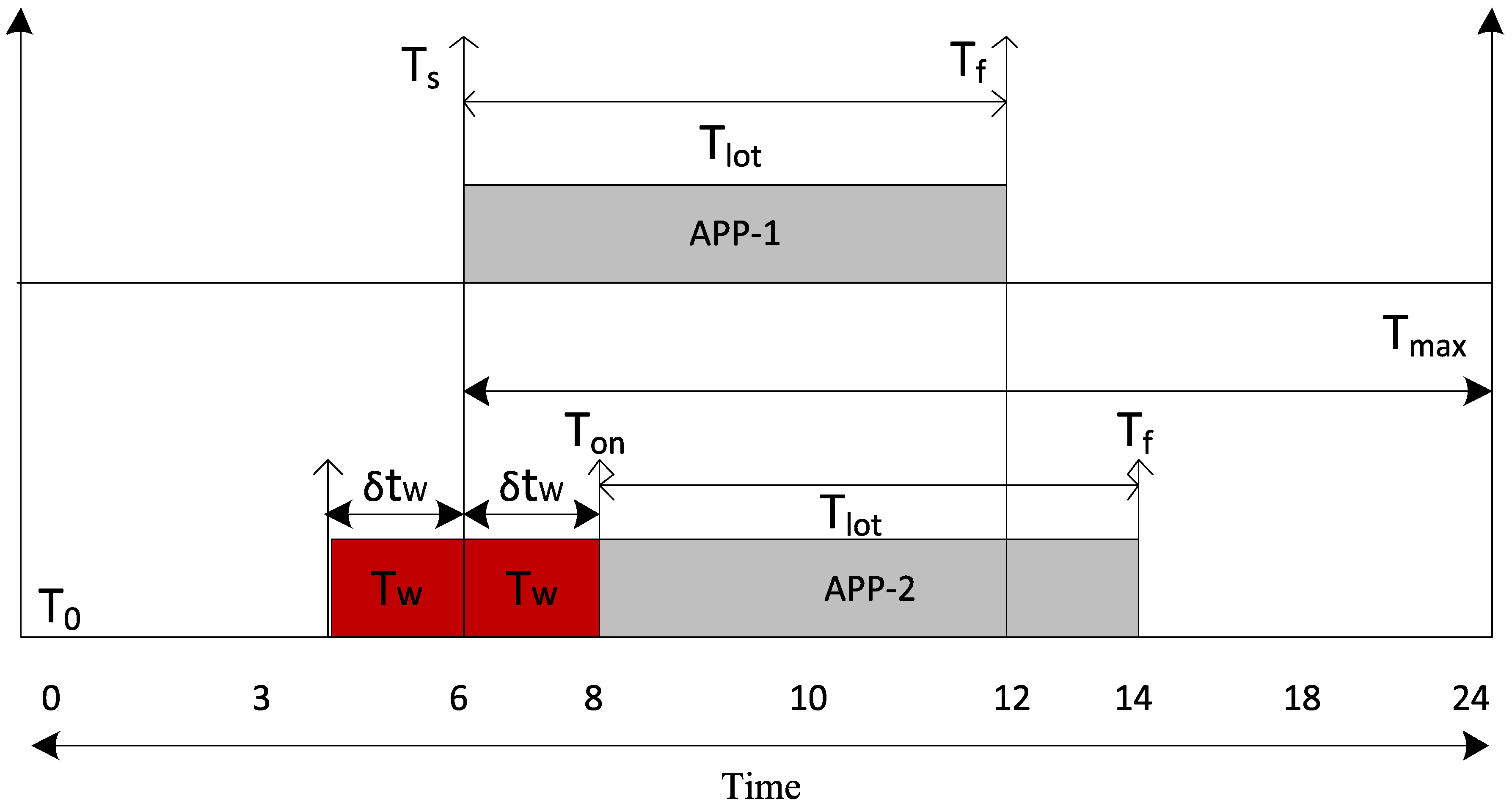
6. System Model
7. Types of Appliances
| Sr. No. | Appliance | Power Rating (kWh) | /(Hours) |
|---|---|---|---|
| 1 | Stove | 3.0 | 9 |
| 2 | Tumble Dryer | 3.3 | 15 |
| 3 | Clothes Dryer | 3.4 | 8 |
| 4 | Washing Machine | 3.0 | 3 |
| 5 | Oven | 3.0 | 13 |
| 6 | Air-conditioner | 5.0 | 7 |
7.1. Class 1
7.2. Class 2
7.3. Class 3
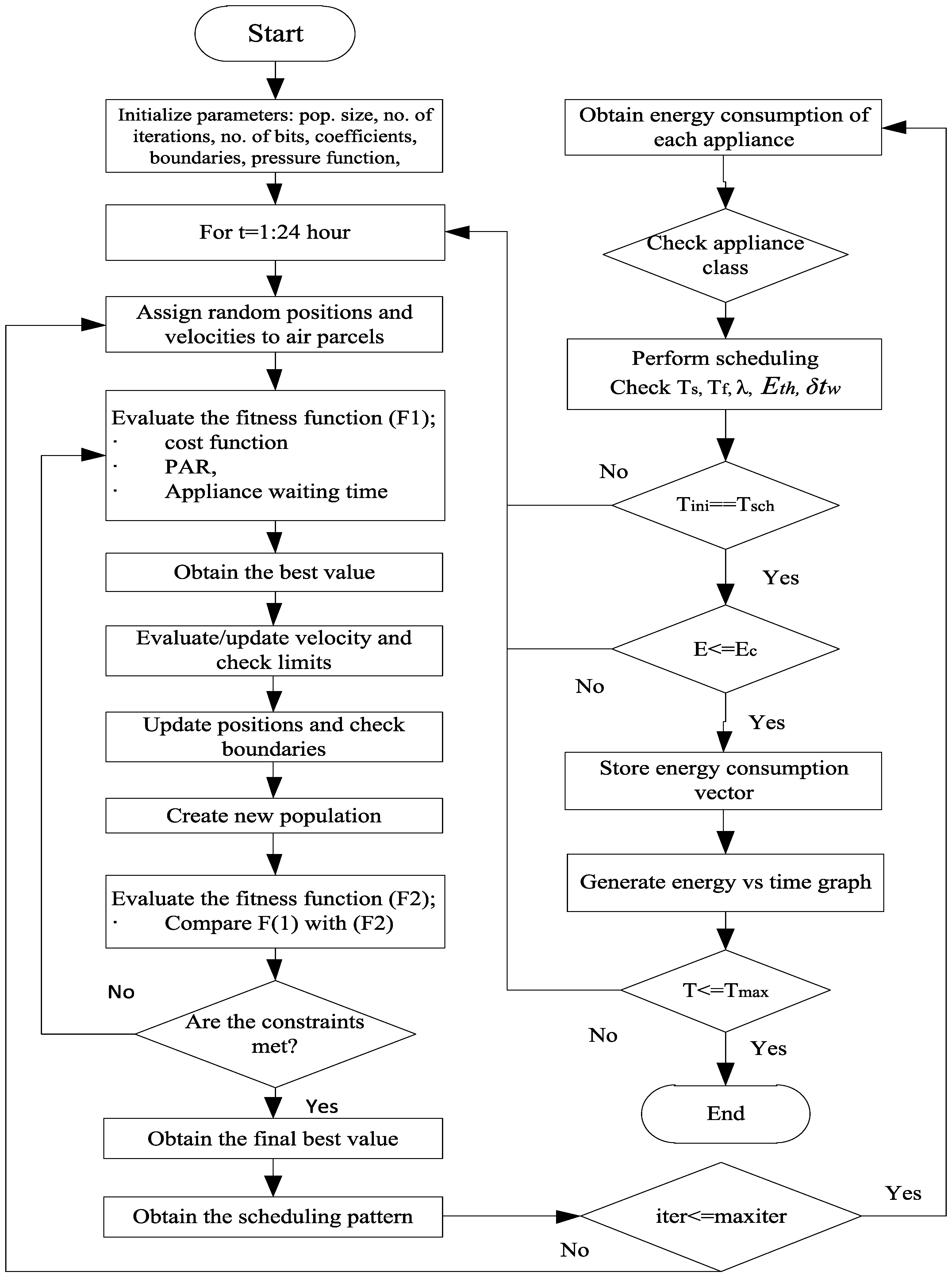
8. Load Optimization and Scheduling
8.1. Scheduling Algorithm
- The first term shows that the air particles continue their movements to the previous path with some opposition of frictional force.
- The second term is gravitational force, which attracts the air particles to the centre (in the coordinate system).
- The third term describes the force exerted on air particles to move them towards the highest pressure location, which is the global best position in the WDO optimization problem.
- The fourth term shows the Coriolis force, which is a deflecting force, because the movement of air particles in one direction is affected by the movement in the second direction. Similarly, in PSO, weights and are used to control the movement of air particles in order to find the global best position.
| Symbol | Description | Symbol | Description |
|---|---|---|---|
| new velocity | v | velocity vector of air particles | |
| current velocity | Coriolis force | ||
| current position | Ω | Earth rotation | |
| optimal position | ρ | density of air particles | |
| pressure at current location | vertical force on air particles | ||
| optimal pressure | sigmoid function | ||
| Coriolis force | local best position | ||
| α | constant in update position | volume of air | |
| R | universal gas constant | sphere function | |
| v | velocity of air particles | ω | inertia factor |
| gravitational force of the Earth | n | total No. of air particles (Equation (23)) | |
| g | gravitational acceleration | T | temperature |
| unit step time | velocity of the i-th particle in n-dimensions | ||
| weights for local and global positions | local best position |
| Algorithm | Evaluation Function | No. of Iterations | Global Pressure/ | Converge |
|---|---|---|---|---|
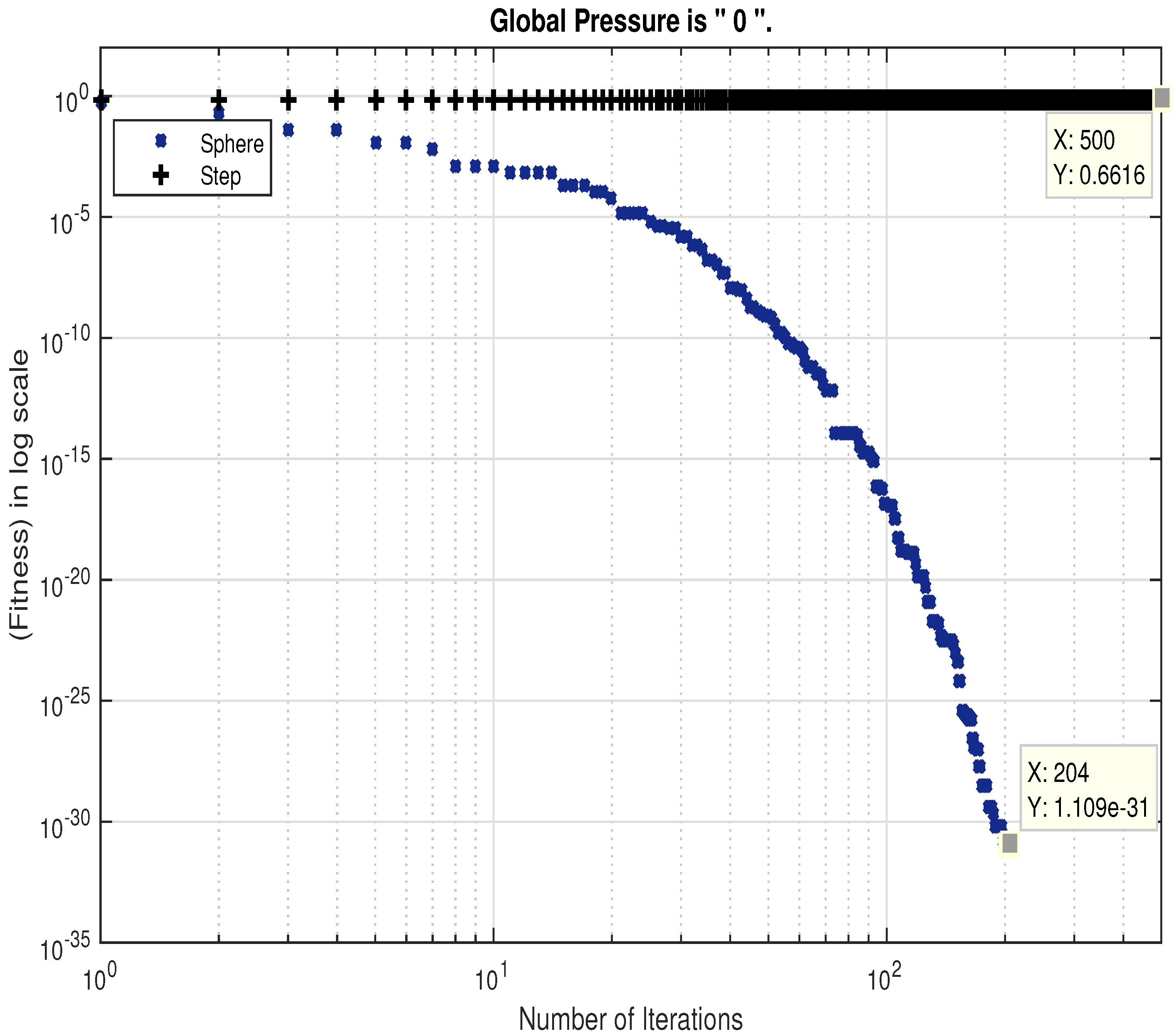
| WDO | Sphere | 204 | 0 | Yes |
| WDO | Step | 500 | 0.6616 | No |
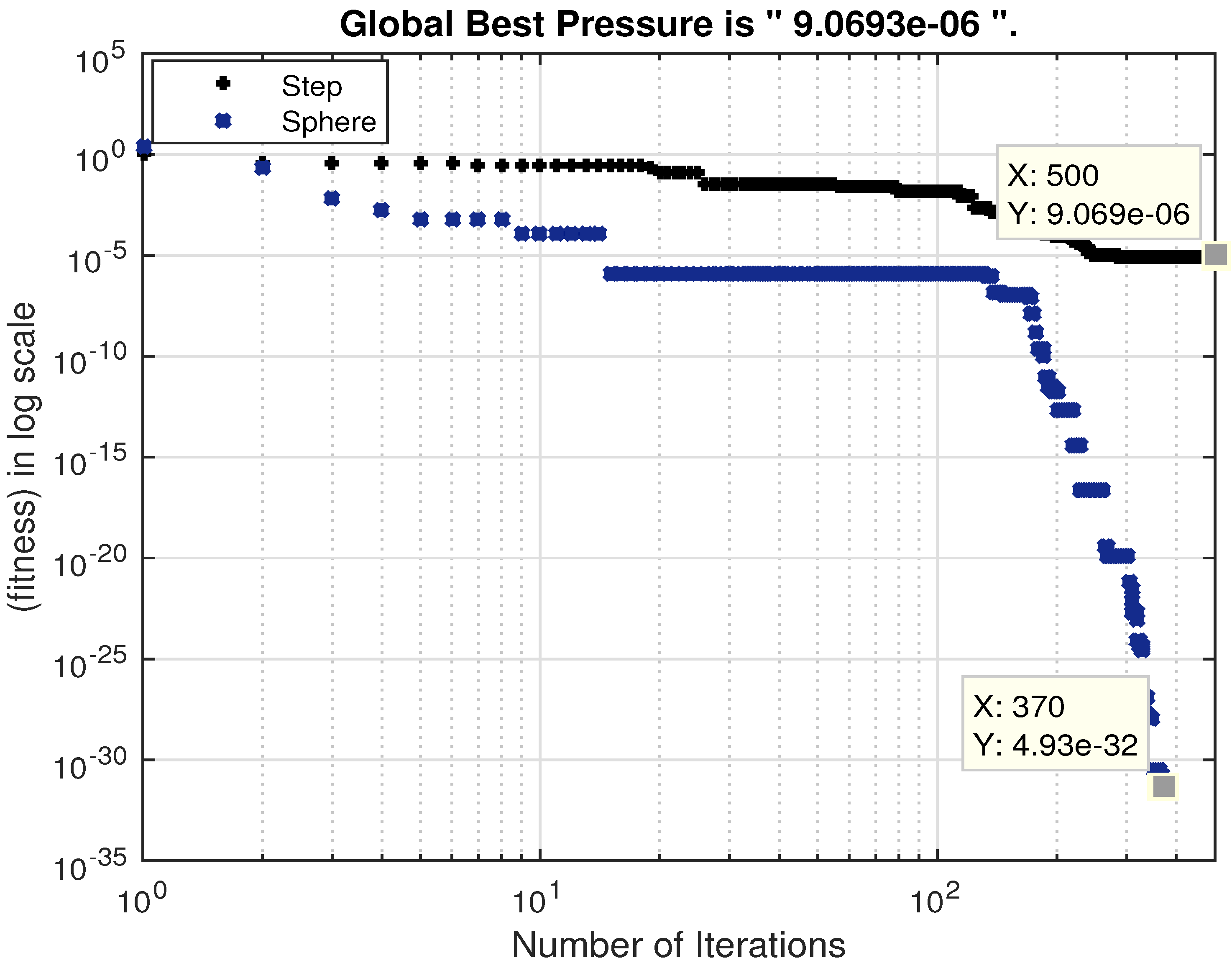
| PSO | Sphere | 500 | No | |
| PSO | Step | 370 | 0 | Yes |
8.1.1. Population Evaluation Functions
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Particle Size | 10 | RT-coefficient | 3 |
| No. of Iterations | 500 | Gravitational const | 0.2 |
| Max-V | 0.4 | Coriolis effect | 0.4 |
| Dimensions | [−1, +1] | α | 0.4 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Particle Size | 10 | 2 | |
| No. of Iterations | 500 | 2 | |
| Max-V | 0.3 | 1.0 | |
| Dimensions | [−1, +1] | 0.4 |
9. Peak-to-Average Ratio
10. Simulation Results and Discussion
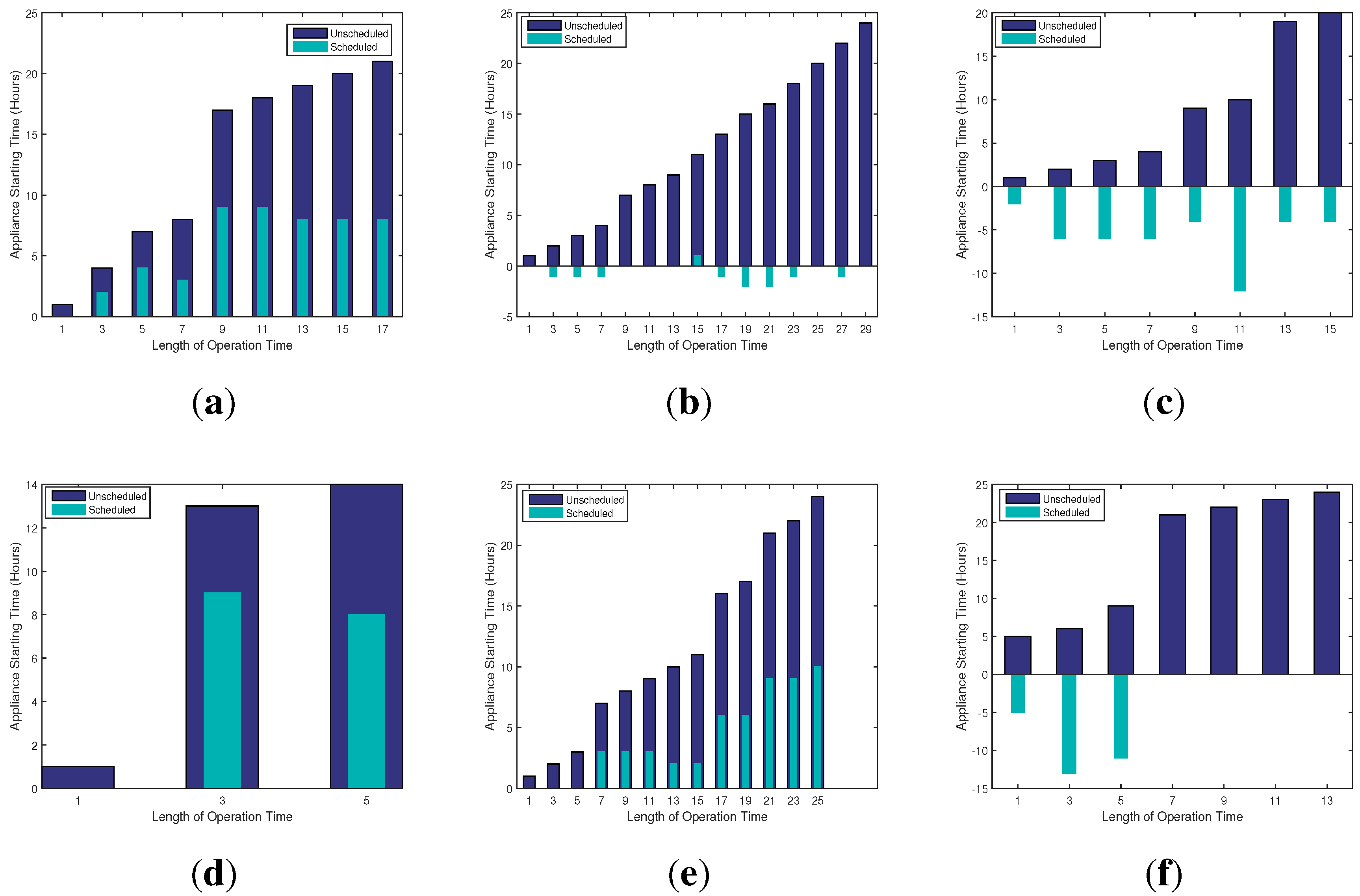
10.1. Electricity Cost vs. Appliance Waiting Time
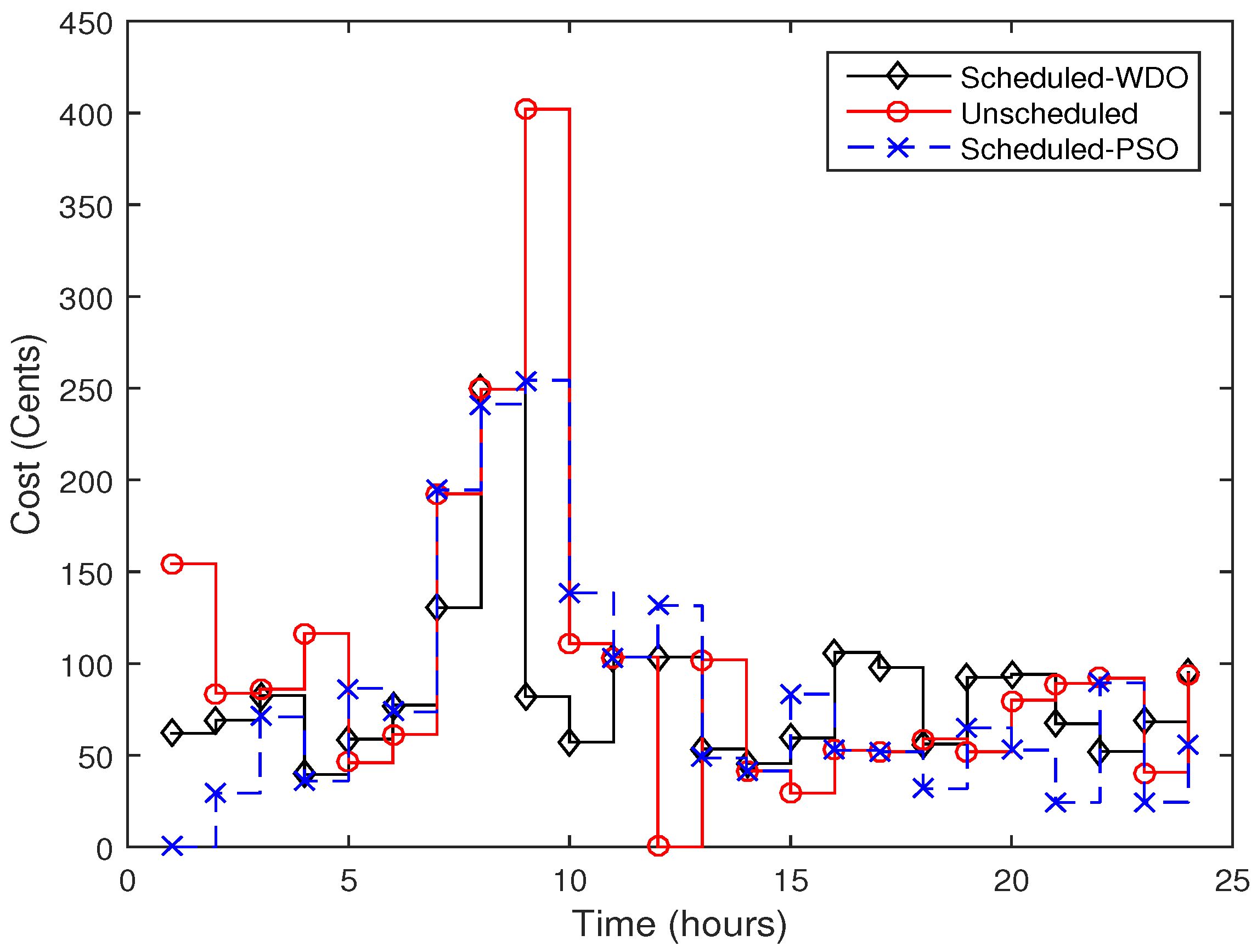
10.2. Electricity Cost vs. Electricity Price
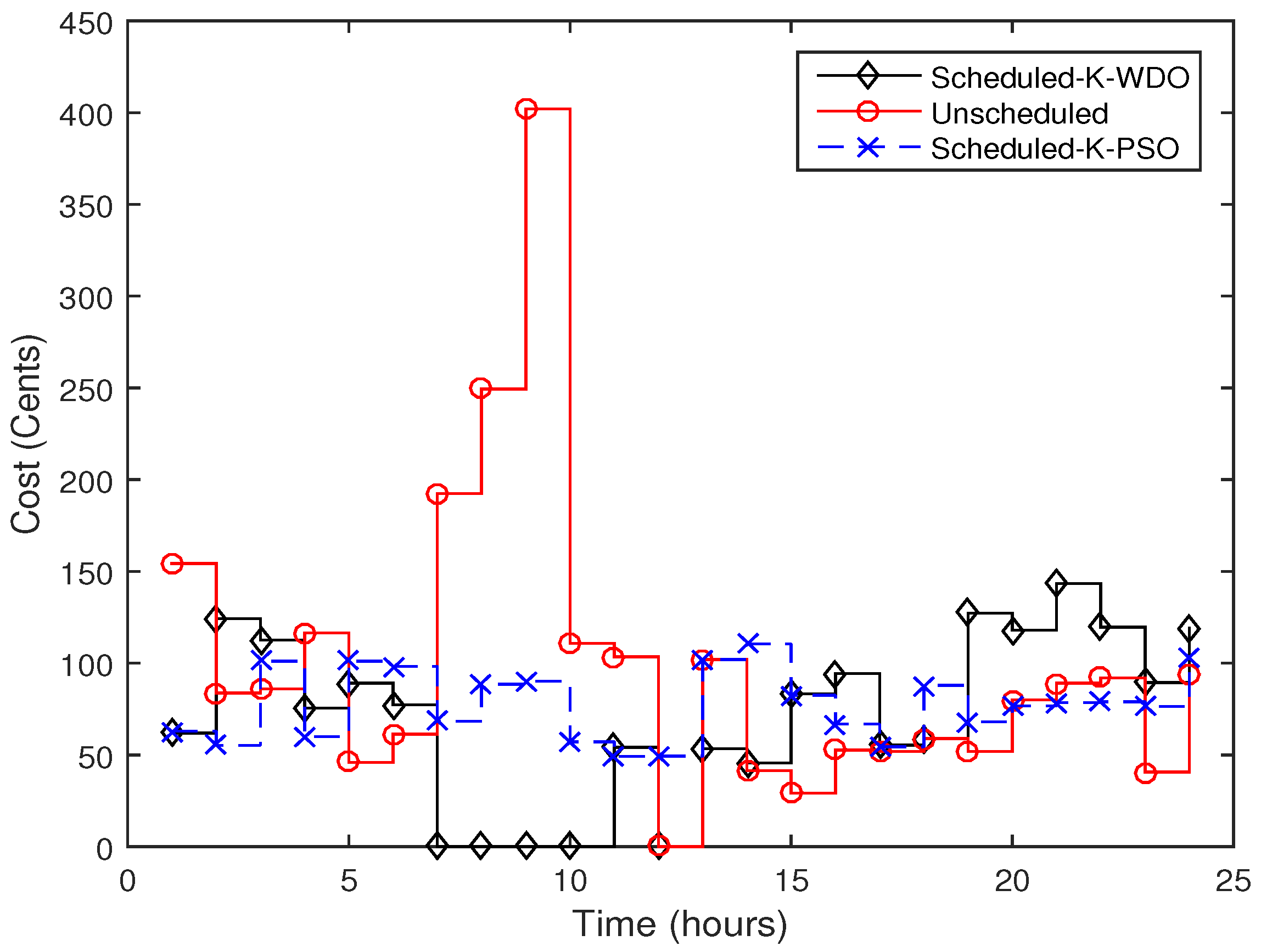
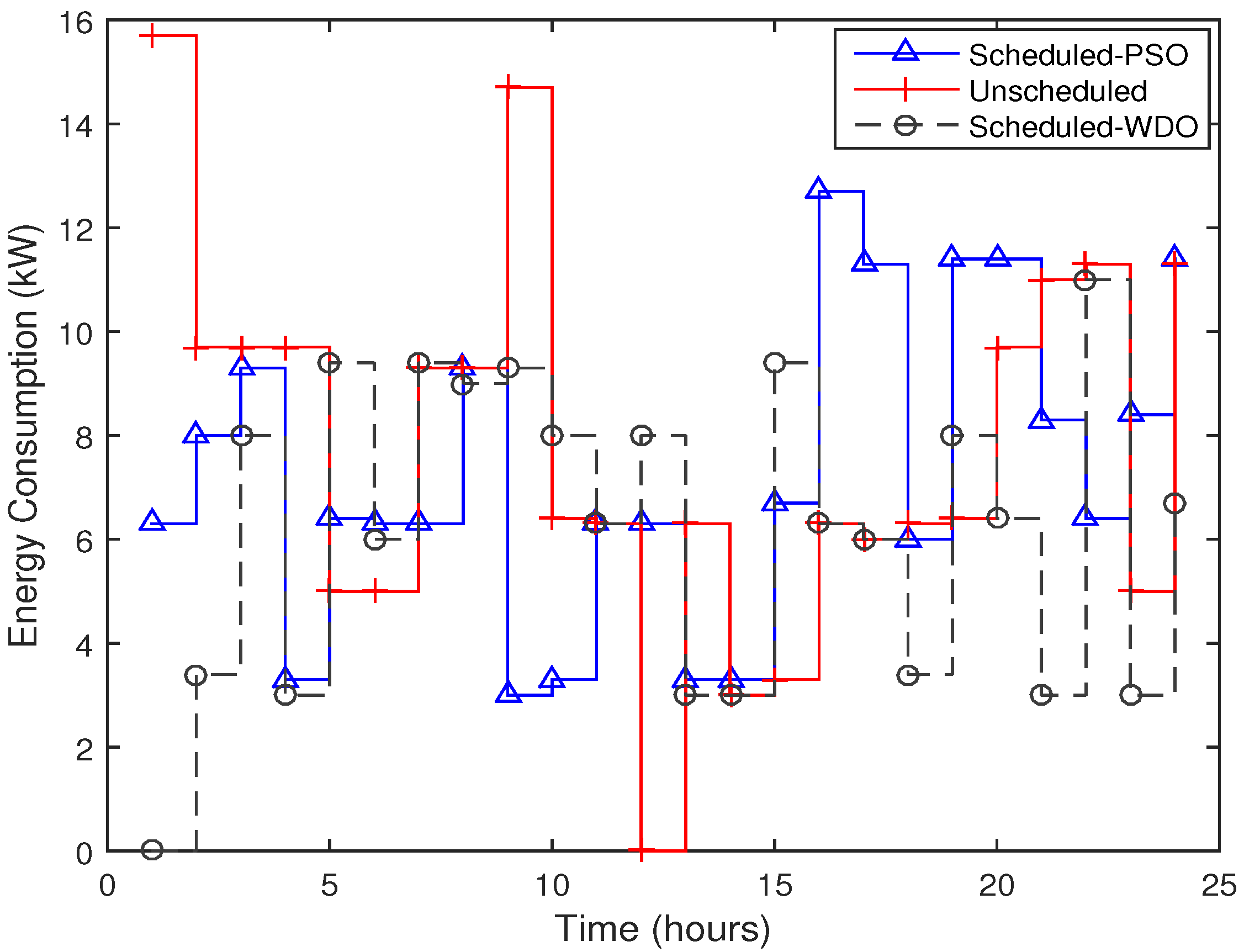
10.3. Energy Consumption
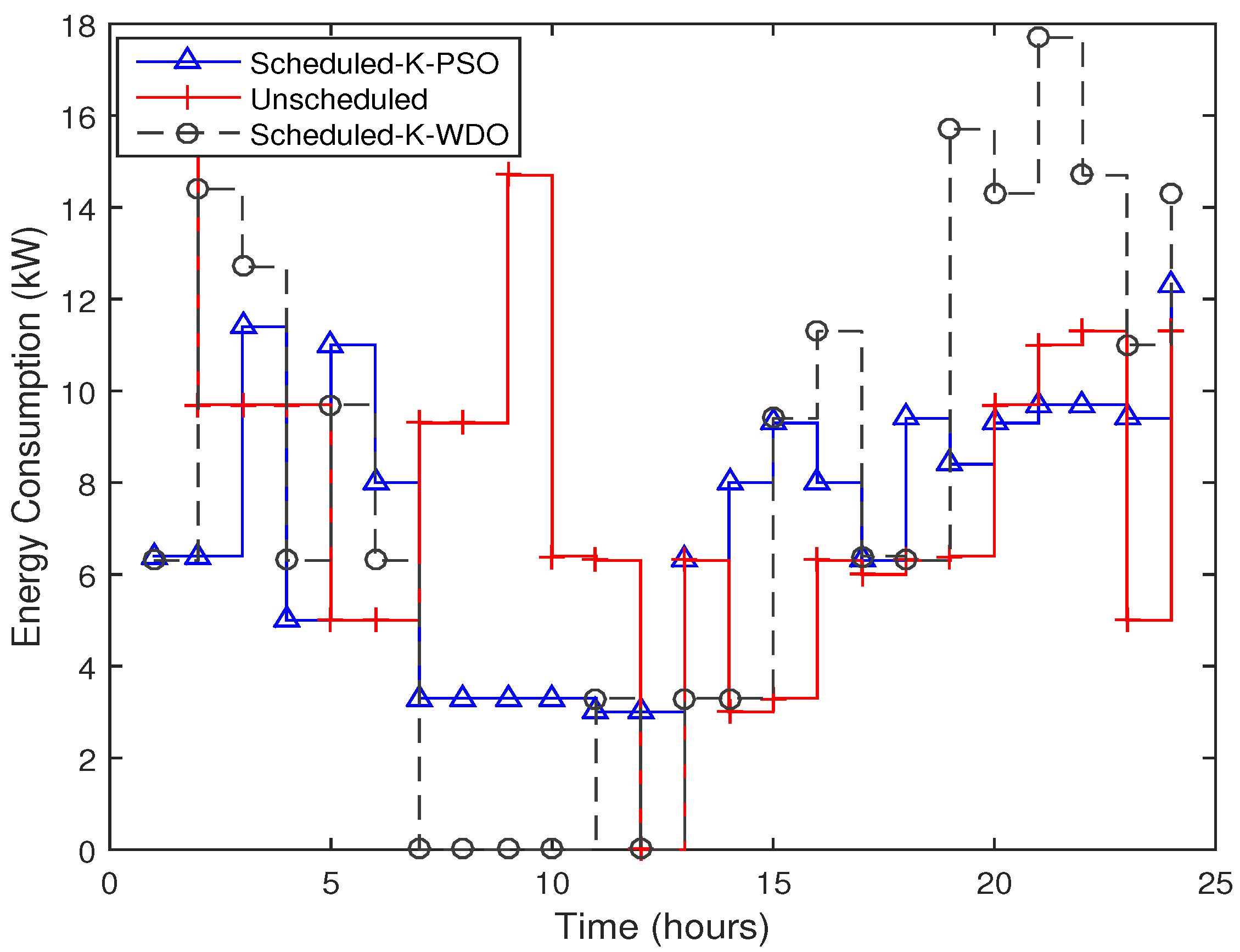
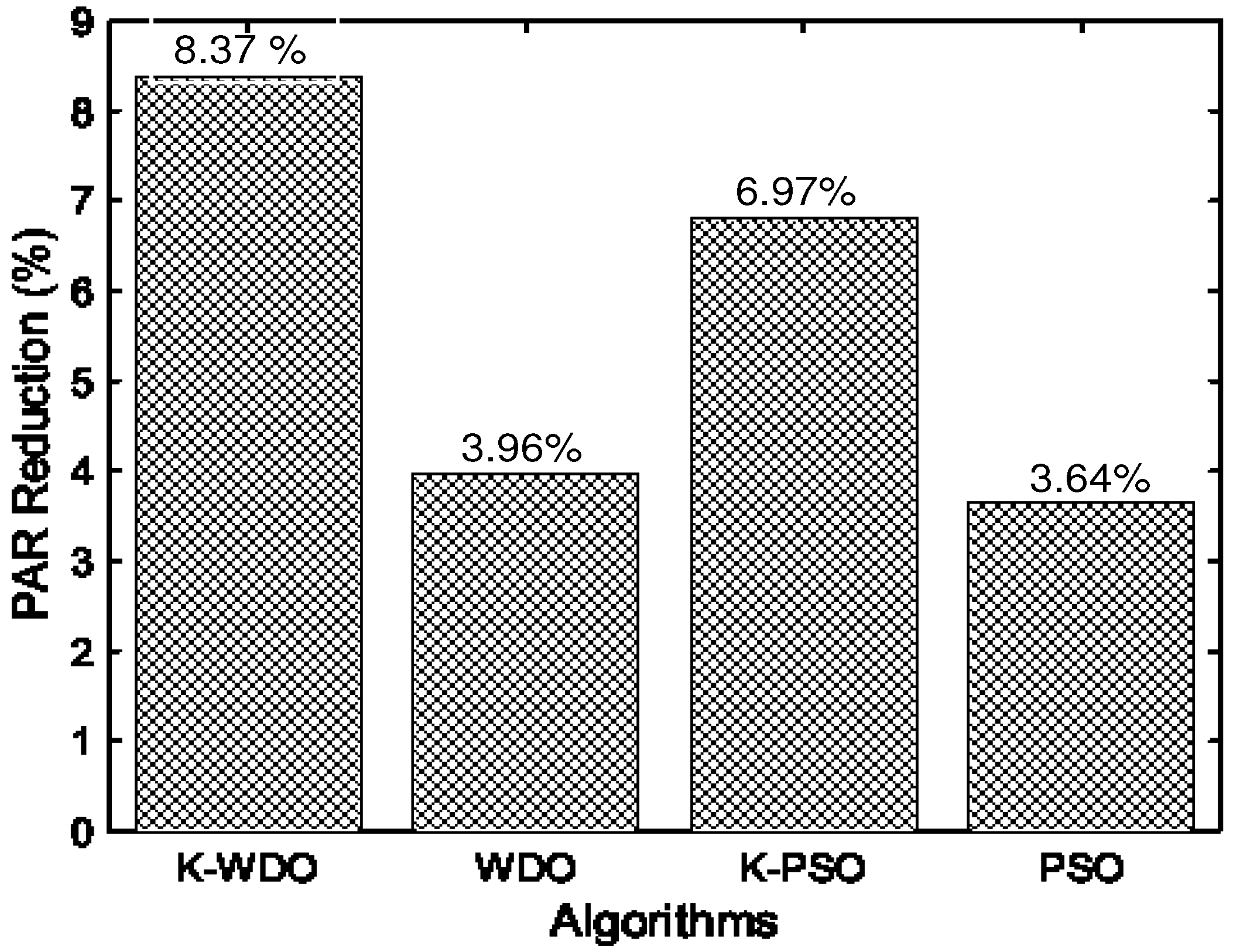
10.4. PAR Reduction
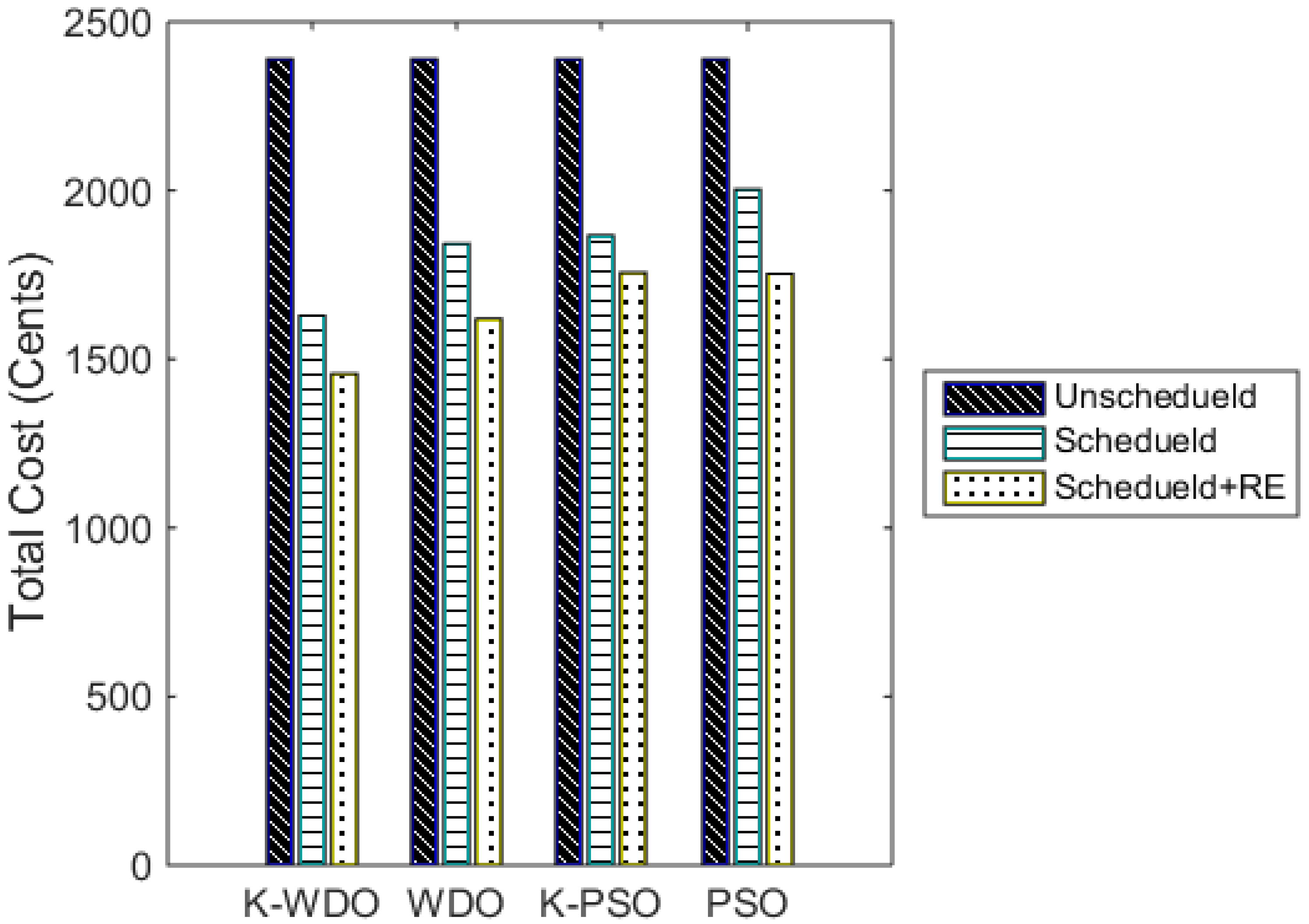
10.5. Electricity Cost with Renewable Sources
11. Conclusions
| Algorithms | Unscheduled Cost (Cents) | Scheduled Cost (Cents) | Saving % Age | Scheduled Cost + RE (Cents) | Saving % Age |
|---|---|---|---|---|---|
| K-WDO | 2390 | 1629 | 31.85 | 1457 | 39.04 |
| WDO | 2390 | 1842 | 22.93 | 1620 | 32.22 |
| K-PSO | 2390 | 1867 | 21.89 | 1756 | 26.16 |
| PSO | 2390 | 2003 | 16.20 | 1753 | 26.66 |
Acknowledgements
Author Contributions
Conflicts of Interest
Nomenclature
| Symbol | Description | Symbol | Description |
| appliance finishing time | appliance scheduled on time | ||
| initial appliance starting time | appliance waiting time | ||
| length of operation time | T | total time horizon | |
| energy consumption of appliance | energy consumption threshold | ||
| minimum energy consumption | energy consumption using scheduler | ||
| maximum energy consumption | energy consumption with delay | ||
| energy consumption of must run appliances | maximum energy consumption | ||
| scheduling horizon | unscheduled appliance starting time | ||
| total energy consumption | boolean variable for on/off status | ||
| set of electricity cost saving for appliance n | minimum electricity cost saving | ||
| maximum electricity cost saving | S | set of all possible scenario | |
| set of all possible solutions | given solution | ||
| optimal solution | maximum regret | ||
| total energy capacity | C | electricity cost | |
| electricity cost with renewable energy source | associated regret of solution s | ||
| maximum electricity load | average electricity load | ||
| energy unit price | small change in time |
References
- Energy Reports. Available online: http://www.enerdata.net/enerdatauk/press-and-publication/energy-features/enerfuture-2007.php (accessed on 1 August 2015).
- Ipakchi, A.; Albuyeh, F. Grid of the future. IEEE Power Energy 2009, 7, 52–62. [Google Scholar] [CrossRef]
- Assessment of Demand Response and Advanced Metering. Available online: http://www.ferc.gov/legal/staff-reports/2010-dr-report.pdf (accessed on 17 January 2014).
- Anadi, M.; Irwin, D.; Shenoy, P.; Kurose, J.; Zhu, T. Greencharge: Managing renewableenergy in smart buildings. IEEE J. Sel. Areas Commun. 2013, 31, 1281–1293. [Google Scholar]
- Mohsenian-Rad, A.H.; Garcia, A.L. Optimal residential load control with price prediction in real-time electricity pricing environments. IEEE Trans. Smart Grid 2010, 1, 120–133. [Google Scholar] [CrossRef]
- Vardakas, J.S.; Zorba, N.; Verikoukis, C.V. A Survey on Demand Response Programs in Smart Grids: Pricing Methods and Optimization Algorithms. Commun. Surv. Tutor. IEEE 2015, 17, 152–178. [Google Scholar] [CrossRef]
- Xiong, G.; Chen, C.; Kishore, S.; Yener, A. Smart (in-home) power scheduling for demand response on the smart grid. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference, Anaheim, CA, USA, 17–19 January 2011.
- Erol-Kantarci, M.; Mouftah, T. Wireless sensor networks for cost-efficient residential energy management in the smart grid. IEEE Trans. Smart Grid 2011, 2, 314–325. [Google Scholar] [CrossRef]
- Samadi, P.; Mohsenian-Rad, A.; Schober, R.; Wong, V.W.S.; Jatskevich, J. Optimal real-time pricing algorithm based on utility maximization for smart grid. In Proceedings of the 1st IEEE International Conference on Smart Grid Communications (SmartGridComm), Gaithersburg, MD, USA, 4–6 October 2010; pp. 415–420.
- Li, Q.; Zhou, M. The future-oriented grid-smart grid. J. Comput. 2011, 6, 98–105. [Google Scholar] [CrossRef]
- Agrawal, P. Overview of DOE microgrid activities. In Proceedings of the Symposium on Microgrids, Montreal, QC, Canada, 23 June 2006; Available online: http://der.lbl.gov/2006 microgrids_files/USA/Presentation_7_Part1_Poonumgrawal.pdf (accessed on 1 August 2015).
- Shahidehpour, M.; Yamin, H.; Li, Z. Market Operations in Electric Power Systems: Forecasting, Scheduling, and Risk Management; Wiley-IEEE Press: New York, NY, USA, 2002. [Google Scholar]
- Popovic, Z.N.; Popovic, D.S. Direct load control as a market-based program in deregulated power industries. In Proceedings of the IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June 2003; Volume 3, p. 4.
- Ng, K.H.; Sheble, G.B. Direct load control-A profit-based load management using linear programming. IEEE Trans. Power Syst. 1998, 13, 688–694. [Google Scholar] [CrossRef]
- Schweppe, F.C.; Daryanian, B.; Tabors, R.D. Algorithms for a spot price responding residential load controller. IEEE Trans. Power Syst. 1989, 4, 507–516. [Google Scholar] [CrossRef]
- Lee, H.; Wilkins, C.L. A practical approach to appliance load control analysis: A water heater case study. IEEE Trans. Power Appl. Syst. 1983, 4, 1007–1013. [Google Scholar] [CrossRef]
- Kurucz, C.N.; Brandt, D.; Sim, S. A linear programming model for reducing system peak through customer load control programs. IEEE Trans. Power Syst. 1996, 11, 1817–1824. [Google Scholar] [CrossRef]
- Pedrasa, M.A.A.; Spooner, T.D.; MacGill, I.F. Coordinated scheduling of residential distributed energy resources to optimize smart home energy services. IEEE Trans. Smart Grid 2010, 1, 134–143. [Google Scholar] [CrossRef]
- Ozturk, Y.; Senthilkumar, D.; Kumar, S.; Lee, G. An intelligent home energy management system to improve demand response. IEEE Trans. Smart Grid 2013, 4, 694–701. [Google Scholar] [CrossRef]
- Salinas, S.; Li, M.; Li, P. Multi-objective optimal energy consumption scheduling in smart grids. IEEE Trans. Smart Grid 2013, 4, 341–348. [Google Scholar] [CrossRef]
- Faria, P.; Soares, J.; Vale, Z.; Morais, H.; Sousa, T. Modified particle swarm optimization applied to integrated demand response and DG resources scheduling. IEEE Trans. Smart Grid 2013, 4, 606–616. [Google Scholar] [CrossRef]
- Conejo, A.J.; Morales, J.M.; Baringo, L. Real-time demand response model. IEEE Trans. Smart Grid 2010, 1, 236–242. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, L.; Fu, Y. Real-time price-based demand response management for residential appliances via stochastic optimization and robust optimization. IEEE Trans. Smart Grid 2012, 3, 1822–1831. [Google Scholar] [CrossRef]
- Hurtado, L.A.; Nguyen, P.H.; Kling, W.L. Multiple objective Particle Swarm Optimization approach to enable smart buildings-smart grids. In Proceedings of the Power Systems Computation Conference (PSCC), Wroclaw, Poland, 18–22 August 2014.
- Fadlullah, Z.; Quan, D.; Kato, N.; Stojmenovic, I. GTES: An optimized game-theoretic demand-side management scheme for smart grid. IEEE Syst. J. 2013, 8, 588–597. [Google Scholar] [CrossRef]
- Maharjan, S.; Zhu, Q.; Zhang, Y.; Gjessing, S.; Basar, T. Dependable demand response management in the smart grid: A Stackelberg game approach. IEEE Trans. Smart Grid 2013, 4, 120–132. [Google Scholar] [CrossRef]
- Ibars, C.; Navarro, M.; Giupponi, L. Distributed demand management in smart grid with a congestion game. In Proceedings of the 1st IEEE International Conference on Smart Grid Communications (SmartGridComm), Gaithersburg, MD, USA, 4–6 October 2010; pp. 495–500.
- Kim, S.J.; Giannakis, G. Scalable and robust demand response with mixed-integer constraints. IEEE Trans. Smart Grid 2013, 4, 2089–2099. [Google Scholar]
- Vandael, S.; Claessens, B.; Hommelberg, M.; Holvoet, T.; Deconinck, G. A scalable three-step approach for demand side management of plug-in hybrid vehicles. IEEE Trans. Smart Grid 2013, 4, 720–728. [Google Scholar] [CrossRef]
- Chen, C.; Nagananda, K.; Xiong, G.; Kishore, S.; Snyder, L. A communication-based appliance scheduling scheme for consumerpremise energy management systems. IEEE Trans. Smart Grid 2013, 4, 56–65. [Google Scholar] [CrossRef]
- Wang, C.; de Groot, M. Managing end-user preferences in the smart grid. In Proceedings of the 1st ACM International Conference on Energy-Efficient Computing and Networking, Passau, Germany, 13–15 April 2010; pp. 105–114.
- Gatsis, N.; Giannakis, G. Residential load control: Distributed scheduling and convergence with lost AMI messages. IEEE Trans. Smart Grid 2012, 3, 770–786. [Google Scholar] [CrossRef]
- Shimomura, Y.; Nemoto, Y.; Akasaka, F.; Chiba, R.; Kimita, K. A method for designing customer-oriented demand response aggregation service. CIRP Ann. Manuf. Technol. 2014, 63, 413–416. [Google Scholar] [CrossRef]
- Liu, B.; Wei, Q. Home energy control algorithm research based on demand response programs and user comfort. In Proceedings of the International Conference on Measurement, Information and Control (ICMIC), Harbin, China, 16–18 August 2013; pp. 995–999.
- Nguyen, D.T.; Le, L.B. Joint optimization of electric vehicle and home energy scheduling considering user comfort preference. IEEE Trans. Smart Grid 2014, 5, 188–199. [Google Scholar] [CrossRef]
- Mohsenian-Rad, A.H.; Garcia, L. Optimal residential load control with price prediction in real-time electricity pricing environments. IEEE Trans. Smart Grid 2010, 1, 120–133. [Google Scholar] [CrossRef]
- Herter, K. Residential implementation of critical-peak pricing of electricity. Energy Policy 2007, 35, 2121–2130. [Google Scholar] [CrossRef]
- Silvano, M.; Toth, P. Knapsack Problems: Algorithms and Computer Implementations; John Wiley and Sons, Inc.: New York, NY, USA, 1990. [Google Scholar]
- Kellerer, H.; Pferschy, U.; Pisinger, D. Introduction to NP-Completeness of Knapsack Problems; Springer: Berlin Heidelberg, Germany, 2004; pp. 483–493. [Google Scholar]
- Haupt, R.L.; Werner, D.H. Genetic Algorithms in Electromagnetics; Wiley-IEEE Press: Hoboken, NJ, USA, 2007. [Google Scholar]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer-Verlag: Berlin, Germany, 2005. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the 9th International Conference of Neural Networkss, Doha, Qatar, 20–23 November 1995; Volume 4, pp. 1942–1948.
- Dorigo, M.; Stutzle, T. Ant Colony Optimization; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Cuckoo search. Available online: https://en.wikipedia.org/wiki/Cuckoo_search (accessed on 23 September 2015).
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Bayraktar, Z.; Komurcu, M.; Bossard, J.; Werner, D.H. The wind driven optimization technique and its application in electromagnetics. IEEE Trans. Antennas Propag. 2013, 61, 2745–2757. [Google Scholar] [CrossRef]
- Bayraktar, Z.; Komurcu, M.; Werner, D.H. Wind Driven Optimization (WDO): A novel nature-inspired optimization algorithm and its application to electromagnetics. In Proceedings of the Antennas and Propagation Society International Symposium (APSURSI), Toronto, AB, Canada, 11–17 July 2010.
- Yao, X.; Liu, Y.; Lin, G. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 1999, 3, 82–102. [Google Scholar]
- Wholesale Solar Home Page. Available online: http://www.wholesalesolar.com/ (accessed on 1 August 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasheed, M.B.; Javaid, N.; Ahmad, A.; Khan, Z.A.; Qasim, U.; Alrajeh, N. An Efficient Power Scheduling Scheme for Residential Load Management in Smart Homes. Appl. Sci. 2015, 5, 1134-1163. https://doi.org/10.3390/app5041134
Rasheed MB, Javaid N, Ahmad A, Khan ZA, Qasim U, Alrajeh N. An Efficient Power Scheduling Scheme for Residential Load Management in Smart Homes. Applied Sciences. 2015; 5(4):1134-1163. https://doi.org/10.3390/app5041134
Chicago/Turabian StyleRasheed, Muhammad Babar, Nadeem Javaid, Ashfaq Ahmad, Zahoor Ali Khan, Umar Qasim, and Nabil Alrajeh. 2015. "An Efficient Power Scheduling Scheme for Residential Load Management in Smart Homes" Applied Sciences 5, no. 4: 1134-1163. https://doi.org/10.3390/app5041134
APA StyleRasheed, M. B., Javaid, N., Ahmad, A., Khan, Z. A., Qasim, U., & Alrajeh, N. (2015). An Efficient Power Scheduling Scheme for Residential Load Management in Smart Homes. Applied Sciences, 5(4), 1134-1163. https://doi.org/10.3390/app5041134








