Development of a Fractional Order Chaos Synchronization Dynamic Error Detector for Maximum Power Point Tracking of Photovoltaic Power Systems
Abstract
:1. Introduction
2. Problem Description and Motives
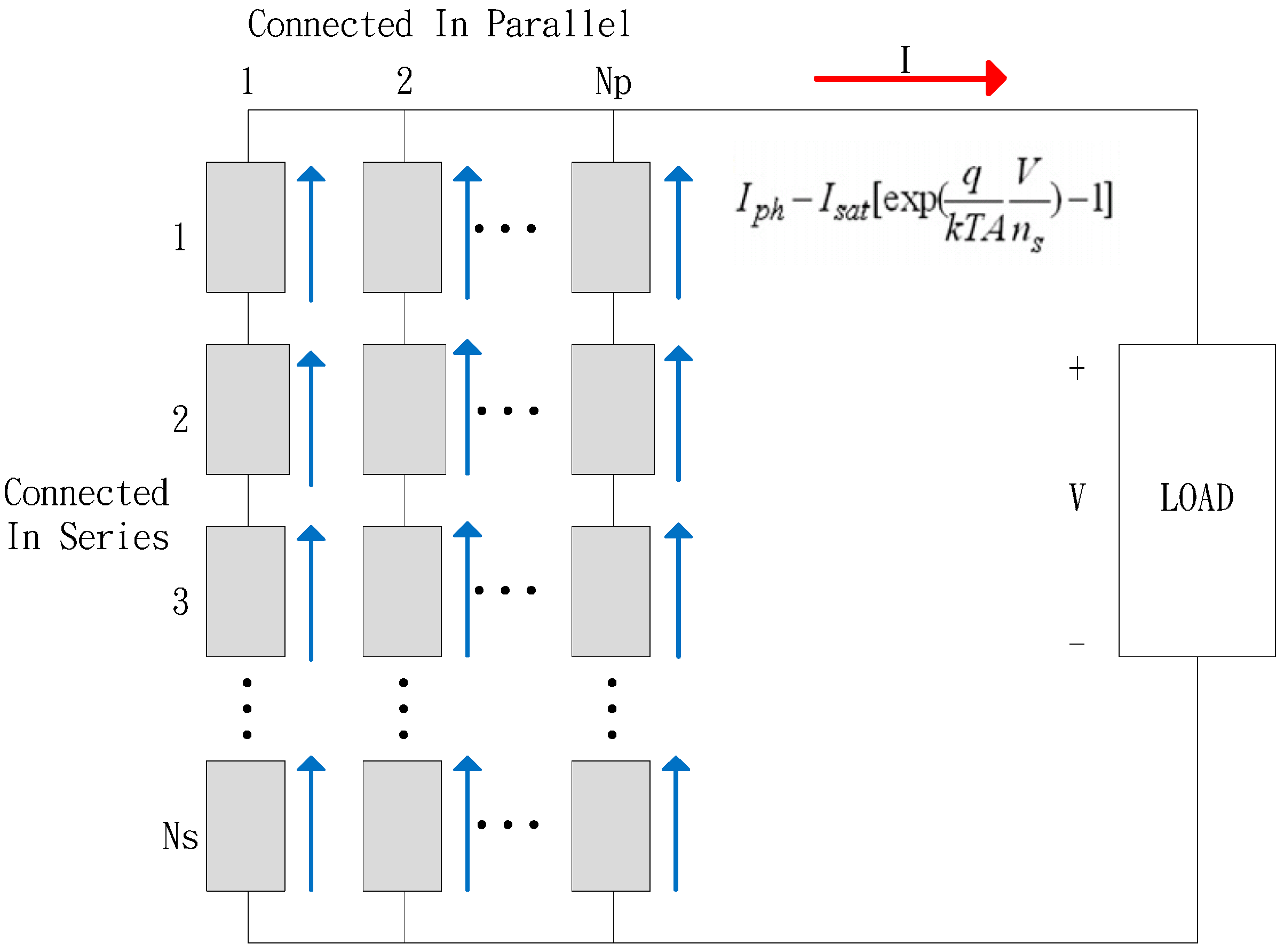
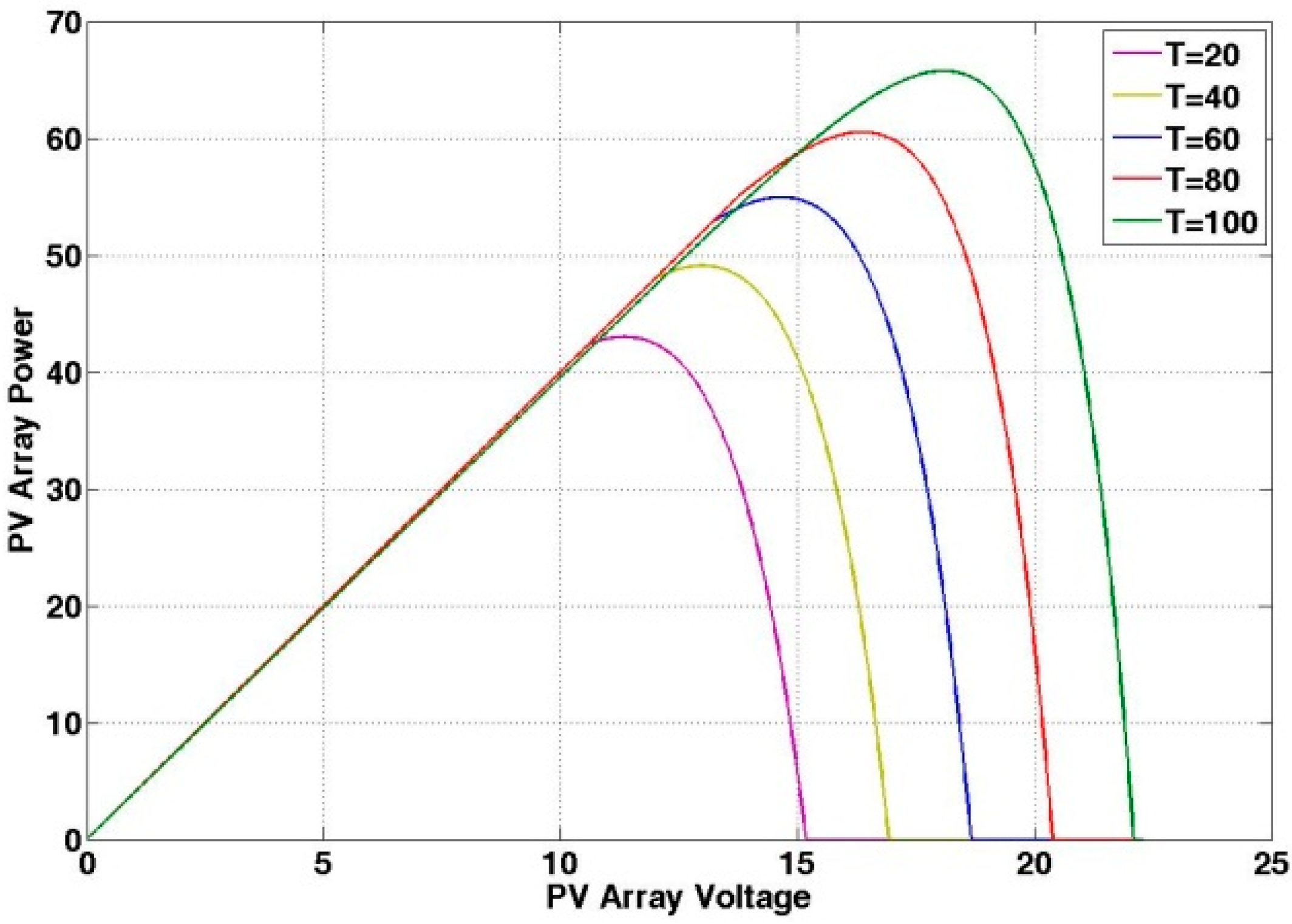
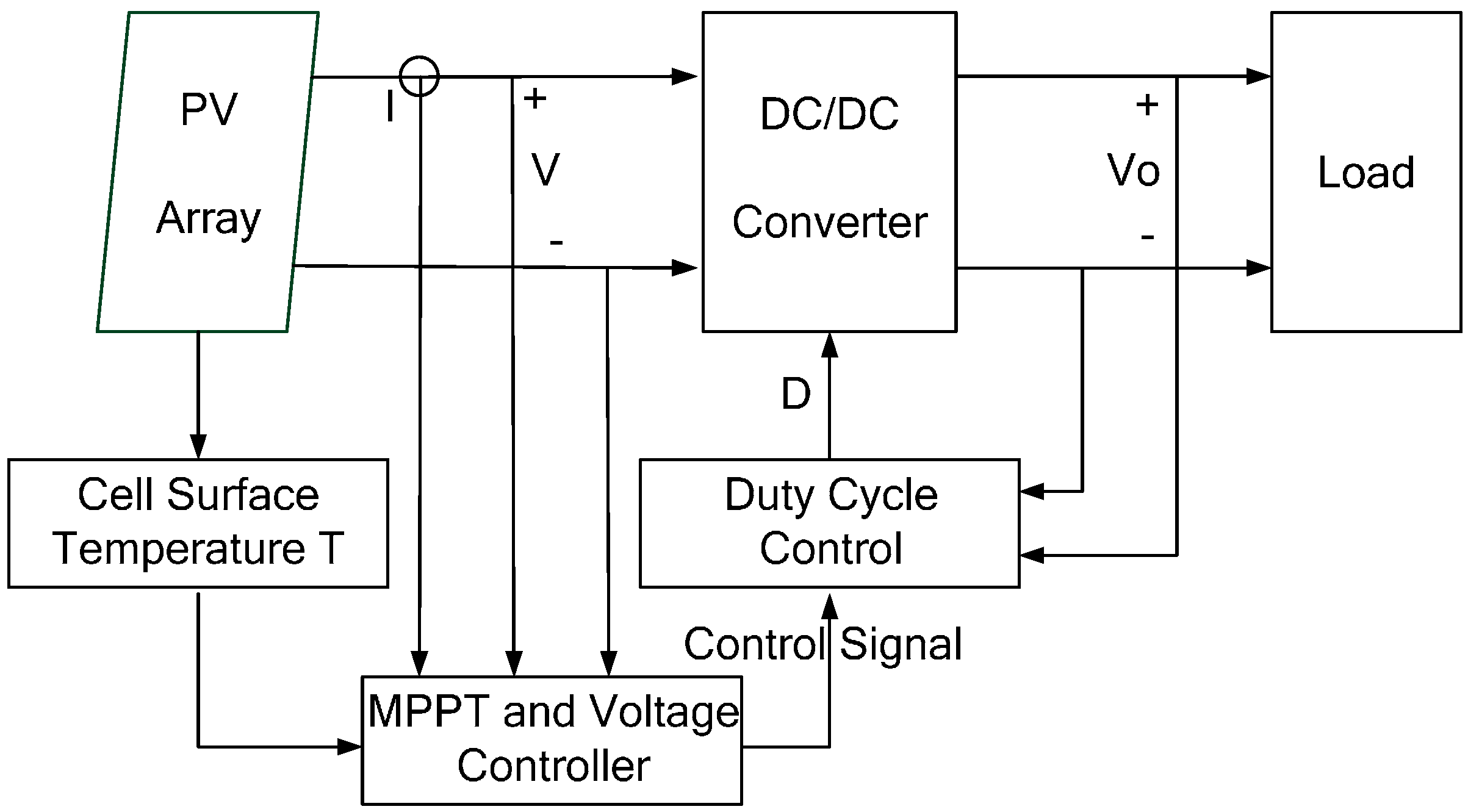
3. Design of Voltage Detector
| Notation | Definition |
|---|---|
| The system states of master system | |
| The system states of slave system | |
| Nonlinear functions | |
| Error states of chaos synchronization system | |
| x | System state of Sprott Chaos System |
| Symbolic function is defined as | |
| a, b | System parameters of Sprott Chaos System |
| Error states of Sprott Chaos System | |
| The value of fractional order | |
| Initial time | |
| Differential with respect to time t | |
| System parameters of fractional order system | |
| Sampling time | |
| The data of expected voltage | |
| The data of real-time test voltage | |
| , | Dynamic error equation as the variables of error judgment of chaos synchronization dynamic error detector |
| , | The set values of error magnitude |
3.1. Chaos Theory and Chaos Synchronization Dynamic Error
3.2. Fractional Order Chaos Synchronization Dynamic Error
3.3. Implementation of Voltage Detector

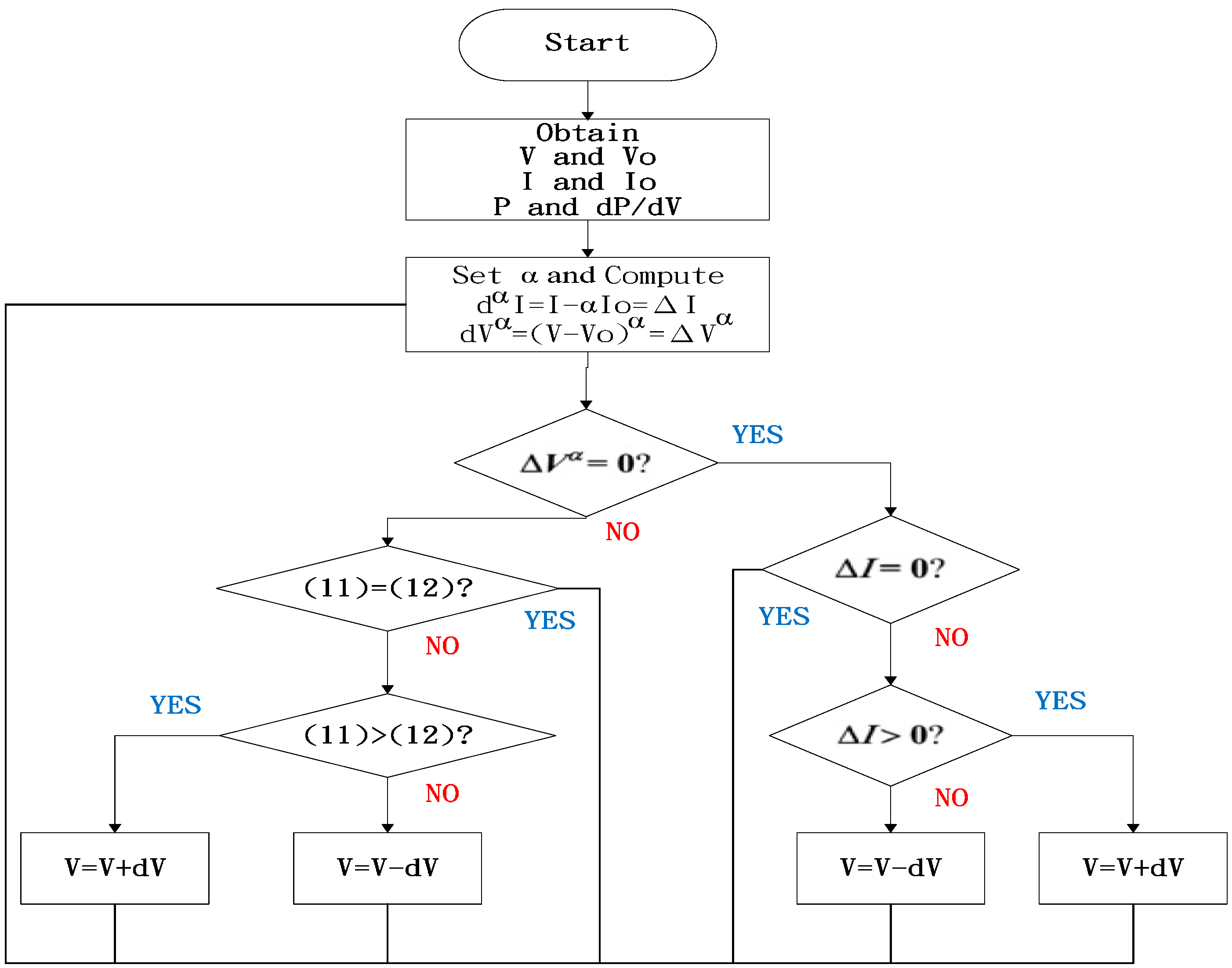
4. Simulation and Experimental Results
4.1. Simulation and Experimental Equipment
| Specific Parameter | Value |
|---|---|
| Maximum Power | 17 (W) |
| Maximum Power Voltage () | 16 (V) |
| Maximum Power Current () | 1.06 (A) |
| Open circuit Voltage () | 21.24 (V) |
| Short circuit Current () | 1.2 (A) |
| Operating Cell temperature Range | −40 °C–85 °C |
4.2. Simulation Results
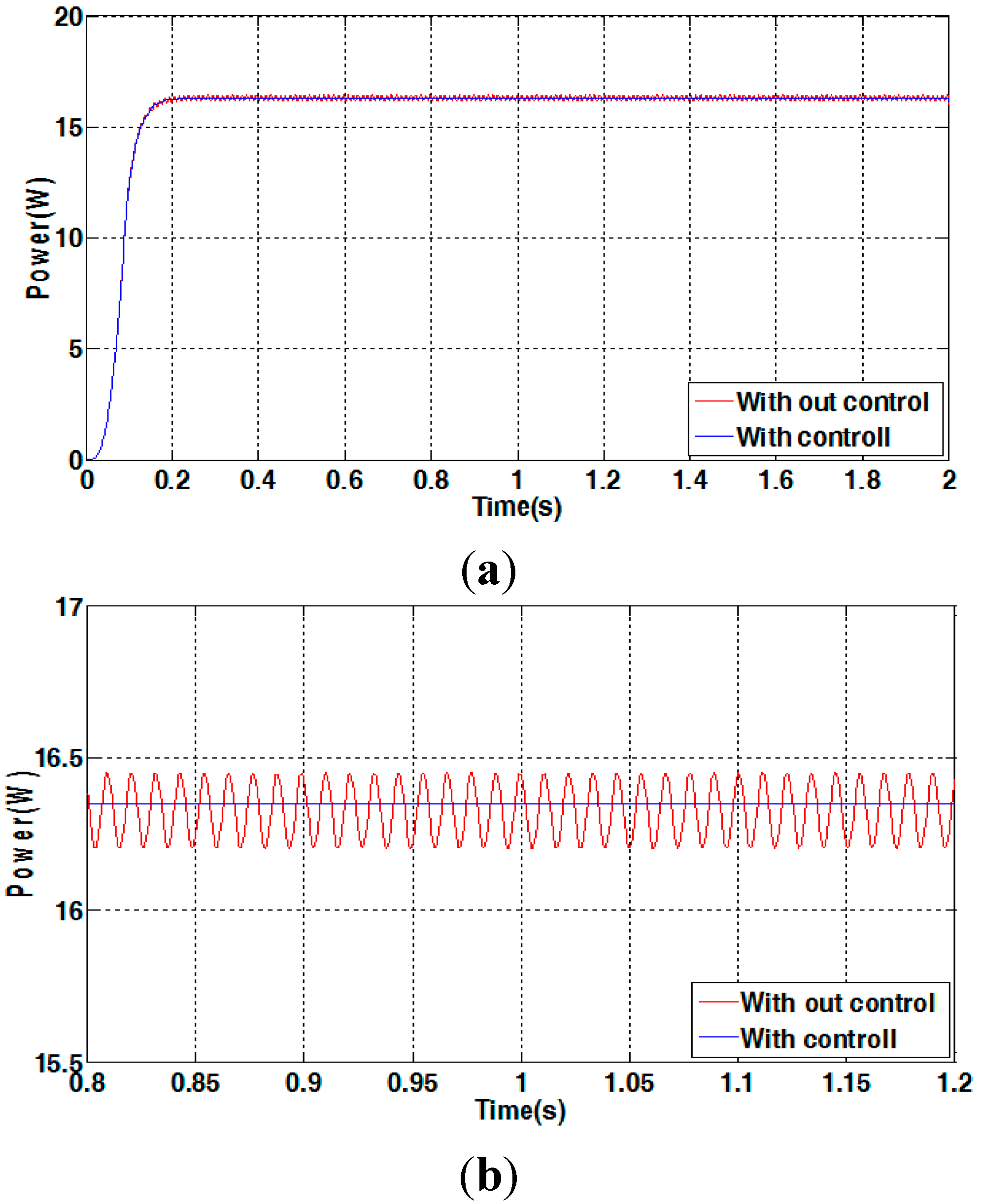
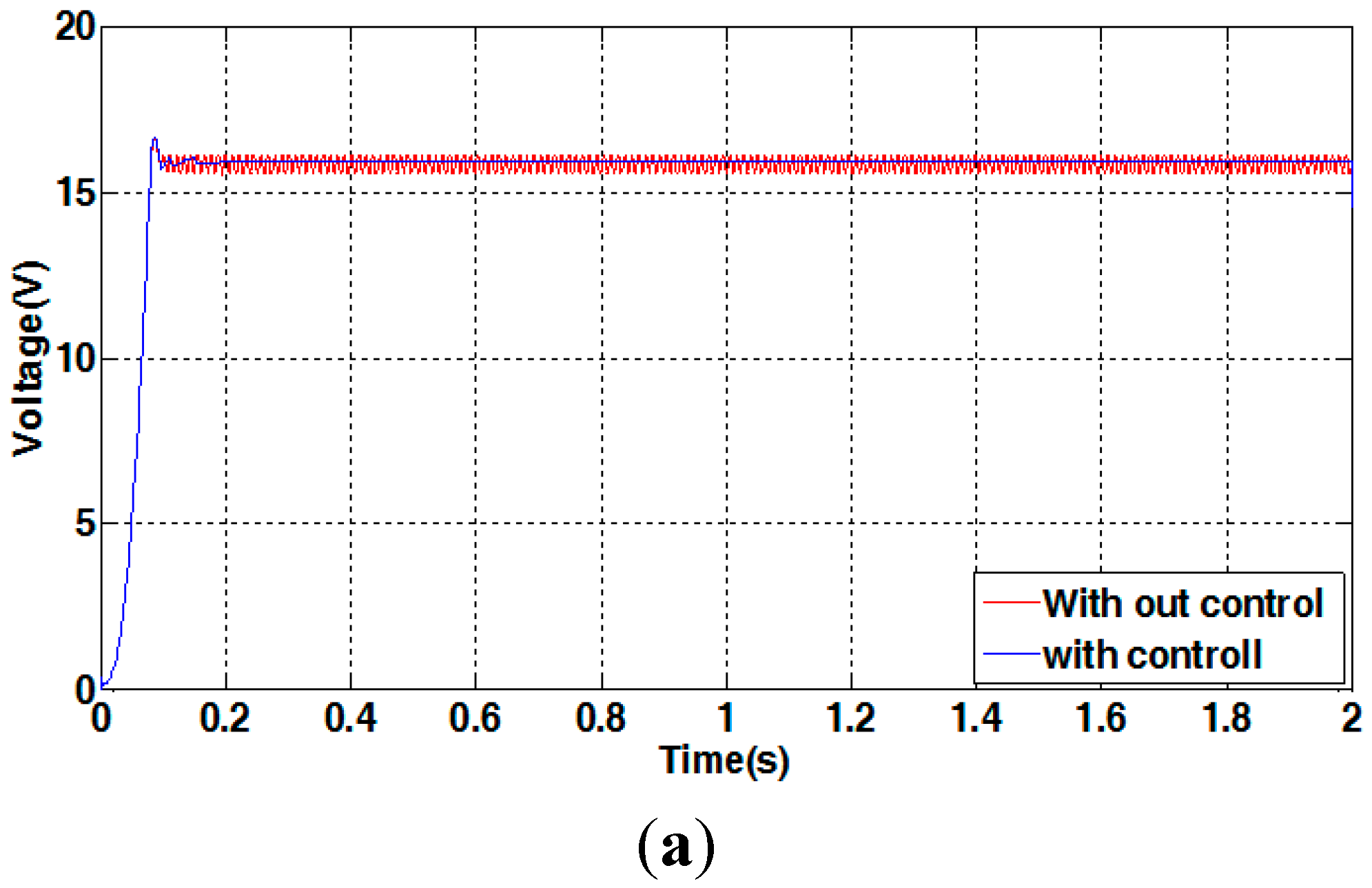
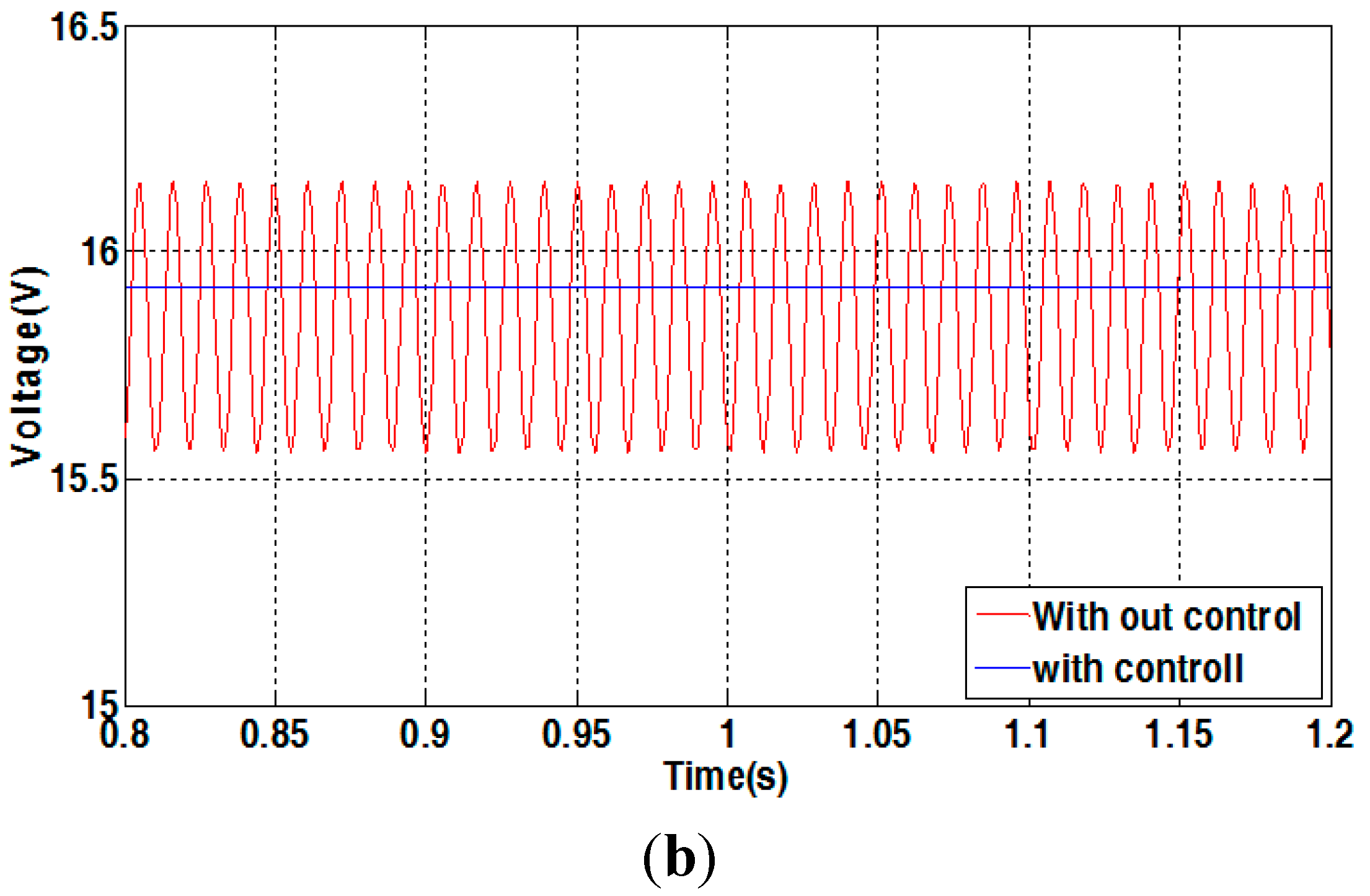
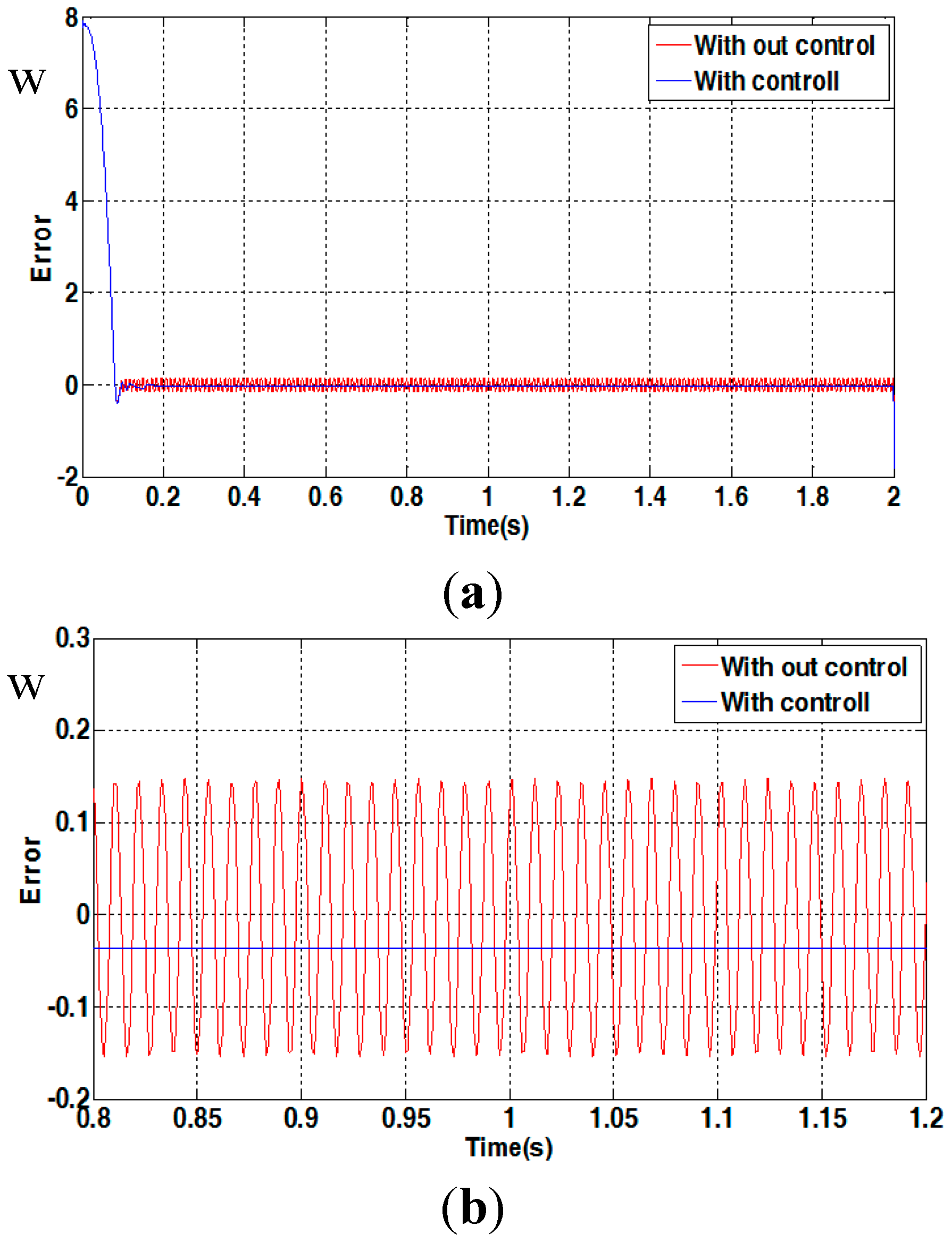
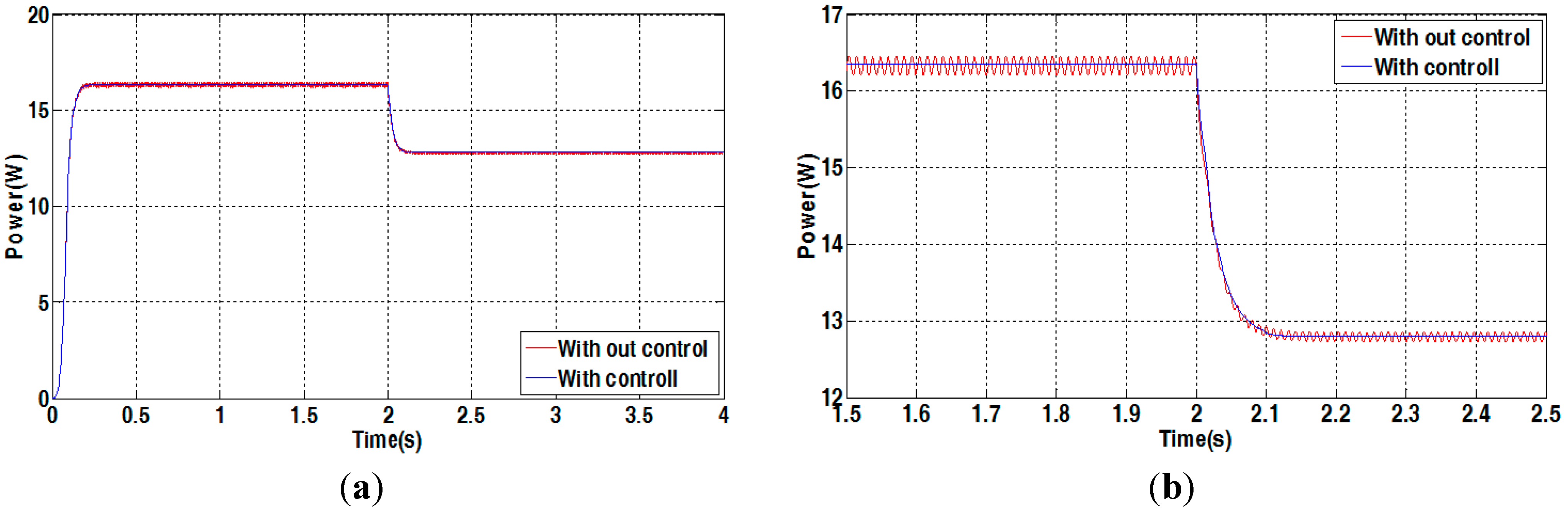
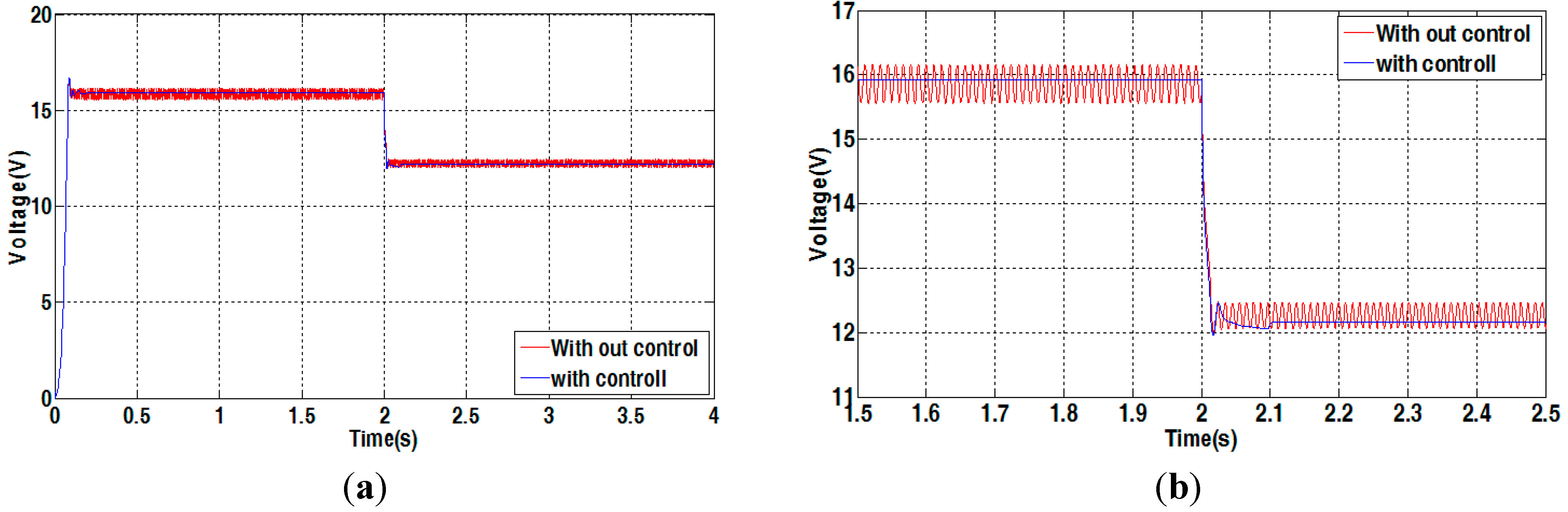
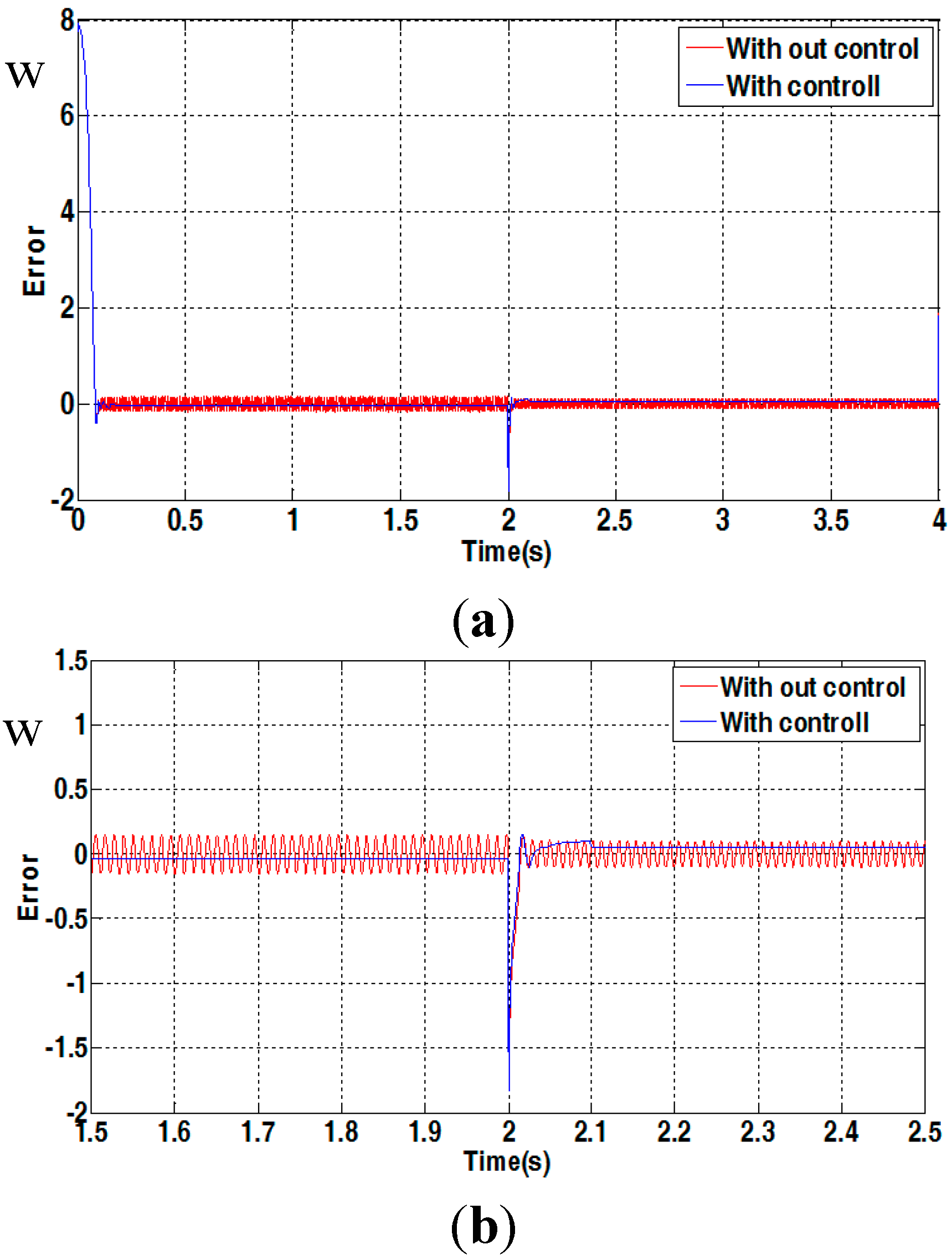
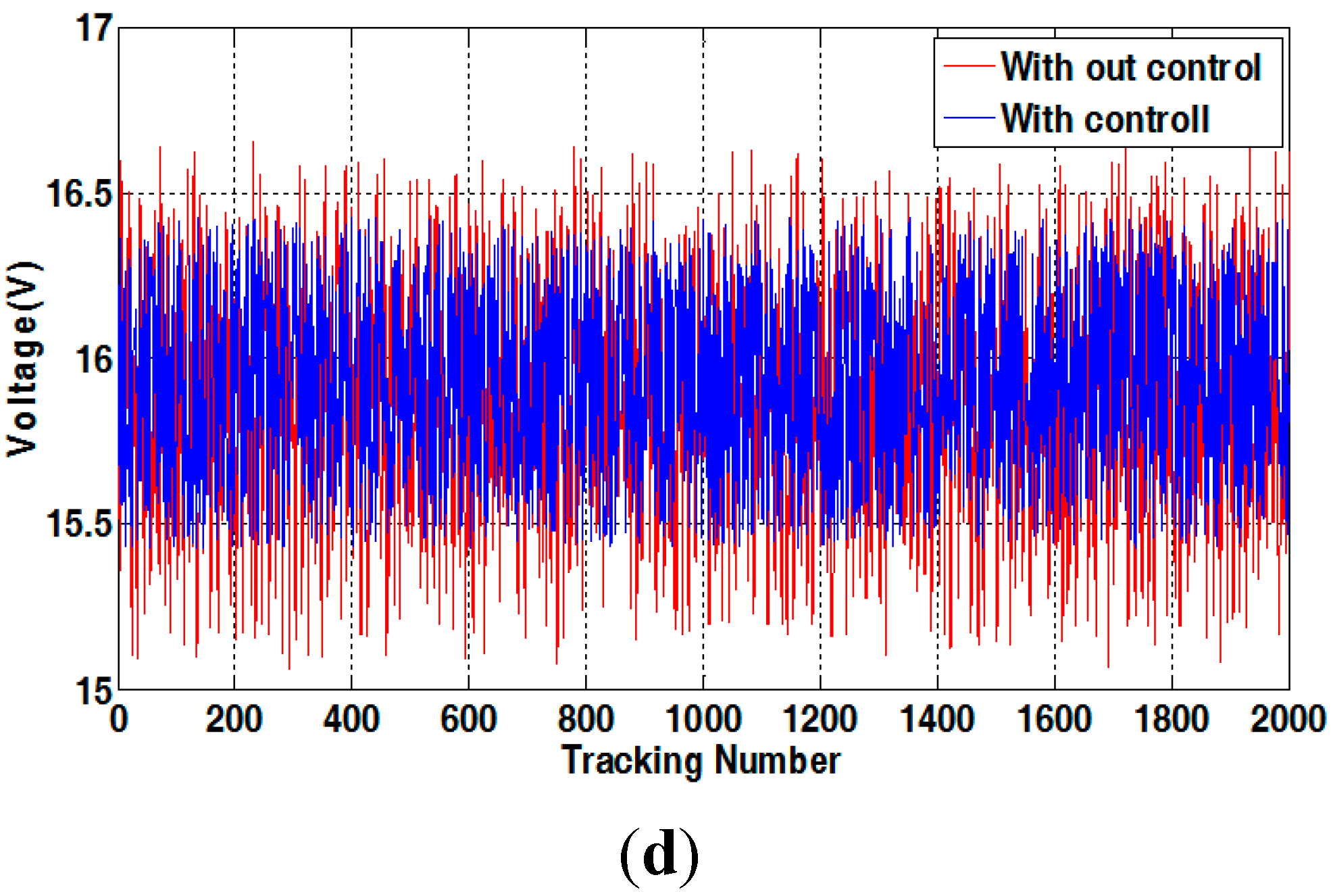
4.3. Experimental Results

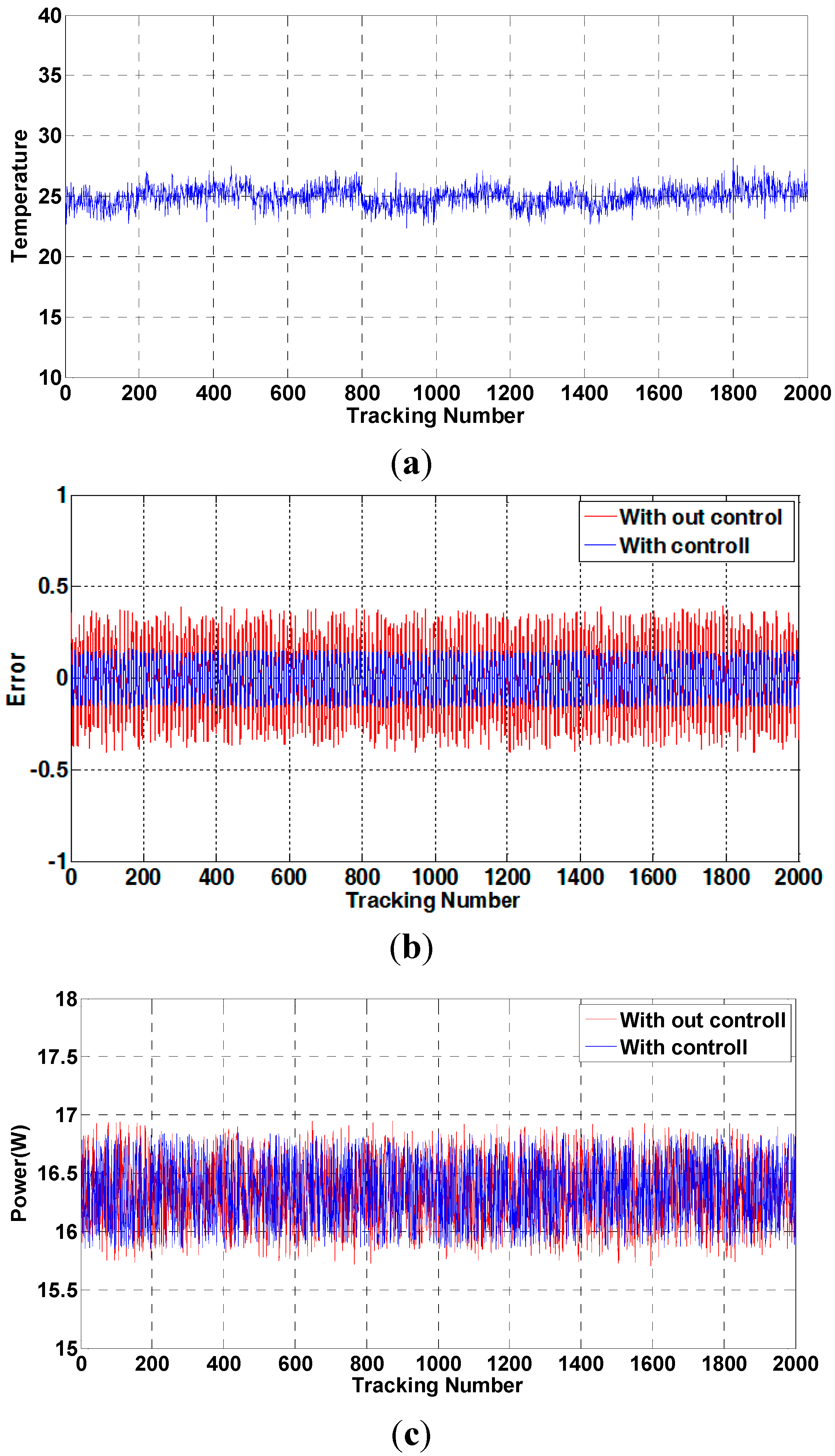
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Di Silvestre, M.L.; Graditi, G.; Riva, S.E. A generalized framework for optimal sizing of Distributed Energy Resources in micro-grids using an Indicator-Based Swarm Approach. IEEE Trans. Ind. Inf. 2014, 10, 152–162. [Google Scholar] [CrossRef]
- Kadri, R.; Gaubert, J.P.; Champenois, G. An Improved Maximum Power Point Tracking for Photovoltaic Grid-Connected Inverter Based on Voltage-Oriented Control. IEEE Trans. Ind. Electron. 2010, 58, 66–75. [Google Scholar] [CrossRef]
- Bendib, B.; Belmili, H.; Krim, F. A survey of the most used MPPT methods: Conventional and advanced algorithms applied for photovoltaic systems. Renew. Sustain. Energy Rev. 2015, 45, 637–648. [Google Scholar] [CrossRef]
- Salas, V.; Olías, E.; Barrado, A.; Lázaro, A. Review of the maximum power point tracking algorithms for stand-alone photovoltaic systems. Sol. Energy Mater. Sol. Cells 2006, 90, 1555–1578. [Google Scholar] [CrossRef]
- Abdullah, M.A.; Yatim, A.H.M.; Tan, C.W.; Saidur, R. A review of maximum power point tracking algorithms for wind energy systems. Renew. Sustain. Energy Rev. 2012, 16, 3220–3227. [Google Scholar] [CrossRef]
- Aurilio, G.; Balato, M.; Graditi, G.; Landi, C.; Luiso, M.; Vitelli, M. Fast Hybrid MPPT Technique for Photovoltaic Applications: Numerical and Experimental validation. Adv. Power Electron. 2014. [Google Scholar] [CrossRef]
- Yu, K.N.; Liao, C.H.; Yau, H.T. A New Fractional-Order Based Intelligent Maximum Power Point Tracking Control Algorithm for Photovoltaic Power Systems. Int. J. Photoenergy 2015. [Google Scholar] [CrossRef]
- Zheng, S.C.; Wang, L.Y. Research on Charging Control for Battery in Photovoltaic System. In Proceedings of the 6th IEEE Conference on Industrial Electronics and Applications (ICIEA), Beijing, China, 21–23 June 2011; pp. 2321–2325.
- Elgammal, A.A.A.; Sharaf, A.M. Self-regulating particle swarm optimised controller for (photovoltaic-fuel cell) battery charging of hybrid electric vehicles. IET Electr. Syst. Trans. 2012, 2, 77–89. [Google Scholar] [CrossRef]
- Gu, B.; Dominic, J.; Lai, J.S.; Zhao, Z.; Liu, C. High Boost Ratio Hybrid Transformer DC-DC Converter for Photovoltaic Module Applications. In Proceedings of the 27th Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 2048–2058.
- Li, H.; Monti, A.; Ponci, F.; D’Antona, G. Voltage Sensor Validation for Decentralized Power System Monitor Using Polynomial Chaos Theory. In Proceedings of the Instrumentation and Measurement Technology Conference (I2MTC), Austin, TX, USA, 3–6 May 2010; pp. 1633–1643.
- Adinolfi, G.; Graditi, G.; Siano, P.; Piccolo, A. Multi-Objective Optimal Design of Photovoltaic Synchronous Boost Converters Assessing Efficiency, Reliability and Cost Savings. IEEE Trans. Ind. Inf. 2015, 11, 1038–1048. [Google Scholar] [CrossRef]
- Graditi, G.; Adinolfi, G.; Tina, G.M. Photovoltaic optimizer boost converters: Temperature influence and electro-thermal design. Appl. Energy 2014, 115, 140–150. [Google Scholar] [CrossRef]
- Graditi, G.; Adinolfi, G.; Femia, N.; Vitelli, M. Comparative Analysis of Synchronous Rectification Boost and Diode Rectification Boost Converter for DMPPT Applications. In Proceedings of the IEEE International Symposium on Industrial Electronics (ISIE 2011), Gdansk, Poland, 27–30 June 2011; pp. 1000–1005.
- Graditi, G.; Adinolfi, G. Energy performances and reliability evaluation of an optimized DMPPT boost converter. In Proceedings of International Conference on Clean Electrical Power (ICCEP 2011), Ischia, Italy, 14–16 June 2011; pp. 69–72.
- Monti, A.; Ponci, F. Uncertainty Evaluation Under Dynamic Conditions Using Polynomial Chaos Theory. IEEE Trans. Instrum. Meas. 2010, 59, 2825–2833. [Google Scholar] [CrossRef]
- Leung, J.Y.-T.; Zhao, H. Minimizing Sum of Completion Times and Makespan in Master-Slave Systems. IEEE Trans. Comput. 2006, 55, 985–999. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Curran, P.F.; Chua, L.O. Robust synthesis for master-slave synchronization of Lur’e systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1999, 46, 846–850. [Google Scholar] [CrossRef]
- Kuo, C.L.; Lin, C.H.; Yau, H.T.; Chen, J.L. Using Self-Synchronization Error Dynamics Formulation Based Controller for Maximum Photovoltaic Power Tracking in Micro-Grid Systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 459–467. [Google Scholar] [CrossRef]
- Chen, S.J.; Zhan, T.S.; Huang, C.H.; Chen, J.L.; Lin, C.H. Nontechnical Loss and Outage Detection Using Fractional-Order Self-Synchronization Error-Based Fuzzy Petri Nets in Micro-Distribution Systems. IEEE Trans. Smart Grid 2014, 6, 411–420. [Google Scholar] [CrossRef]
- Lin, C.H.; Chen, S.J.; Chen, J.L.; Kuo, C.L. Using Sprott Chaos Synchronization-Based Voltage Relays for Protection of Micro distribution Systems Against Faults. IEEE Trans. Power Deliv. 2013, 28, 2092–2102. [Google Scholar] [CrossRef]
- Wu, X.J.; Lin, C.H.; Du, Y.C.; Chen, T. Sprott chaos synchronisation classifier for diabetic foot peripheral vascular occlusive disease estimation. IET Sci. Meas. Technol. 2012, 6, 533–540. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, K.-N.; Yau, H.-T.; Liao, C.-K. Development of a Fractional Order Chaos Synchronization Dynamic Error Detector for Maximum Power Point Tracking of Photovoltaic Power Systems. Appl. Sci. 2015, 5, 1117-1133. https://doi.org/10.3390/app5041117
Yu K-N, Yau H-T, Liao C-K. Development of a Fractional Order Chaos Synchronization Dynamic Error Detector for Maximum Power Point Tracking of Photovoltaic Power Systems. Applied Sciences. 2015; 5(4):1117-1133. https://doi.org/10.3390/app5041117
Chicago/Turabian StyleYu, Kuo-Nan, Her-Terng Yau, and Chi-Kang Liao. 2015. "Development of a Fractional Order Chaos Synchronization Dynamic Error Detector for Maximum Power Point Tracking of Photovoltaic Power Systems" Applied Sciences 5, no. 4: 1117-1133. https://doi.org/10.3390/app5041117
APA StyleYu, K.-N., Yau, H.-T., & Liao, C.-K. (2015). Development of a Fractional Order Chaos Synchronization Dynamic Error Detector for Maximum Power Point Tracking of Photovoltaic Power Systems. Applied Sciences, 5(4), 1117-1133. https://doi.org/10.3390/app5041117





