A Novel Method for Determining the Optimal Transition Point from Surface to Underground Exploitation of Dimension Stone

Abstract

This paper introduces a novel method for determining the optimal exploitation contour, that is, the point of transition from surface to underground exploitation of dimension stone. Exploitation of dimension stone is primarily carried out using surface mining from the main plateau, but it can also be done by underground or combined methods. The decision regarding the mining method—surface, underground, or combined—is made before mining operations commence. This occurs during preliminary, pre-investment, and investment studies. The choice of mining method primarily depends on natural, technological, environmental, and economic factors, which together form a group referred to as techno-economic factors that influence the decision in varying proportions. Using the novel method for comparing techno-economic factors, the optimal transition point (OTP) from surface to underground exploitation of dimension stone deposits was determined. The position of the OTP from surface to underground mining of dimension stone is not a constant value; it changes over time and space according to techno-economic factors.

1. Introduction

Selecting an exploitation method is a key decision that should be made at the very start of a project [1,2,3,4,5]. The selection of the method—surface, underground, or combined—depends on factors such as deposit size, shape, and orientation; rock mass properties; mining capacity and losses; recovery rate; overburden volume; machinery capabilities; environmental and social aspects; climate; discount rate; investment costs; mining costs; depreciation; and profit [6,7,8,9]. The primary objective is to find the most favourable mine contour at which exploitation is economically optimal (profitable), while also ensuring that safety and environmental protection requirements are met.

Underground mining offers several advantages over surface mining, including land reclamation, better control of deposit quality, economic value, operational flexibility, improved safety, and lower environmental impact—which is now a key factor [10,11,12,13]. Accurately determining the optimal exploitation contour for surface, underground, or combined mining is essential for minimising financial investment during mine development [14,15,16].

In the literature, the term optimal depth and final contour of an open pit is stated as the contour within which exploitation is technologically, environmentally, and economically acceptable (profitable); however, this does not apply to dimension stone (DS) deposits [17,18]. Most DS quarries do not recognise the concept of optimal depth, as exploitation is primarily conducted above the basic ground level. Furthermore, optimal depth refers to the one–dimensional field of open pits that develop from the surface towards the deeper parts of the deposit, while the final contour denotes the temporal dimension, usually representing the final state of deposit exploitation. Determining the optimal exploitation contour or optimal transition point (OTP) from surface to underground exploitation is important and should be established during the initial planning phases.

Bastante et al. [19] apply optimisation algorithms—traditionally used for non-stratified deposits such as metal ores—to enhance the exploitation of DS deposits by designing, planning, and scheduling exploitation phases. A deposit model was created that included a block and a financial model of the deposit. The block model of the deposit was represented by the number of recoverable blocks, i.e., stone slabs, while the financial model introduced the relationship between the stripping ratio and the stone slabs.

Using a heuristic algorithm based on an economic block model, Bakhtavar and Shahriar [13] compared the values of blocks for both surface and underground mining methods at each horizon. By identifying the first positive-value blocks for underground mining at a given horizon, they determined the transition point, that is, the depth at which surface mining ends and underground mining begins.

Bakhtavar et al. [20] determined the optimal contour for transitioning from surface to underground exploration using a derived economic-mathematical formula. The method is based on the economically justified overall stripping ratio and the permissible stripping ratio. This methodology is applicable to ore deposits that extend from the surface to the depth.

Opoku and Musingwini [21] consider the current method for determining the optimal transition point from surface to underground exploitation to be insufficiently accurate as it is based on static models that do not account for changes throughout the lifespan of the gold mine. The authors argue that the issue should be approached stochastically, developing several exploitation models (surface, underground, and combined methods) for the same deposit. They emphasize the need to consider the sale price and quality of the mineral resource, geological unpredictability of the ore body, market fluctuations, and many other factors. The authors introduce the concept of a temporally variable “transition point” from surface to underground exploitation of gold deposits.

De Carli et al. [22] analyse the optimal transition point from surface to underground mining, using a gold deposit as a case study. They compared several different scenarios involving combined mining methods, as well as evaluating each method separately, with the aim of maximising the project’s net present value and the quantity of exploited mineral resources. The authors emphasize that determining the optimal transition point is crucial for the continuation of exploitation since an incorrectly defined transition point from surface to underground mining can result in unprofitable underground mining due to an insufficient quantity of mineral resources for exploitation, ultimately leading to project termination.

Bakhtavar et al. [23] introduce a stochastic mathematical model that uses a long-term surface mining plan on an integrated block model of surface and underground exploitation to determine the optimal transition point, i.e., the transition from surface to underground mining. In the block model, ore quality is treated as a random parameter of the main function, and changes in ore quality are constrained, with the main function seeking to maximize the net present value when combining surface and underground mining methods.

When determining the optimal depth for transitioning from surface to underground mining, the use of economic block models and Monte Carlo price simulations is introduced. For instance, in the case of a copper mine, an optimal transition depth of 375 m was established [24]. Badakhshan et al. [25] and Bakhtavar et al. [26] explore similar models in their studies, and depending on geological, economic, and environmental parameters, a wide range of optimal transition depths has been identified, from 62.5 m to as much as 950 m.

To maximize the economic value of the project and its prospective mining operations, it is essential to integrate both surface and underground mining methods from the beginning of the project, rather than planning these approaches independently [27,28].

By applying a stochastic approach to optimisation, models that account for uncertainty in geological data and market prices have demonstrated an increase in net present value (NPV) of up to 9% compared with deterministic approaches [29], while in the case of the gold mine, MacNeil et al. [30] achieved an NPV increase of as much as 23%.

When analysing and selecting the optimal transition point from surface to underground mining, it is necessary to consider various aspects such as safety, technical, and other factors to more reliably determine the point of transition from one mining method to another. Dintwe et al. [31], in their work, introduce the use of numerical models that examine potential occurrences of slope instability, ground subsidence, and collapse of underground chambers. Zhang et al. [32] stated that the safety aspects of this type of mining differ from conventional ones and require specialized protocols and training. According to Soltani Khaboushan et al. [33], equally important criteria, which are increasingly being incorporated into decision-making systems and the selection of optimal solutions for a given project, are environmental and social criteria. From an environmental perspective, underground mining results in a reduced environmental impact, such as lower amounts of waste rock and preservation of the surface cover. Badakhshan et al. [34], using the example of the Sungun copper mine, showed that a transition depth ranging from 887.5 to 950 m, even when including environmental costs, resulted in a net present value (NPV) higher than USD 7.5 billion, with 67.7% of the overall impact being economic in nature, whilst environmental and social factors accounted for 41.7% and 39.8% of the total sustainability assessment, respectively.

Afum and Ben-Awuah [35] present in their work a comprehensive review and analysis of the literature by various authors who, over the past decade, have addressed the topic of transitioning from surface to underground deposit exploitation. The authors state that understanding existing tools and methodologies is crucial for planning the transition from one method of exploitation to another.

Despite the availability of advanced tools and models, the timely and comprehensive planning of transitional phases is still not undertaken during the preparation of mining projects, which leads to suboptimal results and potential long-term consequences [36,37].

Extensive scientific research into the transition from surface to underground mining has been conducted on stratified, massive, and irregular metal deposits. However, the scientific literature does not record any research into the optimal transition point from surface to underground exploitation in dimension stone deposits. In this paper, a novel method for determining the optimal transition point from surface to underground exploitation of dimension stone deposits is presented, based on the analysis of techno-economic factors. The optimal transition point represents the economically optimal contour for surface, underground, or combined exploitation of the dimension stone deposit.

The dimension stone exploitation optimisation method (DS-EOM) represents a significant advancement in the modelling and evaluation of the transition from surface to underground mining for dimension stone deposits. In contrast to traditional methods designed for metal and coal deposits, which often utilize static block models, robust grade estimation, and regular deposit geometry assumptions, DS-EOM addresses the complexity and distinctive features of dimension stone deposits. These deposits are defined by heterogeneous recovery rates—where the economic value is tied to the proportion of marketable blocks rather than mineral grade—along with shallow and highly irregular geometries that make traditional block modelling inefficient and less representative. Additionally, dimension stone deposits are evaluated based on block quality and recoverable volume, not grade, necessitating a departure from grade-centric frameworks.

The DS-EOM method models the deposit as a sequence of exploitable layers instead of a detailed block-by-block approach. This layer-based representation is more flexible and better reflects the actual geological and operational conditions found in dimension stone deposits. Within this framework, blocks (block A, block B, and block C) are designated for either surface or underground exploitation, and techno-economic factors are calculated for each scenario to determine the optimal transition point.

A key innovation of the DS-EOM approach lies in its economic modelling process. Unlike earlier methods that require specialized software for techno–economic calculations, DS-EOM utilizes widely available spreadsheet tools, making the process more accessible and facilitating rapid adjustments in response to market changes. Stakeholders can dynamically evaluate profitability, recovery coefficients (which represent the ratio between the volume of commercial blocks and the total volume of exploited mass $\left(k_i\right)$ and depend on the geological conditions within the deposit [38,39,40,41,42]), and cost structures, leading to real-time updates and greater adaptability in project planning. This capability stands in stark contrast to the rigidity of classical, software-dependent approaches, offering clear improvements in terms of flexibility and responsiveness.

Furthermore, DS-EOM prioritizes the direct calculation of economic impacts resulting from variable recovery rates and fluctuating costs. This enables a tailored determination of the optimal transition contour between surface and underground mining that accommodates the changing nature of both market and operational conditions. As a result, the method delivers a more precise, practical, and adaptable solution for identifying the best transition point, addressing the shortcomings of previous methodologies.

By integrating these conceptual and technical innovations, DS-EOM supports improved project planning and operational decision-making in dimension stone exploitation. The method not only enhances the accuracy of transition modelling but also empowers decision-makers with a tool that reflects the true complexity of dimension stone deposits, ultimately driving better economic outcomes and more sustainable exploitation strategies.

Table 1. DS-EOM vs. classical transition models.

Parameter	DS–EOM Method	Classical Transition Methods
Deposit representation	Layer-based, flexible modelling of shallow/irregular geometries	Static block models, best suited for massive/regular deposits
Grade/value modelling	Focuses on heterogeneous recovery rates and block quality/volume, not mineral grade	Relies on robust grade estimation for economic analysis
Economic evaluation tools	Spreadsheet-based, rapid, and accessible updates; enables real-time adjustments to market changes	Specialized mining software; less flexible and slower to adapt to market changes
Recovery rate handling	Explicitly models spatial variability in recovery rates and block quality	Assumes homogeneous or grade-driven recovery
Geometry adaptability	Optimized for shallow, irregular dimension stone deposits	Optimized for deep, regular metal/coal deposits
Optimal transition point determination	Flexible, scenario-based, tailored to deposit specifics and economic conditions	Rigid, often based on static economic cutoffs
Responsiveness to market/operational changes	Highly adaptable—allows dynamic planning and updates as conditions change	Limited adaptability—requires specialized tools and slower recalibration

presents the principal parameters of DS-EOM in comparison with the classical transition methods.

2. Materials and Methods

The DS-EOM, that is, the determination of the optimal exploitation contour, i.e., the optimal transition point (OTP) from surface to underground exploitation, consists of three main components:

• The first section concerns the identification of the area or section of the deposit to be analysed, as well as the characteristics related to the selected area. This section covers all available data for the chosen location. Based on the collected data, three-dimensional models of the deposit and the terrain surface are created.
• The second section concerns the three-dimensional models of the surface and the underground quarry, namely, the final contours of the quarry obtained through the exploitation of optimisation blocks, as well as the quantities of dimension stone (DS) and waste rock. The final contours of the quarry are determined based on design parameters, while the quarry volumes are calculated by measuring the volume of individual three-dimensional model parts.
• The third section involves determining the economic values of the quarry models, that is, defining and analysing the costs ($T_{E-u}$—costs of underground DS exploitation, EUR; $T_{E-s}$—costs of surface DS exploitation, EUR), revenues, profits, and minimum selling prices of dimension stone blocks obtained through surface and underground exploitation. The position of the optimal exploitation contour, or the OTP from surface to underground exploitation, is established based on a comparative analysis of the economic values of the quarry models. In other words, it is determined which mining method should be used in which part of the deposit to maximise profit.

To determine the OTP from surface to underground exploitation, an algorithm has been developed to select between surface, underground, or combined methods of dimension stone deposit exploitation (see Figure 1).

2.1. First Section

To determine the research area and apply the DS-EOM, it is necessary to consider all available data regarding a specific location, provided that the site is suitable for DS exploitation. By analysing all accessible information about the area, a deposit section is selected for which the greatest amount of data collected during exploration is available (such as geodetic data on the terrain surface, exploratory drilling, geological data, structural elements, details about the rock mass of the area, etc.) or a section for which minimal additional exploration of the site and deposit is required (e.g., exploratory drilling and similar activities) so that it can be chosen as the location where the DS-EOM will be applied.

Based on the available geodetic and geological data for the research area, a digital elevation model (DEM) of the terrain surface and a three-dimensional geological model of the deposit were created.

Within the defined research area, a section with the most available exploration data has been selected, and the DS-EOM will be implemented within the boundaries of this identified section of the research model. The optimisation method will be carried out in segments, meaning specific parts of the deposit—blocks within the selected boundaries—will be designated for either surface or underground exploitation. In this study, three blocks (A, B, and C) have been identified for analysis.

2.2. Second Section

For each block (A, B, and C) in the optimisation model, the final contours of both the surface and underground quarries have been designed. The condition was set that each block (A, B and C) in the optimisation model must be fully exploited, regardless of the chosen mining method or the quarry’s final contour. Additionally, it was specified that due to the specifics of each exploitation method, all activities required to commence the exploitation of block A would be considered preparatory works and would not be considered during the economic analysis of the exploitation methods. The final contours of the surface and underground quarries for blocks A, B, and C continue from the preparatory stage, which is the same across all models.

For each block in the exploitation optimisation model, new surface and underground quarries are designed, along with their final contours, to ensure the entire block is fully exploited. Both surface and underground quarries are modelled based on the established values of the design parameters.

The design process is undertaken in a three-dimensional environment. This approach immediately generates models of the final quarry contours, enabling calculation of exploited volumes of DS and waste rock for both surface and underground quarries.

When calculating the quantities of DS, all rock mass losses can be expressed through the recovery coefficient of the DS deposit $\left(k_i\right)$.

2.3. Third Section

The definition of the economic values of quarries (both surface and underground) is necessary to determine the profitability of exploitation, that is, the limit contour at which exploitation becomes economically justified.

Put simply, underground exploitation of DS is more cost-effective than surface exploitation, according to Expression (1), if mining occurs only in DS layers:

$$T_{E-u} < T_{E-s} + T_{o-s} + T_{r-s},$$

(1)

where

• $T_{E-u}$—costs of underground DS exploitation (EUR),
• $T_{E-s}$—costs of surface DS exploitation (EUR),
• $T_{o-s}$—costs of surface overburden removal (EUR),
• $T_{r-s}$—costs of land reclamation (EUR).

To determine the profitability of exploitation, that is, the limit contour at which exploitation becomes economically justified, it is necessary to establish the economic or market values that can be achieved through the sale of mineral raw materials, as well as the total DS exploitation costs. This is primarily carried out at the very beginning, that is, prior to the commencement of mining activities, through preliminary, pre-investment, and investment studies [43]. To enable a comparison of the economic values of block exploitation by either surface or underground mining, identical parameters have been established for all blocks and all methods of exploitation. The analysis covers the following factors: the volume of DS blocks and the economic values of costs, revenues, and profits from exploitation, as well as the unit cost of exploiting DS stone blocks.

The net value of the quarry can be determined using the following expression:

$$V = (V_i - T_i) · Q_t,$$

(2)

where

• $V$—the value of the deposit expressed as the net profit from the sale of DS blocks (EUR),
• $V_i$—market value of commercial DS blocks (EUR/m³),
• $T_i$—average exploitation costs of commercial DS blocks (EUR/m³),
• $Q_t$—total quantity of commercial DS blocks (m³).

Based on the economic values of surface and underground quarries, an analysis of the results of the final quarries contours is conducted [43].

The quantity of commercial blocks is calculated separately for each productive layer, given that different productive layers have different recovery rates. This is done by multiplying the quantity of exploited rock mass from each productive layer by the recovery coefficient for that layer. The quantity of commercial blocks is determined using the following expression:

$$Q_{uk}= {\sum }_1^n{q}_{DS-n}·k_{i-n},$$

(3)

where

• $q_{DS-n}$—quantity of exploited rock mass from the n-th productive layer,
• $k_{i-n}$—recovery coefficient of the deposit for the n-th productive layer.

The costs of surface exploitation $\left(T_{E-s}\right)$ consist of the costs of exploiting the productive layers $\left(T_{DS-s}\right)$, as well as the costs of exploiting the low wall $\left(T_{lw-s}\right)$ and the overburden $\left(T_{o-s}\right)$. The overburden and the low wall are considered waste rock and will not be valued during the economic analysis. The costs of surface overburden removal and the costs of low wall exploitation can be presented together as the cost of waste rock exploitation $\left(T_{w-s}\right)$:

$$T_{w-s}=T_{o-s}+T_{lw-s},$$

(4)

where

• $T_{w-s}$—cost of waste rock exploitation (EUR),
• $T_{o-s}$—cost of surface overburden removal (EUR),
• $T_{lw-s}$—cost of low wall exploitation (EUR).

The total costs of surface exploitation can be represented as the sum of waste rock removal costs $\left(T_{w-s}\right)$, DS exploitation costs $\left(T_{DS-s}\right)$, and land reclamation costs $\left(T_{r-s}\right)$, as shown in the following expression:

$$T_{E-s}=T_{DS-s}+T_{w-s}+T_{r-s},$$

(5)

where

• $T_{E-s}$—total costs of surface DS exploitation (EUR),
• $T_{DS-s}$—exploitation costs for DS (EUR),
• $T_{w-s}$—waste rock removal costs (EUR),
• $T_{r-s}$—land reclamation costs (EUR).

The total costs of underground exploitation $\left(T_{E-u}\right)$ consist of the costs of exploiting the productive DS layers and overburden and low wall.

In underground exploitation of DS, overburden and low walls are considered as waste rock that must be exploited during the exploitation of the DS layer. Analogous to surface exploitation, the costs of overburden removal $\left(T_{o-u}\right)$ and the costs of low wall exploitation $\left(T_{lw-u}\right)$ can be collectively represented as the costs of waste rock exploitation $\left(T_{w-u}\right)$:

$$T_{w-u}=T_{o-u}+T_{lw-u},$$

(6)

where

• $T_{w-u}$—cost of waste rock exploitation (EUR),
• $T_{o-u}$—cost of underground overburden removal (EUR),
• $T_{lw-u}$—cost of low wall exploitation (EUR).

The costs of underground exploitation $\left(T_{E-u}\right)$ can be represented as the sum of the costs of waste rock exploitation $\left(T_{w-u}\right)$ and the costs of exploiting the productive DS layers $\left(T_{DS-u}\right)$. The costs of land reclamation are entirely omitted, resulting in the following expression:

$$T_{E-u}= T_{DS-u}+ T_{w-u},$$

(7)

where

• $T_{E-u}$—total costs of underground DS exploitation (EUR),
• $T_{DS-u}$—exploitation costs for DS (EUR),
• $T_{w-u}$—underground waste rock exploitation costs (EUR).

Through a comparative analysis of the profit from surface and underground exploitation, it is possible to determine the position of the optimal exploitation contour, that is, the location of the optimal transition point from surface to underground exploitation.

3. Determining the Optimal Transition Point from Surface to Underground DS Exploitation—Case Study

3.1. Research Area

The research area, namely, the “Crvene stijene” deposit, is in Bosnia and Herzegovina, approximately 9 km northeast of town Jajce on the southwestern slopes of Mount Ranče, specifically within the narrower locality of Ovčine (Figure 2). Morphologically, the terrain of the research area is hilly, with the lowest elevation at +900 m above sea level and the highest at +1000 m above sea level. The area is covered with forest and grassy slopes, and occasional rock outcrops can be observed.

The “Crvene stijene” DS deposit is characterised by basal layers of carbonate clastics of Senonian age, which are known as “flysch”. The orientation of the layers in the deposit is approximately north–south, which deviates from the usual Dinaric NW–SE orientation. The layer dips range from 5 to 15 degrees, generally towards the east. Two main productive layers have been identified, which will be exploited as DS (see Figure 3).

The first productive layer is composed of coarse-grained carbonate breccias and is positioned lowest both hypsometrically and stratigraphically. Petrographically, it consists of monomict carbonate breccias, which are light reddish to pink in colour. Generally, it is a single layer with a thickness reaching up to around 30 m. The thickness varies along its extent and dip because of the mechanisms of sedimentation and the shape of the floor at the time of sedimentation. This layer is present throughout the entire deposit.

The second productive layer is composed of coarse-grained carbonate clastics. These include carbonate breccias and carbonate breccia conglomerates. It is separated from the first productive layer by a layer of clayey marl conglomerate, up to 50 cm thick, which often contains a reddish bauxitic binder. The colour of this productive layer is mostly in various shades of grey. Transitions from fine-grained breccias to coarse-grained calcarenites are frequently observed. Subsequent processes of cementation and diagenesis have resulted in a very hard and homogeneous rock with a massive habitus [44].

3.2. Site Modelling

3.2.1. Terrain Modelling

The digital elevation model (DEM) of the terrain (Figure 4) was created based on available data from exploration boreholes, accessible geodetic surveys, and the current situation of the surrounding terrain [44]. The data were processed using Bentley OpenRoads Designer software version 24.00.02.25 [45], in which a triangulated DEM of the terrain was created, and an orthophoto image of the terrain was superimposed onto it [46].

In Figure 4, the boundary of the research model is marked in red, the boundaries of the exploitation model are highlighted in blue, and outcrops of rock that are occasionally visible on the terrain are shown in brown.

3.2.2. Deposit Modelling

The geological model of the deposit was created based on data obtained from exploration drilling [44]. For entering data on exploration boreholes (spatial position of the boreholes and information on lithological members), the “gINT” exploration works database was used, in which all data on lithological units are uniformly displayed and processed [47].

In addition to exploration boreholes, geological profiles were also used [44], which were spatially positioned (Figure 5) to create an integrated three-dimensional model of the deposit. This model was obtained by modelling spatially positioned geological profiles and exploration boreholes (Figure 6).

3.2.3. Defining the Blocks of the Exploitation Optimisation Model

The exploitation optimisation method is implemented segmentally within the boundaries of the research model by defining parts of the deposit—exploitation optimisation blocks—that will be exploited using both surface and underground mining methods. The research model is 230 m wide and 210 m long, occupying a total area of 48,300 m². Within the research model, an exploitation optimisation model was selected, measuring 135 m in width and 180 m in length, with a total area of 24,300 m², as this part of the deposit is the most thoroughly explored. Inside the optimisation model, three identical blocks (block A, block B, and block C) have been defined, each with dimensions of 135 m × 15 m × 15 m (width × height × length), representing sections of the deposit to be exploited using both surface and underground mining methods (Figure 7). The base level of exploitation, i.e., the elevation of the blocks, has been set at +890 m above sea level after analysis of the three–dimensional deposit model. It is important to note that the dimensions of blocks A, B, and C may be adjusted according to the unique characteristics of the dimension stone deposit; however, the minimum dimension is constrained by the used mechanization.

In Figure 7, the boundaries of the research model are shown in red, the boundaries of the exploitation optimisation model are shown in blue, and the designated blocks (A, B, and C) to be analysed are highlighted in purple.

3.3. Defining the Exploitation Parameters and Modelling of Surface and Underground Quarries

The dimension stone surface exploitation parameters are defined based on the Main Mining Project for the exploitation of dimension stone of the “Crvene stijene” exploitation field [44].

The preparatory works required to open the surface quarry shown in Figure 8, Figure 9 and Figure 10 are marked in grey and are the same for all surface and underground exploitation models (Figure 11, Figure 12 and Figure 13), and they are therefore not included in the subsequent analysis.

The final contours of the surface quarries were developed by constructing the base plateau at an elevation of +890 m above sea level, and depending on the block being exploited, benches were developed up to the surface of the terrain (Figure 8).

In Figure 8, Figure 9 and Figure 10, the exploitation optimisation blocks are shown in purple, while the final contours of the surface quarry are shown in green.

The design parameters for the “Crvene stijene” underground quarry were determined based on previous successful examples of dimensioning support pillars and chambers in similar working conditions [48,49]. The final contours of the underground quarries were developed at an elevation of +890 m above sea level within the framework of the exploitation optimisation model, using a selective approach of constructing chambers and leaving support pillars (Figure 11, Figure 12 and Figure 13).

In Figure 11, Figure 12 and Figure 13, the contours of the underground exploitation of DS are shown in green, and the support pillars are marked in orange, while the preparatory works are represented in grey. The exploitation optimisation blocks A, B, and C are overlapping the underground quarry contours and are shown in purple.

4. Results and Discussion

4.1. Analysis of Exploited Volumes

An analysis of the volume values of the exploited parts of the deposit, for both surface and underground exploitation, was conducted using OpenRoads Designer software by measuring the volumes of three-dimensional models of the deposit that were exploited.

4.1.1. Surface Exploitation

The overburden and low walls are considered as waste material and are presented as a cost in the economic analysis of surface and underground quarrying operations. The quantities of the first and second productive layers are shown as valuable mineral raw material—DS. Based on the assumption, if the quantities of overburden and low walls are added together, the total amount of waste that needs to be exploited to obtain DS is obtained. This represents the combined volume values for the first and second productive layers for each optimisation block (

Table 2. Quantities of waste rock and DS from surface quarries.

Block—Quarry Contour	Overburden (m3)	Low Wall (m3)	Waste Rock (m3)	II. Productive Layer	I. Productive Layer	DS (m3)	Total (Waste Rock + DS) (m3)
A	61,931	0	61,931	26,284	26,601	52,885	114,817
B	632,208	192	632,400	127,534	163,363	290,897	923,297
C	2,028,787	19,452	2,048,240	213,541	370,971	584,512	2,632,752

).

The total quantity of DS in relation to the amount of waste rock for block A is almost identical (see Figure 13 and Figure 14), while the ratio starts to change, that is, the difference becomes greater for blocks B and C. For block B, the quantity of waste rock is more than twice the total amount of DS, and the ratio increases further for block C, where it is nearly four times greater. The quantity of waste rock associated with blocks B and C exhibits an upward trend. This increase is due to the parameters of the DS layers, which are dipping relative to the base plateau. As the DS layers dip further away from the base plateau, a greater volume of overburden must be removed to mine the productive layers.

If the quantity of waste rock and DS is expressed as a percentage ratio (see Figure 15), a consistent increase in the amount of waste rock compared with the amount of DS can be observed.

The deposit utilisation coefficient for the first productive layer $\left(k_{i-I}\right)$ is 0.31, and for the second productive layer $\left(k_{i-II}\right)$ it is 0.57 [44]. The product of the quantity of rock mass in the productive layers of DS and the corresponding utilization coefficient represents the total net quantity of DS blocks from surface quarrying (see

Table 3. Total net quantities of DS block from surface quarrying.

Block—Quarry Contour	Quantity of DS Blocks for the I. Productive Layer (m3)	Quantity of DS Blocks for the II. Productive Layer (m3)	Total Net Quantity of DS Blocks (m3)
A	8246	14,982	23,228
B	50,643	72,694	123,337
C	115,001	121,719	236,720

).

4.1.2. Underground Exploitation

Unlike surface mining, in underground exploitation of DS, a selective approach is used with an emphasis on safety as the surface overburden is not removed; instead, the most valuable parts of the deposit are exploited by creating rooms while leaving the less valuable parts of the deposit in protective pillars. This method of exploitation is known as the room and pillar method [50,51], and it is most used in the underground mining of DS.

The calculation of the volume of DS and waste rock in underground mines (

Table 4. Quantities of waste rock and DS from underground quarries.

Block—Quarry Contour	Overburden (m3)	Low Wall (m3)	Waste Rock (m3)	II. Productive Layer	I. Productive Layer	DS (m3)	Total (Waste Rock + DS) (m3)
A	274	0	273	5297	11,227	16,523	16,797
B	1260	136	1396	26,439	110,844	137,283	138,679
C	1303	13,482	14,785	28,589	235,121	263,710	278,496

) was carried out using the same methodology as for surface exploitation.

The quantity of DS for all underground mining optimisation blocks is higher compared with the quantity of waste rock (Figure 16). For block A, the DS quantity is about 60 times greater than the amount of waste rock. In block B, this difference is even more pronounced, with the ratio of DS to waste rock exceeding 98 times, while for block C, the ratio stands at 18 times. The increase in the amount of waste rock for block C is due to the position of the mining optimisation block C and in relation to the deposit, specifically the location of productive DS layers and waste rock.

By comparing the percentage ratios of waste rock and DS, it is evident that the proportion of waste rock in the total quantity of exploited rock is below 10% (Figure 17).

Analogous to the calculation of the volume of DS blocks obtainable through surface quarrying for the I. and II. productive layers, the total quantities of DS block that can be obtained by underground mining of productive layers have been calculated (

Table 5. Total net quantities of DS block from underground quarrying.

Block—Quarry Contour	Quantity of DS Blocks for the I. Productive Layer (m3)	Quantity of DS Blocks for the II. Productive Layer (m3)	Total Net Quantity of DS Blocks (m3)
A	3480	3019	6499
B	34,362	15,070	49,432
C	72,888	16,296	89,183

).

4.2. Economic Values of Surface and Underground Quarries

The optimal transition point (OTP) from surface to underground mining of dimension stone is influenced by key parameters like the discount rate, stone price, and recovery coefficient. A higher discount rate reduces the present value of future revenues, potentially delaying the transition, while a lower rate might justify an earlier transition. Fluctuations in stone prices directly impact profitability, with higher prices favouring an earlier transition and lower prices delaying it. The recovery coefficient, representing the efficiency of stone extraction, also plays a crucial role; higher recovery rates may lead to an earlier transition to underground mining, while lower rates could extend surface operations. By analysing these parameters, we can better understand the proposed method under varying conditions.

The average market value of commercial DS blocks for the “Crvene stijene” deposit has been determined to be 300.00 EUR/m³ [44].

For the calculation of net profit, it is necessary to express the exploitation costs, bearing in mind that the costs of surface and underground exploitation differ since each method has its own specific characteristics.

4.2.1. Surface Quarries Exploitation Costs, Revenue, and Profit

Trial exploitation has determined that the costs of removing the surface overburden are in total 27.52 EUR/m³. According to Jesenko et al. [52], the exploitation costs for the DS layer amount to 27.83 EUR/m³ for a deposit with characteristics like the “Crvene stijene” deposit, and according to Bojčetić et al. [44], the costs of land reclamation are 6.00 EUR/m³. By summing up the individual costs, the total cost of surface DS exploitation comes to 61.35 EUR/m³.

The dominant costs of surface exploitation (

Table 6. Surface exploitation costs.

Block—Quarry Contour	Overburden Removal Costs (EUR)	Low Wall Removal Costs (EUR)	DS Exploitation Costs (EUR)	Land Reclamation Costs (EUR)	Total Surface Exploitation Costs (EUR)
A	1,704,077	0	1,471,951	317,312	3,493,340
B	17,395,613	5355	8,096,494	1,745,379	27,242,840
C	55,823,367	541,428	16,268,665	3,507,072	76,140,533

and Figure 18) for all analysed optimisation blocks are the costs of removing the surface overburden, which for block A account for almost half of the total costs (48.78%). With the exploitation of blocks B and C, these costs increase significantly, and for block C they represent almost three-quarters of the total costs (73.32%). The second most significant costs are DS exploitation costs, the share of which in the total costs decreases—essentially halving from block A to block C.

Through a comparative analysis of total costs (Table 6), profit, and revenue from surface exploitation (

Table 7. Revenue and profit from surface exploitation.

Block—Quarry Contour	Revenue from Selling DS Block (EUR)	Surface Exploitation Profit (EUR)
A	6,968,477	3,475,137
B	37,000,989	9,758,149
C	71,015,850	−5,124,683

), an economic analysis of the surface quarry was obtained, which is presented in Figure 19. For block A, there is almost equalization of costs and profit, while the revenue from the sale of DS blocks is almost twice as high as the profit, that is, the costs of surface exploitation. In the case of block B, the total costs of surface exploitation increase, but so does the revenue from the sale of DS blocks, and the profit from surface exploitation rises by approximately three times. Although the revenue for block C is significantly higher compared with the previous blocks, the profit from surface exploitation is negative, meaning the surface quarry operates at a loss as the total costs of surface exploitation exceed the revenue generated from the sale of DS blocks.

Surface exploitation costs rise non-linearly as terrain elevation increases due to the disproportionately greater volume and complexity of overburden that must be removed. This means that each new mined block not only adds more overburden to be removed but also requires longer haulage distances and more intensive site management, further increasing costs at an accelerating rate.

Key geological and geographical factors exacerbate these cost increases. A steeper geological dip can force the quarry to follow less accessible stone layers, requiring more mining and support. Challenging terrain morphology—such as rugged or uneven ground—demands extra preparation, specialised equipment, and sometimes additional infrastructure such as roads or drainage. Blocks farther from the quarry entrance mean materials must be transported over longer distances, increasing fuel and labour requirements.

4.2.2. Underground Quarry Exploitation Costs, Revenue, and Profit

Jesenko et al. [52] determined that for a deposit with characteristics like the “Crvene stijene” deposit, the total cost of underground exploitation of the DS layer amounts to 45.53 EUR/m³.

An analysis of the underground exploitation costs (

Table 8. Underground exploitation costs.

Block—Quarry Contour	Overburden Removal Costs (EUR)	Low Wall Removal Costs (EUR)	DS Exploitation Costs (EUR)	Total Underground Exploitation Costs (EUR)
A	12,468	0.00	752,311	764,779
B	57,362	6201	6,250,577	6,314,140
C	59,343	613,838	12,006,862	12,680,043

and Figure 20) reveals that the dominant costs are those related to the exploitation of DS, which, for all three optimisation blocks analysed, account for an average of 97% of the total costs of underground exploitation. The costs of removing the waste for blocks A and B are below 2%, while for block C these costs are slightly above 5%.

Through a comparative analysis of total costs (Table 8), profit, and revenue from underground exploitation (

Table 9. Revenue and profit from underground exploitation.

Block—Quarry Contour	Revenue from Selling DS Block (EUR)	Underground Exploitation Profit (EUR)
A	1,949,788	1,185,009
B	14,829,601	8,515,461
C	26,755,0077	14,074,964

), an economic analysis of underground quarries was obtained, which is presented in Figure 21. For block A, a relatively similar situation is observed as with block A of surface exploitation, except that the profit exceeds the total costs of underground exploitation. The profit from underground exploitation continues to increase for block B and is more than seven times higher compared with block A. The upward trend continues for block C, although the profit compared with block B has increased by less than double, the reason for this being the increase in total underground exploitation costs due to the occurrence of low wall, which represents an additional cost.

4.2.3. Comparative Analysis of Quarry Values

A comparative analysis of the total quantities of blocks from surface and underground exploitation (Figure 22) shows that for block A, the quantities of blocks obtained through surface exploitation are approximately four times greater than the total quantities of blocks that can be obtained through underground exploitation. For block B, the quantities of DS blocks obtained by surface exploitation are roughly three times higher than those obtained by underground exploitation, which is also the case for block C.

An analysis of the total costs of surface and underground exploitation (Figure 23) shows that from block A to block C, the total costs of surface exploitation are higher compared with the total costs of underground exploitation. For block A, the costs of surface exploitation are approximately five times higher than the costs of underground exploitation; for block B, the ratio is more than four times, while for block C, it amounts to six times. Additionally, the total costs of surface exploitation increase exponentially, whereas the total costs of underground exploitation rise relatively linearly. The reason for the increase in the total costs of surface exploitation is the growing share of overburden removal costs, which is dictated by the terrain and deposit configuration. In contrast, the costs of underground exploitation are related to the costs of productive layer exploitation.

Analysis of the total revenues from the sale of DS blocks (Figure 24) shows that for block A, there is a difference of approximately four times in favour of revenues from the sale of DS blocks obtained through underground exploitation. For block B, the revenue from the sale of DS blocks through surface exploitation is roughly three times higher than that from underground exploitation, which is also the case for block C. The revenue generated by surface exploitation is considerably higher than that from underground exploitation because greater quantities of DS are obtained by surface methods as parts of the deposit above the boundaries of the optimisation model are also exploited, which is not the case with underground exploitation.

The results of the comparative analysis of the profits from surface and underground exploitation (Figure 25) show an almost linear increase in the profit from underground exploitation across all blocks, that is, the final contours of the underground quarries. The profit from surface exploitation for block A is positive, as is the case for block B. The profit curve from block A to B shows growth; however, after block B, the situation changes, and the curve indicates a decline in profit as the profit for block C is negative. Between blocks B and C, the profits from surface and underground exploitation become equal, and the optimal point for the transition from surface to underground exploitation is identified—namely, the optimal exploitation contour for the DS deposit.

The optimal transition contour or optimal transition point (OTP) is situated between blocks B and C. However, determining the precise location of the OTP requires a more granular approach. This can be achieved by introducing additional blocks within this interval, which will allow for a more precise determination of the OTP. By refining the block segmentation between B and C, it becomes possible to accurately identify the specific location where the shift from surface to underground exploitation should occur. It should be noted that the OTP does not primarily define the optimal depth; rather, it defines the spatial and temporal position for shifting from open pit to underground DS deposit exploitation.

5. Conclusions

One of the challenges in DS exploitation is adapting the exploitation method to the deposit conditions; thus, the same deposit can be exploited by surface, underground, or even a combined method. Given that both exploitation methods differ in their approach and that various techno-economic factors affect each method to different extents, it is essential to accurately define the point at which it is necessary to switch from surface to underground exploitation should the deposit conditions require it.

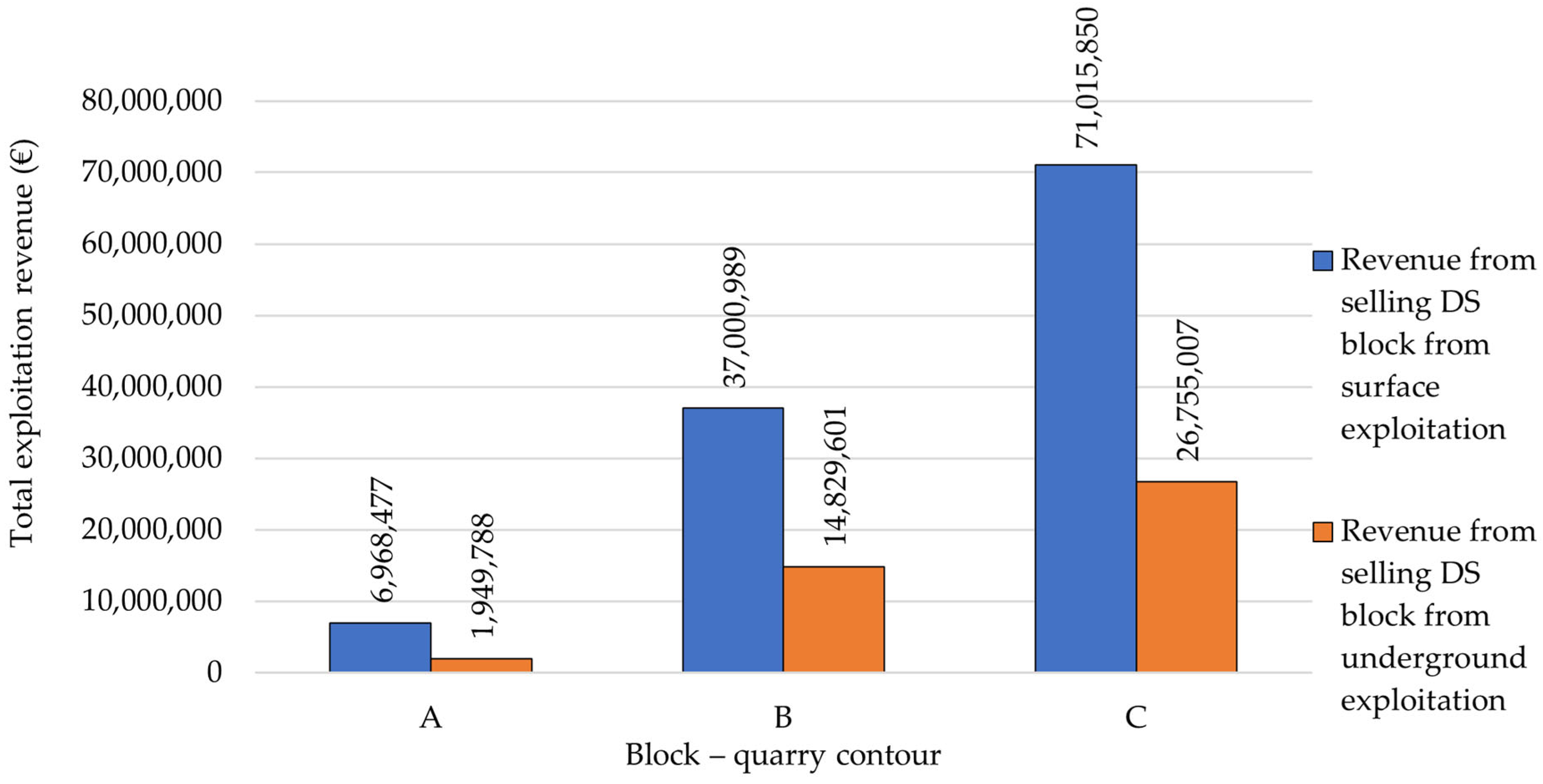
To determine the optimal exploitation method for DS based on the location of mining activities, a research model was selected. Three optimisation model blocks (A, B, and C) were identified, each of which was analysed for the possibility of applying both exploitation methods.

A comprehensive analysis of techno-economic factors—including recovery rates, exploitation costs, revenue generated from the sale of DS blocks, and overall profit—was conducted for each block to determine the optimal transition point (OTP) from surface to underground quarry exploitation. When assessing these techno-economic factors, it is essential to adapt them to the specific conditions present within the deposit, as well as to the prevailing economic circumstances at the location where the method is to be applied.

The DS-EOM method is specifically designed for the determination of the optimal transition point between surface and underground exploitation in dimension stone (DS) deposits. Its application is most effective in deposits where both exploitation methods are technically feasible and where there is sufficient geological, geometric, and economic data to support detailed techno-economic analysis. The method is applicable regardless of the specific lithology or geometry of the DS deposit, provided that the deposit can be discretised into blocks for comparative evaluation. However, the accuracy and reliability of the DS-EOM approach are contingent upon the quality and resolution of input data, as well as the appropriateness of the economic parameters used. The method may be less suitable for deposits with highly irregular geometries or complex tectonic settings or where the economic or technical feasibility of either exploitation method is fundamentally constrained.

Furthermore, as an opportunity for further research, development, and application of this method, a software solution could be created that would enable the new methodology to be efficiently, quickly, simply, and accurately applied depending on deposit conditions. Additionally, the accuracy of the method can be further improved by introducing additional blocks in the analysis. This refinement would allow for a more precise determination of the optimal transition point (OTP), ensuring that the shift from surface to underground exploitation is identified with greater exactness.