FMCW LiDAR Signal Processing Using EMD and Wavelet Transform for Gaussian Noise Suppression

Abstract

Frequency-modulated continuous-wave (FMCW) light detection and ranging (LiDAR) is a high-precision ranging and imaging system that has been widely used in various areas, such as self-driving vehicles and industrial inspection. However, during detection, the system is susceptible to noise interference. This interference results in a decrease in the signal-to-noise ratio (SNR) of mixed signals, which affects the ranging accuracy. In this study, a MATLAB r2021b simulation is used to generate LiDAR transmitted and echo signals, and Gaussian noise is introduced. After mixing, empirical mode decomposition (EMD) and wavelet transform (WT) are used to denoise mixed signals, and the denoising effects of different wavelet basis functions under different SNRs are analysed. Furthermore, an experimental FMCW LiDAR system is set up to collect practical target echo signals, and the simulation results are validated through experiments under various illumination conditions. The results also show that the noise in FMCW LiDAR signals is dominated by Gaussian noise and that the influence of environmental noise is minimal. The combined EMD-WT denoising algorithm and its wavelet basis optimisation strategy proposed in this study can be directly applied to practical scenarios with strict requirements for FMCW LiDAR signal quality, such as autonomous driving, aircraft navigation, and precision industrial measurement, providing theoretical basis and experimental support for wavelet basis selection and denoising strategies in different noise environments.

1. Introduction

Frequency-modulated continuous-wave (FMCW) light detection and ranging (LiDAR) systems combine continuous-wave radar technology and coherent laser detection technology. Their advantages include their high range, high resolution, high velocity sensitivity, and strong antijamming capability. These advanced sensing tools are applied in the field of precision ranging and 3D imaging [1] and have been widely used in scenarios requiring high-accuracy distance information, such as self-driving [2], industrial inspection, and aircraft navigation [3]. FMCW LiDAR systems modulate laser frequencies into linear frequency modulation (LFM) signals that change with time and use the beat frequencies between transmitted and echo signals for ranging. In theory, distance measurements with millimetre-level accuracy can be achieved by FMCW LiDAR systems. However, during detection, an FMCW LiDAR system is affected by factors such as laser frequency nonlinearity, phase noise, and coherence crosstalk in the optical system, resulting in broader beat frequency signals and decreased signal-to-noise ratios (SNRs), which in turn affect the range resolution accuracy and maximum detection range [4]. FMCW LiDAR signals are susceptible to various noise and distortion factors during acquisition and processing. Therefore, high-quality preprocessing and noise suppression of signals are important for achieving high-accuracy detection [5].

Wavelet threshold denoising and empirical mode decomposition (EMD) are commonly applied to meet the denoising requirements of coherent detection signals [6]. These methods can effectively improve the SNR of a signal while retaining its frequency structure and phase information. In some studies, the potential of these methods for improving ranging accuracy and imaging quality has been verified by applying them to the noise reduction and reconstruction of FMCW LiDAR intermediate-frequency (IF) signals. This approach is effective for system performance optimisation [7].

The core mathematical theory of the wavelet transform (WT) was proposed by French scientists Jean Morlet and Alexandre Grossman in the early 1980s [8,9]. In 1998, Kraus et al. [10] at the Vienna University of Technology in Austria applied WT to the filtering of airborne laser scanning data, significantly improving the accuracy of digital terrain model extraction in complex scenes. In 2019, Hua et al. [11] pointed out that WT can effectively suppress Gaussian white noise in Lidar signals through soft thresholding processing, significantly improve the SNR while maintaining the edge features of the signal, and providing higher-quality waveform data for subsequent target detection. However, its threshold function and decomposition levels still rely on empirical settings and lack an adaptive mechanism for low SNR conditions. In 2021, Wang et al. [12] proposed a nonlinear phase estimation and compensation method based on the synchrosqueezed wavelet transform (SSWT). By employing more precise time-frequency analysis to suppress noise and errors, the system’s SNR and resolution ultimately increased, thereby improving the imaging quality of FMCW LiDAR systems. However, it does not conduct a comparison of multiple wavelet basis functions.

EMD was first proposed by Huang et al. [13] in 1998. This technique is applied to decompose complex signals into a series of intrinsic mode functions (IMFs). In 2018, Chang et al. [14] proposed a LiDAR signal denoising method based on correlated-based EMD combined with soft threshold. By distinguishing the relevant and irrelevant IMFs through correlation coefficients and processing them separately, useful information was effectively extracted, achieving a 22.25 dB SNR improvement and a detection range extension of 11 km. It demonstrates superior denoising performance and signal integrity retention capability. However, the setting of regularisation parameters and soft thresholds has a significant impact on the final denoising performance, lacking an adaptive mechanism. In 2020, Zhang et al. [15] proposed a new denoising method based on EMD for processing spatial full-waveform LiDAR signals effectively improving the SNR through signal decomposition and noise removal. In 2023, Jindal et al. [16] applied EMD to denoise differential absorption LiDAR signals and verified the effectiveness of this technique in processing nonlinear and nonstationary signals through experimental analysis. The results showed that this method can adaptively suppress noise while preserving the key features of the original signal.

In this paper, a denoising algorithm that integrates EMD and the WT is employed. By leveraging EMD’s adaptive decomposition capability for nonstationary signals and the WT’s multiresolution analysis advantage in the time-frequency domain, the performance differences in various wavelet basis functions in denoising FMCW LiDAR signals with Gaussian noise is investigated. An experimental platform is established to validate the algorithm’s effectiveness and applicability, providing theoretical foundations and practical guidance for optimal wavelet basis selection and denoising strategy formulation across diverse noise environments. In addition, in view of the deficiencies of the aforementioned research in terms of adaptability and parameter robustness, this paper adopts the dynamically determined decomposition levels and thresholding strategy based on adaptive criteria, which significantly improves the denoising performance and waveform fidelity of LiDAR signals under low-SNR conditions.

The denoising framework and selection criteria proposed in this study provide important reference value for advancing the practical engineering applications of high-precision LiDAR in key fields such as autonomous driving environment perception, precise positioning of industrial robots, and autonomous obstacle avoidance of aircraft.

2. Noise Analysis and Denoising Algorithm Design

In view of denoising FMCW LiDAR signals, the FMCW LiDAR detection process is first analysed, and the main source of LiDAR noise is analysed. Afterwards, the basic theories of WT and EMD are introduced. Finally, the combined EMD-WT denoising algorithm is described, and the implementation process is given in detail to provide a theoretical basis and method framework for subsequent simulation experiments.

2.1. Working Principle of FMCW LiDAR

FMCW LiDAR is based on the principle of coherent detection. High-precision distance measurements are achieved by analysing the beat frequency between the transmitted and echo signals. The detection process consists of four main steps: laser emission, signal propagation, coherent detection, and signal processing [17].

During the laser emission step, the laser generates a continuous-wave light signal, whose frequency varies linearly with time. The typical modulation waveform takes the form of a triangle wave or sawtooth wave, and the frequency modulation (FM) range directly determines the theoretical range resolution of the system [18]. During the signal propagation step, the transmitted light beam is directed towards the target area through the optical system. When the laser beam interacts with the target, part of the energy is reflected to form an echo signal. Owing to the optical path difference, the echo has a time delay relative to the transmitted signal, resulting in a corresponding change in the frequency characteristics of the echo signal. During the coherent detection step, the echo signal and the local reference signal interfere on the surface of the photodetector. This interference process produces a beat-frequency signal that is proportional to the range of the target, and the frequency is jointly determined by the modulation parameters and the range of the target [19]. During the signal processing step, by digitally sampling and performing spectral analysis on the beat-frequency signal, the beat frequency can be extracted to calculate the accurate target range.

2.2. Noise Analysis of FMCW LiDAR

According to the FMCW LiDAR detection process, LiDAR noise can be divided into four types: laser noise, environmental noise, detector noise and digital processing noise [20]. Laser noise includes mainly phase noise and intensity noise. Phase noise broadens the spectrum of the beat-frequency signal and decreases the SNR [21], whereas intensity noise is directly superimposed on the detection signal, increasing the ranging error and false alarm rate [22]. Environmental noise is a noncoherent broadband signal that cannot form a stable beat frequency with the local reference light and thus can be effectively filtered by a coherent detector [23]. The main types of detector noise include shot noise and thermal noise. These noise sources are directly superimposed on the beat-frequency signal during the detection process, reducing the SNR of the system. Digital processing noise includes mainly broadband signals, such as ADC quantization noise and clock jitter [24]. Because the ranging information of the system is encoded in the narrow-band beat-frequency signal, this type of noise has minimal influence on LiDAR. Under normal circumstances, detector noise has the greatest effect [25].

Among the four main types of LiDAR noise, detector noise and a part of digital processing noise are Gaussian noise [26,27].

2.3. WT

The WT represents the signal at different scales and frequencies by projecting the signal onto the wavelet basis function. Through this transform signals are decomposed into approximation coefficients and detail coefficients [28]. The approximation coefficient is the low-frequency component of the signal and describes the main profile and trend of the signal; the detail coefficient is the high-frequency component of the signal and describes the detail, abrupt change and noise of the signal [29]. Noise usually manifests as small-amplitude detail coefficients, and effective signals are concentrated in the approximation coefficients and some large-amplitude detail coefficients. The goal of wavelet threshold denoising is to retain or reduce the detail coefficients through the threshold function, thereby reducing the signal noise [30].

Wavelet threshold denoising requires selecting an appropriate wavelet basis function, the number of decomposition layers, and a threshold. The wavelet basis function must be selected on the basis of the characteristics of the signal to be denoised. In this paper, six types of wavelet basis functions, i.e., the biorthogonal wavelet, Coiflets wavelet, Daubechies wavelet, Fejer–Korovkin wavelet, Symlets wavelet and discrete Meyer wavelet, are selected for comparative analysis. The number of decomposition layers must be adjusted dynamically on the basis of the application performance. If the number of decomposition layers is too small, effectively separating noise and effective signals may not be possible; if the number of decomposition layers is too large, signal distortion may occur, and the effective signals may be filtered out as noise [31]. Thresholds can be divided into hard thresholds and soft thresholds. Coefficients smaller than the threshold are determined to be noise and set to zero; coefficients greater than the threshold are retained or reduced.

The hard threshold function is expressed as follows:

$$w_{hard}(k)=\left\{\begin{array}{c}w(k)\\ 0\end{array}\right.\begin{array}{c},\\ ,\end{array}\begin{array}{c}\left|w(k)\right|>\lambda \\ \left|w(k)\right|\le \lambda \end{array},$$

(1)

The soft threshold function is expressed as follows:

$$w_{soft}(k)=\left\{\begin{array}{c}\mathrm{sgn}\left[w(k)\right](\left|w(k)\right|-\lambda )\\ 0\end{array}\right.\begin{array}{c},\\ ,\end{array}\begin{array}{c}\left|w(k)\right|>\lambda \\ \left|w(k)\right|\le \lambda \end{array},$$

(2)

where $w(k)$ is the original wavelet coefficient and $\lambda$ is the threshold.

2.4. EMD

EMD is a self-adaptive nonlinear signal decomposition method, and the core idea is to decompose noise-containing complex signals into a series of IMFs arranged in a high-to-low-frequency order and a residual component [13], as shown in Equation (3).

$$x(t)={\displaystyle {\sum }_{i=1}^n{c}_i(t)+r(t)},$$

(3)

where $x(t)$ is a complex signal containing noise, $c_i(t)$ is the $i$th IMF component, $r(t)$ is the residual component, and $n$ is the number of IMF components.

After EMD, the noise is concentrated mainly in the high-frequency (lower-order) IMF components, whereas the effective signal is contained mainly in the low-frequency (high-order) IMF components and the residual components. Therefore, during signal reconstruction, some high-frequency IMF components can be discarded, and only the remaining components containing effective signals can be filtered, thereby achieving the goal of noise reduction [32]. The reconstructed signal can be expressed as follows:

$$\tilde{x}(t)={\displaystyle {\sum }_{i=a}^m{c}_i(t)+r(t)},$$

(4)

where $\tilde{x}(t)$ is the reconstructed signal, a is the order of the first retained IMF component, and m is the order of the final retained IMF component.

However, this method has several limitations. Owing to modal aliasing, noise and high-frequency components of the useful signal may coexist in the same IMF, resulting in the loss of some useful information during the denoising process [33]. Therefore, the selection of the threshold affects the final denoising effect.

2.5. Combined EMD-WT Denoising Algorithm

In this study, a combined EMD-WT denoising algorithm based on EMD and wavelet threshold denoising is used. The process is as follows:

• Mixing processing is applied to the transmitted signal and echo signal of the FMCW LiDAR to obtain the beat-frequency signal $S(t)$ containing the target information. EMD is performed on the real part of the beat-frequency signal to obtain $n$ IMF components ($c_1(t)$, $c_2(t)$, ……, $c_n(t)$) and the residual component $r(t)$.
• The signal-dominant IMF components are selected as inputs for subsequent wavelet threshold denoising, and the remaining components are directly retained for signal reconstruction.
• Wavelet threshold denoising is applied to the selected IMFs. First, on the basis of the signal characteristics, the corresponding wavelet is selected as the basis function, Then, the number of decomposition layers is automatically selected on the basis of the energy ratio criterion to ensure that the energy ratio of approximate coefficients is between 0.2 and 0.6 to avoid excessive or insufficient decomposition. Finally, the ddencmp function is employed to adaptively compute the threshold, and the coefficient attenuation is combined to balance denoising effectiveness and signal smoothness.
• The inverse WT is performed on the denoised IMF in the frequency domain to obtain the denoised IMF in the time domain.
• The denoised target IMF component, the unprocessed IMF component and the residual component are superimposed to obtain the final denoised signal:

$$\widehat{S}(t)={\displaystyle {\sum }_{i\in \Omega }\widehat{c_i}(t)+}{\displaystyle {\sum }_{i\notin \Omega }{c}_i(t)+}r(t),$$

(5)

where $\mathrm{\Omega }$ is the set of IMF components after wavelet denoising and $\widehat{c_i}(t)$ is the denoised IMF component.

The decomposition levels and thresholding strategy mentioned above are not fixed empirical values but are dynamically determined based on adaptive criteria. This design ensures that the algorithm can self-adjust according to the noise level and structural characteristics of the input signal, thereby making it applicable to other FMCW Lidar systems.

The proposed method combines the advantages of EMD in adaptive decomposition and the accurate denoising capability of the WT. The specific process of the combined EMD-WT denoising algorithm is shown in Figure 1.

3. Simulation and Analysis

In this study, an FMCW LiDAR signal simulation model is constructed in MATLAB, and the denoising performance of EMD and EMD-WT is systematically compared. The simulation results verify the effectiveness of the combined EMD-WT denoising algorithm under different SNRs. Through quantitative and qualitative analyses, the optimal wavelet basis selection criteria suitable for high- and low-noise scenarios are clarified.

3.1. Signal Simulation

The LiDAR signal simulation and signal processing processes include transmitted signal generation, echo signal simulation, noise addition, mixing processing, EMD, wavelet denoising and signal reconstruction. Finally, the denoising effect is evaluated through time-frequency analysis, spectral comparison, and quantitative indexes.

The FMCW LiDAR signal simulation system is built on the MATLAB platform, and the emitted waveform is a triangular wave. The triangular wave FM signal is divided into a frequency rising section signal and a frequency falling section signal, i.e., a rising edge signal $f_1(t)$ and a falling edge signal $f_2(t)$, and the two formulas are as follows:

$$\begin{array}{l}{f}_1(t)=f_0-{\displaystyle \frac{B}{2}}+K\cdot t\\ f_2(t)=f_0+{\displaystyle \frac{B}{2}}-K\cdot (t-\tau )\end{array},$$

(6)

where $f_0$ is the carrier wave frequency, B is the signal bandwidth, K is the FM slope ($K={\displaystyle \frac{B}{T}}$), T is the signal period, $\tau$ is the time delay of the echo signal relative to the transmitted signal ($\tau ={\displaystyle \frac{2R}{\mathrm{c}}}$), R is the target range, and c is the speed of light. The parameter settings in the simulation are shown in

Table 1. FMCW LiDAR simulation parameters.

Parameter Name	Numerical Value
Speed of light c	$3\times {10}^8\mathrm{m}/\mathrm{s}$
Signal bandwidth B	$4\mathrm{GHz}$
Signal period T	$40.96\mathrm{us}$
$\mathrm{Carrier}\mathrm{wave}\mathrm{frequency}{f}_0$	$0\mathrm{Hz}$
Number of signal sampling points N	20,480
SNR	$10\mathrm{dB}$
Target range R	$15\mathrm{m}$

.

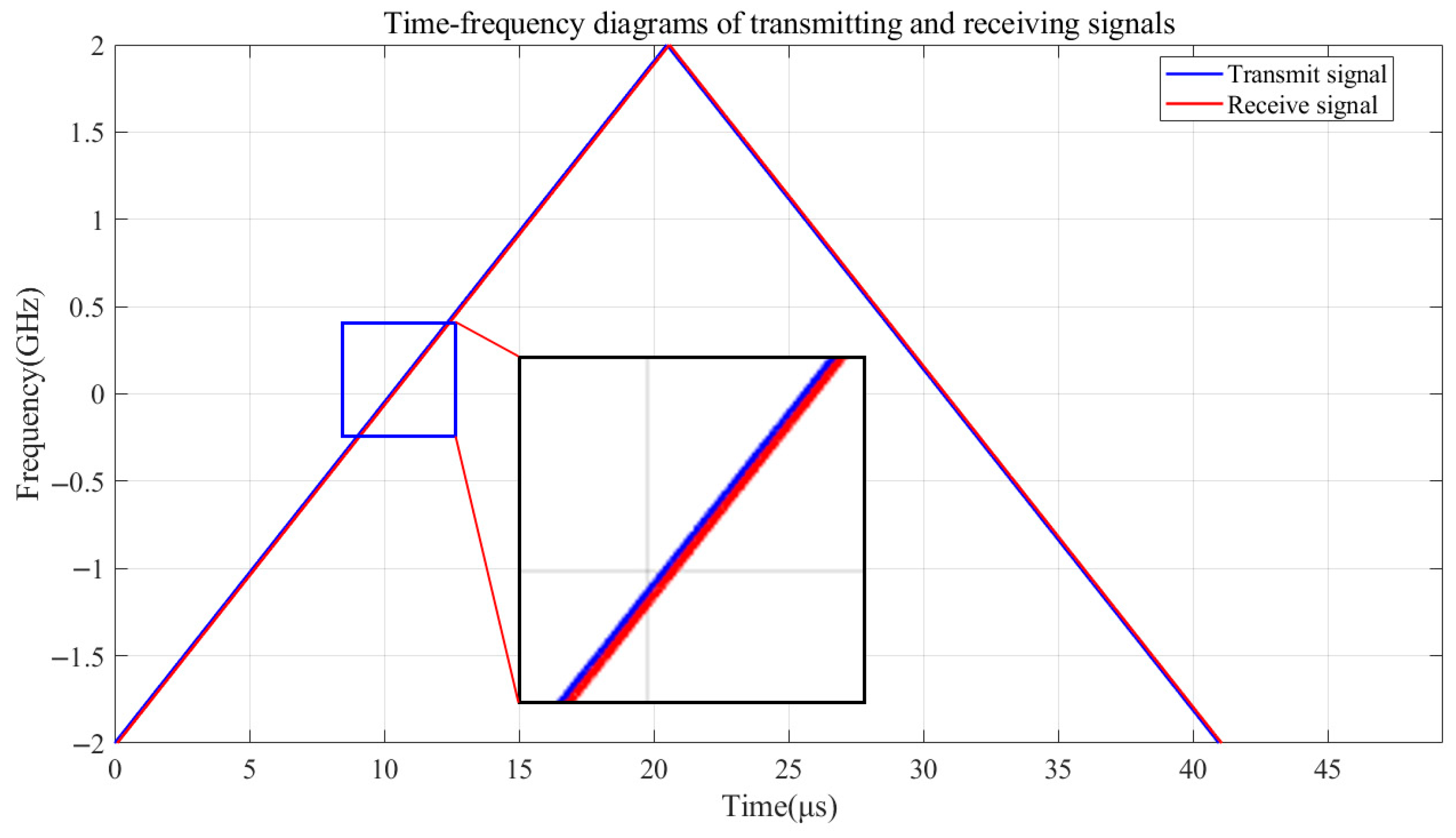
Combining the formulas and parameters, the FM curves of the transmitted and echo signals of the FMCW LiDAR simulated in MATLAB are shown in Figure 2. Because the target range R is relatively small, the time delay $\tau$ of the echo signal relative to the transmitted signal is very small, and the interval between the transmitted and echo signals is very close in the time-frequency diagram.

LiDAR measurements can be contaminated by a variety of noise sources, including a large amount of noise (e.g., thermal noise and shot noise) that is randomly distributed throughout the entire signal and is persistently present throughout the entire measurement process. To simplify the simulation, all the random noises are combined and uniformly modelled as Gaussian white noise. A time-domain comparison of the signal before and after adding noise is shown in Figure 3.

After mixing, the frequency spectra of the rising edge signal and falling edge signal are shown in Figure 4. There is an impulse peak at 156.25 MHz with an amplitude of 26 dB, representing the mixed signal. The remaining peaks arise from noise and must be filtered.

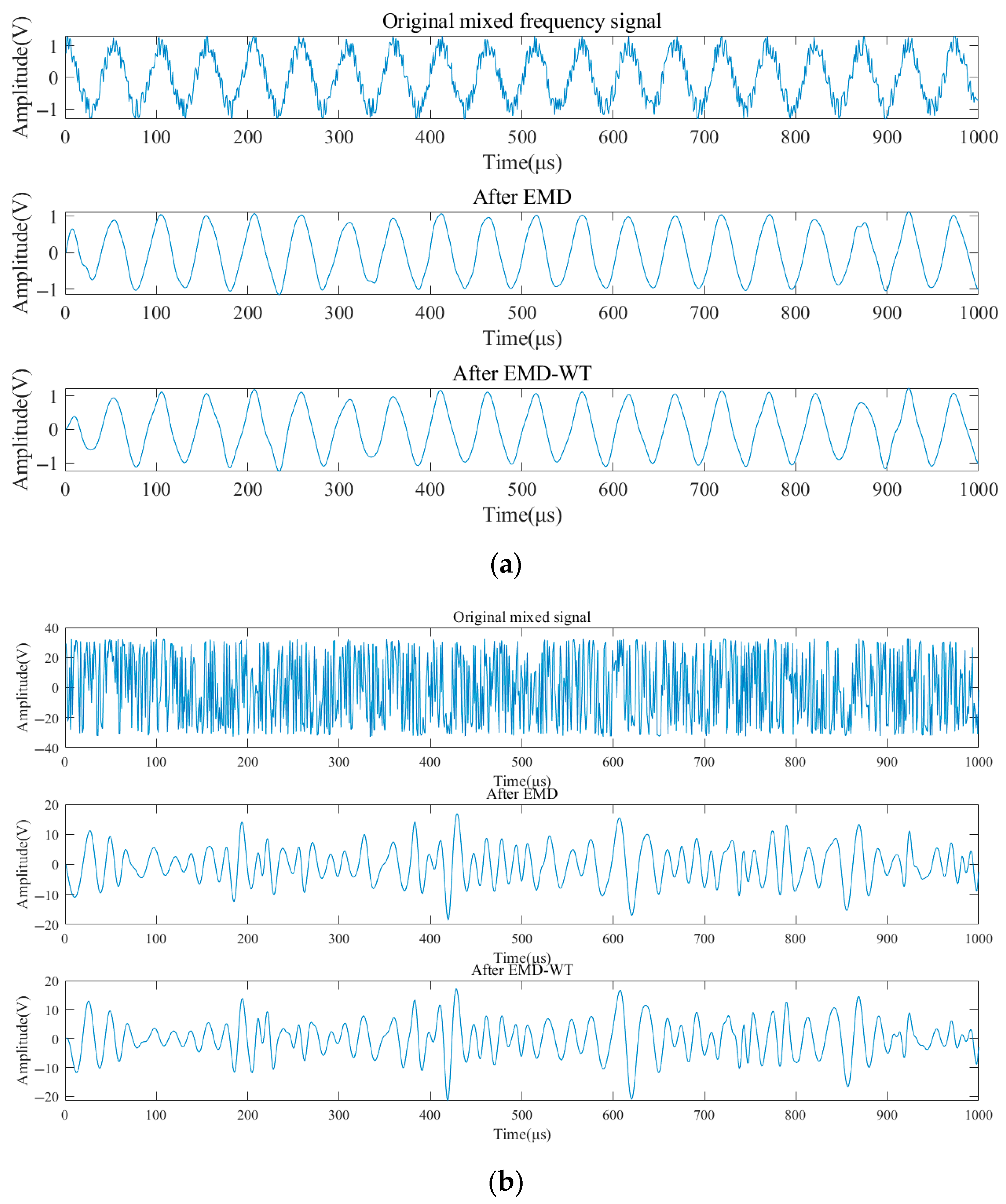
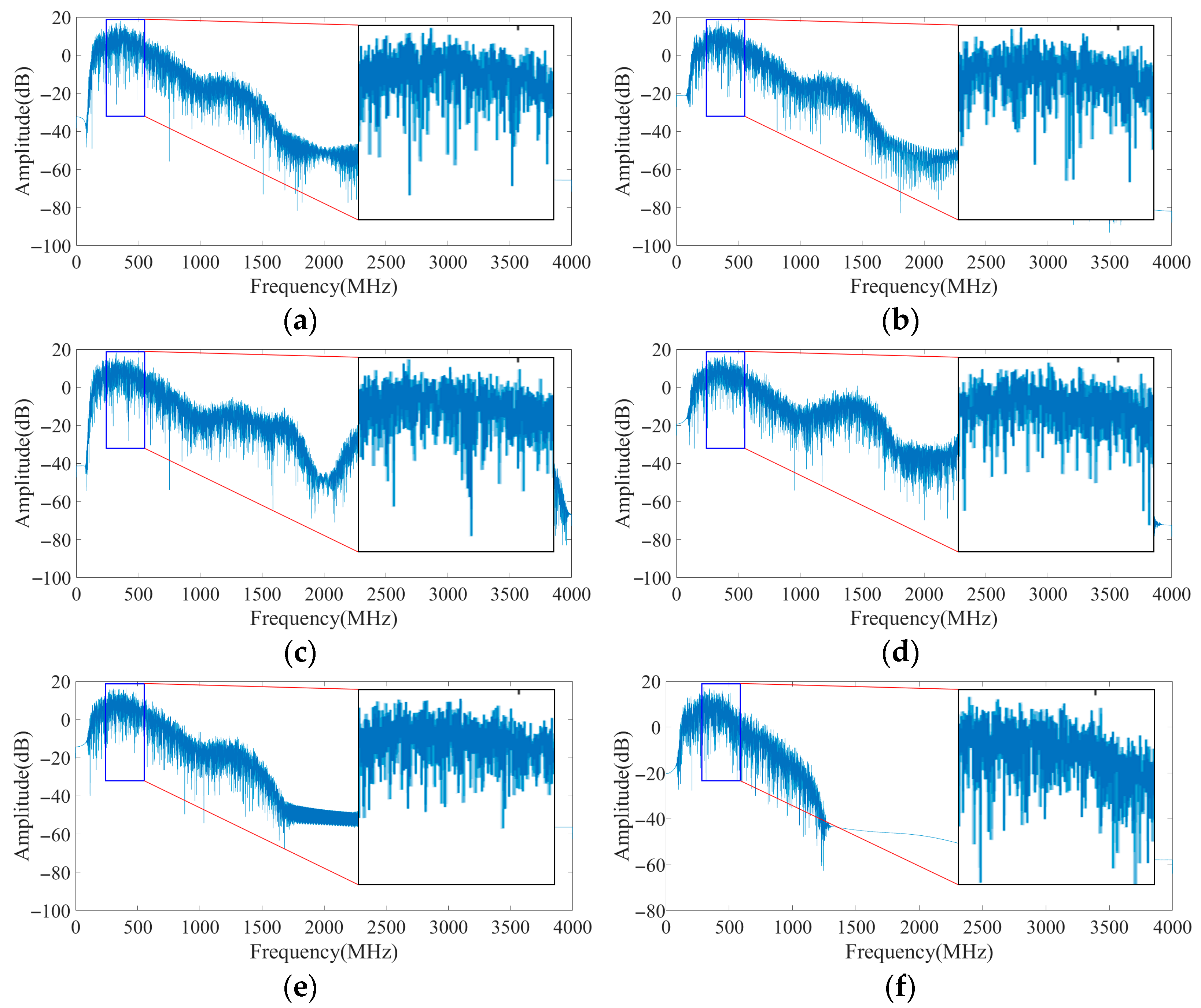
The mixed signal is then denoised. Figure 5 shows a time-domain comparison of the original noise-containing signal, EMD denoised signal, and combined EMD-WT denoised signal. The original signal is severely disturbed by noise, and the amplitude fluctuates drastically. After EMD, the smoothness of the signal improves, but local amplitude distortion is present. After EMD-WT denoising is performed, the noise fluctuations are suppressed, and the amplitude characteristics and trend of the original signal are accurately retained.

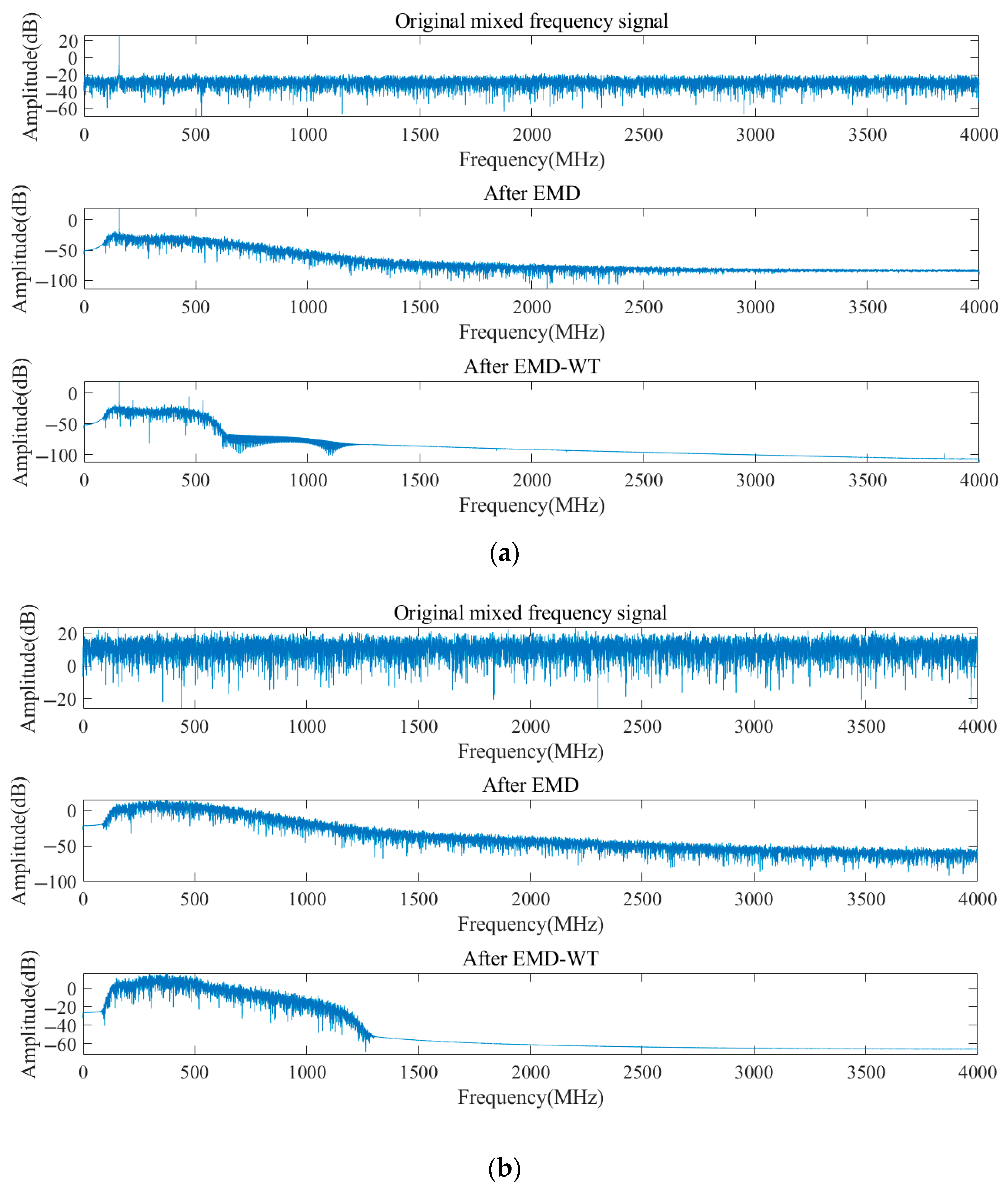
Figure 6 shows the frequency-domain comparison of the three signals. The noise floor in the spectrum of the original noise-containing signal is relatively high, and the peak of the effective signal is masked by the noise. After EMD, the noise floor is reduced to some extent, but residual noise remains near the peak. The noise floor of the EMD-WT denoised signal is significantly reduced, with the peak of the effective signal clearly highlighted and the frequency domain characteristics becoming more pronounced.

3.2. Low-Noise Reduction Simulation and Comparative Analysis

The SNR is used as the denoising performance evaluation index:

$$SNR=10\lg ({\displaystyle \frac{{\displaystyle {\sum }_{k=1}^N{s}^2(k)}}{{\displaystyle {\sum }_{k=1}^N{[s(k)-\widehat{s}(k)]}^2}}}),$$

(7)

where $s(k)$ is the original noiseless signal and $\widehat{s}(k)$ represents the denoised signal. The greater the SNR is, the better the denoising effect.

The six types of wavelet basis functions selected in this study are compared and analysed using MATLAB software: rbio4.4 for the biorthogonal wavelet, coif4.4 for the Coiflets wavelet, dB8 for the Daubechies wavelet, fk8 for the Fejer–Korovkin wavelet, sym8 for the Symlets wavelet, and Demy for discrete Meyer wavelets.

Under low-noise conditions, the frequency spectrum of the signal after EMD-WT denoising is shown in Figure 7.

Under low-noise conditions, the SNRs of the beat-frequency signal, EMD denoised signal, and signal after the EMD-WT denoising are shown in

Table 2. SNR comparison results under low-noise conditions.

Wavelet Basis	Beat-Frequency Signal (dB)	EMD (dB)	EMD-WT/dB
coif4	52.98	56.95	55.62
dB8	52.96	56.74	55.54
fk8	52.96	57.14	55.27
rbio4.4	52.98	59.09	54.69
sym8	52.94	56.83	56.00
Demy	52.94	57.20	57.43

.

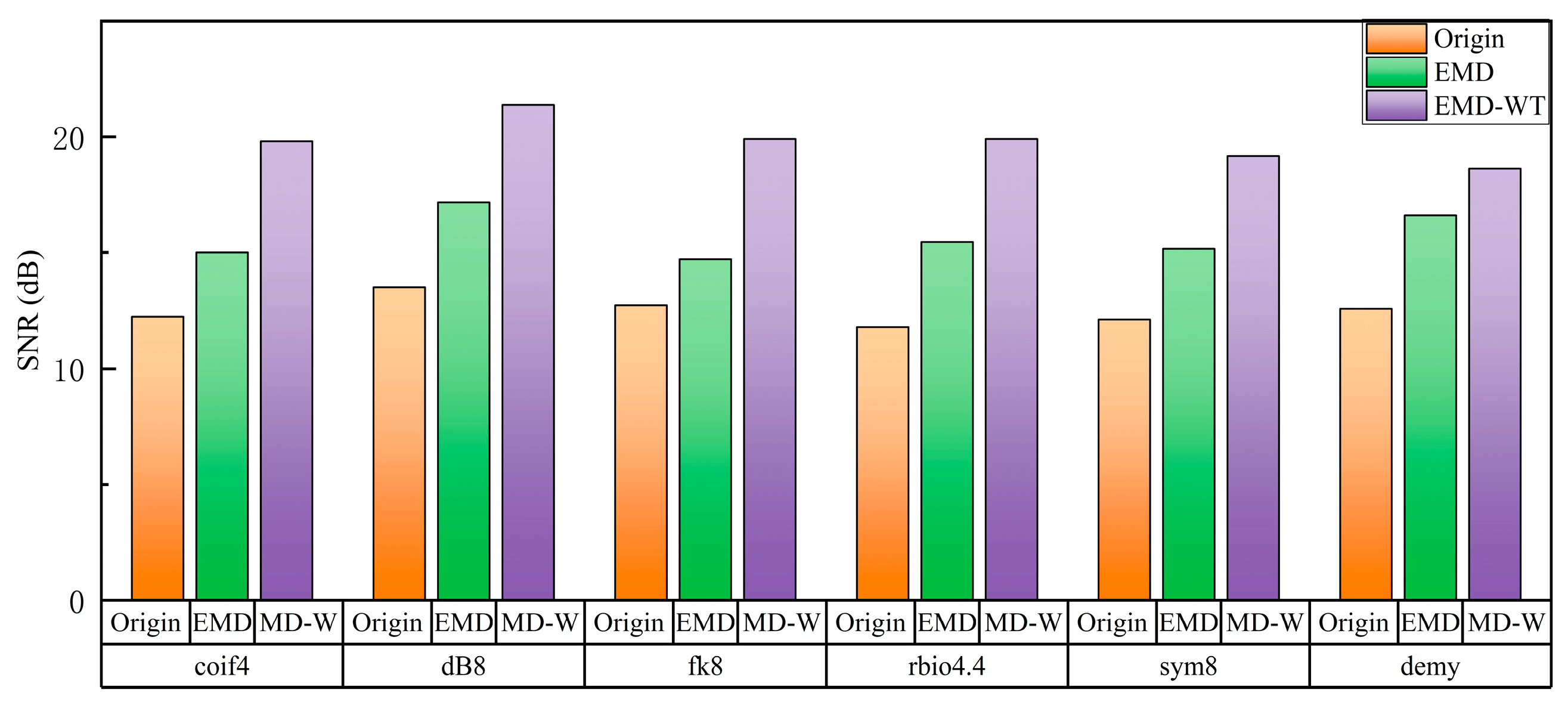
To facilitate comparison, histograms are shown in Figure 8.

Under low-noise conditions, the original signal has a high SNR (approximately 52.94–52.98 dB), and the noise component is relatively weak. At this time, the SNR can be increased to 56.74–59.09 dB by using only EMD and reconstruction, indicating that when the signal is relatively clean, EMD can already satisfactorily separate much of the noise from the useful signal. However, after introducing wavelet threshold denoising, the SNRs of most wavelet basis functions after denoising are not further improved; instead, they decrease slightly.

This phenomenon indicates that under low-noise conditions, excessive wavelet threshold processing may cause the loss of effective signal components, leading to excessive denoising. Nevertheless, the discrete Meyer wavelet (demy) and the Symlets wavelet (sym8) still maintain a relatively high SNR after denoising (57.43 dB and 56.00 dB, respectively), indicating that the excellent frequency domain smoothness and near-symmetrical structure can help preserve signal details more effectively while reducing noise. Therefore, in low-noise environments, a wavelet basis with smooth frequency domain characteristics and minimal phase distortion should be preferred. Alternatively, under some circumstances, only EMD should be used for appropriate denoising.

3.3. High-Noise Reduction Simulation and Comparative Analysis

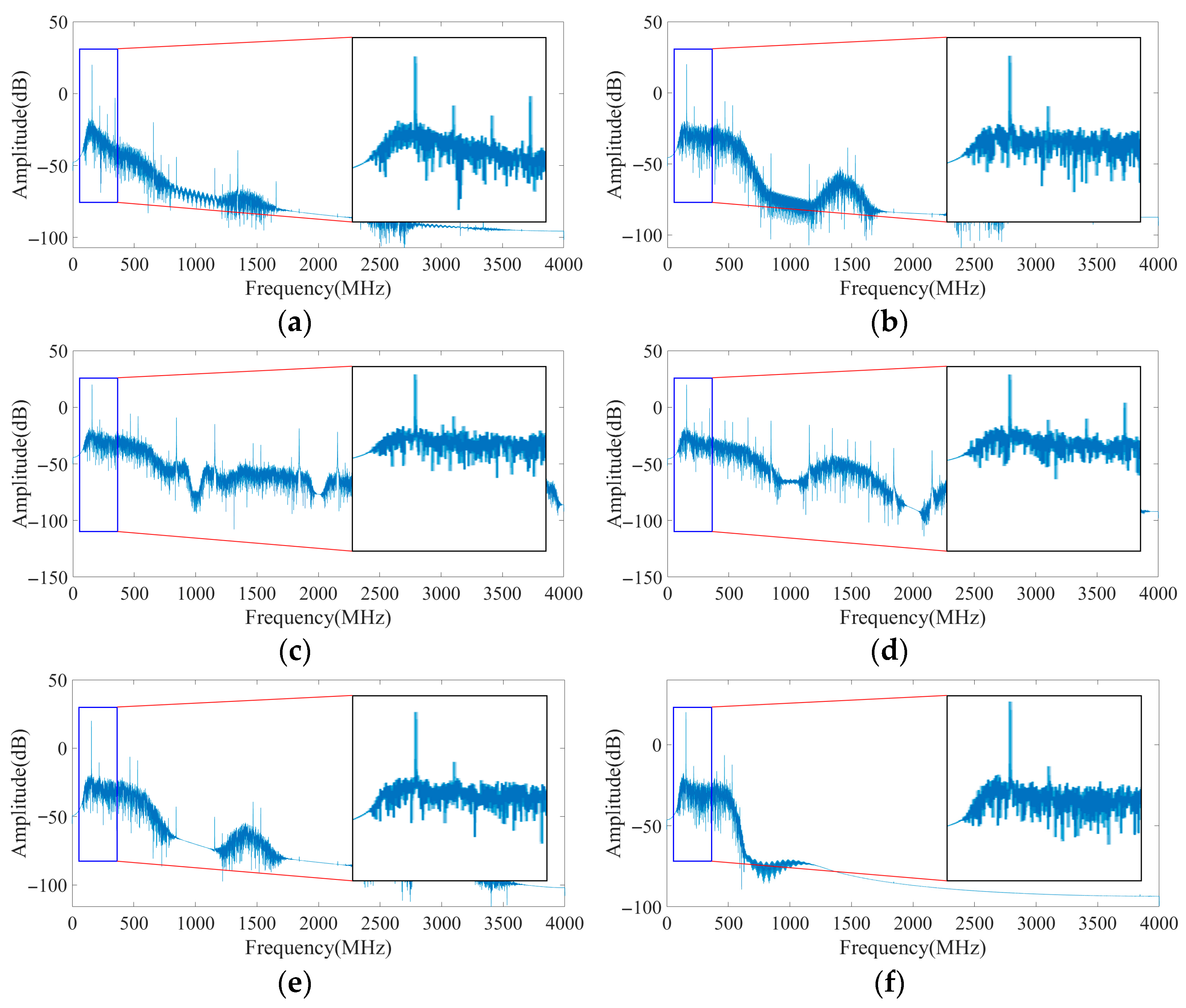
Under high-noise conditions, the frequency spectra of the signal after EMD-WT denoising are shown in Figure 9.

Under high-noise conditions, the SNRs of the beat-frequency signal, the signal after the EMD denoising, and the signal after EMD-WT denoising are shown in

Table 3. Comparison of the SNRs under high-noise conditions.

Wavelet Basis	Beat-Frequency Signal (dB)	EMD (dB)	EMD-WT/dB
coif4	12.24	15.00	19.81
dB8	13.51	17.17	21.38
fk8	12.75	14.72	19.91
rbio4.4	11.79	15.48	19.91
sym8	12.12	15.16	19.16
Demy	12.57	16.60	18.63

.

To facilitate comparison, the histograms are as shown in Figure 10.

Under the high-noise conditions, the SNR of the original beat-frequency signal is relatively low (approximately 11.79 dB–13.51 dB), and the noise interference is severe. After EMD denoising, the SNR of the signal preliminarily increases to 14.72 dB–17.17 dB, indicating that EMD can effectively separate some high-frequency noise. After EMD-WT denoising, a more significant denoising effect is observed for all the wavelet basis functions, and the output SNR further increases to 18.63 dB–21.38 dB, demonstrating the superiority of the combined EMD-WT denoising algorithm in high-noise environments.

The improvement in SNR also reflects the potential enhancement of ranging performance through the denoising process. In FMCW systems, distance information is encoded in the frequency peaks of the beat signal. The increase in SNR results in more distinct spectral peaks and a lower noise floor, which contributes to improved stability in peak detection and greater accuracy in frequency estimation. Consequently, this leads to higher precision and robustness in practical ranging applications.

When comparing the performance of different wavelet basis functions, the Daubechies wavelet (dB8) is most notable. The SNR reaches 21.38 dB after denoising, indicating that the excellent compact support and high-frequency localization capability help effectively preserve signal characteristics in high-noise environments. Biorthogonal wavelet (rbio4.4) and Coiflets wavelet (coif4) also show good overall performance. In contrast, the denoising gain of the discrete Meyer wavelet (demy) is limited in the high-noise environment, which may be due to its limitation in terms of time-domain support. This limitation results in an inadequate ability to suppress nonstationary noise components. The results show that under a high-noise background, a wavelet basis with a strong time-domain localization ability is more suitable for the combined denoising framework.

4. Experiment and Analysis

In this study, an FMCW LiDAR detection system was used to measure the target plate and obtain LiDAR measurement data. Afterwards, a LiDAR measurement data processing programme built in MATLAB was used to read and denoise the data signals and verify the simulation results.

4.1. Experiments

A field experiment was conducted for verification. A LARK LiDAR system from LightIC was used to detect a checkerboard calibration target at a distance of 4 m. The experimental equipment setup is shown in Figure 11. An adjustable power supply was used to power the LiDAR system. An illuminometer was used to measure the light intensity of the LiDAR system. The host computer was used to control the LiDAR system and read the experimental data. A network adapter was used to connect the network ports of the LiDAR systems and the host computer.

Each LiDAR acquisition covered 300 half-cycles. Each half-cycle contained 10 minimum data storage units, and each minimum data storage unit was sampled 2048 times. The processing program was used to extract an entire period from the LiDAR measurement data, consisting of a rising edge and a falling edge. Frequency mixing, EMD, and WT denoising were performed on the rising edge and falling edge signals, and the frequency spectrum was then plotted.

4.2. Experimental Noise Analysis

Experiments were performed under different light intensity conditions. Strong background light corresponds to high environmental noise, and weak background light corresponds to low environmental noise.

The experiments were carried out under background light conditions of 6.7 lux, 57.4 lux, and 106.6 lux, and the wavelet basis function was set to dB8. The frequency domains of the original mixed signal without denoising, the EMD denoised signal, and the EMD-WT denoised signal were compared, as shown in Figure 12.

The SNRs of the beat-frequency signal, the signal after the EMD denoising, and the signal after EMD-WT denoising are shown under different illumination conditions in

Table 4. Comparison of the SNRs under various illumination conditions.

Illumination Intensity/lux	Beat-Frequency Signal (dB)	EMD (dB)	EMD-WT/dB
6.7	16.78	25.70	28.07
57.4	17.33	28.43	29.58
106.6	17.56	28.45	28.86

.

The longitudinal comparison reveals that as the illumination intensity gradually increases, the SNRs of the three types of signals change only slightly, indicating that the background light intensity has minimal influence on the SNR. Therefore, the influence of environmental noise on the FMCW LiDAR system is small, which is consistent with the analysis in Section 2.1.

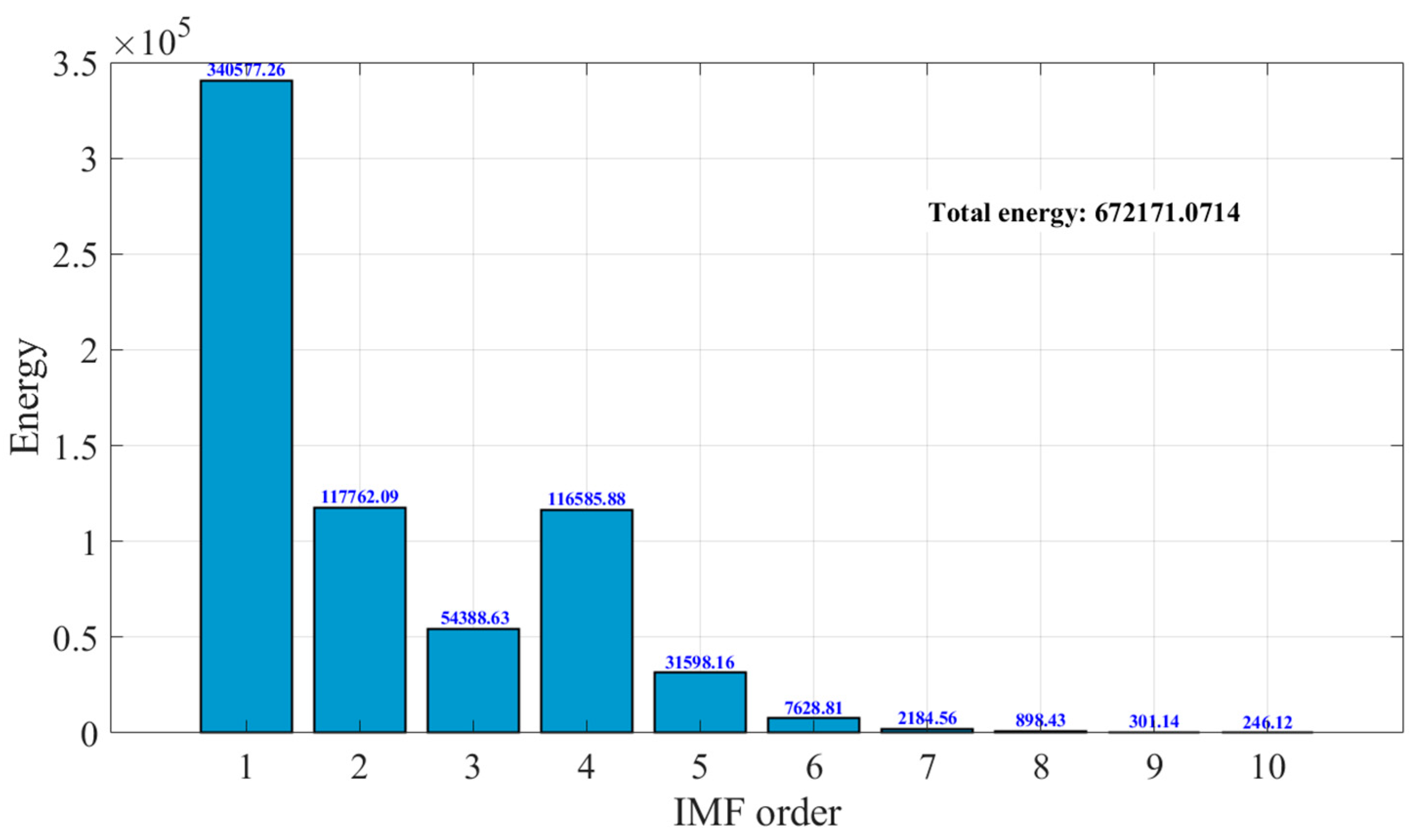
At 6.7 lux, the energy distribution of the signal at each IMF order is shown in Figure 13. The energy of the first- and second-order IMFs account for a very high proportion (approximately 68.2%). Because high-frequency IMF components contain mainly noise signals, the spectrum of high-frequency IMF components can largely reflect the spectrum of noise signals.

At 6.7 lux, the autocorrelation function of the signal at each IMF order is shown in Figure 14. In Figure 14, the high-frequency IMF component is an impulse signal, which is consistent with the low-frequency component of Gaussian noise, indicating that there is a large amount of Gaussian noise in the signal. Therefore, the main noise of the LiDAR system is Gaussian noise. This finding indicates that in Section 3.1, the selection of noise types in the software simulation is reasonable.

4.3. Denoising Experiment and Comparative Analysis

The LiDAR measurement data under 57.4 lux background light conditions were processed using the six selected wavelet basis functions. The frequency spectra of the signal after EMD-WT denoising are shown in Figure 15.

Under the background light condition of 57.4 lux, the SNR of the beat-frequency signal, the signal after the EMD denoising, and the signal after EMD-WT denoising are shown in

Table 5. Comparison of the SNRs at 57.4 lux.

Wavelet Basis	Beat-Frequency Signal (dB)	EMD (dB)	EMD-WT/dB
coif4	17.33	28.43	29.05
dB8	17.33	28.43	30.09
fk8	17.33	28.43	29.58
rbio4.4	17.33	28.43	28.75
sym8	17.33	28.43	29.23
Demy	17.33	28.43	28.01

. Because different wavelet basis functions were used to process the data signal of the same LiDAR measurement, the SNRs of the beat-frequency signals and the signals after EMD were exactly the same among the six groups.

To facilitate comparison, the histograms are as shown in Figure 16.

Under the background light condition of 57.4 lux, after EMD denoising alone, the SNR of the signal increases preliminarily. Except for the demy wavelet, the output SNRs of the other 5 wavelets further improve after applying the combined EMD-WT denoising algorithm. A longitudinal comparison of different wavelet basis functions reveals that dB8 shows the most outstanding performance, achieving a SNR of 30.09 dB after denoising. In addition, rbio4.4 and coif4 also exhibit favourable performance. In contrast, the denoising for demy offers limited gain and may even result in a loss in performance. The simulation results of the denoising algorithm align with the actual conditions described in Section 3.3.

5. Conclusions

The focus of this study was denoising FMCW LiDAR signals, and the EMD-WT denoising algorithm based on EMD and WT was systematically studied. On the basis of the theoretical analysis, software simulation and field tests, the following conclusions are drawn:

• The performance of the combined EMD-WT denoising algorithm is highly dependent on the noise environment and the choice of wavelet basis. The combined EMD-WT denoising algorithm significantly improves the SNR under high-noise background conditions, especially for wavelet basis functions with compact support and high vanishing moments, such as dB8 and rbio4.4. Under low-noise conditions, the advantage of the combined EMD-WT denoising algorithm diminishes. To avoid signal distortion, it is necessary to select wavelet basis functions, such as demy or sym8, that possess strong frequency-domain localization capabilities and good phase-preserving properties.
• The results of the theoretical analysis and field test analysis of the frequency spectrum and autocorrelation function at each IMF order show that Gaussian noise is the dominant form of system noise. Moreover, the experimental results reveal that the environmental noise caused by the change in background light has little influence on the system SNR, thus verifying the inherent strong anti-interference ability of the FMCW LiDAR system.
• Under different noise levels, different denoising algorithms should be selected. Under low-noise conditions, the denoising effect of the EMD algorithm alone is sufficient. The introduction of the WT for further denoising does not produce a significant denoising effect and may even cause a loss in performance. Under high-noise conditions, the use of the combined EMD-WT denoising algorithm is more effective than the use of the EMD denoising algorithm.

In summary, this study not only validates the effectiveness of the combined EMD-WT denoising algorithm in improving the quality of FMCW LiDAR signals but also, more importantly, establishes a complete signal processing strategy through comprehensive comparative analysis, which included noise analysis, algorithm selection, and parameter optimisation. This study holds significant reference value for advancing the high-precision detection capabilities of FMCW LiDAR in complex application scenarios.

However, this study still has the following limitations: Firstly, the algorithm is mainly optimised for Gaussian noise scenarios, and its adaptability to non-Gaussian noise has not been fully evaluated. Secondly, the performance of the algorithm is relatively sensitive to parameters such as the wavelet basis and the number of decomposition layers. Finally, the experiment was conducted under controllable indoor conditions and did not cover complex scenarios such as extreme environments and dynamic targets.

In the future, the combination of more advanced adaptive decomposition methods (e.g., variational mode decomposition (VMD)) and intelligent denoising techniques such as deep learning can be explored to address more complex noise environments.