Abstract
The unified hardening model for clays and sands (CSUH) can adequately represent the stress–strain characteristics of various soil types. However, being an incremental elastoplastic constitutive model, the CSUH model requires extensive iterative computations during parameter identification, resulting in significant computational time. To improve computational efficiency, this study derives the elastoplastic compliance matrix and stress–strain incremental relationships under different stress paths, eliminating the repeated solving of equations typically required during iterative processes. Furthermore, a dynamic step size iterative method is proposed based on the changing slope characteristics of the stress–strain curves. This method divides the total axial strain into two segments: in the initial segment (approximately the first 30% of total strain), where the curve slope is steep, smaller step sizes with arithmetic progression distribution are employed, while in the latter segment (approximately the remaining 70%), characterized by a gentle curve slope, larger and uniformly distributed step sizes are adopted. Comparative analyses between the proposed dynamic step size method and the traditional constant-step iterative method demonstrate that, under the premise of ensuring calculation accuracy, the dynamic step size method significantly reduces the iteration steps from 3000 to 50, thus decreasing the computational time by approximately 47 times. Finally, the proposed method is applied to parameter identification of Fujinomori clay, calcareous sand, and Changhe dam rockfill materials using the CSUH model. The predictions closely match experimental results, confirming the CSUH model’s capability in accurately describing the mechanical behaviors of different soils under various stress paths. The dynamic step size iterative approach developed in this study also provides valuable insights for enhancing computational efficiency and parameter identification of other elastoplastic constitutive models.
1. Introduction
The constitutive relationship of soil, also known as the constitutive model, focuses on the stress–strain behavior of soil, providing a mathematical expression that reflects the complex stress–strain characteristics of soil. It serves as a fundamental theoretical basis in geotechnical engineering and has significant applications in dam construction, railways, and other engineering projects [1,2,3,4]. The Modified Cam-Clay (MCC) model [5,6], a classical elastoplastic constitutive framework, has been widely successful in capturing the mechanical behavior of normally consolidated clay. However, the MCC model shows limitations in capturing the behavior of overconsolidated clays, such as abrupt transitions in stress–strain curves between elastic and plastic responses and an overestimation of peak strength [7]. To better characterize the strain softening and dilatancy behavior of overconsolidated saturated clay, Yao et al. [8,9,10] introduced the Unified Hardening (UH) model based on the MCC model. By modifying only the hardening parameter of the MCC model, the UH model can uniformly describe strain hardening and softening, as well as contraction and dilatancy, in clays with different densities (both normally and overconsolidated clays), demonstrating broad applicability.
In engineering practice, not only clays but also granular soils such as sands, rockfill materials, and railway ballast are encountered. However, the UH model, which is designed for clays, cannot adequately describe the stress–strain behavior of granular soils. To address this, Yao et al. [11] further developed the Unified Hardening model for Clays and Sands (CSUH) based on the UH model. The CSUH model is capable of describing both clays and granular soils and can degenerate into the UH and MCC models, representing a theoretical enhancement and innovative development of the MCC model [12].
Before applying the CSUH model to laboratory experiments and engineering simulations, it is essential to accurately calibrate its parameters. When using inverse methods for parameter calibration, it is necessary to compute the error between the theoretical predictions of the constitutive model and the experimental observations, which requires numerical integration to obtain the theoretical response curves. POPP et al. [13] imported experimental data into Isight and used its optimization algorithms to automatically adjust the model parameters in the finite element software ABAQUS 2025, thereby minimizing the error between the simulated and experimental stress–strain curves for parameter calibration. In recent years, adaptive step-size control in the field of finite element computational methods has received considerable attention in the field of computational mechanics. For instance, Sloan et al. [14,15] proposed an adaptive step-size scheme based on local truncation error estimation, where each substep is computed using both a formula of order p and another of order p + 1. The difference between the results is used to estimate the local error, which then guides the automatic adjustment of the step size. Such methods are known for their robustness and general applicability, especially in finite element integration where the shape of the stress–strain curve is not known a priori. However, these approaches typically require multiple computations and error analyses at each step, resulting in increased computational effort. Other adaptive schemes, such as embedded Runge–Kutta or arc-length methods, are also widely used in related fields.
An alternative approach for computing theoretical constitutive model curves during parameter inversion is explicit iteration [12,16]. Common iterative methods include the forward Euler method and the fourth-order Runge–Kutta method. The fourth-order Runge–Kutta method provides high computational accuracy and stability, but it is computationally expensive. In contrast, the forward Euler method is simple to implement, yet only first-order accurate; when the curves exhibit steep slopes or strong nonlinearities, significant integration errors may occur unless a very small step size is used. Consequently, improving accuracy with the forward Euler method typically requires increasing the number of iterations, which reduces computational efficiency in practical applications.
Among these approaches, the uniform-step forward Euler method is the most commonly used. However, its limited accuracy often necessitates finer discretization, further increasing computational costs. For instance, Yin et al. [17] developed the ErosOpt software for parameter calibration, which can conveniently call the user material subroutine (UMAT) in ABAQUS to compute theoretical response curves for various constitutive models. Nevertheless, because ErosOpt employs the uniform-step forward Euler method and requires assembling the element matrix and solving the system of equations based on boundary conditions at each incremental step, the process consumes significant computational resources, resulting in relatively slow parameter inversion.
Soil stress–strain curves typically exhibit nonlinear characteristics, with significant variations in slope at different stages. Existing methods for solving theoretical constitutive model curves primarily rely on FEM or explicit iteration methods with uniform step sizes, which do not fully consider the influence of stress–strain curve slope variations on the required iteration step size. To improve the computational efficiency of the CSUH model, this study proposes a dynamic iteration method with adaptive step size adjustment. This method adjusts iteration step sizes according to variations in the stress–strain curve slope, significantly reducing the number of iterations while maintaining computational accuracy.
This paper first introduces the flexibility matrix of general elastoplastic constitutive models and presents the stress–strain incremental iteration equations under different stress paths. Subsequently, the fundamental theoretical framework of the CSUH model is outlined, followed by a detailed explanation of the proposed dynamic iteration method. The effectiveness of the dynamic step size iteration method is verified through comparisons with traditional uniform step size iteration methods. Finally, this method is employed for parameter inversion of the CSUH model using Fujinomori clay, calcareous sand, and Changhe dam rockfill material. The prediction results demonstrate that the CSUH model accurately describes the mechanical behavior of different soil types under various stress paths. The findings of this study provide valuable insights for improving the computational efficiency of the CSUH model and other elastoplastic constitutive models.
2. Elastoplastic Constitutive Relationship Theory
2.1. General Elastoplastic Constitutive Relationship
In the elastoplastic constitutive relationship of soil, the elastic part is generally described by Hooke’s Law, while the plastic part consists of the yield condition, flow rule, and hardening law.
The yield condition can be quantitatively described using the yield surface equation, f, which determines the stress condition at which plastic deformation begins. The yield surface equation, f, is a function of stress, σ, and the hardening parameter, H:
The flow rule can be quantitatively described using the plastic potential surface equation g, which defines the direction of plastic strain increments. The plastic potential surface equation, g, is generally expressed as follows:
where C is a constant.
The hardening law essentially determines the hardening parameter, H, which governs the magnitude of plastic strain increments. The hardening parameter, H, is generally a function of plastic strain:
where represents the plastic strain. Different constitutive models adopt different definitions of plastic strain. For example, the MCC model uses the plastic volumetric strain, , as the hardening parameter, i.e., . The CSUH model, on the other hand, adopts a plastic volumetric strain incorporating a stress ratio coefficient as the hardening parameter, expressed as , where η represents the stress ratio, while and denote the potential failure stress ratio and characteristic state stress ratio, respectively. Further details will be introduced later.
2.2. Elastoplastic Stress–Strain Relationship
According to the classical small-strain elastoplastic theory, the total strain, ε, is decomposed into an elastic strain part, , and a plastic strain part, . The elastic strain is calculated using Hooke’s Law, while the plastic strain is determined using plasticity theory. When adopting an incremental formulation, we have the following:
Assuming that the constitutive relationship of the material in the elastic region is given by the following:
where is the elastic compliance matrix. If the elastic strain increment vector, , and the stress increment vector, , are principal strain increments and principal stress increments, respectively, then is a third-order compliance matrix. When both vectors have dimensions of 6 × 1, is a sixth-order compliance matrix.
Since plastic strain increments do not contribute to stress increments, from Equation (5), the relationship between the total stress increment and the total strain increment is given by the following:
Alternatively, this can be rewritten as follows:
where is the plastic compliance matrix. Using incremental plasticity theory, for non-associated flow rules, we can express the formulation as follows:
where Λ is a scalar factor representing the magnitude of the plastic strain increment, referred to as the plastic multiplier.
During plastic loading, the consistency condition df = 0 must be maintained, leading to the following:
Since the hardening parameter, H, is often considered a function of plastic strain or accumulated plastic strain, we have the following:
Substituting Equation (8) into Equation (10):
Substituting Equation (11) into Equation (9) to obtain Λ:
Substitute Equations (8) and (12) into Equation (6):
Equation (13) can also be rewritten in terms of the elastoplastic compliance matrix, forming the stress–strain increment equation:
2.3. Iterative Formula of Stress and Strain Increment Under Different Boundary Conditions
The principal stress and principal strain can be used to simulate common variables in laboratory true triaxial and conventional triaxial tests. The approach to solving the constitutive model’s stress–strain increment iteration equations under different boundary conditions, also known as different stress paths, involves solving a system of equations consisting of the third-order compliance matrix form of the stress–strain increment Equation (16), the intermediate principal stress coefficient Equation (18), and the stress path equation. The maximum principal strain increment, , is used to express the intermediate principal strain increment, , the minimum principal strain increment, , the maximum principal stress increment, , the intermediate principal stress increment, , and the minimum principal stress increment, . From Equation (14), the stress–strain equations expressed in the third-order compliance matrix form can be obtained as follows:
Of course, Equation (15) can also be expressed in the following form:
In experiments, the maximum principal strain increment, , is generally a known quantity, representing the axial strain. To express the remaining five variables in terms of , two additional equations are needed. One equation can be derived from the stress path, while the other can be obtained using the intermediate principal stress coefficient, b, or the stress Lode angle, θ. The definition of the intermediate principal stress coefficient, b, is given as follows:
where b is a constant, provided as an initial condition. This relationship remains valid throughout the increment process:
The increment formulation is independent of the constitutive model, and different models use different compliance matrices. During loading and unloading, the compliance matrix, , is taken as the elastoplastic compliance matrix and the elastic compliance matrix, respectively. The following sections present the incremental formulations for some commonly used stress paths.
2.3.1. Isotropic Compression (ISO) Stress Path
In the isotropic compression stress path, hydrostatic pressure is applied to compress the specimen uniformly in all directions. The stress increments in the three principal stress directions are equal, , and the strain increments are also equal, . Using the condition that the three stress increments are identical, it follows that the intermediate principal stress coefficient b = 0, . By combining this condition with Equation (16), a system of equations consisting of five equations and six variables is obtained:
where b is a known quantity determined from the experiment, and the compliance matrix elements are provided by the constitutive model. Consequently, , , , , and can all be expressed in terms of :
If the initial shear state (initial stress p0 and initial void ratio e0) is known, the MCC and CSUH models can perform iterative calculations based on Equation (20).
2.3.2. Oedometer Compression (K0) Stress Path
The oedometer compression test involves placing a soil sample in a rigid ring that restricts lateral deformation while allowing vertical drainage and compression. The boundary condition for this test is , which implies that the lateral stresses, dσ2 and dσ3, are not equal, but their relationship can be determined. This leads to b = 0. By formulating and solving the system of equations in a manner similar to the isotropic compression stress path, we obtain the following:
2.3.3. Constant σ3 Drained Shear Stress Path
A constant σ3 shear stress path maintains σ3 unchanged throughout the shear process. To obtain different values of σ3, a consolidation (drained compression) test is typically required first. Common consolidation tests include isotropic compression path consolidation tests and K0 consolidation tests. Different consolidation paths lead to different initial stresses and initial void ratios during the shear stage. After consolidation, the pressure conditions and void ratio can be determined, and the shear test can then proceed. In the equation of the constant σ3 shear stress path, dσ3 = 0. By formulating and solving the system of equations in a manner similar to the isotropic compression stress path, we obtain the following:
Conventional triaxial consolidated drained shear (CD) stress path testing is the most common constant σ3 shear test. To solve for the stress–strain relationship in a CD test, one only needs to set b = 0 in Equation (22) and iterate. When b = 1, Equation (22) can be used to calculate a triaxial extension test. It is important to distinguish between triaxial extension tests and triaxial extrusion tests. In a triaxial extension test, the confining pressure σ3 remains unchanged, whereas in a triaxial extrusion test, the axial stress remains unchanged while the confining pressure increases.
2.3.4. Undrained Shear Stress Path with Constant Confining Pressure
The undrained shear stress path is unique as it is a volumetric strain-controlled path. The boundary condition is that the volumetric strain increment satisfies , By formulating and solving the system of equations similarly to the isotropic compression stress path, we obtain the following:
In Equation (23), A, B, and D are defined as follows:
The terms A, B, and D have no physical significance and are only used to simplify the length of Equation (23). When b = 0, Equation (23) reduces to the conventional triaxial consolidated undrained (CU) stress path.
2.3.5. Constant Mean Effective Stress (p) Drained Shear (p0) Stress Path
The constant p drained shear stress path maintains the effective mean principal stress, p, constant during shearing. The condition for this stress path is . By formulating and solving the system of equations, similar to the isotropic compression stress path, we obtain the following:
At this point, the iterative stress–strain increment equations for the five commonly used stress paths have been fully derived.
3. CSUH Model: Framework and Theory
3.1. Three-Dimensional Constitutive Model Framework
Yao Yangping et al. [11] proposed a unified hardening (CSUH) model based on the Modified Cam-Clay (MCC) model, which can describe both overconsolidated clay and sand. The CSUH model effectively captures the stress–strain behavior of various soil types, including clay, sand, and rockfill, under different initial conditions and stress paths. It represents a theoretical advancement and innovative development of the MCC model [12].
To apply the constitutive model to true triaxial laboratory test predictions or engineering practice, it is necessary to extend the model to three dimensions. The Transformed Stress (TS) method, proposed by Yao et al. [18], is a three-dimensional extension approach for constitutive models. Its principal stress formulation is expressed as follows:
where , p, and q represent the principal stresses, mean principal stress, and generalized shear stress in the real stress space, respectively; and denote the principal stresses and generalized shear stress in the transformed stress space, respectively. The varies based on different strength criteria. The mean principal stress ppp in the real stress space is equal to that in the transformed stress space.
Since this method can be formulated based on different strength criteria (such as the SMP criterion, Mohr–Coulomb criterion, Lade criterion, and generalized nonlinear strength criteria), it is applicable to materials with varying strength characteristics. Figure 1 illustrates the transformed stress method based on the SMP strength criterion. Figure 1a shows the SMP strength criterion and the generalized Mises strength criterion in the real stress space. The SMP criterion in the real stress space is transformed into the generalized Mises strength criterion in the transformed stress space, assuming that the constitutive model is established in the transformed stress space. The real stress–strain relationship is obtained by differentiating the yield surface in the transformed stress space with respect to the real stress space. Figure 1b presents the transformation illustration in the π-plane. Figure 1c depicts the yield surface of the CSUH model in both the real principal stress space and the transformed principal stress space. Figure 1d shows the p-q cross-section of Figure 1c, where Me represents the critical state stress ratio under triaxial extension.
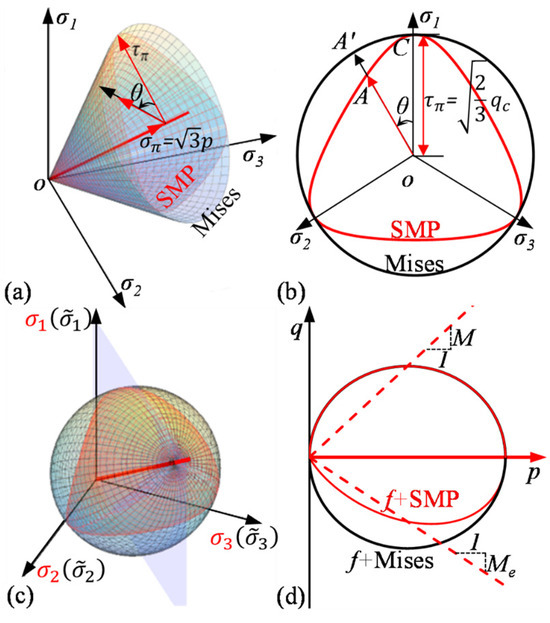
Figure 1.
Transformed stress method: (a) SMP and von Mises Yield Criteria in True Stress Space; (b) Transformation Illustration on the π-Plane; (c) CSUH Model Yield Surface(χ = 0) in Principal Stress Space; (d) Yield Surface in the p–q Plane.
When applying the TS method to extend the CSUH model into three dimensions, it is assumed that the CSUH model is formulated in the transformed stress space. The plastic potential surface equation, g, of the CSUH model in the transformed stress space is expressed as follows:
where and denote the effective mean principal stress and shear stress in the transformed stress space, respectively. The tilde symbol (~) indicates variables in the transformed stress space. The parameter py represents the horizontal coordinate of the plastic potential surface’s intersection with the p-axis. The characteristic state stress ratio, , has a geometric interpretation as the stress ratio at the upper quadrant point of the ellipse.
The yield surface equation, f, of the CSUH model in the transformed stress space is given by the following:
where M is the critical state stress ratio, representing the slope of the conventional triaxial compression critical state line (CSL) in the p-q space. The critical state parameter, χ, adjusts the shape of the yield surface. When χ = 0, the function, f, degenerates into an elliptical yield surface, as shown in Figure 1d. The parameter, ps, represents the hardening parameter. The plastic compression coefficient is defined as , where λ and κ are the compression and rebound indices from isotropic compression tests, respectively. The variable px0 denotes the horizontal coordinate of the initial yield surface intersection with the p-axis under the initial conditions. The term H represents the hardening parameter:
In this equation, represents the current stress ratio in the transformed stress space, is the potential failure stress ratio, and is the increment of plastic volumetric strain. During the shearing process, the characteristic state stress ratio, , and the potential failure stress ratio, , change with the state parameter, , which indicates the current degree of compaction, as shown in Equations (30) and (31). From these equations, it is evident that is also state-dependent.
In these equations, the dilatancy parameter, m, scales the influence of and thereby affects . The state parameter, , is defined as follows:
where ps is the hardening parameter:
The Unified Hardening Model for Clays and Sands (CSUH) has eight fundamental parameters: M, ν, κ, λ, N, Z, χ and m. For the same type of soil, regardless of different stress paths and initial states (initial confining pressure p0 and initial void ratio e0), the same set of parameters is used.
3.2. Third-Order Flexibility Matrix of the Model
Based on Equation (14), the incremental relationship is expressed in the form of a third-order flexibility matrix:
For isotropic materials:
where E is the elastic modulus and ν is Poisson’s ratio.
In Equation (34), the third-order plastic flexibility matrix is given as follows:
where the yield surface equation, , is differentiated with respect to the true stress, σ, and the hardening parameter, , the plastic potential surface equation, , is differentiated with respect to the transformed stress, , and the hardening parameter, , is differentiated with respect to the true strain, . These differentiation processes require the application of the chain rule. The yield surface equation, , and plastic potential surface equation, , are generally expressed as functions of and , while and are functions of stress, . Based on the SMP strength criterion and the transformed stress (TS) method, we obtain the following:
where I1, I2, and I3 are the first, second, and third invariants of the principal stress tensor, respectively, and qc is the transformed generalized shear stress based on the SMP strength criterion. The derivation results for Equation (36) of the CSUH model are provided in [11] and will not be reiterated here. Equation (8) can also be expressed as follows:
The derivative of the hardening parameter with respect to plastic strain can also be expressed as the derivative with respect to plastic volumetric strain. Therefore, for the CSUH model, Equation (36) can be rewritten as follows:
The loading and unloading criteria are defined as follows:
If the strain increment dεd\varepsilondε calculated using the elastic flexibility matrix in Equation (34) indicates loading, the total flexibility matrix, which includes both the elastic and plastic flexibility matrices, should be used to recalculate the stress–strain increment in Equation (34). If the strain increment calculated using only the elastic flexibility matrix indicates unloading, the calculation is considered correct, and the next step of elastic prediction can proceed.
If the trial value, , calculated using the elastic compliance matrix, , in Equation (34) is greater than zero, it indicates loading. In this case, the elastoplastic compliance matrix, which is the sum of the elastic compliance matrix and the plastic compliance matrix, should be used to recalculate the stress–strain increments in Equation (34). Conversely, if the trial value, , calculated using the elastic compliance matrix is less than zero, it indicates unloading, meaning the trial calculation is correct. In this scenario, the stress–strain increments in Equation (34) can be accurately computed using only the elastic compliance matrix, and the next step of the elastic trial calculation can proceed.
4. Dynamic Iteration Method
4.1. Common Iteration Methods
The inversion of constitutive model parameters using optimization algorithms requires extensive computations, with the most time-consuming part being the iterative stress–strain increment calculation, similar to Equation (20). The process of determining constitutive model parameters through optimization involves providing different parameter sets to the constitutive model. The model then computes the theoretical stress–strain curve corresponding to the given parameters and initial conditions from the experiment. The computed theoretical stress–strain curve is compared with the experimental stress–strain curve, and the error is fed back to the optimization algorithm. Based on this error feedback, the optimization algorithm adjusts and attempts to provide improved model parameters. Consequently, the inversion process requires frequent evaluation of stress–strain increments to generate the stress–strain curve.
As previously discussed, different constitutive models can adopt a unified iterative stress–strain increment formulation, similar to Equation (20), for stress–strain curve calculations. Several numerical methods can be applied for iteration, including the forward Euler method, the fourth-order Runge–Kutta (RK4) method, and implicit iteration methods. The RK4 method offers higher computational accuracy and better stability but faces challenges in practical applications due to its complex implementation and high computational cost. Implicit iteration methods, such as the backward Euler method and the Newton-Raphson method, allow for larger incremental steps but require solving nonlinear equations iteratively, which may lead to convergence issues. The semi-implicit return mapping method performs well in handling elastoplastic problems, but its implementation is complex, and its computational efficiency is relatively low.
Due to its simplicity, intuitiveness, and ease of implementation, the forward Euler method is widely used. This method is based on a first-order Taylor expansion, where the stress state of the next step is directly computed using the tangent modulus of the current step. The core concept is to discretize the continuous stress–strain relationship into an incremental form. According to the forward Euler method, the stress–strain increment in Equation (20) and subsequent stress paths can be simplified as :
where represents the stress and strain at step n + 1, represents the stress and strain at step n, Cn is the compliance matrix computed based on the stress state at step n, and is the incremental maximum principal strain.
Figure 2 illustrates the accuracy comparison between the RK4 method and the forward Euler method. While RK4 provides higher accuracy, its computational cost is significantly higher than the forward Euler method. However, it was observed that when the total axial strain is uniformly divided into 3000 increments, the integration curves obtained from both methods with 3000 uniform steps are nearly identical, as shown in Figure 2. This indicates that using 3000 uniform steps can yield an accurate stress–strain curve. Since RK4 requires solving the compliance matrix at four different substep increments, whereas the forward Euler method only requires one calculation, the computational cost of the forward Euler method is significantly lower. Therefore, when the iteration step count reaches 3000, the forward Euler method not only reduces computational effort but also provides satisfactory results, making it the preferred choice for computing the constitutive model stress–strain curve.
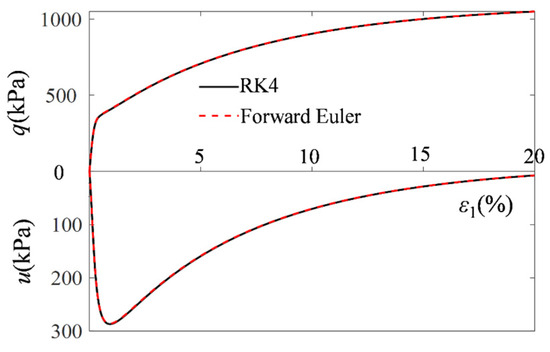
Figure 2.
Stress–strain curves for the CU stress path obtained using different integration methods with 3000 uniform step sizes.
Compared with the computational cost of the optimization algorithm itself, the iterative evaluation of the constitutive model’s stress–strain increment equation is the most time-consuming part of the entire inversion process. Even with 3000 iteration steps using the forward Euler method, the computation time remains excessively long.
4.2. Proposed Dynamic Iterative Method
The slope of the stress–strain curve of soil is not uniform. As shown in Figure 3, the slope of the curve is steep in the front part and gentle in the latter part. By segmentally adjusting the model’s iterative increment step size, the total number of iterations can be reduced, thereby accelerating the speed of parameter inversion.
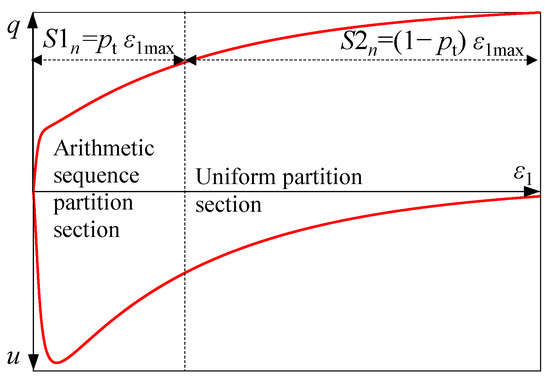
Figure 3.
Segmented adjustment of the iterative increment step size Δε1 in the constitutive model.
When the curve slope is large, a small axial strain increment, Δε1, can cause a significant stress increment, whereas when the curve slope is small, a larger axial strain increment, Δε1, induces only a minor stress increment. If the same iterative increment step size, Δε1, is used regardless of the curve slope, Δε1 must be set sufficiently small to ensure accuracy when the slope is large, which results in a high number of iterations and slow computation.
To enhance the numerical computation efficiency of the constitutive model, a dynamic iterative method that adjusts the iterative increment step size in segments is proposed to reduce the total number of iterations. A smaller iterative step size is adopted when the stress–strain curve slope is large, while a larger step size is used when the slope is small. This approach ensures accuracy while reducing the number of iterations, thereby accelerating the computation speed. Generally, the axial strain distributed in an arithmetic sequence accounts for about 30% of the total axial strain, while the uniformly distributed axial strain accounts for about 70%. The segmentation position dynamically changes with the total axial strain.
As shown in Figure 3, the total axial strain, ε1max, is divided into two parts. The first part adopts an arithmetic sequence distribution, with its axial strain, S1n, accounting for a proportion, pt, of ε1max, where the strain increment, Δε1, follows an arithmetic sequence distribution. The second part adopts a uniform distribution, with axial strain S2n accounting for a proportion (1 − pt) of ε1max, where Δε1 is uniformly distributed.
Given a total number of iterations, Ns, the number of iterations in the uniform distribution part is Ns2 = ptNs, and the corresponding axial strain increment, Δε1, is as follows:
Assuming that the initial iterative step size, a1, in the arithmetic sequence part is 1/10 of the uniform distribution step size Δε1, we have:
Given the total number of iterations Ns, the number of iterations in the arithmetic sequence part is Ns1 = (1 − pt)Ns. The common difference d of the arithmetic sequence and the iterative increment step size, an, can be expressed as follows:
By selecting an appropriate proportion, pt, and a reasonable total iteration count, Ns, a highly accurate stress–strain curve can be obtained with a reduced number of iterations. When ε1max =20%, pt = 0.3, and Ns = 50, the step sizes of different partitions obtained using Equations (42) to (45) are shown in Figure 4.
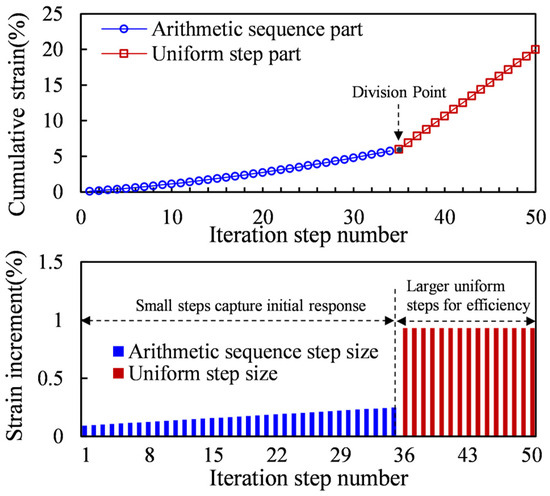
Figure 4.
Step Size for Different Step Partitions.
As shown in Figure 5, the results of 50 steps arithmetic sequence step size (dynamic iteration method parameters pt = 0.3, Ns = 50) are similar to those of 3000 steps uniform step size, indicating that the dynamic iteration method effectively reduces the number of iterations to 1/60 of the original while maintaining accuracy.
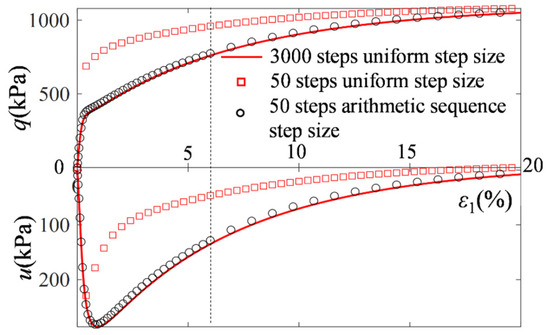
Figure 5.
Comparison of Uniform and Arithmetic Sequence Distributed Iterative Increment Step Sizes.
Figure 2, Figure 5 and Figure 6 present the stress–strain curve of the CSUH model using Toyoura Sand parameters from Table 1 under a confining pressure of 500 kPa and a void ratio of 0.84 in CU tests. According to Equation (16), theoretically, the numerical computation iterative increment step size, dε1, should be infinitely small. However, practical calculations reveal that 3000 steps are generally sufficient for high accuracy (as shown in Figure 2). Since the step size is not infinitely small in actual computation, dε1 is denoted as Δε1, and the same applies to other principal strain and stress increments.
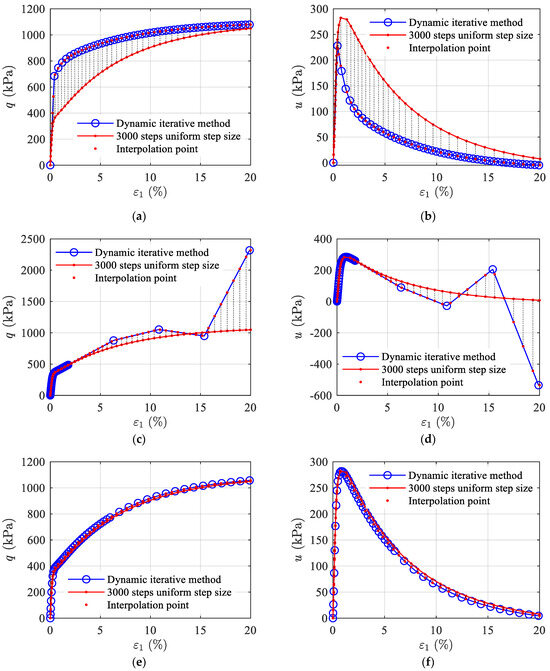
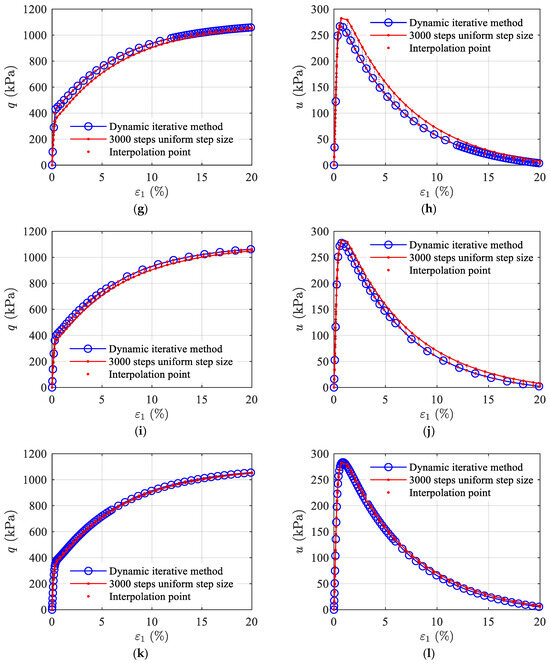
Figure 6.
Differences between dynamic iteration method curves and 3000 uniform step size curves for different pt and Ns values: (a) ε1-q curve at pt = 0, Ns = 50, with MRE = 0.2495; (b) ε1-u curve at pt = 0, Ns = 50, with MRE = 0.5378; (c) ε1-q curve at pt = 0.09, Ns = 50, with MRE = 0.1512; (d) ε1-u curve at pt = 0.09, Ns = 50, with MRE = 3.4802; (e) ε1-q curve at pt = 0.3, Ns = 50, with MRE = 0.0229; (f) ε1-u curve at pt = 0.3, Ns = 50, with MRE = 0.07622; (g) ε1-q curve at pt = 0.6, Ns = 50, with MRE = 0.0619; (h) ε1-u curve at pt = 0.6, Ns = 50, with MRE = 0.1534; (i) ε1-q curve at pt = 0.3, Ns = 30, with MRE = 0.0401; (j) ε1-u curve at pt = 0.3, Ns = 30, with MRE = 0.1331; (k) ε1-q curve at pt = 0.3, Ns = 70, with MRE = 0.0153; (l) ε1-u curve at pt = 0.3, Ns = 70, with MRE = 0.0528.

Table 1.
Parameters used for calculating theoretical curve values of the CSUH model [11].
Figure 6 shows the computational results of the dynamic iteration method with different values of pt and Ns. The red line represents the calculation curve with 3000 uniform steps. Fifty interpolation points are taken at equal arc lengths on the curve to represent the experimental values. Corresponding points to the interpolation points are found on the dynamic iteration method calculation curve. The error between the dynamic iteration method calculation curve and the curve with 3000 uniform steps is measured using mean relative error (MRE) from reference [12]. The dynamic iteration method with pt = 0 and Ns = 50 is equivalent to using 50 uniform step iterations. As shown in Figure 6a,b, the dynamic iteration method (blue dots) differs significantly from the 3000 uniform steps calculation curve (red), with an MRE of 0.2495 for q and 0.5378 for u. The dynamic iteration method with pt = 0.09 and Ns = 50 yields the worst computational results, as shown in Figure 6c,d and Figure 7a.
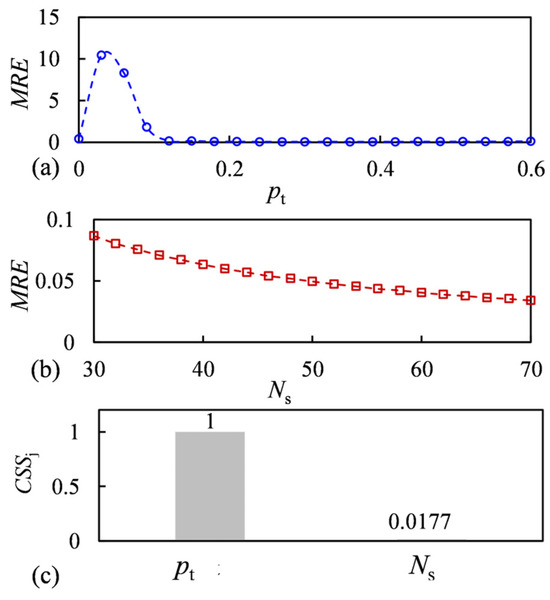
Figure 7.
Sensitivity analysis of pt and Ns: (a) Average MRE of q and u corresponding to different pt when Ns = 50; (b) average MRE of q and u corresponding to different Ns when pt = 0.3; (c) composite scaled sensitivity (CSS) of pt and Ns.
Figure 7 shows the variation in MRE and parameter sensitivity analysis for different pt and Ns values. The sensitivity analysis method adopts a local sensitivity analysis method, namely Composite Scale Sensitivity (CSS) [19]. Figure 7c shows that pt has a larger sensitivity while Ns has a smaller sensitivity, indicating that the choice of pt is the most important in the dynamic iteration method. From Figure 7a, it can be seen that when pt is greater than 0.12, the MRE does not change significantly. Therefore, for this typical stress–strain curve with a slope that is initially large and then small, pt = 0.3 is appropriate. As shown in Figure 7, under the extreme condition where the total number of iteration steps Ns is reduced to 30, the proposed dynamic iteration algorithm still demonstrates excellent numerical stability, with the generated stress–strain curves maintaining a high degree of agreement with the full 3000-step iteration results (MREs of q and u are 0.041 and 0.1331, respectively). In contrast, the traditional numerical scheme with equal step-size iteration encounters complex numbers due to the large initial step size, and both the fourth-order Runge–Kutta method and Euler method exhibit severe numerical divergence. The dynamic iteration method, with a smaller initial step size, improves iteration efficiency by two orders of magnitude while ensuring computational accuracy.
Taking the inversion of the CSUH model parameters for the Changhe dam rockfill in Section 5.3 as an example, the inversion process includes one isotropic compression test and four CD tests, totaling 414 data points. Based on the dynamic iterative method with segmented adjustment of the model iteration increment step size, this paper developed parameter inversion software using VBA language on the Excel platform (website: https://github.com/longbiscuit/ModelParaOpt2.0_Excel_STADE, accessed on 29 April 2025.). The software runs on a Dell Inspiron 13 7000 series laptop (Dell Inc., Austin, TX, USA).. Experimental results show that when the number of iterations is 50, the computation time is about 7 min; when the number of iterations increases to 3000, the required time is 332 min. Compared with the traditional method, the computation time is reduced to 1/47 of the original, as shown in Figure 8.
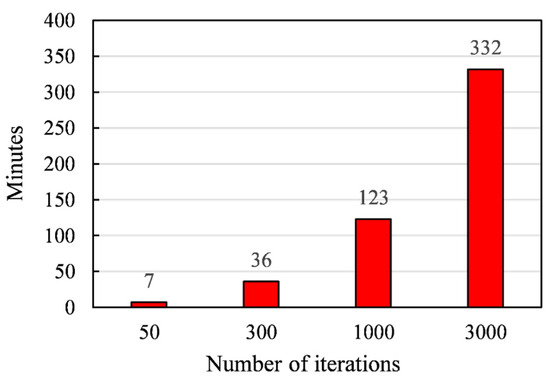
Figure 8.
Computational Time for Inversion with Different Iteration Counts.
In conclusion, the proposed dynamic iterative method with segmented iterative increment step sizes significantly reduces the number of iterations while ensuring prediction accuracy, greatly enhancing the efficiency of parameter inversion.
5. CSUH Model Iterative Inversion Parameters
5.1. Fujinomori Clay
In all parameter inversion calculations presented in Section 5, the dynamic iterative method is consistently used, with parameter pt = 0.3 and Ns = 50. The parameter inversion process refers to references [12,16].
To verify the capability of the CSUH model in describing the stress–strain characteristics of different types of soil, a dynamic iterative method was used to predict the CSUH model parameters for Fujinomori clay. The initial conditions are shown in Table 2.

Table 2.
Initial Shear State of Fujinomori Clay.
For the sample with OCR = 8.0, where p0 = 98 kPa, the process involved first consolidating to the preconsolidation pressure σc = 784 kPa, then unloading to p0 = 98 kPa, and finally performing a constant p shear test at p0 = 98 kPa. The loading and unloading processes for other overconsolidation ratios were similar. The CSUH model parameters are shown in Table 3.

Table 3.
CSUH Model Parameters for Fujinomori Clay.
5.1.1. Constant p Compression Test
As shown in Figure 9, the points represent the experimental results, while the lines represent the CSUH model predictions. The minimum overconsolidation ratio (OCR) is 1.0, corresponding to normally consolidated soil with the lowest density. The maximum OCR is 8, corresponding to heavily overconsolidated soil with the highest density.
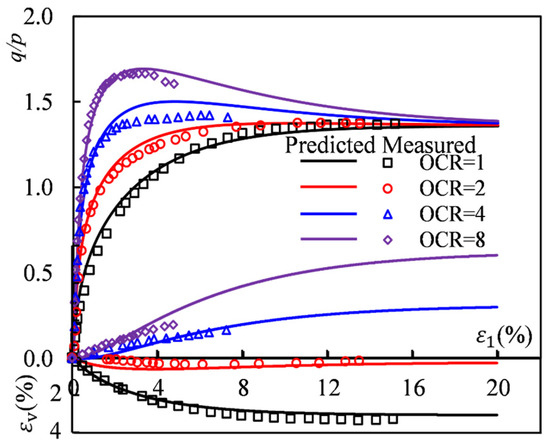
Figure 9.
Comparisons between the constant p compression test results of the Fujinormori clay and the CSUH predictions [20].
Figure 9 shows that normally consolidated clay exhibits strain hardening and shear contraction, while heavily overconsolidated clays display strain softening and volumetric dilation. As the OCR increases, the peak stress ratio gradually increases, and the volumetric deformation transitions from shear contraction to initial shear contraction followed by shear dilation. When OCR = 8, the peak stress ratio is the highest, and the amount of volumetric dilation is the largest. Moreover, the CSUH model predictions align well with the experimental results for clays with different overconsolidation ratios, indicating that the CSUH model can reasonably quantify the differences in dilatancy behavior among soils with varying densities.
5.1.2. True Triaxial Test
The true triaxial test for Fujinomori clay follows the basic procedure of first undergoing isotropic consolidation to p = 196 kPa, followed by a constant p (or constant σm) shear test at an axial strain rate of 1% per day.
As shown in Figure 10, the CSUH model predictions agree well with the experimental results. This further demonstrates that, after incorporating the transformed stress method, the CSUH model can quantitatively describe the differences in the frictional behavior of soils under different stress Lode angles (θ).
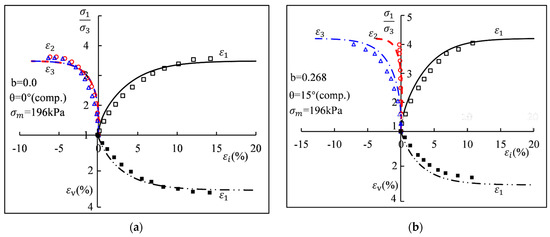
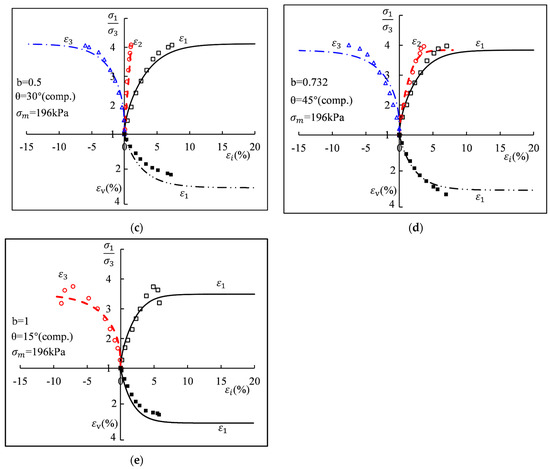
Figure 10.
Comparisons between the true triaxial test measured results under constant p stress path with different medium principal stress coefficient b of the Fujinormori clay and the CSUH predictions [21] (dots: measurements; lines: predictions): (a) Medium principal stress ratio b = 0, equivalent to stress Lode angle θ = 0°; (b) Medium principal stress ratio b = 0.268; (c) Medium principal stress ratio b = 0.5; (d) Medium principal stress ratio b = 0.732; (e) Medium principal stress ratio b = 1.
As shown in Figure 10, the horizontal axis represents εi, where i may denote 1, 2, or 3. The upper part of the vertical axis corresponds to σ1 and the ratio σ1/σ3, while the lower part represents the volumetric stress σv. In Figure 10, lines indicate theoretical calculation results, whereas symbols denote experimental data. Specifically, the black solid square points represent ε1-εv, the black open square points denote ε1-σ1/σ3, the red open circles indicate ε2-σ1/σ3, and the blue open triangles correspond to ε3-σ1/σ3. The relevant explanations have been added to the figure caption.
In summary, the predictions for conventional triaxial and true triaxial tests of saturated Fujinomori clay indicate that the CSUH model can not only quantitatively distinguish the differences in dilatancy behavior among clays with different densities but also accurately capture the variations in frictional characteristics under different stress Lode angles.
5.2. Calcareous Sand
Weng Yiling [22] conducted CD and CU tests on dredged calcareous sand (also known as coral reef sand) from the Nansha Islands. The calcareous sand foundation mainly consists of gravelly sand or gravel soil, which is an uncemented loose material. In this study, experimental data for calcareous sand particles smaller than 0.075 mm were used to validate the model. The CSUH model parameters are listed in Table 4, and the comparison results are shown in Figure 11 and Figure 12.

Table 4.
CSUH model parameters for calcareous silt.
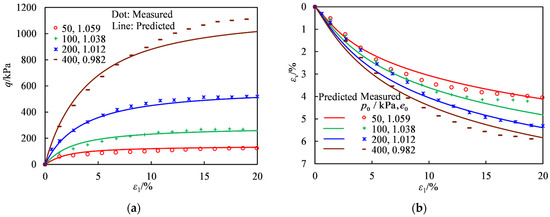
Figure 11.
Comparisons between the CD test measured results of the calcareous silt and the CSUH predictions [22]: (a) Axial Strain vs. Deviatoric Stress; (b) Axial Strain vs. Volumetric Strain.
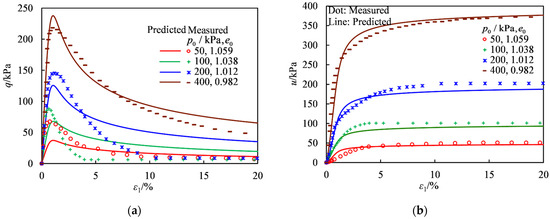
Figure 12.
Comparisons between the CU test measured results of the calcareous silt and the CSUH predictions [22]. (a) Axial Strain vs. Deviatoric Stress; (b) Axial Strain vs. Excess Pore Pressure.
From Figure 11, it can be observed that under different confining pressures, the calcareous sand exhibits strain hardening and shear contraction in the CD tests.
As shown in Figure 12, the calcareous sand reaches peak strength at a relatively small strain, followed by strain softening until the strength nearly approaches zero. Meanwhile, pore pressure rises to a level almost equal to the axial stress, indicating that the soil sample is approaching a liquefied state. Therefore, when analyzing the effective stress ratio, it can be observed that the measured effective stress ratio exhibits anomalies, which were also noted in the literature [22].
5.3. Rockfill Material
Liu et al. [23] conducted isotropic compression, CD, and CU tests on the main rockfill material (composed of hard diorite) from the Changhe dam. The CSUH model parameters for the rockfill material are listed in Table 5.

Table 5.
CSUH model parameters for the rockfill material from the Changhe dam.
5.3.1. Isotropic Compression Test
Figure 13 presents the results of isotropic compression tests on the rockfill material from the Changhe dam, along with the corresponding CSUH model predictions. The comparison between the predicted and experimental results indicates that the CSUH model can effectively describe the compression hardening behavior of large-grained granular soils such as rockfill. Compression hardening refers to the characteristic where the modulus of the soil increases with increasing density during compression, often described as “the more it compresses, the harder it gets” [24].
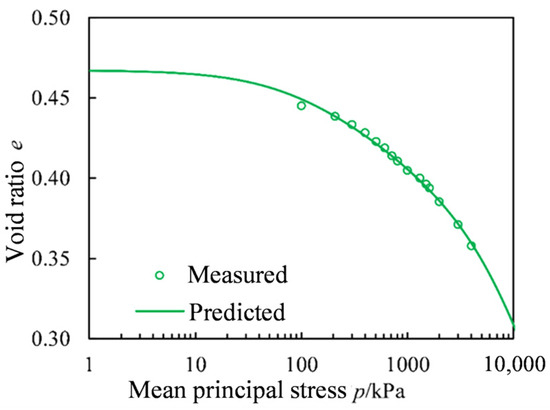
Figure 13.
Comparisons between the isotropic compression test measured results of the rockfill from the Changhe dam and the CSUH predictions [23].
5.3.2. CD Triaxial Compression Test
Figure 14 compares the CD test results of the rockfill material under different confining pressures with the CSUH model predictions. The experimental results indicate that at lower confining pressures, the material exhibits slight strain softening and volume dilation, whereas at higher confining pressures, it exhibits strain hardening with volume contraction throughout. This behavior is primarily attributed to particle breakage in the rockfill material.
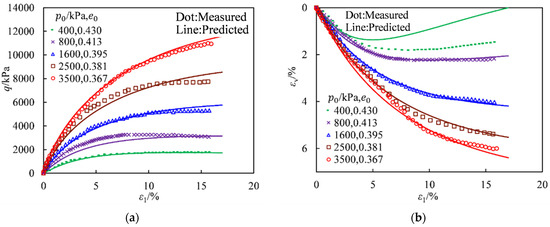
Figure 14.
Comparisons between the CD test measured results of the rockfill from the Changhe dam and the CSUH predictions [23]: (a) Axial Strain vs. Deviatoric Stress; (b) Axial Strain vs. Volumetric Strain.
Since both rockfill and sand exhibit breakage characteristics, their qualitative mechanical behaviors are similar. However, rockfill is more prone to breakage than sand, leading to quantitative differences in test results. For example, in Figure 11, the calcareous sand with an initial state of (400 kPa, 0.982) and in Figure 14, the rockfill with an initial state of (3500 kPa, 0.367) both exhibit a final volumetric strain of approximately 6% after shearing. This suggests that if the initial conditions were the same, the final volumetric strains of the calcareous sand and rockfill would likely be different.
5.3.3. CU Triaxial Compression Test
Figure 15 compares the CU test results of the rockfill material under different confining pressures with the CSUH model predictions. From Figure 15a, it can be observed that under different confining pressures, the rockfill material exhibits strain hardening. Figure 15b shows that as axial strain increases, pore pressure initially rises rapidly and then gradually decreases, indicating a tendency for the rockfill material to undergo initial shear contraction followed by shear dilation in undrained conditions. Additionally, higher confining pressures result in greater pore pressure buildup, which offsets part of the confining pressure. As a result, for the same initial confining pressure, p0, the undrained shear strength, qf, is lower than the drained shear strength.
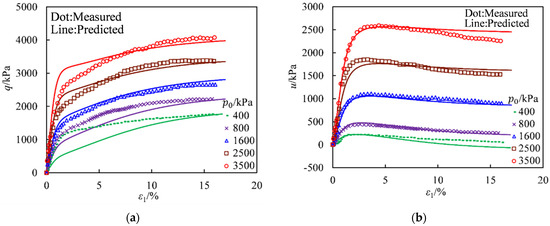
Figure 15.
Comparisons between the CU test measured results of the rockfill from the Changhe dam and the CSUH predictions [23]: (a) Axial Strain vs. Deviatoric Stress; (b) Axial Strain vs. Excess Pore Pressure.
A comparison between Figure 14b and Figure 15b reveals that under an initial confining pressure of 3500 kPa, the rockfill material undergoes continuous shear contraction in the drained test, whereas in the undrained test, it also exhibits dilation. The good agreement between the experimental results and the CSUH model predictions demonstrates that the CSUH model can quantitatively describe the differences in dilation behavior of the same material (rockfill) under different drainage conditions.
6. Conclusions
This study proposes a dynamic iterative method with segmented adjustment of incremental step sizes to improve the efficiency of parameter inversion for the CSUH model. Through theoretical analysis and experimental validation, the following key conclusions are obtained:
- (1)
- The elastoplastic flexibility matrix of the elastoplastic constitutive model and the incremental stress–strain relationships under different boundary conditions are derived. This eliminates the need to solve equation systems when calculating theoretical model curves, thereby accelerating computation speed.
- (2)
- Based on the variation characteristics of the stress–strain curve slope, the iterative step size is distributed using an arithmetic sequence over 30% of the total axial strain range, while a uniform distribution is applied over the remaining 70%. This effectively balances computational accuracy and efficiency. The study shows that this method reduces the number of iterations from the traditional 3000 steps to just 50 steps, decreasing computation time by approximately 47 times while maintaining accuracy comparable to the fourth-order Runge–Kutta method.
- (3)
- The CSUH model accurately describes the stress–strain characteristics of different soil types (such as clay, sand, and rockfill) under various stress paths, including isotropic compression, constant p drained conditions with different intermediate principal stress ratios, CD, and CU tests.
The dynamic iterative method proposed in this study significantly enhances the efficiency of parameter inversion for elasto-plastic models, creating favorable conditions for the practical engineering application of the CSUH model. However, the CSUH model exhibits limitations in characterizing stress–strain behaviors of structured soils, anisotropic formations, and environments influenced by variable water content, prolonged creep processes, or thermal variations. Specialized constitutive formulations are required for these complex scenarios, necessitating tailored parameter recalibration and iterative scheme redevelopment.
In addition, it should be noted that the current validation is primarily performed on datasets used for model calibration and has not yet been extended to independent datasets or new, unseen stress paths. Although the dynamic iterative method demonstrates clear advantages in computational efficiency and accuracy in the present cases, further comprehensive cross-validation and testing on independent datasets and more complex loading conditions are needed in future research to fully establish the generalizability and robustness of the proposed approach.
Author Contributions
Conceptualization, B.Z. and H.Y.; methodology, B.Z.; software, B.Z. and J.Y.; validation, D.C., H.Y. and B.Z.; formal analysis, B.Z.; investigation, Z.B.; resources, D.C.; data curation, M.O.; writing—original draft preparation, B.Z.; writing—review and editing, B.Z. and Z.B.; visualization, B.Z.; supervision, D.C.; project administration, H.Y.; funding acquisition, D.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. U2268216); the Science and Technology Research and Development Program of China State Railway Group Co., Ltd. (Grant No. L2023G009); research projects of China Academy of Railway Sciences Corporation Limited (Grant No. 2023YJ384); and the 2022 Tencent XPLORER PRIZE (Research on Prefabricated Railway Subgrade Structure and Fundamental Theory).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data that support the findings of this study are included within the article.
Acknowledgments
We give thanks to Yangping Yao for his guidance on the unified hardening constitutive model.
Conflicts of Interest
All authors were employed by the company China Academy of Railway Sciences Corporation Limited. The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Yao, Y.; Luo, T.; Hou, W. Soil Constitutive Models; People’s Transportation Publishing House Co., Ltd.: Beijing, China, 2018. [Google Scholar]
- Zhang, Y.; Chen, Y. A constitutive relationship for gravelly soil considering fine particle suffusion. Materials 2017, 10, 1217. [Google Scholar] [CrossRef] [PubMed]
- Cong, S.; Ling, X.; Li, X.; Geng, L.; Xing, W.; Li, G. Elastoplastic model framework for saturated soils subjected to a freeze–thaw cycle based on generalized plasticity theory. Materials 2021, 14, 6485. [Google Scholar] [CrossRef] [PubMed]
- Dong, L.; Tian, S.; Yao, C.; Han, X.; Wang, K. A nonlinear constitutive model for remoulded fine-grained materials used under the Qinghai–Tibet railway line. Materials 2022, 15, 5119. [Google Scholar] [CrossRef] [PubMed]
- Roscoe, K.H.; Schofield, A.N.; Thurairajah, A. Yielding of clays in states wetter than critical. Géotechnique 1963, 13, 211–240. [Google Scholar] [CrossRef]
- Roscoe, K.H.; Burland, J.B. On the generalized stress–strain behaviour of ‘wet clay’. In Engineering Plasticity; Cambridge University Press: Cambridge, UK, 1968. [Google Scholar]
- Hou, W.; Yao, Y. Analysis in behaviors of over-consolidated clays described by cam-clay model and unified hardening model. Ind. Constr. 2011, 41, 18–23+140. [Google Scholar] [CrossRef]
- Yao, Y.P.; Gao, Z.W.; Zhao, J.D.; Wan, Z. Modified UH model: Constitutive modeling of overconsolidated clays based on a parabolic Hvorslev envelope. J. Geotech. Geoenviron. Eng. 2012, 138, 860–868. [Google Scholar] [CrossRef]
- Yao, Y.P.; Hou, W.; Zhou, A. Constitutive model for overconsolidated clays. Sci. China Ser. E-Technol. Sci. 2008, 51, 179–191. [Google Scholar] [CrossRef]
- Yao, Y.P.; Hou, W.; Zhou, A. UH model: Three-dimensional unified hardening model for overconsolidated clays. Géotechnique 2009, 59, 451–469. [Google Scholar] [CrossRef]
- Yao, Y.P.; Liu, L.; Luo, T.; Tian, Y.; Zhang, J.M. Unified hardening (UH) model for clays and sands. Comput. Geotech. 2019, 110, 326–343. [Google Scholar] [CrossRef]
- Zhu, B.; Chen, Z. Calibrating and validating a soil constitutive model through conventional triaxial tests: An in-depth study on CSUH model. Acta Geotech. 2022, 17, 3407–3420. [Google Scholar] [CrossRef]
- Ilie-Octavian, P.; Mihai-Octavian, P.; Mihaela, O.; Gabriela-Petruța, R.; Lucia, C.A. Calibrating DC01 material properties for finite element analysis with Abaqus and Isight. Methodology 2023, 7, 8. [Google Scholar] [CrossRef]
- Sloan, S.W.; Abbo, A.J.; Sheng, D. Refined explicit integration of elastoplastic models with automatic error control. Eng. Comput. 2001, 18, 121–194. [Google Scholar] [CrossRef]
- Sloan, S.W. Substepping schemes for the numerical integration of elastoplastic stress–strain relations. Int. J. Numer. Methods Eng. 1987, 24, 893–911. [Google Scholar] [CrossRef]
- Zhu, B.; Su, X.; Cao, Y.; Yan, F. Determining parameters of the CSUH constitutive model by genetic algorithm. Jpn. Geotech. Soc. Spec. Publ. 2020, 8, 188–193. [Google Scholar] [CrossRef]
- Yin, Z.; Jin, Y. Development of Geotechnical Optimization Platform EROSOPT. In Practice of Optimisation Theory in Geotechnical Engineering; Springer: Singapore, 2019; pp. 243–292. [Google Scholar] [CrossRef]
- Yao, Y.P.; Wang, N. Transformed stress method for generalizing soil constitutive models. J. Eng. Mech. 2014, 140, 614–629. [Google Scholar] [CrossRef]
- Kadlíček, T.; Janda, T.; Šejnoha, M.; Najser, J.; Beneš, Š. Automated calibration of advanced soil constitutive models. Part I: Hypoplastic sand. Acta Geotech. 2022, 17, 3421–3438. [Google Scholar] [CrossRef]
- Nakai, T.; Hinokio, M. A simple elastoplastic model for normally and over consolidated soils with unified material parameters. Soils Found. 2004, 44, 53–70. [Google Scholar] [CrossRef] [PubMed]
- Nakai, T.; Matsuoka, H.; Okuno, N.; Tsuzuki, K. True triaxial tests on normally consolidated clay and analysis of the observed shear behavior using elastoplastic constitutive models. Soils Found. 1986, 26, 67–78. [Google Scholar] [CrossRef] [PubMed]
- Weng, Y. Study on the Shear Strength of Calcareous Soil and Its Influencing Mechanism. Ph.D. Thesis, Guangxi University, Nanning, China, 2017. [Google Scholar]
- Liu, E.; Chen, S.; Li, G.; Zhong, Q.M. Critical state of rockfill materials and a constitutive model considering grain crushing. Rock Soil Mech. 2011, 32, 148–154. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, B.; Zhu, J. Behaviors, constitutive models and numerical simulation of soils. China Civ. Eng. J. 2012, 45, 127–150. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).