Abstract
The width of the pillar is an important factor in the stability of the underground space and the efficiency of resource recovery. This study aims to model the performance of retained walls in panel barrier pillar stopes. By simplifying the three-dimensional problem based on the mining operation, a two-dimensional mechanical model of non-equal-width retained walls was established, and the stress and deflection were solved analytically. The calculated deformation characteristics of equal-width and non-equal-width retained walls were analyzed and compared with numerical simulations. The results indicated that the deformation of retained walls is mainly influenced by the roof loads, the uniaxial compressive strength, and the internal friction angle of backfill materials. For equal-width retained wall design, corresponding to the areas of pillar stopes where the uniaxial compressive strength and internal friction angle of backfill materials are low, great lateral pressure will be created on the retained walls. This results in significant flexural wall deformations in this area, increasing the risk of wall collapses. In comparison, for non-equal-width retained walls, the width is defined based on the surrounding backfill materials, which could greatly reduce the risk of potential damage. For the mining operation at the actual mine, the non-equal-width design with 2.5 m and 4.0 m intervals was adopted for the panel barrier pillar stopes, and the final displacement of the roof of the stope after the completion of the mining is 34 mm, and the two sides of the mine wall remain in good integrity with no significant peeling or cracking identified. This design improves the recovery rate of mineral resources and the stability of mining.
1. Introduction
With the depletion of shallow mineral resources, mining inevitably goes deeper, where the operation faces significantly more additional challenges [1,2,3,4,5]. At shallower depths, the ground stresses around the ore body are low, so only a minimal number of pillars need to be retained as necessary ground supports to ensure the safety of the underground operation [6,7]. However, for deep mining, more in-depth geological investigations are required to help select the best mining method and design the most suitable pillar layout, to make the mining process safe and efficient [8,9].
In deep mining, in situ stresses around the ore body are much higher and it is difficult to effectively control the pressure of surrounding rocks using only pillars. Therefore, in mining practice, a large number of mines try to fill the mined areas with tailings and other mining wastes to bear the stresses of surrounding rocks together with pillars [10]. Back-filling using tailings also brings additional environmental benefits by addressing the issues of accumulated tailings on the ground surface, hence helping promote the restoration of ecological environments after mining [11,12]. At the early stage of the backfilling process, mine pillars are still the main stress-bearing structures and the backfill mainly plays the role of limiting the lateral displacement of mine pillars and improving their bearing capacity [13,14,15,16]. With the development of backfill technology, the strength of backfilled material has been enhanced and the contact area between the backfill and the roof has been gradually increased. Therefore, the overall bearing capacity of the backfill has been increased significantly to improve its ability to limit the movement of the roof strata [17,18,19]. This potentially allows the mining of previously retained pillars to improve the recovery of mineral resources [20]. The original pillars are left temporarily to divide the mining area and to ensure that multiple stopes are mined simultaneously without interfering with each other. Subsequently, these temporary pillars are mined, with only a few thin walls (thin pillars) left permanently underground. These thin walls are mainly used to prevent the mixing of backfill materials and ores at each stope. At the same time, these permanent thin walls can also limit the lateral displacement of backfill materials and build a load-bearing system together with the backfill to maintain the stability of the goaf [21]. There are a significant number of published studies on the load-bearing mechanism of the backfill and pillars in underground space [22,23,24]. Wang et al. [25] investigated the joint bearing mechanism between the backfill and the surrounding rocks using indoor uniaxial compression tests, and the results indicated that pillars could enhance the uniaxial compressive strength and the elastic modulus of the backfill. Zhu et al. [26] used particle flow code numerical simulation software to investigate the load-bearing effects of support pillars consisting of backfill and coal walls under different conditions, and the results indicated that the width of the residual coal pillars had the greatest influence on the stability of the support pillars relative to factors such as mining depth, mining thickness, filling material, and filling ratio. However, most published research focuses on the interaction behavior of a single backfill material with the pillar, and there are few studies on the case of two backfill materials. In practice, more than one backfill material exists because of the economic benefits.
In this study, based on elastic mechanics, the stress and deformation characteristics of permanently retained thin walls in panel barrier pillar stopes are solved when different backfill materials are used in adjacent stopes. The theoretical findings are verified by numerical simulations and collected monitoring data. The results obtained from this study will help design the optimal width of the retained walls to maximize the recovery of mineral resources.
2. Project Overview and Mining Methods
The study area is a mine in China, where direct mining is risky due to the thickness of the ore body and the depth of its burial. The mining method is sublevel open stoping with backfilling. In this operation, the ore body is firstly divided into different panels along the trend; then, a fixed-width barrier pillar is designed between the panels, and the room stopes and pillar stopes are alternately distributed along the panels perpendicular to the ore body trend, as shown in Figure 1. The mining of the ore body is divided into three steps: The first step is to mine the room stopes under the primary support provided by ore pillars on both sides and then backfill the mined stopes using the cemented tailings backfill material. The second step is to mine the pillar stopes under the support of cemented backfills on both sides and then backfill the mine stopes using the full-tailings backfill material. After completing the previous two steps, most of the mineral resources have been recovered. To further improve the recovery of mineral resources, the third step is to mine the panel barrier pillar stopes, and finally backfill the mined area also using the full-tailings backfill material.
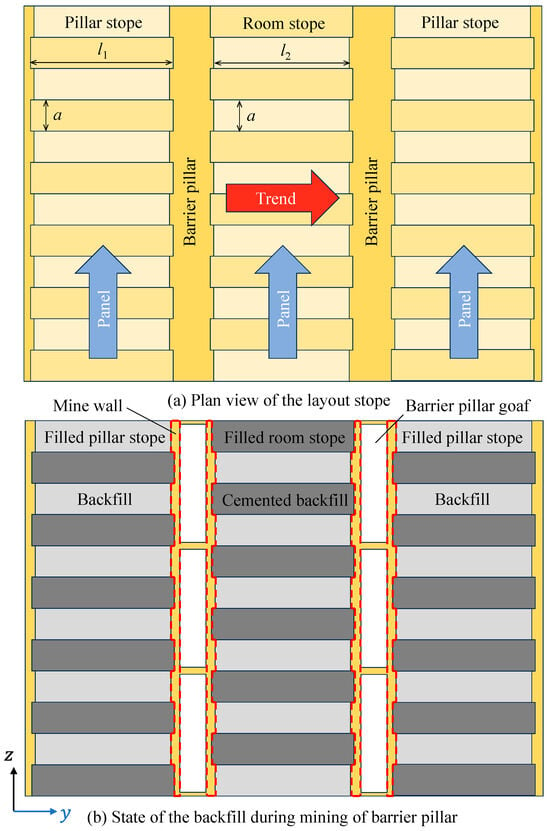
Figure 1.
Schematic diagram of mining and filling sequence.
Although this step-by-step mining process is more complex, it can effectively control the regional stresses and maintain the stability of the stopes throughout the gradual mining and backfilling, and ultimately achieve the goal of less ore loss.
In Figure 1, l1 is the length of the room stope; l2 is the length of the pillar stope; and a is the width of the room stope and pillar stope.
3. Mechanical Modeling of the Permanent Thin Wall
At the third mining step, the thin walls on both sides of the barrier pillar stope are permanently retained in order to prevent mixing of the backfill material with the ore inside the stope. The thin wall has a small direct contact area with the roof compared with the backfill materials, which are the main bearers of the roof loads at this stage. On the horizontal plane, the wall has a large contact area with the backfill materials, so the forces acting on the wall can be simplified to only the lateral loads from the backfill materials. The basic assumptions for the thin walls are as follows: the wall is a continuous, homogeneous, isotropic, and perfectly elastic material, and the magnitude of the wall displacement is much smaller than its own size.
3.1. Mechanical Model of the Thin Wall When Using One Backfill Material
For the case of the same backfill material being used in both the room stopes and pillar stopes, if l1 = l2 (see Figure 1), the width of the thin wall does not change in the z-axis direction, as shown in Figure 2. In this case, it can be assumed that the lateral load q applied by the backfill materials to the thin wall does not change perpendicular to the wall. Therefore, the three-dimensional spatial problem can be simplified to a two-dimensional plane problem.
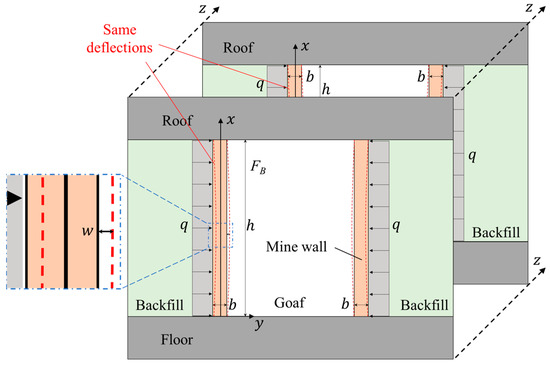
Figure 2.
Mechanical model of the thin wall when using one backfill material.
As can be seen from Figure 2, the thin wall is only bearing lateral loads from backfill materials, and it can be regarded as a beam structure undergoing pure bending deformation; therefore, its deflection and stresses satisfy Equations (1) and (2), respectively.
where Eo is the elastic modulus of the thin wall; Iz is the inertia moment of the wall cross-section about the neutral axis; b is the width of the wall; w is the deflection of the wall; and M(x) is the bending moment of the wall under the lateral load q.
The two ends of the wall are parts of the surrounding rocks, so fixed constraints are applied. From structural mechanics, under uniform load, the bending moment and shear force at the two end points of the beam are as follows:
From Equation (4), the bending moment along the x direction can be derived as follows:
By combining Equations (1) and (5), the deflection equation of the wall can be solved by integration:
where C1 and C2 are undetermined coefficients.
Using Equation (6) and the boundary conditions of
the deflection of the wall can be derived as follows:
As expected, the deflection of the wall is directly proportional to the roof load and inversely proportional to the length of the mine wall, the elastic modulus, and the cube of the width.
3.2. Mechanical Model of the Thin Wall When Using Two Backfill Materials
In practice, pillar stopes are mined under the condition that both sides are backfilled at the first mining step, which uses the cemented tailings backfill material, which has sufficient strength to ensure that the backfill will not fail during the mining process of pillar stopes. After the recovery of pillar stopes, to reduce costs, full-tailings backfill instead of cemented tailings materials are used for the backfill. This results in different lateral loads being applied to the thin walls at different locations. Assuming that the lateral loads applied to the wall by cemented and un-cemented backfill materials are q1 and q2, respectively, the two walls of the same barrier pillar stope will have different deflections, as shown in Figure 3a. In this situation, the deformations of thin walls in adjacent barrier pillar stopes will affect each other, so the three-dimensional problem cannot be simplified into a two-dimensional plane problem.
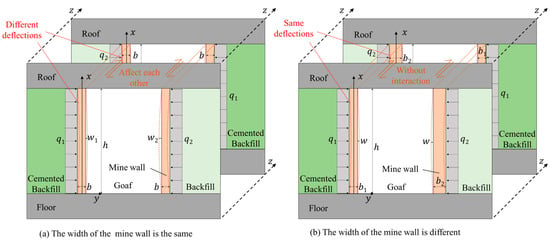
Figure 3.
Mechanical model of the thin wall when using two backfill materials.
Since the thin wall deformation of adjacent barrier pillar stopes is different, the mutual influence is the root cause of the inability to reduce the three-dimensional problem to a two-dimensional one. Then, if it is guaranteed that the thin wall deformation of adjacent barrier pillar stopes is the same, the mutual influence between them will disappear. At this point, they can be regarded as two mutually independent planes, each calculated. As shown in Equation (8), the wall deflection is a function of the lateral load and the wall width. The width of the thin wall can be adjusted according to the lateral loads if it is desired to keep the deflection identical to ensure no interference of wall deformations between adjacent barrier pillar stopes. Based on Equation (8), this situation occurs when the values of wall width satisfy the following relationship:
As the backfill material bears the roof loads under lateral pressure support from the thin wall, the lateral pressure q and the roof pressure p satisfy the following relationship according to the Mohr–Coulomb criterion:
where is the uniaxial compressive strength and is the internal friction angle of the backfill material.
By combining Equations (9) and (10), to achieve the same wall deflection, the width of the thin wall should satisfy the following:
where and are the uniaxial compressive strength values of the backfill materials in room stopes and pillar stopes, respectively; φb1 and φb2 are the internal friction angles of the backfill materials in room stopes and pillar stopes, respectively.
From Equation (11), one can observe that the thin wall width is mainly influenced by the roof load, uniaxial compressive strength, and the internal friction angle of the backfill materials. The wall width needs to increase as the roof load increases, the uniaxial compressive strength decreases, or the internal friction angle decreases. Without considering the influence of internal friction angles, when the roof load is much larger than the uniaxial compressive strength of both backfill materials and the uniaxial compressive strength of both backfill materials is close to each other, the width ratio of the two walls would be close to 1. When the roof load is close to the uniaxial compressive strength of one backfill material, but very different from the uniaxial compressive strengths of the other, the width ratio of the two walls would be far away from 1. From the perspective of internal friction angle, the smaller the difference in the internal friction angle between the two filling materials, the closer the width ratio of the two walls would be to 1. In summary, the different-width walls will be a better choice when the mine pressure and the backfill materials satisfy the following conditions: (a) there is a large difference between the uniaxial compressive strengths of the two backfill materials; (b) there is a large difference between the roof load and the uniaxial compressive strength of one of the backfill materials; and (c) there is a large difference between the internal friction angles of the two backfill materials.
3.3. Optimization of the Width for the Thin Wall
The roof of underground excavations will cave when it loses its support. Engineering practices have indicated [27,28] that the roof will reach a stable state after an arch structure is formed by caving. The arch structure can help re-distribute the ground stresses of the roof strata to unexcavated areas on both sides of the excavation. This stable arch structure formed by the phenomenon of stress redistribution is known as a natural arch.
For the mining operation described in this paper, backfill materials are used to replace the original rocks to support the roof strata. However, as the strength of the backfill materials is far lower than that of the original rock, they cannot completely replace the original rock to bear the stresses from the roof strata, so stress redistribution will inevitably occur. Based on the characteristics of a natural arch, the roof loads will gradually be re-distributed to rocks on both sides of the excavation if the bearing capacity of the substructure is insufficient. This is the case for the mining operation described, where the backfill will only bear the weight of caved loose rocks, as shown in Figure 4.
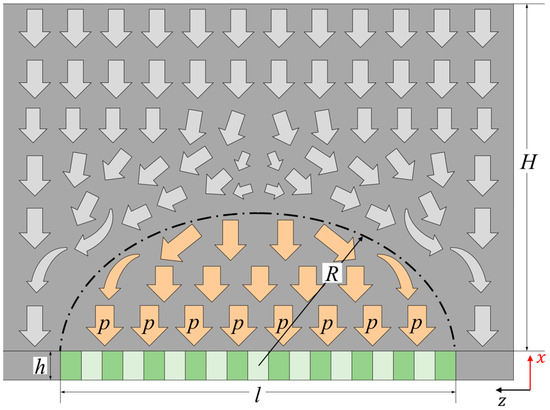
Figure 4.
Schematic diagram of load distribution.
Based on the theory related to natural arches and the findings of our previous studies [29,30], the radius R of the rock mass in the disturbed region surrounding the mine with risk of falling can be determined as:
where is the density of the roof rock, g is the gravity acceleration (9.8 m/s2), H is the depth of the stope from the ground, h is the height of the mine wall, is the cohesion of the roof rock, is the internal friction angle of the roof rock and n is the number of stopes along the direction of the stope width.
The gravitational pressure of the caved rocks, namely, the roof load p, applied to the backfill is
According to the mine site test data, the mechanical parameters of different materials are shown in Table 1. Other required parameters are H = 720 m, n = 19, h = 25 m, and a = 18 m.

Table 1.
Physical and mechanical parameters of different materials.
To ensure the stability of the thin wall, it is required that both the maximum compressive stress and the maximum tensile stress within the mine wall are less than their corresponding strength values. From Equation (5), M(x) is a quadratic function whose maximum appears at x = h/2. When x = h/2, by combining Equations (2), (3) and (5), the stress inside the thin wall can be obtained:
From this equation, the maximum compressive stress in the wall appears at y = b/2, and the maximum tensile stress at y = −b/2. From Equations (10), (12) and (13), when b1 < 1.23 m or b2 < 3.94 m, the tensile stress inside the wall is greater than the tensile strength, and therefore tensile damage may occur. From Equation (11), the deflections of the wall with different widths are the same when b1:b2 = 0.63. In this case, using b1 = 2.48 m and b2 = 3.94 m can ensure that the deflections of both walls are the same, and the wall will not be damaged as it has not exceeded its own ultimate stresses under the lateral loading of the backfill.
4. Numerical Simulation and Engineering Verification
4.1. Numerical Model and Initial Conditions
The geological conditions of the mine were simplified, and a 1000 m × 1200 m × 1200 m (x × y × z) numerical model was constructed using COMSOL Multiphysics 6.2 software, as shown in Figure 5a. The thickness of the roof strata in the upper part of the model is 720 m, the thickness of the ore body in the middle part of the model is 25 m, and the thickness of the floor rocks in the bottom part of the model is 255 m. Figure 5b,c illustrate the location of the ore body in the model and the layout of the stopes within the mine, respectively. The model was meshed using free tetrahedral units. Fine mesh was used in the mining area to ensure the accuracy of the model while coarse mesh was used in areas far away from the stopes to reduce the computational cost, resulting in a total of 640,207 elements. The minimum cell mass is 0.278, the average cell mass is 0.721, and the cell volume ratio is 2.43 × 10−4, giving the mesh a high overall mass. In this case, the Drucker–Prager criterion was used. This criterion is a modified version of the Mohr–Coulomb criterion, retaining the ability to use the Mohr–Coulomb parameters while avoiding the problem of sharp corners that tend to occur in the principal stress space when the Mohr–Coulomb criterion is used. The parameters used in the simulations are listed in Table 1. As the model is large and the excavated area is located in the center of the model, far from the boundary, it can be assumed that there is no displacement at the bottom and only vertical displacement around the surrounding area. The following boundary conditions were used: fixed constraints on the bottom surface of the model, fixed displacement constraints in the normal directions of the four side surfaces of the model, and no constraint for the top surface of the model. Only gravitational loads were considered. The model is the result of a simplification of the actual mine, and in the simulation calculations, it is assumed that all material properties are homogeneous and isotropic, ignoring the anisotropy of materials in the actual geological environment. Moreover, the boundaries are set to be fixed or free, which may deviate from the actual situation. The current model is mainly applicable to laminated rock structures. For geological environments that are unstratified, highly fractured, or where there are a large number of faults, the predictive power of the model may be reduced.
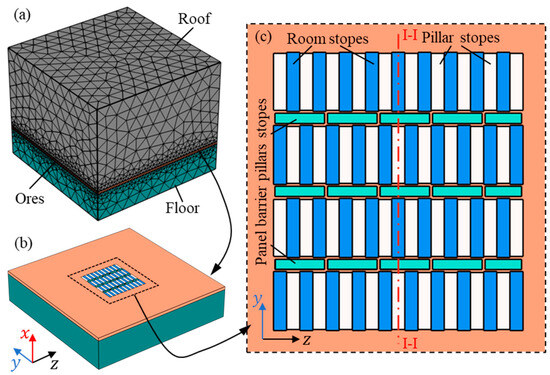
Figure 5.
Numerical model: (a) meshing, (b) the location of the ore body, and (c) the layout of stopes.
4.2. Analysis of Simulation Results
The simulation was conducted according to the three-step mining processes. Figure 6 shows the contour plot of the vertical displacement in cross-section I-I (Figure 5) after the mining of the barrier pillar stopes is completed. The maximum displacement is found to be about 12 cm at the roof of the panel barrier pillar stope. The backfill materials of room stopes and pillar stopes play a partial bearing role and restrict the roof displacement, so the displacement at these locations is about 3 cm. The contour map of the vertical displacements shows a dome structure, which is in general agreement with the assumptions of a caved natural arch formed at the top of the excavation.
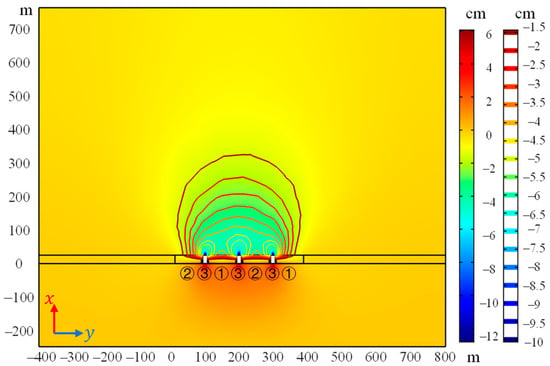
Figure 6.
Contour plot of the vertical displacement on the I-I cross-section.
In this study, simulations were run for both equal-width and non-equal-width thin walls. For the first case, the room stopes and pillar stopes were set to the same size, and the width of the thin walls was set at 3.25 m, as shown in Figure 7a. As different backfill materials were used in the room stopes and pillar stopes, the horizontal displacement of the thin wall near the pillar stope is greater than that near the room stope, which is expected. For the case when the width of the thin walls is different, at 2.5 m and 4 m, respectively, the results are shown in Figure 7b. Compared with Figure 7a, the horizontal displacement of the thin wall close to the room stopes becomes much larger, while the horizontal displacement of the wall close to the pillar stope is slightly reduced.
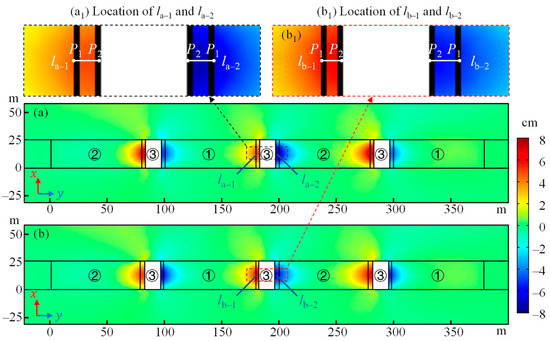
Figure 7.
Horizontal displacement of the thin walls: (a) equal-width walls and (b) non-equal-width walls.
To have a better understanding of the horizontal displacement of the thin wall, the horizontal displacement in the middle of the thin walls from different stopes was extracted and is plotted in Figure 8. la−1, la−2, lb−1, and lb−2 are the four segments, as shown in Figure 7, and their corresponding simulation results are listed in Table 2. When the width of the thin wall is 3.25 m, the average horizontal displacement of the wall close to the room stope is 4.92 cm, while the average horizontal displacement of the wall close to the pillar stope is 7.28 cm. The horizontal displacement of the wall close to the room stopes is only 67.6% of that close to the pillar stopes. In other words, the wall close to the pillar stopes may be damaged first, leading to stress concentration in the walls close to the room stopes which may be subsequently damaged. If the width of the wall was reduced to 2.5 m near the room stopes and increased to 4 m near the pillar stopes, it could be found that the average horizontal displacement of the wall increased to 5.96 cm for the 2.5 m wall and decreased to 5.72 cm for the 4 m wall. In this case, the horizontal displacements of both walls are approximately equal. In other words, the deformations of both walls were relatively more coordinated, and the risk of partial failure and overall collapse was reduced.
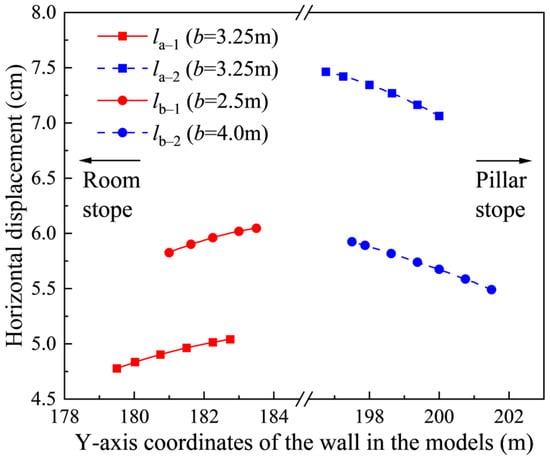
Figure 8.
Horizontal displacement in the middle of the thin wall.

Table 2.
Parameters of selected segments in the middle of the thin wall.
4.3. Verification Against Filed Data
The mine was mined in strict accordance with the design discussed above. From steps 1 to 3, the difficulty of mining gradually increases but the ore recovery rate increases. To understand the wall stability and the roof collapse within the barrier pillar stopes after mining, the Cavity Monitoring System (CMS) developed by Optech Company (Troy, MI, USA), was used to scan the goaf [30]. The collected data were further processed using the Qvol software, and then a 3D model of the goaf was built using the DIMINE modeling software. Examples of the typical cross-sectional profiles of the G6 goaf in the panel barrier pillar stope are shown in Figure 9.
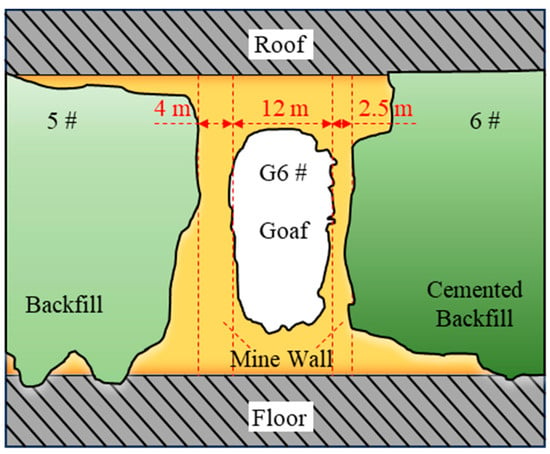
Figure 9.
Typical profiles of the G6 goaf in the panel barrier pillar stope.
The scan results shown in Figure 9 indicate that the width of the retained walls is in good agreement with the design value without significant over-break or under-break. The scanning confirmed that both walls remain in good integrity with no significant peeling or cracking identified. No large quantities of backfill materials were found to have entered the stope during the mining process, and the walls performed well in isolating the backfill from the stopes. In addition, BGK-A3 multi-point displacement gauges were installed on the roof of the barrier pillar stopes to monitor the roof displacements. After 6 months of monitoring, the maximum displacements were 34 mm at the monitoring points in the G6 goaf. It is worth explaining that the maximum displacement monitored by numerical simulation is 12 cm, which is 3.5 times that of the on-site monitoring result, and there is some error. The main reason for this phenomenon is that the on-site monitoring results only represent the maximum displacement near the monitoring point, and do not represent the maximum displacement of the whole roof, so the maximum displacement of the roof on-site will be greater than 34 mm. In addition, the simulation parameters are the average of the rock tests at several sampling points, which may have some differences with the rock at the location of the monitoring point. Also, the simulation process simplifies the strata, and other reasons can lead to these errors. Although there was some error in the modeling and monitoring results, these displacements were within the safe range, proving that the backfill in this case had provided sufficient additional support to the roof strata. The results demonstrated that the backfill, in this case, worked well, the thin wall did not appear to have large deformations or damages, the theoretical and numerical simulation results agreed well, and the layout of non-equal-width walls had a great application value in this type of mining operation.
5. Conclusions
This study modeled the performance of retained walls in panel barrier pillar stopes. By simplifying the three-dimensional problem based on the mining operation, a two-dimensional mechanical model of non-equal-width retained walls was established, and the stress and deflection were solved analytically. The following key conclusions were obtained:
(1) Retained barrier walls will be subjected to bending deformation under the lateral pressure created by the backfill materials. The degree of deformation is mainly influenced by the roof loads, as well as the uniaxial compressive strength and the internal friction angle of the backfill materials. A greater width of the retained walls will be required for higher roof loads, lower uniaxial compressive strength, or a lower internal friction angle of backfill materials.
(2) For the case when different backfill materials with different mechanical properties are used for room stopes and pillar stopes, non-equal width of the retained walls should be designed to ensure that the deformations of the walls are coordinated under the effect of different backfill materials. This will avoid the wall damage caused by over-deformation in part of the retained wall.
(3) The field project chose to use a non-equal-thickness spacing arrangement for the wall in the panel barrier pillar. The monitoring results indicated that the roof displacements of the G6 goaf at the third mining step were 34 mm and both sides of the backfill materials played a good role in supporting the roof. The backfill had sufficient stability in limiting its lateral displacement and the retained walls performed well in preventing the flow of the backfill materials into the stope during the mining operation. The theoretical model has been demonstrated to be able to provide answers to the problems discussed.
Author Contributions
Conceptualization, K.C.; methodology, K.C.; software, Z.Y.; validation, J.L.; resources, K.C.; writing—original draft preparation, K.C.; writing—review and editing, Z.Y.; visualization, J.L.; supervision, J.L.; funding acquisition, K.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Key Scientific Research Project of Colleges and Universities of Henan Province (24A620003).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yao, B.; Wei, J.; Wang, D.; Ma, D.; Chen, Z. Numerical study on seepage property of karst collapse columns under particle migration. CMES Comput. Model. Eng. Sci. 2013, 91, 81–100. [Google Scholar]
- Yang, Z.; Tao, M.; Fei, W.; Yin, T.; Ranjith, P.G. Grain-based coupled thermo-mechanical modeling for stressed heterogeneous granite under thermal shock. Undergr. Space 2025, 20, 174–196. [Google Scholar] [CrossRef]
- Yang, Z.; Tao, M.; Memon, M.B.; Zhuang, D.; Zhao, Y. Microwave irradiation-induced deterioration of rock mechanical properties and implications for mechanized hard rock excavation. J. Rock Mech. Geotech. Eng. 2025, 17, 275–290. [Google Scholar] [CrossRef]
- Bai, J.; Dou, L.; Li, J.; Zhou, K.; Cao, J.; Kan, J. Mechanism of coal burst triggered by Mining-Induced fault slip under High-Stress conditions: A case study. Front. Earth Sci. 2022, 10, 884974. [Google Scholar] [CrossRef]
- Zhao, Y.; Tao, M.; Du, K.; Wu, Y.; Wu, C. Development and application of gas adsorption model for coal based on particle flow code. Gas Sci. Eng. 2023, 110, 204858. [Google Scholar] [CrossRef]
- Tuncay, D.; Tulu, I.; Klemetti, T. Re-analysis of abutment angle method for moderate and deep cover retreat room and pillar mines and investigation of loading mechanics using finite volume modeling. Rock Mech. Rock Eng. 2021, 54, 3447–3468. [Google Scholar] [CrossRef]
- Rastiello, G.; Federico, F.; Screpanti, S. New soft rock pillar strength formula derived through parametric FEA using a critical state plasticity model. Rock Mech. Rock Eng. 2015, 48, 2077–2091. [Google Scholar] [CrossRef]
- Naghadehi, M.; Mikaeil, R.; Ataei, M. The application of fuzzy analytic hierarchy process (FAHP) approach to selection of optimum underground mining method for Jajarm Bauxite Mine, Iran. Expert Syst. Appl. 2009, 36, 8218–8226. [Google Scholar] [CrossRef]
- Guo, J.; Cheng, X.; Lu, J.; Zhao, Y.; Xie, X. Research on factors affecting mine wall stability in isolated pillar mining in deep mines. Minerals 2022, 12, 623. [Google Scholar] [CrossRef]
- Sari, M.; Yilmaz, E.; Kasap, T. Long-term ageing characteristics of cemented paste backfill: Usability of sand as a partial substitute of hazardous tailings. J. Clean. Prod. 2023, 401, 136723. [Google Scholar] [CrossRef]
- Huang, X.; Cai, X.; Bo, J.; Li, S.; Qi, W. Experimental study of the influence of gradation on the dynamic properties of centerline tailings sand. Soil Dyn. Earthq. Eng. 2021, 151, 106993. [Google Scholar] [CrossRef]
- Gao, S.; Li, W.; Yuan, K.; Rong, C. Properties and application of thixotropic cement paste backfill with molybdenum tailings. J. Clean. Prod. 2023, 391, 136169. [Google Scholar] [CrossRef]
- Li, J.; Huang, Y.; Qi, W.; Kong, G.; Song, T. Loose gangues backfill body’s acoustic emissions rules during compaction test: Based on solid backfill mining. Comput. Model. Eng. Sci. 2018, 115, 85–103. [Google Scholar]
- Hou, C.; Zhu, W.; Yan, B.; Yang, L.; Du, J.; Niu, L. Mechanical behavior of backfilled pillar under biaxial loading. J. Cent. South Univ. 2023, 30, 1191–1204. [Google Scholar] [CrossRef]
- Wang, H.; Poulsen, B.; Shen, B.; Xue, S.; Jiang, Y. The influence of roadway backfill on the coal pillar strength by numerical investigation. Int. J. Rock Mech. Min. Sci. 2011, 48, 443–450. [Google Scholar] [CrossRef]
- Hou, C.; Zhu, W.; Yan, B.; Guan, K.; Niu, L. Analytical and experimental study of cemented backfill and pillar interactions. Int. J. Geomech. 2019, 19, 04019080. [Google Scholar] [CrossRef]
- Yan, B.; Ren, F.; Cai, M.; Qiao, C. Influence of new hydrophobic agent on the mechanical properties of modified cemented paste backfill. J. Mater. Res. Technol. 2019, 8, 5716–5727. [Google Scholar] [CrossRef]
- Lu, B.; Li, Y.; Fang, S.; Lin, H.; Zhu, Y. Cemented backfilling mining technology for gently inclined coal seams using a continuous mining and continuous backfilling method. Shock. Vib. 2021, 2021, 6652309. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Li, M.; Gao, F.; Taheri, A.; Huo, B.; Jin, L. Expansion properties of cemented foam backfill utilizing coal gangue and fly ash. Minerals 2022, 12, 763. [Google Scholar] [CrossRef]
- Zhu, W.; Yu, S.; Xuan, D.; Shan, Z.; Xu, J. Experimental study on excavating strip coal pillars using caving zone backfill technology. Arab. J. Geosci. 2018, 11, 554. [Google Scholar] [CrossRef]
- Wang, J.; Qiao, D.; Han, R.; Li, G.; Xie, J. Strength model of cemented backfill in subsequent filling at the stage of open stope and its application. Rock Soil Mech. 2019, 40, 1105–1112. [Google Scholar] [CrossRef]
- Du, X.; Feng, G.; Qi, T.; Guo, Y.; Zhang, Y.; Wang, Z. Failure characteristics of large unconfined cemented gangue backfill structure in partial backfill mining. Constr. Build. Mater. 2019, 194, 257–265. [Google Scholar] [CrossRef]
- Le, Z.; Yu, Q.; Yang, T.; Cao, Y.; Zheng, H.; Deng, W. Compressive bearing and force transmission characteristics of granular backfill under lateral confinement. Rock Soil Mech. 2023, 43, 362–372. [Google Scholar] [CrossRef]
- Wu, D.; Guo, W.; Luo, F.; Li, M.; Wen, P. Stiffness of gangue backfilling body in goaf and its influence mechanism on rock strata control and stress evolution in gangue backfill mining. Environ. Sci. Pollut. Res. 2023, 30, 61789–61807. [Google Scholar] [CrossRef]
- Wang, J.; Fu, J.; Song, W.; Zhang, Y. Mechanical properties, damage evolution, and constitutive model of rock-encased backfill under uniaxial compression. Constr. Build. Mater. 2021, 285, 122898. [Google Scholar] [CrossRef]
- Zhu, X.; Guo, G.; Liu, H.; Peng, X.; Yang, X. Stability analysis of the composite support pillar in backfill-strip mining using particle flow simulation method. Environ. Earth Sci. 2022, 81, 124. [Google Scholar] [CrossRef]
- He, M.; Wang, Q. Excavation compensation method and key technology for surrounding rock control. Eng. Geol. 2022, 307, 106784. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, Y.; Ma, J.; Han, P. Study on stability and bearing characteristics of macroscopic pressure arch of surrounding rock in western deep buried stope of China. Front. Earth Sci. 2023, 11, 1125689. [Google Scholar] [CrossRef]
- Guo, J.; Zhao, Y.; Zhang, W.; Xie, X. Stress analysis of mine wall in panel barrier pillar-stope under multi-directional loads. J. Cent. South Univ. (Sci. Technol.) 2018, 49, 3020–3028. [Google Scholar] [CrossRef]
- Tao, M.; Zhao, Y.; Guo, J. Arch model of roof and optimization of roof-contacted filling rate in two-step mining. Trans. Nonferrous Met. Soc. China 2023, 33, 1893–1905. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).