Reducing Railway Track Vibrations by Applying Particle-Damping Systems
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
- Steel rail: It is the principal component of the testing apparatus to which almost all other devices are connected. The steel rail is two metres long, being a profile of an ASCE (American Society of Civil Engineers) 60 light rail, with a total mass of 60 kg. The rail was positioned sideways, and excited vertically (the original direction concerning lateral vibrations of the mounted rail). The rail is suspended by supports in two locations (discussed in the following topic) and excited at the central portion of its length. The steel rail was tested sideways (when compared to its position during use).
- Supports and ropes: In order to minimise the impact of the fixturing system on the dynamic behaviour of the system, the steel rail was suspended by a pair of racks and ropes. The suspension region was located at the two vibration nodes of the 1st bending mode (slender beam), corresponding to a distance of 22.4% of the total length of the rail, measuring from the closest free edge.
- Speaker: This component was used to provide external excitation to the steel rail. A 6-inch speaker was used, with a power of 90 W RMS (Root Mean Square). The working range of the presented speaker extends from 50 Hz to 5 kHz. The speaker was driven by a signal generator and a 100 W amplifier. The speaker was attached to an inertia block. The entire weight of the rail is maintained by supports, and the rail is positioned to just stay over the speakers (with no force when at rest). The excitation force orientation is parallel to the gravity
- Force transducer and central accelerometer: An impedance head was used to measure the excitation force and acceleration. This measurement device was located between the speaker and the web of the steel rail, placed in the mid-section of its length.
- Accelerometer (edge location): This sensor was used to measure the steel rail’s response under different excitations and with different damping systems, and it was placed 30 mm away from one of the rail ends. More details regarding the measuring system (impedance head and accelerometer) will be provided below.
- Particle reservoir: It is presented in Figure 1d. It consists of a steel box with an adjustable cover, having external dimensions of 550 × 55 × 75 mm. Only one reservoir was used for the present study, located on the web. The reservoir was attached to the rail using a structural adhesive, epoxy. Additionally, its height (75 mm) can be adjusted by two pairs of nuts. This is important since the filling ratio of the particle reservoir can be changed independently of the particle’s total mass. An internal volume of approximately 2 litres is obtained when the cover is positioned at the utmost configuration. The reservoir is attached to the middle section (half length).
3. Results
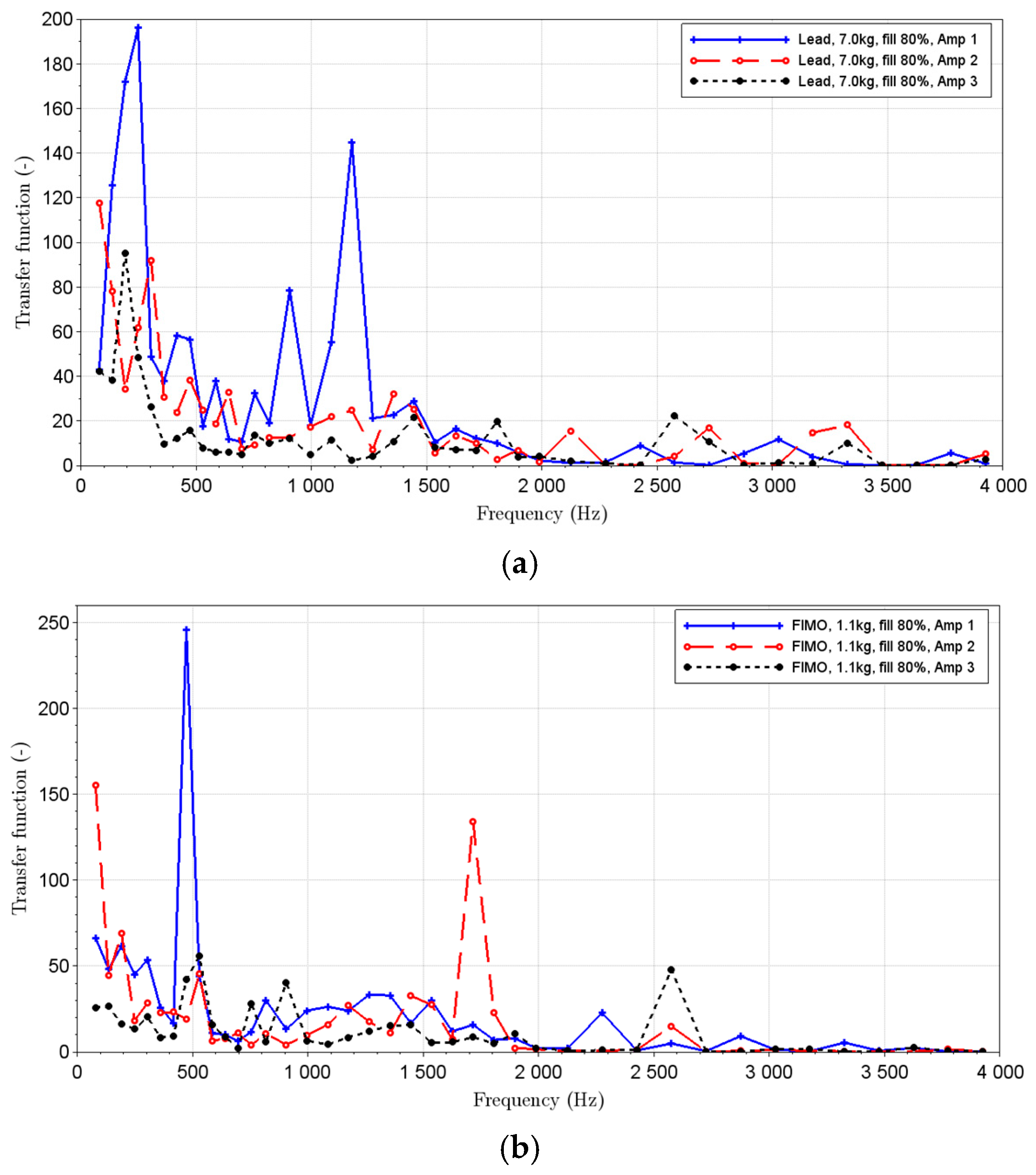
3.1. Lead Particles
3.2. Magnetite Particles
3.3. FIMO and Natural Rubber Particles
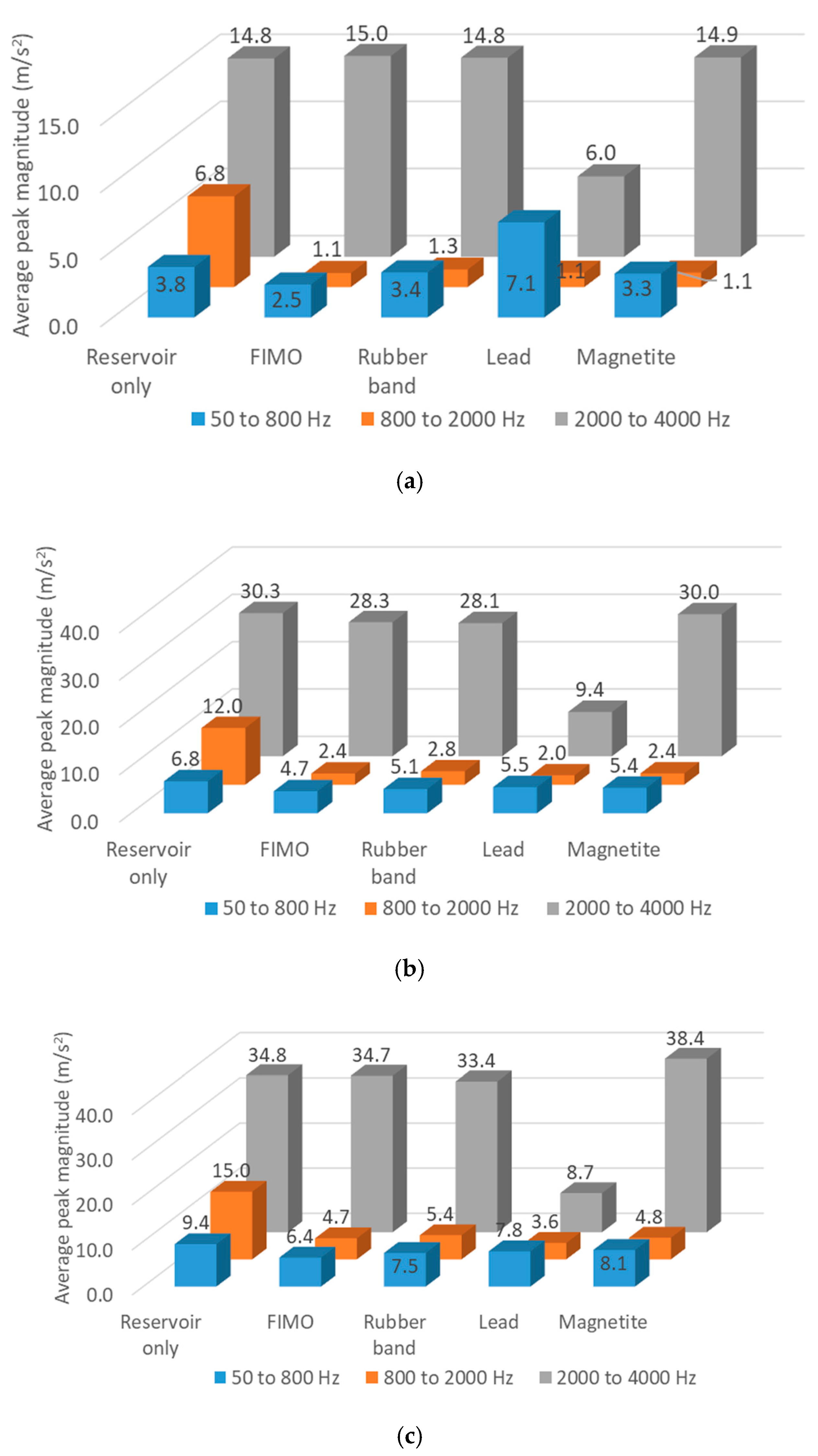
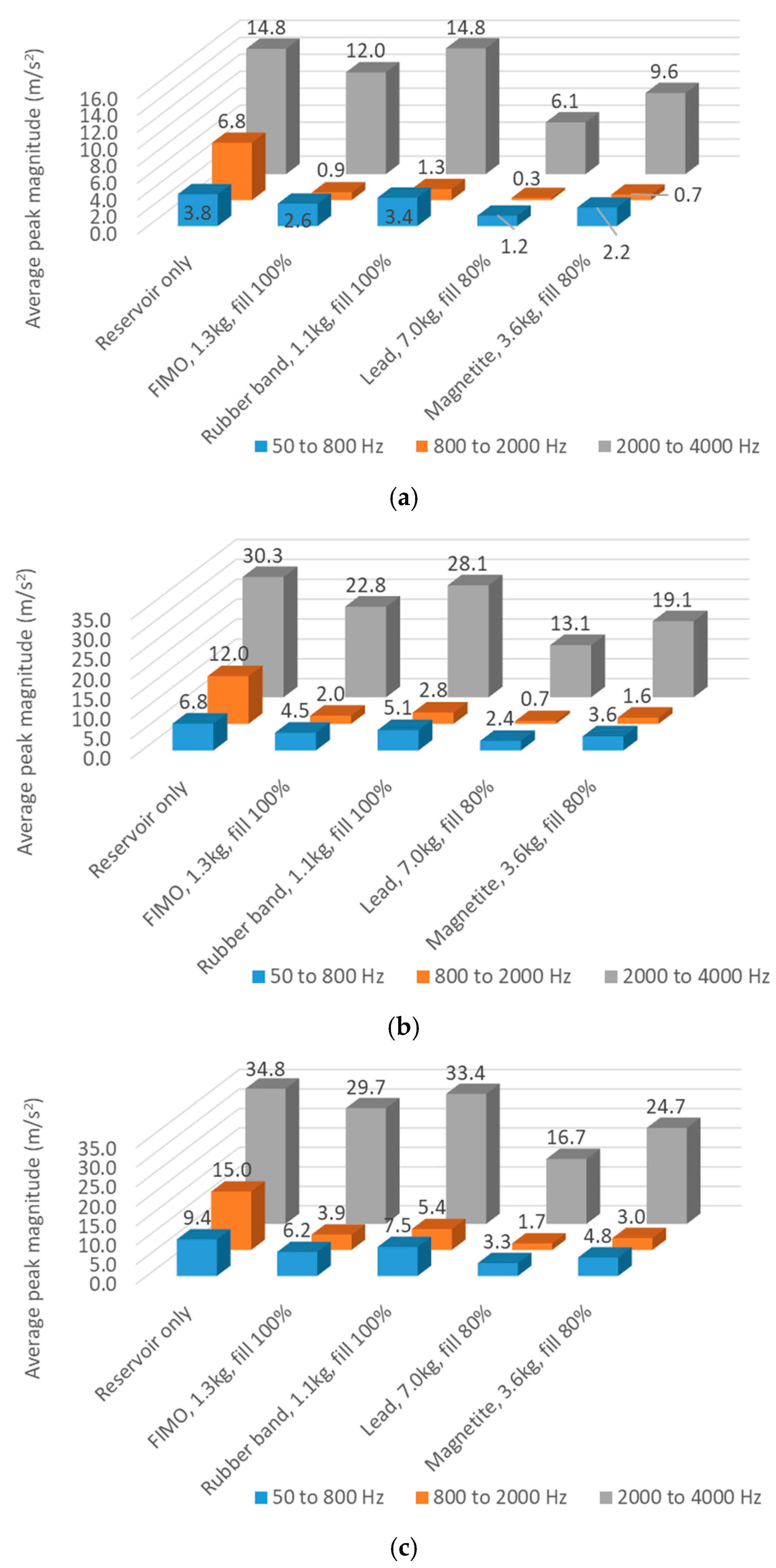
3.4. Equal Mass Comparison
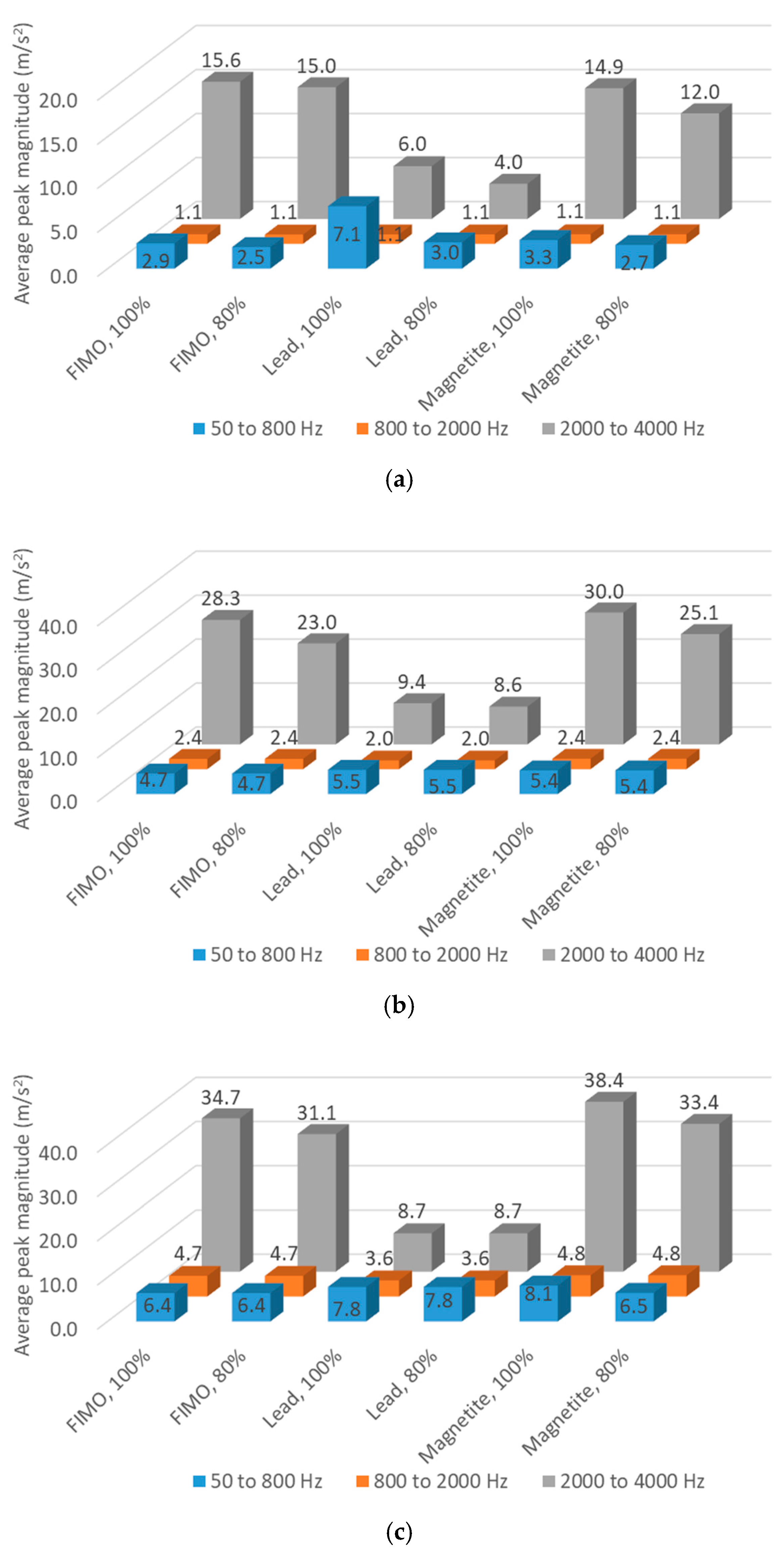
3.5. Effect of Excitation Amplitude
3.6. Summary
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wrótny, M.; Bohatkiewicz, J. Traffic noise and inhabitant health—A comparison of road and rail noise. Sustainability 2021, 13, 7340. [Google Scholar] [CrossRef]
- Maclachlan, L.; Waye, P.K.; Pedersen, E. Exploring perception of vibrations from rail: An interview study. Int. J. Environ. Res. Public Health 2017, 14, 1303. [Google Scholar] [CrossRef] [PubMed]
- Smith, M.G.; Croy, I.; Ögren, M.; Waye, P.K. On the influence of freight trains on humans: A laboratory investigation of the impact of nocturnal low frequency vibration and noise on sleep and heart rate. PLoS ONE 2013, 8, e55829. [Google Scholar] [CrossRef] [PubMed]
- Croy, I.; Smith, M.G.; Waye, K.P. Effects of train noise and vibration on human heart rate during sleep: An experimental study. BMJ Open 2013, 3, e002655. [Google Scholar] [CrossRef]
- Croft, B.; Miller, A.; Küpper, A. Maintenance effects on rolling noise–metro and light rail. Proc. Acoust. 2021, 21, 2022. [Google Scholar]
- Höjer, M.; Bergseth, E.; Olofsson, U.; Nilsson, R.; Lyu, Y. A noise related track maintenance tool for severe wear detection of wheel–rail contact. In Proceedings of the Third International Conference on Railway Technology: Research, Development and Maintenance, Caglinari, Italy, 5–8 April 2016; Civil-Comp Press: Stirlingshire, UK, 2016. [Google Scholar]
- Zhang, J.; Xiao, X.; Wang, D.; Yang, Y.; Fan, J. Source Contribution Analysis for Exterior Noise of a High-Speed Train: Experiments and Simulations. Shock Vib. 2018, 1, 5319460. [Google Scholar] [CrossRef]
- Connolly, D.P.; Marecki, G.P.; Kouroussis, G.; Thalassinakis, I.; Woodward, P.K. The growth of railway ground vibration problems—A review. Sci. Total Environ. 2016, 568, 1276–1282. [Google Scholar] [CrossRef]
- Ogran, M.; GIdlof-Gunnarsson, A.; Smith, M.; Gustavsson, S.; Waye, K.P. Comparison of annoyance from railway noise and railway vibration. Int. J. Environ. 2017, 14, 805. [Google Scholar]
- Sanayei, M.; Maurya, P.; Moore, J.A. Measurement of building foundation and ground-borne vibrations due to surface trains and subways. Eng. Struct. 2013, 53, 102–111. [Google Scholar] [CrossRef]
- Zou, C.; Wang, Y.; Moore, J.A.; Sanayei, M. Train-induced field vibration measurements of ground and over-track buildings. Sci. Total Environ. 2017, 575, 1339–1351. [Google Scholar] [CrossRef]
- Hanson, C.E.; Towers, D.A.; Meister, L.D. Transit Noise and Vibration Impact Assessment; Federal Transit Administration (USA): Washington, DC, USA, 2006. [Google Scholar]
- Abramov, A.; Podorozkina, A.; Bilenko, G.; Ivankova, L.; Okulova, M. Optimization of Freight Train Speeds on Railway Transport. Transp. Res. Procedia 2022, 61, 371–375. [Google Scholar] [CrossRef]
- Thompson, D.J.; Jones, C.J.C. A review of the modelling of wheel/rail noise generation. J. Sound Vib. 2008, 231, 519–536. [Google Scholar] [CrossRef]
- Thompson, D.J. On the relationship between wheel and rail surface roughness and rolling noise. J. Sound Vib. 1996, 193, 149–160. [Google Scholar] [CrossRef]
- Jeong, D.; Choi, H.S.; Choi, Y.J.; Jeong, W. Measuring Acoustic Roughness of a Longitudinal Railhead Profile Using a Multi-Sensor Integration Technique. Sensors 2019, 19, 1610. [Google Scholar] [CrossRef]
- Smith, M.G.; Croy, I.; Hammar, O.; Wayer, K.P. Vibration from freight trains fragments sleep: A polysomnographic study. Sci. Rep. 2016, 6, 24717. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V. Research developments in vibration control of structures using passive tuned mass dampers. Annu. Rev. Control 2017, 44, 129–156. [Google Scholar] [CrossRef]
- Jangid, R.S.; Datta, T.K. Seismic behaviour of base-isolated buildings: A state-of-the art-review. Proc. Inst. Civ. Eng. Struct. Build. 1995, 110, 186–203. [Google Scholar] [CrossRef]
- Saidi, I.; Mohammed, A.D.; Gad, E.F.; Wilson, J.L.; Haritos, N. Optimum Design for Passive Tuned Mass Dampers Using Viscoelastic Materials; Australian Earthquake Engineering Society: Wollongong, Australia, 2007. [Google Scholar]
- Jin, J.; Yang, W.; Koh, H.; Park, J. Development of tuned particle impact damper for reduction of transient railway vibrations. Appl. Acoust. 2020, 169, 107487. [Google Scholar] [CrossRef]
- Lin, C.C.; Wang, J.F.; Chen, B.L. Train-induced vibration control of high-speed railway bridges equipped with multiple tuned mass dampers. J. Bridge Eng. 2005, 10, 398–414. [Google Scholar] [CrossRef]
- Gagnon, L.; Morandini, M.; Ghiringhelli, G.L. A review of particle damping modeling and testing. J. Sound Vib. 2019, 459, 114865. [Google Scholar] [CrossRef]
- Friend, R.D.; Kinra, V.K. Particle impact damping. J. Sound Vib. 2000, 233, 93–118. [Google Scholar] [CrossRef]
- Meyer, N.; Seifried, R. Design of robust particle dampers using inner structures and coated container walls. Granul. Matter 2023, 25, 10. [Google Scholar] [CrossRef]
- Xu, Z.W.; Chan, K.W.; Liao, W.H. An empirical method for particle damping design. Shock Vib. 2004, 11, 647–664. [Google Scholar] [CrossRef]
- Prasad, B.B.; Duvigneau, F.; Woschke, E.; Juhre, D. Application and damping mechanism of particle dampers. Proc. Appl. Math. Mech. 2023, 22, e202200116. [Google Scholar] [CrossRef]
- Veeramuthuvel, P.; Shankar, K.; Sairajan, K.K. Experimental investigation of particle damper-based vibration suppression in printed circuit board for spacecraft applications. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 230, 1299–1311. [Google Scholar] [CrossRef]
- Paul, P.S.; Raja, P.; Aruldhas, P.; Pringle, S.; Shaji, E. Effectiveness of particle and mass impact damping on tool vibration during hard turning process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2018, 232, 776–786. [Google Scholar] [CrossRef]
- Panossian, H.V. Structural Damping Enhancement Via Non-Obstructive Particle Damping Technique. J. Vib. Acoust. 1992, 114, 101–105. [Google Scholar] [CrossRef]
- Prasad, B.B.; Luft, T.; Michaelsen, C.; Rottengruber, H.S. Enhancing Vibroacoustic Performance of Power Electronic Subsystem in Electric Drives Using Particle Dampers. In Proceedings of the DAGA 2024, Hannover, Germany, 18–21 March 2024. [Google Scholar]
- Xin, Y. Deep learning-based investigation of an innovative rail damper using particle damping technology for noise and vibration control. Ph.D. Thesis, The Hong Kong Polytechnic University, Hong Kong, 2024. [Google Scholar]
- Liu, C.; Lai, S.; Ni, Y.; Chen, L. Dynamic modelling and analysis of a physics-driven strategy for vibration control of railway vehicles. Veh. Syst. Dyn. 2024, 1–31. [Google Scholar] [CrossRef]
- Zhang, C.; Kordestani, H.; Shadabfar, M. A combined review of vibration control strategies for high-speed trains and railway infrastructures: Challenges and solutions. J. Low Freq. Noise Vib. Act. Control. 2023, 42, 272–291. [Google Scholar] [CrossRef]
- Jin, J.; Kim, H.; Koh, H.I.; Park, J. Railway noise reduction by periodic tuned particle impact damper with bounce and pitch-coupled vibration modes. Compos. Struct. 2022, 284, 115230. [Google Scholar] [CrossRef]
- Lu, Z.; Zhang, Q.; Fan, Q.; Li, Q. Studies on dissipative characteristics and equivalent model of particle damper in railway application. J. Sound Vib. 2023, 560, 117788. [Google Scholar] [CrossRef]
- Yanning, T.; Yu, D.; Wangqiang, X.; Kun, X. Particle damping-based design for vibration and noise reduction of interior wooden flooring in high-speed railway trains. Railw. Roll. Stock 2024, 1, 85–92. [Google Scholar]
- Cuenot, S.; Frétigny, C.; Demoustier-Champagner, S.; Nysten, B. Surface tension effect on the mechanical properties of nanomaterials measured by atomic force microscopy. Phys. Rev. B 2004, 69, 165410. [Google Scholar] [CrossRef]
- Chicot, D.; Mendoza, J.; Zaoui, A.; Louis, G.; Lepingle, V.; Roudet, F.; Lesage, J. Mechanical properties of magnetite (Fe3O4), hematite (α-Fe2O3) and goethite (α-FeO·OH) by instrumented indentation and molecular dynamics analysis. Mater. Chem. Phys. 2011, 129, 862–870. [Google Scholar] [CrossRef]
- Vo, V.S.; Nguyen, V.; Mahouche-Chegui, S.; Carbonnier, B.; Naili, S. Estimation of effective elastic properties of polymer/clay nanocomposites: A parametric study. Compos. Part B Eng. 2018, 152, 139–150. [Google Scholar] [CrossRef]
- Koblar, D.; Škofic, J.; Boltežar, M. Evaluation of the Young’s Modulus of Rubber-Like Materials Bonded to Rigid Surfaces with Respect to Poisson’s Ratio. J. Mech. Eng. 2014, 60, 506–611. [Google Scholar] [CrossRef]


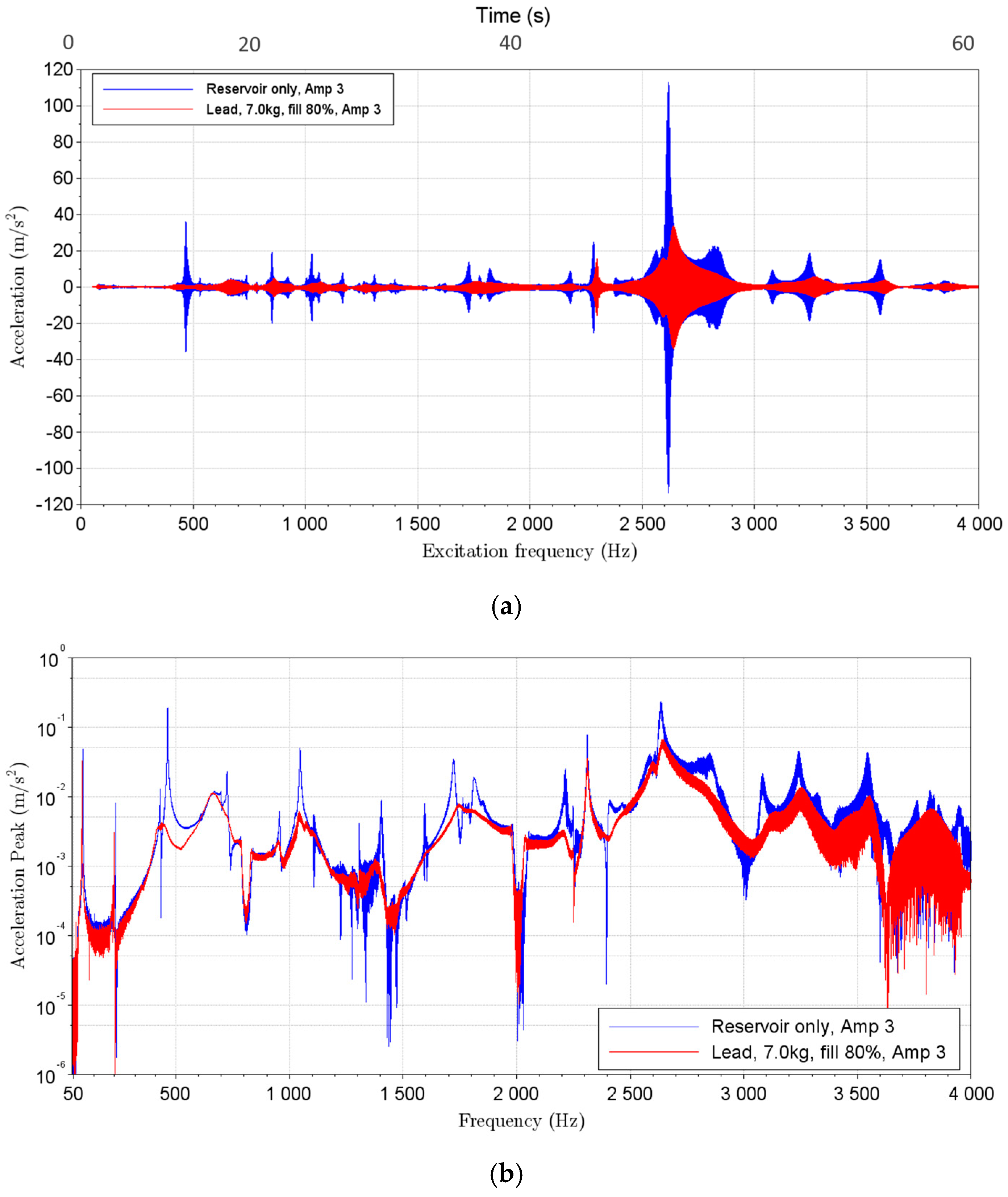
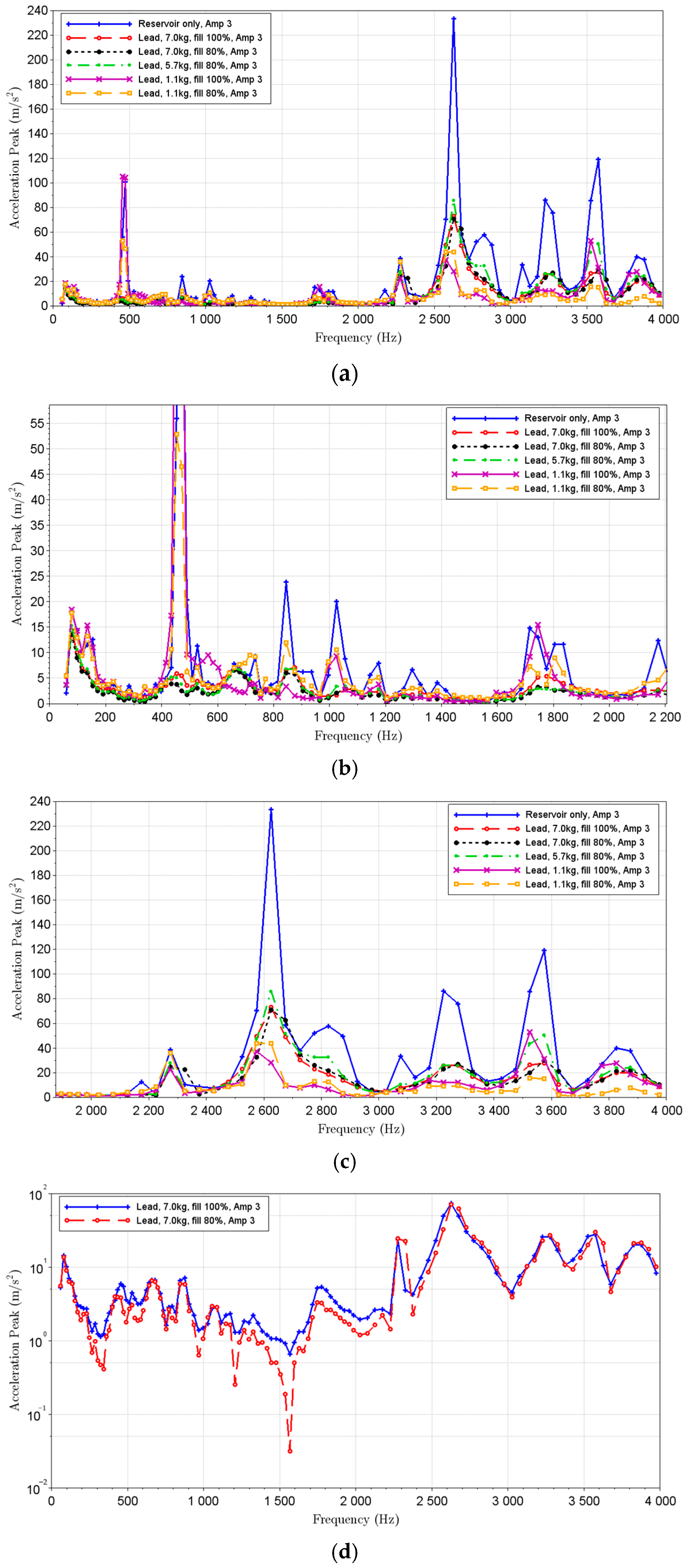
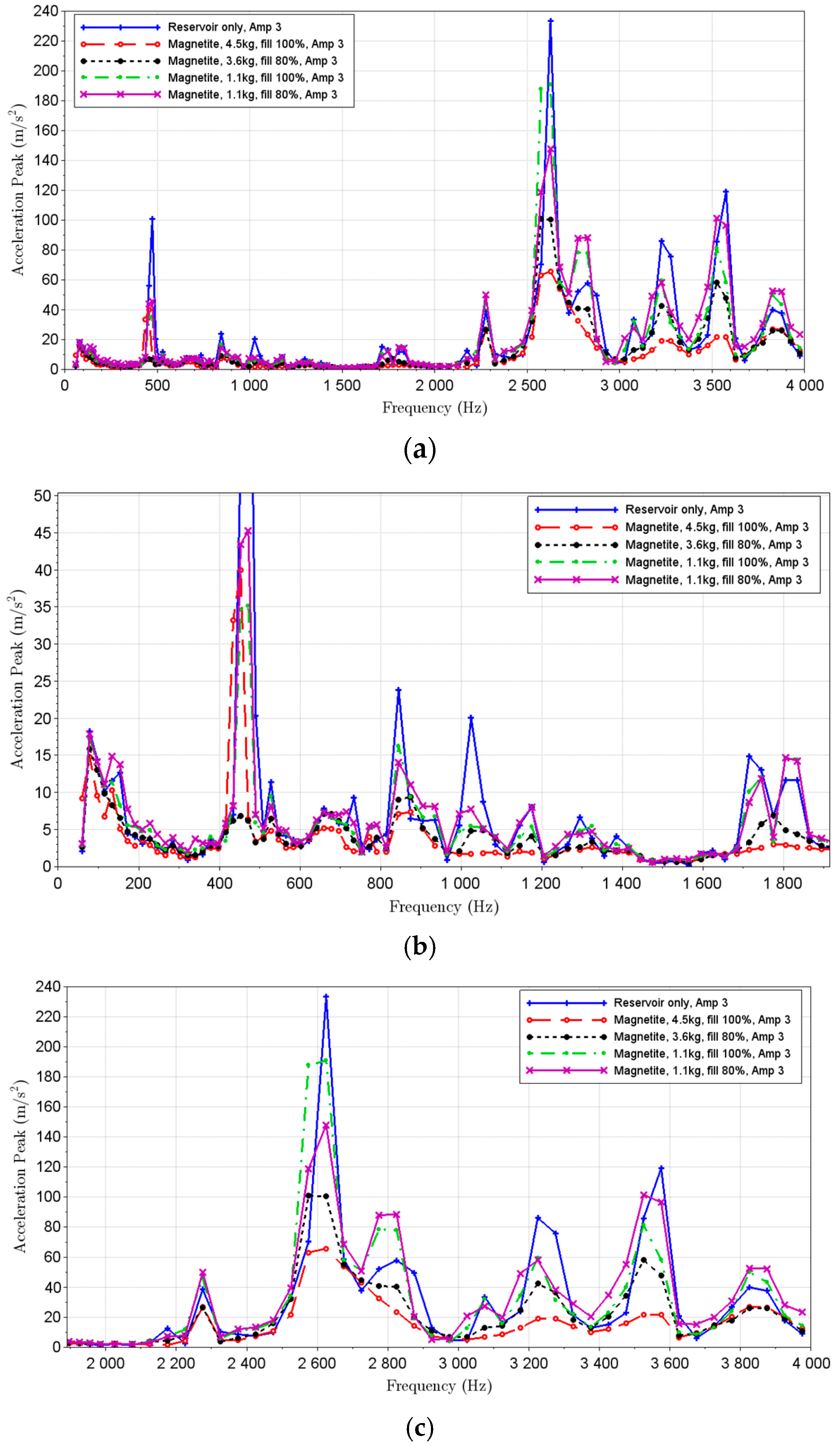

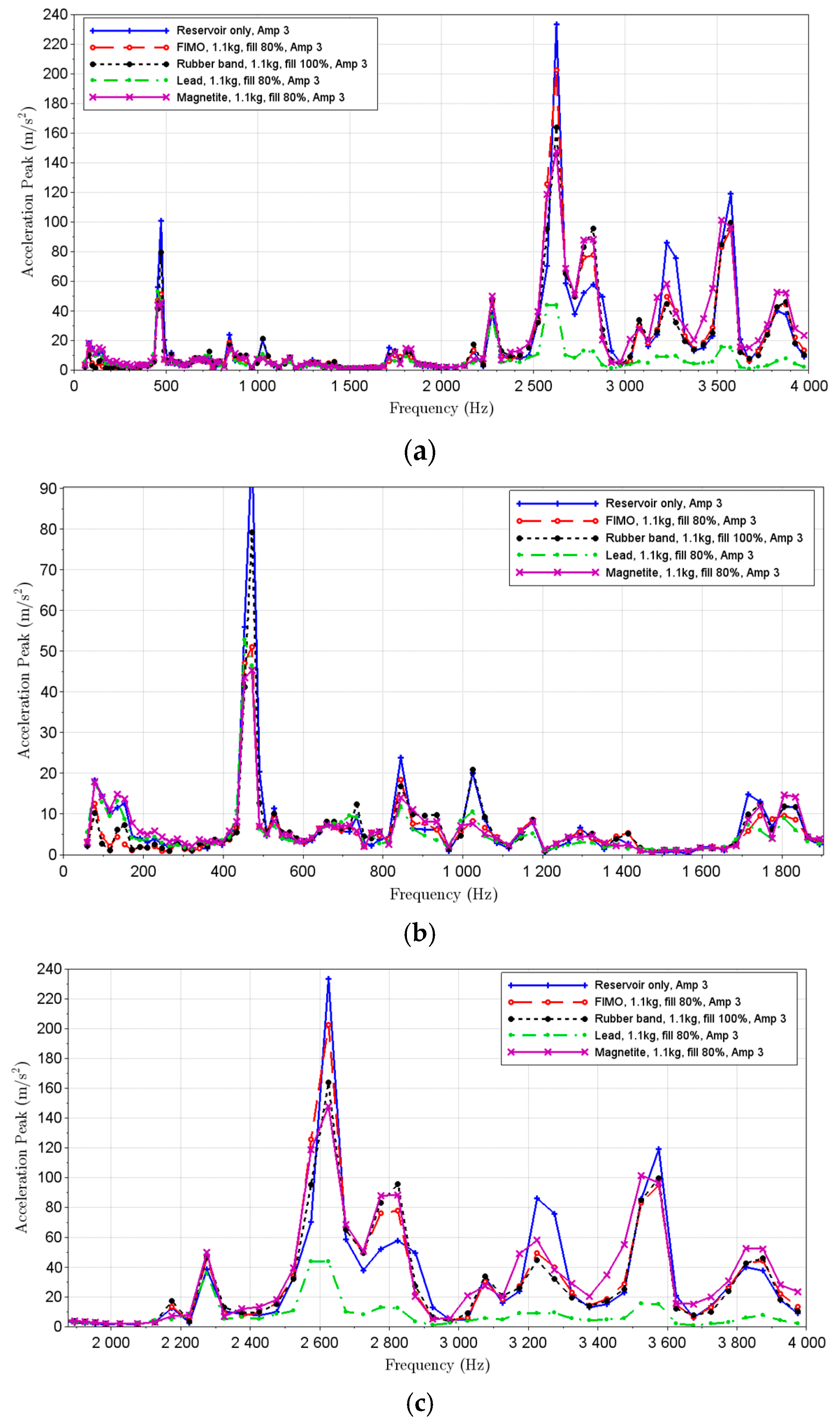
| Sensor | Sensitivity | Measuring Range | |
|---|---|---|---|
| Dytran 5860B—impedance head, Chatsworth, CA, USA | accelerometer | 10.43 mV/(m/s2) | 1.0 to 8000 Hz |
| force transducer | 23.18 mV/N | 1.0 to 8000 Hz | |
| Bruel and Kjaer 4508 b, Nærum, Denmark | accelerometer | 9.73 mV/(m/s2) | 0.3 to 8000 Hz |
| Start Excitation Frequency (Hz) | End Excitation Frequency (Hz) | Excitation Acceleration Amplitude (m/s2) |
|---|---|---|
| 50 | 800 | 4, 8 and 12 |
| 800 | 2000 | 4, 8 and 12 |
| 2000 | 4000 | 4, 8 and 12 |
| Materials | Average Particle Size (mm) | Bulk Density (kg/m3) | Elasticity Modulus (GPa) |
|---|---|---|---|
| Lead spheres | 2.3 | 6500 | 16 [38] |
| Magnetite powder | 0.3 | 2400 | 200 [39] |
| Polymer clay (FIMO) | 3.0 | 700 | 4 [40] |
| Natural rubber | 5.0 | 600 | 3 [41] |
| Materials | Particles Mass (kg) | Filling Ratio (%) |
|---|---|---|
| Lead spheres | 7.9 and 1.1 | 100 |
| 7.9, 5.7 and 1.1 | 80 | |
| Magnetite powder | 4.5 * and 1.1 | 100 |
| 3.5 and 1.1 | 80 | |
| Polymer clay (FIMO) | 1.3 * and 1.1 | 100 |
| 1.1 | 80 | |
| Natural rubber | 1.1 * | 100 |
| 0.9 | 80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiorentin, F.K.; Piehowiak, C.; Salvi, A.Z.; Asaff, Y.E.; Carboni, A.P.; Pinho de Jesus, A.M.; Fiorentin, T.A. Reducing Railway Track Vibrations by Applying Particle-Damping Systems. Appl. Sci. 2025, 15, 5014. https://doi.org/10.3390/app15095014
Fiorentin FK, Piehowiak C, Salvi AZ, Asaff YE, Carboni AP, Pinho de Jesus AM, Fiorentin TA. Reducing Railway Track Vibrations by Applying Particle-Damping Systems. Applied Sciences. 2025; 15(9):5014. https://doi.org/10.3390/app15095014
Chicago/Turabian StyleFiorentin, Felipe Klein, Cristian Piehowiak, Anelize Zomkowski Salvi, Yesid Ernesto Asaff, Andrea Piga Carboni, Abílio Manuel Pinho de Jesus, and Thiago Antonio Fiorentin. 2025. "Reducing Railway Track Vibrations by Applying Particle-Damping Systems" Applied Sciences 15, no. 9: 5014. https://doi.org/10.3390/app15095014
APA StyleFiorentin, F. K., Piehowiak, C., Salvi, A. Z., Asaff, Y. E., Carboni, A. P., Pinho de Jesus, A. M., & Fiorentin, T. A. (2025). Reducing Railway Track Vibrations by Applying Particle-Damping Systems. Applied Sciences, 15(9), 5014. https://doi.org/10.3390/app15095014









