Research on Stochastic Evolutionary Game and Simulation of Carbon Emission Reduction Among Participants in Prefabricated Building Supply Chains
Abstract
1. Introduction
2. Literature Review
2.1. PBSC
2.2. Carbon Reduction in PBSC
2.3. Evolutionary Game Theory
2.4. Research Gap
- Current research demonstrates that participants in each link of the PBSC, from design to dismantling, can reduce carbon emissions. Still, there is less research on how the emission reduction strategies of these participants interact with each other. Compared with studies on secondary and tertiary supply chains, the model constructed in this paper covers the entire PBSC, rather than only partial links or conceptualized upstream and downstream enterprises. This paper’s four-way evolutionary game model reflects participants’ emission reduction strategy choices in the whole PBSC, which is more comprehensive.
- Besides the impact of PBSC participants and external institutions on carbon emission reduction, emission reduction information and PBSC synergy also have a significant effect. Most current studies consider the impact of policy and social factors, such as subsidies, taxes, carbon trading, etc., on carbon emission reduction in PBSC, ignoring the effect of emission reduction information. In addition, current research exists on how synergies and free-rider effects in the supply chain play a role in carbon emission reduction, but there are fewer studies for PBSCs.
- Most studies recognize the impact of stochastic disturbances on carbon emission reduction in PBSCs. Still, few scholars have included them in a systematic analysis to explore the interaction of players’ emission reduction strategies. Most of the existing studies construct evolutionary game models in an ideal state, which lacks authenticity. In addition, there are still fewer methods to study PBSC carbon emission reduction using stochastic evolutionary game models.
3. Model and Analysis
3.1. Problem Raising and Basic Assumptions
3.2. Construction of a Four-Way Evolutionary Game Model
3.2.1. Construction of the Payoff Matrix
3.2.2. Replicator Dynamics Equation
3.3. Construction and Analysis of Stochastic Evolutionary Game Model
3.3.1. Game Model Establishment
3.3.2. Game Model Analysis
3.4. Stochastic Taylor Expansion
4. Results
4.1. Parameter Description
- For PBs, a higher prefabrication ratio significantly reduces carbon emissions [52,72]. Based on the indicators for estimating investment in assembly building projects [73], which provide cost indicators for various types of assembly buildings (PBs), and considering that the cost increase for constructing buildings with a high assembly rate compared to those with a low assembly rate ranges from approximately 12% to 30%, it is abstractly assumed that this incremental cost represents the additional cost incurred by participants in implementing the abatement strategy.
- The regulation on energy conservation in civil buildings stipulates that the government imposes fines of 2–4% of the contract price on companies that exceed emissions [74].
- The Civil Code states that the penalty for breach of contract may not be higher than 30% of the cost of damages [75].
- The Annual Report on China’s carbon market indicates that the carbon trading market offers about a 50% reduction or exemption on carbon trading fees for emission-reducing entities [76]. Several places have also innovated the forms of carbon trading and carbon financial mechanisms, aiming to reduce the cost of emission reduction by lowering the transaction costs of emission-control enterprises [76].
- China grades PBs according to the Evaluation Standard for Assembled Buildings [77], with the higher the grade, the better the environmental benefits [72]. In Beijing, Shanghai, Guangdong, and Shenzhen, financial subsidy policies for assembled buildings with a grade of AA or above provide bonuses of RMB 30–120 per square meter, or approximately 5–10% of the unit cost.
- Referring to the research results related to collaborative emission reduction [41,58,78,79], , set . Based on the research findings on the impact of information on decision-making [56,80], and considering the specific circumstances and expert opinions regarding PBSC emission reduction information, we set .
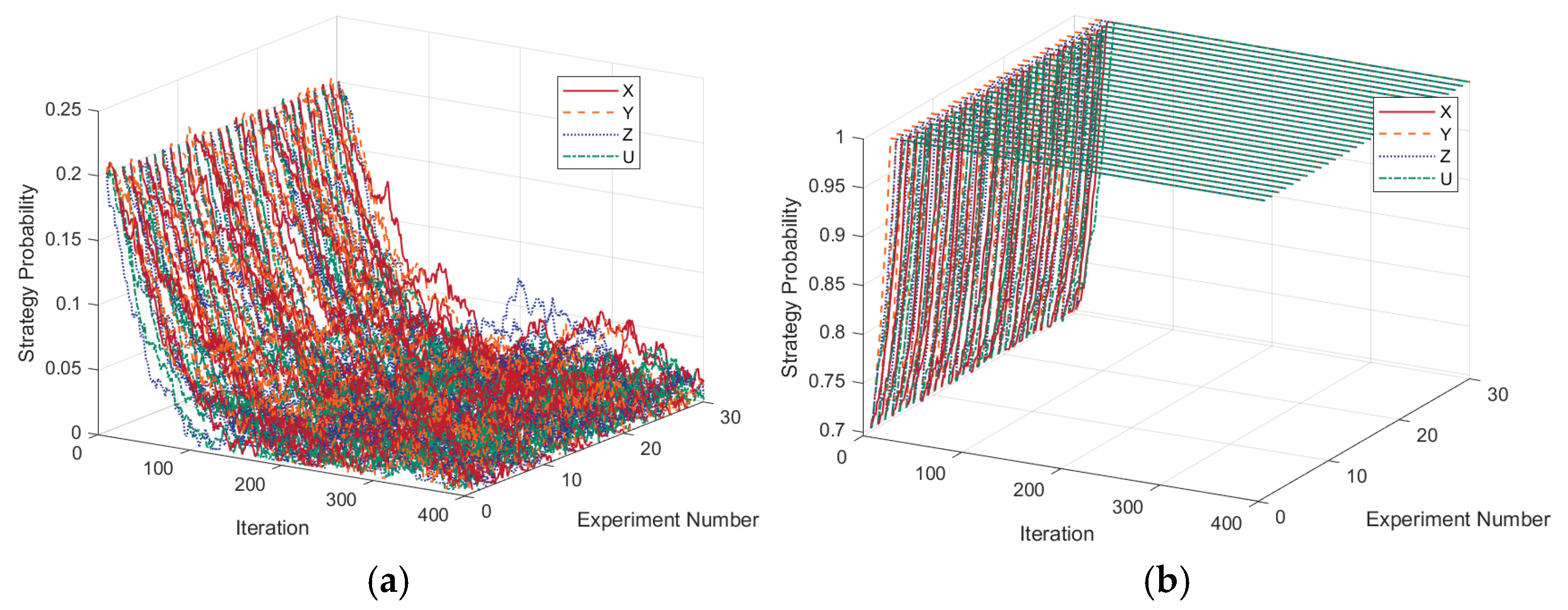
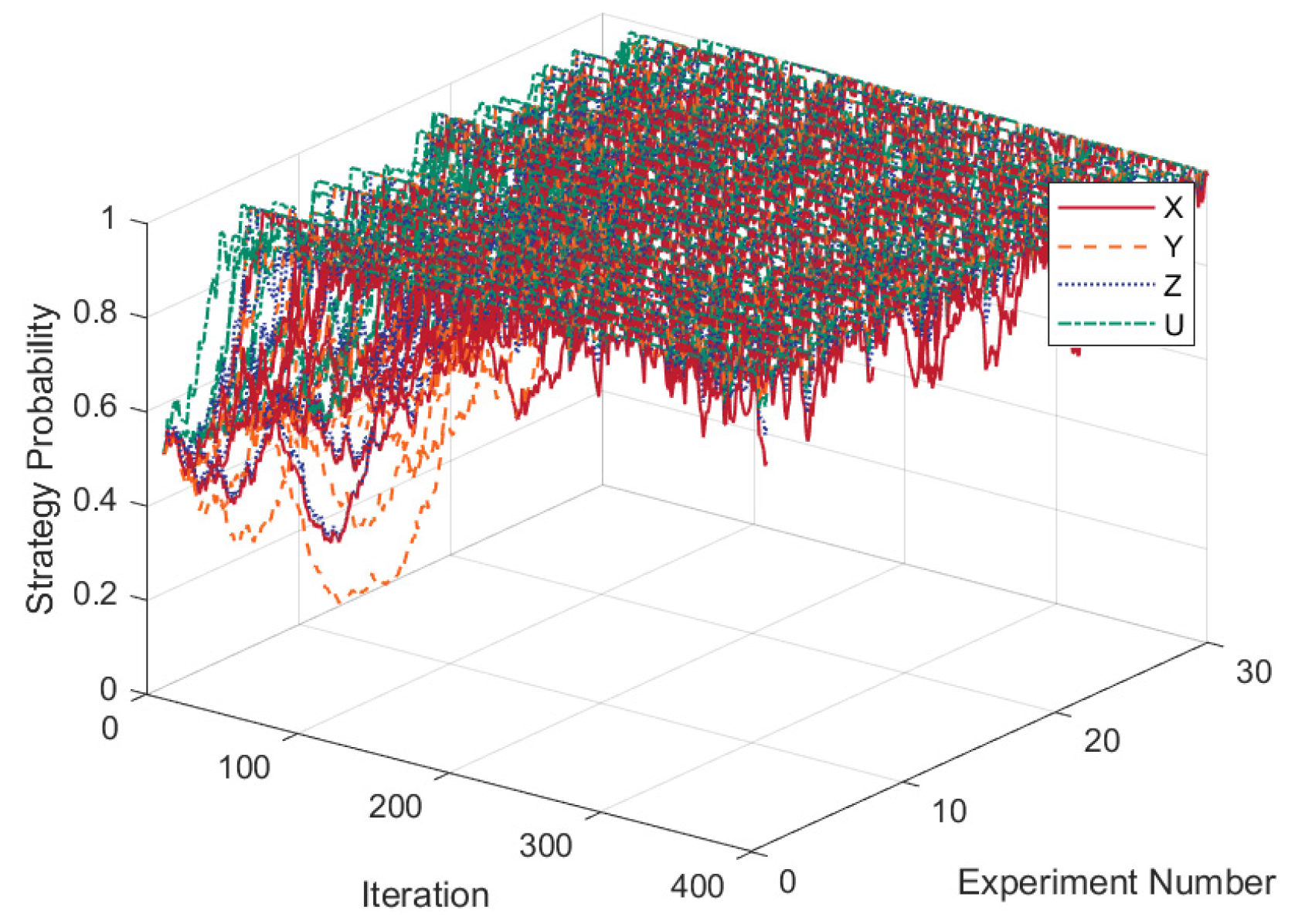
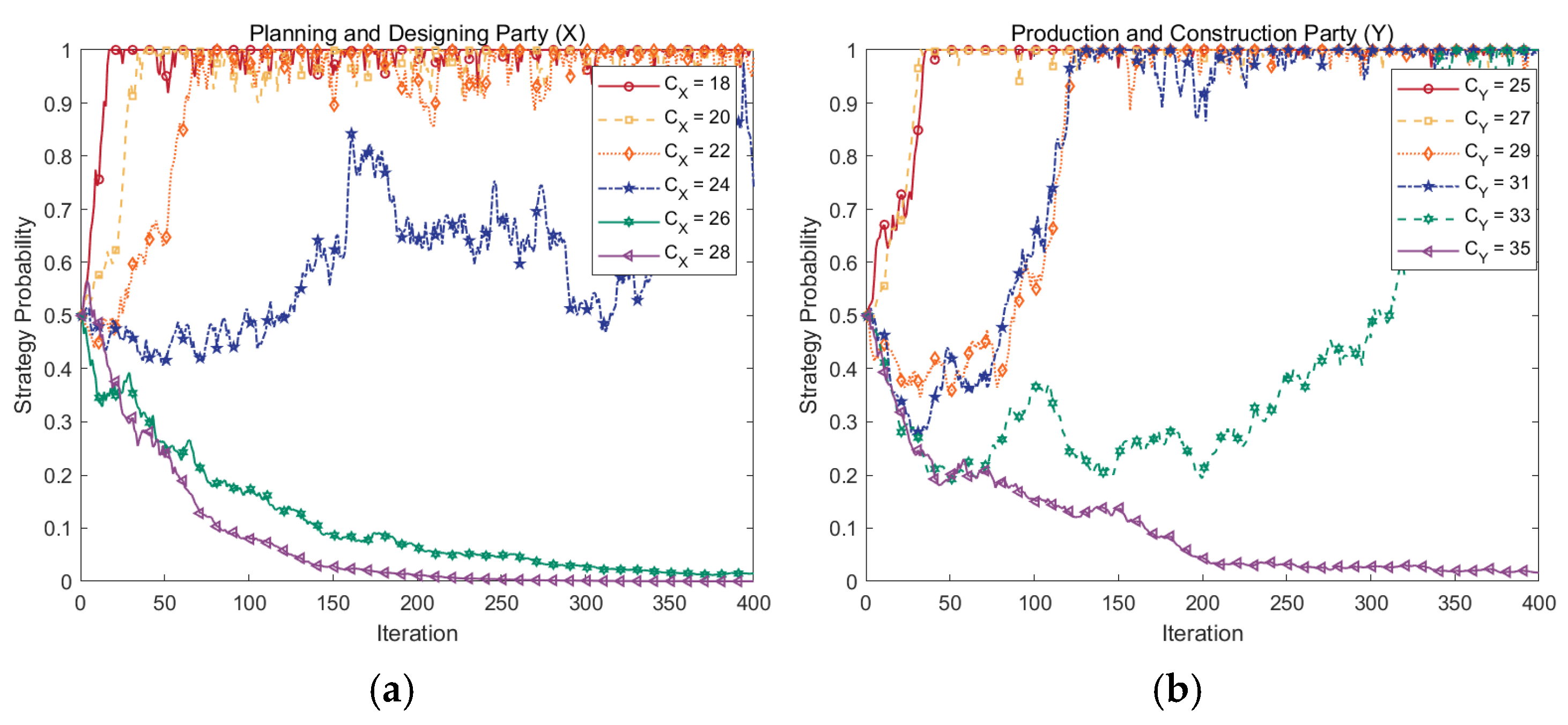
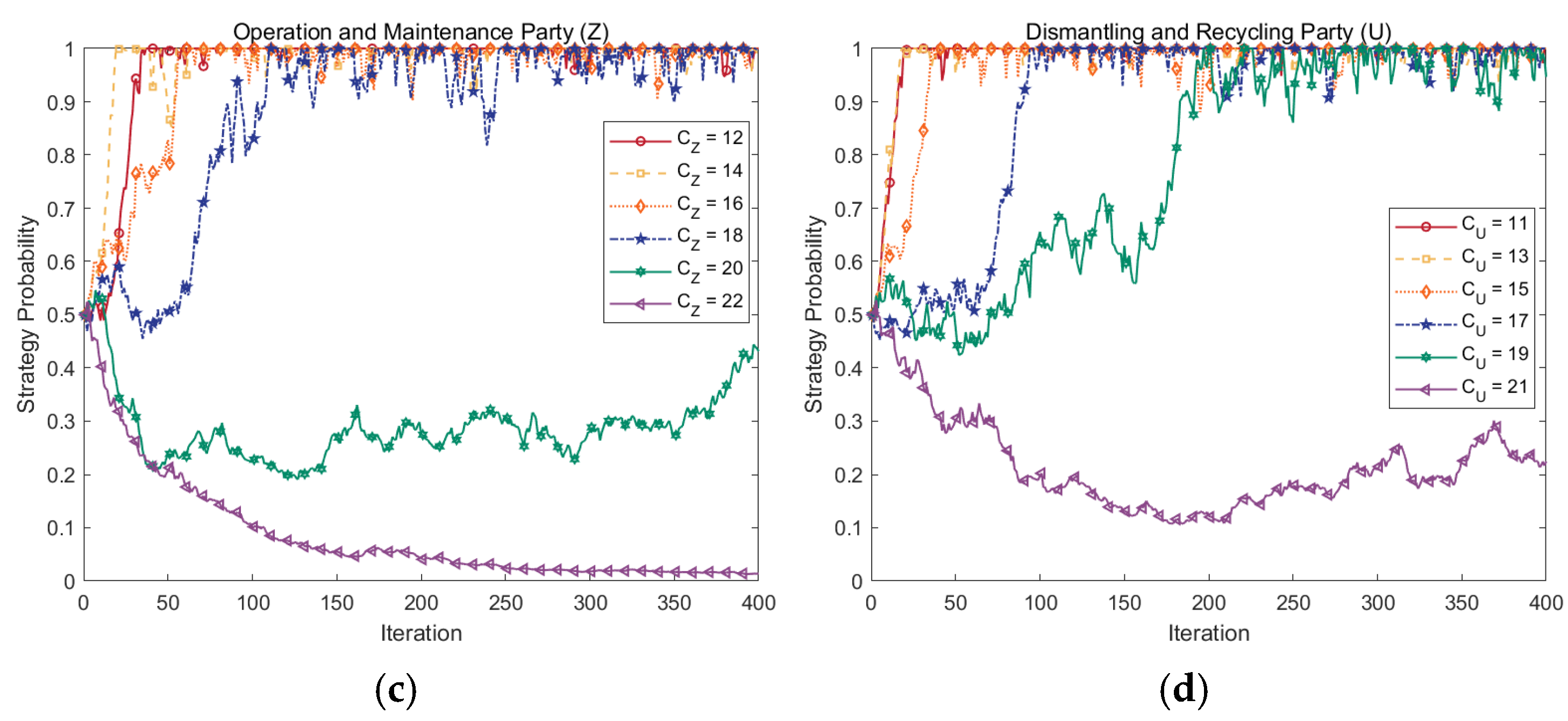
4.2. Validation of Model Credibility and Robustness
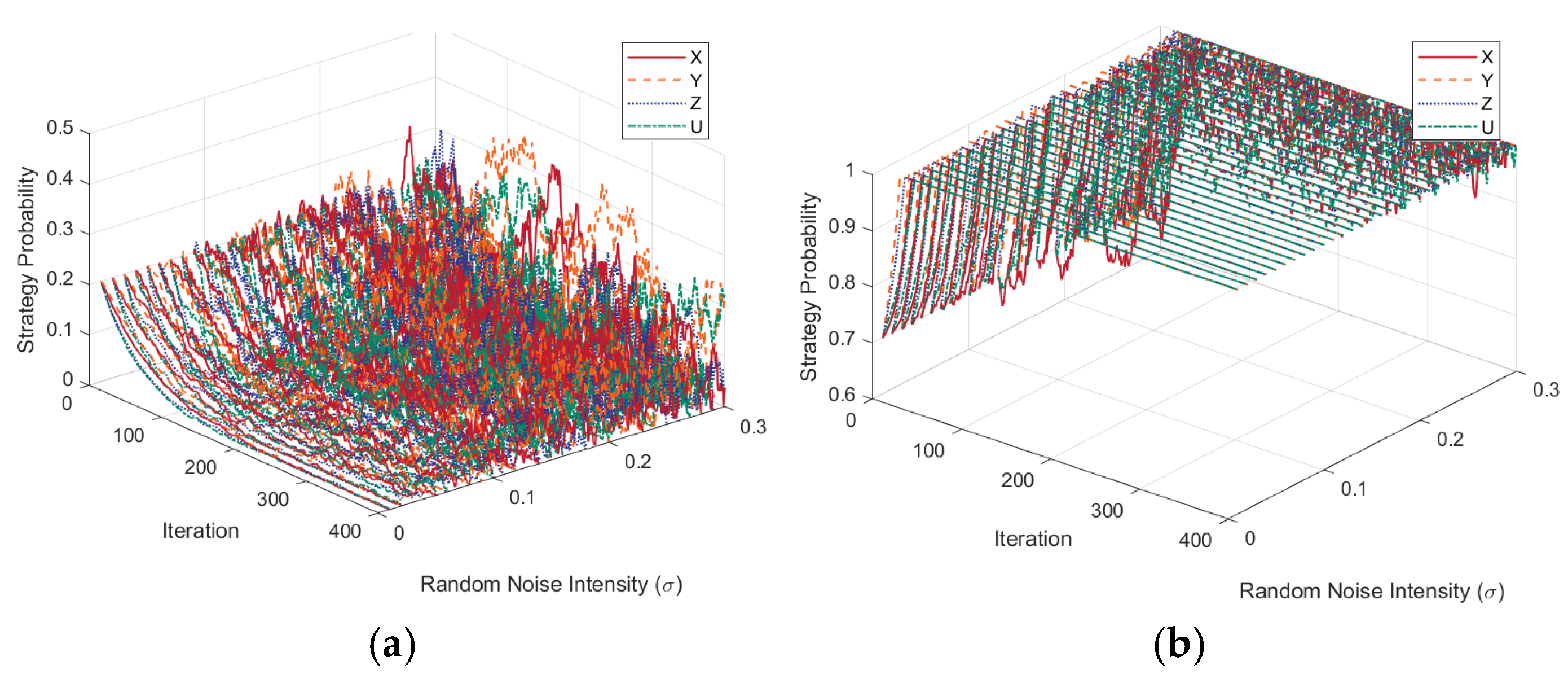
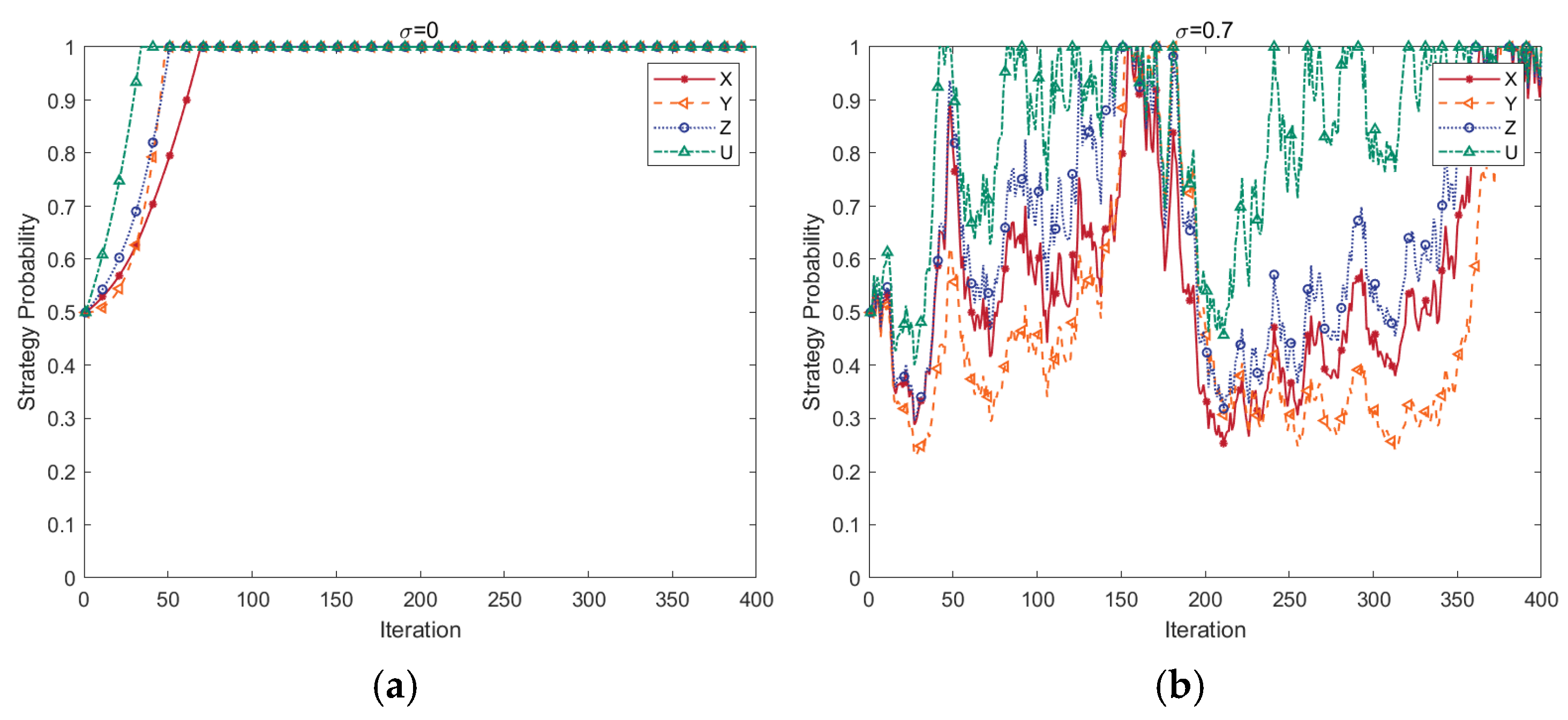
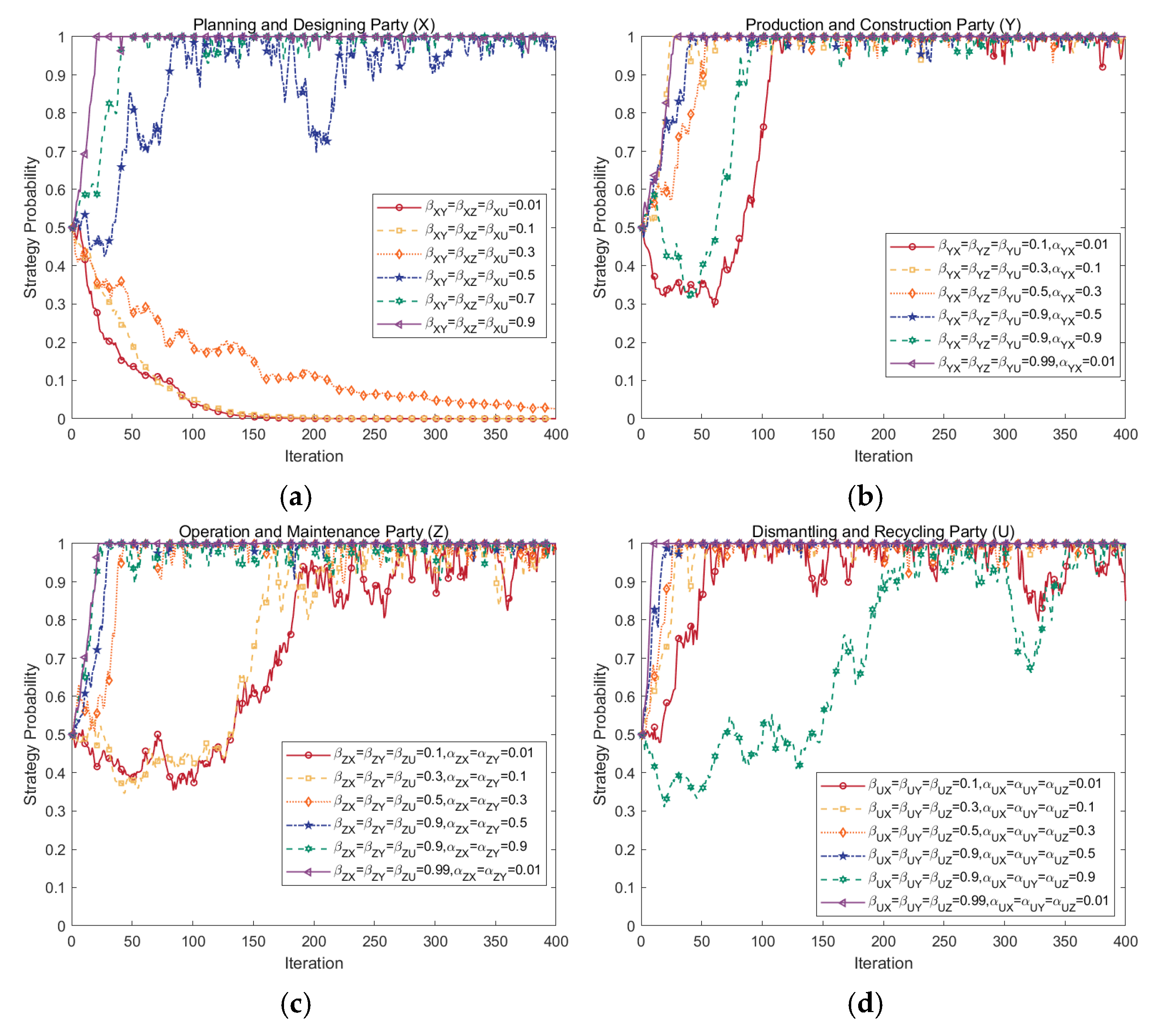
4.3. Effects of Stochastic Perturbations
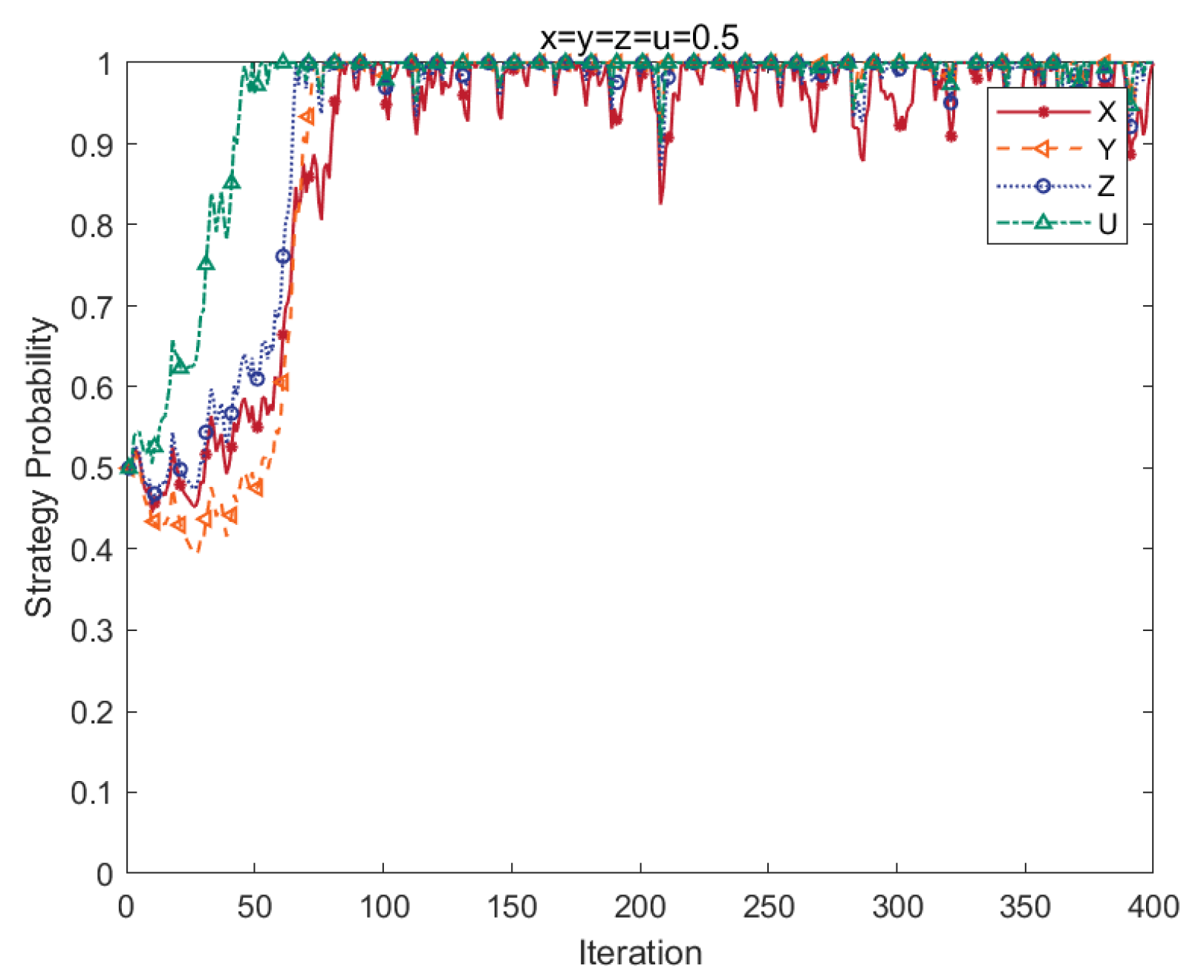
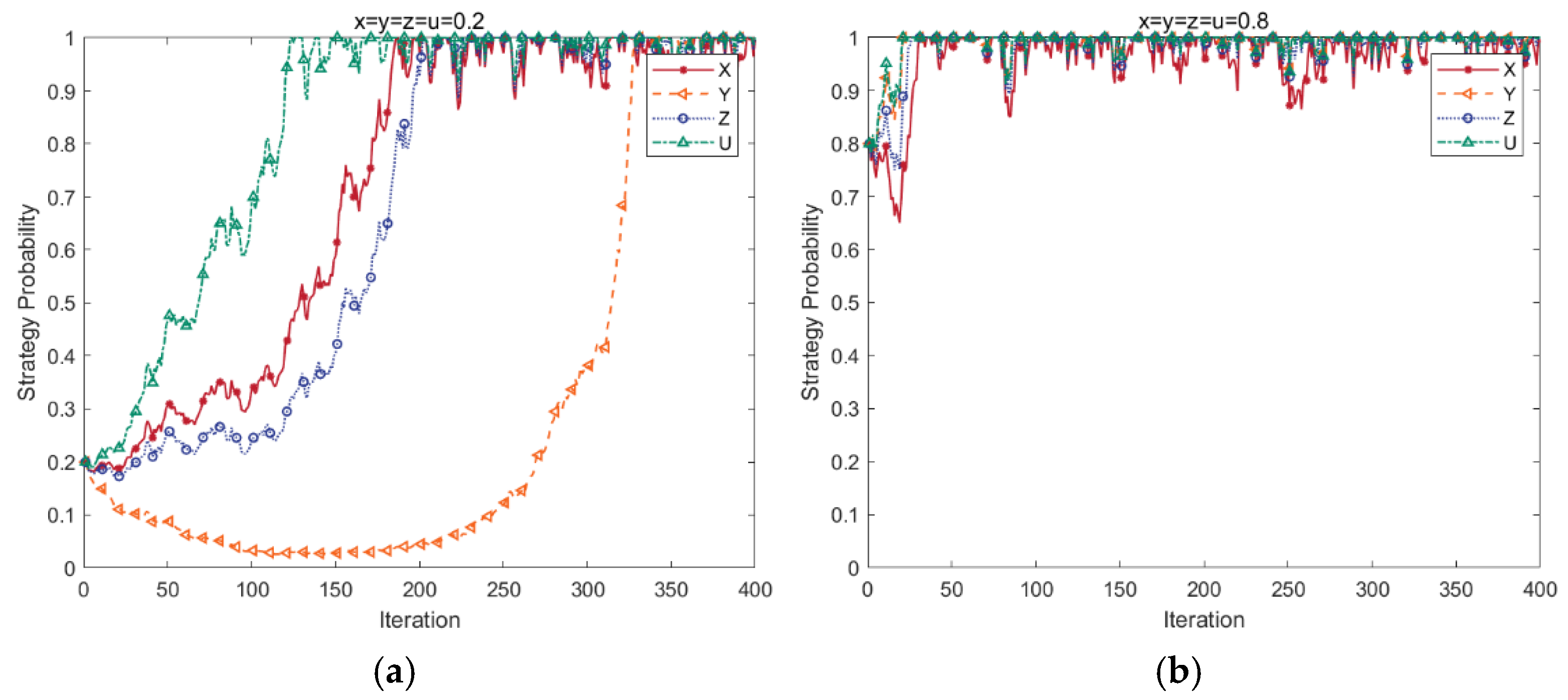
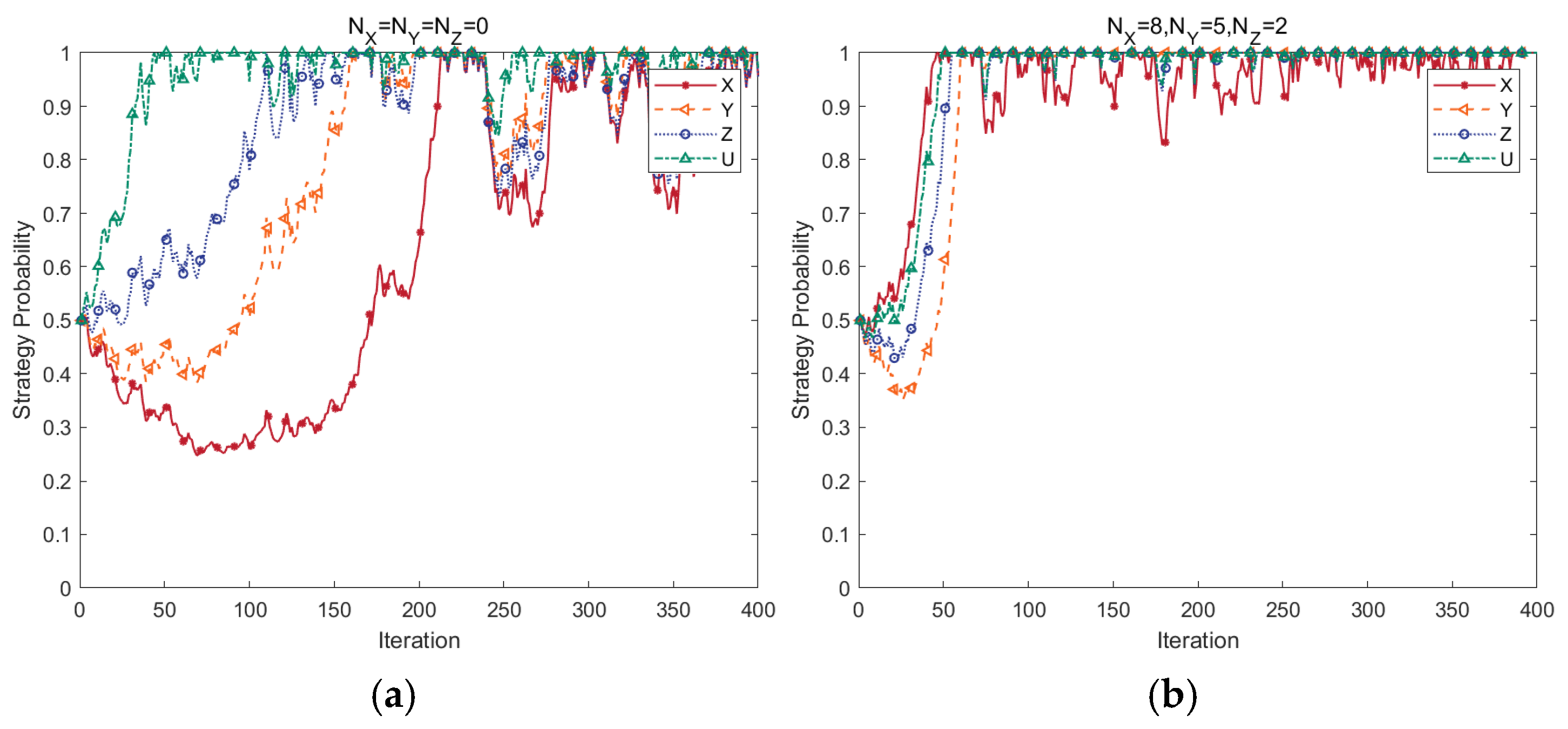
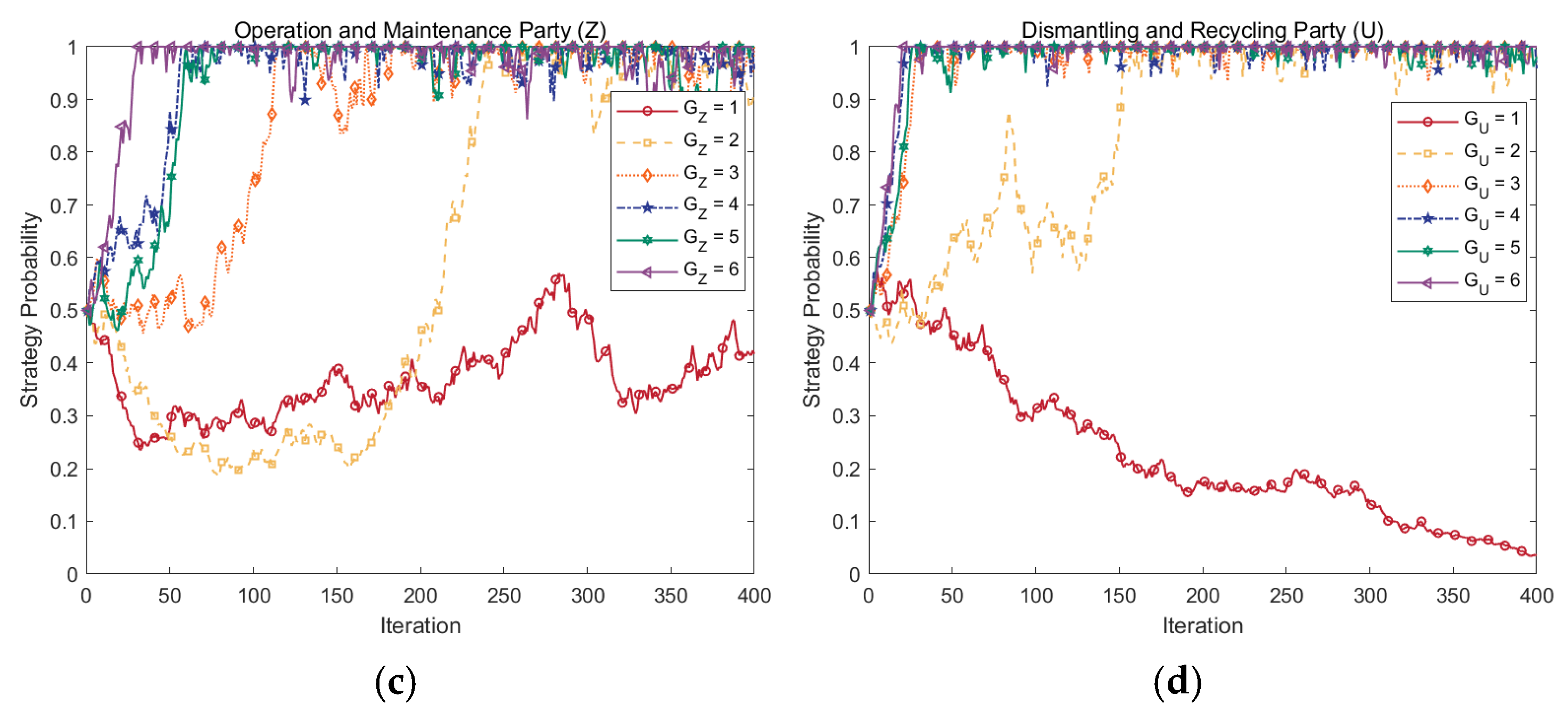
4.4. Effects of Strategy Probability
4.5. Sensitivity Analysis
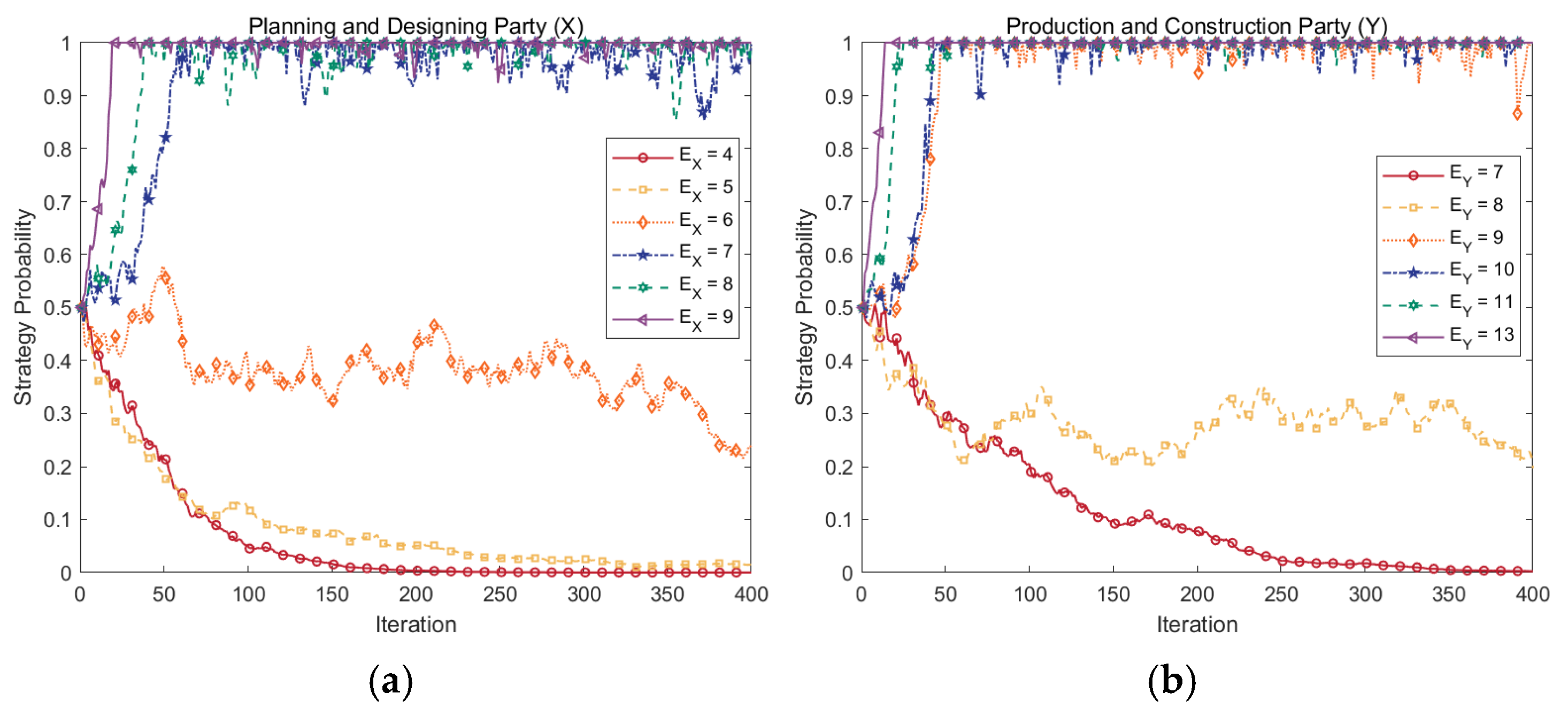
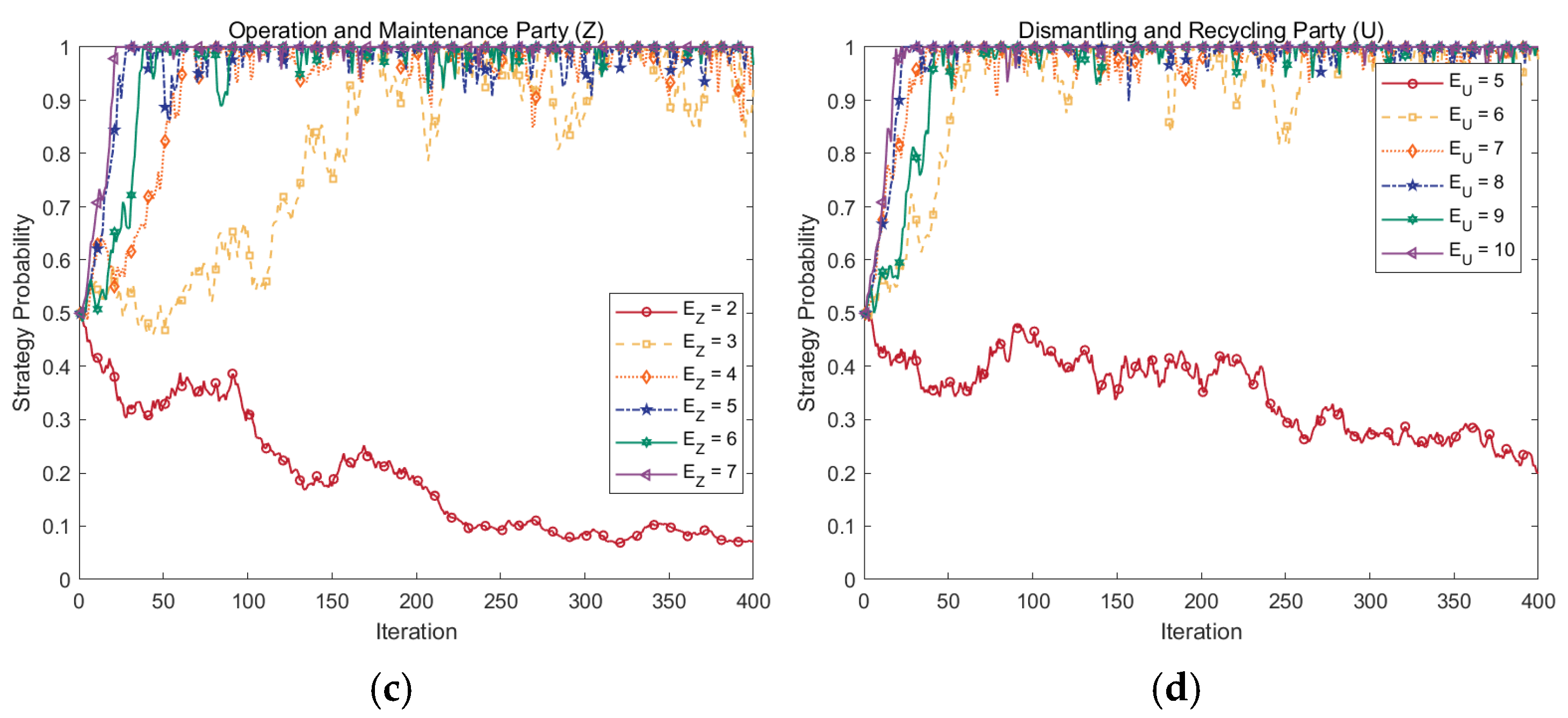
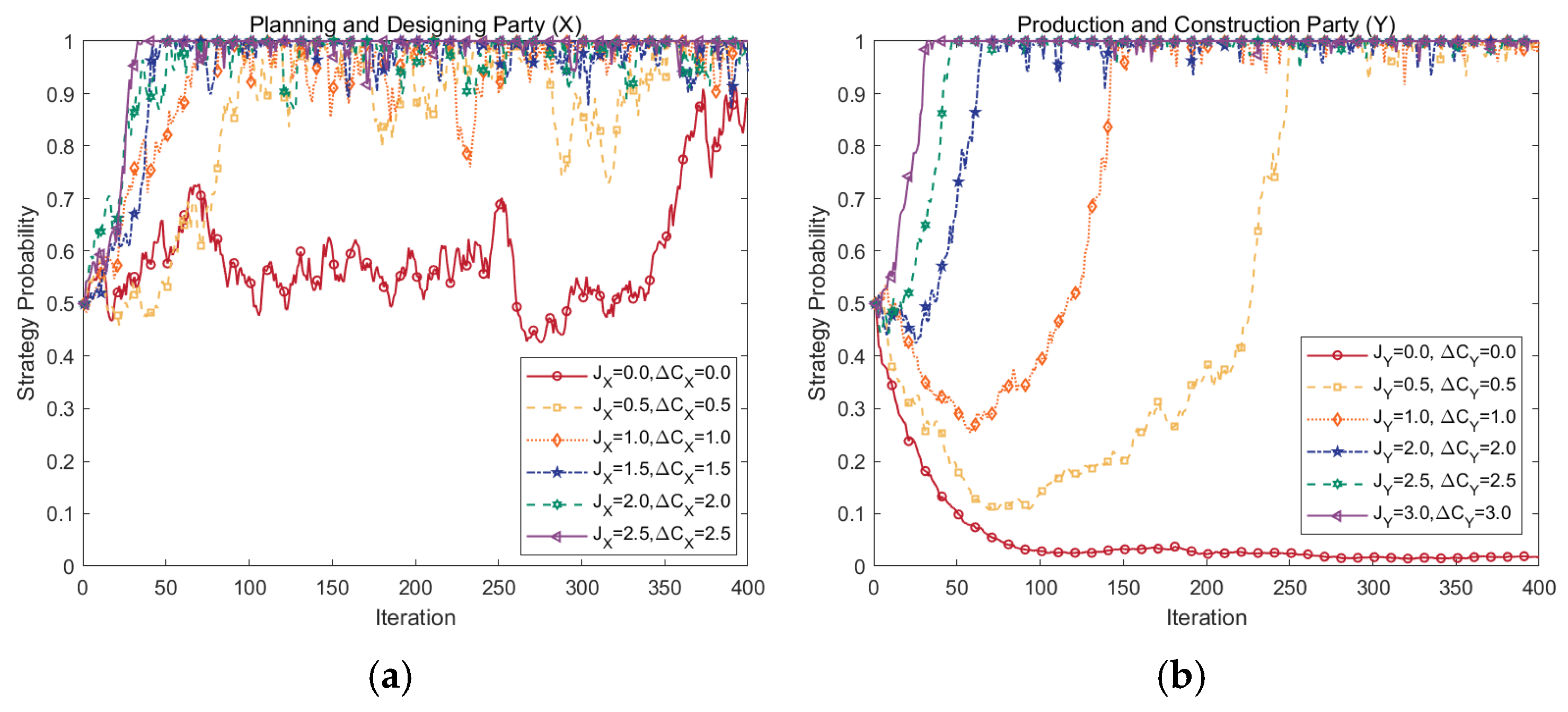
4.5.1. Effects of Abatement Benefits
4.5.2. Effects of Abatement Costs
4.5.3. Effects of Information Absorption and Transformation Efficiency
4.5.4. Effects of Joint Abatement Benefit Coefficients and Free-Riding Benefit Coefficients
4.5.5. Effects of Penalties for Non-Compliance
4.5.6. Effects of External Losses
4.5.7. Effects of External Incentives and Aids
4.5.8. Effects of External Information Content
5. Discussion
5.1. Summary of Findings
- Stochastic perturbation factors and initial strategy probability play a significant role in the gaming system’s evolutionary situation. When the environment in which the PBSC operates is unstable, it lengthens the fluctuation interval and significantly reduces the speed of strategy evolution. Increasing the proportion of the initial carbon emission reduction group is more conducive to accelerating the system’s evolution.
- The agents’ abatement benefits and costs significantly affect the choice of strategy. It is most favorable to promote the abatement strategy when the party’s abatement benefit and cost are at and , respectively. Among them, the Production and Construction Party (Y) is the most sensitive to the benefits and costs of abatement. Consequently, these factors influence Y’s decision to implement abatement strategies.
- The operational status of the PBSC is a key factor in determining participants’ strategies. X at the top and Y at the bottom of the PBSC are most affected by its synergistic capabilities. Establishing an appropriate monitoring mechanism within the PBSC is conducive to increasing the parties’ willingness to reduce emissions and keeping the penalty for non-compliance to less than twice the amount of the base case is conducive to improving the overall effectiveness of PBSC in reducing emissions.
- The external environment’s effect on the agents’ strategies is mainly in terms of the losses caused and the help provided. Continued external pressure on Z to reduce emissions can be an effective driver for continued abatement by Z. For other agents, the external loss is within to push them to implement abatement strategies. External incentives and aids impact the speed of evolution, most prominently on Y, followed by X. Section 4.5.2, Section 4.5.6, and Section 4.5.7 show that, with other factors constant, equal changes in negative and positive incentives lead to different results: Negative incentives may cause subjects to abandon emission reduction, while positive incentives only affect the system’s convergence speed. External losses are more effective than incentives and aid in promoting emission reduction by agents.
- The abatement information content is an essential factor affecting decision-making. The information content positively correlates with the agent’s willingness to reduce emissions. It is optimal to keep the information content to ensure that each agent implements an abatement strategy and avoids wasting resources. The agent’s ability to process information is positively related to the evolutionary speed. It has the most significant effect on X. When , X rejects abatement.
5.2. Recommendation
- Maintaining a stable market, increasing the resilience of the PBSC, and increasing the proportion of emission reduction groups. Section 4.3 and Section 4.4 demonstrate that maintaining system stability and enhancing initial emission reduction intentions can facilitate PBSC emission reduction. The consumer market drives, while the supply market supports. To promote the implementation of emission reduction strategies by participants in the PBSC, the following measures should be taken: (1) Enhance public environmental awareness and acceptance of PB to boost consumers’ willingness to pay [29]. (2) As the general organizer, the government should introduce policies to stabilize the market and prices, alleviating construction companies’ concerns over carbon emission reduction [50]. (3) The PBSC should enhance risk resistance through stronger cooperation among participants to better adapt to market changes.
- Participants in PBSC should reduce costs, increase efficiency, and improve capacity in production, promotion, and co-operation. Section 4.5.1 and Section 4.5.2 indicate that the direct costs and benefits significantly influence enterprises and those engaged in construction should actively participate. The first is to reduce costs via technological innovation and upgrading, corporate R&D cooperation, and construction collaboration [38]. Secondly, use advertising and packaging design to promote emission reduction concepts, expand the market, publicize high-quality projects, and set industry benchmarks to guide more projects to reduce emissions [56]. Thirdly, actively seek opportunities for cooperation [16,37]. For example, reduce employment and training costs via school–enterprise cooperation; lower procurement costs through long-term supplier relationships; decrease R&D costs by collaborating with research institutions; and share resources and complement strengths with peer enterprises via strategic alliances to undertake large-scale projects and achieve standard emission reductions.
- Enhance the internal communication and information-sharing mechanisms within the PBSC, focusing on participants at both ends of the PBSC, with appropriate external intervention for optimization. Section 4.5.4 highlights that focusing on the beginning and end of PBSC agent, enhancing coordination, and avoiding the “free-rider” effect can promote emission reduction. Enhancing information flow within PBSC promotes collaborative emission reduction, while ensuring information security prevents free riding [83]. PBSC participants should form alliances, enhance communication, and optimize the PBSC operation process [36]. Upstream owners should initiate the establishment of an information-sharing platform. Downstream end-user enterprises should actively respond to enhance PBSC synergy, increase joint abatement benefits, and mitigate the adverse impact of free-rider behavior [17]. The information-sharing platform should adopt the following optimization measures: (1) Use API, EDI, and other real-time data exchange technologies to realize real-time data transmission and update and enhance PBSC synergy. (2) Employ firewalls, intrusion detection, and defense systems to enhance privacy protection, ensure data security, and prevent free-riding by downstream participants. (3) Establish a project-centric information-sharing database, reduce information redundancy through standardized design, and enhance collaboration efficiency. The government, industry associations, and other entities can intervene in the PBSC to guide the establishment of a cost-compensation mechanism, optimize the benefit-distribution mechanism, reduce free-riding, and enhance participants’ enthusiasm for emission reduction [41].
- External parties in PBSC should insist on punishment over reward and adopt differentiated instruments. Negative incentives play a significant role in reducing emissions. Section 4.5.6 and Section 4.5.7 reveal that external incentives, whether positive or negative, significantly impact PBSC emission reduction. By strengthening regulatory measures from governments and environmental agencies [50], enhancing consumer awareness of green products, and increasing costs for non-compliant participants, losses can be amplified to compel the main parties to reduce emissions. The focus is on enterprises involved in operation and maintenance. Positive incentives should be targeted at the planning, design, production, and construction stages [4,11,17], with the following measures adopted: (1) The government can reduce uncertainty by introducing supportive policies, guiding public opinion, and providing financial subsidies. (2) The market is the environment for PBSC operation. Stable and orderly building materials, carbon trading, and talent markets facilitate smooth PBSC operations, lower participants’ perceived emission reduction risks, and reduce reserved risk-mitigation costs. (3) Colleges, universities, banks, tech firms, etc., should collaborate via joint training and research, and lower financing thresholds, to help PBSC participants overcome difficulties and promote emission reductions.
- Establish a cross-industry information-sharing platform to optimize PBSC’s information-sharing mechanism and enhance participants’ information processing capabilities [56]. Section 4.5.3 and Section 4.5.8 indicate that both the agent’s information processing capacity and the environmental information content are crucial for PBSC emission reduction. Governments and industry associations should take the lead in establishing a cross-departmental comprehensive information sharing platform, integrating market dynamics, policies, regulations, and technological progress, and breaking information silos. In addition, the platform should actively optimize the information sharing mechanism to reduce participants’ difficulty in collecting and using: (1) Develop harmonized standards to ensure accurate and reliable information. (2) Establish an incentive system to encourage units to share information through financial support, co-operation opportunities, etc. (3) Adopt advanced technologies like cloud computing, big data, IoT, and blockchain to enhance the efficiency and accuracy of information sharing. Within the PBSC, the BIM platform and carbon dashboard can provide digital project information and monitor carbon emissions in real time [84]. They can also link with external information platforms to attract more enterprises to participate in information sharing, increase transparency, and enable participants to obtain personalized information. PBSC participants should enhance their emission reduction awareness, actively seek related technologies, knowledge, and information, establish a professional information analysis team to collect and analyze market-related emission reduction information and feedback from other entities, providing a scientific basis for decision-making, and conduct staff training to improve emission reduction awareness and information processing capabilities, thereby increasing benefits [38].
6. Conclusions
6.1. Implications
6.2. Limitations
6.3. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PBSC | Prefabricated Building Supply Chain |
| PB | Prefabricated Building |
| X | Planning and Designing Party |
| Y | Production and Construction Party |
| Z | Operation and Maintenance Party |
| U | Dismantling and Recycling Party |
Appendix A
Appendix A.1. Existence and Uniqueness Proof
Appendix A.2. Stability Condition Derivation
Appendix B. Expert Interview Process
- Experts generally agree that in PBSCs, X and Y have significant inputs in abatement cost, whereas Z and U have relatively minor inputs.
- In PBSCs, the value-added benefits of joint abatement are approximately 30–70% of those from individual abatement and rarely exceed 100%. Free-riding in emission reduction does exist but can be mitigated through enhanced corporate prevention measures. Free riders are predominantly downstream firms, though some homogeneous firms also engage in free-riding, with the free-riding benefits typically accounting for 0–50% of individual emission reduction benefits.
- Experts generally concur that it is challenging for enterprises to gather all market-related emission reduction information, with collection rates typically ranging from 40% to 90%. University-based experts primarily rely on online platforms for information collection. A few corporate experts noted that their companies have proprietary collection channels, information networks, and public channels. The acquisition of most information is either free or low-cost. However, information processing and benefit realization are complex, demanding time, resources, and labor costs. In addition to the costs of information collation, analysis, and verification, additional costs are incurred to achieve benefits. For example, in selecting emission reduction technology, a comparative study of various information is required to choose the optimal solution, and costs are incurred to introduce the technology. After consulting some experts, it is found that the benefit-to-cost ratio obtained by enterprises through information processing alone generally ranges from 0.5 to 2.
- External policy support for PBSCs is in place but is characterized by its timeliness and regional nature. The overall support intensity aligns broadly with the market situation, and the data in relevant policy documents and reports are sufficient to support the model. However, experts noted that in implementation, factors such as local economic level, enterprise strength, and project-specific conditions can affect the degree and ease of obtaining support.
- Experts generally agree that despite regional variations in losses faced by enterprises without emission reduction, external supervision remains the primary source of these losses. Experts from Beijing noted that the capital’s stringent environmental regulations and dense population lead to a higher probability of uncertain losses due to complaints. Though resident complaints incur losses for enterprises, external supervision is more prominently reflected in economic terms. Experts from Baoding indicated that losses from non-reduction primarily stem from government regulation. Experts agree that the primary damage stems from government regulations, which are consistent and reliable nationwide.
- Experts indicated that in drafting enterprise contracts, clauses involving breach-of-contract fines are strictly formulated by the law, while both parties reasonably negotiate other specific implementation details. In most cases, the parties rigorously adhere to the contract, especially regarding breach-of-contract penalties involving significant interests. However, given the complexity and dynamic nature of PBSC operations, changes may occur in cases of force majeure, major policy shifts, or contract disputes. These cases are rare and can be disregarded in parameter settings.
References
- IPCC. Climate Change 2023: Synthesis Report. In Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Lee, H., Romero, J., Eds.; IPCC: Geneva, Switzerland, 2023; Available online: https://www.ipcc.ch/report/ar6/syr/downloads/report/IPCC_AR6_SYR_LongerReport.pdf (accessed on 12 March 2025).
- Xi, J. Address by President Xi Jinping of the People’s Republic of China at the 75th Session of the United Nations General Assembly. 2020. Available online: https://www.gov.cn/xinwen/2020-09/22/content_5546168.htm (accessed on 11 March 2025).
- The State Council of the People’s Republic of China. Notice on Issuing the Action Plan for Carbon Dioxide Peaking Before 2030. 2021. Available online: https://www.gov.cn/zhengce/content/2021-10/26/content_5644984.htm (accessed on 11 March 2025).
- Han, Y.; Fang, X.; Zhao, X.; Wang, L. Exploring the Impact of Incentive Policy on the Development of Prefabricated Buildings: A Scenario-Based System Dynamics Model. Eng. Constr. Archit. Manag. 2023, 31, 4697–4725. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, Y.; Yu, C.; Zhong, R.Y. Data-Driven Logistics Collaboration for Prefabricated Supply Chain with Multiple Factories. Autom. Constr. 2024, 168, 105802. [Google Scholar] [CrossRef]
- Hussein, M.; Zayed, T. Critical Factors for Successful Implementation of Just-in-Time Concept in Modular Integrated Construction: A Systematic Review and Meta-Analysis. J. Clean. Prod. 2021, 284, 124716. [Google Scholar] [CrossRef] [PubMed]
- Du, Q.; Zhang, Y.; Zeng, L.; Ma, Y.; Li, S. Dynamic Assessment of the Abatement Effects of the Low-Carbon Practices in the Prefabricated Building Supply Chain. Eng. Constr. Archit. Manag. 2024. ahead-of-print. [Google Scholar] [CrossRef]
- Du, Q.; Pang, Q.; Bao, T.; Guo, X.; Deng, Y. Critical Factors Influencing Carbon Emissions of Prefabricated Building Supply Chains in China. J. Clean. Prod. 2021, 280, 124398. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, Y.; Ji, B. Influencing Factors of Resilience of PBSC Based on Empirical Analysis. Buildings 2021, 11, 467. [Google Scholar] [CrossRef]
- Zhu, T.; Liu, G. A Novel Hybrid Methodology to Study the Risk Management of Prefabricated Building Supply Chains: An Outlook for Sustainability. Sustainability 2023, 15, 361. [Google Scholar] [CrossRef]
- Du, Q.; Yang, M.; Wang, Y.; Wang, X.; Dong, Y. Dynamic Simulation for Carbon Emission Reduction Effects of the Prefabricated Building Supply Chain under Environmental Policies. Sustain. Cities Soc. 2024, 100, 105027. [Google Scholar] [CrossRef]
- Liu, Y.; Chang, R.-D.; Zuo, J.; Xiong, F.; Dong, N. What Leads to the High Capital Cost of Prefabricated Construction in China: Perspectives of Stakeholders. Eng. Constr. Archit. Manag. 2022, 30, 805–832. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Y.; Ouyang, H.; Song, L. Sustainability Evaluation of Prefabricated Building Supply Chain Based on Cloud Matter Element Theory. J. Civ. Eng. Manag. 2020, 37, 109–115+122. [Google Scholar] [CrossRef]
- Masood, R.; Lim, J.B.P.; González, V.A. Performance of the Supply Chains for New Zealand Prefabricated House-Building. Sustain. Cities Soc. 2021, 64, 102537. [Google Scholar] [CrossRef]
- Yuan, M.; Li, Z.; Li, X.; Luo, X. Managing Stakeholder-Associated Risks and Their Interactions in the Life Cycle of Prefabricated Building Projects: A Social Network Analysis Approach. J. Clean. Prod. 2021, 323, 129102. [Google Scholar] [CrossRef]
- Liu, L.; Ren, X.; Dai, X. Research on Cooperative Subject Selection of Prefabricated Building Supply Chain for Dynamic Alliance. Constr. Econ. 2021, 42, 61–66. [Google Scholar] [CrossRef]
- Liu, W.; Han, L. Evolution Game Analysis of Supply Chain Synergy Benefits of Prefabricated Building Projects. Appl. Sci. 2023, 13, 11862. [Google Scholar] [CrossRef]
- Koskela, L. Application of the New Production Philosophy to Construction; Stanford University: Espoo, Finland, 1992. [Google Scholar]
- Li, W. The Desing of Construction Supply Chain Operations Reference-Model. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2006. [Google Scholar]
- Tavares, V.; Gregory, J.; Kirchain, R.; Freire, F. What Is the Potential for Prefabricated Buildings to Decrease Costs and Contribute to Meeting EU Environmental Targets? Build. Environ. 2021, 206, 108382. [Google Scholar] [CrossRef]
- State Council of the People’s Republic of China. Action Plan for Energy Conservation and Carbon Reduction (2024–2025). 2024. Available online: https://www.gov.cn/zhengce/zhengceku/202405/content_6954323.htm (accessed on 10 March 2025).
- Aye, L.; Ngo, T.; Crawford, R.H.; Gammampila, R.; Mendis, P. Life Cycle Greenhouse Gas Emissions and Energy Analysis of Prefabricated Reusable Building Modules. Energy Build. 2012, 47, 159–168. [Google Scholar] [CrossRef]
- Miracco, G.; Nicoletti, F.; Ferraro, V.; Muzzupappa, M.; Mattanò, V.M.; Alberti, F. Achieving nZEB Goal through Prefabricated Buildings: Case Study in Italy. Energy Build. 2025, 329, 115301. [Google Scholar] [CrossRef]
- Li, Z.; Shen, G.Q.; Alshawi, M. Measuring the Impact of Prefabrication on Construction Waste Reduction: An Empirical Study in China. Resour. Conserv. Recycl. 2014, 91, 27–39. [Google Scholar] [CrossRef]
- Xu, H.; Kim, J.I.; Chen, J. Improved Framework for Estimating Carbon Emissions from Prefabricated Buildings during the Construction Stage: Life Cycle Assessment and Case Study. Build. Environ. 2025, 272, 112599. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, T.; Yuan, C.; Ping, Y. Assessment of Carbon Emissions at the Logistics and Transportation Stage of Prefabricated Buildings. Appl. Sci. 2023, 13, 552. [Google Scholar] [CrossRef]
- Luo, L.; Wan, P.; Zhong, Z.; Bo, Q.; Yan, X.; Chen, Y. Investigation of Factors and Their Dynamic Influences on Multi-Party Collaboration in Bim-Based Prefabricated Buildings. KSCE J. Civ. Eng. 2025, 29, 100006. [Google Scholar] [CrossRef]
- Yang, W.; Li, H.; Shi, J. Collaborative Innovation in Low-Carbon Supply Chain under Cap-and-Trade: Dual Perspective of Contracts and Regulations. J. Clean. Prod. 2025, 499, 145223. [Google Scholar] [CrossRef]
- Jiang, Y.; Meng, Q.; Guo, Y.; Zhang, Z. Strategic Disclosure of Carrier’s Carbon Emission Reduction Information by Competitive Shippers in Marine Supply Chains. Ocean Coast. Manag. 2024, 253, 107165. [Google Scholar] [CrossRef]
- Liu, J.; Xu, H.; Lyu, Y. Emission Reduction Technologies for Shipping Supply Chains under Carbon Tax with Knowledge Sharing. Ocean Coast. Manag. 2023, 246, 106869. [Google Scholar] [CrossRef]
- Yu, Y.; Zhou, S.; Shi, Y. Information Sharing or Not across the Supply Chain: The Role of Carbon Emission Reduction. Transp. Res. Part E Logist. Transp. Rev. 2020, 137, 101915. [Google Scholar] [CrossRef]
- Wang, L.; Peng, K. Carbon Reduction Decision-Making in Supply Chain under the Pledge Financing of Carbon Emission Rights. J. Clean. Prod. 2023, 428, 139381. [Google Scholar] [CrossRef]
- Qin, J.; Fu, H.; Wang, Z.; Xia, L. Financing and Carbon Emission Reduction Strategies of Capital-Constrained Manufacturers in E-Commerce Supply Chains. Int. J. Prod. Econ. 2021, 241, 108271. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, M.; Tan, Y. Long-Term Emission Reduction Strategy in a Three-Echelon Supply Chain Considering Government Intervention and Consumers’ Low-Carbon Preferences. Comput. Ind. Eng. 2023, 186, 109697. [Google Scholar] [CrossRef]
- Mardyana, R.; Chandra Mahata, G. Impacts of Dual Carbon Emission Reduction Technology and Technology Spillovers of Deterioration Reduction on Supply Chain System’s Performances Considering Government Incentives and Contract Design. J. Clean. Prod. 2024, 468, 142977. [Google Scholar] [CrossRef]
- Meng, C.; Lin, Y. The Impact of Supply Chain Digitization on the Carbon Emissions of Listed Companies—A Quasi-Natural Experiment in China. Struct. Change Econ. Dyn. 2025, 73, 392–406. [Google Scholar] [CrossRef]
- Wang, Q.; Guo, W.; Xu, X.; Deng, R.; Ding, X.; Chen, T. Analysis of Carbon Emission Reduction Paths for the Production of Prefabricated Building Components Based on Evolutionary Game Theory. Buildings 2023, 13, 1557. [Google Scholar] [CrossRef]
- Liu, W.; Fan, G.; Liu, Z. Driving Factors in Carbon Emission Reduction in Prefabricated Building Supply Chains Based on Structural Equation Modelling. Sustainability 2024, 16, 3150. [Google Scholar] [CrossRef]
- Wang, D.; Wang, X. Supply Chain Consequences of Government Subsidies for Promoting Prefabricated Construction and Emissions Abatement. J. Manag. Eng. 2023, 39, 04023029. [Google Scholar] [CrossRef]
- Sun, X.; Wang, Y.; Li, Y.; Zhu, W.; Yan, D.; Li, J. Optimal Pricing and Carbon Emission Reduction Decisions for a Prefabricated Building Closed-Loop Supply Chain under a Carbon Cap-and-Trade Regulation and Government Subsidies. PLoS ONE 2023, 18, e0287684. [Google Scholar] [CrossRef]
- Lin, M.; Liu, H. Evolutionary Game Analysis of Low Carbon Emission Reduction Strategies Under the Influence of Spillover Effect Based on System Dynamics. J. Univ. Electron. Sci. Technol. China (Soc. Sci. Ed.) 2019, 21, 56–68. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, Y. Evolutionary Game Research on Low-carbon Production of Enterprise in Three-level Supply Chain. J. Henan Univ. Sci. Technol. (Soc. Sci.) 2023, 41, 48–56. [Google Scholar] [CrossRef]
- Wang, Y.; Li, F. Game study on green innovation of upstream and downstream enterprises in supply chain under carbon trading regulation. J. Chongqing Univ. Technol. (Nat. Sci.). 2022, 36, 238–244. [Google Scholar] [CrossRef]
- Wang, D.; Wang, K. Evolutionary Game Analysis of Low-carbon Effort Decisions in the Supply Chain Considering Fairness Concerns. Manag. Decis. Econ. 2021, 43, 1224–1239. [Google Scholar] [CrossRef]
- Huang, S.; Hu, J.; Xu, W.; Zhou, J.; Hao, M.; Zhou, J. Different Strategy Choices Analysis Based on Stochastic Evolutionary Game Model for Construction Safety Supervision With/Without Smart Site Technology. Buildings 2025, 15, 603. [Google Scholar] [CrossRef]
- Zhu, Q.; Zong, R.; Xu, M. Three-Party Stochastic Evolutionary Game Analysis of Supply Chain Finance Based on Blockchain Technology. Sustainability 2023, 15, 3084. [Google Scholar] [CrossRef]
- Wang, R.; Tai, Y. How Does Blockchain Mitigate False Advertising in Live Streaming E-Commerce? A Tripartite Stochastic Evolutionary Game Approach. J. Retail. Consum. Serv. 2025, 85, 104287. [Google Scholar] [CrossRef]
- Gao, P.; Li, J.; Zhao, X. How to Promote Public Participation in the Recycling of Floating Debris in the Reservoir Area of Hydropower Projects? A Stochastic Quadripartite Evolutionary Game Analysis. Environ. Dev. 2025, 55, 101215. [Google Scholar] [CrossRef]
- Zhang, P.; Ding, R. How to Achieve Carbon Abatement in Aviation with Hybrid Mechanism? A Stochastic Evolutionary Game Model. Energy 2023, 285, 129349. [Google Scholar] [CrossRef]
- Sun, Q.; Fan, M.; Liu, Z.; Zhao, Z.; Lv, C.; Ma, Q. Strategic Guidance of Carbon Emission Reduction in Industrial Parks Based on Dynamic Evolution Game. Comput. Electr. Eng. 2024, 117, 109210. [Google Scholar] [CrossRef]
- Jiang, Y.; Luo, T.; Wu, Z.; Xue, X. The Driving Factors in the Corporate Proactivity of Carbon Emissions Abatement: Empirical Evidence from China. J. Clean. Prod. 2021, 288, 125549. [Google Scholar] [CrossRef]
- Zhao, W.; Hao, J.L.; Gong, G.; Ma, W.; Zuo, J.; Di Sarno, L. Decarbonizing Prefabricated Building Waste: Scenario Simulation of Policies in China. J. Clean. Prod. 2024, 458, 142529. [Google Scholar] [CrossRef]
- Zhao, Y.; Gao, G.; Zhang, J.; Yu, M. Impact of Carbon Tax on Green Building Development: An Evolutionary Game Analysis. Energy Policy 2024, 195, 114401. [Google Scholar] [CrossRef]
- Duan, Z.; Wei, T.; Xie, P.; Lu, Y. Co-Benefits and Influencing Factors Exploration of Air Pollution and Carbon Reduction in China: Based on Marginal Abatement Costs. Environ. Res. 2024, 252, 118742. [Google Scholar] [CrossRef]
- Li, C.Z.; Tam, V.W.Y.; Lai, X.; Zhou, Y.; Guo, S. Carbon Footprint Accounting of Prefabricated Buildings: A Circular Economy Perspective. Build. Environ. 2024, 258, 111602. [Google Scholar] [CrossRef]
- Zhang, R.; Li, L. Research on Evolutionary Game and Simulation of Information Sharing in Prefabricated Building Supply Chain. Sustainability 2023, 15, 9885. [Google Scholar] [CrossRef]
- Mao, Q.; Zhao, M.; Sun, Q. How Supply Chain Enterprises Achieve Coordination between Green Transition and Profitability under the Carbon Trading Framework. J. Environ. Manag. 2025, 377, 124588. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Pan, G.; Zhang, W. Evolutionary Game Theoretic Analysis of Low Carbon Investment in Supply Chains under Governmental Subsidies. Int. J. Environ. Res. Public. Health 2018, 15, 2465. [Google Scholar] [CrossRef] [PubMed]
- Zhu, M.; Wang, Y.; Liu, R.; Fan, L. Stackelberg Game-Based Method towards Carbon-Economy Equilibrium for the Prefabricated Construction Supply Planning: A Case Study from China. Sustain. Cities Soc. 2024, 106, 105356. [Google Scholar] [CrossRef]
- Wang, X.; Du, Q.; Lu, C.; Li, J. Exploration in Carbon Emission Reduction Effect of Low-Carbon Practices in Prefabricated Building Supply Chain. J. Clean. Prod. 2022, 368, 133153. [Google Scholar] [CrossRef]
- Wang, D.-Y.; Li, Y.; Hong, J. Tax or Subsidy? The Impact Assessment of Environmental Policies on Carbon Allocation and Emissions Abatement of Prefabricated Construction Supply Chain. J. Environ. Manag. 2025, 373, 123451. [Google Scholar] [CrossRef]
- Rangasamy, V.; Yang, J.-B. Interpreting Crucial Barriers to Advancing Prefabricated Construction: An Empirical Study in Taiwan Using ISM-MICMAC Approach. J. Clean. Prod. 2025, 489, 144702. [Google Scholar] [CrossRef]
- Wu, H.; Qian, Q.K.; Straub, A.; Visscher, H. Exploring Transaction Costs in the Prefabricated Housing Supply Chain in China. J. Clean. Prod. 2019, 226, 550–563. [Google Scholar] [CrossRef]
- Arashpour, M.; Bai, Y.; Aranda-mena, G.; Bab-Hadiashar, A.; Hosseini, R.; Kalutara, P. Optimizing Decisions in Advanced Manufacturing of Prefabricated Products: Theorizing Supply Chain Configurations in off-Site Construction. Autom. Constr. 2017, 84, 146–153. [Google Scholar] [CrossRef]
- Poznyak, A.S. 9—Basic Properties of Continuous Time Processes. In Advanced Mathematical Tools for Automatic Control Engineers: Stochastic Techniques; Poznyak, A.S., Ed.; Elsevier: Oxford, UK, 2009; pp. 239–261. ISBN 978-0-08-044673-8. [Google Scholar]
- Habashneh, M.; Ghodousian, O.; Fathnejat, H.; Movahedi Rad, M. Probabilistic Topology Optimization Framework for Geometrically Nonlinear Structures Considering Load Position Uncertainty and Imperfections. Mathematics 2024, 12, 3686. [Google Scholar] [CrossRef]
- Sun, H.; Wang, X.; Xue, Y. Stochastic Evolutionary Game model for Unexpected Incidents Involving Mass Participation Based on Different Scenarios. Oper. Res. Manag. Sci. 2016, 25, 23–30. [Google Scholar]
- Hu, S.; Huang, C.; Wu, F. Stochastic Differential Equations; Science Press: Beijing, China, 2008; ISBN 978-7-03-021380-8. [Google Scholar]
- Baker, C.T.H.; Buckwar, E. Exponential Stability in p-Th Mean of Solutions, and of Convergent Euler-Type Solutions, of Stochastic Delay Differential Equations. J. Comput. Appl. Math. 2005, 184, 404–427. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 1992; ISBN 978-3-642-08107-1. [Google Scholar]
- Liu, X.; Lin, K.; Wang, L.; Zhang, H. Stochastic Evolutionary Game Analysis Between Special Committees and CEO: Incentive and Supervision. Dyn. Games Appl. 2021, 11, 538–555. [Google Scholar] [CrossRef]
- Li, Y.; Gao, Y.; Meng, X.; Liu, X.; Feng, Y. Assessing the Air Pollution Abatement Effect of Prefabricated Buildings in China. Environ. Res. 2023, 239, 117290. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Housing and Urban-Rural Development, China. Regulation on Investment Estimation Indicators for Prefabricated Building Engineering (TY01-02-2023). Available online: http://www.gov.cn/zhengce/zhengceku/202308/content_6901196.htm (accessed on 10 March 2025).
- State Council of the People’s Republic of China. Regulation on Energy Conservation in Civil Buildings. Available online: http://www.gov.cn/flfg/2008-08/07/content_1067062.htm (accessed on 10 March 2025).
- National People’s Congress of China. Civil Code of the People’s Republic of China. Available online: http://www.npc.gov.cn/npc//c2/c30834/202006/t20200602_306457.html (accessed on 10 March 2025).
- First Financial Research Institute. 2023 China Carbon Market Annual Report. 2023. Available online: https://img.cbnri.org/files/2024/05/638525794369200000.pdf (accessed on 11 March 2025).
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Standard for Assessment of Prefabricated Building (GB/T 51129-2017). Available online: https://qzl.njfu.edu.cn/DFS/file/2022/04/30/20220430221413130esp4fi.pdf (accessed on 10 March 2025).
- Ding, C.; Liu, H.; Chen, Y.; Qiu, W. Collaborative Innovation in Construction Supply Chain under Digital Construction: Evolutionary Game Analysis Based on Prospect Theory. Buildings 2024, 14, 2019. [Google Scholar] [CrossRef]
- Xue, H.; Ye, C.; Li, F. Evolutionary Game Analysis of Carbon Emission Reduction in Supply Chain Enterprises under Government Regulation. Soft Sci. 2025, 39, 107–114. Available online: http://kns.cnki.net/kcms/detail/51.1268.G3.20241225.1524.006.html (accessed on 11 March 2025).
- Tang, Q.; Wang, C.; Feng, T. Research on the Group Innovation Information-Sharing Strategy of the Industry–University–Research Innovation Alliance Based on an Evolutionary Game. Mathematics 2023, 11, 4161. [Google Scholar] [CrossRef]
- Ullah, H.; Zhang, H.; Huang, B.; Gong, Y. BIM-Based Digital Construction Strategies to Evaluate Carbon Emissions in Green Prefabricated Buildings. Buildings 2024, 14, 1689. [Google Scholar] [CrossRef]
- Li, X.; Xie, W.; Xu, L.; Li, L.; Jim, C.Y.; Wei, T. Holistic Life-Cycle Accounting of Carbon Emissions of Prefabricated Buildings Using LCA and BIM. Energy Build. 2022, 266, 112136. [Google Scholar] [CrossRef]
- Li, S.; Cui, X.; Huo, B.; Zhao, X. Information Sharing, Coordination and Supply Chain Performance: The Moderating Effect of Demand Uncertainty. Ind. Manag. Data Syst. 2019, 119, 1046–1071. [Google Scholar] [CrossRef]
- Li, X.; Jiang, M.; Lin, C.; Chen, R.; Weng, M.; Jim, C.Y. Integrated BIM-IoT Platform for Carbon Emission Assessment and Tracking in Prefabricated Building Materialization. Resour. Conserv. Recycl. 2025, 215, 108122. [Google Scholar] [CrossRef]
- Ahmad, M.; Li, X.F.; Wu, Q. Carbon Taxes and Emission Trading Systems: Which One Is More Effective in Reducing Carbon Emissions?—A Meta-Analysis. J. Clean. Prod. 2024, 476, 143761. [Google Scholar] [CrossRef]
- Lin, R.; Kwon, S.; Bae, S. Multi-Stage Calibration Framework for a Digital Twin Model in Building Operations: Cold Chain Logistics Centers Case Study. Energy Build. 2025, 337, 115662. [Google Scholar] [CrossRef]







| Parameter | Definition and Explanation |
|---|---|
| Benefits of emission reductions when the agent implements an “abatement” strategy, such as economic benefits from reduced energy consumption and shorter construction periods. | |
| External damages faced by the agent when implementing a “no-abatement” strategy [28], such as fines from environmental protection authorities for exceeding emission standards and conflicts with the public due to environmental pollution. | |
| When X implements an “abatement” strategy, there is a contractual relationship with the downstream party i, requiring i to pay a penalty to X for non-abatement. For example, a contractor’s failure to meet green construction requirements would necessitate payment of liquidated damages to the owner as per the agreement. | |
| Abatement costs are incurred by game players when implementing an “abatement” strategy. These include the cost of purchasing environmentally friendly materials and introducing advanced technology. | |
| The efficiency of absorbing spillover information when the agent implements an “abatement” strategy [56]. This refers to the ratio of the amount of information related to emission reductions obtained by an agent to the total amount of information. | |
| The transformative capacity of an agent to transform information into actual benefits when implementing an “abatement” strategy [56]. When the agent organizes and analyzes the data and decides whether to acquire technology, how much material to acquire, etc., it can lead to economic benefits. This indicator refers to the benefit the agent receives from the unit of information. | |
| Coefficient of value-added return on joint abatement by i for agent i when agent i and agent j implement “abatement” strategies simultaneously [36,41]. | |
| Coefficient of free-rider benefit can be obtained by i when the upstream party j implements an “abatement” strategy and the downstream party i implements a “no-abatement” approach, where [41,57,58]. | |
| Incentives received from the government, industry associations, etc., when the agent of the game implements an “abatement” strategy [34,35], such as government green subsidies, industry honors, and awards. | |
| Costs can be reduced when the agent implements an “abatement” strategy with the assistance of external financial institutions, raw material markets, etc. [32,33]. For example, carbon markets reduce carbon trading costs by waiving transaction fees, and banks reduce financing costs by shortening procedures. | |
| Content of knowledge, technology, and other information outside the PBSC relevant to carbon reduction [29,30,31], such as advanced technologies, incentives, and prices of environmentally friendly materials. |
| Strategy Set | Payoff | Strategy Set | Payoff | Strategy Set | Payoff | Strategy Set | Payoff |
|---|---|---|---|---|---|---|---|
| (1, 1, 1, 1) | (1, 0, 1, 1) | (0, 1, 1, 1) | (0, 0, 1, 1) | ||||
| (1, 1, 1, 0) | (1, 0, 1, 0) | (0, 1, 1, 0) | (0, 0, 1, 0) | ||||
| (1, 1, 0, 1) | (1, 0, 0, 1) | (0, 1, 0, 1) | (0, 0, 0, 1) | ||||
| (1, 1, 0, 0) | (1, 0, 0, 0) | (0, 1, 0, 0) | (0, 0, 0, 0) |
| Production and Construction Party (Y) | Operation and Maintenance Party (Z) | |||
|---|---|---|---|---|
| Abatement (z) | No-Abatement (1 − z) | |||
| Dismantling and Recycling Party (U) | ||||
| Abatement (u) | No-Abatement (1 − u) | Abatement (u) | No-Abatement (1 − u) | |
| Abatement (y) | ||||
| No-abatement (1 − y) | ||||
| Production and Construction Party (Y) | Operation and Maintenance Party (Z) | |||
|---|---|---|---|---|
| Abatement (z) | No-Abatement (1 − z) | |||
| Dismantling and Recycling Party (U) | ||||
| Abatement (u) | No-Abatement (1 − u) | Abatement (u) | No-Abatement (1 − u) | |
| Abatement (y) | ||||
| No-abatement (1 − y) | ||||
| Conditions | Numerical Setting | Stability Point |
|---|---|---|
Condition 1:
| (0, 0, 0, 0) | |
Condition 2:
| (1, 1, 1, 1) |
| Planning and Designing Party (X) | Production and Construction Party (Y) | Operation and Maintenance Party (Z) | Dismantling and Recycling Party (U) | ||||
|---|---|---|---|---|---|---|---|
| 7 | 10 | 5 | 8 | ||||
| 3 | 5 | 5 | 4 | ||||
| 22 | 4 | 2.5 | 1 | ||||
| 1 | 29 | 16 | 15 | ||||
| 1 | 2 | 1 | 1 | ||||
| 2 | 1 | 1 | |||||
| Strategy Probability | Mean | Standard Deviation | Median | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Agent | Max | Min | Mean | Max | Min | Overall | Max | Min | Mean |
| X | 0.96 | 0.79 | 0.93 | 0.24 | 0.08 | 0.15 | 0.99 | 0.86 | 0.98 |
| Y | 0.98 | 0.76 | 0.96 | 0.32 | 0.08 | 0.17 | 1.00 | 1.00 | 1.00 |
| Z | 0.97 | 0.84 | 0.96 | 0.24 | 0.08 | 0.14 | 1.00 | 0.98 | 1.00 |
| U | 0.98 | 0.92 | 0.97 | 0.15 | 0.06 | 0.10 | 1.00 | 1.00 | 1.00 |
| Question Number | Question |
|---|---|
| 1 | What is your age? |
| 2 | What is your gender? |
| 3 | What is your occupation? |
| 4 | What is your current working area? |
| 5 | How many years have you been engaged in work or research related to PBSC carbon emission reduction? |
| Question Number | Question |
|---|---|
| 1 | What is the approximate order of emission reduction input costs among the Planning and Designing Party (X), Production and Construction Party (Y), Operation and Maintenance Party (Z), and Dismantling and Recycling Party (U) in PBSC? |
| 2 | What is the percentage of emission reduction costs in PB projects, and what are the primary related aspects? |
| 3 | What percentage of value-added benefits do enterprises obtain from joint emission reduction in PBSC compared to individual emission reduction benefits? |
| 4 | Is there free-riding in PBSC emission reductions? If so, how is it manifested, and what percentage of free-riding benefits corresponds to the benefits of abatement alone? |
| 5 | What methods do companies typically use to gather emission reduction-related information, and what percentage of market information can be effectively collected? |
| 6 | How do you evaluate enterprises’ ability to process collected emission reduction information? |
| 7 | Have the relevant supporting policies and measures for enterprise carbon emission reduction been effectively implemented? Could you elaborate? |
| 8 | What losses do enterprises face if they do not reduce emissions? Will it have a specific impact on the economy, and how? |
| 9 | Is the contract implementation among PBSC enterprises adequate, and are the provisions related to emission reduction strictly enforced? |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Li, L.; Guo, C.; Zhu, R. Research on Stochastic Evolutionary Game and Simulation of Carbon Emission Reduction Among Participants in Prefabricated Building Supply Chains. Appl. Sci. 2025, 15, 4982. https://doi.org/10.3390/app15094982
Wang H, Li L, Guo C, Zhu R. Research on Stochastic Evolutionary Game and Simulation of Carbon Emission Reduction Among Participants in Prefabricated Building Supply Chains. Applied Sciences. 2025; 15(9):4982. https://doi.org/10.3390/app15094982
Chicago/Turabian StyleWang, Heyi, Lihong Li, Chunbing Guo, and Rui Zhu. 2025. "Research on Stochastic Evolutionary Game and Simulation of Carbon Emission Reduction Among Participants in Prefabricated Building Supply Chains" Applied Sciences 15, no. 9: 4982. https://doi.org/10.3390/app15094982
APA StyleWang, H., Li, L., Guo, C., & Zhu, R. (2025). Research on Stochastic Evolutionary Game and Simulation of Carbon Emission Reduction Among Participants in Prefabricated Building Supply Chains. Applied Sciences, 15(9), 4982. https://doi.org/10.3390/app15094982





