Characteristics of the Damping Ratio of Undisturbed Offshore Silty Clay in Eastern Guangdong, China
Abstract
1. Introduction
2. Experimental Method
2.1. Soil Sample Overview
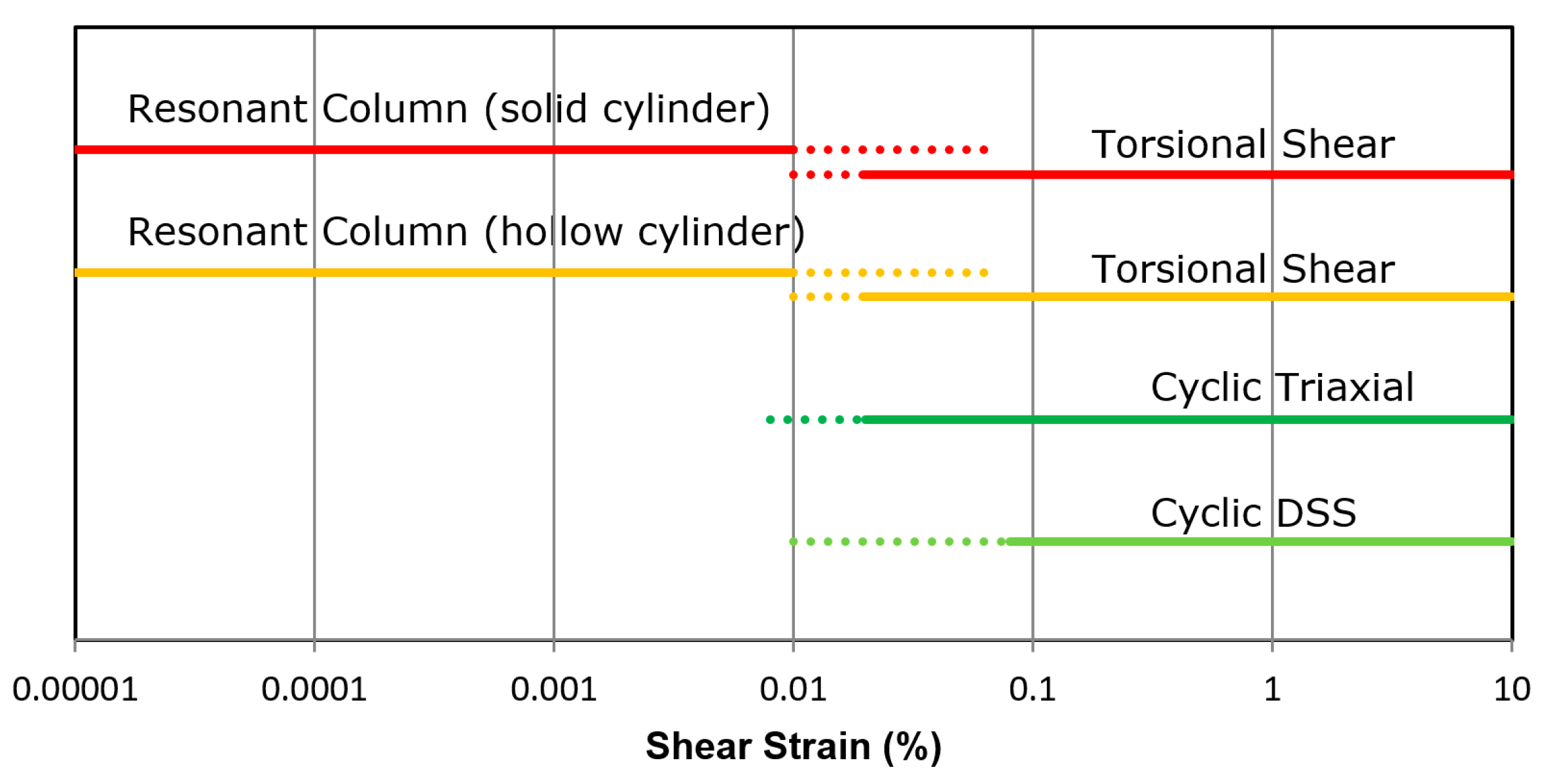
2.2. Experimental Plan
3. Results and Analysis
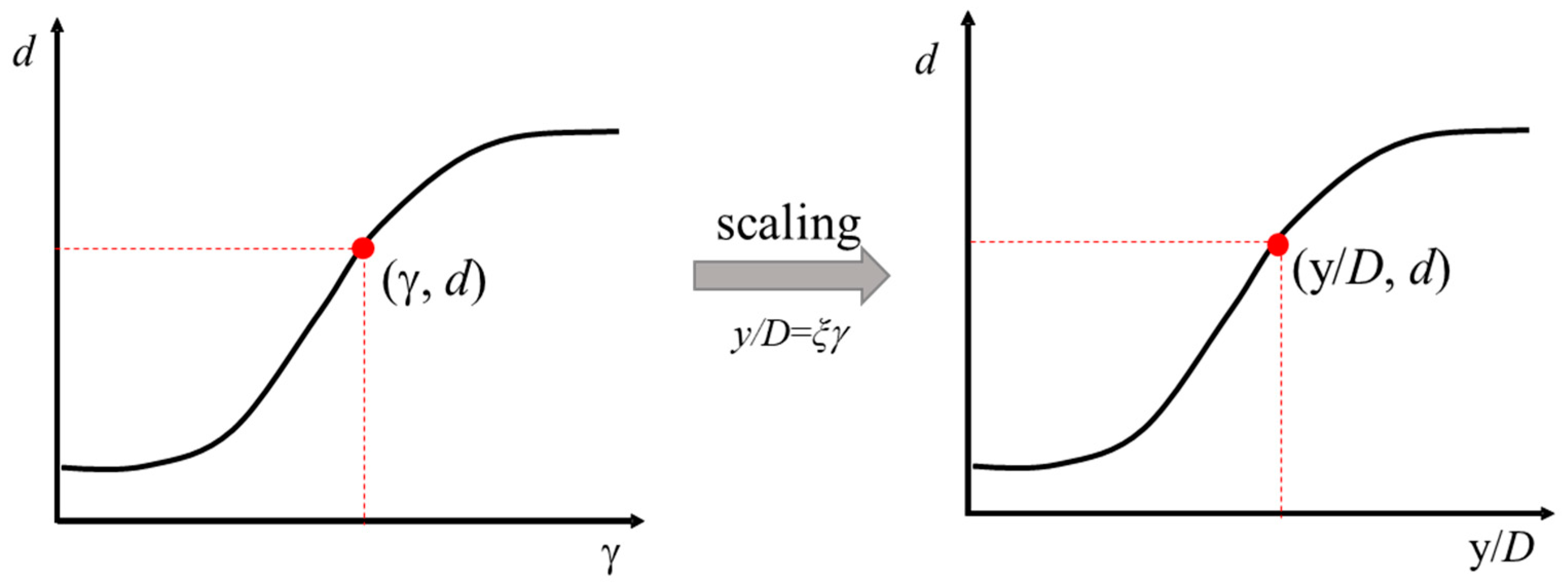
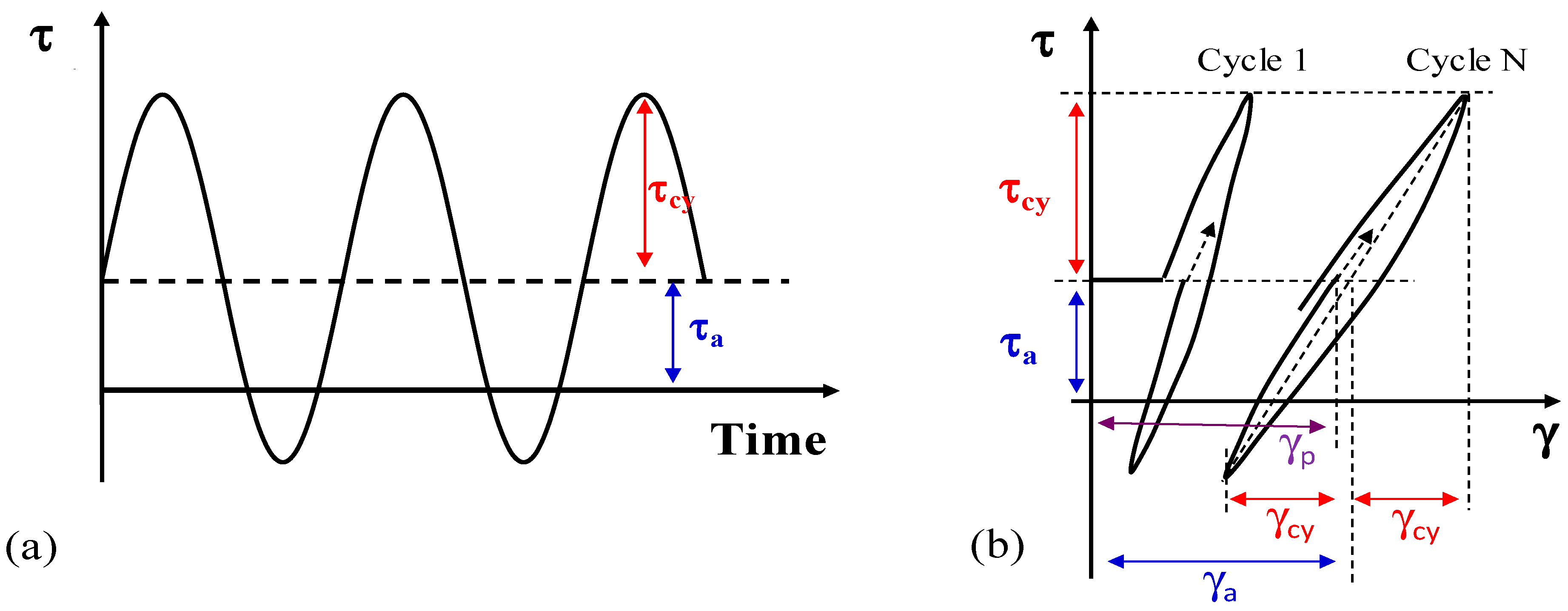
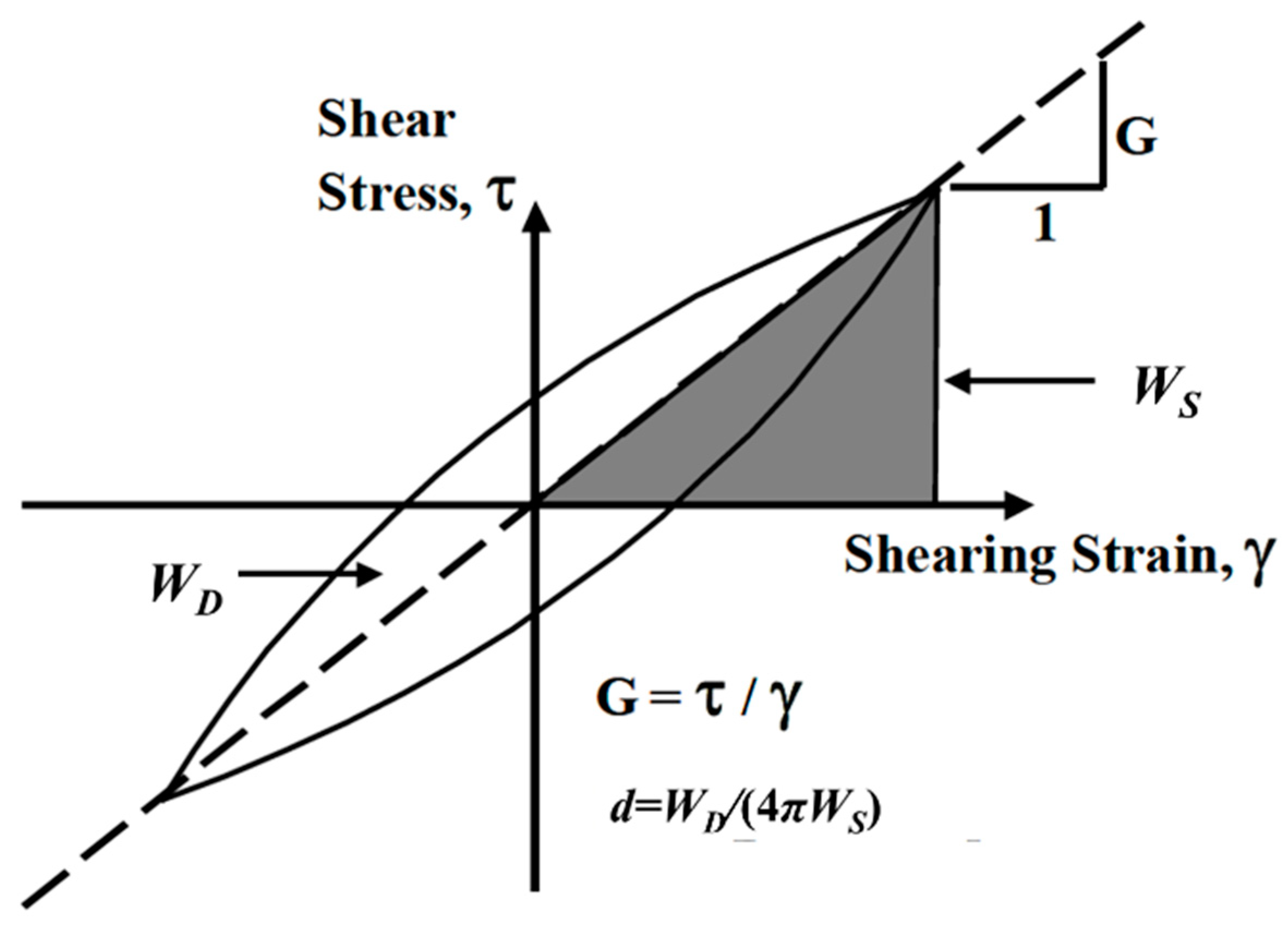
3.1. Damping Ratio Calculation Method
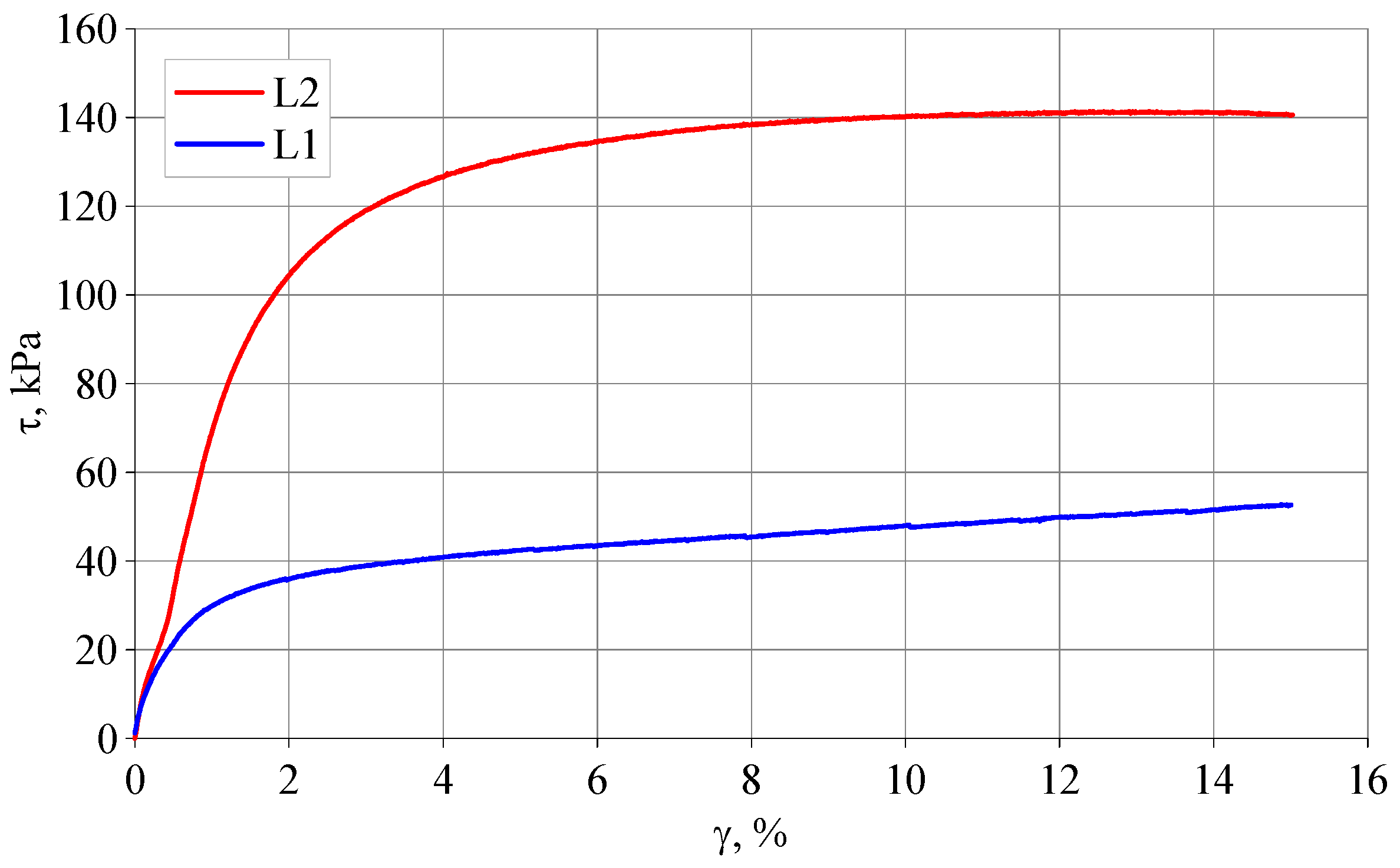
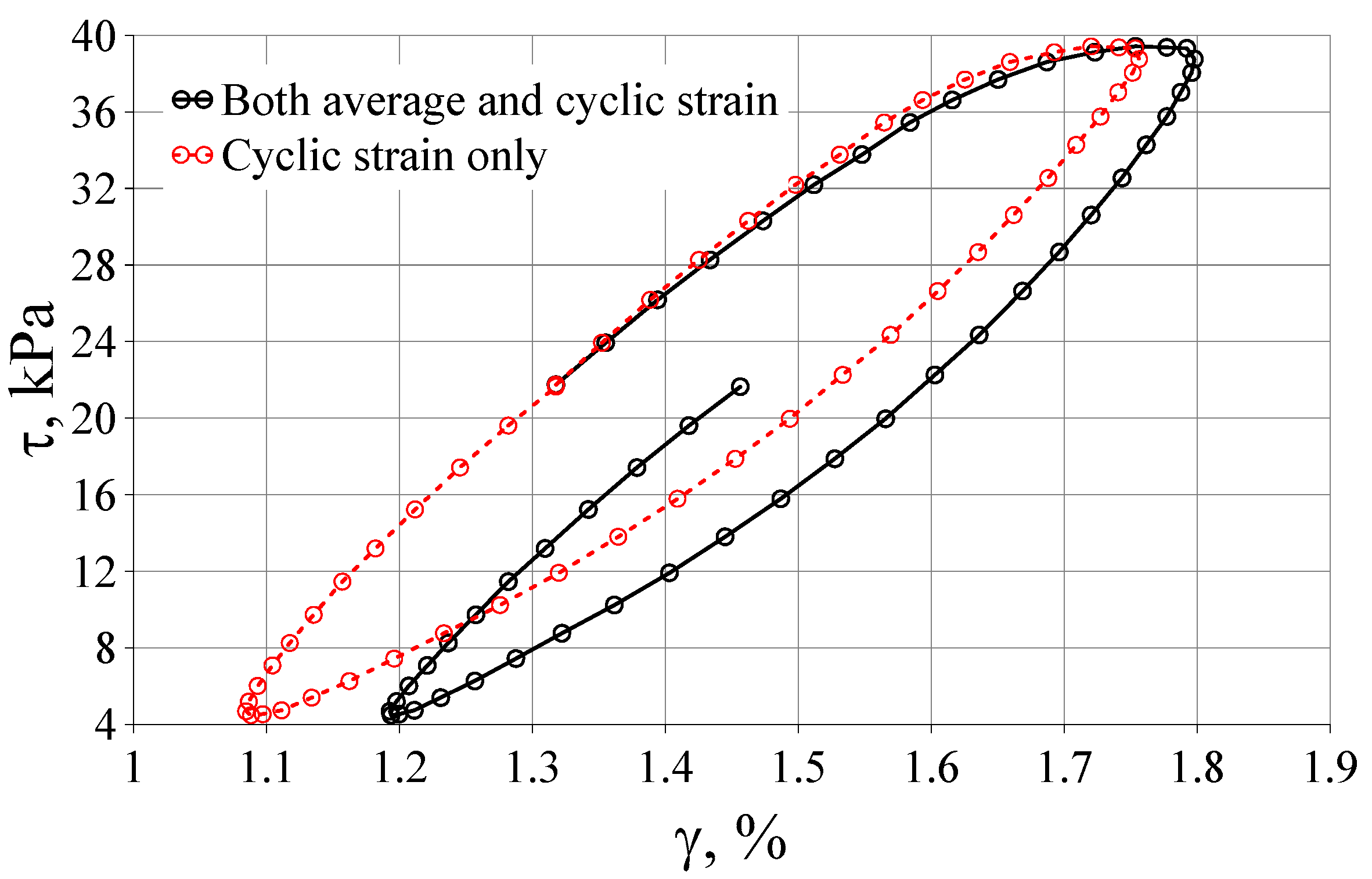
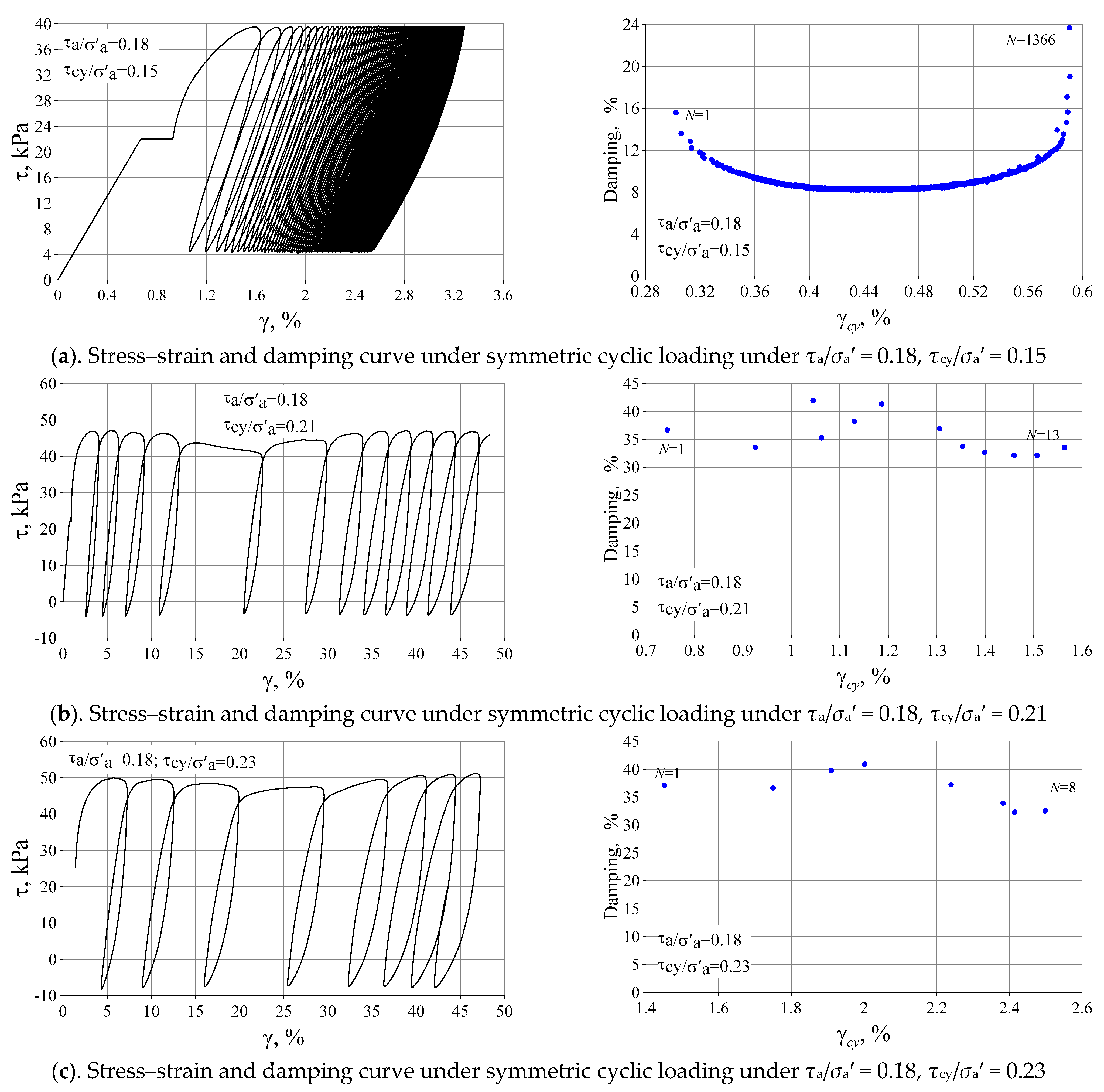
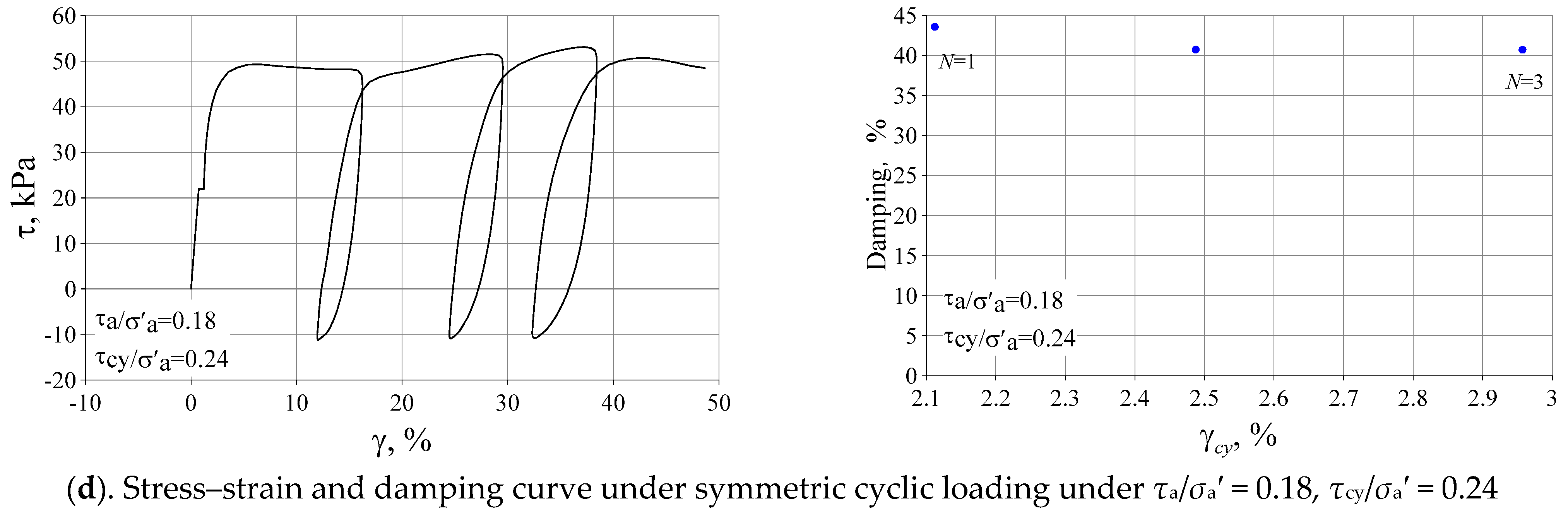
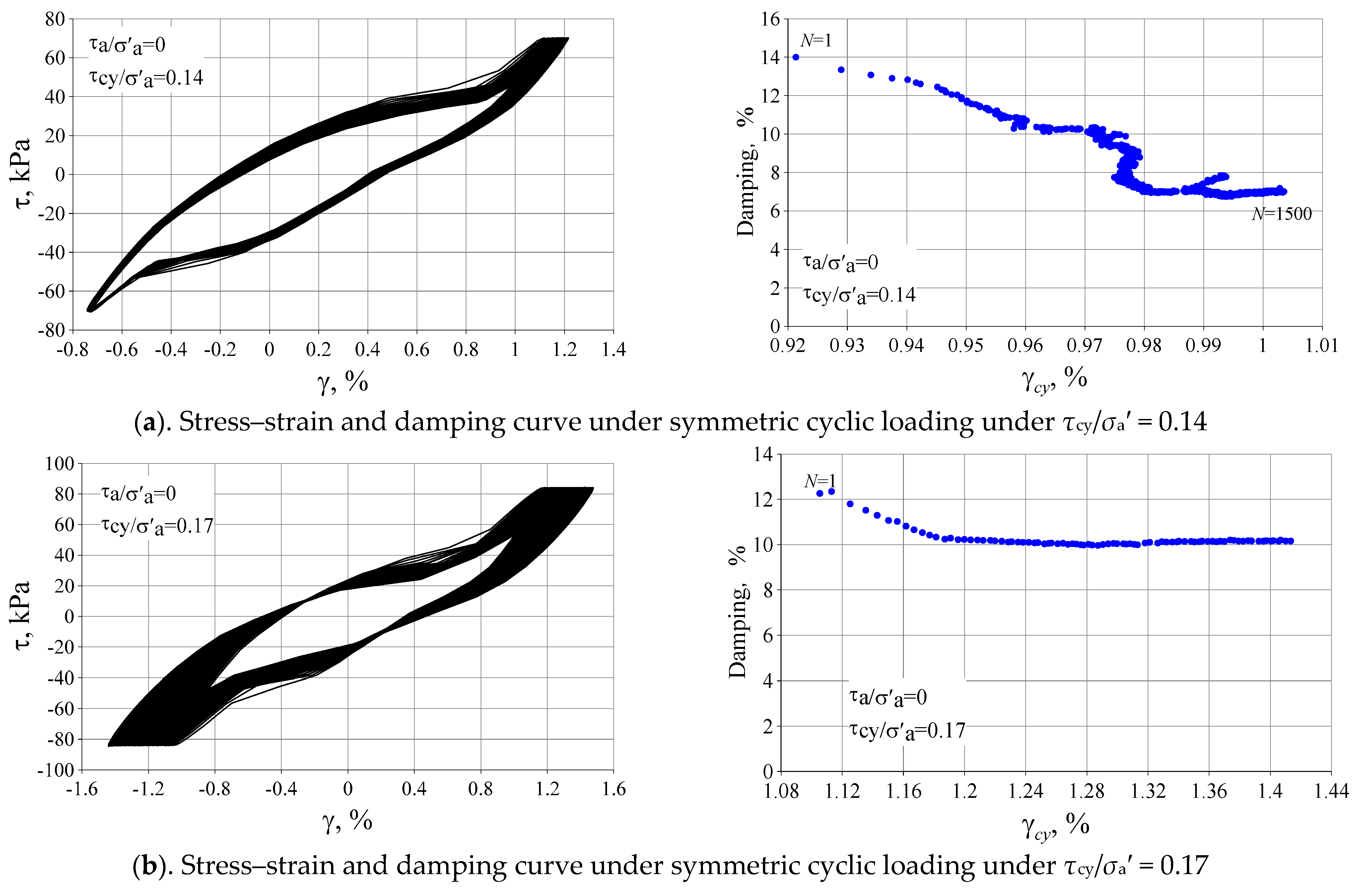
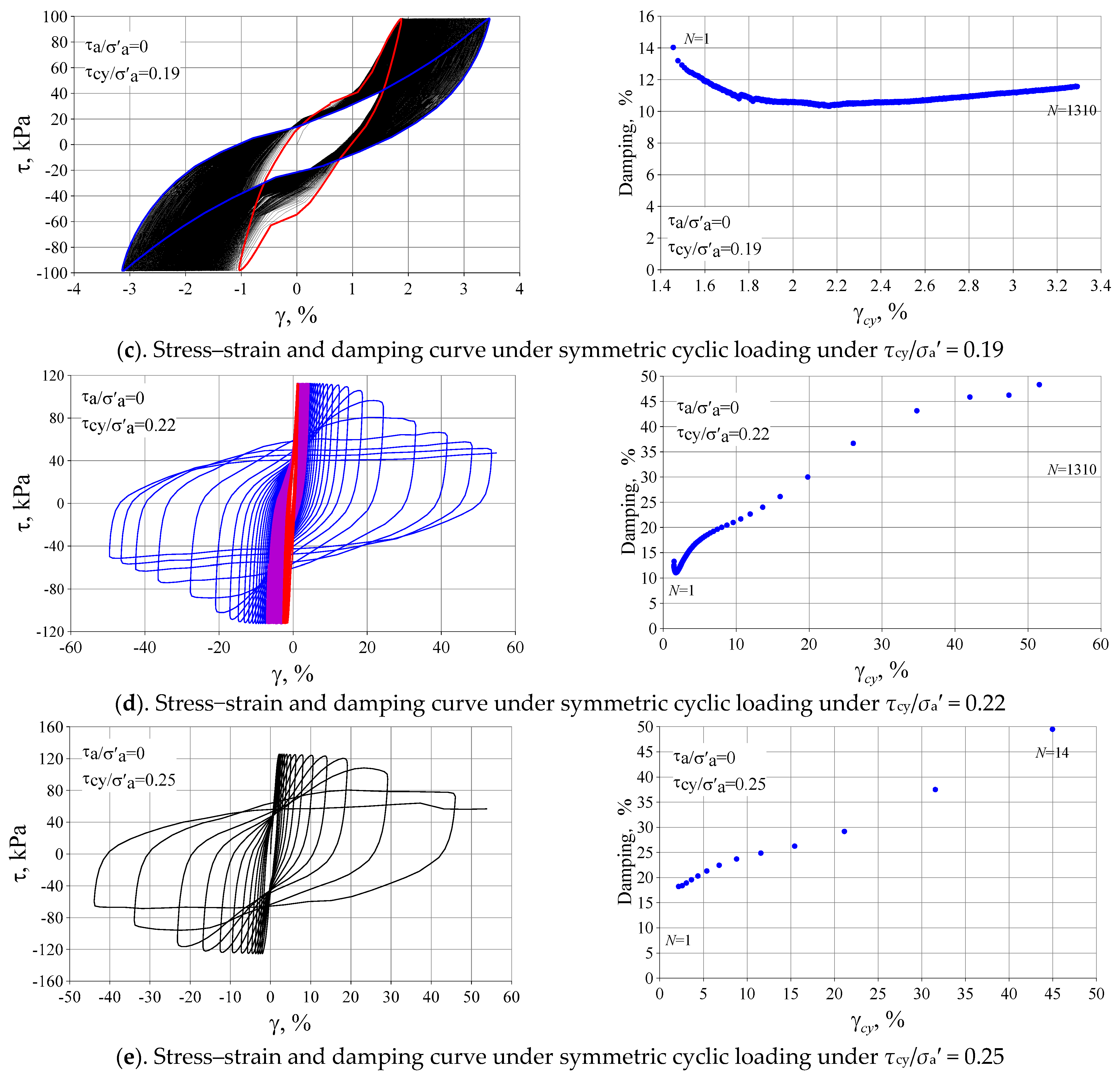
3.2. The Influence of Initial Deviatoric Stress and Cyclic Stress History
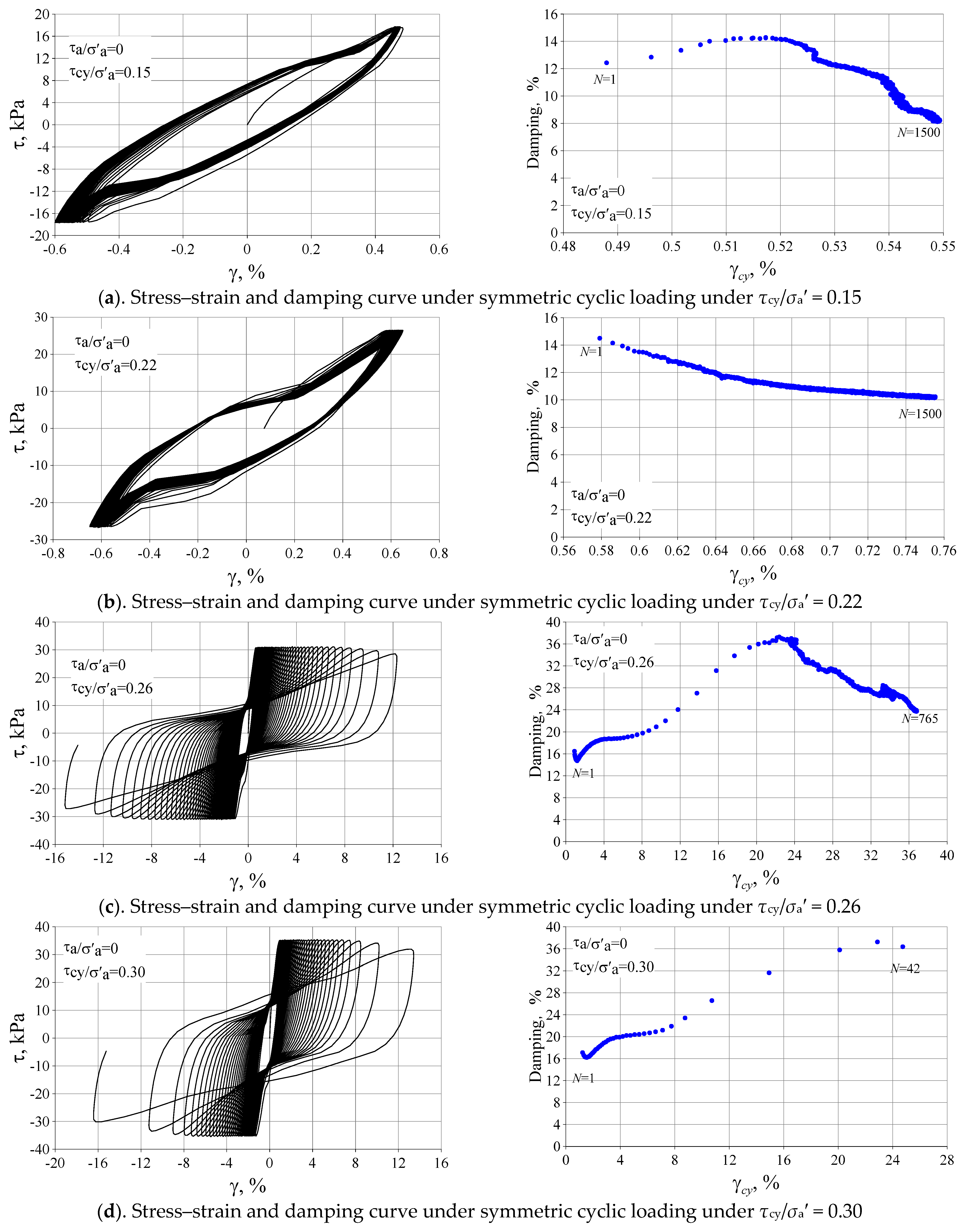
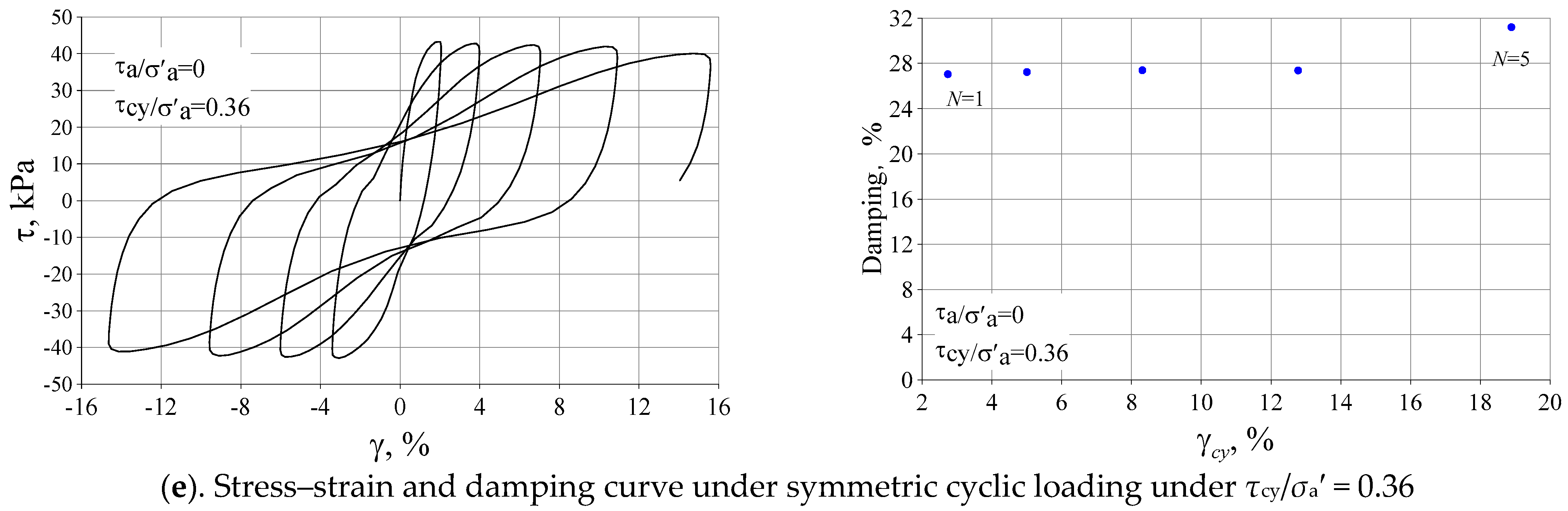
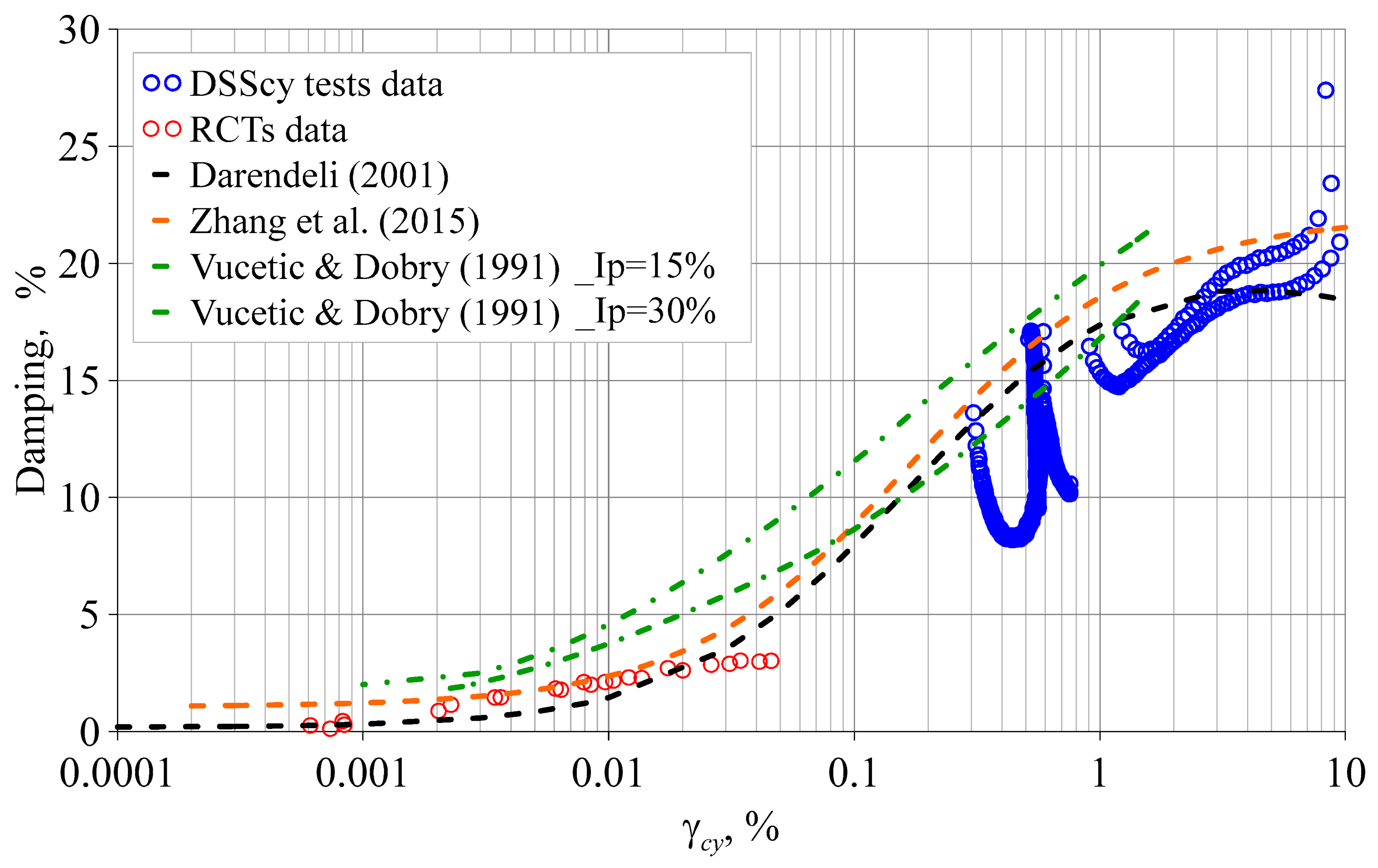
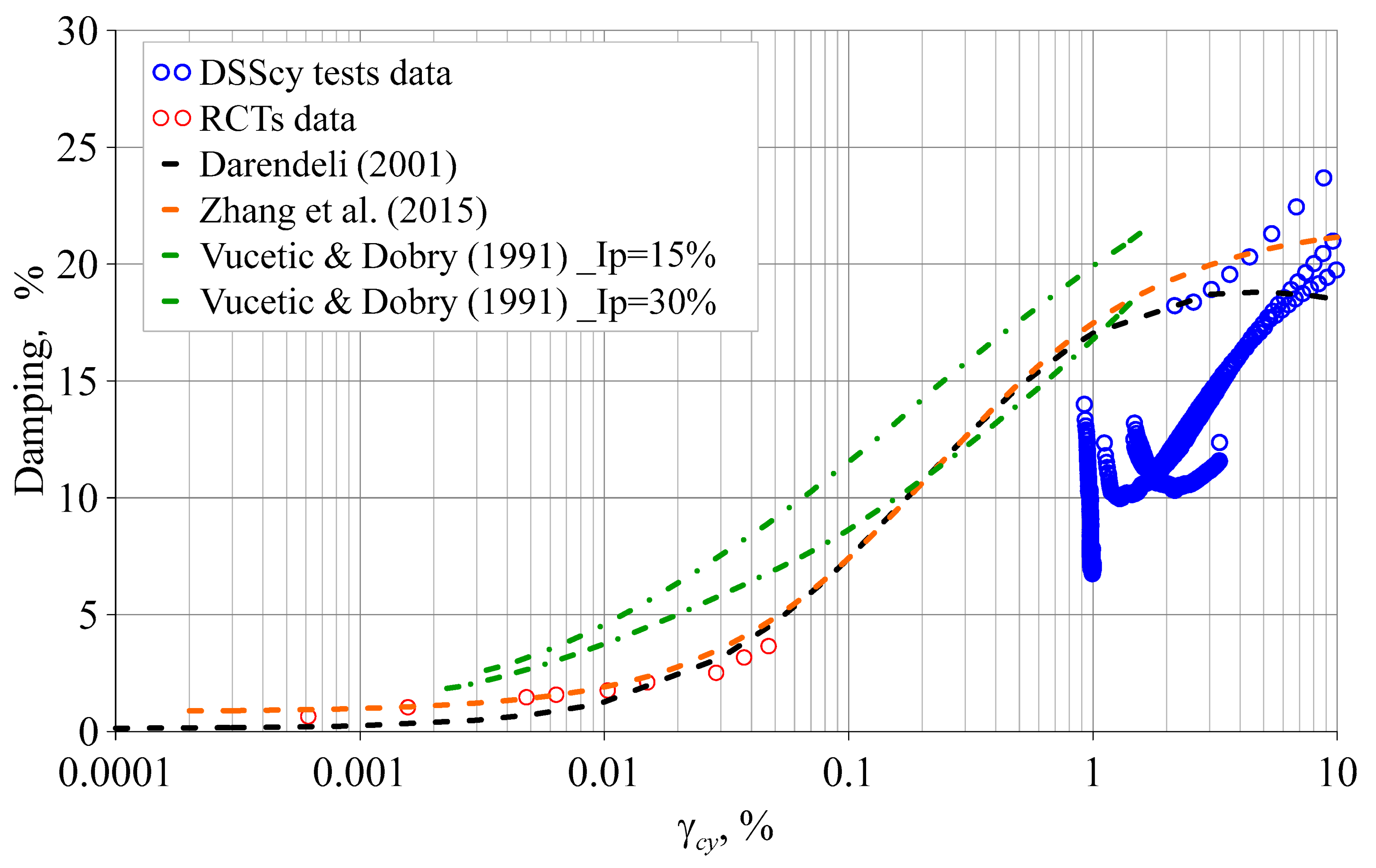
3.3. Damping Ratios of Silty Clay
4. Conclusions
- Soil–pile interaction damping plays a significant role in reducing loads on offshore wind turbine structures, and the soil–element damping ratio is fundamental for studying this interaction. Silty clay, which is widely distributed along China’s coastline, is an important soil type. However, current research on soil damping has primarily focused on clay and sand, with relatively little attention given to silty soils. Therefore, targeted studies on the damping ratio of typical silty clay are essential for optimizing offshore wind power designs in China.
- The damping behaviors of both overconsolidated and normally consolidated silty clay are nearly identical. The influence of cyclic stress history on the damping ratio is significant.
- Currently, no empirical model accurately predicts the damping ratio of silty clay across the entire range of low-to-high strains. While the Darendeli and Zhang et al. models provide relatively accurate predictions at low strain levels, they tend to overestimate the damping of silty clay at medium-to-high strains. This limitation should be considered when empirical models are used in practical engineering applications in place of test data.
- Given the significant challenges and high costs associated with obtaining undisturbed silty clay samples, this study is not exhaustive and does not encompass parametric or mechanistic analyses. Future research should aim to further investigate the damping characteristics of silty clay and silty sand, with the objective of developing a universal empirical damping ratio model for typical silty soils in China. Such a model would have substantial implications for offshore seismic engineering and the optimization of offshore wind power designs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Aamodt, K.K.; Kaynia, A.M. Hysteretic damping model for laterally loaded piles. Mar. Struct. 2021, 76, 102896. [Google Scholar] [CrossRef]
- Assimaki, D.; Kausel, E.; Whittle, A. Model for dynamic shear modulus and damping for granular soils. J. Geotech. Geoenviron. Eng. 2000, 126, 859–870. [Google Scholar] [CrossRef]
- Kovacs, W.D.; Seed, H.B.; Chan, C.K. Dynamic moduli and damping ratios for a soft clay. J. Soil Mech. Found. Div. 1971, 97, 59–75. [Google Scholar] [CrossRef]
- Inci, G.; Yesiller, N.; Kagawa, T. Experimental investigation of dynamic response of compacted clayey soils. Geotech. Test. J. 2003, 26, 125–141. [Google Scholar] [CrossRef]
- Banerjee, S.; Balaji, P. Effect of anisotropy on cyclic properties of Chennai marine clay. Int. J. Geosynth. Ground Eng. 2018, 4, 1–11. [Google Scholar] [CrossRef]
- Mojezi, M.; Biglari, M.; Jafari, M.K.; Ashayeri, I. Determination of shear modulus and damping ratio of normally consolidated unsaturated kaolin. Int. J. Geotech. Eng. 2020, 14, 264–285. [Google Scholar] [CrossRef]
- Hayashi, H.; Yamanashi, T.; Hashimoto, H.; Yamaki, M. Shear Modulus and Damping Ratio for Normally Consolidated Peat and Organic Clay in Hokkaido Area. Geotech. Geol. Eng. 2018, 36, 3159–3171. [Google Scholar] [CrossRef]
- Chehat, A.; Hussien, M.N.; Abdellaziz, M.; Chekired, M.; Harichane, Z.; Karray, M. Stiffness–and damping–strain curves of sensitive Champlain clays through experimental and analytical approaches. Can. Geotech. J. 2018, 29, 364–377. [Google Scholar] [CrossRef]
- Dutta, T.T.; Saride, S. Dynamic properties of compacted cohesive soil based on resonant column studies. In Proceedings of the International Conference on Geo-Engineering and Climate Change Technologies for Sustainable Environmental Management, Allahabad, India, 9–11 October 2015; pp. 1–6. [Google Scholar]
- Galindo-Aires, R.; Lara-Galera, A.; Patiño Nieto, H. Hysteresis model for soft cohesive soils under combinations of static and cyclic shear loads. Int. J. Geomech. 2020, 20, 04020165. [Google Scholar] [CrossRef]
- Patiño, H.; Galindo, R.; Olalla Marañón, C. Cyclic and permanent shear strains of a soft cohesive soil subjected to combined static and cyclic loading. Appl. Sci. 2020, 10, 8433. [Google Scholar] [CrossRef]
- Leng, J.; Ye, G.L.; Ye, B.; Jeng, D.S. Laboratory test and empirical model for shear modulus degradation of soft marine clays. Ocean Eng. 2017, 146, 101–114. [Google Scholar] [CrossRef]
- Hardin, B.O.; Drnevich, V.P. Shear modulus and damping in soils: Measurement and parameter effects (terzaghi leture). J. Soil Mech. Found. Div. 1972, 98, 603–624. [Google Scholar] [CrossRef]
- Kallioglou, P.; Tika, T.; Pitilakis, K. Shear modulus and damping ratio of cohesive soils. J. Earthq. Eng. 2008, 12, 879–913. [Google Scholar] [CrossRef]
- Darendeli, M.B. Development of a New Family of Normalized Modulus Reduction and Material Damping Curves; The University of Texas at Austin: Austin, TX, USA, 2001. [Google Scholar]
- Zhang, J.; Andrus, R.D.; Juang, C.H. Normalized shear modulus and material damping ratio relationships. J. Geotech. Geoenviron. Eng. 2005, 131, 453–464. [Google Scholar] [CrossRef]
- Senetakis, K.; Payan, M. Small strain damping ratio of sands and silty sands subjected to flexural and torsional resonant column excitation. Soil Dyn. Earthq. Eng. 2018, 114, 448–459. [Google Scholar] [CrossRef]
- Lee, C.J.; Sheu, S.F. The stiffness degradation and damping ratio evolution of Taipei Silty Clay under cyclic straining. Soil. Dyn. Earthq. Eng. 2007, 27, 730–740. [Google Scholar] [CrossRef]
- Chen, G.; Wang, B.; Liu, J. Dynamic shear modulus and damping ratio of recently deposited soils in the coastal region of Jiangsu Province. In Geotechnical Engineering for Disaster Mitigation and Rehabilitation: Proceedings of the 2nd International Conference GEDMAR08, Nanjing, China, 30 May–2 June, 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 294–300. [Google Scholar]
- Lan, J.; Liu, H.; Lyu, Y. Dynamic nonlinear parameters of soil in the Bohai Sea and their rationality. J. Harbin Eng. Univ. 2012, 33, 1079–1085. [Google Scholar]
- Li, Y.; Li, P.; Zhu, S. The study on dynamic shear modulus and damping ratio of marine soils based on dynamic triaxial test. Mar. Georesources Geotechnol. 2022, 40, 473–486. [Google Scholar] [CrossRef]
- Song, Q.; Lei, C.; He, W. Experimental study of the dynamic shear modulus and damping ratio of silty clay on Eastern Henan Plain. China Earthq. Eng. J. 2020, 42, 1013–1018. [Google Scholar]
- Song, B.; Sun, Y.; Song, Y.; Zhou, Q.; Liu, Z.; Wang, C.D. Experimental study on the small-strain dynamic properties of offshore seabed soil in Liaodong Bay. China Earthq. Eng. J. 2022, 44, 535–541. [Google Scholar]
- He, W.M.; Li, D.Q.; Yang, J.; Li, Y.Q. Recent progress in research on dynamic shear modulus, damping ratio, and poisson ratio of soils. China Earthq. Eng. J. 2016, 38, 309–317. [Google Scholar]
- Ladd, C.C.; Foott, R. New design procedure for stability of soft clays. J. Geotech. Eng. Div. 1974, 100, 763–786. [Google Scholar] [CrossRef]
- Wang, J.; Yang, T. Cyclic shear modulus and damping ratio of k0 consolidated saturated clays. J. Nat. Disasters 2018, 27, 1–9. [Google Scholar]
- Løvholt, F.; Madshus, C.; Andersen, K.H. Intrinsic soil damping from cyclic laboratory tests with average strain development. Geotech. Test. J. 2020, 43, 194–210. [Google Scholar] [CrossRef]
- Vucetic, M.; Dobry, R. Effect of soil plasticity on cyclic response. J. Geotech. Eng. 1991, 117, 89–107. [Google Scholar] [CrossRef]
- DNV-RP-C212; Offshore Soil Mechanics and Geotechnical Engineering. DNV: Oslo, Norway, 2021.

| Soil Layer No. | Depth Range (m) | Natural Moisture Content (%) | Saturated Unit Weight (kN/m3) | Plasticity Index (%) | Sand Content (0.075–2 mm) (%) | Silt Content (0.005–0.075 mm) (%) | Clay Content (<0.005 mm) (%) |
|---|---|---|---|---|---|---|---|
| L1 | 16–17 | 40.5 | 17.9 | 26.6 | 4.3 | 62.7 | 33 |
| L2 | 17–18 | 38.7 | 18.1 | 20.9 | 7.4 | 72.3 | 20.3 |
| Soil Layer | τa (kPa) | τcy (kPa) | ta/sa′ | tcy/sa′ | sa′ (kPa) | OCR | Ntot | Test | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | L1 | - | - | - | - | 119 | 2 | - | DSS |
| 2 | L1 | - | - | - | - | 119 | 2 | - | RCA |
| 3 | L1 | 0 | 17.6 | 0 | 0.15 | 119 | 2 | >1500 | DSScy |
| 4 | L1 | 0 | 26.4 | 0 | 0.22 | 119 | 2 | >1500 | DSScy |
| 5 | L1 | 0 | 30.8 | 0 | 0.26 | 119 | 2 | 66 | DSScy |
| 6 | L1 | 0 | 35.2 | 0 | 0.30 | 119 | 2 | 38 | DSScy |
| 7 | L1 | 0 | 43 | 0 | 0.36 | 119 | 2 | 5 | DSScy |
| 8 | L1 | 22 | 17.6 | 0.18 | 0.15 | 119 | 2 | 1366 | DSScy |
| 9 | L1 | 22 | 24.9 | 0.18 | 0.21 | 119 | 2 | 13 | DSScy |
| 10 | L1 | 22 | 27.3 | 0.18 | 0.23 | 119 | 2 | 8 | DSScy |
| 11 | L1 | 22 | 28 | 0.18 | 0.24 | 119 | 2 | 3 | DSScy |
| 12 | L2 | - | - | - | - | 506 | 1 | - | DSS |
| 13 | L2 | - | - | - | - | 506 | 1 | - | RCA |
| 14 | L2 | 0 | 70 | 0 | 0.14 | 506 | 1 | >1500 | DSScy |
| 15 | L2 | 0 | 84 | 0 | 0.17 | 506 | 1 | >1500 | DSScy |
| 16 | L2 | 0 | 98 | 0 | 0.19 | 506 | 1 | 270 | DSScy |
| 17 | L2 | 0 | 112 | 0 | 0.22 | 506 | 1 | 191 | DSScy |
| 18 | L2 | 0 | 126 | 0 | 0.25 | 506 | 1 | 10 | DSScy |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, P.; Zhang, Y.; Bi, Q. Characteristics of the Damping Ratio of Undisturbed Offshore Silty Clay in Eastern Guangdong, China. Appl. Sci. 2025, 15, 4954. https://doi.org/10.3390/app15094954
Guo P, Zhang Y, Bi Q. Characteristics of the Damping Ratio of Undisturbed Offshore Silty Clay in Eastern Guangdong, China. Applied Sciences. 2025; 15(9):4954. https://doi.org/10.3390/app15094954
Chicago/Turabian StyleGuo, Peng, Youhu Zhang, and Qian Bi. 2025. "Characteristics of the Damping Ratio of Undisturbed Offshore Silty Clay in Eastern Guangdong, China" Applied Sciences 15, no. 9: 4954. https://doi.org/10.3390/app15094954
APA StyleGuo, P., Zhang, Y., & Bi, Q. (2025). Characteristics of the Damping Ratio of Undisturbed Offshore Silty Clay in Eastern Guangdong, China. Applied Sciences, 15(9), 4954. https://doi.org/10.3390/app15094954





