Abstract
The Bi-directional Evolutionary Structural Optimization (BESO) method, owing to its algorithmic simplicity and strong scalability, has emerged as one of the most prevalent topology optimization methodologies in current research and industrial applications. To overcome the limitations of existing commercial finite element software (e.g., ABAQUS), particularly regarding the closed architecture of topology optimization modules and low efficiency in 3D complex structure optimization, this study proposes an ABAQUS–MATLAB cooperative framework. This innovative approach implements direct read/write operations via Python scripts on CAE/ODB model databases, coupled with MATLAB-based master control programs for sensitivity analysis, mesh filtering, and design variable updating. Compared with conventional integration methods employing INP/FIL file interactions, the proposed framework reduces computational time through MATLAB’s advanced matrix operations while maintaining solution accuracy. Validation cases including 2D cantilever beams and 3D wheel hubs demonstrate the method’s precision and computational efficiency. Practical applications in lightweight design of a hydraulic transmission test bench adapter support achieved 31% volume reduction while satisfying strength and stiffness requirements, significantly lowering material costs. The developed cooperative framework provides an extensible solution for high-efficiency topology optimization of complex engineering structures, balancing algorithmic transparency with practical applicability.
1. Introduction
Structural topology optimization, an engineering technique that seeks optimal material distribution through mathematical methods, aims to maximize structural performance with minimal material consumption. Its essence lies in globally optimizing material layouts to establish efficient load transfer paths rather than performing local dimensional adjustments. Since Bendsøe and Kikuchi pioneered the homogenization theory [1], several representative methodologies have emerged: the Solid Isotropic Material with Penalization (SIMP) method achieves material distribution through continuous density variables [2,3,4]; the Bi-directional Evolutionary Structural Optimization (BESO) method eliminates intermediate densities using discrete 0–1 variable [5]; the Level Set Method (LSM) describes structural boundaries via implicit surface evolution [6,7]; and the Moving Morphable Component (MMC) method employs geometric parameterization for explicit topology representation [8,9]. Originating from Xie and Steven’s Evolutionary Structural Optimization (ESO), BESO overcomes the unidirectional limitations of traditional ESO through bidirectional material addition/removal strategies. It features distinct topological boundaries and rigorous mathematical convergence [10,11,12], having been successfully applied to compliance minimization, frequency-constrained optimization, and multi-scale design, thereby emerging as a mainstream approach for complex structural optimization.
Despite rapid theoretical advancements in topology optimization, significant challenges persist in its practical implementation. The engineering practice of topology optimization demonstrates trends toward multi-objective integration and dynamic coupling. For static structures, Hurtado-Pérez et al. [2] systematically reviewed synergistic design pathways for lightweight satellite structures and additive manufacturing, emphasizing the potential of multi-material optimization in aerospace applications. Ye et al. [13] proposed a hybrid integer programming framework integrating multi-cut optimization and adaptive trust regions, reducing finite element iterations by approximately tenfold and providing efficient solutions for large-scale variable optimization. In dynamic applications, Liu et al. [14] validated the generalizability of the Bi-directional Evolutionary Structural Optimization (BESO) algorithm in 2D flexible mechanisms through explicit finite element analysis, while Alfouneh et al. [15] developed a nonlinear structural power spectral density optimization method based on Moving Isocontour Surfaces (MIST), effectively suppressing dynamic response peaks. Elelwi et al. [4] integrated wing aerodynamics with structural optimization, achieving over 50% weight reduction through concurrent size and topology optimization.
Simultaneously, the field increasingly prioritizes uncertainty quantification in practical engineering. Traditional deterministic methods often neglect uncertainties in material properties, loading conditions, and geometric imperfections, leading to suboptimal designs or reduced robustness. To address these limitations, multidimensional innovations have emerged: Latifi Rostami et al. [16] proposed an Extended Finite Element Method (XFEM)-based framework for continuum structures under geometric uncertainty. The team [17] subsequently introduced a robust topology optimization method using Moving Morphable Components (MMC), balancing robustness, boundary quality, and computational efficiency via adaptive sparse grid techniques. Bai et al. [18] significantly enhanced structural robustness under uncertainty through polynomial chaos expansion and sparse grid quadrature for statistical moment computation. Habashneh et al. [19] established a reliability-based framework incorporating load position uncertainty, integrating geometric nonlinear analysis with normal distributions to validate probabilistic constraint regulation on optimized configurations.
However, challenges persist in multi-scale optimization efficiency [20]. Most open-source topology optimization algorithms developed on MATLAB platforms, while convenient for theoretical validation, are constrained to 2D models with simplified mechanical assumptions, proving inadequate for addressing complex 3D engineering problems [21,22]. Srivastava et al. [5] implemented the Bi-directional Evolutionary Structural Optimization (BESO) method for topology optimization of engine brackets, developing a MATLAB-based algorithm using von Mises stress as the governing parameter, achieving weight reduction while validating structural performance through simulations. Kazakis et al. [23] developed a MATLAB code for concurrent multi-scale topology optimization using BESO, supporting honeycomb/composite materials and single/multi-volume constraints, thereby enabling macro–micro collaborative design and expanding engineering applications. Smith et al. [24] developed a truss optimization program via geometric projection for a parametric design. Chandrasekhar et al. [25] proposed the TOuNN framework mapping density fields to activation functions to eliminate mesh dependency, though constrained to single-objective optimization. Schiffer et al. [26] developed the HiTop 2.0 interactive platform, integrating multi-scale features and manufacturing constraints but lacking nonlinear analysis capabilities. Despite improved accessibility of open-source tools [27,28], limitations remain in commercial software integration and computational scalability. Commercial finite element software (e.g., ABAQUS, ANSYS), despite incorporating 3D topology optimization modules, suffers from closed architectures with black-box algorithms and limited parameter adjustments, hindering compatibility with user-defined optimization strategies.
To bridge the theory-practice gap, researchers have explored integrating commercial FE software with algorithmic platforms: Zuo et al. [21] implemented 3D BESO via ABAQUS scripting with INP file interactions. Chen et al. [29] achieved large-displacement optimization through MATLAB–ANSYS integration. Papazafeiropoulos et al. [30] created the A2M tool for ABAQUS–MATLAB coupling, albeit limited to unidirectional data transfer. Chen et al. [31] proposed Simulated Annealing BESO (SA-BESO) combining stochastic updates and dual-coding mechanisms to escape local optima, yielding lower compliance at reduced costs. Sun et al. [32] introduced a BESO-reinforcement learning hybrid algorithm generating diverse solutions via ε-greedy strategies, balancing quality and diversity in 2D/3D compliance minimization. Teimouri et al. [33] developed a MATLAB–ABAQUS interface for BESO implementation with user-friendly parameter configuration. Lin et al. [34] coded DER-BESO using ANSYS APDL, accelerating convergence for 3D/periodic structures. Silva et al. [35] validated crash optimization feasibility via MATLAB–ABAQUS® iterative interfaces, while Alfouneh et al. [15] formulated a universal nonlinear optimization scheme using MIST with LS-Dyna. Current challenges focus on nonlinear problem decoupling and large-scale parallel acceleration, necessitating standardized interfaces for collaborative computing.
In engineering practice, BESO’s advantages are increasingly evident. Huang et al. [36] addressed ESO limitations via critical boundary constraints, laying BESO’s theoretical foundation. Han [37] developed a multi-material BESO framework using p-norm global stress modeling to reduce stress singularity, demonstrating 21% lower maximum stress versus stiffness-driven designs. Xiong et al. [38] proposed a tri-field BESO method, integrating density, filter radius variables, and isotropic/anisotropic filters to generate plate-like, extruded, and other morphologies, enhancing geometric control and design diversity. Tian et al. [39] optimized jack-up platform legs using BESO, achieving superior load-bearing capacity, dynamic response, and weight reduction compared to traditional K/reverse-K/X-type structures, with experimental validation. Garcez et al. [40] employed BESO for stress-based topology optimization of 2D structures, minimizing p-norm stress via adjoint sensitivity analysis, effectively reducing maximum stress in gravity-loaded structures and outperforming conventional compliance-driven approaches. However, existing studies remain limited to specific cases, lacking universal integrated tools, while 3D optimization efficiency and stability require further improvement.
Compared with previous work, this study proposes an ABAQUS–MATLAB cooperative framework and our contributions are as follows:
- (1)
- A high-efficiency data interaction mechanism, employing Python scripts to directly manipulate ABAEUS CAE model databases and ODB result files, replacing conventional INP/FIL file exchanges.
- (2)
- MATLAB-based BESO algorithm integration, ensuring mathematical convergence and mesh independence, accelerated by advanced matrix operations.
- (3)
- Enhanced compatibility with engineering constraints, including non-design domain binding and multi-loadcase coupling. Applied to the lightweight design of a hydraulic torque converter adapter bracket, the framework achieved 31% volume reduction while meeting strength/stiffness requirements, demonstrating engineering viability.
Next, the sections of this paper are set up as follows: Section 2 details the BESO mathematical formulation. Section 3 presents the architecture and technical implementation of the ABAQUS–MATLAB cooperative framework. Section 4 validates the method accuracy and efficiency through benchmark cases (2D cantilever beam, 3D wheel hub). Section 5 demonstrates an engineering application to a hydraulic transmission test bench adapter support. Conclusions and future directions are discussed in Section 6.
2. Materials and Methods
The BESO method employs discrete variables (0/1) where only a small subset of elements require updates during iterations, and material properties are represented using just two types of elements (solid/void), resulting in low memory consumption. In contrast, the SIMP method utilizes continuous density variables, necessitating thousands of material phases to represent graded densities, which significantly increases memory overhead. For 3D models, BESO avoids the storage and computation of full-density matrices inherent to SIMP by selectively retaining elements based on sensitivity thresholds. This approach mitigates the computational time escalation observed in SIMP for million-element models. Meanwhile, the MMC method relies on predefined parametric components, limiting its ability to freely generate complex internal cavities or curved boundaries. Currently, MMC remains relatively constrained in describing intricate topologies, requiring further methodological advancements.
The BESO method employs finite element analysis (FEA) to define the relative density of elements as design variables. For discrete 0–1 optimization problems, a design variable value of 1 indicates a solid element, while a minimal value (e.g., 0.001) represents a void element. This study adopts the soft-kill strategy [12] where material removal is achieved by transitioning an element’s relative density from 1 to a near-zero value (e.g., 0.001) rather than complete deletion. The mathematical formulation of BESO for compliance minimization under a prescribed volume fraction constraint is expressed as Formula (1):
where denotes the element density variable, represents solid elements and denotes void elements, refers to the mean compliance, is the element displacement vector, is the global force matrix, is the displacement matrix, is the global stiffness matrix, is the element stiffness matrix, is the target volume fraction, and is the penalization factor.
The sensitivity analysis of the objective function is performed using the adjoint method [11], expressed as Formula (2):
where denotes the sensitivity value of the element, quantifying its contribution to the objective function.
The volume fraction at the current iteration step is computed via Formula (3) to establish the threshold for element addition/removal:
where is the number of iterations, is the evolutionary rate, and is the Volume fraction to retain in each iteration.
To mitigate checkerboard patterns and mesh dependency in topology optimization, a mesh-independent filtering scheme is implemented to regularize element sensitivity values, as expressed in Formula (4):
where refers to the linear weighting factor, is the distance between the centroids of element and element , is the filter radius, and is the total number of elements within the filter radius.
The filter radius is typically set to 2–3 times the element size to ensure numerical stability and mitigate mesh dependency. However, in engineering practice, increasing may be necessary to avoid generating excessively fine structural features that complicate manufacturing.
To further enhance convergence and algorithmic stability, a historical sensitivity averaging scheme [11] is introduced, which integrates current and historical sensitivities to mitigate oscillations during the iterative process, as expressed in Formula (6):
where is the number of iterations.
The design variable update scheme of the BESO method is formulated as follows in Formula (7):
where and denote the sensitivity thresholds for material addition and deletion, respectively. Solid elements are removed when their sensitivity values fall below , while void elements are added if their sensitivity values exceed , thereby updating the design variables. In stiffness optimization problems, it is common practice to set , thereby requiring only a single threshold [11].
The iterative process terminates when the convergence criterion in Formula (8) is satisfied:
where denotes the objective function value at the iteration, and is the convergence tolerance (typically τ = 0.001). With N = 5, the algorithm terminates when the relative difference between the sum of the objective function values over the last N iterations and the sum over the preceding N iterations within a continuous 10-iteration window is sufficiently small.
3. Architecture Design and Implementation Workflow of the ABAQUS–MATLAB Cooperative Framework
3.1. Hierarchical Architecture Design of the Cooperative Framework
The ABAQUS–MATLAB collaborative framework proposed in this study achieves organic integration of algorithmic efficiency and industrial-grade engineering capabilities through deep integration and complementary advantages of toolchains. The software version information used in this study is as follows: ABAQUS (Version 2024, Dassault Systèmes, France) and MATLAB (Version R2024a, The MathWorks, Inc., Natick, MA, USA). MATLAB leverages its high-efficiency matrix computation strengths to focus on matrix-intensive calculations in the BESO algorithm (sensitivity analysis, density filtering, and variable updates). However, constructing complex 2D or 3D models in MATLAB remains highly cumbersome. In contrast, ABAQUS utilizes its user-friendly graphical user interface (GUI) to rapidly accomplish complex modeling, analysis configuration, and post-processing tasks, while offering robust finite element solving capabilities, versatility for complex engineering problems, and large-scale computational efficiency, supporting distributed parallel computing (MPI) and GPU acceleration. In the MATLAB-based BESO optimization workflow, critical tasks—including design domain establishment, meshing, finite element computations, and topology visualization—are executed by ABAQUS. The collaborative framework is illustrated in Figure 1. ABAQUS reads updated design variables from MATLAB to refine the topological structure, while MATLAB retrieves structural responses from ABAQUS’s finite element computations to update design variables. This iterative data exchange drives continuous updates until convergence is achieved, completing the topology optimization process.
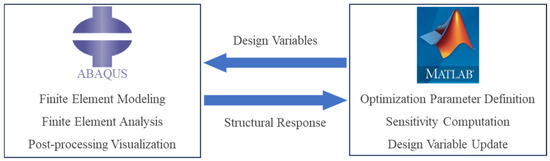
Figure 1.
A schematic of the ABAQUS–MATLAB collaborative framework.
The implementation workflow of the framework is illustrated in Figure 2. Prior to initiating the program, a .cae model file must be preconfigured in ABAQUS via its GUI. This file encompasses the part’s geometric model, material properties, meshing details, boundary conditions, and load definitions.
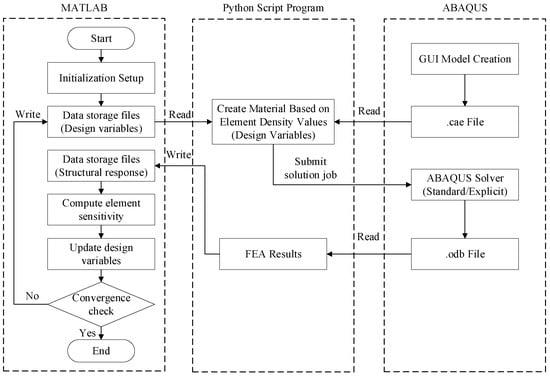
Figure 2.
Detailed flowchart of the ABAQUS–MATLAB integrated framework.
The workflow commences under MATLAB control. Upon task initiation, MATLAB first generates element IDs paired with their corresponding initial design variables (e.g., all set to 1 for BESO initialization) and stores these in a data file (e.g., .xlsx or .txt). Subsequently, MATLAB invokes ABAQUS via the operating system, launching Abaqus CAE to execute a pre-written Python script. The script employs the openMdb function to access the .cae file, extracts part information, and retrieves element/node data. It then reads the design variables from the data file, groups elements based on their density values (design variables), assigns material properties accordingly, and submits the finite element analysis (FEA) job to the ABAQUS solver.
Upon solver completion, the script accesses the. odb results file to extract element output variables (e.g., element strain energy) from the final analysis step (Step 1). A new data file is created to record element IDs and their corresponding output results. MATLAB resumes control, reads the output data, and executes the BESO optimization steps: sensitivity computation, sensitivity filtering, design variable updates, and convergence evaluation. If convergence is unmet, updated design variables are written to the data file, completing one iteration cycle. This loop repeats until the convergence criteria are satisfied.
By leveraging ABAQUS Scripting Interface (ASI), this framework directly manipulates CAE model databases (.cae files) and result databases (.odb files) to enable automated model parameter updates and data exchange, thereby driving the FEA process. The MATLAB-based BESO component follows the core methodology established by Huang and Xie [12].
3.2. MATLAB Master Control Program Design
The topology optimization workflow is driven by the MATLAB master program. After establishing the finite element model and inputting optimization parameters via the ABAQUS/CAE graphical interface, MATLAB initializes design variables and outputs data to the working directory in *.xlsx format. The Python script is invoked through the system command–line interface to trigger ABAQUS solver execution for finite element analysis. The Python script extracts result data from the *.odb database and writes it into the *.xlsx file with element IDs corresponding to their strain energy values. MATLAB reads the *.xlsx file and applies mesh filtering subroutines to process sensitivity information. The filtered sensitivities are used to update design variables through dedicated subroutines. Convergence is evaluated by comparing new and old design variables; if met, optimized results are output; otherwise, the program returns to the design variable output module. The structure of the MATLAB master program is shown in Figure 3.
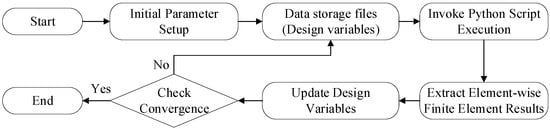
Figure 3.
MATLAB master program.
3.3. Python Scripting Implementation
Upon receiving MATLAB system commands, the Python script executes key operations as depicted in Figure 4. It first reads the *.cae file and design variables from the MATLAB-generated *.xlsx file. The script traverses design domain elements to update material properties, generating a new *.cae file for ABAQUS solver execution. Subsequently, element IDs and their corresponding result data from the *.odb file are extracted and written into a new *.xlsx file. During the first iteration, the script additionally outputs the centroid coordinates of all elements. Reading *.xlsx files via the ABAQUS Scripting Interface requires the openpyxl library. The ABAQUS scripts in this study are written in Python 3.10, which does not include the openpyxl module by default, necessitating its separate download and installation for program execution.
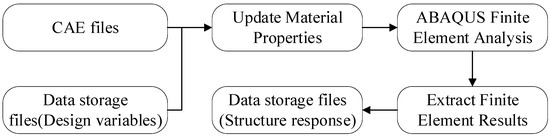
Figure 4.
Python scripting functions.
Specifically, .CAE/.ODB files are binary formats, whereas INP/FIL files are text-based. This study demonstrates that direct read/write operations on .CAE/.ODB files significantly enhance computational efficiency. For scenarios requiring dynamic refinement of local meshes or adjustment of load regions during optimization, the .CAE format enables native manipulation of mesh modules and load managers, offering superior flexibility compared to text-based workflows.
4. Verification Examples
To validate the correctness and efficiency of the proposed ABAQUS–MATLAB cooperative framework, this section conducts comparative tests using a 2D cantilever beam and a 3D wheel hub as benchmark cases.
4.1. Topology Optimization of a 2D Cantilever Beam
A 2D cantilever beam is first tested as a benchmark. The design domain measures 80 mm × 40 mm, with the left end fully fixed and a vertical concentrated load of magnitude 1 applied at the bottom-right corner, as shown in Figure 5.
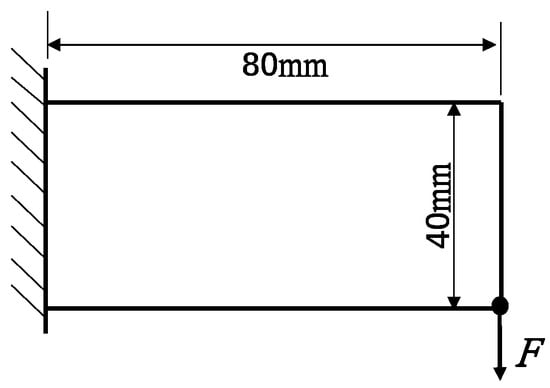
Figure 5.
Original design domain of the cantilever beam.
The CAE model parameters and MATLAB program settings for the proposed ABAQUS–MATLAB cooperative framework are summarized in Table 1. After submitting the topology optimization task, the iterative process is illustrated in Figure 6a–d. The final configuration after 60 iterations is shown in Figure 6d.

Table 1.
Optimization design parameters of 2D cantilever beam.
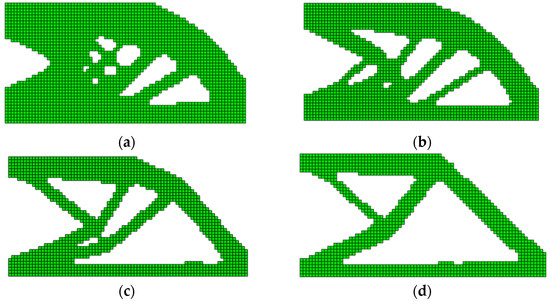
Figure 6.
Iterative optimization process of the cantilever beam. (a) Iteration 14; (b) Iteration 25; (c) Iteration 38; (d) Iteration 60.
The optimized structure exhibits a typical truss-type load transfer path. Compared to the result from the original MATLAB-based program (without ABAQUS integration) [12] in Figure 7, the discrepancies in computational results between the MATLAB framework and the proposed ABAQUS–MATLAB framework stem from differences in element type precision. Consequently, the compliance values obtained by the proposed method are marginally higher than those derived from the MATLAB framework alone. However, the topological configurations of both methods are essentially consistent, with similar evolutionary histories. The final compliance error between the two results is 4%, while the proposed method achieves an iteration time of 18.7 s per cycle and a total optimization duration of 1124 s. The compliance and volume fraction evolution histories of both methods are compared in Figure 8, confirming the validity of the cooperative optimization framework.

Figure 7.
Optimization result from the original MATLAB-based program.
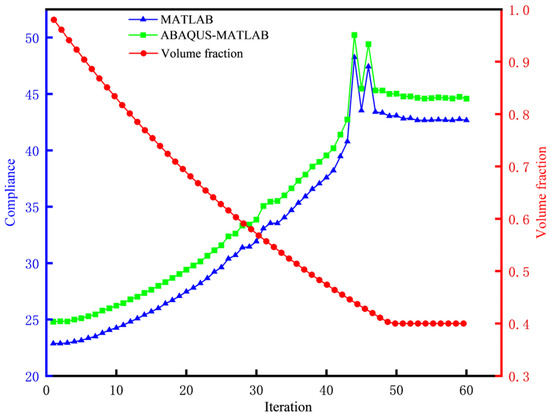
Figure 8.
Compliance and volume fraction evolution histories of the two methods.
To further investigate computational efficiency, we compared the time costs of the MATLAB-only approach and the ABAQUS–MATLAB framework using the cantilever beam model illustrated in Figure 5, with varying element counts. The results are summarized in Table 2.

Table 2.
Computation time comparison between MATLAB and ABAQUS–MATLAB frameworks.
For coarse meshes (e.g., 3200 elements), the MATLAB platform demonstrates significantly higher efficiency than the ABAQUS–MATLAB framework. This disparity arises from the substantial overhead of cross-platform data exchange in the collaborative framework. However, as the element count exceeds 50,000 (e.g., 51,200 elements), the ABAQUS–MATLAB framework outperforms MATLAB due to ABAQUS’s highly efficient solvers—specifically, the standard implicit solver and explicit solver—which dominate the computational workload at scale. These solvers leverage advanced parallelization and optimized algorithms to drastically reduce finite element analysis (FEA) time for large-scale models. The computational overhead associated with cross-platform data exchange becomes negligible when handling models with large-scale element counts.
4.2. Lightweight Design of a 3D Wheel Hub
To further validate the efficiency improvement of the proposed cooperative optimization method for the BESO algorithm, a comparative study is conducted between the proposed framework and the BESO method implemented solely via ABAQUS scripting [21]. A wheel hub model is selected for optimization. The hub dimensions are shown in Figure 9a, with a thickness of 20 mm. The inner and outer annular regions (white) are designated as non-design domains, while the intermediate annular region (blue) serves as the design domain. Radial concentrated loads of 1 N are applied at four equally spaced points on the outer ring, and the inner ring is fully fixed. The meshed model is illustrated in Figure 9b.
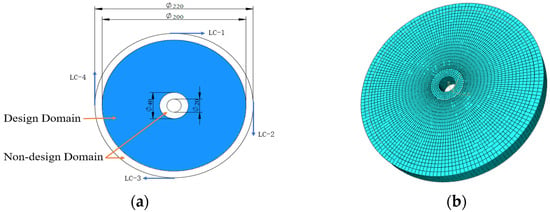
Figure 9.
A 3D wheel hub model. (a) 3D hub model; (b) hub meshing.
The CAE model parameters and MATLAB program settings for the ABAQUS–MATLAB cooperative framework are detailed in Table 3. After submitting the topology optimization task, the iterative process is shown in Figure 10a–d, with the final configuration after 60 iterations (Figure 10d) exhibiting radially distributed stiffening ribs and symmetric void structures. The optimization result from the ABAQUS-only BESO implementation is presented in Figure 11. The compliance and volume fraction evolution histories of both methods are compared in Figure 12.

Table 3.
Optimization design parameters of 3D wheel hub.
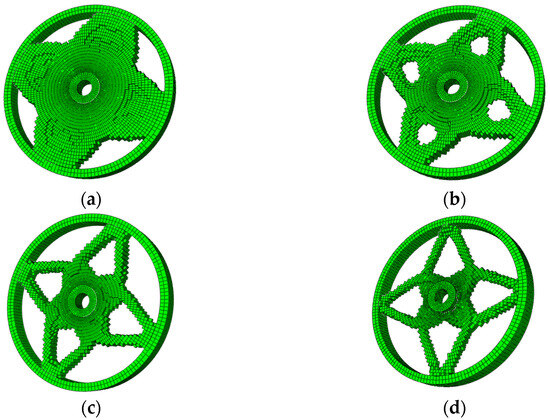
Figure 10.
Iterative optimization process of the 3D wheel hub using the cooperative framework. (a) Iteration 7; (b) Iteration 17; (c) Iteration 27; (d) Iteration 60.

Figure 11.
Optimization results from the ABAQUS-only platform.
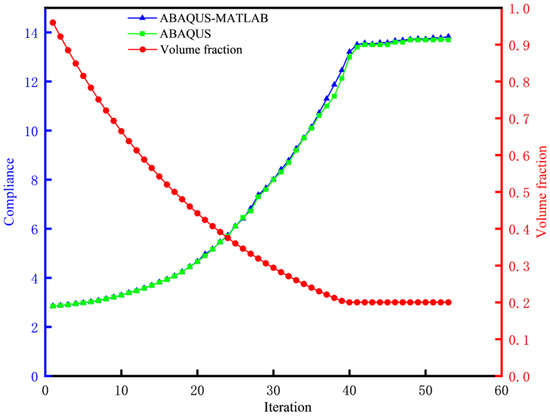
Figure 12.
Compliance and volume fraction evolution histories of the two platforms.
A comparison between the cooperative framework result (Figure 10d) and the ABAQUS-only result (Figure 11) reveals similar topological configurations. Table 4 quantifies the computational efficiency of both platforms, with a more intuitive comparison provided in Figure 13. The ABAQUS-only platform requires 1.65 times more total computation time than the cooperative framework, with grid filtering preparation consuming the majority of time (812 s). In contrast, the cooperative framework reduces grid filtering time to 25.2 s. This disparity arises because Python-based matrix operations in the ABAQUS-only platform iteratively traverse matrix elements, whereas the MATLAB-integrated framework leverages MATLAB’s optimized matrix computation capabilities. Although data exchange between ABAQUS and MATLAB incurs minor overhead, this time is negligible compared to the overall efficiency gains. Notably, the computational gap widens with increasing mesh density.

Table 4.
Computational time comparison between the two platforms.
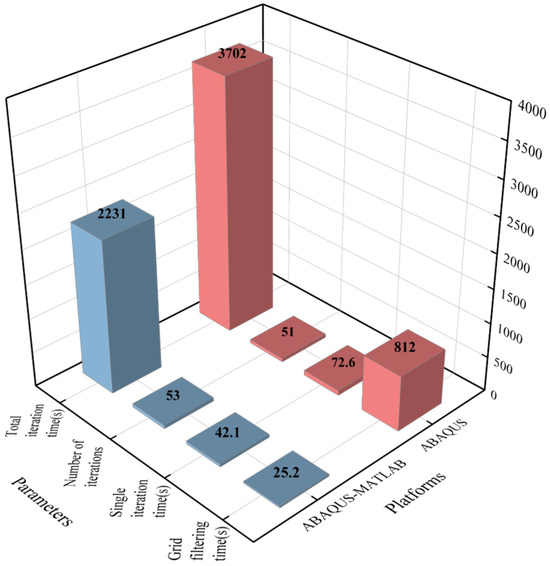
Figure 13.
Computational time comparison between the two platforms.
4.3. Comparative Analysis of 2D Beam and 3D Wheel Hub Optimization
A comparative analysis of the 2D cantilever beam and 3D wheel hub optimization cases is critical to evaluating the framework’s adaptability to varying geometric and computational complexities. Such a comparison highlights how structural features and mesh density influence optimization efficiency, guiding practical applications in industrial design.
As summarized in Table 5, the 3D wheel hub model (15,600 elements) required nearly triple the computation time (3049 s) of the 2D beam (1124 s) despite identical iteration counts (60 cycles). This disparity arises from two factors:

Table 5.
Performance comparison between 2D beam and 3D wheel hub optimization.
- (1)
- An increase in element count: A multiplicative increase in the number of elements substantially prolongs finite element computation time in ABAQUS, while cross-platform data exchange time also rises proportionally.
- (2)
- Geometric complexity: The hub’s radial symmetry and fillets necessitated finer meshing to resolve stress gradients, whereas the beam’s rectilinear geometry allowed for uniform coarser meshes.
These results underscore that geometric intricacy and element count jointly dictate computational demands. While the framework successfully handles both cases, its efficiency for complex 3D structures relies on ABAQUS’s parallelized solvers to mitigate scalability challenges. This insight informs its targeted use in industrial applications requiring high-resolution topology optimization.
5. A Topology Optimization Engineering Application for a Hydraulic Transmission Test Bench Adapter Support
Hydraulic transmissions, as core powertrain components in construction machinery and heavy-duty vehicles, require performance validation and factory testing via test benches to ensure product quality. As shown in Figure 14, the test bench employs a drive motor to simulate engine input and a load motor to simulate operational loads. The mechanical system adopts a modular design, with adapter boxes and driveline configurations, enhancing adaptability to meet testing requirements for various hydraulic transmission models.
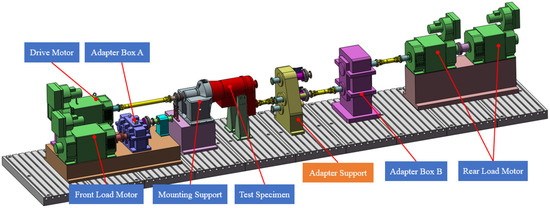
Figure 14.
High-power hydraulic transmission test bench.
The adapter support, located between the test specimen and adapter box, is a critical load-bearing component subjected to complex alternating loads such as torque and vibrational impacts. The initial design, as shown in Figure 15, utilizes gray cast iron HT300, CNC-machined with a volume of 0.1866 m3 and a mass of 1362 kg, ensuring load transmission stability, vibration reduction, and structural rigidity.
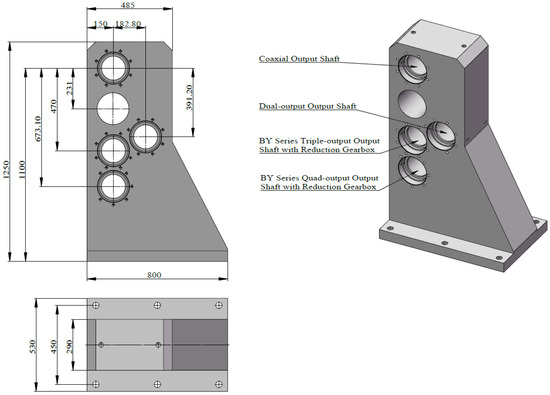
Figure 15.
The initial structural design of the adapter support.
Finite element analysis (FEA) of the initial design reveals displacement and stress distributions. The maximum displacement is 0.808 mm, as shown in Figure 16a, and the maximum stress is 148.2 MPa, as shown in Figure 16b, both well below the material’s allowable limits, indicating significant material redundancy. To reduce manufacturing costs and improve lightweight performance, topology optimization is applied to remove low-stress material while preserving structural integrity.
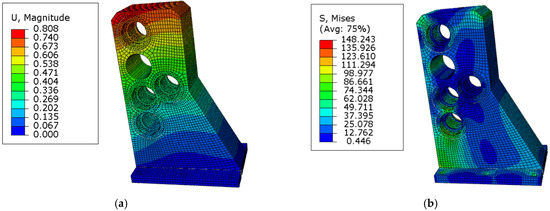
Figure 16.
FEA results of the initial adapter support structure. (a) Displacement nephogram; (b) stress nephogram.
5.1. Optimization Design Implementation
The proposed ABAQUS–MATLAB cooperative framework is applied to optimize the adapter support. To prevent the removal of critical assembly regions during optimization, the support is partitioned into design and non-design domains, as shown in Figure 17a. White regions (non-design domains) interface with adjacent components, while black regions (design domains) undergo optimization. A tie constraint connects these domains in ABAQUS. The CAE model parameters and MATLAB settings are listed in Table 6, with meshing details shown in Figure 17b.
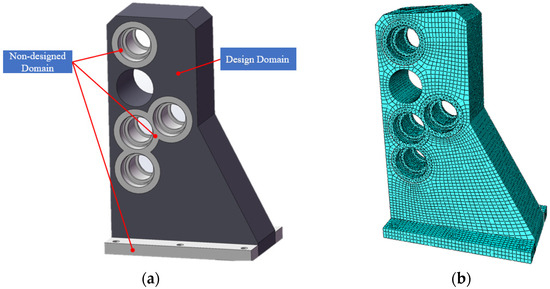
Figure 17.
Design domain partitioning and meshing of the adapter support. (a) Design domain partition; (b) model meshing.

Table 6.
Optimization design parameters of the adapter support.
The use of varying filter radii typically stems from differences in element sizes during mesh generation. In the BESO method, the filter radius should be set to 2–3 times the element size. Generally, to facilitate structural manufacturability and avoid generating excessively fine structural features in the optimization results, the filter radius should be appropriately increased. Under multidimensional constraints (e.g., performance, cost, manufacturability), contextually optimal solutions can be systematically selected rather than passively accepting a single theoretical optimal design.
The iterative optimization process is illustrated in Figure 18a–d, with the final configuration after 38 iterations featuring curved stiffening ribs and honeycomb-like voids, as shown in Figure 18d. The compliance and volume fraction evolution histories are shown in Figure 19.
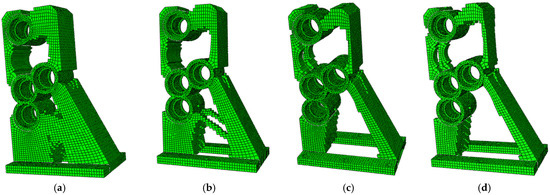
Figure 18.
Iterative optimization process of the adapter support. (a) Iteration 8; (b) Iteration 16; (c) Iteration 25; (d) Iteration 38.
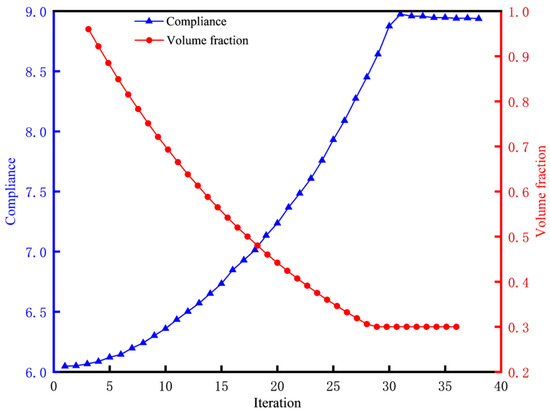
Figure 19.
Compliance and volume fraction evolution histories of the adapter support.
Based on the optimized topology, the redesigned structure (Figure 20) achieves a volume of 0.1287 m3 and a mass of 940 kg, representing a 31% reduction. Post-optimization FEA results (Figure 21a,b) show a maximum displacement of 0.874 mm and maximum stress of 154.6 MPa, compliant with ASME B30.7-2021 standards [41].
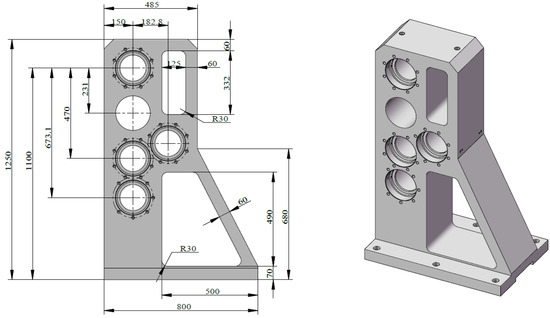
Figure 20.
Optimized structure of the adapter support.
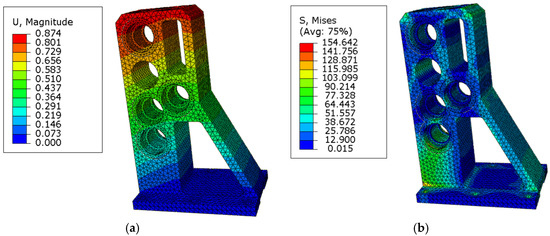
Figure 21.
FEA results of the optimized adapter support. (a) Displacement nephogram; (b) stress nephogram.

Table 7.
A comparison of key parameters before and after optimization.
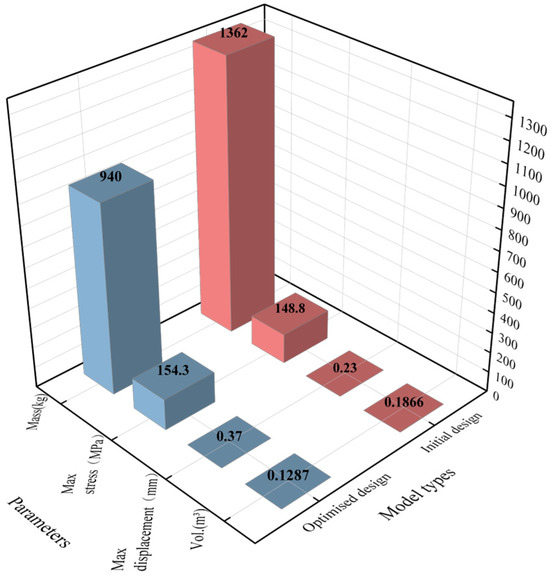
Figure 22.
A comparison of key parameters before and after optimization.
5.2. Engineering Validation and Application Value
The optimized adapter support, CNC-machined and integrated into a 450 kW hydraulic transmission test bench as shown in Figure 23, underwent a comprehensive performance validation. The test bench accommodates performance and factory testing for MA, BY, and SE series products, with a load-end maximum input torque of ≥ 9683 Nm and a maximum input speed of ≥3590 rpm. During testing, the support exhibited no plastic deformation, cracks, or fatigue failure. Results confirm that the optimized component meets strength, stiffness, and dynamic performance requirements while achieving 31% weight reduction, significantly lowering manufacturing costs.

Figure 23.
Engineering application of the optimized adapter support.
6. Conclusions
This study proposes an ABAQUS–MATLAB cooperative optimization framework to overcome the limitations of existing commercial topology optimization tools, such as closed architectures, low efficiency in 3D complex structure optimization, and reliance on time-consuming INP/FIL file interactions. The framework employs a hierarchical architecture where MATLAB manages the BESO-based optimization logic (sensitivity analysis, filtering, and variable updates), ABAQUS handles high-precision finite element modeling and solving with GPU/MPI acceleration, and Python scripts enable real-time parameter updates through direct CAE/ODB database access. This integration eliminates text-based file parsing bottlenecks. Validated through a hydraulic transmission test bench adapter support case, the framework achieved a 31% mass reduction while satisfying strength and stiffness requirements, demonstrating its practical value for topology optimization of heavy machinery components. Scalability tests (Section 4.2) further confirmed its capability to handle industrial-scale problems with several hundred thousand-element models through ABAQUS’s parallel computing.
However, there is still some work that needs to be done. Future efforts will focus on enhancing accessibility via open-source FEA tool compatibility (e.g., CalculiX), integrating real-time visualization and AI-driven parameter tuning, and extending the framework to nonlinear materials and multiphysics problems. These advancements aim to bridge the gap between academic research and industrial deployment, positioning the framework as a versatile platform for both theoretical exploration and real-world engineering applications.
Author Contributions
Conceptualization, D.S., X.Y. and H.Y.; data curation, D.S. and H.L.; formal analysis, D.S.; funding acquisition, X.Y.; methodology, D.S., X.Y., H.L. and H.Y.; supervision, H.Y.; visualization, D.S.; writing—original draft, D.S.; writing—review and editing, D.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Key R&D Program of China (No. 2019YFB1312704), Enterprise project: High power hydraulic transmission and key component supporting construction project (No. 0611-1600130456C).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bendsoe, M.P.; Kikuchi, N. Generating Optimal Topologies in Structural Design Using a Homogenization Method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Hurtado-Pérez, A.B.; Pablo-Sotelo, A.d.J.; Ramírez-López, F.; Hernández-Gómez, J.J.; Mata-Rivera, M.F. On Topology Optimisation Methods and Additive Manufacture for Satellite Structures: A Review. Aerospace 2023, 10, 1025. [Google Scholar] [CrossRef]
- Kim, B.-S.; Han, H.-W.; Chung, W.-J.; Park, Y.-J. Optimization of Gearbox Housing Shape for Agricultural UTV Using Structural-Acoustic Coupled Analysis. Sci. Rep. 2024, 14, 4145. [Google Scholar] [CrossRef]
- Elelwi, M.; Botez, R.M.; Dao, T.-M. Structural Sizing and Topology Optimization Based on Weight Minimization of a Variable Tapered Span-Morphing Wing for Aerodynamic Performance Improvements. Biomimetics 2021, 6, 55. [Google Scholar] [CrossRef]
- Srivastava, S.; Salunkhe, S.; Pande, S. Topology Optimization of Engine Bracket Arm Using BESO. Int. J. Simul. Multidisci. Des. Optim. 2023, 14, 2. [Google Scholar] [CrossRef]
- Gao, J.; Xiao, M.; Zhang, Y.; Gao, L. A Comprehensive Review of Isogeometric Topology Optimization: Methods, Applications and Prospects. Chin. J. Mech. Eng. 2020, 33, 87. [Google Scholar] [CrossRef]
- Wei, P.; Wang, W.; Yang, Y.; Wang, M.Y. Level Set Band Method: A Combination of Density-Based and Level Set Methods for the Topology Optimization of Continuums. Front. Mech. Eng. 2020, 15, 390–405. [Google Scholar] [CrossRef]
- Li, Z.; Xu, H.; Zhang, S. Moving Morphable Component (MMC) Topology Optimization with Different Void Structure Scaling Factors. PLoS ONE 2024, 19, e0296337. [Google Scholar] [CrossRef]
- Li, Z.; Xu, H.; Zhang, S. A Comprehensive Review of Explicit Topology Optimization Based on Moving Morphable Components (MMC) Method. Arch. Comput. Method Eng. 2024, 31, 2507–2536. [Google Scholar] [CrossRef]
- Yang, X.Y.; Xie, Y.M.; Steven, G.P.; Querin, O.M. Bidirectional Evolutionary Method for Stiffness Optimization. AIAA J. 1999, 37, 1483–1488. [Google Scholar] [CrossRef]
- Xia, L.; Xia, Q.; Huang, X.; Xie, Y.M. Bi-Directional Evolutionary Structural Optimization on Advanced Structures and Materials: A Comprehensive Review. Arch. Comput. Method Eng. 2018, 25, 437–478. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y.-M. A Further Review of ESO Type Methods for Topology Optimization. Struct. Multidiscip. Optim. 2010, 41, 671–683. [Google Scholar] [CrossRef]
- Ye, Z.; Pan, W. Discrete Variable Topology Optimization Using Multi-Cut Formulation and Adaptive Trust Regions. Struct. Multidiscip. Optim. 2025, 68, 25. [Google Scholar] [CrossRef]
- Liu, C.-H.; Huang, G.-F.; Chiu, C.-H. An Evolutionary Topology Optimization Method for Design of Compliant Mechanisms with Two-Dimensional Loading. In Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Busan, Republic of Korea, 7–11 July 2015; pp. 1340–1345. [Google Scholar]
- Alfouneh, M.; Tong, L. Topology Optimization of Nonlinear Structures with Damping under Arbitrary Dynamic Loading. Struct. Multidiscip. Optim. 2018, 57, 759–774. [Google Scholar] [CrossRef]
- Rostami, S.A.L.; Ghoddosian, A.; Kolahdooz, A.; Zhang, J. Topology Optimization of Continuum Structures under Geometric Uncertainty Using a New Extended Finite Element Method. Eng. Optim. 2022, 54, 1692–1708. [Google Scholar] [CrossRef]
- Latifi Rostami, S.A.; Kolahdooz, A.; Chung, H.; Shi, M.; Zhang, J. Robust Topology Optimization of Continuum Structures with Smooth Boundaries Using Moving Morphable Components. Struct. Multidiscip. Optim. 2023, 66, 121. [Google Scholar] [CrossRef]
- Bai, S.; Kang, Z. Robust Topology Optimization for Structures under Bounded Random Loads and Material Uncertainties. Comput. Struct. 2021, 252, 106569. [Google Scholar] [CrossRef]
- Habashneh, M.; Cucuzza, R.; Aela, P.; Movahedi Rad, M. Reliability-Based Topology Optimization of Imperfect Structures Considering Uncertainty of Load Position. Structures 2024, 69, 107533. [Google Scholar] [CrossRef]
- Mukherjee, S.; Lu, D.; Raghavan, B.; Breitkopf, P.; Dutta, S.; Xiao, M.; Zhang, W. Accelerating Large-Scale Topology Optimization: State-of-the-Art and Challenges. Arch. Computat. Methods Eng. 2021, 28, 4549–4571. [Google Scholar] [CrossRef]
- Zuo, Z.H.; Xie, Y.M. A Simple and Compact Python Code for Complex 3D Topology Optimization. Adv. Eng. Softw. 2015, 85, 1–11. [Google Scholar] [CrossRef]
- Deng, H.; Vulimiri, P.S.; To, A.C. An Efficient 146-Line 3D Sensitivity Analysis Code of Stress-Based Topology Optimization Written in MATLAB. Optim. Eng. 2022, 23, 1733–1757. [Google Scholar] [CrossRef]
- Kazakis, G.; Lagaros, N.D. Multi-Scale Concurrent Topology Optimization Based on BESO, Implemented in MATLAB. Appl. Sci. 2023, 13, 10545. [Google Scholar] [CrossRef]
- Smith, H.; Norato, J.A. A MATLAB Code for Topology Optimization Using the Geometry Projection Method. Struct. Multidiscip. Optim. 2020, 62, 1579–1594. [Google Scholar] [CrossRef]
- Chandrasekhar, A.; Suresh, K. TOuNN: Topology Optimization Using Neural Networks. Struct. Multidiscip. Optim. 2021, 63, 1135–1149. [Google Scholar] [CrossRef]
- Schiffer, G.; Ha, D.Q.; Carstensen, J.V. HiTop 2.0: Combining Topology Optimisation with Multiple Feature Size Controls and Human Preferences. Virtual Phys. Prototyp. 2023, 18, e2268603. [Google Scholar] [CrossRef]
- Kazakis, G.; Lagaros, N.D. Topology Optimization Based Material Design for 3D Domains Using MATLAB. Appl. Sci. 2022, 12, 10902. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, X.; Zhang, H.; Liang, J.; Zang, H.; Li, H.; Wang, R. Design of Compliant Mechanisms Using Continuum Topology Optimization: A Review. Mech. Mach. Theory 2020, 143, 103622. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, X.; Zhu, B. A 213-Line Topology Optimization Code for Geometrically Nonlinear Structures. Struct. Multidiscip. Optim. 2019, 59, 1863–1879. [Google Scholar] [CrossRef]
- Papazafeiropoulos, G.; Muniz-Calvente, M.; Martinez-Paneda, E. Abaqus2Matlab: A Suitable Tool for Finite Element Post-Processing. Adv. Eng. Softw. 2017, 105, 9–16. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, H.; Wang, W.; Zhang, Q. Topology Optimization Based on SA-BESO. Appl. Sci. 2023, 13, 4566. [Google Scholar] [CrossRef]
- Sun, H.; Ma, L. Structural Topology Optimization by Combining BESO with Reinforcement Learning. J. Harbin Inst. Technol. (New Ser.) 2021, 28, 85–96. [Google Scholar]
- Teimouri, M.; Asgari, M. Developing an Efficient Coupled Function-Based Topology Optimization Code for Designing Lightweight Compliant Structures Using the BESO Algorithm. Optim. Eng. 2024, 25, 575–603. Available online: https://link.springer.com/article/10.1007/s11081-023-09808-w (accessed on 11 March 2025). [CrossRef]
- Lin, H.; Xu, A.; Misra, A.; Zhao, R. An ANSYS APDL Code for Topology Optimization of Structures with Multi-Constraints Using the BESO Method with Dynamic Evolution Rate (DER-BESO). Struct. Multidiscip. Optim. 2020, 62, 2229–2254. [Google Scholar] [CrossRef]
- Silva, C.J.G.; Lopes, R.F.F.; Domingues, T.M.R.M.; Parente, M.P.L.; Moreira, P.M.G.P. Crashworthiness Topology Optimisation of a Crash Box to Improve Passive Safety during a Frontal Impact. Struct. Multidiscip. Optim. 2025, 68, 3. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y.M. A New Look at ESO and BESO Optimization Methods. Struct. Multidiscip. Optim. 2008, 35, 89–92. [Google Scholar] [CrossRef]
- Han, Y. Stress-based bi-directional evolutionary topology optimization for structures with multiple materials. Eng. Comput. 2024, 40, 2905–2923. [Google Scholar] [CrossRef]
- Xiong, Y.; Lu, H.; Yan, X.; He, Y.; Xie, Y.M. Achieving Diverse Morphologies Using Three-Field BESO with Variable-Radius Filter. Eng. Struct. 2025, 322, 119049. [Google Scholar] [CrossRef]
- Tian, X.; Wang, Z.; Liu, D.; Liu, G.; Deng, W.; Xie, Y.; Wang, H. Jack-up Platform Leg Optimization by Topology Optimization Algorithm-BESO. Ocean Eng. 2022, 257, 111633. [Google Scholar] [CrossRef]
- Garcez, G.L.; Pavanello, R.; Picelli, R. Stress-Based Structural Topology Optimization for Design-Dependent Self-Weight Loads Problems Using the BESO Method. Eng. Optim. 2023, 55, 197–213. [Google Scholar] [CrossRef]
- ASME B30.7-2021; Winches (Safety Standard for Cableways, Cranes, Derricks, Hoists, Hooks, Jacks, and Slings). The American Society of Mechanical Engineers: New York, NY, USA, 2021.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).