Abstract
Ventilation systems are susceptible to errors, external disruptions, and nonlinear dynamics. Maintaining stable operation and regulating these dynamics require an efficient control system. This study focuses on the speed control of ventilation systems using a super twisted sliding mode observer (STSMO), which provides robust and efficient state estimation for sensorless control. Traditional SM control methods are resistant to parameter fluctuations and external disturbances but are affected by chattering, which degrades performance and can cause mechanical wear. The STSMO leverages the super twisted algorithm, a second-order SM technique, to minimize chattering while ensuring finite-time convergence and high resilience. In sensorless setups, rotor speed and flux cannot be measured directly, making their accurate estimation crucial for effective ventilation drive control. The STSMO enables real-time control by providing current and voltage estimations. It delivers precise rotor flux and speed estimations across varying motor specifications and load conditions using continuous control rules and observer-based techniques. This paper outlines the mathematical formulation of the STSMO, highlighting its noise resistance, chattering reduction, and rapid convergence. Simulation and experimental findings confirm that the proposed observer enhances sensorless ventilation performance, making it ideal for industrial applications requiring reliability, cost-effectiveness, and accuracy.
1. Introduction
Squirrel cage induction motors (IMs) are widely used in ventilation systems across various applications owing to their cost-effectiveness and mechanical durability. These motors demonstrate remarkable dynamic stability when operated under vector control []. In closed-loop control systems, an input signal representing a controlled state variable is essential for operation. Sensors are commonly employed in vector control systems to gather information on speed along with other state variables []. However, in scenarios involving extreme operational conditions, high-speed applications, or stringent size constraints, sensors such as tachometers and encoders are connected to the motor to acquire speed data. Integrating these devices into the motor reduces system reliability in noisy environments owing to encoder signal degradation. Moreover, additional measures to mitigate noise in such cases increase both design time and costs. Consequently, electric motor control systems primarily utilize sensorless position estimation to address these challenges. Speed sensorless control enables cost savings, simplifies system design, and reduces spatial requirements by eliminating the need for sensor connections [].
Machine-model-based techniques rely on certain variables, such as voltage and current, to estimate speed. These methods allow for reliable and accurate speed estimates, especially at high and medium speeds. The accuracy of the machine model at zero-speed operation is critical to the overall reliability of machine-model-based techniques. Developing reliable estimators for this operational range remains an active area of research within the context of machine-model-based approaches. Previous studies in this field have developed several relevant methods, including the extended Kalman filter [], adaptive flux observer [], reference model adaptive system (MRAS) observer [], and sliding mode observer (SMO) []. Among these, the SMO based on variable structure control theory has recently garnered considerable attention for its desirable attributes, including a fast dynamic response, robustness, insensitivity to parameter fluctuations, and resistance to external distortions.
Recent research has proposed alternatives to the conventional proportional-integral (PI) adaptation mechanism to improve the approximation accuracy of MRAS approaches [,]. A reference model in one MRAS method employs a second-order SMO to estimate rotor flux [,]. Another study has proposed a speed observer utilizing the SM model to measure magnetizing current [].
In most of the above-mentioned studies, an SMO technique was utilized to improve the efficacy of the conventional MRAS methodology. Meanwhile, numerous studies have also introduced fundamental SMO techniques [,,]. These techniques rely on SM functions resulting from the fluxes calculated along the axes in the current estimate. Here, the SM function is integrated into the flux estimation process, enabling rotor speed to be directly derived from the estimated rotor flux and the defined SM functions. The conventional SMO is affected by chattering, which arises from the switching function in the discontinuous control rule.
Consequently, the accuracy of parameter estimation is impacted by the system’s energy consumption and the total harmonic distortion of the motor current, both of which are exacerbated by pronounced chattering. To address these challenges, an enhanced SMO was developed to estimate the position and velocity of IM drives (IMDs) []. In [], the author investigates the asymptotic adaptive appointed-time performance control for electro-hydraulic servo systems affected by unknown, variable linearizable parameters, nonlinear parameters, and disturbances. One study [] proposes a new neural network (NN)-based adaptive dynamic surface asymptotic tracking controller that ensures assured transient performance for n-degrees of freedom (DOF) hydraulic manipulators. This enhanced observer employs a sigmoid function as an alternative to the traditional sign function, effectively reducing chattering. Another study also used the sigmoid function instead of the conventional sign function to estimate rotor position in IMs, reducing chattering []. Previous research has explored various approaches to the SM control law using fuzzy-logic inference systems. A fuzzy-logic-based SMO was established to mitigate chattering and enhance the observer’s resilience to load distortion []. Improved SMOs utilize fuzzy-logic techniques instead of switching functions to estimate rotor flux and speed, effectively eliminating the chattering associated with conventional SMOs []. To address the need for sensorless control in IMs, one study introduced a fuzzy SM speed estimator in which the conventional SMO’s sign function was replaced with a fuzzy-logic system [,]. In [], the author suggested the implementation of sliding mode control (SMC), which relies on the super-twisting observer (STO); hence, achieving second-order sliding mode (SOSM) by continuous control on the designated sliding surface is unfeasible. For the FOC-PMSM drive system, this paper suggests a new speed controller called disturbance-observer-based complementary sliding-mode (DO-CSM) []. One piece of research [] presents a unique control framework for precisely managing the output voltage of floating interleaved boost converters (FIBCs), which have been extensively utilized in fuel cell applications in recent years. The summary of the research studies is shown in the Table 1.

Table 1.
Summarized tabular representation of the research studies.
Meanwhile, high-order SMOs effectively reduce chattering while maintaining system robustness and stability. In a previous study, we adopted a super-twisting slide mode observer (STSMO) to evaluate the speed of IMs. The observer parameters were optimized utilizing the response surface method [] to reduce chattering. In other studies, the STSMO was utilized for speed estimation to achieve the sensorless control of IMs [,]. However, these studies did not evaluate stability, the trade-off between chattering and efficiency under transient conditions, or the impact of observer control law gains on chattering suppression.
This article introduces a novel speed estimate methodology utilizing an STSMO to precisely determine the speed of induction motors (ventilation system) at extremely low and zero speeds while effectively mitigating the chattering issue. Observer gains are adaptively determined based on stability evaluations derived from Lyapunov’s theory. The proposed observer gains are adaptively formulated based on the stability analysis derived from Lyapunov’s theory. The indirect field-oriented control for a sensorless ventilation drive system, utilizing the proposed estimate technique, is developed using MATLAB/Simulink and a LabVIEW-based experimental platform. The modeling and experimental outcomes are shown under several operating scenarios to demonstrate the proposed approach.
2. System Modelling
2.1. IM Modeling
The IM model in the stationary αβ coordinate system is defined by the following equations []:
where p represents the time derivative (d/dt); denotes the stator flux in the αβ orientation; represents the stator current in the αβ orientation; tr denotes the rotor time coefficient; Ls, Lr, and Lm represent the stator, rotor, and mutual inductances, respectively; Rs and Rr denote the stator and rotor resistances, respectively; and denotes the stator voltages in the αβ orientation.
The field-oriented control principle involves aligning the rotor flux vector (Ψr) with the d-axis of the reference frame. The flux angular position (θs) is determined to perform the direct and inverse Park transformations, ensuring that the rotating reference frame is defined as
where is the angle of flux angular position, is the stator speed of the ventilation system, is the reference speed, and is the slip angular speed.
The slip angular speed () can be calculated using the following equation:
2.2. Super-Twisted Slide Mode Observer (ST-SMO) Speed Estimator
The modeling of the super-twisted slide mode observer (ST-SMO) speed observer is as follows.
2.2.1. Super Twisting Algorithm (STA)
The second-order SM technique, known as the STA, provides continuous control based solely on information from the SM surface. The algorithm’s convergence is represented by the rotation of the phase diagram around the origin (S, ). This method employs a control law with two components: u1 and u2. These components represent the discontinuous time derivative and the continuous function, respectively, of the sliding variable, as defined by the following control rule []:
where x denotes the SM surface, a1 and a2 represent control law gains, and Δ1 and Δ2 denote uncertainty terms. The uncertainty terms are bounded as follows:
where δ1 and δ2 are positive constants. Therefore, the system demonstrates asymptotic stability when the gains meet the following specified conditions:
All trajectories converge to the origin within finite time, where this convergence time is given by
Here, V(x) represents a Lyapunov function, x0 denotes the initial state, and λ is a constant dependent on the gains a1 and a2.
The stability of the STA is ensured by the Lyapunov stability theory, as discussed in [].
2.2.2. Current Observer
The sliding surface in the SMO is defined by the state trajectory, which consistently adheres to the switching surface S = 0. A similar control may verify that the state trajectory remains on the sliding surface by ensuring that pS = S = 0.
The surface of the SMO is defined as
where and are the measured stator current components, while and are their estimated counterparts. The estimated currents congregate to the actual currents ( = and = ) as the error trajectories reach the sliding surface (Sn = 0).
where aj > 0 (j = 1, 2, 3, 4) represent the SM control law gains. These gains improve the observer’s robustness by mitigating chattering. These adjustments significantly enhance the observer’s robustness and adaptability. However, higher gain values can exacerbate chattering.
The discontinuous time derivative functions, represented by the first terms of the control law, make a1 and a3 gains more critical than a2 and a4. Among all gains, a1 is more effective in enhancing dynamic performance and reducing chattering. However, the accuracy of estimates depends on the gain a2 [].
2.2.3. Stability Analysis
The stability of the observer is provided by the stability analysis of the current observer by calculating the observer gains a1 and a2. According to Section 2.2.2, (19) and (20) can be calculated as
A Lyapunov function is given as
Lyapunov stability theory maintains that the initial condition mandates the Lyapunov function to be positive definite to fulfill the conditions for a stable current observer, but the succeeding condition demands a negative first derivative.
Equation (26) indicates that the two terms and are negative definite. Consequently, the last two equations should provide negative values, V < 0.
Equations (26) and (27) suggest that the constructed sliding mode surface in (14) is based on the switching functions defined in (27) and (28). The alteration of the slide surface signals results in a modification of and , as delineated in (19) and (20). Therefore, the values of a1 and a2 are established as identical in the specified states. Consequently, (27) and (28) may be restructured as
The subsequent inequalities can be attained by selecting the gains a1 and a2 as exceedingly large positive values. Therefore, the adaptive values of a1 and a2 may be formulated as follows:
Therewith, the values of a1 and a2 can be designed to fulfill the equality, given as
Here, represents a positive number, chosen to satisfy the inequalities (33) and (34) during high-speed operation. To achieve complete adaptation of the gains and the free chattering SMO design, delta can be designated as (). Consequently, the values of gains a1 and a2 are decreased during low-speed operation, thereby eliminating chattering and ensuring stability across varied operating speeds.
2.2.4. Flux and Rotor Speed Observers
By applying Equations (3), (4), (19), and (20), along with the previously stated assumptions, the rotor flux estimate can be expressed as
An alternative representation of the rotor flux estimation, derived from Equations (35) and (36), is given as
Equations (37) and (38) indicate that flux estimation involves the integration of the SM function.
Issues such as DC offset and variations in motor variables affect the pure integration of the SM function, complicating flux estimation. To address this issue, a pure integrator with a negligible negative response is employed as an alternative [].
In this study, using this integrator yields
where ωc represents the cutoff frequency, which has been empirically established to enhance performance throughout the complete speed spectrum. Z(L) denotes the output of the saturation block, which receives the integrator’s output signal, with an amplitude limited to L. The limiting level L must correspond with the actual flux amplitude to efficiently remove the DC element from the output.
The estimated speed is calculated using the following expression:
Figure 1 depicts the configuration of the comprehensive STSMO used for estimating stator current, rotor flux, and rotor speed.
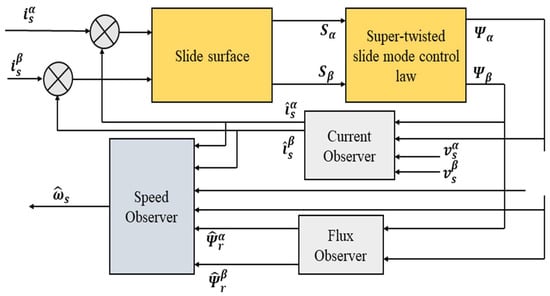
Figure 1.
Schematic view of the proposed STSMO.
3. Experimental Setup and Results
3.1. Experimental Setup
Simulation experiments were conducted in MATLAB/Simulink 2019a to evaluate the performance of the proposed control scheme. The Runge–Kutta technique was used to solve differential equations, with a sampling time of Ts = 10 μs and a converter switching frequency of 15 kHz. The pole-zero cancellation method was employed to determine the control constraints for the vector control method. These parameters were applied consistently in both simulation and experimental validation. The PI parameters for the two current loops were identical in the simulation. For the STSMO controller, the proportional and integral gains were set to kp = 485, ki = 1485 for the current observer and Kp = 4, Ki = 100 for the speed observer.
For a fair comparison, the switching gains were set identically for the simulated and experimental STSMO, with a2 = a4 = 1000. The other gains for the STSMO were set to a1 = a3 = 200. The cutoff frequency in Equation (28) was selected as ωc = 25, and the restraining level L = 0.25 was aligned with the actual flux range. Figure 2 illustrates the vector control system for the sensorless drive based on the STSMO.
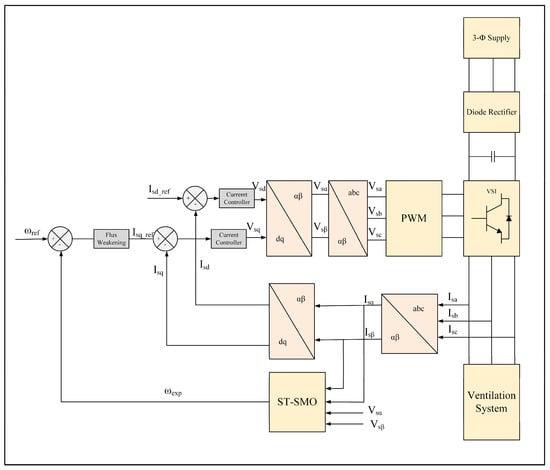
Figure 2.
Control strategy for the sensorless vector control of an IMD using the proposed observer.
The experimental platform, equipped with the STSMO, was designed to evaluate the performance of the speed estimator in controlling the speed of an IMD. The platform consists of a 5.5 kW ventilation system and an AC drive module equipped with an intelligent power element. Figure 2 illustrates the block diagram of our experimental validation setup. The AC drive module comprises a diode rectifier and an insulated-gate-bipolar-transistor-based three-phase inverter. The apparatus utilized in the experiment is depicted in Figure 3.

Figure 3.
Experimental setup for the speed control of an IMD using the STSMO.
3.2. Results and Discussion
In the following cases, the drive was equipped with a sensorless STSMO, where the estimated speed was used for speed control, and the speed sensor was employed primarily for performance assessment. The stability and efficacy of STSMO-based speed observers were evaluated through experiments conducted at low and near-zero speeds, as well as across a broad range of rotor speeds.
- Case 1: Sensorless vector control encounters challenges at near-zero speed during no-load operation. Figure 4a compares the performance of the traditional MRAS with the STSMO-based MRAS. Notably, the STSMO-based MRAS demonstrates stable steady-state performance under the given conditions.
- Case 2: This scenario examines the system’s response to a predetermined reference speed, which challenges the drive’s ability to maintain field orientation at low stator frequencies. The corresponding results are illustrated in Figure 5. As depicted in Figure 5b, the standard SMO demonstrates unsteady performance, with fluctuations observed between −140 and 130 rpm. In contrast, the STSMO-based MRAS achieves stable operation without oscillations (Figure 5a).
- Case 3: This scenario evaluates the encoderless drive’s performance between reference speeds of 345 rpm and −200 rpm. The results for the proposed model are depicted in Figure 6a, while Figure 6b presents the results for the traditional SMO technique. Compared to the traditional SMO with a PI controller, the proposed STSMO-based MRAS achieves consistent performance with minimal steady-state error.
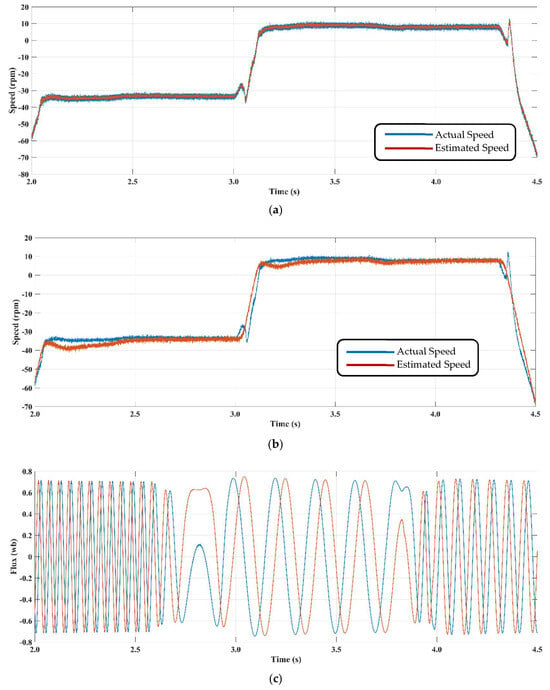
Figure 4.
(a) Sensorless control performance using the proposed STSMO model in the speed range of −35 rpm to 5 rpm. (b) Sensorless control performance using the conventional SMO model in the speed range of −35 rpm to 5 rpm. (c) Change of the flux during the change of the speed from −35 rpm to 5 rpm in proposed method.
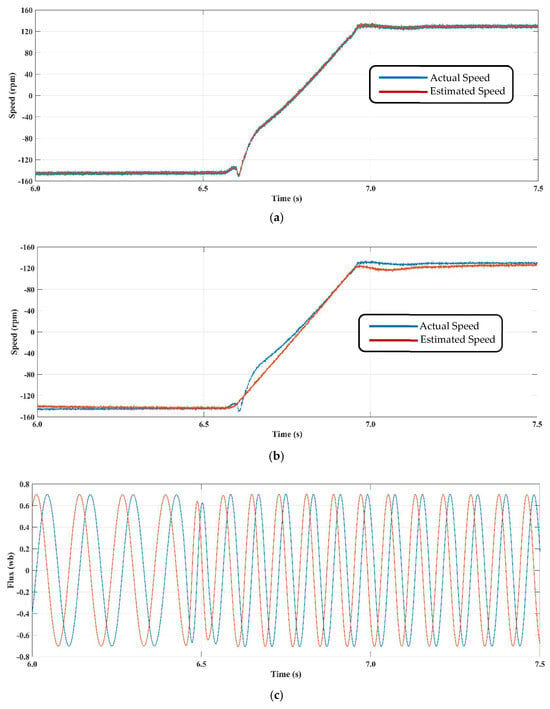
Figure 5.
(a) Sensorless control performance using the proposed STSMO model in the speed range of −140 to 130 rpm. (b) Sensorless control performance using the conventional SMO model in the speed range of −150 to 120 rpm. (c) Change of the flux during the change of the speed from −35 rpm to 5 rpm in proposed method.
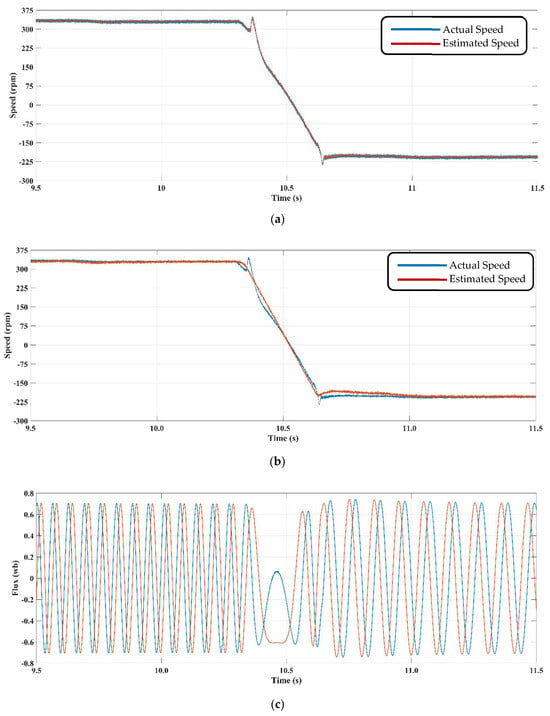
Figure 6.
(a) Sensorless control performance using the proposed STSMO model in the 345 rpm and −200 rpm speed range. (b) Sensorless control performance using the conventional SMO model in the 345 rpm and −200 rpm speed range. (c) Change of the flux during the change of speed from 345 rpm and −200 rpm in the proposed method.
The results indicate that the STSMO-based speed estimator for the ventilation system drive and control algorithm demonstrates improved performance in the low- and medium-speed operational ranges. The efficacy and reliability of the proposed algorithm are validated using various operational cases.
Figure 7 clearly shows that the proposed method has a low THD value of current profile. Table 2 shows the Gain sweep analysis at a2 = 500, 1000, 1500, and 2000, and it clearly demontrates that a2 = 1000 has low convergence time and chattering index.
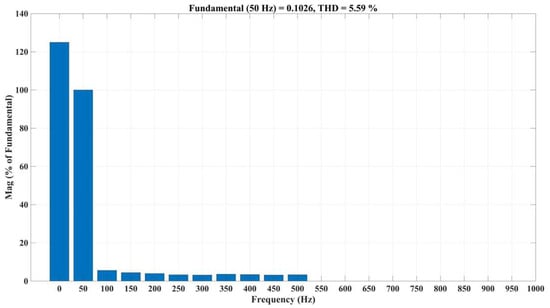
Figure 7.
The total harmonic distortion curve for the proposed method.

Table 2.
Gain sweep analysis at a2 = 500, 1000, 1500, 2000.
Table 3 compares the performance of the proposed model with that of other speed estimators. This investigation focuses on the proposed model’s ability to track speed at low operating speeds. The STSMO-based drive outperforms the previously proposed speed estimators in terms of complexity, robustness, and the minimization of maximum speed estimation error. Consequently, the STSMO is more efficient and reliable than alternative approaches for low-power, high-performance, and cost-effective industrial applications. Our findings conclude that the STSMO model outperforms other speed observers in the low- and medium-speed ranges.

Table 3.
Performance comparison between the proposed speed estimator and other previously proposed estimators.
Table 4 compares the performance of the ST-SMO controller with that of the traditional SMO controller. The results highlight the quick response of the proposed model. While some performance aspects of both methods are similar, the proposed model exhibits superior attributes compared to the traditional SMO controller. In addition to this, the ability of the proposed model to track speed under various operating conditions was evaluated. The findings demonstrate that the STSMO-based drive outperforms the traditional SMO-based system in speed tracking at low speeds, load disturbance rejection, and resistance to parameter fluctuations. These advantages make the proposed model reliable and accurate for industrial applications requiring superior performance, low power consumption, and cost efficiency. To further extend the results, the analysis by incorporating quantitative time-frequency analysis techniques to evaluate and compare the chattering characteristics of various methods is given in Table 5.

Table 4.
Performance comparison of the proposed model and traditional SMO-based vector control.

Table 5.
Quantitative time-frequency analysis techniques to evaluate and compare the chattering characteristics.
4. Conclusions
This study proposes a novel STSMO-based controller to regulate the speed of a ventilation system. The proposed approach overcomes the difficulty in balancing estimation precision with minimizing chattering at low and zero velocities. The performance of the observer is significantly influenced by the coefficients of the SMC rule. Adaptive gain values were derived from the stability analysis of the STA to optimize these coefficients. This enabled quick convergence of predicted variables, improving precision and minimizing chattering at low and zero operating speeds. The results from experiments and simulations indicate that the proposed STSMO model exhibits enhanced efficiency and performance. The findings validate the fact that the proposed observer achieves high estimation precision while effectively suppressing chatter. The research is further extended to the following:
- Further optimization of STSMO performance, such as adaptive tuning strategies or integration with machine-learning algorithms to enhance real-time robustness and adaptability.
- Application of the proposed STSMO to different motor control systems, including permanent magnet synchronous motors (PMSMs) and brushless DC motors (BLDCs), to explore its generalization capability across motor types.
- Hardware implementation considerations, focusing on computational efficiency and implementation on low-cost microcontrollers for industrial use cases.
Author Contributions
All authors contributed to this paper: P. and B.Y. conceived the idea, performed the analysis, and designed the simulations; P. carried out the numerical simulations; and P. and B.Y. co-wrote the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Research Foundation of Korea under Grant NRF-2021R1I1A2045721.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Prince; Hati, A.S.; Chakrabarti, P.; Abawajy, J.H.; Keong, N.W. Development of energy efficient drive for ventilation system using recurrent neural network. Neural Comput. Appl. 2021, 33, 8659–8668. [Google Scholar] [CrossRef]
- Bose, B.K. Power Electronics and AC Drives; Prentice-Hall: Englewood Cliffs, NJ, USA, 1986; 416p. [Google Scholar]
- Prince; Hati, A.S. Temperature and Humidity Dependent MRAS Based Speed Estimation Technique for Induction Motor Used in Mine Ventilation Drive. J. Min. Sci. 2021, 57, 842–851. [Google Scholar] [CrossRef]
- Kumar, P.; Hati, A.S. Sensor-less speed control of ventilation system using extended Kalman filter for high performance. In Proceedings of the 2021 IEEE 8th Uttar Pradesh Section International Conference on Electrical, Electronics and Computer Engineering (UPCON), Dehradun, India, 11–13 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Vas, P. Sensorless Vector and Direct Torque Control; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Orlowska-Kowalska, T.; Dybkowski, M. Stator-current-based MRAS estimator for a wide range speed-sensorless induction-motor drive. IEEE Trans. Ind. Electron. 2009, 57, 1296–1308. [Google Scholar] [CrossRef]
- Ammar, A.; Bourek, A.; Benakcha, A. Sensorless SVM-direct torque control for induction motor drive using sliding mode observers. J. Control. Autom. Electr. Syst. 2017, 28, 189–202. [Google Scholar] [CrossRef]
- Wu, L.; Liu, J.; Vazquez, S.; Mazumder, S.K. Sliding mode control in power converters and drives: A review. IEEE/CAA J. Autom. Sin. 2021, 9, 392–406. [Google Scholar] [CrossRef]
- Bıçak, A.; Gelen, A. Modified Super-Twisting Algorithm-Based Model Reference Adaptive Observer for Sensorless Control of the Interior Permanent-Magnet Synchronous Motor in Electric Vehicles. Machines 2023, 11, 871. [Google Scholar] [CrossRef]
- Lu, Y.; Tan, C.; Ge, W.; Zhao, Y.; Wang, G. Adaptive disturbance observer-based improved super-twisting sliding mode control for electromagnetic direct-drive pump. Smart Mater. Struct. 2022, 32, 017001. [Google Scholar] [CrossRef]
- Yalavarthi, A.; Singh, B. SMO-based position sensorless SRM drive for battery-supported PV submersible pumps. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 3917–3926. [Google Scholar] [CrossRef]
- Sami, I.; Ullah, S.; Basit, A.; Ullah, N.; Ro, J.-S. Integral super twisting sliding mode based sensorless predictive torque control of induction motor. IEEE Access 2020, 8, 186740–186755. [Google Scholar] [CrossRef]
- Wang, H.; Ge, X.; Liu, Y.-C. Second-order sliding-mode MRAS observer-based sensorless vector control of linear induction motor drives for medium-low speed Maglev applications. IEEE Trans. Ind. Electron. 2018, 65, 9938–9952. [Google Scholar] [CrossRef]
- Nurettin, A.; İnanç, N. Sensorless vector control for induction motor drive at very low and zero speeds based on an adaptive-gain super-twisting sliding mode observer. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 4332–4339. [Google Scholar] [CrossRef]
- Lin, S.; Zhang, W. An adaptive sliding-mode observer with a tangent function-based PLL structure for position sensorless PMSM drives. Int. J. Electr. Power Energy Syst. 2017, 88, 63–74. [Google Scholar] [CrossRef]
- Yang, X.; Ge, Y.; Zhu, W.; Deng, W.; Zhao, X.; Yao, J. Adaptive Motion Control for Electro-hydraulic Servo Systems with Appointed-Time Performance. IEEE/ASME Trans. Mechatron. 2025; early access. [Google Scholar]
- Yang, X.; Deng, W.; Yao, J. Neural adaptive dynamic surface asymptotic tracking control of hydraulic manipulators with guaranteed transient performance. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 7339–7349. [Google Scholar] [CrossRef] [PubMed]
- Bist, A.; Jadhav, S.V. Sensorless control based on sliding mode observer for pmsm drive. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 16–19 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Li, Z.; Wang, J.; Wang, S.; Feng, S.; Zhu, Y.; Sun, H. Design of sensorless speed control system for permanent magnet linear synchronous motor based on fuzzy super-twisted sliding mode observer. Electronics 2022, 11, 1394. [Google Scholar] [CrossRef]
- Wang, C.; Cao, D. New sensorless speed control of a hybrid stepper motor based on fuzzy sliding mode observer. Energies 2020, 13, 4939. [Google Scholar] [CrossRef]
- Saghafinia, A.; Ping, H.W.; Uddin, M.N.; Gaeid, K.S. Adaptive fuzzy sliding-mode control into chattering-free IM drive. IEEE Trans. Ind. Appl. 2014, 51, 692–701. [Google Scholar] [CrossRef]
- Chalanga, A.; Kamal, S.; Fridman, L.M.; Bandyopadhyay, B.; Moreno, J.A. Implementation of super-twisting control: Super-twisting and higher order sliding-mode observer-based approaches. IEEE Trans. Ind. Electron. 2016, 63, 3677–3685. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Laghrouche, S.; Depernet, D.; Djerdir, A.; Cirrincione, M. Disturbance-observer-based complementary sliding-mode speed control for PMSM drives: A super-twisting sliding-mode observer-based approach. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 5416–5428. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Ahn, K.K. An improved voltage regulation performance of floating interleaved boost converters for fuel cell applications subject to input variation and load change. Appl. Sci. 2022, 12, 11501. [Google Scholar] [CrossRef]
- Wogi, L.; Morawiec, M.; Ayana, T. Sensorless Control of Induction Motor Based on Super-Twisting Sliding Mode Observer with Speed Convergence Improvement. IEEE Access 2024, 12, 74239–74250. [Google Scholar] [CrossRef]
- Huangfu, L.; Chen, C.; Zhang, T. A sensorless control scheme based on fractional order super-twisting algorithm and improved FLL for PMSM. Adv. Mech. Eng. 2024, 16, 16878132241282013. [Google Scholar] [CrossRef]
- Mishra, A.; Choudhary, P. Speed control of an induction motor by using indirect vector control method. Int. J. Emerg. Technol. Adv. Eng. 2012, 2, 144–150. [Google Scholar]
- Beerens, R.; Bisoffi, A.; Zaccarian, L.; Heemels, W.P.; Nijmeijer, H.; van de Wouw, N. Hybrid PID control for transient performance improvement of motion systems with friction. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 539–544. [Google Scholar]
- Lascu, C.; Andreescu, G.-D. Sliding-mode observer and improved integrator with DC-offset compensation for flux estimation in sensorless-controlled induction motors. IEEE Trans. Ind. Electron. 2006, 53, 785–794. [Google Scholar] [CrossRef]
- Choudhary, M.S.; Saqi, M.S.; Javed, M.R.; Gelani, H.E. Solar powered space vector pulse width modulation based induction motor drive for industry applications. Bull. Electr. Eng. Inform. 2022, 11, 1828–1836. [Google Scholar] [CrossRef]
- Savitha, P.; Divakar, B. Performance comparison of Rotor Flux based and Back EMF Based Model Reference Adaptive System Speed Estimator for 3 Phase Induction Motor. In Proceedings of the2023 IEEE International Conference on Distributed Computing, VLSI, Electrical Circuits and Robotics (DISCOVER), Mangalore, India, 13–14 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 127–133. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).