A Partitioned Rigid Element–Interface Element–Finite Element Method (PRE-IE-FE) for the Slope Stability Analysis of Soil–Rock Binary Structures
Abstract
1. Introduction
2. Common Destabilization Modes of Slopes with Soil–Rock Dichotomies
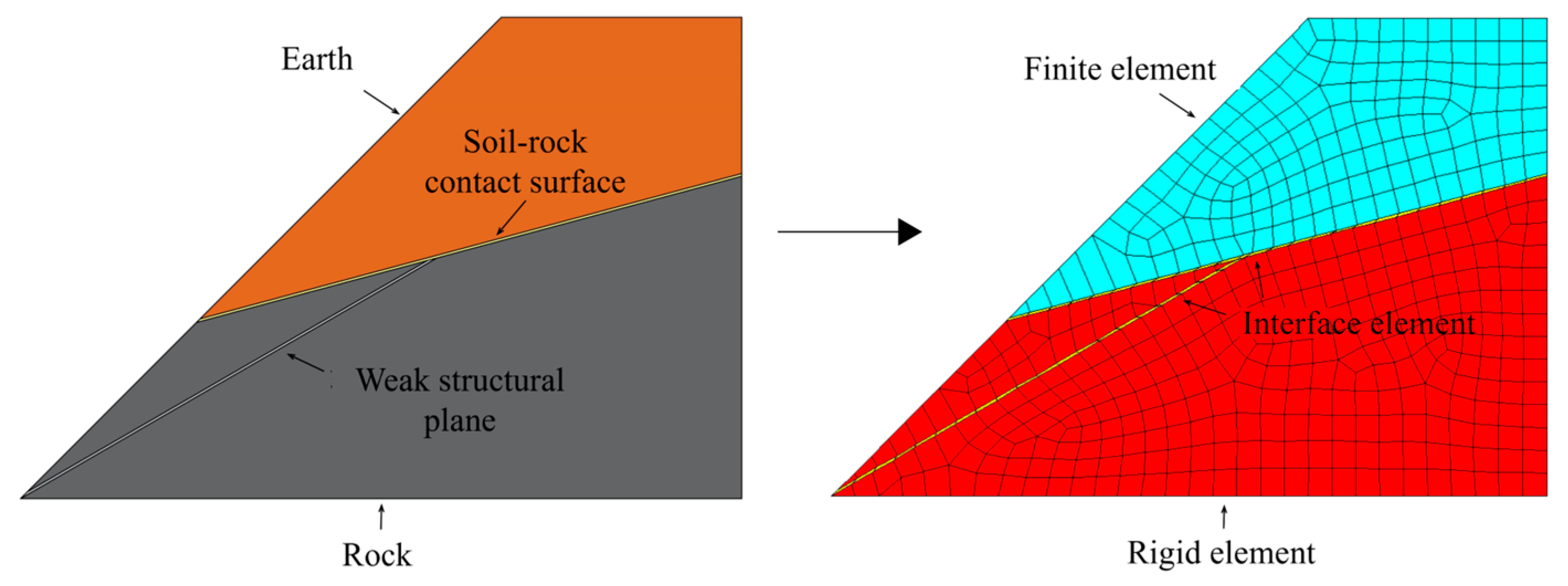
3. PRE-IE-FE
3.1. Core Equations of the PRE-IE Method
3.1.1. Equations of Rigid Element
3.1.2. Equations of Interface Element
3.1.3. Equations of PRE-IE
3.2. The Governing Equations for PRE-IE-FE
3.2.1. Governing Equations of Thin-Layer Interface Elements
3.2.2. Assembly of the Global Stiffness Matrix
3.2.3. Coupled PRE-IE-FE Governing Equations
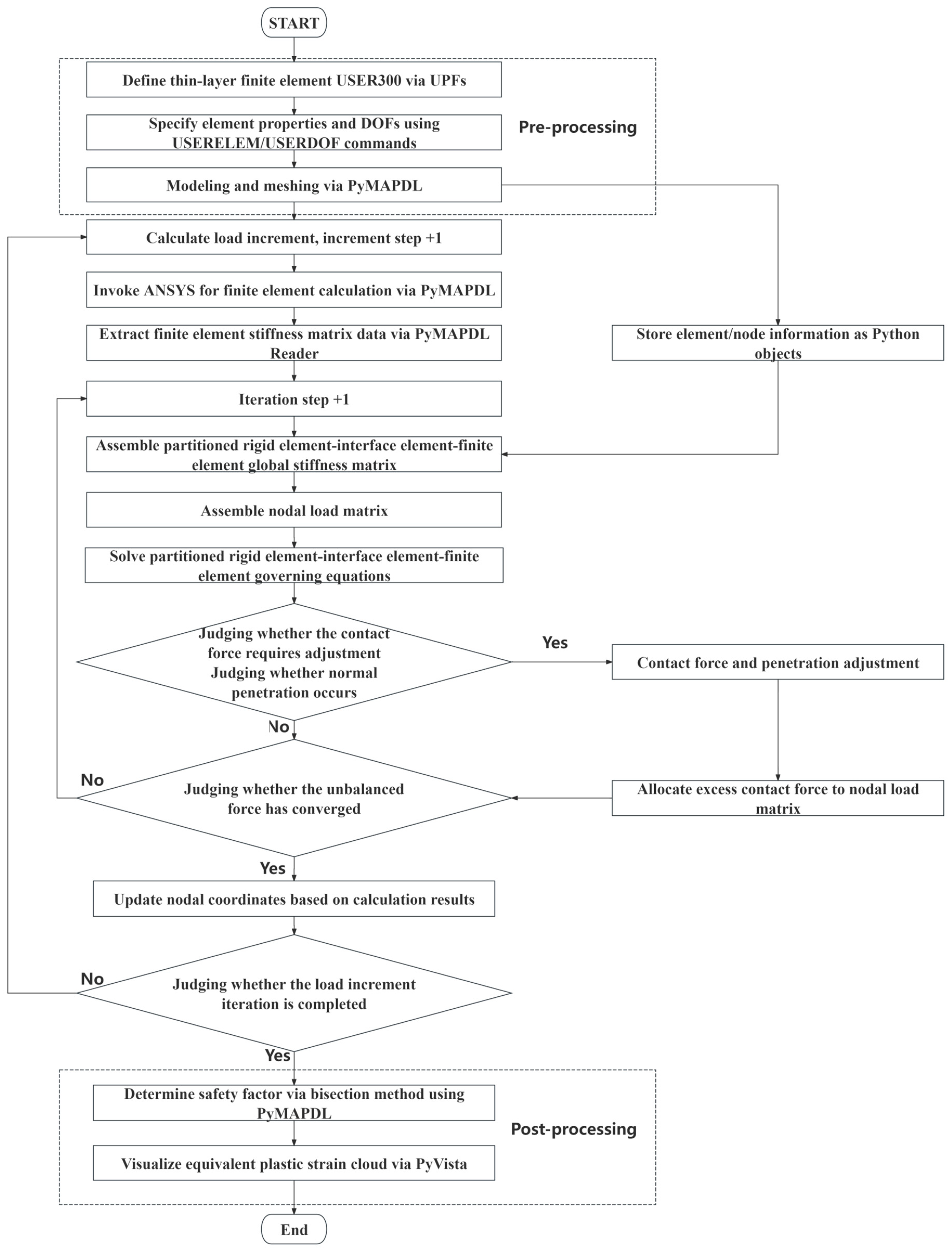
3.3. Calculation Process and Program Development for PRE-IE-FE
3.3.1. Customized Units
3.3.2. Modeling and Meshing
3.3.3. Numerical Calculation
3.3.4. Reprocess
4. Slope Stability Analysis of Soil–Rock Binary Structures Based on the PRE-IE-FE Strength Reduction Method
4.1. Strength Reduction Method
4.2. Instability Criterion for Slopes with Soil–Rock Binary Structure
4.3. Safety Factor Search Method
4.3.1. Identify Potential Slip Surfaces
4.3.2. Determine Strength Reduction Factor Interval
4.3.3. Bisection Method for Safety Factor Search
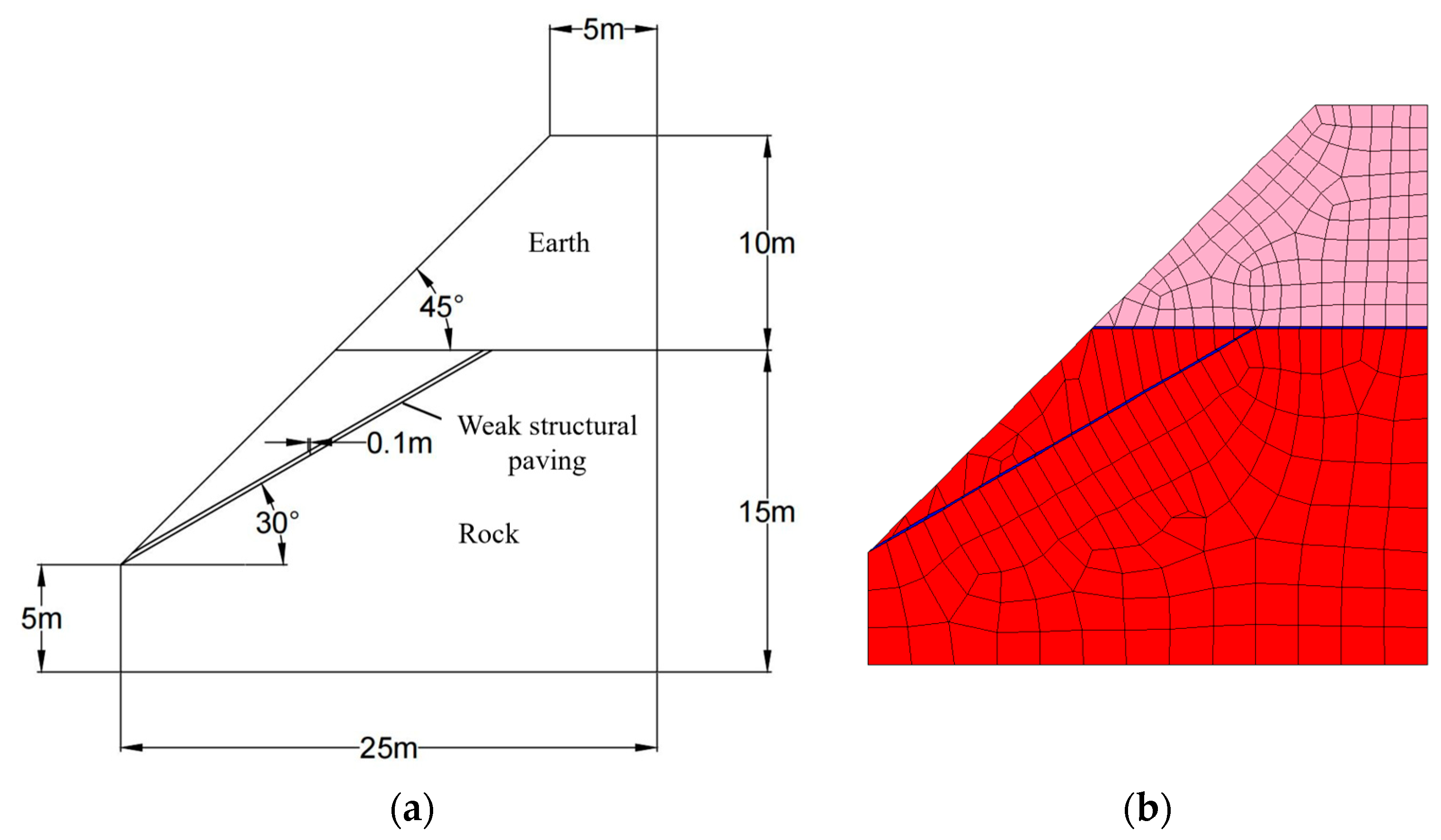
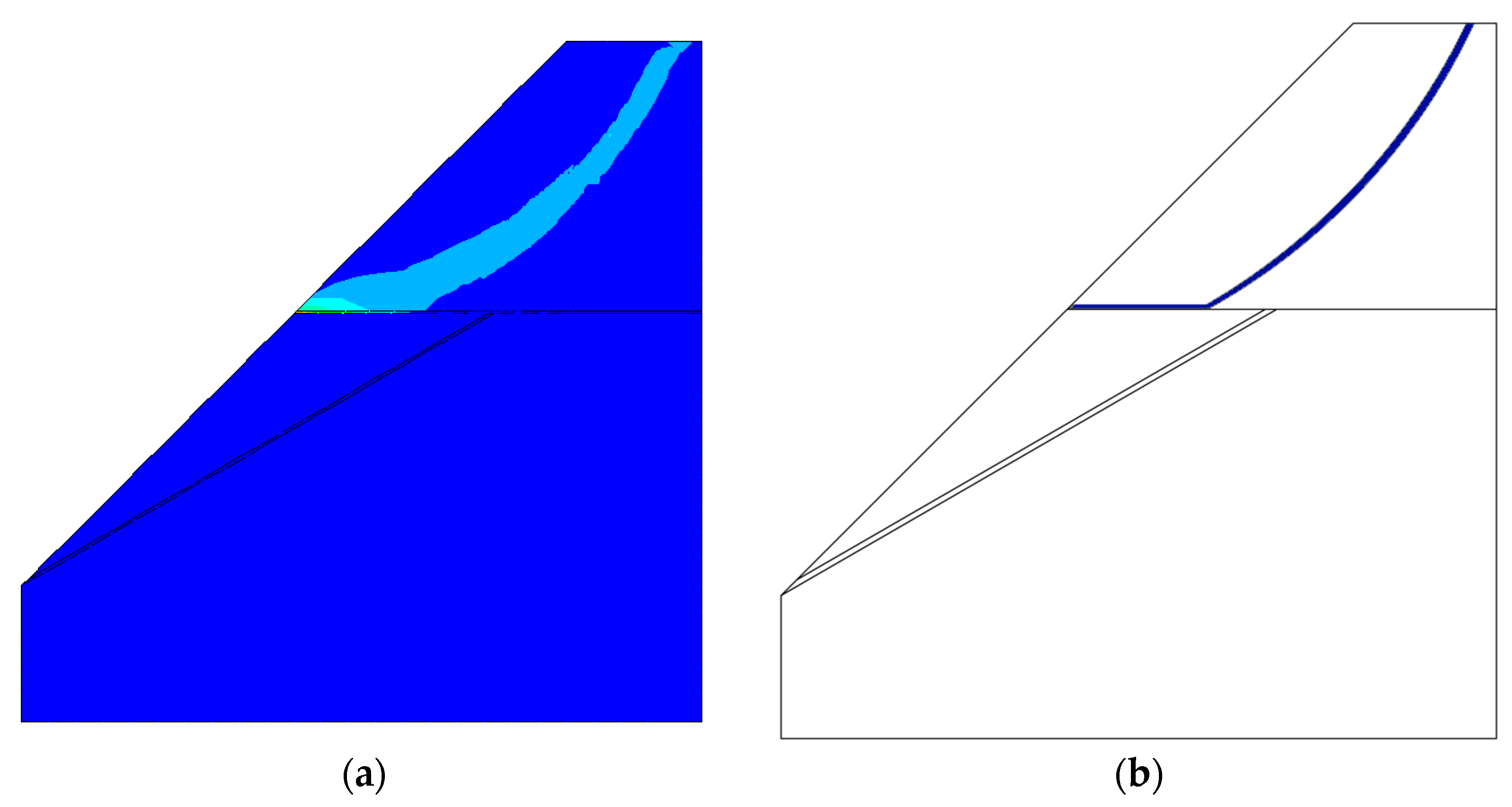
4.4. Example of Slope Stability Analysis of Soil–Rock Binary Structure
5. Conclusions
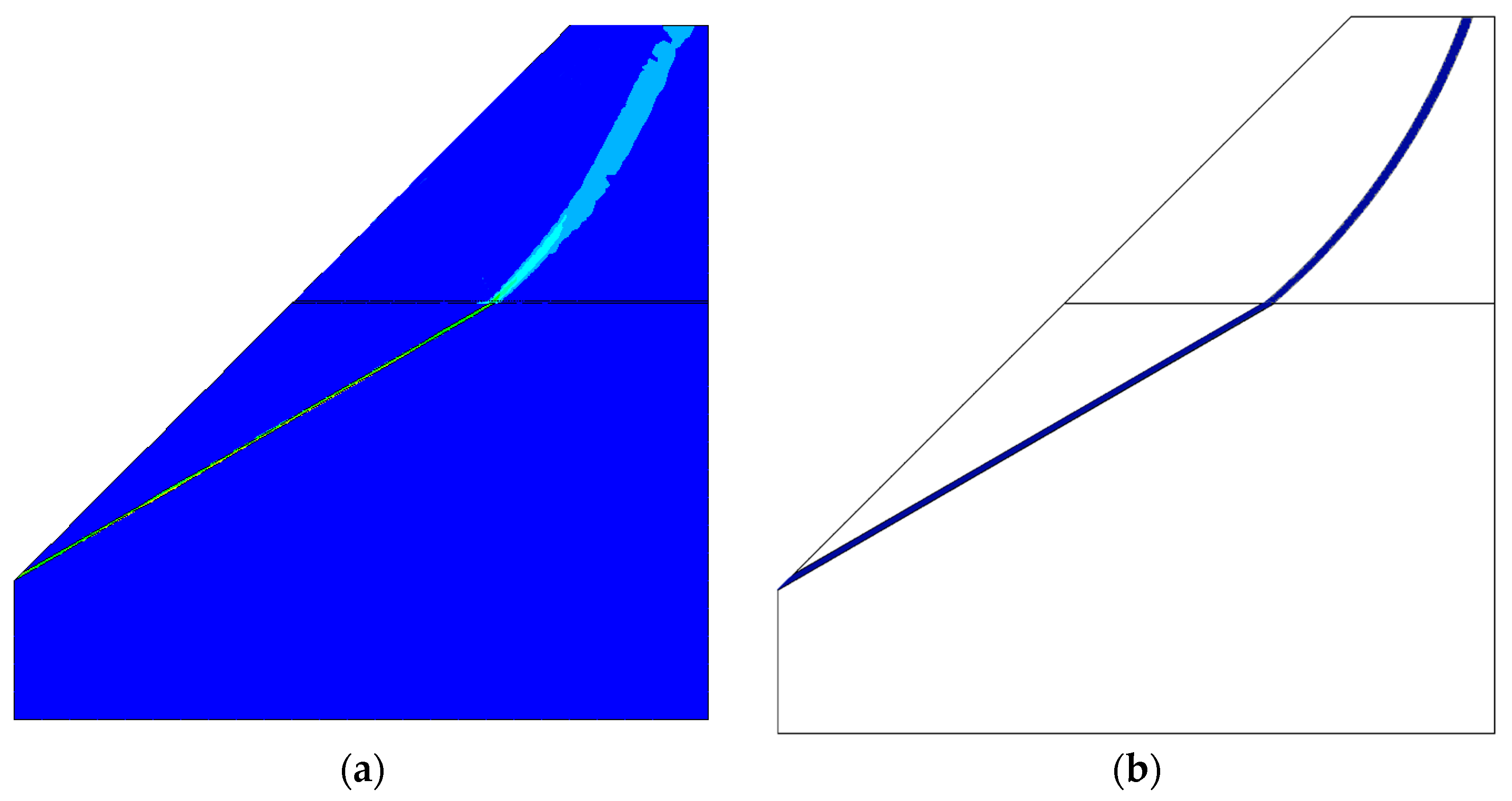
- Type I slopes (loose soil overlying stable bedrock) exhibit composite failure, involving rotational sliding within the soil and linear sliding along the soil–rock interface. Type II slopes (rock masses containing weak structural surfaces) destabilize via planar sliding along these weak structural surfaces, which drives rotational sliding of the overlying soil and forms composite slip surfaces.
- The PRE-IE-FE method couples the overlying soil (modeled as a continuous medium using the FEM) and the underlying rock (simulated as discontinuous rigid elements) through interface elements. This framework simultaneously captures soil elastic deformation and rock contact nonlinearity while maintaining computational efficiency.
- Leveraging ANSYS secondary development and a Python-based hybrid programming framework, a partitioned dynamic stiffness matrix update strategy significantly enhances solving efficiency. Integration with the strength reduction method and a numerical non-convergence criterion enables the rapid determination of safety factors and the visualization of sliding surfaces.
- The safety factors derived from PRE-IE-FE demonstrate close agreement with results obtained from established methods, such as limit equilibrium analysis and FLAC, confirming the method’s reliability in the stability assessment of soil–rock binary slopes.
6. Limitations and Future Work
6.1. Limitations
- All case studies are confined to 2D plane-strain conditions. Extending to 3D would require redefining rigid-body degrees of freedom (e.g., six-DOF motion) and implementing hexahedral interface elements, which would significantly increase computational complexity. Additionally, the framework focuses on static equilibrium, excluding dynamic loads (e.g., seismic effects).
- The method assumes isotropic rock properties, neglecting directional anisotropy (e.g., bedding or joint effects). Furthermore, the displacement compatibility equations for interface elements are derived under small-deformation theory, which may fail to capture geometric nonlinearities in large-displacement scenarios.
- The numerical robustness of the PRE-IE-FE method is supported by its inheritance of mesh-stable characteristics from the original PRE-IE framework [15], where validation cases (e.g., symmetric wedge models) showed consistent results across mesh refinements, indicating minimal sensitivity to volumetric discretization. However, a dedicated mesh-dependency analysis for soil–rock binary slopes was not performed. Additionally, the small-deformation assumption for interface compatibility limits its applicability to large-displacement scenarios, necessitating future integration of adaptive remeshing or finite deformation theory.
6.2. Future Work
- Extend the method to 3D spatial and dynamic problems.
- Incorporate anisotropic strength criteria for structural planes.
- Conduct comprehensive mesh-dependency and large-deformation analyses.
- Validate against field monitoring data for practical engineering applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ministry of Water Resources of the People’s Republic of China. Design Specification for Slopes of Water Conservancy and Hydropower Projects; SL 386-2007; China Water & Power Press: Beijing, China, 2007.
- Sun, W. Study of Instability Mechanism and Intelligent Pre-Warning for Cutting Slope with Soil-Rock Binary Structure. Ph.D. Thesis, Chang’an University, Xi’an, China, 2020. [Google Scholar] [CrossRef]
- Wei, Y.; Qiu, Y. A Brief Analysis of Road Slope Classification Based on Damage Mechanism and Damage Mode. China Investig. Des. 2019, 2, 80–82. [Google Scholar]
- Kou, R. Identification and Determination of Potential Slip Surfaces on Binary Structure Slopes. Ph.D. Thesis, Kunming University of Science and Technology, Kunming, China, 2016. [Google Scholar]
- Tang, X.; Zheng, Y.; Tang, H. Numerical Analysis on the Evolutionary Features of Deformation and Failure Modes of Slope. Appl. Mech. Mater. 2012, 204, 144–154. [Google Scholar] [CrossRef]
- Zhao, L.; Li, T.; Niu, Z. A Mixed finite element method for contact problems with friction and initial gaps. Chin. J. Geotech. Eng. 2006, 28, 2015–2018. [Google Scholar]
- Li, T.; Liu, X.; Zhao, L. An interactive method of interface boundary elements and partitioned finite elements for local continuous/discontinuous deformation problems. Int. J. Numer. Methods Eng. 2014, 100, 534–554. [Google Scholar] [CrossRef]
- Ren, Q. Rigid Body Element Method and Its Application in Stability Analysis of Rock Mass. J. Hohai Univ. (Nat. Sci.) 1995, 23, 1–7. [Google Scholar]
- Ren, Q.; Yu, T. Theory and calculating model of block element method. Eng. Mech. 1999, 16, 67–77. [Google Scholar]
- Zhuo, J. Interface Element Method for Mechanical Problems in Discontinuous Media; Science Press: Beijing, China, 2000. [Google Scholar]
- Zhang, Q.; Zhuo, J. Interface element method and criterion for stability analysis of high slopes in three gorges shiplock. Chin. J. Rock Mech. Eng. 2000, 19, 285–288. [Google Scholar]
- Qi, H.; Li, T.; Liu, X.; Zhao, L.; He, J.; Li, X. A fast local nonlinear solution technique based on the partitioned finite element and interface element method. Int. J. Numer. Methods Eng. 2022, 123, 2214–2236. [Google Scholar] [CrossRef]
- Fan, S.; Li, T.; Liu, X.; Zhao, L.; Niu, Z.; Qi, H. A hybrid algorithm of partitioned finite element and interface element for dynamic contact problems with discontinuous deformation. Comput. Geotech. 2018, 101, 130–140. [Google Scholar] [CrossRef]
- Li, T.; He, J.; Zhao, L.; Li, X.; Niu, Z. Strength reduction method for stability analysis of local discontinuous rock mass with iterative method of partitioned finite element and interface boundary element. Math. Probl. Eng. 2015, 2015, 872834. [Google Scholar] [CrossRef]
- Sheng, T.; Li, T.; Liu, X.; Qi, H. A partitioned rigid-element and interface-element method for rock-slope-stability analysis. Appl. Sci. 2023, 13, 7301. [Google Scholar] [CrossRef]
- Wu, S. Stability Analyses and Mitigation Measures of Typical Slopes in Zhao-Yin Expressway. Soil Eng. Found. 2013, 27, 29–31. [Google Scholar]
- Zhang, L.; Tang, L.; Luo, K. Stability Analysis for Soil-Rock Composite Slope. Geotech. Eng. Tech. 2008, 22, 119–122. [Google Scholar]
- Zhu, D. Revival Mechanism and Deformation Prediction of Typical Accumulative Landslide in the Three Gorges Reservoir. Ph.D. Thesis, China University of Geosciences, Wuhan, China, 2010. [Google Scholar]
- Zou, D.; Zheng, H. Fast Lagrangian Method and Its Applications in Slope Stability Analysis. Min. Res. Dev. 2005, 25, 80–83. [Google Scholar] [CrossRef]
- Zhao, L.; Li, T.; Yang, Q. Numerical simulation method for instability motion and initial surge of soil bank slopes under earthquake action. J. Hydroelectr. 2011, 30, 104–108. [Google Scholar]
- Cheng, L.; Liu, Y.; Yang, Q.; Pan, Y.; Lv, Z. Mechanism and numerical simulation of reservoir slope deformation during impounding of high arch dams based on nonlinear FEM. Comput. Geotech. 2017, 81, 143–154. [Google Scholar] [CrossRef]
- Lin, C.; Li, T.; Zhao, L.; Zhang, Z.; Lin, C.; Liu, X.; Niu, Z. Reinforcement effects and safety monitoring index for high steep slopes: A case study in China. Eng. Geol. 2020, 279, 105861. [Google Scholar] [CrossRef]
- Su, Z.; Shao, L. Three-dimensional slope stability based on the finite element limit equilibrium method. Chin. J. Eng. 2022, 44, 2048–2056. [Google Scholar] [CrossRef]
- Yan, Q.; Lian, X.; Ling, J. Time series finite element analysis of support of slope excavation. J. Traffic Transp. Eng. 2020, 20, 61–71. [Google Scholar] [CrossRef]
- Wang, X. Finite Element Method; Tsinghua University Press: Beijing, China, 2003. [Google Scholar]
- Shi, F. ANSYS Secondary Development and Application Examples in Detail; China Water & Power Press: Beijing, China, 2012. [Google Scholar]

| Criteria for Classification | Typology | Note |
|---|---|---|
| Morphology of soil–rock contact surfaces | Linear contact surface type | The shape of the soil–rock contact surface is straight |
| Folded contact surface type | The shape of the soil–rock contact surface is folded | |
| Arc contact surface type | The shape of the soil–rock contact surface is curved | |
| Irregular contact surface type | Irregular shape of soil–rock contact surfaces | |
| Properties of soil–rock contact surfaces | Horizontal contact surface type | Approximate level of soil–rock contact surface |
| Gently tilting contact surface type | Soil–rock contact surface angle < Integrated slope angle for slopes | |
| Steeply inclined contact surface type | Soil–rock contact surface angle ≥ Integrated slope angle for slopes | |
| Anti-dumping contact surface type | Soil–rock contact surface inclination is opposite to slope inclination | |
| Oblique contact surface type | Soil–rock contact surface inclination at an angle to the slope inclination | |
| Tendency of the top face of the slope | Top climbing type | Slope top surface inclination is the same as the slope inclination |
| Flat-topped | The top surface of the slope is approximately horizontal | |
| Top downhill type | The slope top surface tends to be the opposite of the side slope tendency | |
| Thickness of cladding | Thin layer coverage type | Cladding thickness < 10 m |
| Medium-thickness cover type | 10 m ≤ Cladding thickness < 20 m | |
| Thick cover type | Cladding thickness ≥ 20 m | |
| Number of steps in overburden excavation | Single-stage coverage type | The number of steps in the overburden excavation is 1 |
| Two-stage coverage type | The number of steps in the overburden excavation is 2 | |
| Multi-level coverage type | The number of steps in the overburden excavation is >2 |
| Slope Structure | Slope Modeling | Destabilization Mode | Sliding Surface Pattern |
|---|---|---|---|
| Upper portion is stockpiled soil Stable bedrock below |  |  | 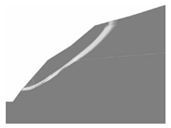 |
| The upper part is an accumulation of soil or fully weathered rock Lower part is a rock body with weak structural surfaces |  |  |  |
| Methodologies | PRE-IE-FE | Simplified Bishop Method | Janbu Method | Morgenstern–Price Method |
|---|---|---|---|---|
| safety factor | 0.832 | 0.833 | 0.825 | 0.829 |
| Ethodologies | PRE-IE-FE | PFE-IE | FDM |
|---|---|---|---|
| safety factor | 1.285 | 1.255 | 1.272 |
| computation time | <1 min | —— | 4 min |
| Software | Version | Organization/Source |
|---|---|---|
| Python | 3.9 | Python Software Foundation, https://www.python.org |
| Ansys Mechanical | 2020 R1 | Ansys Inc., Canonsburg, PA, USA |
| PyMAPDL | 0.63.2 | PyPI, https://pypi.org/project/ansys-mapdl-core/ (accessed on 29 March 2025). |
| PyVista | 0.42.0 | PyPI, https://pypi.org/project/pyvista/ (accessed on 29 March 2025). |
| FLAC | 1.4.3 | Xiph Foundation, https://xiph.org/flac/ (accessed on 29 March 2025). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Sheng, T.; Peng, Y.; Wang, J.; Hu, B. A Partitioned Rigid Element–Interface Element–Finite Element Method (PRE-IE-FE) for the Slope Stability Analysis of Soil–Rock Binary Structures. Appl. Sci. 2025, 15, 4903. https://doi.org/10.3390/app15094903
Xu J, Sheng T, Peng Y, Wang J, Hu B. A Partitioned Rigid Element–Interface Element–Finite Element Method (PRE-IE-FE) for the Slope Stability Analysis of Soil–Rock Binary Structures. Applied Sciences. 2025; 15(9):4903. https://doi.org/10.3390/app15094903
Chicago/Turabian StyleXu, Jianrong, Taozhen Sheng, Yu Peng, Jianxin Wang, and Boyang Hu. 2025. "A Partitioned Rigid Element–Interface Element–Finite Element Method (PRE-IE-FE) for the Slope Stability Analysis of Soil–Rock Binary Structures" Applied Sciences 15, no. 9: 4903. https://doi.org/10.3390/app15094903
APA StyleXu, J., Sheng, T., Peng, Y., Wang, J., & Hu, B. (2025). A Partitioned Rigid Element–Interface Element–Finite Element Method (PRE-IE-FE) for the Slope Stability Analysis of Soil–Rock Binary Structures. Applied Sciences, 15(9), 4903. https://doi.org/10.3390/app15094903





