Study of Concrete Moisture Transfer Characteristics in the Presence of the Concrete Micro–Meso Structure Effect

Abstract

Water and water transfer are the keys of the concrete durability problem; the non-uniform moisture transfer caused by the concrete micro–meso structure has a great effect on the drying shrinkage crack, transfers of inimical ions, etc. For the non-uniform moisture transfer problem, a multi-scale concrete moisture diffusion coefficient model which can consider the effect of Knudsen diffusion was established and verified based on the moisture transfer mechanism of porous medium and the concrete micro–meso structure characteristics. The effects of pore structure, the interfacial transition zone, and aggregate on the concrete moisture diffusion coefficient were studied based on the model, and the non-uniform moisture transfer characteristics and differences in concrete wetting and drying were analyzed via simulations. The results show that the moisture transfers more easily via the pores ranging from 10 nm to 100 nm, the effect of Knudsen diffusion increases with the increasing water-to-cement ratio and decreases with the increasing relative moisture, and Knudsen diffusion is also an effect factor which causes the moisture diffusion coefficient to increase with the increase in moisture. Moisture transfers more easily via the interfacial transition zone at the meso-level and causes a “flow around” phenomenon. The “S” growth relation between the moisture diffusion coefficient and relative moisture can consider the differences in the moisture diffusion coefficient under wetting and drying conditions to a certain extent, which makes concrete wet faster than dry. In addition, the jumping growth of the moisture diffusion coefficient in the relation also leads to an “inflection point” in the concrete moisture distribution.

1. Introduction

The moisture migration and drying shrinkage cracking of concrete have always been one of the main concerns in the engineering field [1,2]. The internal humidity gradient and uneven distribution of concrete are the main reasons for dry shrinkage deformation and surface cracking [3], which have a great impact on the durability of concrete [4,5]. At the same time, moisture is the main medium for concrete deterioration, and a variety of deterioration mechanisms of concrete materials are closely related to its permeability and moisture migration process. Studies show that almost all corrosive media (chloride, sulfate, etc.) enter the concrete mainly through moisture migration [6,7,8], so water and water migration are the core of concrete durability problems.

Previous studies have shown that concrete is a typical non-uniform multi-phase material, which is composed of cement mortar, aggregate, and the interfacial transition zone (ITZ) between them [9]. Each phase material has obvious pore characteristics and is a typical porous medium, and moisture migration is inseparable from its internal micro-structure [10]. Moisture migration also has significant non-uniformity, multi-scale characteristics, and variability during drying and wetting processes [11]. At present, it is difficult to reveal the relation between the microstructure and humidity migration characteristics of concrete by means of experimental testing. Therefore, it is necessary to establish a theoretical model and numerical method of multi-scale moisture migration based on the microstructure of concrete, and to study the moisture migration of concrete from a multi-scale and multi-component perspective (mortar, ITZ, and aggregate).

In recent years, due to the shrinkage and expansion induced by the moisture transfer in concrete, scholars have done a lot of research on the problem of moisture migration of concrete from theoretical, experimental, and numerical aspects, which indicates that the moisture diffusion coefficient of concrete is greatly influenced by the porosity and pore size distribution and the effect mechanism is complicated [12,13,14,15,16]. Studies have shown that the migration of water in concrete pores at the micro scale is closely related to the average pore size and the average free path of water molecules. There are two forms of free diffusion (molecular diffusion) and Knudsen diffusion [17], and, affected by the tortuosity and connectivity of the pore structure, the migration path of humidity is curved and blocked [18]. Macroscopically, it is mainly manifested that the water–cement ratio has a great influence on the moisture diffusion coefficient [19]. At the meso scale, the moisture migration inside the concrete is also affected by the difference in the moisture diffusion coefficients of mortar, aggregate, and ITZ [11]; the “tortuous” and “dilution” effects of aggregates [20] and the loose pore structure of ITZ [9] change the local moisture migration path, resulting in the non-uniformity of moisture migration in concrete. At the same time, the drying and wetting processes of concrete are also quite different [21]. Some scholars suggest adopting two kinds of moisture diffusion coefficients to simulate the moisture migration process in drying and wetting problems, respectively [22,23]. In addition, due to the capillary water absorption of concrete pores at high humidity, a variety of existing concrete moisture diffusion coefficient models [24] (exponential, hyperbolic, “S”, etc.) show that the moisture diffusion coefficient increases with the increase in the relative humidity inside the concrete [25], which makes the moisture migration in the concrete more complicated. It can be seen that the moisture migration of concrete is affected by many factors, such as gel structure, ITZ, pore structure, aggregate, and other microscopic properties, as well as its internal relative humidity. Although the existing research results have explained the reasons for the moisture migration and non-uniform distribution of humidity in concrete to a certain extent, most of them focus on the equivalent moisture diffusion coefficient of concrete as a whole, and the influence of microstructure on the moisture migration of concrete remains to be further studied. Considering that the moisture migration of concrete is directly affected by its internal moisture diffusion coefficient, each part of concrete, consisting of mortar, ITZ, and aggregate, has different moisture diffusion coefficients, leading to more complex internal moisture migration characteristics. It may produce non-uniform moisture changes, causing non-uniform dry shrinkage and wet expansion, thus causing concrete cracking. Therefore, the moisture migration characteristics in concrete are particularly important.

Based on the moisture transfer mechanism of porous media and the microstructure characteristics of concrete, a multi-scale model of the moisture diffusion coefficient of concrete considering Knudsen diffusion is established. The effects of pore structure, ITZ, and aggregate content on the effective moisture diffusion coefficient of concrete were studied. The moisture migration characteristics of concrete during wetting and drying under different aggregate volume fractions were simulated, and the influence of micro-structure on the moisture migration of concrete was analyzed.

2. Multi-Scale Moisture Diffusion Coefficient Model of Concrete

Moisture migration in concrete is generally considered to be a form of moisture migration described by Fick ’s law [11]:

$${\displaystyle \frac{\partial RH}{\partial t}}=D\left({\displaystyle \frac{{\partial }^{\mathit{2}}RH}{\partial x^{\mathit{2}}}}+{\displaystyle \frac{{\partial }^{\mathit{2}}RH}{\partial y^{\mathit{2}}}}+{\displaystyle \frac{{\partial }^{\mathit{2}}RH}{\partial z^{\mathit{2}}}}\right)$$

(1)

where RH is the relative humidity; t is the time, s; and D is the humidity diffusion coefficient, m²/s.

It can be seen from Equation (1) that the difference in moisture migration characteristics of cement paste, mortar, aggregate, and ITZ greatly affects the moisture migration characteristics of concrete at the microscopic scale. Therefore, it is necessary to establish a multi-scale moisture diffusion coefficient model of concrete to determine the moisture diffusion coefficient of each phase in the microstructure of concrete.

2.1. Effective Moisture Diffusion Coefficient of Cement Paste

According to the reference [17], the moisture migration in cement-based materials is affected by both molecular free diffusion and Knudsen diffusion. Therefore, the moisture diffusion coefficient needs to consider the influence of Knudsen diffusion on the basis of molecular diffusion. When considering the influence of Knudsen diffusion, the moisture diffusion coefficient of cement-based materials can be expressed as follows:

$$D_{cm}=k_f{D}_{cm0}$$

(2)

where $D_{cm}$ is the effective moisture diffusion coefficient of cement-based materials considering Knudsen diffusion, m²/s; $D_{cm0}$ is the moisture diffusion coefficient without considering Knudsen diffusion; and $k_f$ is the Knudsen diffusion influence coefficient.

It is also pointed out in reference [17] that Knudsen diffusion should be considered only when the humidity changes phase, and the value of $k_f$ is related to the average pore size of cement-based materials. However, in essence, due to the wide range of pore size distribution of concrete, there is an order of magnitude difference between the maximum pore size and the minimum pore size, so the water migration on the micro scale needs to comprehensively consider the influence of pore structure. The migration of water in concrete pores is affected by the ratio $r$ of the average free path $\lambda$ of water molecules to the pore diameter $d_p$, and there are two forms of free diffusion and Knudsen diffusion. When $r$≤ 0.01, it is free diffusion; when $r$≥ 10, it is Knudsen diffusion, that is, the collision between water molecules and pore walls determines the diffusion of molecules; and when the ratio of the two is between 0.01 and 10, it is mixed diffusion. For a single pore, the diffusion coefficient $D_{fk}$ can be expressed as follows [26]:

$$D_{fk}=\left\{\begin{array}{c}{\displaystyle \frac{\lambda \overline{\nu }}{3}} ,r\le 0.01\\ {\displaystyle \frac{\overline{\nu }\lambda }{3}}\left[1-Exp({\displaystyle \frac{-d_p}{\lambda }})\right],0.01<r<10\\ {\displaystyle \frac{d_p\overline{\nu }}{3}} ,r\ge 10\end{array}\right.$$

(3)

where $\overline{\nu }$ is the average velocity of water molecules relative to air molecules, m/s.

Assuming that the mixed gas in the pores is an ideal gas composed of air and water vapor, the free path $\lambda$ and the average motion rate $\lambda$ of the binary mixed gas can be expressed as follows [27]:

$$\lambda ={\displaystyle \frac{k_b\left(T+273\right)}{\sqrt{2}\pi P_w{d}_w^2+{\pi P}_A{\left(\frac{d_w+d_A}{2}\right)}^{\mathit{2}}\sqrt{1+\frac{m_w}{m_A}}}}$$

(4)

$$\overline{\nu }=\sqrt{{\displaystyle \frac{8R\left(T+273\right)(m_A+m_w)}{\pi m_w{m}_A}}}$$

(5)

where $k_b$ is the Boltzmann constant, 1.380649 × 10⁻²³ J/K; T is the temperature, °C; $d_w$ is the diameter of water molecule, 4 × 10⁻¹⁰ m; $d_A$ is the effective diameter of air molecules, 3.5 × 10⁻¹⁰ m; $m_w$ is the molecular weight of water, 18 g/mol; $m_A$ is the effective molecular weight of air, 29 g/mol; $R$ is the perfect gas constant, 8.314 m³$·\mathrm{P}\mathrm{a}/(\mathrm{m}\mathrm{o}\mathrm{l}·°\mathrm{C})$; and $P_w$ and $P_A$ are the partial pressures of water vapor and air [28], Pa.

$$\left\{\begin{array}{c}{P}_w=610RH·Exp\left({\displaystyle \frac{17.3T}{237.3+T}}\right)\\ P_A=P_{atom}-P_w\end{array}\right.$$

(6)

where $RH$ is the relative humidity; $P_{atom}$ is the standard atmospheric pressure, 100 kPa.

According to Equations (3)–(6), even if there is no phase change, the influence of Knudsen diffusion still exists in the mixed diffusion stage, and the pore size distribution of cement paste also determines the influence of Knudsen diffusion to a certain extent.

Based on Equation (1), for an arbitrary cross-section with an area of Ω, when the humidity gradient is $\nabla RH$, the mass pass through all the pores with a pore size of $d_p$ in unit time can be expressed as follows:

$$Q\left(d_p\right)=D_{fk}\left(d_p\right)A\left(d_p\right)\nabla RH$$

(7)

where $A\left(d_p\right)$ is the total pore area with pore size $d_p$.

Let the relation between the cumulative porosity of cement paste and pore size be ${\varphi }_c={\varphi }_c\left(d_p\right)$, then the total pore area with pore size of $d_p$ can be expressed as follows:

$$A\left(d_p\right)={\displaystyle \frac{\partial {\varphi }_c\left(d_p\right)}{\partial d_p}}\mathsf{\Omega }$$

(8)

According to the conservation of mass in the transmission process, the total mass passing through the cross section per unit time can be expressed as follows:

$$Q={\sum }_{d_{p\text{-}min}}^{d_{p\text{-}max}}{D}_{fk}\left(d_{pi}\right)\mathsf{\Omega }\nabla RH{\displaystyle \frac{\partial {\varphi }_c\left(d_p\right)}{\partial d_p}}$$

(9)

where $d_{p\text{-}min}$ and $d_{p\text{-}max}$ are the minimum pore size and the maximum pore size in the cement paste, m.

Therefore, when considering the influence of Knudsen diffusion, the effective moisture diffusion coefficient $D_{ce}$ of the cross section can be expressed as follows:

$$D_{ce}={\displaystyle \frac{Q}{\mathsf{\Omega }\nabla RH}}={\sum }_{d_{p\text{-}min}}^{d_{p\text{-}max}}{D}_{fk}\left(d_{pi}\right){\displaystyle \frac{\partial {\varphi }_c\left(d_p\right)}{\partial d_p}}$$

(10)

Similarly, the effective moisture diffusion coefficient of the cross section without considering Knudsen diffusion can be expressed as follows:

$$D_{ce0}={\sum }_{d_{p\text{-}min}}^{d_{p\text{-}max}}{\displaystyle \frac{\lambda \overline{\nu }}{3}}·{\displaystyle \frac{\partial {\varphi }_c\left(d_p\right)}{\partial d_p}}$$

(11)

Then, the Knudsen diffusion influence coefficient $k_f$ can be obtained as follows:

$$k_f={\displaystyle \frac{D_{ce}}{D_{ce0}}}$$

(12)

It should be noticed that Equation (11) is the diffusion coefficient in an ideal state within the section $\mathsf{\Omega }$ with a certain free path $\lambda$. Though it seems that Equation (11) can consider the effect of RH while the $\lambda$ has considered the effect of RH via Equations (4) and (6), the $D_{ce0}$ cannot be equal to $D_{cm0}$ directly. This is because the $D_{ce0}$ lacks consideration for hindered diffusion (in the real moisture diffusion process) and different shapes of pores (“bottle neck” effect and “open-pore” effect) [29]. But, Equation (12) is still valid as the $k_f$ in Equation (12) is a relative value with the same ideal state assuming of $D_{ce}$ and $D_{ce0}$.

For the $D_{cm0}$, since the moisture diffusion coefficient of porous material varies with RH, the moisture diffusion coefficient of cement paste can be described an S-shaped curve [19]:

$$D_{cm0}=D_{cm0\text{-}max}{\left[1+{\left(7.5-7.5RH\right)}^4\right]}^{-1}$$

(13)

where the $D_{cm0\text{-}max}$ is the maximum moisture diffusion coefficient of cement paste when RH = 1, and it can be approached via Equation (11).

Though Equation (11) is the diffusion coefficient in an ideal state within the section $\mathsf{\Omega }$ with a certain RH, the $D_{cm0\text{-}max}$ can be calibrated by using $D_{ce0\text{-}max}$ (the maximum of $D_{ce0}$ when RH = 1) due to the quasi-steady state of the local thermodynamic equilibrium [24]. Meanwhile, since the pores in cement paste are tortuous with different shapes, the diffusion path will also be tortuous by the pores. Then, the $D_{ce0\text{-}max}$ for the spatial domain can be modified with the pore tortuosity $\tau$ (which can be defined as a function of porosity $\tau =1-\sqrt{3}\ln {\varphi }_c$ [30]), and the $D_{cm0\text{-}max}$ can be expressed as follows:

$$D_{cm0\text{-}max}={\displaystyle \frac{D_{ce0\text{-}max}}{\tau }}$$

(14)

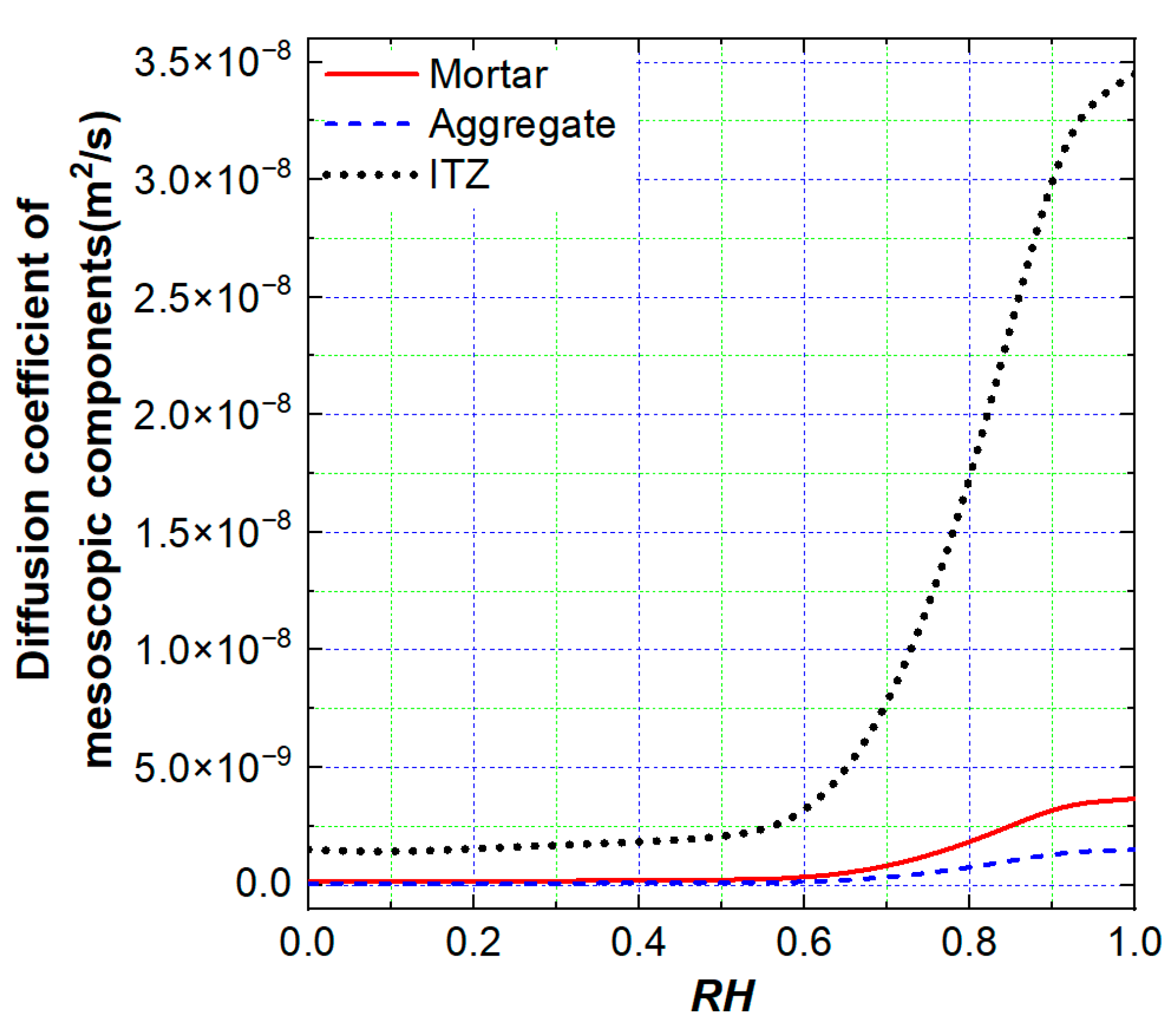
2.2. Effective Moisture Diffusion Coefficient of Mortar and Concrete

Since concrete is a composite binding material, the equivalent diffusion coefficient is essential for engineering applications, and the equivalent moisture diffusion coefficient of composite porous media can be determined by the Maxwell and self-consistent method [31]. Maxwell assumes that the particles in the inclusion phase are far enough away from each other and randomly distributed in the continuous phase, which is suitable for the case of the low dispersed phase [31]. The self-consistent method can better estimate the effective properties of the composite material embedded in the matrix, but there will be a large deviation when the volume of the inclusion phase is greater than 1/3 [31]. If the mortar is regarded as a two-phase composite material composed of fine aggregate (inclusion phase) and cement paste (continuous phase), according to the self-consistent method, the moisture diffusion coefficient relationship between the composite material and the inclusion phase and the continuous phase can be expressed as follows:

$${\displaystyle \frac{D_{\alpha }-D_{eq}}{D_{\alpha }+2D_{eq}}}={\displaystyle \frac{{\mathrm{V}}_{\beta }}{1-{\mathrm{V}}_{\beta }}}{\displaystyle \frac{D_{eq}-D_{\beta }}{D_{\beta }+2D_{eq}}}$$

(15)

where $D_{\alpha }$ is the moisture diffusion coefficient of the continuous phase, $D_{\beta }$ is the moisture diffusion coefficient of the inclusion phase, $D_{eq}$ is the equivalent moisture diffusion coefficient of composite materials, and ${\mathrm{V}}_{\beta }$ is the volume fraction of the inclusion phase.

Considering that the volume fraction of mortar fine aggregate is greater than 1/3 in practical engineering, the “mortar” containing 1/3 volume fraction of fine aggregate can be regarded as a continuous phase, and the remaining fine aggregate can be regarded as an inclusion phase. The self-consistent equation is iterated again to obtain the moisture diffusion coefficient at a higher volume fraction of fine aggregate. Assume that the equivalent moisture diffusion coefficient in Equation (15) is $D_{eq}=D_{eq}({\mathrm{V}}_{\beta },D_{\alpha },D_{\beta })$, then the effective moisture diffusion coefficient $D_m$ of mortar with different volume fractions of fine aggregate can be expressed as follows:

$$D_m=\left\{\begin{array}{cc}{D}_{eq}\left({\mathrm{V}}_{\beta },D_{\alpha },D_{\beta }\right),\hfill & \hfill 0<{\mathrm{V}}_{\beta }\le 0.33\\ D_{eq}({\mathrm{V}}_{\beta 1},D_{\alpha 1},D_{\beta }),\hfill & \hfill 0.33<{\mathrm{V}}_{\beta }\le 0.56\\ D_{eq}({\mathrm{V}}_{\beta 2},D_{\alpha 2},D_{\beta }),\hfill & \hfill 0.56<{\mathrm{V}}_{\beta }\le 0.70\\ D_{eq}({\mathrm{V}}_{\beta 3},D_{\alpha 3},D_{\beta }),\hfill & \hfill 0.70<{\mathrm{V}}_{\beta }\le 0.80\end{array}\right.$$

(16)

where $D_{\alpha 1}$, $D_{\alpha 2}$, and $D_{\alpha 3}$ are the moisture diffusion coefficients of the continuous phase in the three iterations; ${\mathrm{V}}_{\beta 1}$, ${\mathrm{V}}_{\beta 2}$, and ${\mathrm{V}}_{\beta 3}$ are the residual volume fractions of inclusion phase in three iterations.

Concrete is usually regarded as a three-phase composite material composed of mortar, coarse aggregate, and ITZ, but the Maxwell and self-consistent method are equivalent methods of two-phase composite materials. In order to deduce the effective moisture diffusion coefficient of concrete, ITZ and aggregate can be regarded as a “composite” structure, and then, concrete can be analyzed as a two-phase composite material composed of mortar and the “composite”, as shown in Figure 1.

Since the volume fraction of coarse aggregate in the “composite” is much larger than 1/3, if the self-consistent method is used, a large deviation will be generated. Therefore, the generalized Maxwell equation [32] is used to consider the equivalent mass transfer coefficient of non-uniform composite materials with an arbitrary shape and spatial distribution as follows:

$$D_{rc}=D_{ITZ}+{\displaystyle \frac{V_{rc}{D}_{ITZ}(D_r-D_{ITZ})}{D_{ITZ}+\frac{1}{3}(1-V_{rc})(D_r-D_{ITZ})}}$$

(17)

where $D_r$ is the moisture diffusion coefficient of coarse aggregate, m²/s; $D_{ITZ}$ is the moisture diffusion coefficient of ITZ, m²/s; and $V_{rc}$ is the volume fraction of coarse aggregate in the “composite”.

$$V_{rc}={\left({\displaystyle \frac{r_r}{r_r+∆r_r}}\right)}^3$$

(18)

where $r_r$ is the coarse aggregate radius, mm; $∆r_r$ is the thickness of ITZ, mm.

Then, the concrete is regarded as a two-phase composite consisting of “composite” and mortar. Similarly, the effective moisture diffusion coefficient of concrete can be obtained by using Equation (16).

Since the moisture diffusion coefficients of aggregate and ITZ are needed for the effective moisture diffusion coefficient calculations of the mortar and concrete, it is assumed that the pore size distribution of each phase in concrete is similar. Thus, the moisture diffusion coefficient of each phase can be considered by the effect of porosity. According to the reference [33], the porosity of the aggregate with better texture is about 3%, which is about 0.1 times that of the cement paste; the porosity of ITZ is about 2.1~2.5 times that of cement paste [34], and the median value is about 2.3 times. Then, by analogy with porosity, we can have $D_r$ = 0.1 $D_{ce}$ and $D_{ITZ}$ = 2.3 $D_{ce}$, and the thickness of ITZ is suggested at about 50 μm [34].

According to the above relations of the moisture diffusion coefficient of each phase in concrete, the effective moisture diffusion coefficient of concrete from the micro to the macro scale considering the influence of Knudsen diffusion can be obtained by combining Equations (2) and (16).

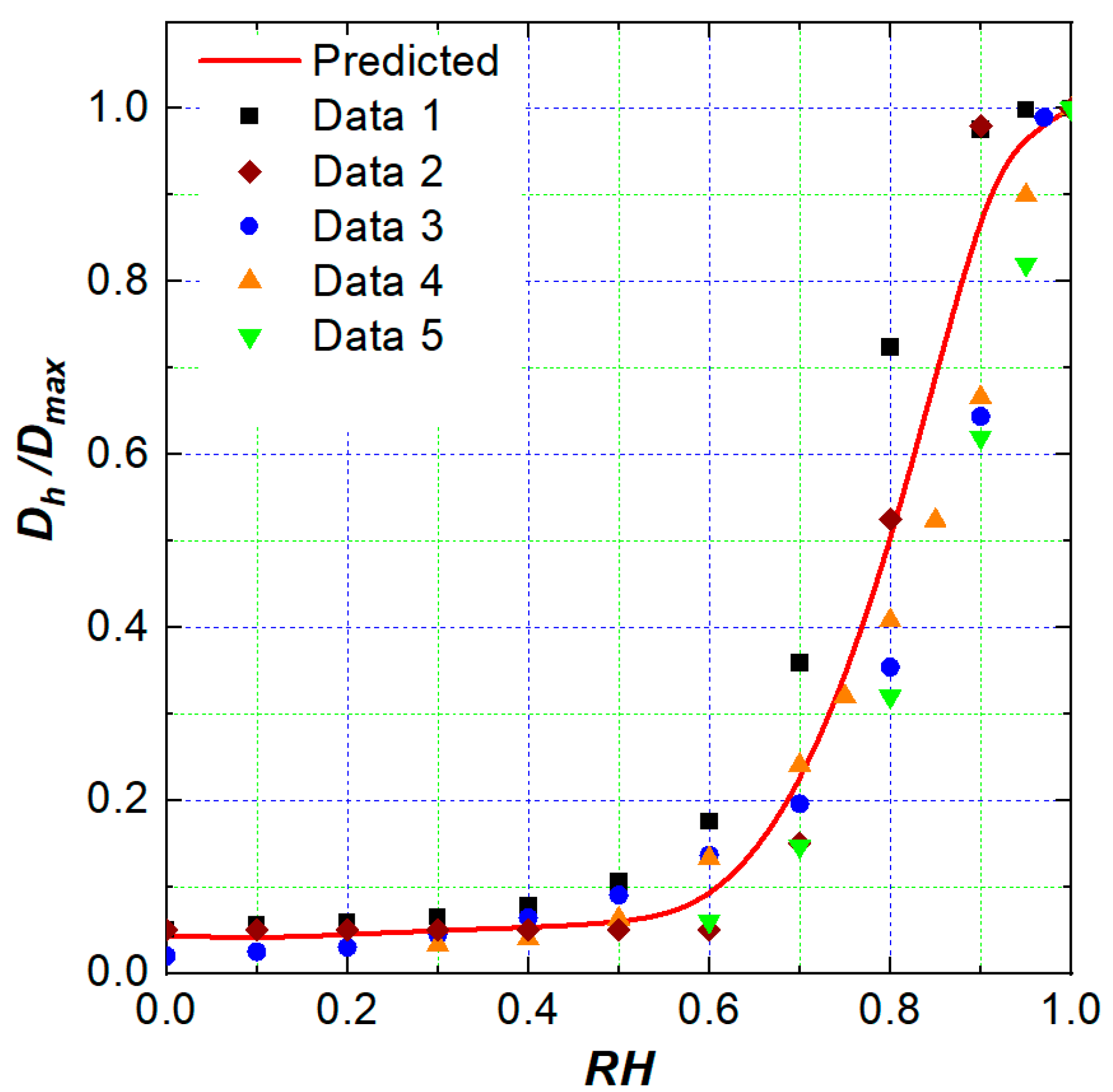
2.3. Model Validation

In order to verify the reliability of the multi-scale moisture diffusion coefficient model of concrete in this paper, the data obtained from the empirical equations in the CEB-FIP (2010) code [35] and some experimental data in the references [16,36,37,38,39] were chosen to compare with the model calculation result. Considering the influence of the concrete mix ratio difference on the moisture diffusion coefficient in the reference, a similar mix ratio (in which the water–cement ratio is around 0.5) is selected as far as possible, and the dimensionless moisture diffusion coefficient $D_h/D_{max}$ is used for comparative analysis and verification.

According to the empirical Equation (19) in the CEB-FIP (2010) code [35], the moisture diffusion coefficient of concrete can be expressed as follows:

$$D_h=D_{max}\left\{m+{\displaystyle \frac{1-m}{1+{\left[\left(1-H\right)/\left(1+H_c\right)\right]}^n}}\right\}$$

(19)

where $D_{max}$ is the maximum value of $D_h$ when RH = 1, m²/s; $H_c$ is the relative humidity when $D_h=0.5 D_{max}$, and the code recommendation $H_c$= 0.8; $m$ and $n$ are the empirical coefficients; and it is recommended that $m$= 0.05, $n$= 15.

The pore size distribution curve required in the multi-scale moisture diffusion coefficient model was obtained via the data in reference [39], and the temperature is selected at room temperature (20 °C). The comparison results are shown in Figure 2, which indicate that the predicted data of the moisture diffusion coefficient model is in good agreement with the empirical and reference date, and the model can effectively describe the moisture diffusion coefficient of the multi-scale of concrete.

3. Meso-Scale Simulation of Moisture Transfer Characteristics

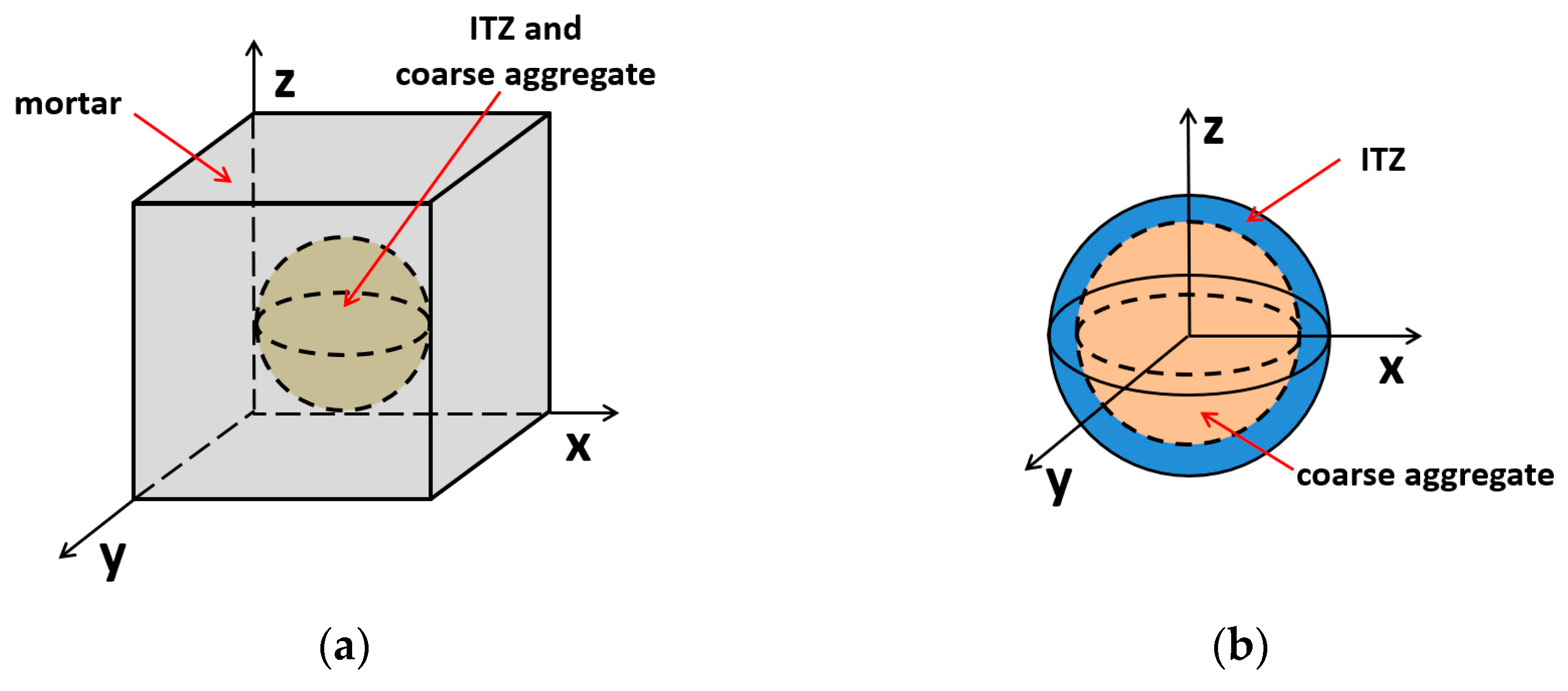
3.1. Calculation Parameters and Models

Considering the difference between the wetting and drying process of concrete, this paper uses the finite element method (COMSOL Multiphysics) to analyze the moisture migration characteristics of concrete in the wetting and drying process. Only mortar, coarse aggregate, and ITZ are considered in the analysis, and the mesoscopic calculation parameters are obtained according to the reference [39]. The moisture diffusion coefficients of mortar, coarse aggregate, and ITZ were obtained according to Section 2 as shown in Figure 3. At the same time, a self-written program was utilized to generate a random aggregate distribution, with sizes varying between 5 mm and 10 mm according to the Fuller grading curve. The mesoscopic model is in the size of 10 cm × 10 cm (two-dimensional model), and three kinds of coarse aggregate volume fractions (0.30, 0.45, and 0.6) were used to consider the influence of the coarse aggregate volume fraction. In addition, the ITZ thickness was set as 0.50 mm to avoid the local element inconsistency caused by significant size differences between aggregate and ITZ. Triangular elements in the size of 0.5 mm~5 m were used in the simulations and the meshed simulation models are shown in Figure 4.

Meanwhile, the same RH difference of the boundary was used in the wetting and drying process. Considering that it is difficult for the RH inside the concrete under the real climatic and environmental conditions to reach 0, the RH boundary in the simulation is set as 0.5~1, and only the left side ($x=0 \mathrm{c}\mathrm{m}$) of the model is applied to the wetting and drying boundary, and the other side is the dehumidification boundary, as shown in

Table 1. Boundary conditions of wetting and drying.

Working Condition	Boundary Position	Boundary RH	Internal Initial RH
Wetting process	$x=0 \mathrm{c}\mathrm{m}$	1	0.5
Drying process	$x=0 \mathrm{c}\mathrm{m}$	0.5	1

. At the same time, considering that the wetting time of concrete is shorter than the drying time [7], the transient process of wetting for 72 h and drying for 168 h were used in the simulations.

3.2. Mesoscopic Moisture Migration Characteristics in Wetting and Drying

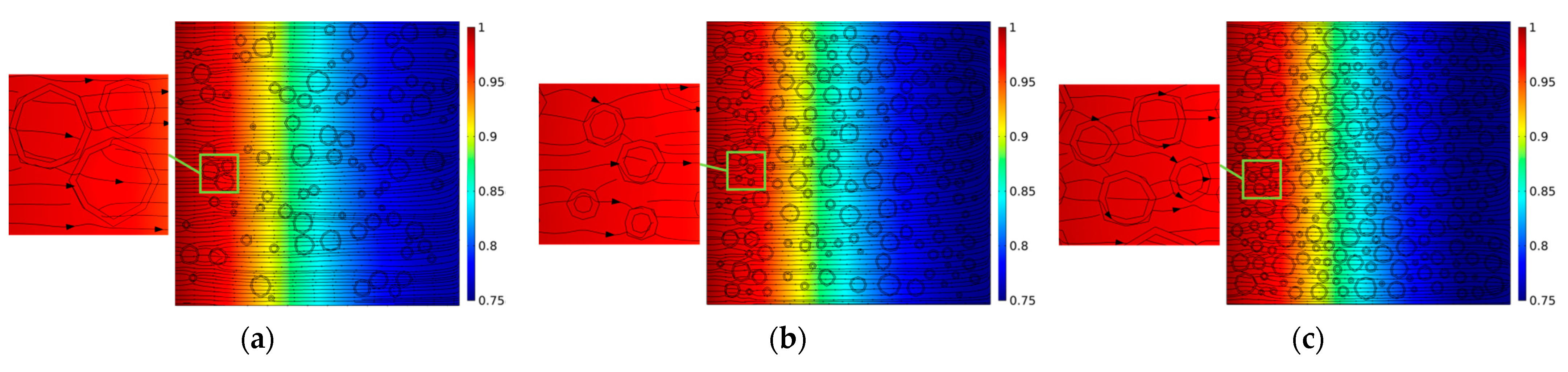
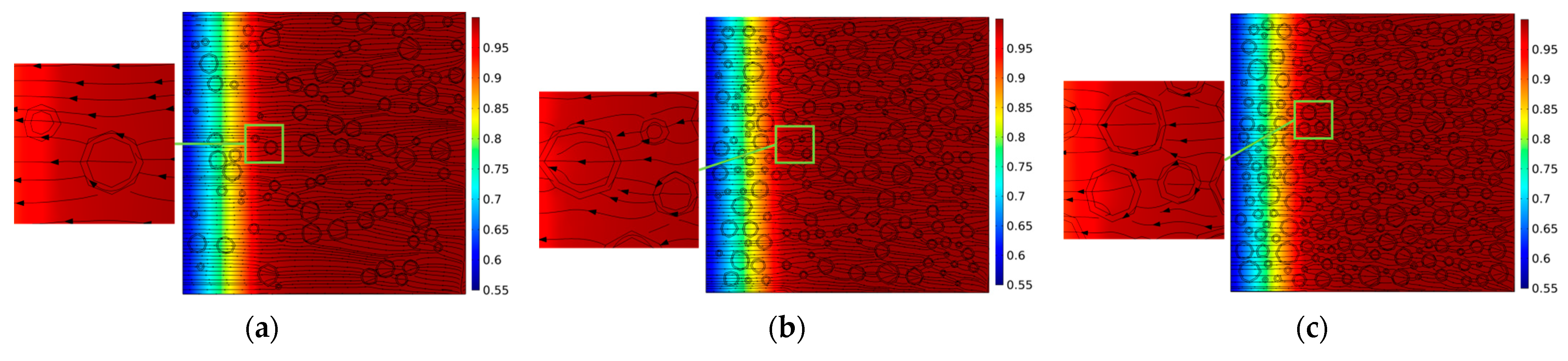
3.2.1. RH Distribution and “Flow Around” Phenomenon in Wetting and Drying

(1)

Wetting process

The calculation results at 72 h of wetting are shown in Figure 5. The internal RH of concrete is between 0.75 and 1. Due to the presence of random aggregate, the moisture migration path inside the concrete has a detailed “bending” phenomenon, and the humidity distribution is uneven. The RH at $x$ = 5 cm in concrete with a coarse aggregate volume fraction of 0.30, 0.45, and 0.60 is 0.855, 0.843, and 0.836, respectively. The larger the volume fraction of the coarse aggregate, the lower the moisture migration rate. At the same time, the local diffusion path around the coarse aggregate shows that the humidity is more inclined to migrate through the ITZ, resulting in an obvious “flow-around” phenomenon near the coarse aggregate and ITZ, and with the increase in the aggregate volume fraction, the “flow-around” phenomenon is more obvious, resulting in a non-uniform distribution of humidity. According to the moisture diffusion coefficient model, it can be seen that the moisture diffusion coefficients of each phase are significantly different when RH > 0.8, so the “flow around” phenomenon is more likely to occur in the higher part of RH.

(2)

Drying process

The calculation results at 168 h of drying are shown in Figure 6. The relative humidity inside the concrete is between 0.55 and 1, which is the same as the wetting process. The relative humidity distribution inside the concrete during the drying process also shows non-uniformity and an obvious “flow around” phenomenon. The relative humidity at x = 2 cm inside the concrete with a coarse aggregate volume fraction of 0.30, 0.45, and 0.60 is 0.877, 0.881, and 0.887, respectively. The larger the aggregate volume fraction, the lower the moisture migration rate in the drying process. At the same time, it can be seen from the above humidity distribution law that the volume fraction of coarse aggregate has little effect on the humidity distribution, but the larger the volume fraction of coarse aggregate, the slower the water migration, whether it is wet or dry. The moisture diffusion characteristics under different aggregate volume fractions also further prove that, when the aggregate volume fraction increases, the effect of the additional ITZ on the surface on the moisture diffusion coefficient of concrete is less than that of the aggregate volume fraction.

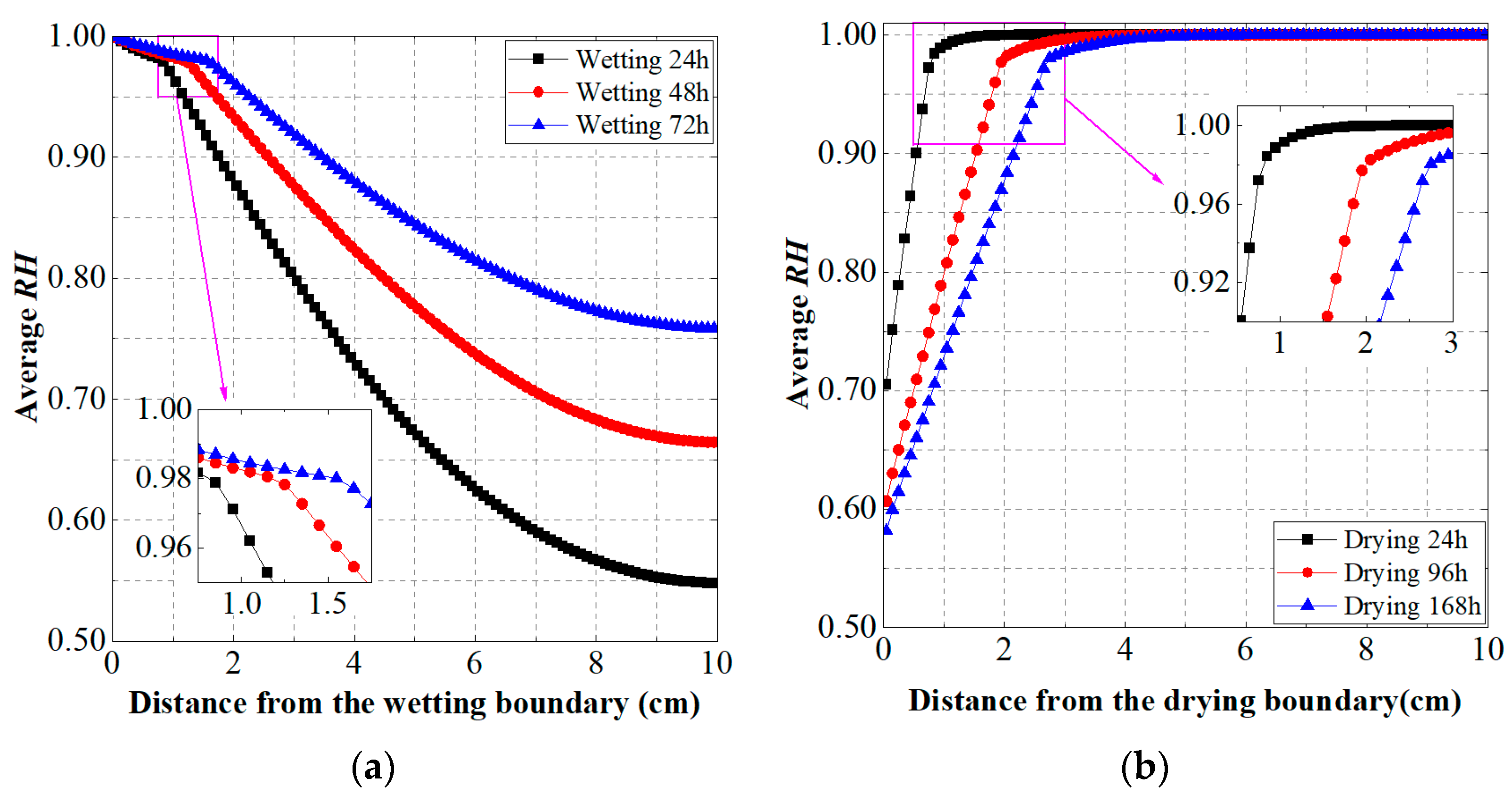
3.2.2. Difference in Moisture Diffusion Characteristics Between Wetting and Drying

In order to further explain the difference in the moisture migration characteristics between the concrete wetting and drying process, the average humidity distribution inside concrete is obtained according to the calculation results, as shown in Figure 7. The results show that there is an obvious “inflection point” in the average humidity distribution inside the concrete whether in the wet or dry process. According to Equation (1), the solution of concrete humidity distribution should be a smooth quadratic curve in general. However, due to the “S” growth relationship between the moisture diffusion coefficient and RH, the slope of the quadratic curve changes, which leads to the occurrence of the “inflection point”. Since the moisture diffusion coefficient reaches the maximum when RH ≥ 0.9, the “inflection point” will appear at a higher relative humidity. At the same time, the difference in the humidity distribution under different aggregate volume fractions gradually increases with the increase in the humidity migration distance. This is mainly due to the influence of the increase in the aggregate volume fraction on the overall moisture diffusion coefficient of concrete, which makes the humidity evolution of the same part have a time difference. At the same time, the continuity of wet migration in space makes the time difference accumulate with the wet migration process, which eventually leads to the increasing difference in the spatial distribution of humidity. Although this difference is small, the difference in wetting is greater than that in drying.

Considering the time difference between the wetting and drying process and the phenomenon of the “inflection point”, the average relative humidity distribution at different moments was obtained by taking the model with an aggregate volume fraction of 0.3 as an example, as shown in Figure 8. The results show that the distance from the boundary to the “inflection point” in the wetting and drying process increases with the increase in time, and the change in RH at the “inflection point” is small, but it is always greater than 0.9. This is due to the fact that in the wetting process, the boundary x = 0 is the first part where the humidity starts to rise. This is due to the wetting process. The boundary x = 0 is the first part where the humidity began to rise. According to Equation (1), it can be seen that the “point of inflection” on the left side of the humidity gradient is small, and the right side of the humidity gradient is larger, so in the process of wetting, the “point of inflection” on the left side of the humidity changes slower than the right side, while the drying process is the opposite.

In addition, the wetting process of concrete is faster than the drying process, because the RH of the wet boundary is 1, the moisture diffusion coefficient at the boundary is the largest, and the wet boundary transmits water to the concrete with a large moisture diffusion coefficient. The RH of the drying boundary is 0.5, and the moisture diffusion coefficient at the drying boundary is small, so the boundary transports moisture outward with a small moisture diffusion coefficient. Since the other boundaries of the concrete are moisture-proof conditions, according to the conservation of mass, the moisture migrating from the boundary during drying is less than that migrating from the boundary during wetting at the same time, so the drying process is longer than the wetting process, and the internal humidity changes slower than the wetting process. It can be seen that the “S”-type growth between the moisture diffusion coefficient of concrete and RH includes the difference in the moisture diffusion coefficient between the wetting and drying process.

In summary, since the simulation results of concrete wetting and drying processes confirm to the general cognitive laws and can reflect the differences in moisture transfer characteristics in both processes, the model established in this paper can also be further validated by the results.

4. Discussion

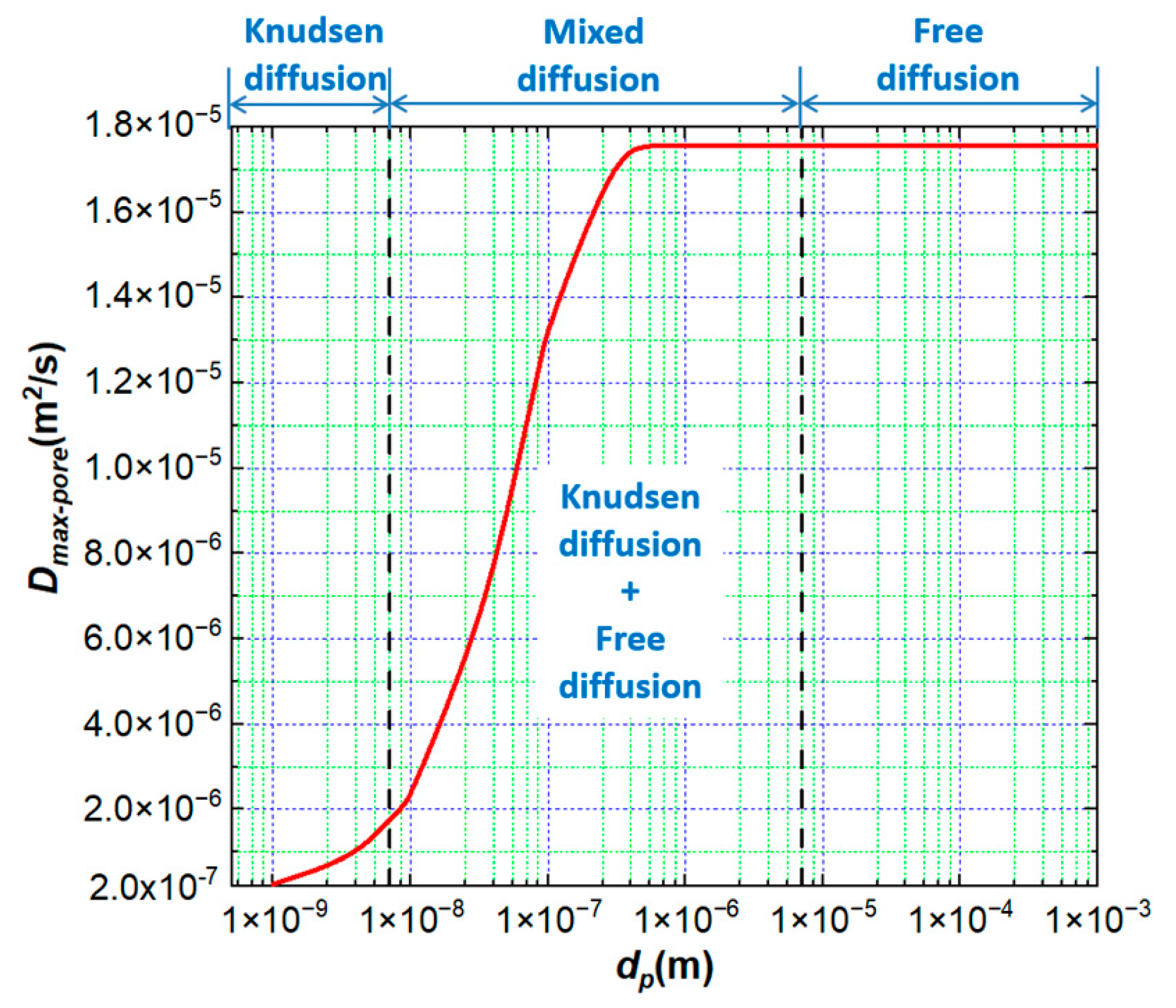
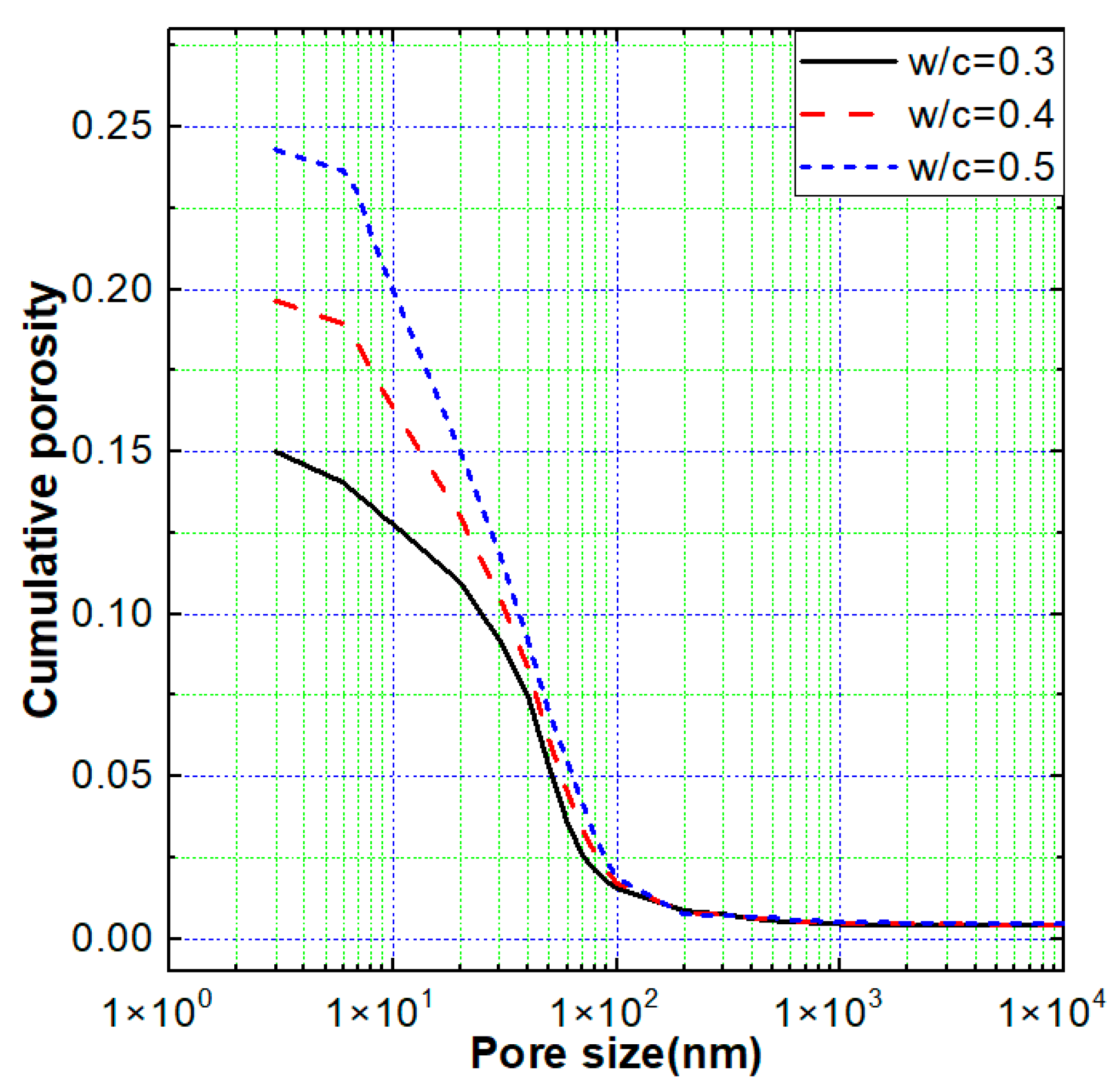
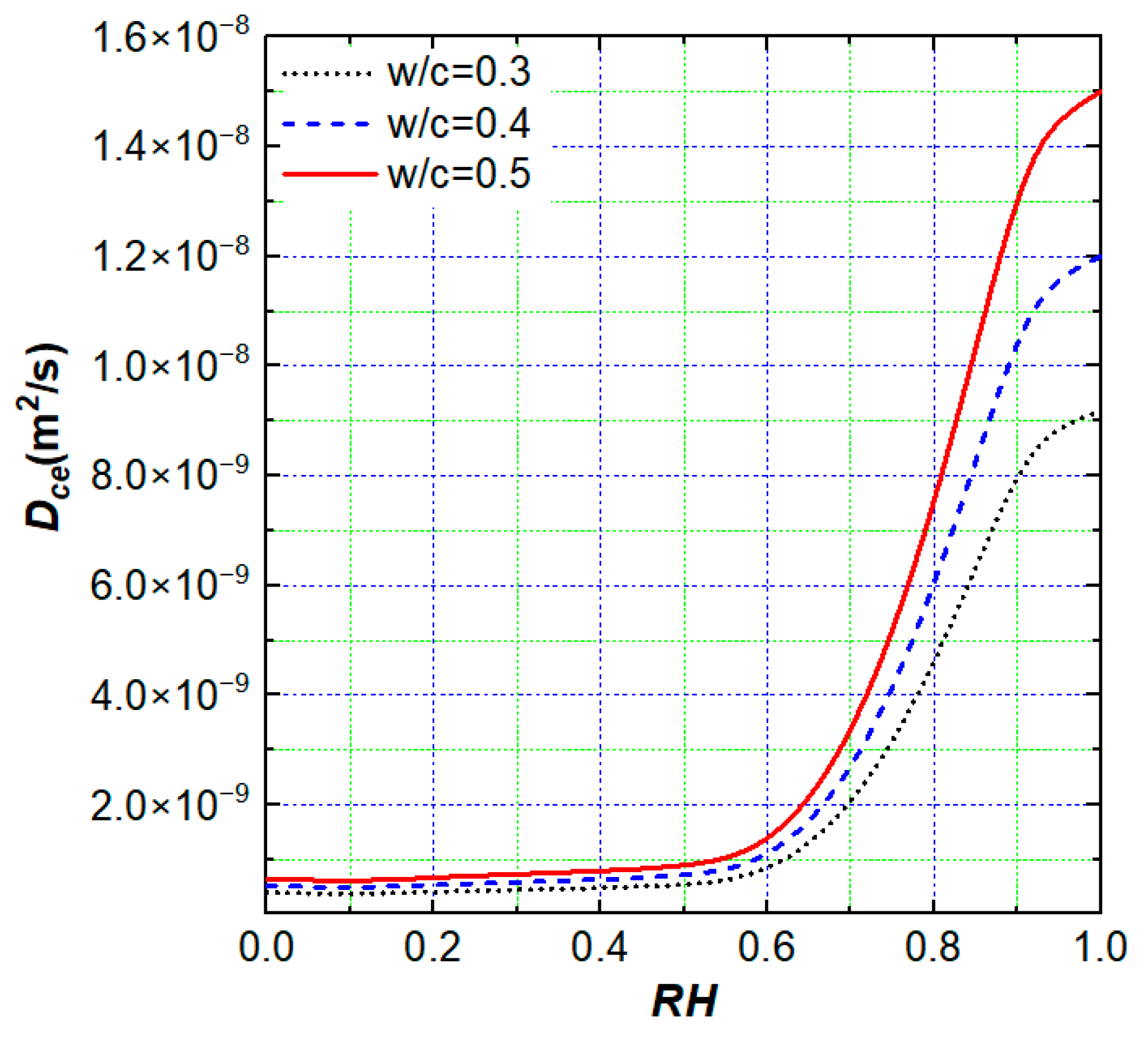
4.1. The Effect of Pore Size and Water-to-Cement Ratio on Moisture Transfer

Considering that the moisture diffusion coefficient of concrete is the accumulation of moisture migration in a single pore, the relationship between the moisture diffusion coefficient of a single pore and the pore size is shown in Figure 9, when the RH is 1 according to the moisture diffusion coefficient model in this paper. The results show that the moisture diffusion coefficient of a single pore increases with the increase in pore size, and finally tends to be stable. The growth rate of the diffusion coefficient increases first and then decreases. This is mainly due to the fact that when the pore size is small (about <7 nm), the moisture migration in the pores is mainly Knudsen diffusion, and the diffusion coefficient is mainly determined by the pore size. Between the pore size of about 7~700 nm, it is a mixed diffusion. The size of the diffusion coefficient is determined by the pore size and the free path. With the increase in the pore size, the proportion of Knudsen diffusion gradually decreases, and the proportion of free diffusion gradually increases. When the pore size is large (about >700 nm), the moisture migration in the pores is mainly free diffusion, and the diffusion coefficient is only determined by the free path.

At the same time, according to the pore size distribution (PSD) curve of 28 days in reference [39] (Figure 10), the equivalent moisture diffusion coefficient of cement paste under different water–cement ratios was calculated, as shown in Figure 11. The results show that the moisture diffusion coefficient of cement paste increases with the increase in the water–cement ratio at the micro scale. Additionally, with the increase in RH, the “S”-type growth law is presented, which is consistent with the macroscopic law of concrete. It is noteworthy that the free path of water molecules increases with the decrease in RH, so the proportion of Knudsen diffusion in the pores of cement paste increases when the RH is low. Because the moisture diffusion coefficient of Knudsen diffusion is much smaller than that of free diffusion, Knudsen diffusion is also one of the reasons why the moisture diffusion coefficient increases with the increase in RH. In addition, combined with the effect of pore size on the moisture diffusion coefficient in Figure 9, the results in Figure 11 also show that the micro-scale moisture diffusion coefficient is greatly affected by the pore size distribution of cement paste.

In order to further illustrate the influence of pore size distribution on moisture migration, the contribution of pores with different pore size ranges to the overall moisture diffusion coefficient is calculated according to the moisture diffusion coefficient model (i.e., $\left[D_{ce\text{-}dp1}-D_{ce\text{-}dp2}\right]/D_{ce}$, considering that when RH is about greater than 0.6, $D_{ce}$ begins to increase, so the effective moisture diffusion coefficients when RH is 0.6, 0.8, and 1 are selected as the benchmarks, respectively), as shown in Figure 12. The results show that under the influence of the free path difference in water molecules at different RHs, with the increase in RH, the migration proportion of water molecules in macropores increases, that is, the influence of Knudsen diffusion decreases gradually, and the proportion of free diffusion increases gradually. At the same time, the contribution of pores with a pore size of 10~100 nm to the overall moisture diffusion coefficient of cement paste is dominant, and with the increase in the water–cement ratio, water molecules are more likely to migrate through small pores, that is, the greater the water–cement ratio, the greater the influence of Knudsen diffusion. This is mainly due to the fact that the volume ratio of 10~100 nm pores in cement paste is the largest, and as the water–cement ratio increases, the volume ratio of small pores increases.

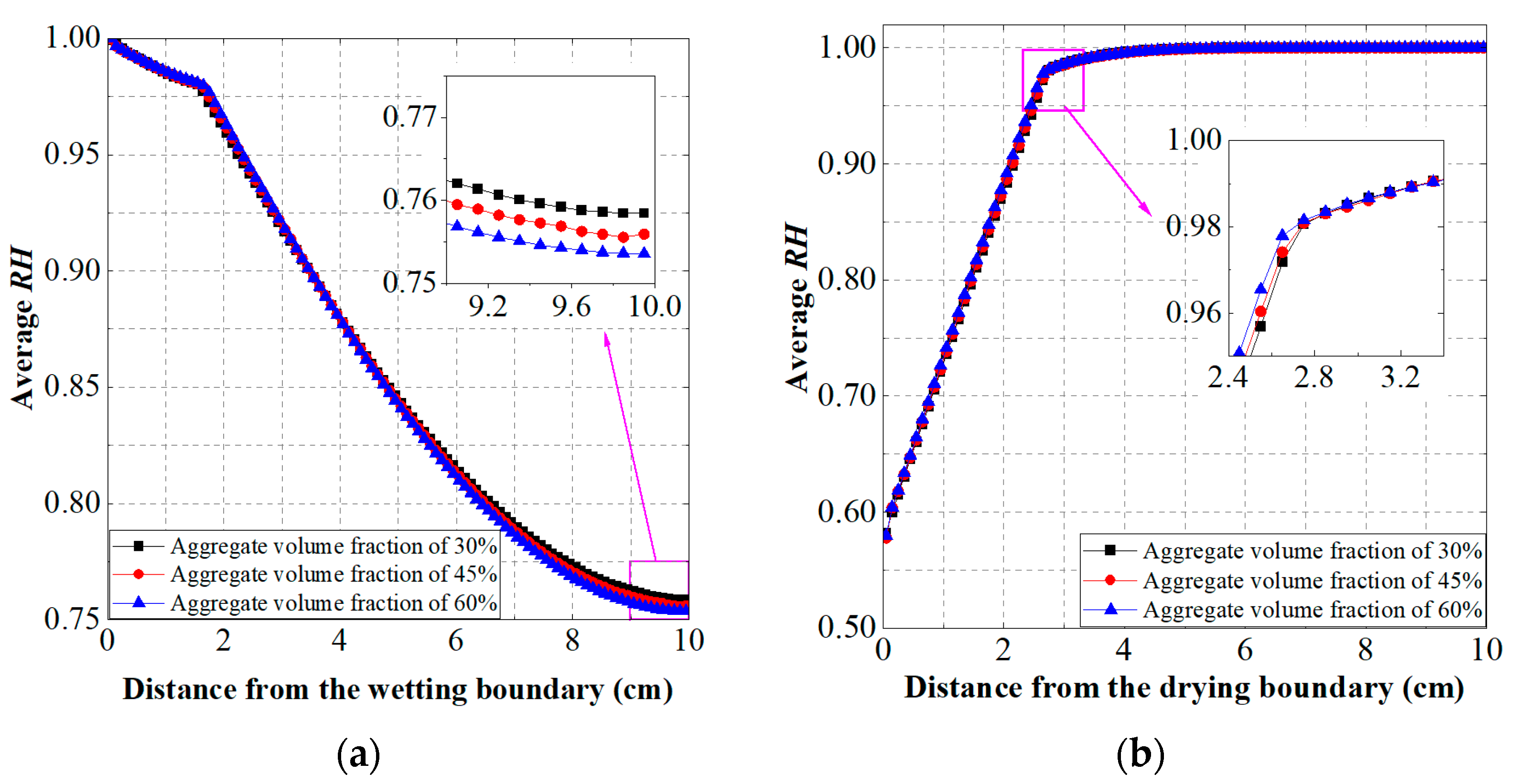
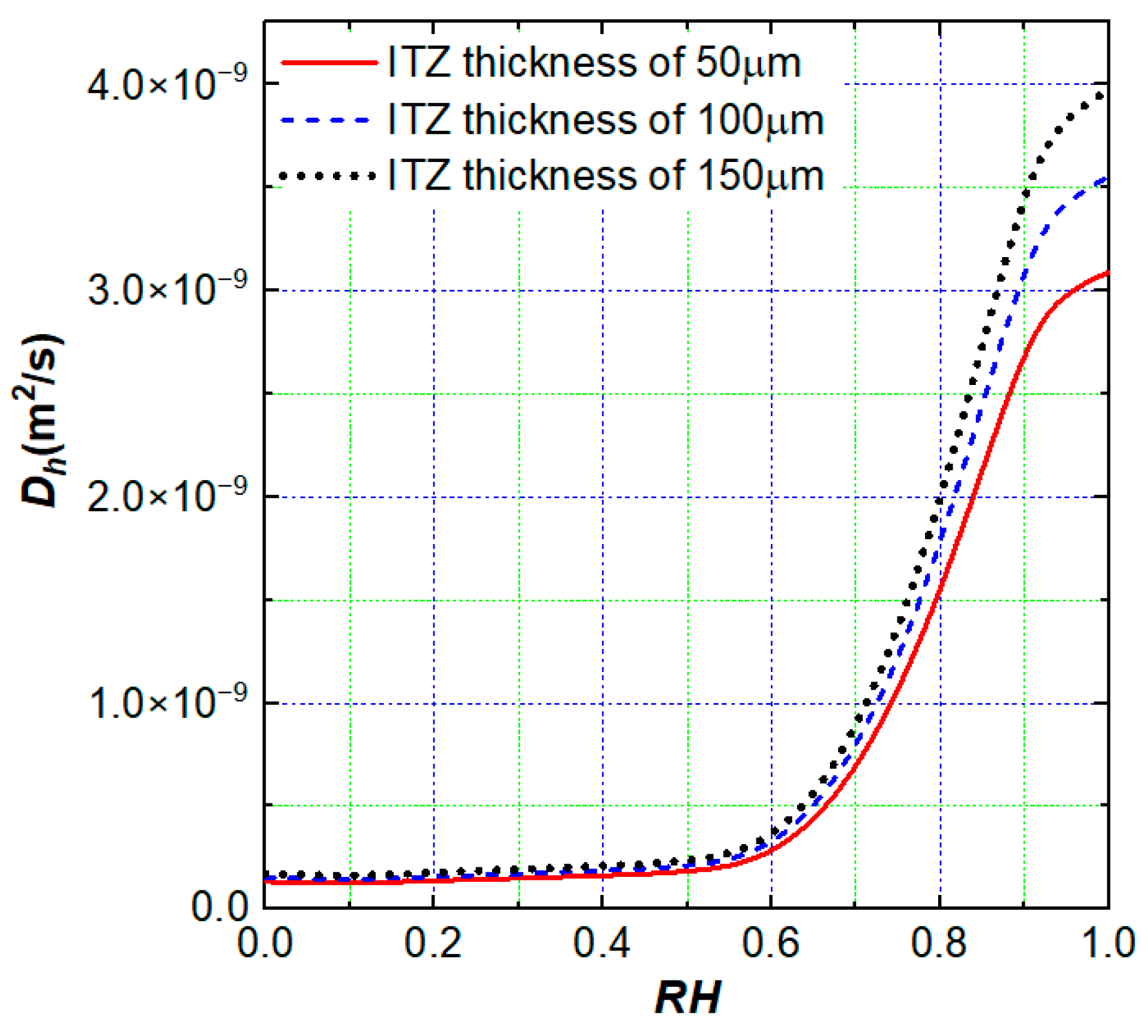
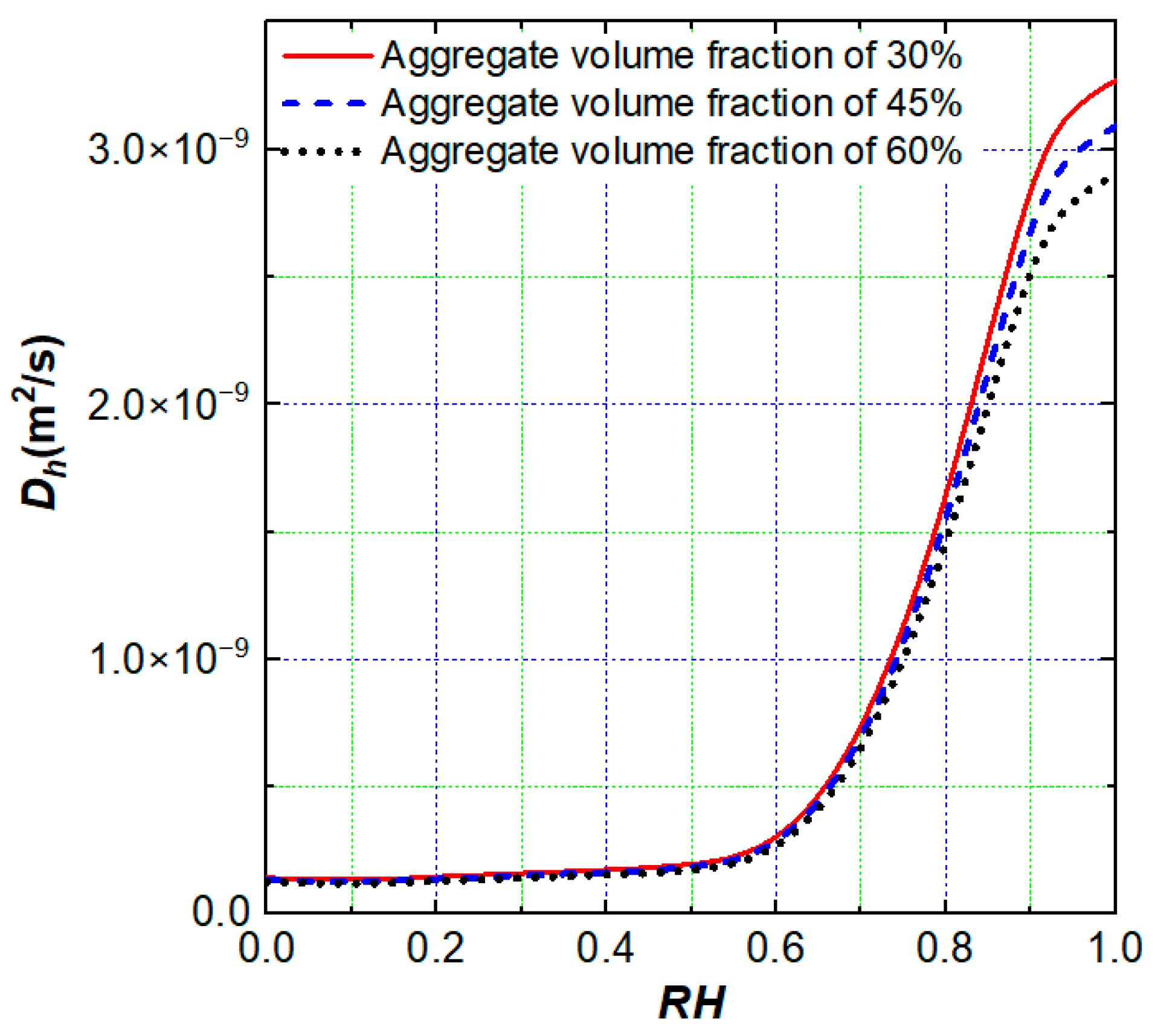
4.2. The Effect of ITZ Thickness and Aggregate Volume Fraction on Moisture Transfer

At the same time, according to the reference [37], concrete with a water–cement ratio of 0.5 and a volume ratio of cement paste, fine aggregate, and coarse aggregate of about 0.3: 0.25: 0.45 was selected. The influence of the thickness of ITZ on the overall moisture diffusion coefficient of concrete was analyzed, as shown in Figure 13. The results show that the moisture diffusion coefficient of concrete increases with the increase in the thickness of ITZ; especially when the internal RH of concrete is larger, the influence of ITZ is very significant. The reason is that the ITZ structure is loose and has a higher moisture diffusion coefficient than mortar and coarse aggregate. The increase in the thickness of the ITZ makes the concrete have more moisture migration channels, resulting in more moisture migration through the ITZ. It can be seen that although the volume of ITZ in concrete is relatively small, the influence of ITZ on the effective moisture diffusion coefficient of concrete cannot be ignored. When analyzing the effective moisture diffusion coefficient of concrete, it is necessary to consider the reasonable thickness of ITZ.

Similarly, the effect of the aggregate volume fraction on the effective moisture diffusion coefficient of concrete is shown in Figure 14. The results show that although the moisture diffusion coefficient of concrete increases with the increase in the aggregate volume fraction, the influence of aggregate is not very significant. The reason is that although the increase in the aggregate volume fraction enhances its “dilution” effect, the volume fraction of ITZ with a larger moisture diffusion coefficient also increases with the increase in the aggregate volume fraction, which weakens the “dilution” effect of aggregate to a certain extent. Therefore, when the volume fraction of aggregate increases, the influence of the additional ITZ on the surface on the overall moisture diffusion coefficient of concrete is less than the “dilution” effect of aggregate.

5. Conclusions

A multi-scale moisture diffusion coefficient model of concrete is established for the non-uniformity of moisture migration in concrete in this paper. The influence of microstructure on the moisture migration of concrete is discussed. The main conclusions are as follows:

(1)

The moisture diffusion coefficient model of concrete considering microstructure quantifies the role of Knudsen diffusion in moisture migration, which can effectively consider the effects of pore size distribution, aggregate content, and excessive interface on moisture migration;

(2)

The pore size distribution has a great influence on the humidity diffusion coefficient, and the humidity is more likely to migrate through the pores of 10~100 nm. Knudsen diffusion reduces the moisture diffusion coefficient of concrete to a certain extent, and its influence increases with the increase in the water–cement ratio and decreases with the increase in relative humidity, which also leads to the increase in the moisture diffusion coefficient with the increase in relative humidity to a certain extent;

(3)

The transient moisture migration of concrete has obvious non-uniformity. There is a “flow around” phenomenon at the edge of aggregate, and water is more likely to be transmitted through the excessive interface. With the increase in the aggregate volume fraction, the excessive interface with a higher moisture diffusion coefficient also increases, but the influence of the additional excessive interface on the overall moisture diffusion coefficient is less than that of the aggregate “dilution” effect;

(4)

The “S”-type growth relationship between the moisture diffusion coefficient and relative humidity of concrete includes the difference in the moisture diffusion coefficient between the wetting and drying process, which makes wetting faster than drying. At the same time, the jump growth of the moisture diffusion coefficient is also the main reason for the “inflection point” of the humidity distribution inside the concrete during the wetting and drying process.

In this study, the effect of microstructure on moisture migration in concrete is investigated by a multi-scale moisture diffusion model based on Knudsen diffusion, which can consider the cracking damage of pores induced by dry shrinkage from non-uniform moisture transfer and provide a theoretical basis for improving pore structure and moisture migration to reduce dry shrinkage and enhance the durability of concrete. In addition, for concrete subjected to gas or ion corrosion, the non-uniform transport and diffusion of ions and gas in the concrete can be studied according to the multi-scale diffusion model proposed in this study and the effect of concrete microstructure on the diffusion of ions and gas can be obtained.

In view of possible future developments, the variation in environmental temperature and the changes in concrete components and microstructures during the service have a significant influence on moisture transfer in concrete. Therefore, in future research, changes in temperature and the effect of load should be considered to further develop the multi-scale diffusion model. Additionally, experiments on moisture transfer should be conducted by considering the changes in concrete components and microstructures. The porosity, pore structure, and mineral composition can be experimentally measured. The experimental results can be used to validate and improve the multi-scale moisture diffusion model proposed in this study. Furthermore, the effect of temperature variation, load action, component, and microstructure changes on the moisture transfer in concrete can be investigated, which can provide a theoretical basis for reducing the dry shrinkage cracking and improving the durability of concrete in the service period.