Design of 3D Scanning Technology Using a Method with No External Reference Elements and Without Repositioning of the Device Relative to the Object
Abstract
1. Introduction
2. Materials and Methods
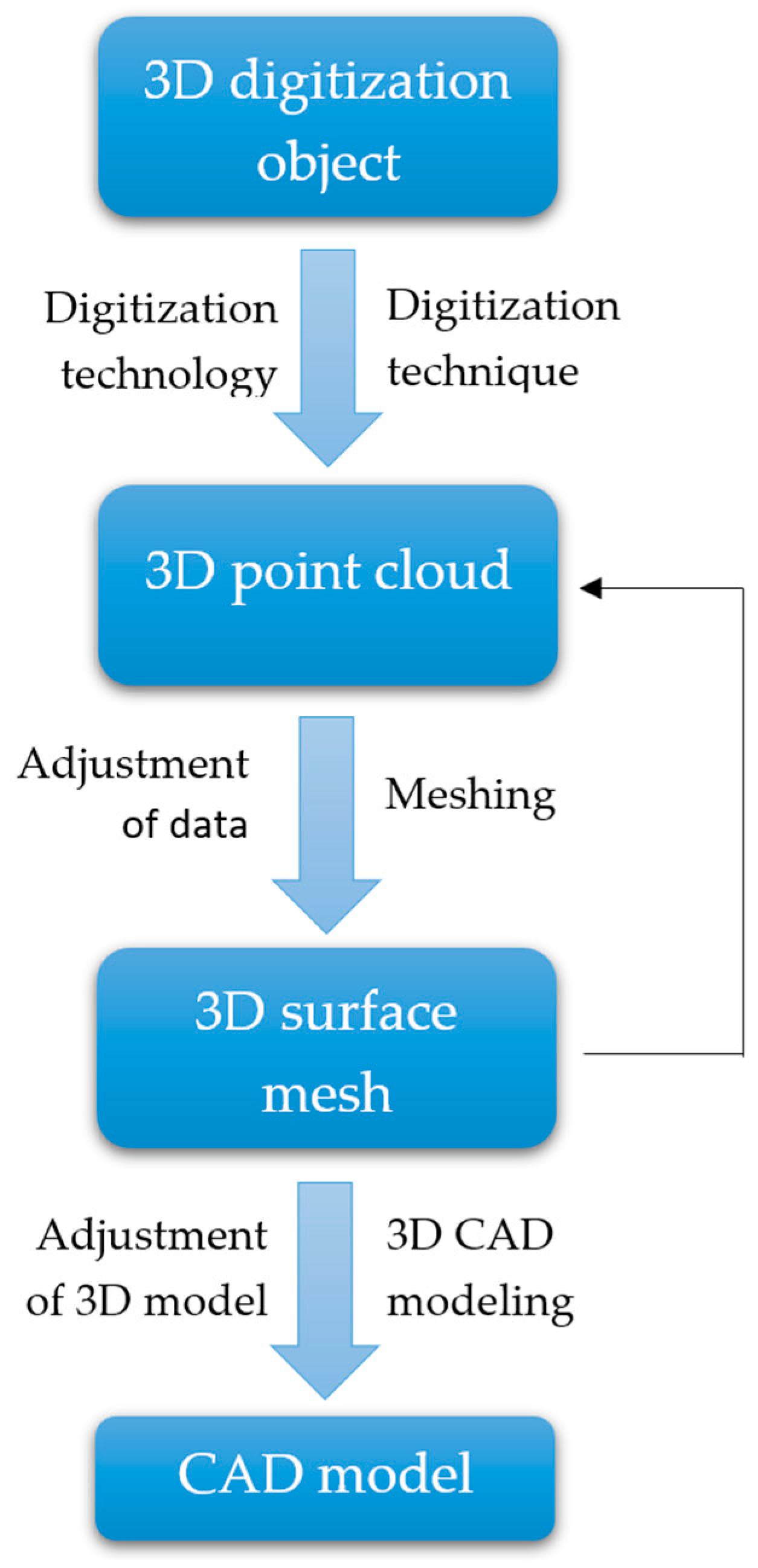
2.1. Reverse Engineering and 3D Surface Digitization
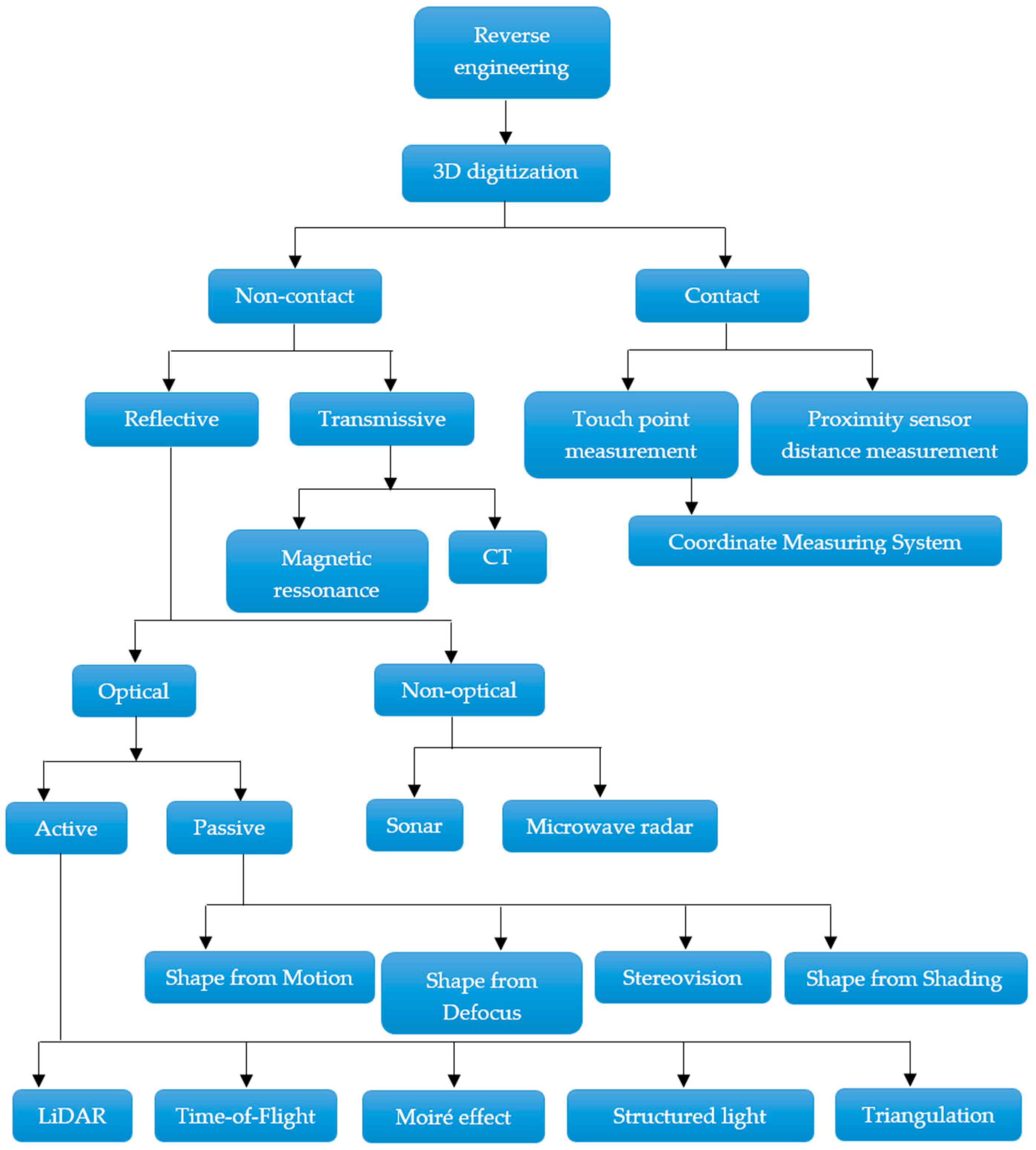
2.2. Reverse Engineering Techniques and Technologies
- portability—they should be lightweight and easily portable and be able to operate in confined spaces or harsh environments;
- accuracy—the range of distances between the values obtained and the actual values;
- range—the functional range of distances between the device and the object to be digitized;
- requirements for the physical properties of the digitized objects—size, surface characteristics, shape constancy and complexity of the object, etc.;
- repeatability—determines the extent of changes on the acquired data within several measurements of the same object by the same device and without changing the parameters;
- dynamic accuracy—the range of the number of measurements per unit time within which the specified accuracy can be achieved;
- calibration—making a comparison of the data obtained from a device relative to known values;
- volume, size, wattage and power parameters—the material and physical parameters of the equipment;
- safety—the extent to which there is a risk of harm, injury or death when working with the digitizing device;
- usability—the ability of the device to capture and measure multiple surface aspects of physical objects;
- cost—the sum of the purchase price and the operating costs over the required time horizon for the use of the device;
- output data—the method of display and representation of the acquired and retrieved data and the output format of the recorded data;
- ergonomics—design criteria for the physical and ergonomic demands of working with the device;
- robustness and durability—the ability of the equipment to withstand external influences and forces applied when working with the equipment;
- the nature, manner and extent of changes made and caused by the digitizing device to the digitized object as part of the digitization process [16].
- 1.
- Digitization using photogrammetry:
- A technique based on camera movement (Shape from Motion, SfM);
- Digitization using video (Shape from Video, SfV).
- 2.
- Stereo vision (Shape from Stereo, SfS) using dual sensing:
- Stereo vision with two optical sensors outside the head of the device;
- Stereo vision with two optical sensors located on the head of the device.
- 3.
- Stereo vision based on dual optics and single optical sensor sensing:
- channel with split optics;
- dual aperture optics;
- dual optical channel with prismatic lens;
- dual aperture optics with interlaced image;
- dual aperture optics with Complimentary Multiband Band-pass Filters (CMBF);
- variable optical path system;
- an off-axis static aperture system and a rotating disc.
- 4.
- Digitization based on the use of structured light:
- structured light technique with optical light guiding device;
- the structured light technique with a projection device on the external side of the endoscope;
- structured light technique based on phase shift analysis;
- structured light technique with spectrally encoded light pattern;
- a stereoscopic sensor pair using structured light;
- structured light technique with a multi-component coupled optical system sensor.
- 5.
- Digitization using endoscopic equipment with one optical channel:
- a technique based on differential focusing of the image and astigmatic projection of the light pattern;
- ToF reflected light Time of Flight calculation technique;
- holographic optics technique with a sensor on the endoscope head;
- holographic optics technique, light guided through an optical channel and a sensor outside the endoscope head;
- Shape from Shading (SfSh) technique;
- Shape from Defocus (SfD) technique of the sensor optics;
- SfD based technique for projected light patterns, 3D measurement technique using laser beams [20].
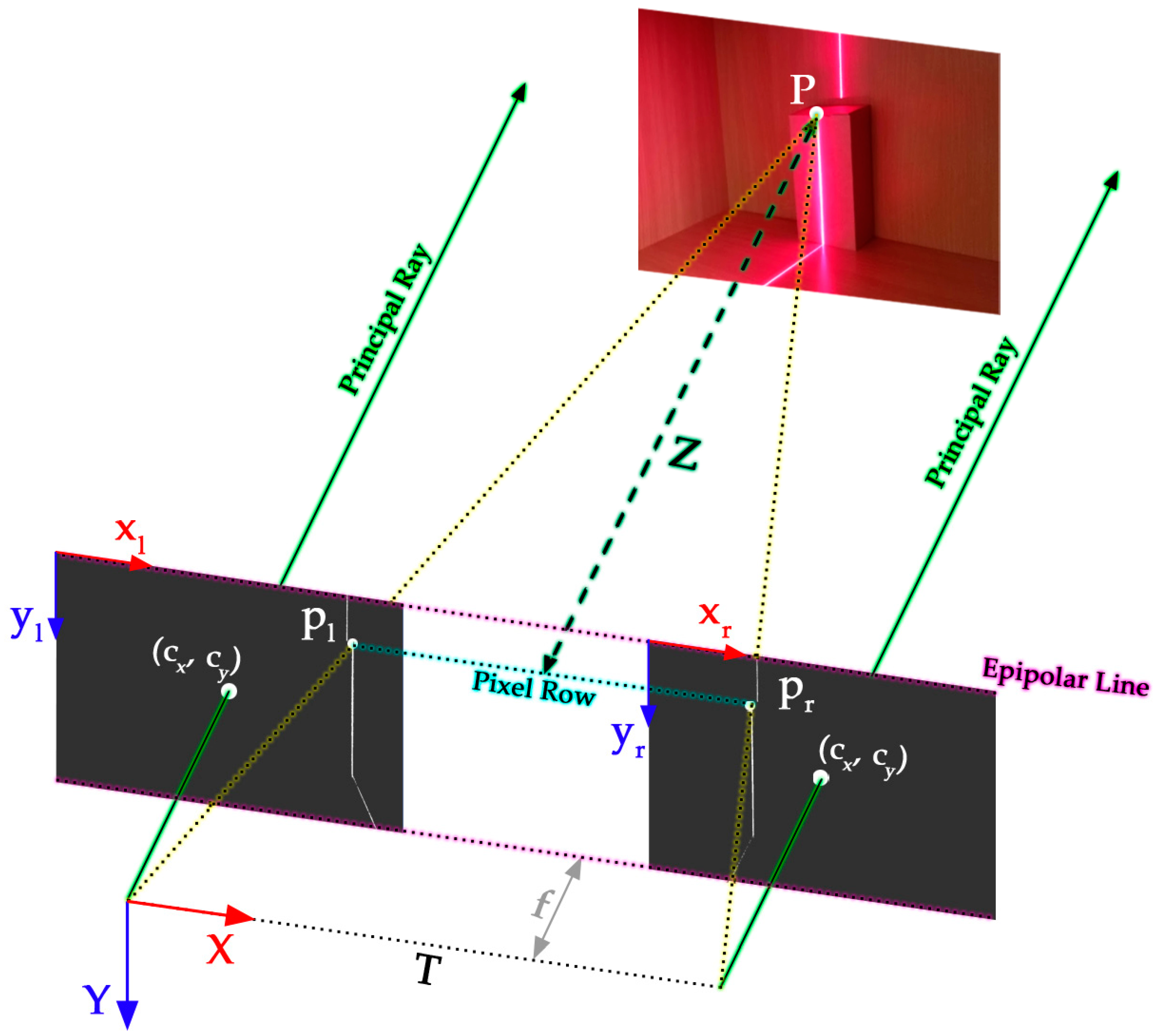
2.3. Shape from Stereo SfS
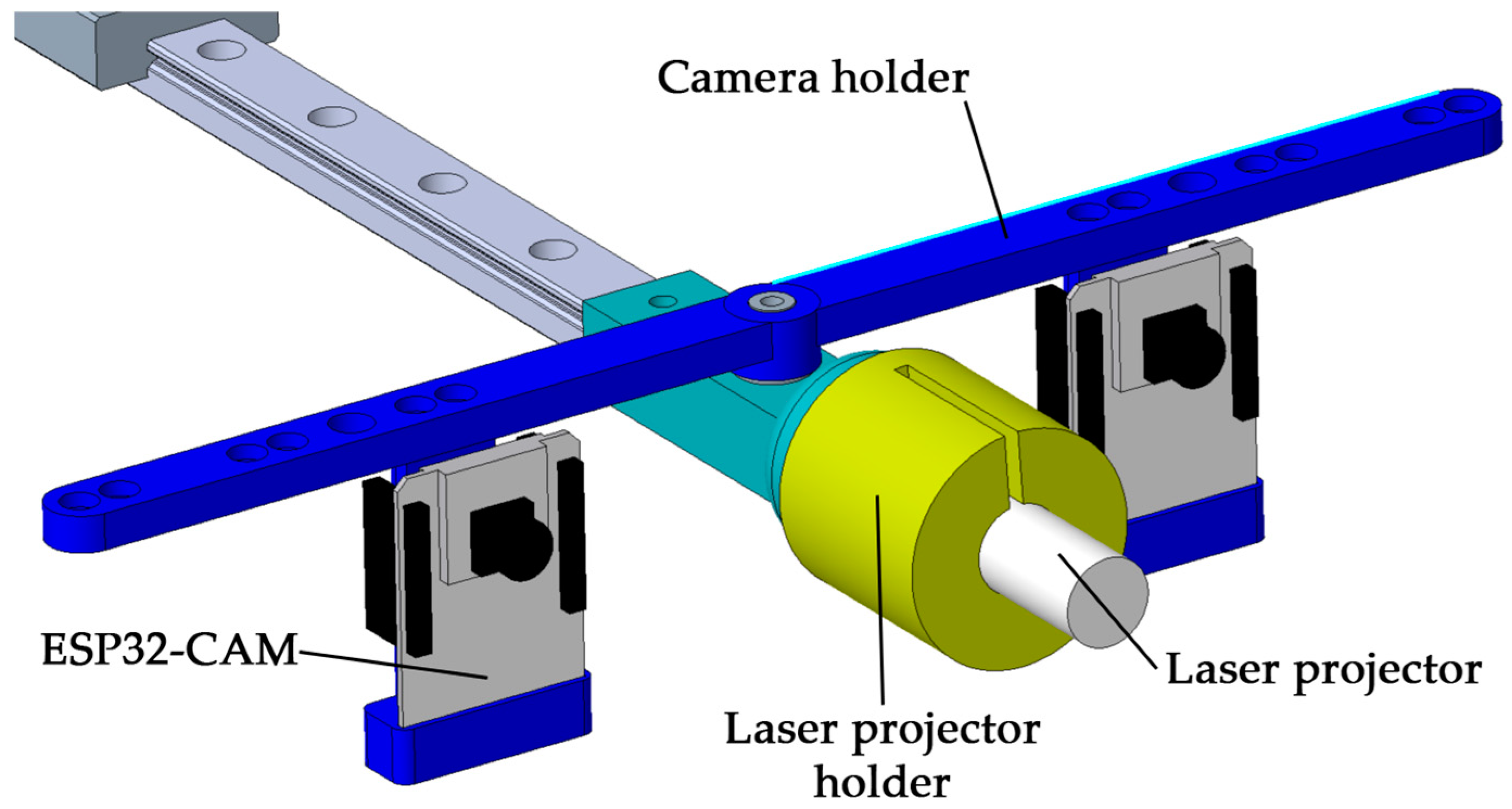
2.4. Initial Design of the Device
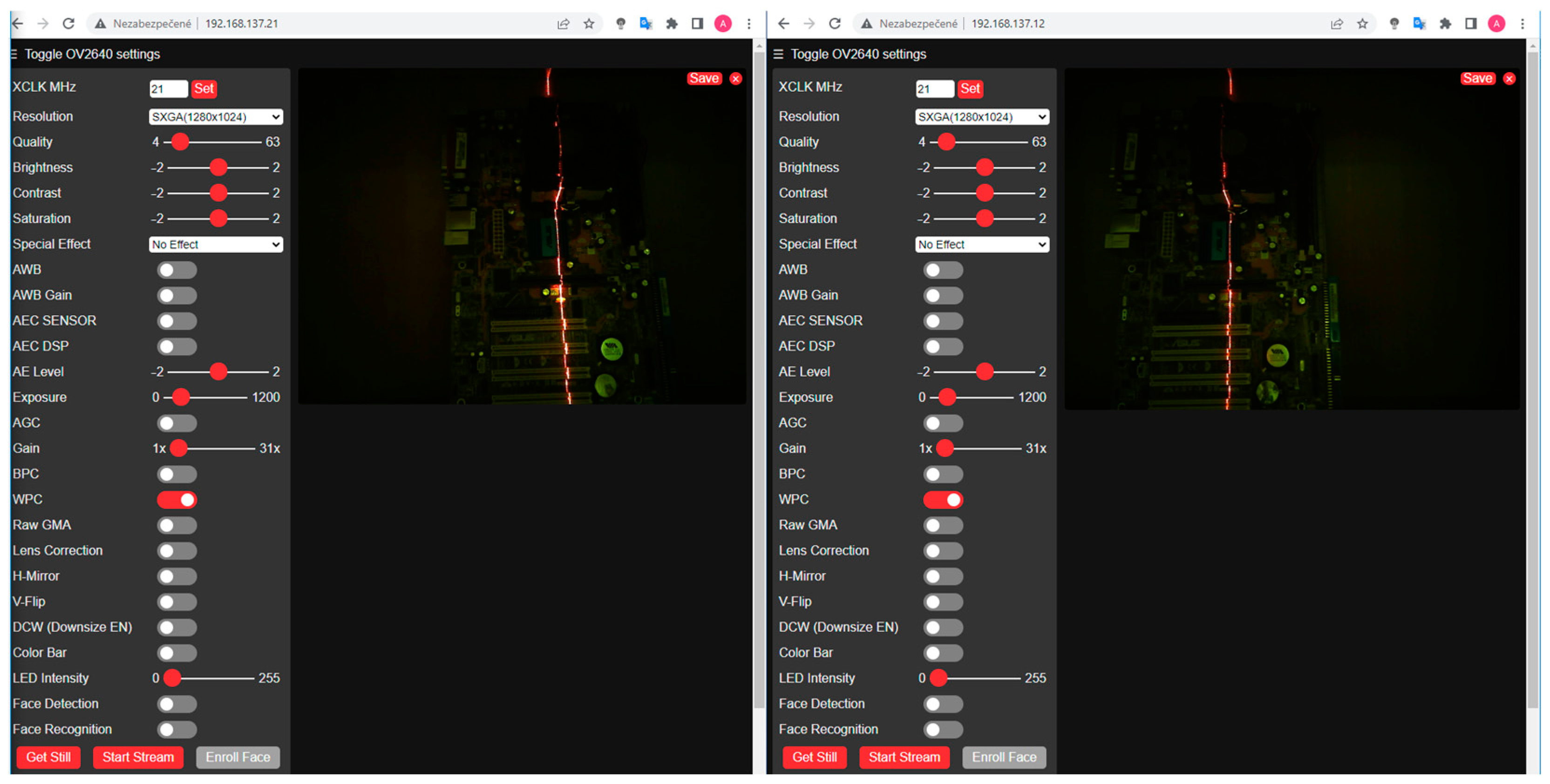
2.5. Calibration of Device
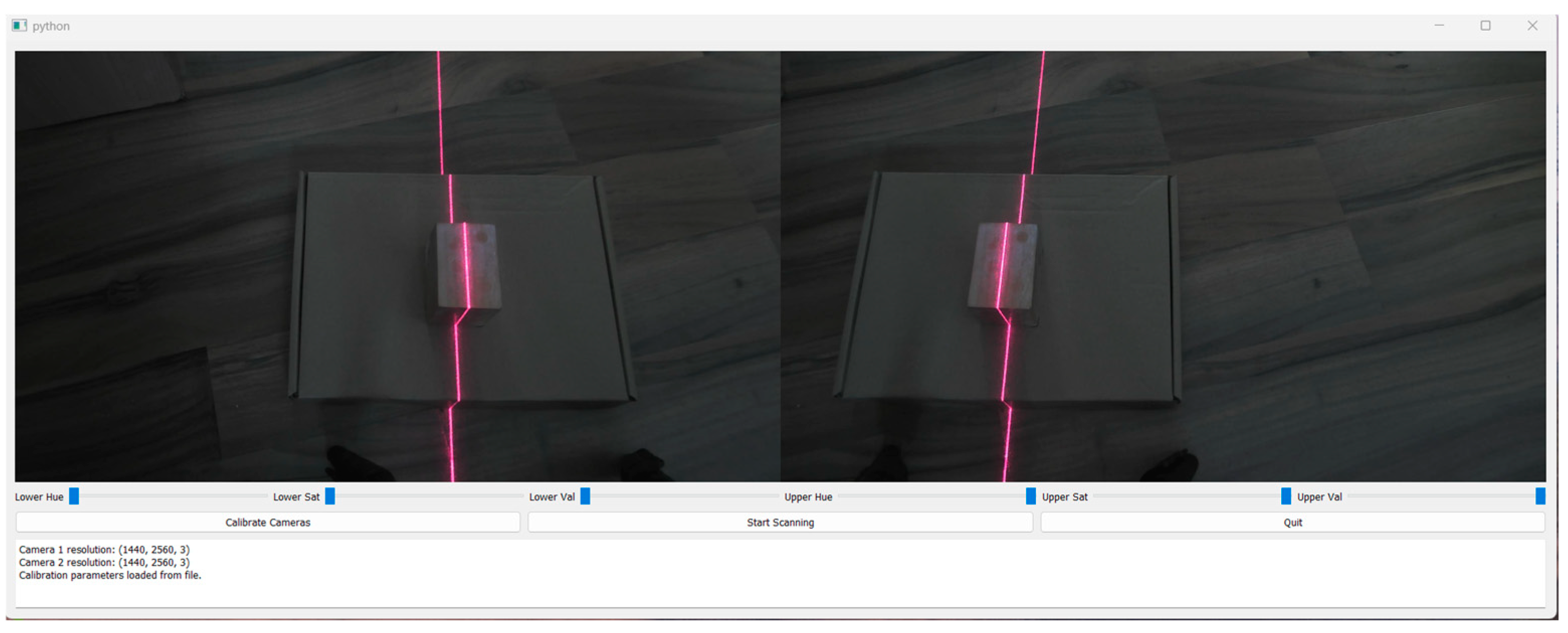
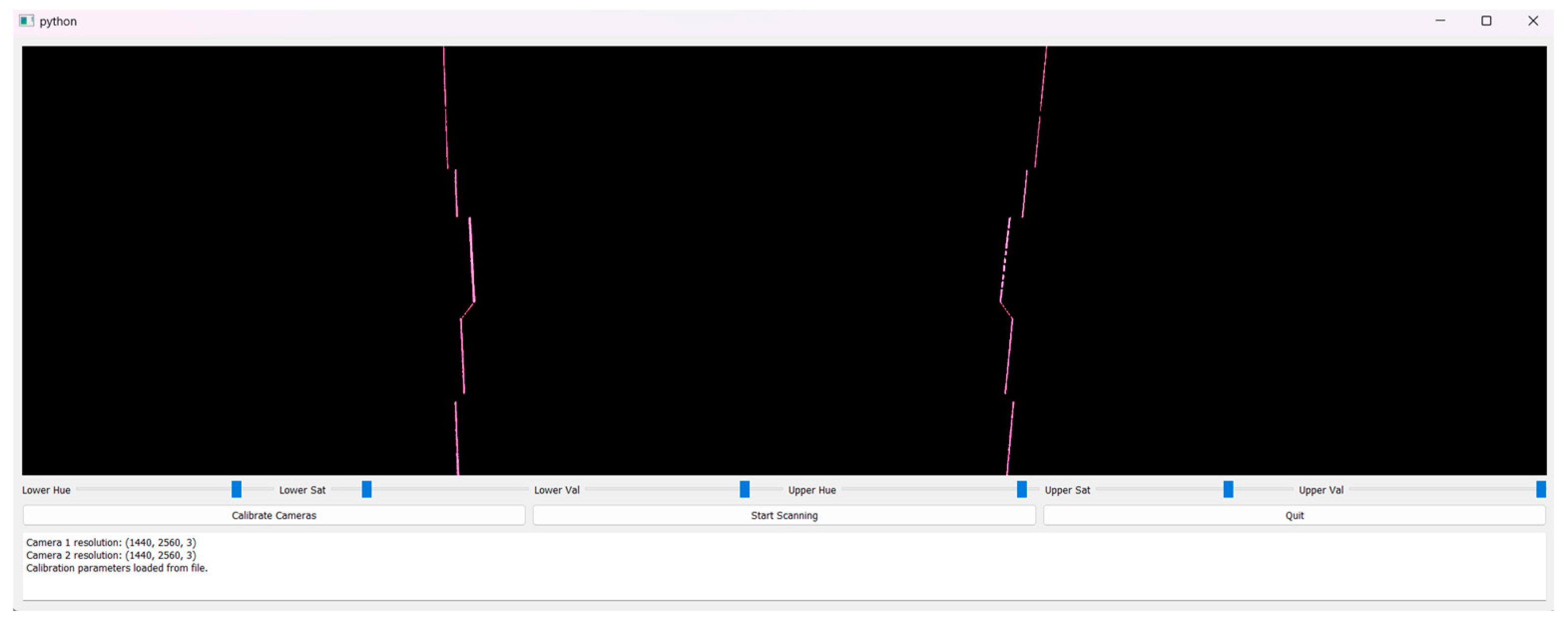
2.6. Image Processing for Calculating 3D Surface Coordinates
3. Results
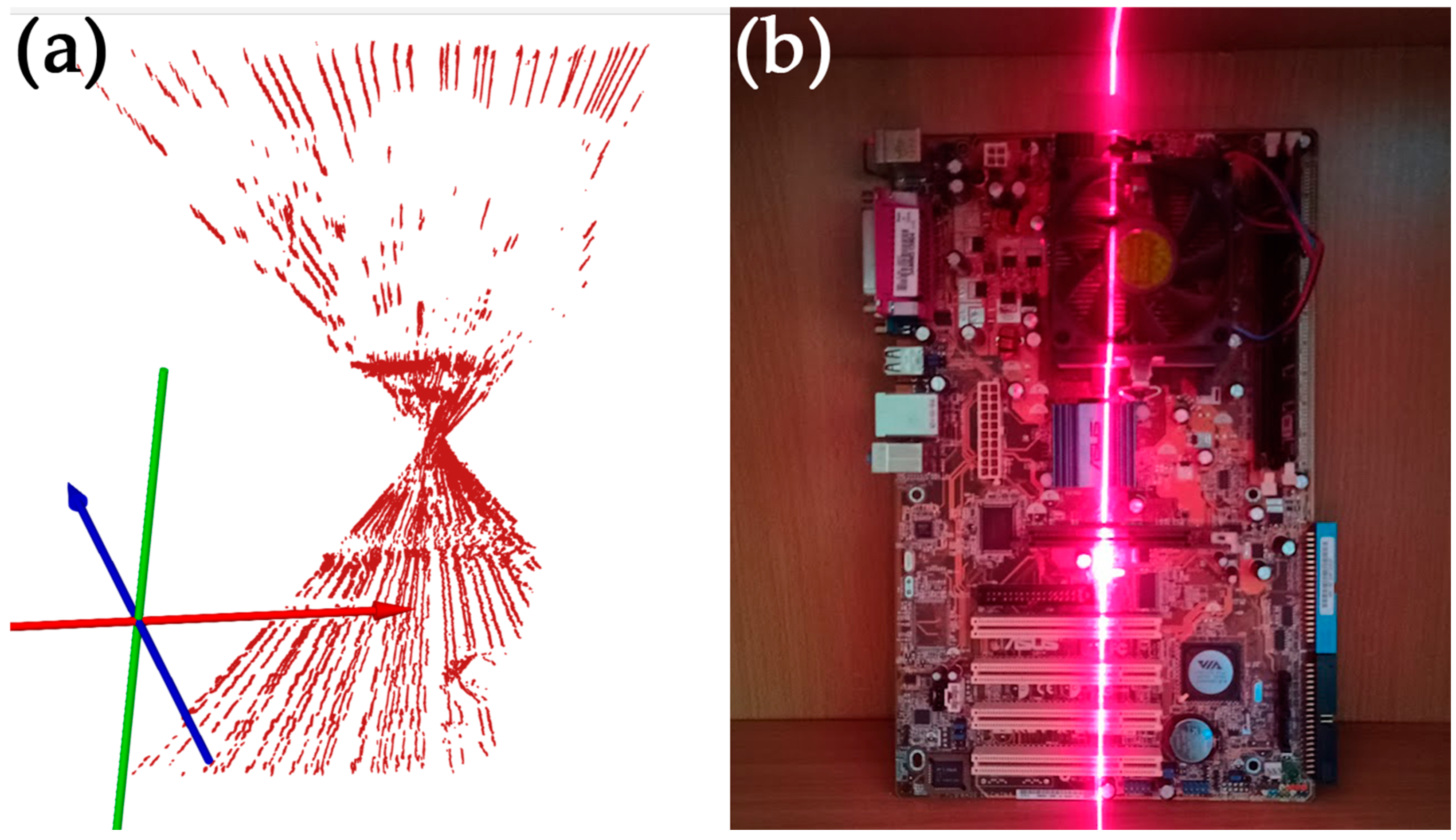
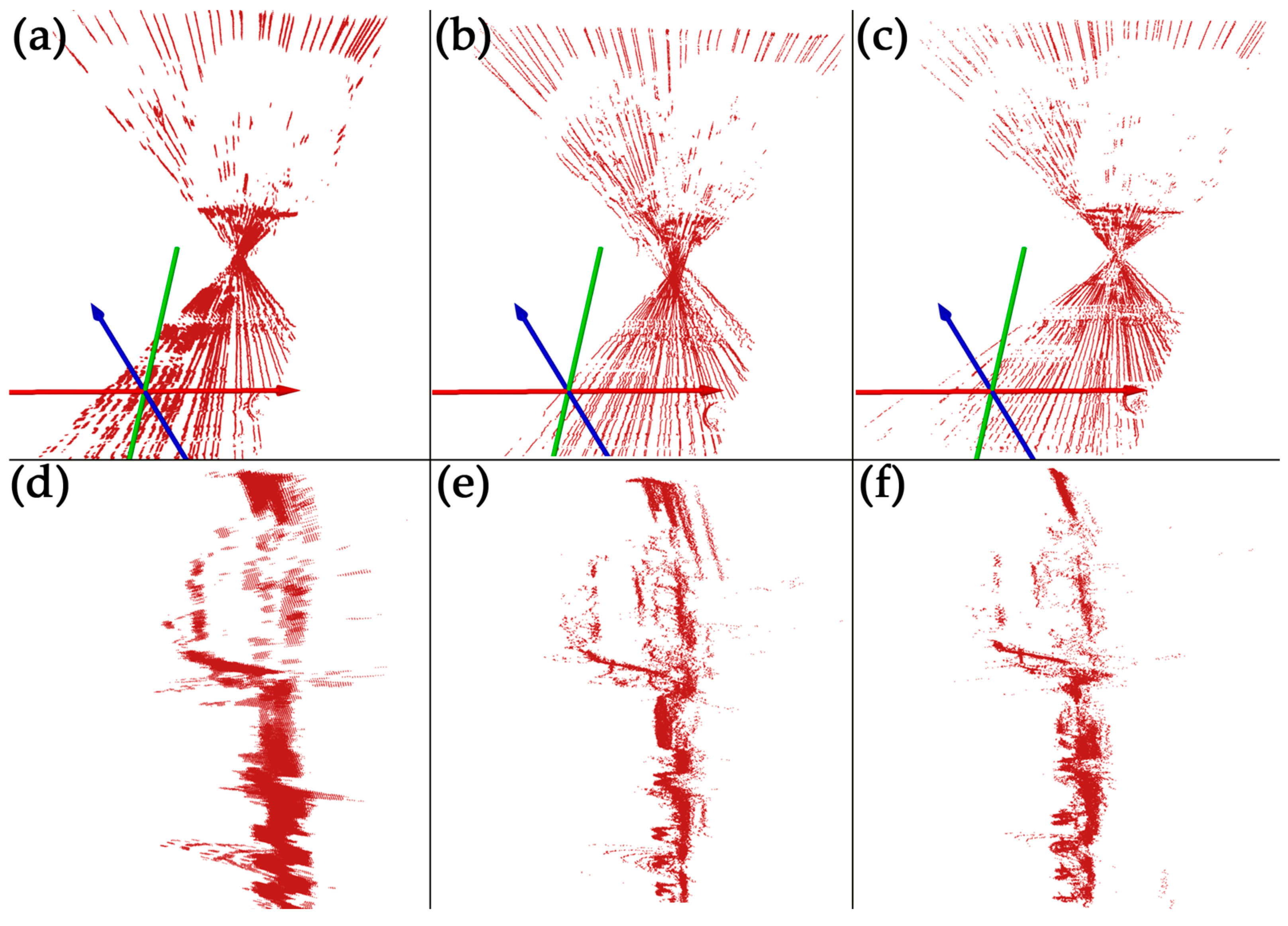
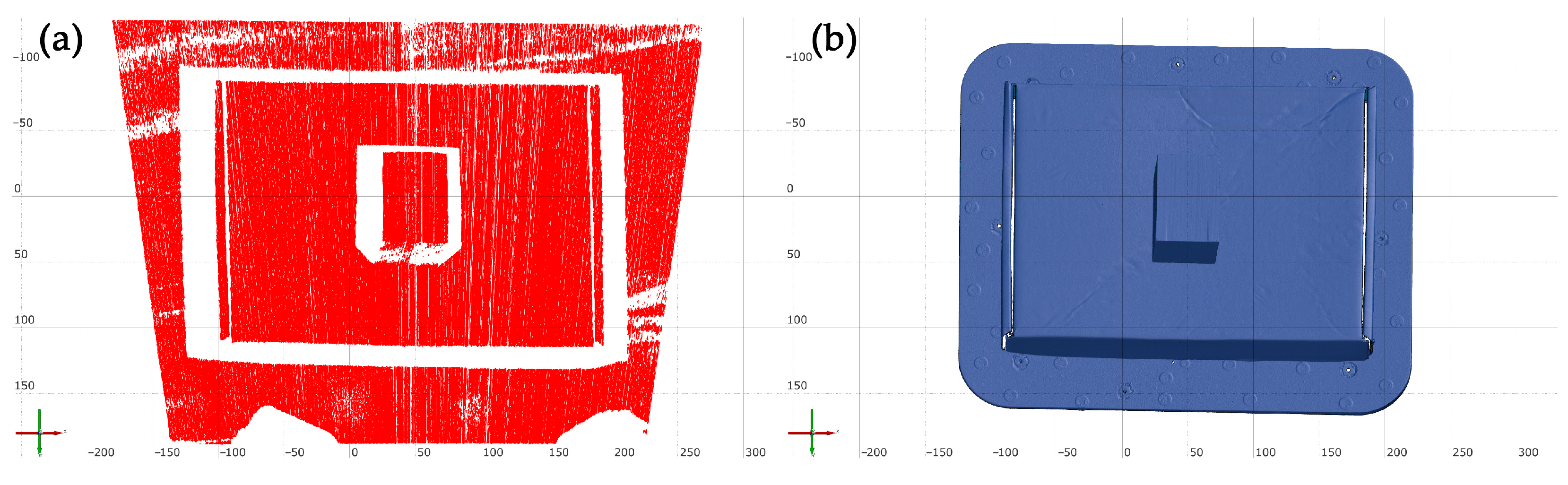
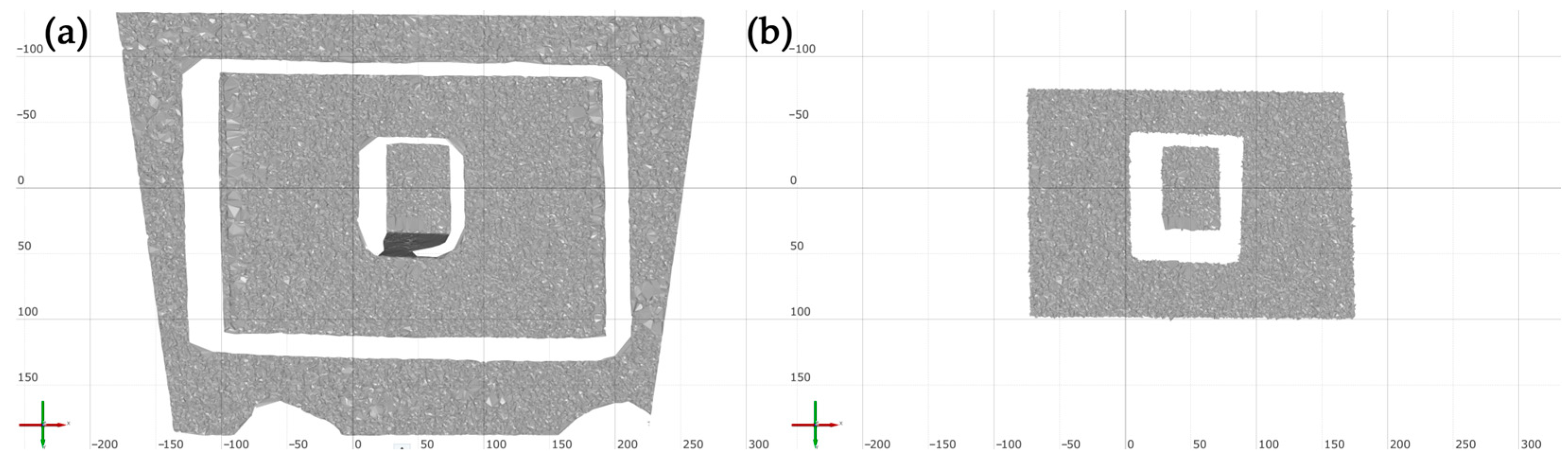
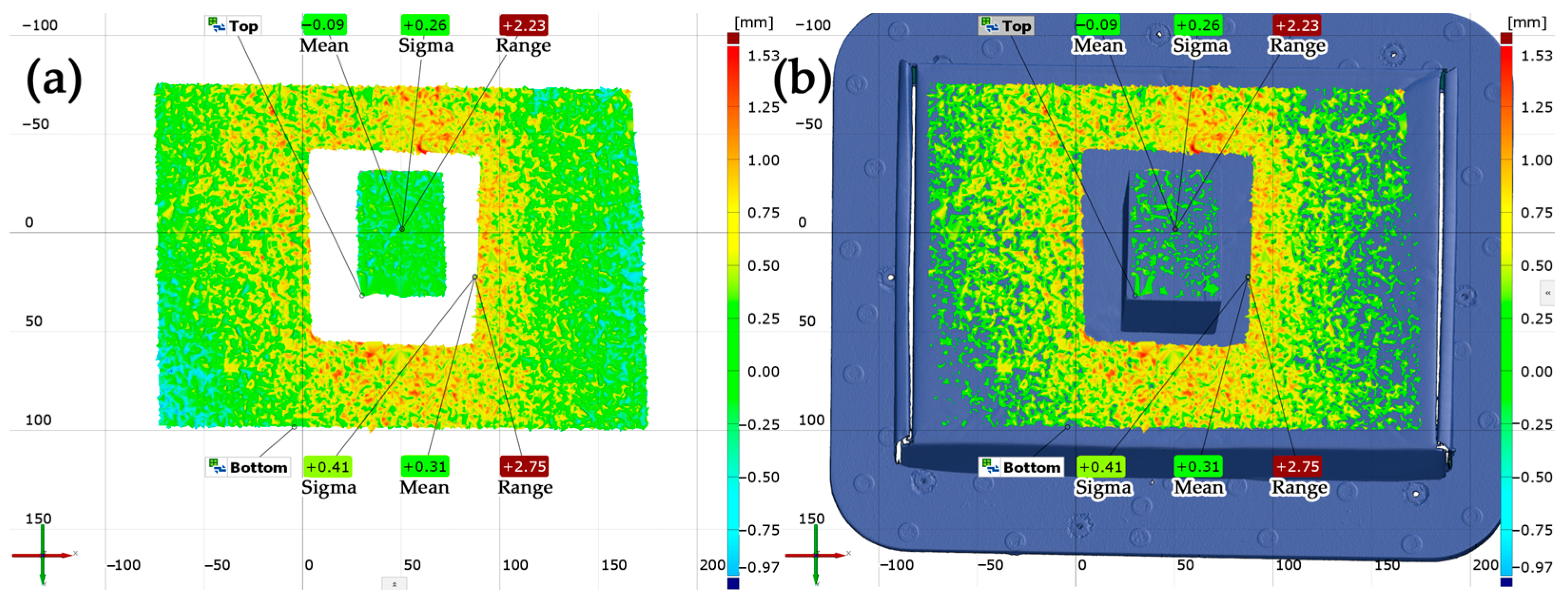
3.1. Scan Result Analysis
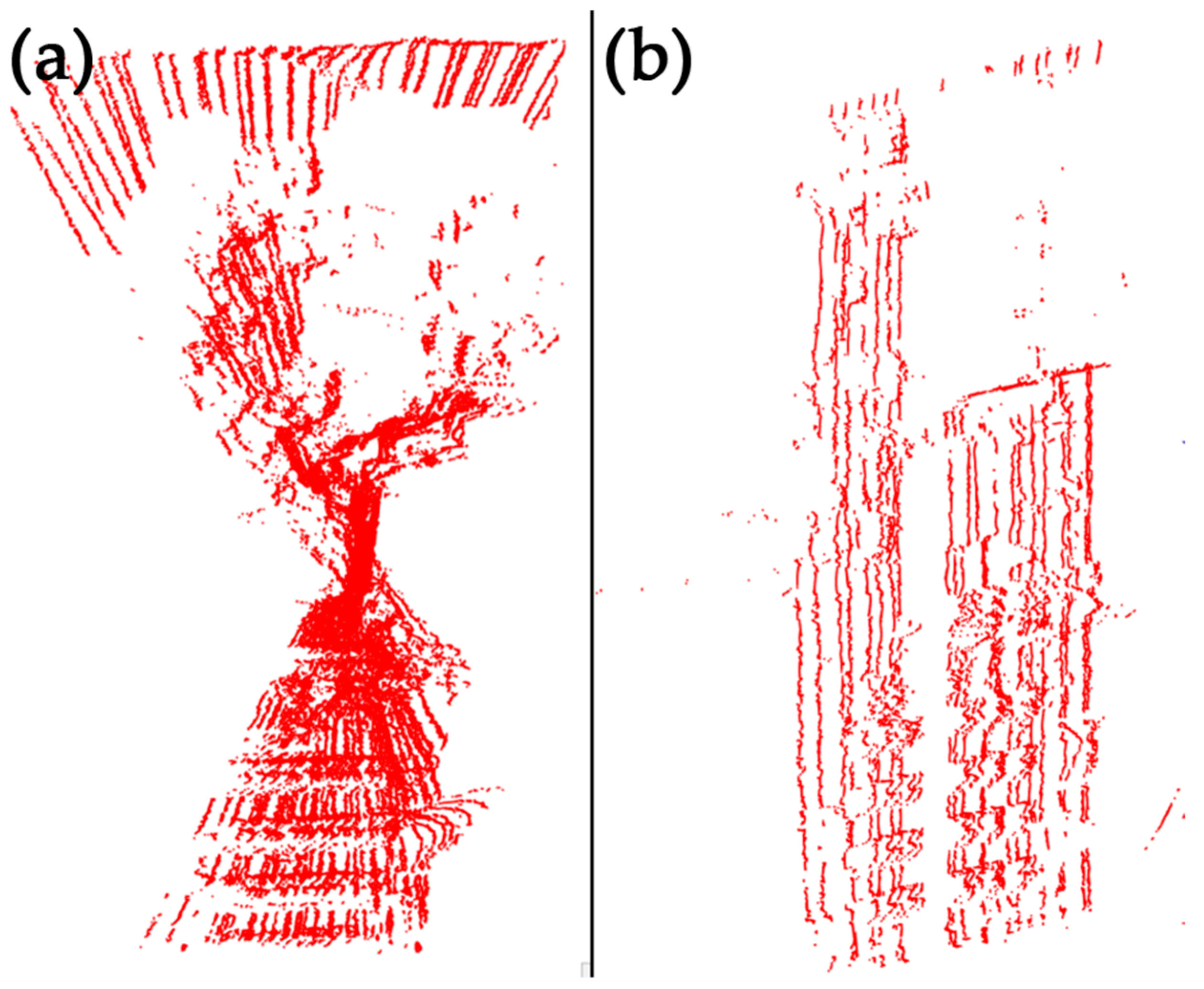
3.2. Further Design Improvements and Adjustments
3.3. Verification of the Performance of the Improved Prototype Design
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 3D | Three-dimensional |
| 2D | Two-dimensional |
| ICP | Iterative Closest Point |
| SLAM | Simultaneous Localization and Mapping |
| CAD | Computer Aided Design |
| CMM | Coordinate Measuring Machine |
| LiDAR | Light Detection and Ranging |
| ToF | Time of Flight |
| SfM | Shape from Motion |
| SfS | Shape from Stereo |
| CMBF | Complimentary Multiband Band-pass Filters |
| SfSh | Shape from Shading |
| SfD | Shape from Defocus |
| BM | Block Matching |
| SGBM | Semi-Global Block Matching |
| WiFi | Wireless Fidelity |
| FFF | Fused Filament Fabrication |
| GPIO | General Purpose Input/Output |
| RAM | Random Access Memory |
| PSRAM | Pseudo-Static Random Access Memory |
| LED | Light Emitting Diode |
| IP | Internet Protocol |
| AWB | Auto White Balance |
| AEC | Automatic Exposure Control |
| AE | Automatic Exposure |
| GMA | Gamma |
| BPC | Black Pixel Correction |
| WPC | White Pixel Correction |
| MPx | Megapixels |
| RGB | Red Green Blue |
| HSL | Hue Saturation Lightness |
| HSV | Hue Saturation Value |
References
- Wakjira, Y.; Kurukkal, N.S.; Lemu, H.G. Assessment of the Accuracy of 3D Printed Medical Models through Reverse Engineering. Heliyon 2024, 10, e31829. [Google Scholar] [CrossRef] [PubMed]
- Strzępek, P. The Assessment of Abrasion Resistance of Casted Non-Ferrous Metals and Alloys with the Use of 3D Scanning. Processes 2024, 12, 2200. [Google Scholar] [CrossRef]
- Borthakur, P.P. The Role and Future Directions of 3D Printing in Custom Prosthetic Design. Eng. Proc. 2025, 81, 10. [Google Scholar] [CrossRef]
- Szalai, V.; Stratan, A.; Ciutina, A.; Clepe, A.D.; Ene, A. Procedure for Generation of Finite Element Models of Steel Members from 3D Scanned Data. In Lecture Notes in Civil Engineering; Springer Nature Switzerland: Cham, Switzerland, 2024; pp. 154–164. ISBN 9783031577994. [Google Scholar]
- Daneshmand, M.; Helmi, A.; Avots, E.; Noroozi, F.; Alisinanoglu, F.; Arslan, H.S.; Gorbova, J.; Haamer, R.E.; Ozcinar, C.; Anbarjafari, G. 3D Scanning: A Comprehensive Survey. arXiv 2018, arXiv:1801.08863. [Google Scholar]
- Vodilka, A.; Kočiško, M.; Kaščak, J. Design of a Prototype of an Innovative 3D Scanning Technology for Use in the Digitization of Hard-to-Reach Places. Appl. Sci. 2025, 15, 2817. [Google Scholar] [CrossRef]
- Zhou, Q.-Y.; Park, J.; Koltun, V. Open3D: A Modern Library for 3D Data Processing. arXiv 2018, arXiv:1801.09847. [Google Scholar]
- Macario Barros, A.; Michel, M.; Moline, Y.; Corre, G.; Carrel, F. A Comprehensive Survey of Visual SLAM Algorithms. Robotics 2022, 11, 24. [Google Scholar] [CrossRef]
- Teo, T.-A.; Huang, S.-H. Surface-Based Registration of Airborne and Terrestrial Mobile LiDAR Point Clouds. Remote Sens. 2014, 6, 12686–12707. [Google Scholar] [CrossRef]
- Silva, R.; Silva, B.; Fernandes, C.; Morouço, P.; Alves, N.; Veloso, A. A Review on 3D Scanners Studies for Producing Customized Orthoses. Sensors 2024, 24, 1373. [Google Scholar] [CrossRef] [PubMed]
- Török, J.; Vodilka, A.; Kaščak, J.; Kočiško, M. Design of Personalized Orthoses with Support of PTC Creo and FDM Technology. In Lecture Notes in Mechanical Engineering; Springer Nature Switzerland: Cham, Switzerland, 2024; pp. 149–162. ISBN 9783031564581. [Google Scholar]
- Rothstock, S.; Weiss, H.-R.; Krueger, D.; Kleban, V.; Paul, L. Innovative Decision Support for Scoliosis Brace Therapy Based on Statistical Modelling of Markerless 3D Trunk Surface Data. Comput. Methods Biomech. Biomed. Engin. 2020, 23, 923–933. [Google Scholar] [CrossRef] [PubMed]
- Cheng, D.; Shi, H.; Xu, A.; Schwerin, M.; Crivella, M.; Li, L.; Choset, H. Visual-Laser-Inertial SLAM Using a Compact 3D Scanner for Confined Space. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Chen, R.; Chen, F.; Xu, G.; Li, X.; Shen, H.; Yuan, J. Precision Analysis Model and Experimentation of Vision Reconstruction with Two Cameras and 3D Orientation Reference. Sci. Rep. 2021, 11, 3875. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Sun, Q.; Gao, C.; Ren, Z.; Dai, W. A Three-Dimensional Vision Measurement Method Based on Double-Line Combined Structured Light. Sci. Rep. 2023, 13, 18660. [Google Scholar] [CrossRef] [PubMed]
- Messler, R.W., Jr. Reverse Engineering: Mechanisms, Structures, Systems & Materials; McGraw-Hill Professional: New York, NY, USA, 2013; ISBN 9780071825160. [Google Scholar]
- Kumar, A.; Jain, P.K.; Pathak, P.M. Reverse Engineering in Product Manufacturing: An Overview. In DAAAM International Scientific Book 2013; DAAAM International Vienna: Vienna, Austria, 2013; pp. 665–678. ISBN 9783901509940. [Google Scholar]
- Wang, W. Reverse Engineering: Technology of Reinvention; CRC Press: Boca Raton, FL, USA, 2010; ISBN 9781439806302. [Google Scholar]
- Vasco, J.C. Additive Manufacturing for the Automotive Industry. In Additive Manufacturing; Elsevier: Amsterdam, The Netherlands, 2021; pp. 505–530. ISBN 9780128184110. [Google Scholar]
- Geng, J.; Xie, J. Review of 3-D Endoscopic Surface Imaging Techniques. IEEE Sens. J. 2014, 14, 945–960. [Google Scholar] [CrossRef]
- Luhmann, T.; Robson, S.; Kyle, S.; Boehm, J. Close-Range Photogrammetry and 3D Imaging, 4th ed.; De Gruyter: Berlin, Germany, 2023; ISBN 9783111029351. [Google Scholar]
- ESP32-CAM Camera Development Board. Available online: https://docs.ai-thinker.com/en/esp32-cam (accessed on 13 March 2025).
- Brahmbhatt, S. Practical OpenCV, 1st ed.; APress: Berlin, Germany, 2013; ISBN 9781430260790. [Google Scholar]
- OpenCV: Camera Calibration with OpenCV. Available online: https://docs.opencv.org/4.x/d4/d94/tutorial_camera_calibration.html (accessed on 14 March 2025).
- Vaishya, A. Mastering OpenCV with Python: Use NumPy, Scikit, TensorFlow, and Matplotlib to Learn Advanced Algorithms for Machine Learning Through a Set of Practical Projects; Orange Education: Delhi, India, 2023; ISBN 9789390475797. [Google Scholar]
- OpenCV: Camera Calibration with Square Chessboard. Available online: https://docs.opencv.org/4.x/dc/d43/tutorial_camera_calibration_square_chess.html (accessed on 14 March 2025).
- Bradski, G.R.; Kaehler, A. Learning OpenCV: Computer Vision with the OpenCV Library, 2nd ed.; O’Reilly Media: Sebastopol, CA, USA, 2015; ISBN 9781449314651. [Google Scholar]
- Chen, J. Learn OpenCV with Python by Examples: Implement Computer Vision Algorithms Provided by OpenCV with Python for Image Processing, Object Detection and Machine Learning, 2nd ed.; James Chen, 2023; ISBN 9781738908448. [Google Scholar]
- CR-Scan Raptor. Available online: https://www.creality.com/products/creality-cr-scan-raptor (accessed on 27 March 2025).
- Vodilka, A.; Pollák, M.; Kočiško, M. Polygonization of the Surface Digitized Using Helios2 Time-of-Flight Camera. In EAI/Springer Innovations in Communication and Computing; Springer International Publishing: Cham, Switzerland, 2023; pp. 31–43. ISBN 9783031227189. [Google Scholar]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vodilka, A.; Kočiško, M.; Pollák, M.; Kaščak, J.; Török, J. Design of 3D Scanning Technology Using a Method with No External Reference Elements and Without Repositioning of the Device Relative to the Object. Appl. Sci. 2025, 15, 4533. https://doi.org/10.3390/app15084533
Vodilka A, Kočiško M, Pollák M, Kaščak J, Török J. Design of 3D Scanning Technology Using a Method with No External Reference Elements and Without Repositioning of the Device Relative to the Object. Applied Sciences. 2025; 15(8):4533. https://doi.org/10.3390/app15084533
Chicago/Turabian StyleVodilka, Adrián, Marek Kočiško, Martin Pollák, Jakub Kaščak, and Jozef Török. 2025. "Design of 3D Scanning Technology Using a Method with No External Reference Elements and Without Repositioning of the Device Relative to the Object" Applied Sciences 15, no. 8: 4533. https://doi.org/10.3390/app15084533
APA StyleVodilka, A., Kočiško, M., Pollák, M., Kaščak, J., & Török, J. (2025). Design of 3D Scanning Technology Using a Method with No External Reference Elements and Without Repositioning of the Device Relative to the Object. Applied Sciences, 15(8), 4533. https://doi.org/10.3390/app15084533






