Study on the Mechanical Properties and Interaction Mechanism of Fractured Rock Subjected to Freeze–Thaw Cycles
Abstract
1. Introduction
2. Test Materials and Program
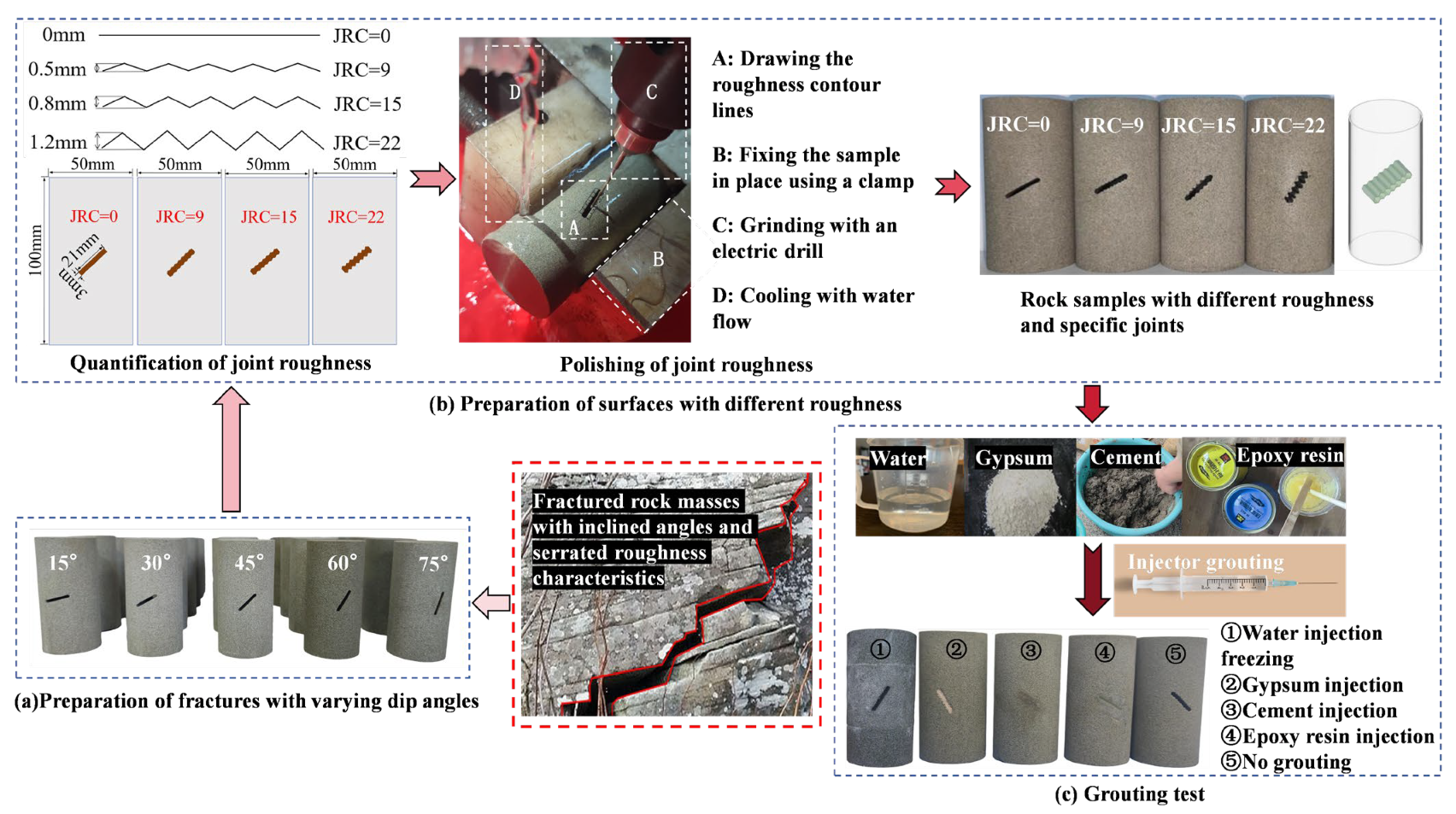
2.1. Sample Preparation
2.2. Experimental Design
2.3. Test Methods
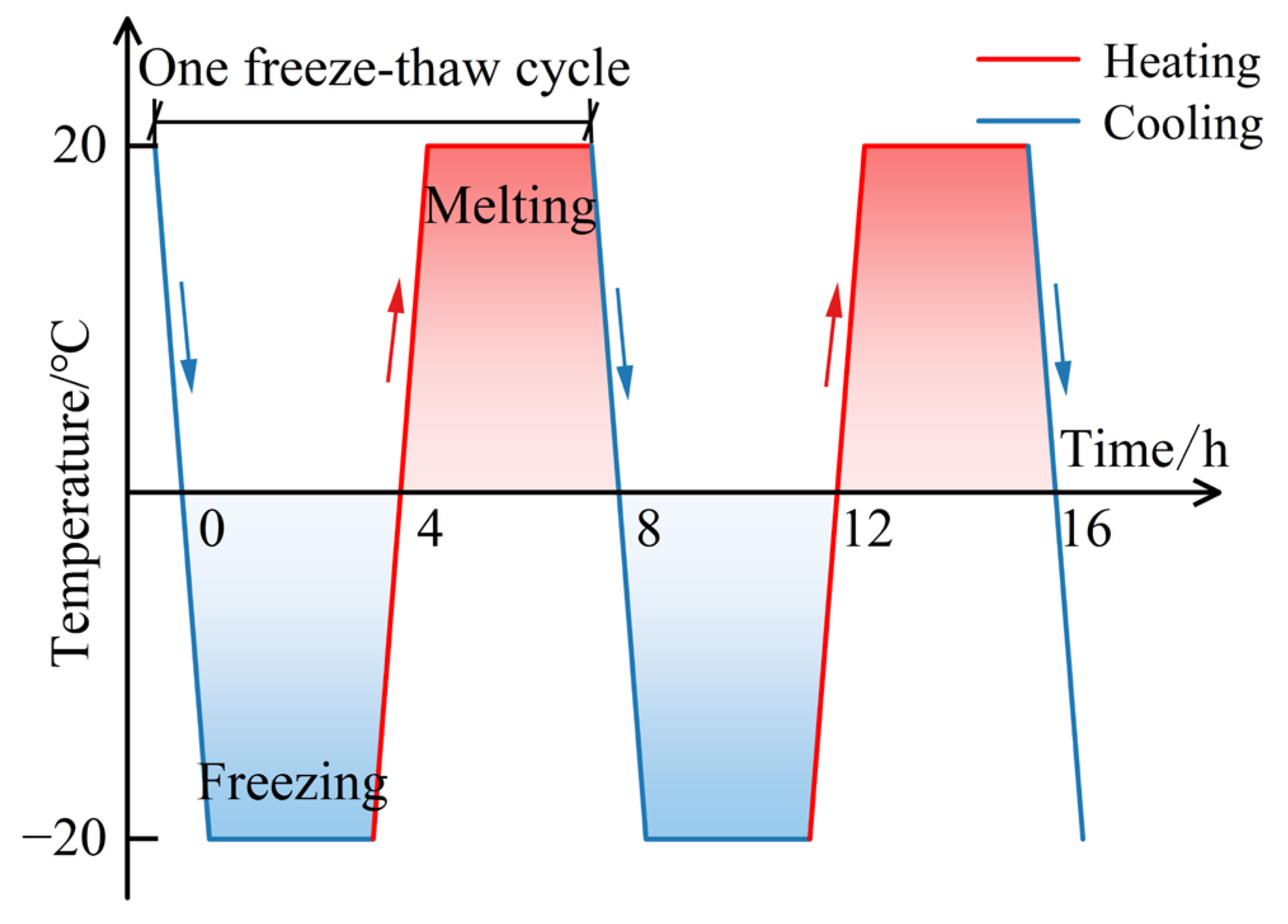
2.3.1. Freeze–Thaw Cycling Test
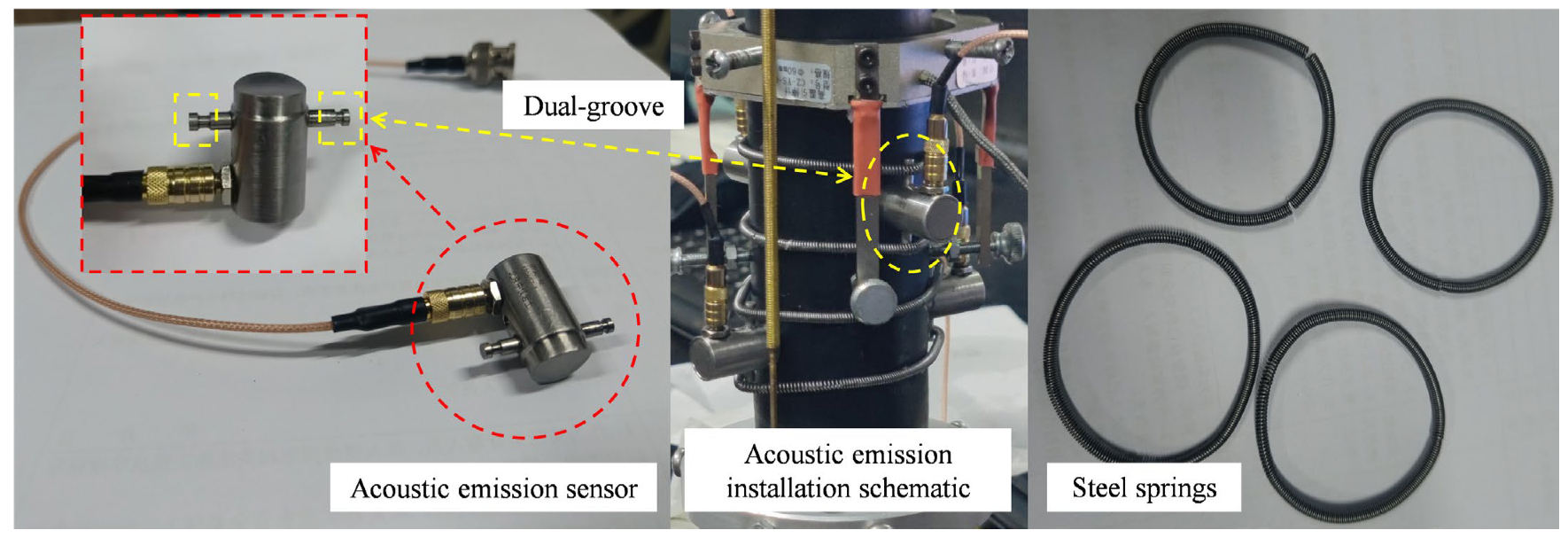
2.3.2. Uniaxial and Triaxial Compression Tests
3. Analysis of Test Results
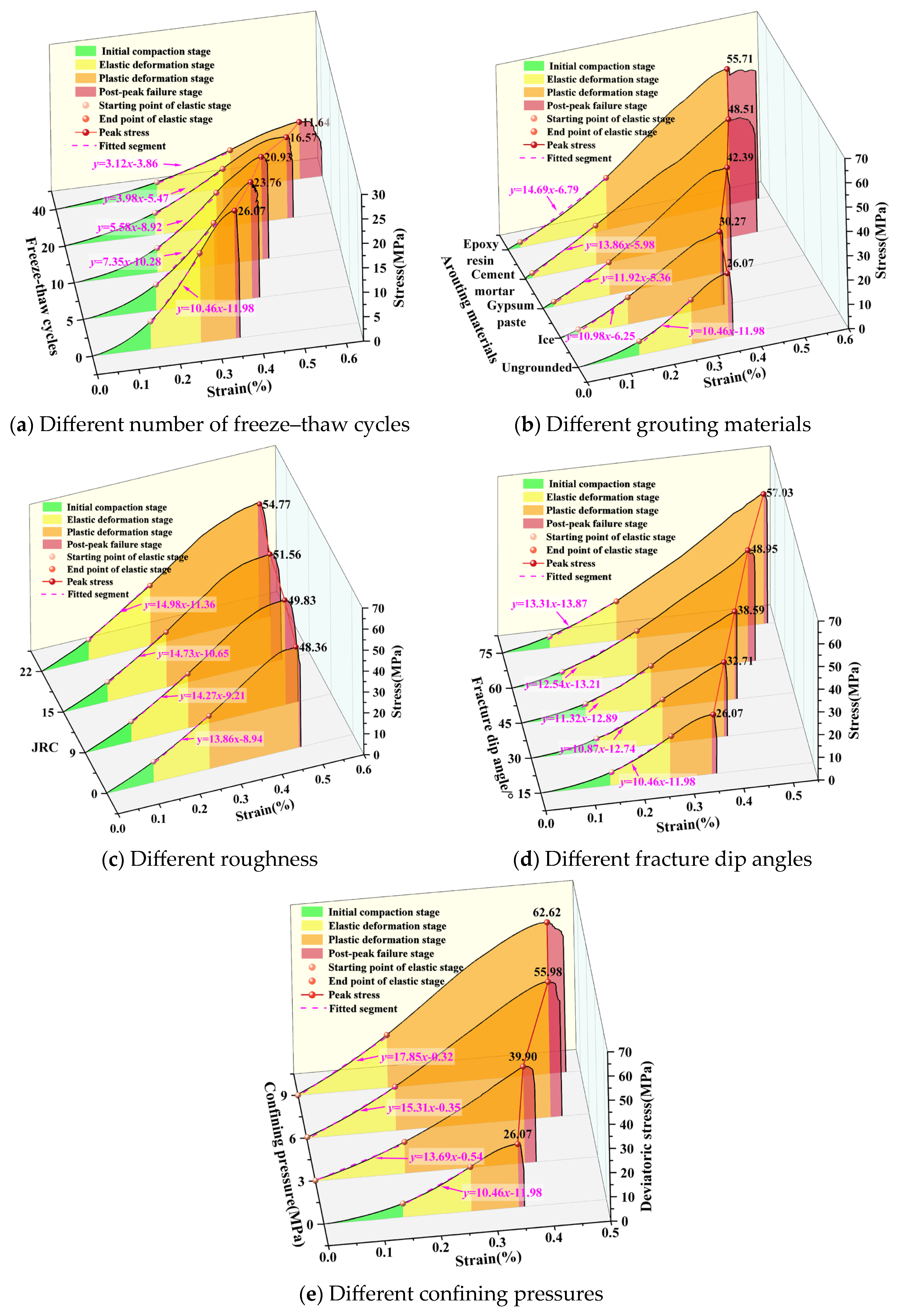
3.1. Mechanical Properties of Sandstone Under the Action of a Single Factor
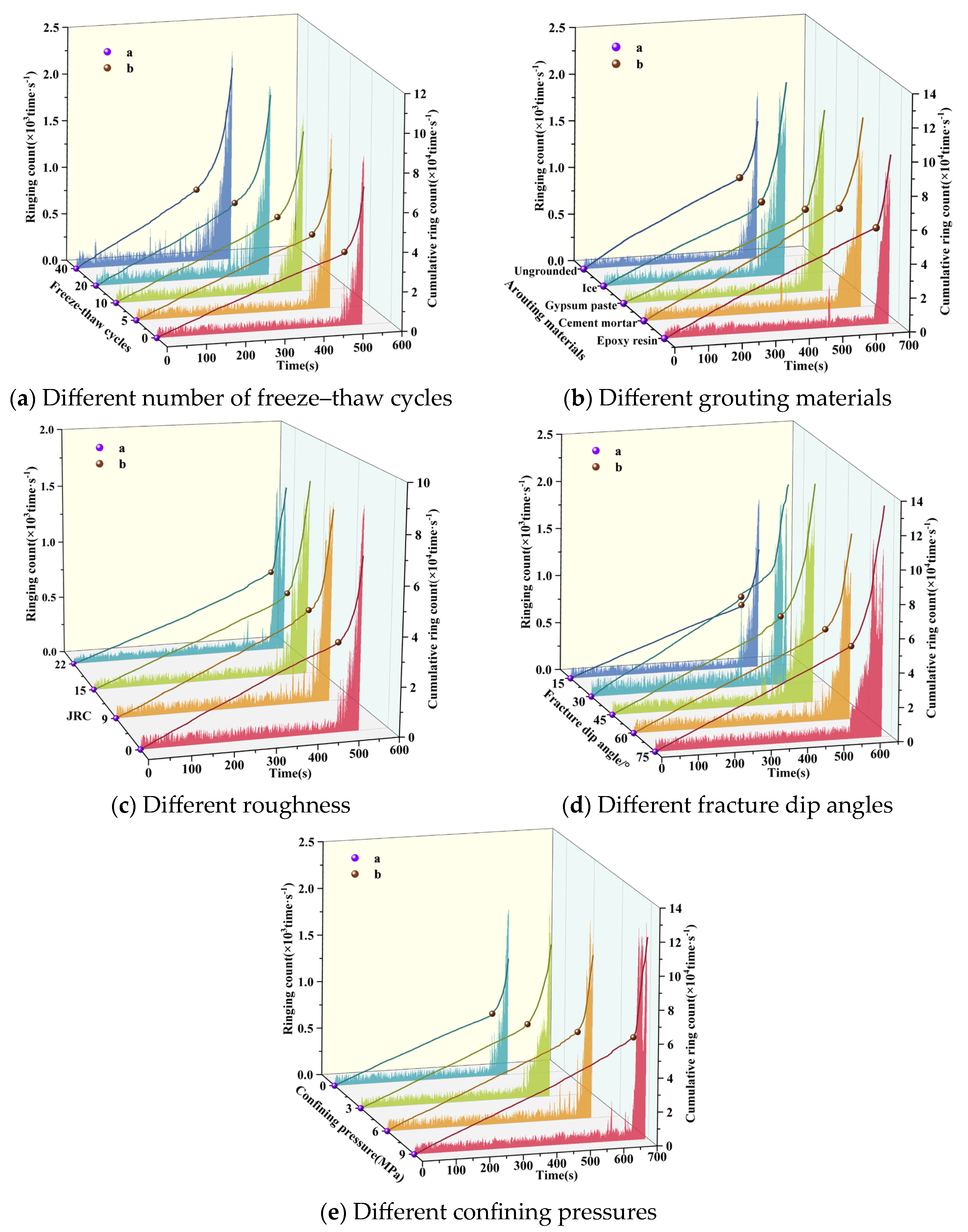
3.2. Characterization of the Acoustic Emission Evolution of Sandstone Under the Action of a Single Factor
3.3. Rock Mechanical Properties Under the Interaction of Multiple Factors
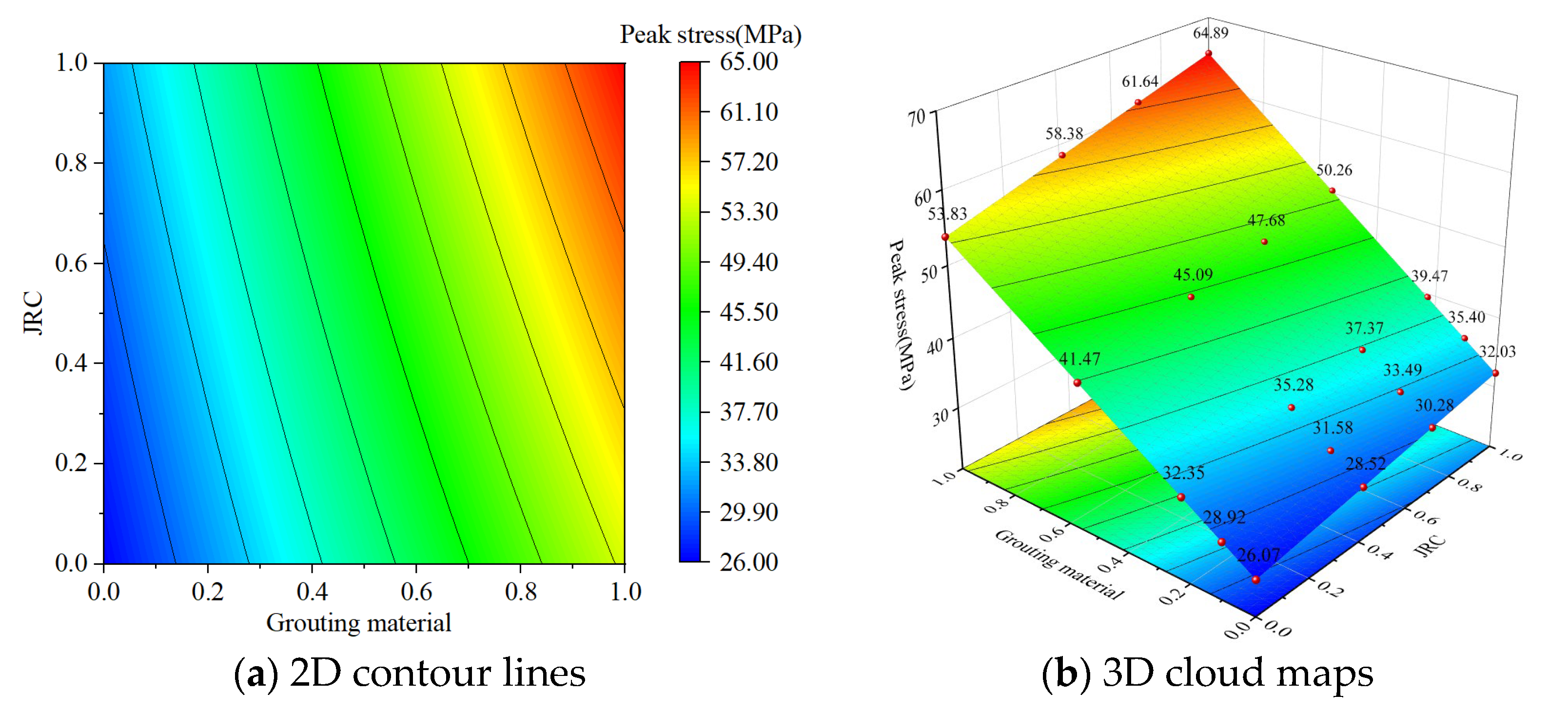
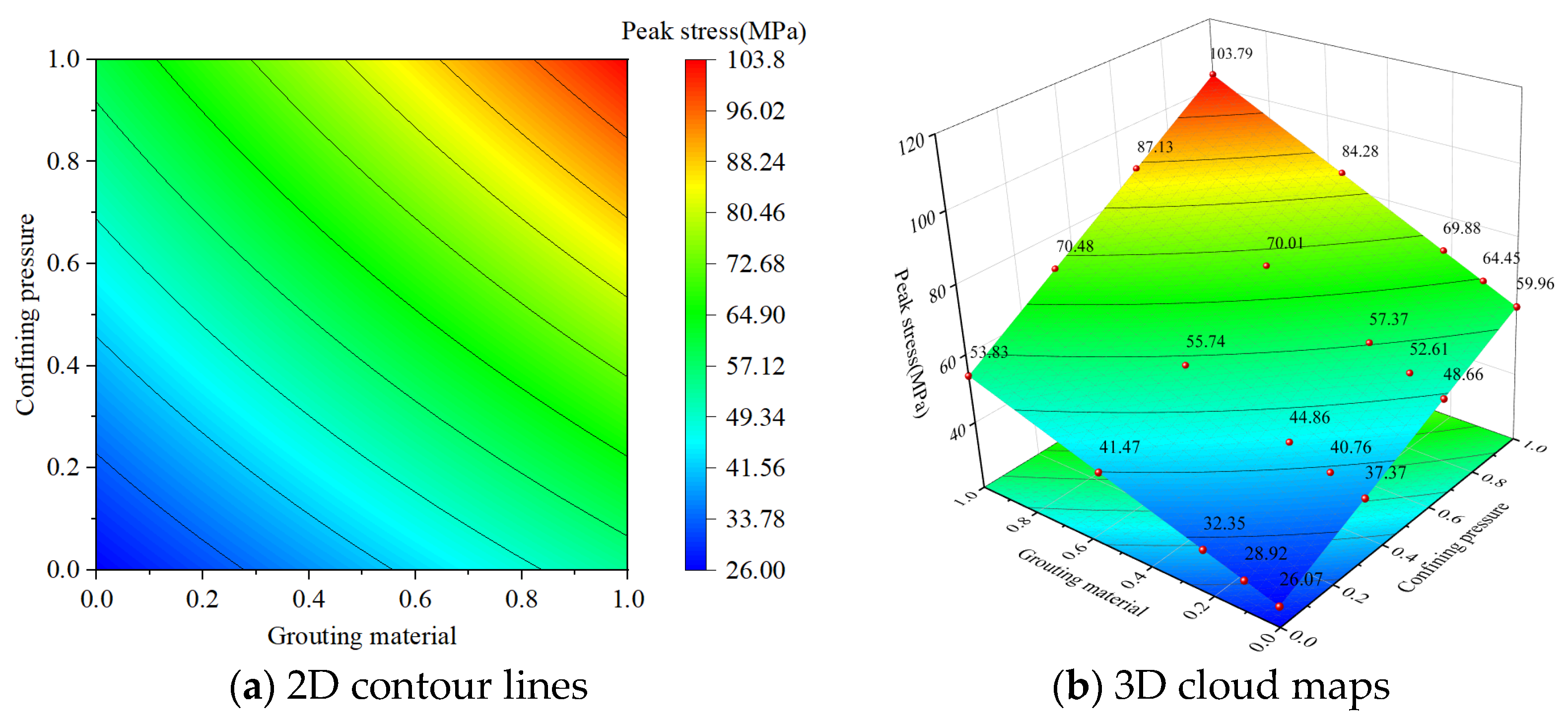
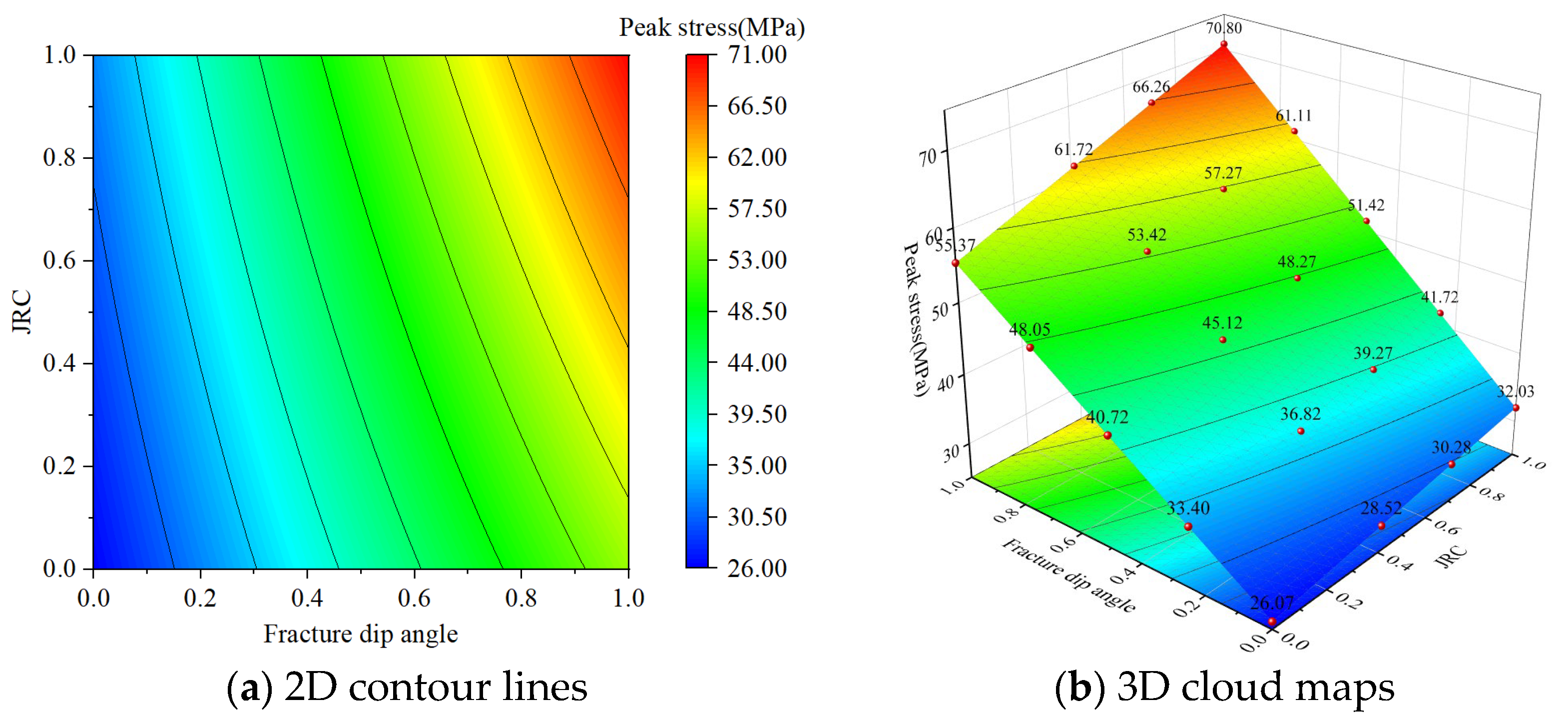
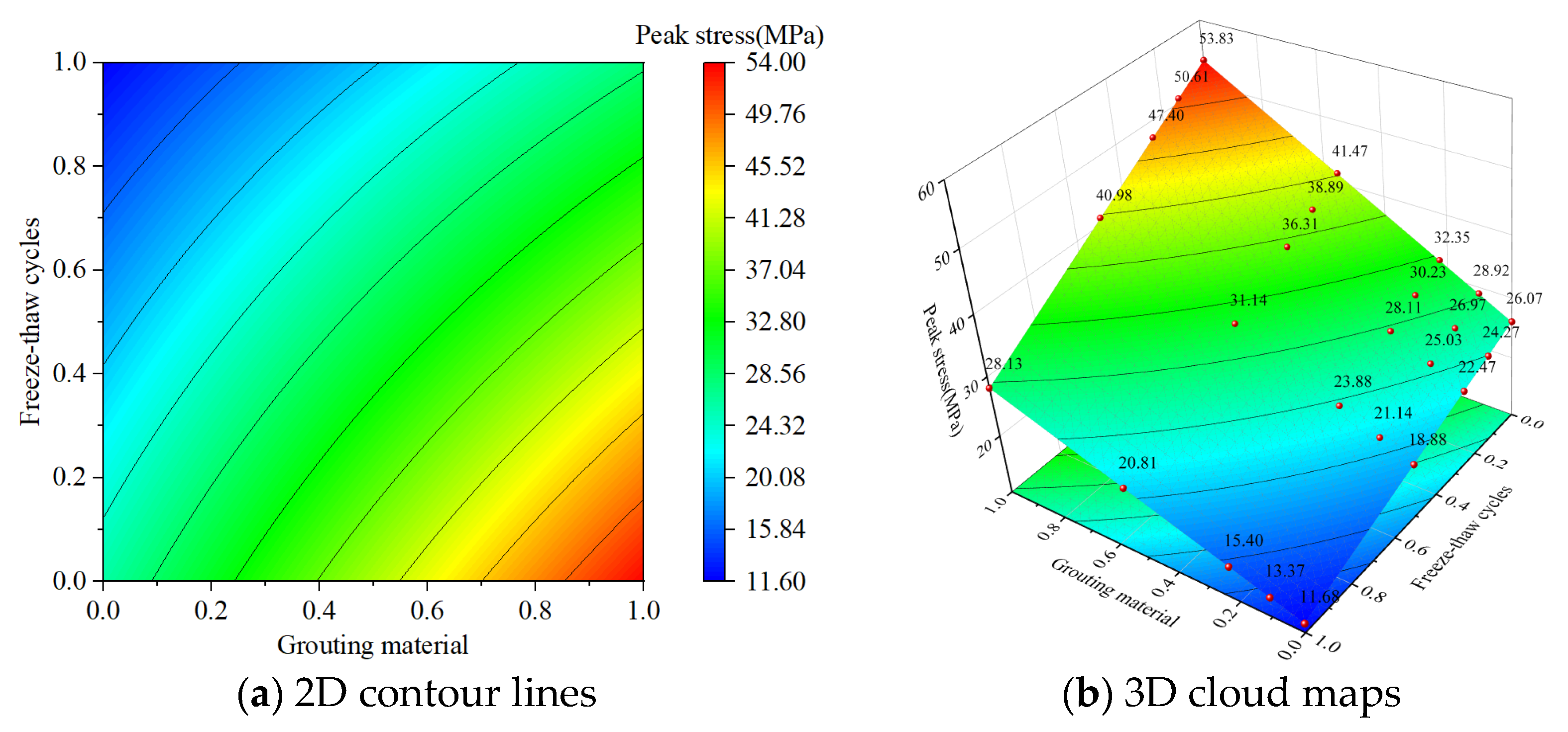
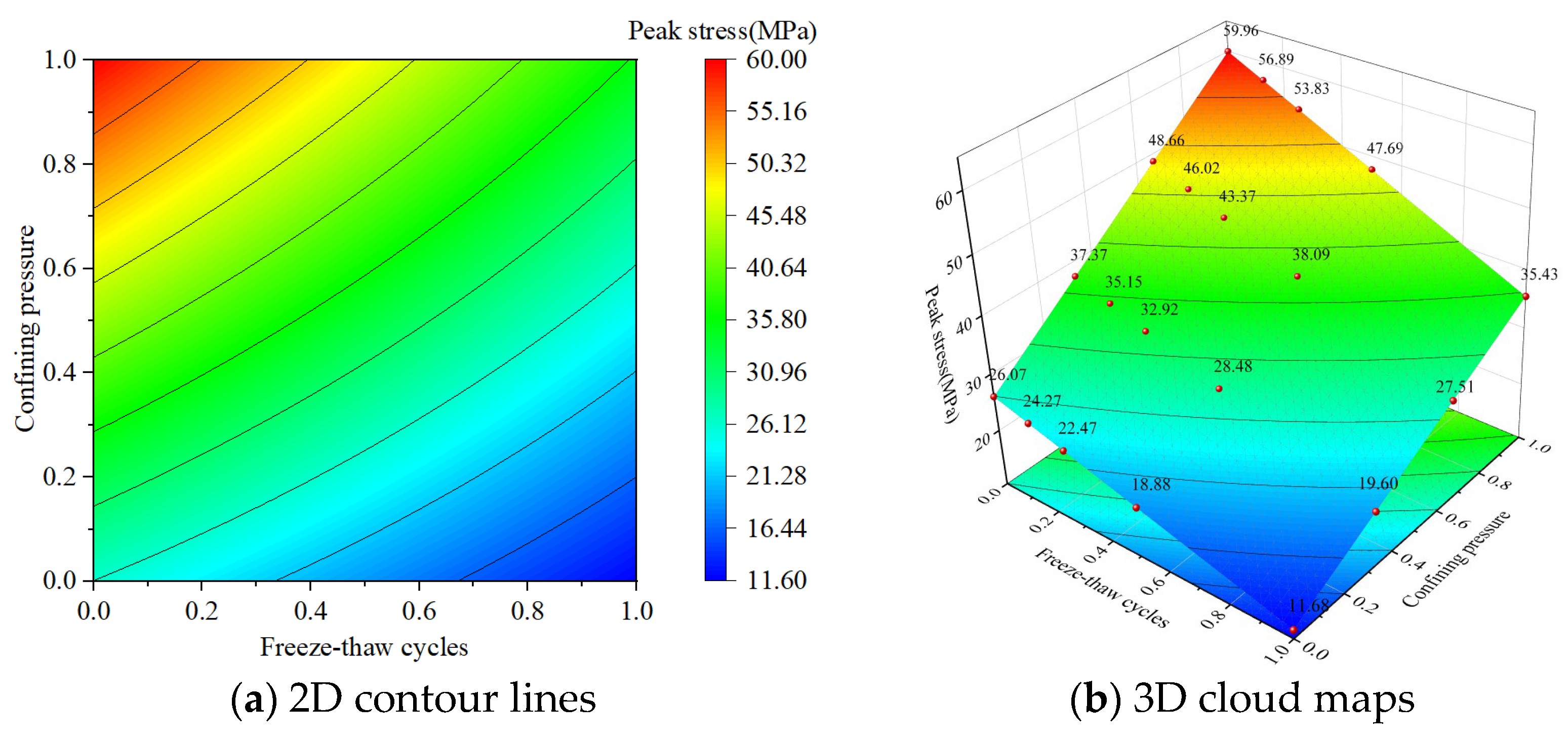
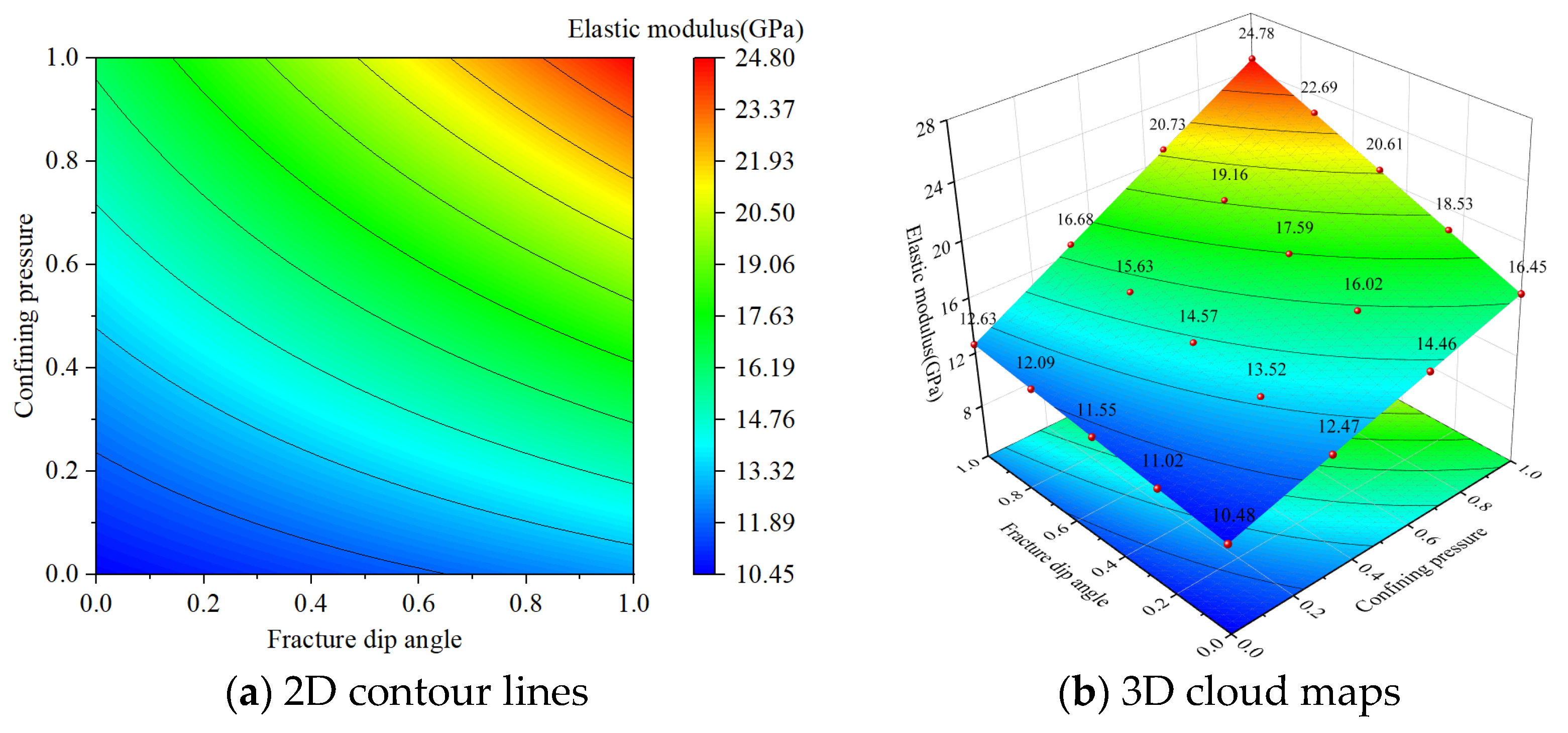
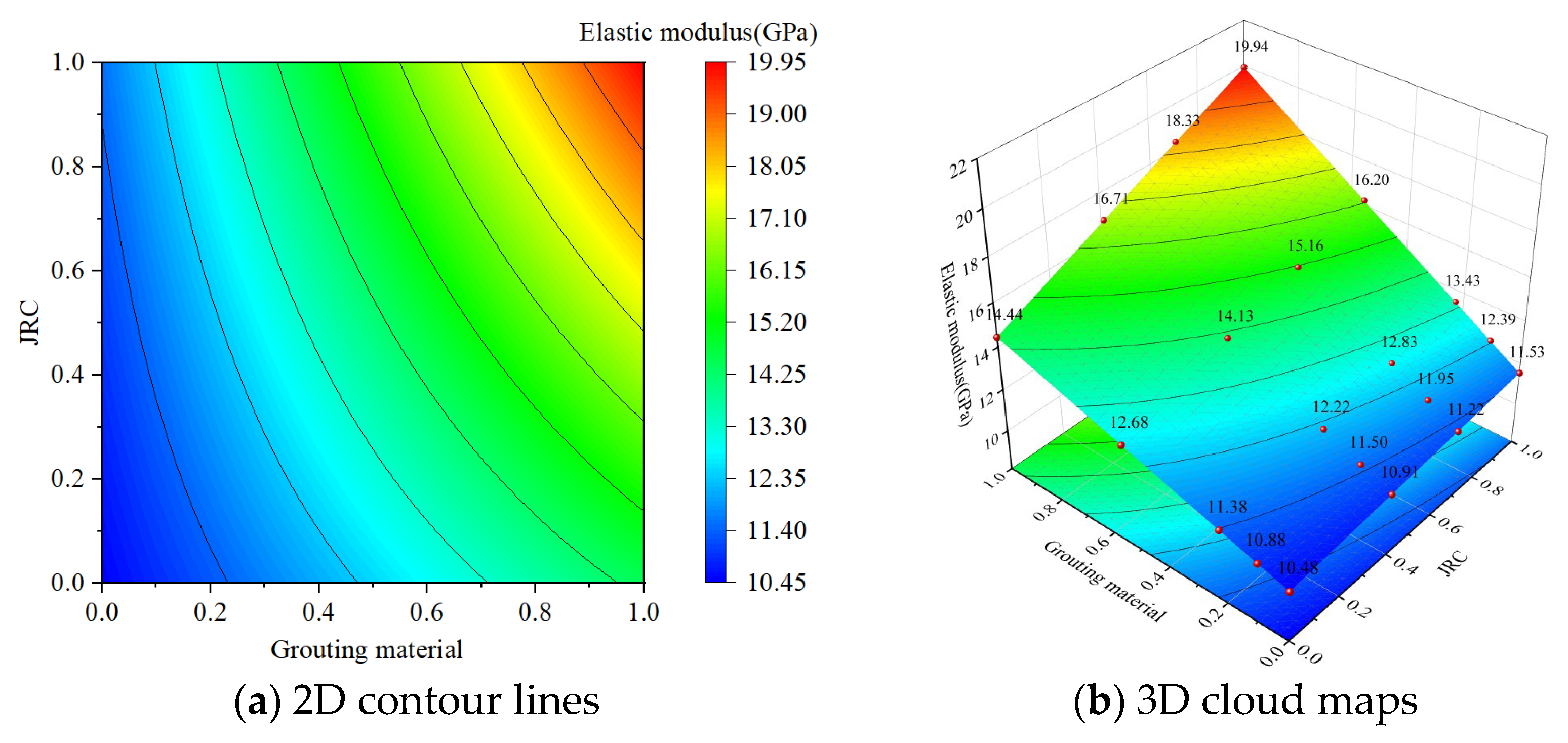
3.3.1. Analysis of Interaction Effects
3.3.2. Factor Interactions on Peak Stresses
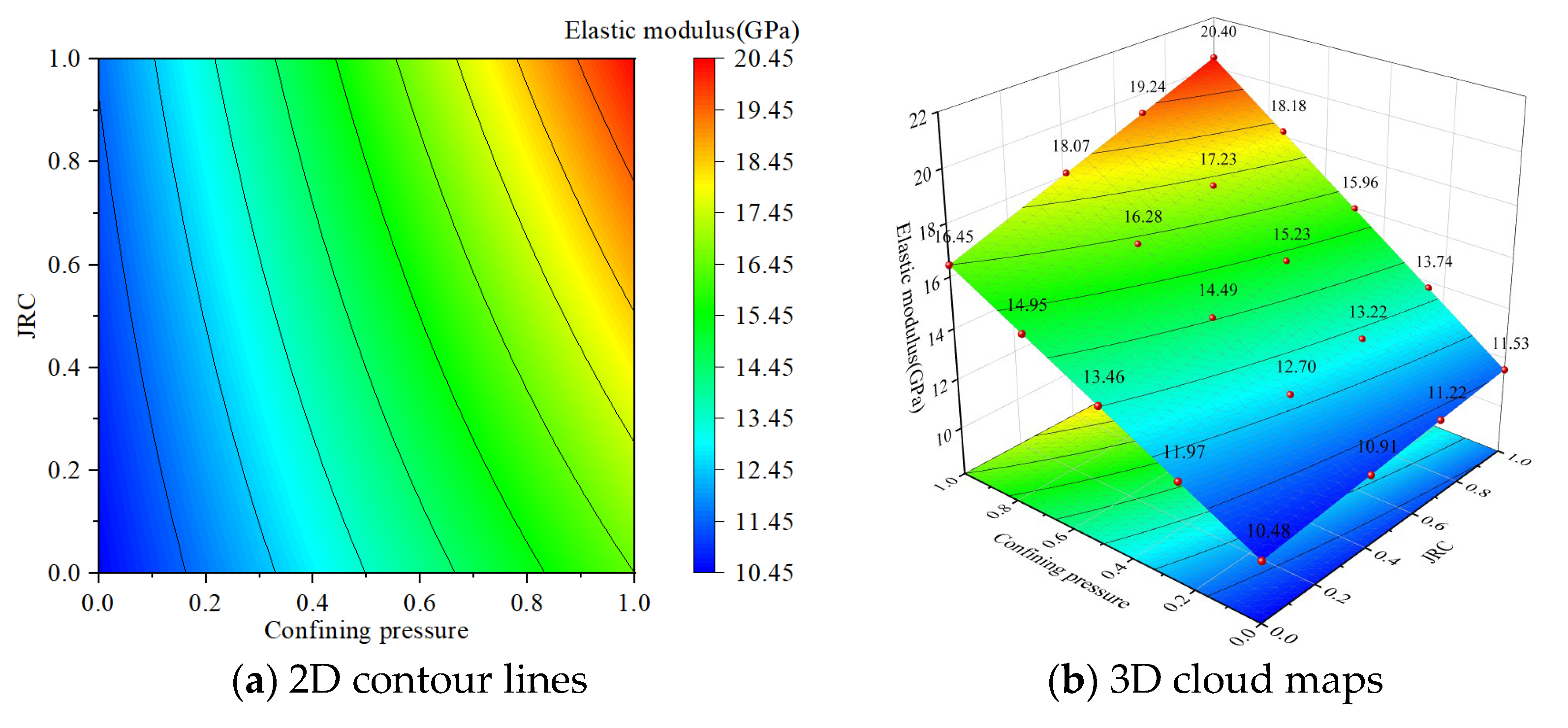
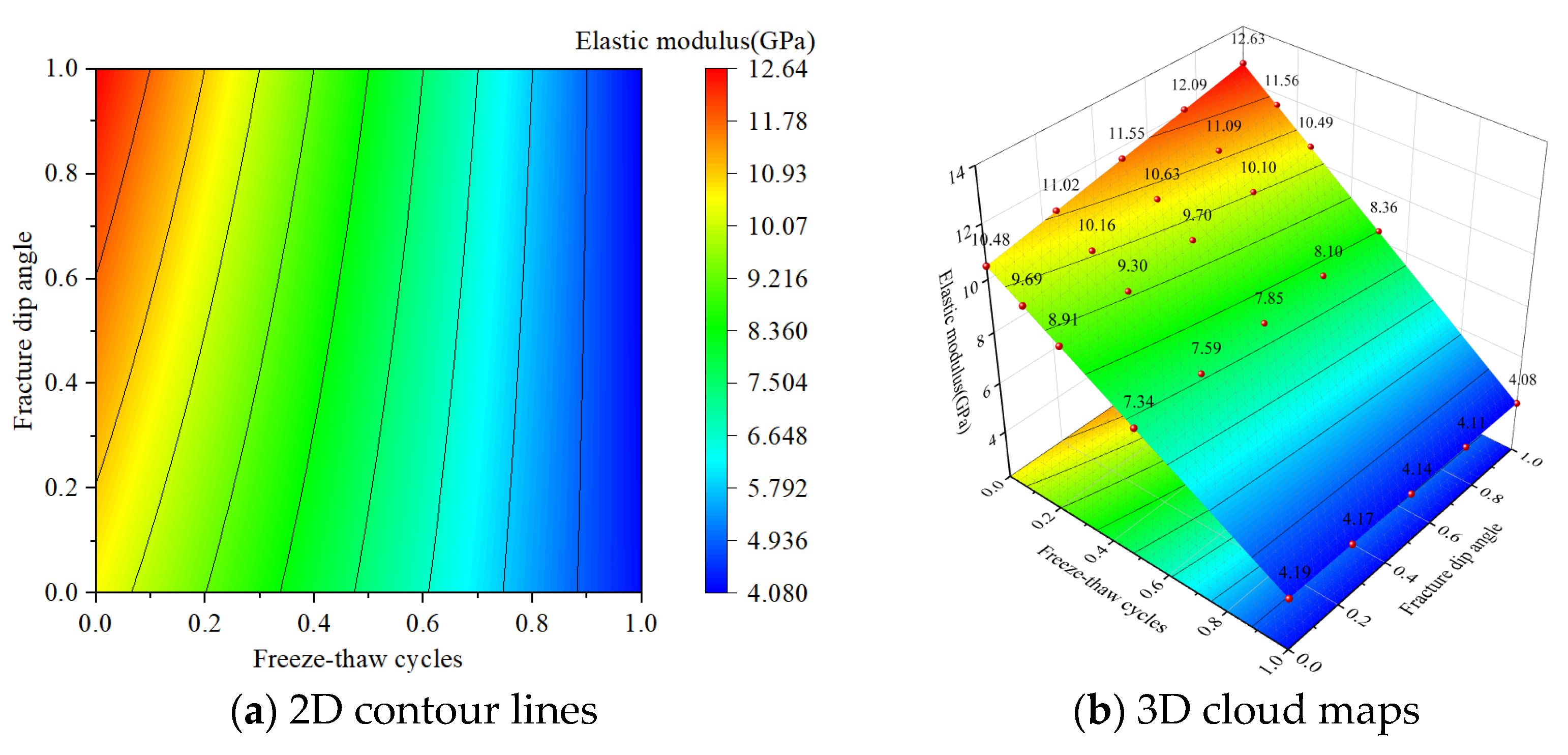
3.3.3. Factor Interaction on Elastic Modulus
4. Conclusions
- (1)
- The degree of influence of each factor on the peak stress of sandstone under the action of each factor is ranked as follows: confining pressure > fracture dip angle > grouting material > number of freeze–thaw cycles > roughness. The degree of influence on the elastic modulus is ranked as follows: number of freeze–thaw cycles > confining pressure > grouting material > fracture dip angle > roughness. Freeze–thaw cycles lead to the expansion of microfractures and the deterioration of the pore structure, which is expressed as a weakening effect. Grouting materials have a strengthening effect by improving the adhesion and support of the rock, the dip of the fissures improves the efficiency of stress transmission, roughness enhances the anchoring effect of the grout, and confining pressure improves the compactness of the rock specimen and limits deformation.
- (2)
- Under the interactive effect of grouting materials and roughness, high-strength grouting materials and high-roughness fissure surfaces form a strong anchoring system, which can effectively disperse external stress and reduce the stress concentration, resulting in a significant gain in peak stress. Under the interactive effect of grouting material and confining pressure, confining pressure effectively inhibits crack sliding, and grouting material enhances the bonding force of the crack surface, and the synergistic effect of the two significantly increases the peak stress of the rock specimen. Under the interactive effect of crack inclination and roughness, high crack inclination and high roughness enhance the anchoring effect and anti-sliding ability of the crack surface, relieve the stress accumulation at the crack tip, and result in a significant increase in peak stress. By making reasonable use of the above-mentioned interactive enhancement mechanism, the bearing capacity of the rock mass can be effectively improved.
- (3)
- Under the interactive effect of confining pressure and fracture dip angle, high confining pressure and high fracture dip angle promote the reconstruction of the fracture network, the microfractures are fully compacted, the contact area of the particles increases, and the external stress is more effectively transmitted through the particle contact surface, resulting in a significant increase in the elastic modulus of the rock specimen. Under the interactive effect of grouting material and roughness, high-strength grouting material effectively reinforces the cracks, while high roughness provides more anchor points, further significantly increasing the elastic modulus of the rock specimen; under the interactive effect of confining pressure and roughness, high confining pressure and high roughness work together to compact the cracks and enhance the frictional resistance, significantly increasing the elastic modulus of the rock specimen. By reasonably utilizing the aforementioned interactive enhancement mechanisms, the deformation resistance of the rock mass can be effectively improved.
- (4)
- Under the interactive effect of grouting material and the number of freeze–thaw cycles, and the number of freeze–thaw cycles and confining pressure, both high levels of grouting material and confining pressure can reduce the impact of freeze–thaw cycles on peak stress. However, a high level of freeze–thaw cycles inhibits the reinforcing effect of grouting material and the strengthening effect of confining pressure, and there is an interactive inhibition mechanism for peak stress. Under the interactive effect of the number of freeze–thaw cycles and the inclination angle of the crack, the freeze–thaw cycle induces the expansion of microcracks near the surface of the crack with a high inclination angle. The direction of expansion of the microcracks has an adverse interaction with the direction of the principal stress, which in turn reverses the trend of the elastic modulus with the inclination angle of the crack. There is an interactive reversal mechanism.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary
| Dry density of sandstone, g/cm3 | |
| Saturated density of sandstone, g/cm3 | |
| Dry mass of the specimen, g | |
| Saturated mass of the specimen, g | |
| Cross-sectional area of the specimen, cm2 | |
| Height of the specimen, cm | |
| Saturated moisture content of sandstone, % | |
| Porosity of sandstone, % | |
| Volume of the sandstone specimen, cm3 | |
| Density of the pore water within the rock, assumed to be 1.0 g/cm3 for calculation purposes | |
| Average base length of the joint roughness, mm | |
| Average height of the joint roughness, mm | |
| Fractal dimension of the joint | |
| Joint roughness coefficient | |
| Root mean square of the first derivative | |
| , | Heights of consecutive data points |
| , | Corresponding positions of the data points |
| Total number of data points | |
| Peak stress | |
| Elastic modulus | |
| Grouting material | |
| Number of freeze–thaw cycles | |
| Fracture dip angle | |
| Confining pressure | |
| Roughness |
References
- Mortazavi, A.; Maadikhah, A. An investigation of the effects of important grouting and rock parameters on the grouting process. Geomech. Geoengin. 2016, 11, 219–235. [Google Scholar] [CrossRef]
- Cui, P.; Chen, R.; Xiang, L.; Su, F. Analysis of mountain disasters and their risks in the Tibetan Plateau under the background of climate warming. Prog. Clim. Change Res. 2014, 10, 103–109. [Google Scholar]
- Zhang, G.; Chen, G.; Xu, Z.; Yang, Y.; Lin, Z. Crack failure characteristics of different rocks under the action of frost heaving of fissure water. Front. Earth Sci. 2020, 8, 13. [Google Scholar] [CrossRef]
- Dan, R.; Bai, Y.; Sun, P.; Wu, Y.; Sui, S.; Yuan, H. Experimental study on freezing and expansion force characteristics of fractured red sandstone. J. China Coal Soc. 2019, 44, 1742–1752. [Google Scholar]
- Zhao, J.; Xie, M.; Yu, J.; Zhao, W. Experimental study on mechanical properties and damage evolution law of fracture-containing rocks under freeze-thaw action. J. Eng. Geol. 2019, 27, 1199–1207. [Google Scholar]
- Tian, S.; Zhao, Y.; Si, H.; Zhu, C.; Li, Q. Experimental study on freeze-thaw damage characteristics and mechanical properties of fractured rock mass of surface mine slope in cold region. J. China Coal Soc. 2024, 49, 4687–4700. [Google Scholar]
- Wu, X.; Ni, Z.; Zhu, J.; Qin, K.; Tang, K. Mechanical properties and crack extension characteristics of fissured chert under freeze-thaw cycles. J. Chongqing Univ. 2025; in press. [Google Scholar]
- Lu, Y.; Li, X.; Wu, X. Mechanism of crack penetration in freeze-thawed single-fissure rock specimens under triaxial compression conditions. Rock Soil Mech. 2014, 35, 1579–1584. [Google Scholar]
- Liu, Y.; Guo, Y.; Huang, S.; Cai, Y.; Li, K.; Wang, L.; Li, W. Study on fracture characteristics and strength loss of fissure-like sandstone under freeze-thaw action. Rock Soil Mech. 2018, 39, 62–71. [Google Scholar]
- Fu, H.; Zhang, J.; Huang, Z.; Huang, H.; Shi, Y. Study on elastic parameters and uniaxial compressive strength of slate under freeze-thaw cycle. Rock Soil Mech. 2017, 38, 2203–2212. [Google Scholar]
- Yang, H.; Zhang, J.; San, R.; Wu, F. Experimental study on mechanical properties of frozen water-saturated single-fissure rock body. Rock Soil Mech. 2018, 39, 1245–1255. [Google Scholar]
- Lv, S.; Zhu, J.; Wang, B.; Zhu, Y. Macroscopic and fine-scale damage modeling of open-fractured sandstone under freeze-thaw load coupling. Chin. J. Rock Mech. Eng. 2023, 42, 1124–1135. [Google Scholar]
- Liu, H.; Liu, Y.; Xing, C.; Zhang, L.; Ma, M. Experimental study on damage destruction of jointed rock mass under cyclic freezing and thawing conditions. Rock Soil Mech. 2014, 35, 1547–1554. [Google Scholar]
- Yang, L.; Zhang, Y.; Tang, M.; Li, R.; Xu, Z.; Yin, H. Mechanical properties and damage mode of split grouting and solidification in water-rich and weak surrounding rock. J. Cent. South Univ. (Sci. Technol.) 2024, 55, 649–664. [Google Scholar]
- Lu, H.; Zhang, Q. Investigations on shear properties of soft rock joints under grouting. Rock Mech. Rock Eng. 2021, 54, 1875–1883. [Google Scholar]
- Liu, Q.; Lei, G.; Lu, C.; Peng, X.; Zhang, J.; Wang, J. Experimental study on the effect of grouting reinforcement on the mechanical properties of rock fracture. Chin. J. Rock Mech. Eng. 2017, 36, 3140–3147. [Google Scholar]
- Zhu, Y.; Ren, H.; Wang, P.; Li, P.; Wang, X.; Wei, M. Analysis of grouting test and reinforcement mechanism in rocks with single penetration rupture surface. Rock Soil Mech. 2022, 43, 3221–3230. [Google Scholar]
- Niu, Y.; Hu, Y.; Wang, J. Cracking characteristics and damage assessment of filled rocks using acoustic emission technology. Int. J. Geomech. 2023, 23, 04023013. [Google Scholar] [CrossRef]
- Tang, J.; Liu, Q.; Dai, Z.; Wang, Y. Research on mechanical properties and damage mode of grouted fissured sandy mudstone. Chin. J. Undergr. Space Eng. 2021, 17, 1028–1037. [Google Scholar]
- Shen, J.; Liu, B.; Chen, J.; Li, Y.; Cheng, Y.; Song, Y. Experimental study on the physical and mechanical properties of grouting in gabbroic fissures. Chin. J. Rock Mech. Eng. 2020, 39, 2804–2817. [Google Scholar]
- Brown, E.T. Rock Characterization, Testing and Monitoring: ISRM Suggested Methods; Pergamon Press: Oxford, UK, 1981; pp. 107–110. ISBN 978-0-080-27308-2. [Google Scholar]
- Culshaw, M.G.; Ulusay, R. (Eds.) The ISRM suggested methods for rock characterization, testing and monitoring: 2007–2014: Cham, Switzerland: Springer. Bull. Eng. Geol. Environ. 2015, 74, 1499–1500. [Google Scholar]
- ASTM D4543-19; Standard Practices for Preparing Rock Core as Cylindrical Test Specimens and Verifying Conformance to Dimensional and Shape Tolerances. ASTM International: West Conshohocken, PA, USA, 2019.
- Xie, H. Fractal description of rock joints. Chin. J. Geotech. Eng. 1995, 17, 18–23. [Google Scholar]
- Chen, S.J.; Zhu, W.C.; Wang, C.Y.; Zhang, F. Review of research progresses of the quantifying joint roughness coefficient. Chin. J. Theor. Appl. Mech. 2017, 49, 239–256. [Google Scholar]
- Jia, H.L.; Zhao, S.Q.; Ding, S.; Wang, T.; Dong, Y.H.; Tan, X.J. Study on the evolution and influencing factors of frost heaving force of waterbearing cracks during freezing-thawing process. Chin. J. Rock Mech. Eng. 2022, 41, 1832–1845. [Google Scholar]
- Liu, H.; Lin, J.H.; Yang, G.S.; Yun, Y.; Zhang, H.; Liang, B.; Zhang, Y. Acoustic emission test on tensile damage characteristics of sandstone under freeze-thaw cycle. J. Min. Saf. Eng. 2020, 38, 830–839. [Google Scholar]
- Amini, M.; Younesi, H.; Bahramifar, N. Statistical modeling and optimization of the cadmium biosorption process in an aqueous solution using Aspergillus niger. Colloids Surf. A Physicochem. Eng. Asp. 2009, 337, 67–73. [Google Scholar]
- Yetilmezsoy, K.; Demirel, S.; Vanderbei, R.J. Response surface modeling of Pb (II) removal from aqueous solution by Pistacia vera L.: Box-Behnken experimental design. J. Hazard. Mater. 2009, 171, 551–562. [Google Scholar]
- Li, H.; Zhang, G.; Li, X.; Zhang, H.; Zhang, Q.; Liu, W.; Mu, G. Calibration of the discrete element method parameters in living juvenile Manila clam (Ruditapes Philippinarum) and seeding verification. Agriengineering 2021, 3, 894–906. [Google Scholar] [CrossRef]


| Quartz | Calcite | Albite | Kaolin | Chlorite |
|---|---|---|---|---|
| 45.2 | 6.8 | 32.1 | 7.5 | 8.4 |
| Longitudinal Wave Velocity (m·s−1) | Dry Density (g·cm−3) | Saturated Density (g·cm−3) | Saturated Moisture Content (%) | Porosity (%) |
|---|---|---|---|---|
| 2.968 | 1.561 | 1.638 | 4.928 | 7.695 |
| Material | Uniaxial Compressive Strength (MPa) | Young’s Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|
| Ice (−20 °C) | 6.7 | 4.6 | 0.28 |
| Gypsum paste | 14.8 | 2.1 | 0.24 |
| Cement mortar | 36.2 | 8.4 | 0.27 |
| Epoxy resin | 65.3 | 4.8 | 0.39 |
| Rock Specimen Number | Grouting Material | Freezing–Thawing Cycles | Fissured Angles (°) | JRC | Confining Pressures (MPa) |
|---|---|---|---|---|---|
| 1 | / | 0 | 15 | 0 | 0 |
| 2 | / | 5 | 30 | 9 | 3 |
| 3 | / | 10 | 45 | 15 | 6 |
| 4 | / | 20 | 60 | 22 | 9 |
| 5 | Ice | 0 | 30 | 15 | 9 |
| 6 | Ice | 5 | 15 | 22 | 6 |
| 7 | Ice | 10 | 60 | 0 | 3 |
| 8 | Ice | 20 | 45 | 9 | 0 |
| 9 | Gypsum paste | 0 | 45 | 22 | 3 |
| 10 | Gypsum paste | 5 | 60 | 15 | 0 |
| 11 | Gypsum paste | 10 | 15 | 9 | 9 |
| 12 | Gypsum paste | 20 | 30 | 0 | 6 |
| 13 | Cement mortar | 0 | 60 | 9 | 6 |
| 14 | Cement mortar | 5 | 45 | 0 | 9 |
| 15 | Cement mortar | 10 | 30 | 22 | 0 |
| 16 | Cement mortar | 20 | 15 | 15 | 3 |
| 17 | Epoxy resin | 40 | 75 | 0 | 0 |
| 18 | Epoxy resin | 40 | 75 | 9 | 3 |
| 19 | Epoxy resin | 40 | 75 | 15 | 6 |
| 20 | Epoxy resin | 40 | 75 | 22 | 9 |
| 21 | / | 0 | 75 | 0 | 3 |
| 22 | Ice | 5 | 75 | 9 | 0 |
| 23 | Gypsum paste | 10 | 75 | 15 | 9 |
| 24 | Cement mortar | 20 | 75 | 22 | 6 |
| 25 | Epoxy resin | 0 | 15 | 9 | 6 |
| 26 | Epoxy resin | 5 | 30 | 0 | 9 |
| 27 | Epoxy resin | 10 | 45 | 22 | 0 |
| 28 | Epoxy resin | 20 | 60 | 15 | 3 |
| 29 | / | 40 | 15 | 15 | 0 |
| 30 | Ice | 40 | 30 | 22 | 3 |
| 31 | Gypsum paste | 40 | 45 | 0 | 6 |
| 32 | Cement mortar | 40 | 60 | 9 | 9 |
| 33 | / | 5 | 45 | 9 | 3 |
| 34 | / | 10 | 30 | 0 | 6 |
| 35 | Ice | 0 | 60 | 0 | 0 |
| 36 | Ice | 20 | 15 | 0 | 9 |
| Factor | Effect on Strength | Effect on Stiffness | Influence Mechanism |
|---|---|---|---|
| Freeze–thaw Cycles | Peak stress decreases by 55.37% | Elastic modulus decreases by 76.78% | Freeze–thaw cycles cause microcrack expansion and deterioration of pore structure, resulting in a gradual decrease in strength and stiffness, exhibiting typical cumulative damage effects. |
| Grouting Material | Peak stress increases by 113.61% | Elastic modulus increases by 40.44% | Grouting materials improve adhesion and support, extending residual strength, enhancing peak stress, and improving overall stiffness. |
| Roughness (JRC) | Peak stress increases by 13.25% | Elastic modulus increases by 8.08% | Roughness improves slurry anchoring, optimizes stress distribution, delays crack propagation, and enhances the rock’s stability, thereby improving mechanical properties. |
| Fracture Dip Angle | Peak stress increases by 118.76% | Elastic modulus increases by 27.25% | Fracture dip angle optimizes stress transfer, reduces slippage and cracking, increasing elastic modulus and peak stress, thereby enhancing stability. |
| Confining Pressure | Peak stress increases by 140.2% | Elastic modulus increases by 70.65% | Confining pressure increases rock density, limits deformation, enhances stiffness and strength, and promotes the transition from brittle to ductile failure. |
| Explanatory Variable | Coefficient of Influence | Standard Error | t-Value | p-Value (Pr > |t|) | |
|---|---|---|---|---|---|
| interception | 26.0712 | 1.301 | 19.761 | <2 × 10−16 | *** |
| grouting material | 27.754 | 1.866 | 7.907 | <2 × 10−16 | *** |
| number of freeze–thaw cycles | −14.392 | 1.658 | −5.867 | <2 × 10−16 | *** |
| fracture dip angle | 29.299 | 2.046 | 7.479 | <2 × 10−16 | *** |
| confining pressure | 33.886 | 2.755 | 12.301 | <2 × 10−16 | *** |
| roughness, respectively | 5.957 | 1.267 | 2.364 | 0.00494 | ** |
| grouting material: number of freeze–thaw cycles | −11.307 | 2.594 | 10.268 | <2 × 10−16 | *** |
| grouting material: confining pressure | 16.075 | 2.785 | 13.496 | <2 × 10−16 | *** |
| grouting material: roughness, respectively | 5.111 | 2.81 | 2.887 | 0.00414 | ** |
| number of freeze–thaw cycles: confining pressure | −10.134 | 3.434 | −5.571 | 5.11 × 10−8 | *** |
| fracture dip angle: roughness, respectively | 9.476 | 2.949 | 4.909 | 1.42 × 10−6 | *** |
| R2 = 0.9613 | |||||
| Explanatory Variable | Coefficient of Influence | Standard Error | t-Value | p-Value (Pr > |t|) | |
|---|---|---|---|---|---|
| interception | 10.4785 | 0.4236 | 29.162 | <2 × 10−16 | *** |
| grouting material | 3.9654 | 0.5481 | 5.216 | <2 × 10−16 | *** |
| number of freeze–thaw cycles | −6.2846 | 0.6117 | −7.894 | <2 × 10−16 | *** |
| fracture dip angle | 2.1523 | 0.4296 | 3.218 | <2 × 10−16 | *** |
| confining pressure | 5.9667 | 0.6701 | 7.106 | <2 × 10−16 | *** |
| roughness, respectively | 1.0471 | 0.6646 | 2.208 | 0.03564 | * |
| grouting material: roughness, respectively | 4.4513 | 0.9278 | −4.798 | 3.58 × 10−6 | *** |
| number of freeze–thaw cycles: fracture dip angle | −2.2635 | 0.4853 | 3.406 | 0.000828 | ** |
| fracture dip angle: confining pressure | 6.1807 | 0.7806 | 9.801 | <2 × 10−16 | *** |
| confining pressure: roughness, respectively | 2.9091 | 0.8633 | −3.370 | <2 × 10−16 | *** |
| R2 = 0.9529 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bi, R.; Gan, W. Study on the Mechanical Properties and Interaction Mechanism of Fractured Rock Subjected to Freeze–Thaw Cycles. Appl. Sci. 2025, 15, 4101. https://doi.org/10.3390/app15084101
Bi R, Gan W. Study on the Mechanical Properties and Interaction Mechanism of Fractured Rock Subjected to Freeze–Thaw Cycles. Applied Sciences. 2025; 15(8):4101. https://doi.org/10.3390/app15084101
Chicago/Turabian StyleBi, Ran, and Weijian Gan. 2025. "Study on the Mechanical Properties and Interaction Mechanism of Fractured Rock Subjected to Freeze–Thaw Cycles" Applied Sciences 15, no. 8: 4101. https://doi.org/10.3390/app15084101
APA StyleBi, R., & Gan, W. (2025). Study on the Mechanical Properties and Interaction Mechanism of Fractured Rock Subjected to Freeze–Thaw Cycles. Applied Sciences, 15(8), 4101. https://doi.org/10.3390/app15084101






