Network Topology-Driven Vertiport Placement Strategy: Integrating Urban Air Mobility with the Seoul Metropolitan Railway System
Abstract
1. Introduction
2. Literature Review
2.1. Location-Allocation Planning in Transportation: Traditional Approaches and Network Perspectives
2.2. Airport Location-Allocation Strategies
2.3. Strategic Approaches to Vertiport Location Allocation in the Context of UAM
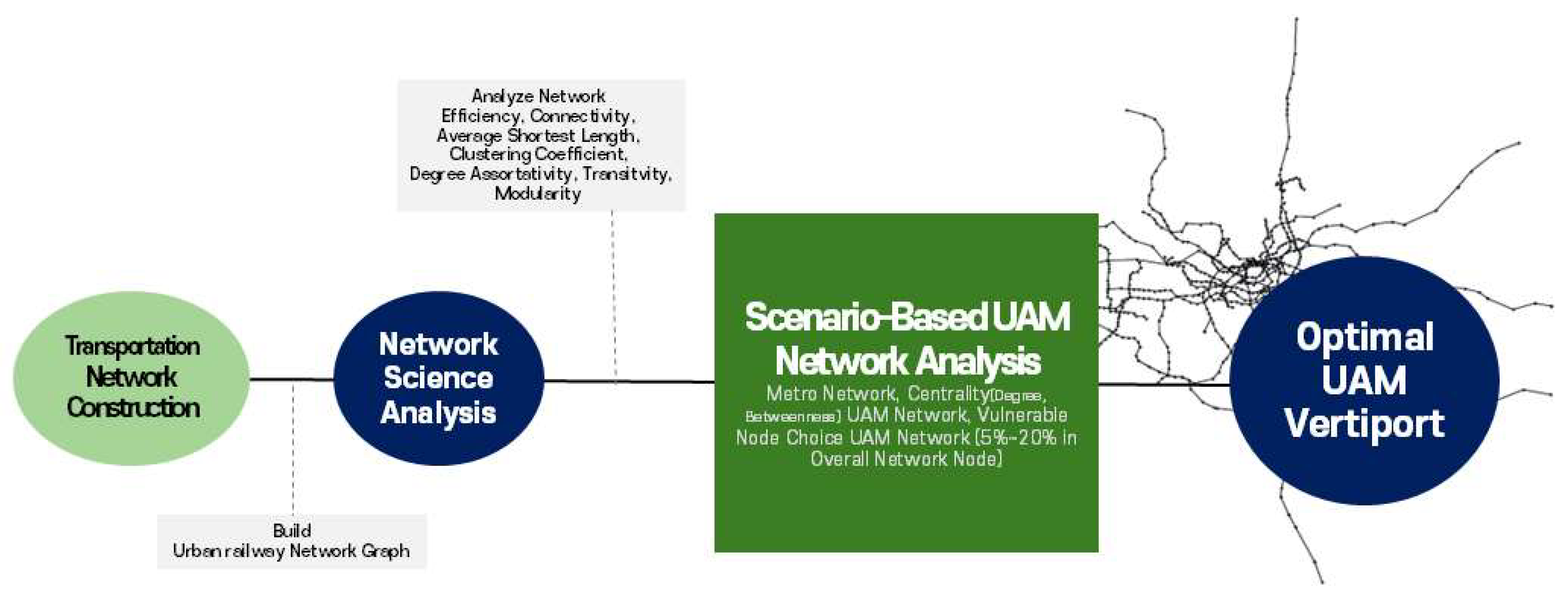
3. Methodology
3.1. Overall Research Landscape
3.2. Network Topology Analysis Methodology
- : Number of nodes;
- : Shortest path length between node i and j.
- (1)
- Connectivity of Nodes
- : Minimum set of nodes that must be removed to disconnect the network;
- : Set of all nodes in graph .
- (2)
- Connectivity of Edges
- : Minimum set of edges that must be removed to disconnect the network;
- : Set of all edges in graph G.
- : Number of nodes;
- : Shortest path length between node i and j.
- : Number of triangles formed by the neighbors of node ;
- : Degree of node i.
- : Second smallest eigenvalue of the network’s Laplacian matrix.
- : Degree of node i
- : 1 if nodes i and j are connected; otherwise, 0;
- : Number of overall edges.
- : Adjacency matrix indicating whether nodes i and j are connected;
- : Degree of node i and j;
- : Number of overall edges;
- : if nodes i and j belong to the same community; otherwise, 0.
3.3. Node Centrality and Vulnerability Assessment Methodology Based on Network Topology
- : Node ;
- : if nodes and are connected; otherwise, 0.
- : Number of shortest paths between node s and node t;
- : Number of shortest paths between node s and node t that pass through node v.
- : Selected set of nodes
- : Neighboring nodes of
4. Results
4.1. Base Network
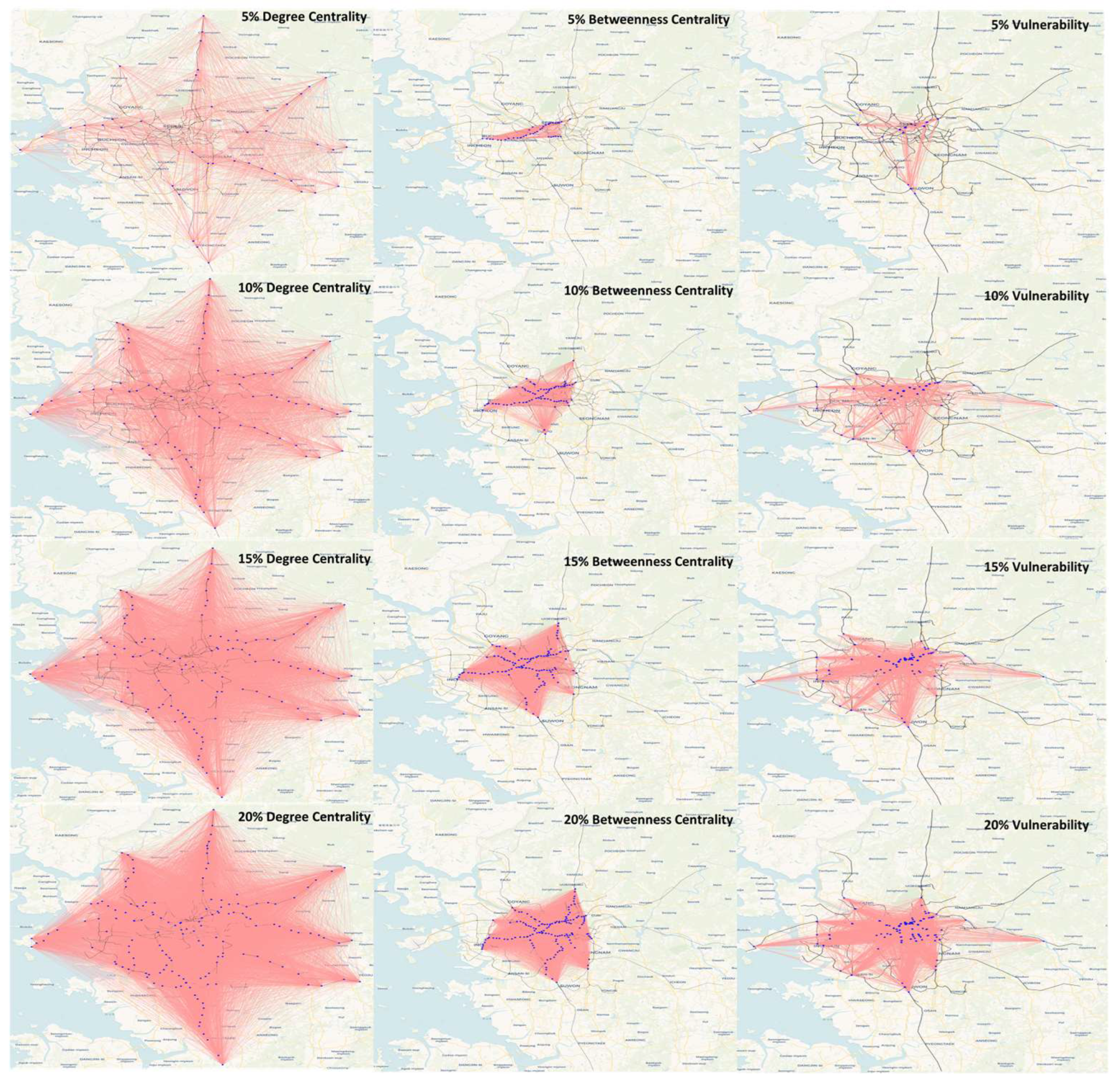
4.2. Scenario Evaluation Outcomes
4.3. Comprehensive Analysis Findings
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Feng, T. Strategic integration of vertiport planning in multimodal transportation for urban air mobility: A case study in Beijing, China. J. Clean. Prod. 2024, 467, 142988. [Google Scholar]
- Mendonca, N.; Murphy, J.; Patterson, M.D.; Alexander, R.; Juarex, G.; Harper, C. Advanced air mobility vertiport considerations: A list and overview. In Proceedings of the AIAA AVIATION 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022; p. 4073. [Google Scholar]
- Brunelli, M.; Ditta, C.C.; Postorino, M.N. New infrastructures for Urban Air Mobility systems: A systematic review on vertiport location and capacity. J. Air Transp. Manag. 2023, 112, 102460. [Google Scholar]
- Rothfeld, R.; Fu, M.; Balać, M.; Antoniou, C. Potential urban air mobility travel time savings: An exploratory analysis of munich, paris, and san francisco. Sustainability 2021, 13, 2217. [Google Scholar] [CrossRef]
- Chen, S.; Zhuang, D. Evolution and evaluation of the Guangzhou metro network topology based on an integration of complex network analysis and GIS. Sustainability 2020, 12, 538. [Google Scholar] [CrossRef]
- Park, C.; Sohn, S.Y. An optimization approach for the placement of bicycle-sharing stations to reduce short car trips: An application to the city of Seoul. Transp. Res. Part A Policy Pract. 2017, 105, 154–166. [Google Scholar] [CrossRef]
- Mohring, H. Optimization and scale economies in urban bus transportation. Am. Econ. Rev. 1972, 62, 591–604. [Google Scholar]
- Mandl, C.E. Evaluation and optimization of urban public transportation networks. Eur. J. Oper. Res. 1980, 5, 396–404. [Google Scholar]
- Archetti, C.; Peirano, L.; Speranza, M.G. Optimization in multimodal freight transportation problems: A Survey. Eur. J. Oper. Res. 2022, 299, 1–20. [Google Scholar] [CrossRef]
- Ríos-Mercado, R.Z.; Borraz-Sánchez, C. Optimization problems in natural gas transportation systems: A state-of-the-art review. Appl. Energy 2015, 147, 536–555. [Google Scholar]
- Zitrický, V.; Gašparík, J.; Pečený, L. The methodology of rating quality standards in the regional passenger transport. Transp. Probl. 2015, 10, 59–72. [Google Scholar]
- Abramović, B.; Zitricky, V.; Biškup, V. Organisation of railway freight transport: Case study CIM/SMGS between Slovakia and Ukraine. Eur. Transp. Res. Rev. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Bukvić, L.; Pašagić Škrinjar, J.; Abramović, B.; Zitrický, V. Route selection decision-making in an intermodal transport network using game theory. Sustainability 2021, 13, 4443. [Google Scholar] [CrossRef]
- Stopka, O.; Zitricky, V.; Abramović, B.; Marinov, M.V.; Ricci, S. Innovative technologies for sustainable passenger transport. J. Adv. Transp. 2019, 2019, 1–2. [Google Scholar]
- Chen, M.; Lu, H. Analysis of transportation network vulnerability and resilience within an urban agglomeration: Case study of the greater Bay Area, China. Sustainability 2020, 12, 7410. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, M.; Wang, Y. Location decision of emergency medical supply distribution centers under uncertain environment. Int. J. Fuzzy Syst. 2024, 26, 1567–1603. [Google Scholar]
- Bulková, Z.; Čamaj, J.; Šperka, A.; Jursová, S. Simulation of travel document purchase measures aimed at preventing the spread of COVID-19–Case study from Slovakia. Transp. Res. Interdiscip. Perspect. 2023, 20, 100853. [Google Scholar]
- Čamaj, J.; Nedeliaková, E.; Šperka, A.; Ližbetinová, L. The planning of investment activities in field of railway transport with support of simulation tools. Transp. Res. Procedia 2021, 53, 39–49. [Google Scholar]
- Mašek, J.; Kolarovszki, P.; Čamaj, J. Application of RFID technology in railway transport services and logistics chains. Procedia Eng. 2016, 134, 231–236. [Google Scholar]
- Gerhátová, Z.; Zitrický, V.; Klapita, V. Industry 4.0 implementation options in railway transport. Transp. Res. Procedia 2021, 53, 23–30. [Google Scholar]
- Wu, Q.; Li, Y.; Dan, P. Optimization of urban rail transit station spacing for minimizing passenger travel time. J. Rail Transp. Plan. Manag. 2022, 22, 100317. [Google Scholar]
- Macias, J.E.; Khalife, C.; Slim, J.; Angeloudis, P. An integrated vertiport placement model considering vehicle sizing and queuing: A case study in London. J. Air Transp. Manag. 2023, 113, 102486. [Google Scholar]
- Tuncal, A. Operational Challenges and Prioritization of Potential Solutions for Integrating Vertiports into Airports. Türkiye İnsansız Hava Araçları Derg. 2024, 6, 42–55. [Google Scholar] [CrossRef]
- Kopardekar, P.; Rios, J.; Prevot, T.; Johnson, M.; Jung, J.; Robinson, J.E. Unmanned aircraft system traffic management (UTM) concept of operations. In Proceedings of the AIAA AVIATION Forum and Exposition, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Schweiger, K.; Preis, L. Urban air mobility: Systematic review of scientific publications and regulations for vertiport design and operations. Drones 2022, 6, 179. [Google Scholar] [CrossRef]
- Liu, J.; Lu, H.; Chen, M.; Wang, J.; Zhang, Y. Macro perspective research on transportation safety: An empirical analysis of network characteristics and vulnerability. Sustainability 2020, 12, 6267. [Google Scholar] [CrossRef]
- Koumoutsidi, A.; Pagoni, I.; Polydoropoulou, A. A new mobility era: Stakeholders’ insights regarding urban air mobility. Sustainability 2022, 14, 3128. [Google Scholar] [CrossRef]
- Aydin, N.; Seker, S.; Özkan, B. Planning location of mobility hub for sustainable urban mobility. Sustain. Cities Soc. 2022, 81, 103843. [Google Scholar]
- Lazari, V.; Chassiakos, A. Multi-objective optimization of electric vehicle charging station deployment using genetic algorithms. Appl. Sci. 2023, 13, 4867. [Google Scholar] [CrossRef]
- Rouhana, F.; Jawad, D. Transportation network resilience against failures: GIS-based assessment of network topology role. Int. J. Disaster Resil. Built Environ. 2021, 12, 357–370. [Google Scholar]
- Perera, P.; Hewage, K.; Sadiq, R. Electric vehicle recharging infrastructure planning and management in urban communities. J. Clean. Prod. 2020, 250, 119559. [Google Scholar]
- Hong, J.; Tamakloe, R.; Lee, S.; Park, D. Exploring the topological characteristics of complex public transportation networks: Focus on variations in both single and integrated systems in the Seoul Metropolitan Area. Sustainability 2019, 11, 5404. [Google Scholar] [CrossRef]
- Lim, E.; Hwang, H. The selection of vertiport location for on-demand mobility and its application to Seoul metro area. Int. J. Aeronaut. Space Sci. 2019, 20, 260–272. [Google Scholar] [CrossRef]
- Akbarzadeh, M.; Memarmontazerin, S.; Derrible, S.; Salehi Reihani, S.F. The role of travel demand and network centrality on the connectivity and resilience of an urban street system. Transportation 2019, 46, 1127–1141. [Google Scholar] [CrossRef]
- Hensher, D.A. Stated preference analysis of travel choices: The state of practice. Transportation 1994, 21, 107–133. [Google Scholar] [CrossRef]
- Leitham, S.; McQuaid, R.W.; Nelson, J.D. The influence of transport on industrial location choice: A stated preference experiment. Transp. Res. Part A Policy Pract. 2000, 34, 515–535. [Google Scholar] [CrossRef]
- Fulton, M.; Hoch, L.C. Transportation factors affecting locational decisions. Econ. Geogr. 1959, 35, 51–59. [Google Scholar] [CrossRef]
- Ahas, R.; Krisp, J.M.; Toivonen, T. Methodological aspects of using geocoded data from mobile devices in transportation research. J. Locat. Based Serv. 2017, 11, 75–77. [Google Scholar] [CrossRef]
- Jia, G.-L.; Ma, R.-G.; Hu, Z.-H. Urban transit network properties evaluation and optimization based on complex network theory. Sustainability 2019, 11, 2007. [Google Scholar] [CrossRef]
- Hammad, M.A.; Elgazzar, S.; Sternad, M. A Conceptual Framework to Establish and Operate a Global Logistics Energy Hub. Sustainability 2021, 13, 10976. [Google Scholar] [CrossRef]
- Zhang, X.; Miller-Hooks, E.; Denny, K. Assessing the role of network topology in transportation network resilience. J. Transp. Geogr. 2015, 46, 35–45. [Google Scholar] [CrossRef]
- Ganin, A.A.; Kitsak, M.; Marchese, D.; Keisler, J.M.; Seager, T.; Linkov, I. Resilience and efficiency in transportation networks. Sci. Adv. 2017, 3, e1701079. [Google Scholar] [CrossRef]
- Saaty, T.L. The analytic hierarchy process (AHP). J. Oper. Res. Soc. 1980, 41, 1073–1076. [Google Scholar]
- Min, H. Location planning of airport facilities using the analytic hierarchy process. Logist. Transp. Rev. 1994, 30, 79. [Google Scholar]
- Ballis, A. Airport site selection based on multicriteria analysis: The case study of the island of Samothraki. Oper. Res. 2003, 3, 261–279. [Google Scholar]
- Liao, Y.; Bao, F. Research on airport site selection based on triangular fuzzy number. Appl. Mech. Mater. 2014, 505, 507–511. [Google Scholar]
- Zhang, H.; Sun, F.; Qian, J. An optimization based on general airport of complex condition. In Proceedings of the 2019 International Conference on Computer, Information and Telecommunication Systems (CITS), Beijing, China, 28–31 August 2019; pp. 1–5. [Google Scholar]
- Sennaroglu, B.; Celebi, G.V. A military airport location selection by AHP integrated PROMETHEE and VIKOR methods. Transp. Res. Part D Transp. Environ. 2018, 59, 160–173. [Google Scholar]
- Zhao, S.; Sun, P. Scheme Comparison of New Airport Site Selection Based on Lattice Order Decision Making Method in the Integrated Transportation System. Int. J. Online Eng. 2013, 9, 95. [Google Scholar]
- Alves, C.J.P.; da Silva, E.J.; Müller, C.; Borille, G.M.R.; Guterres, M.X.; Arraut, E.M.; Peres, M.S.; dos Santos, R.J. Towards an objective decision-making framework for regional airport site selection. J. Air Transp. Manag. 2020, 89, 101888. [Google Scholar]
- Wang, M.; Li, H.; Cui, J.; Deng, K.; Bhowmick, S.S.; Dong, Z. Pinocchio: Probabilistic influence-based location selection over moving objects. IEEE Trans. Knowl. Data Eng. 2016, 28, 3068–3082. [Google Scholar]
- Gao, Y.; Zheng, B.; Chen, G.; Li, Q. Optimal-location-selection query processing in spatial databases. IEEE Trans. Knowl. Data Eng. 2009, 21, 1162–1177. [Google Scholar]
- Jiang, X.; Cao, S.; Mo, B.; Cao, J.; Yang, H.; Tang, Y.; Hansen, M.; Zhao, J.; Sengupta, R. Simulation-Based Optimization for Vertiport Location Selection: A Surrogate Model With Machine Learning Method. Transp. Res. Rec. 2024, 2678. [Google Scholar] [CrossRef]
- Kotwicz Herniczek, M.T.; German, B.J. Scalable Combinatorial Vertiport Placement Method for an Urban Air Mobility Commuting Service. Transp. Res. Rec. 2024, 2678, 1624–1641. [Google Scholar] [CrossRef]
- Yoon, D.; Jeong, M.; Lee, J.; Kim, S.; Yoon, Y. Integrating Urban Air Mobility with Highway Infrastructure: A Strategic Approach for Vertiport Location Selection in the Seoul Metropolitan Area. arXiv 2025, arXiv:2502.00399. [Google Scholar]
- Rahman, B.; Bridgelall, R.; Habib, M.F.; Motuba, D. Integrating urban air mobility into a public transit system: A GIS-based approach to identify candidate locations for vertiports. Vehicles 2023, 5, 1803–1817. [Google Scholar] [CrossRef]
- Chae, M.; Kim, S.H.; Kim, S.H.; Kim, M.; Park, H.-T. Vertiport Locations Optimization in Discrete Search Space. In Proceedings of the 2023 IEEE/AIAA 42nd Digital Avionics Systems Conference (DASC), Barcelona, Spain, 1–5 October 2023; pp. 1–6. [Google Scholar]
- Kim, W.-J.; Park, J.-H. A study on the factors affecting UAM vertiport location selection. J. Urban Stud. Real Estate 2022, 13, 119–137. [Google Scholar]
- Cohen, M.M. The Vertiport as an Urban Design Problem; 0148-7191; SAE Technical Paper; SAE: Warrendale, PA, USA, 1996. [Google Scholar]
- Wang, J.; Zhang, S.; Guo, H.; Tian, Y.; Liu, S.; Du, C.; Wu, J. Stereoscopic monitoring of transportation infrastructure. Autom. Constr. 2024, 164, 105472–105485. [Google Scholar] [CrossRef]
- Bozzo, E.; Franceschet, M.; Rinaldi, F. Vulnerability and power on networks. Netw. Sci. 2015, 3, 196–226. [Google Scholar] [CrossRef]
- Latora, V.; Marchiori, M. Efficient behavior of small-world networks. Phys. Rev. Lett. 2001, 87, 198701. [Google Scholar]
- Vragović, I.; Louis, E.; Díaz-Guilera, A. Efficiency of informational transfer in regular and complex networks. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2005, 71, 036122. [Google Scholar]
- Menger, K. Zur allgemeinen kurventheorie. Fundam. Math. 1927, 10, 96–115. [Google Scholar]
- Derrible, S.; Kennedy, C. The complexity and robustness of metro networks. Phys. A Stat. Mech. Its Appl. 2010, 389, 3678–3691. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Lee, S. An Analysis of the Relationship between Neighborhood Road Network Structure and Pedestrian Traffic Accidents: Focusing on Seoul TAAS Data (2012–2014). J. Korea Plan. Assoc. 2017, 52, 141–161. [Google Scholar] [CrossRef]
- Fiedler, M. Algebraic connectivity of graphs. Czechoslov. Math. J. 1973, 23, 298–305. [Google Scholar] [CrossRef]
- Wei, P.; Chen, L.; Sun, D. Algebraic connectivity maximization of an air transportation network: The flight routes’ addition/deletion problem. Transp. Res. Part E Logist. Transp. Rev. 2014, 61, 13–27. [Google Scholar] [CrossRef]
- Newman, M.E. Assortative mixing in networks. Phys. Rev. Lett. 2002, 89, 208701. [Google Scholar] [CrossRef]
- Chang, H.; Su, B.-B.; Zhou, Y.-P.; He, D.-R. Assortativity and act degree distribution of some collaboration networks. Phys. A Stat. Mech. Its Appl. 2007, 383, 687–702. [Google Scholar] [CrossRef]
- Newman, M.E. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Shanmukhappa, T.; Ho, I.W.-H.; Chi, K.T.; Leung, K.K. Recent development in public transport network analysis from the complex network perspective. IEEE Circuits Syst. Mag. 2019, 19, 39–65. [Google Scholar] [CrossRef]
- Newman, M.E. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar]
- Xu, M.; Pan, Q.; Muscoloni, A.; Xia, H.; Cannistraci, C.V. Modular gateway-ness connectivity and structural core organization in maritime network science. Nat. Commun. 2020, 11, 2849. [Google Scholar]
- Freeman, L.C. Centrality in social networks: Conceptual clarification. Soc. Netw. Crit. Concepts Sociol. Lond. Routledge 2002, 1, 238–263. [Google Scholar]
- Chen, L.; Wandelt, S.; Dai, W.; Sun, X. Scalable vertiport hub location selection for air taxi operations in a metropolitan region. INFORMS J. Comput. 2022, 34, 834–856. [Google Scholar] [CrossRef]
- Bryan, D.L.; O′kelly, M.E. Hub-and-spoke networks in air transportation: An analytical review. J. Reg. Sci. 1999, 39, 275–295. [Google Scholar]
- Peksa, M.; Dandl, F.; Bogenberger, K. Hierarchical Vertiport Network for an Urban Air Mobility System: Munich Metropolitan Area Case Study. In Proceedings of the 2023 IEEE/AIAA 42nd Digital Avionics Systems Conference (DASC), Barcelona, Spain, 1–5 October 2023; pp. 1–6. [Google Scholar]
- Willey, L.C.; Salmon, J.L. A method for urban air mobility network design using hub location and subgraph isomorphism. Transp. Res. Part C Emerg. Technol. 2021, 125, 102997. [Google Scholar]


| Category | Node | Link |
|---|---|---|
| Road Network | 153,120 | 196,850 |
| Road and Railway Network | 156,354 | 338,289 |
| Railway Network | 1924 | 2058 |
| Urban Railway Network | 834 | 1018 |
| Group | Global Efficiency | Average Shortest Path Length | Algebraic Connectivity | Clustering Coefficient | Degree Assortativity | Transitivity | Modularity |
|---|---|---|---|---|---|---|---|
| Urban Railway Network | 0.06080 | 24.20161 | 0.00212 | 0.05422 | 0.52806 | 0.18000 | 0.87862 |
| Ratio | Betweenness UAM Network | Degree UAM Network | Vulnerable UAM Network |
|---|---|---|---|
| 5% | 0.08706 | 0.08948 | 0.09556 |
| 10% | 0.12753 | 0.12932 | 0.14703 |
| 15% | 0.16842 | 0.16566 | 0.19674 |
| 20% | 0.19971 | 0.21665 | 0.23825 |
| Ratio | Betweenness UAM Network | Degree UAM Network | Vulnerable UAM Network |
|---|---|---|---|
| 5% | 17.3005 | 16.0882 | 15.8778 |
| 10% | 12.2384 | 11.9723 | 10.6847 |
| 15% | 9.7350 | 9.8296 | 8.2023 |
| 20% | 8.7287 | 7.3651 | 7.0458 |
| Ratio | Betweenness UAM Network | Degree UAM Network | Vulnerable UAM Network |
|---|---|---|---|
| 5% | 0.00293 | 0.00356 | 0.00326 |
| 10% | 0.00440 | 0.00568 | 0.00362 |
| 15% | 0.00510 | 0.00645 | 0.00449 |
| 20% | 0.00550 | 0.00920 | 0.00646 |
| Ratio | Betweenness UAM Network | Degree UAM Network | Vulnerable UAM Network |
|---|---|---|---|
| 5% | 0.05072 | 0.05081 | 0.04053 |
| 10% | 0.07646 | 0.07530 | 0.06419 |
| 15% | 0.10154 | 0.09937 | 0.09321 |
| 20% | 0.12815 | 0.12606 | 0.12512 |
| Ratio | Betweenness UAM Network | Degree UAM Network | Vulnerable UAM Network |
|---|---|---|---|
| 5% | 0.91335 | 0.89679 | 0.87188 |
| 10% | 0.97169 | 0.96848 | 0.95549 |
| 15% | 0.98427 | 0.98409 | 0.97476 |
| 20% | 0.98920 | 0.98782 | 0.98188 |
| Ratio | Betweenness UAM Network | Degree UAM Network | Vulnerable UAM Network |
|---|---|---|---|
| 5% | 0.65703 | 0.68810 | 0.66245 |
| 10% | 0.31077 | 0.30245 | 0.28555 |
| 15% | 0.12937 | 0.14362 | 0.12440 |
| 20% | 0.07310 | 0.07711 | 0.06092 |
| Ratio | Betweenness UAM Network | Degree UAM Network | Vulnerable UAM Network |
|---|---|---|---|
| 5% | 0.94994 | 0.92884 | 0.89724 |
| 10% | 0.94004 | 0.93193 | 0.88948 |
| 15% | 0.92365 | 0.92317 | 0.85936 |
| 20% | 0.90299 | 0.89032 | 0.81274 |
| Group | Network Strategy Effect (p-Value) | Ratio Effect (p-Value) |
|---|---|---|
| Global Efficiency | 0.0097 | 0.0000 |
| Average Shortest Path Length | 0.0053 | 0.0000 |
| Algebraic Connectivity | 0.0276 | 0.0051 |
| Clustering Coefficient | 0.0067 | 0.0000 |
| Degree Assortativity | 0.0005 | 0.0039 |
| Transitivity | 0.0378 | 0.0000 |
| Modularity | 0.0540 | 0.0000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, K.-H.; Lee, H. Network Topology-Driven Vertiport Placement Strategy: Integrating Urban Air Mobility with the Seoul Metropolitan Railway System. Appl. Sci. 2025, 15, 3965. https://doi.org/10.3390/app15073965
Song K-H, Lee H. Network Topology-Driven Vertiport Placement Strategy: Integrating Urban Air Mobility with the Seoul Metropolitan Railway System. Applied Sciences. 2025; 15(7):3965. https://doi.org/10.3390/app15073965
Chicago/Turabian StyleSong, Ki-Han, and HaJeong Lee. 2025. "Network Topology-Driven Vertiport Placement Strategy: Integrating Urban Air Mobility with the Seoul Metropolitan Railway System" Applied Sciences 15, no. 7: 3965. https://doi.org/10.3390/app15073965
APA StyleSong, K.-H., & Lee, H. (2025). Network Topology-Driven Vertiport Placement Strategy: Integrating Urban Air Mobility with the Seoul Metropolitan Railway System. Applied Sciences, 15(7), 3965. https://doi.org/10.3390/app15073965






