Comprehensive Analysis of Deposition Parameters and Energy-Dispersive X-Ray Spectroscopy Characterization in Cataphoretic Coating Processes
Abstract
1. Introduction
2. Materials and Methods
2.1. Material Selection—VDA 239-100 CR4
2.2. Experimental Conditions
2.2.1. Sample Preparation
2.2.2. The Process of Cataphoretic Coating
2.3. Measurement Methods
2.4. Analysis of Prediction Model
3. Results and Discussion
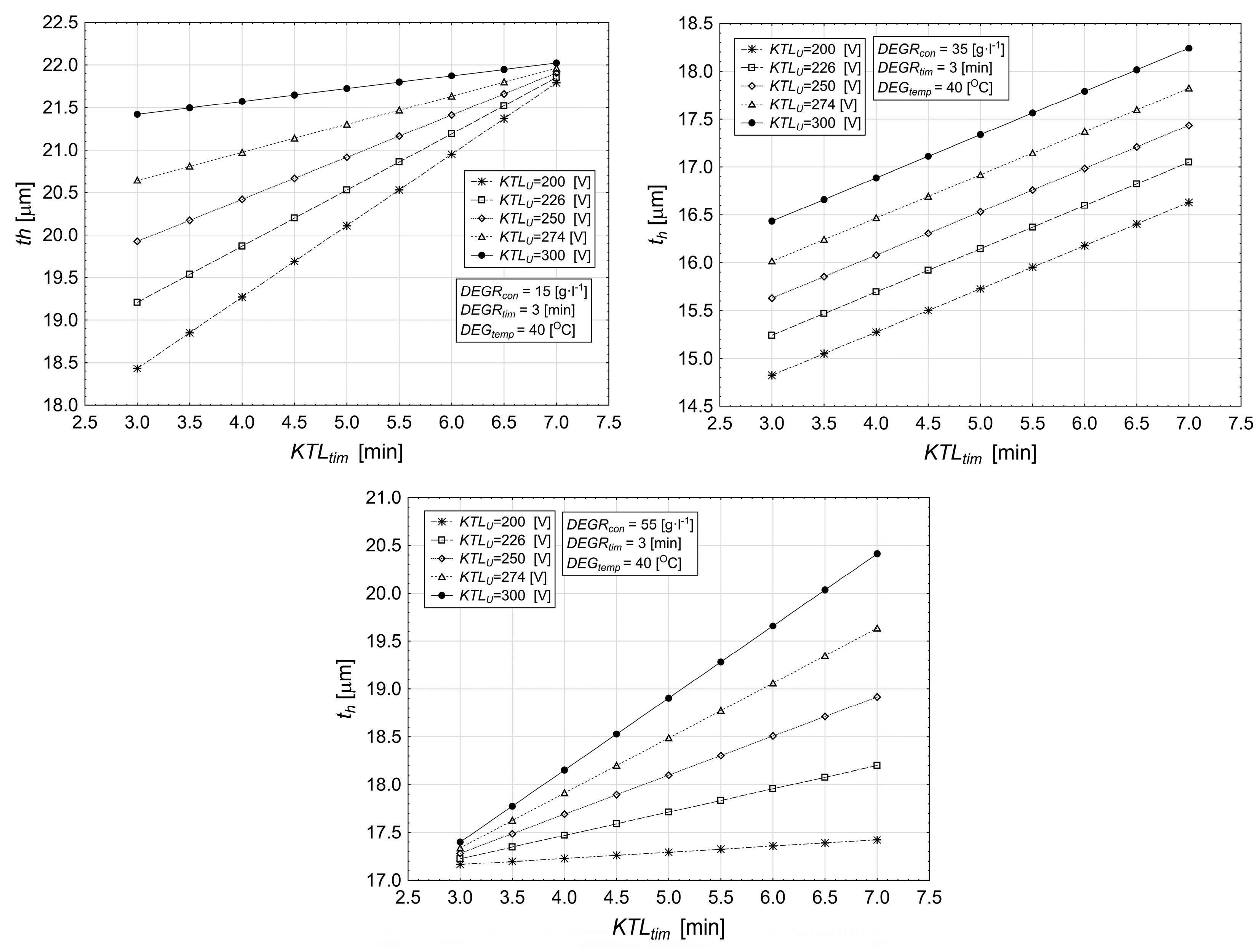
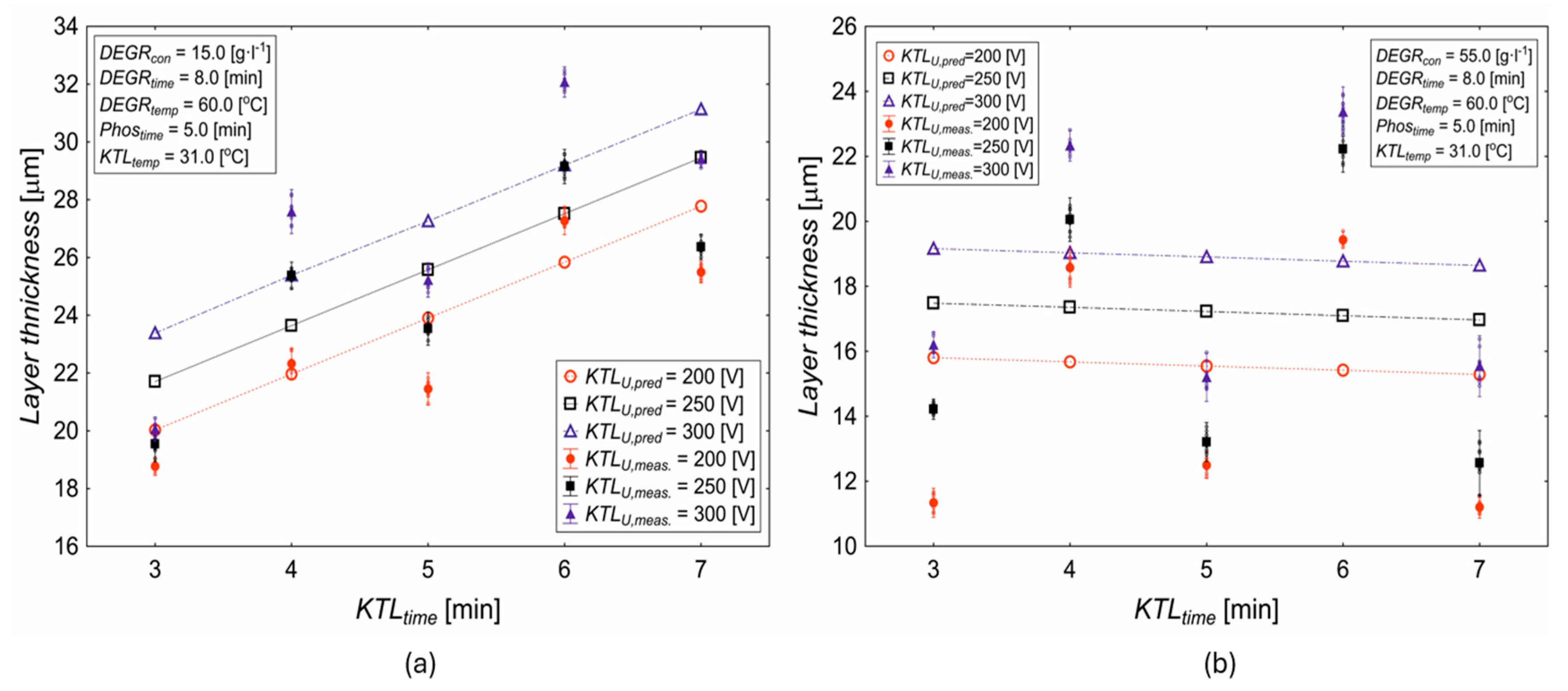
3.1. Influence of Deposition Time and Cataphoretic Voltage on Coating Characteristics
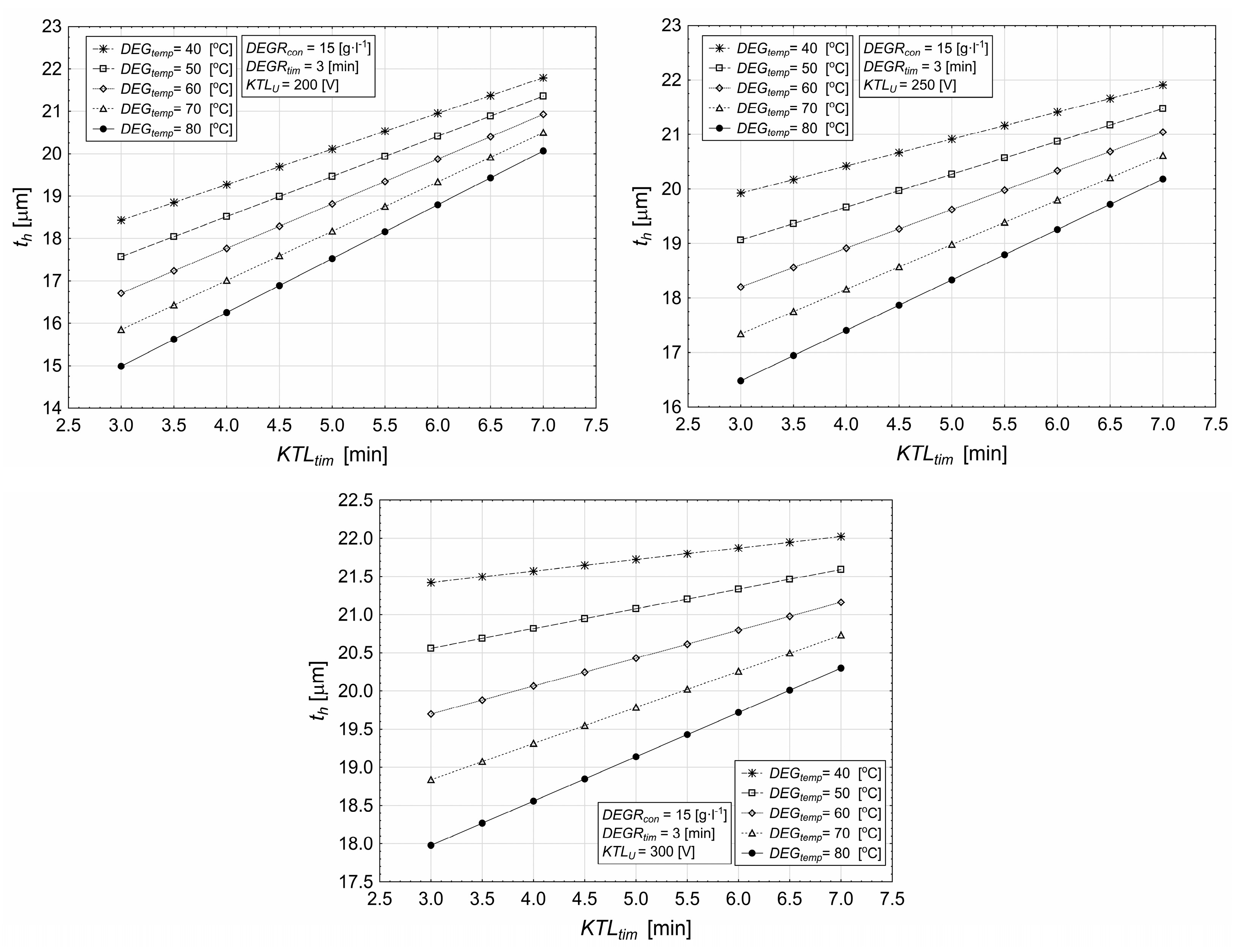
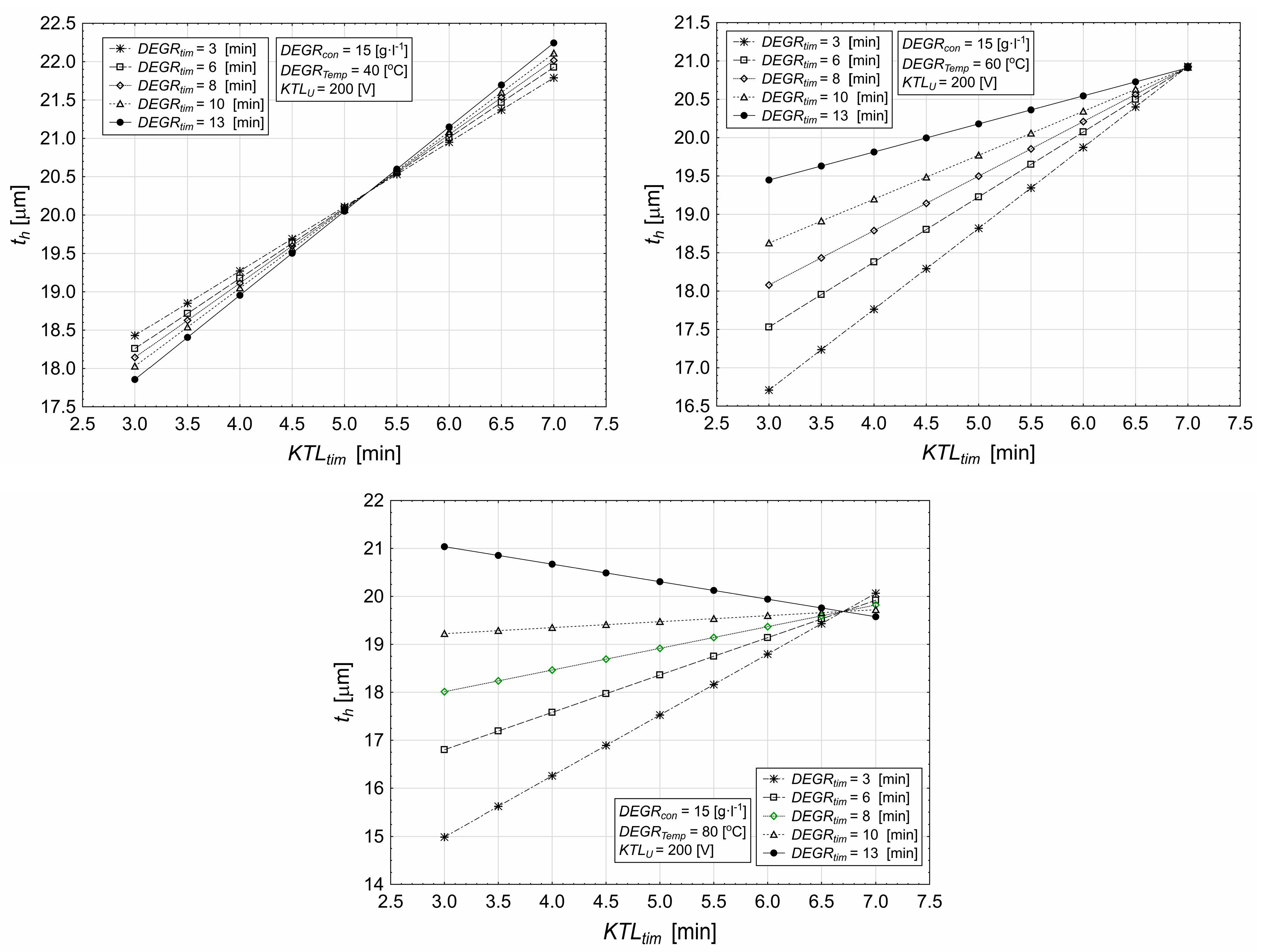
3.2. Influence of Deposition Time and Degreasing Temperature on Coating Characteristics
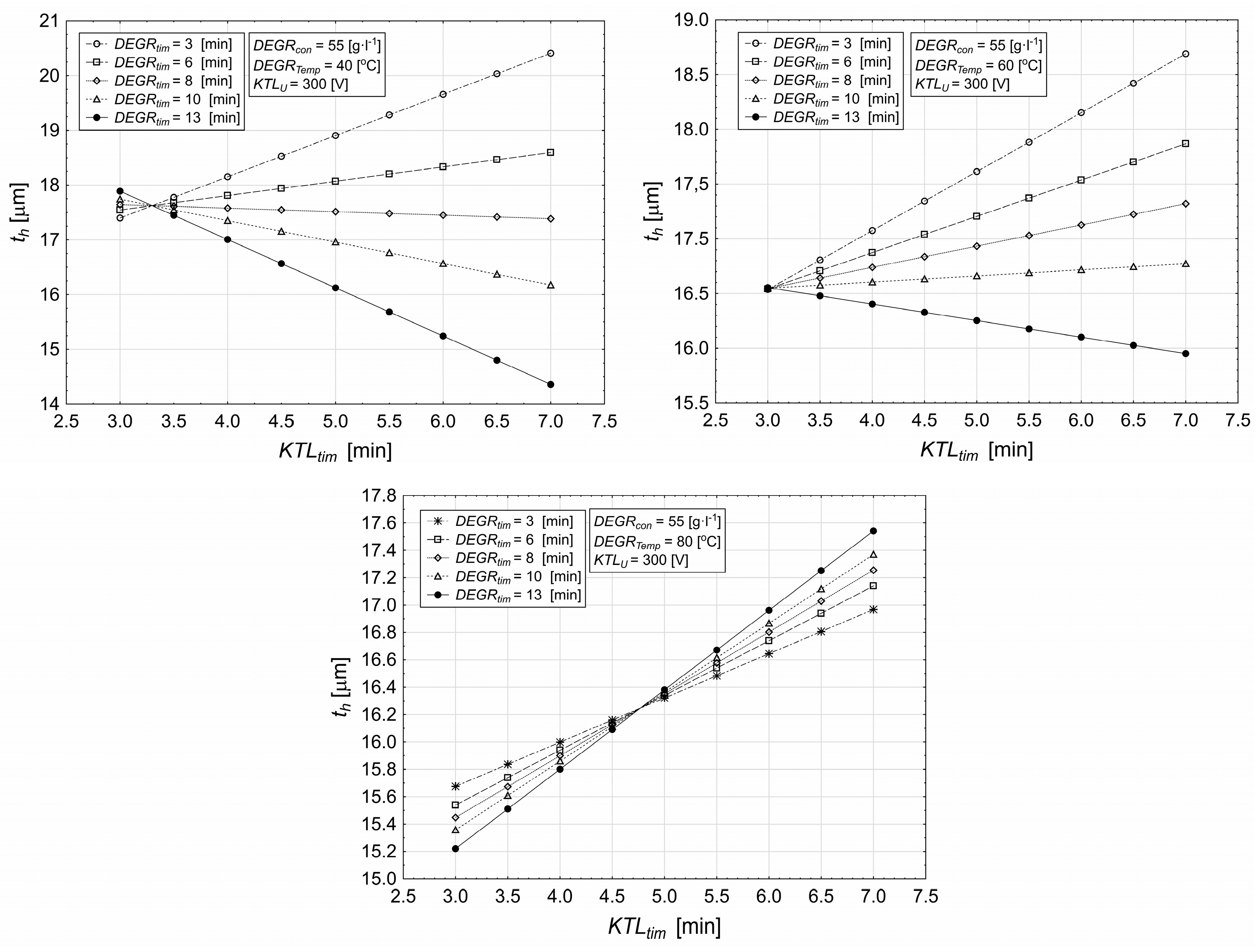
3.3. Influence of Cataphoretic Deposition and Degreasing Deposition on Coating Characteristics
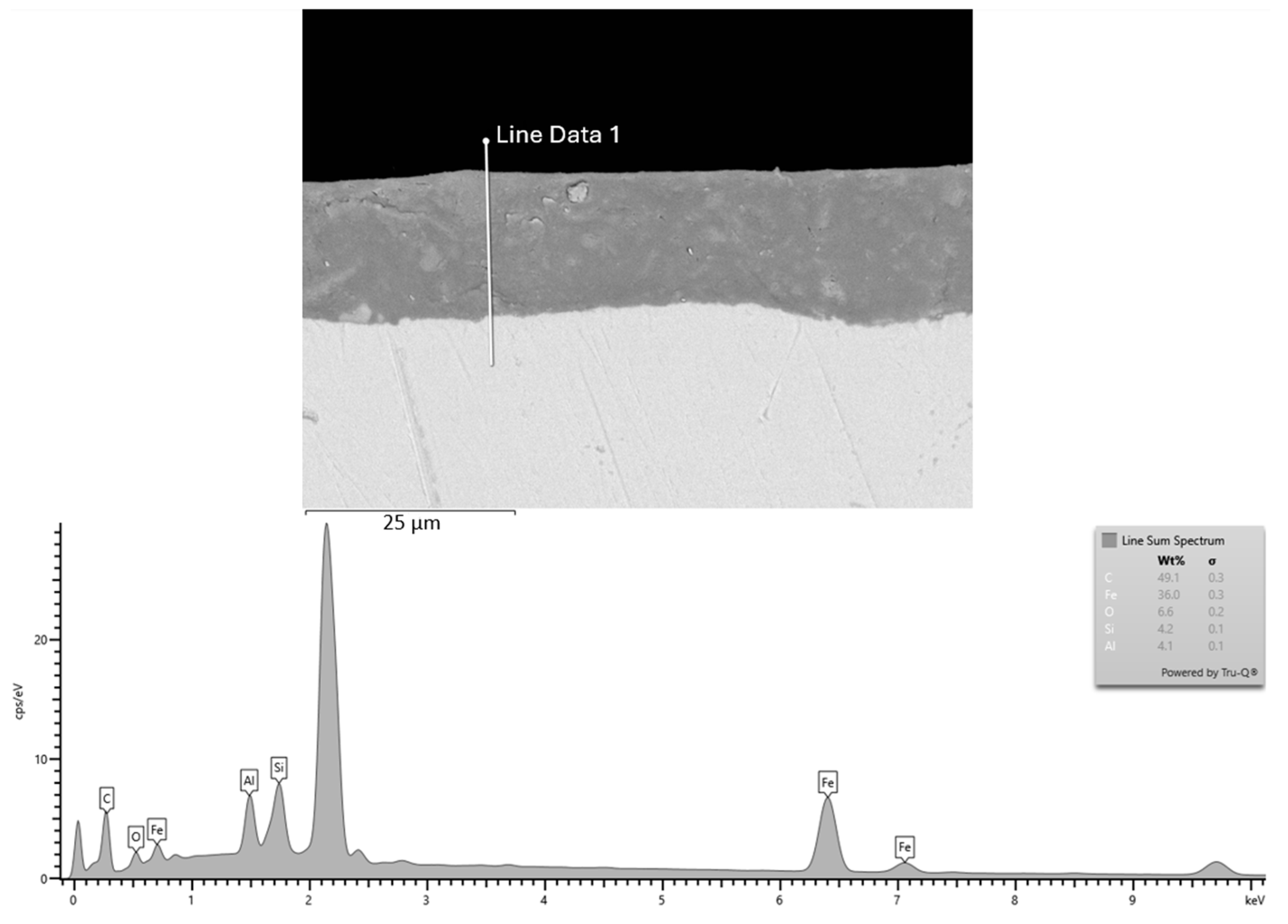
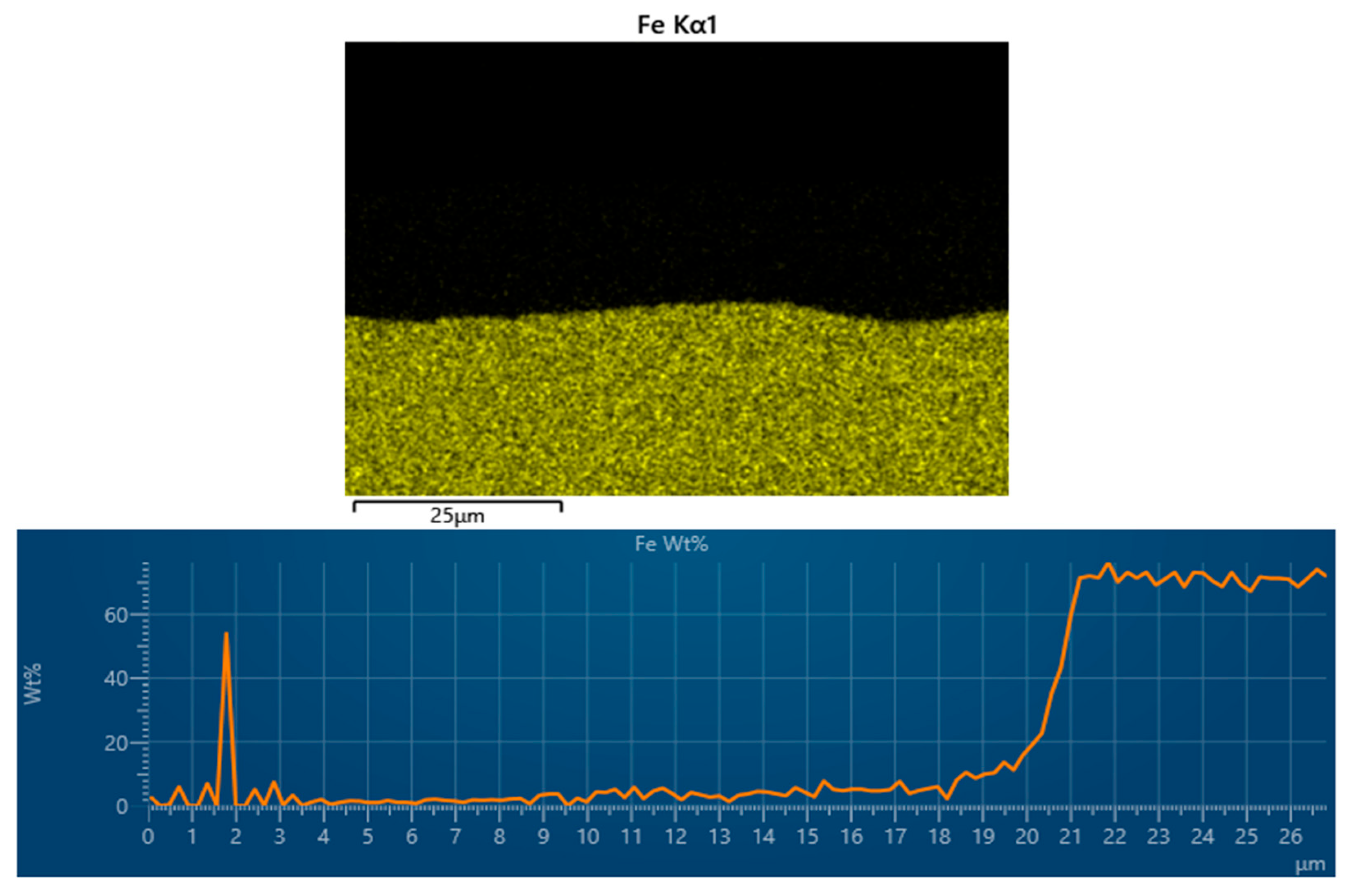
3.4. Energy-Dispersive X-Ray Spectroscopy (EDX) of Cataphoretic Layer
3.5. Summary of Results
4. Conclusions
- The layer thickness increases with KTL deposition time, with the maximum thickness achieved at 7 min, while shorter times (e.g., 3 min) result in thinner coatings.
- The applied voltage significantly influences the layer thickness; at 300 V, the layer thickness increases more steeply, and the reduction over time is minimal, indicating a higher material accumulation in the early stages of deposition.
- Lower degreasing temperatures (e.g., 40 °C) lead to higher layer thickness, while higher temperatures (e.g., 80 °C) result in a reduction in thickness.
- The optimal combination of voltage and temperature (e.g., 60 °C) leads to more uniform layer thicknesses across different deposition times.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ouchi, T.; Sadoway, D.R. Positive current collector for Li∥Sb-Pb liquid metal battery. J. Power Sources 2017, 357, 158–163. [Google Scholar] [CrossRef]
- Kirchgeorg, T.; Weinberg, I.; Hoernig, M.; Baier, R.; Schmid, M.J.; Brockmeyer, B. Emissions from corrosion protection systems of offshore wind farms: Evaluation of the potential impact on the marine environment. Mar. Pollut. Bull. 2018, 136, 257–268. [Google Scholar] [CrossRef] [PubMed]
- Flores, J.F.; Neville, A.; Kapur, N.; Gnanavelu, A. Assessing the resistance of metal matrix composites and their microstructural integrity under erosion-corrosion. Wear 2011, 271, 1331–1340. [Google Scholar] [CrossRef]
- Babaei, N.; Yeganeh, H.; Gharibi, R. Anticorrosive and self-healing waterborne poly(urethane-triazole) coatings made through a combination of click polymerization and cathodic electrophoretic deposition. Eur. Polym. J. 2019, 112, 636–647. [Google Scholar] [CrossRef]
- Moradi, M.; Yeganeh, H.; Pazokifard, S. Synthesis and assessment of novel anticorrosive polyurethane coatings containing an amine-functionalized nanoclay additive prepared by the cathodic electrophoretic deposition method. RSC Adv. 2016, 6, 28089–28102. [Google Scholar] [CrossRef]
- Aghili, M.; Yazdi, M.K.; Ranjbar, Z.; Jafari, S.H. Anticorrosion performance of electro-deposited epoxy/amine functionalized graphene oxide nanocomposite coatings. Corros. Sci. 2021, 179, 109143. [Google Scholar] [CrossRef]
- Zivkovic, L.S.; Jegdic, B.V.; Andric, V.; Rhee, K.Y.; Bajat, J.B.; Miskovic-Stankovic, V.B. The effect of ceria and zirconia nanoparticles on the corrosion behaviour of cataphoretic epoxy coatings on AA6060 alloy. Prog. Org. Coat. 2019, 136, 105219. [Google Scholar] [CrossRef]
- Oliviera, M.G.; Romano, A.P.; Vandermiers, C.; Mathieu, X.; Poelman, M. Influence of the stress generated during an ageing cycle on the barrier properties of cataphoretic coatings. Prog. Org. Coat. 2008, 63, 323–329. [Google Scholar] [CrossRef]
- Garcia, S.J.; Rodriguez, M.T.; Izquierdo, R.; Suay, J. Evaluation of cure temperature effects in cataphoretic automotive primers by electrochemical techniques. Prog. Org. Coat. 2007, 60, 303–311. [Google Scholar] [CrossRef]
- Zanella, C.; Pedrotti, A.; Fedel, M.; Deflorian, F. Influence of the electrochemical behavior of metal substrates on the properties of cataphoretic clearcoat. Prog. Org. Coat. 2014, 77, 1987–1992. [Google Scholar] [CrossRef]
- Calovi, M.; Russo, F.; Rossi, S. Synergic behavior of graphene-based filler and thermochromic pigments in cataphoretic coatings. Prog. Org. Coat. 2021, 2021, 105978. [Google Scholar]
- Darowicki, K.; Slepski, P.; Szocinski, M. Novel application of dynamic electrochemical impedance monitoring to a cataphoretic coating process. Prog. Org. Coat. 2020, 149, 105906. [Google Scholar]
- Sternadelova, K.; Krupova, H.; Matysek, D.; Mohyla, P. Quality assessment of the vitreous enamel coating applied to the weld joint. MM Sci. J. 2023, 2023, 6333–6338. [Google Scholar]
- Brüggemann, M.; Rach, A. Electrocoat: Formulation and Technology; Vincentz Network: Hannover, Germany, 2020. [Google Scholar]
- Goldschmidt, A.; Streitberger, H.J. BASF Handbuch Lackiertechnik; Vincentz Network: Hannover, Germany, 2014. [Google Scholar]
- Brock, T.; Groteklaes, M.; Mischke, P. European Coatings Handbook, 2nd ed.; Vincentz Network: Hannover, Germany, 2010. [Google Scholar]
- Ovsik, M.; Manas, M.; Stanek, M.; Dockal, A.; Mizera, A.; Fluxa, P.; Bednarik, M.; Adamek, M. Nano-mechanical properties of surface layers of polyethylene modified by irradiation. Materials 2020, 13, 929. [Google Scholar] [CrossRef]
- Akafuah, N.K.; Poozesh, S.; Salaimeh, A.; Patrick, G.; Lawler, K.; Saito, K. Evolution of the automotive body coating process-A Review. Coatings 2016, 6, 24. [Google Scholar] [CrossRef]
- Skotnicki, W.; Jedrzejczyk, D. The comparative analysis of the coatings deposited on the automotive parts by the cataphoresis method. Materials 2021, 14, 6155. [Google Scholar] [CrossRef]
- Jaczewski, M. Industrial Paint Coatings for Metal Surfaces. In Tikkurila Protective Coating Guide, 2nd ed.; Tikkurila: Vantaa, Finland, 2008. [Google Scholar]
- Javidi, A.; Rieger, U.; Eichlseder, W. The effect of machining on the surface integrity and fatigue life. Int. J. Fatigue 2008, 30, 2050–2055. [Google Scholar] [CrossRef]
- Rivera, J.L.; Reyes-Carrillo, T. A framework for environmental and energy analysis of the automobile painting process. Procedia CIRP 2014, 15, 171–175. [Google Scholar]
- Goeke, S.; Biermann, D.; Stickel, D.; Stemmer, P.; Fischer, A.; Geenen, K.; Huth, S.; Theisen, W. Enhancing the surface integrity of tribologically stressed contacting surfaces by an adjusted surface topography. Procedia CIRP 2014, 13, 214–218. [Google Scholar]
- VDA 239-100; Spray and Micro-Dosage Application—Technical Cleanliness of Components in Contact with Fluids. Normservis, 2016. Available online: https://eshop.normservis.sk/norma/vda-239-100-1.5.2016.html (accessed on 15 January 2025).
- Marine Steels. DIN EN 10130 DC01 Steel—Cold Rolled Low Carbon Steel Plate. Available online: https://sk.marinesteels.com/stainless-steel/stainless-steel-plate/din-en-10130-dc01-steel.html (accessed on 18 January 2025).
- Dean, A.; Voss, D.; Dragulijc, D. Design and Analysis of Experiments; Springer International Publishing AG: Cham, Switzerland, 2017; ISBN 978-3-319-52250-0. [Google Scholar]
- KTL s.r.o. Princip Činnosti. KTL s.r.o. Available online: https://www.ktlpresov.sk/princip-cinnosti (accessed on 24 January 2025).
- ISO 16232:2018; Road Vehicles—Cleanliness of Components and Systems. International Organization for Standardization: London, UK, 2018. Available online: https://www.iso.org/standard/71583.html (accessed on 25 January 2025).
- Built In. Shapiro-Wilk Test: A Guide to Normality Testing. Available online: https://builtin.com/data-science/shapiro-wilk-test (accessed on 25 January 2025).
- Garcia, S.J.; Suay, J. Optimization of deposition voltage of cataphoretic automotive primers assessed by EIS and AC/DC/AC. Prog. Org. Coat. 2009, 66, 306–313. [Google Scholar]
- Kamas, T.; Tekkalmaz, M. Coupled field modeling of E/M impedance of piezoelectric wafer active sensor for cataphoretic coating thickness measurement. Smart Mater. Struct. 2017, 26, 045035. [Google Scholar]
- Krenicky, T.; Goncharov, O.Y.; Kuchar, J.; Sapegina, I.V.; Kudlacek, J.; Faizullin, R.R.; Korshunov, A.I.; Cerny, D. Chemical vapor deposition of tantalum carbide in the TaBr5-CCl4-Cd system. Coatings 2024, 14, 547. [Google Scholar] [CrossRef]
- Kania, H.; Saternus, M.; Kudlacek, J. Impact of Bi and Sn on microstructure and corrosion resistance of zinc coatings obtained in Zn-AlNi bath. Materials 2020, 13, 3788. [Google Scholar] [CrossRef] [PubMed]
- Hamera, P.; Bennison, A.D. TIB Clean A300—lowering the temperature of alkaline degreasing. Ochr. Przed Koroz. 2021, 64, 144–147. [Google Scholar]
- Wang, C.S.; Cai, N.; Zhang, D.V.; Zhang, J.X.; Chang, T.H.; Li, S.M.; Chao, Y.Q.; Hu, J.Q. Preparation of optimum degreasing-sintering process for metal-polymer blending low temperature 3D printing. Rapid Prototyp. J. 2019, 25, 515–529. [Google Scholar] [CrossRef]
- Swierczynski, T. Leraclen® ATR and Lerabilt® 268—low-temperature, alkaline products for degreasing prior to hot-dip galvanizing and electroplating. Ochr. Przed Koroz. 2022, 65, 324–326. [Google Scholar]
- Rossi, S.; Calovi, M.; Fedel, M. Corrosion protection of aluminum foams by cataphoretic deposition of organic coatings. Prog. Org. Coat. 2017, 109, 144–151. [Google Scholar]
- Calovi, M.; Dire, S.; Ceccato, R.; Deflorian, F.; Rossi, S. Corrosion protection properties of functionalised graphene-acrylate coatings produced via cataphoretic deposition. Prog. Org. Coat. 2019, 136, 105261. [Google Scholar]
- Su, Y.; Zhitomirsky, I. Cataphoretic assembly of cationic dyes and deposition of carbon nanotube and graphene films. J. Colloid Interf. Sci. 2013, 399, 46–53. [Google Scholar]
- Li, C.H.; He, Y.; Zhao, Y.; Li, Z.J.; Sun, D.; Li, H.J.; Chen, W.; Yan, J.; Wu, G.Y.; Yuan, X. Cataphoretic deposition of an epoxy coating with the incorporation of Ti3C2Tx@Mg-Al layered double hydroxide for long-term active corrosion protection effect. Prog. Org. Coat. 2023, 175, 107333. [Google Scholar] [CrossRef]
- Kania, H.; Saternus, M.; Kudlacek, J.; Svoboda, J. Microstructure Characterization and Corrosion Resistance of Zinc Coating Obtained in a Zn-AlNiBi Galvanizing Bath. Coatings 2020, 10, 758. [Google Scholar] [CrossRef]
- Nam, D.; Opanasyuk, A.S.; Koval, P.V.; Ponomarev, A.G.; Jeong, A.R.; Kim, G.Y.; Jo, W.; Cheong, H. Composition variations in Cu2ZnSnSe4 thin films analyzed by X-ray diffraction, energy dispersive X-ray spectroscopy, particle induced X-ray emission, photoluminescence, and Raman spectroscopy. Thin Solid Films 2014, 562, 109–113. [Google Scholar] [CrossRef]
- Lovejoy, T.C.; Ramasse, Q.M.; Falke, M.; Kaeppel, A.; Terborg, R.; Zan, R.; Dellby, N.; Krivanek, O.L. Single atom identification by energy dispersive x-ray spectroscopy. Appl. Phys. Lett. 2012, 100, 154101. [Google Scholar] [CrossRef]
- Qi, P.; Samadi, N.; Martinson, M.; Ponomarenko, O.; Bassey, B.; Gomez, A.; George, G.N.; Pickering, I.J.; Chapman, L.D. Wide field imaging energy dispersive X-ray absorption spectroscopy. Sci. Rep. 2019, 9, 17734. [Google Scholar]
- D’Alfonso, A.J.; Freitag, B.; Klenov, D.; Allen, L.J. Atomic-resolution chemical mapping using energy-dispersive x-ray spectroscopy. Phys. Rev. B 2010, 81, 100101. [Google Scholar] [CrossRef]
- Tromp, R.M. Energy-dispersive X-ray spectroscopy in a low energy electron microscope. Ultramicroscopy 2024, 259, 113935. [Google Scholar] [CrossRef]
- Sanchez, D.F.; Simionovici, A.S.; Lemelle, L.; Cuartero, V.; Mathon, O.; Pascarelli, S.; Bonnin, A.; Shapiro, R.; Konhauser, K.; Grolimund, D.; et al. 2D/3D Microanalysis by Energy Dispersive X-ray Absorption Spectroscopy Tomography. Sci. Rep. 2017, 7, 16453. [Google Scholar] [CrossRef]

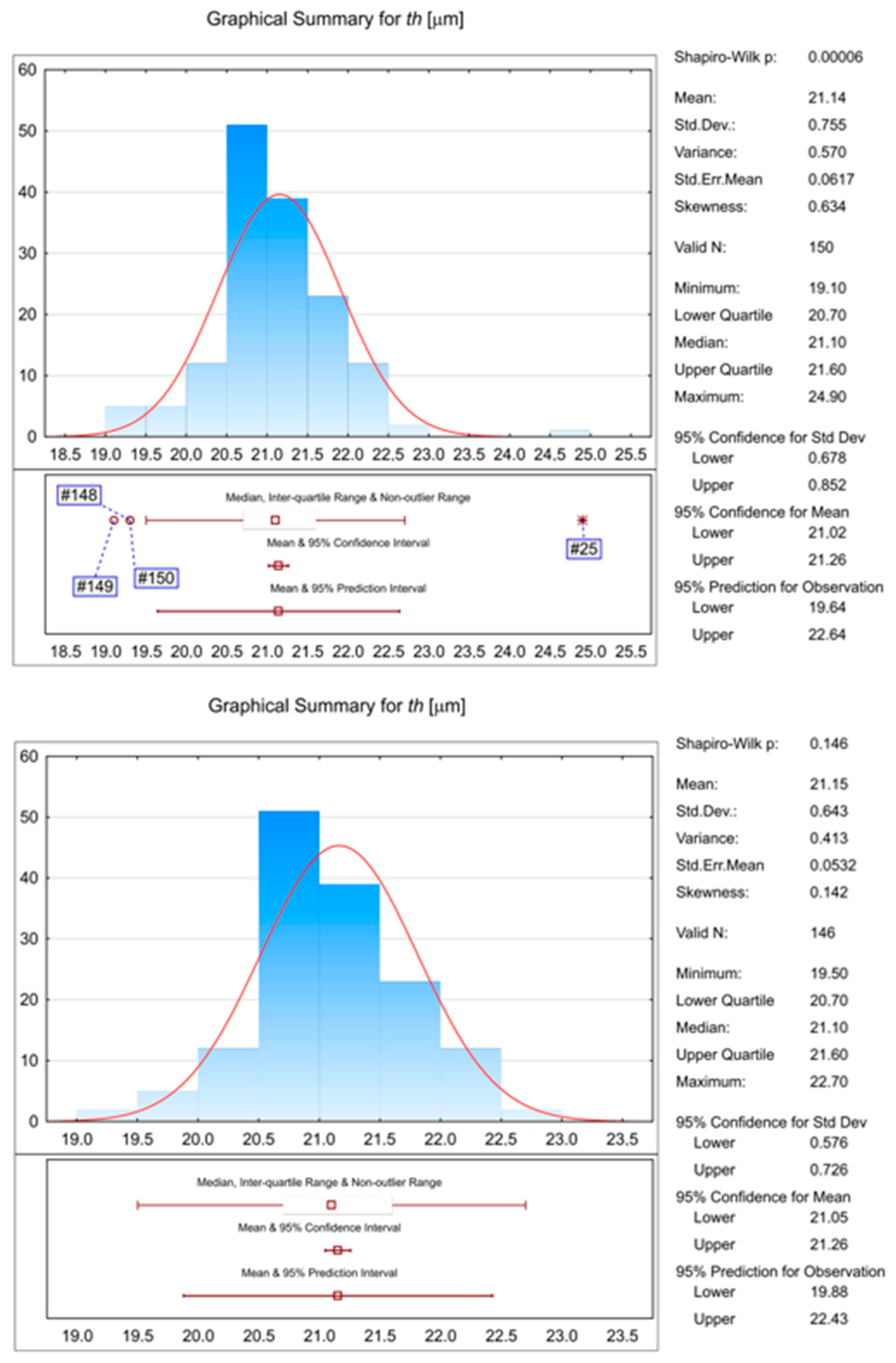
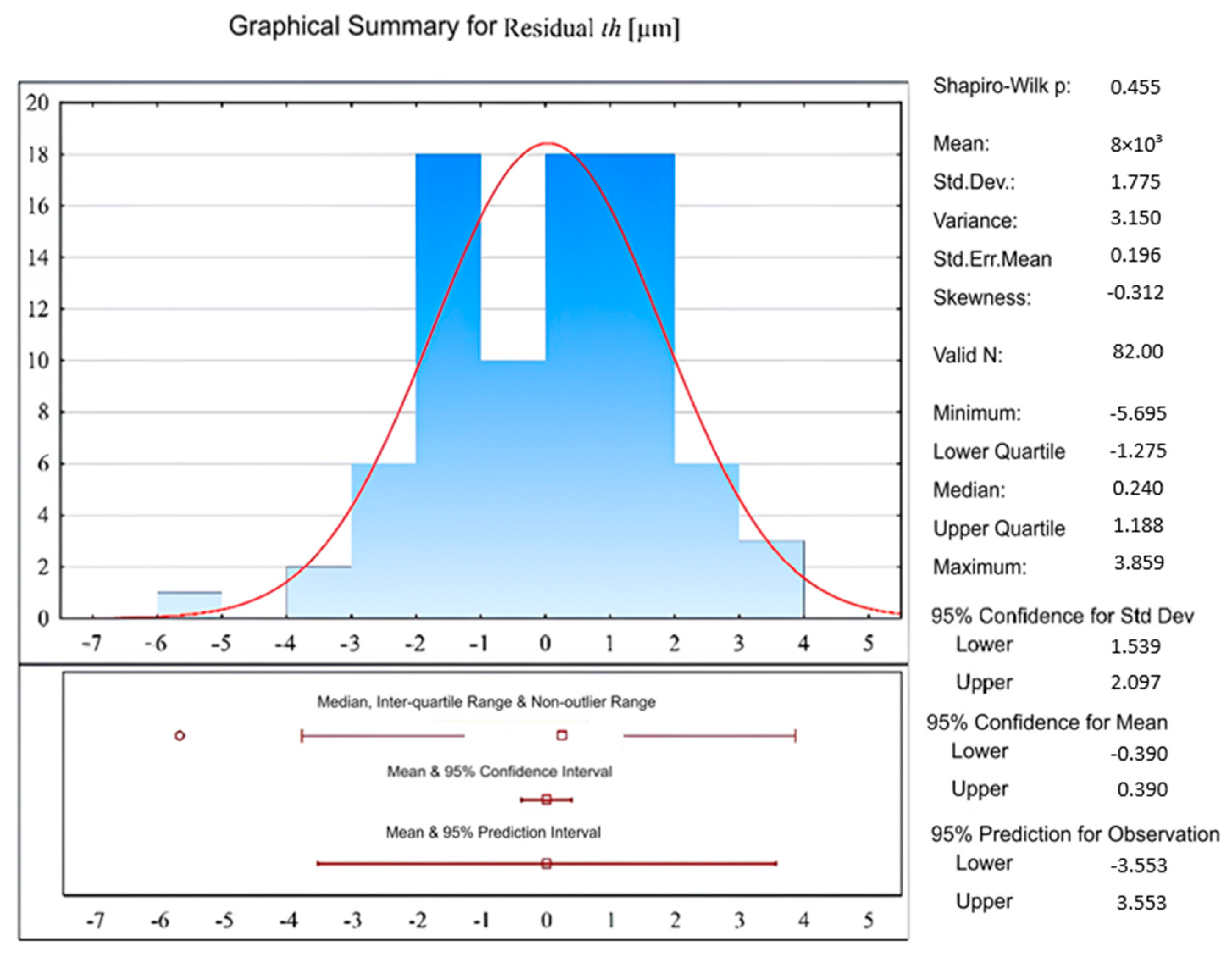




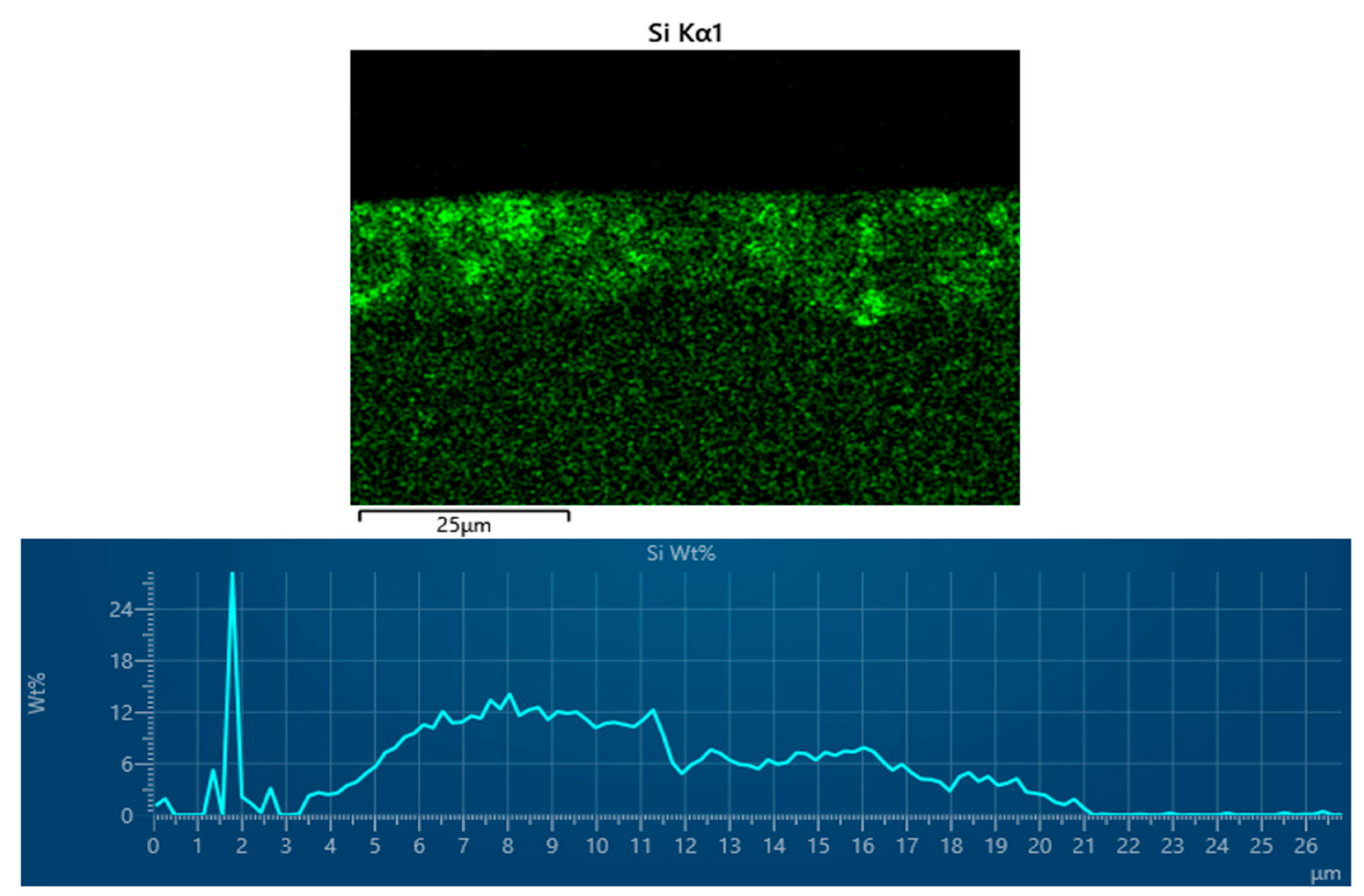
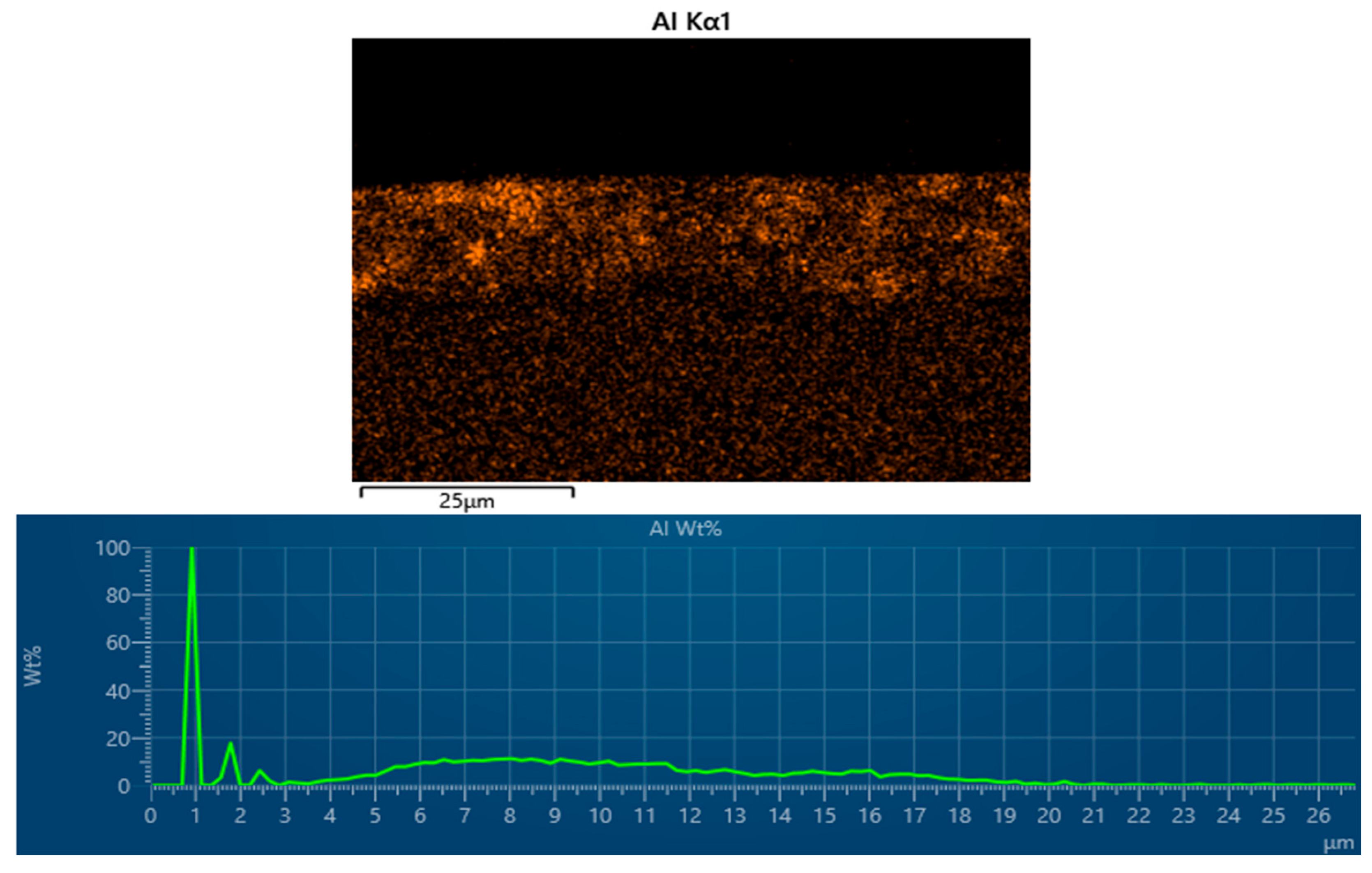
| Property | Value |
|---|---|
| Yield strength (Rp0,2) | 140–180 MPa |
| Tensile strength (Rm) | 270–330 MPa |
| Hardness by Brinell HBW | 267 |
| Elongation (A80) | ≥39% |
| r-value (r90/20) | ≥1.9 |
| r-value m/20 | ≥1.6 |
| n-value (n10–20/Ag) | ≥0.20 |
| Chemical Element | Concentration [%] |
|---|---|
| Sodium carbonate (Na2CO3) | 20–30 |
| Sodium metasilicate (Na2SiO3 × 5H2O) | 20–30 |
| Sodium hydroxide (NaOH) | 20–30 |
| Fatty tallowamine (POE), ethoxylate (5EO) | 3–5 |
| Factor Code | Variable | Unit | Level of Factors | ||||
|---|---|---|---|---|---|---|---|
| −2.05464 | −1 | 0 | 1 | +2.05464 | |||
| x1 | kODM | g·L−1 | 15 | 25 | 35 | 45 | 55 |
| x2 | tODM | min | 3 | 6 | 8 | 10 | 13 |
| x3 | TODM | °C | 40 | 50 | 60 | 70 | 80 |
| x4 | tFOSF | min | 1 | 3 | 5 | 7 | 9 |
| x5 | tKTL | min | 3 | 4 | 5 | 6 | 7 |
| x6 | UKTL | V | 200 | 226 | 250 | 274 | 300 |
| x7 | tPOLY | min | 13 | 17 | 20 | 23 | 27 |
| x8 | TPOLY | °C | 150 | 176 | 200 | 224 | 250 |
| Source | Value |
|---|---|
| RSquare | 0.751148 |
| RSquare Adj | 0.707869 |
| Root Mean Square Error | 1.922936 |
| Mean of Response | 17.71049 |
| Observations (or Sum Wgts) | 82 |
| Source | DF | Sum of Squares | Mean Square | F Ratio | Prob > F |
|---|---|---|---|---|---|
| Model | 12 | 770.1278 | 64.1773 | 17.3561 | <0.0001 |
| Error | 69 | 255.1402 | 3.6977 | - | - |
| C. Total | 81 | 1025.268 | - | - | - |
| Source | DF | Sum of Squares | Mean Square | F Ratio | Prob > F | Max RSq |
|---|---|---|---|---|---|---|
| Lack Of Fit | 30 | 135.09267 | 4.50309 | 1.4629 | 0.1312 | 0.8829 |
| Pure Error | 39 | 120.04749 | 3.07814 | - | - | - |
| Total Error | 69 | 255.14016 | - | - | - | - |
| Term | Estimate | Std Error | t Ratio | Prob > |t| | Lower 95% | Upper 95% |
|---|---|---|---|---|---|---|
| Intercept | 15.24063 | 0.480734 | 31.7 | <0.0001 | 14.28159 | 16.19966 |
| x1 | −2.08862 | 0.225926 | −9.24 | <0.0001 | −2.53933 | −1.63791 |
| x5 | 0.903898 | 0.225926 | 4 | 0.0002 | 0.453188 | 1.354608 |
| x6 | 0.805741 | 0.225926 | 3.57 | 0.0007 | 0.355031 | 1.256451 |
| x3 | −0.58184 | 0.225926 | −2.58 | 0.0122 | −1.03255 | −0.13113 |
| x1·x1 | 3.453701 | 0.680272 | 5.08 | <0.0001 | 2.096597 | 4.810806 |
| x1·x5 | −0.51656 | 0.240367 | −2.15 | 0.0351 | −0.99608 | −0.03704 |
| x1·x2 | −0.68031 | 0.240367 | −2.83 | 0.0061 | −1.15983 | −0.20079 |
| x3·x2 | 0.71 | 0.240367 | 2.95 | 0.0043 | 0.230481 | 1.189519 |
| x1·x5·x3 | 0.51625 | 0.240367 | 2.15 | 0.0352 | 0.036731 | 0.995769 |
| x1·x1·x1·x1 | −0.47839 | 0.168911 | −2.83 | 0.0061 | −0.81536 | −0.14142 |
| x1·x5·x6·x2 | −0.68906 | 0.240367 | −2.87 | 0.0055 | −1.16858 | −0.20954 |
| x1·x5·x3·x2 | 0.94625 | 0.240367 | 3.94 | 0.0002 | 0.466731 | 1.425769 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fejko, P.; Peti, D.; Dobránsky, J.; Gombár, M.; Michalík, P. Comprehensive Analysis of Deposition Parameters and Energy-Dispersive X-Ray Spectroscopy Characterization in Cataphoretic Coating Processes. Appl. Sci. 2025, 15, 3760. https://doi.org/10.3390/app15073760
Fejko P, Peti D, Dobránsky J, Gombár M, Michalík P. Comprehensive Analysis of Deposition Parameters and Energy-Dispersive X-Ray Spectroscopy Characterization in Cataphoretic Coating Processes. Applied Sciences. 2025; 15(7):3760. https://doi.org/10.3390/app15073760
Chicago/Turabian StyleFejko, Patrik, Damián Peti, Jozef Dobránsky, Miroslav Gombár, and Peter Michalík. 2025. "Comprehensive Analysis of Deposition Parameters and Energy-Dispersive X-Ray Spectroscopy Characterization in Cataphoretic Coating Processes" Applied Sciences 15, no. 7: 3760. https://doi.org/10.3390/app15073760
APA StyleFejko, P., Peti, D., Dobránsky, J., Gombár, M., & Michalík, P. (2025). Comprehensive Analysis of Deposition Parameters and Energy-Dispersive X-Ray Spectroscopy Characterization in Cataphoretic Coating Processes. Applied Sciences, 15(7), 3760. https://doi.org/10.3390/app15073760









