Machine Learning Strategies for Forecasting Mannosylerythritol Lipid Production Through Fermentation: A Proof-of-Concept

Featured Application

Fermentation- and culture-based products are widely used across many industries, such as food, health, polymers, and waste management. Nevertheless, developing new fermentation-based industrial-scale products is lengthy, expensive, and time-consuming. The work presented here aims to contribute to the development of data-driven and machine-learning-based workflows to be used in the design and monitoring of new fermentation-based protocols, utilizing common culture parameters, such as products, substrates, and gas concentrations. Further investment in these computational tools may pave the way for the faster scale-up of new fermentation processes while generating more knowledge about the impact of different culture strategies tested.

Abstract

Fermentations are complex and often unpredictable processes. However, fermentation-based bioprocesses generate large volumes of data that are currently underexplored. These data can be used to develop data-driven models, such as machine learning (ML) models, to improve process predictability. Among various fermentation products, biosurfactants have emerged as promising candidates for several industrial applications. Nevertheless, the large-scale production of biosurfactants is not yet cost-effective. This study aims to develop forecasting methods for the concentration of mannosylerythritol lipids (MELs), a type of biosurfactant, produced in Moesziomyces spp. cultivation. Three ML models, neural networks (NNs), support vector machines (SVMs), and random forests (RFs), were used. An NN provided predictions with a mean squared error (MSE) of 0.69 for day 4 and 1.63 for day 7 and a mean absolute error (MAE) of 0.58 g/L and 1.1 g/L, respectively. These results indicate that the model’s predictions are sufficiently accurate for practical use, with the MAE showing only minor deviations from the actual concentrations. Both results are promising, as they demonstrate the possibility of obtaining reliable predictions of the MEL production on days 4 and 7 of fermentation. This, in turn, could help reduce process-related costs, enhancing its economic viability.

1. Introduction

Fermentations are, in general, inherently complex biological processes for the production of valuable compounds, characterized by interactions among various intrinsic and extrinsic variables. Intrinsic factors, such as metabolism, genetic variability, and cellular responses, interact dynamically with extrinsic variables, such as nutrient availability, pH, and oxygen levels, influencing the dynamics and output of the process. These variables are often interdependent and can vary over time, making fermentation processes unpredictable and challenging to control. This complexity impacts the consistency and efficiency of consecutive process batches, leading to variability in yield and quality. As a result, there is a demand for advanced strategies to enable the real-time monitoring, modeling, and consequent optimization of processes. Such improvements are essential to enhance reproducibility and increase productivity, ultimately leading to cost efficiency, which is essential for scaling these bioprocesses to the industrial scale. The large volumes of data that can be generated during fermentation bioprocesses, from online monitoring and offline sampling, present a still underexplored opportunity to develop data-driven models, such as those based on machine learning (ML), which in turn could be used to understand the process better and improve its predictability, contributing to a higher process efficiency.

Fermentation bioprocesses have historically been used for food production and conservation and to improve food’s taste and texture [1]. In recent years, precision fermentation has attracted significant interest as a sustainable method for producing high-value ingredients, such as proteins, vitamins, and other bioactive compounds, for the alternative protein industry [2]. Beyond food, fermentation technologies have been widely developed for the production of biofuels, industrial chemicals, and pharmaceutical products [3]. Among these various fermentation products, biosurfactants have emerged as a promising class of biomolecules due to their unique physicochemical properties and broad industrial applications, including the cosmetic, cleaning, and pharmaceutical industries [4].

Surfactants are molecules that reduce the surface or interfacial tension between liquids, a liquid and a gas, or a liquid and a solid and are used extensively across various industries. Synthetic surfactants, mostly produced by the petrochemical industry, are commonly used, but presently, several concerns regarding their toxicity are emerging, as they affect the microbial world, soil, plants, and aquatic life [5]. With environmental issues becoming a pressing concern for both the public and industry, there is an urgent need to identify greener, more sustainable alternatives to petrochemical surfactants. Biosurfactants offer an appealing solution, as they are naturally derived and produced as secondary metabolites by bacteria or fungi, making their production more environmentally friendly and sustainable [6].

Mannosylerythritol lipids (MELs), a type of glycolipid compounds, are among the most interesting biosurfactants. MELs are surface-active agents with hydrophobic and hydrophilic moieties that allow them to reduce surface and interfacial tension [7]. The hydrophobic moieties that compose these molecules consist of a mannose and an erythritol, specifically 4-O-$\beta$-D-mannopyranosyl-meso-erythritol, and the hydrophilic moiety is composed of fatty acids and acetyl groups [8]. Their exceptional surface-active properties, versatile biochemical functions, non-toxicity, biodegradability, and environmental compatibility, among other attributes, make MELs an interesting potential option for various applications [8].

Despite the advantage of using MELs or other biosurfactants instead of the current less environmentally friendly alternatives, their production remains economically challenging [9]. This can be attributed to low product yields, high production costs, and the complex interplay of process variables that influence biosurfactant synthesis. These challenges emphasize the need to optimize production processes to enhance their viability for commercialization and industrial adoption [9]. This is, in general, a common problem for most biosurfactants since their production is affected by a variety of factors, such as the carbon [10] and nitrogen sources used [11], the consequent carbon-to-nitrogen ratio [12], and abiotic factors, such as temperature, oxygen [13], and pH [14], among others. Moreover, the high variability in the production process makes it challenging to predict the success of each fermentation run. This challenge is amplified further when using agro-industrial residues, such as residual oils or cheese whey [15], due to their possible variable composition.

Due to the many variables involved in biosurfactant production, testing each factor individually is both time-consuming and expensive. A more efficient approach gaining popularity is the use of data-driven models, like machine learning. These models can analyze past data to extract insights and predict outcomes without needing prior knowledge of the reaction mechanisms. This emerging approach could lead to new technologies that optimize fermentation processes and reduce the production costs of biosurfactants. Although the application of machine learning in bioengineering is still in its early stages, several studies have already demonstrated the potential of these models to predict biological processes, using unsupervised [16] and supervised learning approaches [17].

Neural networks (NNs) are the most common models used in the field of ML applied to bioreactors to predict the product concentration, as they are very flexible due to their several possible adjustable parameters and topologies [18]. The use of NNs dates back to 1990, when Thibault et al. [19] used a fairly simple NN, with only one hidden layer, to predict the concentration of cells and substrate at the next sampling interval in a continuously stirred bioreactor by giving the algorithm the dilution rate and the concentration of cells and substrate at the current sampling interval, achieving fairly accurate predictions. It is worth noting that the NN was used to predict the simulation results and was not applied to a real-world case. More recently, Zhang et al. [20] also used an NN to successfully predict the concentrations of biomass for two strains of Clostridium butyricum, glycerol, and 1,3-propanediol in both batch and fed-batch modes in a 5 L bioreactor. When using a double-input NN, the predictions were successful for the fermentation process for strain I of Clostridium butyricum, but they failed for strain II. After adjusting the model by adding two more input variables, the model reduced its error rate, but the predictions for strain II were still significantly different from reality.

Another popular model is random forests (RFs) since they are fairly simple to implement and provide high accuracy, even for small datasets. An RF possess several parameters that can be adjusted as needed, such as the number of trees and the maximum depth of each tree, to name a few [21]. Zhang et al. [22] used two ML models—RF and gradient boost regression—to optimize and predict the bio-oil production from the hydrothermal liquefaction of algae. In this study, although the gradient boosting regression model outperformed RF, the model still achieved a coefficient of determination (R²) of approximately 0.90, successfully predicting the oil yield, oxygen, and nitrogen content.

Although there are quite a few studies in which ML techniques are applied to forecasting the product concentration in bioreactors, there are only a handful of studies that have focused specifically on biosurfactant production. Among these few studies, Jovic et al. [23] forecasted the biosurfactant yield, emulsification index (E24), and reduction in surface tension using a support vector machine (SVM). Similarly and more recently, Bustamante et al. [24] predicted the biosurfactant concentration, E24, and surface tension reduction in biosurfactant production, both in Erlenmeyer flasks and bioreactors, using an NN model. To the best of our knowledge, no studies have been published on the use of ML algorithms to optimize MEL production process.

In this work, three different ML models (NN, SVM, and RF) were tested for predicting the MEL concentration in the cultivation of Moesziomyces spp. in Erlenmeyer flasks.

This work aims to enhance the predictability and efficiency of MEL production by applying ML models, an area that is still under-explored, with few reported examples in the literature. We compare several models that are expected to anticipate the fermentation outcomes, enabling corrective actions to adjust the process trajectory or terminate unsuccessful batches earlier. This approach has the potential to improve the process consistency and reduce costs while also serving as an essential first step toward applying machine learning to large-scale MEL production forecasting, process control, and optimization. Additionally, we provide an open-access dataset and codebase, promoting reproducibility and future advancements in fermentation modeling.

2. Materials and Methods

Figure 1 showcases a simplified workflow of the methodology used in this work, which is detailed further in the following sections. First, the dataset was constructed using previous experiments conducted by the research team. Then, data preprocessing techniques were applied to the data to make them compatible with the different models used. After this, feature engineering was performed, which included feature extraction and feature selection techniques. This resulted in a clean dataset. Machine learning models were then trained, and hyperparameter tuning using a grid search was applied simultaneously. Finally, unseen data were given to the models to see whether they could generalize over new data.

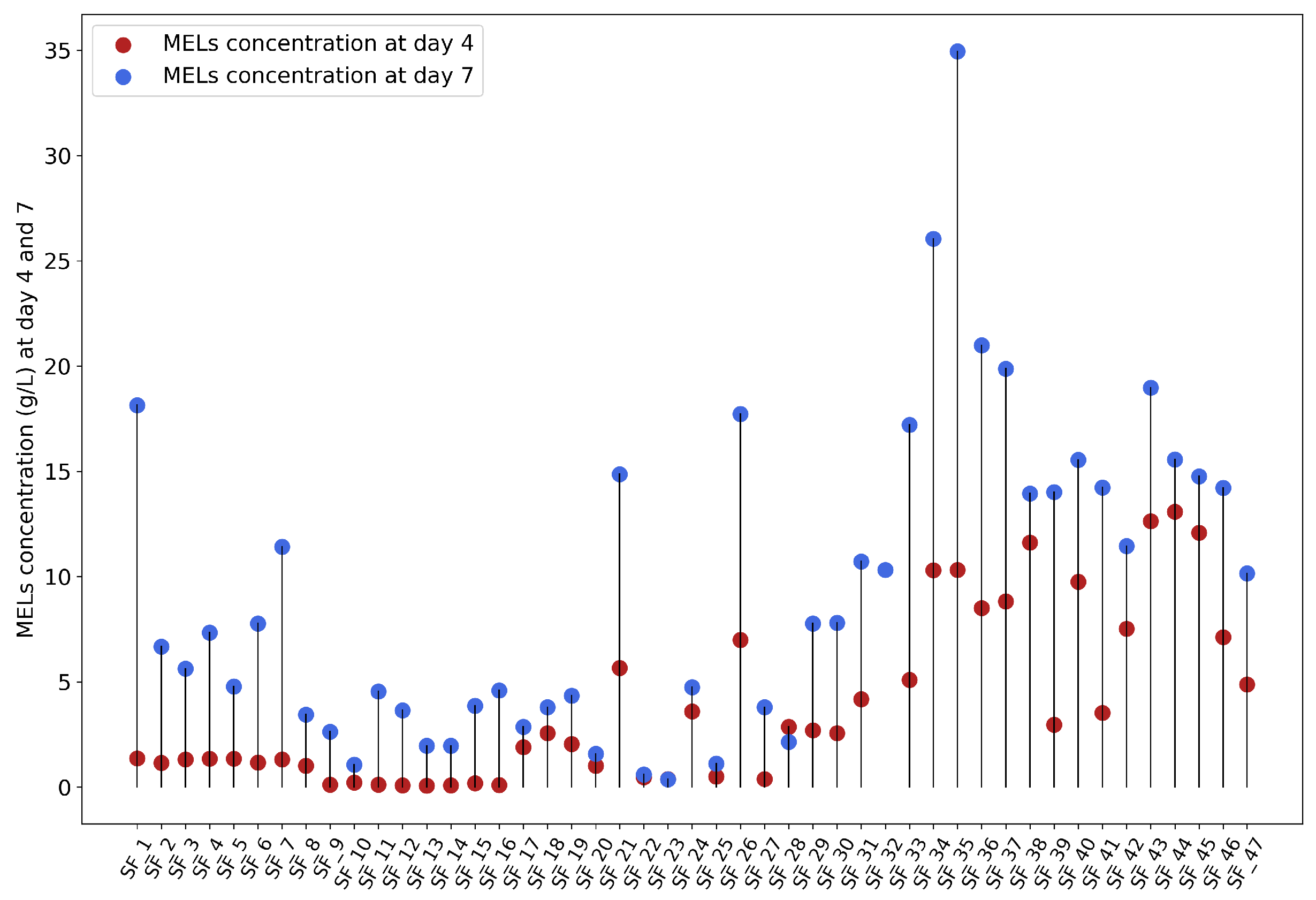
2.1. Dataset

The dataset used in this study was compiled from four different groups of experiments previously carried out by the research group [15,25,26,27,28], with the aim of producing MELs.

In all experiments, the concentrations of biomass, carbon, and nitrogen were assessed at the beginning of the experiment (day 0) and on day 2, day 4, and day 7 and, for longer experiments, on days 10, 14, and 18 as well. Furthermore, the MEL and lipid concentrations were measured on days 4 and 7 and, for longer experiments, on days 10, 14, and 18 as well. Possible carbon sources, both hydrophilic (glucose, glycerol, cheese whey, or no carbon sources) and hydrophobic (soybean oil, fish oil, sunflower oil, rapeseed oil, and waste frying oil), constituted the categorical variables. Sodium nitrate was consistently used as the nitrogen source. The final dataset is composed of 47 samples, with each shake flask run considered a sample, and includes 42 features. Although the experiments aimed at the production of MELs, they followed different strategies, varying in the carbon source used, feeding strategy, initial biomass, headspace volume, carbon-to-nitrogen ratio, and duration. The shortest experiment was concluded after 7 days of fermentation, while the longest experiment was extended to 18 days. Figure S1 (Supplementary Material, Figure S1) shows the evolution of biomass throughout the first 7 days for all of the experiments. Figures S2 and S3 (Supplementary Material, Figures S2 and S3) depict the consumption of carbon and nitrogen, respectively, throughout the first 7 days for all experiments.

-

Experiment 1 included 18 samples, a duration of 18 days, and a volume of 50 mL. D-glucose or glycerol (or simply no hydrophilic carbon source) was used in combination with a hydrophobic carbon source, such as soybean oil, rapeseed oil, or waste frying oil.

-

Experiment 2 included 10 samples, a duration of 10 days, and a volume of 50 mL. Waste frying oil was used as the hydrophobic carbon source, while D-glucose and cheese whey (CW) were used as the hydrophilic carbon sources.

-

Experiment 3 comprised 8 samples, a duration of 7 days, and the consistent use of D-glucose and waste frying oil as the hydrophilic and hydrophobic carbon sources, respectively. Four different volumes were tested (200 mL, 100 mL, 50 mL, and 25 mL), with each set of conditions run in duplicate.

-

Experiment 4 included 11 samples, with each running for 10 days with a volume of 50 mL. D-glucose was used as the hydrophilic carbon source, while the hydrophobic carbon sources were varied between residual fish oil and sunflower oil.

2.2. Data Preprocessing

After assembling the dataset, data preprocessing was required before testing the ML models. As previously stated, the dataset consists of both numerical and categorical features. To use the categorical features as inputs, they were encoded into numerical values using the one-hot encoding technique, where each categorical feature was represented by 0 for its absence and 1 for its presence [29]. For example, if glucose was used in a sample, it would be represented by 1, while all other carbon sources would be represented by 0.

Additionally, the dataset contained some missing values that were not due to the different experimental durations but rather to normal experimental unexpected issues. Therefore, value imputation was necessary for the analysis, as most models cannot handle missing data. To select the most appropriate imputation method, 5% of the known values of the dataset were randomly removed, and then several methods were used to predict the removed values. These methods included simple and commonly used techniques, such as the mean and median, as well as machine learning algorithms like k-Nearest Neighbor, RFs, Decision Trees (DTs), Bayesian Ridge, and SVMs. The performance of each method was assessed by comparing the mean squared error (MSE) [30]. Analyzing the results obtained using the different methods, the k-Nearest Neighbor regressor with two neighbors achieved the lowest MSE (42.16). Therefore, it was selected for imputing the true missing values in the dataset.

After completing this step, the data were scaled, as not all of the features had the same order of magnitude. Scaling the data ensures that each variable contributes equally to the analysis. The z-score method was applied, which standardizes each feature to have a mean of zero and a standard deviation of one [31]. After scaling, 80% of the data (37 samples) were used for training and the remaining 20% for testing (10 samples) the classifiers.

2.3. Feature Engineering

After completing the data preprocessing, new features were extracted from the original ones to provide additional information not directly available in the initial feature set. The carbon-to-nitrogen ratio for each day was calculated and added as a new feature. Next, based on our knowledge of the process, the biomass growth rate, $\mu$, was calculated using Equation (1), where $X_v$ represents the biomass concentration at time t, and $X_{v_0}$ represents the initial biomass concentration.

$$X_v=X_{v_0}\times e^{\mu t}$$

(1)

Glucose and nitrogen consumption rates were calculated by subtracting the final concentration from the initial concentration (day 0) and then dividing by the total duration of the experiment. The biomass/substrate yield was calculated by dividing the biomass concentration at the end of the experiment by the substrate consumption throughout the days. Moreover, the specific rates of nitrogen and glucose consumption were also calculated using Equation (2). In Equation (2), S represents the glucose concentration when calculating the glucose consumption rate and nitrogen when calculating the nitrogen consumption rate.

$$q_S={\displaystyle \frac{1}{X_v}}\times {\displaystyle \frac{dS}{dt}}$$

(2)

Finally, the increases or decreases that the substrate, nitrogen, MEL, or lipid concentration experienced between each day (Equation (3)) were also added as new features.

$$\Delta X_i=X_i-X_{i-1}$$

(3)

where $\Delta X_i$ represents the change (increase or decrease) in the concentration of the variable X (e.g., substrate, nitrogen) on day i, $X_i$ represents the concentration of the variable on the current day (i), and $X_{i-1}$ represents the concentration of the variable on the previous day $i-1$.

At the end of the feature extraction process, the final dataset was composed of 47 samples and 74 features.

Feature selection methods were also applied to the dataset to ensure that only relevant information was provided to the models and to assess which features would have the greatest impact and be most relevant to predicting the MEL concentration. Five different feature selection methods were tested, therefore creating five different feature subsets.

A principal component analysis (PCA) was the first method explored for feature selection. It creates several principal components, where each component is a linear combination of the original features. To reduce the dimensionality of the dataset, the number of principal components was first selected to ensure that they explained 90% of the total variance. Then, the mean contribution of each original feature across all of the selected principal components was calculated. Features with an overall negative mean contribution were discarded, as they pn average contributed inversely to the variance captured by the principal components that explained 90% of the variance [32].

The dimensionality was also reduced using the analysis of variance (ANOVA) method. In the context of feature selection, an ANOVA is used to rank the features by calculating the ratio of the variances between and within groups [33,34]. Then, the same number of features previously obtained from the PCA was selected from the feature ranking.

The Least Absolute Shrinkage and Selection Operator (LASSO) technique was also used for feature reduction. LASSO is a regression method that incorporates a penalty term, known as L1 regularization. The L1 regularization term is the sum of the absolute values of the regression coefficients, multiplied by a tuning parameter. LASSO works by simultaneously finding the coefficient values that minimize the sum of the squared differences between the predicted and actual values (the residual sum of squares) and minimizing the L1 regularization term. As a result, LASSO shrinks some coefficients towards zero, which can then be used to reduce the feature set by eliminating those with a coefficient of zero [35,36].

Dimensionality reduction through the removal of correlated features was also carried out using Pearson’s correlation, which measures the linear relationship between two features. Correlation values can range between −1 and 1, indicating that the features are completely correlated, negatively or positively, respectively, while 0 means there is no correlation between such features [37]. In this work, when two features had an absolute correlation greater than 60%, one of them was removed [38].

Finally, the last method used was recursive feature elimination (RFE). This method starts with all features and recursively eliminates them based on their importance to a given estimator. In other words, a model is built and fitted with the whole set of features, and then an importance score for each feature is calculated. The least important feature is removed, and the previous process is repeated until a specific number of features is reached. The model chosen was the support vector regressor with a linear kernel [39].

The features selected by each method for day 4 are represented in Tables S1 and S2 (Supplementary Material, Tables S1 and S2) for day 7.

2.4. Machine Learning Techniques

Different machine learning techniques were employed to forecast the MEL concentrations at the end of days 4 and 7. This study used three supervised ML algorithms: a support vector machine, random forest, and neural network. These models were chosen for different reasons. Random forest models are easy to implement and allow the path back to the output to be tracked, support vector machines are very efficient in high-dimensional spaces, and neural networks can model the complex, non-linear relationships in data. Additionally, these three models are among the most commonly applied machine learning techniques in bioprocess forecasting studies [20,22,23,24].

Real-world data often exhibit non-linear separability, making it challenging to distinguish between classes in the original feature space and to determine the separation surface effectively. To address this challenge, kernel functions are employed to transform the data into a higher-dimensional feature space where the classes become more easily separable. Among the several existing kernels, the most common ones are linear, polynomial, the radial basis function (RBF), and sigmoid. A support vector machine is an algorithm used for both classification and regression tasks. The SVM uses this kernel-based mapping to transform the data into a higher-dimensional space, where it then searches for the optimal hyperplane that can separate the data. The construction of the hyperplane is mainly dependent on the support vectors, which are created through data points from the training set and support the margins of the hyperplane. The choice of kernel function is a key hyperparameter in the SVM since it allows the model to operate in a high-dimensional feature space without explicitly calculating the coordinates in that space. This is essential because high-dimensional spaces are often too large to compute directly, making the calculations slow or even impractical for large datasets. A detailed description of the method can be found in Zhang, 2020 [40].

The random forest model was also used in this study. Random forest is an ensemble learning method, a combination of several inducers, more specifically decision trees (DTs). Each DT in the forest is a simple model that has low accuracy individually since it only uses a subset of the features. By aggregating the DTs, using averaging for regression or majority voting for classification, the RF algorithm can construct complex decision surfaces that effectively separate the classes. One of the advantages of RF is its ability to achieve a high accuracy even with limited data relative to the number of features, as it utilizes bootstrap sampling to generate diverse training subsets for each tree. More information about this model is presented in Cutler, 2012 [21].

Finally, predictions were also made using a feed-forward neural network (NN). Briefly, an NN is divided into three parts: an input layer, hidden layers, and an output layer. NN algorithms are inspired by the neural networks present in the human brain, where an external stimulus is received and propagated by a neural network connected by synapses that process the information and return a final command. In this approach, the input data are provided to the algorithm, which will activate certain nodes (or neurons) in the input layer, which will, in turn, activate other nodes in the hidden layers through the weight connections associated with a bias. These interactions generate an output based on the connections from the input layer through the hidden layers. Training data must be provided to the algorithm so it can learn the weights that connect the various neurons, enabling accurate predictions. The weight learning process is carried out through backpropagation, which is a cost function minimization through gradient descent. When test data are provided to the network, it should be able to predict these new and unseen entities based on the learning from the training set [41].

This type of algorithm requires a very large dataset for training because increasing the number of layers significantly raises the number of parameters that need to be optimized.

The final step in the process was to optimize the hyperparameters of each model. Several combinations of hyperparameters were tested for each subset of features. Therefore, the combinations that produced lower errors with a certain subset may not have been the best combination when applied to another subset. For the RF model, the parameters tested included the number of trees, a criterion to measure the quality of a split, the maximum tree depth, the minimum number of samples required to be at a leaf node, the maximum number of features to consider when looking for the best split, and whether bootstrap samples were used when building trees. Regarding the SVM, four different kernels were tested, along with different values for the regularization parameter, and finally, different gamma and epsilon values were also tested. Moreover, in the case of the polynomial kernel, several polynomial degrees were tested. Finally, different hyperparameters were also tested for the NN. The parameters tested were different numbers of hidden layers, the neurons present in these layers, and the batch size given to the NN. It is also worth noting that the NN had a maximum number of epochs of 100 and incorporated a monitor function, stating that if the validation loss increased in more than 5 epochs, the training was stopped, and the best model was saved. All models were trained during this process, and the weights were saved at the end of the training, so the same trained model could be applied to the testing set and the results would stay consistent. The NN configuration that achieved the best result for the forecasting of day 4 had three hidden layers with 64, 32, and 16 neurons, respectively, and a single-neuron output layer. Data samples were processed in batches of eight. The loss function used was the MSE, and the learning technique applied was the adaptive moment estimation method (ADAM). As for the forecasting of day 7, the configuration of the NN consisted of 2 hidden layers with 128 and 64 neurons, an output layer with 4 neurons (the prediction was the average between the 4), and a batch size of 4. The loss function used was once again the MSE, and the learning technique applied the ADAM method.

Table 1. Hyperparamaters selected for each model for forecasting the concentration of MELs on day 4 and day 7 of the process.

Model	Hyperparameter	Day 4	Day 7
Random Forest	Number of estimators	10	1
	Criterion	Absolute error	Squared error
	Maximum depth	None	None
	Minimum sample split	3	3
	Maximum features	Sqrt	Sqrt
	Bootstrap	True	True
Support Vector Machine	Kernel	RBF	Polynomial
	Epsilon	0.001	0.001
	Gamma	1	0.001
	C	0.1	75
Neural Network	Number of layers and neurons	[64, 32, 16]	[128, 64]
	Loss function	MSE	MSE
	Output layer	1	4
	Batch size	8	4

summarizes the hyperparameters selected for each model for forecasting the MEL concentration on day 4 and day 7 of the fermentation process.

To evaluate the performance of the models, two different metrics were chosen, the mean squared error and the mean absolute error (MAE), represented by the following equations:

$$MSE={\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-\widehat{y_i})}^2$$

(4)

$$MAE={\displaystyle \frac{1}{n}}\sum _{i=1}^n|\widehat{y_i}-y_i|$$

(5)

where $y_i$ and $\widehat{y_i}$ are the observed value and the predicted value, respectively.

All the code in this study was implemented in Python version 3.11.4. The SVM and the RF were applied using the library scikit-learn [42], while the NN was constructed using the libraries tensorflow [43] and keras [44]. The experiments were run on a computer with an Intel i7 7th quad-core processor with an NVIDIA 1060 GPU and 16 GB of RAM. The source code, as well as the dataset, is available in the GitHub MELs-forecasting (further details are given in the data availability statement).

3. Results and Discussion

Before applying the ML workflow (Figure 1), data characterization was carried out. Firstly, the MEL concentrations on days 4 and 7 are represented in Figure 2 and show no clear pattern between the two time points. However, when Pearson’s correlation was calculated for these two variables, a value of 0.78 was obtained, revealing a strong positive correlation. Spearman’s test, which measures the strength and direction of a monotonic relation, was also used, revealing a correlation coefficient of 0.82, further reinforcing the Pearson’s correlation results. Given the established relationship between the two variables, it is reasonable to hypothesize that predicting the MEL concentration on day 4 could serve as an early indicator of the outcome on day 7. This baseline could help forecast whether a particular shake flask would achieve the desired MEL concentration, allowing for a more informed decision on whether to proceed with the fermentation process or not.

As previously stated, three different machine learning models were trained to predict the MEL concentration at the end of days 4 and 7 using 37 samples. Therefore, 10 samples were kept aside for testing in a different file to avoid data leakage, corresponding to a train–test split of 80/20. The testing set was chosen at random so as not to introduce any human bias. This split ensures that the model is trained on most of the data while still being tested on a significant portion that remains unseen during training. Then, from the training set, 7 samples were chosen to serve as the validation set, while the remaining 30 samples were used to train the models. This validation set was used to assess the performance of the model on the training set.

As described in Section 2.4, all of the models were trained during the hyperparameter optimization step. Although the models obtained low errors when asked to predict the validation set, it was important to check for their ability to generalize over unseen data.

It is also important to note that the dataset used was relatively small, and a larger dataset could further enhance the accuracy of the predictions.

Table 2. MSE values for predictions for day 4 of MEL production. Five predictions were attained for each model by using each of the five feature subsets used as input for model training. Lower MSE results achieved by each model are represented in bold.

	All Features	RFE	Correlation	LASSO	ANOVA	PCA
Neural Network	1.77	12.88	0.69	2.83	2.63	1.63
Random Forest	4.45	9.22	11.01	7.35	3.45	4.15
Support Vector	29.12	29.52	28.24	30.76	30.04	28.64

shows the MSE obtained for each model using each subset of the features for day 4, and in

Table 3. Comparison of experimental values for MEL production on the fourth day of fermentation with RF, NN, and SVM predictions. The prediction errors represent the absolute error between the predictions and actual values and are on the line below the predictions.

Experimental Values (g/L)	RF Predictions (g/L) ± Error	NN Predictions (g/L) ± Error	SVM Predictions (g/L) ± Error
0.08	0.14	0.00	1.41
	± 0.06	± 0.08	± 1.33
4.17	7.19	4.59	1.54
	± 3.02	± 0.42	± 2.63
3.60	5.24	3.11	1.67
	± 1.64	± 0.49	± 1.93
13.08	10.16	10.81	1.91
	± 2.92	± 2.27	± 11.17
9.76	9.92	10.00	1.58
	± 0.16	± 0.24	± 8.18
1.17	3.32	1.42	1.24
	± 2.15	± 0.25	± 0.07
0.12	2.00	0.59	1.50
	± 1.88	± 0.47	± 1.38
0.38	0.50	1.20	1.61
	± 0.12	± 0.82	± 1.23
6.99	4.62	6.56	1.76
	± 2.37	± 0.43	± 5.23
8.82	8.32	8.52	1.91
	± 0.50	± 0.30	± 6.91

, the experimental values, the predicted values, and the prediction errors are presented. The same information for the day 7 predictions can be found in

Table 4. MSE values for predictions for day 7 of MEL production. Five predictions were attained for each model by using each of the five feature subsets used as input for model training. Lower MSE results achieved by each model are represented in bold.

	All Features	RFE	Correlation	LASSO	ANOVA	PCA
Neural Network	7.01	3.76	6.47	10.31	1.63	4.2
Random Forest	12.99	13.82	27.07	9.48	59.39	27.96
Support Vector	44.21	37.36	41.34	45.01	36.63	36.25

and

Table 5. Comparison of experimental values for MEL production on the seventh day of fermentation with RF, NN, and SVM predictions. The prediction errors represent the absolute error between the predictions and actual values and are on the line below the predictions.

Experimental Values (g/L)	RF Predictions (g/L) ± Error	NN Predictions (g/L) ± Error	SVM Predictions (g/L) ± Error
15.45	10.16	15.64	6.73
	± 5.29	± 0.19	± 8.72
1.97	4.23	3.62	5.84
	± 2.26	± 1.65	± 3.87
3.65	4.23	4.77	5.73
	± 0.58	± 1.12	± 2.08
4.34	4.74	6.71	6.58
	± 0.40	± 2.37	± 2.24
10.32	13.83	11.79	7.06
	± 3.51	± 1.47	± 3.26
7.77	5.62	9.24	7.74
	± 2.15	± 1.47	± 0.03
11.42	5.62	10.74	6.74
	± 5.80	± 0.68	± 4.68
20.99	18397	20.75	7.74
	± 2.02	± 0.24	± 13.25
7.77	5.62	8.67	6.89
	± 2.15	± 0.90	± 0.88
13.94	13.01	14.93	6.72
	± 0.93	± 0.99	± 7.22

.

Overall, the predictions for day 4 were more successful than those for day 7, which was not expected since the features used for the forecasting of day 4 included only the first two days of fermentation. It is also worth noting that the models benefited from the feature selection process since a lower MSE was achieved by each model when feature reduction techniques were applied.

3.1. MEL Production Forecasting: Day 4

Given the small dataset, consisting of four distinct experiments with different initial conditions, the train–test split inevitably caused the under-representation of some initial conditions, making certain samples more challenging to predict. Nevertheless, the overall results were generally satisfactory.

The results of the MEL production forecasting for day 4 using the NN model, combined with the correlation-derived feature subset, achieved the lowest error among all tested configurations. This combination obtained an MSE of 0.69 and an MAE of 0.58, which can be considered high-accuracy. The MAE of 0.58 suggests that the average deviation of the predictions is only 0.58 $g_{MELs}/L$. A closer examination of Table 3, which compares the values predicted by each model, shows that the NN prediction errors are below 1 g/L in 9 out of the 10 samples.

The RF achieved its lowest MSE when the ANOVA feature selection method was used, with an MSE of 3.45 and an MAE of 1.49 g/L. Although the RF model’s best MSE result was higher than most of the NN model’s MSE results, it provided the most accurate MEL concentration estimate for sample 1 on day 4. The experimental value was 0.08 g/L, while the model predicted 0.14 g/L.

The SVM consistently produced MSE values around 30, regardless of the feature selection method applied. This poor performance is likely due to a mismatch between the data’s complexity and the model’s capacity to capture it. The predictions made by the SVM were extremely narrow, ranging from 1.24 g/L to 1.91 g/L, while the actual target values varied significantly from 0.08 to 13.08 g/L. This indicates that the SVM failed to identify the optimal hyperplane for separating the data and instead settled on a region in the feature space that represented the true relationship between the features and the target variable poorly.

The success of the NN can be attributed to its capacity to capture non-linear relationships within the data and its adaptive learning method. Furthermore, the NN also benefited from the feature reduction techniques since when comparing the MSE obtained using all of the features to that achieved after removing the correlated features, there was a 61% reduction.

Figure 3 is a visual representation of the predictions made by the three models, highlighting their overall accuracy in forecasting the experimental values. The plot further supports earlier observations regarding the performance of the models. Interestingly, sample 44 not only poses a forecasting challenge for the NN but also the RF, potentially due to the small size of the dataset, causing the under-representation of some initial conditions, which can lead to difficulties in the forecasting.

3.2. MEL Production Forecasting: Day 7

After estimating the MEL production on day 4, the prediction of the concentration of the MELs was carried out on day 7, the last time point common to all of the experiments in the dataset. As shown in Table 4, the NN model demonstrates a superior performance, consistently outperforming the other models. The model achieved the lowest MSE using the feature subset selected by the ANOVA, with an MSE of 1.63 and an MAE of 1.1 g/L, meaning that the average deviation of the predictions from the experimental values was approximately 1 $g_{MELs}$/L. Furthermore, an analysis of Table 5 reveals a prediction with an error greater than 2 g/L which only occurs for the model’s prediction of the concentration of sample 19. This sample belonged to experiment 2, which was the only experiment where CW was used as the hydrophilic substrate source, making this condition under-represented in the dataset. As a result, the model had limited examples to learn from during training, which likely affected its ability to generalize to this specific condition.

The RF models’ performance declined when forecasting the MEL production for day 7, with the lowest MSE achieved being 9.48. Furthermore, the predictions made revealed that the RF model presented only seven distinct values. This lack of variability likely resulted from the RF models’ decision trees grouping the testing samples into identical nodes, leading to limited differentiation between the predicted values. This may have occurred because the testing samples were assigned to the same leaf nodes when passing through the trees.

The SVM models’ performance for day 7 is similar to that for day 4, with high MSEs and a narrow prediction range. The model failed to find the optimal hyperplane for separating the data, even when tested with different kernels.

The NN model achieved its best result for both days 4 and 7 when the ANOVA-derived feature subset was used. This method selects features based on significant differences between independent groups, more specifically by calculating the ratio of the variance between and within groups. This approach takes into consideration the target value when applied, which can enhance the NN’s ability to learn the patterns within the data. The success of the neural network across this work can be attributed once again to its robustness and flexibility.

Finally, Figure 4 reinforces the previous conclusions about the three models but also shows that the NN model struggles to forecast sample 14 and sample 32. Once again, the dataset used in this work comprises four different experiments with different initial conditions, such as different carbon and lipid sources. As a result, some of the initial conditions appear less frequently than others, which impacts the models’ performance due to the limited number of examples available for learning during training. For example, sample 14’s initial conditions were glucose for the hydrophilic carbon source and rapeseed oil for the hydrophobic source. Rapeseed oil was only used in 6 out of 47 samples, resulting in this hydrophobic source being under-represented in the learning set.

The predictions for day 4 were more successful than those for day 7, likely due to the non-linear relationship between the variables and the different ways the MEL production depends on specific features at each time point. For day 4, the MEL production may have been more strongly influenced by a particular feature present in the dataset, simplifying the prediction task. In contrast, by day 7, the relationship between MEL production and the available features may have shifted or become more complex since MELs are secondary metabolites, produced mainly after the primary growth phase, reducing the models’ ability to accurately capture the dynamics of this process. Finally, for the forecasting for day 4, the data used were evenly spaced, with a consistent two-day interval. However, for day 7, the last available time point was day 4, resulting in a three-day jump, which may have contributed to the better results observed for day 4.

3.3. Benchmarking

As previously mentioned, although ML techniques have not yet been applied to forecasting MEL concentrations, some studies have focused on predicting biosurfactant production. Unfortunately, none of the existing articles have published their code or datasets. In the work by Jovic et al. [23], the authors predicted biosurfactant concentrations, achieving a test root mean squared error (RMSE) of 0.53, which improved to 0.31 after applying the firefly algorithm. The authors also calculated the R² for their test predictions, achieving a value of 0.98 before applying the firefly algorithm and 0.99 after. To enable a comparison, the R² values for the best result for each model and each day in the present study were also calculated and are presented in

Table 6. R² values for the lowest MSE obtained for each of the models.

	Random Forest	Neural Network	Support Vector Machine
R2—day 4	0.82	0.96	−0.47
R2—day 7	0.70	0.95	−0.15

. It is also important to note that Jovic et al. did not provide information about the size of the dataset or the inputs given to the model. To ensure the reproducibility of the results, the methodology used in the present study has been made publicly available.

A different study [24] also explored forecasting biosurfactant concentrations using an NN. The authors provided information about the input features used and used particle swarm optimisation to optimize the weights and bias of the NN. This work was able to achieve an R² of 0.94, which is in line with the values obtained in our study.

Finally, Ahmad et al. [45] used an NN to predict the biosurfactant yield. The authors used a dataset with 27 samples, with 19 used to train the model, 4 for validation, and 4 for testing. Similar to that in the previously mentioned work, an R² of 0.94 was achieved for the testing set, with an RMSE of 1.22. However, the authors noted that the weights varied with each run of the NN, resulting in inconsistent outcomes. In contrast, in the present work, all of the model weights were saved after training to ensure reproducibility and consistency in the results.

4. Conclusions

Mannosylerythritol lipids are high-value biosurfactants with diverse industrial applications, yet their production processes remain suboptimal and more costly than those for conventional surfactants derived from the petrochemical industry. One of the factors behind these limitations is the complexity of microbial fermentation. To accelerate bioprocess development/optimization, we envision machine learning and data-driven models playing a crucial role, as they can tackle large datasets, potentially avoiding the need for several rounds of individual parameter testing and improving the overall understanding of and control over the process. ML models also allow for the detection of deviations from the expected fermentation trajectories and the identification of early signs of contamination, equipment failure, or experimental errors. This allows for timely corrective actions, preventing batch failures before they occur or stopping a potentially failed process, saving time and reducing costs. A critical first step towards achieving this is the establishment of models capable of predicting the fermentation performance, in this work, in terms of the final MEL concentration, by relying solely on early-stage data.

In this study, we presented MEL concentration forecasting on days 4 and 7 of the fermentation process, using three different ML models and applying several dimensionality reduction techniques. Between the three ML models tested, the neural network had the best performance for both the day 4 and day 7 predictions, especially when coupled with feature selection techniques.

The results for day 4 were quite impressive, as the models were being fed solely with data from days 0 and 2 and achieved an average deviation from the experimental values of 0.58 g/L and an R² of 0.96, which indicated that the model was well fitted to the data. The ability to forecast the MEL concentration for day 7 with data from the first 4 days of fermentation is quite promising as an early batch quality assessment metric. Considering that the average deviation from the experimental values was nearly 1 g/L on day 4, production could be stopped, avoiding more resource waste and reducing the associated costs. Interestingly, the predictions for day 4 were more accurate than those for day 7, likely because the MEL production in the early stages of fermentation is more strongly influenced by a specific feature or set of features. As the process progresses, the metabolic complexity increases, leading to non-linear interactions between the variables and MEL concentrations, making the forecasting task more challenging for the models.

This work presents a significant contribution to the field of MEL production and fermentation bioprocess development, as there are still few reported examples of the application of ML techniques to forecasting production outcomes, and to the best of our knowledge, none of these studies have focused on MEL production. Moreover, the work presented here aims to be a foundation for the more transparent and open development of such forecasting tools, as it not only provides a dataset of MEL fermentation experiments but also the complete codebase required to reproduce our results. The framework demonstrated here can also be used directly for other datasets and adapted with minimal modifications to address different problems, such as bioprocesses with other microbial or animal cell types. The four experiments that compose the dataset are meant to reflect the real-life variability in fermentation and to cover a variety of initial conditions. While this study focuses on shake flask fermentations, this serves as an essential first step before scaling up the process. Future work opportunities include the use of bioreactor data to improve the process predictability. Such advancements could play an important role in broader industrial applications and more efficient biomanufacturing systems.