Improving Cost Contingency Estimation in Infrastructure Projects with Artificial Neural Networks and a Complexity Index
Abstract
1. Introduction
- (1)
- To select high-performing ML models for cost contingency prediction;
- (2)
- To investigate whether integrating a complexity index can improve prediction performance;
- (3)
- To develop interval predictions and assess whether the incorporation of a complexity index improves their accuracy.
2. Literature Review
2.1. Cost Contingency Prediction
2.2. Traditional Approaches to Contingency Estimation
2.3. Machine Learning Applications in Contingency Estimation
| Algorithms | Theoretical Underpinnings | Strengths |
|---|---|---|
| Linear regression | Linear regression assumes a linear relationship between the input variables and the target: where is the predicted target, represents the input variables, are the coefficients (weights) that quantify the influence of each input on the target, and is the intercept. The optimal coefficients are achieved by minimizing the ordinary least squares [11]: , where is the actual value, is the predicted value, and is the number of observations. The coefficients in the linear regression model quantify the influence of each input variable on the target. | Simplicity, interpretability, and computational efficiency |
| SVR | Similar to linear regression, SVR fits the function WTX + b while allowing a margin of tolerance . To handle non-linear relations, it performs the kernel trick, which maps data to a higher-dimensional space where linear separation is achievable. Common kernel options include linear (), polynomial, and radial basis function [27]. | Capability to address outliers and model non-linear relationships |
| Decision trees | Decision trees split data into branches based on features that best reduce impurity. Impurity is a measure of the homogeneity of the data within a node, aiming to make each split as “pure” as possible. It can be calculated using metrics like Gini impurity and entropy for classification and variance for regression models [25]. Specifically, Gini impurity is calculated as: , where is the proportion of class in the node ; and entropy is measured as: . | Capability to model non-linear relationship and effectively identify important features |
| Random forest | Random forest improves predictive accuracy by combining multiple decision trees. Each tree is trained on a random subset of data and features, reducing variance and overfitting [26]. The final prediction is the average outcome across all trees: , where is the total number of trees. | Robustness to overfitting |
| Gradient boosting | Gradient boosting builds an ensemble of decision trees sequentially, with each new tree focused on reducing the errors of the previous one [36]. At each step , the model updates predictions as: , where is the learning rate controlling the contribution of each tree. The final model combines these sequentially trained trees, each contributing based on its ability to minimize prior errors. | Promising predictive accuracy through interactive error correction |
| XGBoost | XGBoost employs regularization and optimization techniques to enhance model performance. Regularization, which prevents overfitting by penalizing model complexity, includes two techniques: L1 and L2 [31]. L1 regularization applies a penalty based on the absolute magnitude of coefficients, given by , while L2 uses the squared magnitude, i.e., , where are model parameters, and and control the strength of L1 and L2 regularization, respectively. XGBoost also uses optimization techniques, like second-order approximation and shrinkage. | High predictive accuracy through optimization |
| ANN | An ANN consists of interconnected neuron layers: input, hidden, and output. Each neuron in layer l receives weighted inputs from the previous layer : , where and refer to the weight and bias, respectively. The activation function introduces non-linearity: . During training, the ANN adjusts these weights using backpropagation which calculates the gradient of the loss function (a measure of prediction error) with respect to each weight [28]. | Ability to model complex relationships |
2.4. Interval Estimation in Machine Learning
2.5. Project Complexity and Estimation Accuracy
2.6. Research Gap
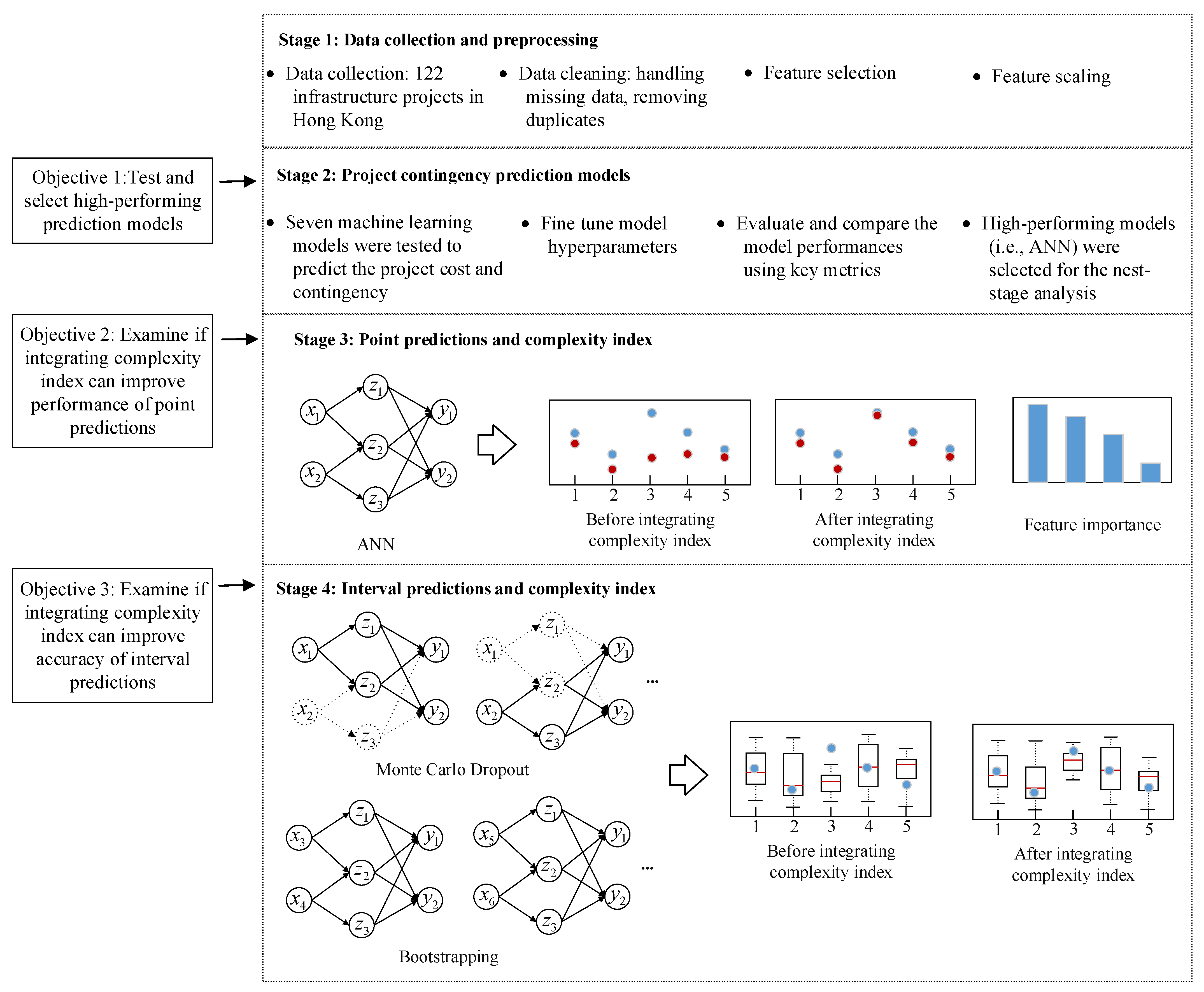
3. Materials and Methods
3.1. Stage 1: Data Collection and Preprocessing
3.2. Stage 2: Project Contingency Prediction Models
3.3. Stage 3: Point Estimation and Complexity Index
3.4. Stage 4: Interval Predictions and Complexity Index
- (a)
- Monte Carlo dropout
- (i)
- Train the model using the original training dataset, with dropout enabled during both training and inference;
- (ii)
- Perform multiple stochastic forward passes (n passes) through the trained model for the same test case x, with dropout activated to introduce randomness in each pass;
- (iii)
- Generate a set of n predictions for the test case x from the stochastic forward passes;
- (iv)
- Calculate the lower and upper bounds of the prediction interval, using the formulas presented below [61]:
- (b)
- Bootstrapping
4. Results
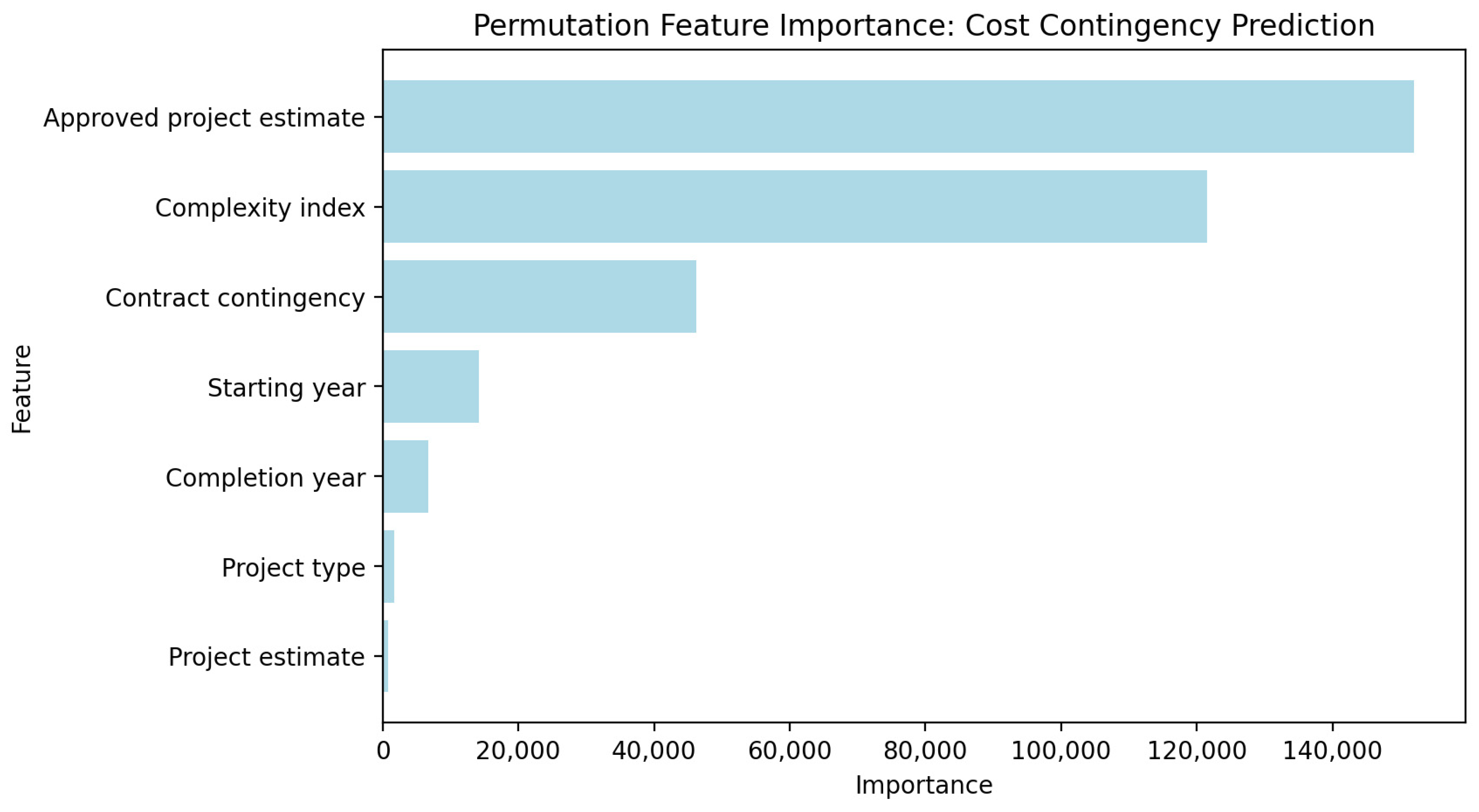
4.1. Feature Selection
4.2. Development of Cost Contingency Prediction Models
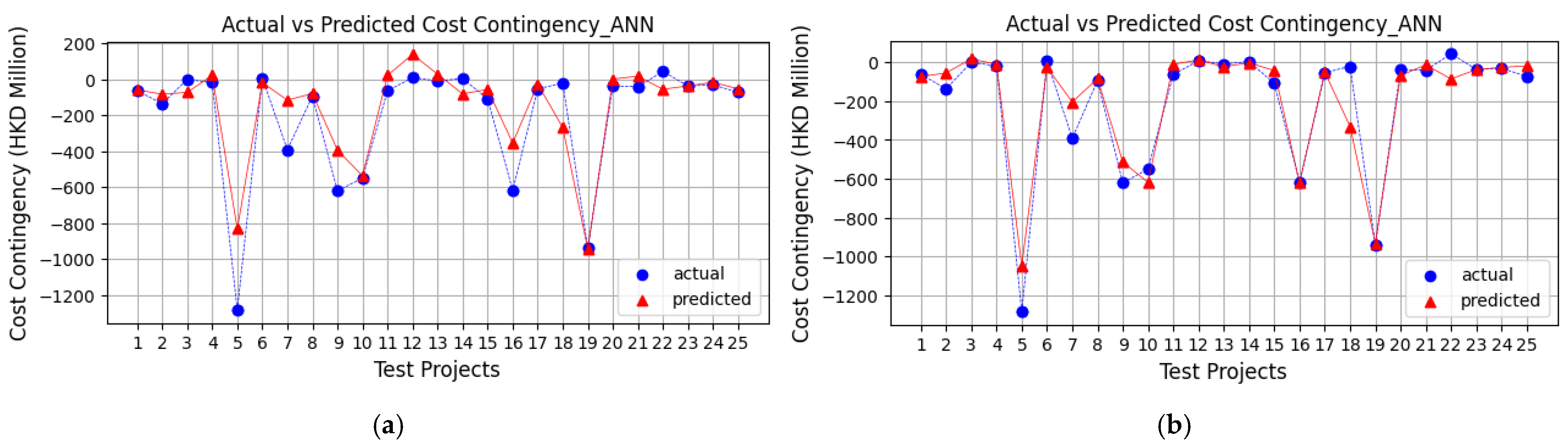
4.3. Integrating the Complexity Index into Point Estimation
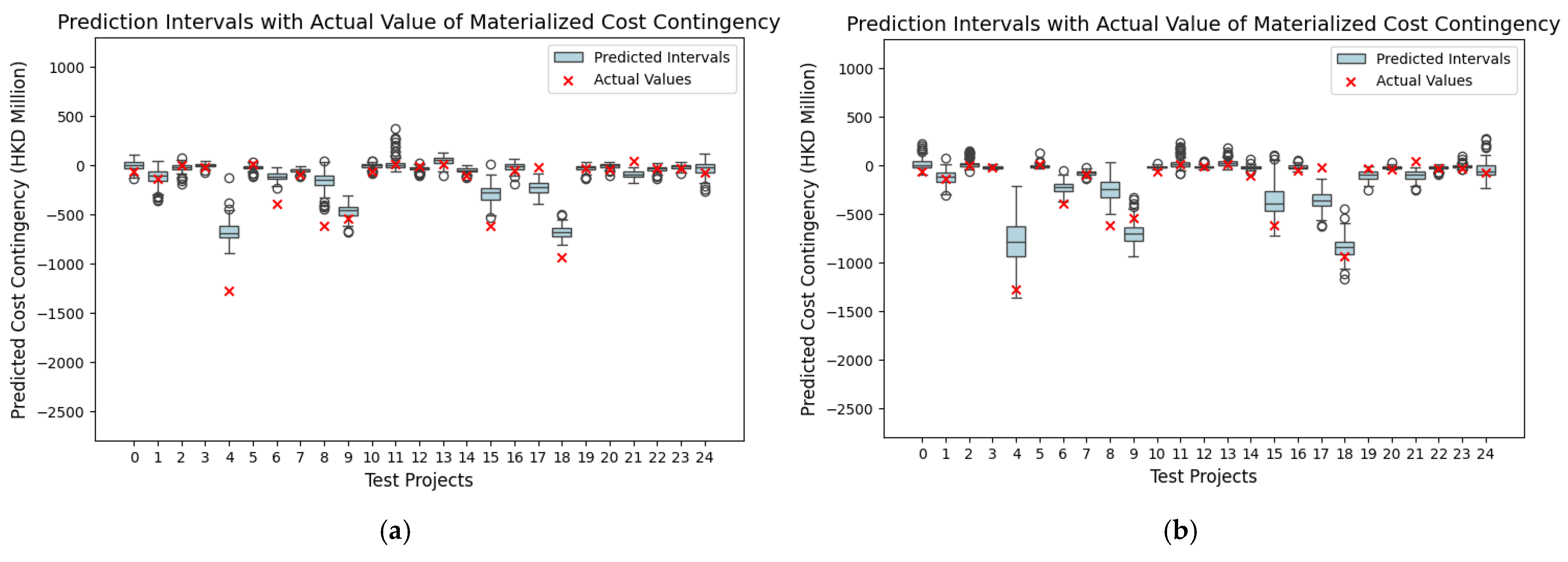
4.4. Integrating the Complexity Index into Interval Estimation
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lhee, S.C.; Flood, I.; Issa, R.R.A. Development of a two-step neural network-based model to predict construction cost contingency. J. Inf. Technol. Constr. 2014, 19, 399–411. [Google Scholar]
- Hoseini, E.; Bosch-Rekveldt, M.; Hertogh, M. Cost contingency and cost evolvement of construction projects in the preconstruction phase. J. Constr. Eng. Manag. 2020, 146, 5020006. [Google Scholar]
- Hammad, M.W.; Abbasi, A.; Ryan, M.J. Allocation and Management of Cost Contingency in Projects. J. Manag. Eng. 2016, 32, 04016014. [Google Scholar]
- Enshassi, A.; Ayyash, A. Factors affecting cost contingency in the construction industry–Contractors’ perspective. Int. J. Constr. Manag. 2014, 14, 191–208. [Google Scholar]
- Islam, M.S.; Prasad, M.; Skitmore, M.; Drogemuller, R. Automation in Construction Risk induced contingency cost modeling for power plant projects. Autom. Constr. 2021, 123, 103519. [Google Scholar] [CrossRef]
- Cardebat, J.-M.; Figuet, J.-M.; Paroissien, E. Expert opinion and Bordeaux wine prices: An attempt to correct biases in subjective judgments. J. Wine Econ. 2014, 9, 282–303. [Google Scholar]
- Lu, Y.; Luo, L.; Wang, H.; Le, Y.; Shi, Q. Measurement model of project complexity for large-scale projects from task and organization perspective. Int. J. Proj. Manag. 2015, 33, 610–622. [Google Scholar]
- Lin, W.; Wang, G.; Ning, Y.; Ma, Q.; Dai, S. The effects of performance measurement on megaproject performance: The moderating effects of project complexity. Eng. Constr. Archit. Manag. 2025, 32, 172–193. [Google Scholar]
- Elmousalami, H.H. Artificial intelligence and parametric construction cost estimate modeling: State-of-the-art review. J. Constr. Eng. Manag. 2020, 146, 3119008. [Google Scholar]
- El-Kholy, A.M.; Tahwia, A.M.; Elsayed, M.M. Prediction of simulated cost contingency for steel reinforcement in building projects: ANN versus regression-based models. Int. J. Constr. Manag. 2022, 22, 1675–1689. [Google Scholar]
- Ammar, T.; Abdel-Monem, M.; El-Dash, K. Regression-based model predicting cost contingencies for road network projects. Int. J. Constr. Manag. 2024, 1–15. [Google Scholar] [CrossRef]
- Han, Y.; Yang, Q.; Tian, P. The fundamentals of boosting high-quality development by megaprojects: A systematic literature review. Proj. Leadersh. Soc. 2024, 5, 100140. [Google Scholar]
- Flyvbjerg, B. What you should know about megaprojects and why: An overview. Proj. Manag. J. 2014, 45, 6–19. [Google Scholar] [CrossRef]
- Luo, L.; He, Q.; Jaselskis, E.J.; Xie, J. Construction project complexity: Research trends and implications. J. Constr. Eng. Manag. 2017, 143, 4017019. [Google Scholar]
- Project Management Institute. Project Management Body of Knowledge (Pmbok® Guide); Project Management Institute: Newtown Square, PA, USA, 2021. [Google Scholar]
- Doyle, A.; Hughes, W. The influence of project complexity on estimating accuracy. In Proceedings of the 16th Annual ARCOM Conference, Glasgow, UK, 6–8 September 2000. [Google Scholar]
- Sonmez, R.; Ergin, A.; Birgonul, M.T. Quantiative methodology for determination of cost contingency in international projects. J. Manag. Eng. 2007, 23, 35–39. [Google Scholar]
- Calford, E.M. Uncertainty aversion in game theory: Experimental evidence. J. Econ. Behav. Organ. 2020, 176, 720–734. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1050–1059. [Google Scholar]
- Bruce, P.; Bruce, A.; Gedeck, P. Practical Statistics for Data Scientists: 50+ Essential Concepts Using R and Python; O’Reilly Media: Sebastopol, CA, USA, 2020; ISBN 1492072915. [Google Scholar]
- Idrus, A.; Nuruddin, M.F.; Rohman, M.A. Expert Systems with Applications Development of project cost contingency estimation model using risk analysis and fuzzy expert system. Expert Syst. Appl. 2011, 38, 1501–1508. [Google Scholar] [CrossRef]
- Musa, M.M.; Zubairu, I.K.; Bala, K. Appraisal of the performance of contingency cost provision for building projects in Nigeria. ATBU J. Environ. Technol. 2011, 4, 41–48. [Google Scholar]
- Barraza, G.A.; Asce, M.; Bueno, R.A. Cost Contingency Management. J. Manag. Eng. 2007, 23, 140–146. [Google Scholar]
- Thal, A.E., Jr.; Cook, J.J.; Iii, E.D.W. Estimation of Cost Contingency for Air Force Construction Projects. J. Constr. Eng. Manag. 2010, 136, 1181–1188. [Google Scholar]
- Maulud, D.; Abdulazeez, A.M. A review on linear regression comprehensive in machine learning. J. Appl. Sci. Technol. Trends 2020, 1, 140–147. [Google Scholar]
- Khodabakhshian, A. Machine Learning for Risk Management in Construction Projects. Ph.D. Thesis, Politecnico di Milano, Milan, Italy, 2023. [Google Scholar]
- Sohrabi, H.; Noorzai, E. Risk-supported case-based reasoning approach for cost overrun estimation of water-related projects using machine learning. Eng. Constr. Archit. Manag. 2024, 31, 544–570. [Google Scholar]
- Darko, A.; Glushakova, I.; Boateng, E.B.; Chan, A.P.C. Using machine learning to improve cost and duration prediction accuracy in green building projects. J. Constr. Eng. Manag. 2023, 149, 4023061. [Google Scholar]
- Yun, J.; Ryu, K.R.; Ham, S. Spatial analysis leveraging machine learning and GIS of socio-geographic factors affecting cost overrun occurrence in roadway projects. Autom. Constr. 2022, 133, 104007. [Google Scholar] [CrossRef]
- Wang, R.; Asghari, V.; Hsu, S.-C.; Lee, C.-J.; Chen, J.-H. Detecting corporate misconduct through random forest in China’s construction industry. J. Clean. Prod. 2020, 268, 122266. [Google Scholar]
- Chakraborty, D.; Elhegazy, H.; Elzarka, H.; Gutierrez, L. A novel construction cost prediction model using hybrid natural and light gradient boosting. Adv. Eng. Inform. 2020, 46, 101201. [Google Scholar]
- Coffie, G.H.; Cudjoe, S.K.F. Using extreme gradient boosting (XGBoost) machine learning to predict construction cost overruns. Int. J. Constr. Manag. 2023, 24, 1742–1750. [Google Scholar]
- Matel, E.; Vahdatikhaki, F.; Hosseinyalamdary, S.; Evers, T.; Voordijk, H. An artificial neural network approach for cost estimation of engineering services. Int. J. Constr. Manag. 2022, 22, 1274–1287. [Google Scholar]
- Nabawy, M.; Gouda Mohamed, A. Risks assessment in the construction of infrastructure projects using artificial neural networks. Int. J. Constr. Manag. 2024, 24, 361–373. [Google Scholar]
- Wang, R.; Asghari, V.; Man, C.; Hsu, S.; Lee, C. Automation in Construction Assessing effects of economic factors on construction cost estimation using deep neural networks. Autom. Constr. 2022, 134, 104080. [Google Scholar] [CrossRef]
- Meharie, M.G.; Mengesha, W.J.; Gariy, Z.A.; Mutuku, R.N.N. Application of stacking ensemble machine learning algorithm in predicting the cost of highway construction projects. Eng. Constr. Archit. Manag. 2022, 29, 2836–2853. [Google Scholar]
- Hon, C.K.H.; Sun, C.; Xia, B.; Jimmieson, N.L.; Way, K.A.; Wu, P.P.-Y. Applications of Bayesian approaches in construction management research: A systematic review. Eng. Constr. Archit. Manag. 2022, 29, 2153–2182. [Google Scholar]
- Milanés-Hermosilla, D.; Trujillo Codorniú, R.; López-Baracaldo, R.; Sagaró-Zamora, R.; Delisle-Rodriguez, D.; Villarejo-Mayor, J.J.; Núñez-Álvarez, J.R. Monte Carlo dropout for uncertainty estimation and motor imagery classification. Sensors 2021, 21, 7241. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Mohamed, E.; Jafari, P.; AbouRizk, S. Machine Learning–Based Bayesian Framework for Interval Estimate of Unsafe-Event Prediction in Construction. J. Constr. Eng. Manag. 2023, 149, 4023118. [Google Scholar]
- Vaysse, K.; Lagacherie, P. Using quantile regression forest to estimate uncertainty of digital soil mapping products. Geoderma 2017, 291, 55–64. [Google Scholar]
- Gondia, A.; Siam, A.; El-Dakhakhni, W.; Nassar, A.H. Machine learning algorithms for construction projects delay risk prediction. J. Constr. Eng. Manag. 2020, 146, 4019085. [Google Scholar]
- Vassilev, H.; Laska, M.; Blankenbach, J. Uncertainty-aware point cloud segmentation for infrastructure projects using Bayesian deep learning. Autom. Constr. 2024, 164, 105419. [Google Scholar]
- Vidal, L.; Marle, F. Understanding project complexity: Implications on project management. Kybernetes 2008, 37, 1094–1110. [Google Scholar] [CrossRef]
- Qazi, A.; Quigley, J.; Dickson, A.; Kirytopoulos, K. Project Complexity and Risk Management (ProCRiM): Towards modelling project complexity driven risk paths in construction projects. Int. J. Proj. Manag. 2016, 34, 1183–1198. [Google Scholar]
- Hatamleh, M.T.; Hiyassat, M.; Sweis, G.J.; Sweis, R.J. Factors affecting the accuracy of cost estimate: Case of Jordan. Eng. Constr. Archit. Manag. 2018, 25, 113–131. [Google Scholar]
- Boonstra, A.; Reezigt, C. A complexity framework for project management strategies. Proj. Manag. J. 2023, 54, 253–267. [Google Scholar]
- Floricel, S.; Michela, J.L.; Piperca, S. Complexity, uncertainty-reduction strategies, and project performance. Int. J. Proj. Manag. 2016, 34, 1360–1383. [Google Scholar]
- Chen, Y.; Ahiaga-Dagbui, D.D.; Thaheem, M.J.; Shrestha, A. Toward a deeper understanding of optimism bias and transport project cost overrun. Proj. Manag. J. 2023, 54, 561–578. [Google Scholar]
- Asmussen, J.N.; Kristensen, J.; Wæhrens, B.V. Cost estimation accuracy in supply chain design: The role of decision-making complexity and management attention. Int. J. Phys. Distrib. Logist. Manag. 2018, 48, 995–1019. [Google Scholar]
- Tsamardinos, I.; Greasidou, E.; Borboudakis, G. Bootstrapping the out-of-sample predictions for efficient and accurate cross-validation. Mach. Learn. 2018, 107, 1895–1922. [Google Scholar]
- Cismondi, F.; Fialho, A.S.; Vieira, S.M.; Reti, S.R.; Sousa, J.M.C.; Finkelstein, S.N. Missing data in medical databases: Impute, delete or classify? Artif. Intell. Med. 2013, 58, 63–72. [Google Scholar]
- Emmanuel, T.; Maupong, T.; Mpoeleng, D.; Semong, T.; Mphago, B.; Tabona, O. A survey on missing data in machine learning. J. Big Data 2021, 8, 140. [Google Scholar] [CrossRef]
- Pham, T.Q.D.; Le-Hong, T.; Tran, X. V Efficient estimation and optimization of building costs using machine learning. Int. J. Constr. Manag. 2023, 23, 909–921. [Google Scholar] [CrossRef]
- Hossain, R.; Timmer, D. Machine learning model optimization with hyper parameter tuning approach. Glob. J. Comput. Sci. Technol. D Neural Artif. Intell. 2021, 21, 31. [Google Scholar]
- Adnan, M.; Alarood, A.A.S.; Uddin, M.I.; ur Rehman, I. Utilizing grid search cross-validation with adaptive boosting for augmenting performance of machine learning models. PeerJ Comput. Sci. 2022, 8, e803. [Google Scholar]
- Belete, D.M.; Huchaiah, M.D. Grid search in hyperparameter optimization of machine learning models for prediction of HIV/AIDS test results. Int. J. Comput. Appl. 2022, 44, 875–886. [Google Scholar]
- AlKheder, S.; Al Otaibi, H.; Al Baghli, Z.; Al Ajmi, S.; Alkhedher, M. Analytic hierarchy process (AHP) assessment of Kuwait mega construction projects’ complexity. Eng. Constr. Archit. Manag. 2025, 32, 1903–1946. [Google Scholar]
- Nguyen, A.T.; Nguyen, L.D.; Le-Hoai, L.; Dang, C.N. Quantifying the complexity of transportation projects using the fuzzy analytic hierarchy process. Int. J. Proj. Manag. 2015, 33, 1364–1376. [Google Scholar]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation importance: A corrected feature importance measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [PubMed]
- Gürsoy, M.İ.; Alkan, A. Investigation of diabetes data with permutation feature importance based deep learning methods. Karadeniz Fen Bilim. Derg. 2022, 12, 916–930. [Google Scholar]
- Saraiva, S.V.; de Oliveira Carvalho, F.; Santos, C.A.G.; Barreto, L.C.; Freire, P.K. de M.M. Daily streamflow forecasting in Sobradinho Reservoir using machine learning models coupled with wavelet transform and bootstrapping. Appl. Soft Comput. 2021, 102, 107081. [Google Scholar]
- Miok, K.; Nguyen-Doan, D.; Zaharie, D.; Robnik-Šikonja, M. Generating data using Monte Carlo dropout. In Proceedings of the 2019 IEEE 15th International Conference on Intelligent Computer Communication and Processing (ICCP), Cluj-Napoca, Romania, 5–7 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 509–515. [Google Scholar]
- Offei-Nyako, K.; Ohene Tham, L.C.; Bediako, M.; Adobor, C.D.; Oduro Asamoah, R. Deviations between contract sums and final accounts: The case of capital projects in Ghana. J. Constr. Eng. 2016, 2016, 2814126. [Google Scholar]
- De Marco, A.; Narbaev, T.; Ottaviani, F.M.; Vanhoucke, M. Influence of cost contingency management on project estimates at completion. Int. J. Constr. Manag. 2024, 24, 935–945. [Google Scholar]
| Research | Algorithm | Input Variables | Target | Advantages/Disadvantages |
|---|---|---|---|---|
| Lhee et al. (2014) [1] | ANN | Number of bidders, project letting year, project duration, and contract value | Predicted contingency amount | The ANN model demonstrated promising accuracy in predicting cost contingency. However, the input variables are limited, and the lack of consideration for project complexity factors restricts the model’s generalizability to infrastructure projects. |
| Islam et al. (2021) [5] | Fuzzy Bayesian belief networks | Cost overrun-related risks, including 27 independent risks and 14 dependent risks | Probability of cost overrun | It predicted the probability of cost overrun. However, limited project cases (12 cases) used for prediction model, computational complexity, and reliance on subjective data constrain its application. |
| El-Kholy et al. (2022) [10] | ANN | Sensitivity analysis ratio of steel reinforcement prices, ratio of the direct cost of steel reinforcement to the total project cost, probability distribution types for risk variables (triangular and normal), and contractor trend in dealing with risk (gambler, neutral, and conservative) | Predicted cost contingency percentage | This study demonstrated that the ANN model outperformed regression-based models in predictive accuracy. However, the limited number of project cases (30 cases) and the focus on the influence of steel reinforcement prices on cost contingency, constrain its broader applicability. |
| Ammar et al. (2024) [11] | Linear regression | Cost overrun-related factors, such as inaccurate cost estimate, design changes, scope changes, and variation orders | Predicted contingency amount | This study revealed promising predictive performance for linear regression. However, it lacks diverse project features as input variables and relies on subjective input data. |
| Prediction Models | Hyperparameters |
|---|---|
| Linear regression | ElasticNet (‘alpha’ = 1, ‘l1_ratio’ = 1) |
| SVM | SVR(‘C’ = 500, ‘degree’ = 2, ‘epsilon’ = 2, ‘gamma’ = ‘scale’, ‘kernel’ = ‘linear’) |
| Decision tree | DecisionTreeRegressor (‘criterion’ = ‘poisson’, ‘max_depth’ = None, ‘max_features’ = None, ’min_samples_split’ = 2) |
| Random forest | RandomForestRegressor (n_estimators = 100, criterion = ‘squared_error’, max_depth = None, min_samples_split = 2, min_samples_leaf = 1) |
| Gradient boosting | GradientBoostingRegressor (‘learning_rate’ = 0.1, ‘loss’ = ‘huber’, ‘n_estimators’ = 100) |
| XGBoosting | XGBRegressor (objective = ‘reg:squarederror’, n_estimators = 300, learning_rate = 0.01, max_depth = 3, subsample = 0.8, colsample_bytree = 1, gamma = 0, min_child_weight = 20, reg_alpha = 0, reg_lambda = 0, random_state = 31) |
| ANN | MLPRegressor (hidden_layer_sizes = (256, 128), activation = ‘relu’, solver = ‘adam’, alpha = 0.0001, max_iter = 600, random_state = 0, learning_rate = ‘constant’, learning_rate_init = 0.001, shuffle = True, verbose = True, validation_fraction = 0.1, momentum = 0.9) |
| Model Variables | Description | Value | ||||
|---|---|---|---|---|---|---|
| Data Type | Min. | Max. | Mean | Standard Deviation | ||
| Input | ||||||
| Project estimate (PE) (HKD) | A cost estimate prepared by a client before receiving any bids from contractors for a construction project. It is based on the design, specifications, and other known factors. | Numerical value | 32.55 million | 44,878.95 million | 1508.99 million | 4701.69 million |
| Contract contingency allowed in PE (HKD) | A specific allowance to cover unforeseen costs or risks (e.g., design changes or unexpected site conditions) that might arise during the construction project. | Numerical value | 2.35 million | 2665.22 million | 114.16 million | 308.88 million |
| Approved PE (HKD) | The officially sanctioned project estimate that has been reviewed and endorsed by the client. | Numerical value | 34.00 million | 44,798.40 million | 1826.55 million | 5167.11 million |
| Project type | Project type refers to the category of public infrastructure projects classified by their purpose. Five main types are identified: land development projects (LDPs), roads and highways (RH), water treatment projects (WTPs), sewage treatment projects (STPs), and other public functional projects (PFPs, e.g., hospitals, schools, and government offices) | Five string values: LDPs (26%), RH (11%), WTPs (7%), STPs (11%), PFPs (45%) | -- | -- | -- | -- |
| Starting year | The year in which the construction work for a project begins on site. | Integer | 1998 | 2021 | -- | -- |
| Completion year | The year when all construction activities are finished, and the project is considered complete. | Integer | 2002 | 2024 | -- | -- |
| Output | ||||||
| Materialized cost contingency (HKD) | The portion of the allocated cost contingency that has actually been used to cover unforeseen risks or changes during the project construction process. | Numerical value | −7518.71 million | 1418.48 million | −233.66 million | 784.91 million |
| Prediction Targets | Metrics | Linear Regression | SVM | Decision Tree | Random Forest | Gradient Boosting | XGBoosting | ANN |
|---|---|---|---|---|---|---|---|---|
| Materialized cost contingency | R2 | 0.397 | 0.360 | 0.084 | 0.725 | 0.782 | 0.785 | 0.808 |
| MAE | 156 | 141 | 156 | 94 | 86 | 86 | 93 | |
| MSE | 66,709 | 70,870 | 101,470 | 30,412 | 24,095 | 23,876 | 21,236 | |
| RMSE | 258 | 266 | 318 | 174 | 155 | 157 | 145 |
| Prediction Target | Metrics | Without Complexity Index | With Complexity Index |
|---|---|---|---|
| Materialized cost contingency | R2 | 0.808 | 0.889 |
| MAE | 93 | 68 | |
| MSE | 21,236 | 11,080 | |
| RMSE | 145 | 105 |
| Features | Value | Rank |
|---|---|---|
| Approved project estimate | 151,976.32 | 1 |
| Complexity index | 121,533.38 | 2 |
| Contract contingency | 46,223.72 | 3 |
| Starting year | 14,185.36 | 4 |
| Completion year | 6729.28 | 5 |
| Project type | 1650.03 | 6 |
| Project estimate | 803.49 | 7 |
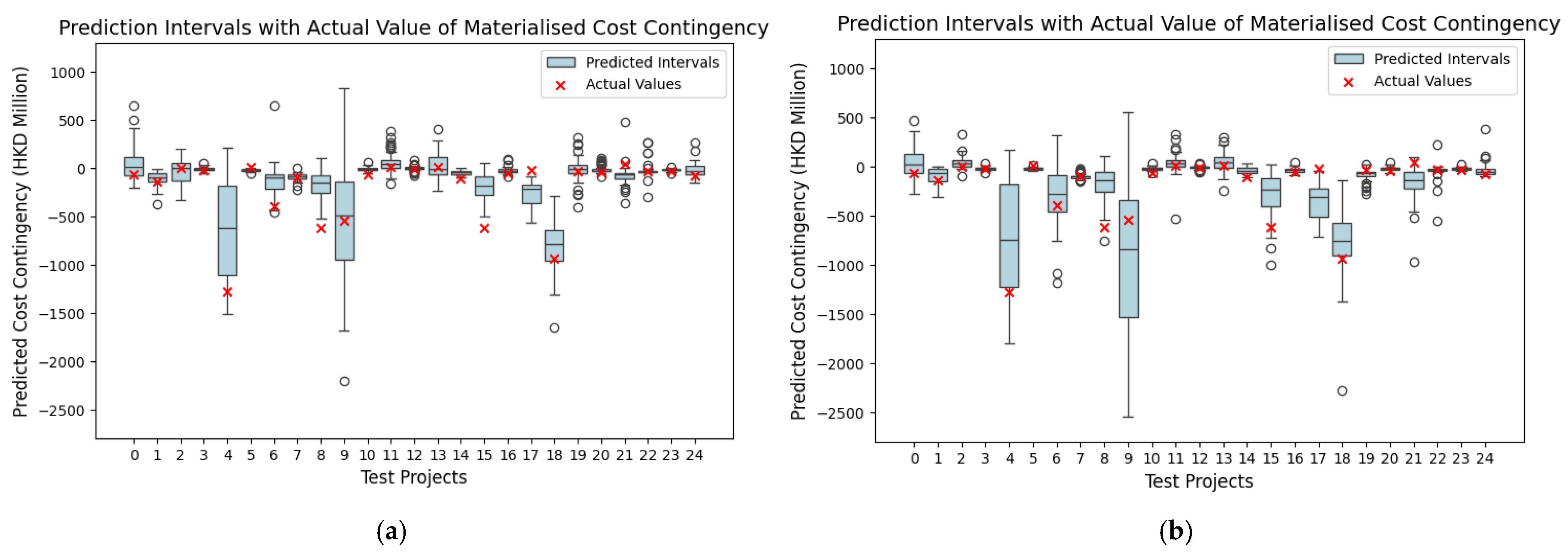
| Prediction Target | Methods | Without Complexity Index (Uncertainty Accuracy, %) | With Complexity Index (Uncertainty Accuracy, %) |
|---|---|---|---|
| Cost contingency prediction | Monte Carlo dropout | 60 | 76 |
| Bootstrapping | 80 | 88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sing, M.C.P.; Ma, Q.; Gu, Q. Improving Cost Contingency Estimation in Infrastructure Projects with Artificial Neural Networks and a Complexity Index. Appl. Sci. 2025, 15, 3519. https://doi.org/10.3390/app15073519
Sing MCP, Ma Q, Gu Q. Improving Cost Contingency Estimation in Infrastructure Projects with Artificial Neural Networks and a Complexity Index. Applied Sciences. 2025; 15(7):3519. https://doi.org/10.3390/app15073519
Chicago/Turabian StyleSing, Michael C. P., Qiuwen Ma, and Qinhuan Gu. 2025. "Improving Cost Contingency Estimation in Infrastructure Projects with Artificial Neural Networks and a Complexity Index" Applied Sciences 15, no. 7: 3519. https://doi.org/10.3390/app15073519
APA StyleSing, M. C. P., Ma, Q., & Gu, Q. (2025). Improving Cost Contingency Estimation in Infrastructure Projects with Artificial Neural Networks and a Complexity Index. Applied Sciences, 15(7), 3519. https://doi.org/10.3390/app15073519








