Verifiable Key-Aggregate Searchable Encryption Scheme for Fog-Based Internet of Autonomous Vehicles

Abstract

The fog-based Internet of Autonomous Vehicles (FB-IAV) collects extensive sensing data to enhance its understanding of the environment. As vehicles generate unique keys for encryption and receive keyword details from data requesters for the secure transmission of specialized environmental data, FB-IAV increases the risk of key leakage increases. Additionally, the fog server may be manipulated to alter search results. Current approaches do not adequately consider the potential for vehicles to inadvertently disclose keyword details of data requesters. Moreover, the cost of verifying search results is substantial for these systems. To tackle these problems, we offer a new blockchain-verifiable, multiple-keyword searching method for FB-IAV. At first glance, the proposed scheme is based on key-aggregate searchable encryption, which achieves safe key aggregation by using blockchain technology and an oblivious search request. The method uses a dual-verified technique to provide efficient verification for the outcomes of the search. The suggested plan can achieve authorization, requester privacy, accountability, and dual validation, in addition to ensuring secure search. Furthermore, the efficiency of the suggested scheme in accomplishing the specified security goals is demonstrated by the security analysis and proof. Lastly, the performance study shows that the proposed scheme is both significantly feasible and scalable.

1. Introduction

To date, the fog-based Internet of Autonomous Vehicles (FB-IAV) has demonstrated a remarkable ability to sense vast amounts of environmental data, including traffic conditions, road status, and safety route directions [1,2]. Vehicle sensors are designed to collect environmental sensing data within an FB-IAV system. To ensure efficient data storage, management, and sharing, this information is uploaded to a fog server (FS).

Nevertheless, despite the ease of data exchange in Federated Blockchain-based Intelligent Autonomous Vehicles (FB-IAVs), there is growing concern regarding the unintentional detection of data leaks [3]. Such leaks can compromise vehicle privacy and potentially distort accurate environmental data. Therefore, it is essential to maintain data privacy throughout the sharing process in FB-IAV. A common solution to these challenges is for vehicles to encrypt all their data before transmitting it to the Federated Server (FS) [4]. This approach allows individuals who possess the decryption keys to later retrieve and decrypt the data. However, the encryption complicates the process for the data requester $\left(dr\right)$, making it difficult to search for and obtain only the data that contain a specific keyword (k).

Numerous searchable encryption (SE)-based solutions have been proposed to address the aforementioned issues [5]. SE utilizes the computational power of function sharing (FS) for k searches without compromising anonymity. However, in large-scale applications involving billions of files and millions of vehicles, the implementation of such a system may be impeded by practical challenges related to effective key management [6]. In practice, it is often necessary to use different encryption keys for various files to enable vehicles to share encrypted data with specific users. Nevertheless, the expenses of setting up trapdoors, carefully keeping keys, and distributing keys rise in tandem with the volume of shared files.

Searchable encryption using a key aggregate (KSE) is commonly employed to address the aforementioned challenges [7]. In KSE, vehicles can produce an aggregate key from various classes containing the term $dr$ by utilizing their secret keys. Although it is a single key, this aggregate key possesses the capability to search for ciphertexts across multiple classes. Moreover, without requiring all of the decryption keys, $dr$ is authorized to decode vehicle data using the aggregate key, provided that patient consent has been obtained.

Nevertheless, certain issues persist [7]. Firstly, existing key search encryption (KSE) methods do not consider the potential for automobiles to provide $dr$ with k information. If the $dr$ is unable to supply k information, vehicles cannot generate aggregate keys. Secondly, the Function Server (FS) may not be entirely reliable, which raises the possibility of data manipulation. A straightforward approach involves using the data generator ($d{g}_i$) to create a bilinear aggregated signature for encrypted text data and contracting with the FS to manage the signature, along with the k ciphertexts [8]. The FS then provides the matching aggregate signature, along with the corresponding ciphertexts, to the $dr$. The aggregated signature can then be used by the $dr$ to confirm the accuracy of the plaintext data that correspond to the encrypted data. Nevertheless, the verification algorithm uses bilinear pairing, which raises the cost considerably.

Here, we propose a verified search technique for FB-IAV utilizing secure multiple-key aggregation (MKA). The MKA scheme aggregates keys and generates trapdoors for an authorized $dr$ by employing key search encryption (KSE) and blockchain technologies [9,10,11]. Vehicles can securely collect keys from various categories that contain relevant ks, even when they are unaware of the specific k details associated with the $dr$. Additionally, it incorporates an enhanced oblivious method [12] to prevent vehicles from discerning the k details of the $dr$. To ensure efficient verification of the search results, we develop a dual provable method that does not rely on bilinear pairings. The main contributions are described as follows.

• We utilize smart contracts $\left(SCs\right)$, oblivious search inquiries, and key search encryption (KSE) to develop a Multi-Key Access (MKA) scheme. The aggregation of secure keys and the generation of trapdoors for permitted data retrieval (denoted as $dr$) can be accomplished by integrating KSE with an $SC$. The leakage of k information related to $dr$ is effectively mitigated through the use of oblivious search requests.
• A dual-verifiable technique is also developed by our team, which utilizes two homomorphic hash functions and their properties. This approach enables the effective verification of the overall search outcome. Additionally, this method notably decreases the communication and computational costs through collaborative confirmation. Additionally, bilinear pairing is not employed in the dual-verifiable algorithm.
• We validate the suggested system and perform a thorough security study, showcasing its strong security features. Additionally, we conduct comprehensive testing to assess its performance, demonstrating its effectiveness in terms of processing and transmission expenses.

This article is structured as follows: In Section 2, we review related works. Section 3 outlines our preliminary findings, the system model, security threats, and security goals. Section 4 introduces the proposed plan, followed by Section 5 and Section 6, which analyze its security and performance, respectively. Finally, our work is summarized in Section 7.

2. Related Work

We performed a thorough literature assessment of key searchable encryption (KSE) and verifiable key-aggregate searchable encryption.

The concept of searchable encryption (SE), a search method that permits the searching of encrypted data while concurrently protecting individual privacy, was first formally described by Xiaoding et al. [13] with reference to key searchable encryption (KSE). Searchable symmetric encryption and searchable asymmetric encryption are the two main components of SE. However, the seeking of authorization for a particular dataset one of the disadvantages of these methods. In [14], researchers presented searchable encryption using key aggregation as a solution to this problem. For this approach to allow for search capabilities over a set of files, a $d{g}_i$ is required give a user an aggregate key. Then, in order to perform searches on the shared dataset, the user has to send a trapdoor. However, this strategy is susceptible to both k assumption and attacks on the chosen k. Wen et al. [15] successfully addressed the identified vulnerabilities, especially those pertaining to guessing other users’ private keys. Nevertheless, searching across multi-generator data is not supported by these systems. To overcome this limitation, Pareek et al. [16] proposed an efficient key-aggregate scheme that satisfies all key-aggregate efficiency requirements, allowing a data owner to enforce dynamic updates in user access rights much more efficiently than existing methods. Additionally, some schemes [17,18] have been proposed with the aim of aggregating multi-generator keys.

The authors of [17] developed a technique that enables users to utilize a query trapdoor to search through the document sets of multiple generators. This technique significantly enhances the query performance of current key searchable encryption (KSE) schemes. Later, Trivedi et al. [18] succeeded in achieving a multi-generator setting, making sure that the aggregation key’s size stayed constant, irrespective of the quantity of records. Similarly, Liu et al. [14] proposed a method to produce a constant-size key. Although this approach successfully addresses the issue of key leakage during data exchange in the authentication process, it has a significant flaw. This flaw allows unauthorized individuals to access any arbitrary set of files stored in the fog server and forge the authentication key. Subsequently, Liu et al. [19] developed a key aggregation searchable encryption system with auxiliary input, which may improve resistance to key disclosure. The previously described efforts accomplished aggregated keys. Yin et al. [20] introduced a novel decentralized ciphertext policy attribute-based encryption scheme to address the single point of failure and the limited research focusing on the privacy concerns of user identity during the key generation process. However, they failed to consider the potential for vehicles to inadvertently disclose sensitive k information. Consequently, we propose an efficient and secure method for aggregated multi-key management.

In the field of verifiable searchable key-aggregate encryption, Li et al. [21] proposed an effective technique to ensure the integrity of search results. They introduced appropriate confirmation flags generated by the $d{g}_i$ with the assistance of a server. However, if the assistance server is compromised, the security of the system is at risk. To address this issue, Lee et al. [7] suggested an efficient verifiable searchable encryption method utilizing aggregate keys. Additionally, Liu et al. [19] employed a Bloom filter to validate the search results. Long et al. [22] introduced a certificateless verifiable public k-searchable encryption scheme to mitigate the problem of a semi-trusted third party providing incorrect search results, thereby conserving computational and bandwidth resources. Nevertheless, due to its high false-positive rate, the Bloom filter may yield inaccurate verified results.

Nevertheless, the verification procedure incurs a significant cost due to its reliance on bilinear pairings. Liu et al. [19] subsequently suggested a searchable encryption technique that makes use of aggregate keys for authentication and verification. This method employs information obtained from the data user’s interactions with the file server (FS) to confirm the ciphertexts’ integrity.

However, the reliance of the verification technique on bilinear pairings was blamed for the high verification costs. However, these techniques are unable to effectively verify the search results. Based on the relevant research covered in this section, we suggest an effective verification scheme.

3. Preliminaries

3.1. Cryptographic Assumptions

Definition 1. 

(Decisional Bilinear Diffie–Hellman Problem (DBDH)).

A multiplicative group of the same large prime order with bilinear maps ($\widehat{e}:\mathcal{G}\times \mathcal{G}\to \mathbb{G}$) and an additive group of large prime order (q) are also considered. Let $a,b,c,x\in Z_q^{*}$ and P be a generator in $\mathcal{G}$. The following is the definition of the DBDH problem:

The next step is to calculate $\widehat{e}{(P,P)}^{abc}$ consideringan input tuple $(P\in \mathcal{G},aP\in \mathcal{G},bP\in \mathcal{G},cP\in \mathcal{G})$. Ref. [7] defines the advantage ($Dv$) of a polynomial time ($\mathrm{\Phi }$) in resolving the DBDH problem.

$$D{v}_{\mathrm{\Phi }}^{DBDH}\left(\beta \right)=\left|\begin{array}{c}\hfill Pr\left[\mathrm{\Phi }(\widehat{e},P,aP,bP,cP,\widehat{e}{(P,P)}^{abc}=1)\right]\\ \hfill -Pr\left[\mathrm{\Phi }(\widehat{e},P,aP,bP,cP,\widehat{e}{(P,P)}^x=1)\right]\end{array}\right|\le \mu$$

(1)

DBDH Assumption: Assume that an adversary ($\mathbb{A}$) has an advantage of $D{v}_{\mathrm{\Phi }}^{DBDH}\left(\beta \right)\le \mu$, where $\mu$ is a negligible number and is able to distinguish between $\widehat{e}{(P,P)}^{abc}$ and $\widehat{e}{(P,P)}^x$. In polynomial time, the DBDH problem is thought to be challenging to solve.

Definition 2. 

 $\left(\right(\mathbf{F},\mathbf{n})$–Diffie–-Hellman Additive $(\mathbf{F},\mathbf{n})-DEA\left)\right)$. Using bilinear mappings ($\widehat{e}:\mathcal{G}\times \mathcal{G}\to \mathbb{G}$), consider groups $\mathcal{G}$ and $\mathbb{G}$ of order q. In $\mathcal{G}$ and $\delta \in Z_q^{*}$, let P be a generator. The $(\mathbf{F},\mathbf{n})-DEA$ problem is formulated as follows:

A polynomial function ($\mathbf{F}\left(x\right)\in Z_q\left[x\right]$) of degree ${\mathbf{n}}^{\prime }$ is given for ${\mathbf{n}}^{\prime }>\mathbf{n}$ and $P,\delta P,{\delta }^{2}P,\dots ,{\delta }^{\mathbf{n}}P$, and the $(\mathbf{F},\mathbf{n})-DEA$ problem is used to determine ($\mathbf{F}\left(x\right),\mathbf{F}\left(\delta \right)P)$.

$(\mathbf{F},\mathbf{n})-DEA$ Assumption: Suppose that an adversary ($\mathbb{A}$) has a larger chance of solving the $(\mathbf{F},\mathbf{n})-DEA$ problem than ${\mu }^{\prime }$, where ${\mu }^{\prime }$ is an insignificant value. It is thought to be challenging to solve the $(\mathbf{F},\mathbf{n})-DEA$ issue in polynomial time.

3.2. Dual-Verifiable Encryption

Motivated by convergence encryption [23], which offers solely data authenticity validation and does not provide multi-data assurance, we build two provable encryption methods for multi-data verification. In the proposed method, we use two homomorphic hash functions [17] to achieve double validation. The protocol we propose comprises the algorithms listed below:

• Key $(n,d_1,\dots ,d_n,{\hslash }_1)\to {\left\{s{k}_i\right\}}_{i\in [1,n]}:$ Enter the files amounts (n) for n files ${\left\{d_i\right\}}_{i\in [1,n]}$, and generate key ${\left\{Y_i\right\}}_{i\in [1,n]}$ using homomorphic hash ${\hslash }_1$.
• AggKey $(n,{\left\{Y_i\right\}}_{i\in [1,n]})\to Y_{i_{agg}}$: This algorithm generates the aggregate key ($Y_{i_{agg}}$) after receiving as inputs the amount of files (n) and key ${\left\{Y_i\right\}}_{i\in [1,n]}$.
• Encrypt $(d_1,\dots ,d_n,{\hslash }_1,{\hslash }_2)\to ({\{E_{1i},{\alpha }_{2i}\}}_{i\in [1,n]},{\alpha }_M^{\prime })$. This algorithm generates n ciphertexts (${\{{\alpha }_{1i},{\alpha }_{2i},\}}_{i\in [1,n]}$) and an aggregated ciphertext (${\alpha }_M^{\prime },{\alpha }_2^{\prime }$), obtaining n files (${\left\{m_i\right\}}_{i\in [1,n]}$) and two homomorphic hashes (${\hslash }_1$ and ${\hslash }_2$).
• Verify $(s{k}_{agg},{\alpha }_M^{\prime },{\alpha }_2^{\prime })\to M^{\prime }$: Initially, this method determines if ${\hslash }_2({\alpha }_M^{\prime }·s{k}_{agg})={\alpha }_2^{\prime }$. Environmental data ciphertexts (${\alpha }_M^{\prime },{\alpha }_2^{\prime }$) are accurate if this equation is true. Then, it decrypts ${\alpha }_M^{\prime }$ using key $s{k}_{agg}$, yielding decrypted data ($M^{\prime }$). Additionally, it determines whether ${\hslash }_1\left(M^{\prime }\right)=s{k}_{agg}$. This equation indicates that several files have not been altered if it is correct. It returns the original data ($M^{\prime }$) at the end.

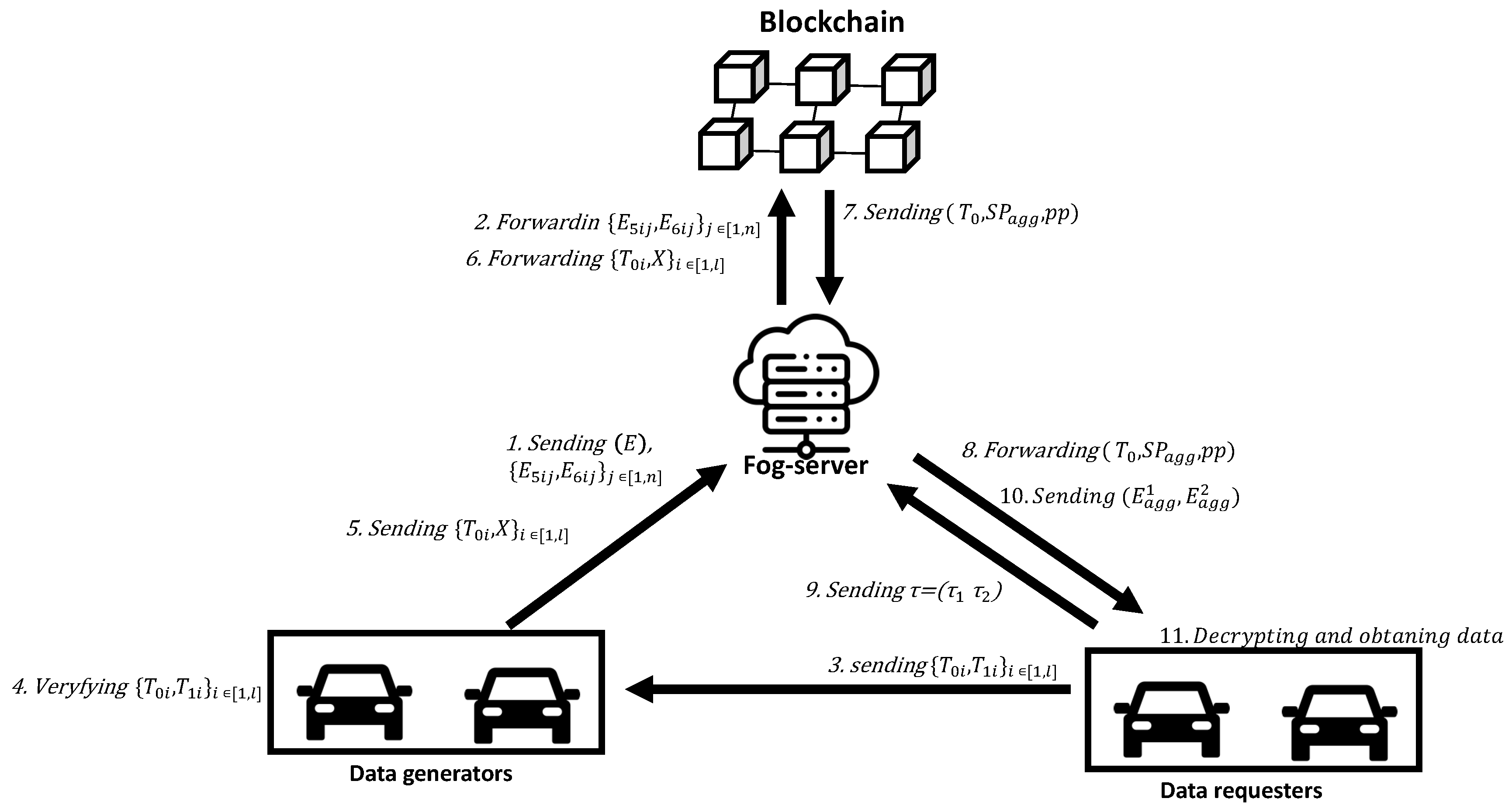
3.3. System Model

As illustrated in Figure 1, the proposed design comprises four components: the implementation of a smart contract $\left(SC\right)$ on a blockchain platform, a fog server ($FS$), a data generator ($d{g}_i$), and a data requester ($dr$).

• Data generators ($d{g}_i$) are conceptualized as entities that interact with sensors to produce environmental sensing data. To generate environmental data ciphertexts and k ciphertexts, $d{g}_i$ encrypts various types of environmental data using distinct keys and their associated k. Subsequently, the FS receives these ciphertexts to share environmental information with $dr$. Additionally, the keyword-encrypted data are added to the blockchain for future processing.
• Vehicle insurance companies are among the entities requesting access to environmental data on automobiles. While maintaining the confidentiality of the search term, the requester transmits search requests to the data guardian, along with a token and supporting evidence. The data guardians are provided with proof to verify that the k is part of the approved k set. Once the proof is successfully verified, the data guardians transmit permission to the blockchain. To conduct searches for the desired terms, the requester can utilize the blockchain to access a search trapdoor. Additionally, the requester can confirm the accuracy of the decrypted environmental data and the precision of the encrypted environmental data retrieved from the file system.
• The responsibility of maintaining encrypted environmental data and the corresponding k ciphertexts transmitted by $d{g}_i$ lies with the fog server (FS). Additionally, it is accountable for providing search services.
• Smart contracts are implemented using blockchain technology. The Aggregate Smart Contract (ASC) refers to the blockchain $SC$. The ASC performs three primary functions: creating a search trapdoor for approved $dr$s, combining the various keys from $d{g}_i$s, and collecting keys from environmental data.

3.4. Security Threats

To ensure the accurate execution of activities, the $SC$ is implemented within a secure environment as proposed. However, the following security risks may be posed by external entities:

The data generators are not entirely trustworthy. They may genuinely transmit the k ciphertexts of the FS and environmental data ciphertexts; however, they might attempt to disclose the $dr$ keyword information.

The FS may exhibit malevolent behavior. By examining the algorithms for ciphertext storage and query retrieval, one might attempt to access sensitive data. Furthermore, a rogue server might not honestly perform the query.

Requesters of authorized data are not always truthful. Within a group of files that are not inside the $dr$’s trapdoor, they might try to look for ks. They might also attempt to create a new trapdoor out of an old one, which could be quite dangerous. Furthermore, some malevolent attackers might try to retrieve more information from the blockchain’s recorded k and trapdoor ciphertexts.

3.5. Security Goals

In light of these challenges, we determined four security objectives that necessitate careful consideration.

Secure search. Only authorized workers (designated as $dr$) have access to the environmental data of $d{g}_i$ and can perform k searches. The opponent cannot deduce any other private information from the trapdoor or distinguish between the ks supplied in the trapdoor and the k ciphertexts.

Dual verification. Possible search result manipulation could arise from $d{g}_i$ and the FS working together. In order to detect any malicious behavior from the FS or $d{g}_i$, the suggested approach needs to validate the search results. Initially, the $dr$ might be permitted to confirm the correctness of ciphertexts that contain environmental information retrieved from the FS. The $dr$ can access the decrypted environmental data and carry out additional checks to verify its accuracy following a successful verification.

Accountability and access control. Only one k from the specified k collection shows up in the $dr$ search trapdoor, thanks to accountability. Once the $d{g}_i$ has found a valid k from the k collection, it can call the $SC$ to create a trapdoor for the matching $dr$. Regarding access control, a k search cannot be carried out by an attacker or an unauthorized $dr$ without $d{g}_i$’s permission. Stated differently, they are not allowed to look for the k in files that have nothing to do with the known trapdoor. Additionally, attempting to construct a new trapdoor for a different collection of files than the one that is currently in place is strictly prohibited.

Requester privacy. By utilizing the request tokens from the $dr$ or employing search trapdoors, both the FS and the $d{g}_i$ can access the term. The two k ciphertexts remain indistinguishable to any potential adversary. This ensures that the privacy of the $dr$ is consistently safeguarded.

4. Proposed Scheme

4.1. Overview

The proposed scheme consists of six steps: system setup, ciphertext generation, trapdoor generation, verification and aggregation, search, and decryption. During the setup phase, the system creates and publishes public parameters. Consequently, the $d{g}_i$ and $dr$ must generate their respective pairs of public and private keys, denoted as $(Y_i,y_i)$ and $(X,x)$, respectively.

To create environmental data ciphertexts (E), each $d{g}_i$ encrypts its unique original environmental data using a distinct key during the ciphertext generation stage. k ciphertexts are employed to encrypt the associated ks. The file server (FS) is responsible for maintaining these ciphertexts and supplying a search function for the $dr$. Subsequently, the FS sends pair $(E,k)$ to the $dr$. Additionally, k ciphertexts (${\{E_{5ij},E_{6ij}\}}_{j\in [1,n]}$) are transmitted to the blockchain to facilitate easy access to the related files by the authorized $dr$.

To safeguard k privacy, the $dr$ first encrypts k during the trapdoor creation stage to generate a token ($\tau$). To ensure its accuracy, the $dr$ simultaneously creates a k proof (${\phi }_i$). They then pass $\tau ,{\phi }_i)$ to the $d{g}_i$, which checks whether the token’s k is part of the approved k set. If the verification is unsuccessful, the token is canceled. Nevertheless, if the verification is successful, each $d{g}_i$ sends verification result ($T_i$) back to the $dr$ and the authorization $(T_i,\tau ,X)$ to the blockchain’s aggregation $SC$. Subsequently, the request $(X,\widehat{k})$ is sent to the aggregate $SC$ by the $dr$.

When $(T_i,\tau ,X)$ and $(X,\widehat{k})$ are received, the aggregation $SC$ produces the searchable and symmetric keys $(P_{agg},S_{agg)}$ and retrieves corresponding keys that include the keyword ($\widehat{k}$). These keys are then combined to create the symmetric key $(P{P}_{agg},S{S}_{agg)}$ and a single searchable key. Additionally, the aggregated $SC$ produces an encoded symmetric $S{P}_{agg}$ and a trapdoor ($T_i$). The true trapdoor ($T_i$) is subsequently obtained by the decryption routine($dr$) using their private key (x) after it sends $(T_0,S{P}_{agg})$. Lastly, the file server (FS) receives the actual trapdoor ($T_i$).

The FS uses $T_i$ to query k ciphertexts during the search phase. If the matching k ciphertexts are discovered, the FS forwards relevant environmental ciphertexts to the $dr$.

The $dr$ confirms the accuracy of the environmental data ciphertexts ($E_i^{\prime }$) during the decryption and verification phase. The $dr$ decrypts $E_i^{\prime }$ and retrieves the original environmental data ($d_i^{\prime }$) if the verification is successful. Additionally, they must verify the decrypted environmental data ($d_i^{\prime }$) once more. The $dr$ obtains the intended original environmental data if this verification is successful. If not, the $dr$ terminates the procedure for those environmental data. Some frequently used notations in this work are listed in

Table 1. Notations.

Notation	Description
$\mathcal{G}$	The additive group
$\mathbb{G}$	The multiplicative group
P	The generator of $\mathcal{G}$
$P_t$	The public system parameter
$dg$	The data generator
$dr$	The data requester
$(Y_i,y_i)$	The public key for the data generator
$(X,x)$	The private key for the data generator
E	The environmental data ciphertexts
k	Keyword ciphertexts
$\tau$	The token generated by the data generator
${\phi }_i$	A keyword proof created by the data generator
$(P_{agg},S_{agg)}$	The aggregated searchable and symmetric key
$T_i$	The trapdoor created by the aggregation smart contract
$S{P}_{agg}$	The encrypted symmetric key created by the aggregation smart contract

.

4.2. Details of the Proposed Scheme

Phase 1: System Setup

The public parameter ($P_t$) of the system is generated by the trust server. To initialize the system, it selects the security parameter (${\rm Y}$) as follows:

• A bilinear pairing mapping and an additive group ($\mathcal{G}$) are chosen so that $\widehat{e}:\mathcal{G}\times \mathcal{G}\to \mathbb{G}$. A multiplicative group is represented by $\mathbb{G}$. Keep in mind that the order number (q) is the same for $(\mathcal{G},\mathbb{G})$.
• A point generator ($P\in \mathcal{G}$) and the number (n) of secret keys ($s\in Z_q^{*}$) are selected to compute ${\lambda }_j=s^{j}P$ for $j\in [1,n]$, where n is the maximum limit of stored files.
• Two homomorphic hash algorithms (${\hslash }_1:\{0,1\}\to Z_q^{*}$ and ${\hslash }_2=\mathbb{G}\to Z_{q_z}^{*}$) and a collision-resistant hash algorithm ($H:\mathbb{G}\to Z_q^{*}$) are selected.
• n keywords are generated ($K=\{k_i\in [i,n]\}$).

The trust server publishes $P_t=\{q,\mathcal{G},\mathbb{G},\widehat{e},P,{\left\{{\lambda }_j\right\}}_{i\in [1,n]},{\hslash }_1,{\hslash }_2,H,K\}$.

Registration

Each system’s entity is in charge of generating its public and private keys, as described below.

• Data generators $\left(dg\right)$ registration. Each $d{g}_i$ generates its key pair, where $Y_i={\left\{y_i^{j}P\right\}}_{j\in [1,n]}$ is a public key and $y_i\in Z_q^{*}$ is a private key.
• Data requester $dr$ registration. Each $dr$ generates its key pair, where $X=xP$ is a public key and $x\in Z_q^{*}$ is a private key.

Phase 2: Ciphertext generation.

Each data generator $d{g}_i$ first chooses a keyword ($k\in K$) and selects $r_{ij}\in Z_q^{*}$. It then encrypts its data ($d_i$) and the selected k as follows:

• $E_{0ij}={\hslash }_1\left(d_i^j\right)$
• $E_{1ij}=E_{0ij}\oplus d_i^j$
• $E_{2ij}=E_{1ij}^{E_{0ij}}$
• $E_{3ij}=r_{ij}P$
• $E_{4ij}=\widehat{e}(E_{3ij},(y_i+k_i)P)$
• $E_{5ij}=k\oplus E_{0ij}^{y_i}$
• $E_{6ij}=y_i{\lambda }_j$

After that, the $d{g}_i$ sends the ciphertext ($E=\left({\{E_{1ij},E_{2ij},E_{3ij},E_{4ij}\}}_{j\in [1,n]}\right)$) to the FS and sends ${\{E_{5ij},E_{6ij}\}}_{j\in [1,n]}$ to the blockchain.

Phase 3: Trapdoor generation.

Each $dr$ chooses a keyword ($\widehat{k}\in K$) and uses its private key (x) to generate a trapdoor as follows.

• $T_{0i}=\left(x{y}_i\right)P+\left(x\widehat{k}\right)P$
• $T_{1i}={\displaystyle \frac{1}{x}}(Y_i+\widehat{k}P)$

After that, the $dr$ sends $T_i=\left({\{T_{0i},T_{1i}\}}_{i\in [1,l]}\right)$ to the data generators ($dg$), where l is the number of data generators ($dg$s).

Phase 4: Verification and aggregation.

Verification. When the data generator ($d{g}_i$) receives $T_i$ from the $dr$, it first verifies the validity of the keyword as follows.

$${\phi }_i={\displaystyle \frac{\widehat{e}((y_i+k)P,P)}{\widehat{e}(T_{1i}+T_{0i},P)}}=1$$

(2)

The trapdoor is closed if the equation is not true, which means that the keyword is $\widehat{k}\notin K$. Otherwise, the authorization ($(T_{0i},X)$) is sent to the blockchain by each data generator ($dg$) and to the $dr$ by each data generator. Therefore, the authorized $dr$ transmits $(X,\widehat{k})$ as a request to the blockchain after receiving $(T_{0i},X)$.

Correctness: The test algorithm is considered correct when the encrypted keyword and the trapdoor keyword match.

$$\begin{array}{cc}\hfill {\phi }_i& ={\displaystyle \frac{\widehat{e}((y_i+k)P,P)}{\widehat{e}(T_{1i}+T_{0i},P)}}\hfill \\ & ={\displaystyle \frac{\widehat{e}((y_i+k)P,P)}{\widehat{e}(\frac{1}{x}(Y_i+\widehat{k}P+\left(x{y}_i\right)P+(x\widehat{k})P,P)}}\hfill \\ & ={\displaystyle \frac{\widehat{e}((y_i+k)P,P)}{\widehat{e}(\frac{1}{x}(y_i+\widehat{k})P+x(y_i+\widehat{k})P,P)}}\hfill \\ & ={\displaystyle \frac{\widehat{e}((y_i+k)P,P)}{\widehat{e}((y_i+\widehat{k})P,P)}}=1,ifk=\widehat{k}\hfill \end{array}$$

Aggregation.

Following receipt of the permission $(T_{0i},X)$ and request $(X,\widehat{k})$, the blockchain’s aggregation smart contact confirms that the $dr$ is a valid requester. The aggregation smart contact calculates $(E_{0ij}^{y_i}=\widehat{k}\oplus E_{5ij})$ if the validation is successful. The index set ($Z_i$, where $Z_i\in [1,n]$) is then where j is stored. It then extracts many keys from a collection of file indices (${\left\{Z_i\right\}}_{i\in [1,n]}$) that are shared by l distinct data generators ($dg$s) in the manner described below:

• $P_{agg}={\sum }_{j\in Z_i}{E}_{6ij}$
• $S_{agg}={\sum }_{j\in Z_i}{E}_{0ij}$

Next, it selects $w_i\in Z_q^{*}$ and computes multi-key aggregation as follows:

• $pp=w_{i}P$
• $P{P}_{agg}={\sum }_{i\in l}{P}_{agg}$
• $S{S}_{agg}={\sum }_{i\in l}{S}_{agg}$
• $S{P}_{agg}=H\left(w_{i}X\right)\oplus S{S}_{agg}$

Finally, it generates a trapdoor as follows:

• ${\mu }_0=P{P}_{agg}+T_{0i}$
• ${\mu }_1=E_{4ij}·\widehat{e}(P{P}_{agg},X^{-1})$

The blockchain sends $\vartheta =({\mu }_0,{\mu }_1,S{P}_{agg},pp)$ to the $dr$.

Token.

After receiving $\vartheta$ from the blockchain, the $dr$ utilizes its private key (x) and selects $u_i\in Z_q^{*}$ randomly to compute

• ${\tau }_1={\mu }_1^{u_i}$
• ${\tau }_2={\displaystyle \frac{u_i}{x}}{\mu }_0$

Then, the $dr$ sends $\tau =({\tau }_1,{\tau }_2)$ to the FS.

Phase 5: Search.

Upon acquiring the trapdoor ($\tau$) from the $dr$, the FS initially confirms its legitimacy by calculating the subsequent equation:

$$\alpha ={\displaystyle \frac{{\tau }_1}{\widehat{e}(E_{3ij}+{\tau }_2,P)}}=1$$

(3)

The FS combines several ciphertexts $(E_{agg}^1={\sum }_{i\in [1,n],j\in Z_i}{E}_{1ij},E_{agg}^2={\sum }_{i\in [1,n],j\in Z_i}{E}_{2ij})$ if the equation is true. Then, it sends the result $(E_{agg}^1,E_{agg}^2)$ to the $dr$, granting permission to access the original sensing data. If not, it rejects access to the data and aborts the outcome.

Correctness: The correctness of $\alpha$ is determined as follows:

$$\begin{array}{cc}\hfill \alpha & ={\displaystyle \frac{{\tau }_1}{\widehat{e}({\sum }_{i\in [1,l],j\in Z_i}{E}_{3ij}+{\tau }_2,P)}}\hfill \\ & ={\displaystyle \frac{{[E_{4ij}·\widehat{e}(P{P}_{agg},X^{-1})]}^{u_i}}{\widehat{e}(E_{3ij}+{\tau }_2,P)}}\hfill \\ & ={\displaystyle \frac{\widehat{e}{(E_{3ij},(y_i+k_i)P)}^{u_i}·\widehat{e}{(P{P}_{agg},X^{-1})}^{u_i}}{\widehat{e}(E_{3ij},P)\widehat{e}({\tau }_2,P)}}\hfill \\ & ={\displaystyle \frac{\widehat{e}{(r_{ij}P,(y_i+k_i)P)}^{u_i}·\widehat{e}{({\mathrm{\Sigma }}_{j\in Z_i}{E}_{6ij},\frac{1}{x}P)}^{u_i}}{\widehat{e}(E_{3ij},P)\widehat{e}(\frac{u_i}{x}{\mu }_0,P)}}\hfill \\ & ={\displaystyle \frac{\widehat{e}{(r_{ij}P,(y_i+k_i)P)}^{u_i}·\widehat{e}{({\mathrm{\Sigma }}_{j\in Z_i}{y}_i{\lambda }_j,\frac{1}{x}P)}^{u_i}}{\widehat{e}(E_{3ij},P)\widehat{e}(\frac{u_i}{x}(P{P}_{agg}+T_{0i}),P)}}\hfill \\ & ={\displaystyle \frac{\widehat{e}{(r_{ij}P,(y_i+k_i)P)}^{u_i}·\widehat{e}{({\mathrm{\Sigma }}_{j\in Z_i}{y}_i{\lambda }_j,\frac{1}{x}P)}^{u_i}}{\widehat{e}(E_{3ij},P)\widehat{e}(\frac{u_i}{x}P{P}_{agg},P)\widehat{e}(\frac{u_i}{x}{T}_{0i},P)}}\hfill \\ & ={\displaystyle \frac{\widehat{e}{({\mathrm{\Sigma }}_{j\in Z_i}{\lambda }_j+(y_i+k_i)P,P)}^{\frac{r_{ij}{y}_i{u}_i}{x}}}{\widehat{e}(E_{3ij},P)\widehat{e}(\frac{u_i}{x}{\mathrm{\Sigma }}_{j\in Z_i}{y}_i{\lambda }_j,P)\widehat{e}(u_i(y_i+\widehat{k})P,P)}}\hfill \\ & ={\displaystyle \frac{\widehat{e}{({\mathrm{\Sigma }}_{j\in Z_i}{\lambda }_j+(y_i+k_i)P,P)}^{\frac{r_{ij}{y}_i{u}_i}{x}}}{\widehat{e}(r_{ij}P,P)\widehat{e}{({\mathrm{\Sigma }}_{j\in Z_i}{\lambda }_j,P)}^{\frac{u_i{y}_i}{x}}\widehat{e}{((y_i+\widehat{k})P,P)}^{u_i}}}\hfill \\ & ={\displaystyle \frac{\widehat{e}{({\mathrm{\Sigma }}_{j\in Z_i}{\lambda }_j+(y_i+k_i)P,P)}^{\frac{r_{ij}{y}_i{u}_i}{x}}}{\widehat{e}{({\mathrm{\Sigma }}_{j\in Z_i}{\lambda }_j+(y_i+\widehat{k})P,P)}^{\frac{r_{ij}{u}_i{y}_i}{x}}}}\hfill \end{array}$$

Phase 6: Decryption.

Upon receiving ciphertexts $(E_{agg}^1,E_{agg}^2)$ from the FS, the $dr$ is able to access encrypted sensing data by using its private key (x) to perform the following computation:

• $S{S}_{agg}=S{P}_{agg}H\left(xpp\right)$
• $d_i=S{S}_{agg}\oplus E_{agg}^1$

This algorithm provides the $dr$ with a lightweight decryption process.

5. Security Analysis

This section will evaluate the effectiveness of the proposed solution in meeting its security objectives.

5.1. Secure Search

When a search is secure, it can withstand keyword selection attacks. For instance, an attacker may select specific terms to deduce or reveal private information.

Theorem 1. 

Under the DBDH assumption, the proposed solution is capable of withstanding the specified keyword attacks.

Proof. 

The chosen keyword attack (CKA) game can be won with a minimal advantage, denoted as $xi$, if $\mathcal{A}$ is a polynomial-time adversary. To participate in the CKA game with $\mathcal{A}$, we construct a challenger ($\mathcal{C}$) within a bilinear group. □

Setup. The system parameters ($P_t=\{q,\mathcal{G},\mathbb{G},\widehat{e},P,{\{{\lambda }_j\}}_{i\in [1,n]},{\hslash }_1,{\hslash }_2,H,K\}$) are calculated by $\mathcal{C}$. $\mathcal{C}$ creates an aggregate key $P{P}_{agg}={\sum }_{i\in l}{P}_{agg}$ for file set $Z_i$. It then chooses a value ($y_i\in Z_q^{*}$) at random and computes $Y_i={\left\{y_i^{j}P\right\}}_{j\in [1,n]}$. The file set $(P_t,P{P}_{agg},Y_i)$ is sent to $\mathcal{A}$, together with the public parameters and public key, by $\mathcal{C}$.

Phase 1. Some inquiries are performed by $\mathcal{A}$.

Query 1. The adversary ($\mathcal{A}$) uses the phrase expressed as $\widehat{k}\in K$ to query a token. Using a random number ($y_i$) as his private key, $\mathcal{C}$ computes the following:

${\left\{T_{0i}\right\}}_{i\in [1,k]}=\left(x{\mathrm{\Pi }}_{\widehat{k}\ne k}{y}_i\right)P+\left(x{\Pi }_{\widehat{k}\ne k}\widehat{k}\right)P$

It then sends $T_i=\left({\{T_{0i},T_{1i}\}}_{i\in [1,l]}\right)$ to $\mathcal{A}$.

Query 2. Using a collection of files ($Z_i$), the adversary ($\mathcal{A}$) executes aggregate queries. $\mathcal{C}$ transmits $(P{P}_{agg},S{S}_{agg})$ to $\mathcal{A}$ and responds to the aggregation key as follows: ($P{P}_{agg}={\sum }_{i\in l}{P}_{agg},S{S}_{agg}={\sum }_{i\in l}{S}_{agg})$.

Query 3.

$\mathcal{A}$ uses phrase $\widehat{k}$ to execute a trapdoor query. After computing $\tau =({\tau }_1,{\tau }_2)$, $\mathcal{C}$ forwards the result to $\mathcal{A}$.

Challenge. Two keywords $(k_0,k_1)$ are chosen by $\mathcal{A}$, where $(k\ne k_0\ne k_1)$. $\mathcal{C}$ aborts and makes a random guess if $k_0=k_1$. If not, $\mathcal{C}$ computes the keyword ciphertext for $k_b$ by randomly selecting a bit ($b\in \{0,1\}$). $\mathcal{C}$ sets $(E_{3ij},E_{4ij})$ after selecting a random number ($r_{ij}\in Z_q^{*}$), which it sends to $\mathcal{A}$; it then sends $E_{ij}=({\{E_{3ij},E_{4ij}\}}_{j\in [1,n]})$.

Phase 2. As in step 1, $\mathcal{C}$ answers the questions. The trapdoor $(·)$ on query terms $k_0$ and $k_1$ cannot be issued by $\mathcal{A}$.

Guess. A guess ($b\in \{0,1\}$) is sent to $\mathcal{C}$ by $\mathcal{A}$. $\mathcal{A}$ is the winner of the game if $b^{\prime }=b$, meaning that $\widehat{e}({\lambda }_j,(y_i,k_b)r_{ij}P)=\widehat{e}{(P,P)}^{\theta }$. In any other case, $\mathcal{A}$ loses the game.

In the guessing phase, the ciphertext ($E_{ij}$) is a correct keyword ciphertext of keyword $k_y$ if $\widehat{e}({\lambda }_j,(y_i,k_b)r_{ij}P)=\widehat{e}{(P,P)}^{\theta }$. In this instance, the DBDH problem is solved by $\mathcal{A}$ with a minor $\xi$ benefit. That aligns with the DBDH presumption. Therefore, the suggested plan may withstand the ASCunder the DBDH assumption.

5.2. Accountability

Definition. Accountability indicates that the token’s keyword derives from a single authorized term. It encompasses the scenario in which an adversary can forge proof for a legitimate token.

Theorem 2. 

According to the $(f,n)$-DHE assumption, the suggested approach can guarantee accountability.

Proof. 

Suppose that an adversary ($\mathcal{A}$) can solve the $(f,n)$-DHE problem in polynomial time with a negligible advantage (${\xi }^{\prime }$). Using $\mathcal{A}$ [12], we develop a $\mathcal{C}$ solution to the $(f,n)$-DH problem. □

Setup. The system parameters ($P_t=\{P,{\left\{{\lambda }_j\right\}}_{i\in [1,n]}\}$) are calculated by $\mathcal{C}$. A random number ($y_i$) is chosen using $\mathcal{C}$, which then computes $Y_i={\left\{y_i^{j}P\right\}}_{j\in [1,n]}$. A public key $(P_t,Y_i)$ is then submitted to $\mathcal{A}$.

Challenge. Two keyword sets $({\overline{k}}_1,{\overline{k}}_2)$ are selected by $\mathcal{A}$, where ${\overline{k}}_1\le n$ and ${\overline{k}}_1>1$. $\mathcal{C}$ computes the token $(T_{0i},T_{1i})$ by selecting a value (x) at random as the private key of the $dr$. The token $(T_{0i},T_{1i})$ is then sent to $\mathcal{A}$ by $\mathcal{C}$.

Win. $\mathcal{C}$ can solve the $(f,n)$-DHE problem with the corresponding negligible advantage (${\xi }^{\prime }$) if the $\mathcal{A}$ has a negligible advantage (${\xi }^{\prime }$) in breaching accountability. Consequently, accountability can be realized by the suggested plan.

5.3. Decryption

Data generators encrypt the file ($E=({\{E_{1ij},E_{2ij},E_{3ij},E_{4ij}\}}_{j\in [1,n]})$) with the suggested framework. They then transmit the ciphertext (E) to the FS in order to exchange sensing data. The $dr$ uses its private key (x) to decrypt $S{P}_{agg}$ and retrieve the symmetric key ($S{S}_{agg}$) after receiving the result $(E_{agg}^1,E_{agg}^2)$ from the FS. After that, the $dr$ computes $d_i=S{S}_{agg}\oplus E_{agg}^1$ to retrieve the sensing data. Therefore, the suggested plan prevents a third party from decrypting the ciphertext.

5.4. Access Control

Assume that l data generators ($dg=\{d{g}_i,i\in [1,l]\}$) are involved in the system in the suggested manner. Data generators create a search trapdoor for the $dr$ using an $SC$ in the blockchain to accomplish access control. First, each data generator checks ${\phi }_i$ to confirm that the keyword ($\widehat{k}\in K$) is genuine. The aggregated contract calculates $(E_{0ij}^{y_i}=\widehat{k}\oplus E_{5ij})$ after obtaining the data generators’ authorization $(T_{0i},X)$ and request $(X,\widehat{k})$. It then extracts the corresponding file keys $(P_{agg},S_{agg})$ that compose the targeted keyword ($\widehat{k}$) in the file set ($Z_i$). After that, using a searchable key ($P{P}_{agg}$) for the permitted $dr$, it creates a search trapdoor ($\tau =({\tau }_1,{\tau }_2)$). Only the authorized $dr$ may use the search trapdoor (${\tau }_2$) to look for term $\widehat{k}$. Nevertheless, the $dr$ is unable to generate additional trapdoors for a new set (${Z\prime }_i$) and search for ks in files that have nothing to do with recognized trapdoors. Additionally, the plan creates a search trapdoor and extracts the relevant file keys using the aggregate $SC$. Thus, access control can be achieved with our technique.

5.5. Requester Privacy

A keyword token ($T_i=\left({\{T_{0i},T_{1i}\}}_{i\in [1,l]}\right)$) is created to safeguard the $dr$’s keyword privacy. The data generator checks to see if the keyword is $\widehat{k}\in K$ when it receives $T_i$ from the $dr$. The data generator does not pick up any keyword information from $T_i$ during this operation. Additionally, the aggregated contract creates a search trapdoor (${\tau }_2$) and aggregates several keys in a searchable key $P_{agg}$. Following receipt of the trapdoor ($\tau$), the FS computes $\alpha$ to confirm its authenticity. If it is found to be legitimate, it aggregates several ciphertexts $(E_{agg}^1,E_{agg}^2)$. The original sensing data are then made available to the $dr$ by sending the result $(E_{agg}^1,E_{agg}^2)$. During the $dr$’s searching process, data generators and the FS are completely unaware of any information regarding files or keywords. This prevents any private information pertaining to the $dr$’s keywords from being accessed by data generators or the FS. Thus, the secrecy of the $dr$ is successfully protected.

6. Performance Evaluation

Hyperledger Caliper Fabric was utilized as the blockchain network technology in this study. We implemented the proposed cryptographic techniques using Java and the JPBC package. We then analyzed the communication and computational overheads of the proposed scheme. Additionally, we implemented the $SC$ on Hyperledger Caliper and assessed its blockchain performance [24].

We built a consortium blockchain using the Hyperledger Caliper Fabric v2.0 platform. The test environment comprises four peers and three orderers, representing both peer and orderer organizations. The peer organizations provide $SC$ capabilities and process transactions for regular clients, while the orderer organization consists of consensus nodes that package and rank transactions. In this testing environment, ordering services are facilitated through the Raft consensus algorithm. The virtual environment is set up and managed using Docker and Docker Compose. To develop an $SC$ that executes within the designated channel inside a Docker container, we utilize Go version 1.18.7. The client tests the $SC$ and uploads transactions to the blockchain.

6.1. Comparison of Security Properties

This section compares the security features of the proposed scheme with those of other studies, including those by Jihyeon et al. [25], Haijiang et al. [26], Liu et al. [19], and Ali et al. [24]. Ali et al. [24] proposed a homomorphic encryption strategy to ensure secure searching and keyword-based access to the database, as indicated in

Table 2. Comparison of security properties.

Property	Ali et al. [24]	Liu et al. [19]	Haijiang et al. [26]	Jihyeon et al. [25]	Proposed
Secure search	√	√	√	√	√
Accountability	×	×	×	×	√
Access control	√	√	√	√	√
Requester privacy	×	×	×	×	√
Key-leakage resistance	√	√	×	√	√
Dual verifiable search	×	×	×	×	√

.

This plan is effective for approved data searches and IoT data sharing, yet it was not built for multiple-generator searches. Liu et al. [19] introduced FB-IAV, a searchable encryption system that utilizes key aggregation and auxiliary input, facilitating the secure sharing of encrypted data. Nevertheless, the secret information associated with the $dr$ keyword is not adequately protected. Haijiang et al. [26] introduced an efficient attribute-based data encryption system with a concealed strategy to achieve restricted access. However, this initiative suffers from inadequate key management. Jihyeon et al. [25] also implemented a blockchain and aggregated key method with mutual authentication to provide access control and verifiable search. However, this approach incurs significant computational costs due to its authentication algorithm. Among the five proposed plans, only the suggested plan can ensure both accountability and the protection of requester privacy.

6.2. Communication Overhead

The sizes of the environmental data ciphertexts, denoted as $|{\mathbf{E}}_{sym}|$, $\left|\mathbf{E}\right|$, $\left|\mathcal{G}\right|$, $\left|\mathbb{G}\right|$, and $\left|Z\right|$ bytes, respectively, indicate that $E=({\{E_{1ij},E_{2ij},E_{3ij},E_{4ij}\}}_{j\in [1,n]})$ is a component in $\mathcal{G}$, $\mathbb{G}$, and $Z_q$.

Table 3. Communication overhead of the proposed scheme.

Scheme	Aggregate	Trapdoor	Searching	Encryption
Liu et al. [19]	$2\left|\mathcal{G}\right|$	$2\left|\mathcal{G}\right|$	$3\left|\mathcal{G}\right|+2\left|\mathbb{G}\right|$	$n3\left(\right|\mathcal{G}|+|\mathbb{G}\left|\right)$
Jihyeon et al. [25]	$3\left|\mathcal{G}\right|$	$2\left|\mathcal{G}\right|$	$l\left(4\right|\mathcal{G}|+2|\mathbb{G}|+|Z\left|\right)$	$n\left(4\right|\mathcal{G}|+|\mathbb{G}|+2|Z\left|\right)$
Proposed scheme	$|{\mathbf{E}}_{sym}|+|\mathcal{G}|$	$\left|\mathcal{G}\right|$	$|{\mathbf{E}}_{sym}|+|\mathbf{E}|$	$n\left(\right|{\mathbf{E}}_{sym}|+|\mathbf{E}|+|\mathcal{G}|+|\mathbb{G}\left|\right)$

illustrates the four stages of communication costs: ciphertexts, aggregation, trapdoor, and search. While current techniques typically consider only one $d{g}_i$, the proposed scheme accommodates multiple $d{g}_i$s. Consequently, we focus on a single $d{g}_i$ here for comparison with other methods. During the ciphertext phase, the $d{g}_i$ transmits k ciphertexts and environmental ciphertexts $(E_{d_i},k)$ to the FS for storage. With n representing the number of files, these ciphertexts’ overall length is $n\left(\right|{\mathbf{E}}_{sym}|+|\mathbf{E}|+|\mathcal{G}|+|\mathbb{G}\left|\right)$ bytes. The length of the encrypted symmetric key and trapdoor $(T_i,S{P}_{agg})$ sent to the $dr$ by the aggregation $SC$ during the aggregation phase is $|{\mathbf{E}}_{sym}|+|\mathcal{G}|$ bytes. The $dr$ then provides a search trapdoor ($T_i$) to the FS after recovering the trapdoor using the private key. The trapdoor’s overall length is $\left|\mathcal{G}\right|$ bytes.In the process of the search, the FS provides the matching environmental data ciphertexts ($E_i$) to the $dr$. The length for the data search is $|{\mathbf{E}}_{sym}|+|\mathbf{E}|$ bytes.

We evaluate the communication overhead against two comparable systems, represented by the number of n files: those proposed by Liu et al. [19] and Jihyeon et al. [25]. Compared to the method of Liu et al. [19], the proposed solution incurs a higher communication overhead during the ciphertext phase, as indicated in Table 3. In the trapdoor phase, the method proposed by Jihyeon et al. [25] outperforms the proposed scheme in terms of communication costs. However, in contrast to the other two strategies, the proposed scheme incurs only a minimal transmission cost during the data search.

In summary, regarding communication overhead during the search phase, the recommended method outperforms both of the proposed alternatives.

6.3. Computational Cost

By altering the quantity of files and $d{g}_i$ in

Table 4. Computational cost of the proposed scheme.

Algorithm	Trapdoor	Search	Encryption	Encryption
$n=100$ and $l=40$	27	53	5160	9
$l=100$ and $n=100$	27	53	5160	9

, we used the cryptographic primitives and assessed the computational cost of the suggested algorithms. We can calculate the computing cost of the proposed design using this method. The proposed technique uses the Encrypt algorithm to construct keyword ciphertexts (k) and environmental data ciphertexts ($E_{d_i}$). To ascertain whether the keyword in the token ($\tau$) provided by the $dr$ is a member of the keyword set (K), the $d{g}_i$ performs a verification process.The $dr$ can utilize the Trapdoor algorithm to obtain a trapdoor ($T_i$) if the verification is successful. The trapdoor ($T_i$) is then sent to the FS, enabling the Search algorithm to efficiently locate the desired keywords. Finally, the $dr$ decrypts the environmental data ciphertexts ($E_{d_i}^{\prime }$) using the symmetric key ($S{S}_{agg}$) in the decryption and verification procedures.

As shown in Table 4, we ran the algorithms with a file count of 100 and a total of 40 data generators ($l=40$) in each situation. We observe that the amount of files (n) affects the computational costs of all algorithms, as they all operate with the files. Additionally, we used 100 $d{g}_i$s to implement the algorithms while keeping the file count at $n=100$. The findings show that when the number of $d{g}_i$ rises, the computational costs of the encryption, trapdoor, decryption, and verification algorithms remain effective. The reason for this efficiency is that these algorithms use the $d{g}_i$ values of information to execute pairing computations.

Additionally, the computational cost analysis of each algorithm in the proposed scheme is compared with other relevant studies. While maintaining a fixed graph degree for the $d{g}_i$, amounting to $l=40$, the methods proposed by Liu et al. [19] and Jihyeon et al. [25] are taken into consideration. As illustrated in Figure 2, the computation cost of encryption for each solution fluctuates in direct proportion to the quantity of files, denoted as n.

Among the three schemes, Liu et al.’s [19] scheme incurs the highest computational cost. This is primarily due to its reliance on a greater number of bilinear operations in comparison with the other works. Additionally, the trapdoor algorithm in the scheme proposed by Oh et al. [25] necessitates extra computations operations, further increasing its cost relative to that of Liu et al.’s [19] scheme and the proposed scheme.

With a file size of $n=100$, we examine the computational cost of each procedure for different values of $d{g}_i$ and l. For the methods proposed by Liu et al. [19] and Jihyeon et al. [25], the computational cost of encryption is significantly higher than that of the proposed approach, as illustrated in Figure 2. As the number of $d{g}_i$s increases, the computational cost exhibits a linear rise. This is due to the encryption technique employed in the proposed system, which requires relatively few hash functions and bilinear pairing computations. Jihyeon et al. [25] and Liu et al. [19] indicated that the trapdoor algorithm incurs a greater computational cost than the proposed scheme, as it necessitates more complex calculations. According to Jihyeon et al. [25], each $d{g}_i$ must perform several bilinear pairing operations during the search process. Consequently, the computational cost increases with the number of $d{g}_i$s because additional bilinear pairing operations are required. In contrast, the computational cost of the proposed strategy remains constant, as it is independent of the number of $d{g}_i$s. According Liu et al. [19] assert that the decryption and verification algorithm has a higher computational cost than the other two systems. This is attributed to the use of bilinear pairing operations, which escalate computing costs as the number of $d{g}_i$s increases. However, since the proposed strategy does not utilize bilinear pairing operations, it has the lowest computational cost. The comparisons presented above indicate that the proposed method is less computationally expensive than the other two methods.

6.4. Smart Contract Time Consumption

The time needed to send a transaction to the blockchain is impacted by the size of the data. In this investigation, we look at a number of blockchain-based $SC$ functions that transfer data. $l\left(\right|\mathcal{G}|+|\mathbf{E}|$, $\left|\mathcal{G}\right|$, and $\left(\right|\mathcal{G}|+|\mathbf{E}\left|\right)$ bytes are the lengths of the key-aggregate, key-extract, and trapdoor-aggregate functions, respectively. Let $l=10$ stand for the number of $d{g}_i$s in this case for $\left|\mathcal{G}\right|$ and $\left|\mathbf{E}\right|$. The lengths of the transactions are 560, 57, and 27 bytes for the extract key, aggregate key, and aggregate trapdoor, respectively. We utilize the Hyperledger Fabric platform to execute these transactions. The time overheads are presented in

Table 5. Computational cost of the proposed scheme.

Metric	Key Extract	Key Aggregate	Trapdoor Aggregate
Transaction size (bytes)	560	57	27
Execution time (ms)	$68.20$	$59.70$	$31.70$

, where the execution times for the key-extract, key-aggregate, and trapdoor-aggregate functions are $68.20$ ms, $59.70$ ms, and $31.70$ ms, respectively.

7. Conclusions

In this paper, we present a novel multi-keyword searchable scheme for FB-IAV utilizing a verified blockchain. First, we introduce a multi-keyword aggregation (MKA) technique that securely aggregates keys by leveraging blockchain technology and keyword search encryption (KSE). This approach employs an oblivious method to prevent vehicles from accessing the keyword information of the $dr$. Second, we propose a dual-verifiable technique that does not rely on bilinear pairing, thereby providing lightweight verification for search results. Furthermore, the proposed scheme underwent rigorous security analysis and verification, demonstrating its ability to achieve the desired security objectives. We also conducted a comprehensive assessment of communication and computation costs. To validate the effectiveness and feasibility of the proposed scheme, we tested resource consumption and deployed the smart contract on the Hyperledger platform.