Modeling and Reliability Evaluation of the Motion and Fluid Flow Characteristics of Spark Bubbles in a Tube
Abstract
1. Introduction
2. Materials and Methods
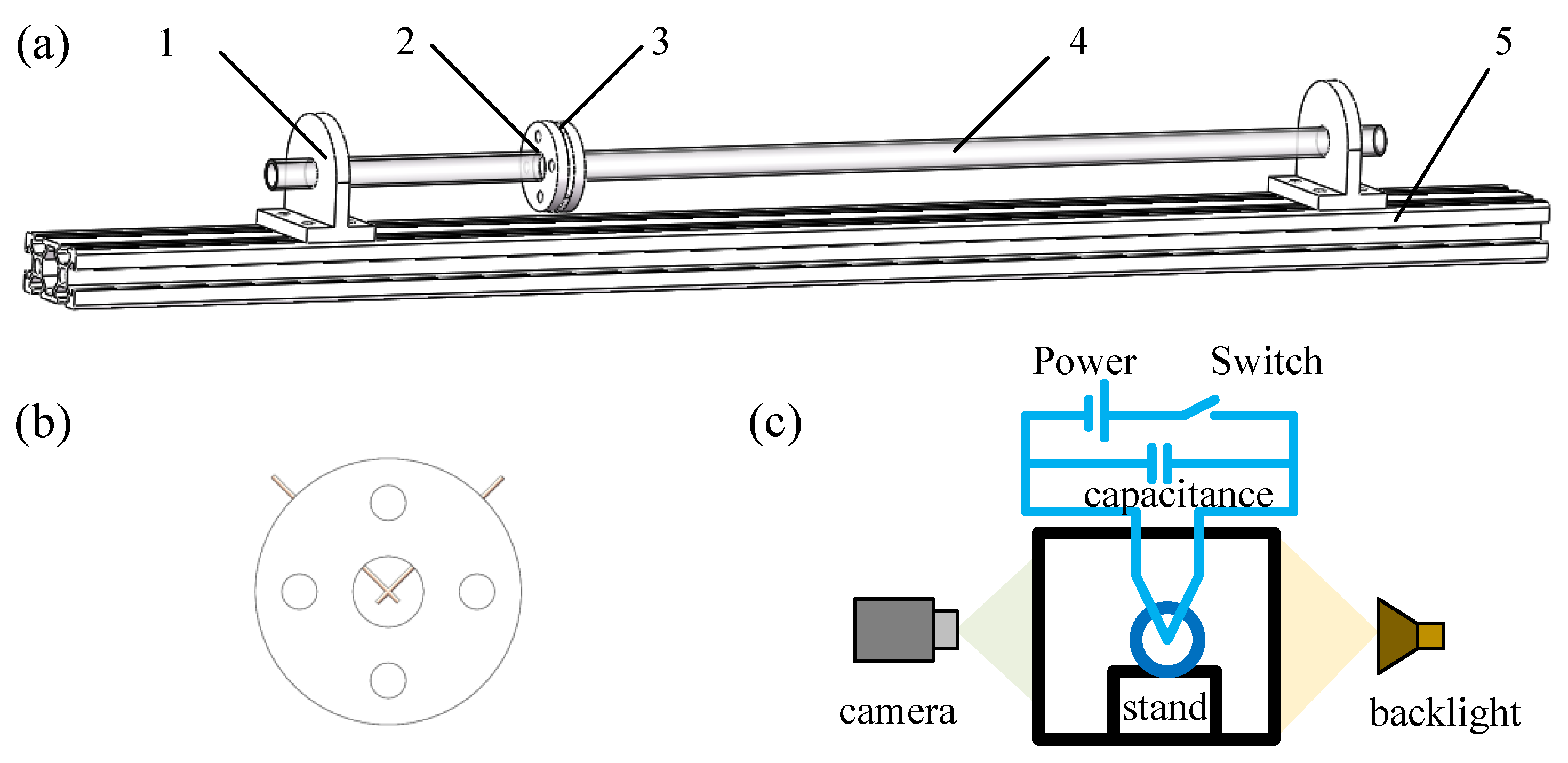
2.1. Experimental Setup
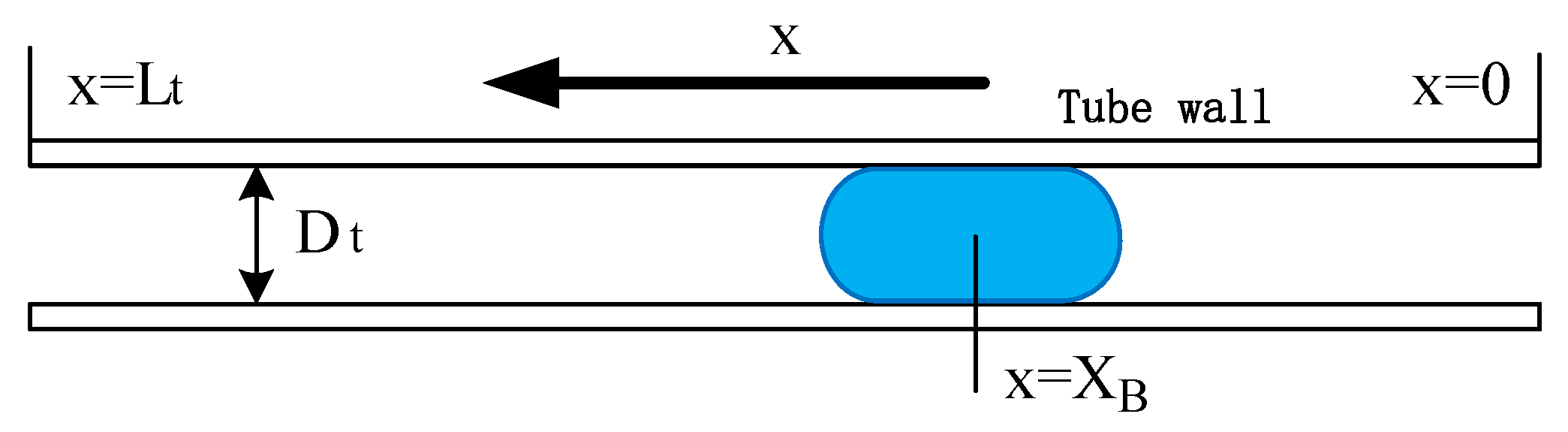
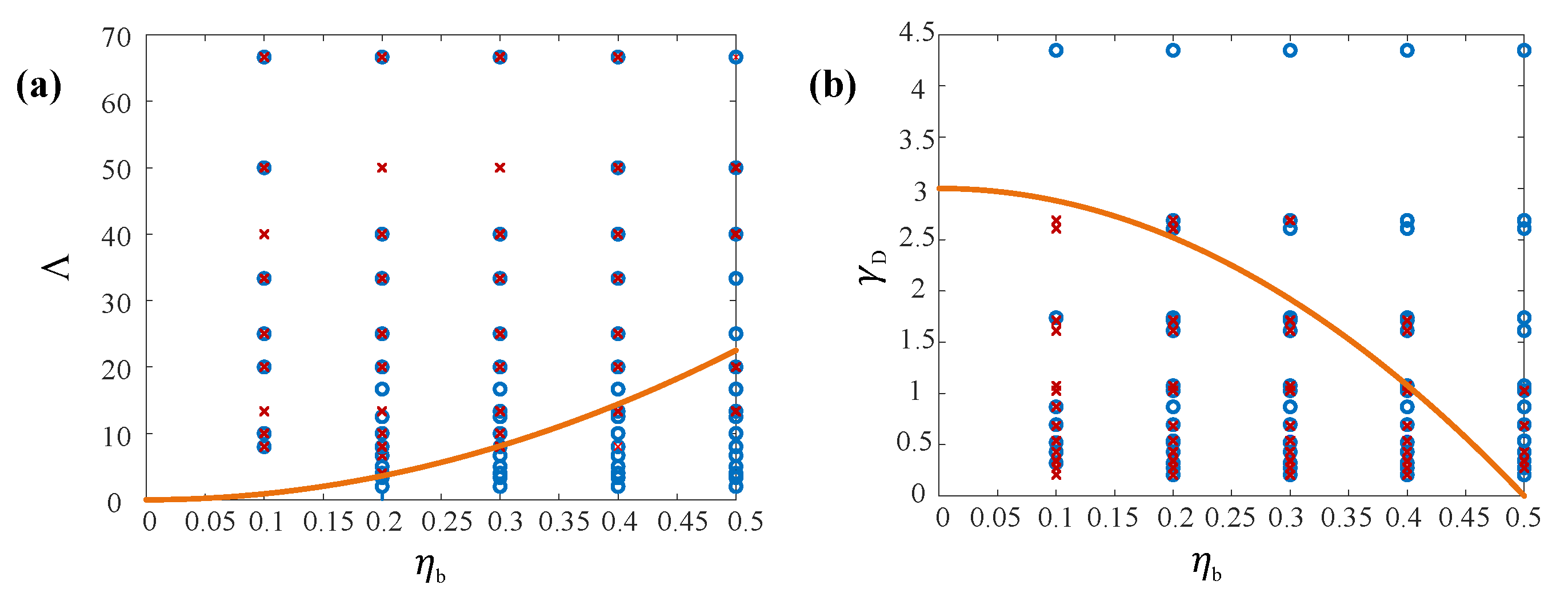
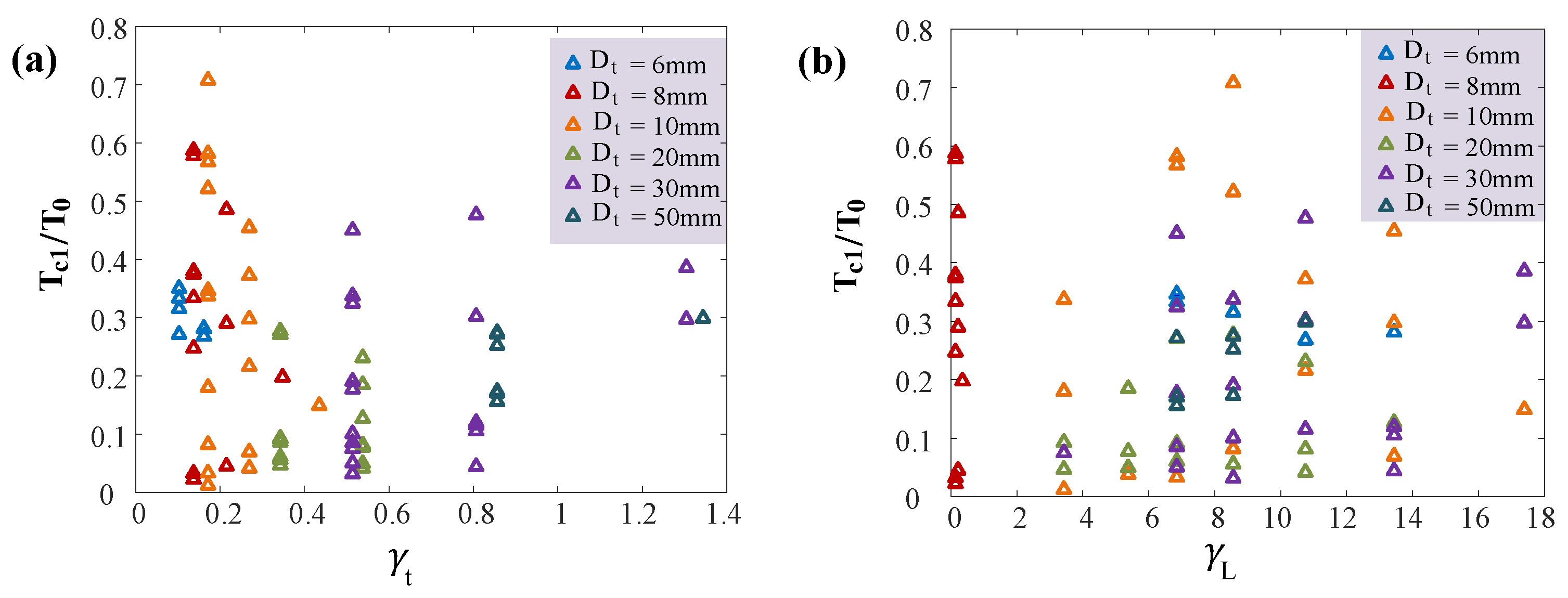
2.2. Dimensionless Parameters
3. Numerical Simulation Verification of Bubble Morphology in Tubes
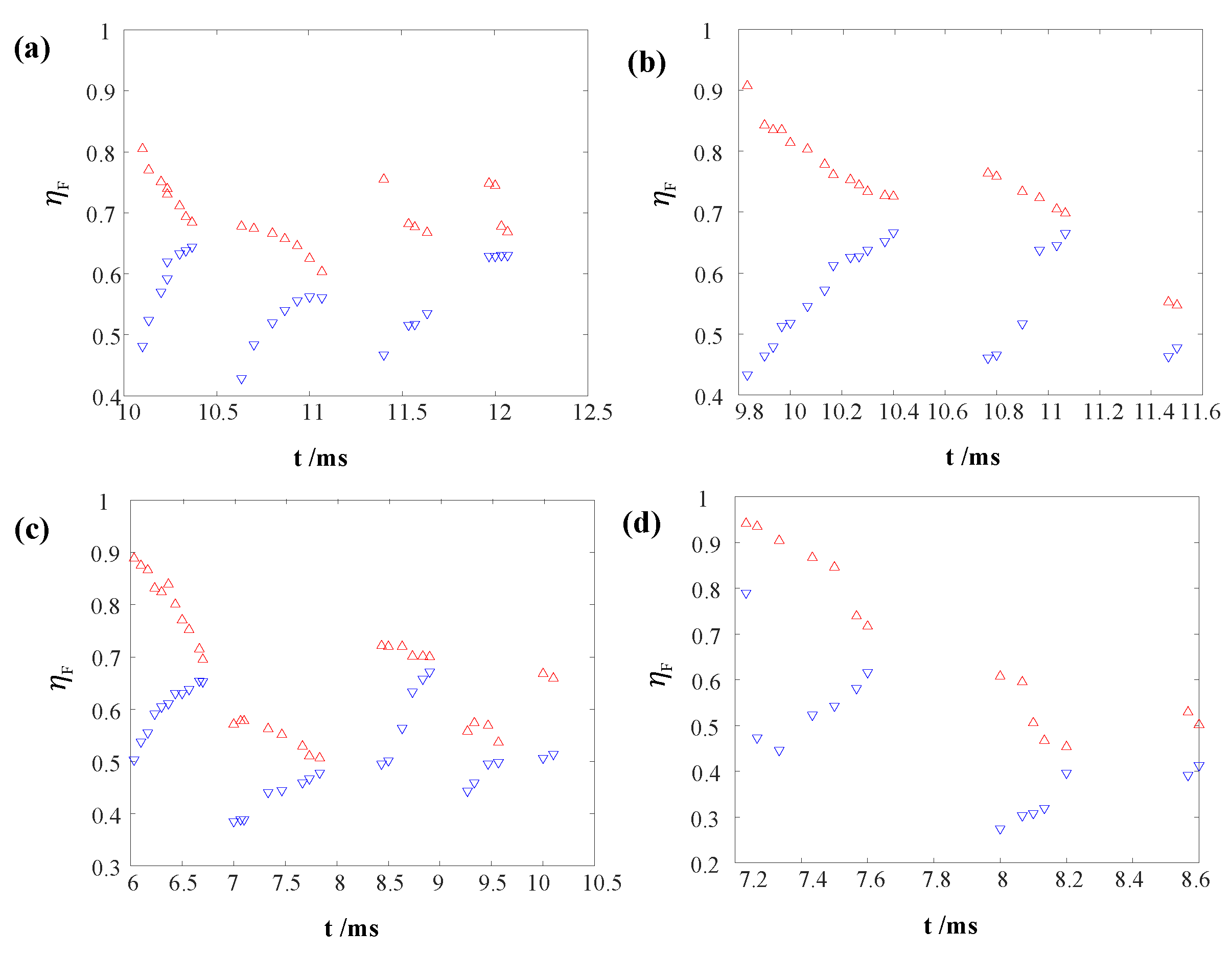
4. Dynamic Characteristics of a Bubble in Short Tubes
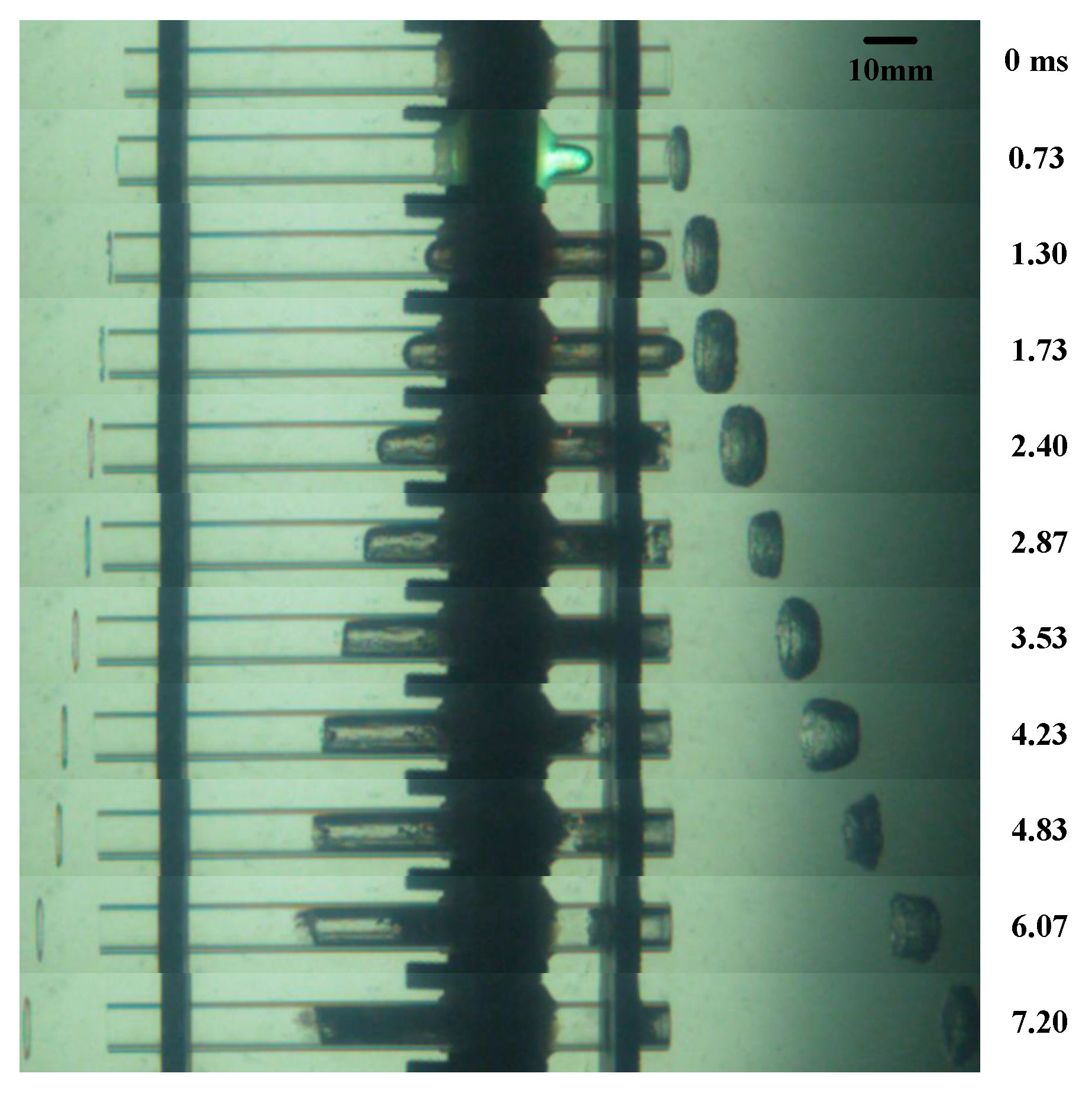
4.1. Bubble Collapse
4.1.1. Symmetric Bubble Collapse
4.1.2. Asymmetric Bubble Collapse
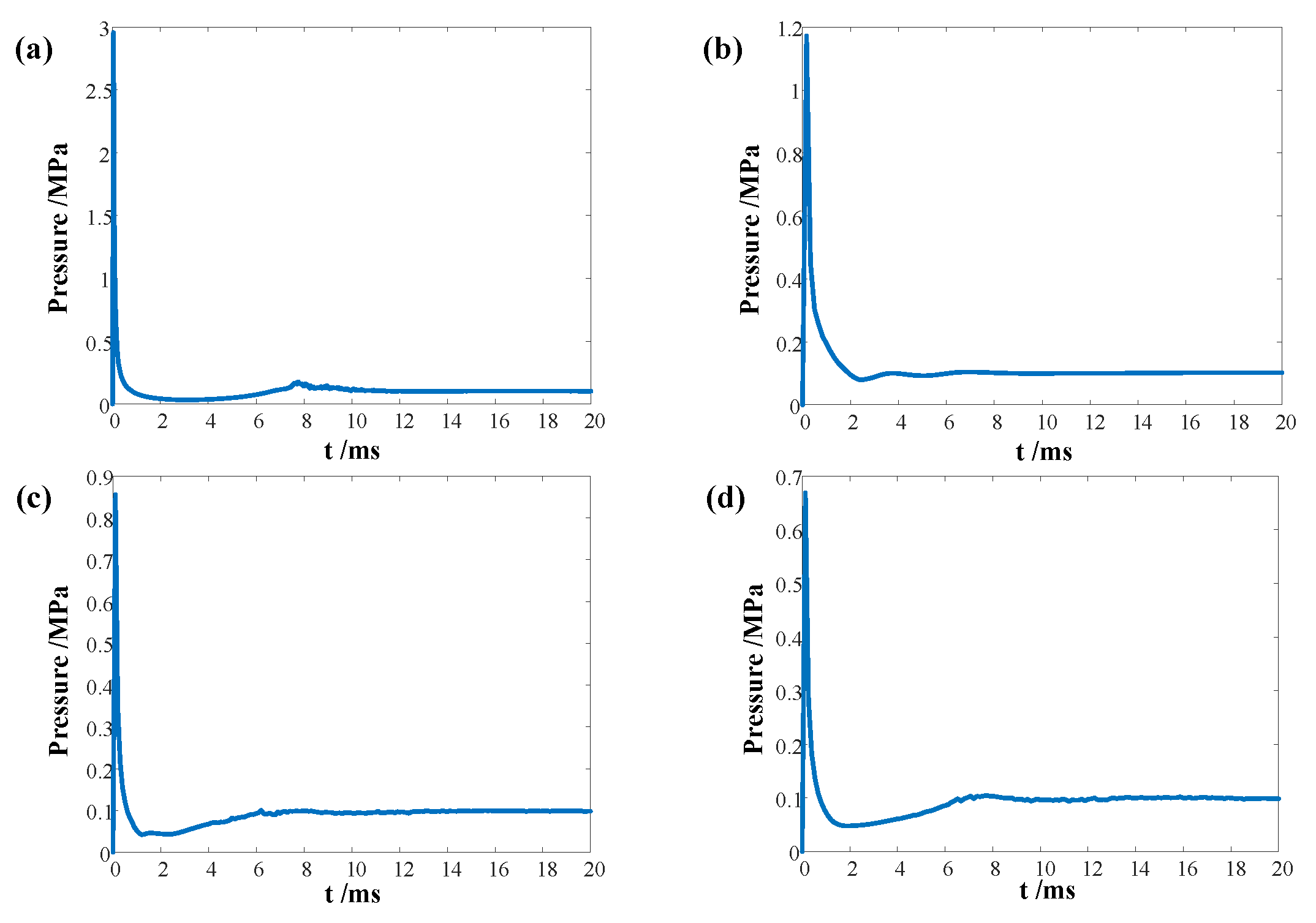
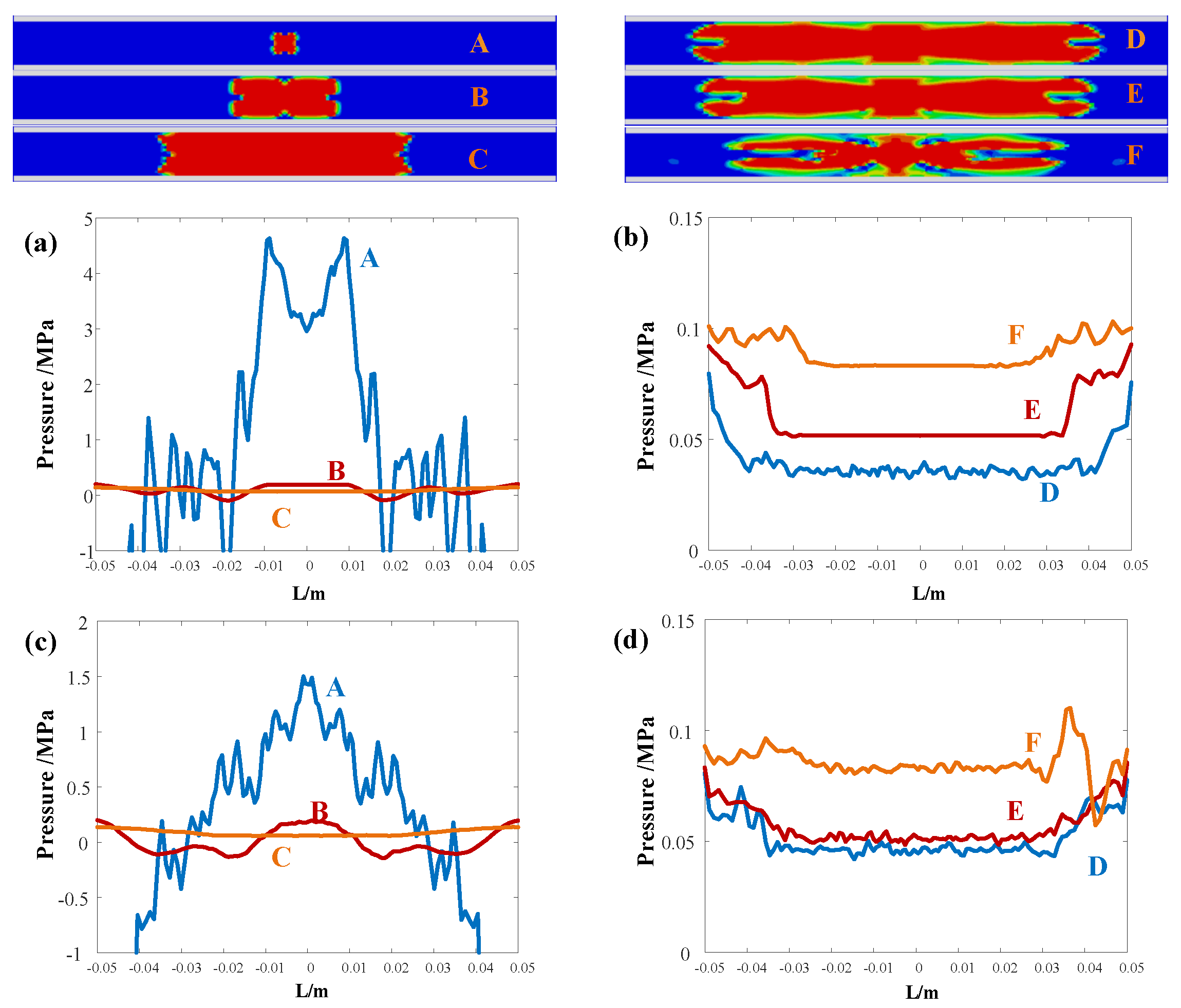
4.2. Pressure in the Tube
4.3. Vortex Ring Oscillation Period
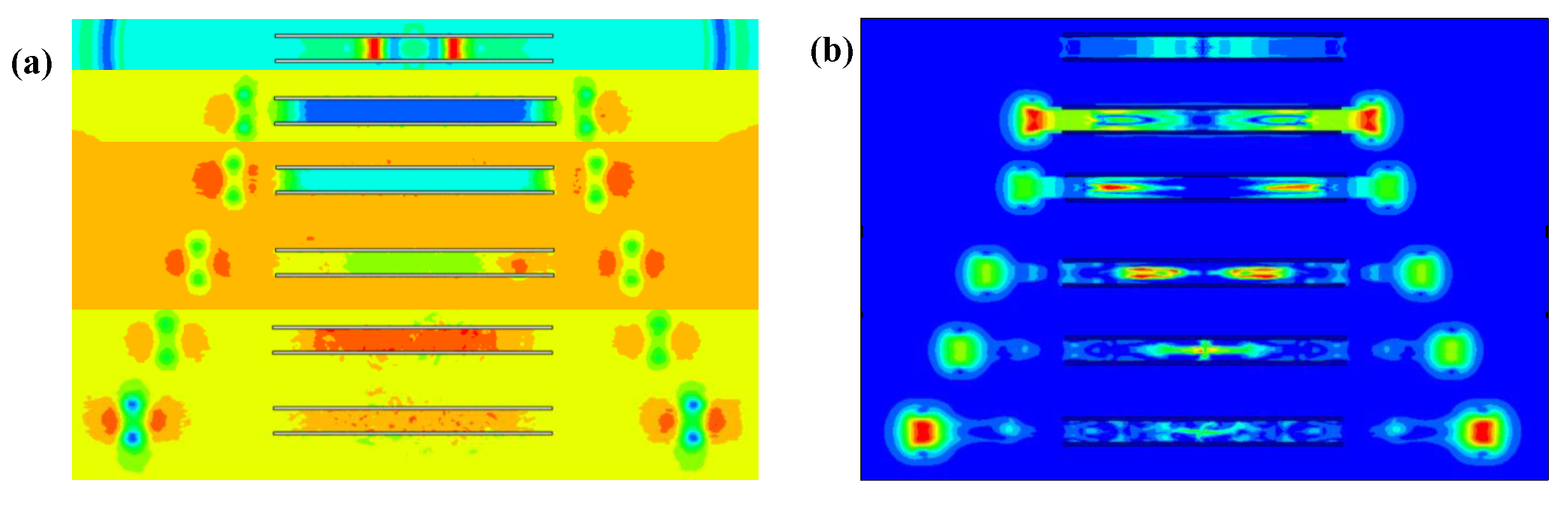
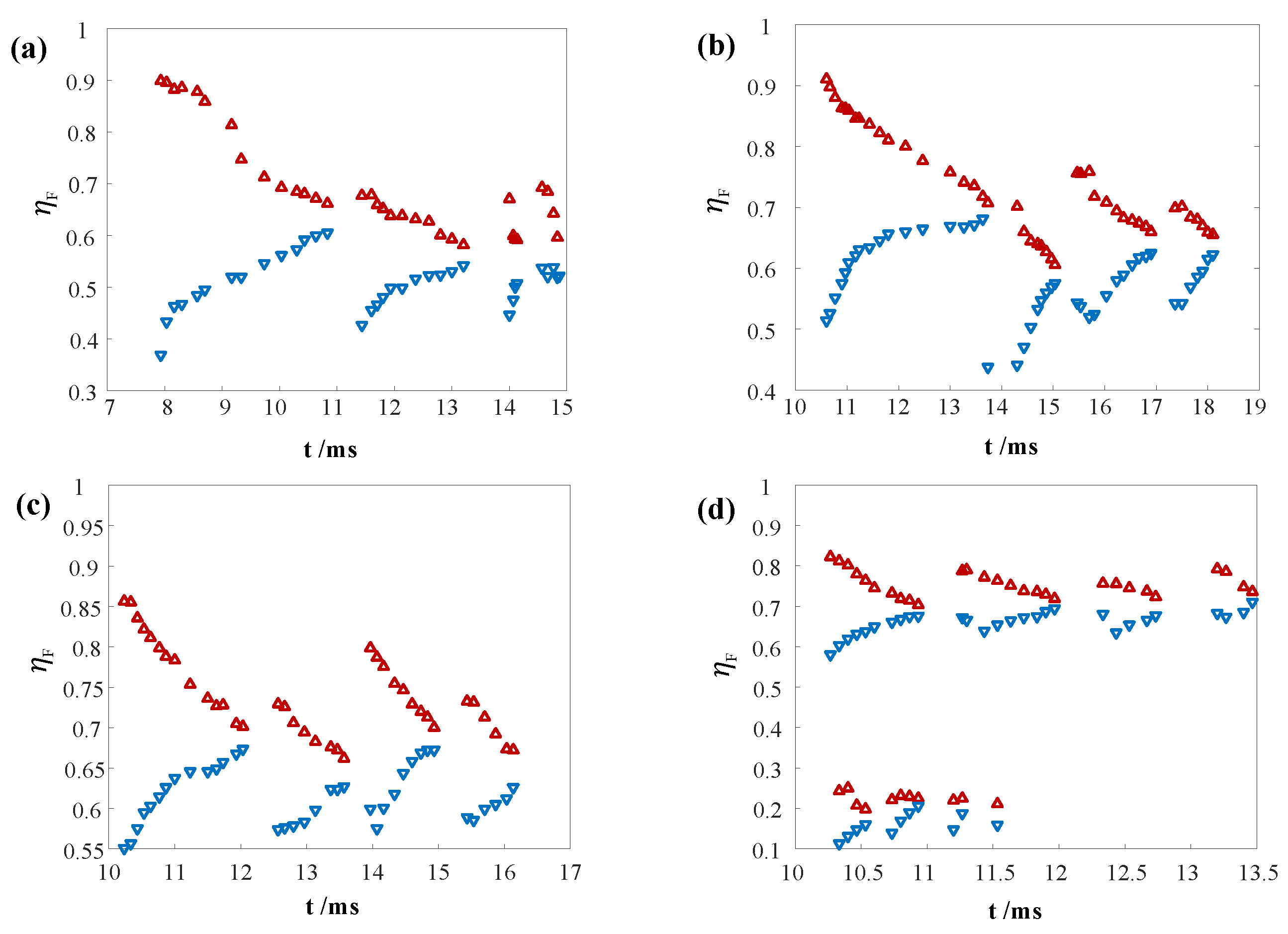
5. Dynamic Characteristics of a Bubble in Longer Tubes
5.1. Bubble Collapse
5.1.1. Symmetric Bubble Collapse
5.1.2. Asymmetric Bubble Collapse
5.2. Discovery of Secondary Cavitation
6. Dynamic Characteristics of a Bubble in Long Tubes
6.1. Bubble Collapse
6.1.1. Symmetrical Bubble Collapse
6.1.2. Asymmetric Bubble Collapse
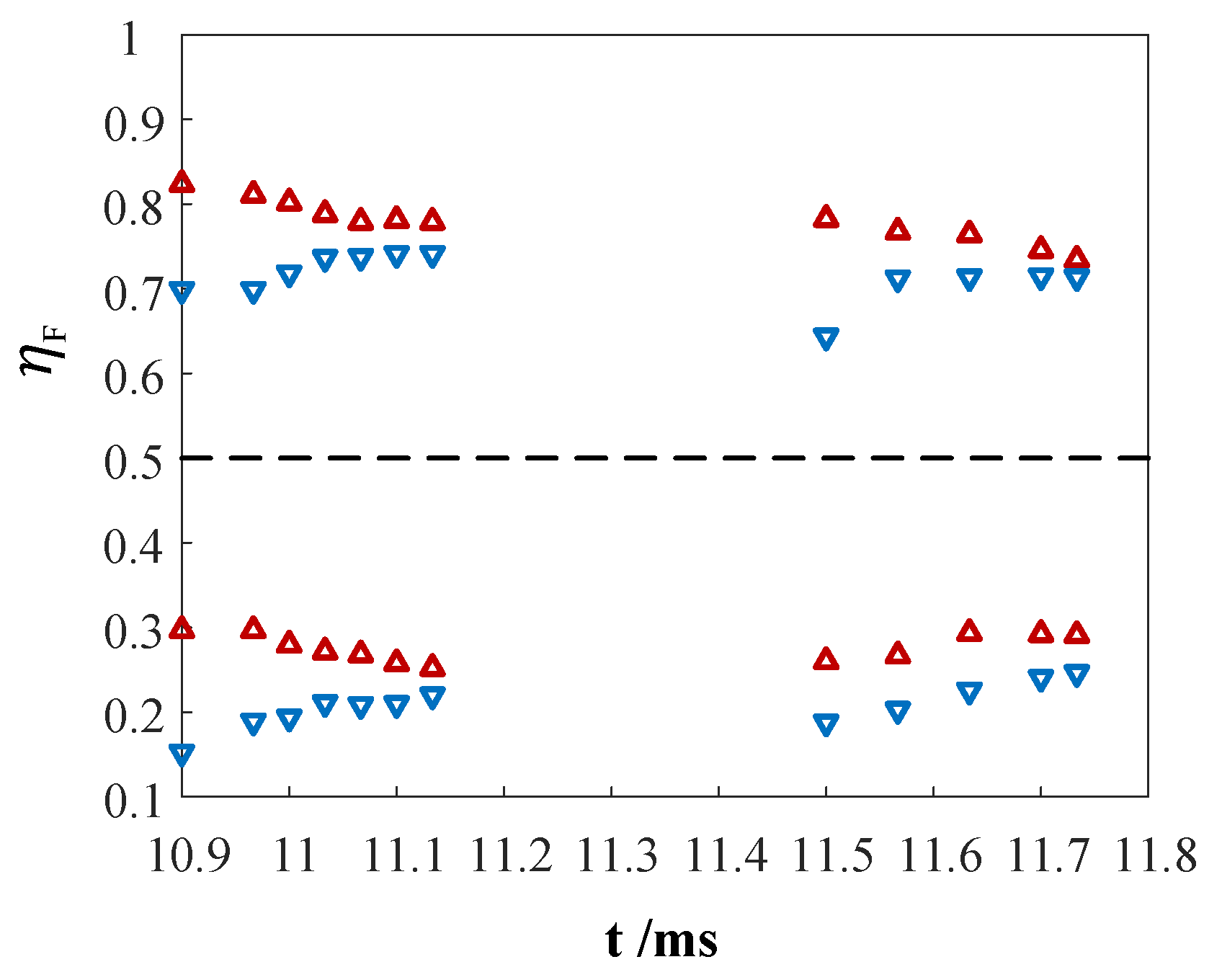
6.2. Multiple Cavitation
6.2.1. Conditions for the Generation of Multiple Cavitations
6.2.2. Multiple Cavitation Generation Position
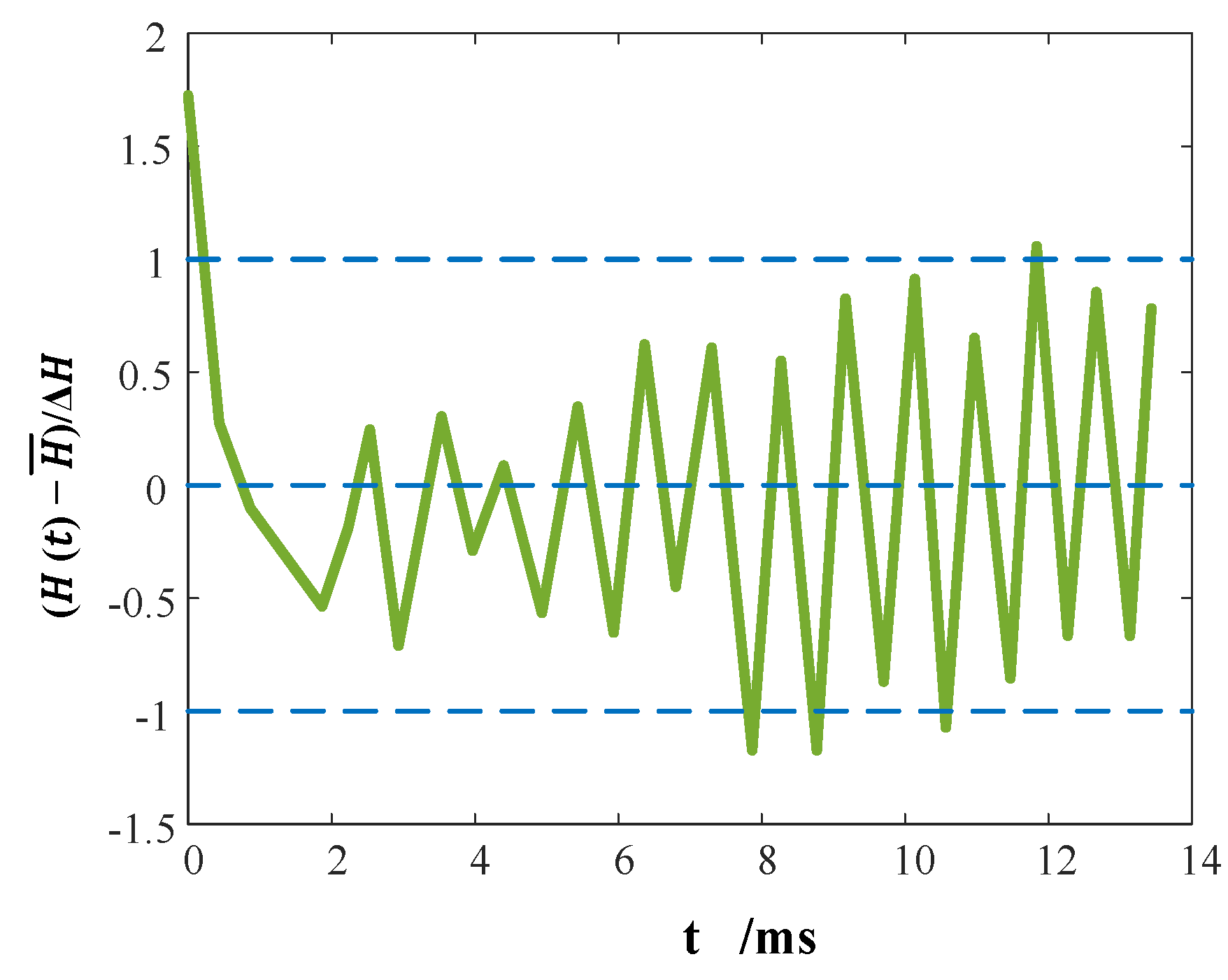
6.2.3. Multiple Cavitation Cycles
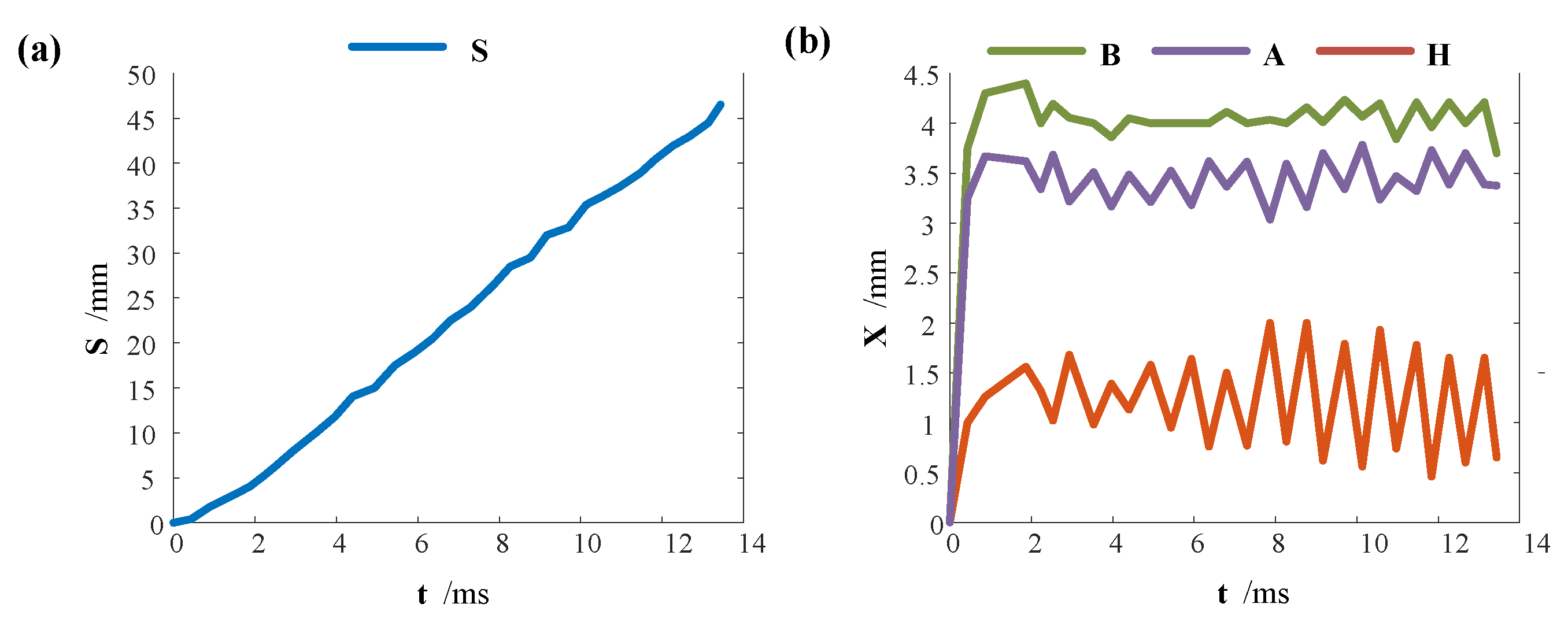
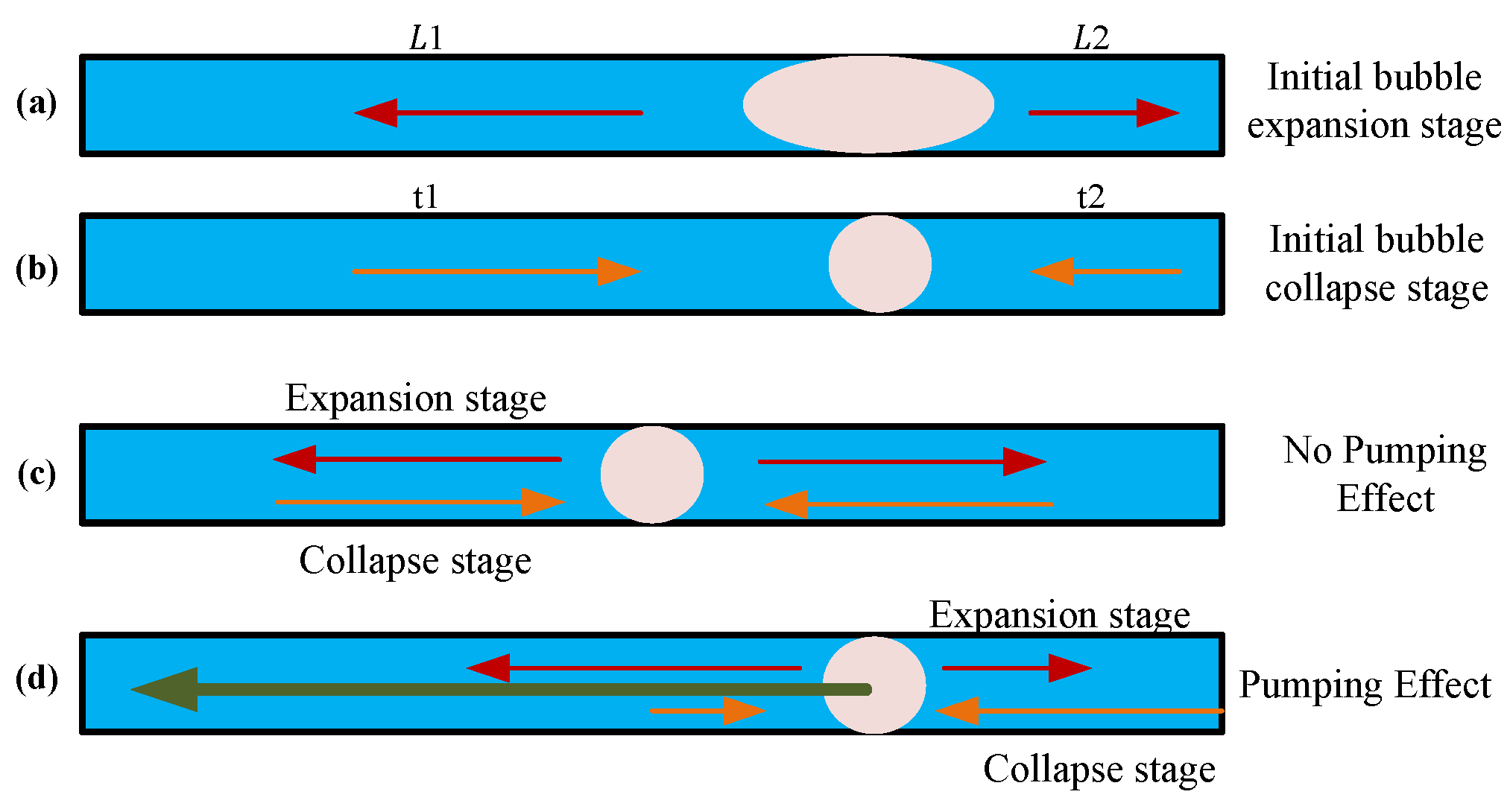
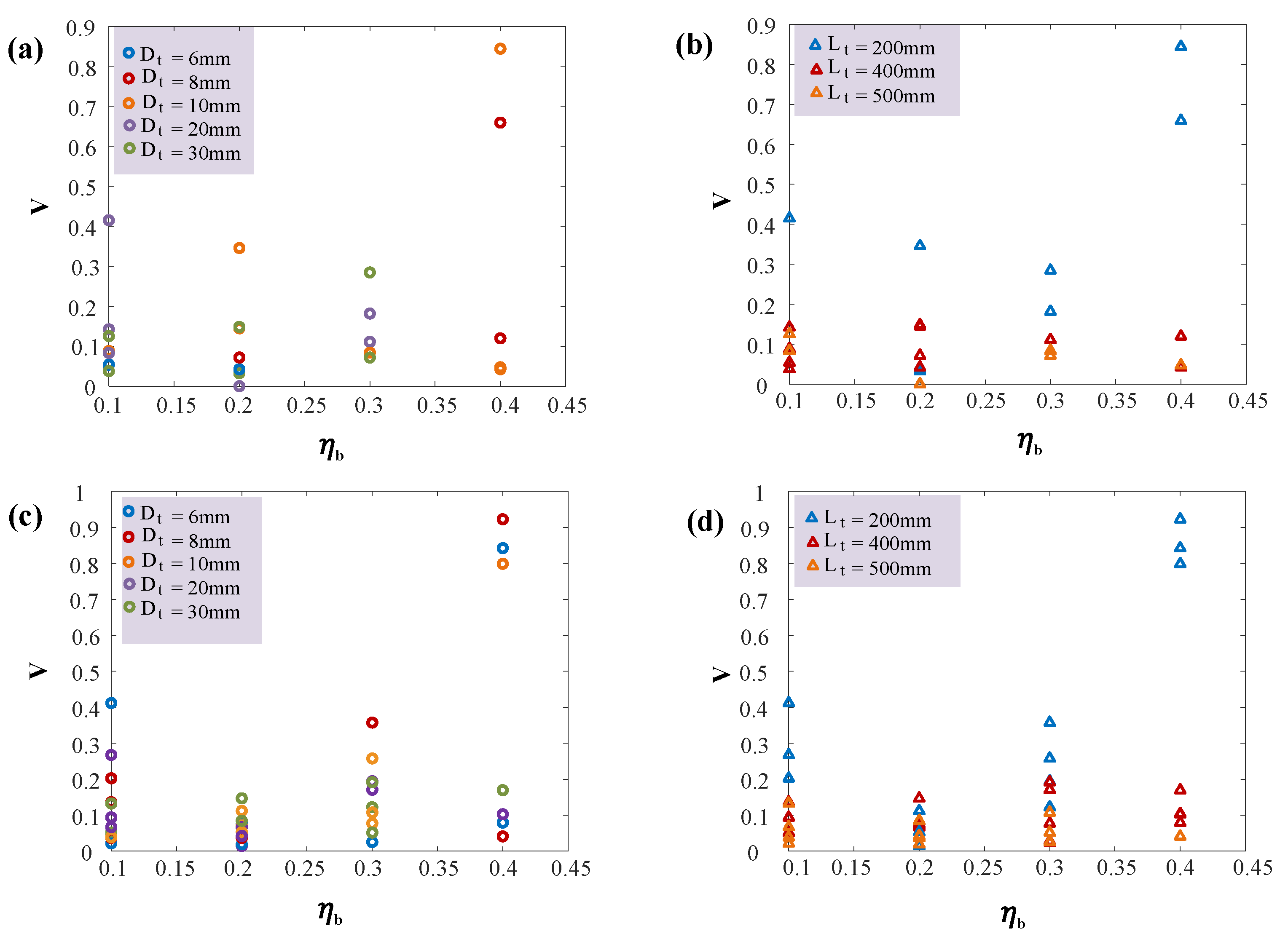
6.3. Pumping Effect and Speed
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Ishida, H.; Nuntadusit, C.; Kimoto, H.; Nakagawa, T.; Yamamoto, T. Cavitation bubble behavior near solid boundaries. cav2001: SessionA5. 003. 2001. Available online: https://resolver.caltech.edu/CAV2001:sessionA5.003 (accessed on 1 February 2025).
- Manmi, K.M.; Aziz, I.A.; Arjunan, A.; Saeed, R.K.; Dadvand, A. Three-dimensional oscillation of an acoustic microbubble between two rigid curved plates. J. Hydrodyn. 2021, 33, 1019–1034. [Google Scholar] [CrossRef]
- Su, B.; Yao, X.; Cui, X. Experimental research of underwater explosion bubble dynamics between two parallel plates with various distances. Appl. Ocean. Res. 2022, 122, 103081. [Google Scholar] [CrossRef]
- Gong, S.; Ohl, S.; Klaseboer, E.; Khoo, B. Interaction of a spark-generated bubble with a two-layered composite beam. J. Fluids Struct. 2018, 76, 336–348. [Google Scholar] [CrossRef]
- Soroureddin, A.; Shervani-Tabar, M.T.; Aminfar, H. Numerical investigation into the effect of viscosity on bubble dynamics in a narrow channel. Sci. Iran. 2020, 27, 2419–2432. [Google Scholar]
- Gonzalez-Avila, S.R.; Van Blokland, A.C.; Zeng, Q.; Ohl, C.D. Jetting and shear stress enhancement from cavitation bubbles collapsing in a narrow gap. J. Fluid Mech. 2020, 884, A23. [Google Scholar] [CrossRef]
- Zeng, Q.; Gonzalez-Avila, S.R.; Ohl, C.D. Splitting and jetting of cavitation bubbles in thin gaps. J. Fluid Mech. 2020, 896, A28. [Google Scholar] [CrossRef]
- Mohammadzadeh, M.; Li, F.; Ohl, C.D. Shearing flow from transient bubble oscillations in narrow gaps. Phys. Rev. Fluids 2017, 2, 014301. [Google Scholar] [CrossRef]
- Brujan, E.A.; Zhang, A.M.; Liu, Y.L.; Ogasawara, T.; Takahira, H. Jetting and migration of a laser-induced cavitation bubble in a rectangular channel. J. Fluid Mech. 2022, 948, A6. [Google Scholar] [CrossRef]
- Yang, S.; De Jesus, A.M.; Meng, D.; Nie, P.; Darabi, R.; Azinpour, E.; Zhu, S.P.; Wang, Q. Very high-cycle fatigue behavior of steel in hydrogen environment: State of the art review and challenges. Eng. Fail. Anal. 2024, 166, 108898. [Google Scholar] [CrossRef]
- Yang, S.; Meng, D.; Díaz, A.; Yang, H.; Su, X.; Jesus, A.M.d. Probabilistic modeling of uncertainties in reliability analysis of mid-and high-strength steel pipelines under hydrogen-induced damage. Int. J. Struct. Integr. 2025, 16, 39–59. [Google Scholar] [CrossRef]
- Yuan, H.; Prosperetti, A. The pumping effect of growing and collapsing bubbles in a tube. J. Micromechan. Microeng. 1999, 9, 402. [Google Scholar] [CrossRef]
- Ory, E.; Yuan, H.; Prosperetti, A.; Popinet, S.; Zaleski, S. Growth and collapse of a vapor bubble in a narrow tube. Phys. Fluids 2000, 12, 1268–1277. [Google Scholar] [CrossRef]
- Ni, B.Y.; Zhang, A.M.; Wang, Q.X.; Wang, B. Experimental and numerical study on the growth and collapse of a bubble in a narrow tube. Acta Mech. Sin. 2012, 28, 1248–1260. [Google Scholar] [CrossRef]
- Zou, J.; Li, B.; Ji, C. Interactions between two oscillating bubbles in a rigid tube. Exp. Therm. Fluid Sci. 2015, 61, 105–112. [Google Scholar] [CrossRef]
- Ji, C.; Li, B.; Zou, J. Secondary cavitation in a rigid tube. Phys. Fluids 2017, 29, 082107. [Google Scholar] [CrossRef]
- Wang, S.P.; Wang, Q.; Zhang, A.M.; Stride, E. Experimental observations of the behaviour of a bubble inside a circular rigid tube. Int. J. Multiph. Flow 2019, 121, 103096. [Google Scholar] [CrossRef]
- Li, H.; Huang, J.; Wu, X.; Zhang, J.; Wang, J.; Wang, Y.; Huang, C. Dynamic behaviors of a laser-induced bubble and transition mechanism of collapse patterns in a tube. AIP Adv. 2020, 10, 035210. [Google Scholar] [CrossRef]
- Aghdam, A.H.; Khoo, B.; Farhangmehr, V.; Shervani-Tabar, M. Experimental study on the dynamics of an oscillating bubble in a vertical rigid tube. Exp. Therm. Fluid Sci. 2015, 60, 299–307. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, Y.; Yang, J.; Sun, M. Liquid jets produced by an immersed electrical explosion in round tubes. Phys. Fluids 2017, 29, 062102. [Google Scholar] [CrossRef]
- Ren, Z.; Li, B.; Xu, P.; Wakata, Y.; Liu, J.; Sun, C.; Zuo, Z.; Liu, S. Cavitation bubble dynamics in a funnel-shaped tube. Phys. Fluids 2022, 34. [Google Scholar] [CrossRef]
- Luo, X.; Chen, T.; Xiao, W.; Yao, X.; Liu, J. The dynamics of a bubble in the internal fluid flow of a pipeline. Phys. Fluids 2022, 34. [Google Scholar] [CrossRef]
- Sugimoto, Y.; Hamamoto, M. Measurements of laser induced bubble behavior in elastic tube and temperature around bubble in TUL treatment. J. Flow Control. Meas. Vis. 2020, 8, 134. [Google Scholar] [CrossRef]
- Jang, N.W.; Gracewski, S.M.; Abrahamsen, B.; Buttaccio, T.; Halm, R.; Dalecki, D. Natural frequency of a gas bubble in a tube: Experimental and simulation results. J. Acoust. Soc. Am. 2009, 126, EL34–EL40. [Google Scholar] [CrossRef]
- Liu, Y.; Luo, J. Experimental study on damage mechanism of blood vessel by cavitation bubbles. Ultrason. Sonochem. 2023, 99, 106562. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhang, A.; Liu, Y.; Zeng, D. Numerical simulation of bubble dynamics in an elastic vessel. Eur. Phys. J. E 2013, 36, 119. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Wang, Q.; Leppinen, D.; Zhang, A.; Liu, Y. Acoustic bubble dynamics in a microvessel surrounded by elastic material. Phys. Fluids 2018, 30. [Google Scholar] [CrossRef]
- Xie, Y.; Hu, J.; Lei, W.; Qian, S. Prediction of vascular injury by cavitation microbubbles in a focused ultrasound field. Ultrason. Sonochem. 2022, 88, 106103. [Google Scholar] [CrossRef]
- Meng, D.; Yang, S.; De Jesus, A.M.; Fazeres-Ferradosa, T.; Zhu, S.P. A novel hybrid adaptive Kriging and water cycle algorithm for reliability-based design and optimization strategy: Application in offshore wind turbine monopile. Comput. Methods Appl. Mech. Eng. 2023, 412, 116083. [Google Scholar] [CrossRef]
- Yang, S.; Meng, D.; Yang, H.; Luo, C.; Su, X. Enhanced soft Monte Carlo simulation coupled with SVR for structural reliability analysis. In Proceedings of the Institution of Civil Engineers-Transport; Emerald Publishing Limited: Bingley, UK, 2024; pp. 1–41. [Google Scholar]
- Meng, D.; Yang, H.; Yang, S.; Zhang, Y.; De Jesus, A.M.; Correia, J.; Fazeres-Ferradosa, T.; Macek, W.; Branco, R.; Zhu, S.P. Kriging-assisted hybrid reliability design and optimization of offshore wind turbine support structure based on a portfolio allocation strategy. Ocean. Eng. 2024, 295, 116842. [Google Scholar] [CrossRef]
- Johnson, V.E., Jr.; Chahine, G.L.; Lindenmuth, W.T.; Conn, A.F.; Frederick, G.S.; Giacchino, G.J., Jr. Cavitating and Structured Jets for Mechanical Bits to Increase Drilling Rateart I: Theory and Concepts. J. Energy Resour. Technol. 1984, 106, 282–288. [Google Scholar] [CrossRef]


























Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gou, Y.; Shi, D.; Wang, J. Modeling and Reliability Evaluation of the Motion and Fluid Flow Characteristics of Spark Bubbles in a Tube. Appl. Sci. 2025, 15, 2569. https://doi.org/10.3390/app15052569
Gou Y, Shi D, Wang J. Modeling and Reliability Evaluation of the Motion and Fluid Flow Characteristics of Spark Bubbles in a Tube. Applied Sciences. 2025; 15(5):2569. https://doi.org/10.3390/app15052569
Chicago/Turabian StyleGou, Yuxin, Dongyan Shi, and Jiuqiang Wang. 2025. "Modeling and Reliability Evaluation of the Motion and Fluid Flow Characteristics of Spark Bubbles in a Tube" Applied Sciences 15, no. 5: 2569. https://doi.org/10.3390/app15052569
APA StyleGou, Y., Shi, D., & Wang, J. (2025). Modeling and Reliability Evaluation of the Motion and Fluid Flow Characteristics of Spark Bubbles in a Tube. Applied Sciences, 15(5), 2569. https://doi.org/10.3390/app15052569




